Dynamic Temperature–Vacuum Swing Adsorption for Sustainable Direct Air Capture: Parametric Optimisation for High-Purity CO₂ Removal

Abstract

Direct air capture (DAC), as a complementary strategy to carbon capture and storage (CCS), offers a scalable and sustainable pathway to remove CO₂ directly from the ambient air. This study presents a detailed evaluation of the amine-functionalised metal-organic framework (MOF) sorbent, mmen-Mg₂(dobpdc), for DAC using a temperature–vacuum swing adsorption (TVSA) process. While this sorbent has demonstrated promising performance in point-source CO₂ capture, this is the first dynamic simulation-based study to rigorously assess its effectiveness for low-concentration atmospheric CO₂ removal. A transient one-dimensional TVSA model was developed in Aspen Adsorption and validated against experimental breakthrough data to ensure accuracy in capturing both the sharp and gradual adsorption kinetics. To enhance process efficiency and sustainability, this work provides a comprehensive parametric analysis of key operational factors, including air flow rate, temperature, adsorption/desorption durations, vacuum pressure, and heat exchanger temperature, on process performance, including CO₂ purity, recovery, productivity, and specific energy consumption. Under optimal conditions for this sorbent (vacuum pressure lower than 0.15 bar and feed temperature below 15 °C), the TVSA process achieved ~98% CO₂ purity, recovery over 70%, and specific energy consumption of about 3.5 MJ/KgCO₂. These findings demonstrate that mmen-Mg₂(dobpdc) can achieve performance comparable to benchmark DAC sorbents in terms of CO₂ purity and recovery, underscoring its potential for scalable DAC applications. This work advances the development of energy-efficient carbon removal technologies and highlights the value of step-shape isotherm adsorbents in supporting global carbon-neutrality goals.

1. Introduction

The continued rise in atmospheric CO₂—driven by population growth, urbanisation, and industrialisation—has intensified global climate change, making carbon mitigation a critical priority for long-term environmental sustainability. Despite growing efforts to decarbonise, fossil fuels such as coal, oil, and natural gas remain the dominant energy sources, and account for over 75% of anthropogenic CO₂ emissions [1,2,3,4,5]. While renewable energy technologies (e.g., wind, solar, hydro, and bioenergy) offer low-carbon alternatives, their adoption is challenged by intermittency, storage limitations, and spatial constraints [6,7,8,9,10,11]. While the global energy transition is underway, the pace of decarbonisation remains insufficient to meet the targets set by the Paris Agreement and ensure climate sustainability. Atmospheric CO₂ levels have risen from approximately 180 parts per million (ppm) during the last three glacial cycles to about 426 ppm as of May 2024, with an ongoing annual increase of around 2 ppm [12,13]. To limit the global temperature rise to below 2 °C, with an aspirational target of 1.5 °C above pre-industrial levels, as outlined in the Paris Agreement, large-scale removal of atmospheric CO₂ is required, with estimates indicating a need to extract 10 GtCO₂/year by 2050, increasing to 20 GtCO₂/year thereafter [14,15].

Direct air capture (DAC) has emerged as a promising negative emission technology to address both current and historical CO₂ emissions, complementing traditional carbon capture, utilisation, and storage (CCUS) technologies that primarily target point sources [7,16]. Among the available DAC technologies, absorption using liquid solvents is the most widely applied due to its high CO₂ capacity and relatively low cost. However, its application in DAC is limited by challenges such as complex waste management, solvent degradation, evaporation losses, and high thermal energy demand for regeneration, especially under variable atmospheric conditions [17,18,19]. While alternatives like ionic liquids offer improved thermal stability, their practical use is constrained by thermal decomposition and high cost [20,21,22,23]. These limitations have shifted attention towards adsorption-based DAC processes, which offer the advantage of partially overcoming the limitations associated with absorption [24].

Various porous materials, including carbon, zeolites, silica, resin, and metal-organic frameworks (MOFs), have been investigated for CO₂ separation [25,26,27,28,29,30,31]. While activated carbons (ACs) and zeolites have been widely studied for DAC due to their porosity and thermal stability, both exhibit significant limitations under ambient conditions. ACs exhibit reduced CO₂ capacity under humid environments and may degrade thermally during repeated regeneration, particularly at high desorption temperatures [32,33], though modifications, such as hydrophobic surface treatments and potassium carbonate incorporation, offer partial improvements [34,35,36]. Zeolites offer high CO₂ selectivity and strong structural stability but suffer from moisture sensitivity and loss adsorption capacity above 100 °C, requiring high regeneration energy [37,38,39]. To overcome these issues, approaches such as core–shell hydrophobic coatings and ion exchange have been investigated, with Fe-modified 13X zeolites showing enhanced performance [21]. Recent advances have positioned MOFs as promising candidates, offering extremely high surface areas (up to 7140 m²/g, and theoretically even 10,000 m²/g) and structural tunability through metal-organic coordination, with over 88,000 MOF structures reported and many more possible [40,41]. The mechanisms and strategies for optimising CO₂ capture in MOFs under high-concentration conditions are well established, resulting in the development of highly stable and high-performing materials that are now commercialised for industrial use. For example, CALF-20, a MOF developed for flue gas CO₂ capture, features channel-like pores of approximately ~3 Å and demonstrated a CO₂ uptake of 4.07 mmol g⁻¹ at 293 K and 1.2 bar, with an IAST selectivity of 230 for a 10/90 CO₂/N₂ mixture [42]. Similarly, UTSA-16, an ultra-microporous MOF based on citric acid, achieves a CO₂ uptake of 4.25 mmol g⁻¹ with pore dimensions of 3.3 × 5.4 ⁰A² [43]. Moreover, recent developments in MOF design have explored the integration of catalytic sites for simultaneous CO₂ capture and conversion, broadening the potential application of these materials beyond pure adsorption processes [44,45]. However, for capturing CO₂ directly from the air, with its extremely low partial pressure, these MOFs, like CALF-20 and UTSA-16, often underperform due to weak binding sites [42,43] and moisture-induced degradation [46].

For low-concentration CO₂ capture, chemisorption is advantageous by providing strong binding affinity. In particular, amine-functionalisation of porous materials via physical impregnation, chemical grafting, or in situ polymerisation has proven effective in improving both CO₂ capture capacity and selectivity [14,47,48]. This approach has been particularly successful with MOFs, enabling the design of highly tuneable materials (via linker or metal–ligand modifications) and superior CO₂ selectivity and capacity through strong Lewis base sites [49,50]. A prominent example is mmen-Mg₂(dobpdc), developed by grafting N, N′ dimethyl ethylene diamine (mmen) and ethylene diamine (ED) onto the Mg₂(dobpdc) framework [25]. This sorbent exhibits exceptional CO₂ capacity at low pressures (2.0 mmol/g (8.1 wt %) at 0.39 mbar and 25 °C) and benefits from fast adsorption kinetics and cooperative adsorption mechanisms that enhance efficiency [51]. In addition, mmen-Mg₂(dobpdc) demonstrated favourable recyclability and thermal stability. McDonald et al. [49] reported consistent performance over multiple adsorption–desorption cycles, while later research confirmed structural integrity during vacuum or N₂-based regeneration up to 150 °C and its tolerance to moderate humidity [52]. These characteristics further reinforce its suitability for long-term DAC operation. Subsequent studies have confirmed its potential under DAC conditions [38,50,53,54,55]. However, Darunte et al. [56] evaluated its performance for CO₂ capture from ultra-dilute feeds and observed a reduced CO₂ capture fraction due to the unique stepped isotherm and kinetic characteristics of this sorbent. Further investigation under 1000 ppm CO₂ confirmed the high working capacity of mmen-Mg₂(dobpdc) despite mass transfer limitations [57].

To maximise DAC efficiency, the choice of regeneration strategy has a critical role in determining the overall process efficiency. TVSA has been identified as the most suitable regeneration strategy for amine-functionalised solid sorbents, offering high working capacities and lower energy demands without requiring extreme vacuum or temperature [58,59,60], which makes it well suited for DAC, where careful balance between sorbent efficiency and the regeneration energy demand is essential. Phase-change adsorbents like mmen-Mg₂(dobpdc), which exhibit sharp stepwise isotherm transitions, particularly benefit from TVSA because it enables effective regeneration with minimal energy input [51].

While several studies have explored the application of different amine-functionalised MOFs for CO₂ capture from flue gas [61,62] and the indoor environment [57], this study specifically targets the 400 ppm CO₂ concentration typical of DAC, where lower partial pressures intensify both kinetic and thermodynamic challenges. A dynamic simulation of a modular DAC process is developed using the amine-functionalised MOF, mmen-Mg₂(dobpdc), known for its distinctive step-shaped CO₂ adsorption isotherm. A one-dimensional TVSA framework, implemented in Aspen Adsorption, incorporates mass, energy, and momentum balances to simulate the transient behaviour of adsorption–desorption cycles at lab scale. Sensitivity analysis is conducted to evaluate the effects of key operating parameters—feed flow rate and temperature, vacuum pressure, and step durations—on critical performance metrics, including CO₂ purity, recovery, productivity, and specific energy consumption. The findings establish operational guidelines to improve process efficiency and provide valuable insights for the design and optimisation of energy-efficient MOF-based DAC systems, aligning with broader environmental sustainability goals.

2. Materials and Methods

During adsorption, CO₂ is captured by high-affinity porous material, followed by a regeneration step that releases CO₂ and restores the sorbent’s capacity. The efficiency of this process depends on the sorbent properties, operating conditions, and regeneration strategy. In this study, a TVSA process was simulated in an axial-flow fixed-bed reactor, where mmen-Mg₂(dobpdc) was used as the adsorbent. TVSA combines mild heating and vacuum pressure reduction to desorb CO₂ while restoring the sorbent’s adsorption capacity for subsequent cycles [63]. The released CO₂ was collected through a condenser to ensure high purity, while a heat exchanger was integrated within the bed to optimise thermal management during adsorption and desorption.

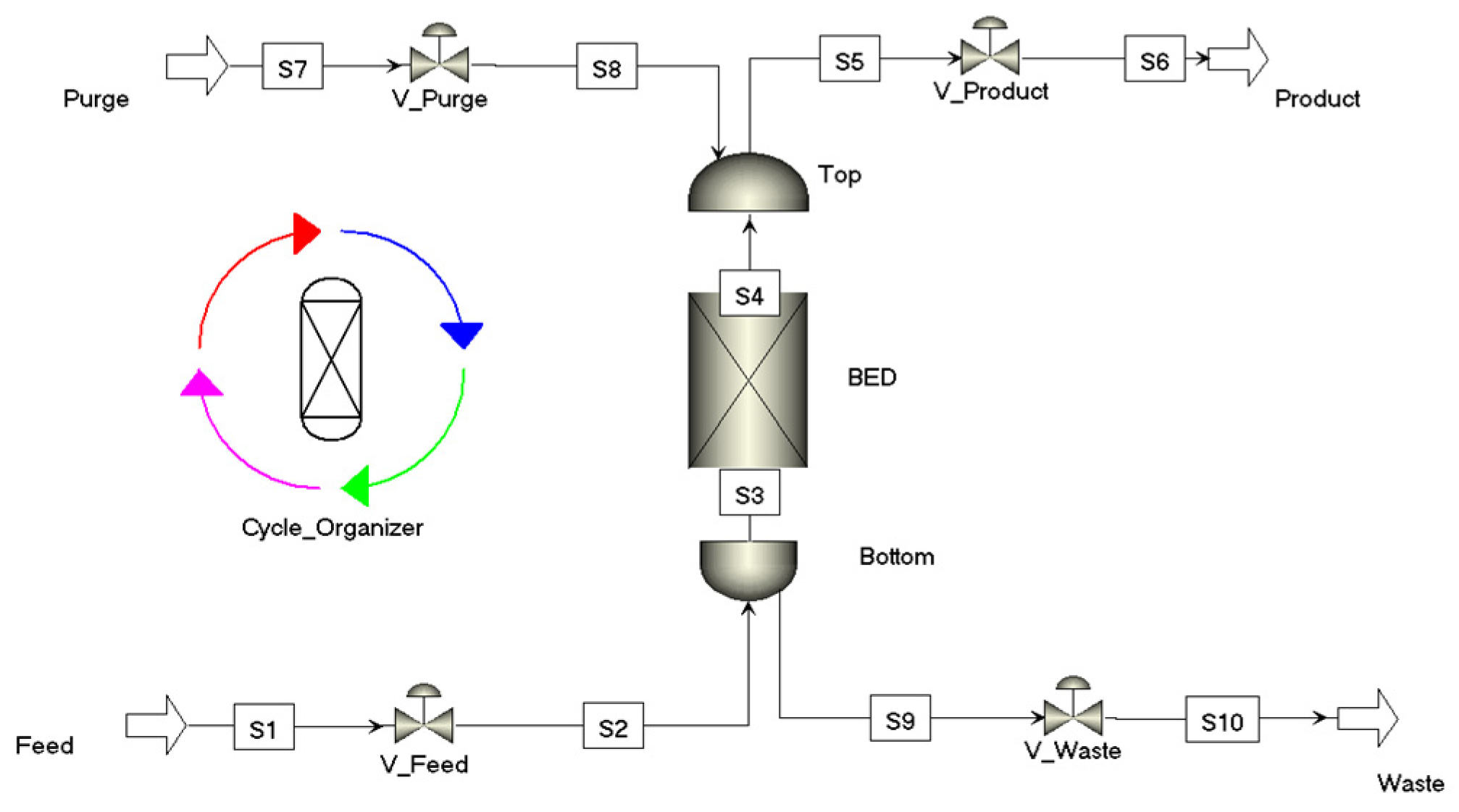
2.1. Simulation Framework (Numerical Modelling and Assumption)

A dynamic model for non-isothermal, adiabatic TVSA was developed in Aspen Adsorption to evaluate the technical performance of mmem-Mg₂(dobpdc) under DAC conditions. The software simulates the complete adsorption/desorption cycle, incorporating mass, energy, and momentum balances to predict system behaviour and evaluate process parameters (Aspen Adsorption V14). To solve the coupled partial differential equations (PDEs) under specified boundary conditions, this study applied a set of assumptions to simplify the computational complexity while maintaining model accuracy, as follows:

• The sorbent has a spherical shape with uniform, continuous properties, as the selected particles used in the experimental studies were derived from MOF powders composed of fine crystallites that were agglomerated and sieved to obtain particles with controlled and consistent size [56].
• The gas phase follows ideal gas behaviour, which is a reasonable approximation under the low operating pressures and dilute CO₂ concentrations typical of DAC systems.
• Constant adsorbed phase heat capacity is assumed because the amount of adsorbed CO₂ is small in DAC.
• The column thickness effect is ignored, assuming the adiabatic conditions.
• No parasitic reactions between the gas and the adsorbent.
• A one-dimensional model incorporating convection.
• The air flow mixture consists of CO₂ and N₂, with CO₂ as the sole adsorbed component.
• CO₂ adsorption kinetics differ below and above Pₛₜₑₚ, and the model captures this through dual-regime rate constants derived from experimental fitting [56].

These assumptions are consistent with prior TVSA modelling studies [53,54,64,65], allowing focus on parametric influences rather than complex 2D effects or humidity interactions.

The exceptional CO₂ selectivity of mmen-Mg₂(dobpdc) allows the exclusion of N₂ and O₂ from adsorption considerations. McDonald [49] reported that CO₂/N₂ selectivity of this sorbent exceed 49,000, with negligible uptake of O₂ and N₂. Mason et al. [66] further confirmed that N₂ adsorption was undetectable in mixed-gas conditions. Based on these findings, N₂ and O₂ can be treated as inert gases in this model. Additionally, the effect of water adsorption was not considered in the present study, as experimental results have consistently demonstrated that the presence of H₂O has minimal influence on CO₂ adsorption in mmen-Mg₂(dobpdc). Notably, CO₂ uptake under humid conditions is comparable to, or slightly higher than, that observed in dry environments [49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66]. Similarly, breakthrough experiments conducted at 50% relative humidity under DAC conditions illustrated an increase in CO₂ capture capacity from 2.16 mmol/g to 2.41 mmol/g [67].

2.1.1. Packed-Bed Specification

The packed-bed reactor was designed based on the experimental parameters reported by Darunte [56]. The air feed conditions were set at 1.1013 bar and 25 °C, with a molar composition of 99.96% N₂ and 0.04% CO₂.

Table 1. Design and operating parameters of the packed bed used for simulation [56].

Parameters	Unit	Values
Bed Length	m	0.055
Bed Internal Radius	m	0.004
Desorption Temperature	°C	115
Adsorption Temperature	°C	23
Particle Radius	m	2.25 × 10−4
Crystal Density	Kg/m3	860
Bed Porosity	fraction	0.32
Adsorbent Weight	g	60
Particle Porosity	fraction	0.85
Feed Flow rate	N mL/min	17.2

lists the key design parameters for the packed-bed reactor model used in this study. These parameters define the physical characteristics of the adsorption column and operating conditions, which govern adsorption behaviour and system performance by influencing flow dynamics, mass transfer, and adsorbent capacity.

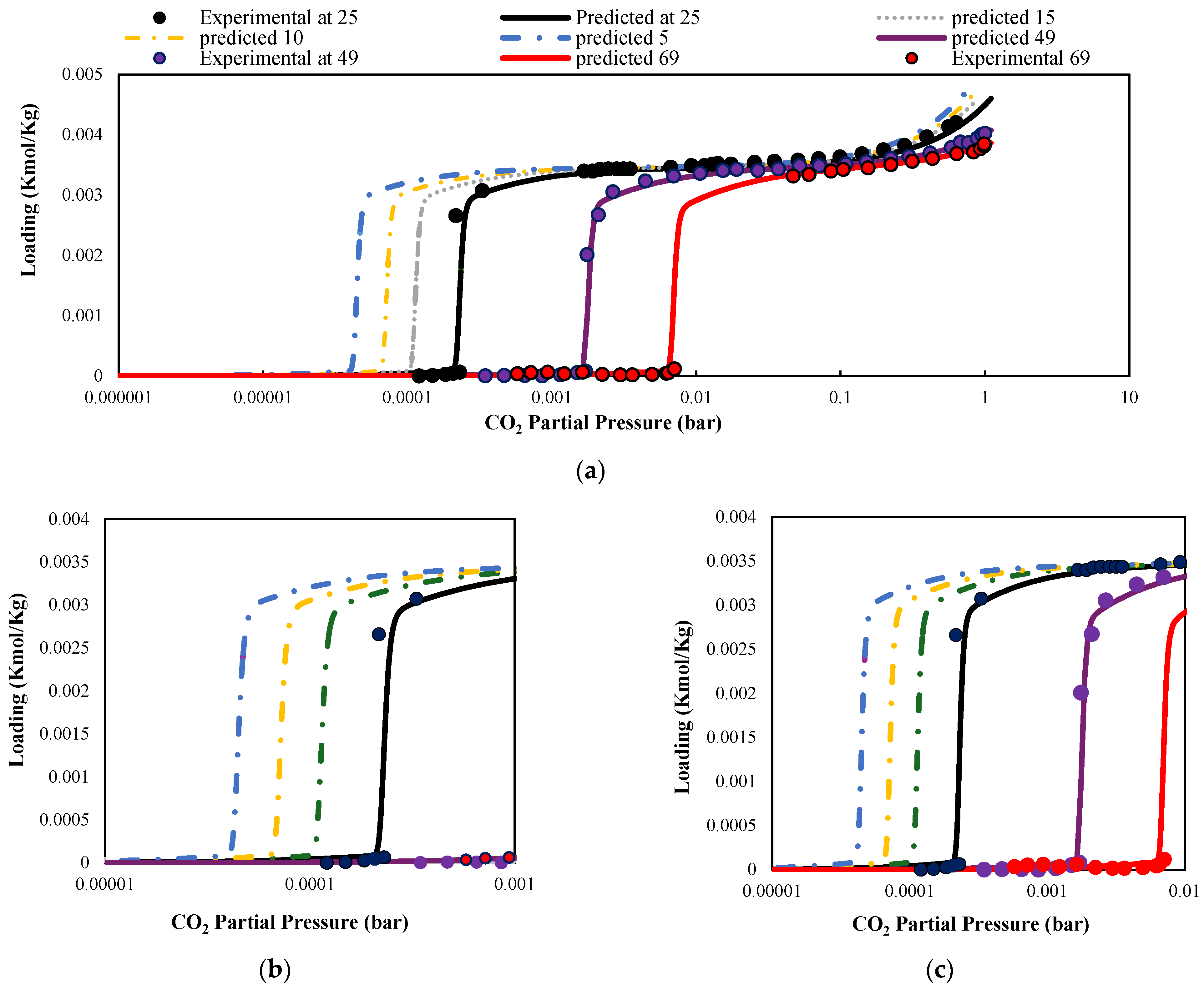
2.1.2. Adsorption Equilibrium and Kinetics

The development of the model required accurate adsorption characteristics. The relevant thermal properties used in the simulation are summarised in Table 2.

Table 2. Thermal characteristics of mmen-Mg₂(dobpdc) and adsorbates.

Parameters	Unit	Values	Reference
CO2 heat of adsorption	KJ/mol	−71	[68]
N2 heat of adsorption	KJ/mol	−18	[57]
Heat capacity of the crystal	KJ/Kg·K	1.6	[51]
CO2 heat capacity	KJ/Kmol·K	37.4673	(Aspen Plus)
N2 heat capacity	KJ/Kmol·K	29.1806	(Aspen Plus)
Thermal conductivity	W/m·K	0.3	[69]

Table 2. Thermal characteristics of mmen-Mg₂(dobpdc) and adsorbates.

Parameters	Unit	Values	Reference
CO2 heat of adsorption	KJ/mol	−71	[68]
N2 heat of adsorption	KJ/mol	−18	[57]
Heat capacity of the crystal	KJ/Kg·K	1.6	[51]
CO2 heat capacity	KJ/Kmol·K	37.4673	(Aspen Plus)
N2 heat capacity	KJ/Kmol·K	29.1806	(Aspen Plus)
Thermal conductivity	W/m·K	0.3	[69]

The adsorption behaviour of mmen-Mg₂(dobpdc) follows step-shape (S-shape) CO₂ adsorption isotherm, characterised by two distinct adsorption regimes. Below isotherm transition pressure (P_step), CO₂ adsorption occurs through the reaction of two free amine groups with CO₂, forming ammonium carbamate, similar to conventional amine functionalised sorbents. Above P_step, the cooperative adsorption mechanism is observed, where both ends of the diamine participate in CO₂ binding, leading to the formation of one-dimensional ammonium carbamate chains aligned along the Mg²⁺ framework [51]. This study employed the model proposed by Darunte et al. [56], which builds upon Hefti’s framework [54], incorporating the Sips isotherm to accurately describe CO₂ adsorption below P_step, as defined by Equations (1)–(8). Here, ${\mathrm{q}}_1^{\mathrm{*}}$ and ${\mathrm{q}}_2^{\mathrm{*}}$ describe CO₂ uptake before and after P_step, respectively, $\mathrm{w}$ presents a smooth transition function between two regions, ${\mathrm{q}}_{\mathrm{L}}$, ${\mathrm{q}}_{\mathrm{H}}$, and ${\mathrm{q}}_{\mathrm{U}}$ represent the affinity of sorbents, and n reflects the surface homogeneity factor. The temperature dependence of P_step is calculated by Equation (8), where ${\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p},0}$ = 0.8 mbar at T₀ = 313.5 ⁰K, and $∆{\mathrm{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$ represent the enthalpy change associated with the adsorption transition [51]. Darunte et al. [56] fitted the isotherm model to the experimental data to determine the isotherm parameters. The fitted parameters with the formula of temperature-dependent parameters are presented in

Table 3. Isotherm fitting parameters and equations for temperature-dependent variables [56].

Parameters	Unit	Value	Parameters	Unit	Values
${\mathrm{q}}_{\mathrm{L}}$	mol/Kg	28.25	$∆{\mathrm{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$	KJ/mol	−62.49
${\mathrm{b}}_{\mathrm{L}0}$	1/bar	2.51 × 10−15	$∆{\mathrm{H}}_{\mathrm{L}}$	KJ/mol	70.74
${\mathrm{n}}_0$	-	0.518	$∆{\mathrm{H}}_{\mathrm{n}}$	KJ/mol	1.35
${\mathrm{q}}_{\mathrm{H}}$	mol/Kg	3.46	$∆{\mathrm{H}}_{\mathrm{H}}$	KJ/mol	67.72
${\mathrm{b}}_{\mathrm{H}0}$	1/bar	2.42 × 10−11	$∆{\mathrm{H}}_{\mathrm{u}}$	KJ/mol	18.67
${\mathrm{q}}_{\mathrm{u}0}$	mol/Kg.bar	5.27 × 10−4	${\mathsf{\lambda }}_1$	-	1.74 × 10−2
ϒ	-	4	${\mathsf{\lambda }}_2$	1/0K	6.53
Temperature-dependent variables’ formulas
${\mathrm{b}}_{\mathrm{U}}={\mathrm{b}}_{\mathrm{L}0}\exp \left({\displaystyle \frac{∆{\mathrm{H}}_{\mathrm{L}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{g}}}}\right)$			${\mathrm{q}}_{\mathrm{U}}={\mathrm{q}}_{\mathrm{u}0}\exp \left({\displaystyle \frac{∆{\mathrm{H}}_{\mathrm{u}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{g}}}}\right)$
$\mathsf{\sigma }={\mathsf{\lambda }}_1\mathrm{e}\mathrm{x}\mathrm{p}\left[{\mathsf{\lambda }}_2\left({\displaystyle \frac{1}{{\mathrm{T}}_0}}-{\displaystyle \frac{1}{{\mathrm{T}}_{\mathrm{g}}}}\right)\right]$			${\mathrm{b}}_{\mathrm{H}}={\mathrm{b}}_{\mathrm{H}0}\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{∆{\mathrm{H}}_{\mathrm{H}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{g}}}}\right)$
$\mathrm{n}={\mathrm{n}}_0\mathrm{e}\mathrm{x}\mathrm{p}\left({\displaystyle \frac{∆{\mathrm{H}}_{\mathrm{L}\mathrm{n}}}{\mathrm{R}{\mathrm{T}}_{\mathrm{g}}}}\right)$

:

$${\mathrm{q}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}={\mathrm{q}}_1^{\mathrm{*}}+{\mathrm{q}}_2^{\mathrm{*}}$$

(1)

$${\mathrm{q}}_1^{\mathrm{*}}={\mathrm{q}}_{\mathrm{l}\mathrm{o}\mathrm{w}}\times \left(1-\mathrm{w}\right)+{\mathrm{q}}_{\mathrm{s}\mathrm{a}\mathrm{t}}\times \mathrm{w}$$

(2)

$${\mathrm{q}}_2^{\mathrm{*}}=({\mathrm{q}}_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}-{\mathrm{q}}_{\mathrm{s}\mathrm{a}\mathrm{t}})\times \mathrm{w}$$

(3)

$${\mathrm{q}}_{\mathrm{l}\mathrm{o}\mathrm{w}}={\displaystyle \frac{{\mathrm{q}}_{\mathrm{L}}{\left({\mathrm{b}}_{\mathrm{L}}\mathrm{p}\right)}^{{\mathrm{n}}_{\mathrm{L}}}}{1+{\left({\mathrm{b}}_{\mathrm{L}}\mathrm{p}\right)}^{{\mathrm{n}}_{\mathrm{L}}}}}$$

(4)

$${\mathrm{q}}_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h}}={\displaystyle \frac{{\mathrm{q}}_{\mathrm{H}}{\mathrm{b}}_{\mathrm{H}}\mathrm{p}}{1+{\mathrm{b}}_{\mathrm{H}}\mathrm{p}}}+{\mathrm{q}}_{\mathrm{U}}\mathrm{p} \mathrm{p}<{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$$

(5)

$${\mathrm{q}}_{\mathrm{s}\mathrm{a}\mathrm{t}}={\displaystyle \frac{{\mathrm{q}}_{\mathrm{L}}{\left({\mathrm{b}}_{\mathrm{L}}{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\right)}^{\mathrm{n}}}{1+{\left({\mathrm{b}}_{\mathrm{L}}{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\right)}^{\mathrm{n}}}} \mathrm{p}>{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$$

(6)

$$\mathrm{w}={\left[{\displaystyle \frac{\mathrm{e}\mathrm{x}\mathrm{p}\left(\frac{\log \left(\mathrm{p}\right)-\mathrm{l}\mathrm{o}\mathrm{g}\left({\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\right)}{\mathsf{\sigma }}\right)}{1+\exp \left(\frac{\log \left(\mathrm{p}\right)-\log \left({\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\right)}{\mathsf{\sigma }}\right)}}\right]}^{\mathsf{\gamma }}$$

(7)

$${\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}\left(\mathrm{T}\right)={\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p},0}\mathrm{e}\mathrm{x}\mathrm{p}\left[-{\displaystyle \frac{∆{\mathrm{H}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}}{\mathrm{R}}}\left({\displaystyle \frac{1}{{\mathrm{T}}_0}}-{\displaystyle \frac{1}{\mathrm{T}}}\right)\right]$$

(8)

The parameters ${\mathrm{b}}_{\mathrm{L}}$ and ${\mathrm{b}}_{\mathrm{H}}$ represent the temperature-dependent adsorption equilibrium constants for the low-affinity (L) and high-affinity (H) sites, respectively. The terms $∆{\mathrm{H}}_{\mathrm{L}}$ and $∆{\mathrm{H}}_{\mathrm{H}}$ denote the heat of adsorption for low- and high-affinity sites, respectively, while $∆{\mathrm{H}}_{\mathrm{u}}$ corresponds to the heat of adsorption for uniform adsorption sites. The parameter $\mathsf{\sigma }$ characterises the sharpness of the phase transition in the cooperative adsorption mechanism. To describe the adsorption kinetic (${\displaystyle \frac{\partial W_i}{\partial \mathrm{t}}}$), a dual-kinetic approach based on the work of Darunte et al. [56] was adopted. Their study demonstrated that the conventional linear driving force (LDF) model alone could not adequately capture the experimental kinetic data. Consequently, they proposed two different kinetic models based on CO₂ partial pressure: an LDF model for pressure below the step pressure (${\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$), where CO₂ adsorption proceeds via ammonium carbamate formation with a 2:1 amine-to-CO₂ stoichiometry [51,70] (Equation (9)), and an Avrami fractional-order model for pressures above p_step. At these higher pressures, CO₂ adsorption is governed by cooperative insertion, characterised by a rapid saturation of amine sites due to 1:1 stoichiometry and chain propagation effects (Equation (10)) [56]:

$${\displaystyle \frac{\partial W_i}{\partial t}}=K_k\left({w^{*}}_i-w_i\right) \mathrm{p}<{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$$

(9)

$${\displaystyle \frac{\partial W_i}{\partial t}}=K_A^{n_A}{t}^{n_A-1}\left({w^{*}}_i-w_i\right) \mathrm{p}>{\mathrm{p}}_{\mathrm{s}\mathrm{t}\mathrm{e}\mathrm{p}}$$

(10)

In Equation (9), the initial value of the overall mass transfer coefficient $K_k$(1/s) is estimated using a lumped resistance model, as expressed in Equation (11), which accounts for both external film resistance and macropore diffusion [71]. Since such correlations alone are often insufficiently precise, the initial estimate was subsequently refined by calibrating the simulation results against experimental observations:

$${\displaystyle \frac{1}{K_k}}={\displaystyle \frac{r_p}{3K_{fk}}}+{\displaystyle \frac{r_p^2}{15 {\epsilon }_p{K}_{pk}}}$$

(11)

In Equation (11), $r_p$ and ${\epsilon }_p$ represent particle radius (m) and intraparticle void fraction, respectively. The film resistance coefficient $K_{fk}$ (m/s) is calculated using Equations (12)–(15). The $K_{pk}$ is the macropore diffusion coefficient (m²/s), which is calculated by Equations (16) and (17):

$$K_{fk}={sh}_k{\displaystyle \frac{D_{mk}}{2r_p}}$$

(12)

$${sh}_k=2+1.1\times {Sc}_k^{1/3}{Re}^{0.6}$$

(13)

$${Sc}_k={\displaystyle \frac{\mu }{D_{mk}{\rho }_g}}$$

(14)

$$Re={\displaystyle \frac{v_{g}2r_p{\rho }_g}{\mu }}$$

(15)

$${\displaystyle \frac{1}{K_{pk}}}=\tau ({\displaystyle \frac{1}{D_{Kk}}}+{\displaystyle \frac{1}{D_{mk}}})$$

(16)

$$D_{Kk}=97r_p{\left({\displaystyle \frac{T}{M_k}}\right)}^{0.5}$$

(17)

The Sherwood (${sh}_k$), Reynolds ($Re$), and Schmidt numbers (${Sc}_k$) are defined in Equations (12)–(15). The Knudsen diffusion coefficient $D_{Kk}$ (m²/s), shown in Equation (17), is a function of temperature (⁰K), molar mass $M_k$ (g/mol), and pore radius. The total molecular diffusion ($D_{mk}$) is estimated using data from the Aspen Properties database.

In Equation (10), the Avrami parameters k_A, t, ${w^{*}}_i$, and n_A represent the Avrami rate constant, time, saturation capacity, and Avrami fractional constant, respectively. The constant parameters ($K_A$ and $n_A$) were fitted to experimental data, with values of 4.36 × 10⁻⁵ (1/s) and 1.5 for 0.4 mbar CO₂ partial pressure [56].

2.1.3. Energy Balance

In a non-isothermal system, energy balance applies to both gas and solid phases. The energy balance for the solid phase is expressed as Equation (18). This equation includes a contribution from heat transfer through convection, the heat released during adsorption, the heat capacity of the adsorbed phase, and the heat transfer between the gas and solid phase. The gas phase energy balance accounts for the effects of convection, heat accumulation, heat transfer between the gas and solid phases, and the heat of reaction, which are outlined in Equation (19). The adsorbed-phase heat capacity and heat transfer coefficient were estimated by using Aspen V14 software:

$${\rho }_s{C}_{ps}{\displaystyle \frac{\partial T_s}{\partial t}}+\sum H_k+{\rho }_s\sum \left(∆H_k{\displaystyle \frac{\partial w_k}{\partial t}}\right)-HTC{a}_p(T_g-T_s)=0$$

(18)

Here, ${\mathsf{\rho }}_{\mathrm{s}}$ denotes solid phase density (Kg/m³), ${\mathrm{C}}_{\mathrm{p}\mathrm{s}}$ is the specific heat capacity of the solid phase (MJ/Kmol·K), ${\mathrm{T}}_{\mathrm{g}}$ and ${\mathrm{T}}_{\mathrm{s}}$ represent the temperatures of solid and gas phases (K), ${\mathrm{H}}_{\mathrm{k}}$ is the heat of adsorption for component K (J/Kg), $\mathrm{H}\mathrm{T}\mathrm{C}$ refers to the heat transfer coefficient between the gas and solid (W/m²·K), and ${\mathrm{a}}_{\mathrm{p}}$ is the external surface area per unit volume of the particle (1/m):

$$C_{vg}{v}_g{\rho }_g{\displaystyle \frac{\partial T_g}{\partial z}}+{\epsilon }_t{C}_{vg}{\rho }_g{\displaystyle \frac{\partial T_g}{\partial t}}+HTC a_p\left(T_g-T_s\right)+a_{Hx}{Q}_{Hx}=0$$

(19)

In this equation, ${\mathrm{C}}_{\mathrm{v}\mathrm{g}}$ represents the specific heat capacity of the gas phase (MJ/kmol·K), ${\mathrm{v}}_{\mathrm{g}}$ is the superficial gas velocity (m/s), ${\mathsf{\rho }}_{\mathrm{g}}$ is the gas density (Kg/m³), and ${\mathsf{\epsilon }}_{\mathrm{t}}$ denotes the total bed porosity. Additionally, ${\mathrm{a}}_{\mathrm{H}\mathrm{x}}$ is the heat exchanger surface area per unit volume (1/m), and ${\mathrm{Q}}_{\mathrm{H}\mathrm{x}}$ refers to the heat supplied or removed by the heat exchanger (W/m³).

2.1.4. Pressure Drop

Since the system operates at a constant mass flow rate with uniform adsorbent distribution, steady-state conditions were assumed for pressure drop across the bed. Consequently, the Ergun equation (Equation (20)) was applied to describe the total pressure drop, accounting for both viscous and kinetic energy loss in the fixed bed. In this equation, ${\mu }_g$ refers to gas viscosity (N.s/m²), $u_g$ is the superficial velocity of the gas phase (m/s), $r_p$ represents the particle radius (m), $\epsilon$ is the interparticle voidage fraction (m³_(Void)/m³_(Bed)), and ${\rho }_g$ is the gas phase density (Kg/m³):

$$-{\displaystyle \frac{\partial P_{total}}{\partial z}}=150{\displaystyle \frac{{\mu }_g{\left(1-\epsilon \right)}^2}{{\epsilon }^3{\left(2r_p\right)}^2}}{u}_g+1.75{\displaystyle \frac{(1-\epsilon ){\rho }_g}{2r_p{\epsilon }^3}}{u}_g^2$$

(20)

2.2. Process Design: Basis and Criteria

A cyclic adsorption model was developed as the basis for evaluating mmem-Mg₂(dobpdc) under DAC conditions. The process flowchart diagram is depicted in Figure 1. The TVSA sequences were defined in five sequential steps, as outlined below:

• Adsorption: Ambient air flows through the packed bed, where CO₂ is selectivity adsorbed onto the sorbent while CO₂-depleted air is released.
• Evacuation: The system pressure is reduced to remove N₂.
• Heating + Evacuation: The bed is heated using a heat exchanger to reach the regeneration temperature while maintaining vacuum conditions to promote efficient CO₂ desorption.
• Cooling: The heat exchanger cools the bed to maintain thermal stability, prevent amine degradation, and facilitate the next adsorption step.
• Pressurisation: The system is returned to atmospheric pressure by gradually reintroducing air, initiating the next adsorption cycle.

The initial process cycle duration, considering the breakthrough behaviour, is detailed in

Table 4. Process cycle durations for the base case.

Cycles of Process	Unit	Duration
Adsorption	s	7200
Evacuation	s	6
Heating + Evacuation	s	10,000
Cooling	s	Temperature matched the feed temperature
Pressurising	s	Pressure matched the atmospheric pressure

. An event-driven approach was applied to the cooling and pressurisation step to eliminate unnecessary idle time and improve overall cycle efficiency.

2.3. Performance Metrics

To evaluate the steady-state performance of the TVSA process, four key performance indicators—recovery, CO₂ purity, productivity, and specific energy consumption—were evaluated, with their respective definitions provided in

Table 5. Formulas for performance indicators.

Performance Indicators	Unit	Formula
CO2 Purity	%	${\displaystyle \frac{{\int }_0^{t_{cycle}}{F}_{product} y_{{CO}_2}dt}{{\sum }_{i=1}^m{\int }_0^{t_{cycle}}{F}_{product} y_{i}dt}}$
Recovery	%	${\displaystyle \frac{{\int }_0^{t_{cycle}}(y_{product,{CO}_2}{\left.F_{product}\right|}_{z=L})dt}{{\int }_0^{t_{cycle}}(y_{feed,{CO}_2}{\left.F_{feed}\right|}_{z=0})dt}}$
Productivity	Kmol/Kg·year	${\displaystyle \frac{3600\times {\int }_0^{t_{cycle}}{(F}_{product} y_{{CO}_2})dt}{w_{adsorbent}{t}_{cycle}}}$
SEC (vacuum)	MJ/Kg CO2	${\displaystyle \frac{{\int }_0^{t_{cycle}}\frac{F_{vac}{P}_{vac}\gamma }{\eta (\gamma -1)}\left[{\left(\frac{P_{feed}}{P_{vac}}\right)}^{1-\frac{1}{\gamma }}-1\right]dt}{{\int }_0^{t_{cycle}}{F}_{product}{y}_{product,{CO}_2}dt}}$

. The total energy demand comprises the electrical energy required for the vacuum pump and the thermal energy for the heat exchanger. The electrical energy consumption of the vacuum pump was estimated using the corresponding thermodynamic expression shown in Table 5, with a vacuum pump efficiency (ƞ) assumed to be 0.8. The heat capacity ratio (C_p/C_v), $\gamma$, was taken as 1.4, which is the typical value for air and CO₂. Thermal energy input associated with the heat exchanger was calculated directly using Aspen Adsorption. Given the negligible pressure drop across the bed under experimental conditions, fan energy consumption was considered insignificant and excluded from the overall energy analysis.

3. Results and Discussion

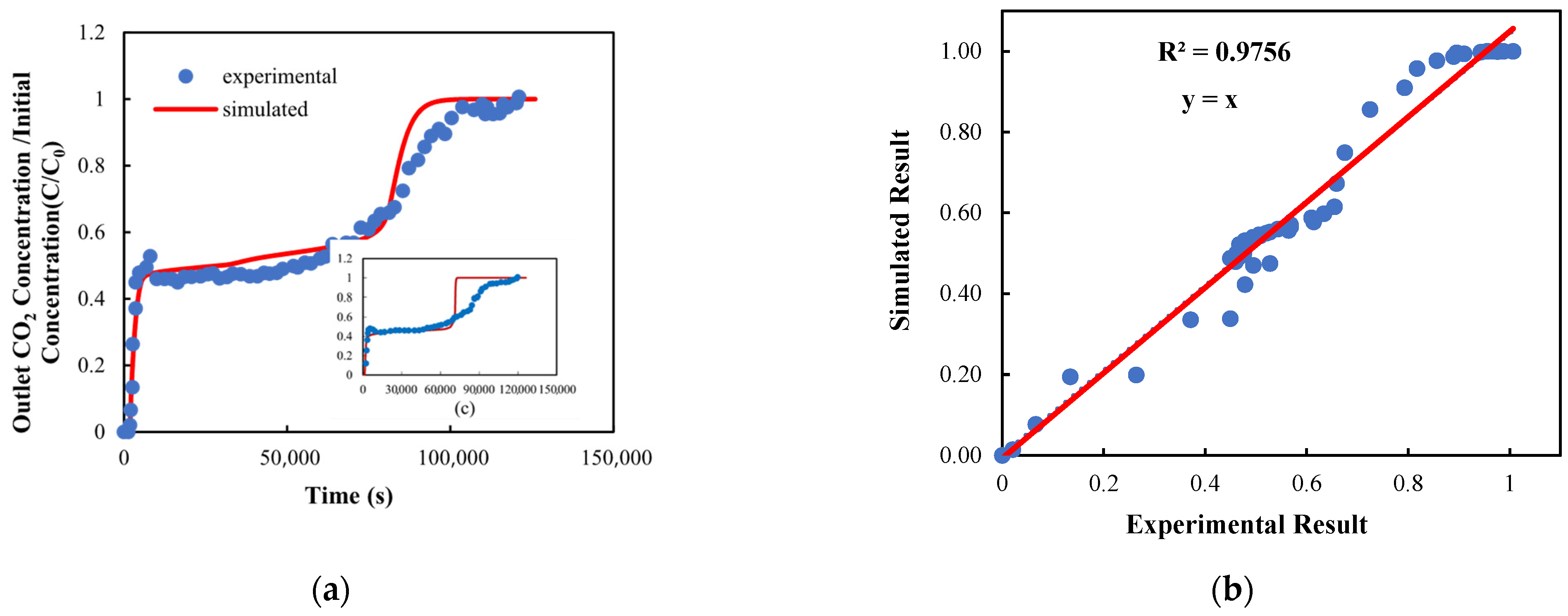
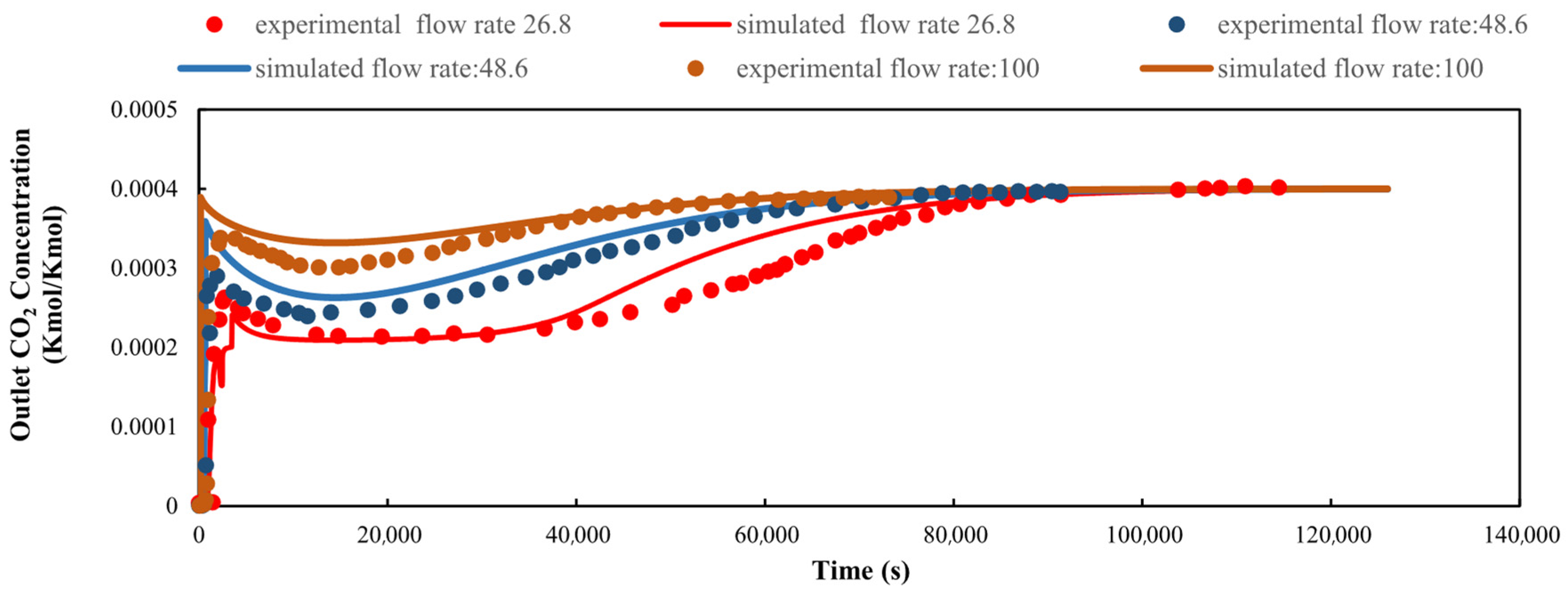
3.1. Mass Transfer Coefficient (MTC) Validation: Breakthrough Curve Comparison

To achieve accurate modelling of breakthrough dynamics, the reliability of the isotherm model was first established. Figure 2a–c demonstrate the close alignment between simulated and experimental CO₂ adsorption isotherms at 25, 49, and 69 °C, which are shown in different ranges of CO₂ partial pressure. The model also reproduced the adsorption behaviour trend at lower temperatures, supporting its suitability for DAC simulations under reduced temperature conditions. The validated isotherm model was utilised to simulate breakthrough performance, which was subsequently compared with experimental data. Figure 3a presents the breakthrough curves at 23 °C and a flow rate of 17.2 N mL/min. Quantitatively, the predicted breakthrough time deviated by about 3% (Figure 3b), underscoring the model’s predictive accuracy. Further validation at different inlet flow rates (Figure 4) demonstrated the model’s robustness across varying operational conditions. For flow rates of 26.8, 48.6, and 100 NmL/min, the average absolute relative deviation (AARD) values were 8.18%, 7.24%, and 4.97%, the root mean squared error (RMSE) values were 2.99 × 10⁻⁵, 3.10 × 10⁻⁵, and 2.88 × 10⁻⁵, and the R² values were 0.81, 0.72, and 0.80, respectively.

Validation against experimental breakthrough curves at different flow rates led to the adjustment of the initial estimation of the mass transfer coefficient to 0.05 S⁻¹ for pressure before the step. The values of Avrami equation parameters reported in [56] effectively describe the breakthrough behaviour beyond the step pressure. The simulation results demonstrated that applying a dual-kinetic approach provided a more accurate representation of the adsorption process compared to using the LDF model alone (Figure 3a).

The LDF model captured the initial sharp breakthrough resulting from mmen-Mg₂(dobpdc)’s cooperative adsorption behaviour. This sorbent exhibited a step-shaped isotherm, where CO₂ uptake began abruptly once a threshold partial pressure was reached. At low loading, strong exothermic chemisorption drove the rapid formation of ammonium carbamate chains, producing a steep concentration front and a sharp breakthrough transition [51]. However, the LDF model alone was not sufficient to reproduce the gradual uptake observed at the intermediate and high CO₂ loading. This later-stage behaviour was attributed to moderate chemisorption and weak physisorption, driven by enthalpy-dependent adsorption mechanisms [47].

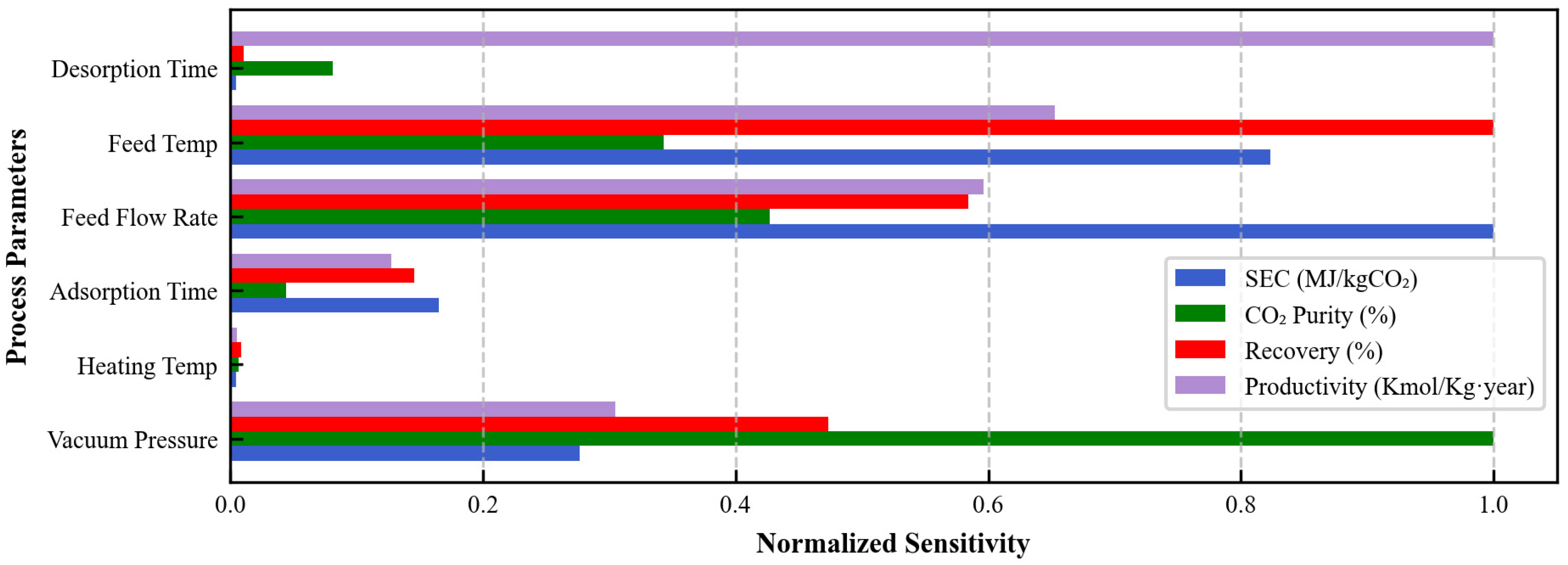
3.2. Parametric Evaluation

The performance of mmen-Mg₂(dobpdc) in DAC was governed by its relatively slow adsorption kinetics and step-shaped isotherm. While the sorbent exhibited high theoretical CO₂ capacity, enhancing recovery depends not only on its intrinsic uptake potential but also on its kinetics behaviour. At ambient CO₂ concentration, adsorption proceeded in two distinct stages: an initial chemisorption phase with slower kinetics, followed by a faster cooperative insertion step at higher loading. These kinetic characteristics resulted in a sharp breakthrough, followed by a gradual saturation phase, leading to prolonged adsorption times. Therefore, careful tuning of process parameters is essential to enable the sorbent to approach equilibrium loading. A systematic investigation of key process parameters, such as feed flow rate, temperature, and step durations, is critical to overcoming mass transfer limitations and improving overall process performance.

This section evaluates the effects of ambient temperature, inlet flow rate, vacuum pressure, heat exchanger temperature, and step durations on the performance of the DAC process. Parametric analysis provides a systematic framework for assessing the sensitivity of system outputs to these variables and defining optimal conditions for improving process efficiency. A related techno-economic analysis of solid-sorbent DAC systems demonstrated how variations in process conditions and bed geometry affect both energy requirements and cost, highlighting the importance of identifying the most influential parameters to balance CO₂ capture efficiency with operational feasibility [72]. The results of this study identified effective operating windows and illustrated the trade-offs among CO₂ recovery, specific energy consumption, and system scalability under varying conditions.

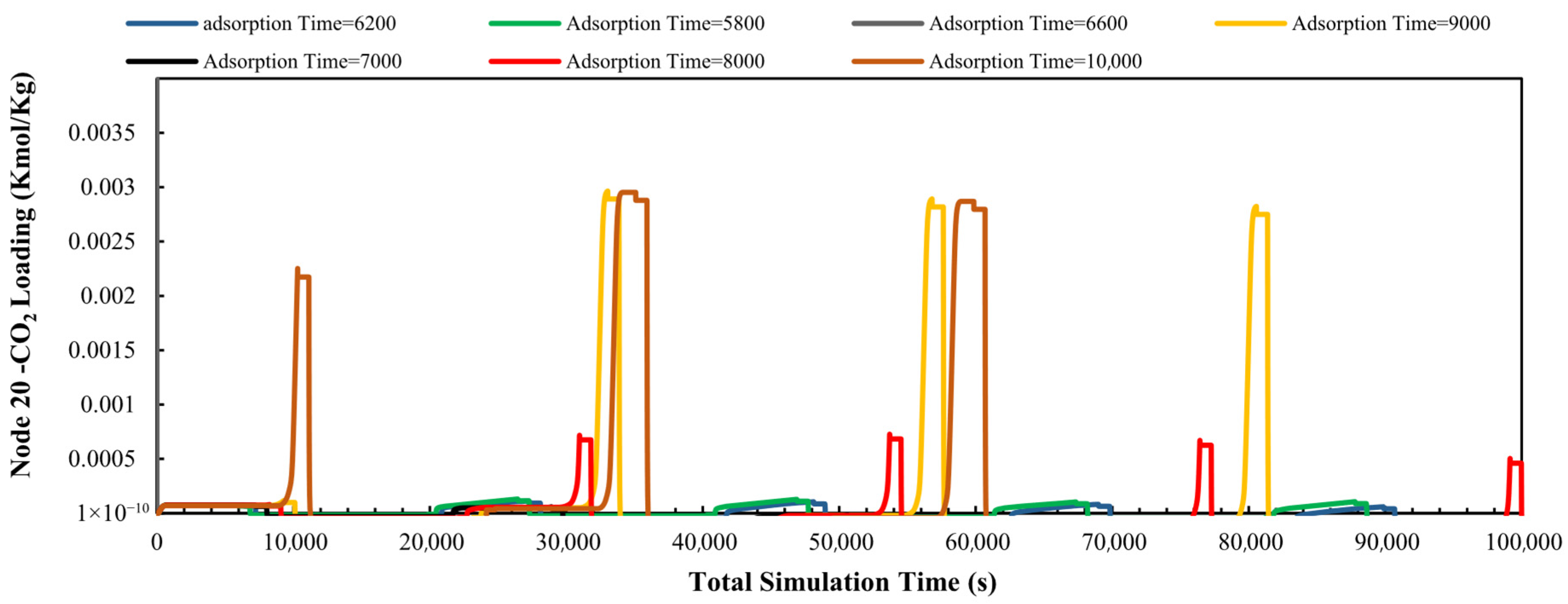
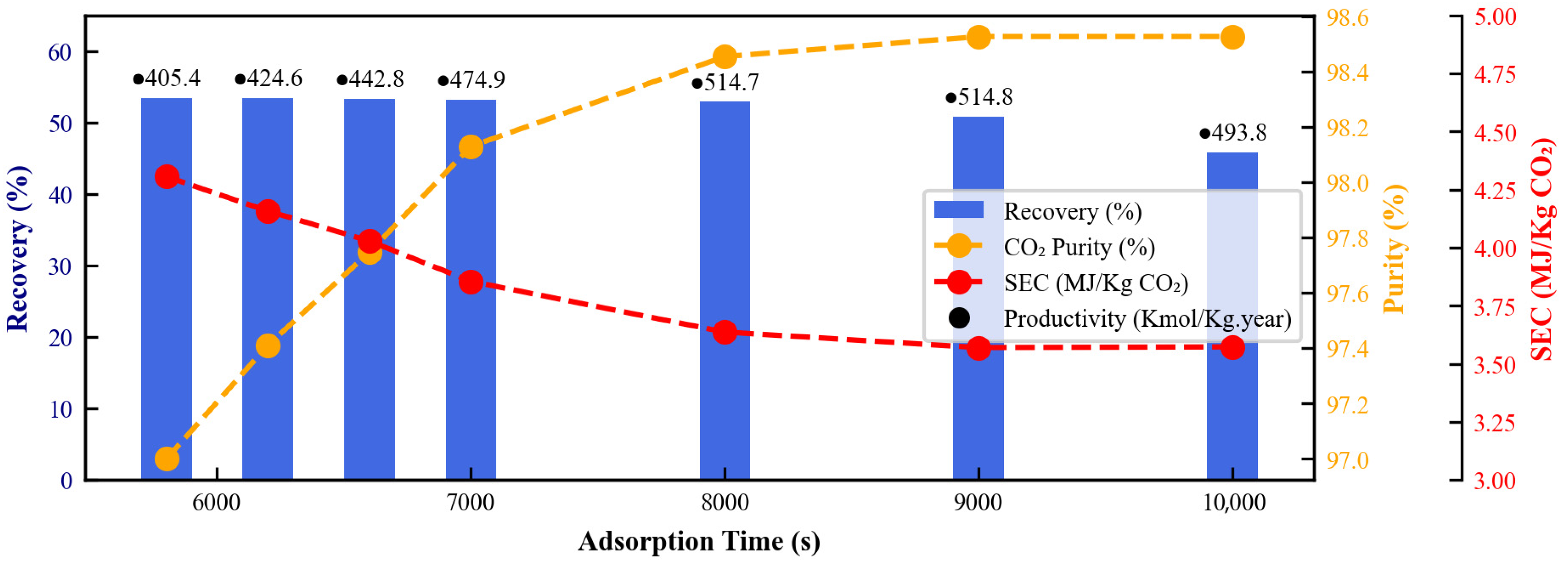
3.2.1. Adsorption Time

During the adsorption step, the primary objective was to maximise CO₂ uptake and achieve full bed saturation [73]. This study examined the effect of extending the adsorption time from 5000 to 10,000 s on overall process efficiency. While saturation was consistently achieved at nodes 1 and 10—representing the inlet and midpoint of the bed—the saturation level at node 20—located near the bed outlet—increased with longer adsorption durations. As shown in Figure 5, full saturation at node 20 was attained only when the adsorption time exceeded 9000 s, indicating improved bed utilisation with an extended adsorption period. The prolonged bed saturation was primarily attributed to the limited CO₂ mass transfer rate of the sorbent, as reflected in the breakthrough curve profile. As shown in Figure 3a, the curve exhibits a distinct plateau phase following the initial breakthrough front, during which CO₂ continues to adsorb gradually, particularly in the downstream segments of the bed. This observation aligns with the work of Stampi-Bombelli et al. [73], who argued that, due to the inherently slow CO₂ mass transfer in DAC processes, the adsorption step should be sufficiently long to ensure saturation of the entire column. They proposed defining adsorption time based on the saturation of the final bed segment rather than relying solely on the breakthrough time, particularly because, in DAC systems, the CO₂ recovery constraint is less stringent than in post-combustion capture, allowing for longer adsorption durations to prioritise bed saturation.

However, this extended adsorption period introduces a trade-off. While longer adsorption times improved bed utilisation and allowed the bed to approach full saturation, they also coincided with the plateau region of the breakthrough curve, where the adsorbent was no longer able to capture all incoming CO₂. Consequently, CO₂ recovery slightly decreased by approximately 2%. As shown in Figure 6, increasing the adsorption time enhanced specific energy consumption and CO₂ purity, with both metrics plateauing around 9000 s, signifying that the system approached equilibrium and the adsorption bed was saturated with CO₂ (Figure 5). Meanwhile, beyond 9000 s, process productivity declined, as fewer operational cycles could be completed annually. This reflects a performance limitation—while prolonging the adsorption phase initially improved overall performance, it eventually led to diminishing returns in both productivity and CO₂ recovery.

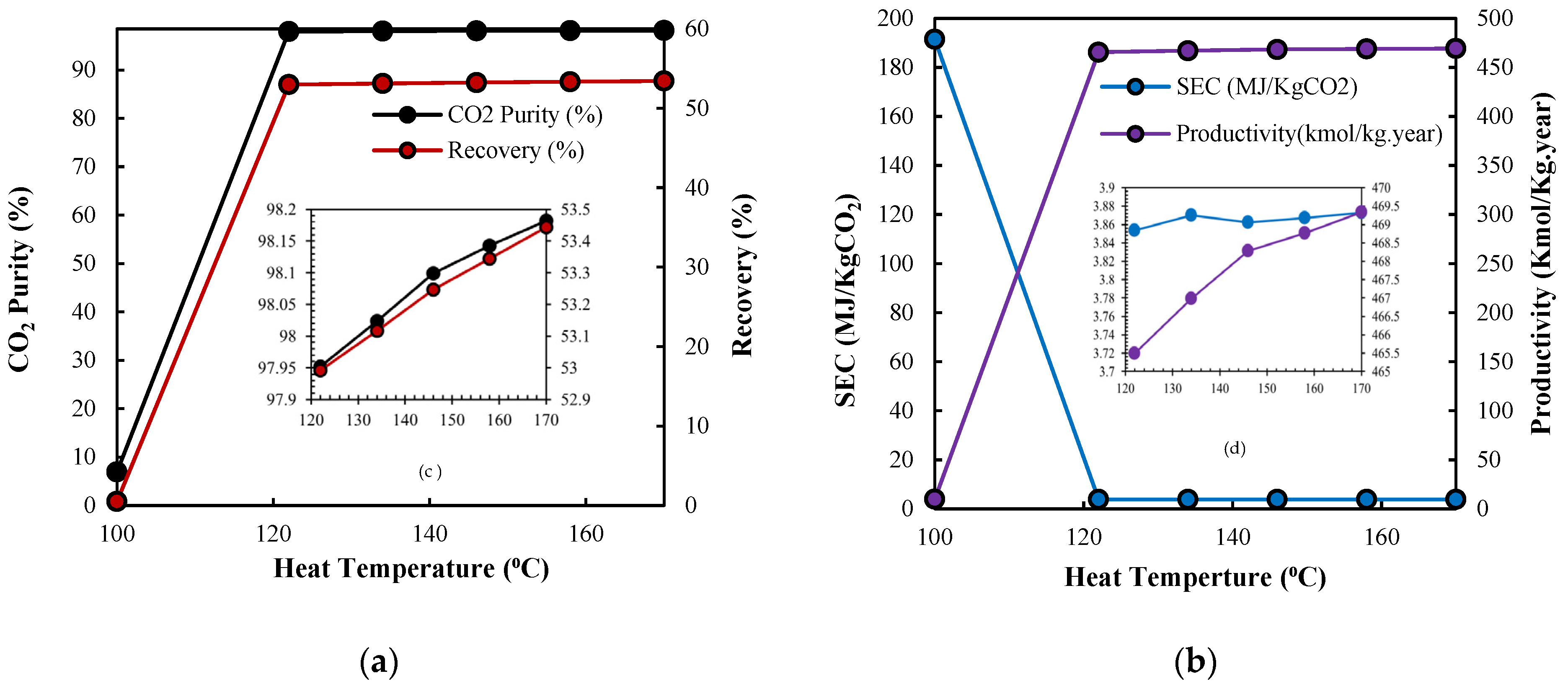
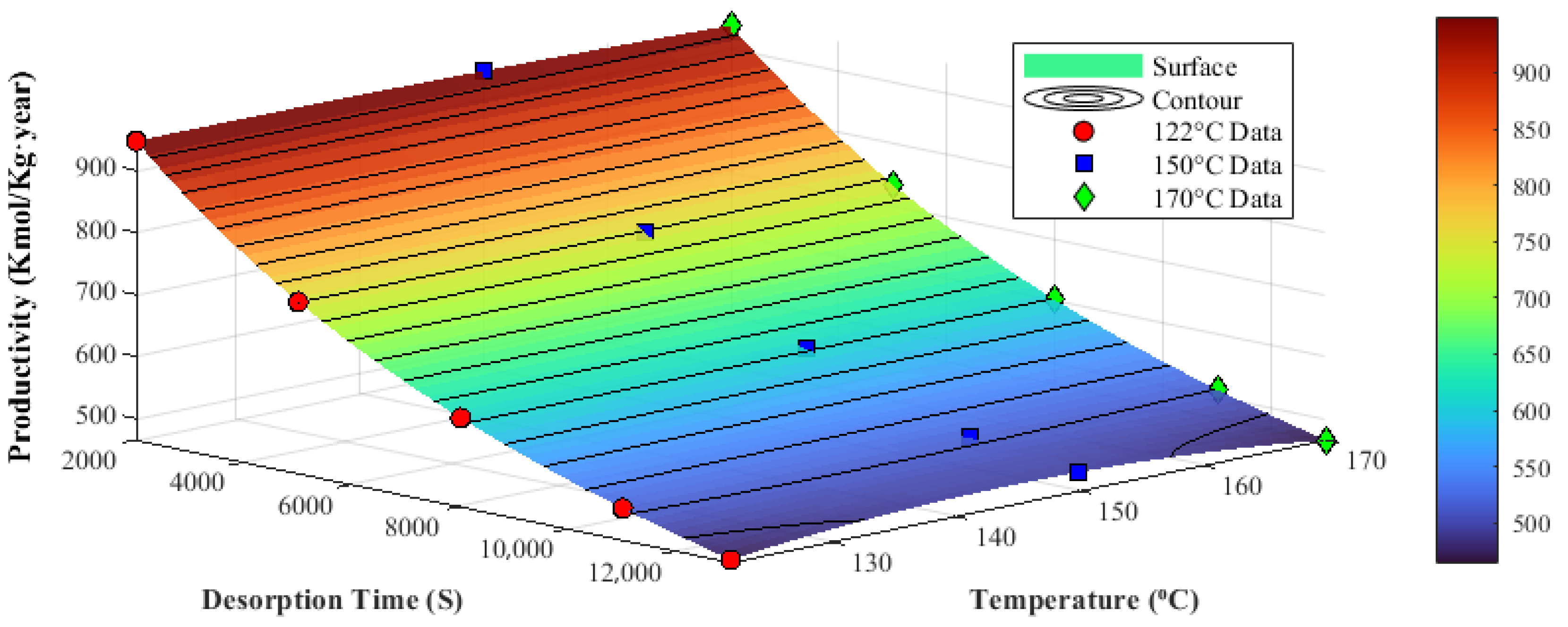
3.2.2. Desorption Temperature

In a TVSA process, regeneration of the adsorbent is achieved by applying both elevated temperature and reduced pressure, which together enhance the thermodynamic driving force for CO₂ desorption [57,73,74]. Therefore, the selection and optimisation of desorption temperature and vacuum pressure are closely interdependent.

Figure 7a,b present the effect of desorption temperature under a fixed vacuum pressure (P_eva = 0.09 bar) on performance indexes. As shown, CO₂ recovery and productivity remained negligible at temperatures around 100 °C but increased sharply once a specific threshold temperature was reached, approximately 120 °C. However, increasing the desorption temperature beyond 120 °C had minimal impact on further improving process performance, reflecting the cooperative desorption mechanism of mmen-Mg₂(dobpdc) associated with its characteristic step-shaped isotherm and temperature-dependent kinetics. These frameworks exhibited long induction periods near the step temperature, with desorption only becoming significant once a critical temperature was reached [75]. Importantly, the desorption threshold temperature was influenced by the applied vacuum level. Under deeper vacuum pressure, the equilibrium partial pressure of CO₂ decreased, enabling desorption at lower temperatures [76]. These findings establish a practical threshold that can guide the optimisation of regeneration strategies in DAC systems employing this sorbent.

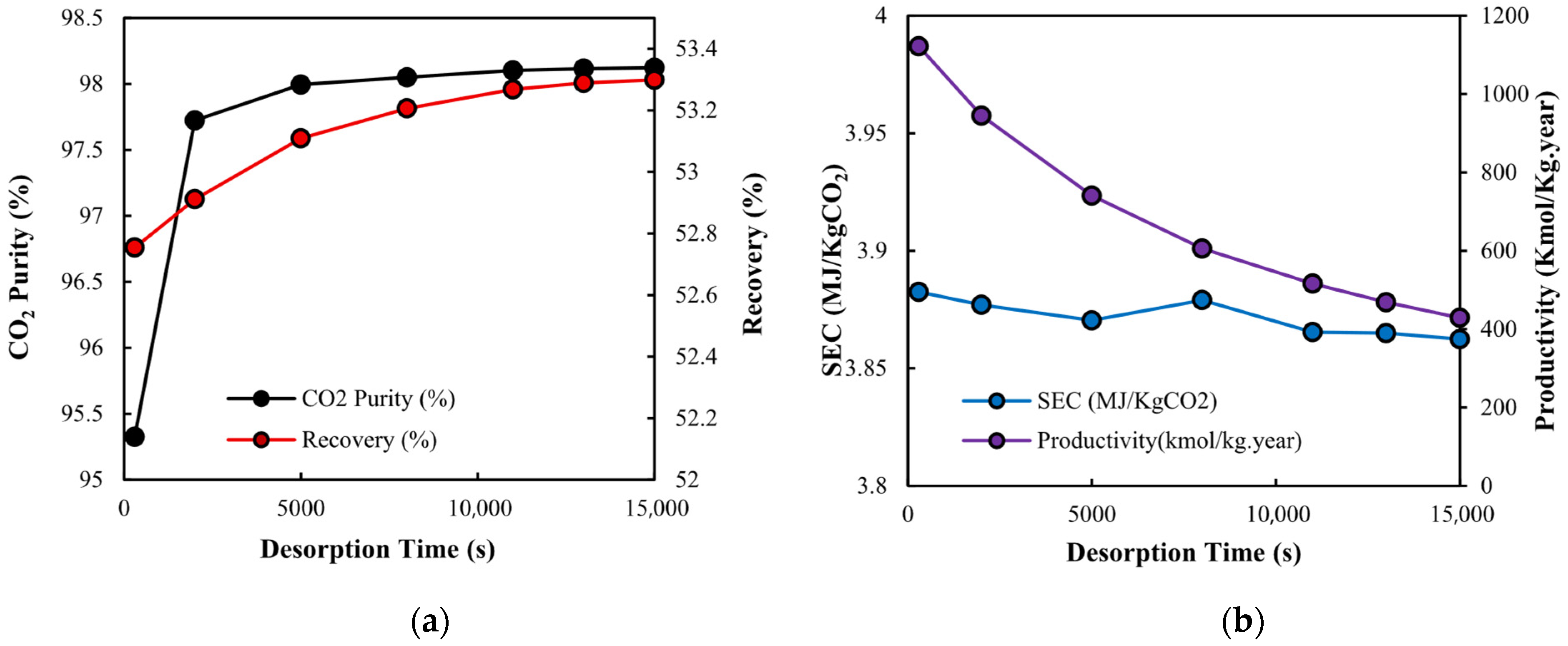
3.2.3. Desorption Time

Figure 8a,b illustrate the variation in productivity, CO₂ purity, recovery, and specific energy consumption across different desorption durations under a constant evacuation pressure (P_eva = 0.09). Extending the desorption time beyond 500 s had minimal impact on specific energy consumption (which remained nearly constant) and CO₂ recovery (which stabilised around 52.8–53.2%) since the bed reached its target temperature early in the desorption stage, and both metrics subsequently stabilised. However, desorption time showed a more significant influence on CO₂ purity and overall process productivity. Increasing the duration up to 2000 s improved purity, as more CO₂ was removed from the bed. Beyond this point, further improvement in purity was negligible (<0.2%), indicating that the sorbent’s desorption capacity was nearly exhausted at 120 °C. Meanwhile, longer desorption times reduced the number of process cycles that could be completed annually, thereby decreasing overall productivity. Previous studies have demonstrated that an optimal desorption duration exists that maximises CO₂ yield with minimal energy input [73]. Similarly, findings from multi-objective optimisations of TVSA cycles using amine-functionalised solid sorbents showed that prolonged desorption offers diminishing returns in terms of purity and recovery, while significantly reducing productivity due to extended cycle times [77]. Moreover, Figure 9 shows the variation in productivity with desorption temperatures between 120 and 170 °C across desorption durations ranging from 2000 to 12000 s. The curve indicates that the desorption temperature exceeded the identified threshold (~120 °C), making the desorption duration increasingly influential. In this regime, rather than further increasing the temperature, reducing the desorption time becomes a more effective strategy for improving annual productivity without compromising separation performance.

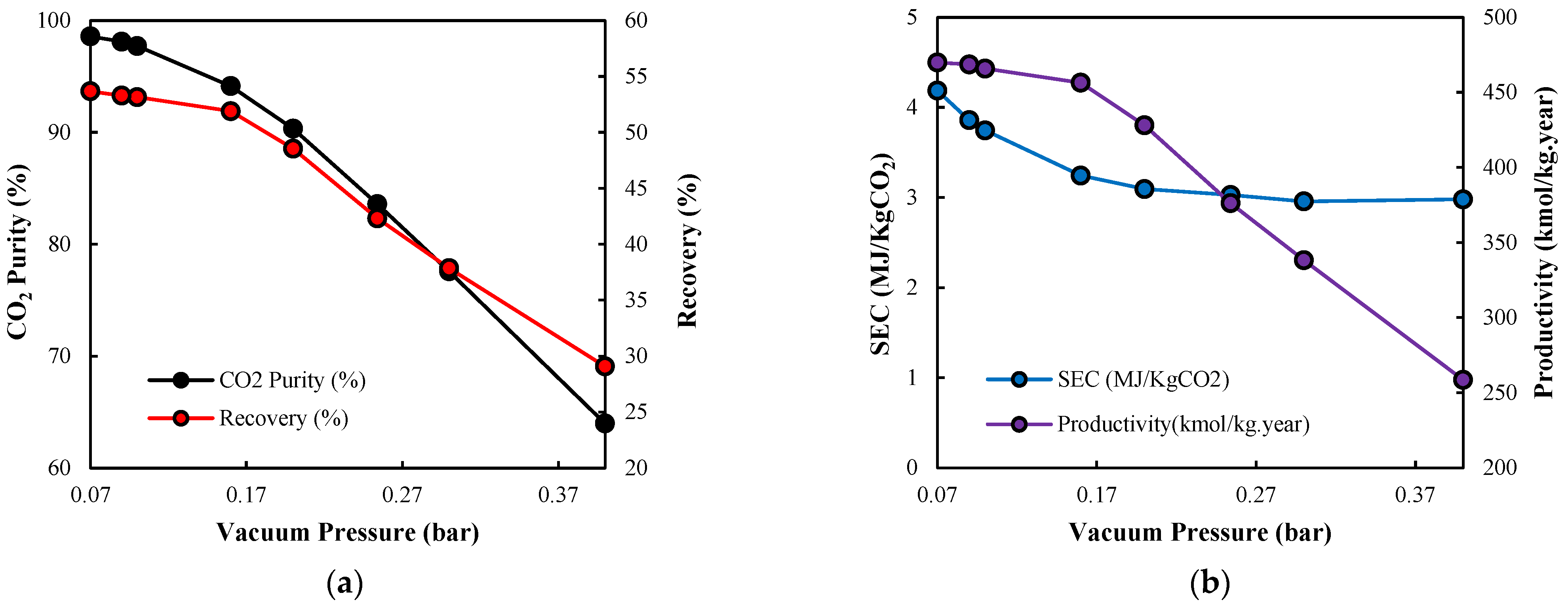
3.2.4. Evacuation Pressure

One of the important objectives of DAC processes is to achieve high CO₂ purity, ensuring that the captured product meets the quality requirements for downstream applications. This necessitates the effective removal of residual air from the adsorption bed before initiating the desorption step. Moreover, this step also helps prevent oxygen-induced degradation of amine-functionalised sorbents during subsequent heating [78].

Figure 10a,b compare CO₂ purity, productivity, specific energy consumption, and recovery for different evacuation pressures, ranging from 0.07 to 0.4 bar. As shown in the figure, there was a gradual reduction in purity, recovery, and productivity with increasing vacuum pressure up to 0.15 bar, followed by a more pronounced drop beyond this point. Additionally, a slight trade-off existed between specific energy consumption and CO₂ purity, recovery, and productivity. While operating at higher vacuum pressures reduced the energy demand of the vacuum pump—thereby reducing specific energy consumption—this benefit became less significant beyond 0.15 bar, as the weakened desorption driving force led to a decline in CO₂ recovery. The findings indicate that lower evacuation pressures significantly enhanced CO₂ recovery, purity, and productivity by enabling more complete regeneration of the sorbent. This improvement was attributed to the stronger thermodynamic driving force for desorption at lower pressures, which facilitated more efficient CO₂ release from the adsorbent [73]. By increasing the pressure differential between the adsorbed CO₂ and the surrounding gas phase, lower evacuation pressures enhanced the effectiveness of sorbent regeneration. However, the energy savings achieved at higher vacuum pressures were offset by corresponding reductions in recovery and productivity.

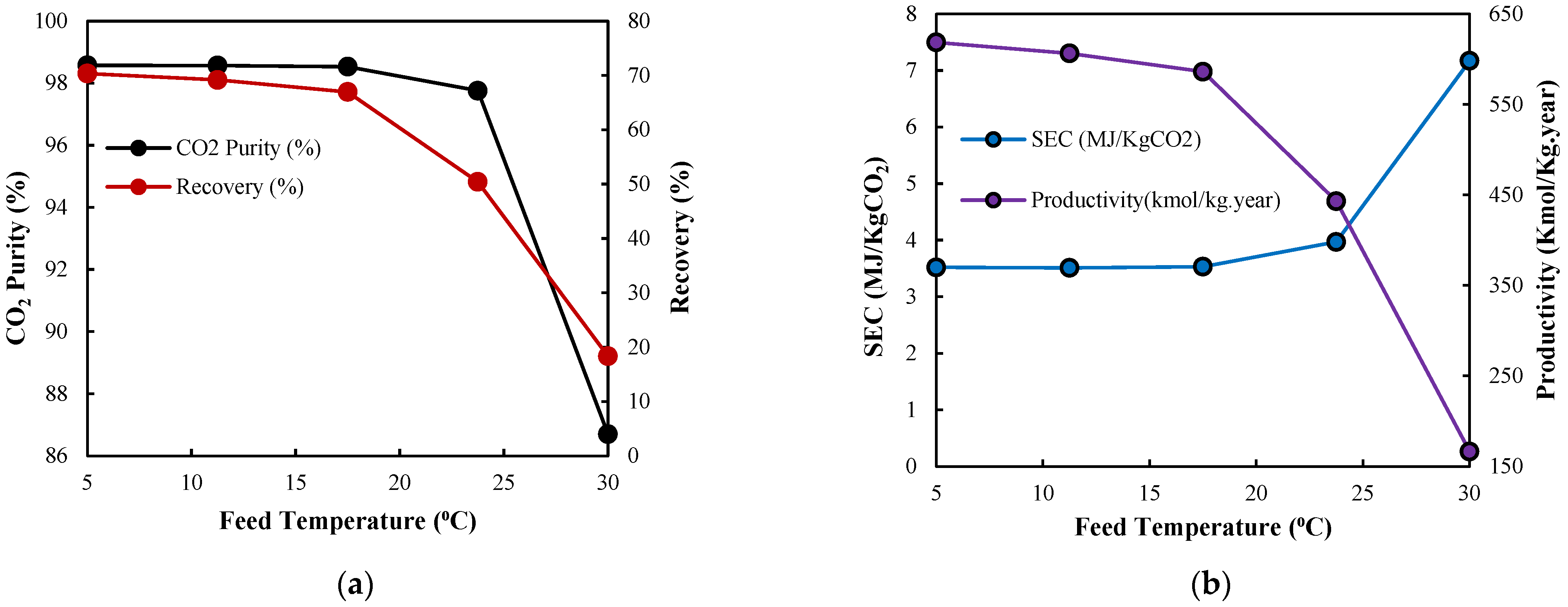
3.2.5. Inlet Feed Temperature

The effect of feed temperature on CO₂ purity, recovery, productivity, and specific energy consumption was investigated to consider different ranges of environmental temperatures. According to the simulation results in Figure 11a,b, CO₂ purity, recovery, and productivity remained relatively stable at feed temperatures below 20 °C. As the temperature increased beyond this point, all three performance indicators exhibited a consistent downward trend. This suggests that lower ambient (feed) temperatures were more favourable for achieving optimal DAC process performance using mmen-Mg₂(dobpdc), particularly in maintaining high product purity and maximising sorbent utilisation.

This behaviour can be attributed to the thermodynamics of the sorbent’s cooperative adsorption mechanism, in which CO₂ is captured through insertion into metal–amine bonds, forming extended chains of ammonium carbamate along the one-dimensional channels [49,79]. This process is exothermic and highly temperature sensitive [49]. As a result, at elevated temperatures, the formation of ammonium carbamate chains becomes thermodynamically less favourable, with reduced CO₂ uptake and diluted product streams. This trend was also observed by Martell et al. [75], who reported more favourable adsorption kinetics and thermodynamics at lower temperatures due to cooperative chemisorption mechanisms in diamine-appended Mg₂(dobpdc) frameworks.

Higher feed temperatures also led to increased specific energy consumption. This was primarily due to the reduced amount of CO₂ captured, which outweighed the benefit of lower heating energy input required to reach the target desorption (Figure 11b).

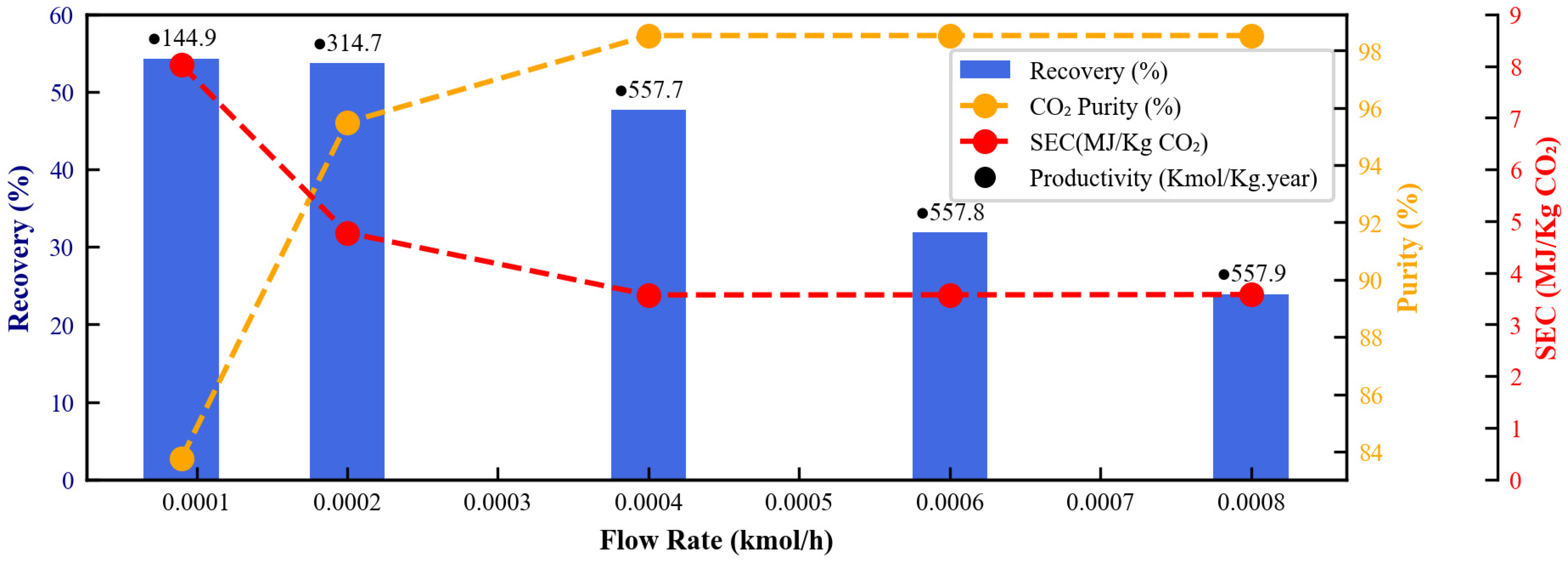
3.2.6. Inlet Feed Flow Rate

The sensitivity analysis on feed flow rate, conducted under constant feed temperature (23 °C) and evacuation pressure (0.09 bar), revealed that increasing the inlet air flow rate beyond 0.0004 Kmol/h had a minimal influence on CO₂ purity, productivity, and specific energy consumption. However, a significant decline in CO₂ recovery was observed (column plot in Figure 12). This reduction was attributed to the insufficient gas residence time within the adsorption bed, which restricted CO₂ diffusion and hindered effective adsorption onto the sorbent surface. Consequently, a significant fraction of CO₂ bypassed the bed without being captured. Conversely, at lower flow rates, extended gas–solid contact time enabled the sorbent to approach full saturation, thereby improving CO₂ recovery. The stability of CO₂ purity, specific energy consumption, and productivity at higher flow rates can be explained by the dynamic balance between adsorption kinetics and process throughput. Although increasing the flow rate reduced the contact time, the high velocity also increased the mass transfer driving force, allowing CO₂ to be quickly adsorbed.

3.3. Optimal Design Discussion

To complement the individual parameter investigations, a normalised sensitivity analysis was conducted to compare the relative impact of each process parameter on four key performance indicators: SEC, CO₂ purity, recovery, and productivity. The study considered the following parameter ranges: adsorption time (5000–10,000 s), desorption time (300–15,000 s), feed temperature (5–30 °C), feed flow rate (0.0001–0.0008 Kmol/h), and vacuum pressure (0.07–0.4 bar). According to Figure 13, feed temperature consistently demonstrated a strong influence across all metrics, significantly affecting SEC, recovery, and productivity. Its role in controlling the thermal and mass transport within the bed made it particularly impactful. Vacuum pressure also strongly influenced recovery and purity, as it governed the thermodynamic driving force for CO₂ desorption. Desorption time significantly affected productivity by limiting the number of annual operational cycles, while also influencing CO₂ purity through its impact on bed regeneration. By contrast, adsorption time showed minimal influence across all indicators in the sensitivity analysis, indicating that once sufficient bed saturation was achieved, further increases in adsorption time had a negligible effect on system performance. Finally, heating temperature appeared to have a minimal impact in this analysis, which aligns with prior findings in Section 3.2.2, where it was demonstrated that heating temperatures above 120 °C did not substantially improve performance due to the system reaching equilibrium; hence, the effect of further increases within the 120–170 °C range was limited.

Translating the insights from the sensitivity analysis into process improvements, the base case performance was compared with optimised condition performance. Table 6 succinctly summarises the resulting performance indicators for both the baseline and optimised scenarios. The optimised configuration demonstrated substantial enhancement over the base case. Specifically, it achieved a significant improvement in CO₂ recovery (from 53.26 to 75%) and productivity (from 474.85 to 1373 Kmol/Kg·year). Crucially, these gains were realised while maintaining a consistently high CO₂ purity of 98% and notably reducing the specific energy consumption from 3.85 to 3.64 MJ/Kg CO₂. These improvements were primarily attributable to strategic adjustments in operating conditions, including a reduction in vacuum pressure to 0.08 bar, a decrease in desorption time to 1000 s, an extension of adsorption time to 8200 s, and lowering the feed temperature to below 7 °C. These adjustments align directly with the sensitivities identified for each parameter and collectively support the development of more energy-efficient and sustainable DAC systems.

To further contextualise the performance of our developed system, Table 6 also incorporates a comparison with three established benchmark sorbents reported in the DAC literature. One of these was Lewatit VP OC 1065, evaluated under a packed-bed TVSA process, which closely aligns with our system’s bed configuration and process type. The other two sorbents were mmen-Mg₂(dobpdc) and MIL-101(cr)-PEI-800, employing novel coated monolith adsorption beds. Additionally, the table presents performance data from the Climeworks commercial DAC process to provide a broader industrial benchmark.

This analysis focused on purity, recovery, and specific energy consumption, providing a comprehensive assessment of the system’s operational efficiency and effectiveness. Our optimised system highlighted competitive capabilities, particularly in achieving lower specific energy consumption alongside enhanced purity and recovery rates. These improvements indicate the potential for reduced operational costs and increased process sustainability. The calculated energy requirement in our benchmark case was approximately 59% lower than the reported value for the Climeworks system. This deviation was anticipated, as our model represents a highly idealised and optimised scenario. For example, Climeworks adsorption bed configuration [80] likely limits full bed saturation due to practical design constraints, whereas our simulation assumes optimal sorbent utilisation. Several additional factors contribute to this difference:

• The current model assumes negligible pressure drop, thereby excluding blower energy consumption.
• Real-world vacuum equipment typically operates at lower efficiencies than assumed in ideal models.
• The Climeworks contactor design includes additional flow resistance due to the parallel flow path through structured adsorbent sheets, whereas the current model assumes axial flow through a thin sorbent layer, reducing resistance and energy loss.
• The current study does not consider the presence of water in the feed and associated energy required for water–CO₂ separation. These factors would likely increase the energy demand in real-word systems.

Among the benchmark sorbents considered, the Lewatit VP OC 1065, evaluated by Deschamps et al. [81], stood out for its relatively high energy consumption despite operating under idealised process conditions. This can be attributed, in part, to the inclusion of moisture and its interactions with CO₂, a level of complexity not considered in the current study. Additionally, the sorbent demonstrated the ability to achieve high CO₂ purity without the need for deep vacuum conditions.

Furthermore, the study by Sinha et al. [53] investigated mmen-Mg₂(dobpdc) and MIL-101(cr)-PEI-800 under experimental conditions using a monolithic adsorption configuration. The predicted energy consumption for mmen-Mg₂(dobpdc) in their study was slightly lower than that reported in the present study. This variation can be attributed to differences in bed configuration and the higher CO₂ purity achieved in our system, which was facilitated by operating at deeper vacuum levels. Although such conditions increase energy demand, they also enhance separation performance. In contrast, the use of MIL-101(cr)-PEI-800 in monolithic configurations resulted in substantially higher energy consumption and lower CO₂ recovery, indicating that this sorbent may be a less promising candidate for DAC applications compared to mmen-Mg₂(dobpdc) under the applied condition.

Table 6. Performance comparison of the optimised mmen-Mg₂(dobpdc) packed-bed TVSA system with established benchmark sorbents for DAC.

Performance Indicators	Process	Purity	Recovery	Specific Energy Consumption	Productivity	Reference
Unit		%	%	MJ/Kg	Kmol/Kg·year
Base case	Packed bed, TVSA	98.13	53.26	3.85	474.85	This work
Designed case	Packed bed, TVSA	98.05	75	3.64	1373	This work
Climeworks amine-based sorbent	TVSA	99.9	85.4	6.12–8.18	1344	[82,83]
Lewatit VP OC 1065	Packed bed, TVSA	99	77	5.42	1090	[81]
Mmen-Mg2(dobpdc)	Coated monolith Steam assistance, TVSA	95	60	3.52	-	[53]
MIL-101(cr)-PEI-800	Coated monolith Steam assistance, TVSA	95	50	5.34	-	[53]

Table 6. Performance comparison of the optimised mmen-Mg₂(dobpdc) packed-bed TVSA system with established benchmark sorbents for DAC.

Performance Indicators	Process	Purity	Recovery	Specific Energy Consumption	Productivity	Reference
Unit		%	%	MJ/Kg	Kmol/Kg·year
Base case	Packed bed, TVSA	98.13	53.26	3.85	474.85	This work
Designed case	Packed bed, TVSA	98.05	75	3.64	1373	This work
Climeworks amine-based sorbent	TVSA	99.9	85.4	6.12–8.18	1344	[82,83]
Lewatit VP OC 1065	Packed bed, TVSA	99	77	5.42	1090	[81]
Mmen-Mg2(dobpdc)	Coated monolith Steam assistance, TVSA	95	60	3.52	-	[53]
MIL-101(cr)-PEI-800	Coated monolith Steam assistance, TVSA	95	50	5.34	-	[53]

4. Conclusions and Prospect

This study evaluated the performance of mmen-Mg₂(dobpdc) under realistic DAC process conditions using a dynamic simulation framework. This metal-organic framework, known for its distinctive step-shaped isotherm, was evaluated within a TVSA process in Aspen Adsorption. After validating the simulation model against experimental breakthrough data and confirming its reliability, a sensitivity analysis was conducted to identify the most influential process parameter (vacuum pressure, adsorption and desorption times, feed temperature, feed flow rate, and heat exchanger temperature) on CO₂ purity, recovery, productivity, and specific energy consumption. Beyond demonstrating high CO₂ purity and recovery, the analysis highlighted the complex and interdependent relationships between process variables and their implications for system performance and design.

A key insight from this work was the trade-off between CO₂ recovery and productivity. While lower feed temperatures and extended adsorption time enhanced recovery by increasing sorbent loading and saturation levels, they concurrently reduced the frequency of adsorption–desorption cycles, thus lowering productivity. Another significant finding was the dual role of vacuum pressure: deeper vacuums improved desorption efficiency and boosted both CO₂ purity and recovery. However, this came at the expense of increased SEC, particularly from mechanical work. The interplay between feed temperature and vacuum pressure was particularly noteworthy—lower feed temperatures shifted the isotherm’s step pressure downward, enabling effective desorption at milder vacuum conditions, and thus offering potential energy saving if properly tuned. This study also revealed a threshold effect for desorption temperature, beyond which further heating yielded marginal benefit. At a deeper vacuum level, effective regeneration can occur at lower temperatures, provided sufficient desorption time is allowed. This introduces a critical design trade-off where longer desorption times reduce thermal energy demand (lowering SEC), but again, may compromise overall productivity.

Although the current study was conducted at an experimental scale and did not explicitly account for humidity fluctuations or long-term material stability, the demonstrated performance underscores the potential of this sorbent for DAC applications. These results provide a robust foundation for sustainable DAC process development, offering guidance for future research aimed at optimising the process and improving system scalability. Future investigation is needed into the sorbent degradation mechanism under cyclic operation, as well as the scalability of the adsorption bed design for industrial-scale development. Further work will also prioritise a comprehensive evaluation of competitive adsorption between H₂O and CO₂ under realistic atmospheric conditions. Furthermore, the insights gained from this study revealed the interconnected dynamics among process variables, highlighting the limitations of isolated parameter tuning and emphasising the need for system-level optimisation. The complexity of balancing CO₂ purity, recovery, SEC, and productivity justifies the application of advanced multi-objective optimisation techniques to define operating strategies that achieve optimal performance across these key indicators and support the development of sustainable carbon removal technologies.