Abstract
This paper calculates the expected cost of uncertainty in solar and wind energy using the uncertainty cost function (UCF), with a primary focus on computational processing time. The comparison of processing time for the uncertainty cost quantification (UCQ) is conducted through three methods: the Monte Carlo simulation method (MC), numerical integration method, and analytical method. The MC simulation relies on random simulations, while numerical integration employs established numerical formulations. These methods are commonly used for solving cost optimization problems in power systems. However, the analytical method is a less conventional approach. The analytical method for calculating uncertainty costs is closely related to the UCF, as it relies on a mathematical representation of the impact of uncertainty on costs, which is modeled through the UCF. A multi-objective approach was employed for scheduling an energy management system, that is to say, thermal–wind–solar energy systems, proposing a simplified method for modeling controllable renewable generation through UCF with an analytical method, instead of the complex probability distributions typically used in traditional methods. This simplification reduces complexity and computational processing time in optimization problems, offering greater accuracy in approximating real distributions and adaptability to various scenarios. The simulations performed yielded positive results in improving cost estimation and computational efficiency, making it a promising tool for enhancing economic distribution and grid operability.
1. Introduction
With the integration of renewable energy sources, the topic of optimal power flow in energy systems has received a lot of interest within the research community. Power flow optimization is crucial for reliable and efficient operation, maximizing the use of renewable energy resources while minimizing system costs. However, as these systems become more complex, computational processing times emerge as a critical challenge. Traditionally, uncertainty cost modeling has relied on conventional methods such as the Monte Carlo (MC) simulation and numerical integration. However, the MC method requires extensive random sampling to estimate uncertainty costs, resulting in prolonged processing times and high computational resource demands. On the other hand, while more efficient than MC, the numerical integration method involves solving complex integrals based on nonlinear probability functions (e.g., log-normal for solar or Weibull for wind power), significantly increasing computational load, particularly in large-scale systems with multiple renewable sources. Efforts to replace these methods with analytical approaches have faced major limitations. For instance, analytical methods have often been restricted to specific probability distributions (e.g., log-normal for solar generation), limiting their applicability to broader uncertainty scenarios. However, in [1,2,3,4,5] they expanded these formulations to incorporate additional probability functions, improving their versatility. The adaptive geometry estimation-based multi-objective differential volution (AGE-MODE), combined with a multi-objective optimization approach, is the innovative strategy presented in this research for computation in thermal–wind–solar power systems. The authors propose uncertainty-based cost functions due to the involvement of renewable energy sources such as solar and wind power. The computational processing time was compared using three methods: the Monte Carlo simulation method (MC), numerical integration method, and analytical method. Typically, the analysis of such optimization problems involves extensive and complex mathematical functions, especially due to the number of simulations and modeled functions, as seen in the cases of the MC and numerical integration methods. However, the cost functions developed through the analytical method provide algebraic representations of the uncertainties associated with renewable electricity costs, making the analysis of this complex problem much simpler. This approach reduces computational cost while ensuring more accurate data. The proposed technique can be incorporated into optimization software, as it demonstrates substantial savings in computational simulation time compared to traditional methods.
While existing studies have extensively explored uncertainty cost functions (UCFs) for solar and wind energy [6,7,8,9,10], recent advances have extended these methods to hydropower systems, particularly small hydroelectric plants (SHP). As shown in [9,11,12,13], UCFs can effectively model water flow uncertainty using Gumbel probability distributions for river discharge (f(Q)), enabling analytical cost quantification similar to solar/wind approaches. This broader applicability underscores the versatility of UCFs across renewable sources and justifies their adoption for integrated energy systems.
Uncertainty in power systems incorporating renewable energy refers to the inherent variability and unpredictability associated with renewable generation (e.g., solar irradiance, wind speed), load demand, and grid conditions, which challenge system planning, operation, and control. This uncertainty arises from the stochastic nature of renewables, forecasting errors, and grid dynamics. Due to uncertainties, renewable generation presents a challenge for optimal power flow (OPF) as it is increasingly integrated into electrical grids, applying underestimation and overestimation uncertainty cost functions (UCFs) to evaluate the values of photovoltaic generation (PVG), wind energy generation (WEG), and plug-in electric vehicles (PEV) [1,2]. Existing approaches for modeling these uncertainties often rely on complex probability distributions, which significantly increase computational burden [3]. This paper employs uncertainty cost functions (UCFs) through an analytical method as a novel approach to address this issue, as explored in previous papers, replacing the numerical integration method, which relies on Monte Carlo simulations for solar distribution and Weibull probability functions for wind distribution [4]. This approach demonstrates a simpler and less complex formulation, reducing computational processing time. This method offers several benefits, including lower computational overhead, better accuracy in capturing the true distribution of solar irradiance, and adaptability to various scenarios, enabling the planning and evaluation of electrical assets in the short, medium, and long term [5,6,7].
The analytical form of these UCFs is a key component that allows them to be easily integrated into any power system optimization solver currently in use. The authors in [8] presented operational scheduling results by applying this type of function, considering probability distribution and uncertainty, using the DEEPSO (differential evolutionary particle swarm optimization) heuristic optimization algorithm. This eliminates the need for complex mathematical operations and facilitates the application of the proposed strategy within existing OPF frameworks, potentially extending the concept of uncertainty costs in the operation of energy systems containing renewable sources (solar and wind) to power systems with small hydropower plants (SHPs) [9]. This approach enables a more accurate and efficient estimation of uncertainty costs in renewable generation by addressing the computational complexities of traditional methods. Ultimately, this will lead to a more stable and reliable operation of electrical grids with high penetration of these valuable renewable energy sources [10]. In multi-objective optimal power flow (MOOPF) problems with multiple objectives, the proposed UCF approach provides a useful way to overcome computational bottlenecks, especially when considering the uncertainties of solar photovoltaic and wind generation. This method paves the way for more effective and reliable MOOPF solutions for hybrid energy systems, ultimately improving grid stability and operation by significantly reducing computation time while maintaining accurate uncertainty cost estimates [1,2,3,4,8,9,11].
Given that solar and wind energies are uncertain energy resources, we can develop uncertain cost functions to optimize them [12,13]. We can develop optimization and decision-making tools for power systems’ distribution operators by performing expected value calculations of uncertain cost quantification to improve processing time [14,15,16,17]. These tools are designed to be developed and integrated into frameworks capable of handling these uncertainties in energy generation and mitigating the overall impact on costs [18,19,20,21].
In both the solar and wind industries, as well as in any sector involving uncertainty in production forecasts and associated costs, traditional approaches have relied on Monte Carlo methods. Recently, more advanced techniques have been considered, such as polynomial chaos expansion, stochastic collocation, Gaussian process regression, and analytical methods like the one proposed in this article. Unlike conventional approaches, this latter method is based on single-data-point sampling, meaning data collection and decision-making occur through a single scenario while encompassing outlier values of the analyzed energy source. This method typically demonstrates greater efficiency compared to Monte Carlo [13,14,15,16], combined with the function representing the behavior of the relevant energy source (depending on the model’s properties), and can generate computationally cheaper surrogate models. Furthermore, data-driven surrogate models have garnered significant interest, particularly for representation and decision-making purposes. Recent trends in uncertainty quantification, specifically in optimization and decision-making, are becoming increasingly prevalent in applications involving renewable energy integration into power systems.
In summary, the application of UCF with an analytical method for power system cost quantification (UCQ) has significant relevance in optimal power flow (OPF) problems, energy management systems (EMS), and large-scale investment planning, enhancing the performance, accuracy of results, and minimizing the computational burden on the power system while notably reducing processing time compared to traditional methods. Additionally, the simplicity of the proposed tool greatly aids in real-time decision-making regarding costs.
In this paper, Section 1 presents the introduction based on a literature review related to the system costs due to the behavior of renewable energy sources, while Section 2 addresses the problem formulation for expected value calculation in uncertainty cost quantification (UCQ) and uncertainty cost functions (UCFs). The problem solution through estimation methods for cost calculation is presented in Section 3. Section 4 showcases the simulation and validation of UCF results in contrast with other methods applied to the same cost optimization problem. The results of the entire process and a comparison with the analytical method, implementing an evolutionary algorithm, are detailed in Section 5, followed by the conclusions in Section 6.
2. Problem Formulation: Expected Value Calculation for Uncertainty Cost Quantification (UCQ) and Uncertainty Cost Function (UCF)
Uncertainty cost quantification (UCQ) based on renewable energy resources is the process of measuring or quantifying the total cost associated with uncertainty in a system, focusing on assessing the financial impact of associated uncertainties. These costs can be represented as functions or mathematical models, specifically uncertainty cost functions (UCFs). UCFs can be utilized as a tool within the UCQ process, beginning by defining a cost function (UCF) that describes how uncertainty affects costs, and then using this function to quantify the total cost (UCQ) associated with different levels of uncertainty. Models such as Monte Carlo simulations, numerical integration methods, and analytical approaches are employed to quantify the uncertainties related to renewable energy generation [3].
In this paper, we propose calculations using an analytical approach to handle model uncertainties that occur in renewable energy generation, such as solar irradiance, wind speed, and small hydropower plants [4]. These models are used to improve the decision-making, operation, and planning of renewable energy systems by leveraging the inherent variability and unpredictability of renewable energy resources [6].
Uncertain cost quantification is counting the whole available power (Pav) cases produced from the renewable energy resource generation [7]. For this purpose, the cost for a case is given by:
where ΔP is the difference between the available power (Pav) and the scheduled power (Ps), multiplied by a penalty factor (PF), resulting in the total cost (C).
Ps is defined by the power system operator using optimal scheduling tools, while Pav is the available power from the renewable source at that time. The penalty factor is divided into two cases: overestimation and underestimation. The total cost scenarios are calculated from all possible available power. Pav is then determined from the probability distribution of the primary energy source. In the cases considered, we have log-normal distribution for solar irradiation, Weibull distribution for wind speed, and Gumbel distribution for hydropower flow [8].
2.1. Overestimated Cost
Overestimated cost reflects the penalty incurred when the power scheduling model allocates more power to the generator than what is actually available from the energy source at that time. If the supplied power is less than the scheduled power , grid operators will need to draw on reserve energy from storage systems or the grid itself to ensure a continuous power supply to consumers. In this scenario, the penalty is used to leverage backup energy and compensate for the remaining deficit to meet the scheduled power.
The expected penalty cost due to overestimation is given by:
where:
- is the expected value of the cost due to overestimation;
- is the penalty cost coefficient for generator i;
- is denoted for scheduled power set by the model in generator i;
- is the minimum power output available for the generator i;
- is the probability of determined available power given by the PDF of the energy source (solar, wind, small hydro);
- is the minimum power output of the generator.
2.2. Underestimated Cost
Underestimated cost represents the penalty incurred when the power scheduling model allocates less power to the generator compared to the actual availability from the energy source at that time. If the provided power exceeds the scheduled power, the surplus energy may go unused, and the grid operators would be responsible for the penalty cost. The penalty cost associated with the surplus of renewable energy can be defined as follows:
where:
- is the expected value of the cost due to underestimation;
- is the penalty cost coefficient for generator i;
- is denoted for the scheduled power set by the model in generator i;
- is the minimum power output available for the generator i;
- is the probability of determined available power given by the PDF of the energy source (solar, wind, small hydro);
- is the minimum power output of the generator.
3. Problem Solution
To calculate the expected cost, we have three ways to estimate expected value calculation.
3.1. Monte Carlo Simulation
The Monte Carlo simulation method is a probabilistic approach used to estimate the outcome of a complex process or system by repeatedly generating random samples. It is used to calculate the probability of different outcomes in situations where there is uncertainty, variability, or a high degree of complexity in the mathematical models.
MC evaluates the expected penalty cost due to the underestimation and overestimation of the power generated by a renewable energy source. Initially, the parameters for each renewable source associated with the system under analysis are defined. Table 1 outlines the parameters considered in this article.

Table 1.
Initial parameters.
A probability distribution is defined for each case, such as the log-normal distribution for solar energy (3) and the Weibull distribution (4) or Rayleigh (5) for wind energy.
The method relies on generating thousands of random rates or samples (n = 10,000) based on these distributions, which are then used to calculate the associated costs using the generation equations of each renewable source, solar energy (6) and (7) and wind energy (8).
Equation (6) is defined as the power produced (WPV(G)) in Part A of solar generation, corresponding to the standard irradiance (G), and representing values below the reference solar irradiance Rc. Meanwhile, Equation (7) defines the power produced in Part B of solar generation in relation to irradiance, representing values above the reference solar irradiance. The output power of the wind turbine () is discrete at certain wind speeds, as indicated by Equation (8). Specifically, the turbine’s output power will be zero when the wind speed (υ) is below the cut-in speed (υin) or above the cut-out speed (υout). However, the turbine will reach its rated power when the wind speeds fall within the range of the rated speed (υr) and the cut-out speed (υout). In [4], the MC simulation method was used for the calculation of solar energy.
The overestimation and underestimation costs will depend on the previously determined results in relation to the scheduled power defined by the grid operator.
3.2. Numerical Integral Calculations
The numerical integral calculations are based on both underestimation and overestimation cases. The use of this method heavily relies on understanding and applying the probability functions and power equations for each renewable energy source.
The main contribution of this article is the reduction of computational processing time through the use of UCFs via the analytical method. However, it is necessary to first develop the numerical integration model for each system.
3.2.1. Solar Case
For the numerical integration model, it is assumed that solar irradiance behaves like a log-normal probability density function (PDF). The log-normal PDF is given by Equation (3), where G is the solar irradiance, is the corresponding log-normal PDF, and λ and β are the location (mean) and scale (standard deviation) parameters of the log-normal distribution.
To determine the relationship between solar irradiance and the active power generated by a photovoltaic solar plant (WPV), the following conditions of the energy conversion function are defined, as presented in [11], depending on a reference irradiance value (Rc) according to the specific geographical location.
The analysis of solar power generation considers two conditions related to the critical reference irradiance (Rc), which can be defined as an irradiance threshold that determines changes in the photovoltaic system’s behavior, and the actual incident solar irradiance (G) on the photovoltaic panels. The variable Gr represents the standard reference solar irradiance (1000 W/m2) used for system calibration. This formulation provides a robust theoretical framework for analyzing the statistical behavior of photovoltaic generation in relation to the spatial and temporal variability of solar irradiance.
Condition A
Condition A refers to when the relationship Rc = G > 0 is satisfied. In this case, the quadratic transformation and the notation of the function g(G) are used, which represent the WPV power in terms of G.
Applying the change of variable expression, the WPV probability distribution function expressed for solar photovoltaic power is obtained
Then, replacing the inverse of g and its derivate of (9) in (10), the PDF (3) of the power of the photovoltaic generator for condition A is obtained (11).
Finally, Equation (11) is substituted into (2) or (3) in the probability function portion, depending on the uncertainty cost to be calculated.
Condition B
Condition B refers to when the relationship G > Rc is satisfied. In this case, the quadratic transformation and the notation of the function g(G) are used, which represent the WPV power in terms of G.
Then, replacing the inverse of g and its derivate of (12) in (10), the PDF (3) of the power of the photovoltaic generator for condition A is obtained (13).
Finally, Equation (13) is substituted into (2) or (3) in the probability function portion, depending on the uncertainty cost to be calculated.
3.2.2. Wind Case
The numerical integration method for wind energy assumes that wind speed follows a probability density function (PDF). According to the Weibull PDF, with a shape factor (β) and a scale factor (α), the wind speed distribution can be modeled as expressed in Equation (4). The wind power probabilities in these discrete zones can be calculated using the following equations or conditions:
Condition A
In this case, the power generated (WW) due to insufficient wind energy or saturation in the generator is 0. The probability of the wind power output being zero coincides with the sum of the probability of wind speed being smaller than υin plus the probability of wind speed being larger than υout.
Condition B
In the zone between the cut-in speed (υin) and the rated speed (υr), the wind turbine’s output power is continuous. For a continuous zone, the probability can be calculated as follows.
Condition C
In this case, there is a constant power output with respect to the wind speed. Based on the wind PDF, the following PDF is obtained for the wind power Ww values in the range of wind speed condition C, using the probability of wind speed between and :
Finally, Equations (14)–(16) are substituted into the probability functions of Equations (2) and (3), where they will be used depending on the uncertainty cost to be calculated. Equations (17) and (18) represent the UCF for overestimation and underestimation, respectively, where is the scheduled power of the wind turbine.
3.3. Analytical Method
The objective of the ED model is to properly allocate the scheduled power to minimize both underestimation and overestimation costs along with the production cost. The proposed UCF is obtained by summing the costs associated with underestimation and overestimation.
The penalty cost for underestimation arises when the ED model schedules an amount of power in a generator that is less than the available power from the source. In this case, there is a penalty for not utilizing the full available power from the source . On the other hand, the penalty cost for overestimation occurs when the ED model schedules more power in a generator than what is available from the source, necessitating the activation of another source to meet the demanded load, with the relationship
The analytical method primarily builds on the numerical integration model, which serves as the basis for cost estimation. The computational processing time of the numerical integration method is lengthy due to the complexity of the established equation or model. However, the proposed UCF significantly reduces processing time while also improving result accuracy.
3.3.1. Solar Case
Regarding the penalty cost due to underestimation, for the solar case, we have two scenarios in the analytical formulations.
The first scenario occurs when WRc is greater than the scheduled power of the solar panel (WPV,s). Substituting Equation (12) associated with condition A into (3) forms the analytical expression for the underestimation part “A” (20). As a result, Equation (23) is expressed as follows:
It is possible to use the variable change theorem for integrals as follows:
The integral limits for the variable change integral can be defined as follows:
By solving the integrals through the error function identities of Appendix A, the expected value of the cost function in terms of the limits σ1 and σ2 is obtained:
The second case is associated with condition B, where WRc is less than Ws. The analytical expression for the underestimate part “B” involves substituting Equation (14) into (2), as shown in the following expression:
It is possible to use the variable change theorem for integrals as follows:
The integral limits for the variable change integral can be defined as follows:
By solving the integrals through the error function identities of Appendix A, the expected value of the cost function in terms of the limits σ3 and σ4 is obtained:
Similar to the penalty cost due to underestimation, the penalty cost due to overestimation also presents two cases in the analytical formulations. The first case is when WRc is greater than Ws. Substituting Equation (12) associated with condition A into Equation (3) forms the analytical expression for the overestimation part “A”. As a result, Equation (28) is expressed as follows:
The second case is associated with condition B, where WRc is less than Ws. The analytical expression for the overestimate part “B” involves substituting Equation (14) into (3), as shown in the following expression (29):
3.3.2. Wind Case
The penalty cost due to underestimation for the wind case is derived from Equation (19), resulting in the following analytical expression (30):
The penalty cost due to overestimation is derived from Equation (18). The analytical expression is given by Equation (31):
4. Simulation and Validation for Enhancing the Processing Time in UCF
The simulation and validation process compares three different methodologies for estimating the uncertainty cost associated with solar and wind energy generation. The Monte Carlo simulation generates approximately one million random scenarios of solar irradiance and wind speed using the log-normal distribution and the Weibull distribution, respectively. These scenarios are then used to estimate the generated power Wav,i and compare it with the scheduled power set by the operator. In this MC simulation process, the costs due to underestimation (CO) and overestimation (CU) of the generated power are calculated.
The expected cost of uncertainty for both underestimation and overestimation cases can be estimated using numerical integrals through the numerical integration method (NIM). This involves using lambda (λ) and beta (β) functions of the log-normal distribution for the solar case, and shape (k) and scale (c) factors for the wind case, to demonstrate the probability density functions (PDFs) for both cases. The calculation is based on the UCF model applying the probability function for each case and integrating the equation within specified limits.
The selected parameters for the log-normal distribution of solar irradiance (λ = 6, β = 0.25) are grounded in empirical measurements and established conventions within the literature. The logarithmic mean (λ = 6, corresponding to a median irradiance of ~403 W/m2) reflects typical conditions at mid-latitudes, as documented in reference studies for photovoltaic systems [11,13]. This value aligns with some standards for the PV system performance assessment [13]. The logarithmic standard deviation (β = 0.25) constrains dispersion to capture diurnal and seasonal variability while preventing physically unrealistic irradiance values (>1200 W/m2), as demonstrated by hourly distribution analyses in [4,17]. This parameter combination achieves an optimal balance between physical realism and computational tractability, enabling the derivation of precise analytical UCFs [19,20,21,22,23] without compromising climatic representativeness.
Additionally, the analytical method estimates the expected cost of uncertainty using analytical formulas for both underestimation and overestimation. Finally, the algorithm code displays histograms to visualize the distribution (log-normal and Weibull), the available generated power, and the costs associated with both methods, underestimation, and overestimation.
The main objective of this paper is to show the difference in computational processing time for each method. The processing time results (Table 4, Table 5 and Table 6 for the solar case and Table 8, Table 9 and Table 10 for the wind case) display the costs and processing times for different scheduled powers for the established cases. Table 2, Table 3, and Table 7 present the initial parameters for the solar and wind cases, respectively.
4.1. UCF for Solar Case
The following results are a comparison of the costs and processing times for the power levels of 15, 40, and 60 MW across the different methods used.

Table 2.
Solar Parameters’ settings.
Table 2.
Solar Parameters’ settings.
| Variable 1 | Quantify | Value |
|---|---|---|
| WPVr | Power rated pv | 65 MW |
| Gstd | Irradiance standard | 1000 W/m2 |
| Rc | Irradiance | 150 W/m2 |
| Wmax | Maximum power pv | 100 MW |
1 The parameters may vary depending on the desired adjustment of the probability curve. The cost values fluctuate according to the operator’s criteria. Other parameters are included for practicality in the analysis.

Table 3.
Economic parameters’ settings.
Table 3.
Economic parameters’ settings.
| Variable 1 | Quantify | Value |
|---|---|---|
| λ | Media = μ | 6 |
| Β | Deviation standard = σ | 0.25 |
| Cu | Cost of underestimation | $30 |
| Co | Cost of overestimation | $70 |
1 The parameters may vary depending on the desired adjustment of the probability curve. The cost values fluctuate according to the operator’s criteria. Other parameters are included for practicality in the analysis.

Table 4.
Cost and elapsed time for WPV,s = 15 MW.
Table 4.
Cost and elapsed time for WPV,s = 15 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 363.3898 | 4.652178 | 441.61 × 103 |
| Integral Method | 363.1972 | 0.007402 | 602.8 |
| Analytical Method | 363.1972 | 0.001053 | 0 (baseline) |

Table 5.
Cost and elapsed time for WPV,s = 40 MW.
Table 5.
Cost and elapsed time for WPV,s = 40 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 927.4409 | 4.656728 | 442.13 × 103 |
| Integral Method | 926.8113 | 0.005475 | 419.8 |
| Analytical Method | 926.8113 | 0.000869 | 0 (baseline) |

Table 6.
Cost and elapsed time for WPV,s = 60 MW.
Table 6.
Cost and elapsed time for WPV,s = 60 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 2.3065 × 103 | 4.651972 | 441.68 × 103 |
| Integral Method | 2.3063 × 103 | 0.005523 | 527.2 |
| Analytical Method | 2.3063 × 103 | 0.000878 | 0 (baseline) |
Solar irradiation, power, and costs for underestimation–overestimation are shown in Figure 1.
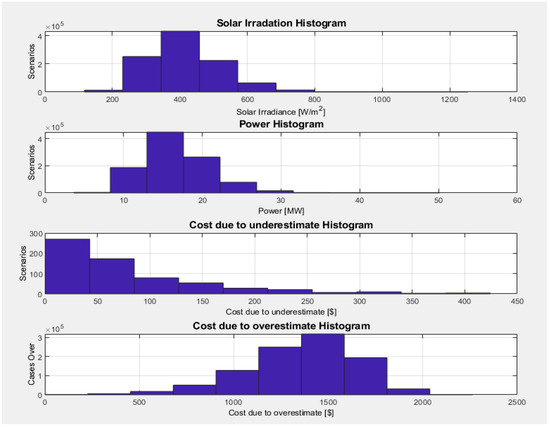
Figure 1.
Histogram of solar case.
4.2. UCF for Wind Case
The following results are a comparison of the costs and processing times for the power levels of 10, 80, and 150 MW across the different methods used.

Table 7.
Parameters’ settings.
Table 7.
Parameters’ settings.
| Variable 1 | Quantify | Value |
|---|---|---|
| Vi | Cut-in speed | 5 m/s |
| Vr | Rated speed | 15 m/s |
| Vo | Cut-out speed | 45 m/s |
| Wr | Rated power | 150 MW |
| A | Linear coefficient | 15 MW/m/s |
| B | Linear coefficient | −75 MW |
| Sg | Scale parameter Rayleigh distribution | 16 |
| C | Scale factor | |
| K | Scale shape | 2 |
| N | Number of simulations | 100,000 |
| CU | Cost of underestimation | 30 $/MW |
| CO | Cost of overestimation | 70 $/MW |
1 The parameters may vary depending on the desired adjustment of the probability curve. The cost values fluctuate according to the operator’s criteria. Other parameters are included for practicality in the analysis.

Table 8.
Cost and elapsed time for Ws = 10 MW.
Table 8.
Cost and elapsed time for Ws = 10 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 3.3550 × 103 | 0.548882 | 84.75 × 103 |
| Integral Method | 3.3522 × 103 | 0.026638 | 4018 |
| Analytical Method | 3.3522 × 103 | 0.000647 | 0 (baseline) |

Table 9.
Cost and elapsed time for Ws = 80 MW.
Table 9.
Cost and elapsed time for Ws = 80 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 2.2242 × 103 | 0.559076 | 86.85 × 103 |
| Integral Method | 2.2252 × 103 | 0.025671 | 3892 |
| Analytical Method | 2.2252 × 103 | 0.000643 | 0 (baseline) |

Table 10.
Cost and elapsed time for Ws = 150 MW.
Table 10.
Cost and elapsed time for Ws = 150 MW.
| Method | Cost in $ | Elapsed Time in Seconds | % Error |
|---|---|---|---|
| Monte Carlo Simulation | 2.1653 × 103 | 0.554730 | 86.7 × 103 |
| Integral Method | 2.1492 × 103 | 0.023300 | 3546 |
| Analytical Method | 2.1492 × 103 | 0.000639 | 0 (baseline) |
The results demonstrate that the Monte Carlo method exhibits significant computational time variability (441,612–442,130% slower for solar; 84,757–86,856% slower for wind) compared to the analytical approach, while maintaining cost estimation errors below 0.1% for both energy sources. This consistent accuracy despite computational inefficiency reinforces its reliability as a benchmark for validating faster methods. While unsuitable for real-time applications, it remains valuable for offline studies prioritizing precision over speed.
The wind speed, power, and costs for underestimation–overestimation are shown in Figure 2.
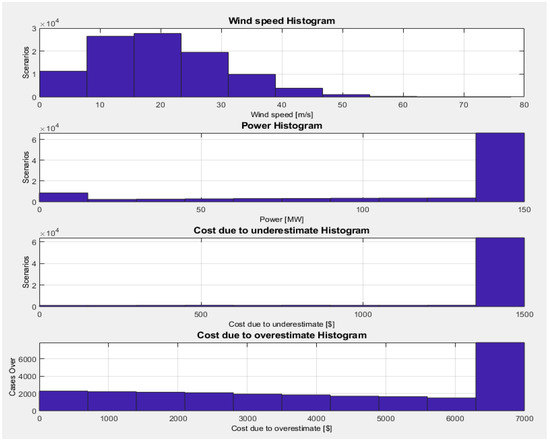
Figure 2.
Histogram of wind case.
Figure 3 presents a histogram of total uncertainty cost functions, by adding the overestimation and underestimation parts.
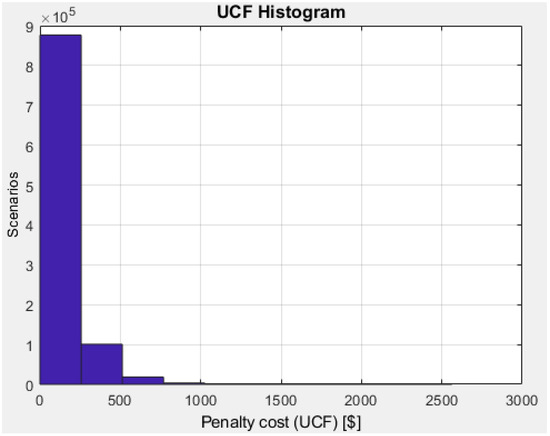
Figure 3.
UCF histogram.
The comparison of the results obtained (previous tables) between the proposed methods (MC simulation, numerical integration method, and analytical method) shows the precision of the expected costs of uncertainty and the notable reduction in processing time. It must be considered that these times and values are only part of the calculation of the uncertainty cost of each renewable source, and not the total calculation of the analysis (UCQ).
5. Simulation and Validation for Enhancing the Processing Time in UCQ Using the AGE-MODE Method
The main objective of this study is to quantify the uncertainty costs associated with various renewable energy sources exhibiting this behavior, with the goal being optimization through the minimization of total costs. The simulations were conducted using MATLAB R2020b, supported by the Matpower toolbox, to perform power flow calculations and compute the fitness function value for all candidate solutions in the initial population.
This section discusses multi-objective optimal power flow based on renewable energy sources, using an optimization algorithm to calculate the lowest operational cost of generation. This optimization is associated with various objectives related to environmental management and the main electrical system, particularly due to the integration of renewable energy sources.
The base case is derived from a multi-objective optimal power flow of a thermal-wind-solar power system, utilizing adaptive geometry estimation-based multi-objective differential evolution (AGE-MODE) [4]. The proposed methodology establishes a predictive modeling approach for wind and photovoltaic power generation outputs using Weibull and log-normal probability distribution functions, respectively. Through extensive case studies, the research examines multiple optimization scenarios incorporating combinations of two, three, and four objective functions. The generation cost structure for these renewable energy sources incorporates direct operational costs along with financial considerations for estimation errors, including penalty costs associated with power underestimation and reserve costs required for overestimation scenarios. This comprehensive cost framework provides a robust foundation for an economic analysis of renewable energy integration in modern power systems. The results are highly favorable for the analysis of multi-objective optimization costs in systems incorporating non-conventional energy sources. However, the computational time required is extensive, primarily due to the large number of objectives and the methods employed (Monte Carlo simulation and numerical integration) for calculating power generated by renewable sources. These methods significantly increase the complexity of the problem and demand more computational time to define the optimal front. To address computational processing time limitations, analytical methods have been proposed, as demonstrated in [11], which develop analytical formulations for uncertainty penalty and reserve costs associated with solar and wind energy generation, as well as electric vehicle integration, through mathematical expected value derivation. These formulations incorporate probability distribution functions (PDFs) of primary energy sources, with analytical validity confirmed via Monte Carlo simulation verification.
Demonstration, Simulation, and Validation
The referenced article [4] employs the numerical integration method and Monte Carlo simulations to calculate wind and solar generation, respectively. The complexity or modeling of these methods impacts the processing time for system evaluation.
The results shown in Table 11, using the analytical method [11], demonstrate that the proposed approach significantly reduces calculation time, allowing for more accurate conclusions regarding the system’s efficiency and viability for real-time or near-real-time applications. These results also show that the analytical method reduces certain outcomes as the number of objectives increases, while still maintaining optimal values for costs, emissions, losses, and voltages, and achieving adequate computational speed.

Table 11.
Comparison of times with the proposed methods.
The proposed analysis framework is based on a combination of multi-objective optimization, uncertainty cost functions, and an efficient algorithm to manage the uncertainties inherent in renewable energy sources, aiming to improve the optimization of power flow in thermo–wind–solar energy systems. In [4], the expression for solar generation, originally based on a Monte Carlo simulation, is replaced with analytical expressions through uncertainty cost functions addressing both overestimation and underestimation for solar energy. Similarly, the numerical integral method for wind generation is substituted with uncertainty cost functions for the overestimation and underestimation of wind energy. This approach resolves computational challenges, accelerates calculations, and provides a clearer understanding of how the system responds under various circumstances.
In [4], which handles eight multi-objective study cases, the first four are related to the IEEE-30bus system and the rest to the IEEE-57bus system. Cases 1 and 2 analyze the costs of energy generation, together with CO2 emissions and power losses, respectively, in the 30-bus system. The same occurs with cases 5 and 6 with respect to the 57-bus system. Cases 3, 4, 7, and 8, with their respective study systems, address the objectives of generation costs, CO2 emissions, losses, and voltage deviations. Table 12 shows a comparison of the results from case 1 in the IEEE-30 bus system between the methods used in [4] and the analytical method proposed in this paper, derived from the study in [11].

Table 12.
Comparison of results of methods used in [4] and analytical method for IEEE-30bus system case 1.
Figure 4 illustrates the relationship between emission costs, measured in tons per hour, and the operational costs of the involved sources (case 1) in the IEEE-30 bus system. Figure 4a presents the results from the study in [4], which applies the Monte Carlo simulation and numerical integration methods. In contrast, Figure 4b displays the values obtained using the analytical method from [11].
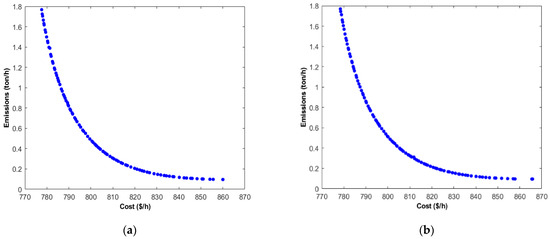
Figure 4.
Pareto front for case 1 of the IEEE-30 bus system obtained by the following: (a) MC simulation and numerical integration method; (b) analytical method.
Table 12 presents a comparison of all system objectives in relation to the applied method. The first column shows the results obtained for each objective using the methods established in [4], while the second column represents the final values obtained using the method indicated in [11]. However, columns 3 and 4 display results for the entire process when applying the analytical method exclusively to a single renewable source. The similarity between the values in the first and fourth columns demonstrates that the Monte Carlo simulation method is more time-consuming and less precise than the numerical integration or analytical methods. The use of analytical methods shows a reduction in computational time for the second and fourth columns, with the Monte Carlo simulation being the method causing delays in the scheduling process.
The same applies when using the analytical method for the IEEE-57 bus system.
Table 13
presents the simulation results for the system, while
Figure 5
illustrates the Pareto front in relation to the objectives of operational cost, gas emissions’ cost, power losses’ cost in transmission lines, and voltage variation (case 8).

Table 13.
Comparison of results of methods used in [4] and analytical method for IEEE-57 bus system case 1.
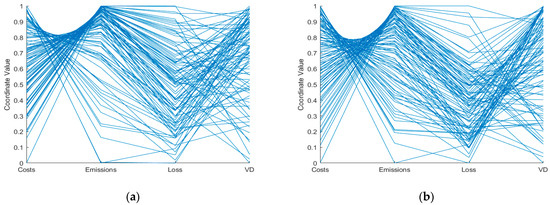
Figure 5.
Pareto front for case 8 of the IEEE-57 bus system obtained by the following: (a) MC simulation and numerical integration method; (b) analytical method.
6. Conclusions
In this paper, three methods were compared to achieve results in terms of processing time with minimal cost. To this end, the algorithm code compares the three methodologies by calculating the expected cost of uncertainty. These methods include the Monte Carlo simulation method, the numerical integration method, and the analytical method.
A multi-objective approach has been introduced that incorporates the uncertainty cost functions for solar and wind generation, along with a brief definition for optimal power flows in thermo–solar–wind energy systems. The latter addresses the calculation process time and the unpredictability of renewable energy supply. A tolerable method has been proposed that, despite increasing objectives, offers a significant advantage over traditional systems by calculating process duration, simulations, and method validations. The streamlined method enhances model resolution based on its tractability and simple cost of uncertainty by combining uniform probability functions that generate quadratic-shaped functions for solar and wind generation. Furthermore, the effectiveness and profitability of the proposed approach are demonstrated, providing more precise and reliable energy flow optimization through the analytical method in a thermo–solar–wind energy system. This offers invaluable insights into viable approaches for optimal energy flow in renewable energy systems, including the management of thermal, wind, and solar power systems for system durability and sustainability efforts and performance enhancement.
Author Contributions
Conceptualization, L.C.P.G. and S.R.R.R.; methodology, L.C.P.G. and S.R.R.R.; software, L.C.P.G.; validation, L.C.P.G., S.R.R.R. and G.I.-O.; formal analysis, L.C.P.G., S.R.R.R. and G.I.-O.; investigation, S.R.R.R.; resources, L.C.P.G. and S.R.R.R.; data curation, L.C.P.G. and S.R.R.R.; writing—original draft preparation, L.C.P.G. and S.R.R.R.; writing—review and editing, L.C.P.G., S.R.R.R. and G.I.-O.; visualization, L.C.P.G.; supervision, S.R.R.R. and G.I.-O.; project administration, S.R.R.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author(s).
Conflicts of Interest
The authors have no conflicts of interest to declare that are relevant to the content of this article.
Appendix A. Error Function Identities
References
- Reyes, E.; Bretas, A.; Rivera, S. Marginal Uncertainty Cost Functions for Solar Photovoltaic, Wind Energy, Hydro Generators, and Plug-In Electric Vehicles. Energies 2020, 13, 6375. [Google Scholar] [CrossRef]
- Leon, L.; Bretas, A.; Rivera, S. Quadratically Constrained Quadratic Programming Formulation of Contingency Constrained Optimal Power Flow with Photovoltaic Generation. Energies 2020, 13, 3310. [Google Scholar] [CrossRef]
- Bernal-Rubiano, J.; Neira, J.; Rivera, S. Mathematical Uncertainty Cost Functions for Controllable Photo-Voltaic Generators considering Uniform Distributions. WSEAS Trans. Math. 2019, 18, 137–142. [Google Scholar]
- Huy, T.H.B.; Thanh, H.D.; Vo, D.; Lee, K.; Kim, D. Multi-objective optimal power flow of thermal-wind-solar power system using an adaptive geometry estimation based multi-objective differential evolution. Appl. Soft Comput. 2023, 149, 110977. [Google Scholar] [CrossRef]
- Hertlein, T.A.; Mladenovic, I.; Weindl, C. A Novel Approach for the Grid-Serving Implementation of Charging Infrastructures and Their Techno-Economic Integration in the Existing Power Grid. Energies 2025, 18, 431. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Long, Z.; Chen, Y. A Novel Dual-Scale Deep Belief Network Method for Daily Urban Water Demand Forecasting. Energies 2018, 11, 1068. [Google Scholar] [CrossRef]
- Lopez Alzate, Y.; Gómez-Luna, E.; Vasquez, J.C. Innovative Microgrid Services and Applications in Electric Grids: Enhancing Energy Management and Grid Integration. Energies 2024, 17, 5567. [Google Scholar] [CrossRef]
- De Oliveira-De Jesus, P.M.; Yusta, J.M. Optimal Power Dispatch for Maximum Energy Community Welfare by Considering Closed Distribution Systems and Renewable Sources. Energies 2024, 17, 4707. [Google Scholar] [CrossRef]
- Molina, F.; Pérez, S.; Rivera, S. Uncertainty Cost Function Formulation in Small Hydropower Plants Inside a Microgrid. Ing. USBMed 2017, 8, 29–36. [Google Scholar] [CrossRef]
- Dai, L.; Ye, R.; You, D.; Yin, X. Security-Constrained Multi-Stage Robust Dynamic Economic Dispatch with Bulk Storage. Energies 2025, 18, 1073. [Google Scholar] [CrossRef]
- Bonilla, J.A.; Santos, F.; Rivera, S. Uncertainty cost functions for solar photovoltaic generation, wind energy generation, and plug-in electric vehicles: Mathematical expected value and verification by Monte Carlo simulation. Int. J. Power Energy Convers. 2019, 10, 171–207. [Google Scholar] [CrossRef] [PubMed]
- Hamideh, B.; Akond, M. Optimal operation of energy storage to minimize wind spillage and mitigate wind power forecast errors. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016. [Google Scholar]
- Barati, M.; Mohammadi, M. Uncertainty Quantification in Renewable Energy Systems: A Review. Renew. Sustain. Energy Rev. 2019, 107, 412–428. [Google Scholar]
- Liu, Y.; Wang, H. Quantification of Uncertainties in Wind Power Generation: A Review. IEEE Trans. Sustain. Energy 2019, 10, 227–236. [Google Scholar]
- Botterud, M.; Wang, J.B. Uncertainty Quantification in Solar Power Forecasting: A Review. Sol. Energy 2019, 185, 452–467. [Google Scholar]
- Zadeh, S.; Soares, A. Uncertainty Quantification in Photovoltaic Power Forecasting: Challenges and Opportunities. IEEE Trans. Sustain. Energy 2018, 9, 1294–1303. [Google Scholar]
- Romero, R.J.; Georgilakis, P.S. Probabilistic Assessment of Renewable Energy Sources: A Comprehensive Review. Renew. Energy 2018, 126, 594–611. [Google Scholar]
- Zhang, H.; Li, Y. Quantifying Uncertainties in Biomass Energy Production: A Survey. Bioresour. Technol. 2019, 273, 647–656. [Google Scholar]
- Pereira, L.M.C.; Palomino, A.L.P.L.M. Uncertainty Quantification in Geothermal Energy Production: Challenges and Solutions. Geothermics 2020, 87, 101770. [Google Scholar]
- Petrucelli, M.S.; Catalão, J.P.S. Uncertainty in Wave Energy Resource Assessment: A Review. Ocean Eng. 2018, 159, 107–118. [Google Scholar]
- Chang, Z.; Liu, X.; Zhang, Q.; Zhang, Y.; Wang, Z.; Zhang, Y.; Li, W. Consideration of Wind-Solar Uncertainty and V2G Mode of Electric Vehicles in Bi-Level Optimization Scheduling of Microgrids. Energies 2025, 18, 823. [Google Scholar] [CrossRef]
- Garcia-Guarin, J.; Alvarez, D.; Bretas, A.; Rivera, S. Schedule Optimization in a Smart Microgrid Considering Demand Response Constraints. Energies 2020, 13, 4567. [Google Scholar] [CrossRef]
- Rodriguez-Gil, J.A.; Mojica-Nava, E.; Vargas-Medina, D.; Arevalo-Castiblanco, M.F.; Cortes, C.A.; Rivera, S.; Cortes-Romero, J. Energy management system in networked microgrids: An overview. Energy Syst. 2024. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).