Advances in Illumination of Lengthy Road Tunnels by Means of Innovative Vaulting and Sustainable Control of Flicker Perturbations
Abstract
1. Introduction
2. The Flicker Effect
3. Materials and Methods: Several Proposals to Avoid the Flicker Effect in Tunnels and Very Long Underground Roads (VLURs)
- (1)
- Decrease of the luminance required inside the tunnel through interventions in the portal surroundings, like forestation or introduction of scaled surfaces, to reflect the sunlight out of the L20 cone from the approaching drivers’ eyes. This decrease results in less emitted flux and lower contrasts between light cones and darker areas, contributing to the elimination of the flicker effect.
- (2)
- Installation of continuous stripes of LED along the whole tunnel or underground road, as shown in Figure 3. These stripes can be placed at least in the interior zone where the flicker effect is more prone to buildup. Although the intensity emitted by these relatively new products is much lower than that emitted by classical high-pressure sodium projectors, the luminance on the road can be enough to fulfill the requests in this zone, even at the nighttime level.
- (3)
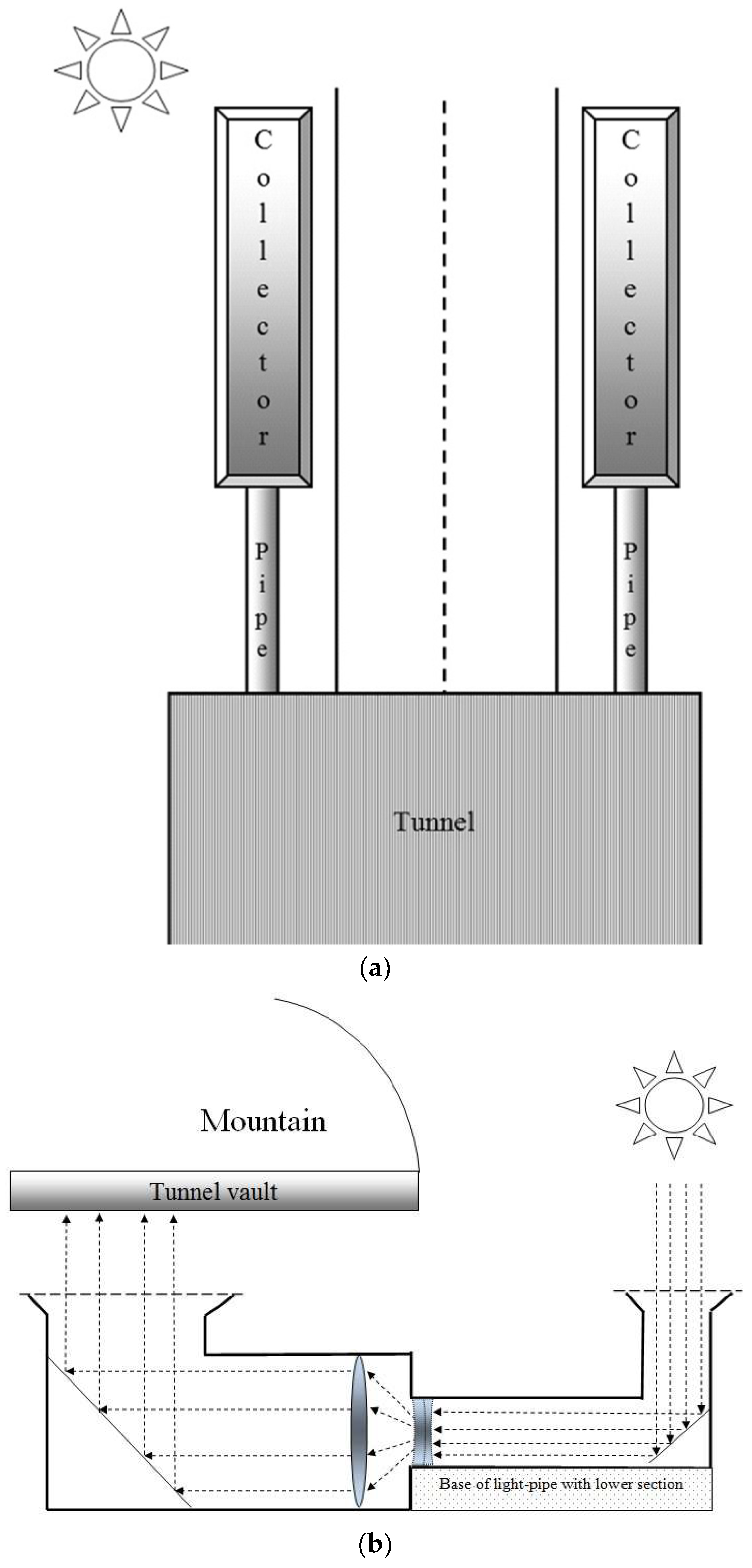
- Supplementing sunlight to the electrical lighting. Although most strategies using sunlight in road tunnels are designed to achieve a good visual adaptation when entering the threshold zone, some of them could be useful in the interior zone to achieve better uniformity.
- -
- The lower chamber of the light-pipes on the ground and shoulders of the road.
- -
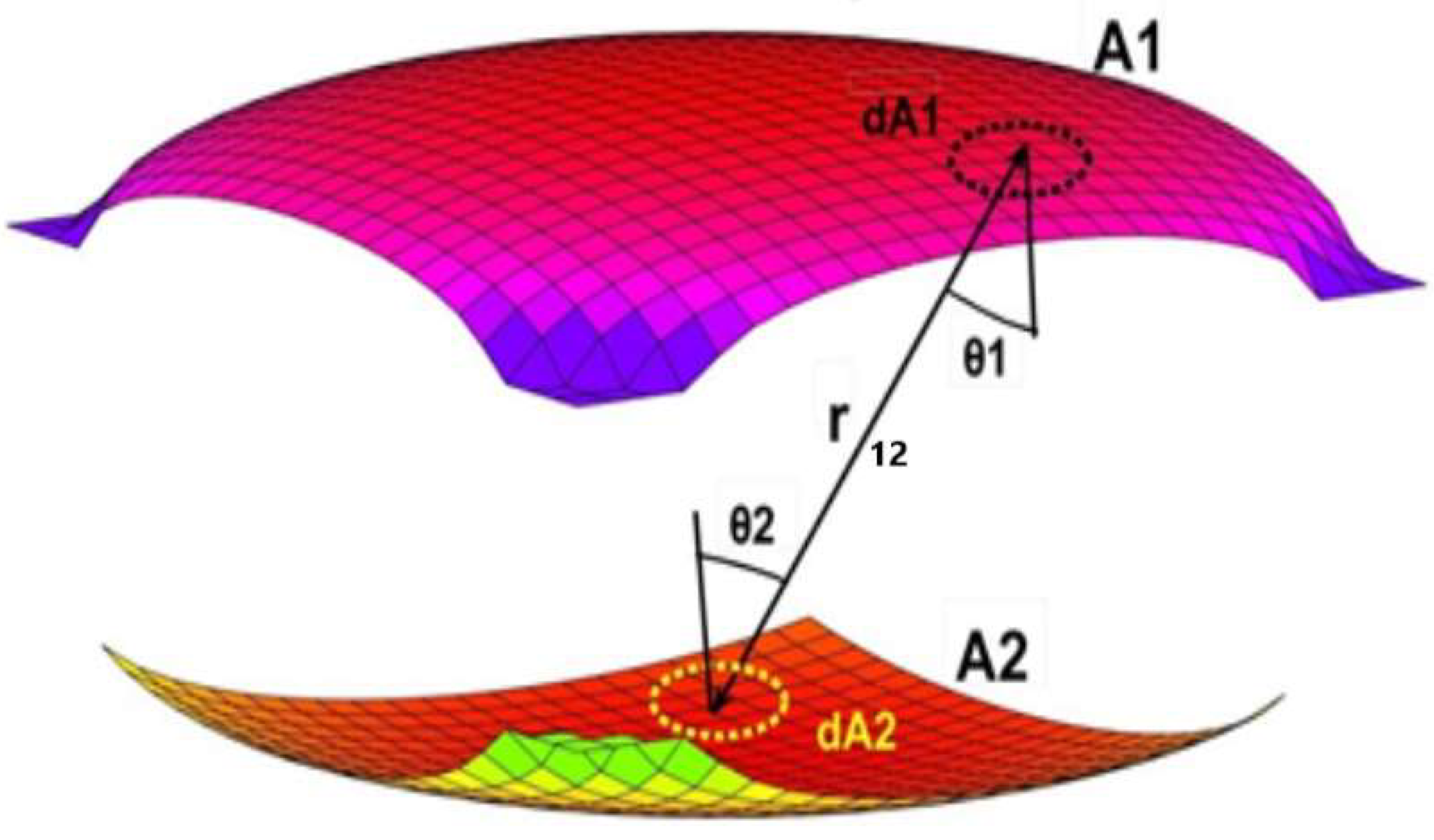
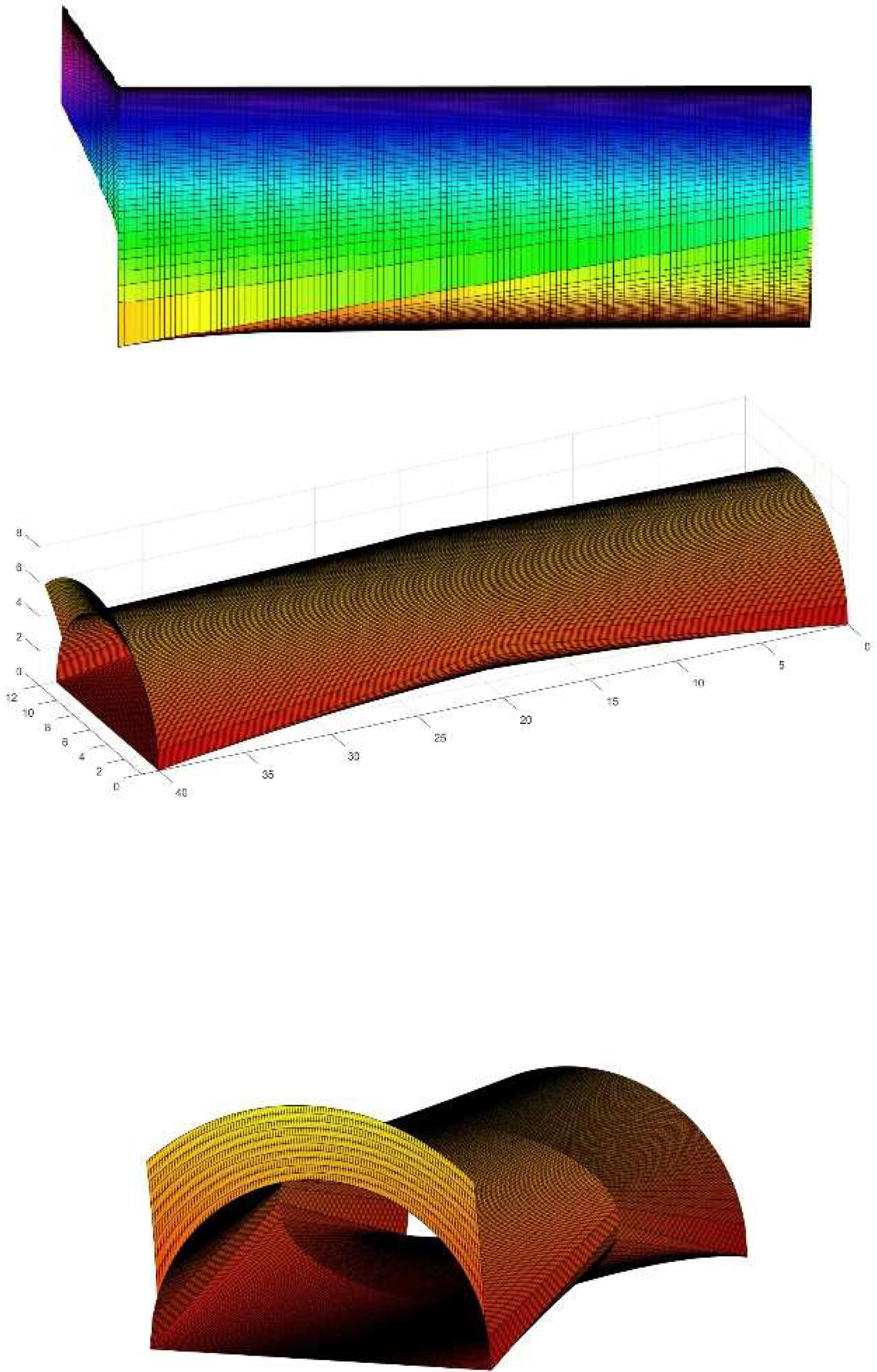
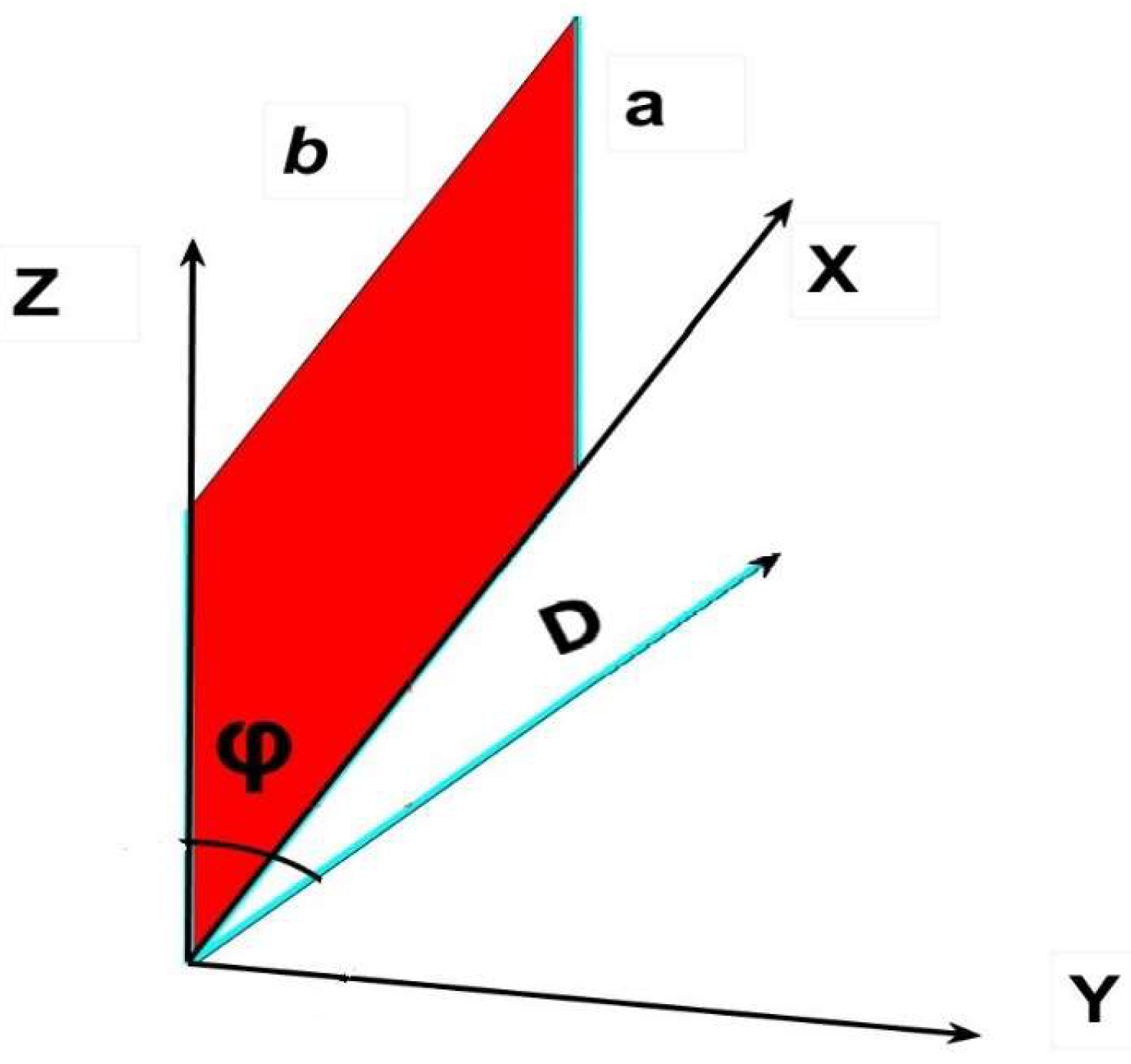
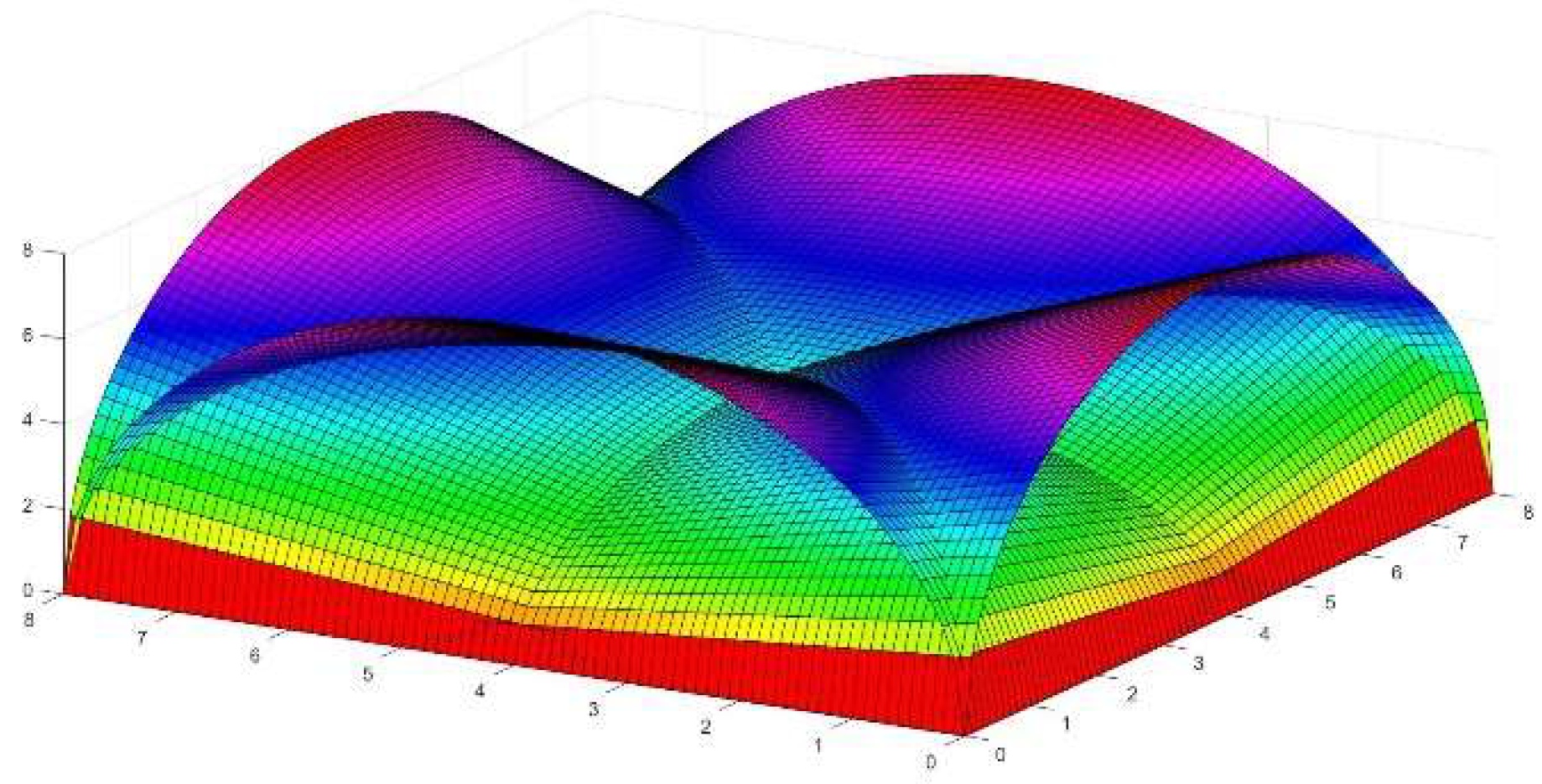
- The construction of a complex-shaped vault of camber geometry with sufficient capacity to reflect and diffuse the solar flux transported by the light-pipes homogeneously on the pavement.
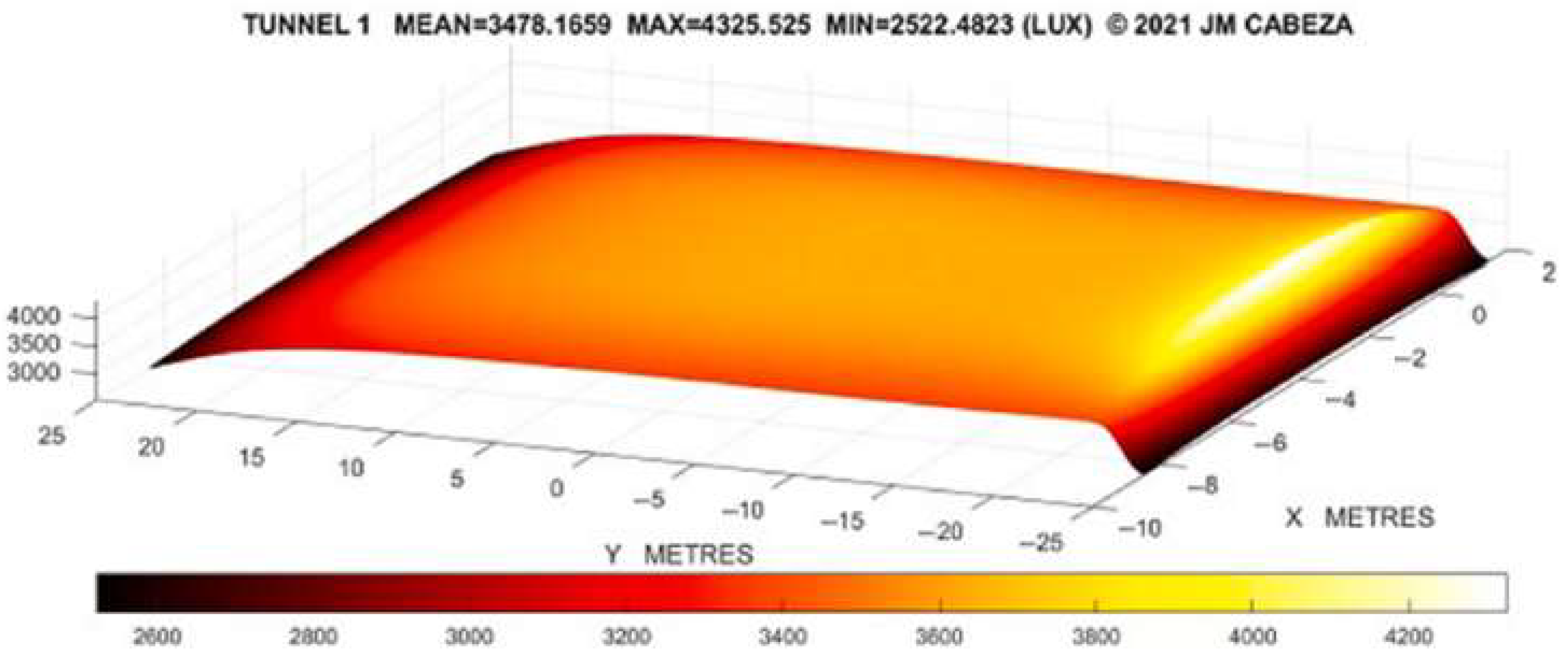
4. Discussion and Early Results
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Amundsen, F.H.; Ranes, G. Studies on traffic accidents in Norwegian road tunnels. Tunn. Undergr. Space Technol. 2000, 15, 3–11. [Google Scholar] [CrossRef]
- Caliendo, C.; De Guglielmo, M.L. Accident Rates in Road Tunnels and Social Cost Evaluation. Procedia Soc. Behav. Sci. 2012, 53, 166–177. [Google Scholar] [CrossRef]
- Danishmal, M.; Zainullah, S. Investigating the Importance of Tunnel Lighting and its Role in Reducing Traffic Accidents. Acad. J. Res. Sci. Publ. 2021, 3, 39–57. [Google Scholar] [CrossRef]
- Li, Z.; Xing, G.; Zhao, X.; Li, H. Impact of the connected vehicle environment on tunnel entrance zone. Accid. Anal. Prev. 2021, 157, 106145. [Google Scholar] [CrossRef] [PubMed]
- Commission Internationale de l’Éclairage (CIE). Guide for the Lighting of Road Tunnels and Underpasses; CIE Publications: Vienna, Austria, 2004; p. 88. [Google Scholar]
- Gil-Martín, L.M.; Espín-Estrella, A.; Aznar-Dols, F. Energy saving in road tunnels by means of transparent tension structures. In Proceedings of the International Conference on Renewable Energies and Power Quality (ICREPQ’10), Granada, Spain, 23–25 March 2010. [Google Scholar]
- Larue, G.S.; Rakotonirainy, A.; Pettitt, A.N. Driving performance impairments due to hypovigilance on monotonous roads. Accid. Anal. Prev. 2011, 43, 2037–2046. [Google Scholar] [CrossRef] [PubMed]
- Qin, X.; Zhang, N.; Zhang, W.; Meitner, M. How does tunnel interior color environment influence driving behavior? Quantitative analysis and assessment experiment. Tunn. Undergr. Space Technol. 2020, 98, 103320. [Google Scholar] [CrossRef]
- Miller, E.E.; Boyle, L.N. Driver behavior in road tunnels: Association with driver stress and performance. Transp. Res. Rec. 2015, 2518, 60–67. [Google Scholar] [CrossRef]
- Flø, M.; Jenssen, G.D. Drivers’ perception of long tunnels. Studies from the Quinling Shongnan Tunnel in China as well as the Lærdal tunnel and the World longest subsea tunnel (Rogfast) in Norway. In Proceedings of the 4th International Conference-Traffic and Safety in Road Tunnels, Hamburg, Germany, 25–27 April 2007. [Google Scholar]
- Chen, P.; Chen, F.; Zhang, L.; Ma, X.; Pan, X. Examining the influence of decorated sidewaall in road tunnels using fMRI technology. Tunn. Undergr. Space Technol. 2020, 99, 103362. [Google Scholar] [CrossRef]
- Sasaki, K. View factor of a spheroid and an ellipse from a plate element. J. Quant. Spectrosc. Radiat. Transf. 2024, 326, 109102. [Google Scholar] [CrossRef]
- Schröder, P.; Hanrahan, P. On the Form Factor between Two Polygons. In SIGGRAPH ‘93: Proceedings of the 20th Annual Conference on Computer Graphics and Interactive Techniques; ACM Press: New York, NY, USA, 1993; pp. 163–164. [Google Scholar] [CrossRef]
- Camaraza-Medina, Y.; Hernandez-Guerrero, A.; Luviano-Ortiz, J.L. View factor for radiative heat transfer calculations between triangular geometries with common edge. J. Therm. Anal. Calorim. 2023, 148, 4523–4539. [Google Scholar] [CrossRef]
- Commission Internationale de l’Éclairage. ILV: International Lighting Vocabulary; CIE Publications: Vienna, Austria, 2011; S017/E:2015. [Google Scholar]
- Howell, J.R. A Catalogue of Radiation Heat Transfer Configuration Factors. Factor C-43b. Available online: http://www.thermalradiation.net/sectionc/C-43b.html (accessed on 10 August 2024).
- Howell, J.R. A Catalogue, Factor C-140b. Available online: http://www.thermalradiation.net/sectionc/C-140b.html (accessed on 10 August 2024).
- Iacomussi, P.; Radis, M.; Rossi, G. Flicker effects in tunnel lighting. In Proceedings of the CIE 2017 Midterm Meetings and Conference on Smarter Lighting for Better Life, Jeju, Republic of Korea, 10–13 October 2018; pp. 641–648. [Google Scholar]
- Gil-Martín, L.; Peña-García, A.; Hernández-Montes, E.; Espín-Estrella, A. Tension structures: A way towards sustainable lighting in road tunnels. Tunn. Undergr. Space Technol. 2011, 26, 223–227. [Google Scholar] [CrossRef]
- Peña-García, A.; Gil-Martín, L.-M.; Escribano, R.; Espín-Estrella, A. A Scale Model of Tension Structures in Road Tunnels to Optimize the Use of Solar Light for Energy Saving. Int. J. Photoenergy 2011, 2011, 9. [Google Scholar] [CrossRef]
- Peña-García, A.; Escribano, R.; Gil-Martín, L.; Espín-Estrella, A. Computational optimization of semi-transparent tension structures for the use of solar light in road tunnels. Tunn. Undergr. Space Technol. 2012, 32, 127–131. [Google Scholar] [CrossRef]
- Gil-Martín, L.M. Study of pergolas for energy savings in road tunnels. Comparison with tension structures. Tunn. Undergr. Space Technol. 2013, 35, 172–177. [Google Scholar] [CrossRef]
- Gil-Martín, L.; Gómez-Guzmán, A.; Peña-García, A.M. Use of diffusers materials to improve the homogeneity of sunlight under pergolas installed in road tunnels portals for energy savings. Tunn. Undergr. Space Technol. 2015, 48, 123–128. [Google Scholar] [CrossRef]
- Peña-García, A.; Gil-Martín, L.M.; Rabaza, O. Application of translucent concrete for lighting purposes in civil infrastructures and its optical characterization. Key Eng. Mater. 2015, 663, 148–156. [Google Scholar] [CrossRef]
- Salam, A.O.A.; Mezher, K.A. Energy saving in tunnels lighting using shading structures. In Proceedings of the 2014 International Renewable and Sustainable Energy Conference (IRSEC), Ouarzazate, Morocco, 17–19 October 2014; pp. 519–524. [Google Scholar]
- Ramswamy, G.S. Design and Construction of Concrete Shell Roofs; CBS Publishers & Distributors: New Delhi, India, 2005. [Google Scholar]
- Drakou, D.; Burattini, C.; Bisegna, F.; Gugliermetti, F. Study of a daylight “filter”zone in tunnels. In Proceedings of the IEEE 15th International Conference on Environment and Electrical Engineering (EEEIC), Rome, Italy, 10–13 June 2015; pp. 649–652. [Google Scholar]
- Saraiva, L.; Martzloff, J.C.; Baldini, J.; Dhombres, J. História Das Ciências Matemáticas: Portugal e o Oriente—History of Mathematical Sciences: Portugal and East Asia; Fundação Oriente: Lisboa, Portugal, 2000. [Google Scholar]
- Grayson, J.H. Korea: A Religious History; Routledge Curzon: London, UK, 2002; ISBN 0-7007-1605-X. [Google Scholar]
- Kerr, A.; Sokol, A.K. Another Kyoto; Penguin Press: New York, NY, USA, 2018; ISBN 978-0141988337. [Google Scholar]
- Bunko, T. Memoirs of the Research Department of the Toyo Bunko (the Oriental Library); Publications-Toyo Bunko. Ser. B.; Toyo Bunko: Tokyo, Japan, 1926. [Google Scholar]
- Drakou, D.; Celucci, L.; Burattini, C.; Nardecchia, F.; Gugliermetti, F. Study for optimizing the daylight “filter” in a pre-tunnel structure. In Proceedings of the IEEE 16th International Conference on Environment and Electrical Engineering (EEEIC), Florence, Italy, 7–10 June 2016; p. 4. [Google Scholar]
- Drakou, D.; Burattini, C.; Mangione, A.; Bisegna, F. Exploring the daylight simulation of filter panels in a pre-tunnel structure. In Proceedings of the 2017 IEEE International Conference on Environment and Electrical Engineering and 2017 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Milan, Italy, 6–9 June 2017; pp. 1–5. [Google Scholar]
- Cantisani, G.; D’Andrea, A.; Moretti, L. Natural lighting of road pre-tunnels: A methodology to assess the luminance on the pavement—Part I. Tunn. Undergr. Space Technol. 2018, 73, 37–47. [Google Scholar] [CrossRef]
- Cantisani, G.; D’ANdrea, A.; Moretti, L. Natural lighting of road pre-tunnels: A methodology to assess the luminance on the pavement—Part II. Tunn. Undergr. Space Technol. 2018, 73, 170–178. [Google Scholar] [CrossRef]
- Doganoff, I. Berechnung Von Kugelschalen Über Rechteckigem Grundriss: Mit Berechnungsdiagrammen; Mitteilungen aus dem Institut für Massivbau Hannover; Werner: Düsseldorf, Germany, 1962. [Google Scholar]
- Gil-Martín, L.; Peña-García, A.M.; Jiménez, A.; Hernández-Montes, E. Study of light-pipes for the use of sunlight in road tunnels: From a scale model to real tunnels. Tunn. Undergr. Space Technol. 2014, 41, 82–87. [Google Scholar] [CrossRef]
- Peña-García, A.M.; Gil-Martín, L.; Hernández-Montes, E. Use of sunlight in road tunnels: An approach to the improvement of light-pipes’ efficacy through heliostats. Tunn. Undergr. Space Technol. 2016, 60, 135–140. [Google Scholar] [CrossRef]
- Peña-García, A.; Cabeza-Lainez, J. Daylighting of road tunnels through external ground-based light-pipes and complex reflective geometry. Tunn. Undergr. Space Technol. 2023, 131, 104788. [Google Scholar] [CrossRef]
- Qin, X.; Zhang, X.; Qi, S.; Han, H. Design of Solar optical fiber lighting system for enhanced lighting in highway tunnel threshold zone: A case study of Huashuyan tunnel in China. Int. J. Photoenergy 2015, 2015, 10. [Google Scholar] [CrossRef]
- Perdahci, C.; Sogodok, Y. Comparative study of solar optical fibre and electrical light for daylighting in tunnel threshold zone. Light Eng. 2021, 29, 95–101. [Google Scholar] [CrossRef] [PubMed]
- Peña-García, A. The SLT equation: A tool to predict and evaluate energy savings in road tunnels with sunlight systems. Tunn. Undergr. Space Technol. 2017, 64, 43–50. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J. Architectural Characteristics of Different Configurations Based on New Geometric Determinations for the Conoid. Buildings 2022, 12, 10. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J. A New Principle for Building Simulation of Radiative Heat Transfer in the Presence of Spherical Surfaces. Buildings 2023, 13, 1447. [Google Scholar] [CrossRef]
- Doganoff, I.; Hoffmann, C.; Rühle, H. Shell and Fold Structure Roofs out of Precast, Pre-Stressed Reinforced Concrete Elements; Nixe Verlag: Düsseldorf, Germany, 1964. [Google Scholar]
- Andujar, F.S.; Rodriguez-Cunill, I.; Cabeza-Lainez, J.M. The Problem of Lighting in Underground Domes, Vaults, and Tunnel-Like Structures of Antiquity; An Application to the Sustainability of Prominent Asian Heritage (India, Korea, China). Sustainability 2019, 11, 5865. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J. Innovative Tool to Determine Radiative Heat Transfer Inside Spherical Segments. Appl. Sci. 2023, 13, 8251. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, T.; Qi, F. A correction method for calculating sky view factor in urban canyons using fisheye images. Build. Environ. 2024, 262, 111834. [Google Scholar] [CrossRef]
- Gomez-Gil, A.; Cabeza-Lainez, J. Ferrer House at Rocafort, an Early Case of Brise-Soleil’s Design for the Mediterranean Region in Valencia. Designs 2024, 8, 96. [Google Scholar] [CrossRef]
- Cabeza-Lainez, J. New Geometric Theorems Derived from Integral Equations Applied to Radiative Transfer in Spherical Sectors and Circular Segments. Mathematics 2024, 12, 2875. [Google Scholar] [CrossRef]
- Cross, H. The Column Analogy. Univ. Ill. Bull. 1930, XXVIII. University of Illinois. Engineering Experiment Station. Bulletin No. 215. Available online: https://www.ideals.illinois.edu/items/5207 (accessed on 25 September 2022).
- Cabeza-Lainez, J.M.; Salguero-Andújar, F.; Rodríguez-Cunill, I. Prevention of Hazards Induced by a Radiation Fireball through Computational Geometry and Parametric Design. Mathematics 2022, 10, 387. [Google Scholar] [CrossRef]
- Rodríguez Cunill, M.I. Medio ambiente, videoinstalaciones y otras propuestas artísticas audiovisuales. In Medios de Comunicación y Medio Ambiente; Gutiérrez-SanMiguel; Miguel, B.G.S., Ed.; University of Salamanca: Salamanca, Spain, 2002; Available online: https://dialnet.unirioja.es/servlet/articulo?codigo=294636 (accessed on 19 December 2024).












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabeza-Lainez, J.; Peña-García, A. Advances in Illumination of Lengthy Road Tunnels by Means of Innovative Vaulting and Sustainable Control of Flicker Perturbations. Sustainability 2025, 17, 6680. https://doi.org/10.3390/su17156680
Cabeza-Lainez J, Peña-García A. Advances in Illumination of Lengthy Road Tunnels by Means of Innovative Vaulting and Sustainable Control of Flicker Perturbations. Sustainability. 2025; 17(15):6680. https://doi.org/10.3390/su17156680
Chicago/Turabian StyleCabeza-Lainez, Joseph, and Antonio Peña-García. 2025. "Advances in Illumination of Lengthy Road Tunnels by Means of Innovative Vaulting and Sustainable Control of Flicker Perturbations" Sustainability 17, no. 15: 6680. https://doi.org/10.3390/su17156680
APA StyleCabeza-Lainez, J., & Peña-García, A. (2025). Advances in Illumination of Lengthy Road Tunnels by Means of Innovative Vaulting and Sustainable Control of Flicker Perturbations. Sustainability, 17(15), 6680. https://doi.org/10.3390/su17156680






