The Application of Wind Power Prediction Based on the NGBoost–GRU Fusion Model in Traffic Renewable Energy System

Abstract

In the context of the “double carbon” goals and energy transformation, the integration of energy and transportation has emerged as a crucial trend in their coordinated development. Wind power prediction serves as the cornerstone technology for ensuring efficient operations within this integrated framework. This paper introduces a wind power prediction methodology based on an NGBoost–GRU fusion model and devises an innovative dynamic charging optimization strategy for electric vehicles (EVs) through deep collaboration. By integrating the dynamic feature extraction capabilities of GRU for time series data with the strengths of NGBoost in modeling nonlinear relationships and quantifying uncertainties, the proposed approach achieves enhanced performance. Specifically, the dual GRU fusion strategy effectively mitigates error accumulation and leverages spatial clustering to boost data homogeneity. These advancements collectively lead to a significant improvement in the prediction accuracy and reliability of wind power generation. Experiments on the dataset of a wind farm in Gansu Province demonstrate that the model achieves excellent performance, with an RMSE of 36.09 kW and an MAE of 29.96 kW at the 12 h prediction horizon. Based on this predictive capability, a “wind-power-charging collaborative optimization framework” is developed. This framework not only significantly enhances the local consumption rate of wind power but also effectively cuts users’ charging costs by approximately 18.7%, achieving a peak-shaving effect on grid load. As a result, it substantially improves the economic efficiency and stability of system operation. Overall, this study offers novel insights and robust support for optimizing the operation of integrated energy systems.

1. Introduction

Against the background of the “double carbon” goal and energy transformation, energy integration has become a key trend in the coordinated development of energy and transportation. Energy integration aims to break through the traditional boundaries of energy and transportation systems, achieving efficient energy utilization and low-carbon, intelligent development of transportation through integrated infrastructure and collaborative operation mechanisms. The rapid development of renewable energy power generation technologies, represented by wind power and photovoltaics, has provided crucial support for energy exchange integration. For instance, offshore wind power generation technology continues to make breakthroughs. New control methods, such as multi-model three-level fuzzy control based on the active rotating inertial actuator (ARID), can effectively address dynamic load challenges in complex marine environments and ensure stable wind power output [1]. In the transportation sector, the number of electric vehicles as a green travel carrier is steadily increasing. Research on relevant energy management strategies, such as adaptive energy management strategies based on micro-stroke identification for extended-range electric vehicles, has significantly improved fuel economy and energy efficiency [2]. The development of intelligent transportation systems has also driven the advancement of traffic data processing technologies. The synchronous spatio-temporal graph converter network can effectively model the non-local spatio-temporal relationships of traffic data, offering a novel solution for traffic flow prediction [3]. The multi-agent reinforcement learning framework provides a novel approach for achieving adaptive collaborative transportation systems [4]. Additionally, the trajectory prediction model that takes driving style into account enhances the accuracy of predicting target vehicle behavior in intelligent transportation scenarios [5]. The Hybrid Renewable Energy System (HRES), which combines photovoltaic (PV) systems and battery energy storage systems, is commonly used in remote areas. It significantly improves energy sustainability and reduces carbon dioxide emissions [6]. However, the high-cost investment and operational maintenance challenges impede its widespread adoption in these regions.

In offshore wind power, harsh natural conditions like ice loads severely threaten wind turbine structural fatigue reliability. Machine learning-based structural fatigue reliability assessment has enhanced efficiency, accuracy, and adaptability [7], but further exploration is needed for its engineering application. The 6G large-scale antenna system, despite theoretical advantages, faces limits in practical use due to hardware costs, energy use, and compatibility with current communication standards, hindering wide-scale deployment [8]. In power electronic equipment optimization, the improved modulation strategy of the single-phase three-level neutral-point-clamped converter cuts switching losses [9], but reliability and thermal management in high-power settings require more study to ensure long-term stable equipment operation. In wind turbine control, the pitch controller with robust cyclic shaping design boosts the wind turbine system’s stability and dynamic performance [10]. However, there is still room for enhancing adaptive control capabilities under complex wind conditions to further optimize energy capture efficiency and reduce load fluctuations. In target vehicle behavior prediction, the short-term lateral behavior reasoning architecture based on driver preview characteristics has improved prediction accuracy [11]. Nevertheless, prediction accuracy and real-time performance in multi-vehicle interaction scenarios need enhancement to meet the high safety requirements of autonomous driving systems.

The integration of energy and transportation aims to achieve deep integration and collaborative optimization of the two systems. Viewed from the energy supply side, wind power prediction technology is advancing continuously. The prediction method based on numerical weather prediction correction and adaptive spatio-temporal graph feature information fusion has greatly improved prediction accuracy and thus strongly supports power grid dispatching [12]. In the energy storage field, the robust energy storage planning method that takes extreme weather impacts into account (e.g., the ESS planning model in hurricane scenarios) enhances the grid’s disaster resistance and wind power integration efficiency [13]. From the traffic demand perspective, optimizing electric vehicle charging strategies is crucial for integration. By adopting intelligent energy management strategies (such as dynamic charging control based on wind power prediction), electric vehicles can be transformed into flexible grid-regulation resources. While satisfying travel needs, this also promotes renewable energy consumption and stable grid operation. Lidar data processing technology advances have bolstered the environmental perception capabilities of intelligent transportation systems. By leveraging rotating lidar data to jointly optimize scene flow estimation and moving target segmentation, the intelligence of automatic driving and traffic management has been enhanced [14]. Research on a synchronous information and power transmission system, which relies on magnetron modulation characteristics, offers a novel approach to integrating energy transmission and information communication. Its effectiveness has been confirmed through theoretical and numerical analysis [15]. In-ahead day power prediction for wind farm clusters, accuracy has been significantly improved by identifying the inherent predictable components of wind power and isolating interference components [16,17,18], introducing a new method for such predictions.

Although the above research has laid a solid technical foundation for the convergence of traffic and energy, there are still gaps in the synergistic optimization of wind power prediction and electric vehicle charging management, the seamlessness of system integration, and the broad practical applicability.

Wind power prediction is a key technology to support the efficient operation of the “transportation-energy integration” system. Its research progress mainly focuses on the physical model method [19,20], statistical learning method [21,22], and deep learning method [23,24]. Although the mechanism of numerical weather prediction (NWP) [25] is well-defined, its complex calculations make it difficult to respond to local meteorological disturbances in real time. Statistical learning methods, such as the Auto-regressive Moving Average Model (ARMA) [26] and Support Vector Machine (SVM) [27], have inherent limitations in capturing the strong non-stationarity and long-term time-series dependencies of wind power. In recent years, deep learning models have become mainstream due to their powerful feature extraction capabilities. For example, recurrent neural networks, represented by Long Short-Term Memory (LSTM) [28], can effectively model temporal dynamic features through their gating mechanisms. Among them, the Gated Recurrent Unit (GRU) [29] demonstrates remarkable engineering advantages in wind power time-series dynamic modeling due to its lightweight gating mechanism. In contrast, Convolutional Neural Networks (CNNs) [30] concentrate on extracting spatial meteorological features and have introduced improved attention-based models, such as Attention-GRU [31], to enhance short-term prediction accuracy. Furthermore, Transformer [32], with its self-attention mechanism, has emerged as a new research direction in time-series forecasting due to its growing advantages in handling long-sequence dependencies. Although Transformer overcomes long-term dependency modeling issues via its self-attention mechanism, it is constrained by computational complexity and local feature capture ability. To boost prediction robustness, ensemble learning methods like Extreme Gradient Boosting (XGBoost) [33] and Light Gradient Boosting Machine (LightGBM) [34] are widely applied. At the same time, probabilistic prediction models, such as NGBoost (Natural Gradient Boosting) [35], have drawn much attention due to their ability to quantify prediction uncertainty. However, existing research on integrating deep time-series models with probabilistic prediction methods still has notable deficiencies. Moreover, these studies also need to better address the rapid distribution drift of wind power data [36].

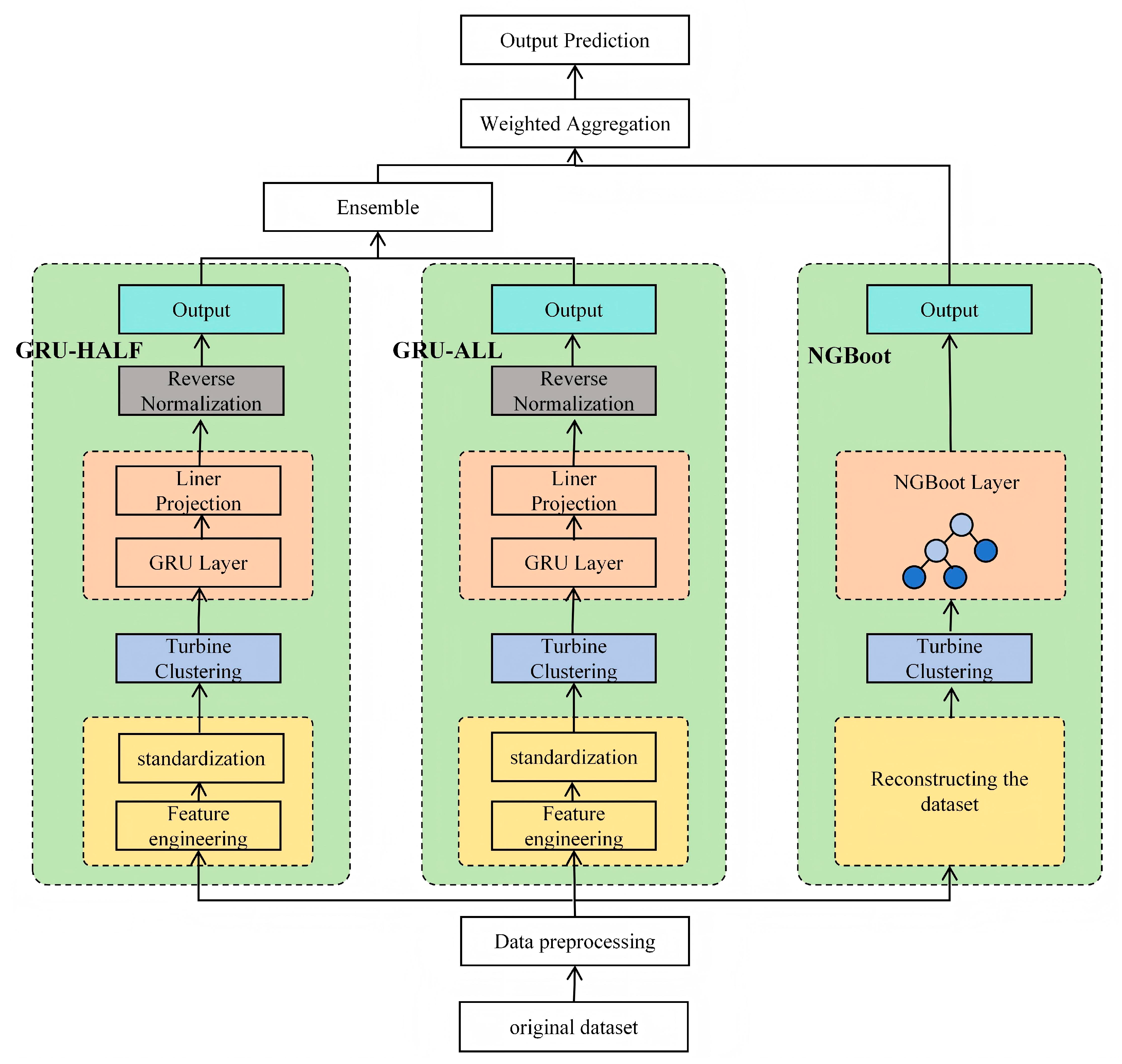
To address existing wind power prediction method deficiencies in deep fusion time-series dynamic modeling, probabilistic prediction, and adaptation to rapid data distribution drift, this paper proposes a wind power prediction method based on an NGBoost–GRU fusion model. It also designs a deeply coordinated dynamic charging optimization strategy for electric vehicles. The prediction model innovatively integrates the core advantages of the Gated Recurrent Unit (GRU) and Natural Gradient Boosting (NGBoost). With its efficient gating mechanism, GRU significantly enhances its ability to extract dynamic features of complex non-stationarity and long-term time-series dependence in wind power series. NGBoost robustly models the complex nonlinear relationships between input features and accurately quantifies predictive uncertainty through its conditional probability distribution-based gradient boosting framework. Unlike traditional prediction methods that depend on single physical models, statistical learning, or deep learning, this integration strategy not only enhances point prediction accuracy but also overcomes the intrinsic limitations of conventional deterministic prediction models in risk quantification. NGBoost equips the model with the capability to output a full probability distribution. The resulting prediction intervals (e.g., confidence intervals) dynamically mirror prediction reliability—narrow during stable periods and wide during volatile ones. This provides critical uncertainty quantification for downstream decisions like grid scheduling and charging strategy optimization, thus significantly boosting the system’s robustness against wind power fluctuations and distribution shifts. Our key contributions are as follows:

• A wind power collaborative forecasting model that integrates time-series modeling and probabilistic prediction is proposed. The model innovatively combines the advantages of GRU in capturing complex time-series dynamics and NGBoost in modeling nonlinear relationships and quantifying uncertainty. Through key technologies such as dual GRU fusion and spatial clustering, the model’s prediction accuracy and uncertainty quantification reliability are enhanced.
• An EV dynamic charging coordination strategy based on probabilistic forecasting has been designed. A “global-real-time” dual-mode optimization framework is constructed to deeply integrate wind power forecasts (point and interval estimates) with grid status (including electricity prices and constraints) and user demand. This ensures precise spatiotemporal matching between wind power and charging loads, thereby maximizing wind power utilization and achieving peak load shifting.
• The proposed strategy effectively balances system efficiency and economic interests by enhancing wind power utilization, reducing user charging costs, and alleviating grid peak-shaving pressures, thus maximizing energy efficiency and minimizing social and economic costs.

This paper is organized as follows: Section 2 details the wind power prediction method using the NGBoost–GRU fusion model and the electric vehicle dynamic charging strategy based on this prediction model. Section 3 validates the effectiveness and advantages of the proposed method through experiments. Section 4 deeply discusses the research results, analyzing the model’s strengths, potential applications, and future research directions. Section 5 summarizes the work and draws the research conclusions.

2. Methodology

2.1. Combinatorial Model Architecture

The core challenge of wind power prediction lies in simultaneously capturing the dynamic characteristics of time series (such as wind speed mutation and power fluctuation) and complex nonlinear relationships (such as the coupling effect of environmental variables and power), while quantifying prediction uncertainty to support power grid risk-based decision-making. To address these requirements, this paper proposes a novel probabilistic-time-series collaborative framework: the NGBoost–GRU fusion forecasting model. By integrating GRU’s time-series modeling capabilities and NGBoost’s probabilistic prediction advantages, the model achieves high-precision point prediction and dynamic uncertainty quantification. The architecture of the NGBoost–GRU fusion forecasting model is illustrated in Figure 1.

The combined model consists of an NGBoost probabilistic forecasting module and a GRU time-series modeling module. To more accurately capture the dynamic characteristics of wind power sequences and address the challenges of long-sequence predictions, we designed two GRU sub-models with different output lengths: GRU-Half focuses on predicting the first half of the target-length sequence, while GRU-ALL predicts the entire sequence. The core design replaces the first half of the GRU-ALL prediction results with those from GRU-Half. This leverages GRU-Half’s high-precision capture of the sequence’s initial short-term dynamics (e.g., the initial response to wind speed mutations). When GRU-ALL predicts long sequences, errors in the initial part of the sequence can easily accumulate and propagate backward, which may affect the overall prediction accuracy. By shortening the prediction range, GRU-Half can model the complex details of the sequence’s initial stage more intensively and accurately. The proposed replacement strategy effectively suppresses error accumulation in the first half of the sequence. At the same time, it retains GRU-ALL’s ability to capture the overall trend and long-term dependencies of the sequence. This approach enables the complementary integration of the two models’ advantages. In addition, due to the wake effect of adjacent wind turbines, similarities in power generation performance may occur, as shown in Figure 1. Before data is fed into the GRU network, a key step is added: cluster analysis based on the spatial location of the wind turbines. Wind turbines with similar power generation performance are grouped together, which significantly enhances the training set’s homogeneity. This allows the models trained for each group (including subsequent GRU-Half, GRU-ALL, and NGBoost) to focus on learning the group’s common and clearer power change patterns. It reduces noise from individual fan differences, thereby improving the model’s generalization ability and prediction accuracy. At the same time, Pearson correlation coefficient (PCC)-based feature selection becomes more targeted. For the NGBoost component, data preprocessing is also conducted. Through feature fusion (combining original environment/operating condition features, spatial information, and high-level temporal features extracted by GRU, etc.), new training data that better captures complex nonlinear relationships is generated for it. Finally, each wind turbine in the wind farm (or its cluster group) generates three models: NGBoost, GRU-Half, and GRU-ALL. The prediction results from NGBoost and the fusion-modified GRU sequence prediction (combining the first half of GRU-Half with the second half of GRU-ALL) are integrated via variable-weight combination to produce the final prediction output.

2.2. NGBoost Section

As a gradient boosting probability framework, the core of NGBoost (Natural Gradient Boosting) is to iteratively optimize the conditional probability distribution $P(y|x)$ through the addition model.

Different from the traditional point prediction model, NGBoost outputs the complete probability distribution, which provides the basis of uncertainty quantification for the dynamic scheduling of the power grid. Part of the NGBoost algorithm flow is shown in Figure 2. This module contains the following key processes.

2.2.1. Data Filling

Aiming at the problem of missing wind power data due to equipment maintenance and power grid regulation, a time-aware dynamic filling strategy is adopted [37]. Let the original dataset be $\mathcal{D}={\{(x_t,y_t)\}}_{t=1}^T$, where the feature vector $x_t\in {ℝ}^d$ (d-dimensional variable). For the missing value $x_{t,j}$ (the j-th feature at time t), based on the assumption of time continuity, a two-way exponential weighted interpolation is constructed:

$${\widehat{x}}_{t,j}={\displaystyle \frac{{\displaystyle \sum _{k=-L}^L{e}^{-\alpha |k|}}\cdot x_{t+k,j}}{{\displaystyle \sum _{k=-L}^L{e}^{-\alpha |k|}}}},$$

(1)

the window width $L$ ensures that the filling value reflects the local dynamic characteristics. The attenuation factor $\alpha$ makes the weight of adjacent data points higher, and avoids the non-physical jump of key variables such as wind speed and power.

2.2.2. Outlier Processing

The wind power anomaly is caused by extreme turbulence or sensor failure, which needs to be filtered by combining physical constraints and statistical criteria. First, the physical boundary constraints of the device are applied, as shown in

Table 1. Abnormal range of wind power parameters.

Characteristic Parameters	Anomaly Extension
Active power (Patv)	Patv ≤ 0
Wind speed (Wspd)	Wspd > 2.5
Pitch angle of blade 1 (Pad1)	Pab1 > 89°
The pitch angle of blade 2 (Pad2)	Pab2 > 89°
Pitch angle of blade 3 (Pad3)	Pab3 > 89°
Angle of yaw (Ndir)	Ndir > 720° or Ndir < −720°
Angle between wind direction and turbine position (Wdir)	Wdir > 180° or Wdir < −180°

:

Secondly, dynamic interquartile range (IQR) detection was used [38]. The robust quartile ${\widehat{Q}}_1,{\widehat{Q}}_3$ (based on Tukey’s double weight estimation) of the power series is calculated, and the boundary is adjusted in combination with the wind speed fluctuation:

$$\mathrm{UB}={\widehat{Q}}_3+2.5\cdot \mathrm{IQR}\cdot {\displaystyle \frac{{\sigma }_{t,\mathrm{Wspd}}}{{\overline{\sigma }}_{\mathrm{Wspd}}}},$$

(2)

where ${\sigma }_{t,\mathrm{Wspd}}$ is the standard deviation of wind speed at time $t$; ${\overline{\sigma }}_{\mathrm{Wspd}}$ is the global standard deviation.

This design allows the boundary to adaptively expand by 20–40%during turbulent periods. Finally, the local outlier factor (LOF) is used to detect the anomaly of the feature space: for the sub-clusters after DBSCAN clustering, the samples with LOF > 3 (defined as ${\mathrm{LOF}}_k={\displaystyle \frac{1}{|N_k|}}{\displaystyle \sum _{o\in N_k}\frac{\mathrm{lrd}(o)}{\mathrm{lrd}(k)}}$, where the local reachable density ${\mathrm{LOF}}_k={\displaystyle \frac{1}{|N_k|}}{\displaystyle \sum _{o\in N_k}\frac{\mathrm{lrd}(o)}{\mathrm{lrd}(k)}}$) are removed.

2.2.3. Feature Reconstruction

To fully leverage and enhance the information in wind power data and boost the prediction model’s ability to learn wind power variation patterns, we reconstruct the original features. A series of new features reflecting the sequence’s local statistical characteristics is constructed. Specifically, rolling mean, maximum, minimum, and standard deviation are created based on historical sequence data. This strengthens the model’s capacity to capture wind power’s dynamic changes.

For a given time series $x_i$, where $i$ is the first data point $i$ in the time series, we define a rolling window of length $w$ to calculate the following characteristics:

Rolling average (${\mu }_t$): The rolling average at the time point $t$ is used to reflect the central trend of the sequence in the local window. The calculation formula is:

$${\mu }_t={\displaystyle \frac{1}{w}}{\displaystyle \sum _{i=t-w+1}^t{x}_i},$$

(3)

where $w$ denotes the length of the scrolling window; $t$ denotes the current time point.

The rolling average makes it easier for the model to capture long-term trends by smoothing short-term fluctuations.

The rolling maximum (${\max }_t$): The rolling maximum at the time point T is used to highlight the highest value of the sequence in the window. The calculation formula is:

$${\max }_t=\max (x_{t-w+1},x_{t-w+2},\dots ,x_t)$$

(4)

This feature provides the upper bound information of the data range for the model, which helps to perceive the abnormal peak of the data.

The rolling minimum (${\min }_t$): The rolling minimum of $t$ at the time point is used to highlight the minimum value of the sequence in the window. The calculation formula is:

$${\min }_t=\min (x_{t-w+1},x_{t-w+2},\dots ,x_t)$$

(5)

This feature provides the lower bound information of the data range for the model, which helps to perceive the abnormal trough of the data.

Rolling standard deviation (${\sigma }_t$): The rolling standard deviation at the time point $t$ is used to quantify the degree of data dispersion of the sequence in the window. The calculation formula is:

$${\sigma }_t=\sqrt{{\displaystyle \frac{1}{w}}{\displaystyle \sum _{i=t-w+1}^t{(x_i-{\mu }_t)}^2}}$$

(6)

The standard deviation enables the model to assess data stability, with larger values indicating higher volatility.

These new features offer the model a more comprehensive view of sequence information, enhancing its ability to accurately predict wind power trends. By providing diverse feature space perspectives, they help the model better grasp the intrinsic patterns of wind power data, thereby improving prediction performance.

2.2.4. K-Means Clustering Based on Spatial Location

This paper employs a clustering method based on the spatial location of wind turbines, which proves more effective than clustering based on the statistical correlation of power series. Its core advantage stems from the inherent physical characteristics of wind farms. Specifically, the geographical location of a wind turbine directly determines its comprehensive influence from topography, local meteorological conditions (like wind speed profiles and turbulence intensity), and the wake effect of adjacent turbines. Wind turbines in close spatial proximity often experience similar micro-meteorological environments, leading to highly spatially homogeneous power fluctuation patterns. In contrast, correlation-based clustering methods (such as those using the Pearson correlation coefficient) are vulnerable to short-term random fluctuations or measurement noise. They might group turbines with large spatial distances but occasional statistical similarities into one category. Such grouping overlooks the real physical spatial connections and shared environmental drivers between turbines, weakening the model’s ability to capture key meteorological dynamics with spatial continuity. Spatial clustering ensures that turbines in the same cluster share a real-world physical environment through geographical proximity. This significantly enhances the homogeneity of training data and the generalization performance of the model.

The K-means clustering method is chosen primarily for its computational efficiency and suitability for large-scale engineering problems. By minimizing the sum of squared Euclidean distances from samples to their cluster centers, it efficiently converges and generates compactly distributed wind turbine groups. Its near-linear computational complexity makes it ideal for processing large-scale wind farm position data. Moreover, K-means’ hard clustering feature provides clear boundaries for spatial clusters, facilitating subsequent independent model training (e.g., NGBoost and GRU) for each cluster. This strategy enables customized modeling of unique meteorological features in different regions, reduces interference from mixed regional features, and improves prediction accuracy with low computational overhead.

The spatial position information of the wind turbine is an important factor affecting the wind power change mode. Through K-means clustering based on spatial location [39], wind turbines with similar power generation characteristics can be grouped to improve the training efficiency and prediction accuracy of the model. The K-means clustering method is selected mainly based on its computational efficiency and applicability to large-scale engineering problems. Firstly, we represent the spatial position of each fan as a two-dimensional coordinate $(x_i,y_i)$, and construct a position matrix $L={[(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)]}^{\top }$ (where $N$ is the number of fans).

The goal of the K-means algorithm is to divide the fan into $K$ clusters, so that the position difference of the fan in the cluster is minimized and the difference between the clusters is maximized. Specifically, we achieve clustering by minimizing the following objective function:

$${\min }_{\{C_1,C_2,\dots ,C_K\}}{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{i\in C_k}\Vert (}}{x}_i,y_i)-{\mu }_k{\Vert }^2,$$

(7)

where $C_k$ denotes the $k$-th cluster; ${\mu }_k$ is the center coordinate of the $k$ cluster (i.e., the mean value of the position of the fan in the cluster).

In the clustering process, we initialize $K$ random center points and continuously adjust the cluster allocation and center position through iterative optimization. For each fan $i$, calculate its distance to the center of each cluster:

$$d_{ik}=\Vert (x_i,y_i)-{\mu }_k\Vert$$

(8)

The fan $i$ is assigned to the nearest $C_k$ cluster. Then, update the center position of each cluster:

$${\mu }_k={\displaystyle \frac{1}{|C_k|}}{\displaystyle \sum _{i\in C_k}(x_i,y_i)}$$

(9)

Repeat this process until cluster assignments stabilize or the maximum iterations are reached. Each turbine is then assigned to a specific cluster $C_k$. This spatial-location-based clustering ensures that turbines in the same cluster have similar generation patterns, enhancing training data homogeneity and prediction accuracy. The clustering results also offer a basis for subsequent feature selection and model training, boosting the model’s adaptability to complex wind farm environments.

2.2.5. Probabilistic Modeling and Optimization

The core of the NGBoost module is to achieve uncertainty quantification and high-precision point prediction through probability modeling. We first define the conditional probability distribution $P(Y|X)$ of the target variable $Y$ (i.e., wind power), where $X$ is the input feature vector. NGBoost iteratively optimizes the conditional probability distribution through the addition model, and its basic form is:

$$P(Y|X)={\displaystyle \prod _{i=1}^{n}P}(Y_i|X_i;{\theta }_i),$$

(10)

where ${\theta }_i$ is the model parameter.

In order to optimize the model parameters, we use the maximum likelihood estimation (MLE) method to maximize the log-likelihood function:

$$\mathcal{L}(\theta )={\displaystyle \sum _{i=1}^n\log }P(Y_i|X_i;{\theta }_i)$$

(11)

In NGBoost, the parameter update is achieved by the natural gradient descent method. The natural gradient is defined as:

$$G={\mathbb{E}}_{P(Y|X;\theta )}\left[{\nabla }_{\theta }\log P(Y|X;\theta )\right]$$

(12)

The parameter update formula is:

$${\theta }^{(t+1)}={\theta }^{(t)}+\eta G,$$

(13)

where $\eta$ is the learning rate and controls the step size.

In addition, in order to prevent overfitting and improve the generalization ability of the model, we introduce a regularization term in the optimization process. the optimization objective is:

$${\mathcal{L}}_{\mathrm{regularized}}(\theta )=\mathcal{L}(\theta )-\lambda \Vert \theta {\Vert }^2,$$

(14)

where $\lambda$ is the regularization strength, which balances the weights of the likelihood term and the regularization term.

Through the above probability modeling and optimization process, NGBoost can output a complete conditional probability distribution, which not only provides point prediction values (such as mean $\mu$), but also quantifies the uncertainty of prediction (such as variance ${\sigma }^2$).

2.3. GRU Section

Gated Recurrent Units (GRUs) are neural network structures designed for temporal data processing. They excel at capturing long-term dependencies and dynamic features in sequential data, making them crucial for modeling wind speed and power time-series variations in wind power prediction. The GRU workflow mainly includes feature engineering, normalization, and training optimization, as shown in Figure 3. Data preprocessing and clustering stages here are the same as those in the NGBoost component and will not be repeated.

2.3.1. Feature Engineering

In terms of feature engineering, this study uses the Pearson correlation coefficient [40] to assist feature screening, aiming to extract a feature set that is highly correlated with wind power, so as to enhance the input quality of the GRU model and improve the prediction accuracy. Specifically, we first calculate the Pearson correlation coefficient between each input feature (such as wind speed, wind direction, ambient temperature, etc.) and the target variable wind power. The formula is:

$$r_{x,y}={\displaystyle \frac{{\displaystyle \sum _{i=1}^n(x_i-\overline{x})}(y_i-\overline{y})}{\sqrt{{\displaystyle \sum _{i=1}^n{(x_i-\overline{x})}^2}}\sqrt{{\displaystyle \sum _{i=1}^n{(y_i-\overline{y})}^2}}}},$$

(15)

where $x$ denotes the input feature; $x$ is wind power; $\overline{x}$ and $\overline{y}$ are the mean values of $x$ and $y$, respectively.

By setting the correlation threshold, the features with significant linear correlation with wind power are screened out, and the redundant or irrelevant features are eliminated, thereby reducing the input dimension, so that GRU can focus more on the learning of key information, avoid the noise interference caused by invalid features, and improve the training efficiency and final prediction performance of the model.

2.3.2. Standardization

In order to ensure that the input data of the GRU model has the appropriate scale, facilitates the optimal training of the network, and accelerates the convergence, this study uses Z-score to standardize the filtered feature data. The Z-score standardized formula is:

$$x^{\prime }={\displaystyle \frac{x-\mu }{\sigma }},$$

(16)

where $x$ is the original data point; $\mu$ represents the mean value of the feature data; $\sigma$ is the standard deviation.

After normalization, each feature has a zero-mean, unit-variance distribution. This standardization allows for comparison and learning across features with different dimensions and ranges on a unified scale. It enhances GRU’s sensitivity and feature discrimination, setting a solid foundation for time-series modeling.

2.3.3. Training Optimization

For GRU training optimization, this study designs two sub-models, GRU-ALL and GRU-Half, to address long-sequence prediction challenges. Both use an encoder–decoder structure for precise sequence prediction, as shown in Figure 4. The encoder extracts and encodes input-sequence features, mapping temporal information to a fixed-dimensional hidden state. The decoder then predicts the target-sequence output using this hidden state.

For the GRU-ALL model, the goal is to predict the wind power sequence of the entire target length. The input sequence is F, and the encoder converts it into a hidden state sequence SS. The decoder generates a prediction sequence RGRTE based on D, where EER represents the full length of the target prediction sequence.

For the GRU-ALL model, the goal is to predict the wind power sequence of the entire target length. The input sequence is $X=[x_1,x_2,\dots ,x_T]$, and the encoder converts it into a hidden state sequence $H=[h_1,h_2,\dots ,h_T]$. The decoder generates a prediction sequence ${\widehat{Y}}_{ALL}=[{\widehat{y}}_1^{ALL},{\widehat{y}}_2^{ALL},\dots ,{\widehat{y}}_L^{ALL}]$ based on $H$, where $L$ represents the full length of the target prediction sequence.

The GRU-Half model focuses on predicting the first half of the target length sequence. Under the same input sequence $X$, the encoder also generates a hidden state sequence $X$, but the decoder only generates the first half of the prediction sequence ${\widehat{Y}}_{Half}=[{\widehat{y}}_1^{Half},{\widehat{y}}_2^{Half},\dots ,{\widehat{y}}_{L/2}^{Half}]$ at this time, that is, the prediction sequence length is $L/2$.

In the practical application of the replacement strategy, the prediction result ${\widehat{Y}}_{Half}$ of GRU-Half is replaced by the first half of the prediction result $[{\widehat{y}}_1^{ALL},{\widehat{y}}_2^{ALL},\dots ,{\widehat{y}}_{L/2}^{ALL}]$ of GRU-ALL, forming the final prediction sequence ${\widehat{Y}}_{Final}=[{\widehat{Y}}_{Half},{\widehat{Y}}_{ALL}^{\mathrm{latter}\mathrm{part}}]$ after fusion, where ${\widehat{Y}}_{ALL}^{\mathrm{latter}\mathrm{part}}=[{\widehat{y}}_{L/2+1}^{ALL},\dots ,{\widehat{y}}_L^{ALL}]$. This approach integrates GRU-Half’s high-precision capture of short-term sequence dynamics with GRU-ALL’s ability to grasp overall trends and long-term dependencies. It effectively suppresses error accumulation in long-sequence predictions, optimizes prediction performance, and enables the model to handle wind power’s complex time-series characteristics more accurately. This enhances prediction stability and reliability.

2.4. Weighted Integration

In order to realize the robustness optimization of the prediction results, this model adopts the dynamic weighted integration strategy to adaptively fuse the NGBoost probability prediction output ${\widehat{y}}_N^{(t)}$ and the fusion modified GRU sequence prediction ${\tilde{y}}_G^{(t)}$. Based on the principle of prediction timeliness attenuation, the weight function of time step $t$ ($t=1,2,\dots ,T$) is defined: the weight of GRU correction sequence ${\tilde{y}}_G^{(t)}$ decreases exponentially with the increase in $t$, while the weight of NGBoost point prediction ${\widehat{y}}_N^{(t)}$ corresponds to increasing $w_G^{(t)}=\exp \left(-\lambda t\right)$, where the attenuation coefficient $\lambda$ is determined by verification set optimization.

The final predicted value is fused by weighted average:

$${\widehat{y}}^{(t)}=\underset{\mathrm{GRU}\mathrm{weight}}{\underbrace{\exp \left(-\lambda t\right)}}\cdot {\tilde{y}}_G^{(t)}+\underset{\mathrm{NGBoost}\mathrm{weight}}{\underbrace{\left(1-\exp \left(-\lambda t\right)\right)}}\cdot {\widehat{y}}_N^{(t)}$$

(17)

The design embodies the timing-probability coordination mechanism: in the initial stage of the sequence (when $t$ is small), $\exp \left(-\lambda t\right)\approx 1$ makes GRU dominate the prediction, making full use of its high-precision capture ability for short-term dynamics such as wind speed mutations; as the prediction time increases ($t$ increases), $1-\exp \left(-\lambda t\right)\to 1$ transitions to NGBoost dominance, giving full play to its robust modeling advantages for complex nonlinear relationships such as coupling effects of environmental variables. The $\lambda$ weight coefficient is optimized by minimizing the weighted average absolute error of the validation set:

$${\lambda }^{*}=\underset{\lambda }{\mathrm{argmin}}{\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T\left|\exp \left(-\lambda t\right)\cdot {\tilde{y}}_G^{(t)}+\left(1-\exp \left(-\lambda t\right)\right)\cdot {\widehat{y}}_N^{(t)}-y_{\mathrm{true}}^{(t)}\right|}$$

(18)

2.5. Wind-Power-Charging Collaborative Optimization Framework

This paper designs a comprehensive three-tier wind-power-charging collaborative optimization framework (Figure 5) based on the NGBoost–GRU fusion model’s wind power prediction capabilities. The NGBoost–GRU fusion model underpins both global and real-time optimization strategies within this framework. At the input level, it supplies high-precision wind power point forecasts (expected trajectories) and confidence intervals for uncertainty quantification. Along with real-time grid status (e.g., electricity prices, network constraints) and user requirements (e.g., charging time windows, power limits), these outputs inform optimization decision-making.

Specifically, the NGBoost–GRU fusion model supports global optimal scheduling (offline) based on mixed-integer linear programming (MILP) by providing a 24 h ahead wind power point prediction sequence. This lays a data foundation for solving cost-optimal day-ahead charging plans. Its prediction accuracy directly determines the economic viability of the plan and the potential for wind power consumption. In the real-time optimization control (online) phase, the model enables dynamic decision-making by rolling out the latest short-term point predictions and key confidence intervals. The confidence interval is central to improving decision-making accuracy. During stable periods with high prediction confidence (narrow interval), the system can aggressively use wind power and trigger high-power charging (e.g., when real-time electricity prices are below dynamic thresholds and predicted output is sufficient). This maximizes wind power consumption and cost savings. When prediction uncertainty surges (evidenced by a significantly widened interval), such as during extreme weather or rapid system-state changes, the confidence interval effectively warns of potential prediction deviations. It triggers risk-aversion mechanisms (e.g., reducing charging power, delaying non-emergency charging, or activating backup plans). This mitigates potential grid impacts and ensures system safety and stability. The optimization layer’s dual-mode decision-making mechanism, together with the output layer’s execution system, achieves three goals: smoothing the grid load curve, maximizing wind power consumption, and saving user costs. This is carried out by precisely matching wind power output, grid status, and user demand. The NGBoost–GRU fusion model’s precise point prediction and uncertainty quantification (confidence interval) are central to supporting the framework’s global optimization foresight and real-time control robustness. The framework’s implementation and engineering application will be analyzed in depth from three aspects: objective function, constraint condition, and optimization strategy design.

2.5.1. Objective Function (Minimizing Total Charging Cost)

The charging cost function is defined as the difference between the grid electricity purchase cost and wind power sales revenue. Electricity price fluctuations affect the purchase cost, while sales revenue depends on wind power output and real-time electricity prices. By optimizing the charging strategy, the system maximizes wind power utilization, meets charging demands, reduces overall charging costs, and achieves a balance between economic and environmental benefits.

The calculation formulas for electricity purchase cost and sales revenue are as follows:

$$\mathrm{Total}\mathrm{Cos}\mathrm{t}={\displaystyle \sum _{t=1}^T\left(P_{\mathrm{charge},t}\cdot C_{\mathrm{grid},t}-P_{\mathrm{wind},t}\cdot C_{\mathrm{wind},t}\right)}\cdot \Delta t,$$

(19)

where $P_{\mathrm{charge},t}$ is the charging power (kW) of period $t$; $P_{\mathrm{wind},t}$ is the wind power prediction value (kW) of the period $t$; $C_{\mathrm{grid},t}$ is the grid electricity price (yuan/kWh) of the time period $t$; $C_{\mathrm{wind},t}$ is wind power feed-in tariff (yuan/kWh); $\Delta t$ is the time interval (hours); $T$ is the total number of optimized periods.

2.5.2. Constraint Conditions

Charging power constraint: The charging power cannot exceed the maximum charging power of the electric vehicle.

$$0\le P_{\mathrm{charge},t}\le P_{\max },$$

(20)

where $P_{\max }$ is the maximum charging power of the electric vehicle.

Charging power constraint: Charging power must meet the needs of users.

$${\displaystyle \sum _{t=1}^T{P}_{\mathrm{charge},t}}\cdot \Delta t\ge E_{\mathrm{demand}},$$

(21)

where $E_{\mathrm{demand}}$ is the user’s charging demand (kWh).

Grid power balance constraint: The total power output of the grid must be equal to the total power demand.

$$P_{\mathrm{grid},t}=P_{\mathrm{load},t}+P_{\mathrm{charge},t}-P_{\mathrm{wind},t},$$

(22)

where $P_{\mathrm{grid},t}$ is the output power of the grid; $P_{\mathrm{load},t}$ is other load power.

2.5.3. Optimization Strategy Design

• Global optimization strategy (offline scheduling)

For a given complete prediction sequence, solve the global optimization problem:

$$\min {\displaystyle \sum _{t=1}^T\left(P_{\mathrm{charge},t}\cdot C_{\mathrm{grid},t}-P_{\mathrm{wind},t}\cdot C_{\mathrm{wind},t}\right)}\cdot \Delta t$$

(23)

The problem is a convex optimization problem, which is solved by the sequential least squares method, and the computational complexity is $O(T^2)$.

2.

Real-time optimization strategy (online control)

Based on the current wind power forecast value and electricity price, heuristic decision rules are adopted:

$$P_{\mathrm{charge},t}=\left\{\begin{array}{ll}{P}_{\max }\hfill & \mathrm{if}{C}_{\mathrm{grid},t}\le \theta \cdot C_{\mathrm{avg}}\mathrm{and}{P}_{\mathrm{wind},t}\ge \varphi \cdot P_{\mathrm{wind},\mathrm{avg}}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.,$$

(24)

where $\theta$ is the electricity price threshold coefficient; $\varphi$ is the power reduction coefficient; $C_{\mathrm{avg}}$ is the average electricity price; $P_{\mathrm{wind},\mathrm{avg}}$ is the average wind power.

Under the integrated transportation-energy system framework, this EV dynamic charging strategy based on the NGBoost–GRU fusion forecasting model improves charging efficiency, cuts user costs, and eases grid-load pressure. By capturing both the point prediction of wind power and its uncertainty interval, the strategy aligns wind power output forecasts with grid status, user demand, and time-of-use electricity prices. It guides EV charging behavior to boost local renewable wind energy consumption, curb reliance on fossil-fuel-based power, and enhance the system’s environmental performance. Meanwhile, the strategy balances electricity pricing, economic benefits, and grid-load dynamics to support safe and stable grid operations.

In summary, the wind-power-charging collaborative optimization framework offers solid technical support and a theoretical basis for the efficient and coordinated operation of smart grids and electric vehicles. This is highly significant for promoting renewable energy utilization and ensuring the stable development of smart grids.

3. Results

3.1. Dataset

The data used in this paper is the spatial dynamic wind power prediction dataset of a wind farm in Guazhou City, Gansu Province, issued by Longyuan Power Group Co., Ltd. in 2022 [41]. There are 134 wind turbines in total, and the data is collected every 10 min. The data from each wind turbine is collected 144 times a day. Each wind turbine has a total of 144 × 245 = 35,280 continuous data points. The distribution of wind farms is shown in Figure 6a.

The dataset provides key external features that affect wind power generation, such as wind speed, wind direction, and ambient temperature, as well as basic internal features, such as internal temperature of the blade, cabin direction, and pitch angle. In addition, there is a separate file that provides the spatial location information of each fan in the coordinate form of (x, y). The detailed description of each variable is shown in

Table 2. Variable description of wind power data set.

Column	Column Name	Specification
1	TurbID	Wind turbine ID
2	Day	Day of the record
3	Tmstamp	Created time of the record
4	Wspd 1 (m/s)	The wind speed recorded by the anemometer
5	Wdir 2 (°)	The angle between the wind direction and the position of turbine nacelle
6	Etmp 3 (°C)	Temperature of the surounding environment
7	Itmp 4 (°C)	Temperature inside the turbine nacelle
8	Ndir 5 (°)	Nacelle direction, i.e., the yaw angle of the nacelle
9	Pab 6 1 (°)	Pitch angle of blade 1
10	Pab2 (°)	Pitch angle of blade 2
11	Pab3 (°)	Pitch angle of blade 3
12	Prtv (kW)	Reactive power
13	Patv 7 (kW)	Active power (target variable)

In conjunction with Figure 6b, this paper describes the variables in the wind power dataset as follows, and the meaning of each variable in Table 2 is: ¹ The variable Wspd is the real-time wind speed recorded by the anemometer on the turbine. ² The variable Wdir is the angle between the wind direction and the turbine nacelle. ³ The variable Etmp is the monitored ambient temperature around the turbine. ⁴ The variable Itmp is the monitored temperature in the turbine nacelle. ⁵ The variable Ndir is the yaw angle of nacelle. ⁶ The variable Pab is the pitch angle of the wind turbine blade. ⁷ The variable Patv is the active power output by the wind turbine, which is the target variable of the wind power prediction in this paper.

.

3.2. Experimental Environment and Parameter Configuration

In order to verify the effectiveness of the NGBoost–GRU fusion model proposed in this paper, all of this paper is implemented using Python 3.8 code, and the development tool PyCharm 2023 is used to remotely connect to the cloud server provided by the AI Galaxy platform for experiments. The model uses the PyTorch 1.13.1 framework and runs in a GPU computing environment equipped with a GeForce RTX 3090 (24 GB). The Adam optimizer is used in the training process, and the initial learning rate is set to 0.01. The batch size is set to 32, and the dataset is divided into a 60% training set, a 20% validation set, and a 20% test set. Each model undergoes 200 training cycles to ensure full learning and optimal performance. In order to compare the performance of the model fairly, the parameter settings of the baseline model follow the original paper, and the training configurations, such as learning rate and batch size, are consistent with the model.

3.3. Evaluation Indicators

In order to quantitatively evaluate the performance of the NGBoost–GRU fusion model proposed in this paper in wind power prediction tasks, the following two widely used regression evaluation indicators are used: mean absolute error (MAE) and root mean square error (RMSE). The indicators are defined as follows:

3.3.1. Mean Absolute Error (MAE)

MAE represents the mean value of the absolute error between the predicted value and the true value. The calculation method is:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n\left|y_i-{\widehat{y}}_i\right|},$$

(25)

where $y_i$ is the real active power value of the $i$-th sample (unit: kW); ${\widehat{y}}_i$ is the corresponding predicted value, and $n$ is the total number of samples. MAE is not sensitive to outliers and can directly reflect the absolute level of prediction error.

3.3.2. Root Mean Squared Error (RMSE)

RMSE is the square root of MSE, which is defined as:

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}},$$

(26)

RMSE has the same dimension (kW) as the target variable, which is convenient to intuitively explain the actual physical meaning of the prediction error. Compared with MAE, RMSE is more sensitive to extreme errors and can effectively reflect the stability of prediction results.

The above indicators together constitute a multi-dimensional assessment of prediction performance. MAE provides robust estimation of errors, and RMSE focuses on identifying large deviation samples (in wind power forecasting, extreme errors may lead to grid scheduling risks). The experiment will report the results of each index on the test set, respectively, to comprehensively verify the effectiveness of the model.

3.4. Baseline Model

In order to comprehensively evaluate the prediction performance of the NGBoost–GRU fusion model proposed in this paper, five representative advanced prediction models were selected as baseline methods, covering two mainstream paradigms of deep learning and ensemble learning. Here is a selection of comparison algorithms:

• Long Short-Term Memory (LSTM) [42]: Long-term memory and key information extraction of historical dynamic features are realized by using the cell state and a gating unit to selectively retain and transmit timing information.
• Convolutional Neural Network (CNN) [43]: By sliding the one-dimensional convolution kernel in the temporal dimension, local spatial features (such as wind speed mutation, power fluctuation mode) are extracted and predicted.
• Extreme Gradient Boosting (XGBoost) [44]: The decision tree combination is iteratively optimized by the addition training strategy, and the regularization term is introduced to control the complexity of the model. Its advantages are efficient processing of structured features (such as ambient temperature, pitch angle), automatic processing of missing values, and nonlinear modeling capabilities for feature interaction, which are robust in wind power feature engineering.
• Light Gradient Boosting Machine (LightGBM) [45]: Gradient-based one-sided sampling (GOSS) and mutually exclusive feature binding (EFB) techniques are used to significantly improve training efficiency and memory utilization. Compared with XGBoost, its histogram algorithm accelerates feature splitting, which is especially suitable for large-scale processing of high-dimensional wind turbine data (such as multi-unit spatial position and operating condition parameters).
• Transformer [32]: Abandon the loop structure and rely entirely on the self-attention mechanism (self-attention) to dynamically calculate the global dependence weight of sequence elements. By injecting timing information through position coding, its multi-head attention layer can capture the long-range correlation and multivariate interaction of wind speed series in parallel and realize prediction.

3.5. Main Results

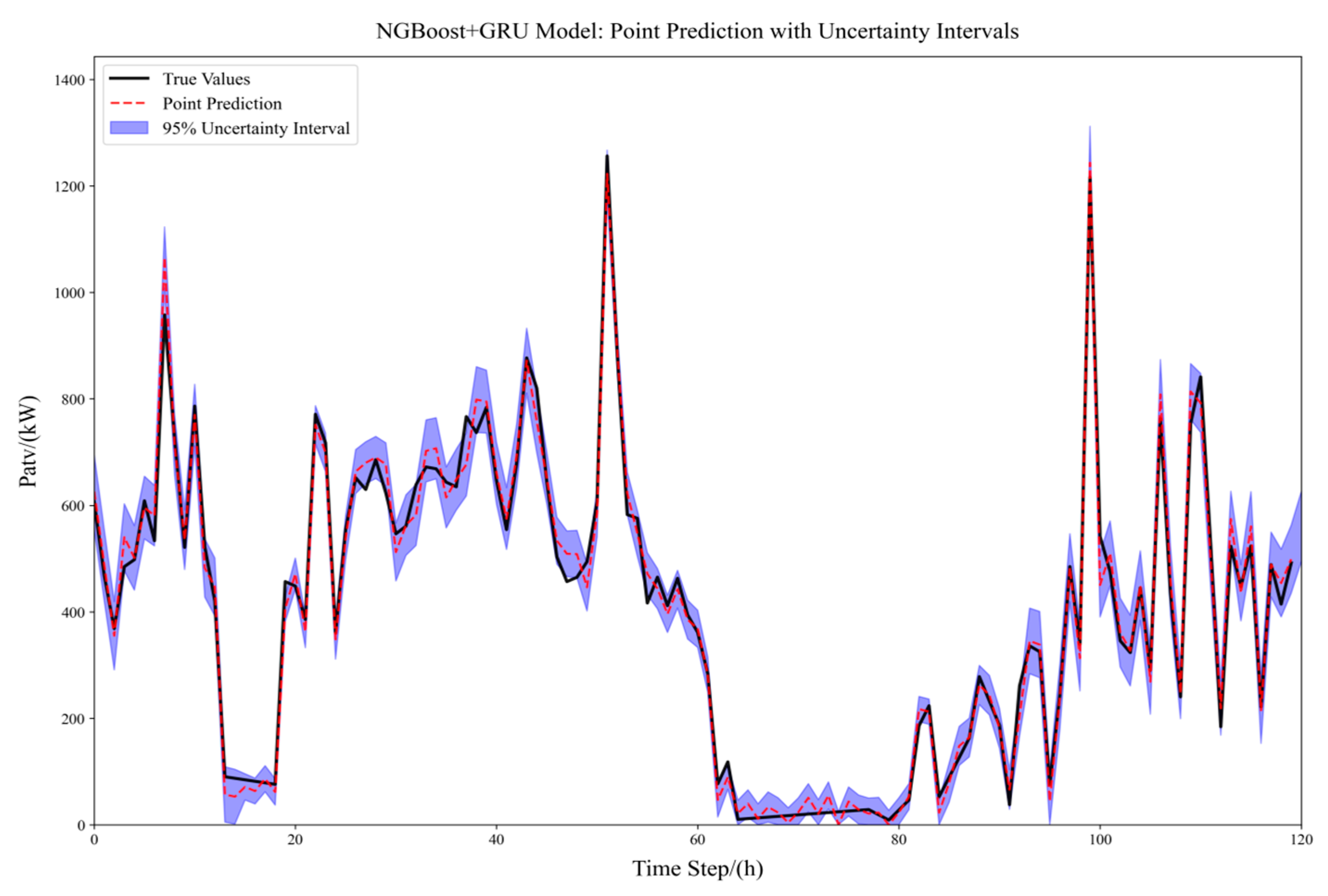
We selected the prediction results of a wind turbine for 120 consecutive hours for visual display. Figure 7 shows the point prediction and uncertainty interval visualization results of the NGBoost–GRU fusion model in the wind power prediction task. By combining GRU’s timing modeling ability with NGBoost’s probabilistic prediction characteristics, the model achieves the dual goals of high-precision point prediction and quantitative uncertainty.

The point prediction value of the model output (red dotted line in Figure 7) is highly consistent with the real power curve (black solid line). When the wind speed is stable (such as 0–40 h), the predicted value is almost completely consistent with the real value; during the wind speed mutation period (such as 60–80 h), the model captures the dynamic characteristics in time through the GRU gating mechanism and responds to power fluctuations quickly. This performance verifies the strong representation ability of the model of the nonlinear dynamic characteristics in the wind power time series.

The light-blue area denotes the 95% confidence interval for NGBoost’s probabilistic forecasting. It reflects the prediction’s reliability: the interval narrows during wind-speed stability (e.g., 20–30 h), indicating high prediction confidence, and widens during extreme weather (e.g., a strong wind mutation at 60 h), warning of potential predictive risks. This dynamic quantification of uncertainty offers key risk indicators for power grid security scheduling. Grid operators can activate backup power supply plans to prevent frequency instability caused by prediction deviations.

In summary, the NGBoost–GRU fusion model proposed in this paper achieves remarkable performance in wind power prediction. Its point predictions align closely with the actual power curve. Thanks to GRU’s gating mechanism and NGBoost’s probabilistic prediction features, the model accurately captures dynamic characteristics and quantifies uncertainty in both stable and volatile wind speed periods. This provides reliable early warnings for grid security dispatching, confirming the model’s strong ability to characterize nonlinear dynamic features in wind power time series.

3.6. Comparative Experiment

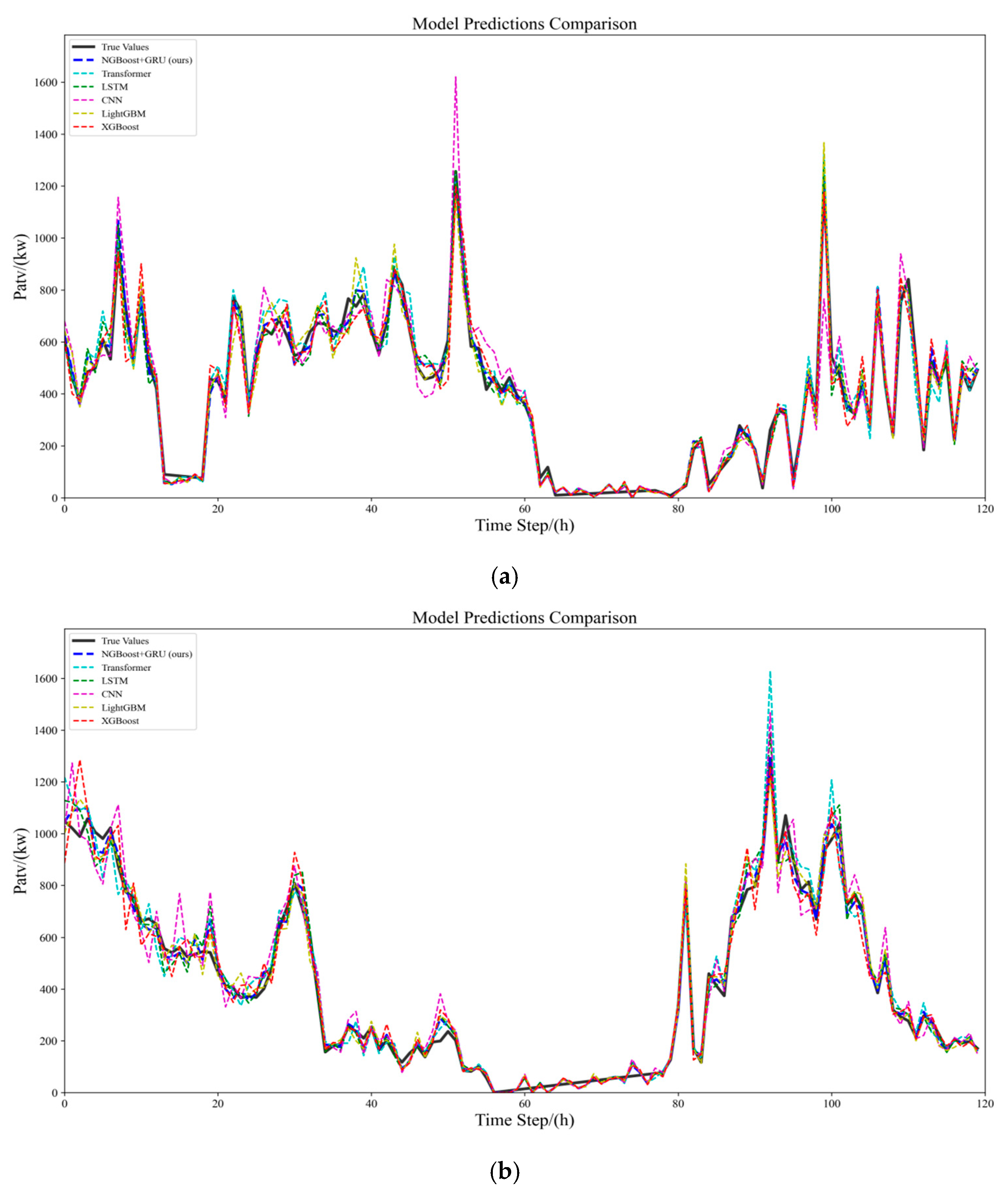
This paper compares the NGBoost–GRU fusion forecasting model with five other algorithms using real wind farm data.

Table 3. Comparison of different forecasting methods.

Algorithm	RMSE/MAE
	3 h	6 h	9 h	12 h
LSTM	43.73/31.03	47.9/35.68	51.74/41.89	56.17/48.09
CNN	90.64/51.51	103.35/64.39	116.43/77.27	128.19/92.72
XGBoost	57.07/37.33	63.29/43.67	69.19/51.51	75.5/59.72
LightGBM	51.45/34.88	56.83/41.16	61.96/47.09	67.09/54.07
Transformer	59.08/40.29	66.06/48.35	73.56/58.42	80.36/68.49
NGBoost–GRU	29.97/21.71	32.14/24.31	34.18/27.13	36.09/29.96

The best results are marked in bold font.

shows the RMSE and MAE values for prediction horizons of 3 h, 6 h, 9 h, and 12 h.

As shown in Table 3, the NGBoost–GRU fusion model outperforms all other algorithms in both long-term and short-term predictions across all evaluation metrics on the real-world dataset. While prediction errors increase with time for all models, the NGBoost–GRU fusion model exhibits the slowest error growth, indicating superior long-term time-series dependency modeling. Compared to models like Transformer and XGBoost, the NGBoost–GRU fusion model effectively reduces prediction bias by integrating GRU’s temporal feature extraction and NGBoost’s nonlinear feature capture capabilities.

To visually compare NGBoost–GRU fusion model predictions with other algorithms, we randomly selected Turb 1 and Turb 2 from the wind farm dataset, predicted 120 h, and visualized the results. Figure 8 shows the prediction curves.

The results show that our model performs well on the real dataset of wind farms. The reason may be that the model combines the strong ability of NGBoost in dealing with nonlinear relationships and uncertainties and the advantages of GRU in capturing long-term dependencies of time series data, which can more accurately describe the complex patterns and dynamic changes in wind power generation data, so as to achieve excellent prediction results on each prediction time scale.

3.7. Ablation Experiment

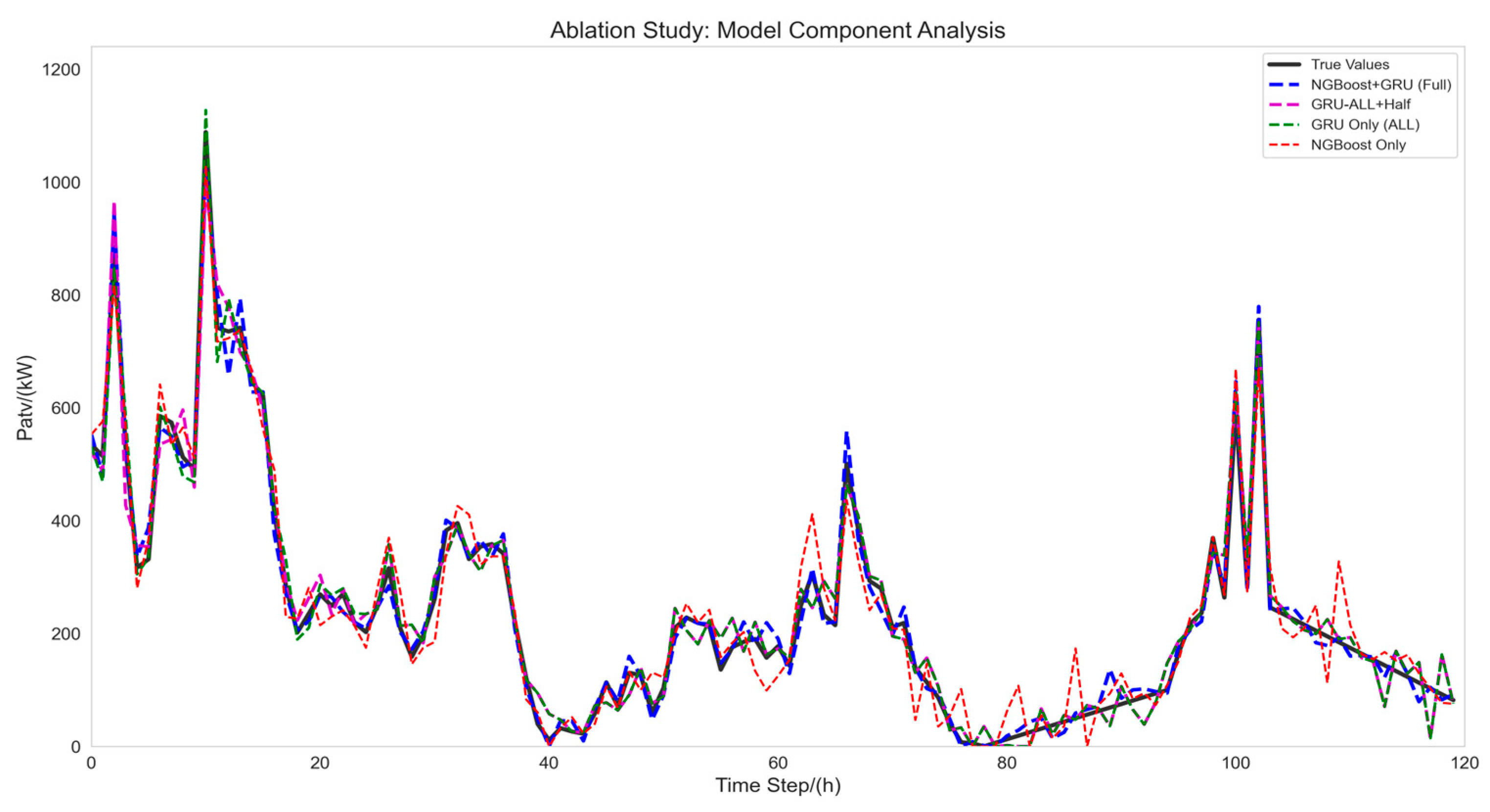
To explore each component’s contribution to the NGBoost–GRU fusion model performance and their synergistic mechanisms, ablation experiments with four model configurations were conducted: NGBoost-Only, GRU-Only, GRU-ALL + Half hybrid, and the Full NGBoost + GRU model. Experimental results are presented in

Table 4. Comparison of ablation experimental results.

Model Configuration	RMSE/MAE
	3 h	6 h	9 h	12 h
NGBoost Only	51.99/44.47	55.76/55.28	59.28/61.56	62.61/64.44
GRU Only (ALL)	46.09/33.22	49.43/32.03	52.56/40.14	55.51/40.91
GRU-ALL + Half	40.74/29.65	43.69/29.99	46.46/38.68	49.06/37.62
NGBoost + GRU (Full)	28.87/20.24	30.95/21.89	32.91/28.79	34.76/24.47

The best results are marked in bold font.

and Figure 9.

It can be seen from Table 4 that the model using only NGBoost shows the highest prediction error on all prediction time scales. This is because the dynamic features and long-term dependencies of time series data play a key role in wind power prediction, and NGBoost itself is not good at capturing these time series features. Specifically, the RMSE and MAE of NGBoost Only were 51.99 and 44.47, respectively, which were significantly higher than those of the complete model, NGBoost + GRU (28.87 and 20.24, respectively).

In contrast, the model using only GRU (GRU Only (ALL)) performs well in capturing the dynamic characteristics of time series data. The gating mechanism of GRU can effectively filter and retain valuable historical information for prediction, thus showing good performance in time series prediction tasks. For example, in the 3 h prediction, the RMSE and MAE of GRU Only (ALL) were 46.09 and 33.22, respectively, which were significantly improved compared with NGBoost Only. However, there are still some limitations in relying solely on GRU, because it mainly focuses on the extraction of time series features, and the processing ability of nonlinear relationships and uncertain factors in the data is relatively insufficient.

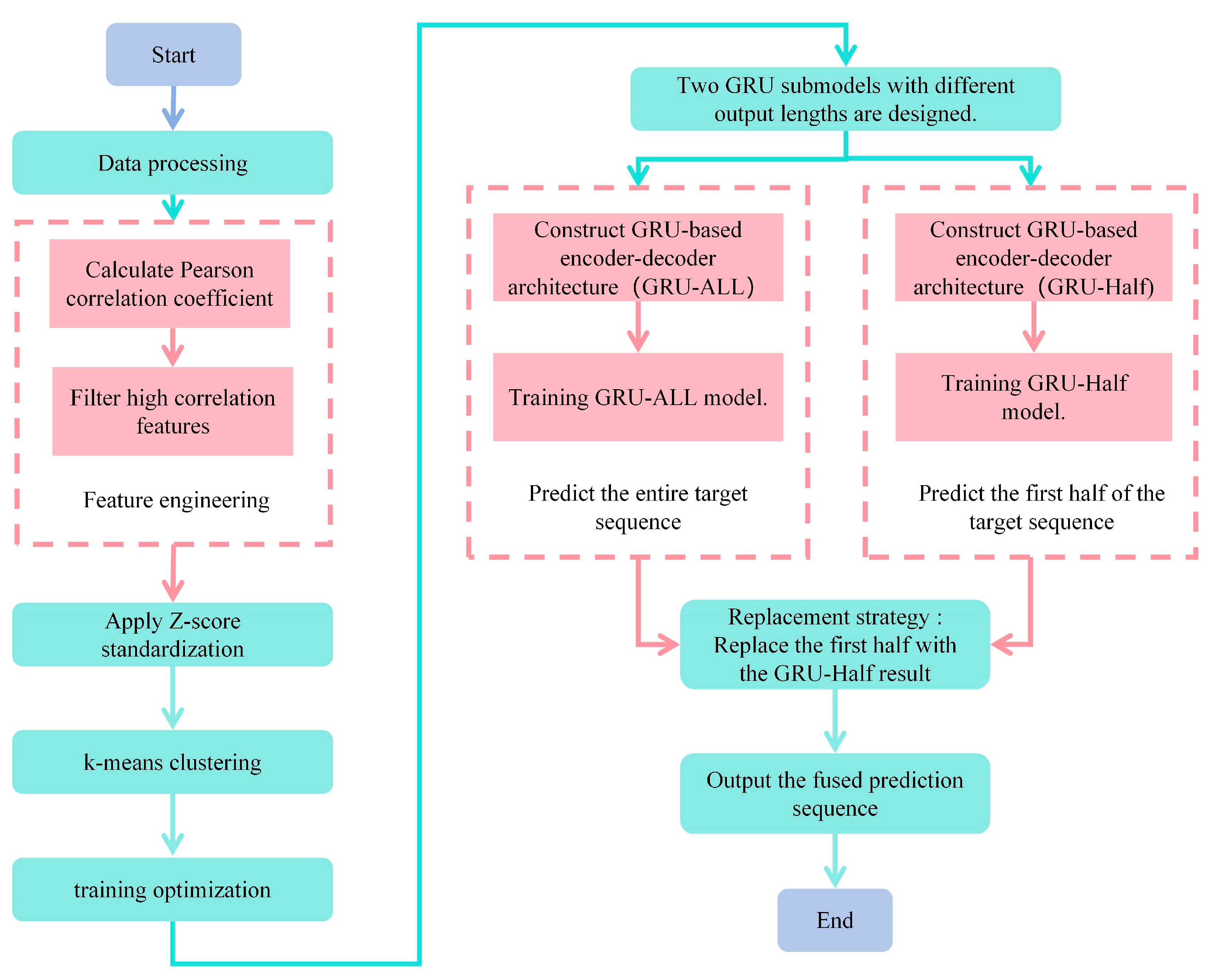
It is worth noting that this paper designs a GRU-ALL + Half hybrid model, which effectively suppresses the error accumulation in the first half of the sequence by combining the prediction results of the first half of GRU-Half with the prediction results of the second half of GRU-ALL. The experimental results show that this hybrid strategy significantly improves the prediction accuracy: in the 3 h prediction, the RMSE (40.74) and MAE (29.65) of GRU-ALL + Half are 11.6% and 10.8% lower than those of GRU Only, respectively. This improvement takes advantage of GRU-Half’s high-precision capture of short-term dynamics of sequence initiation and makes up for the defect of GRU-ALL’s error accumulation in the initial part of long sequence prediction.

The complete model, NGBoost + GRU, gives full play to the respective advantages of NGBoost and GRU. NGBoost can accurately capture the nonlinear relationship and uncertainty factors in the data, such as the complex correlation between variables, such as ambient temperature, pitch angle, and active power. The temporal features extracted by GRU provide high-quality input for NGBoost, which enables it to model the probability distribution more accurately. This synergy makes the complete model achieve the lowest prediction error at each prediction time scale. For example, in the 12 h prediction, the RMSE and MAE of the complete model are 34.76 and 24.47, respectively, which are significantly better than other models.

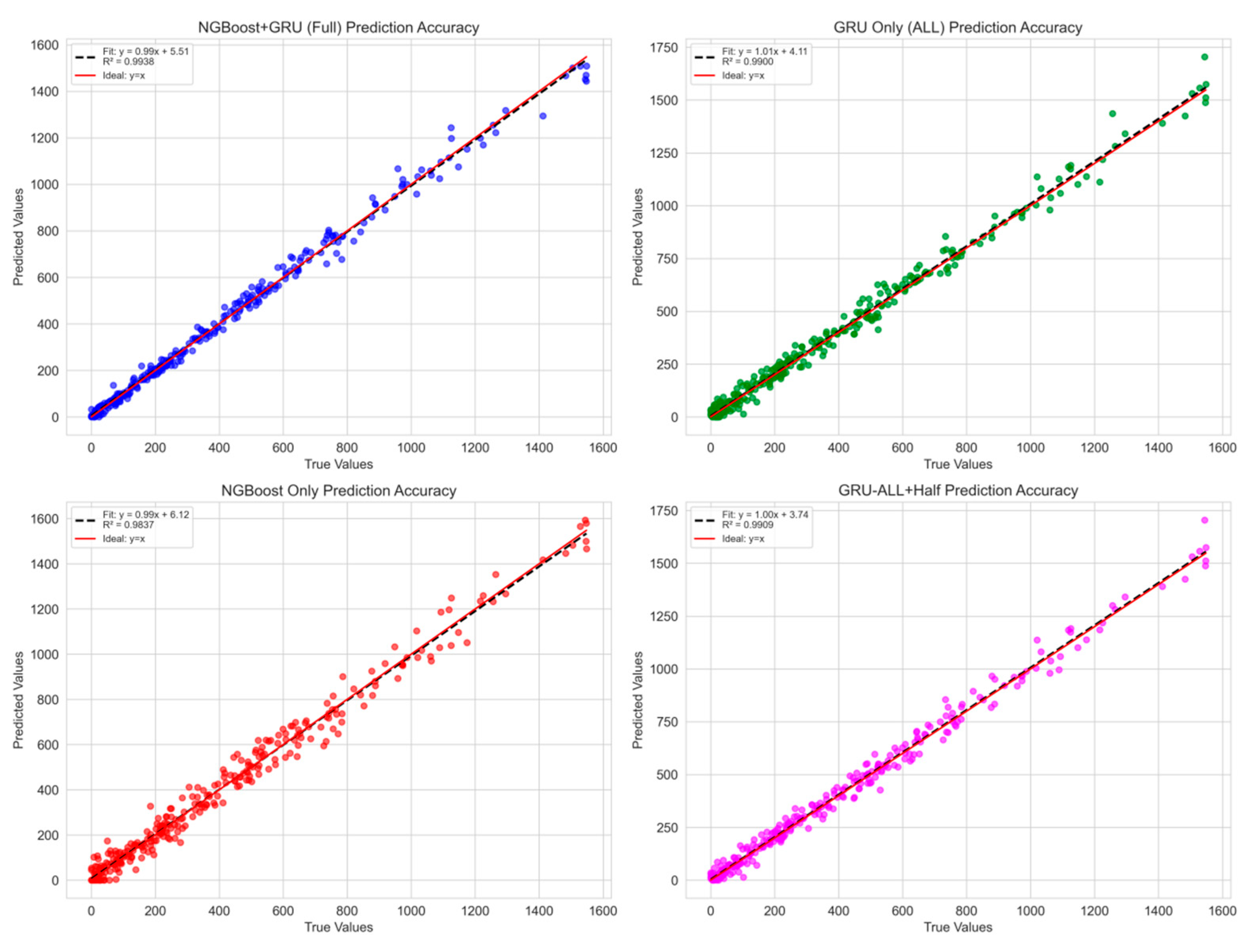
Figure 10 shows the scatter plot of the predicted value and the true value of the complete model, NGBoost + GRU. It can be seen from the figure that the predicted value is highly consistent with the real value, and most of the points are closely distributed near the diagonal, indicating that the model prediction results are consistent with the actual values. This further verifies the effectiveness of the synergy between NGBoost and GRU in wind power prediction tasks. The complete model not only performs well in the error index, but also is significantly better than the single-component model in the accuracy of the actual prediction results.

In summary, the ablation experimental results show that NGBoost and GRU play an irreplaceable role in the complete model, and their synergistic effect significantly improves the accuracy and stability of wind power prediction.

3.8. Dynamic Charging Analysis of Electric Vehicles Based on NGBoost–GRU Fusion Combined Prediction Model

The NGBoost–GRU fusion model achieves high-precision point prediction of power fluctuation and reliable quantification of its uncertainty interval in wind power prediction, which provides key support for subsequent real-time decision optimization. Based on this prediction ability, we design a dynamic charging strategy for electric vehicles, which aims to optimize charging efficiency, reduce user costs, and relieve grid load pressure. In order to rigorously evaluate the applicability and effectiveness of the strategy in actual scenarios, this study constructed a simulation dataset that meets the current charging characteristics of wind power and electric vehicles for experimental analysis. The core idea of this strategy is to intelligently match the predicted wind power output information with the grid state, user demand, and time-of-use electricity price structure, and dynamically guide the charging behavior of electric vehicles.

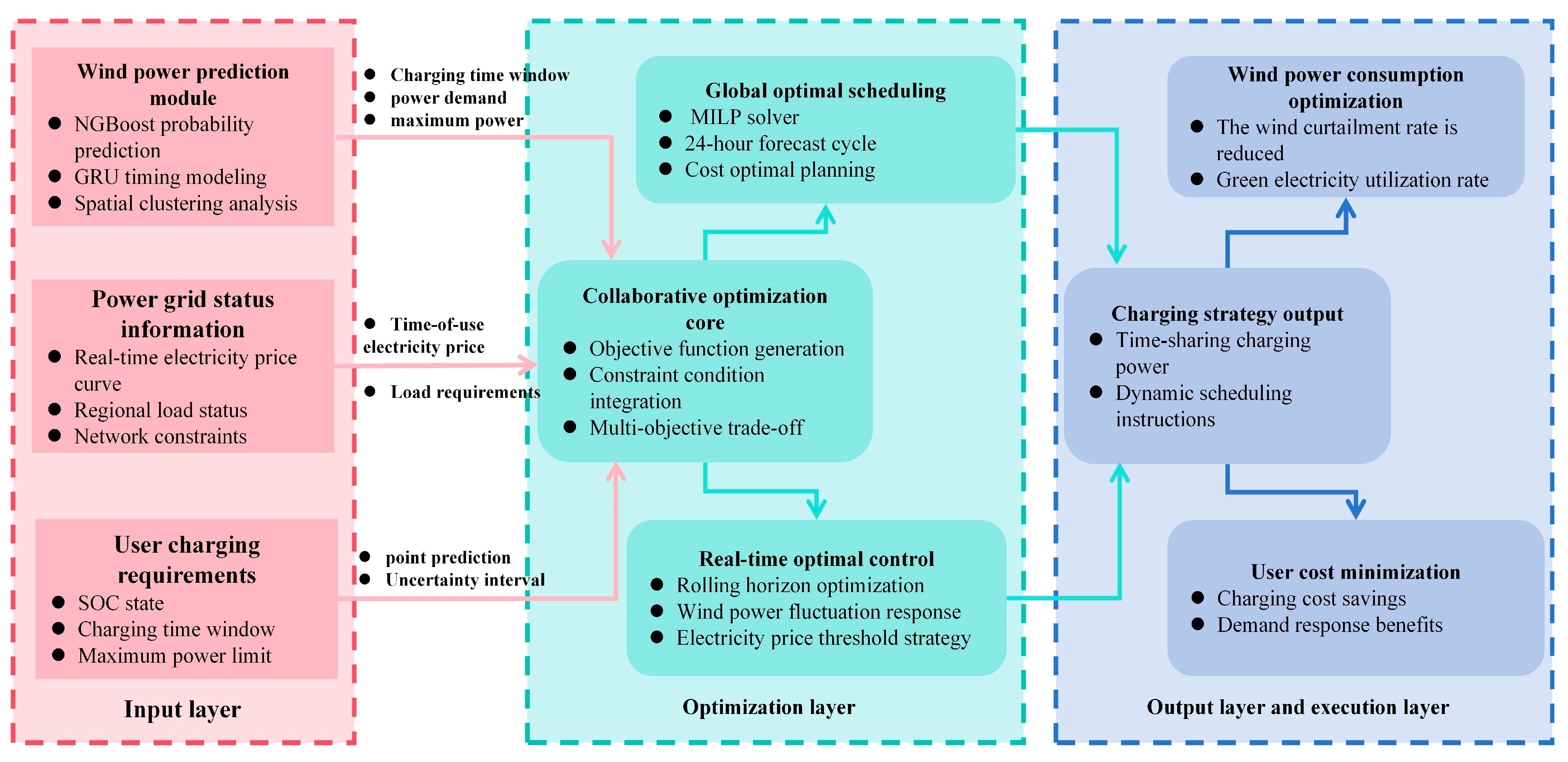
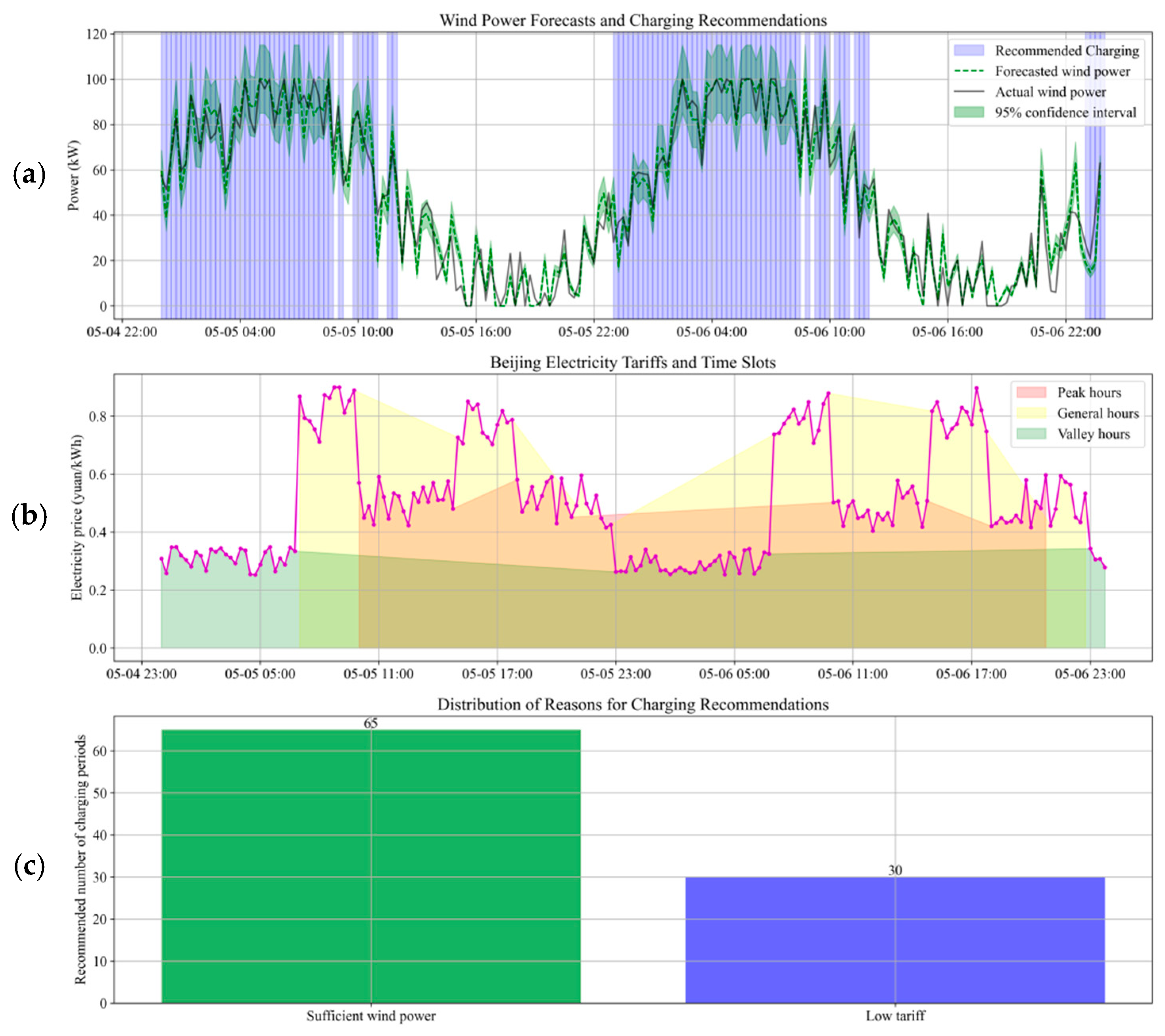
Figure 11 shows a schematic diagram of wind power prediction and electric vehicle charging scheduling. It contains three key subgraphs, which together constitute a complete energy decision support visualization system.

The first subgraph is wind power prediction and charging period recommendation. The GRU-NGBoost model is used to effectively predict wind power. At the same time, the confidence interval is used to provide a risk boundary for decision-making. The confidence interval of this paper is set to 95%, which can intuitively quantify the uncertainty of prediction. The blue area marker image shows the recommended charging period for the charging recommendation.

The second sub-graph clearly shows the peak-valley electricity price structure (magenta curve) of Beijing (2025). The time period is divided into the following: red area—peak period (10:00–15:00, 18:00–21:00, electricity price ≈ 0.8 yuan/kWh); yellow area—normal period (7:00–10:00, 15:00–18:00, 21:00–23:00, electricity price ≈ 0.5 yuan/kWh); green area—valley period (23:00–7:00, electricity price ≈ 0.3 yuan/kWh). The electricity cost and power grid load intuitively show the optimization effect. Provide strong support for decision-making.

The third subgraph shows the optimization results of electric vehicle charging scheduling. More than 70% of the charging suggestions are directly triggered by the dynamic charging strategy designed by the system with sufficient wind power and a low electricity price.

The dynamic charging strategy of electric vehicles based on the NGBoost–GRU fusion prediction model is closely related to the collaborative optimization of wind power prediction and electric vehicle charging demand. In order to achieve the expected goal of the strategy, the following will be an in-depth analysis from three aspects: prediction-driven charging period decision, coordinated optimization of electricity price and economy, and dynamic balance of power grid load, as follows:

• Prediction-Driven Charging Period Decision:

The NGBoost + GRU model’s point prediction (the green dotted line in Figure 11a) accurately depicts the expected trajectory of future wind power. Based on this, the strategy actively identifies and recommends periods of high wind power output (e.g., the blue marked area in Figure 11a). By guiding the centralized charging of electric vehicles during these periods, the strategy maximizes the local consumption of renewable wind energy, reduces reliance on traditional fossil-fuel power generation, and enhances the system’s environmental performance. The model’s output uncertainty interval (the light-green area in Figure 11a) provides crucial risk boundary information for decision-making. During stable periods with high prediction confidence (narrow interval), the strategy enables more aggressive use of wind power. When prediction uncertainty increases significantly, the strategy triggers a risk-aversion mechanism. It recommends reducing or avoiding charging or initiating a backup scheduling plan. This buffers the grid impact from prediction deviations and ensures the system’s safe and stable operation.

2.

Coordinated Optimization of Electricity Price and Economy:

The strategy integrates wind power forecasts with time-of-use electricity pricing structures (as shown by the magenta curve and red/yellow/green zones in Figure 11b). This ensures users meet their charging needs at the lowest possible cost. Specifically, it guides users to charge during high-wind-power-output off-peak and regular periods (green and yellow zones in Figure 11b). This approach offers two benefits: users cut costs by charging at low-price periods, and grid power-purchase costs are reduced, especially during peak periods when high-cost marginal units would otherwise be needed, from Equation (19), it can be calculated that this strategy effectively reduces the user’s charging cost by approximately 18.7%. The model’s prediction accuracy ensures the effectiveness of this “wind-chasing and peak-avoidance” strategy, preventing users from being misled to charge during high-price periods due to prediction errors.

3.

Dynamic balance of grid load:

By dynamically adjusting the charging power curve of electric vehicles (as shown in Figure 11c), the strategy aims to smooth the net load curve of the grid, reduce the peak load, and fill the load trough. For example, in the period when it is predicted that the wind power output is about to decline and the grid load will enter the peak period (combined with the peak period of Figure 11b and the downward trend of wind power in Figure 11a), the strategy can reduce the charging power in advance or delay some non-emergency charging requirements (combined with the charging completion time window set by the user), thereby effectively alleviating the peak shaving pressure of the grid, reducing the risk of line congestion, and improving the utilization rate of transmission and distribution equipment. The optimization results shown in Figure 11c (such as the increase in charging power in the valley period) are the intuitive embodiment of this dynamic balance effect.

Based on the wind power prediction ability of the NGBoost–GRU fusion prediction model, this paper designs a dynamic charging strategy for electric vehicles, which shows significant advantages in optimizing charging efficiency, reducing user costs, and alleviating grid load pressure. It provides strong technical support and theoretical basis for the efficient coordinated operation of the smart grid and electric vehicles, and is of great significance for promoting the consumption of renewable energy and the stable development of the smart grid.

4. Discussion

The NGBoost–GRU fusion-based wind power prediction and EV dynamic charging strategy offer innovative solutions for optimizing AC energy integration systems. By combining GRU’s temporal feature extraction and NGBoost’s probabilistic prediction, the model enhances wind power prediction accuracy and reliability, effectively supporting EV charging strategy optimization. Accurate wind power prediction aids grid operators in devising scientific scheduling plans, pre-planning energy storage charging/discharging, and traditional thermal power output adjustments, thus improving grid operation stability and economy. The strategy also guides EV charging behavior, enabling users to enjoy low-cost charging while supporting grid operations. This fosters a user-grid win-win scenario and promotes the coordinated development of transportation electrification and energy transformation.

However, this study has some limitations in practical application, mainly reflected in the following aspects. First of all, the research assumes that the power grid capacity is not limited, and the practical problems of power grid expansion are not fully considered. At present, under the background of the rapid development of electric transportation and renewable energy charging infrastructure, the power grid complex is facing huge expansion pressure. Wind farms are connected to high-voltage and ultra-high-voltage networks, and electric vehicle charging stations are mostly connected to low-voltage networks. The entire power grid complex is involved, but increasing the capacity of transmission lines and substations requires a lot of time and resources. Secondly, this strategy is mainly applicable to the slow charging station scenario, which requires a large number of electric vehicles to be connected to the slow charging station and implement the charging algorithm, while reducing the electricity price to attract users. However, this mode does not apply to the fast charging station network. When the battery power is insufficient and the driver plans to continue driving, it is difficult to effectively control the fast charging demand using this strategy, thus limiting the scale of the adjustable load. In addition, the complexity and high cost of automatic control systems and communication channels are not considered in the study. Controlling such a large-scale equipment complex requires a large number of communication channels and automatic control system support, which undoubtedly increases the financial burden of actual implementation. Therefore, although the strategy has obvious advantages in theory, its cost-effectiveness ratio has not been fully evaluated, which poses a major limitation to its practical application.

In summary, although the NGBoost–GRU fusion prediction model and the dynamic charging strategy of electric vehicles proposed in this paper have significant advantages and broad application prospects in theory, they still face many challenges in practical applications. Future research should focus on the following directions: First, develop a lightweight and efficient model architecture to reduce the computational complexity and improve the real-time performance of the model in large-scale data scenarios. Second, expand the scope of research, comprehensively consider the deep coupling mechanism of different types of loads (such as electric buses, electric trucks, etc.) and renewable energy sources such as wind power, and build a more comprehensive integrated energy system model. Third, deepen the research on uncertainty quantification and risk assessment, and develop a refined risk assessment index system and early warning mechanism based on advanced theories to provide more forward-looking guidance for power grid dispatching decision-making. Fourth, carry out model verification and optimization in multiple regions and multiple scenes to improve the adaptability and generalization ability of the model. Fifth, evaluate the cost-effectiveness ratio of the implementation of the strategy, comprehensively consider the actual factors such as power grid expansion and communication system construction, and propose solutions with economic feasibility. Through these efforts, it is expected to promote the integration of energy exchange technology to play a greater role in practical applications, and help achieve global energy transformation and carbon emission reduction targets.

5. Conclusions

This paper makes practical contributions to the integration of traffic and energy by focusing on wind power prediction and EV dynamic charging strategies. First, it proposes an NGBoost–GRU fusion combined model for high-precision wind power prediction. This model not only accurately forecasts wind power expectations but also quantifies prediction uncertainty, offering crucial risk warnings for grid dispatching. Second, based on this predictive ability, the paper designs a dynamic EV charging optimization strategy. By aligning with the spatiotemporal fluctuations of wind power generation, time-of-use electricity prices, and user demand, this strategy enables precise scheduling of EV charging loads. In practice, it reduces user charging costs by approximately 18.7%, boosts local wind power consumption, achieves grid load peak-shaving, and enhances system economic and operational stability.

The study focuses on model prediction performance and strategy optimization but faces practical engineering challenges like grid expansion limits, strategy adaptability to fast-charging scenarios, and the complexity and cost of large-scale control systems. Future research should develop lighter, more efficient models for better real-time performance, expand strategies to handle diverse loads and complex scenarios, deepen uncertainty-based risk assessment, and verify the optimization model’s cost-effectiveness across multi-region and multi-scenario settings. This will facilitate large-scale energy integration technology application and support energy transformation and “dual-carbon” goals.