Experimental Study on Impact Responses of Geofoam Reinforced Sand Cushion for Rockfall Hazard Mitigation

Abstract

In rockfall hazard mitigation, geofoam has been used in the cushion layer to improve the sustainability of the rockfall gallery, such as impact resistance enhancement and dead load reduction. Impact tests were conducted to study the effect of geofoam type, thickness, and impact energy on the impact responses of the sand cushion layer. The test results showed that placing geofoam in the sand cushion can reduce the peak impact force of the rockfall and the peak acceleration of the gallery slab by up to 80%. While the peak impact stress at the cushion layer bottom can also be reduced by geofoam under low impact energy, thicker geofoam layers (e.g., 4 and 6 cm) increased peak impact stress when the rockfall had high impact energy. Placing geofoam at the bottom of the cushion to replace one third of the sand cushion thickness can enhance the impact resistance of the cushion layer. Under low impact energy, expandable polyethylene (EPE) foam resulted in lower impact force on the rockfall, reduced impact stress within the sand cushion, and diminished vibration of the gallery slab compared with polystyrene (EPS) foam with a constant thickness. However, EPS foam is suitable for use in sand cushions of rockfall galleries subjected to high-energy rock impacts. Moreover, EPE foam exhibits superior resilience, resulting in less damage compared to EPS foam.

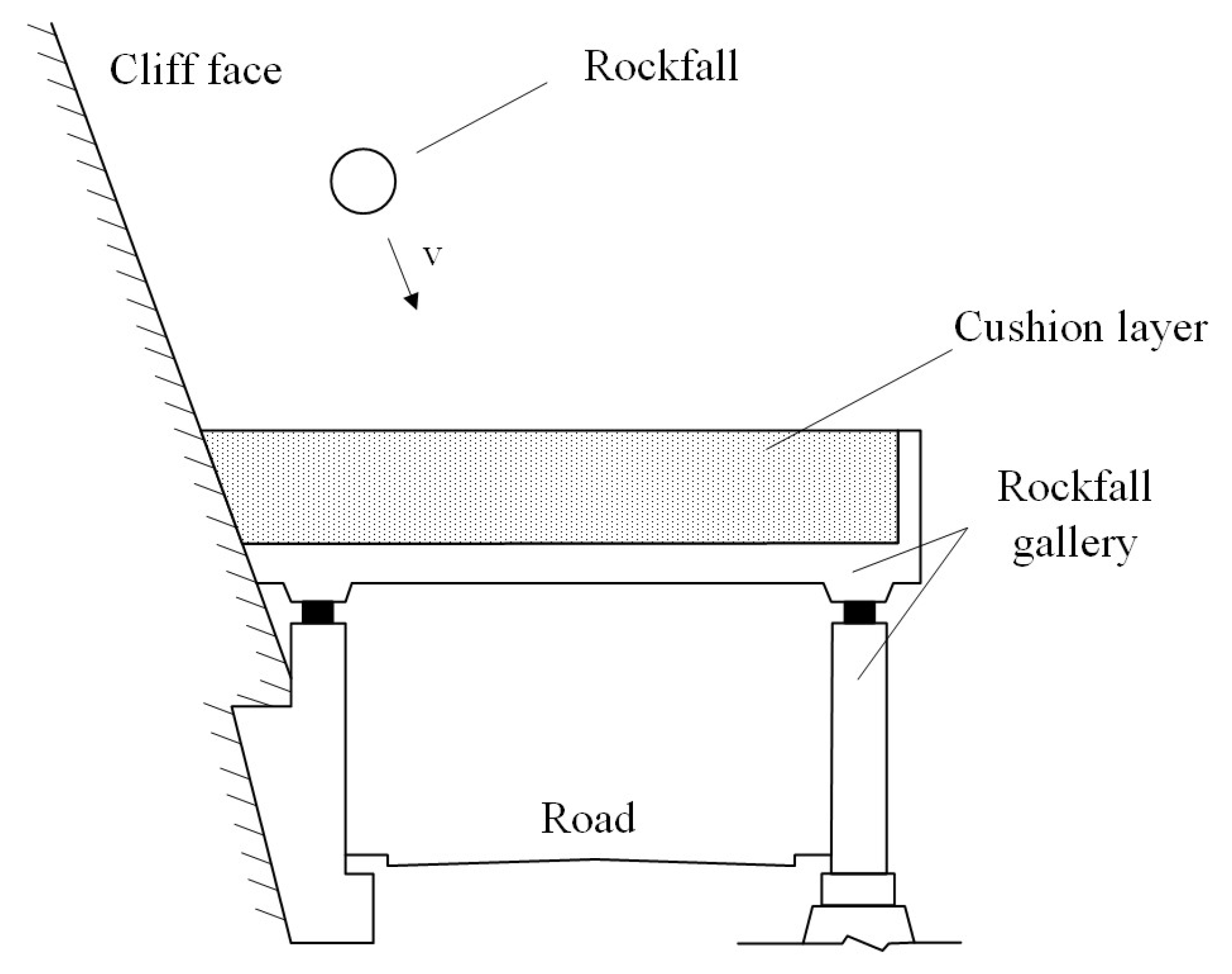
1. Introduction

Unstable rockfalls from high, steep slopes possess high impact energy, and may cause severe damage to humans and infrastructures [1,2,3]. Due to the less predictable volume and occurrence of rockfalls, protection measures cannot be placed in time to defend against the rock impact. Passive protection structures (e.g., rockfall galleries and retaining walls) are set up to intercept and stop rockfalls, while active protection measures (e.g., wire meshes and anchor stocks) are used to fix the unstable rock in place. Because the placement of active protection measures is limited by the terrain and elevation of the high, steep slope, passive protection structures are widely installed in potential rockfall areas.

A rockfall gallery covered with a cushion layer (Figure 1) is one of the most efficient rigid passive protection measures against rock impact. The cushion layer works as a buffer to prevent the direct collision between the rock and the gallery, thus potentially improving the impact resistance of the rockfall gallery. In practice, readily available river sand, crushed stone, and clay are commonly used as cushion material [4,5,6]. The impact resistance of the cushion layer is affected by many parameters, such as the cushion particle size, thickness, density, material, and structure. Kawahara and Muro [7] showed that the impact pressure within the sand cushion increased with an increase in the dry density of the cushion material and a decrease in the cushion thickness. Zhu et al. [8] reported that thin, gravel cushions can lead to a high coefficient of restitution of the cushion layer based on laboratory test results. Shen et al. [9] conducted an experimental and numerical investigation on the buffering effect of a cushion with uniformly graded soil particles. The results indicated that the impact resistance of the cushion layer improved with the decrease in soil particle size. Perera et al. [10] characterized the flexural behavior of a gabion layer placed in front of a reinforced concrete wall against boulder impact. Meng et al. [11] conducted impact tests to investigate the effect of geogrid location and layer number on the dynamic behaviors of a sand cushion for a rock shed. The results indicated that one-third-height of sand cushion is an optimum location for placing geogrid to reduce the impact force and contact stresses against rockfall impact. For traditional cushion materials (e.g., sand, crushed stone, and clay), a thick cushion is often needed to obtain favorable impact resistance in the cushion layer for the rockfall gallery. Previous studies showed that the increase in cushion thickness can reduce the rock impact force, increase the duration of rock impact, and distribute the impact stress within the cushion layer [12,13,14]. However, the improvement in the cushion impact resistance will become smoother when the cushion thickness increases to a threshold. In other words, there are limitations to the improvement in the buffering effect of the cushion layer only by increasing the cushion thickness. Therefore, the recommended optimum cushion thickness is 1.5 and 0.9 m, in the Chinese standard [15] and the Japanese practice [16], respectively. In addition, a high dead weight of the thick cushion layer will lead to challenges for the bearing capacity and construction cost of the rockfall gallery.

To improve the capacity of energy absorption, while reducing the dead weight of the structure, the cushion layer of the rockfall gallery can be partly or completely replaced by lightweight cushion materials. Ng et al. [17] conducted large-scale pendulum impact tests and found that using a cellular glass cushion resulted in maximum impact force on the rock, and the transmitted load on the concrete wall decreased by 25 and 50%, as compared with the gabion cushion. Furthermore, Kwan et al. [18] showed the feasibility of ethylene-vinyl acetate foam and a recycled glass cullet cushion placed in front of the concrete wall subjected to rockfall impact. Sun et al. [19] conducted impact tests and indicated that a used tire filled with sand or gravel had better impact resistance against rock impact than an unfilled tire. Meree et al. [20] found low impact force and vertical deformation when placing an airbag under the sand cushion. However, these materials (e.g., air bag and cellular glass) are not widely used, due to the complex construction technique and high cost.

Geofoam (e.g., EPS and EPE), a conventional packaging material, has been widely used as a buffer to dissipate energy in structural and geotechnical applications thanks to its favorable vibration resistance, light weight, and low cost [21,22]. EPS foam can also absorb the rock impact energy due to its high compressive strain [23]; thus, it is gradually being adopted to replace the traditional cushion partly or completely in rockfall hazard protection. Bhatti [24] reported that the high thickness and low density of EPS foam can result in remarkable impact resistance for an EPS–sand cushion of a reinforced concrete girder. Yan et al. [25] conducted combined finite and discrete element simulation by embedding cohesive interface elements between the finite elements to characterize the microscopic behaviors of the EPS-foam-reinforced sand cushion against rock impact. Zhao et al. [26] showed that thick EPS foam can amplify the effect of the rock shape on the impact responses of a cushion layer. EPS foam will have local brittle failure of punching shear under the high impact energy of a rockfall, resulting in decreased energy absorption of the EPS–sand cushion. Compared with the EPS foam, the EPE foam had better ductility and less cracking against rock impact. Therefore, increasingly more attention has been given to the impact responses of the EPE–sand cushion. Zhao et al. [27] showed that the EPE foam was only slightly caved while the EPS foam had punching shear failure in the sand cushion under a constant impact energy level. Yu et al. [28] studied the influence of EPE position on the dynamic responses of a sand cushion when placing the EPE foam between two sand layers.

For improving the sustainability of the rockfall gallery, although some studies indicated that the EPE–sand cushion exhibited better impact responses than the EPS–sand cushion [29,30], the preferable use of EPE or EPS foam in a sand cushion against rock impact may be limited by some specific conditions, such as the geofoam (e.g., density, thickness, position), cushion (e.g., thickness, material), and impact energy. Based on this background, this study focuses on investigating the feasibility of placing geofoam (i.e., EPS and EPE) in a sand cushion for a rockfall gallery against rock impact. Reduced-scale model impact tests were conducted to investigate the effect of geofoam type, thickness, and impact energy on the impact force of a rockfall, the impact stress within a cushion layer, and the vibration of a gallery slab. Meanwhile, the damage pattern of EPS and EPE foams was compared and discussed. Furthermore, the applicability condition of EPS and EPE foams was proposed. This study not only compared the impact responses between EPS and EPE foams but also identified the optimal foam thickness in a sand cushion, which could provide guidance for rockfall hazard mitigation.

2. Cushion Materials

2.1. Sand

Air-dried river sand was used in this study as cushion material above a rockfall gallery. It had a uniformity coefficient ($C_u$) of 5.9, a curvature coefficient ($C_c$) of 1.5, and a mean particle size ($d_{50}$) of 0.5 mm; thus it was classified as well-graded sand [31]. The cushion layer for the rock gallery was used to absorb the impact energy. Sand with large compressibility can provide favorable deformation to dissipate the impact energy of a rockfall. Therefore, sand with a relative compaction of 0.28 and a density of 1610 kg/m³ was used in this study. In addition, the sand had a peak friction angle of 36.7°, resulting from the direct shear test. The sand cushions were strictly controlled with mass and compaction in different tests to maintain uniformity.

2.2. Geofoam

To investigate the effect of geofoam type and thickness on the impact resistance of the sand cushion, EPS and EPE foams with the same density were selected, as shown in Figure 2. EPS and EPE had densities of 14.7 and 14.9 kg/m³, respectively, based on laboratory tests. The tensile test results showed that the tensile strength of these foams was 0.20 and 0.34 MPa, respectively. Three replicates of the EPS or EPE foam were applied in the uniaxial compression test to obtain the mechanical properties of the geofoam. During the compression tests, monotonic loading with a constant rate of 0.2 mm/s was applied until the specimens failed. Then, the geofoam specimens were unloaded and unconstrained for 3 min to obtain the resilience rate. The resilience rate was calculated by the geofoam thickness after 3 min of standing divided by the thickness before the compression test.

Figure 3 shows the stress–strain curves of the EPS and EPE foams under uniaxial compression. The deformation of EPS under uniaxial compression can be divided into elastic, plastic, and densification stages. The linear elastic behavior of EPS (i.e., the elastic stage) began with the bending of the cell walls of EPS. With the increase in the loading, the cell walls started to collapse, accompanied by a large amount of gas expelled. As a result, EPS underwent plastic deformation. During this plastic stage, a large amount of energy was absorbed due to the collapse of the cell walls [32]. EPS entered the densification stage as soon as the collapsed cell walls made contact with each other. The stress increased steeply with the increase in loading until the specimen failed. Unlike the EPS foam, the deformation of EPE foam under uniaxial compression had no clear boundary between the three stages. The stress–strain behavior of EPE foam could be characterized by an exponential power function. The stress of EPE foam increased with the increase in strain. At the same time, the tangent modulus of EPE foam increased gradually. In addition, the resilience rates of EPS and EPE foams were 44% and 95%, respectively. Clearly, EPE foam had better resilience performance than EPS foam, indicating that EPE has good durability when subjected to loading.

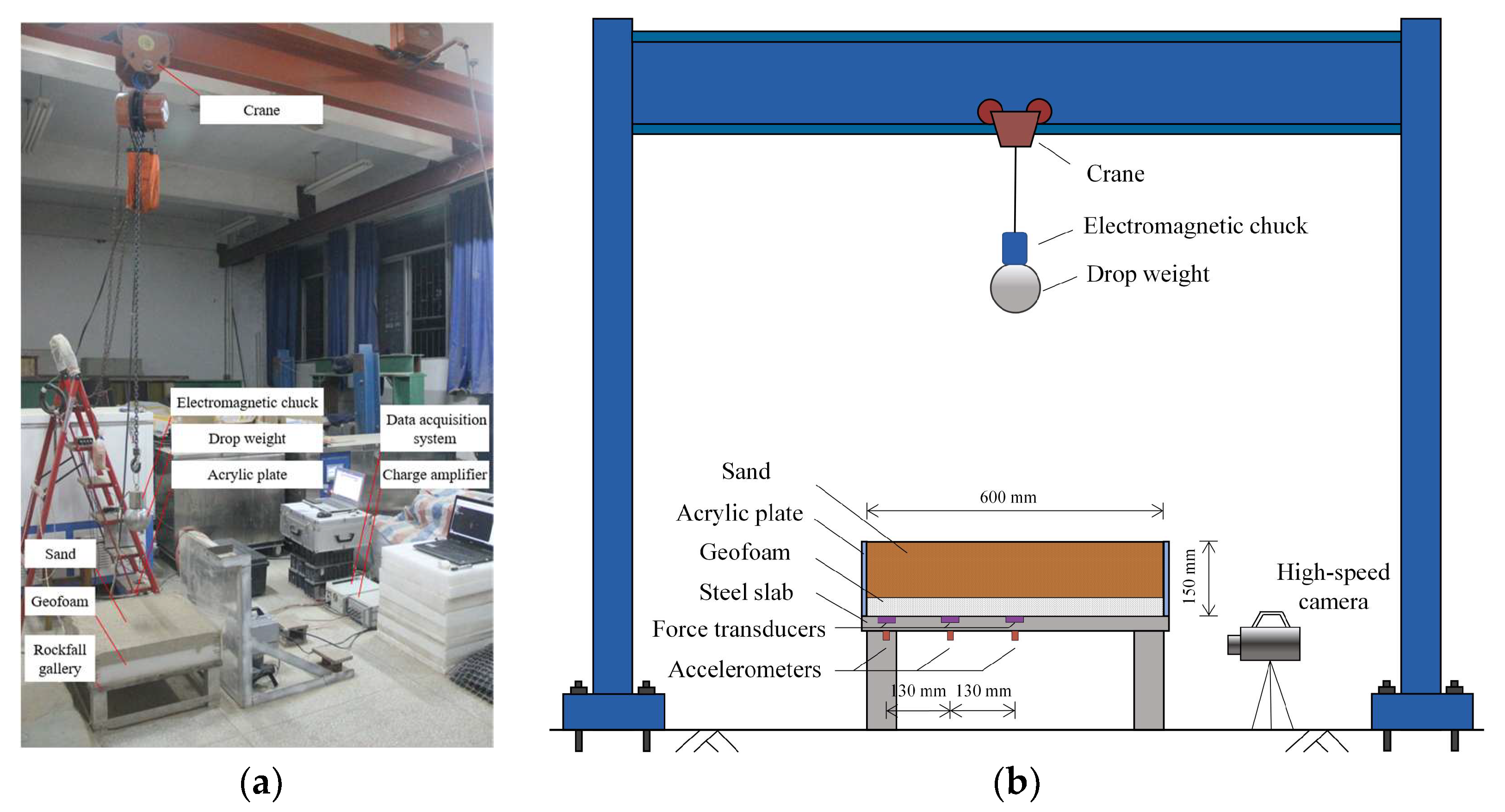
3. Experimental Procedure

3.1. Scaling Factor Design

The cushion placed above the rockfall gallery works as a buffer to dissipate impact energy when a rockfall hazard occurs. Cushion thicknesses in practical applications range from 0.5 to ~2 m [17,24], which means that conducting an impact test on a prototype cushion and a rockfall gallery is difficult. Reduced-scale tests are commonly used for parametric investigations. In this study, reduced-scale model tests were used to investigate the influence of geofoam type and thickness on the impact resistances of a sand cushion under rock impact, as shown in Figure 4. Meanwhile, the law of similitude was applied in the reduced-scale model test design. It is worth mentioning that this study mainly focused on investigating the feasibility of using geofoam to improve the impact responses of a sand cushion for a rockfall gallery, instead of reproducing a certain practical rockfall event. In this study, acceleration and impact force were key parameters characterizing the impact responses of a geofoam-reinforced sand cushion, and the impact force of the rockfall can be obtained by acceleration multiplied by rock mass. Therefore, acceleration was the primary choice for the control variable with a scaling factor of 1. Density was used as the control variable with a scaling factor of 1, as the cushion material used in the reduced-scale model test was the same as that in practice. In addition, the scaling factor of the cushion geometry size was set as 1/6. Thus, the slab (0.6 m × 0.6 m) used in the model test can simulate a practical rockfall gallery with a single lane (3.6 m × 3.6 m). Furthermore, the other main variables can be deduced by the Buckingham π theorem [33], as shown in

Table 1. The scaling factors of the model test.

Type	Physical Quantity	Symbol	Scaling Factor
Geometry property	Length	$S_l$	1/6
	Displacement	$S_s$	1/6
Material property	Density	$S_{\rho }$	1
	Elastic modulus	$S_E$	1/6
	Mass	$S_m$	(1/6)3
Dynamic property	Impact energy	$S_W$	(1/6)4
	Impact force	$S_P$	(1/6)3
	Acceleration	$S_a$	1
	Duration time	$S_t$	(1/6)0.5
	Stress	$S_{\sigma }$	1/6
	Strain	$S_{\epsilon }$	1

. A steel drop weight with a diameter of 0.13 m was used to simulate the rockfall instead of stone or concrete to obtain a higher impact energy. For the convenience of repeated tests, a steel slab was used to represent the rockfall gallery. Meanwhile, the cushion layer was restrained by acrylic plates above the steel slab. Based on the scaling factor of the cushion geometry size, the cushion thickness was 0.15 m in the model test to simulate the cushion in practice. In general, the weight of a rockfall ranges from 100 to 10,000 kg, and the falling height ranges from 5 to 50 m [34,35,36]. For the reduced-scale test, a drop weight of 9.5 kg was lifted by an electromagnetic chuck attached to the crane up to 0.5, 1.0, and 1.5 m, and then released freely to hit the cushion layer. The drop heights of 0.5, 1.0, and 1.5 m in the impact tests corresponded to 3.0, 6.0, and 9.0 m in a practical rockfall event. In other words, the rock impact energies of 47.5, 95.0, and 142.5 J in the impact tests can simulate the rock impact energies of 61.6, 123.1, or 184.7 kJ in practice, respectively, which are in the common impact energy range (5 to 5000 kJ) of a practical rockfall event [34,35,36]. In addition, the impact energies of 47.5 and 142.5 J were described as low and high impact energies, respectively, in the model tests.

3.2. Setup of Impact Test

The motion of the drop weight was measured by an accelerometer A0 during the test process, which was installed in the drop weight. On one hand, the velocity and penetration depth of the rockfall (i.e., drop weight) into the cushion can be calculated by the first and second integration of the acceleration, respectively. On the other hand, the peak impact force can be evaluated by the measured peak acceleration multiplied by the drop weight mass. The impact stress within the cushion bottom can be obtained by the force transducers installed along the symmetric axis of the top surface of the gallery slab. The force transducer F1 was placed on the center of the slab as shown in Figure 5a, and there was a gap of 130 mm between the force transducers F1, F2, and F3. Slab vibration can also characterize the impact resistance of the cushion. Therefore, accelerometers were placed on the slab bottom to evaluate the slab vibration. Accelerometers A1, A2, and A3 corresponded to the locations of the sensors F1, F2, and F3, as shown in Figure 5b. Meanwhile, the displacement at the slab center was monitored with a high-speed camera during the collision between the drop weight and cushion. The high-speed camera had a shooting frequency of 7 kHz to capture the displacement of the slab subjected to the drop weight impact.

The geofoam–sand cushion consisted of a geofoam layer and a sand cushion. The geofoam was used as the bottom layer and the sand cushion was placed above the geofoam layer. In this study, a single geofoam block was placed on the bottom of the sand cushion. No edge restraint was needed to fix the geofoam in the cushion layer, but the foam blocks should be placed closely and layer-by-layer to meet the requirement of the cushion size in practical applications. Nine model tests with different geofoam types and thicknesses were designed, as shown in

Table 2. Model test variables.

Model Test	Geofoam Type	Geofoam Thickness (m)	Sand Thickness (m)
U	None	None	0.15
S1	EPS	0.01	0.14
S2	EPS	0.02	0.13
S4	EPS	0.04	0.11
S6	EPS	0.06	0.09
E1	EPE	0.01	0.14
E2	EPE	0.02	0.13
E4	EPE	0.04	0.11
E6	EPE	0.06	0.09

. The symbols U, S, and E represent the unreinforced, EPS–sand, and EPE–sand cushions, respectively, and the numbers behind the symbols denote the geofoam thickness and the rock drop height. For example, E6-1.0 indicates the test where the EPS–sand cushion with an EPS thickness of 6 cm is hit by the weight dropped from 1.0 m, while U-1.5 represents the test where the unreinforced sand cushion is hit by the weight dropped from 1.5 m. Furthermore, the other symbols are defined in the same way in the following sections.

4. Test Results

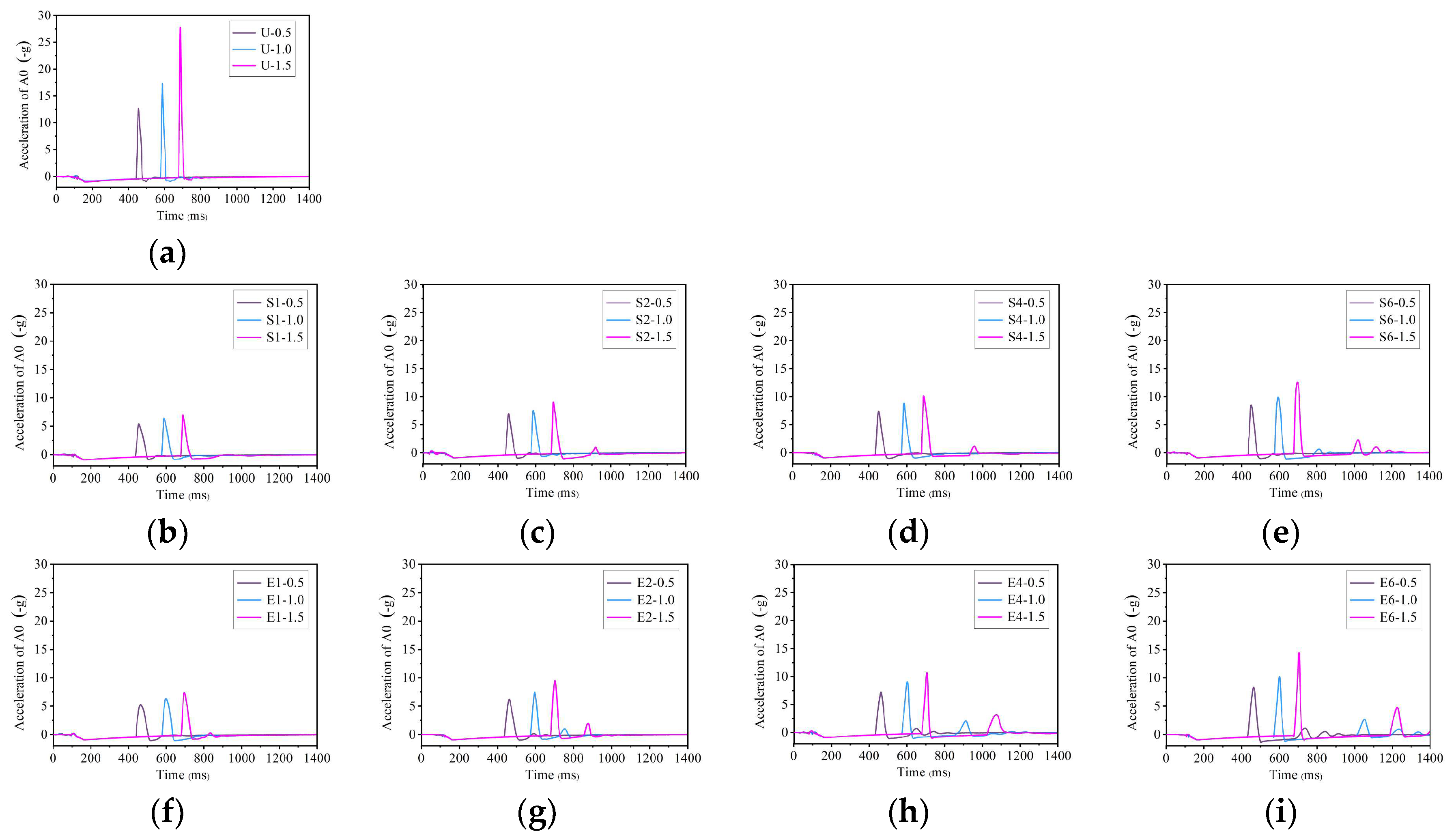
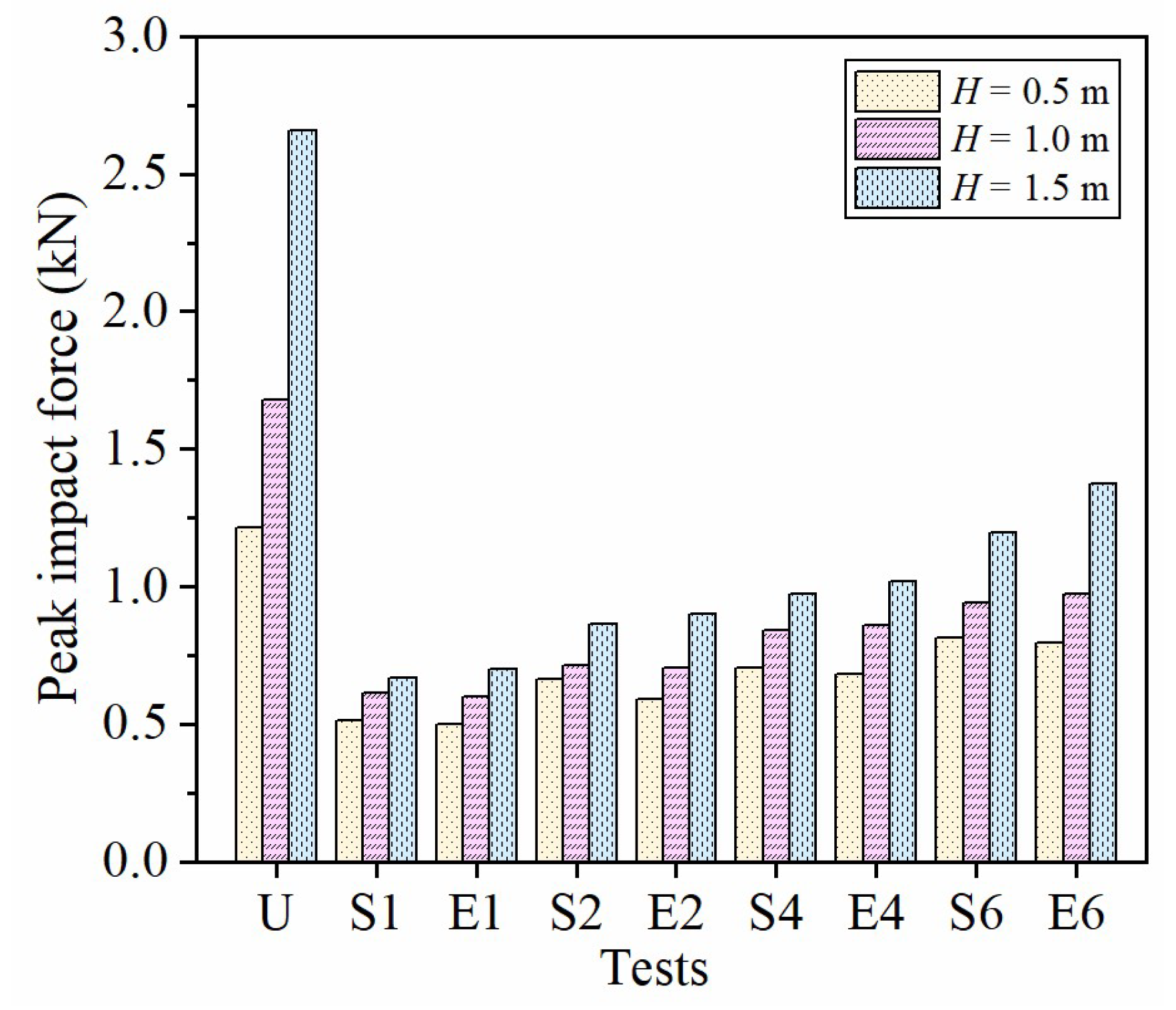
4.1. Impact Responses of the Drop Weight

During the descent of the drop weight (i.e., rockfall) after release, its motion was captured by the accelerometer A0. Figure 6 shows the acceleration responses of the drop weight in the impact tests with and without geofoam in the sand cushion. It should be pointed out that the direction of gravity is regarded as positive in this study. The drop weight started falling when it was released from the crane. The unhooking between the crane and drop weight resulted in jitters in the accelerometer A0 at the beginning of the impact test, as shown in Figure 6. Then, the acceleration of the drop weight increased immediately to gravitational acceleration while the drop weight started to free fall. Before the drop weight hit the cushion, the velocity of the drop weight increased gradually due to the positive acceleration. At the same time, the air resistance of the drop weight increased with the increase in velocity. Therefore, the acceleration decreased with the increase in air drag before the drop weight hit the cushion. When the falling weight made contact with the cushion, the sand cushion with or without geofoam acted as a damper to dissipate the impact energy. With the increase in resistance provided by the cushion, the acceleration of the drop weight decreased rapidly to zero and then increased immediately to the peak value with the opposite direction. Meanwhile, the velocity decreased rapidly to zero until the peak impact acceleration was obtained. Then, the drop weight stopped or bounced up, resulting in a decrease in acceleration, as shown in Figure 6. If the weight still had high kinetic energy after the first impact, the drop weight would bounce up and down on the cushion until coming to a complete stop, especially in tests with the geofoam-reinforced sand cushion.

Figure 6 shows that the peak acceleration of the drop weight increased with the increase in impact energy. For example, the drop weight that was released from 0.5 m and hit the cushion U led to a peak acceleration of 12.7 g. When the drop height increased from 0.5 to 1.0 and 1.5 m, the peak accelerations rose to 17.7 and 27.9 g, respectively. Furthermore, the peak acceleration in the acceleration–time curve (i.e., Figure 6) multiplied by the rock mass was used to calculate the peak impact force of the drop weight. It should be mentioned that only the normal contact between the rock and cushion layer was considered for impact force evaluation in this study. Figure 7 indicates that the peak impact force of the rockfall decreased by 33.1~74.9% when using geofoam to replace the sand cushion with a certain thickness. When the drop weight was released from 0.5 m to hit the geofoam-reinforced sand cushion, the EPE–sand cushion caused a lower peak impact force than the EPS–sand cushion did. This is possibly because the strain of the foam was at a low level under the impact energy of 47.5 J. The EPE foam had a lower stress than the EPS foam when the strain was below 0.34, as shown in Figure 3. When the rockfall released from 1.0 m, placing a 1 or 2 cm thick EPE foam in the sand cushion still resulted in a lower peak impact force than using EPS foam. However, the EPE foam led to a higher peak impact force with the thickness of 4 or 6 cm. In addition, the EPE–sand cushion also showed a higher peak impact force than the EPS–sand cushion in the tests where the drop weight was released from 1.5 m. The foam strain increased with the increase in the impact energy and foam thickness. As the strain exceeded 0.34, the stress of the EPE foam was higher than that of the EPS foam (Figure 3), which contributed to the higher peak impact force in the tests with the EPE–sand cushion. Meanwhile, as compared with the EPS foam, the high resilience rate (i.e., 95%) of the EPE foam also led to a higher peak impact force. Clearly, the impact energy of the drop weight cannot be dissipated by a single impact, due to the high resilience rate of EPE foam. As a result, the EPE–sand cushion had more rockfall ricochets than the EPS–sand cushion (Figure 6), and the ricochets of the rockfall on the EPE–sand cushion had an increased bounce duration and acceleration magnitude in comparison with the EPS-reinforced sand cushion.

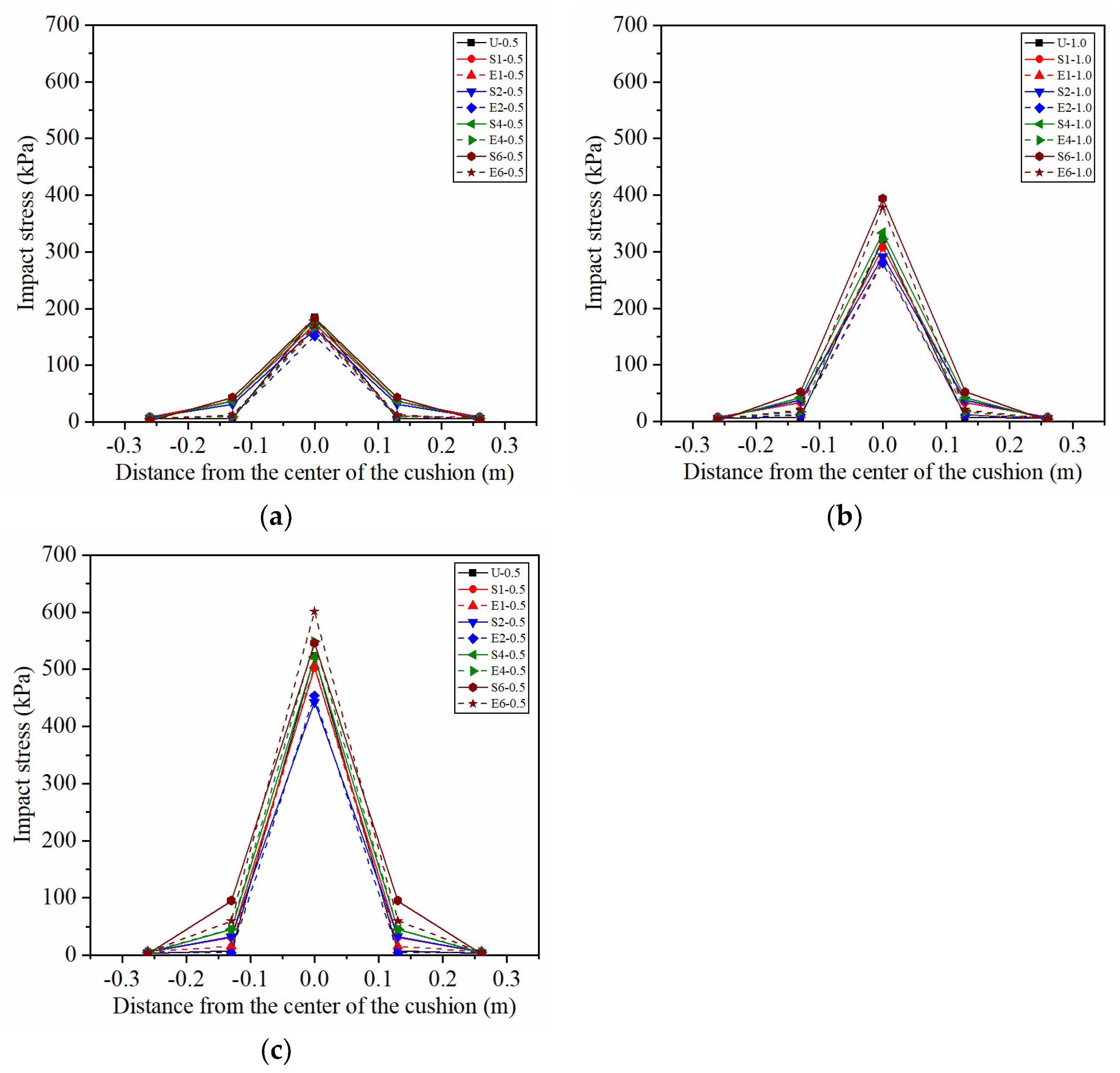
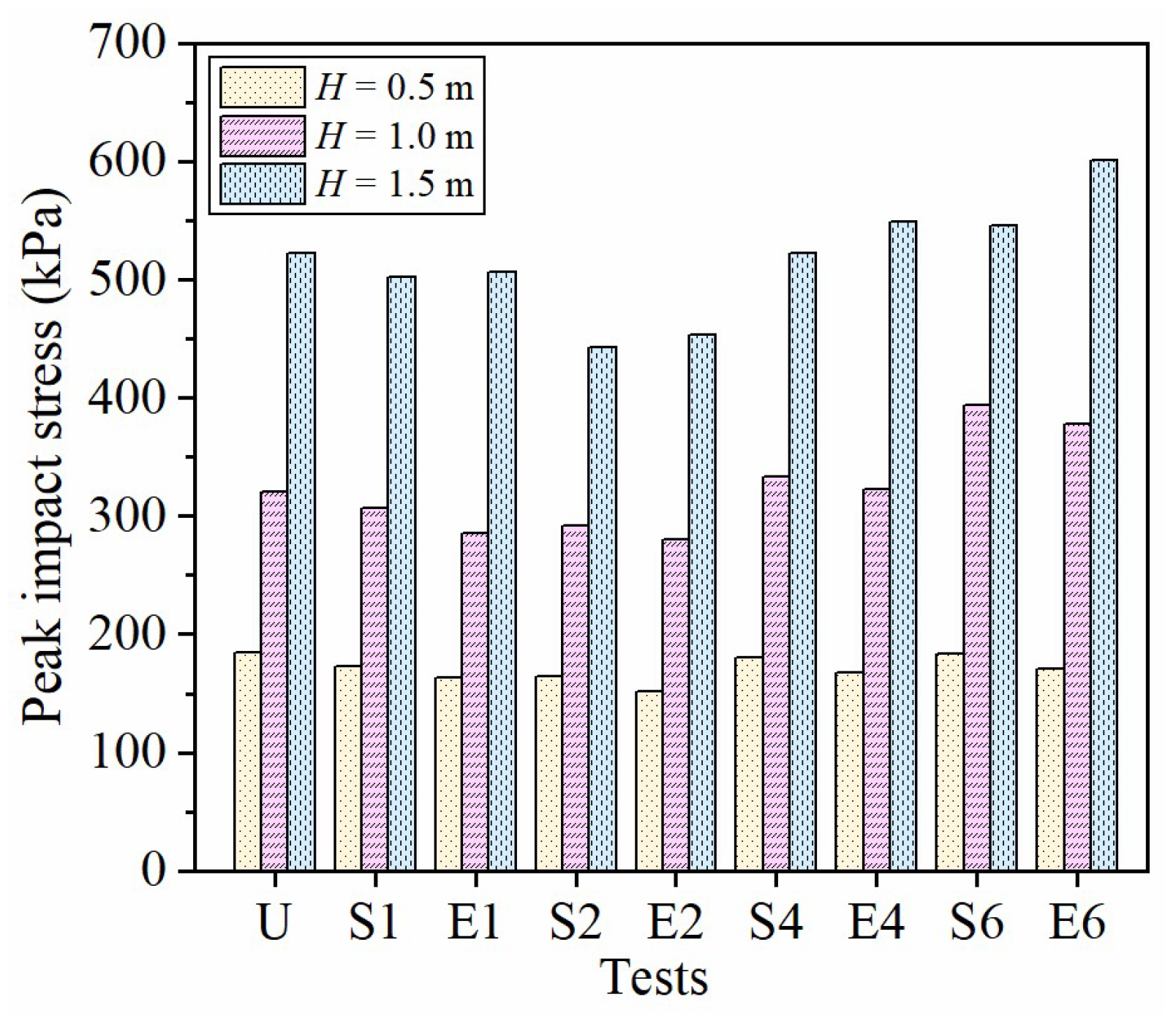
4.2. Stress Distribution at Cushion Bottom

The sand cushion reinforced by geofoam works as a buffer to distribute the rock impact energy. The impact stress distributed at the cushion bottom can directly affect the safety of the rockfall gallery. A spherical rockfall was used in this study to conduct the impact tests; thus, the impact stress distributed at the cushion bottom can be assumed to be symmetrical along the centerline of the gallery slab. As a result, the impact stress distribution on the cushion bottom is shown in Figure 8. Apparently, the peak impact stress occurred at the impact point (i.e., cushion bottom center). Furthermore, the impact stress decreased with increasing distance away from the cushion bottom center. Compared with the impact stress at the cushion center, there was a steep drop 0.13 m away from the cushion center. Meanwhile, the impact stress decreased slightly as the distance increased from 0.13 to 0.26 m.

Figure 9 shows the impact stress at the cushion bottom center. When the rock was dropped from 0.5 m, using geofoam as reinforcement in the sand cushion can decrease the impact stress significantly. The peak impact stress was 184.3 kPa at the bottom of the sand cushion without geofoam, and the peak impact stress of the geofoam-reinforced sand cushion was reduced by 0.6~17.6% in comparison with the sand cushion without geofoam. However, when the rock fell from 1.0 and 1.5 m, the thick geofoam (e.g., 4 and 6 cm) may result in a higher peak impact stress than that in test U. For example, the peak impact stress at the cushion bottom increased by 5.3 and 5.0% in tests E6-1.0 and E6-1.5, respectively. All the geofoam-reinforced sand cushions followed the same trend: the peak impact stress at the bottom of the sand cushion decreased first and then increased with the increase in geofoam thickness. The sand cushion can move to the surrounding area for energy dissipation against rockfall impact. Meanwhile, the geofoam had good deformability and resilience to absorb and release the impact energy. Clearly, a certain thick sand cushion is needed to provide sufficient deformation for the penetration of a rockfall. Furthermore, a geofoam layer with a suitable thickness in the sand cushion is conducive to dissipating the impact energy by its compressibility. However, thick geofoam will decrease the thickness of the sand cushion. When the rock had high impact energy, the thick geofoam was highly compressed and resulted in a high resistance to rock penetration. Thanks to the large deformation, the resilience of thick geofoam would release lots of energy. The up-layer sand cushion had a decreased energy absorption capacity limited by its thickness. When energy was partly dissipated to the gallery slab, there was increased impact stress within the sand cushion in the tests with thick geofoam compared with the tests without geofoam, especially under high impact energy. In this study, the low thickness of geofoam (e.g., 1 and 2 cm) effectively reduced the peak impact stress of the cushion in comparison with the cushion layer in test U. Furthermore, using the 2 cm thick geofoam to replace the sand cushion can obtain the minimum peak impact stress at the cushion bottom.

It should be mentioned that the EPE–sand cushion had a lower impact stress than the EPS–sand cushion when the rockfall started from 0.5 or 1.0 m. On the contrary, the EPE foam led to a higher impact stress within the sand cushion compared to the EPS foam when the rock was dropped from 1.5 m. This is possibly because the strain of EPS and EPE geofoam below 0.34 was subjected to low-energy rockfall impacts (i.e., 47.5 or 95.0 J). Therefore, the stress of EPE foam was lower than that of EPS foam with the same strain, as shown in Figure 3, and the increasing strain resulted in a decreased stress difference between EPE and EPS foams after the elastic stage of the EPS foam. However, the high impact energy of the rockfall may result in a large deformation of geofoam when the rock falls from 1.5 m. EPE foam showed a higher stress than EPS foam when the foam strain was larger than 0.34. Meanwhile, the stress difference between EPE and EPS foams increased with the increase in the foam strain. As a result, Figure 9 shows that EPE foam may have a higher stress than EPS foam against rock impact with high energy.

4.3. Vibration of the Gallery Slab

In addition to the impact energy absorbed by the cushion layer, the energy of the rockfall can be partly dissipated by the rockfall gallery. The gallery slab vibration can be measured by the accelerometers, which were placed on the slab bottom. Peak acceleration occurred when rock hit the cushion layer. Then, the acceleration varied up and down before finally settling on zero with time [11]. Figure 10 shows the peak acceleration at different positions of the gallery slab. The peak acceleration decreased significantly when the EPS or EPE foam was used to replace sand with a certain thickness in the cushion layer. For example, the peak acceleration of the unreinforced sand cushion was 4.4 m/s² at the slab bottom center (i.e., the position of accelerometer A1) when the rock fell from 0.5 m. Compared with the sand cushion without geofoam, the peak acceleration of A1 in the tests with the geofoam-reinforced sand cushion decreased by 56.2~86.0%. Furthermore, with the rockfall drop height increased to 1.0 and 1.5 m, the peak acceleration reduced significantly (around 80%) when geofoam was placed in the sand cushion. In addition, a position far away from the slab center had a lower acceleration, as shown in Figure 10. The stress wave induced by the rockfall propagated to the surrounding area within the cushion layer. Therefore, the vibration of the slab decreased with increasing distance far away from the slab center. For instance, the peak acceleration of A1 was 4.0 m/s² in test E1-1.5. The peak acceleration of A2 and A3 decreased by 19.1 and 44.9%, respectively, in comparison with the peak acceleration of A1. Similar to the impact stress, the peak acceleration of the slab decreased first and then increased with increasing foam thickness. Optimum foam thicknesses of 2 and 4 cm, respectively, can reduce the slab vibration when the sand cushion is partly replaced by EPS and EPE foams.

Slab displacement is another parameter characterizing slab vibration. Based on the random speckle pattern sprayed on the accelerometer A1, the displacement of the slab center was obtained by comparing the pixel intensity array subsets on the images captured by the high-speed camera. The displacement of the slab center decreased by 31.1~72.5% when geofoam was placed on the sand cushion bottom. Figure 10 indicates that the EPE foam resulted in a lower acceleration on the gallery slab than the EPS foam in the geofoam-reinforced sand cushion. Although there was a low displacement magnitude (below 0.1 mm), the displacement of the slab center showed a similar trend as the acceleration response of the slab center. In other words, the EPE-reinforced sand cushion led to a smaller slab displacement as compared with the EPS-reinforced sand cushion. As mentioned above, the collapse of the cell walls occurred in the EPS foam when the reinforced cushion was subjected to rockfall impact with high energy. In this way, the high impact energy of the rockfall can be partly dissipated by the plastic deformation of EPS foam. However, the resilience of EPE foam (i.e., 95%) was more than twice as high as that of the EPS foam (i.e., 44%). The majority of the absorbed impact energy by the deformation of EPE foam will be released to the sand cushion by its resilience, resulting in the low acceleration and displacement level of the gallery slab.

5. Discussion

Some studies were conducted to compare the impact responses of EPS and EPE foams, and it was proposed that the EPE foam was more favorable than the EPS foam when placing it within the sand cushion against rock impact [27,29]. In this study, the impact test results showed that the impact responses of geofoam were affected by the foam type, thickness, and impact energy. As mentioned above, the EPE-reinforced sand cushion had favorable energy absorption capacity in comparison with the EPS-reinforced sand cushion when the rockfall had low impact energy (e.g., drop heights were 0.5 and 1.0 m). Figure 11 shows the typical damage pattern of the geofoam and omits the tests with no visible plastic damage on the foam surface. Generally, geofoam damage increased with the increase in foam thickness and drop height. When the rock fell from 0.5 m, there was no visible plastic damage on the foam surface that contacted with the sand layer, even in the tests with 6 cm thick geofoam (Figure 11a,e). Furthermore, cracks began to generate on the EPS and EPE foams as the thickness increased to 4 and 6 cm when the rock drop height was 1.0 m. The small number of cracks indicated that the EPS and EPE geofoams had a low strain level. Therefore, the EPE foam may lead to lower impact stress than the EPS foam, as shown in Figure 3.

However, the EPS-reinforced sand cushion led to a lower impact force and impact stress than the EPE-reinforced sand cushion subjected to high impact energy (e.g., drop height of 1.5 m). On one hand, the EPS foam had a lower stress than the EPE foam resulting from the large strain caused by the high impact energy (Figure 3). On the other hand, the EPS foam had more plastic damage than the EPE foam with the same thickness under high-energy rock impact, as shown in Figure 11. Punching shear failure occurred on the EPS and EPE foams against rock impact. Cracks were easily generated along the cell walls of EPS foam. To dissipate the high impact energy, the small cracks propagated and connected to form a large fracture, finally resulting in damage to the EPS foam, as shown in Figure 11p. Unlike the EPS foam, small cracks generated around the impact point on EPE foam and no penetrating crack occurred (Figure 11l). Thus, there were fewer cracks on the EPE foam than the EPS foam under the same energy level. The layered expandable polyethylene was compressed under rock impact until punching shear failure occurred. The EPE foam exhibited remarkable compressive deformation to absorb the high impact energy. Furthermore, the absorbed impact energy was instantly released to the sand cushion and gallery slab thanks to the good resilience of EPE foam. The EPS foam can absorb more energy due to the fracture, thus exhibiting lower impact stress on the gallery slab than the EPE foam.

The placement of a suitable type of geofoam to replace the sand cushion of an appropriate thickness for the rock gallery could decrease the impact force of falling rock, reduce the impact stress within the sand cushion, and minimize the vibration of the gallery slab. In this way, the sand layer and geofoam layer can work together to improve the energy absorption capacity of the gallery cushion under rock impact. The EPE foam had remarkable impact resistance when being placed in the sand cushion subjected to low-energy rock impact. Meanwhile, the EPE foam had good durability thanks to its high resilience, which is effective against multiple rock impacts. Compared with EPE foam, the EPS foam can absorb more impact energy under high-energy rock impact, resulting from the crack generation and propagation. However, the failure of EPS foam will result in difficulties for the maintenance of the cushion layer. Furthermore, when thick EPS and EPE foams were placed on the bottom of the sand cushion, the resilience of the foams may lead to higher impact stress on the gallery slab compared with the unreinforced sand cushion, especially under high-energy rock impact (Figure 9). The test results indicate that a favorable geofoam thickness is below one third of the cushion thickness. In this way, the sand cushion obtained enough deformation against rockfall penetration. Geofoam could make good use of its resilience to absorb the impact energy.

6. Conclusions

Impact tests were conducted in this study to investigate the impact resistance of EPS–sand and EPE–sand cushions for improving the sustainability of a rockfall gallery. The effect of geofoam type, thickness, and impact energy on the impact characteristics of a geofoam-reinforced sand cushion was analyzed and discussed. The following specific conclusions are drawn:

• There was an increased rockfall impact force, impact stress on the cushion bottom, geofoam damage, and vibration level of the gallery slab with the increase in impact energy. The impact stress and slab vibration concentrated on the impact point and decreased with increasing distance from the center of the cushion bottom.
• The geofoam can significantly improve the impact responses of the sand cushion for the rockfall gallery. The rockfall impact force and the acceleration of the gallery slab reduced by 33.1~74.9% and 56.2~86.0%, respectively, when geofoam was placed on the sand cushion bottom. The peak impact stress at the cushion bottom was also reduced by the geofoam against a 47.5 J rockfall impact. However, the sand cushion reinforced with thick geofoam (i.e., 4 and 6 cm) against higher impact energy (i.e., 95.0 and 142.5 J) led to increased impact stress in comparison with the sand cushion without geofoam.
• The impact resistance of the geofoam-reinforced sand cushion increased first and then decreased with increasing foam thickness. A sand cushion with a certain thickness is needed to provide sufficient deformation for the geofoam-reinforced sand cushion to undergo rockfall penetration. Placing geofoam with a thickness below one third of the cushion thickness on the sand cushion bottom could obtain a favorable impact resistance of the cushion layer against rock impact.
• The EPE foam exhibited a better behavior in reducing impact force, impact stress, and slab vibration than the EPS foam did in the sand cushion under low impact energy. However, thick EPE foam may lead to a higher rock impact force than the EPS foam. Compared with the EPE foam, the EPS foam-reinforced sand cushion showed decreased impact force, impact stress, and bounce times as well as an increased slab vibration when the rockfall had high impact energy. Moreover, there was less damage to the EPE foam as compared with the EPS foam thanks to its good resilience.