Abstract
This paper investigates the impact of carbon emissions trading schemes (CETSs) on agricultural green total factor productivity (AGTFP) using a multi-temporal DID model. Using Chinese prefecture-level city data collected from 2004 to 2022, we find that CETSs enhance AGTFP through technological innovation, with stronger effects in eastern and western regions and positive spillover to neighboring cities. These findings underscore the significant role of CETSs in influencing agricultural productivity and highlight the various factors that contribute to improving AGTFP.
1. Introduction
The Emission Gap Report 2021 published by the United Nations Environment Programme (UNEP) states that global emissions of carbon dioxide currently exceed 40 billion tons per year. To prevent detrimental effects on climate, significant emission reductions are needed over the next decade [1,2]. Agriculture, accounting for approximately 24% of global emissions, is a critical sector necessitating action, requiring sustainable practices to balance productivity and environmental goals [3,4]. The Organization for Economic Cooperation and Development [5] further notes that market-based instruments, such as CETSs, play an important role in facilitating technological innovation and regional diffusion, which can increase agricultural productivity while reducing emissions. As such, China has committed to achieving peak carbon emissions by 2030 and carbon neutrality by 2060, known as the “double carbon” goal, through a combination of command-and-control measures and market-based tools like carbon emissions trading schemes (CETSs). While command-and-control approaches result in reduced emissions, their high costs and industry pushback limit industrial restructuring. A CETS, by contrast, allocates carbon emission allowances to enterprises, fostering green, low-carbon development through market mechanisms. In 2011, seven provinces—Beijing, Tianjin, Shanghai, Chongqing, Shenzhen, Hubei, and Guangdong—initiated carbon emissions trading schemes, progressively broadening the range of industries participating in the carbon emissions trading market [6,7]. In 2021, the inaugural compliance cycle of China’s national carbon emissions trading saw annual emissions from enterprises in the carbon emissions trading market reach 4.5 billion tons, with the amount of traded carbon reaching 167 million tons, which illustrates the growing significance of carbon emissions trading [8].
Although the total carbon emissions from agriculture are comparatively lower than those from industrial sources, the factors contributing to agricultural carbon emissions are more intricate. Additionally, the significant rise in agricultural production has been accompanied by a corresponding increase in agricultural carbon emissions [9]. In 2021, agricultural greenhouse gas (GHG) emissions constituted between 20% and 25% of global GHG emissions. By 2050, greenhouse gas emissions from the agricultural sector are projected to increase by 58%, making agricultural emissions some of the most challenging to manage [10]. Therefore, it is essential to decrease carbon emissions within the agricultural sector to support the achievement of the “double carbon” objective. The effort to reduce agricultural carbon emissions faces considerable obstacles. On the one hand, the need for a reduction in agricultural carbon emissions is likely to adversely affect agricultural production activities, potentially impacting agricultural development and farmers’ income [11,12]. On the other hand, agricultural production in China continues to depend heavily on chemical fertilizers and pesticides. The shift towards more sustainable farming methods aimed at reducing carbon emissions faces several challenges, particularly the increasing demand for food [13,14]. Consequently, it is essential to integrate agricultural economic development with carbon emission reduction efforts within a cohesive framework.
The theory of economic growth posits that total factor productivity (TFP) is the primary metric for evaluating economic advancement. It further asserts that disparities in TFP growth are the fundamental drivers of economic inequalities between nations and regions [15]. The process of agricultural modernization is primarily marked by a rise in TFP’s contribution to the growth of the agricultural economy [16,17]. However, the traditional approach to measuring agricultural total factor productivity (ATFP) focuses on evaluating factor inputs and desired outputs, often overlooking the impact of undesired outputs. With the increasing utilization of modern agricultural inputs, including pesticides, agricultural films, fertilizers, and machinery, total carbon emissions from agriculture are also increasing, paralleling the growth in agricultural output [18,19]. This phenomenon gives rise to the designation of agriculture as a “high carbon nature” sector [20]. It is evident that assessing the quality of agricultural growth necessitates considering the environmental costs associated with agricultural production, which include carbon emissions and the pollution of agricultural land [21]. As a result, AGTFP is considered a more scientifically sound metric for assessment.
The trading of carbon emissions is a market-driven method for regulating environmental impacts, facilitating a cost-efficient approach to managing carbon outputs while considering external costs. Within the framework of the global advancement of carbon emissions trading practices, studies undertaken by researchers around the world regarding the mechanisms of carbon emissions trading predominantly focus on two main areas. The first is the overall effectiveness of carbon emissions trading at the macro level. Scholarly consensus indicates that carbon emissions trading is an effective strategy for reducing emissions, offering environmental benefits and significantly impacting neighboring communities [22,23]. Moreover, some researchers contend that carbon emissions trading can promote economic growth while concurrently reducing emissions [24,25]. Nevertheless, various researchers have found that the expected reduction in emissions from the implementation of a carbon emissions trading policy has not been achieved. Furthermore, they have highlighted potential limitations in the effectiveness of the carbon market in fostering regional economic growth [26]. The other area of focus is the micro-level effectiveness of carbon emissions trading. In line with Porter’s hypothesis, some scholars argue that the environmental regulations embedded in carbon emissions trading schemes can foster a mutually beneficial relationship between economic growth and environmental sustainability [27]. They further suggest that the implementation of a carbon emissions trading scheme can improve companies’ financial performance, encourage greater investment in research and development, and promote technological innovation within organizations, ultimately resulting in an increase in their overall value [28,29]. Nevertheless, some scholars, on the basis of the “constraint hypothesis”, contend that carbon emissions trading will engender augmented costs for enterprises, which can impede enterprise profit maximization and, to a certain extent, will hinder the innovative performance of enterprises, which may reduce their value [30].
Scholars have presented useful discussions of the policy effects and mechanisms of carbon emissions trading, indicating that as a market-based environmental policy tool, it can encourage technological innovation and emission reduction through carbon pricing, but no consistent conclusions have yet been reached; this is especially true for the agricultural sector, on which fewer studies have been conducted, with most focusing on the provincial level and lacking heterogeneity and attribution analyses for different regions. Most existing studies have focused on the industrial and energy sectors, exploring the impact of CETSs on emissions, economic growth, and enterprise performance. However, insufficient attention has been paid to the direct role of green total factor productivity (GTFP) in agriculture, with few studies addressing the criticality of agriculture as a high-carbon emission industry in sustainable development. Furthermore, although the difference (DID) method is often adopted in research to analyze policy effects, the spatial dimension is less often considered, and the inter-regional technology diffusion and spillover effects caused by CETSs have not been fully elucidated. In this context, based on a multi-temporal DID model, this paper investigates the impact of CETSs on AGTFP using city-scale panel data recorded from 2004 to 2022. Furthermore, it investigates the mechanisms of this impact and the potential spatial spillover. Our goal is to provide a reference for the ongoing enhancement of the carbon emissions trading market and support the promotion of sustainable development practices within the agricultural sector.
This study makes several contributions to the existing body of literature. First, it broadens the discourse on the economic impacts of CETSs, a topic that has garnered significant interest from both researchers and practitioners. In numerous studies, researchers have investigated the diverse economic consequences of CETSs. These studies include investigations into firm debt financing [31], carbon productivity [32], carbon emission performance [33], overall firm performance [34], stock returns [35], technology transfer [36], and green economy efficiency [37], among others. In this paper, we illustrate that the adoption of a carbon emissions trading scheme can substantially improve agricultural green total factor productivity by fostering innovation.
Second, we contribute to the current literature on green total factor productivity by emphasizing the different methodologies employed in prior studies. Many studies have employed the DEA method to proxy different forms of total factor productivity, including urban [38,39], corporate [40,41], forestry [42], grain [43], and transportation [44] green total factor productivity, among others. This paper primarily concentrates on measuring green total factor productivity from an agricultural perspective, emphasizing the unique contributions and challenges within this sector. Using the super-efficient Slacks-Based Measurement-Directional Distance Function (SBM-DDF) model, we measure agricultural green total factor productivity in Chinese prefecture-level cities.
Third, we advance research on the determinants of AGTFP by identifying essential factors that affect its growth and sustainability in the agricultural sector. Existing evidence suggests many variables can significantly impact AGTFP, such as digital finance and digital economy [45,46,47,48], agricultural insurance [49,50], green finance [51], green trade barriers [52], and agricultural credit [53]. Moreover, various studies examine the influence of environmental policy on AGTFP, concentrating on elements like environmental regulation [54] and climate change [55]. Like other environmental policies, we perform an empirical analysis of the connection between CETSs and agricultural green total factor productivity. Additionally, this study supports the theory that CETSs enhance AGTFP by encouraging innovation.
The rest of this article is structured as follows. Section 2 presents the theoretical framework and research hypothesis; the methodology is introduced in Section 3, including the identification strategy, the data source, and a description of the variables; Section 4 investigates the association between CETSs and AGTFP; and Section 5 concludes the study.
2. Theoretical Analysis and Research Hypothesis
The environmental harm resulting from excessive carbon emissions generates significant negative externalities. Carbon emissions trading addresses these by adhering to the “polluter pays” principle, effectively internalizing the costs associated with carbon emissions. According to the Coase theorem, negative externalities can be mitigated through market mechanisms if property rights are clearly defined, thereby providing a direct theoretical foundation for carbon emissions trading. Firstly, under the framework of clearly defined property rights, carbon emissions trading enables enterprises with carbon emission quotas to engage in the carbon trading market according to established rules and transparent procedures. Enterprises that possess surplus emission rights can derive external benefits by selling their quotas, while those with excess emissions incur higher costs, thereby incentivizing them to reduce their carbon emissions, as it is more cost-effective. Specifically, as the price of carbon rises, the cost of acquiring carbon credits for companies increases, prompting them to actively pursue methods to reduce their emissions. Additionally, carbon emissions trading generates positive returns for leading companies in emission control and carbon reduction, motivating more companies to adopt low-carbon production practices, thereby establishing a foundation for achieving significant reductions in carbon emissions. The cost–benefit approach of carbon emissions trading uses market instruments to drive companies to meet their carbon reduction targets. In particular, carbon emissions trading has a strong signaling role, sending a clear signal to major carbon emitters and to society as a whole to reduce their emissions. This approach will not only directly encourage low-carbon choices among stakeholders, prompting companies to adopt more proactive measures to reduce carbon emissions and select low-carbon production methods, but will also stimulate consumer demand for low-carbon products. Consequently, this increased demand will drive companies to enhance their production processes and further reduce carbon emissions from the demand side. Ultimately, the local government’s policy preference for low-carbon emission reduction, along with the social reputation linked to emissions trading, will motivate companies to actively participate in carbon emissions trading. This involvement, in turn, encourages them to implement more carbon-reducing practices. Consequently, this paper argues that carbon emissions trading can enhance AGTFP by effectively lowering carbon emissions and minimizing undesirable outputs.
Carbon emissions trading addresses the negative external costs associated with carbon emissions by establishing a clear price for carbon and delineating the costs of emission reduction. This mechanism compels companies to pursue green transformation initiatives while also accelerating research and development (R&D) and innovation in carbon reduction technologies by fostering a platform that facilitates the flow and diffusion of capital and technology. In agriculture, CETSs facilitate the adoption of low-carbon technologies by freeing up capital from surplus allowances, which firms can reinvest into innovative practices. Technologies such as drip irrigation and soil moisture sensors reduce energy-intensive water pumping [56]. Similarly, precision agriculture tools, like GPS-guided equipment and variable rate technology, optimize input use, reducing emissions, enhancing water-use efficiency, and improving AGTFP [57]. The adoption of such technologies is often supported by capital freed up through emissions trading, as firms with surplus allowances can invest in innovative practices. Additionally, carbon emissions trading as a means of reducing emissions by “capping total emissions and trading allowances” brings additional benefits to those with low energy usage. If enterprises improve their energy structure and energy use efficiency through technological innovation in the production process, they can reduce their energy consumption while increasing output, achieving both environmental and economic benefits. For agricultural enterprises with insufficient research and development capacity, adopting energy-efficient irrigation systems or methane capture technologies for livestock results in immediate emission reductions while maintaining output [58,59]. These advancements, supported by CETSs, not only lower compliance costs, but also stimulate technological upgrades in upstream equipment manufacturing, fostering the broader diffusion of low-carbon innovations across the agricultural sector [60]. Furthermore, the government will create policy conditions that align with carbon reduction within the framework of carbon emissions trading, incentivizing companies engaged in the carbon trading market to pursue technological innovation, such as conservation tillage or renewable-energy-powered equipment. This initiative aims to promote research and development, as well as the adoption of low-carbon technologies by businesses, thereby contributing to the reduction in carbon emissions [8]. Consequently, this paper contends that carbon emissions trading can enhance AGTFP through technological innovation. In essence, CETSs provide both economic impetus and financial pathways for agricultural enterprises to invest in, adopt, and widely disseminate green technologies, ultimately fostering a more sustainable and productive agricultural sector.
The above provides a comprehensive overview of the impact of carbon emissions trading on AGTFP. However, it is important to note that the effects may vary significantly across regions, as they are closely linked to regional environmental conditions and resource endowments. Theoretically speaking, the influence of CETSs on regional heterogeneity can be understood from the perspective of economic geography, which holds that the spatial differences in economic development and resource allocation determine policy outcomes. In China, the persistent imbalance in regional development has led to different economic and institutional backgrounds. The more developed regions, especially the eastern part of China, have sound infrastructure, attract high-tech enterprises and high human capital, and create an environment conducive to the effective implementation of CETSs and the adoption of green technologies. On the contrary, the economically underdeveloped central and western regions may face resource constraints, but they will benefit from the policy-driven catch-up effect, because CETSs encourage low-carbon agricultural practices. This suggests that the influence of carbon emissions trading on AGTFP may differ based on the level of regional development. To demonstrate this heterogeneity, we divide China into eastern, central, and western regions to reflect their different levels of economic development and resource endowments [61]. Moreover, public environmental policy is also influenced by regional environmental policy preferences. The stronger the environmental awareness of the local government, the more likely it is to provide relatively lenient environmental financial support to stimulate the development of regional green transformation; moreover, enterprises will tend to choose environmentally friendly technology in the production process and use cleaner production methods to adapt to social and environmental preferences. As a comprehensive environmental policy instrument, the effectiveness of carbon emissions trading in reducing emissions is also shaped by regional environmental policy preferences. Consequently, this paper posits that the impact of carbon emissions trading on AGTFP varies according to the levels of regional economic development, environmental policy preferences, and other influencing factors.
According to Tobler’s first law of geography, neighboring things are more closely related than distant things. New Economic Geography also suggests that inter-regional economic linkages are closely related to spatial distance, i.e., carbon emissions trading may impact AGTFP through spatial transmission mechanisms. For ATFCP, due to the mobility of GHGs and the geographical linkages between regions, changes in carbon emissions in one region will affect neighboring regions, and many studies point to the diffusion of this effect through technological advances. Therefore, this paper contends that carbon emissions trading exerts a spatial spillover effect on AGTFP.
3. Methodology and Materials
3.1. Model Construction
3.1.1. DID Model
In October 2011, the General Office of the National Development and Reform Commission (NDRC) released a circular concerning pilot initiatives for carbon emissions trading, which granted authorization to seven provinces and municipalities to implement pilot projects in this area. Subsequently, Shenzhen, Beijing, Shanghai, Tianjin, and Guangdong officially launched their carbon emissions trading schemes in 2013, with Chongqing and Hubei following suit in 2014. This paper utilizes the two batches of carbon emissions trading initiatives from 2013 and 2014 as quasi-natural experiments and constructs a multi-temporal DID model to examine the impact of carbon emissions trading on AGTFP. The DID approach effectively captures temporal and spatial dependencies, suitable for the spatially heterogeneous nature of CETS policies. In contrast, alternative counterfactual approaches, such as the Synthetic Control Method (SCM), were considered but deemed less suitable than DID for this study. The SCM constructs a synthetic control unit as a weighted combination of untreated units to approximate the counterfactual outcome for the treated unit [62]. While the SCM is advantageous for single-unit or small-sample treatment scenarios, it is less effective in settings with multiple treated units and complex spatial interactions, as is the case here. Therefore, we build the model as follows:
where AGTFP is the agricultural green total factor productivity; is the core explanatory variable, indicating whether city i implemented carbon emissions trading in year t, and its estimated coefficient β1 is used to measure the implementation effect; represents the control variables; and are the controlling locality fixed effect and time fixed effect, respectively; and is a random disturbance term.
3.1.2. SBM Model
In this paper, drawing on the work of Fukuyama and Weber (2009) [63], the SBM model is employed to assess AGTFP. It is assumed that the entire sample consists of independent decision-making units. In this context, N, M, and I represent the inputs, desired outputs, and undesired outputs of each decision unit, with their respective sets denoted as A, B, and C. The entire sample is assumed to consist of K individually independent decision units, and N, M, and I are the inputs, expected outputs, and undesired outputs of each decision unit, whose set is denoted by , , and , respectively. The specific SBM directional distance function with a variable scale reward is constructed as follows:
where xt,k′, yt,k′, and bt,k′ are the vectors of the inputs, desired outputs, and undesired outputs for the kth decision unit in period t; gx, gy, and gb are the vectors of positive directions for input reductions, desired output increases, and undesired output decreases, with , , and ; , , and are the slack variables for the inputs, desired outputs, and undesired outputs; and is a constant vector representing the weight of each decision unit.
3.1.3. Mediation Effect Model
To investigate the impact mechanism of carbon emissions trading on AGTFP, with reference to Baron and Kenny (1986) [64], this paper constructed a mediating effect model for analysis, where Mit represents the mediating variable of city i in year t, and definitions of the remaining variables are the same as in Formula (1).
3.1.4. Spatial DID Model
To satisfy the stability hypothesis of the individual treatment effect, bias in the estimation coefficient should be avoided [65]. This paper further develops a spatial DID model, following the approach of Zhang et al. (2024) [66], to examine the spatial spillover effects of carbon emissions trading on AGTFP. Spatial DID models better accommodate these dynamics by explicitly modeling spatial relationships and allowing for heterogeneous treatment effects across multiple units, thereby providing a more robust framework for estimating both the direct and indirect effects of carbon emissions trading on AGTFP. The specific model is shown below:
where ρ is the spatial autoregressive coefficient; λ is the spatial autocorrelation coefficient; N is the number of cities; and is the spatial weight matrix. This paper includes a spatial adjacency matrix, a spatial geography weight matrix, an inverse distance matrix, and a distance-squared matrix. are spatial lag terms for the explained variable, explanatory variable, and control variables, respectively, and is the average spillover effect of the city where the pilot policy is located to neighboring cities.
Our study employs four spatial weighting matrices—neighborhood, spatial geography, inverse distance, and distance squared—to model spatial relationships between Chinese prefecture-level cities from 2004 to 2022. CETSs are expected to generate spatial spillover effects because the environmental and economic policies of a city may affect neighboring regions through technology diffusion, trade, or resource flows [67]. The neighborhood matrix, based on shared boundaries, captures local policy diffusion [68], while the spatial geography matrix accounts for topographic variations affecting spatial interactions. The inverse distance matrix reflects linearly diminishing economic and environmental impacts with distance, and the distance-squared matrix further emphasizes the attenuation of impacts with distance, making it suitable for capturing long-distance, albeit weaker, spillover effects [69].
3.2. Variables
3.2.1. Explained Variable: AGTFP
In accordance with the definitions provided by Wang et al. (2021) [70] and Song et al. (2022) [71], this study focuses on agriculture in a narrow sense, specifically cultivation, and identifies input variables in terms of land, capital, and labor. Land inputs are quantified as thousands of hectares of cultivated area. Capital inputs are categorized into machinery, irrigation, fertilizer, pesticide, agro-film, and diesel inputs. The total power of agricultural machinery is quantified as the machinery input. This is then multiplied by the proportion of the total agricultural output value relative to the combined output value of agriculture, forestry, husbandry, and fishing, and converted into plantation machinery power, with a measurement unit of 10,000 kilowatts. Irrigation input is quantified as the effective irrigated area in thousands of hectares. Fertilizer input is measured as the amount of fertilizer applied to agricultural holdings in tons, while pesticide input is expressed as the quantity of pesticide used in tons. Agro-film input is represented by the amount of plastic film utilized in agriculture in tons. Diesel input is quantified as the amount of diesel consumed on farms, also in tons. Labor input is calculated by multiplying the share of total agricultural output among the overall output of agriculture, forestry, husbandry, and fishing by the number of individuals employed in agriculture, yielding a value representing the number of persons engaged in plantation activities. The desired output variable is expressed in terms of gross agricultural output, adjusted to constant 2009-based prices in millions of RMB to mitigate the effects of price fluctuations. The undesired output variable is represented by carbon emissions, using six indirect carbon emission sources—agricultural tilling, irrigation, fertilizer, pesticide, agro-film, and diesel fuel—with a unit of 10,000 tons.
where E is the total amount of agricultural carbon emissions in tons; Ti is a carbon emission source; and is the emission coefficient of each carbon emission source. Specifically, in accordance with the definitions provided by Wu et al. (2007) [72] and Li et al. (2011) [73], the carbon emission coefficient of agricultural plowing is 312.6 kg/km2; that of agricultural irrigation is 20.476 kg/hm2; that of fertilizer is 0.8956 kg/kg; that of pesticide is 4.9341 kg/kg; that of agricultural film is 5.18 kg/kg; and that of diesel is 0.5927 kg/kg.
3.2.2. Core Explanatory Variable: Carbon Emissions Trading Schemes
This paper identifies carbon emissions trading schemes as the primary explanatory variable. In the model, the DID variable serves as the policy variable representing carbon emissions trading. The value of treati is as follows: i takes a value of 1 for the experimental group if i represents prefecture-level cities in Beijing, Tianjin, Shanghai, Chongqing, Guangdong, and Hubei, and 0 for the control group if i represents other cities. Since carbon emissions trading is carried out in batches, the value of postit is as follows: when i represents prefecture-level cities in Beijing, Shanghai, Tianjin, and Guangdong and t ≥ 2013, or i represents prefecture-level cities in Chongqing and Hubei and t ≥ 2014, the value of postit is 1; otherwise, it is 0.
3.2.3. Mediation Variable: Urban Innovation Index
Technological innovation includes a wide array of technologies, artifacts, or products aimed at minimizing environmental pollution and decreasing the consumption of raw materials and energy. This serves as an effective strategy to promote low-carbon development. In this paper, the level of technological innovation is characterized using an urban innovation index. This index is constructed using micro-level big data from two primary sources: patent data from the China National Intellectual Property Administration (CNIPA) and newly registered enterprise data from the State Administration for Market Regulation (SAMR). Specifically, we utilize invention patents granted by the CNIPA. While CNIPA patents include invention patents, utility models, and design patents, invention patents are chosen for this study because they have a higher bar for novelty, inventiveness, and practical applicability, making them a more robust indicator of true innovation capacity compared to utility models or design patents. It is also important to note that simply using the number of patents can be inaccurate. Patent holders must pay annual fees to maintain patent validity, and generally, older patents with longer lifespans tend to have greater private value. Therefore, to more accurately reflect innovation, we estimate the value of each granted invention patent using the patent renewal model proposed by Pakes and Schankerman (1984) [74]. The estimated values of individual patents are then aggregated to the city level, resulting in a comprehensive urban innovation index for each city.
3.2.4. Control Variables
To address potential omitted-variable bias, and with reference to relevant studies [19,52,75], this paper incorporated several factors influencing AGTFP, including industrial structure rationalization; industrial structure advancement; education expenditure level; educational attainment; environmental regulation level; agricultural economic development level; and road area per capita.
3.3. Data
The comprehensive data utilized in this study were primarily sourced from the China Urban Statistical Yearbook (2005–2023), China Statistical Yearbook (2005–2023), China Environmental Statistical Yearbook (2005–2023), China Agricultural Statistical Yearbook (2005–2023), China Animal Husbandry Yearbook (2005–2023), China Forestry and Grassland Statistical Yearbook (2005–2023), China Carbon Emission Database (CEADs), IPCC emission causes sub-database, and China patent database. Additionally, logarithmic transformations, linear interpolation for missing values, and outlier elimination for certain indices were conducted. The descriptive statistics of the data are shown in Table 1.

Table 1.
Descriptive Statistics.
This table provides the summary statistics for the complete sample, which comprises 5396 city-year observations spanning from 2004 to 2022. Detailed definitions of all variables can be found in Table A1.
4. Results
4.1. Baseline Results
Table 2 illustrates the baseline regressions evaluating the effects of CETSs on AGTFP. Specifically, Column (1) shows the estimation results from the DID regression without control variables, while Column (2) presents the results obtained upon incorporating the effects of control variables. Furthermore, both Columns (1) and (2) include clustered robust standard errors at the city level. The results in Column (1) reveal that CETSs positively influence AGTFP, which remains valid even after including the control variables in Column (2).

Table 2.
Baseline Results.
4.2. Parallel Trend Test
The analysis based on the DID method relies on the premise that there are no systematic disparities between the treatment and control groups before the policy intervention. This implies that there are no statistically significant variations in AGTFP prior to CETS implementation. To further validate the baseline findings [76,77], we employ an event study methodology and construct a dynamic model. In this reassessment, the year prior to the implementation of CETSs is designated as the reference group. Figure 1 illustrates the estimated coefficients for the primary interaction terms, accompanied by their corresponding 95% confidence intervals.
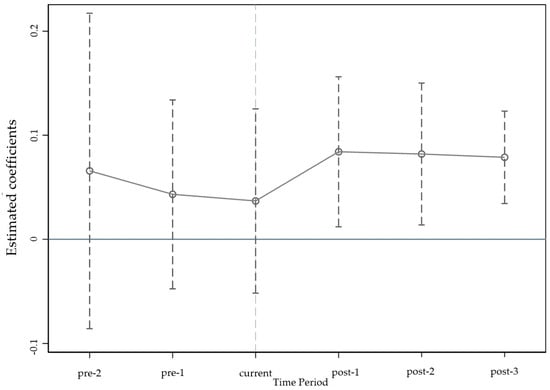
Figure 1.
Results of parallel trend tests.
Figure 1 clearly illustrates that the estimated coefficients for the primary interaction terms do not reach statistical significance prior to the implementation of CETSs. This indicates that there was no significant difference in AGTFP between the pilot and non-pilot regions before the enactment of this policy. Conversely, the coefficients for the interaction terms exhibit substantial significance following the policy shock, suggesting that the introduction of CETSs has a meaningful positive impact on AGTFP. These findings support the validity of using the DID approach to analyze the effects of CETSs on AGTFP.
4.3. Heterogeneity Analysis
4.3.1. Regional Heterogeneity
The benchmark regression results suggest that carbon trading policies typically improve green total factor productivity in agriculture. In this section, we explore whether this relationship varies among different sub-samples. First, we analyze regional differences, with the findings summarized in Table 3. Column (1) of Table 3 presents the results for the eastern region, while Columns (2) and (3) display the findings for the central and western regions, respectively.

Table 3.
Results of Heterogeneity Analysis: By Different Regions.
In contrast to the eastern and central regions, the western region is comparatively less developed regarding agricultural production levels, exhibiting fewer advancements in agricultural technology, management expertise, and infrastructure [69]. The western region is a vast area, with considerable variation in its climate and land dynamics, economic underdevelopment, transportation, and other factors limiting its technological development; therefore, in the absence of policy, because it has a low baseline of productivity, it has the potential for higher marginal production efficiency. The introduction of carbon trading policies may yield greater marginal benefits for the western region. These policies create new incentives and facilitate resource reallocation, leading to a notable enhancement in agricultural green total factor productivity in the western region.
Meanwhile, the eastern region exhibits superior overall technological standards and enhanced competitiveness in agricultural green technology relative to other regions. Consequently, this region can absorb some of the costs associated with enhancing AGTFP, benefiting from lower expenses related to agricultural green technology innovation and achieving more effective outcomes in green innovation.
4.3.2. Quantile Regression
To examine the impact of carbon emissions trading policies on AGTFP across different quartiles, additional validation is conducted using a two-way stationary quartile model, as detailed in Table 4. The findings presented in Table 4 indicate a significant positive effect of CETSs on AGTFP across the first four quartiles, with this effect decreasing as the level of AGTFP increases, demonstrating diminishing marginal benefits. Quantile regressions allow us to estimate the conditional effects of CETSs on different parts of AGTFP distribution, capturing the heterogeneity in policy impacts, which might be masked by average treatment effects. Specifically, cities with lower AGTFP quantiles typically represent less developed or less agriculturally intensive regions, such as the western region, where resource constraints and lower baseline productivity create greater potential for CETS-driven technological innovations, such as the adoption of low-carbon agricultural technologies [78].

Table 4.
Quantile Regression.
4.4. Endogeneity
CETSs may not be entirely exogenous, as they can be influenced by the political power of a city. In line with the methodology suggested by Hering and Poncety (2014) [79], we use the ventilation coefficient—an indicator of meteorological conditions that affect the dispersion rate of pollutants in the atmosphere—as an instrumental variable. Our hypothesis is that adverse meteorological conditions that impede pollutant dispersion are likely to lead to the adoption of stricter environmental regulations. As a result, a lower ventilation coefficient increases the chances of a city being chosen as a participant in a carbon emissions trading scheme. Additionally, the ventilation coefficient is shaped by natural environmental factors, such as meteorological geography, and is not linked to other unobserved factors that could influence carbon emissions. This reinforces the hypothesis concerning the exogeneity of instrumental variables. To determine the air ventilation coefficient for each prefecture-level city, we utilize the product of wind speed and boundary layer height. The results of the 2SLS regressions are presented in Table 5.

Table 5.
Results of 2SLS Regressions.
In the first stage, we conduct a regression analysis where the CETS variable is regressed against the instrumental variable and various control variables, as presented in Column (1). The significant positive coefficient of the instrumental variable confirms its validity. In the second stage, as depicted in Column (2), we analyze the relationship between AGTFP and the estimated CETS variable from the first stage, while also including additional control variables. The results from this second-stage regression are consistent with those of the baseline regressions, as evidenced by the statistically significant positive coefficient for CETSs in Column (2). This indicates that the results shown in Table 2 remain unaffected by any issues related to endogenous selection.
To address the issue of multicollinearity in the second-stage estimation of the 2SLS method, we conduct a multicollinearity diagnostic for the independent variables used in the second stage to ensure the accuracy and robustness of coefficient estimates and to enhance the reliability of the results [80]. Table 6 presents the results of the multicollinearity diagnostics for the independent variables in the second stage of the 2SLS regression.

Table 6.
Results of the Multicollinearity Regression.
We conducted a multicollinearity test for the independent variables involved in the second stage of the 2SLS regression, as presented in Column (1). The coefficients from the VIF test are all below 2, indicating no multicollinearity among these variables. Column (2) shows the reciprocals of the VIF test coefficients, which suggest that the results of the 2SLS regression for addressing endogeneity are not affected by multicollinearity among the variables.
4.5. Robustness Checks
4.5.1. Robustness Tests with Alternative Sample
In China, municipalities and provincial capitals often accumulate many political and production resources, significantly facilitating policy implementation. This resource accumulation may lead to an overestimation of the emission reduction effects of carbon emissions trading policies. To ensure robustness, we re-evaluate the relationship between CETSs and AGTFP using alternative samples, as presented in Table 6. In Column (1), the results are derived from a sample that excludes municipalities, while Column (2) further excludes both municipalities and provincial capitals. Table 7 indicates that the significantly positive coefficients for CETSs remain consistent.

Table 7.
Robustness Tests with Alternative Sample.
4.5.2. Sample After Winsorization at 1% Level
Financial data are frequently vulnerable to outliers (extreme data points), which can disproportionately affect statistical analyses and compromise the reliability of the results. There are several statistical techniques available to assess the influence of outliers or to reduce their impact, such as winsorization [81,82]. The findings obtained after applying winsorization to the sample are shown in Table 8, where the variables have been winsorized at the 1% level. Table 8 demonstrates a robust and significant effect of CETSs on AGTFP after winsorization.

Table 8.
Robustness Tests with the Sample after Winsorization at the 1% and 99% levels.
4.5.3. PSM-DID Test
While the carbon emissions trading pilot policy demonstrates a significant positive effect on AGTFP, this impact may be influenced by potential self-selection bias. To address this concern, we utilize the PSM method. We start by selecting covariates and calculating propensity scores through nearest neighbor matching using a caliper. By identifying and matching participants, we aim to minimize potential self-selection bias within the groups, thereby establishing new treatment and control groups. Ultimately, we apply the DID model to identify and evaluate the treatment effects. The estimation results from the PSM-DID analysis are presented in Table 8.
The nearest neighbor matching method is employed to pair the experimental group with the most closely aligned control group in Columns (1) to (4) of Table 9. A matching ratio of 1:2 is utilized in Column (1), while ratios of 1:3, 1:4, and 1:5 are reported in Columns (2) to (4). Additionally, the outcomes of radius matching and kernel matching are shown in Columns (5) and (6) of Table 8. The coefficient of the PSM-DID estimator is positive and statistically significant at the 5% level. Consequently, the carbon emissions trading pilot policy continues to significantly improve AGTFP at the city level, suggesting that our findings are robust.

Table 9.
Robustness Tests with PSM-DID.
4.6. Spatial Geography Regressions
While the main identification model indicates a positive causal relationship between the implementation of CETSs and AGTFP, it is crucial to acknowledge the interconnectedness of neighboring cities, as highlighted by Tobler’s first law of geography (1970) [83]. This principle suggests that the effects of a pilot policy may extend into adjacent areas, potentially violating the Stable Unit Treatment Value Assumption (SUVTA) [84], which is vital for ensuring the credibility of the identification outcomes. Essentially, although the primary regression model relaxes this assumption, it does not sufficiently account for the policy impacts associated with neighborhood spillover. Consequently, in line with the approaches of Delgado and Florax (2015) [85] and Du et al. (2022) [86], we implement the Spatial DID model, which integrates the DID model within a spatial econometric context. This technique allows us to assess the potential spatial spillover effects of the introduction of regional pilot CETSs.
Prior to implementing the Spatial DID model, we initially calculate the global Moran’s index to assess the spatial correlation between cities. The results, presented in Table 10, indicate that AGTFP exhibits a notable positive spatial correlation among cities from 2004 to 2022.

Table 10.
Global Moran’s Index.
Next, we perform an LR test and a Wald test to determine the most appropriate spatial econometric model. After applying these filtering techniques, including the LR test and Wald test, we can identify the most suitable model for our analysis. The results presented in Table 11 indicate that the SAR is the most fitting choice for this study.

Table 11.
LR and Wald Tests.
To further investigate the spatial spillover effects, we decompose the policy margin effects of CETSs into local effects (direct effects), spillover effects (indirect effects), and total effects. The findings of this analysis are significant, as shown in Table 12. The coefficients in Columns (1) and (2) across all panels are significantly positive at the 1% significance level, thereby reinforcing the primary regression results discussed in Section 4.1. Moreover, the parameters in Column (3), which represent spillover effects, are statistically significant and positive at the 5% significance level, suggesting that the implementation of CETSs has a beneficial impact on the AGTFP of neighboring cities.

Table 12.
Results of Spatial Geography Regressions.
4.7. Mechanism Analysis
Building on the previous analysis, it is clear that the carbon emissions trading pilot policy significantly contributes to the enhancement of AGTFP. The next investigation focuses on the mechanisms that drive this effect. As stated in the research hypotheses, carbon emission allowances are considered a commodity and promote improvements in AGTFP through technological advancements, particularly by boosting the urban innovation index.
The carbon emissions trading pilot policy acts as a catalyst for businesses to engage in innovation, thereby promoting the growth of AGTFP. Firstly, this policy incentivizes firms to innovate by allowing them to improve their production methods without compromising on output or exhausting their limited free carbon emission allowances. By achieving greater emission reductions through the employment of innovative approaches, companies can sell any surplus allowances, resulting in increased profits. As a result, the carbon emissions trading pilot policy not only encourages enterprises to innovate, but also supports more sustainable production practices, ultimately leading to a decrease in CO2 emissions.
Furthermore, innovation plays a crucial role in enhancing AGTFP by boosting productivity and reducing production costs. On the one hand, innovation can improve AGTFP by alleviating production expenses. Specifically, costs may rise due to the inefficient use of materials, inadequate operational management, and other contributing factors. In these situations, innovation can aid businesses by lowering material costs, enabling the use of alternative energy sources, and optimizing management processes, ultimately resulting in enhanced AGTFP in urban regions.
Conversely, innovation can strengthen AGTFP by improving production efficiency. Firstly, green innovation can enhance product quality by reducing the incidence of defective outputs and speeding up sales, which, in turn, boosts both output efficiency and AGTFP. Secondly, innovation allows businesses to adopt production reforms, thereby enhancing their competitive edge and further elevating AGTFP. Additionally, innovation contributes to AGTFP by increasing labor productivity per unit.
Building on the previous analysis, this paper examines the mechanism of innovation in Table 13. Column (1) indicates that the estimated coefficient for CETSs is positive and significant at the 5% level, suggesting that the carbon emissions trading pilot policy has led to improvements in innovation within the pilot regions. Following this, Column (2) presents the regression results for the dependent variable, AGTFP, in relation to the primary variable, CETSs, and the intermediary variable, innovation. The results reveal that the estimated coefficient for innovation is positive and statistically significant at the 5% level, indicating that innovation enhances the effect of CETSs on AGTFP. This finding illustrates that fostering innovation is advantageous for promoting AGTFP, consistent with the earlier theoretical analysis.

Table 13.
Results of Mediating Regressions.
5. Conclusions
Encouraging a transition to a green low-carbon economy is crucial for attaining high-quality technological development. In this regard, China has implemented various initiatives aimed at decreasing carbon emissions. This study provides empirical evidence regarding the economic impacts of the carbon emissions trading pilot policy on AGTFP. We explore the mechanisms through which the carbon emissions trading pilot policy contributes to the improvement of AGTFP.
Our results reveal that the carbon emissions trading pilot policy boosts AGTFP by encouraging innovation, which holds true across multiple reliability tests. Importantly, this positive impact is especially significant in both the eastern and western regions. Additionally, the adoption of a carbon emissions trading scheme can have favorable spillover effects on agricultural green total factor productivity in neighboring cities. Despite these insights, our study has certain limitations. First, potential self-selection issues may arise, as cities participating in CETS pilots might inherently possess stronger environmental awareness or economic capacity, possibly inflating the estimated effects. Second, uncontrolled exogenous shocks, such as the COVID-19 pandemic (2019), could influence agricultural production and CETS implementation, confounding our results. Third, the uneven quality of CETS implementation at the local level, driven by variations in administrative capacity and policy enforcement, may lead to inconsistent outcomes across cities.
The policy implications drawn from our findings are as follows. First, the positive impact of CETSs on AGTFP highlights its capacity for reducing agricultural carbon emissions while promoting high-quality agricultural growth through innovation. Regionally tailored policies are essential to maximize these benefits. In Eastern China, where institutional capacity and advanced agricultural structures support robust CETS implementation, policies should focus on scaling up green technology adoption and market integration. In the central and western regions, with varying institutional capacities and less intensive agricultural systems, policies should prioritize capacity-building, financial incentives, and technical support to enhance CETSs’ effectiveness. Furthermore, we must develop a strong coordinated approach to carbon emission reduction involving collaborative regional prevention and control initiatives. Second, the significant spatial spillover effects of CETSs on AGTFP underscore the need for regional cooperation. To counter beggar-thy-neighbor governance, it is critical to establish a balanced national carbon trading market supported by coordinated regional prevention and control initiatives to amplify emission reductions. Future research could extend the spatial DID model to farming households to capture the micro-level impacts of CETSs, dynamically test technological performance to assess innovation sustainability, or explore the interactions of CETSs with other environmental policies, such as green subsidies, to optimize policy synergies for sustainable agricultural development.
Author Contributions
Conceptualization, Y.X., Z.Z. and Y.Z.; Data curation, Y.X.; Formal analysis, Y.X.; Funding acquisition, Z.Z.; Methodology, Y.X.; Writing—original draft, Y.X., Z.Z. and Y.Z.; Writing—review and editing, Z.Z. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China [grant number 72303087].
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Variable Definitions.
Table A1.
Variable Definitions.
| Variable | Definition |
|---|---|
| AGTFP | Agricultural green total factor productivity, which is defined based on the model of super-efficient SBM-DDF |
| UI | Urban innovation index, which is defined as the average value of each type of patent |
| ISA | Industrial structure advanced, which is defined as the ratio of the added value of the tertiary industry to the added value of the secondary industry |
| ISR | Industrial structure rationalization, which is defined as the ratio of the value of output to the share of employees for each industry |
| EE | Education expenditure, which is defined as the ratio of education expenditure to general government expenditure |
| EA | Educational attainment, which is defined as the ratio of the number of students enrolled in general higher education to the total population at the end of the year |
| ER | Environmental regulation, which is measured as the comprehensive utilization rate of general industrial solid waste |
| AED | Agricultural economic development, which is defined as the ratio of primary sector value added to primary sector employees |
| RA | Road area, which is defined as the ratio of urban road area to total population at the end of the year |
References
- Levine, M.D.; Steele, R.V. Climate change: What we know and what is to be done. Wiley Interdiscip. Rev. Energy Environ. 2021, 10, e388. [Google Scholar] [CrossRef]
- Lomborg, B. Welfare in the 21st century: Increasing development, reducing inequality, the impact of climate change, and the cost of climate policies. Technol. Forecast. Soc. Change 2020, 156, 119981. [Google Scholar] [CrossRef]
- FAO. The State of Food and Agriculture 2020: Overcoming Water Challenges in Agriculture; Food and Agriculture Organization of the United Nations: Rome, Italy, 2020. [Google Scholar]
- IPCC. Climate Change 2022: Mitigation of Climate Change; Contribution of Working Group III to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; The Intergovernmental Panel on Climate Change: Geneva, Switzerland, 2022. [Google Scholar]
- OECD. Agricultural Policy Monitoring and Evaluation 2021: Addressing the Challenges Facing Food Systems; Organisation for Economic Co-Operation and Development: Paris, France, 2021. [Google Scholar]
- Dai, S.; Qian, Y.; He, W.; Wang, C.; Shi, T. The spatial spillover effect of China’s carbon emissions trading policy on industrial carbon intensity: Evidence from a spatial difference-in-difference method. Struct. Change Econ. Dyn. 2022, 63, 139–149. [Google Scholar] [CrossRef]
- Feng, X.; Zhao, Y.; Yan, R. Does carbon emission trading policy has emission reduction effect?—An empirical study based on quasi-natural experiment method. J. Environ. Manag. 2024, 351, 119791. [Google Scholar] [CrossRef]
- Li, R.H.; Du, H. Emission Reduction Effect and Regional Differences of Carbon Emission Trading Pilots Under the “Dual Carbon” Goals. Res. Econ. Manag. 2023, 44, 25–44. [Google Scholar]
- Liu, M.; Yang, L. Spatial pattern of China’s agricultural carbon emission performance. Ecol. Indic. 2021, 133, 108345. [Google Scholar] [CrossRef]
- Liu, L.; Hu, X.; Li, L.; Sun, Z.; Zhang, Q. Understanding China’s agricultural non-carbon-dioxide greenhouse gas emissions: Subnational insights and global trade dynamics. Environ. Impact Assess. Rev. 2024, 106, 107487. [Google Scholar] [CrossRef]
- Fujimori, S.; Wu, W.; Doelman, J.; Frank, S.; Hristov, J.; Kyle, P.; Sands, R.; van Zeist, W.-J.; Havlik, P.; Domínguez, I.P.; et al. Land-based climate change mitigation measures can affect agricultural markets and food security. Nat. Food 2022, 3, 110–121. [Google Scholar] [CrossRef]
- Guo, Y.; Chen, Y.; Searchinger, T.D.; Zhou, M.P.D.; Pan, D.; Yang, J.; Wu, L.; Cui, Z.; Zhang, W.; Zhang, F.; et al. Air quality, nitrogen use efficiency and food security in China are improved by cost-effective agricultural nitrogen management. Nat. Food 2020, 1, 648–658. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, C.; Hu, R. Determinants and overuse of pesticides in grain production: A comparison of rice, maize and wheat in China. China Agric. Econ. Rev. 2020, 12, 367–379. [Google Scholar] [CrossRef]
- Zhang, Y.; Long, H.; Wang, M.Y.; Li, Y.; Ma, L.; Chen, K.; Zheng, Y.; Jiang, T. The hidden mechanism of chemical fertiliser overuse in rural China. Habitat Int. 2020, 102, 102210. [Google Scholar] [CrossRef]
- Siller, M.; Schatzer, T.; Walde, J.; Tappeiner, G. What drives total factor productivity growth? An examination of spillover effects. Reg. Stud. 2021, 55, 1129–1139. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, C.; Peng, J. Financial inclusion and agricultural total factor productivity growth in China. Econ. Model. 2021, 96, 68–82. [Google Scholar] [CrossRef]
- Zhang, X.; Hu, L.; Yu, X. Farmland Leasing, misallocation Reduction, and agricultural total factor Productivity: Insights from rice production in China. Food Policy 2023, 119, 102518. [Google Scholar] [CrossRef]
- Chen, Y.; Miao, J.; Zhu, Z. Measuring green total factor productivity of China’s agricultural sector: A three-stage SBM-DEA model with non-point source pollution and CO2 emissions. J. Clean. Prod. 2021, 318, 128543. [Google Scholar] [CrossRef]
- Song, M.; Peng, L.; Shang, Y.; Zhao, X. Green technology progress and total factor productivity of resource-based enterprises: A perspective of technical compensation of environmental regulation. Technol. Forecast. Soc. Chang. 2022, 174, 121276. [Google Scholar] [CrossRef]
- Zhao, Z.; Bai, Y.; Deng, X.; Chen, J.; Hou, J.; Li, Z. Changes in livestock grazing efficiency incorporating grassland productivity: The case of Hulun Buir, China. Land 2020, 9, 447. [Google Scholar] [CrossRef]
- Xia, F.; Xu, J. Green total factor productivity: A re-examination of quality of growth for provinces in China. China Econ. Rev. 2020, 62, 101454. [Google Scholar] [CrossRef]
- Dong, Z.; Xia, C.; Fang, K.; Zhang, W. Effect of the carbon emissions trading policy on the co-benefits of carbon emissions reduction and air pollution control. Energy Policy 2022, 165, 112998. [Google Scholar] [CrossRef]
- Li, Z.; Wang, J. Spatial emission reduction effects of China’s carbon emissions trading: Quasi-natural experiments and policy spillovers. Chin. J. Popul. Resour. Environ. 2021, 19, 246–255. [Google Scholar] [CrossRef]
- Hong, Q.; Cui, L.; Hong, P. The impact of carbon emissions trading on energy efficiency: Evidence from quasi-experiment in China’s carbon emissions trading pilot. Energy Econ. 2022, 110, 106025. [Google Scholar] [CrossRef]
- Xu, J.; Wei, W. Would carbon tax be an effective policy tool to reduce carbon emission in China? Policies simulation analysis based on a CGE model. Appl. Econ. 2022, 54, 115–134. [Google Scholar] [CrossRef]
- Narassimhan, E.; Gallagher, K.S.; Koester, S.; Alejo, J.R. Carbon pricing in practice: A review of existing emissions trading systems. Clim. Policy 2018, 18, 967–991. [Google Scholar] [CrossRef]
- Li, X.; Shu, Y.; Jin, X. Environmental regulation, carbon emissions and green total factor productivity: A case study of China. Environ. Dev. Sustain. 2022, 24, 2577–2597. [Google Scholar] [CrossRef]
- Shao, S.; Cheng, S.; Jia, R. Can low carbon policies achieve collaborative governance of air pollution? Evidence from China’s carbon emissions trading scheme pilot policy. Environ. Impact Assess. Rev. 2023, 103, 107286. [Google Scholar] [CrossRef]
- Verde, S.F.; Borghesi, S. The international dimension of the EU emissions trading system: Bringing the pieces together. Environ. Resour. Econ. 2022, 83, 23–46. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.J. Does China’s carbon emissions trading scheme affect the market power of high-carbon enterprises? Energy Econ. 2022, 108, 105906. [Google Scholar] [CrossRef]
- Huang, N.; He, R.; Luo, L.; Shen, H. Carbon emission trading scheme and firm debt financing. J. Contemp. Account. Econ. 2024, 20, 100384. [Google Scholar] [CrossRef]
- Zhou, D.; Liang, X.; Zhou, Y.; Tang, K. Does Emission Trading Boost Carbon Productivity? Evidence from China’s Pilot Emission Trading Scheme. Int. J. Environ. Res. Public Health 2020, 17, 5522. [Google Scholar] [CrossRef]
- Zheng, Y.; Sun, X.; Zhang, C. Can emission trading scheme improve carbon emission performance? Evidence from China. Front. Energy Res. 2021, 9, 759572. [Google Scholar] [CrossRef]
- Sun, R.; Wang, K.; Wang, X.; Zhang, J. China’s Carbon Emission Trading Scheme and Firm Performance. Emerg. Mark. Financ. Trade 2022, 58, 837–851. [Google Scholar] [CrossRef]
- Oestreich, A.M.; Tsiakas, I. Carbon emissions and stock returns: Evidence from the EU Emissions Trading Scheme. J. Bank. Financ. 2015, 58, 294–308. [Google Scholar] [CrossRef]
- Cai, H.; Wang, Z.; Zhang, Z.; Xu, X. Carbon emission trading schemes induces technology transfer: Evidence from China. Energy Policy 2023, 178, 113595. [Google Scholar] [CrossRef]
- Yan, X.; He, T. Wish fulfilment or wishful thinking?–Assessing the outcomes of China’s pilot carbon emissions trading scheme on green economy efficiency in China’s cities. Energy Policy 2024, 192, 114261. [Google Scholar] [CrossRef]
- Liu, Y.; Peng, Y.; Wang, W.; Liu, S.; Yin, Q. Does the pilot zone for green finance reform and innovation policy improve urban green total factor productivity? The role of digitization and technological innovation. J. Clean. Prod. 2024, 471, 143365. [Google Scholar] [CrossRef]
- Wen, H.; Hu, K.; Nghiem, X.; Acheampong, A.O. Urban climate adaptability and green total-factor productivity: Evidence from double dual machine learning and differences-in-differences techniques. J. Environ. Manag. 2024, 350, 119588. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, L.; Sun, C. How does urban environmental legislation guide the green transition of enterprises? Based on the perspective of enterprises’ green total factor productivity. Energy Econ. 2022, 110, 106032. [Google Scholar] [CrossRef]
- Zhou, L.; Fan, J.; Hu, M.; Yu, X. Clean air policy and green total factor productivity: Evidence from Chinese prefecture-level cities. Energy Econ. 2024, 133, 107512. [Google Scholar] [CrossRef]
- Chen, C.; Ye, F.; Xiao, H.; Xie, W.; Liu, B.; Wang, L. The digital economy, spatial spillovers and forestry green total factor productivity. J. Clean. Prod. 2023, 405, 136890. [Google Scholar] [CrossRef]
- Wang, J.; Long, F. Grain industrial agglomeration and grain green total factor productivity in China: A dynamic spatial durbin econometric analysis. Heliyon 2024, 10, e26761. [Google Scholar] [CrossRef]
- Yang, X.; Jia, Z.; Yang, Z. How does technological progress impact transportation green total factor productivity: A spatial econometric perspective. Energy Rep. 2021, 7, 3935–3950. [Google Scholar] [CrossRef]
- Hong, M.; Tian, M.; Wang, J. Digital Inclusive Finance, Agricultural Industrial Structure Optimization and Agricultural Green Total Factor Productivity. Sustainability 2022, 14, 11450. [Google Scholar] [CrossRef]
- Jiang, Y.; Han, G.; Yu, D. Digital finance and agricultural green total factor productivity: The mediating role of digital village development. Financ. Res. Lett. 2024, 67, 105948. [Google Scholar] [CrossRef]
- Shen, Y.; Guo, X.; Zhang, X. Digital Financial Inclusion, Land Transfer, and Agricultural Green Total Factor Productivity. Sustainability 2023, 15, 6436. [Google Scholar] [CrossRef]
- Zhang, Y.; Ji, M.; Zheng, X. Digital Economy, Agricultural Technology Innovation, and Agricultural Green Total Factor Productivity. SAGE Open 2023, 13, 1935527700. [Google Scholar] [CrossRef]
- Fang, L.; Hu, R.; Mao, H.; Chen, S. How crop insurance influences agricultural green total factor productivity: Evidence from Chinese farmers. J. Clean. Prod. 2021, 321, 128977. [Google Scholar] [CrossRef]
- Li, H.; Tang, M.; Cao, A.; Guo, L. Assessing the relationship between air pollution, agricultural insurance, and agricultural green total factor productivity: Evidence from China. Environ. Sci. Pollut. Res. Int. 2022, 29, 78381–78395. [Google Scholar] [CrossRef]
- Li, G.; Jia, X.; Khan, A.A.; Khan, S.U.; Ali, M.; Luo, J. Does green finance promote agricultural green total factor productivity? Considering green credit, green investment, green securities, and carbon finance in China. Environ Sci. Pollut. Res. Int. 2023, 30, 36663–36679. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, M.; Li, Q.; Zhao, X. The impact of green trade barriers on agricultural green total factor productivity: Evidence from China and OECD countries. Econ. Anal. Policy 2023, 78, 319–331. [Google Scholar] [CrossRef]
- Wang, F.; Du, L.; Tian, M. Does Agricultural Credit Input Promote Agricultural Green Total Factor Productivity? Evidence from Spatial Panel Data of 30 Provinces in China. Int. J. Environ. Res. Public Health 2022, 20, 529. [Google Scholar] [CrossRef]
- Sun, Y. Environmental regulation, agricultural green technology innovation, and agricultural green total factor productivity. Front. Environ. Sci. 2022, 10, 955954. [Google Scholar] [CrossRef]
- Zhou, D.; Tang, M.; Li, H. Investigating the nonlinear effects of climate change on agricultural green total factor productivity: Findings from the PSTR approach. Environ. Dev. Sustain. 2024, 26, 24453–24471. [Google Scholar] [CrossRef]
- Rana, B.; Parihar, C.M.; Jat, M.L.; Patra, K.; Nayak, H.S.; Reddy, K.S.; Sarkar, A.; Anand, A.; Naguib, W.; Gupta, N.; et al. Combining sub-surface fertigation with conservation agriculture in intensively irrigated rice under rice-wheat system can be an option for sustainably improving water and nitrogen use-efficiency. Field Crops Res. 2023, 302, 109074. [Google Scholar] [CrossRef]
- Getahun, S.; Kefale, H.; Gelaye, Y. Application of precision agriculture technologies for sustainable crop production and environmental sustainability: A systematic review. Sci. World J. 2024, 2024, 2126734. [Google Scholar] [CrossRef]
- Andrews, H.M.; Homyak, P.M.; Oikawa, P.Y.; Wang, J.; Jenerette, G.D. Water-conscious management strategies reduce per-yield irrigation and soil emissions of CO2, N2O, and NO in high-temperature forage cropping systems. Agric. Ecosyst. Environ. 2022, 332, 107944. [Google Scholar] [CrossRef]
- Tauseef, S.M.; Premalatha, M.; Abbasi, T.; Abbasi, S.A. Methane capture from livestock manure. J. Environ. Manag. 2013, 117, 187–207. [Google Scholar] [CrossRef]
- Huang, Z.; Du, X. Toward green development? Impact of the carbon emissions trading system on local governments’ land supply in energy-intensive industries in China. Sci. Total Environ. 2020, 738, 139769. [Google Scholar] [CrossRef]
- Wu, X.R.; Zhang, J.B.; Tian, Y.; Li, P. Agricultural carbon emissions in China’s provincial areas:A study on the measurement, efficiency changes and influencing factors—Based on the DEA-Malmquist index decomposition method and the application of Tobit model. Resour. Sci. 2014, 36, 129–138. [Google Scholar]
- Rehkopf, D.H.; Basu, S. A new tool for case studies in epidemiology—The synthetic control method. Epidemiology 2018, 29, 503–505. [Google Scholar] [CrossRef]
- Fukuyama, H.; Weber, W.L. A directional slacks-based measure of technical inefficiency. Socio-Econ. Plan. Sci. 2009, 43, 274–287. [Google Scholar] [CrossRef]
- Baron, R.M.; Kenny, D.A. The moderator–mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations. J. Personal. Soc. Psychol. 1986, 51, 1173. [Google Scholar] [CrossRef] [PubMed]
- Kolak, M.; Anselin, L. A spatial perspective on the econometrics of program evaluation. Int. Reg. Sci. Rev. 2020, 43, 128–153. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhao, Z.; Teng, Z.; Wang, J. Can an energy-consuming rights trading system control environmental inequality? Energy Environ. 2024. [Google Scholar] [CrossRef]
- Shao, S.; Fan, M.T.; Yang, L.L. Economic Structural Adjustment, Green Technology Progress and China’s Low-Carbon Transition Development—An Empirical Examination Based on the Perspectives of Overall Technology Frontier and Spatial Spillover Effects. Manag. World 2022, 38, 46–69+4–10. [Google Scholar]
- Huang, D.H.; Ding, S.J. Agricultural Technological Progress, Spatial Effects and Urban-Rural Income Gap-Analysis Based on Provincial Panel Data. China Agric. Resour. Zoning 2022, 43, 239–248. [Google Scholar]
- Wang, L.L.; Xu, Y.X.; Chai, Y.Y.; Xu, X.; Lv, J. Study on the impact of agricultural mechanization level on the intensity of agricultural carbon emissions based on the panel data test of 30 provinces from 2004 to 2021. China Agric. Resour. Zoning 2025, 1–14. Available online: https://slib.tzc.edu.cn/articlesearch/web_searchingDetail?id=2031556995739 (accessed on 25 June 2025).
- Wang, M.; Xu, M.; Ma, S. The effect of the spatial heterogeneity of human capital structure on regional green total factor productivity. Struct. Change Econ. Dyn. 2021, 59, 427–441. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, B.; Wang, J.; Kwek, K. The impact of climate change on China’s agricultural green total factor productivity. Technol. Forecast. Soc. Chang. 2022, 185, 122054. [Google Scholar] [CrossRef]
- Wu, F.L.; Li, L.; Zhang, H.L.; Chen, F. Effects of conservation tillage on net carbon release from agroecosystems. J. Ecol. 2007, 26, 2035–2039. [Google Scholar]
- Li, B.; Zhang, J.B.; Li, H.P. Spatial and temporal characteristics of agricultural carbon emissions in China and decomposition of influencing factors. China Popul. Resour. Environ. 2011, 21, 80–86. (In Chinese) [Google Scholar]
- Pakes, A.; Schankerman, M. The rate of obsolescence of patents, research gestation lags, and the private rate of return to research resources. In R&D, Patents, and Productivity; University of Chicago Press: Chicago, IL, USA, 1984; pp. 73–88. [Google Scholar]
- Huang, X.; Feng, C.; Qin, J.; Wang, X.; Zhang, T. Measuring China’s agricultural green total factor productivity and its drivers during 1998–2019. Sci. Total Environ. 2022, 829, 154477. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.J.; Li, P.; Lu, Y. Career concerns and multitasking local bureaucrats: Evidence of a target-based performance evaluation system in China. J. Dev. Econ. 2018, 133, 84–101. [Google Scholar] [CrossRef]
- Liu, J.; Liu, X. Effects of carbon emission trading schemes on green technological innovation by industrial enterprises: Evidence from a quasi-natural experiment in China. J. Innov. Knowl. 2023, 8, 100410. [Google Scholar] [CrossRef]
- Wang, F.T.; Wang, H.; Kong, F.B. The enhancement effect of rural digital development on total factor carbon productivity in agriculture. China Popul.-Resour. Environ. 2024, 34, 79–90. [Google Scholar]
- Hering, L.; Poncety, S. Environmental policy and exports: Evidence from Chinese cities. J. Environ. Econ. Manag. 2014, 68, 296–318. [Google Scholar] [CrossRef]
- Davino, C.; Romano, R.; Vistocco, D. Handling multicollinearity in quantile regression through the use of principal component regression. METRON 2022, 80, 153–174. [Google Scholar] [CrossRef]
- Chang, X.; Chen, Y.; Wang, S.Q.; Zhang, K.; Zhang, W. Credit Default Swaps and Corporate Innovation. J. Financ. Econ. 2019, 134, 474–500. [Google Scholar] [CrossRef]
- Li, J.; Shan, Y.; Tian, G.; Hao, X. Labor Cost, Government Intervention, and Corporate Innovation: Evidence from China. J. Corp. Financ. 2020, 64, 101668. [Google Scholar] [CrossRef]
- Tobler, W. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Rubin, D.B. Formal Modes of Statistical Inference For Causal Effects. J. Stat. Plan. Inference 1990, 25, 279–292. [Google Scholar] [CrossRef]
- Delgado, M.S.; Florax, R.J.G.M. Difference-in-differences techniques for spatial data: Local autocorrelation and spatial interaction. Econ. Lett. 2015, 123–126. [Google Scholar] [CrossRef]
- Du, M.; Feng, R.; Chen, Z. Blue sky defense in low-carbon pilot cities: A spatial spillover perspective of carbon emission efficiency. Sci. Total Environ. 2022, 846, 157509. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).