A Sustainable Framework for Realism Evaluation and Optimization of Virtual Fabric Drape Effect
Abstract
1. Introduction
2. Research Methodology
2.1. Fabric Selection
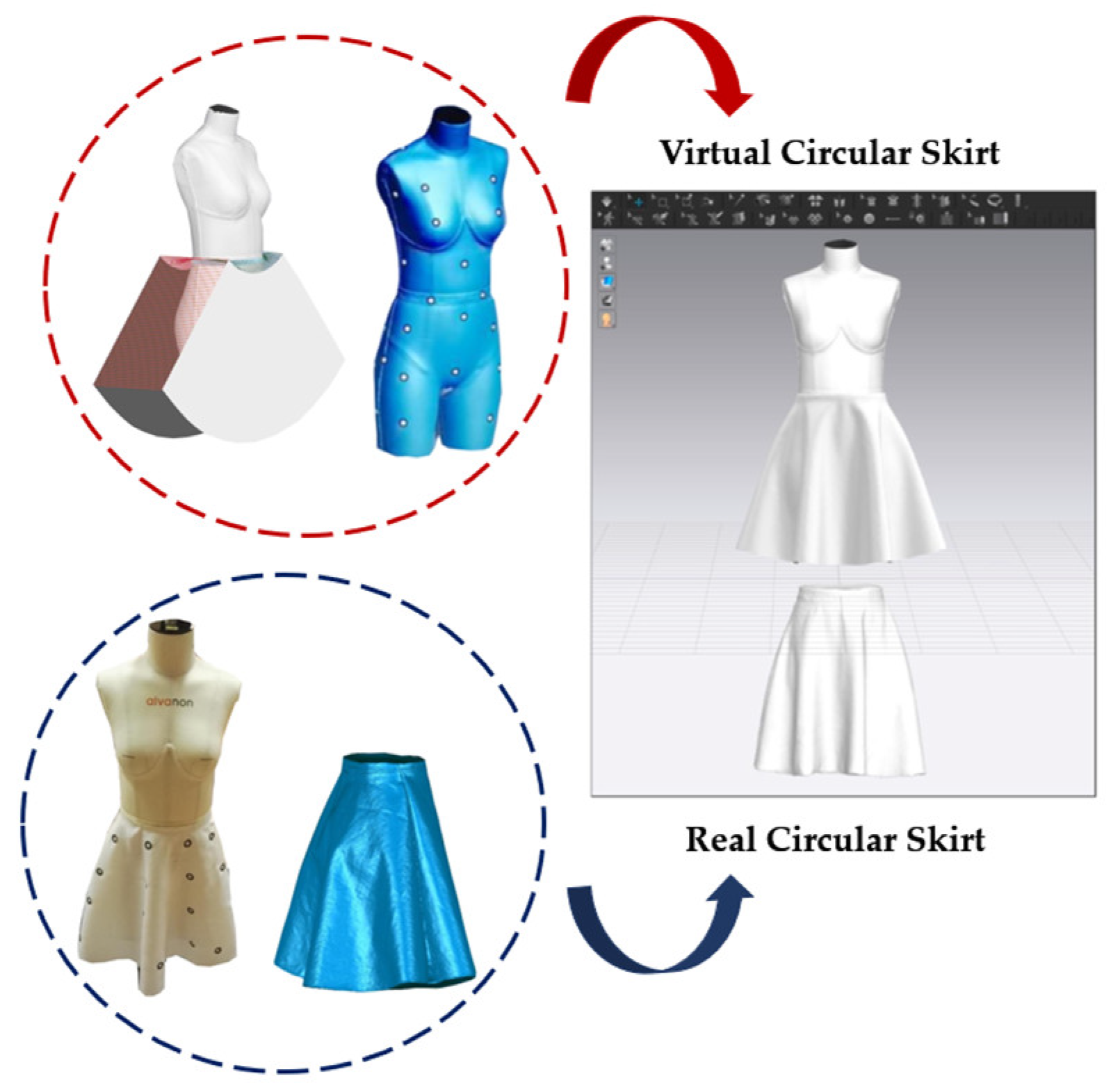
2.2. Generation of Virtual Fabric
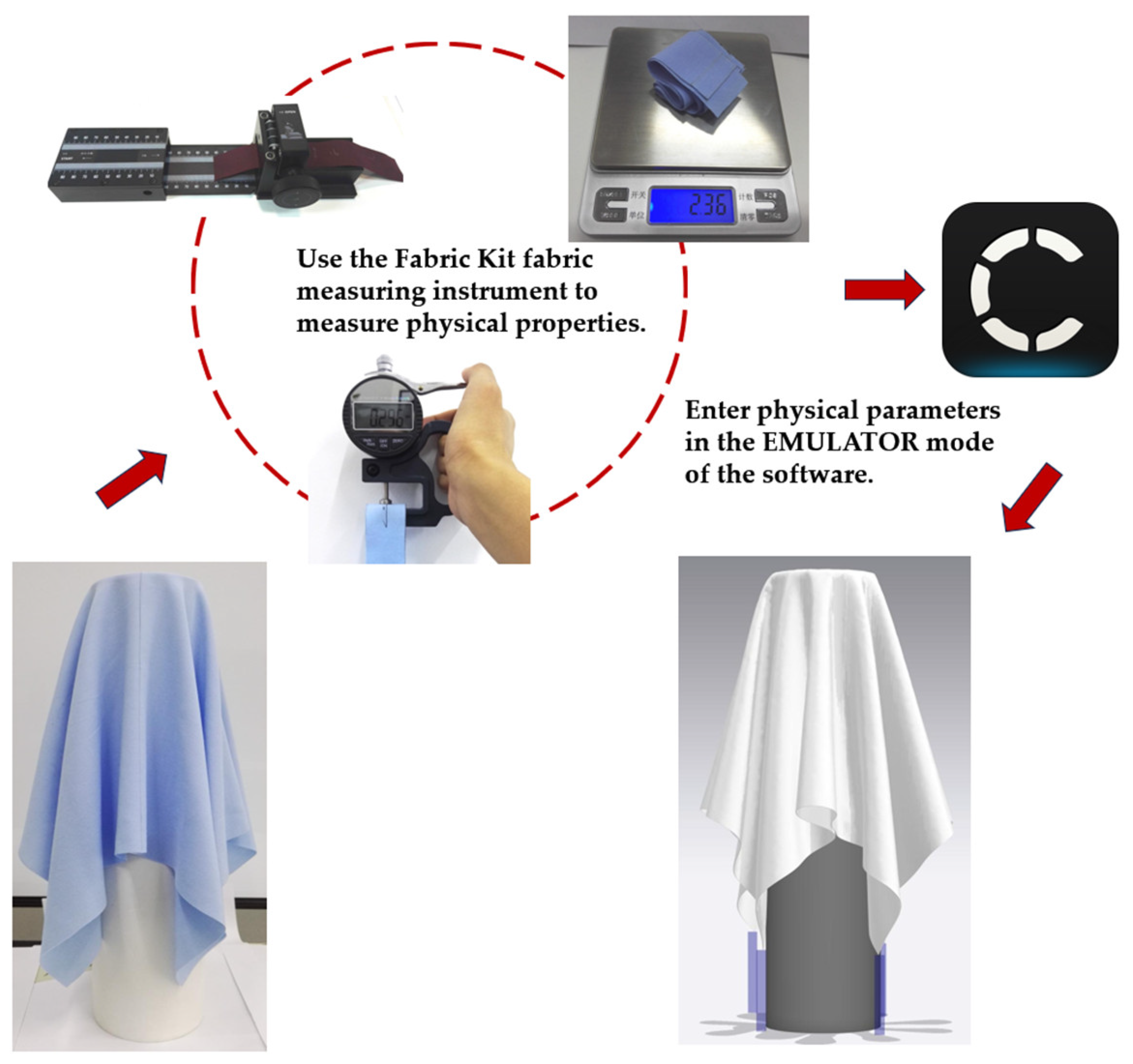
2.3. Drape Tests in Real and Virtual Environments
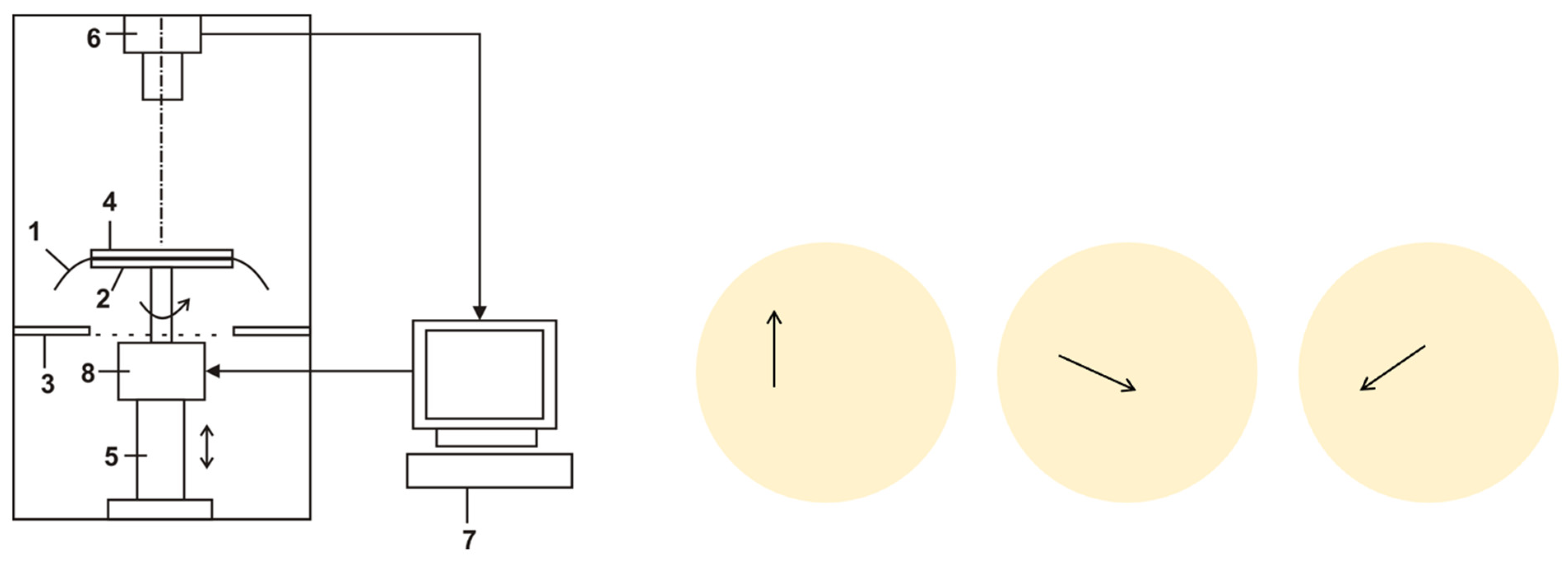
2.3.1. Real Fabric Drape Experiment
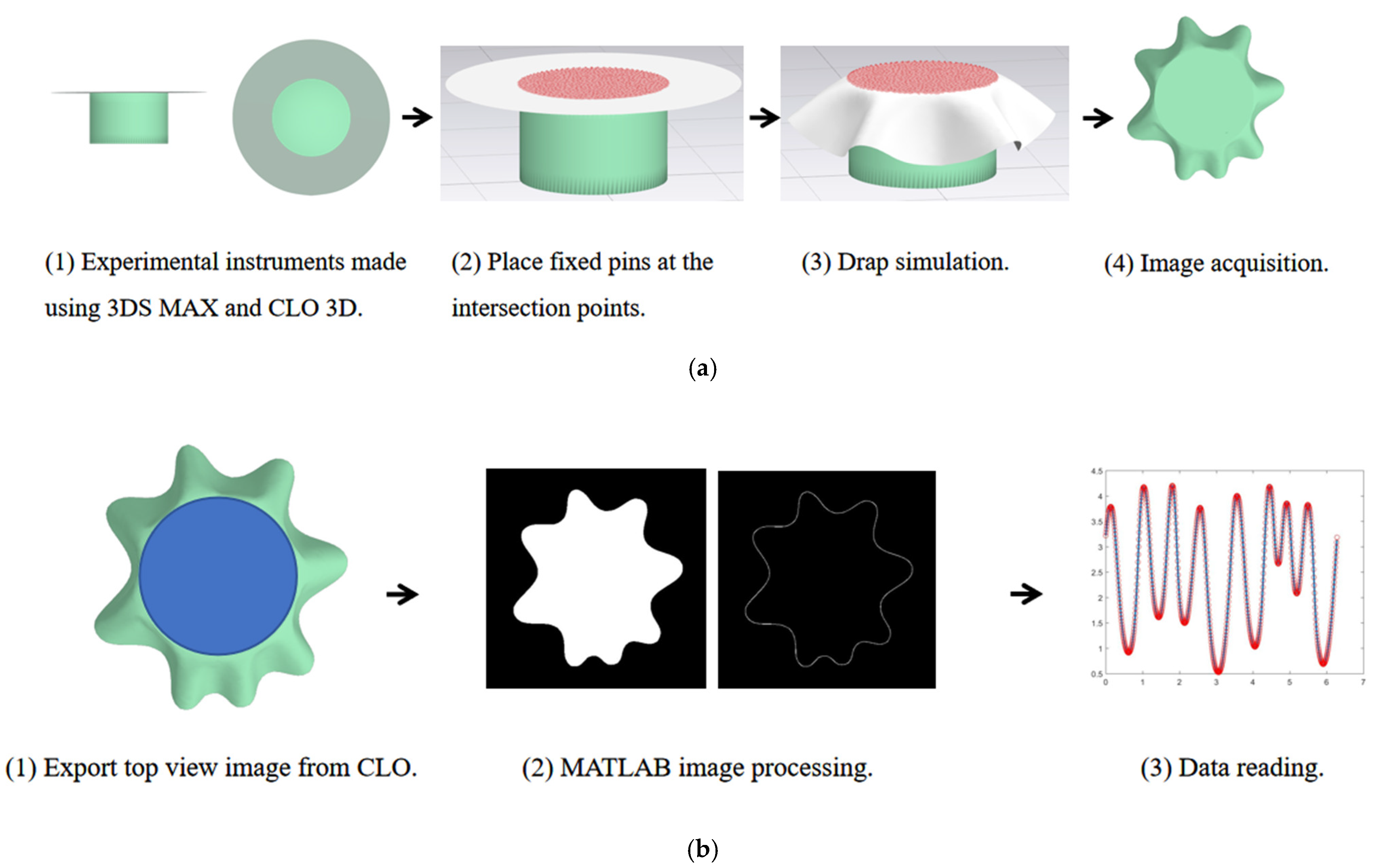
2.3.2. Virtual Drape Test
2.4. Statistical Analysis
2.4.1. Objective Evaluation of Reality
2.4.2. Classification System Development Using Fuzzy Clustering Analysis
2.4.3. Subjective Evaluation of Reality
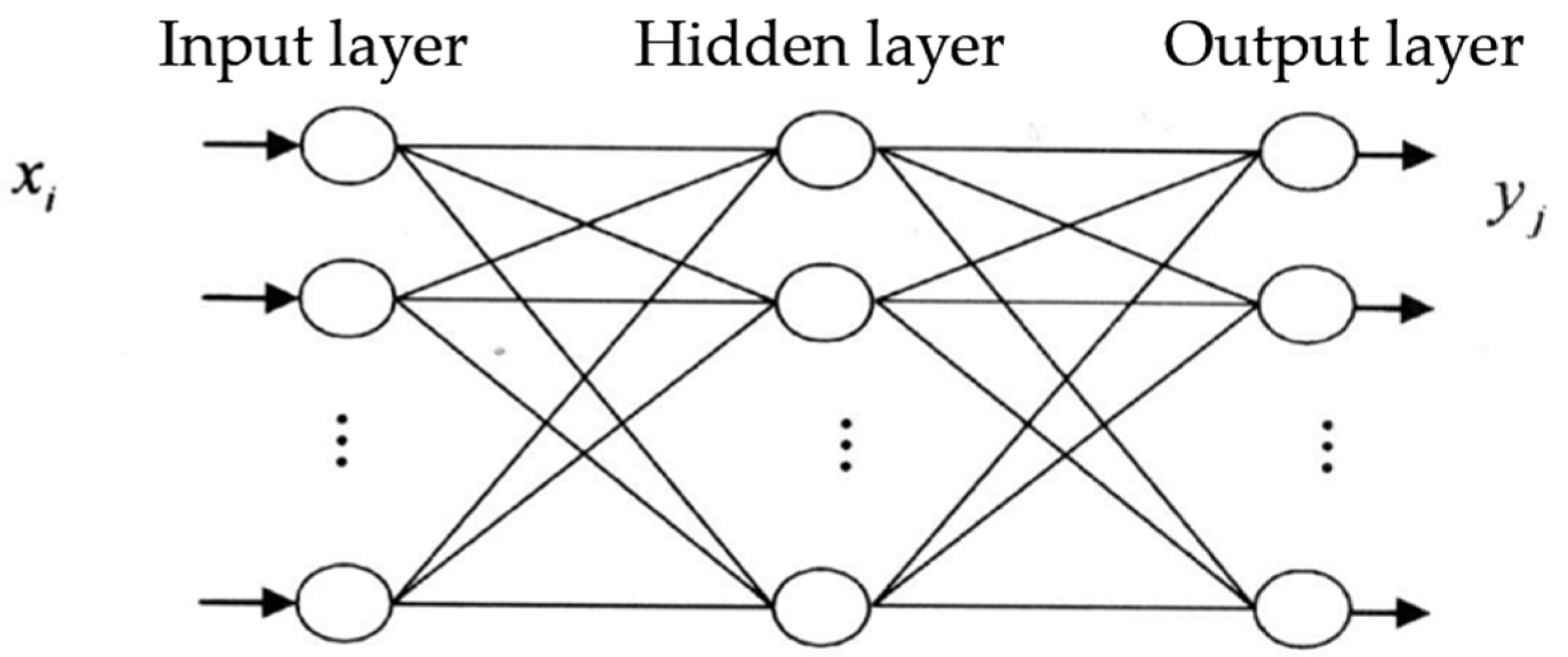
2.5. The BP Neural Network Modeling
2.5.1. Data Preprocessing
2.5.2. BP Neural Network Construction
3. Results and Discussion
3.1. Paired t-Tests
3.2. Results of Fuzzy Clustering Classification
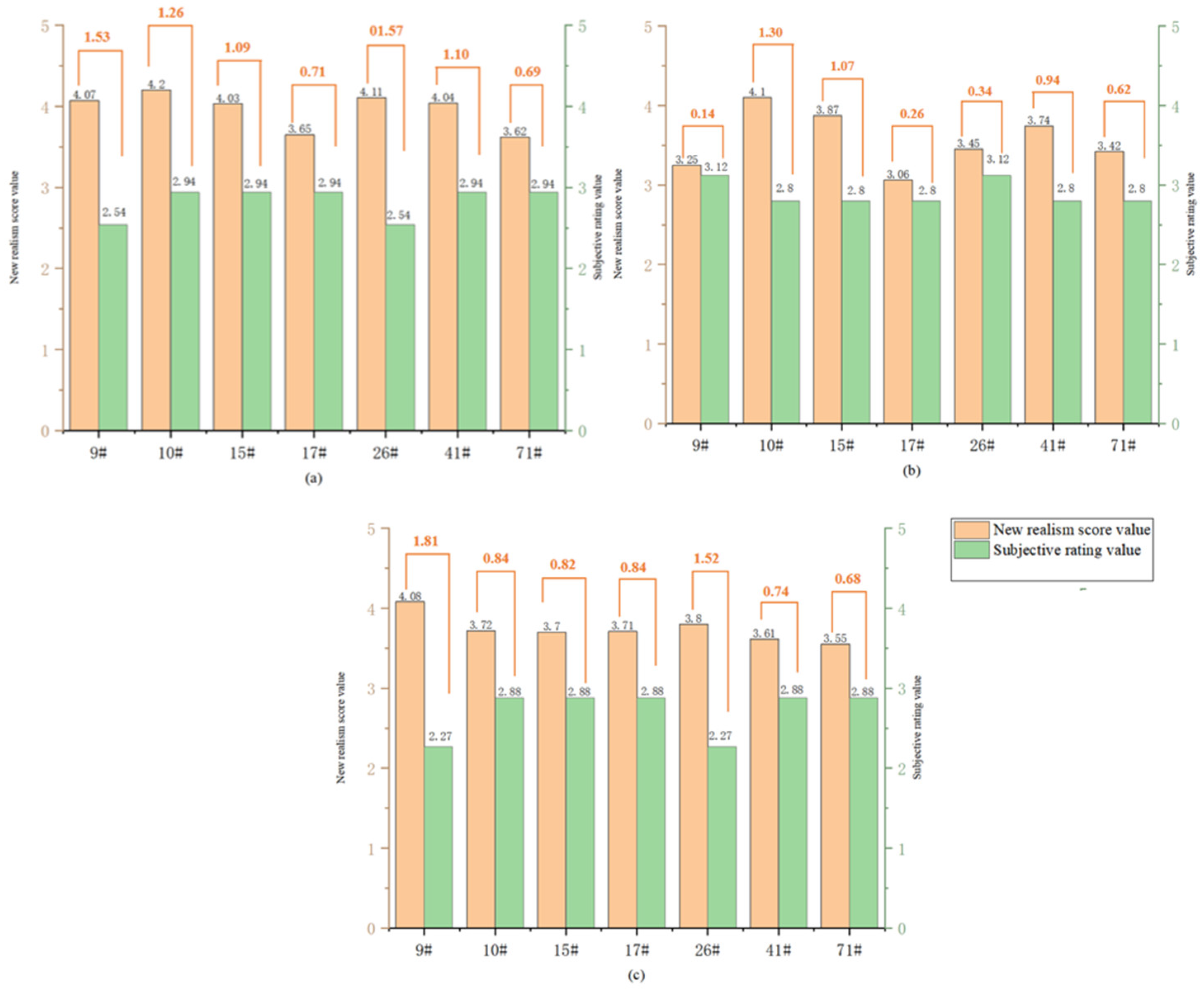
3.3. Subjective Evaluation Results
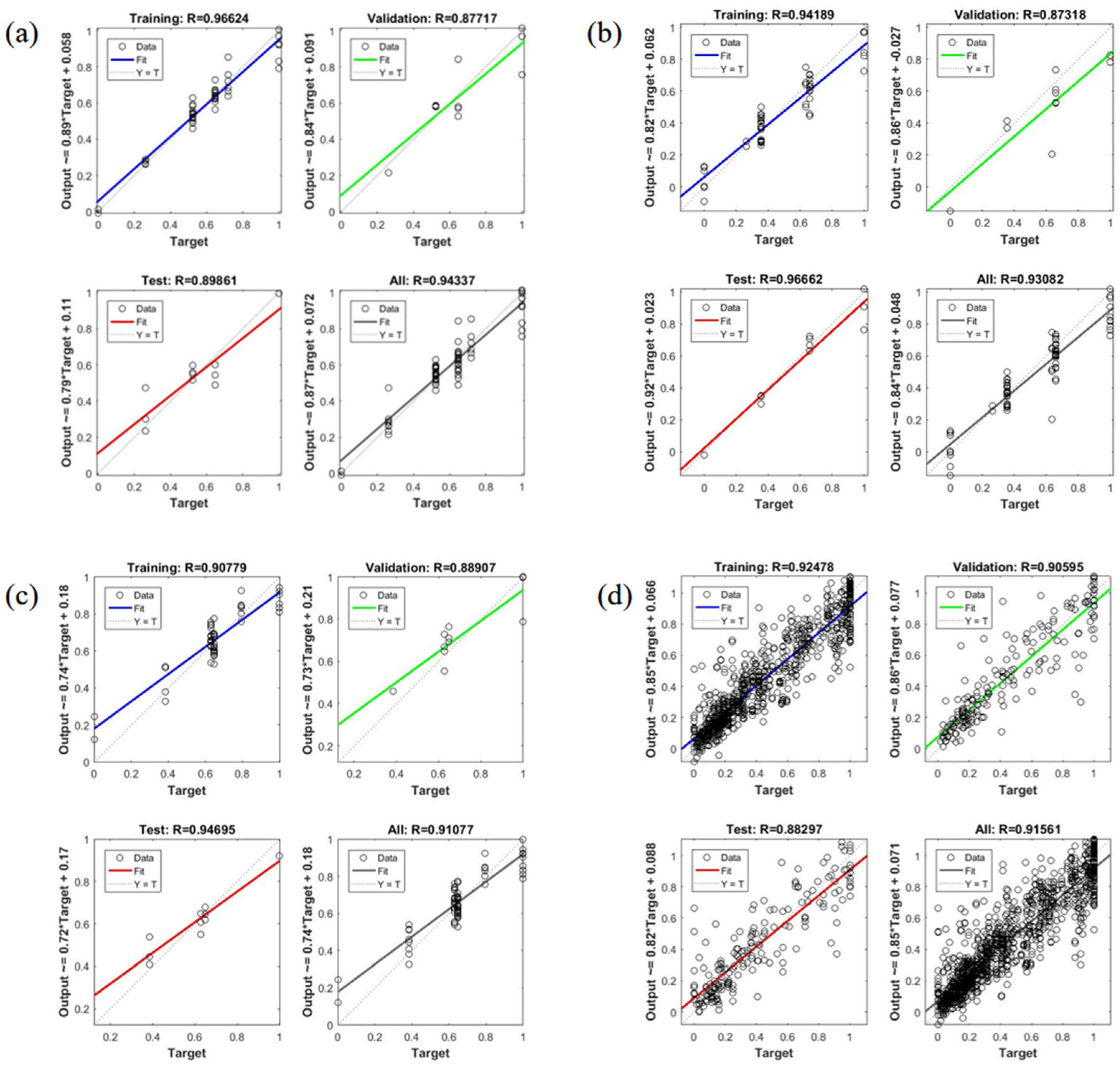
3.4. Prediction Models Verification of BP Neural Network
4. Limitations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Marin, I. Research regarding new sustainable methods of garment pattern drafting. J. Text. Eng. Fash. Technol. 2022, 8, 140–143. [Google Scholar] [CrossRef]
- Fan, W.; Wang, Y.; Liu, R.; Zou, J.; Yu, X.; Liu, Y.; Zhi, C.; Meng, J. Textile production by additive manufacturing and textile waste recycling: A review. Environ. Chem. Lett. 2024, 22, 1929–1987. [Google Scholar] [CrossRef]
- Bertola, P.; Teunissen, J. Fashion 4.0. Innovating fashion industry through digital transformation. Res. J. Text. Appar. 2018, 22, 352–369. [Google Scholar] [CrossRef]
- Pal, R.; Jayarathne, A. Digitalization in the textiles and clothing sector. In The Digital Supply Chain; Elsevier: Amsterdam, The Netherlands, 2022; pp. 255–271. [Google Scholar]
- Bottino, A.; Laurentini, A.; Scalabrin, S. Quantitavely Comparing Virtual and Real Draping of Clothes. 2001. Available online: http://wscg.zcu.cz/wscg2001/Papers_2001/R159.pdf (accessed on 10 June 2025).
- Wang, H.; Hecht, F.; Ramamoorthi, R.; O’Brien, J.F. Example-based wrinkle synthesis for clothing animation. In Proceedings of the ACM SIGGRAPH 2010 Papers, Los Angeles, CA, USA, 26–30 July 2010; pp. 1–8. [Google Scholar]
- Kim, D.-E.; LaBat, K. An exploratory study of users’ evaluations of the accuracy and fidelity of a three-dimensional garment simulation. Text. Res. J. 2013, 83, 171–184. [Google Scholar] [CrossRef]
- Chang, W.; Xu, X. Research on design thinking of pleated clothing inspired by fractal geometry. Int. J. Cloth. Sci. Technol. 2025, 37, 22–47. [Google Scholar] [CrossRef]
- Petrak, S.; Mahnić Naglić, M.; Rogale, D.; Geršak, J. Analysis of polygonal computer model parameters and influence on fabric drape simulation. Materials 2021, 14, 6259. [Google Scholar] [CrossRef]
- Peirce, F.T. 26—The “handle” of cloth as a measurable quantity. J. Text. Inst. Trans. 1930, 21, T377–T416. [Google Scholar] [CrossRef]
- Youn, S.; Knowles, C.G.; Mills, A.C.; Mathur, K. Comparative study of physical and virtual fabric parameters: Physical versus virtual drape test using commercial 3D garment software. J. Text. Inst. 2025, 116, 33–46. [Google Scholar] [CrossRef]
- Liu, C.; Feng, H. Real performance analysis of drape of virtual cotton fabric based on Style3D. Int. J. Cloth. Sci. Technol. 2025, 37, 48–59. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, J.S. Investigating parameters affecting the real and virtual drapability of silk fabrics for traditional Hanbok. Fash. Text. 2024, 11, 21. [Google Scholar] [CrossRef]
- Lu, X.; Zhu, H.; Wang, X. Comparative study on drapability of virtual silk fabrics. J. Silk 2022, 59, 38–45. [Google Scholar]
- Buyukaslan, E.; Jevsnik, S.; Kalaoglu, F. Comparative analysis of drape characteristics of actually and virtually draped fabrics. Int. J. Cloth. Sci. Technol. 2018, 30, 286–301. [Google Scholar] [CrossRef]
- Wang, P.; Liu, J. Method of fabric drape test based on 3D scanning technology. J. Silk 2018, 55, 25–30. [Google Scholar]
- Kim, H.-A.; Ryu, H.-S.; Lee, J.-H.; Nam, Y.-J. A study on the comparing visual images between the real garment and the 3D garment simulation of flare skirts. Sci. Emot. Sensib. 2011, 14, 385–394. [Google Scholar]
- Buyukaslan, E.; Kalaoglu, F.; Jevsnik, S. Drape simulation and subjective assessment of virtual drape. IOP Conf. Ser. Mater. Sci. Eng. 2017, 254, 162002. [Google Scholar] [CrossRef]
- Grieves, M. Digital twin: Manufacturing excellence through virtual factory replication. White Pap. 2014, 1, 1–7. [Google Scholar]
- Tao, F.; Qi, Q.; Wang, L.; Nee, A. Digital twins and cyber–physical systems toward smart manufacturing and industry 4.0: Correlation and comparison. Engineering 2019, 5, 653–661. [Google Scholar] [CrossRef]
- Hu, J.; Chan, Y.-F. Effect of fabric mechanical properties on drape. Text. Res. J. 1998, 68, 57–64. [Google Scholar] [CrossRef]
- Shao, Y. The Study on Relationship between Drape Aesthetic Perception and Property of Mechanics. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2011. [Google Scholar]
- Wang, X. Simulation of Drapability of 3D Virtual Fabric Based on BP Neural Network. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2022. [Google Scholar]
- GB/T 23329-2009; Textiles—Determination of Drapability of Fabrics. China Textile Industry Association: Beijing, China, 2009.
- Bhatti, N.B.; Siyal, A.A.; Qureshi, A.L.; Bhatti, I.A. Socio-economic impact assessment of small dams based on t-paired sample test using SPSS software. Civ. Eng. J. 2019, 5, 153–164. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Zhang, W. Pattern Making for Fashion Design; China Textile & Apparel Press: Beijing, China, 2006; p. 321. [Google Scholar]
- Liang, J.; Zhou, J.; Hu, X.; Luo, H.; Cao, G.; Liu, L.; Xiao, K. Digital Grading the Color Fastness to Rubbing of Fabrics Based on Spectral Reconstruction and BP Neural Network. J. Imaging 2023, 9, 251. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. The Effect Size. Statistical Power Analysis for the Behavioral Sciences; Routledge: Abingdon, UK, 1988; pp. 77–83. [Google Scholar]


| Fabric | Variety | Suitable Clothing |
|---|---|---|
| Cotton | Poplin—plain weave, small figured plain weave | Shirts, trousers, jackets, outerwear, etc |
| Cotton | Khaki—twill about 70° | Outerwear such as trench coats |
| Cotton | Corduroy—weft double layer, soft handfeel, clear grain, round and plump ridges | All kinds of men’s and women’s clothing and apparel items |
| Silk | Chiffon | Summer fabric |
| Nylon | Nylon | Down jacket |
| Number | Fabric Composition | Weight (g/m²) | Number | Fabric Composition | Weight (g/m²) |
|---|---|---|---|---|---|
| 1# | 100% Viscose Rayon | 133 | 37# | 98% Rayon, 2% Silver Thread | 109 |
| 2# | 100% Polyester | 63 | 38# | 50% Cotton, 50% Tencel | 138 |
| 3# | 80% Rayon, 20% Silk | 193 | 39# | 100% Tencel | 172 |
| 4# | 100% Silk | 84 | 40# | 60% Cotton, 40% Polyester | 127 |
| 5# | 95% cotton, 5% polyurethane (PU faux leather) | 104 | 41# | 100% Cotton | 100 |
| Number | Test Type | F (%) | N | MaxCR (cm) | MinCR (cm) | MaxCA (deg) | MinCA (deg) | CVR (%) | CVA (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1# | Real fabric drape test | 17.78 | 8 | 3.21 | 2.27 | 126.84 | 61.42 | 11.08 | 26.30 |
| Virtual drape test | 33.15 | 7 | 4.37 | 3.79 | 117.50 | 74.77 | 5.22 | 15.94 | |
| 2# | Real fabric drape test | 10.67 | 8 | 2.42 | 1.85 | 107.82 | 83.12 | 9.57 | 8.93 |
| Virtual drape test | 17.75 | 11 | 3.40 | 1.72 | 88.12 | 46.40 | 17.61 | 19.11 | |
| 3# | Real fabric drape test | 10.85 | 8 | 2.31 | 1.61 | 104.48 | 73.77 | 11.27 | 12.29 |
| Virtual drape test | 17.54 | 9 | 3.50 | 2.64 | 94.80 | 73.77 | 9.84 | 9.26 | |
| 4# | Real fabric drape test | 17.98 | 7 | 3.57 | 2.73 | 118.50 | 88.12 | 10.27 | 11.93 |
| Virtual drape test | 22.14 | 8 | 3.65 | 3.08 | 97.80 | 83.45 | 5.85 | 5.34 | |
| 5# | Real fabric drape test | 67.22 | 7 | 5.46 | 4.87 | 140.19 | 69.10 | 3.72 | 26.39 |
| Virtual drape test | 70.22 | 7 | 5.62 | 5.00 | 129.18 | 70.10 | 3.82 | 22.47 |
| Category | Fabric Number | Real Fabric | Virtual Fabric | Category | Fabric Number | Real Fabric | Virtual Fabric |
|---|---|---|---|---|---|---|---|
| 1.1 | 4# |  |  | 2.2 | 9# |  |  |
| 1.2 | 1# |  |  | 3.1 | 50# |  |  |
| 2.1 | 17# |  |  | 3.2 | 8# |  |  |
| Paired Differences | t | df | Sig. (2-Tailed) | d | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std. Deviation | Std. Error Mean | 95% Confidence Interval of the Difference | |||||||
| Lower | Upper | |||||||||
| 1 | F2–F1 | 8.16549 | 8.39263 | 0.99602 | 6.17899 | 10.15200 | 8.198 | 70 | 0.000 | 0.973 |
| 2 | N2–N1 | 0.634 | 1.268 | 0.150 | 0.334 | 0.934 | 4.213 | 70 | 0.000 | 0.500 |
| 3 | MaxWC2–MaxWC1 | 0.28380 | 0.58658 | 0.06961 | 0.14496 | 0.42264 | 4.077 | 70 | 0.000 | 0.484 |
| 4 | MinWC2–MinWC1 | 0.55704 | 0.63611 | 0.07549 | 0.40648 | 0.70761 | 7.379 | 70 | 0.000 | 0.876 |
| 5 | MaxCA2–MaxCA1 | −20.58225 | 28.30962 | 3.35973 | −27.28303 | −13.88148 | −6.126 | 70 | 0.000 | −0.727 |
| 6 | MinCA2–MinCA1 | 3.88085 | 26.14489 | 3.10283 | −2.30755 | 10.06924 | 1.251 | 70 | 0.215 | 0.148 |
| 7 | CVR2–CVR1 | −3.54127 | 4.04292 | 0.47981 | −4.49821 | −2.58432 | −7.381 | 70 | 0.000 | −0.876 |
| 8 | CVA2–CVA1 | −7.36254 | 8.85209 | 1.05055 | −9.45779 | −5.26728 | −7.008 | 70 | 0.000 | −0.832 |
| Category | Cluster Center | Threshold Range | Corresponding Fabric Sample |
|---|---|---|---|
| Category 1 | 8.34793029565442 | 3.000~15.370 | 1#, 2#, 3#, 4#, 5#, 6#, 7#, 11#, 12#, 13#, 14#, 16#, 19#, 20#, 21#, 22#, 23#, 24#, 25#, 27#, 28#, 29#, 30#, 32#, 33#, 34#, 35#, 37#, 39#, 43#, 45#, 49#, 52#, 53#, 54#, 57#, 59#, 61#, 63#, 64#, 65#, 66#, 68#, 69#, 70# |
| Category 2 | 22.6995760042544 | 17.988~30.110 | 9#, 10#, 15#, 17#, 18#, 26#, 31#, 41#, 58#, 71# |
| Category 2 | −2.65507031633409 | −11.037~2.598 | 8#, 36#, 38#, 40#, 42#, 44#, 46#, 47#, 48#, 50#, 51#, 55#, 56#, 60#, 62#, 67# |
| Category | F (%) | N | MaxCR (cm) | MinCR (cm) | MaxCA (deg) | MinCA (deg) | CVR (%) | CVA (%) |
|---|---|---|---|---|---|---|---|---|
| Category 1.1 | 3.757~13.767 | 0.333~3.333 | −0.214~1.184 | −0.263~1.055 | −74.771~−9.680 | −36.718~20.028 | −14.432~8.046 | −27.784~12.695 |
| Category 1.2 | 3.000~15.370 | −2.000~0.667 | −0.005~1.289 | 0.046~1.524 | −29.040~54.075 | −4.673~66.426 | −10.172~2.321 | −20.738~9.940 |
| Category 2.1 | 17.988~30.110 | −1.000~2.333 | −0.061~1.421 | 0.443~1.666 | −104.478~27.038 | −39.722~26.036 | −8.937~−1.626 | −20.961~11.484 |
| Category 2.2 | 24.851~29.472 | −3.000~−1.000 | 0.506~2.034 | 1.382~2.775 | −0.668~17.024 | 77.107~106.481 | −8.195~−6.841 | −32.433~−26.797 |
| Category 3.1 | −4.202~2.013 | −1.000~1.000 | −0.311~0.301 | −0.108~0.498 | −29.708~16.022 | −16.690~26.036 | −3.644~0.012 | −11.837~6.006 |
| Category 3.2 | −11.037~2.598 | 0.667~2.667 | −1.054~0.122 | −0.832~0.192 | −74.771~−37.385 | −26.370~9.346 | −10.377~2.644 | −19.279~−4.386 |
| Score | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Corresponding meaning | Poor | Fair | acceptable | Good | Excellent |
| Fabric Number | Evaluation Aspect | Result (Average Value) | Fabric Number | Evaluation Aspect | Result (Average Value) |
|---|---|---|---|---|---|
| 4# | Overall Feeling | 3.53 | 1# | Overall Feeling | 3.34 |
| Degree of Draping | 3.60 | Degree of Draping | 3.23 | ||
| Draping Form | 3.27 | Draping Form | 3.30 | ||
| 17# | Overall Feeling | 2.94 | 9# | Overall Feeling | 2.54 |
| Degree of Draping | 2.80 | Degree of Draping | 3.12 | ||
| Draping Form | 2.88 | Draping Form | 2.27 | ||
| 50# | Overall Feeling | 3.64 | 8# | Overall Feeling | 4.07 |
| Degree of Draping | 3.57 | Degree of Draping | 4.01 | ||
| Draping Form | 3.53 | Draping Form | 3.86 |
| Number | Initial Simulated Drape Renderings | Simulated Drape Renderings After Optimization |
|---|---|---|
| 9# |  |  |
| 10# |  |  |
| 15# |  |  |
| 17# |  |  |
| 26# |  |  |
| 41# |  |  |
| 71# |  |  |
| Number | F (%) | N | MaxCR (cm) | MinCR (cm) | MaxCA (deg) | MinCA (deg) | CVR (%) | CVA (%) |
|---|---|---|---|---|---|---|---|---|
| 9# | −13.16 | 0 | 0.01 | 0.19 | −16.02 | 14.35 | −0.03 | −10.66 |
| 10# | −1.37 | 3 | −0.27 | −0.39 | −69.10 | −47.73 | 0.22 | −0.62 |
| 15# | 2.29 | 2 | −0.16 | 0.02 | −47.07 | −51.07 | −1.92 | 4.87 |
| 17# | −7.15 | 0 | 0.07 | 0.15 | 15.69 | 22.03 | −0.22 | −4.08 |
| 26# | −3.03 | 1 | 0.06 | −0.79 | −65.42 | 16.02 | 8.32 | −25.71 |
| 41# | 0.86 | 3 | −0.48 | −0.12 | −59.08 | −42.06 | −3.76 | −0.83 |
| 71# | −1.47 | 1 | 0.22 | 0.14 | −15.35 | −2.00 | −0.43 | −2.78 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Fang, F.; Chen, Q. A Sustainable Framework for Realism Evaluation and Optimization of Virtual Fabric Drape Effect. Sustainability 2025, 17, 5550. https://doi.org/10.3390/su17125550
Wang R, Fang F, Chen Q. A Sustainable Framework for Realism Evaluation and Optimization of Virtual Fabric Drape Effect. Sustainability. 2025; 17(12):5550. https://doi.org/10.3390/su17125550
Chicago/Turabian StyleWang, Rulin, Fang Fang, and Qiaoqiao Chen. 2025. "A Sustainable Framework for Realism Evaluation and Optimization of Virtual Fabric Drape Effect" Sustainability 17, no. 12: 5550. https://doi.org/10.3390/su17125550
APA StyleWang, R., Fang, F., & Chen, Q. (2025). A Sustainable Framework for Realism Evaluation and Optimization of Virtual Fabric Drape Effect. Sustainability, 17(12), 5550. https://doi.org/10.3390/su17125550





