Unravelling Landscape Evolution and Soil Erosion Dynamics in the Xynias Drained Lake Catchment, Central Greece: A GIS and RUSLE Modelling Approach
Abstract
1. Introduction
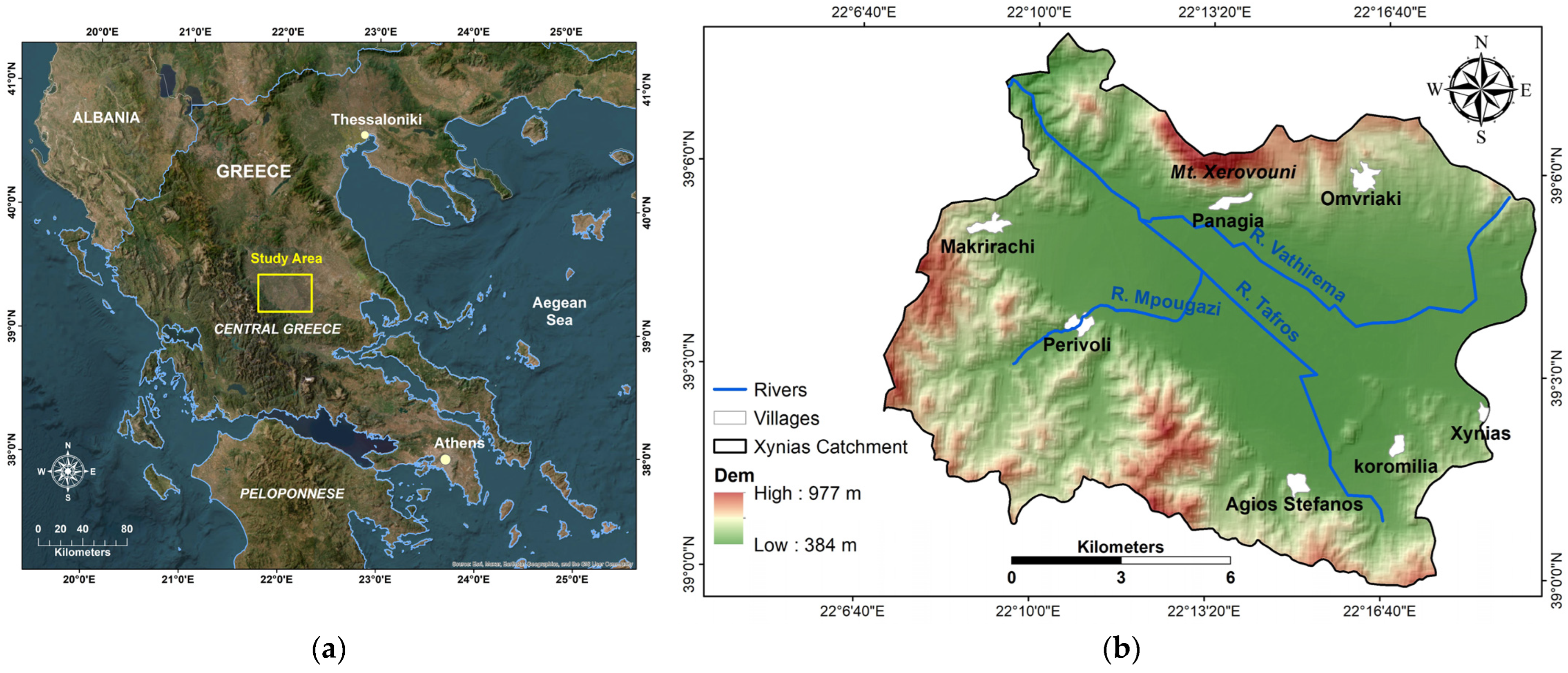
2. Study Area Characteristics
3. Materials and Methods
3.1. Input Data
3.2. Geomorphological Variables
3.2.1. Framework
3.2.2. Basic Principles
3.3. The Revised Universal Soil Loss Equation (RUSLE)
4. Results and Discussion
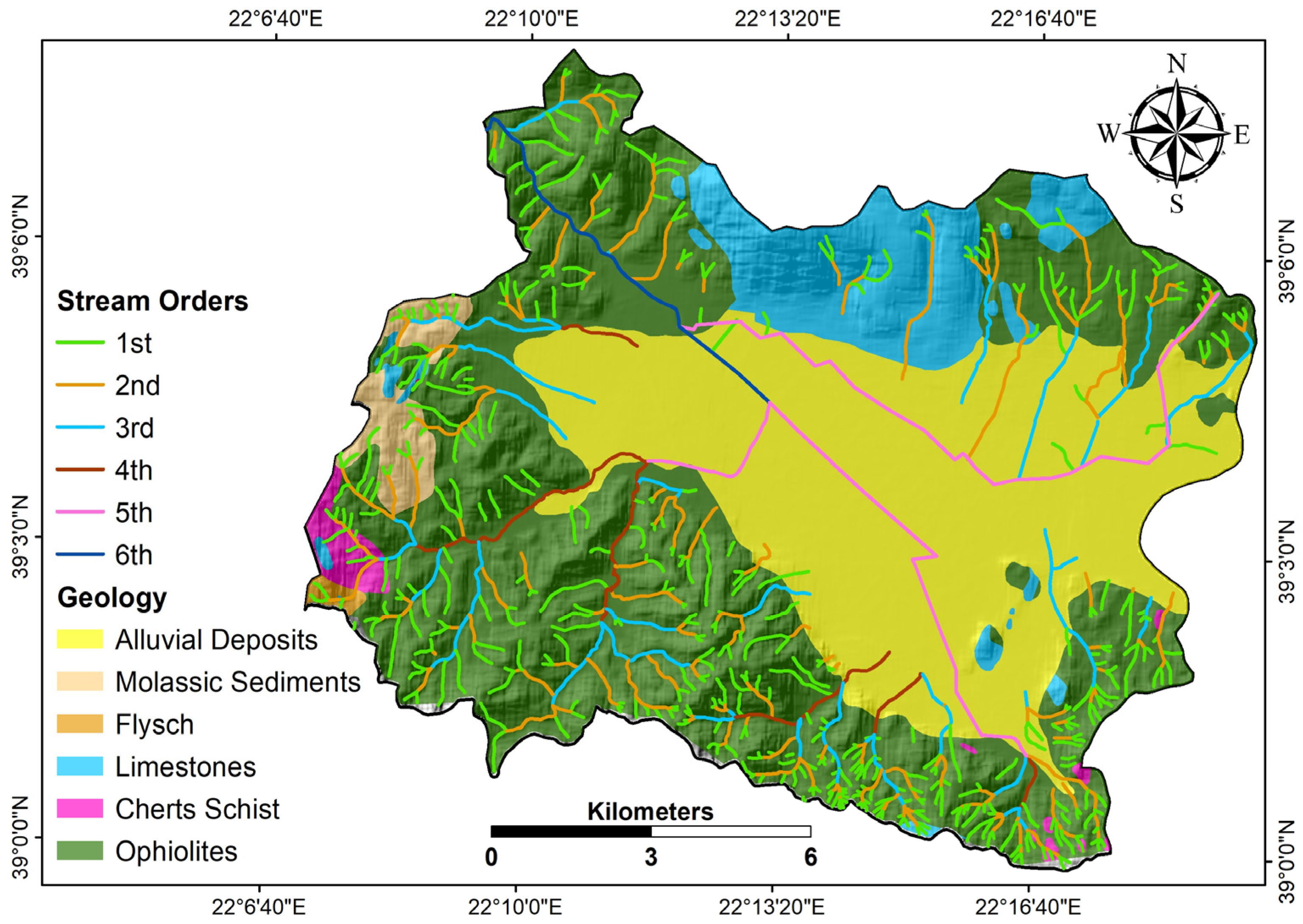
4.1. Geomorphological Analysis
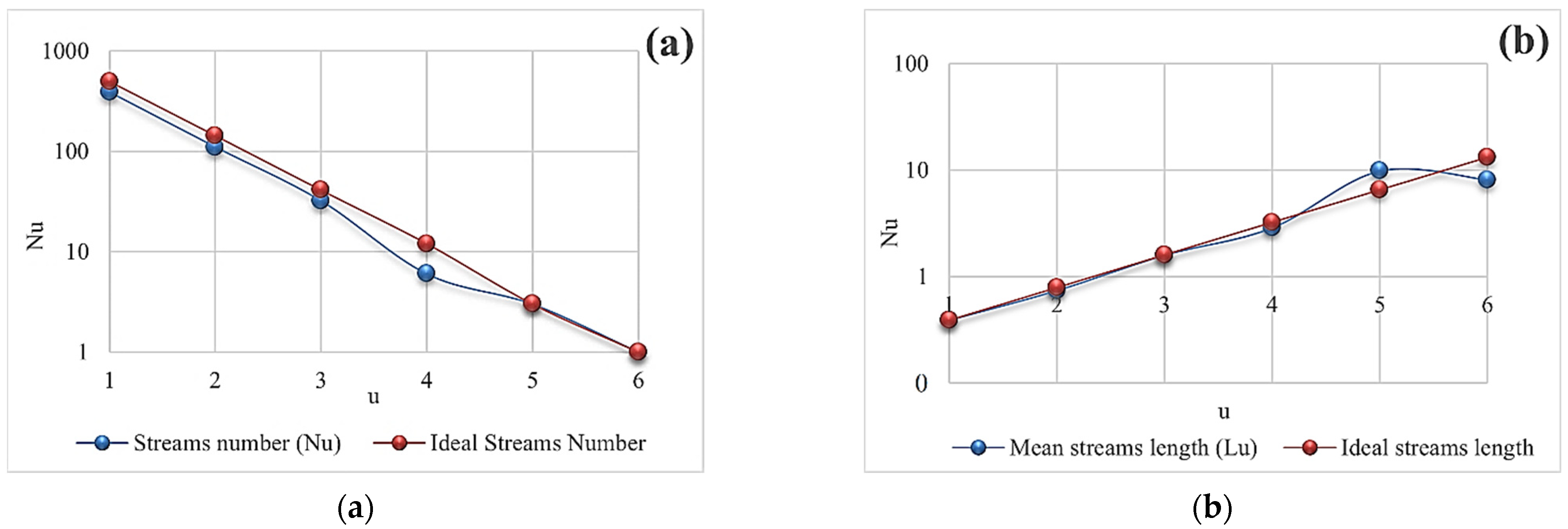
4.1.1. Horton’s First Law
4.1.2. Horton’s Second Law
4.1.3. Drainage Density (D)
4.1.4. Drainage Frequency (F)
4.1.5. Relief Ratio (Rh)
4.1.6. Circularity (Cu)
4.1.7. Elongation Ratio (Er)
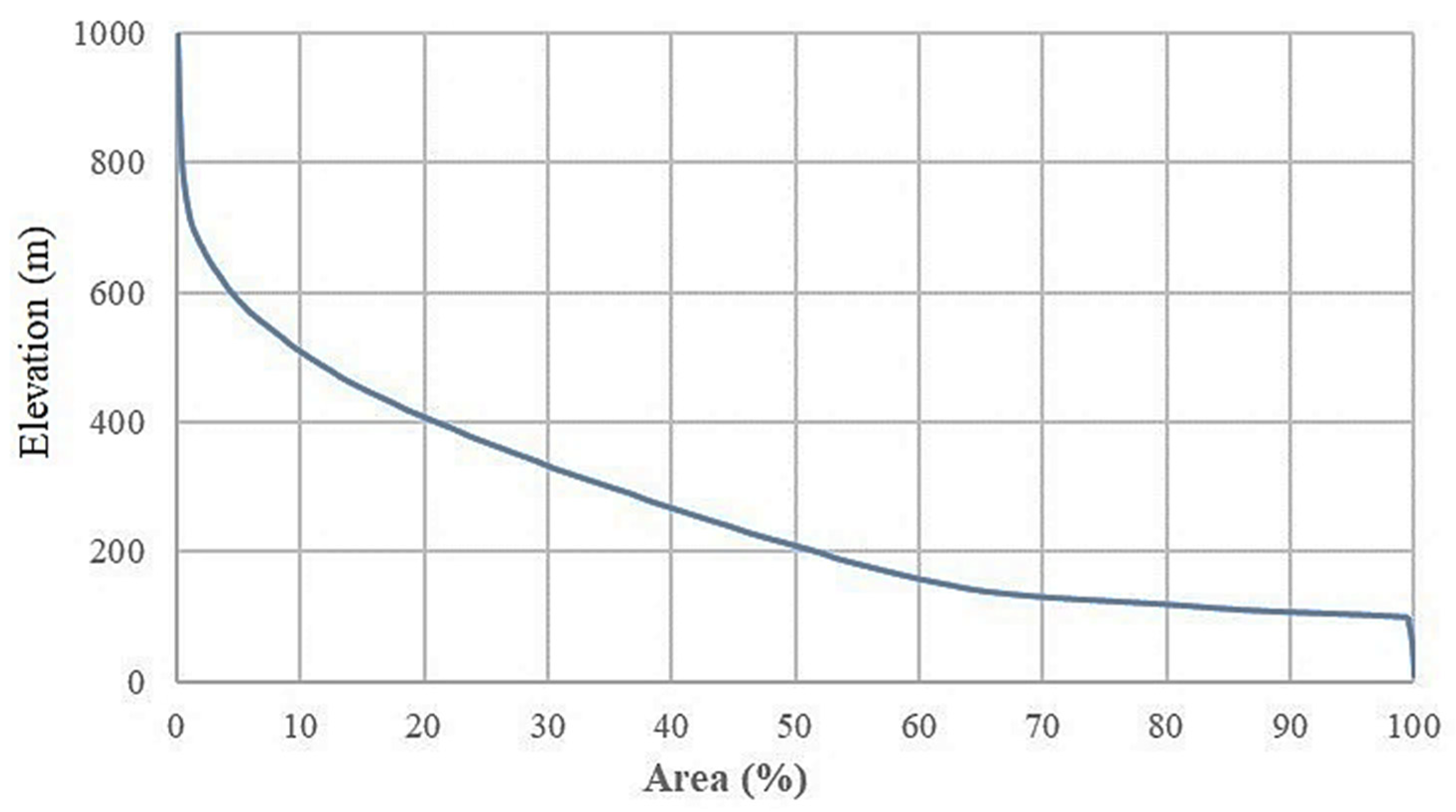
4.1.8. Hypsometric Integral (Hi)
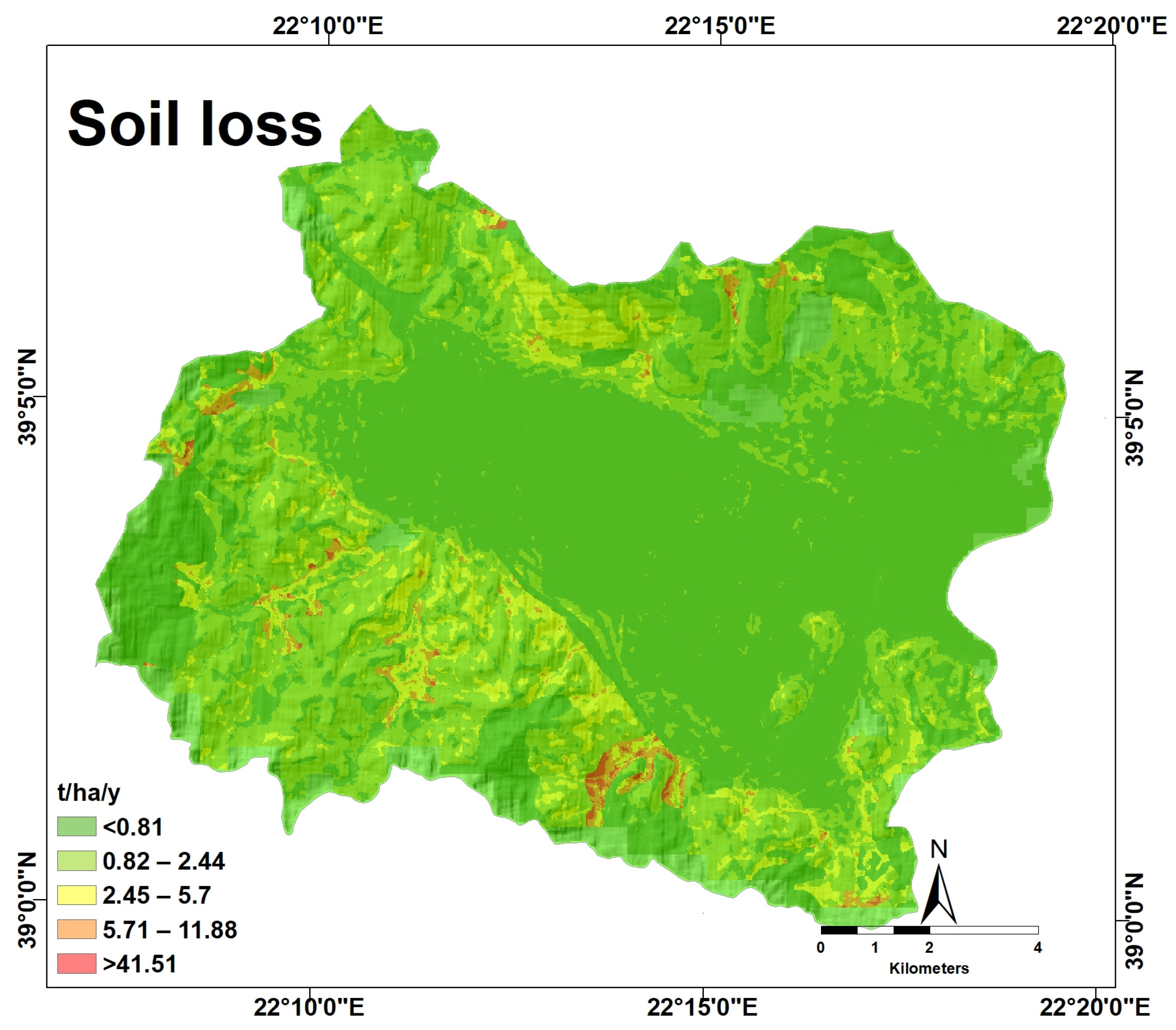
4.2. Soil Erosion Analysis
4.3. Policy and Methodological Implications for Soil Health and Sustainability Goals
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Psomiadis, E.; Charizopoulos, N.; Soulis, K.X.; Efthimiou, N. Investigating the Correlation of Tectonic and Morphometric Characteristics with the Hydrological Response in a Greek River Catchment Using Earth Observation and Geospatial Analysis Techniques. Geosciences 2020, 10, 377. [Google Scholar] [CrossRef]
- Prakash, K.; Rawat, D.; Singh, S.; Chaubey, K.; Kanhaiya, S.; Mohanty, T. Morphometric Analysis Using SRTM and GIS in Synergy with Depiction: A Case Study of the Karmanasa River Basin, North Central India. Appl. Water Sci. 2019, 9, 13. [Google Scholar] [CrossRef]
- Psomiadis, E.; Migiros, G.; Antoniou, V. Geomorphological Quantitative Analysis of Sperchios River Basin Area (Central Greece) Utilizing Geographical Information Systems. Bull. Geol. Soc. Greece 2013, 47, 325. [Google Scholar] [CrossRef][Green Version]
- Psomiadis, E. Research of Geomorphological and Environmental Changes in the Sperchios’ River Basin Utilizing New Technologies. Ph.D. Thesis, Agricultural University of Athens, Athina, Greek, 2010. (In Greek). [Google Scholar]
- Tucker, G.E.; Hancock, G.R. Modelling Landscape Evolution. Earth Surf. Process. Landforms 2010, 35, 28–50. [Google Scholar] [CrossRef]
- Charizopoulos, N.; Mourtzios, P.; Psilovikos, T.; Psilovikos, A.; Karamoutsou, L. Comptes Rendus-Geoscience Morphometric Analysis of the Drainage Network of Samos Island (Northern Aegean Sea): Insights into Tectonic Control and Fl Ood Hazards. Comptes Rendus-Geosci. 2019, 351, 375–383. [Google Scholar] [CrossRef]
- Waikar, M.L.; Nilawar, A.P. Morphometric Analysis of a Drainage Basin Using Geographical Information System: A Case Study. Int. J. Multidiscip. Curr. Res. 2014, 2, 179–184. [Google Scholar]
- Ganasri, B.P.; Ramesh, H. Assessment of Soil Erosion by RUSLE Model Using Remote Sensing and GIS-A Case Study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin Characteristics. Eos Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Horton, R.E. An Approach Toward a Physical Interpretation of Infiltration-Capacity. Soil Sci. Soc. Am. J. 1941, 5, 399–417. [Google Scholar] [CrossRef]
- Horton, R.E. Erosional Development of Streams and Their Drainage Basins; Hydrophysical Approach to Quantitative Morphology. GSA Bull. 1945, 56, 275–370. [Google Scholar] [CrossRef]
- Strahler, A.N. Hypsometric (Area-Altitude) Analysis of Erosional Topography. GSA Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Strahler, A.N. Quantitative Analysis of Watershed Geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Dapin, I.G.; Ella, V.B. GIS-Based Soil Erosion Risk Assessment in the Watersheds of Bukidnon, Philippines Using the RUSLE Model. Sustainability 2023, 15, 3325. [Google Scholar] [CrossRef]
- Mantilla, R.; Gupta, V.K. A GIS Numerical Framework to Study the Process Basis of Scaling Statistics in River Networks. IEEE Geosci. Remote Sens. Lett. 2005, 2, 404–408. [Google Scholar] [CrossRef]
- Cao, Q.; Miao, Y.; Li, F.; Gao, X.; Liu, B.; Lu, D.; Chen, X. Developing a New Crop Circle Active Canopy Sensor-Based Precision Nitrogen Management Strategy for Winter Wheat in North China Plain. Precis. Agric. 2017, 18, 2–18. [Google Scholar] [CrossRef]
- Harsha, J.; Ravikumar, A.S.; Shivakumar, B.L. Evaluation of Morphometric Parameters and Hypsometric Curve of Arkavathy River Basin Using RS and GIS Techniques. Appl. Water Sci. 2020, 10, 86. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Jones, A.; Robinson, D.A. A 1 Billion Euro Mission: A Soil Deal for Europe. Eur. J. Soil Sci. 2024, 75, e13466. [Google Scholar] [CrossRef]
- Pandey, A.; Himanshu, S.K.; Mishra, S.K.; Singh, V.P. Physically Based Soil Erosion and Sediment Yield Models Revisited. CATENA 2016, 147, 595–620. [Google Scholar] [CrossRef]
- Covelli, C.; Cimorelli, L.; Pagliuca, D.N.; Molino, B.; Pianese, D. Assessment of Erosion in River Basins: A Distributed Model to Estimate the Sediment Production over Watersheds by a 3-Dimensional LS Factor in RUSLE Model. Hydrology 2020, 7, 13. [Google Scholar] [CrossRef]
- Poesen, J.W.; Torri, D.; Bunte, K. Effects of Rock Fragments on Soil Erosion by Water at Different Spatial Scales: A Review. CATENA 1994, 23, 141–166. [Google Scholar] [CrossRef]
- Smets, T.; Poesen, J.; Bochet, E. Impact of Plot Length on the Effectiveness of Different Soil-Surface Covers in Reducing Runoff and Soil Loss by Water. Prog. Phys. Geogr. 2008, 32, 654–677. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Poesen, J.; Ballabio, C.; Lugato, E.; Meusburger, K.; Montanarella, L.; Alewell, C. The New Assessment of Soil Loss by Water Erosion in Europe. Environ. Sci. Policy 2015, 54, 438–447. [Google Scholar] [CrossRef]
- Borrelli, P.; Märker, M.; Panagos, P.; Schütt, B. Modeling Soil Erosion and River Sediment Yield for an Intermountain Drainage Basin of the Central Apennines, Italy. CATENA 2014, 114, 45–58. [Google Scholar] [CrossRef]
- Funk, R.; Völker, L.; Deumlich, D. Landscape Structure Model Based Estimation of the Wind Erosion Risk in Brandenburg, Germany. Aeolian Res. 2023, 62, 100878. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, Y.; Vaze, J.; Lane, P.; Xu, S. Impact of Bushfire and Climate Variability on Streamflow from Forested Catchments in Southeast Australia. Hydrol. Sci. J. 2015, 60, 1340–1360. [Google Scholar] [CrossRef]
- Shroder, J.F.; Bishop, M.P. Mass Movement in the Himalaya: New Insights and Research Directions. Geomorphology 1998, 26, 13–35. [Google Scholar] [CrossRef]
- Kirkby, M.J.; Irvine, B.J.; Jones, R.J.A.; Govers, G.; Boer, M.; Cerdan, O.; Daroussin, J.; Gobin, A.; Grimm, M.; Le Bissonnais, Y.; et al. The PESERA Coarse Scale Erosion Model for Europe. I.—Model Rationale and Implementation. Eur. J. Soil Sci. 2008, 59, 1293–1306. [Google Scholar] [CrossRef]
- Dragičević, N.; Karleuša, B.; Ožanić, N. A Review of the Gavrilović Method (Erosion Potential Method) Application. Gradjevinar 2016, 68, 715–725. [Google Scholar] [CrossRef]
- Flanagan, D.C.; Gilley, J.E.; Franti, T.G. Water Erosion Prediction Project (WEPP): Development History, Model Capabilities, and Future Enhancements. Trans. ASABE 2007, 50, 1603–1612. [Google Scholar] [CrossRef]
- De Roo, A.P.J.; Hazelhoff, L.; Burrough, P.A. Soil Erosion Modelling Using ‘Answers’ and Geographical Information Systems. Earth Surf. Process. Landforms 1989, 14, 517–532. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2005. 2005. Available online: https://swat.tamu.edu/media/1292/swat2005theory.pdf (accessed on 1 February 2025).
- Laflen, J.M.; Lane, L.J.; Foster, G.R. WEPP: A New Generation of Erosion Prediction Technology. J. Soil Water Conserv. 1991, 46, 34–38. [Google Scholar] [CrossRef]
- Karydas, C.G.; Panagos, P. The G2 Erosion Model: An Algorithm for Month-Time Step Assessments. Environ. Res. 2018, 161, 256–267. [Google Scholar] [CrossRef] [PubMed]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; United States Science, Education Administration, Purdue University Agricultural Experiment Station, Eds.; USDA Publications, Department of Agriculture, Science and Education Administration, U.S. Government Printing Office: Washington, DC, USA, 1978. [Google Scholar]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.I. RUSLE Revised Universal Soil Loss Equation; United States Department of Agriculture (USDA), Agricultural Research Service (ARS): Beltsville, MD, USA, 1991. [Google Scholar]
- Kouli, M.; Soupios, P.; Vallianatos, F. Soil Erosion Prediction Using the Revised Universal Soil Loss Equation (RUSLE) in a GIS Framework, Chania, Northwestern Crete, Greece. Environ. Geol. 2009, 57, 483–497. [Google Scholar] [CrossRef]
- Alexiou, S.; Efthimiou, N.; Karamesouti, M.; Papanikolaou, I.; Psomiadis, E.; Charizopoulos, N. Measuring Annual Sedimentation through High Accuracy UAV-Photogrammetry Data and Comparison with RUSLE and PESERA Erosion Models. Remote Sens. 2023, 15, 1339. [Google Scholar] [CrossRef]
- Efthimiou, N.; Psomiadis, E.; Panagos, P. Fire Severity and Soil Erosion Susceptibility Mapping Using Multi-Temporal Earth Observation Data: The Case of Mati Fatal Wildfire in Eastern Attica, Greece. CATENA 2020, 187, 104320. [Google Scholar] [CrossRef]
- Efthimiou, N.; Lykoudi, E.; Karavitis, C. Comparative Analysis of Sediment Yield Estimations Using Different Empirical Soil Erosion Models. Hydrol. Sci. J. 2017, 62, 2674–2694. [Google Scholar] [CrossRef]
- Brini, I.; Alexakis, D.D.; Kalaitzidis, C. Linking Soil Erosion Modeling to Landscape Patterns and Geomorphometry: An Application in Crete, Greece. Appl. Sci. 2021, 11, 5684. [Google Scholar] [CrossRef]
- Stefanidis, S.P.; Proutsos, N.D.; Solomou, A.D.; Michopoulos, P.; Bourletsikas, A.; Tigkas, D.; Spalevic, V.; Kader, S. Spatiotemporal Monitoring of Post-Fire Soil Erosion Rates Using Earth Observation (EO) Data and Cloud Computing. Nat. Hazards 2024, 121, 2873–2894. [Google Scholar] [CrossRef]
- González Bonorino, G.; Osterkamp, W.R.; Colombo Piñol, F. An Averaging Procedure for Applying the Revised Universal Soil Loss Equation (RUSLE) to Disturbed Mountain Watersheds. Geogaceta 2002, 33, 51–54. [Google Scholar]
- Bircher, P.; Liniger, H.P.; Prasuhn, V. Comparison of Long-Term Field-Measured and RUSLE-Based Modelled Soil Loss in Switzerland. Geoderma Reg. 2022, 31, e00595. [Google Scholar] [CrossRef]
- Getu, L.A.; Nagy, A.; Addis, H.K. Soil Loss Estimation and Severity Mapping Using the RUSLE Model and GIS in Megech Watershed, Ethiopia. Environ. Chall. 2022, 8, 100560. [Google Scholar] [CrossRef]
- Demir, S.; Dursun, İ. Assessment of Pre- and Post-Fire Erosion Using the RUSLE Equation in a Watershed Affected by the Forest Fire on Google Earth Engine: The Study of Manavgat River Basin. Nat. Hazards 2024, 120, 2499–2527. [Google Scholar] [CrossRef]
- Nourizadeh, M.; Naghavi, H.; Omidvar, E. Correction to: The Effect of Land Use and Land Cover Changes on Soil Erosion in Semi-Arid Areas Using Cloud-Based Google Earth Engine Platform and GIS-Based RUSLE Model. Nat. Hazards 2024, 120, 8095–8099. [Google Scholar] [CrossRef]
- Gupta, S.; Ojha, C.S.P.; Singh, V.P.; Adeloye, A.J.; Jain, S.K. Pixel-Based Soil Loss Estimation and Prioritization of North-Western Himalayan Catchment Based on Revised Universal Soil Loss Equation (RUSLE). Sustainability 2023, 15, 15177. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Event Soil Loss, Runoff and the Universal Soil Loss Equation Family of Models: A Review. J. Hydrol. 2010, 385, 384–397. [Google Scholar] [CrossRef]
- Li, P.; Zang, Y.; Ma, D.; Yao, W.; Holden, J.; Irvine, B.; Zhao, G. Soil Erosion Rates Assessed by RUSLE and PESERA for a Chinese Loess Plateau Catchment under Land-cover Changes. Earth Surf. Process. Landforms 2020, 45, 707–722. [Google Scholar] [CrossRef]
- Kaffas, K.; Pisinaras, V.; Al Sayah, M.J.; Santopietro, S.; Righetti, M. A USLE-Based Model with Modified LS-Factor Combined with Sediment Delivery Module for Alpine Basins. CATENA 2021, 207, 105655. [Google Scholar] [CrossRef]
- De Vente, J.; Poesen, J.; Verstraeten, G.; Govers, G.; Vanmaercke, M.; Van Rompaey, A.; Arabkhedri, M.; Boix-Fayos, C. Predicting Soil Erosion and Sediment Yield at Regional Scales: Where Do We Stand? Earth-Sci. Rev. 2013, 127, 16–29. [Google Scholar] [CrossRef]
- Polykretis, C.; Alexakis, D.D.; Grillakis, M.G.; Manoudakis, S. Assessment of Intra-Annual and Inter-Annual Variabilities of Soil Erosion in Crete Island (Greece) by Incorporating the Dynamic “Nature” of R and C-Factors in RUSLE Modeling. Remote Sens. 2020, 12, 2439. [Google Scholar] [CrossRef]
- Efthimiou, N.; Psomiadis, E.; Papanikolaou, I.; Soulis, K.X.; Borrelli, P.; Panagos, P. A New High Resolution Object-Oriented Approach to Define the Spatiotemporal Dynamics of the Cover-Management Factor in Soil Erosion Modelling. CATENA 2022, 213, 106149. [Google Scholar] [CrossRef]
- Psomiadis, E.; Papazachariou, A.; Soulis, K.X.; Alexiou, D.S.; Charalampopoulos, I. Landslide Mapping and Susceptibility Assessment Using Geospatial Analysis and Earth Observation Data. Land 2020, 9, 133. [Google Scholar] [CrossRef]
- Sidi Almouctar, M.A.; Wu, Y.; Zhao, F.; Dossou, J.F. Soil Erosion Assessment Using the RUSLE Model and Geospatial Techniques (Remote Sensing and GIS) in South-Central Niger (Maradi Region). Water 2021, 13, 3511. [Google Scholar] [CrossRef]
- Ghosh, A.; Rakshit, S.; Tikle, S.; Das, S.; Chatterjee, U.; Pande, C.B.; Alataway, A.; Al-Othman, A.A.; Dewidar, A.Z.; Mattar, M.A. Integration of GIS and Remote Sensing with RUSLE Model for Estimation of Soil Erosion. Land 2022, 12, 116. [Google Scholar] [CrossRef]
- Liu, B.Y.; Nearing, M.A.; Risse, L.M. Slope Gradient Effects on Soil Loss for Steep Slopes. Trans. Am. Soc. Agric. Eng. 1994, 37, 1835–1840. [Google Scholar] [CrossRef]
- Michalopoulou, M.; Depountis, N.; Nikolakopoulos, K.; Boumpoulis, V. The Significance of Digital Elevation Models in the Calculation of LS Factor and Soil Erosion. Land 2022, 11, 1592. [Google Scholar] [CrossRef]
- Jothimani, M.; Mulualem, W. Drainage Morphometric Characterization of Megech River Watershed, North Western Ethiopia, Using Geospatial Tools. Ethiop. J. Nat. Comput. Sci. 2021, 1, 37–52. [Google Scholar] [CrossRef]
- Gajbhiye, S.; Mishra, S.K.; Pandey, A. Prioritizing Erosion-Prone Area through Morphometric Analysis: An RS and GIS Perspective. Appl. Water Sci. 2013, 4, 51–61. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.; Pramanik, M.; Chaudhary, S.; Negi, M.S. Soil Erodibility Mapping Using Watershed Prioritization and Morphometric Parameters in Conjunction with WSA, SPR and AHP-TOPSIS Models in Mandakini Basin, India. Int. J. River Basin Manag. 2024, 22, 143–165. [Google Scholar] [CrossRef]
- Farhan, Y.; Anbar, A.; Al-Shaikh, N.; Mousa, R.; Farhan, Y.; Anbar, A.; Al-Shaikh, N.; Mousa, R. Prioritization of Semi-Arid Agricultural Watershed Using Morphometric and Principal Component Analysis, Remote Sensing, and GIS Techniques, the Zerqa River Watershed, Northern Jordan. Agric. Sci. 2016, 8, 113–148. [Google Scholar] [CrossRef]
- Shekar, P.R.; Mathew, A.; Abdo, H.G.; Almohamad, H.; Abdullah Al Dughairi, A.; Al-Mutiry, M. Prioritizing Sub-Watersheds for Soil Erosion Using Geospatial Techniques Based on Morphometric and Hypsometric Analysis: A Case Study of the Indian Wyra River Basin. Appl. Water Sci. 2023, 13, 160. [Google Scholar] [CrossRef]
- Bottema, S. Pollen Analytical Investigations in Thessaly (Greece). Palaeohistoria 1979, 21, 19–40. [Google Scholar]
- Harrison, S.P.; Digerfeldt, G. European Lakes as Palaeohydrological and Palaeoclimatic Indicators. Quat. Sci. Rev. 1993, 12, 233–248. [Google Scholar] [CrossRef]
- Yu, G.; Harrison, S.P. Holocene Changes in Atmospheric Circulation Patterns as Shown by Lake Status Changes in Northern Europe. Boreas 1995, 24, 260–268. [Google Scholar] [CrossRef]
- Digerfeldt, G.; Sandgren, P.; Olsson, S. Reconstruction of Holocene Lake-Level Changes in Lake Xinias, Central Greece. Holocene 2007, 17, 361–367. [Google Scholar] [CrossRef]
- Charizopoulos, N.; Stamatis, G.; Psilovikos, A. Water Balance and Temporal Changes of the Surface Water Quality in Xynias Basin (SW Thessaly). In Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2011; pp. 275–281. [Google Scholar] [CrossRef]
- Charizopoulos, N.; Psilovikos, A. Hydrologic Processes Simulation Using the Conceptual Model Zygos: The Example of Xynias Drained Lake Catchment (Central Greece). Environ. Earth Sci. 2016, 75, 777. [Google Scholar] [CrossRef]
- Charizopoulos, N.; Zagana, E.; Stamatis, G. Hydrogeochemical Investigations in a Drained Lake Area: The Case of Xynias Basin (Central Greece). Environ. Monit. Assess. 2016, 188, 480. [Google Scholar] [CrossRef]
- Karmis, P.; Karmis, P. Electromagnetic Geophysical Survey Survey in the Area of Drained Lake Xyniada; Report Series; Institute of Geology and Mineral Exploration: Athens, Greece, 2010. [Google Scholar]
- Charizopoulos, N. Investigation on Mechanisms of Quantitative and Qualitative Deterioration of Water and Soil Recourses in Domokos Basin by Natural an Anthropogenic Process. Ph.D. Thesis, Agricultural Unversity of Athens, Athens, Greece, 2013. (In Greek). [Google Scholar]
- Mountrakis, D. Geology of Greece; Scientific Research Publishing: Irvine, CA, USA, 1985. (In Greek) [Google Scholar]
- Hynes, A.J.; Nisbet, E.G.; Smith, G.A.; Welland, M.J.P.; Rex, D.C. Spreading and Emplacement Ages of Some Ophiolites in the Othris Region (Eastern Central Greece). Z. Deutsch. Geol. Ges. 1972, 123, 455–468. [Google Scholar] [CrossRef]
- Caputo, R.; Pavlides, S. Late Cainozoic Geodynamic Evolution of Thessaly and Surroundings (Central-Northern Greece). Tectonophysics 1993, 223, 339–362. [Google Scholar] [CrossRef]
- Marinos, G.; Anastopoulos, J.; Maratos, N.; Melidonis, N.; Andronopoulos, B. Geological Map of Greece, Sheets Anavra and Domokos, 1:50,000; Hellenic Survey of Geology & Mineral Exploration: Athens, Greece, 1957; 1 Sheet. [Google Scholar]
- Marinos, G.; Anastopoulos, J.; Maratos, N.; Melidonis, N.; Andronopoulos, B. Geological Map of Greece, Sheet Leontarion, 1:50,000; Hellenic Survey of Geology & Mineral Exploration: Athens, Greece, 1962; 1 sheet. [Google Scholar]
- Tóth, G.; Jones, A.; Montanarella, L. The LUCAS Topsoil Database and Derived Information on the Regional Variability of Cropland Topsoil Properties in the European Union. Environ. Monit. Assess. 2013, 185, 7409–7425. [Google Scholar] [CrossRef]
- Orgiazzi, A.; Ballabio, C.; Panagos, P.; Jones, A.; Fernández-Ugalde, O. LUCAS Soil, the Largest Expandable Soil Dataset for Europe: A Review. Eur. J. Soil Sci. 2018, 69, 140–153. [Google Scholar] [CrossRef]
- Planchon, O.; Darboux, F. A Fast, Simple and Versatile Algorithm to Fill the Depressions of Digital Elevation Models. CATENA 2002, 46, 159–176. [Google Scholar] [CrossRef]
- Argyriou, A.V.; Teeuw, R.M.; Soupios, P.; Sarris, A. Neotectonic Control on Drainage Systems: GIS-Based Geomorphometric and Morphotectonic Assessment for Crete, Greece. J. Struct. Geol. 2017, 104, 93–111. [Google Scholar] [CrossRef]
- Babu, K.J.; Sreekumar, S.; Aslam, A. Implication of Drainage Basin Parameters of a Tropical River Basin of South India. Appl. Water Sci. 2016, 6, 67–75. [Google Scholar] [CrossRef]
- Schumm, S.A. Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Keller, E.A. Active Tectonics: Earthquakes, Uplift, and Landscape, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2002; ISBN 0130882305. [Google Scholar]
- Miller, V.C. A Quantitative Geomorphic Study of Drainage Basin Characteristics in the Clinch Mountain Area, Virginia and Tennessee; Technical Report 3; Columbia University Department of Geology: New York, NY, USA, 1953. [Google Scholar]
- Apollov, B.A. A Study of Rivers; Moscow University: Moscow, Russia, 1963. [Google Scholar]
- Verstappen, H. The Applied Geomorphology; International Institute for Aerial Survey and Earth Science (I.T.C): Enschede, The Netherlands, 1983. [Google Scholar]
- Kumar, A.; Samuel, S.K.; Vyas, V. Morphometric Analysis of Six Sub-Watersheds in the Central Zone of Narmada River. Arab. J. Geosci. 2015, 8, 5685–5712. [Google Scholar] [CrossRef]
- Farhan, Y.; Anbar, A.; Enaba, O.; Al-shaikh, N. Quantitative Analysis of Geomorphometric Parameters of Wadi Kerak, Jordan, Using Remote Sensing and GIS. J. Water Resour. Prot. 2015, 7, 456–475. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-Relief Ratio, Hypsometric Integral, and Geomorphic Area-Altitude Analysis. Bull. Geol. Soc. Am. 1971, 82, 1079–1083. [Google Scholar] [CrossRef]
- Magesh, N.S.; Chandrasekar, N. GIS Model-Based Morphometric Evaluation of Tamiraparani Subbasin, Tirunelveli District, Tamil Nadu, India. Arab. J. Geosci. 2014, 7, 131–141. [Google Scholar] [CrossRef]
- Morisawa, M. Rivers: Form and Process; Clayton, K.M., Ed.; Geomorphology Texts 7; Longman: Harlow, UK, 1985; ISBN 0582489822. [Google Scholar]
- Strahler, A.N. Quantitative Geomorphology of Drainage Basin and Channel Networks; Chow, V., Ed.; Handbook of Applied Hydrology; McGraw Hill, Open Access Library: New York, NY, USA, 1964. [Google Scholar]
- Van Der Knijff, J.M.; Jones, R.J.A.; Montanarella, L.; European Soil Bureau. Soil Erosion Risk Assessment Italy, Soil Erosion Risk Assessment in Europe; European Commission Directorate General, Joint Research Center, Space Applications Institute: Rome, Italy.
- Fox, D.G. Judging Air Quality Model Performance. A Summary of the AMS Workshop on Dispersion Model Performance. B. Am. Meteorol. Soc. 1981, 62, 599. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Johnson, C.B.; Cross, B.W. A Soil Erodibility Nomograph for Farmland and Construction Sites. J. Soil Water Conserv. 1971, 26, 189–193. [Google Scholar]
- Ditzler, C.; Scheffe, K.; Monger, H. Soil Survey Manual; Soil Science Division Staff, Ed.; Agriculture Handbook No. 18; United States Department of Agriculture: Washington, DC, USA, 2017. [Google Scholar]
- Rawls, W.J.; Brakensiek, C.L.; Saxton, K.E. Estimation of Soil Water Properties. Trans.-Am. Soc. Agric. Eng. 1982, 25, 1316–1320. [Google Scholar] [CrossRef]
- Angulo-Martínez, M.; López-Vicente, M.; Vicente-Serrano, S.M.; Beguería, S. Mapping Rainfall Erosivity at a Regional Scale: A Comparison of Interpolation Methods in the Ebro Basin (NE Spain). Hydrol. Earth Syst. Sci. 2009, 13, 1907–1920. [Google Scholar] [CrossRef]
- Panagos, P.; Meusburger, K.; Alewell, C.; Montanarella, L. Soil Erodibility Estimation Using LUCAS Point Survey Data of Europe. Environ. Model. Softw. 2012, 30, 143–145. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K. A New European Slope Length and Steepness Factor (LS-Factor) for Modeling Soil Erosion by Water. Geosciences 2015, 5, 117–126. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. A GIS Procedure for Automatically Calculating the USLE LS Factor on Topographically Complex Landscape Units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar] [CrossRef]
- de Vente, J.; Poesen, J.; Govers, G.; Boix-Fayos, C. The Implications of Data Selection for Regional Erosion and Sediment Yield Modelling. Earth Surf. Process. Landforms 2009, 34, 1994–2007. [Google Scholar] [CrossRef]
- Wang, G.; Wente, S.; Gertner, G.Z.; Anderson, A. Improvement in Mapping Vegetation Cover Factor for the Universal Soil Loss Equation by Geostatistical Methods with Landsat Thematic Mapper Images. Int. J. Remote Sens. 2002, 23, 3649–3667. [Google Scholar] [CrossRef]
- Efthimiou, N. Object-oriented Soil Erosion Modelling: A Non-Stationary Approach towards a Realistic Calculation of Soil Loss at Parcel Level. CATENA 2023, 222, 106816. [Google Scholar] [CrossRef]
- Panagos, P.; Borrelli, P.; Meusburger, K.; van der Zanden, E.H.; Poesen, J.; Alewell, C. Modelling the Effect of Support Practices (P-Factor) on the Reduction of Soil Erosion by Water at European Scale. Environ. Sci. Policy 2015, 51, 23–34. [Google Scholar] [CrossRef]
- Leopold, L.B.; Langbein, W.B. The Concept of Entropy in Landscape Evolution; Professional Paper; United States Government Printing Office: Washington, DC, USA, 1962; pp. A1–A20. [CrossRef]
- Shreve, R.L. Statistical Law of Stream Numbers. J. Geol. 1966, 74, 17–37. [Google Scholar] [CrossRef]
- Cooper, A.H.; Farrant, A.R.; Price, S.J. The Use of Karst Geomorphology for Planning, Hazard Avoidance and Development in Great Britain. Geomorphology 2011, 134, 118–131. [Google Scholar] [CrossRef]
- Parcharidis, I.; Psomiadis, E.; Stamatis, G. Using Landsat TM Images to Study the Karstic Phenomenon. Int. J. Appl. Earth Obs. Geoinf. 1998, 1998, 118–123. [Google Scholar]
- Pareta, K.; Pareta, U. Quantitative Morphometric Analysis of a Watershed of Yamuna Basin, India Using ASTER (DEM) Data and GIS. Int. J. Geomatics Geosci. 2011, 2, 248–269. [Google Scholar]
- Chow, V.T. Handbook of Applied Hydrology: A Compendium of Water-Resources Technology; McGraw-Hill book Co.: New York, NY, USA, 1964. [Google Scholar]
- Singh, S.; Singh, M.C. Morphometric Analysis of Kanhar River Basin. Natl. Geogr. J. India 1997, 43, 31–43. Available online: https://www.scirp.org/reference/referencespapers?referenceid=1451679 (accessed on 21 January 2025).
- Samarinas, N.; Tsakiridis, N.L.; Kalopesa, E.; Zalidis, G.C. Soil Loss Estimation by Water Erosion in Agricultural Areas Introducing Artificial Intelligence Geospatial Layers into the RUSLE Model. Land 2024, 13, 174. [Google Scholar] [CrossRef]


| Parameter | Formula | Description | References |
|---|---|---|---|
| Horton’s first law of stream numbers | (1) | The numbers of streams of successively lower orders in each catchment tend to form a geometric progression | [10] |
| Horton’s second law of stream lengths | (2) | The mean stream length segments of each of the successive orders tend to approximate a direct geometric series, with stream length increasing towards a higher order of streams | [10] |
| Drainage density, D (km−1) | (3) | The aggregate length of streams per unit area | [9,11] |
| Channel frequency, F (km−2) | (4) | The total number of streams per unit area | [9,11] |
| Relief ratio, Rh (%) | (5) | The ratio of basin relief to basin length | [84] |
| Circularity | (6) | Circularity is defined as the ratio of the catchment to the area of a circle having the same perimeter as the catchment | [86] |
| Elongation ratio | (7) | The elongation ratio is the ratio between the diameter of the circle of the same area as the catchment and the maximum length of the catchment | [84] |
| Hypsometric integral, Hi (%) | (8) | The area below the hypsometric curve, which represents the relative proportion of the watershed area below (or above) a given height | [85] |
| Morphometric Parameters | Values |
|---|---|
| Area (km2) | 167.9 |
| Drainage density (km/km2) | 2.02 |
| Drainage frequency (n/km2) | 3.21 |
| The maximum length of the catchment (km) | 19.8 |
| Catchment width (km) | 8.5 |
| Perimeter (km) | 66.2 |
| Maximum Elevation Hmax (m) | 977 |
| Minimum Elevation Hmin (m) | 384 |
| Total relief (m) | 593 |
| Mean Elevation—Hmean (m) | 540 |
| Relief ratio (%) | 2.98 |
| Circularity | 0.48 |
| Elongation ratio | 0.74 |
| Hypsometric integral (%) | 26.3 |
| Stream Order (u) | Stream Number (Nu) | Bifurcation Ratio | Mean Bifurcation Ratio | Ideal Stream Number | Deviation (%) | Stream Length (Lu) | Mean Stream Length | Length Ratio | Mean Length Ratio | Ideal Mean Stream Length | Deviation (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 387 | 3.46 | 495 | −21.81 | 152.9 | 0.39 | 2.02 | 0.39 | 0.0 | ||
| 2 | 110 | 3.52 | 143 | −23.08 | 82.2 | 0.74 | 1.89 | 0.79 | −6.33 | ||
| 3 | 32 | 3.44 | 41 | −21.95 | 50.8 | 1.59 | 2.15 | 1.60 | −0.62 | ||
| 4 | 6 | 5.33 | 12 | −50.00 | 17.2 | 2.87 | 1.80 | 3.23 | −11.15 | ||
| 5 | 3 | 2 | 3 | 0 | 29.5 | 9.83 | 3.42 | 6.52 | 50.77 | ||
| 6 | 1 | 3 | 1 | 0 | 8.1 | 8.1 | 0.82 | 13.17 | −38.50 | ||
| ΣNu = 539 | ΣLu = 340.7 (km) | ||||||||||
| Land Use Type | CORINE LU Code | C Factor |
|---|---|---|
| Discontinuous urban fabric | 0.001 | |
| Construction sites | 133 | 0.01 |
| Non-irrigated arable land | 211 | 0.3 |
| Permanently irrigated land | 212 | 0.15 |
| Complex cultivation patterns | 242 | 0.18 |
| Land occupied by agriculture | 243 | 0.07 |
| Broad-leaved forest | 311 | 0.003 |
| Coniferous forest | 312 | 0.002 |
| Natural grassland | 321 | 0.05 |
| Sclerophyllous vegetation | 323 | 0.03 |
| Transitional woodland shrub | 324 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Charizopoulos, N.; Alexiou, S.; Efthimiou, N.; Psomiadis, E.; Arvanitis, P. Unravelling Landscape Evolution and Soil Erosion Dynamics in the Xynias Drained Lake Catchment, Central Greece: A GIS and RUSLE Modelling Approach. Sustainability 2025, 17, 5526. https://doi.org/10.3390/su17125526
Charizopoulos N, Alexiou S, Efthimiou N, Psomiadis E, Arvanitis P. Unravelling Landscape Evolution and Soil Erosion Dynamics in the Xynias Drained Lake Catchment, Central Greece: A GIS and RUSLE Modelling Approach. Sustainability. 2025; 17(12):5526. https://doi.org/10.3390/su17125526
Chicago/Turabian StyleCharizopoulos, Nikos, Simoni Alexiou, Nikolaos Efthimiou, Emmanouil Psomiadis, and Panagiotis Arvanitis. 2025. "Unravelling Landscape Evolution and Soil Erosion Dynamics in the Xynias Drained Lake Catchment, Central Greece: A GIS and RUSLE Modelling Approach" Sustainability 17, no. 12: 5526. https://doi.org/10.3390/su17125526
APA StyleCharizopoulos, N., Alexiou, S., Efthimiou, N., Psomiadis, E., & Arvanitis, P. (2025). Unravelling Landscape Evolution and Soil Erosion Dynamics in the Xynias Drained Lake Catchment, Central Greece: A GIS and RUSLE Modelling Approach. Sustainability, 17(12), 5526. https://doi.org/10.3390/su17125526







