Time-Varying Reliability Assessment of Urban Traffic Network Based on Dynamic Bayesian Network
Abstract
1. Introduction
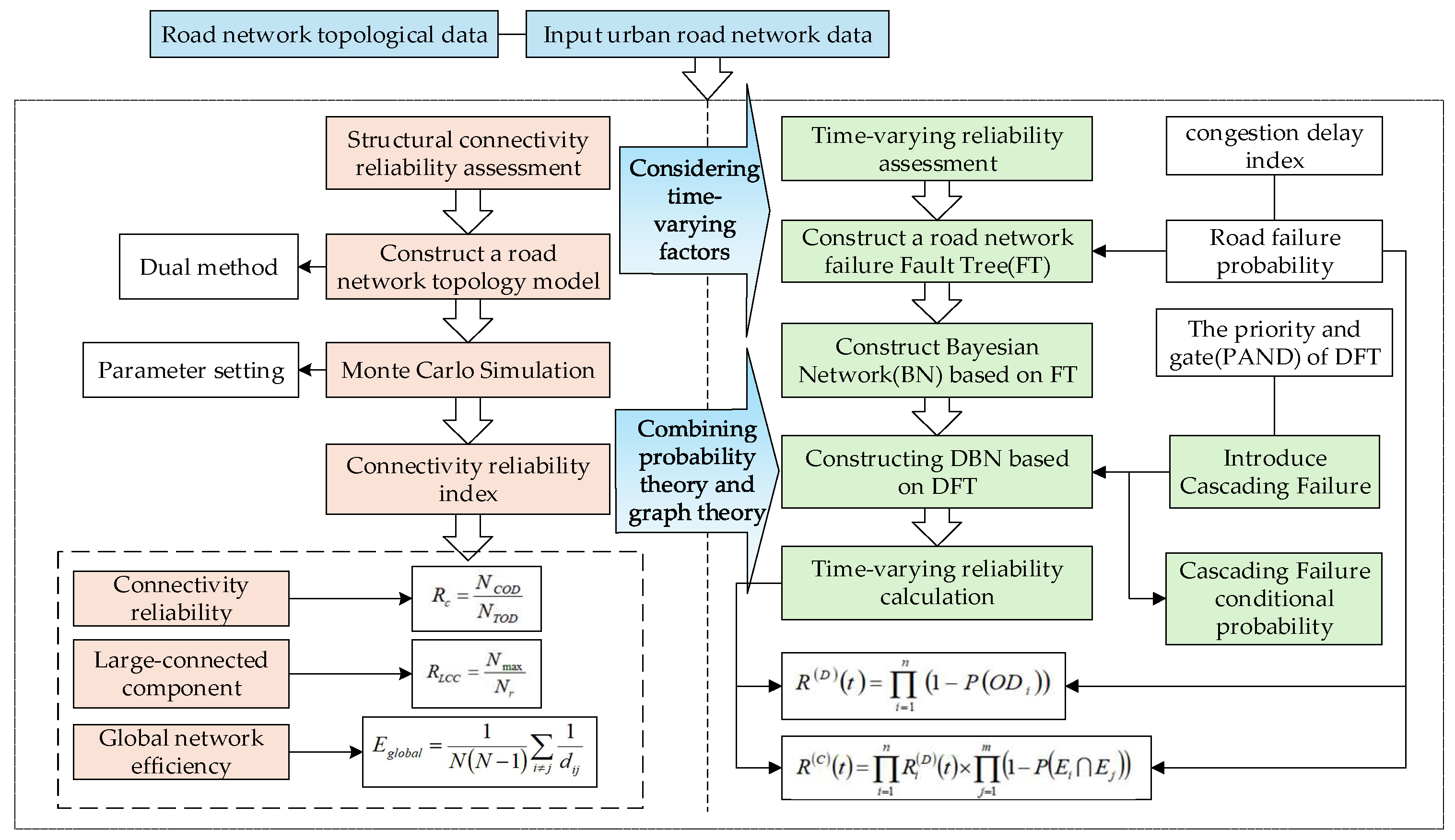
2. Methods and Models
2.1. Structural Connectivity Reliability Modeling and Assessment
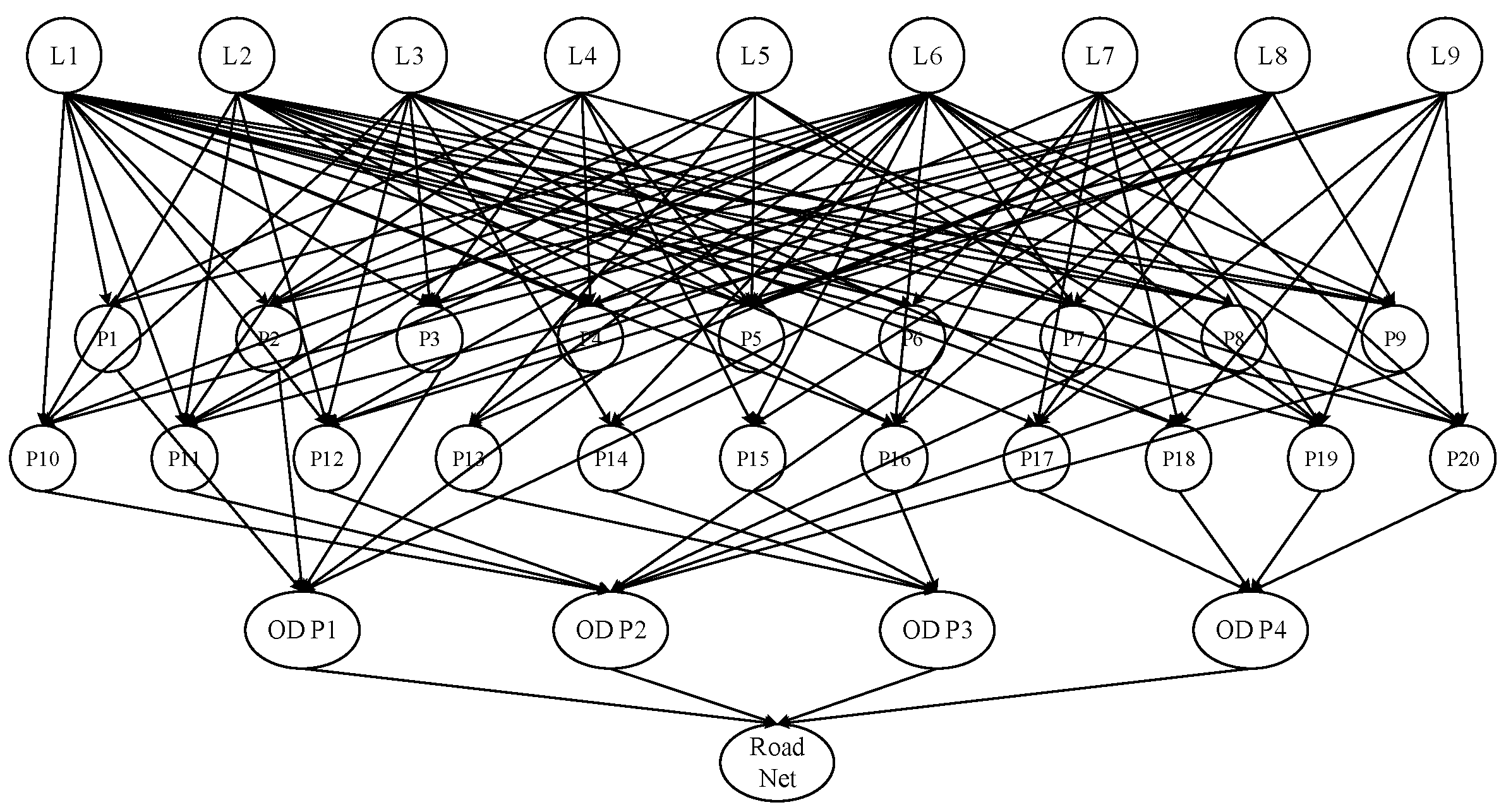
2.1.1. Road Network Connectivity Reliability Modeling
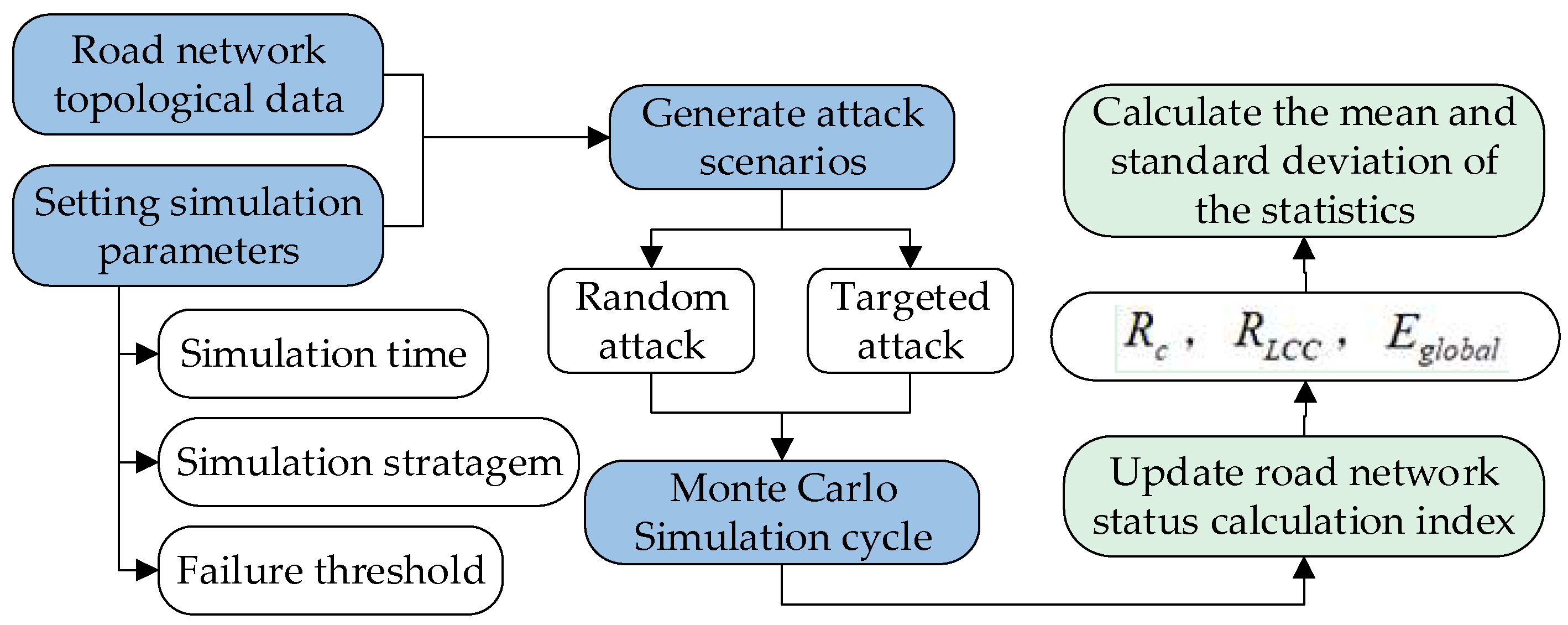
2.1.2. Road Network Reliability Assessment Based on MCS
2.2. Time-Varying Connectivity Reliability Modeling and Assessment
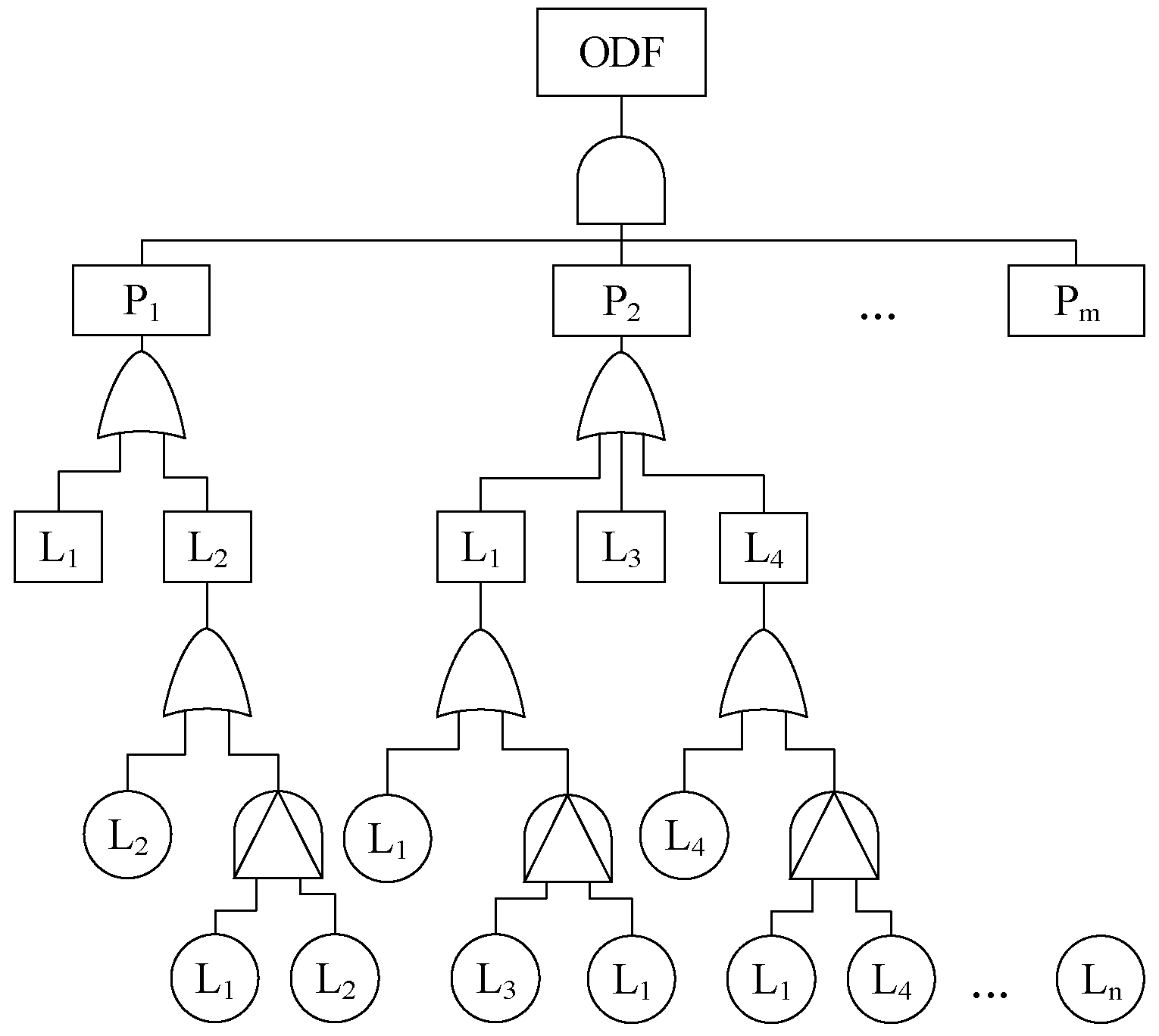
2.2.1. Road Network Time-Varying Reliability Modeling
- (1)
- Reliability modeling without considering cascading failures
- (2)
- Reliability modeling considering cascading failure
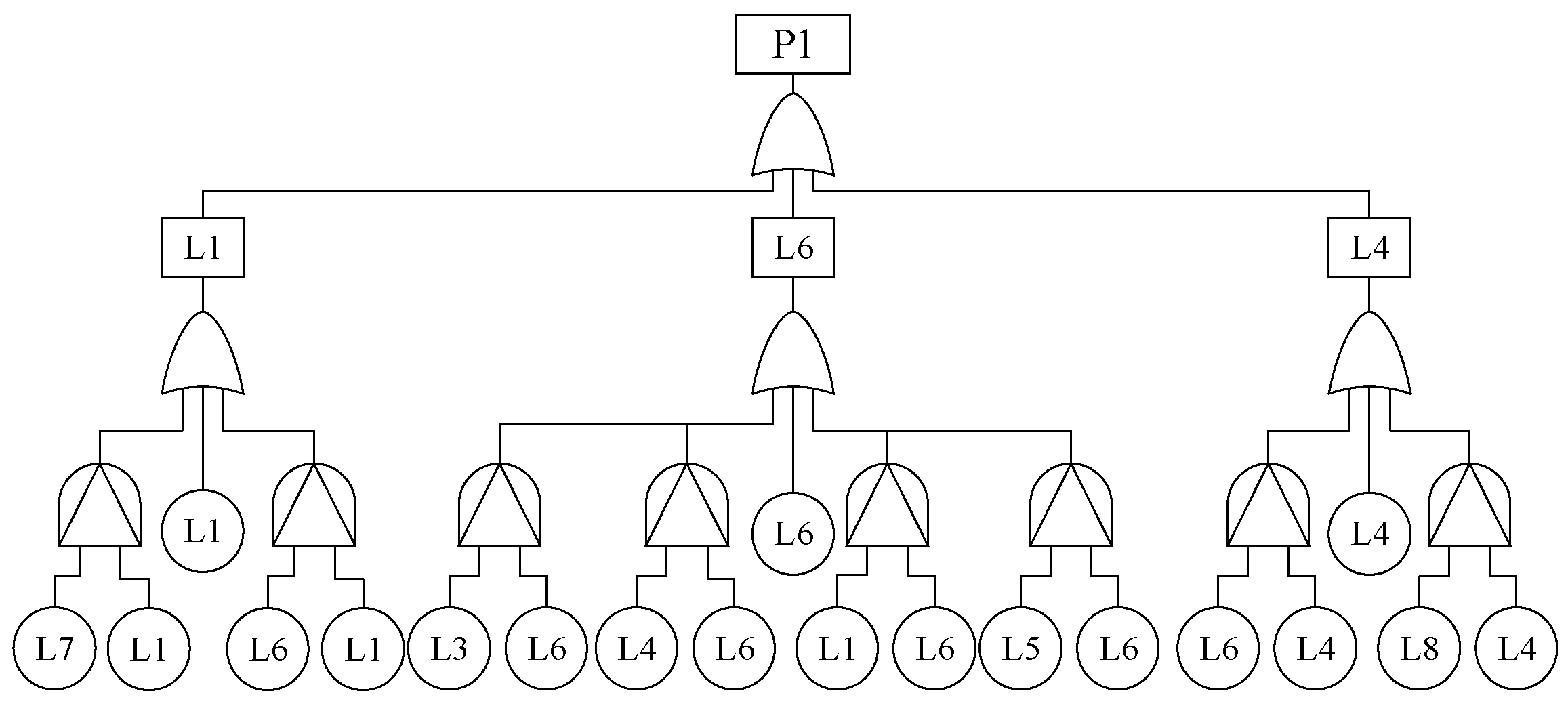
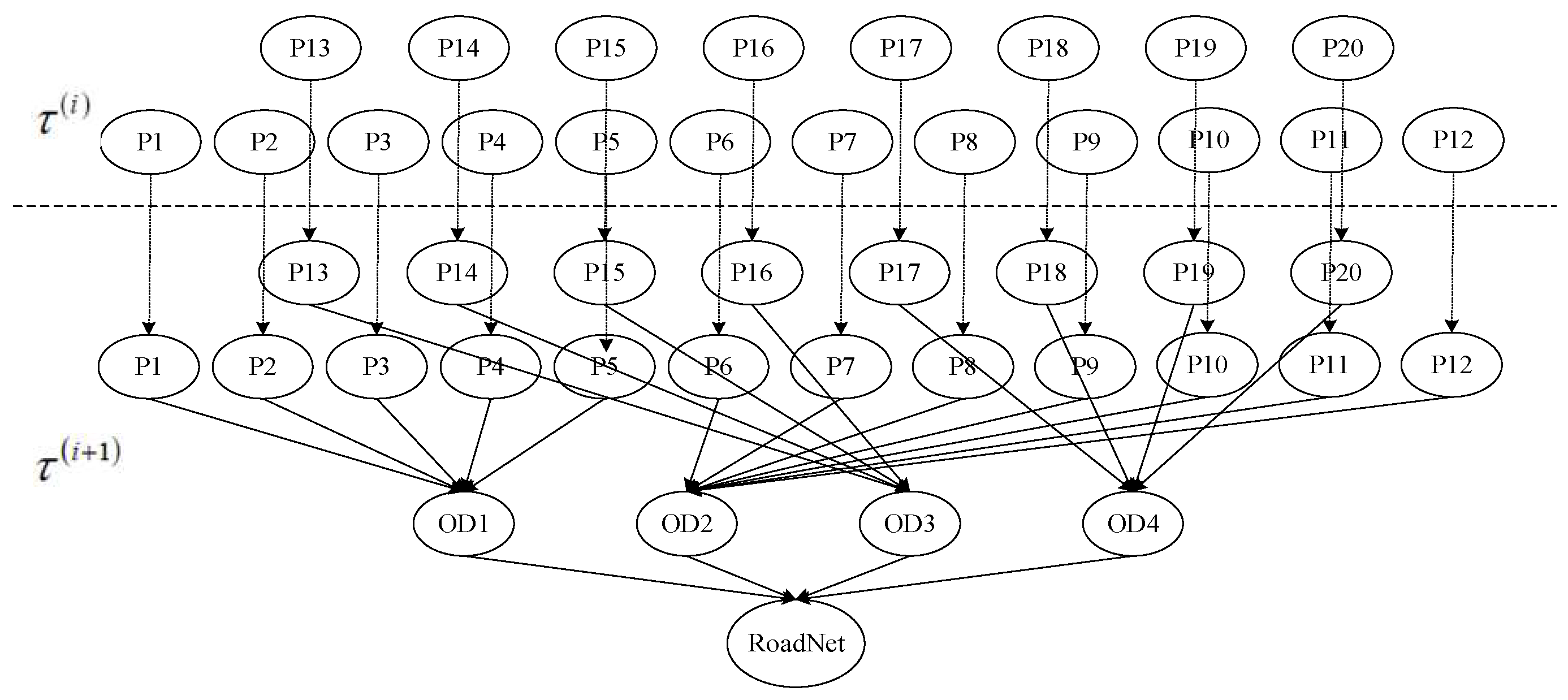
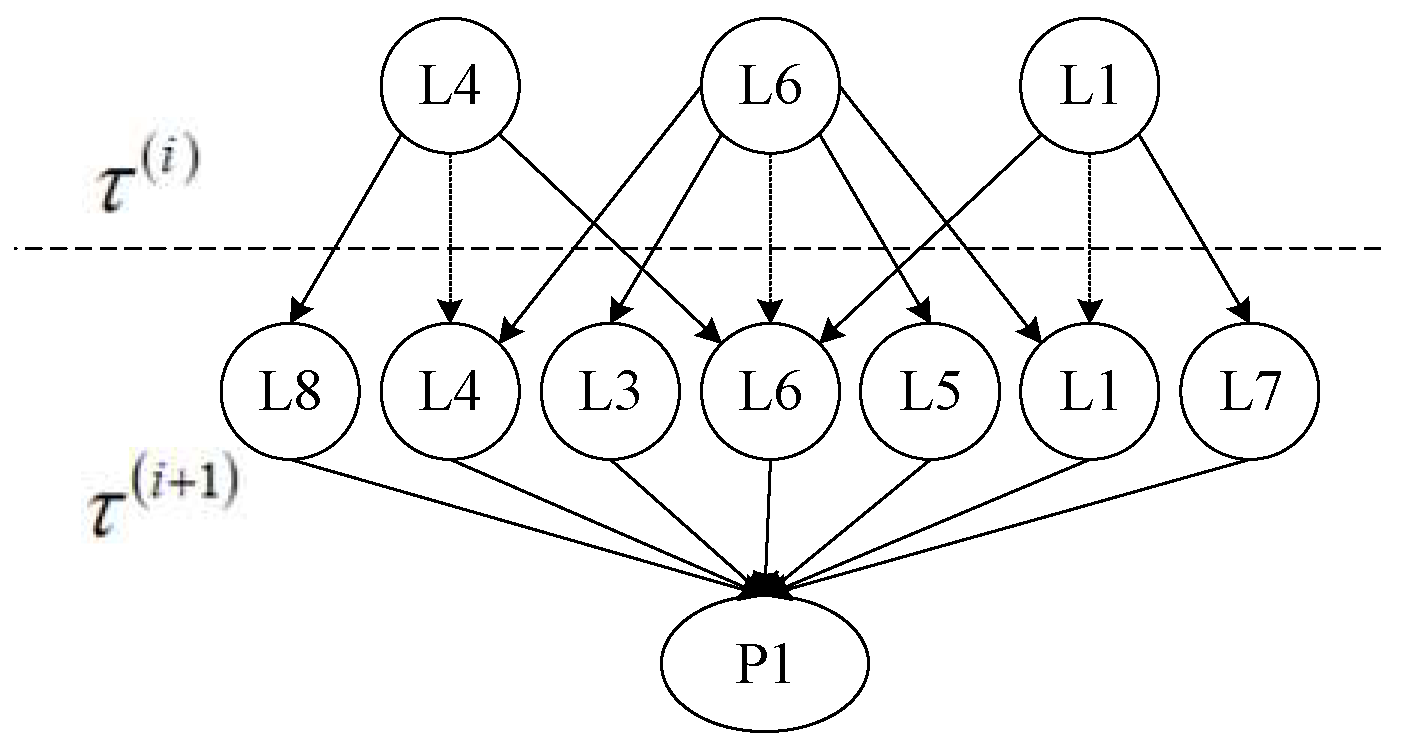
2.2.2. Road Network Reliability Assessment Based on FT-DBN
| Model Type | Conversion Type | Conversion Rules | Conversion Diagrams |
|---|---|---|---|
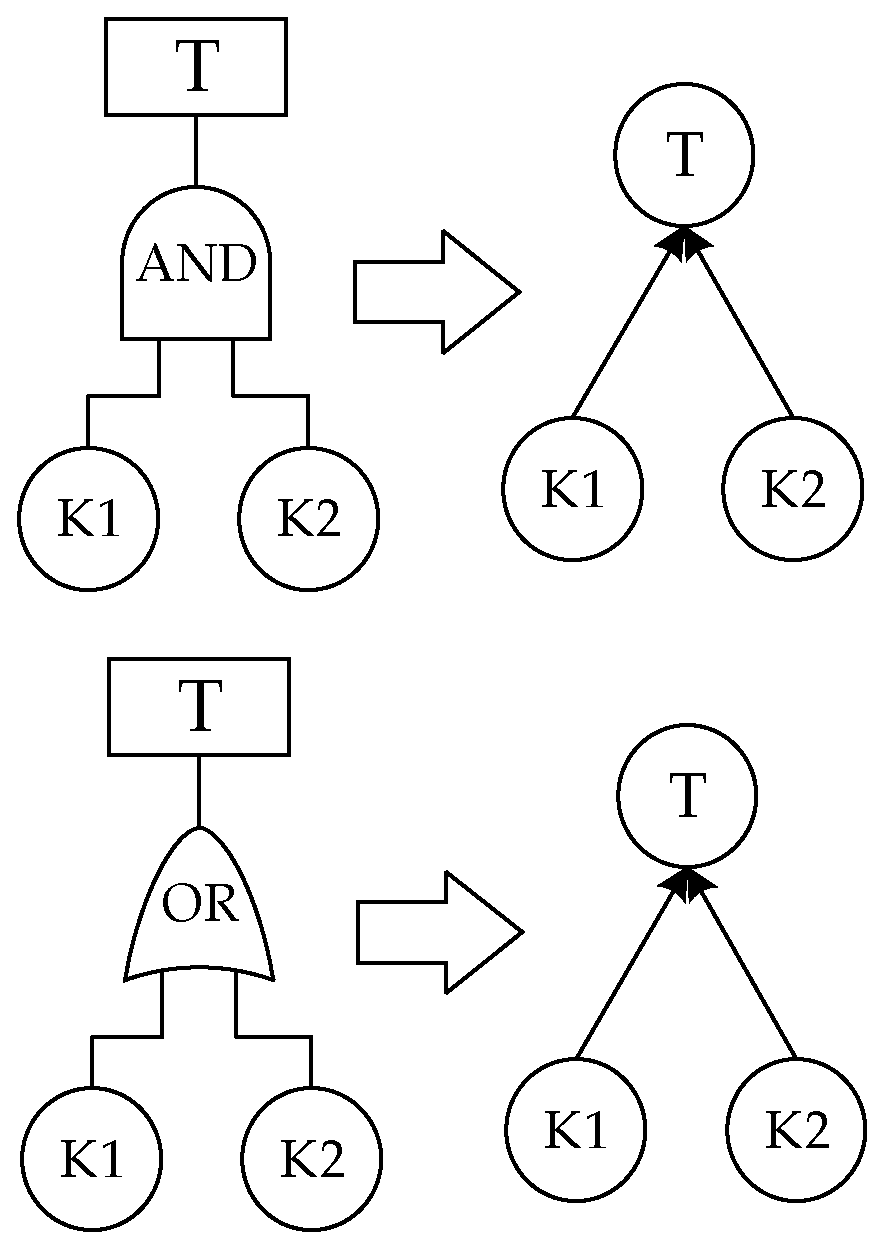
| Reliability assessment model without considering cascading failures | FT to BN | ① The bottom events of FT correspond to the root nodes of BN; ② The logic gates of FT correspond to the intermediate nodes of BN; ③ The parent nodes of BN are connected to the child nodes corresponding to the logic gates; ④ The prior probabilities of the root nodes are determined by the failure distributions; ⑤ The CPTs of non-root nodes are determined by the logic gates of FT. | Figure 6 |
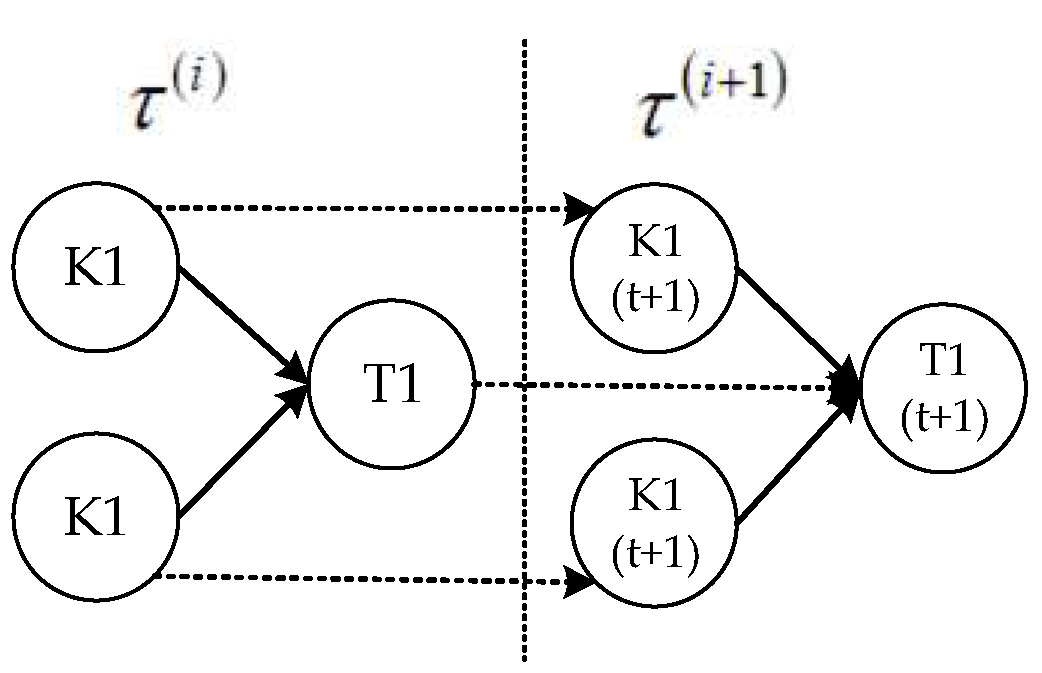
| BN to DBN | Continuous time is divided into a finite number of discrete time steps , and cross-time arcs are added to connect the same nodes in adjacent time steps. | Figure 7 | |
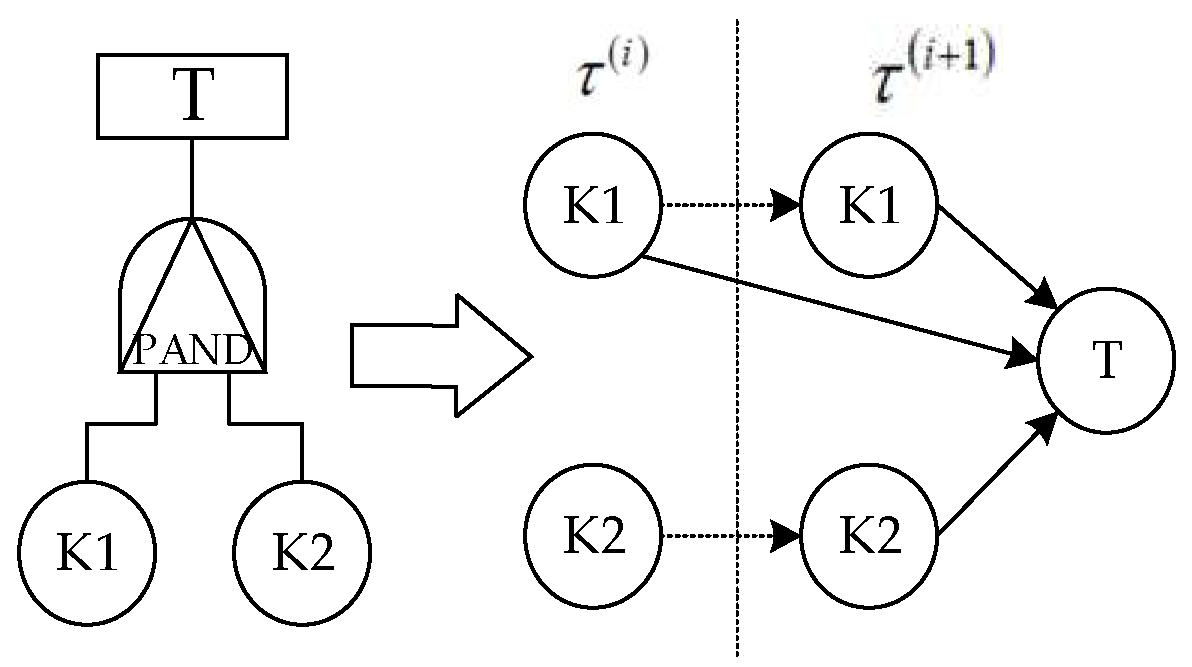
| Reliability assessment model considering cascading failures | DFT to DBN | ① The PAND gate in DFT corresponds to the time-dependent node in DBN; ② The CPT in DBN quantifies the conditional probability of cascading failures; ③ On the basis of the 2D-DBN, cross-node cross-time arcs are added to connect related nodes in adjacent time steps. | Figure 8 |
3. Case Analysis
3.1. Assessment of Road Network Structural Connectivity Reliability
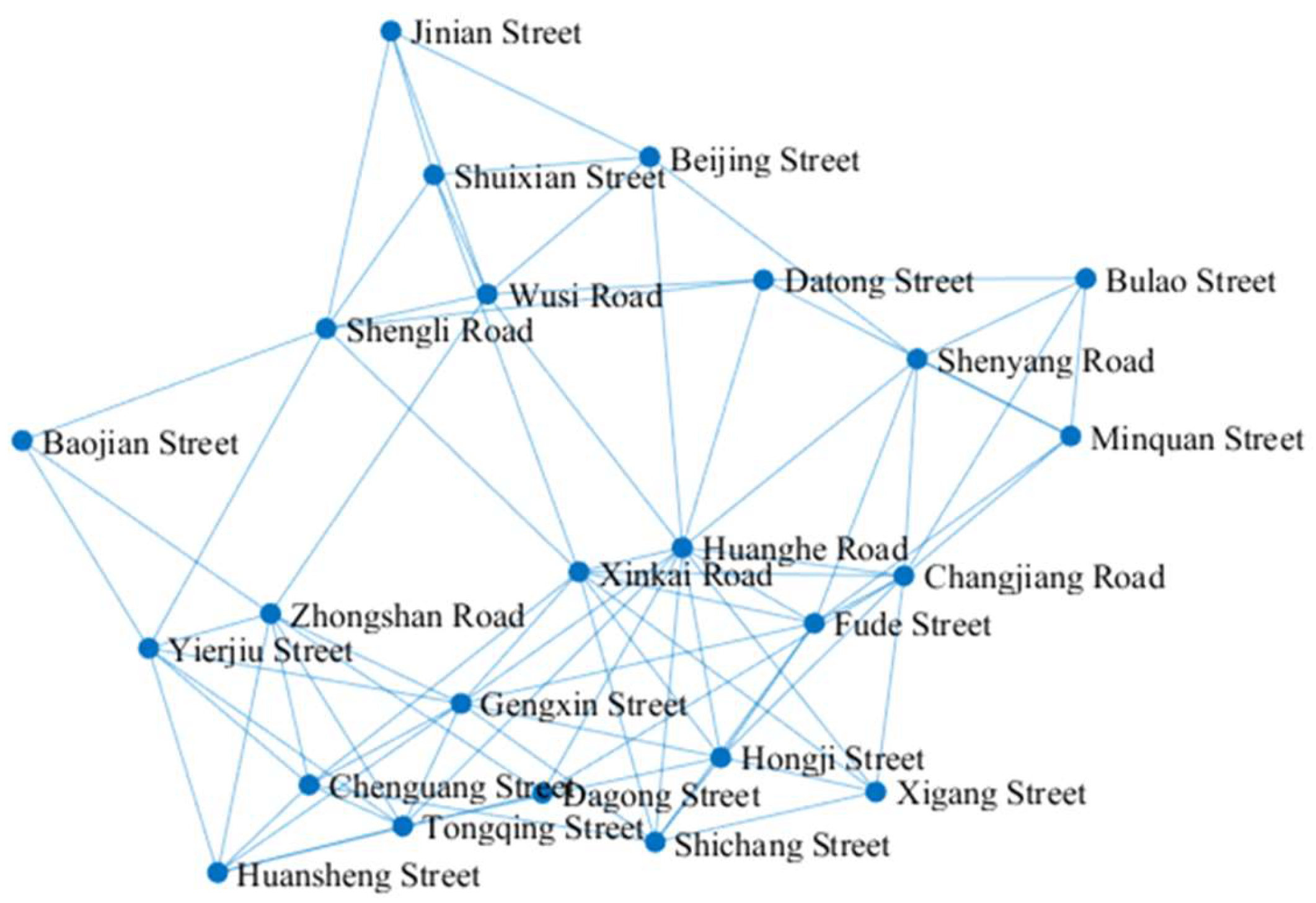
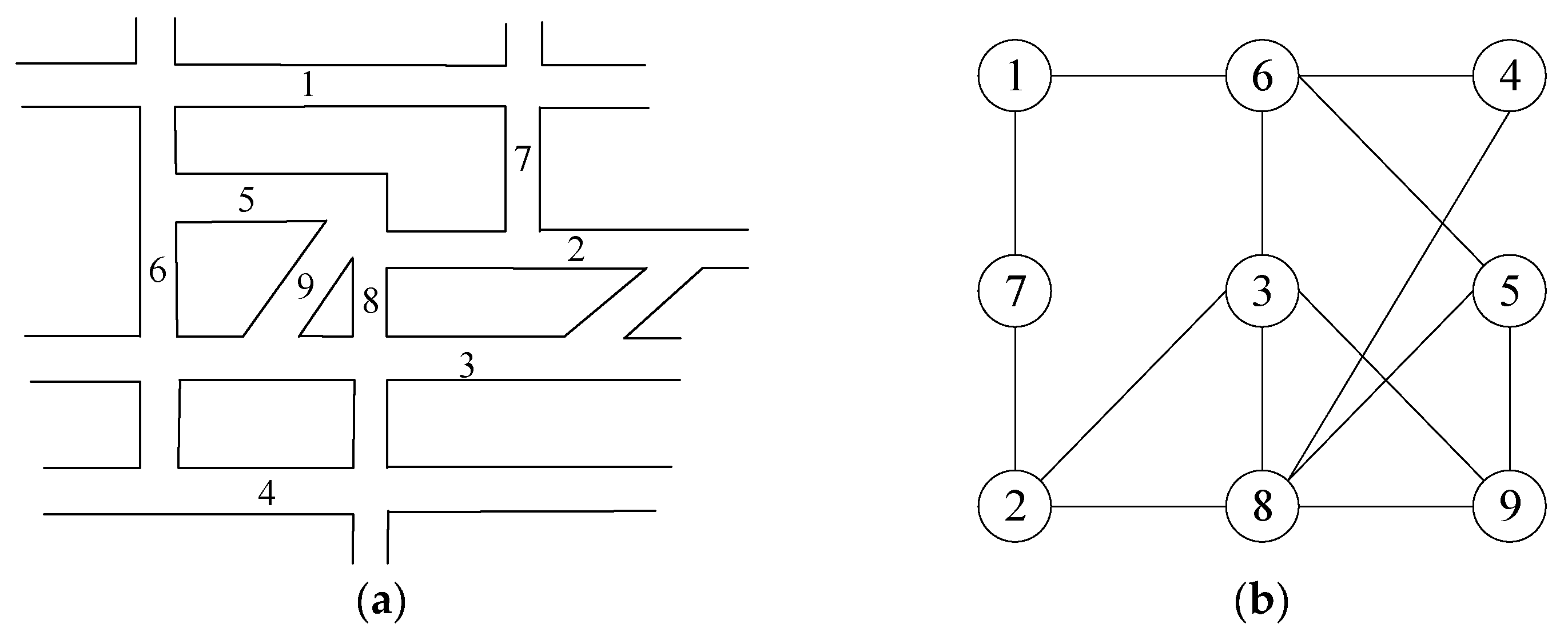
3.1.1. Analysis of Road Network Basic Characteristics
3.1.2. Assessment of Road Network Structural Reliability
3.2. Assessment of Road Network Time-Varying Connectivity Reliability
3.2.1. Reliability Assessment Model Without Considering Cascading Failures
3.2.2. Reliability Assessment Model Considering Cascading Failures
3.2.3. Assessment of Road Network Time-Varying Reliability
4. Discussion and Analysis
5. Conclusions
- (1)
- A road network structural connectivity reliability assessment method based on MCS is proposed. The dual method is used to construct the road network topology model, and network parameters are used to describe the structural connectivity reliability of the road network. Combined with MCS, the redundancy and vulnerability characteristics of the road network under random and targeted attack strategies are revealed. The structural connectivity reliability of a partial road network in Dalian is analyzed, confirming the effectiveness of this method in addressing system uncertainty and reducing accidental error. The failure of key nodes significantly accelerates the risk of network collapse, providing theoretical support for optimizing road network structural redundancy design.
- (2)
- A road network time-varying connectivity reliability assessment method based on FT-DBN is proposed. A Failure Fault Tree of the road network is constructed to establish the failure logic relationship from road sections to the entire road network. The hierarchical element associations and their impacts on overall road network reliability are analyzed. The congestion delay index is introduced to construct a Bayesian Network, which is expanded into a Dynamic Bayesian Network based on Conditional Probability Tables to quantify the failure correlation. This breaks through the static limitations of traditional Fault Trees and reveals the laws of road network reliability changes over time without considering cascading failures. In terms of failure propagation modeling, a road network failure probability model is proposed by converting Dynamic Fault Trees into a Dynamic Bayesian Network. The time delay mechanism is introduced to construct the conditional probability table of cascading failures, establishing a non-linear mapping from traffic congestion states to topological connectivity. This accurately characterizes the time-varying evolution laws of road network reliability under cascading failure scenarios. The empirical analysis using traffic data from Dalian shows that ignoring cascading effects can lead to a maximum reliability assessment deviation of 0.3, especially during morning peak hours. The failure of key nodes triggers cascading propagation, causing the road network reliability to drop by 58%. Through multidimensional indicator comparisons, the proposed method is proven to have significant advantages over traditional methods in terms of structural vulnerability point identification accuracy and emergency resource allocation efficiency. The adaptability of the model to complex dynamic scenarios is verified, and it can provide more accurate traffic congestion warnings and resource allocation suggestions for traffic management departments. It provides a theoretical basis for the sustainable resilience planning of urban traffic networks.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DBN | Dynamic Bayesian Network |
| MCS | Monte Carlo simulation |
| CPT | Conditional Probability Table |
| FT | Fault Tree |
| BN | Bayesian Network |
| DFT | Dynamic Bayesian Network |
| GNN | Graph Neural Network |
References
- Peiravian, F.; Derrible, S. Multi-dimensional geometric complexity in urban transportation systems. arXiv 2015, arXiv:1507.03607. [Google Scholar] [CrossRef]
- Reisi, M.; Sabri, S.; Agunbiade, M.; Rajabifard, A.; Li, Y. Transport sustainability indicators for an enhanced urban analytics data infrastructure. Sustain. Cities Soc. 2020, 59, 102095. [Google Scholar] [CrossRef]
- Yangyang, M. Vulnerability Comparisons of Various Complex Urban Metro Networks Under Multiple Failure Scenarios. Sustainability 2024, 16, 9603. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Y.; Li, C.; Chen, T. A complex network approach to quantifying flood resilience in high-density coastal urban areas: A case study of Macau. Int. J. Disaster Risk Reduct. 2025, 119, 105335. [Google Scholar] [CrossRef]
- Dumedah, G.; Garsonu, E.K. Characterising the structural pattern of urban road networks in Ghana using geometric and topological measures. Geo Geogr. Environ. 2021, 8, e00095. [Google Scholar] [CrossRef]
- Liu, J.; Jia, H.; Lin, J.; Hu, H. Seismic Damage Rapid Assessment of Road Networks considering Individual Road Damage State and Reliability of Road Networks in Emergency Conditions. Adv. Civ. Eng. 2020, 2020, 9631804. [Google Scholar] [CrossRef]
- Shuwen, L. Improve the reliability index of power supply—Strengthen reliability management and reduce the average power outage time of customers. Sci. Technol. 2017, 212, 1. [Google Scholar]
- Zhang, H.; Wang, M.; Tang, M.; Yang, H. The reliability measures model of multilayer urban distribution network. Soft Comput. 2018, 22, 107–118. [Google Scholar] [CrossRef]
- Shao, F.; Shao, H.; Wang, D.; Lam, W.H. A multi-task spatio-temporal generative adversarial network for prediction of travel time reliability in peak hour periods. Phys. A Stat. Mech. Its Appl. 2024, 638, 129632. [Google Scholar] [CrossRef]
- Jiang, L.; Huang, S. Analyzing connectivity reliability and critical units for highway networks in high-intensity seismic region using Bayesian network. J. Infrastruct. Intell. Resil. 2022, 1, 100006. [Google Scholar] [CrossRef]
- Menghan, Q. Dynamic Estimation and Reliability Calculation Method of Urban Arterial Travel Time. Ph.D. Thesis, Chongqing Jiaotong University, Chongqing, China, 2020. [Google Scholar]
- Kato, T.; Uchida, K.; Lam, W.H.; Sumalee, A. Estimation of the value of travel time and of travel time reliability for heterogeneous drivers in a road network. Transportation 2021, 48, 1639–1670. [Google Scholar] [CrossRef]
- Luo, X.Q.; Hou, Q.H.; Duan, Y.Q. The research of the road network capacity based on the unblocked reliability. Biotechnol. Indian J. 2014, 10, 12628–12634. [Google Scholar]
- Kuang, A.; Tang, Z.; Shan, L. Road network capacity reliability considering travel time reliability. Procedia-Soc. Behav. Sci. 2013, 96, 1818–1827. [Google Scholar] [CrossRef][Green Version]
- Liu, Z.; Sun, D.J.; Chen, H.; Hao, W.; Wang, Z.; Tang, F. Resilience-based post-disaster repair strategy for integrated public transit networks. Transp. B Transp. Dyn. 2024, 12, 1–25. [Google Scholar] [CrossRef]
- Monfared, M.A.S.; Rezazadeh, M.; Alipour, Z. Road networks reliability estimations and optimizations: A Bi-directional bottom-up, top-down approach. Reliab. Eng. Syst. Saf. 2022, 222, 108427. [Google Scholar] [CrossRef]
- Yang, W.; Mu, L.; Jiang, H.; Li, X.; Hou, K. Fault Spread and Recovery Strategy of Urban Rail Transit System Based on Complex Network. J. Phys. Conf. Ser. 2021, 2037, 012049. [Google Scholar] [CrossRef]
- Qingguo, W. Comprehensive analysis of urban road importance evaluation methods. Surv. Mapp. Bull. 2018, 4, 124–127. [Google Scholar]
- Xing, C.; Guohua, C.; Hao, W.; Shenghua, C.; Yun, Z. Reliability analysis method of power system based on GT-RBD. J. Shenyang Univ. Technol. 2023, 45, 17–23. [Google Scholar]
- Du, J.; Cui, J.; Ren, G.; Thompson, R.G.; Zhang, L. Cascading failures and resilience evolution in urban road traffic networks with bounded rational route choice. Phys. A Stat. Mech. Its Appl. 2025, 664, 130456. [Google Scholar] [CrossRef]
- Cao, Y.; Lu, C. Reliability analysis for continuous degrading systems subject to multi-level failure dependence. Qual. Eng. 2025, 37, 79–91. [Google Scholar] [CrossRef]
- Zhou, S.; Li, Z.; Wang, J. Reliability analysis of Dynamic fault trees with Priority-AND gates using conditional binary decision diagrams. Reliab. Eng. Syst. Saf. 2025, 253, 110495. [Google Scholar] [CrossRef]
- Zhang, R.; Song, S. Bayesian network approach for Dynamic fault tree with common cause failures and interval uncertainty parameters. Maint. Reliab. 2024, 26, 190379. [Google Scholar] [CrossRef]
- Dou, Q.; Lu, D.G.; Zhang, B.Y. Physical resilience assessment of road transportation systems during post-earthquake emergency phase: With a focus on restoration modeling based on Dynamic Bayesian network. Reliab. Eng. Syst. Saf. 2025, 257, 110807. [Google Scholar] [CrossRef]
- Jiang, L.; Wang, G.; Feng, X.; Yu, T.; Lei, Z. Study on cascading failure vulnerability of the 21st-century Maritime Silk Road container ship network. J. Transp. Geogr. 2024, 117, 103891. [Google Scholar]
- Liu, C.; Jia, G. Industrial Big Data and Computational Sustainability: Multi-Method Comparison Driven by High-Dimensional Data for Improving Reliability and Sustainability of Complex Systems. Sustainability 2019, 11, 4557. [Google Scholar] [CrossRef]
- Meiling, L. Research on the Invulnerability of High-Speed Railway Network in China Based on Complex Network Theory. Ph.D. Thesis, Beijing Jiaotong University, Beijing, China, 2025. [Google Scholar]
- Jing, H. Study on the Evaluation Method of Road Network Failure Degree and Safety Level. Ph.D. Thesis, Shanghai Jiaotong University, Shanghai, China, 2010. [Google Scholar]
- Lei, J. Research on Reliability and Availability Modeling and Evaluation Methods of High-Speed Railway Signal Systems. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2020. [Google Scholar]
- Barahimi, A.H.; Eydi, A.; Aghaie, A. Urban transportation network reliability calculation considering correlation among the links comprising a route. Sci. Iran. 2022, 29, 1742–1754. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. Graph neural network surrogate for seismic reliability analysis of highway bridge systems. J. Infrastruct. Syst. 2024, 30, 4. [Google Scholar] [CrossRef]
- Liu, T.; Meidani, H. Optimizing seismic retrofit of bridges: Integrating efficient graph neural network surrogates and transportation equity. Proc. Cyber-Phys. Syst. Internet Things Week 2023, 2023, 367–372. [Google Scholar]
- Ziqiang, G. Study on the Resilience of Dynamic Heterogeneous Urban Road Traffic Network Considering the Influence of Information Conditions. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2021. [Google Scholar]









| Parameter | Meaning |
|---|---|
| Number of nodes | The number of nodes in the network |
| Number of edges | The number of edges in the network |
| Average degree | The average value of the degrees of all nodes in the network |
| Average path length | The average distance between any two nodes in the network |
| Average clustering coefficient | The average clustering coefficient of all nodes in the network |
| Global network efficiency | The average of the reciprocals of the shortest path lengths between all pairs of nodes in the network |
| Parameter | Number of Nodes | Number of Edges | Average Degree | Average Path Length | Average Clustering Coefficient | Global Network Efficiency |
|---|---|---|---|---|---|---|
| Feature value | 24 | 80 | 6.6667 | 1.9094 | 0.55476 | 0.61202 |
| Indicator | Random Attack | Targeted Attack | Mean Difference | Confidence Interval | p-Value |
|---|---|---|---|---|---|
| Number of attacks required for collapse | 28.3 ± 4.2 | 9.1 ± 1.5 | 19.2 | [17.8, 20.6] | <0.001 *** |
| Decrease rate of the largest connected component per attack | −3.2% (±0.5%)/Attack | −10.5% (±1.2%)/Attack | 7.3% | [6.5%, 8.1%] | <0.001 *** |
| Decrease rate of global efficiency per attack | −2.1% (±0.3%)/Attack | −8.7% (±1.0%)/Attack | 6.6% | [5.9%, 7.3%] | <0.001 *** |
| Number of Attacked Nodes | Reliability Under Random Attack | Reliability Under Targeted Attack |
|---|---|---|
| 1 | 0.988 | 0.752 |
| 5 | 0.985 | 0.403 |
| 10 | 0.961 | 0.211 |
| 20 | 0.856 | 0.032 |
| Number | Road Name | Connected Road Numbers | PF-Peak | PF-Non-Peak |
|---|---|---|---|---|
| L1 | Zhonghua West Road | L6, L7 | 0.1 | 0.0087 |
| L2 | Yangtze Road | L3, L7, L8 | 0.2 | 0.0091 |
| L3 | Yellow River Road | L2, L6, L8, L9 | 0.05 | 0.0032 |
| L4 | Digital Road | L6, L8 | 0.15 | 0.0067 |
| L5 | North China Road | L6, L8, L9 | 0.08 | 0.0043 |
| L6 | Southwest Road | L1, L3, L4, L5 | 0.3 | 0.0098 |
| L7 | Northeast Expressway | L1, L2 | 0.25 | 0.0084 |
| L8 | Xi’an Road | L2, L3, L4, L5, L9 | 0.12 | 0.0072 |
| L9 | Zhongchang Street | L3, L5, L8 | 0.18 | 0.0079 |
| Triggering Event | Affected Road Section | Conditional Failure Probability | Propagation Delay Time |
|---|---|---|---|
| Failure of L1 | L6 | 0.4577 | 30 min |
| Failure of L1 | L7 | 0.3728 | 15 min |
| Failure of L6 | L1 | 0.4278 | 15 min |
| Failure of L6 | L3 | 0.3897 | 15 min |
| Failure of L6 | L4 | 0.2738 | 30 min |
| Failure of L6 | L5 | 0.5637 | 30 min |
| Failure of L4 | L6 | 0.4359 | 30 min |
| Failure of L4 | L8 | 0.4893 | 45 min |
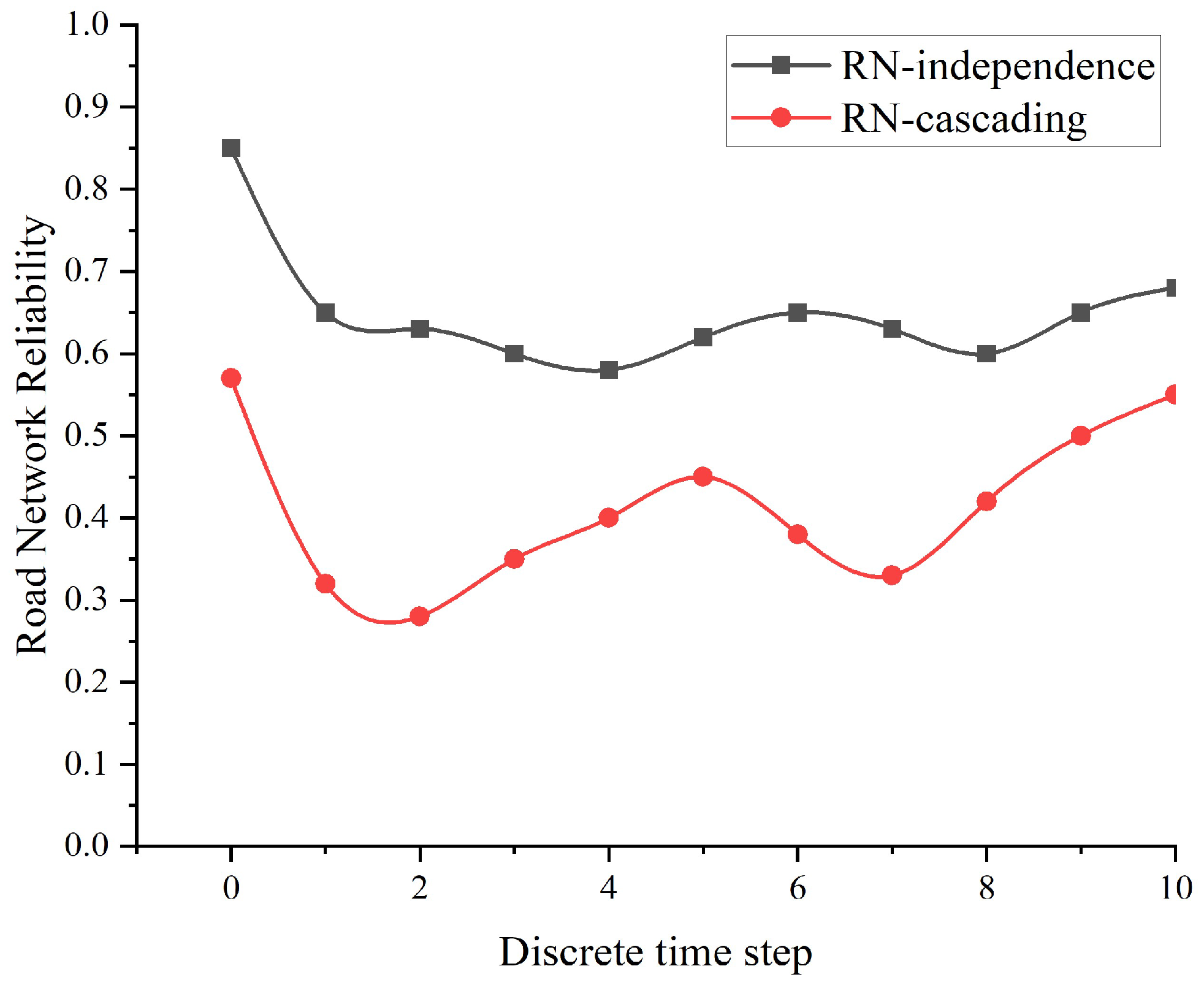
| ) | Time (Minutes) | R(D)(t) | R(C)(t) | Key Event Description |
|---|---|---|---|---|
| 0 | 0 | 0.85 | 0.57 | Initial state |
| 1 | 15 | 0.65 | 0.32 | Early peak starts, cascading triggered from L1 to L6 |
| 2 | 30 | 0.63 | 0.28 | Cascading spreads to L3 |
| 3 | 45 | 0.60 | 0.35 | Partial effectiveness of repair mechanism |
| 4 | 60 | 0.58 | 0.40 | Peak ends, pressure relieved |
| 5 | 75 | 0.62 | 0.45 | Traffic flow stabilizes |
| 6 | 90 | 0.65 | 0.38 | Evening peak starts, secondary cascading from L6 to L4 |
| 7 | 105 | 0.63 | 0.33 | Cascading impact expands |
| 8 | 120 | 0.60 | 0.42 | Secondary effectiveness of repair mechanism |
| 9 | 135 | 0.65 | 0.50 | System stabilizes |
| 10 | 150 | 0.68 | 0.55 | Low traffic flow period at night |
| Road Number | Prior Probability | Posterior Probability (Independent Failure) | Posterior Probability (Cascading Failure) | Keyness Ranking (Independent Failure) | Keyness Ranking (Cascading Failure) | Keyness Analysis and Cascading Failure Analysis |
|---|---|---|---|---|---|---|
| L1 | 0.10 | 0.15 | 0.78 | 6 | 1 | Triggering cascading failures of L6 and L7 |
| L2 | 0.20 | 0.28 | 0.31 | 2 | 6 | Secondary impact |
| L3 | 0.05 | 0.12 | 0.42 | 8 | 3 | Affected by L6 |
| L4 | 0.15 | 0.20 | 0.35 | 5 | 5 | Affected by L6 and L8 |
| L5 | 0.08 | 0.10 | 0.18 | 9 | 8 | Connecting L6 and L8 |
| L6 | 0.30 | 0.45 | 0.65 | 1 | 2 | Connecting L3, L4, and L5 |
| L7 | 0.25 | 0.25 | 0.31 | 3 | 7 | Affected by L1 |
| L8 | 0.12 | 0.18 | 0.38 | 7 | 4 | Multiple path dependencies |
| L9 | 0.18 | 0.20 | 0.22 | 4 | 9 | Minimal impact |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, S.; Jia, N.; Li, S.; Zou, Y. Time-Varying Reliability Assessment of Urban Traffic Network Based on Dynamic Bayesian Network. Sustainability 2025, 17, 5402. https://doi.org/10.3390/su17125402
Dong S, Jia N, Li S, Zou Y. Time-Varying Reliability Assessment of Urban Traffic Network Based on Dynamic Bayesian Network. Sustainability. 2025; 17(12):5402. https://doi.org/10.3390/su17125402
Chicago/Turabian StyleDong, Sihui, Ni Jia, Shiqun Li, and Yazhuo Zou. 2025. "Time-Varying Reliability Assessment of Urban Traffic Network Based on Dynamic Bayesian Network" Sustainability 17, no. 12: 5402. https://doi.org/10.3390/su17125402
APA StyleDong, S., Jia, N., Li, S., & Zou, Y. (2025). Time-Varying Reliability Assessment of Urban Traffic Network Based on Dynamic Bayesian Network. Sustainability, 17(12), 5402. https://doi.org/10.3390/su17125402






