A Stochastic Knapsack Model for Sustainable Safety Resource Allocation Under Interdependent Safety Measures
Abstract
1. Introduction
2. Literature Review
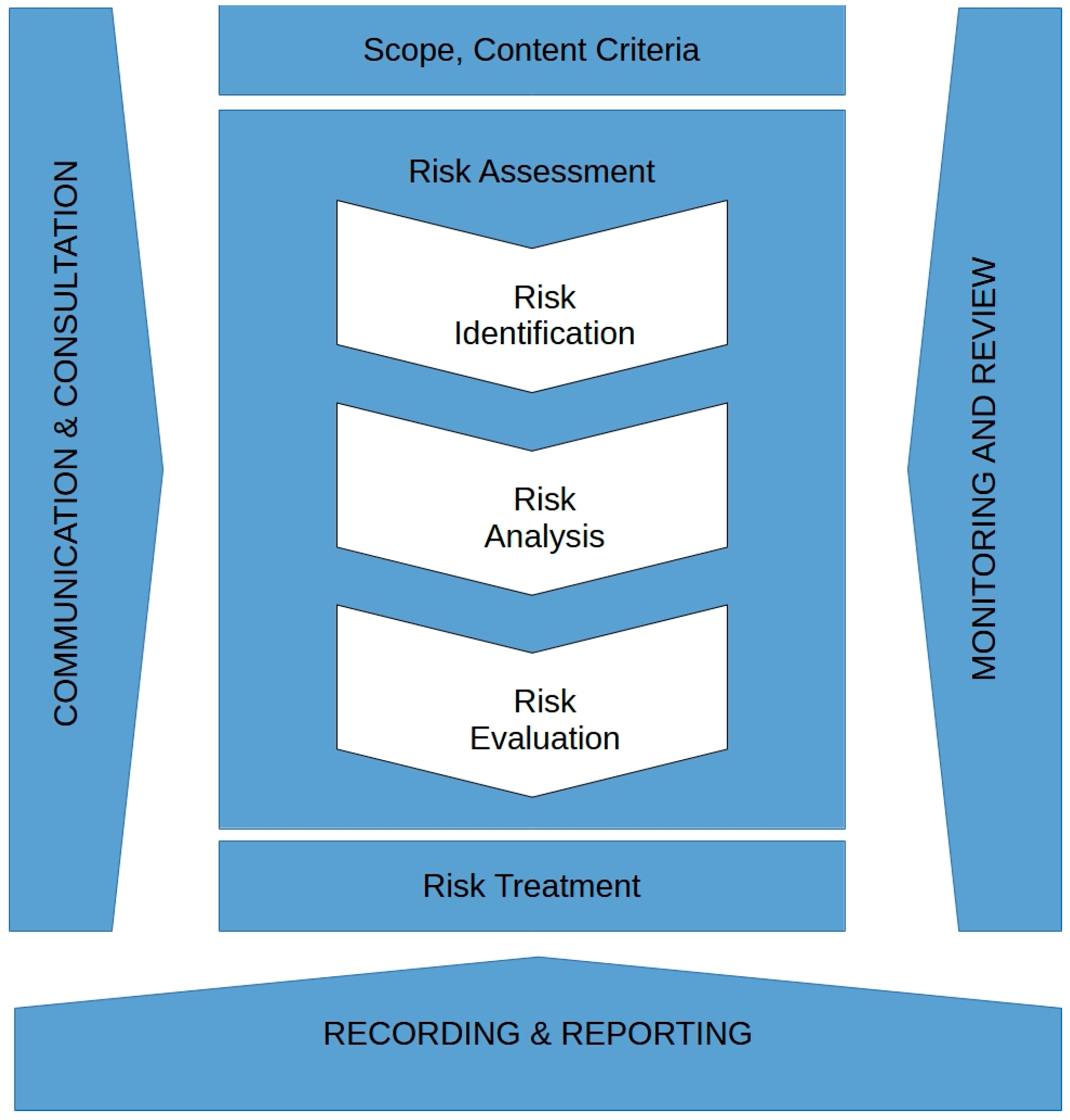
2.1. Risk Assessment Process and Methods
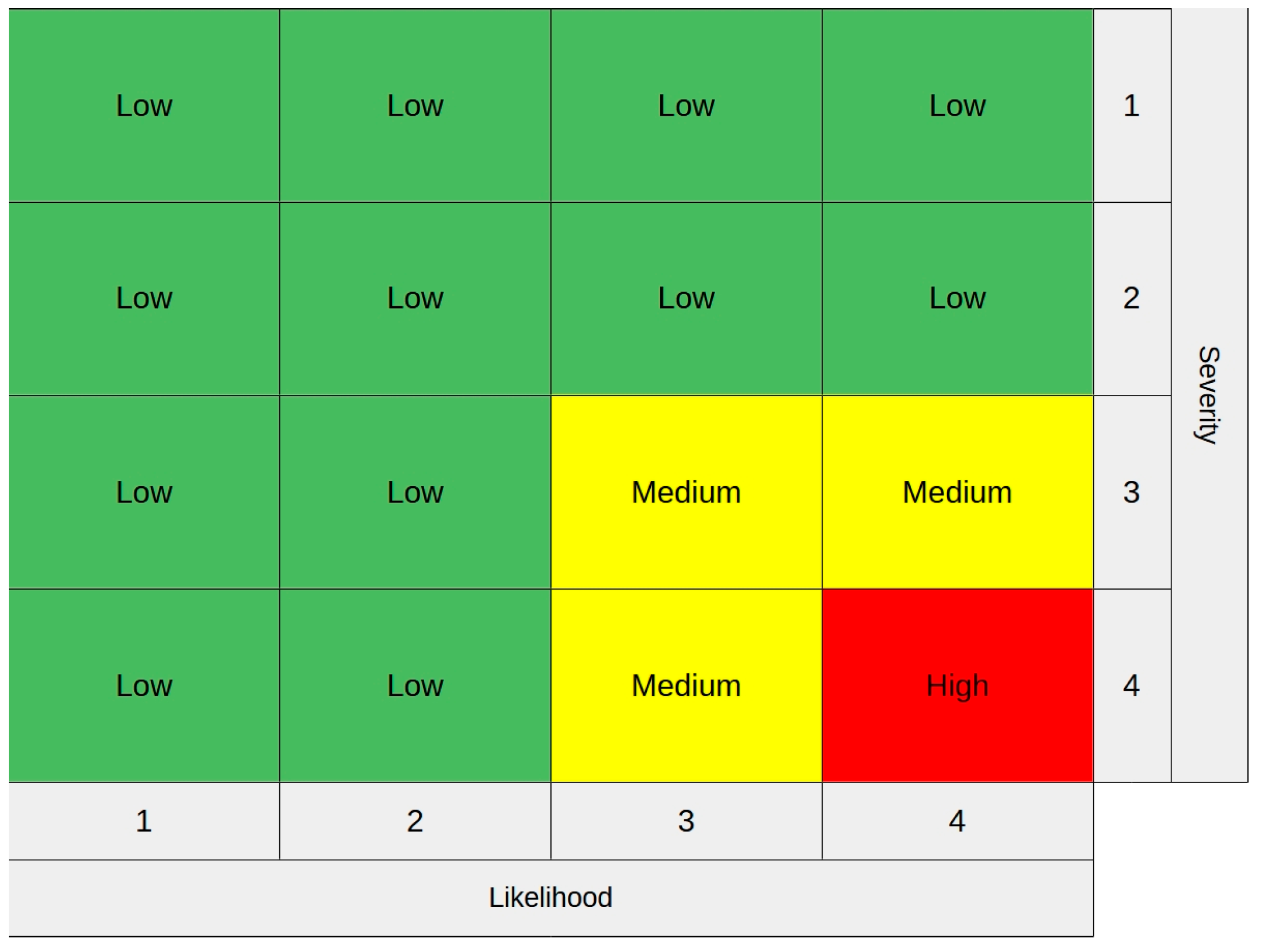
2.2. Risk Matrices and Their Limitations
2.3. Probability Estimation via Expert Judgment
2.4. SM Impact Probability
2.5. Challenges in the Optimal Assignment of SMs and the Research Gap
3. The Proposed Models
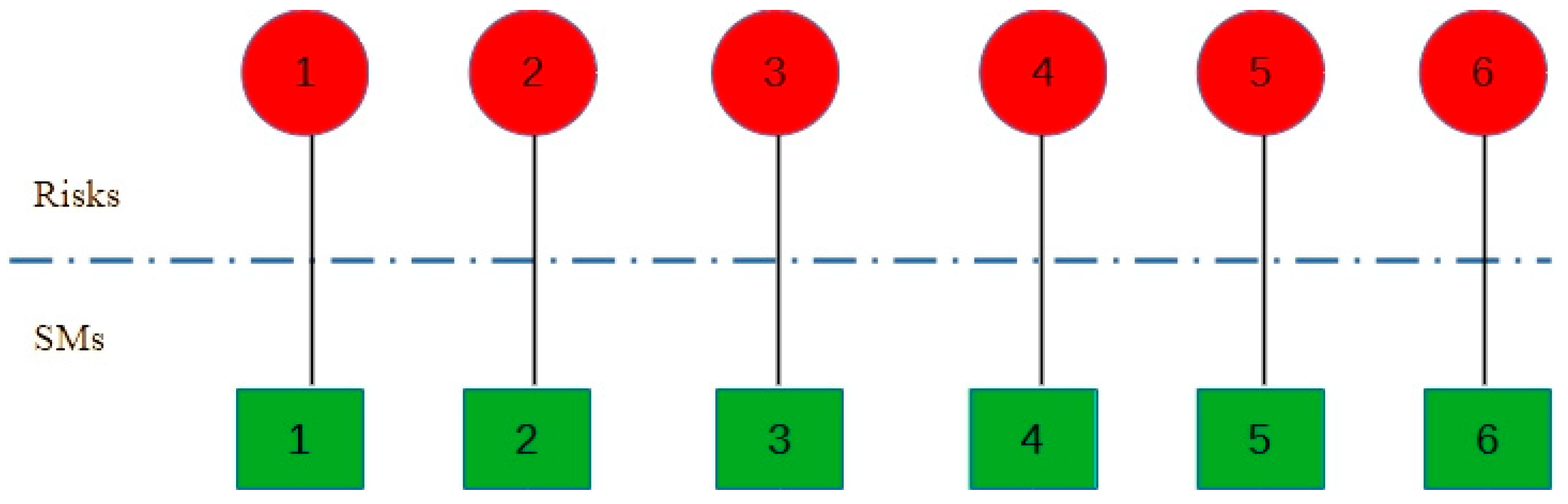
3.1. One-to-One Relationship Model
- i.
- Only one SM can be used for each risk;
- ii.
- Each SM can affect only one risk;
- iii.
- An SM cannot be partially applied (fully applied or not);
- iv.
- SMs do not pose an additional risk;
- v.
- Severity and likelihood levels, assessed by experts, are independent of each other;
- vi.
- Risks do not change during the review process;
- vii.
- The effects of the applied SMs on risks are stochastic;
- viii.
- If an SM is invested in, it will be implemented during the review period.
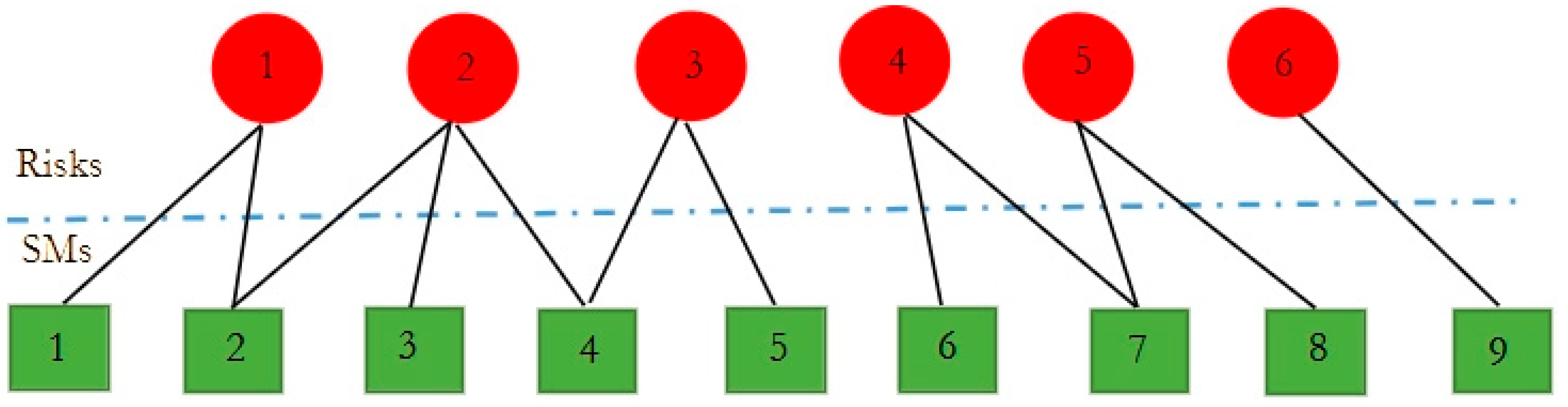
3.2. Multiple-Relationship Model
- i.
- Several SMs can be taken for a risk;
- ii.
- An SM can affect more than one risk;
- iii.
- SMs cannot be partially applied (fully applied or not);
- iv.
- SMs do not pose an additional risk;
- v.
- The impacts of the SM bundles on risks are stochastic;
- vi.
- The probability (effects of SM bundles), severity, and likelihood values are dependent to SMs when implementing an SM bundle;
- vii.
- Risks do not change during the review process;
- viii.
- If an SM bundle is invested, it will be implemented during the review period.
3.3. Multiple-Relationship Model Sample Problem
Solution for the Sample Problem and Implications
4. Limitations and Challenges of the Proposed Models
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SDG | Sustainable Development Goal |
| SM | Safety Measure |
| OHS | Occupational Health and Safety |
| DP | Dynamic Programming |
| CBA | Cost–Benefit Analysis |
| Eq. | Equation |
| s.t. | Subject To |
| SMEs | Small- and Medium-Sized Enterprises |
| VSS | Value of the Stochastic Solution |
References
- Baybutt, P. Designing Risk Matrices to Avoid Risk Ranking Reversal Errors. Process. Saf. Prog. 2016, 35, 41–46. [Google Scholar] [CrossRef]
- Coppola, D.P. Chapter 3—Risk and Vulnerability. In Introduction to International Disaster Management, 4th ed.; Coppola, D.P., Ed.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 177–265. ISBN 978-0-12-817368-8. [Google Scholar]
- Mentges, A.; Halekotte, L.; Schneider, M.; Demmer, T.; Lichte, D. A Resilience Glossary Shaped by Context: Reviewing Resilience-Related Terms for Critical Infrastructures. Int. J. Disaster Risk Reduct. 2023, 96, 103893. [Google Scholar] [CrossRef]
- Mohamed, A.-M.O.; Paleologos, E.K.; Howari, F.M. Pollution Assessment for Sustainable Practices in Applied Sciences and Engineering; Butterworth-Heinemann: Oxford, UK, 2021; ISBN 978-0-12-809582-9. [Google Scholar]
- Bao, C.; Li, J.; Wu, D. A Fuzzy Mapping Framework for Risk Aggregation Based on Risk Matrices. J. Risk Res. 2018, 21, 539–561. [Google Scholar] [CrossRef]
- Dai, Y.; Tong, X.; Wang, L. Workplace Safety Accident, Employee Treatment, and Firm Value: Evidence from China. Econ. Model. 2022, 115, 105960. [Google Scholar] [CrossRef]
- Li, J.; Bao, C.; Wu, D. How to Design Rating Schemes of Risk Matrices: A Sequential Updating Approach. Risk Anal. 2018, 38, 99–117. [Google Scholar] [CrossRef]
- Xu, H.; Mei, Q.; Liu, S.; Zhang, J.; Khan, M.A.S. Understand, Track and Develop Enterprise Workplace Safety, and Sustainability in the Industrial Park. Heliyon 2023, 9, e16717. [Google Scholar] [CrossRef]
- Elmonstri, M. Review of the Strengths and Weaknesses of Risk Matrices. J. Risk Anal. Crisis Response 2014, 4, 49–57. [Google Scholar] [CrossRef]
- Nguembi, I.P.; Yang, L.; Appiah, V.S. Safety and Risk Management of Chinese Enterprises in Gabon’s Mining Industry. Heliyon 2023, 9, e20721. [Google Scholar] [CrossRef]
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development, A/RES/70/1; United Nations Department of Economic and Social Affairs: New York, NY, USA, 2015. [Google Scholar]
- Mazzi, A. Environmental and Safety Risk Assessment for Sustainable Circular Production: Case Study in Plastic Processing for Fashion Products. Heliyon 2023, 9, e21352. [Google Scholar] [CrossRef]
- Varadharajan, S.; Bajpai, S. Chronicles of Security Risk Assessment in Process Industries: Past, Present and Future Perspectives. J. Loss Prev. Process Ind. 2023, 84, 105096. [Google Scholar] [CrossRef]
- ISO 31000:2018; Risk Management—Guidelines. International Organization for Standardization: Geneva, Switzerland, 2018.
- PMI. The Standard for Risk Management in Portfolios, Programs, and Projects; PMI: Newtown Square, PA, USA, 2019. [Google Scholar]
- Albanesi, B.; Godono, A.; Plebani, F.; Mustillo, G.; Fumagalli, R.; Clari, M. Exploring Strategies and Tools to Prevent Accidents or Incidents in Atypical Scenarios. A Scoping Review. Saf. Sci. 2023, 163, 106124. [Google Scholar] [CrossRef]
- Choo, B.L.; Go, Y.I. Energy Storage for Large Scale/Utility Renewable Energy System—An Enhanced Safety Model and Risk Assessment. Renew. Energy Focus 2022, 42, 79–96. [Google Scholar] [CrossRef]
- Langdalen, H.; Abrahamsen, E.B.; Abrahamsen, H.B. A New Framework to Idenitfy and Assess Hidden Assumptions in the Background Knowledge of a Risk Assessment. Reliab. Eng. Syst. Saf. 2020, 200, 106909. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G.; Khakzad, N.; Yang, M. Operational Safety Economics: Foundations, Current Approaches and Paths for Future Research. Saf. Sci. 2021, 141, 105326. [Google Scholar] [CrossRef]
- Levine, E.S. Improving Risk Matrices: The Advantages of Logarithmically Scaled Axes. J. Risk Res. 2012, 15, 209–222. [Google Scholar] [CrossRef]
- Manuele, F.A. Advanced Safety Management Focusing on Z10 and Serious Injury Prevention, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1-118-84098-6. [Google Scholar]
- Marhavilas, P.K.; Koulouriotis, D.E. A Risk-Estimation Methodological Framework Using Quantitative Assessment Techniques and Real Accidents’ Data: Application in an Aluminum Extrusion Industry. J. Loss Prev. Process. Ind. 2008, 21, 596–603. [Google Scholar] [CrossRef]
- Altenbach, T.J. Comparison of Risk Assessment Techniques from Qualitative to Quantitative. In Proceedings of the American Society of Mechanical Engineers, Pressure Vessels and Piping Division, Hono lulu, HI, USA, 23–27 July 1995; Volume 296. [Google Scholar]
- Duijm, N.J. Recommendations on the Use and Design of Risk Matrices. Saf. Sci. 2015, 76, 21–31. [Google Scholar] [CrossRef]
- Wanner, P.; Freis, M.; Peternell, M.; Kelm, V. Risk Classification of Contaminated Sites—Comparison of the Swedish and the German Method. J. Environ. Manag. 2023, 327, 116825. [Google Scholar] [CrossRef]
- Wilkinson, G.; David, R. Back to Basics: Risk Matrices and ALARP. In Safety-Critical Systems: Problems, Process and Practice, Proceedings of the 17th Safety-Critical Systems Symposium, SSS 2009, Brighton, UK, 3–5 February 2009; Springer: London, UK, 2009. [Google Scholar]
- Xu, Y.; Reniers, G.; Yang, M.; Yuan, S.; Chen, C. Uncertainties and Their Treatment in the Quantitative Risk Assessment of Domino Effects: Classification and Review. Process. Saf. Environ. Prot. 2023, 172, 971–985. [Google Scholar] [CrossRef]
- Baybutt, P. Guidelines for Designing Risk Matrices. Process. Saf. Prog. 2018, 37, 49–55. [Google Scholar] [CrossRef]
- Ball, D.J.; Watt, J. Further Thoughts on the Utility of Risk Matrices. Risk Anal. 2013, 33, 2068–2078. [Google Scholar] [CrossRef]
- Wall, K.D. The Trouble with Risk Matrices; Naval Postgraduate School (DRMI): Monterey, CA, USA, 2011; p. 26. [Google Scholar]
- Markowski, A.S.; Mannan, M.S. Fuzzy Risk Matrix. J. Hazard. Mater. 2008, 159, 152–157. [Google Scholar] [CrossRef] [PubMed]
- Marhavilas, P.K.; Filippidis, M.; Koulinas, G.K.; Koulouriotis, D.E. The Integration of HAZOP Study with Risk-Matrix and the Analytical-Hierarchy Process for Identifying Critical Control-Points and Prioritizing Risks in Industry—A Case Study. J. Loss Prev. Process Ind. 2019, 62, 103981. [Google Scholar] [CrossRef]
- Cheng, Y.-C.; Liao, S.-W.; Alauddin, M.; Amyotte, P.; Shu, C.-M. Redefining of Potential Dust Explosion Risk Parameters for Additives in the Petrochemical Manufacturing Process. Process. Saf. Environ. Prot. 2023, 169, 472–480. [Google Scholar] [CrossRef]
- Comberti, L.; Demichela, M. Customised Risk Assessment in Manufacturing: A Step towards the Future of Occupational Safety Management. Saf. Sci. 2022, 154, 105809. [Google Scholar] [CrossRef]
- Seker, S. A Model for Risk Assessment in Glass Manufacturing Using Risk Matrix Technique and IVIF-TOPSIS Method. J. Intell. Fuzzy Syst. 2021, 42, 541–550. [Google Scholar] [CrossRef]
- Du, M.; Zhang, S.M.; Shang, W.J.; Yan, W.X.; Liu, Q.; Qin, C.Y.; Liu, M.; Liu, J. 2022 Multiple-Country Monkeypox Outbreak and Its Importation Risk into China: An Assessment Based on the Risk Matrix Method. Biomed. Env. Sci. 2022, 35, 878–887. [Google Scholar]
- Lohmann, D.; Lang-Welzenbach, M.; Feldberger, L.; Sommer, E.; Bücken, S.; Lotter, M.; Ott, O.J.; Fietkau, R.; Bert, C. Risk Analysis for Radiotherapy at the Universitätsklinikum Erlangen. Z. Für Med. Phys. 2022, 32, 273–282. [Google Scholar] [CrossRef]
- Mbah, L.T.; Molua, E.L.; Bomdzele, E.; Egwu, B.M.J. Farmers’ Response to Maize Production Risks in Cameroon: An Application of the Criticality Risk Matrix Model. Heliyon 2023, 9, e15124. [Google Scholar] [CrossRef]
- Durdyev, S.; Mohandes, S.R.; Tokbolat, S.; Sadeghi, H.; Zayed, T. Examining the OHS of Green Building Construction Projects: A Hybrid Fuzzy-Based Approach. J. Clean. Prod. 2022, 338, 130590. [Google Scholar] [CrossRef]
- Spasenic, Z.; Makajic-Nikolic, D.; Benkovic, S. Integrated FTA-Risk Matrix Model for Risk Analysis of a Mini Hydropower Plant’s Project Finance. Energy Sustain. Dev. 2022, 70, 511–523. [Google Scholar] [CrossRef]
- Tian, Z.; Chen, Q.; Zhang, T. A Method for Assessing the Crossed Risk of Construction Safety. Saf. Sci. 2022, 146, 105531. [Google Scholar] [CrossRef]
- Bolbot, V.; Theotokatos, G.; McCloskey, J.; Vassalos, D.; Boulougouris, E.; Twomey, B. A Methodology to Define Risk Matrices—Application to Inland Water Ways Autonomous Ships. Int. J. Nav. Archit. Ocean. Eng. 2022, 14, 100457. [Google Scholar] [CrossRef]
- Georgiev, K. Aviation Safety Training Methodology. Heliyon 2021, 7, e08511. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Sattari, F.; Lefsrud, L.; Macciotta, R. Human Vulnerability Modeling and Risk Analysis of Railway Transportation of Hazardous Materials. J. Loss Prev. Process. Ind. 2022, 80, 104882. [Google Scholar] [CrossRef]
- Sun, S.; Gao, G.; Li, Y.; Zhou, X.; Huang, D.; Chen, D.; Li, Y. A Comprehensive Risk Assessment of Chinese High-Speed Railways Affected by Multiple Meteorological Hazards. Weather. Clim. Extrem. 2022, 38, 100519. [Google Scholar] [CrossRef]
- Firoozzare, A.; Ghazanfari, S.; Yousefian, N. Designing and Analyzing the Motivational Risk Profile of Healthy Food and Agricultural Products Purchase. J. Clean. Prod. 2023, 432, 139693. [Google Scholar] [CrossRef]
- Domínguez, C.R.; Martínez, I.V.; Piñón Peña, P.M.; Rodríguez Ochoa, A. Analysis and Evaluation of Risks in Underground Mining Using the Decision Matrix Risk-Assessment (DMRA) Technique, in Guanajuato, Mexico. J. Sustain. Min. 2019, 18, 52–59. [Google Scholar] [CrossRef]
- Hao, M.; Nie, Y. Hazard Identification, Risk Assessment and Management of Industrial System: Process Safety in Mining Industry. Saf. Sci. 2022, 154, 105863. [Google Scholar] [CrossRef]
- Sánchez-Squella, A.; Fernández, D.; Benavides, R.; Saldias, J. Risk Analysis, Regulation Proposal and Technical Guide for Pilot Tests of Hydrogen Vehicles in Underground Mining. Int. J. Hydrog. Energy 2022, 47, 18799–18809. [Google Scholar] [CrossRef]
- Landell, H. The Risk Matrix as a Tool for Risk Analysis. Master’s Thesis, University of Gävle, Gävle, Sweden, 2016; p. 32. [Google Scholar]
- Asgary, A.; Ozdemir, A.I. Global Risks and Tourism Industry in Turkey. Qual. Quant. 2020, 54, 1513–1536. [Google Scholar] [CrossRef]
- Cook, R. Simplifying the Creation and Use of the Risk Matrix. In Improvements in System Safety; Redmill, F., Anderson, T., Eds.; Springer: London, UK, 2008; pp. 239–264. ISBN 978-1-84800-099-5. [Google Scholar]
- Cox, L.A. What’s Wrong with Risk Matrices? Risk Anal. 2008, 28, 497–512. [Google Scholar] [CrossRef]
- Liu, P.; Lyu, X.; Qiu, Y.; He, J.; Tong, J.; Zhao, J.; Li, Z. Identifying Key Performance Shaping Factors in Digital Main Control Rooms of Nuclear Power Plants: A Risk-Based Approach. Reliab. Eng. Syst. Saf. 2017, 167, 264–275. [Google Scholar] [CrossRef]
- Sutton, I. Offshore Safety Management; William Andrew: NY, USA, 2014; ISBN 978-0-323-26206-4. [Google Scholar]
- IEC 31010:2019; Risk Management—Risk Assessment Techniques. ISO: Geneva, Switzerland, 2019.
- Kaya, G.K.; Ward, J.; Clarkson, J. A Review of Risk Matrices Used in Acute Hospitals in England. Risk Anal. 2019, 39, 1060–1070. [Google Scholar] [CrossRef] [PubMed]
- Ni, H.; Chen, A.; Chen, N. Some Extensions on Risk Matrix Approach. Saf. Sci. 2010, 48, 1269–1278. [Google Scholar] [CrossRef]
- Smith, E.D.; Siefert, W.T.; Drain, D. Risk Matrix Input Data Biases. Syst. Eng. 2009, 12, 344–360. [Google Scholar] [CrossRef]
- Vatanpour, S.; Hrudey, S.; Dinu, I. Can Public Health Risk Assessment Using Risk Matrices Be Misleading? Int. J. Environ. Res. Public Health 2015, 12, 9575–9588. [Google Scholar] [CrossRef]
- Lengyel, D.M.; Mazzuchi, T.A.; Vesely, W.E. Establishing Risk Matrix Standard Criteria for Use in the Continuous Risk Management Process. J. Space Saf. Eng. 2023, 10, 276–283. [Google Scholar] [CrossRef]
- Jensen, R.C.; Bird, R.L.; Nichols, B.W. Risk Assessment Matrices for Workplace Hazards: Design for Usability. Int. J. Environ. Res. Public Health 2022, 19, 2763. [Google Scholar] [CrossRef]
- Jordan, S.; Mitterhofer, H.; Jørgensen, L. The Interdiscursive Appeal of Risk Matrices: Collective Symbols, Flexibility Normalism and the Interplay of ‘Risk’ and ‘Uncertainty’. Account. Organ. Soc. 2018, 67, 34–55. [Google Scholar] [CrossRef]
- Monat, J.P.; Doremus, S. An Alternative to Heat Map Risk Matrices for Project Risk Prioritization. J. Mod. Proj. Manag. 2018, 6, 104–113. [Google Scholar]
- Pickering, A.; Cowley, S. Risk Matrices: Implied Accuracy and False Assumptions. J. Health Saf. Res. Pract. 2010, 2, 9–16. [Google Scholar]
- Baybutt, P. Addressing Uncertainty and Subjectivity in Using Risk Matrices for Process Safety. Loss Prev. Bull. 2016, 17. [Google Scholar]
- Amer, M.; Daim, T. Expert Judgment Quantification. In Research and Technology Management in the Electricity Industry: Methods, Tools and Case Studies; Daim, T., Oliver, T., Kim, J., Eds.; Springer: London, UK, 2013; pp. 31–65. ISBN 978-1-4471-5097-8. [Google Scholar]
- Aven, T. Risk, Surprises and Black Swans: Fundamental Ideas and Concepts in Risk Assessment and Risk Management; Routledge: Abingdon, UK, 2014; ISBN 978-1-317-62632-9. [Google Scholar]
- Aven, T.; Reniers, G. How to Define and Interpret a Probability in a Risk and Safety Setting. Saf. Sci. 2013, 51, 223–231. [Google Scholar] [CrossRef]
- McAndrew, T.; Wattanachit, N.; Gibson, G.C.; Reich, N.G. Aggregating Predictions from Experts: A Review of Statistical Methods, Experiments, and Applications. Wiley Interdiscip. Rev. Comput. Stat. 2021, 13, e1514. [Google Scholar] [CrossRef]
- Tian, D.; Yang, B.; Chen, J.; Zhao, Y. A Multi-Experts and Multi-Criteria Risk Assessment Model for Safety Risks in Oil and Gas Industry Integrating Risk Attitudes. Knowl.-Based Syst. 2018, 156, 62–73. [Google Scholar] [CrossRef]
- Clemen, R.T.; Reilly, T. Making Hard Decisions with Decision Tools, 3rd ed.; South-Wester/Cengage Learning: Mason, OH, USA, 2013; ISBN 13: 978-0-538-79757-3. [Google Scholar]
- Chhibber, S.; Apostolakis, G.; Okrent, D. A Taxonomy of Issues Related to the Use of Expert Judgments in Probabilistic Safety Studies. Reliab. Eng. Syst. Saf. 1992, 38, 27–45. [Google Scholar] [CrossRef]
- Surowiecki, J. The Wisdom of Crowds: Why the Many Are Smarter than the Few and How Collective Wisdom Shapes Business, Economies, Societies, and Nations; Doubleday & Co.: New York, NY, USA, 2004; Volume 27, ISBN 978-0-349-11605-1. [Google Scholar]
- Lee, M.D.; Danileiko, I. Using Cognitive Models to Combine Probability Estimates. Judgm. Decis. Mak. 2014, 9, 258–272. [Google Scholar] [CrossRef]
- Clemen, R.T.; Winkler, R.L. Limits for the Precision and Value of Information from Dependent Sources. Oper. Res. 1985, 33, 427–442. [Google Scholar] [CrossRef]
- Baron, J.; Mellers, B.A.; Tetlock, P.E.; Stone, E.; Ungar, L.H. Two Reasons to Make Aggregated Probability Forecasts More Extreme. Decis. Anal. 2014, 11, 133–145. [Google Scholar] [CrossRef]
- Winkler, R.L.; Grushka-Cockayne, Y.; Lichtendahl, K.C.; Jose, V.R.R. Probability Forecasts and Their Combination: A Research Perspective. Decis. Anal. 2019, 16, 239–260. [Google Scholar] [CrossRef]
- Yuan, Z.; Khakzad, N.; Khan, F.; Amyotte, P.; Reniers, G. Risk-Based Design of Safety Measures to Prevent and Mitigate Dust Explosion Hazards. Ind. Eng. Chem. Res. 2013, 52, 18095–18108. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelagagge, P.M.; Palumbo, M. Economic Optimization of Industrial Safety Measures Using Genetic Algorithms. J. Loss Prev. Process. Ind. 2011, 24, 541–551. [Google Scholar] [CrossRef]
- Abrahamsen, E.B.; Moharamzadeh, A.; Abrahamsen, H.B.; Asche, F.; Heide, B.; Milazzo, M.F. Are Too Many Safety Measures Crowding Each Other Out? Reliab. Eng. Syst. Saf. 2018, 174, 108–113. [Google Scholar] [CrossRef]
- Tian, D.; Chen, J.; Wu, X. A Two Stage Risk Assessment Model Based on Interval-Valued Fuzzy Numbers and Risk Attitudes. Eng. Appl. Artif. Intell. 2022, 114, 105086. [Google Scholar] [CrossRef]
- Cox, L.A. Evaluating and Improving Risk Formulas for Allocating Limited Budgets to Expensive Risk-Reduction Opportunities. Risk Anal. 2012, 32, 1244–1252. [Google Scholar] [CrossRef]
- Caputo, A.C.; Pelagagge, P.M.; Salini, P. A Multicriteria Knapsack Approach to Economic Optimization of Industrial Safety Measures. Saf. Sci. 2013, 51, 354–360. [Google Scholar] [CrossRef]
- Chen, C.; Reniers, G. Chapter Eleven—Economic Approaches for Making Prevention and Safety Investment Decisions in the Process Industry. In Methods in Chemical Process Safety; Khan, F.I., Amyotte, P.R., Eds.; Elsevier: Amsterdam, The Netherlands, 2020; Volume 4, pp. 355–378. ISBN 2468-6514. [Google Scholar]
- Eslami Baladeh, A.; Cheraghi, M.; Khakzad, N. A Multi-Objective Model to Optimal Selection of Safety Measures in Oil and Gas Facilities. Process. Saf. Environ. Prot. 2019, 125, 71–82. [Google Scholar] [CrossRef]
- Safie, S. Words into Action Guidelines: National Disaster Risk Assessment; UNDRR: Geneva, Switzerland, 2017. [Google Scholar]
- Reniers, G.L.L.; Sörensen, K. An Approach for Optimal Allocation of Safety Resources: Using the Knapsack Problem to Take Aggregated Cost-Efficient Preventive Measures. Risk Anal. 2013, 33, 2056–2067. [Google Scholar] [CrossRef]
- Cox, L.A. Risk Analysis of Complex and Uncertain Systems; Springer: Boston, MA, USA, 2009; Volume 129, ISBN 978-0-387-89013-5. [Google Scholar]
- Meyer, T.; Reniers, G. Engineering Risk Management; De Gruyter: Berlin, Germany, 2022; ISBN 978-3-11-066533-8. [Google Scholar]
- Reniers, G.L.L.; Van Erp, H.R.N. Operational Safety Economics: A Practical Approach Focused on the Chemical and Process Industries; Wiley: Newark, NJ, USA, 2016; ISBN 978-1-118-87151-5. [Google Scholar]
- Reniers, G.L.L.; Sörensen, K. Optimal Allocation of Safety and Security Resources. Chem. Eng. Trans. 2013, 31, 397–402. [Google Scholar]
- Gonen, A. Optimal Risk Response Plan of Project Risk Management. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Singapore, 6–9 December 2011. [Google Scholar]
- Todinov, M.; Weli, E. Optimal Risk Reduction in the Railway Industry by Using Dynamic Programming. Int. J. Ind. Manuf. Eng. 2013, 7, 1342–1346. [Google Scholar]
- Todinov, M. Optimal Allocation of Limited Resources among Discrete Risk Reduction Options. Artif. Intell. Res. 2014, 3, 5298. [Google Scholar] [CrossRef]
- Yuan, Z.; Khakzad, N.; Khan, F.; Amyotte, P. Risk-Based Optimal Safety Measure Allocation for Dust Explosions. Saf. Sci. 2015, 74, 79–92. [Google Scholar] [CrossRef]
- Syed, Z.; Lawryshyn, Y. Multi-Criteria Decision-Making Considering Risk and Uncertainty in Physical Asset Management. J. Loss Prev. Process. Ind. 2020, 65, 104064. [Google Scholar] [CrossRef]
- Qazi, A.; Akhtar, P. Risk Matrix Driven Supply Chain Risk Management: Adapting Risk Matrix Based Tools to Modelling Interdependent Risks and Risk Appetite. Comput. Ind. Eng. 2020, 139, 105351. [Google Scholar] [CrossRef]
- Qazi, A.; Shamayleh, A.; El-Sayegh, S.; Formaneck, S. Prioritizing Risks in Sustainable Construction Projects Using a Risk Matrix-Based Monte Carlo Simulation Approach. Sustain. Cities Soc. 2021, 65, 102576. [Google Scholar] [CrossRef]
- Marhavilas, P.K.; Koulouriotis, D.E. A Combined Usage of Stochastic and Quantitative Risk Assessment Methods in the Worksites: Application on an Electric Power Provider. Reliab. Eng. Syst. Saf. 2012, 97, 36–46. [Google Scholar] [CrossRef]
- ISO 45001:2018; Occupational Health and Safety Management Systems—Requirements with Guidance for Use. ISO: Geneva, Switzerland, 2018.
- Dorman, P. The Economics of Safety, Health, and Well-Being at Work: An Overview; ILO: Geneva, Switzerland, 2000. [Google Scholar]
- Martello, S.; Toth, P. Knapsack Problems: Algorithms and Computer Implementations; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1990; ISBN 0-471-92420-2. [Google Scholar]
- Cacchiani, V.; Iori, M.; Locatelli, A.; Martello, S. Knapsack Problems—An Overview of Recent Advances. Part I: Single Knapsack Problems. Comput. Oper. Res. 2022, 143, 105692. [Google Scholar] [CrossRef]
- Cacchiani, V.; Iori, M.; Locatelli, A.; Martello, S. Knapsack Problems—An Overview of Recent Advances. Part II: Multiple, Multidimensional, and Quadratic Knapsack Problems. Comput. Oper. Res. 2022, 143, 105693. [Google Scholar] [CrossRef]
| SDG No | Short Description | Goal |
|---|---|---|
| 3 | Good Health and Well-Being | Ensure healthy lives and promote well-being for all at all ages |
| 8 | Decent Work and Economic Growth | Promote sustained, inclusive, and sustainable economic growth, full and productive employment, and decent work for all |
| 9 | Industry, Innovation, and Infrastructure | Build resilient infrastructure, promote inclusive and sustainable industrialization, and foster innovation |
| 12 | Responsible Consumption and Production | Ensure sustainable consumption and production patterns |
| 13 | Climate Action | Take urgent action to combat climate change and its impacts |
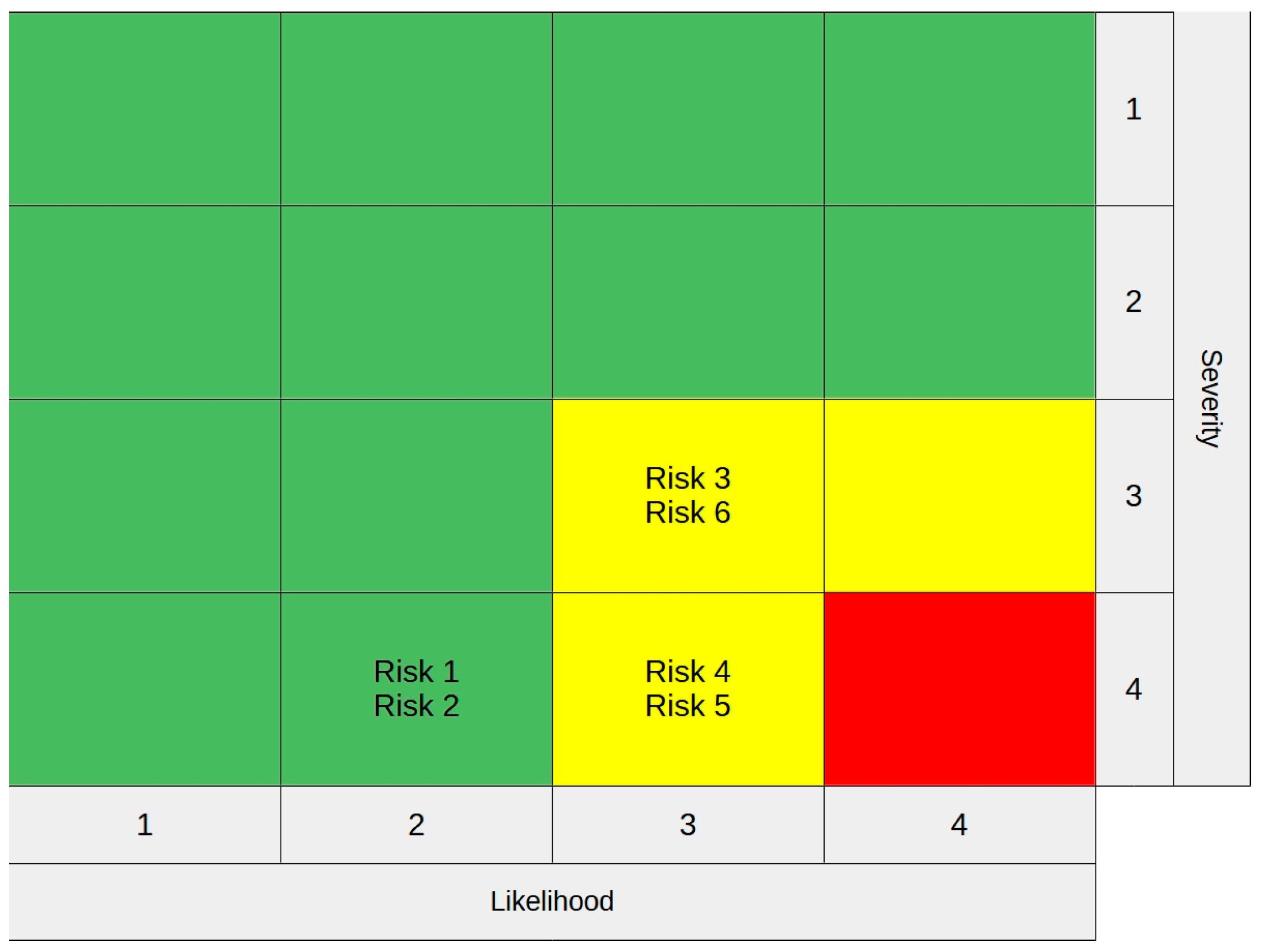
| Scale | Severity (in Monetary Units/Period) | Scale | Likelihood (/Period) | ||
|---|---|---|---|---|---|
| 1 | Negligible | <10,000 | 1 | Impossible | <0.001 |
| 2 | Marginal | [10,000; 100,000) | 2 | Improbable | [0.001; 0.01) |
| 3 | Critical | [100,000; 1,000,000) | 3 | Occasional | [0.01; 0.1) |
| 4 | Catastrophe | [1,000,000; 10,000,000] | 4 | Frequent | [0.1; 1] |
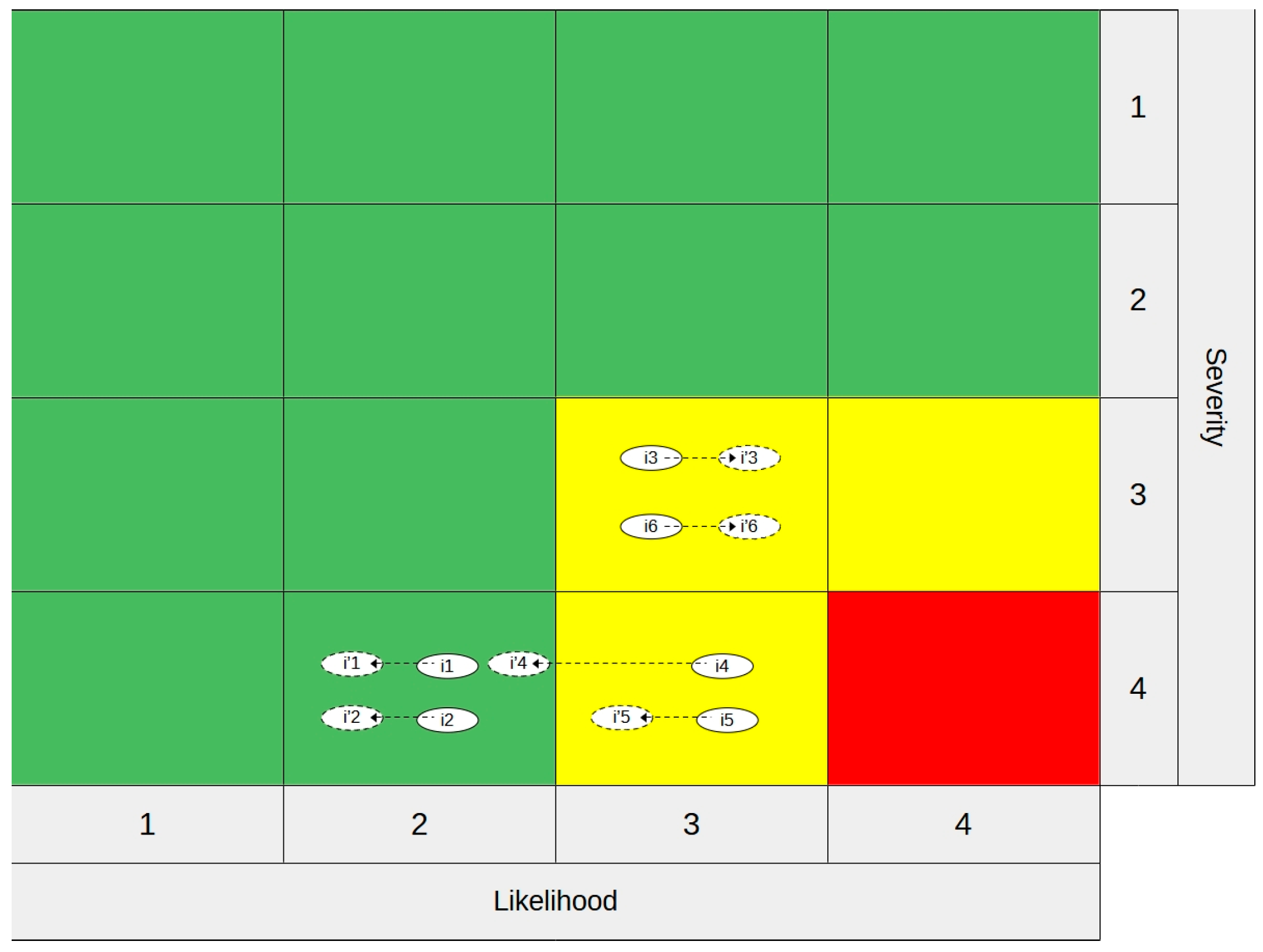
| i | Risks | Likelihood Score | Severity Score | Li | Si |
|---|---|---|---|---|---|
| 1 | Fire | 2 | 4 | 0.0055 | 5,500,000 |
| 2 | Electric shock | 2 | 4 | 0.0055 | 5,500,000 |
| 3 | Tripping over objects | 3 | 3 | 0.055 | 550,000 |
| 4 | Falling from a height | 3 | 4 | 0.055 | 5,500,000 |
| 5 | Falling materials from height | 3 | 4 | 0.055 | 5,500,000 |
| 6 | Manual lifting and transportation of heavy materials | 3 | 3 | 0.055 | 550,000 |
| q | SM | Cq (USD) |
|---|---|---|
| 1 | Sprinkler system construction | 20,000 |
| 2 | Leakage current relay installation | 500 |
| 3 | Buying an insulation mat | 1500 |
| 4 | Maintenance of electrical installation | 2500 |
| 5 | Continuous monitoring to ensure there is no material left in the work area | 13,000 |
| 6 | Safety net stretching | 10,000 |
| 7 | Purchasing personal protective equipment | 4000 |
| 8 | Redesign of fallible materials to prevent falls | 10,000 |
| 9 | Purchasing a pallet truck | 9000 |
| Bundle j | |
|---|---|
| M1 | {1, 2, {1, 2}} |
| M2 | {2, 3, 4, {2, 3}, {2, 4}, {3, 4}, {2, 3, 4}} |
| M3 | {4, 5, {4, 5}} |
| M4 | {6, 7, {6, 7}} |
| M5 | {7, 8, {7, 8}} |
| M6 | {9} |
| Diq | Bundles Including SM q | Diq | Bundles Including SM q |
|---|---|---|---|
| i = 1, q = 1 | {1, {1, 2}} | i = 3, q = 5 | {5, {4, 5}} |
| i = 1, q = 2 | {2, {1, 2}} | i = 4, q = 6 | {6, {6, 7}} |
| i = 2, q = 2 | {2, {2, 3}, {2, 4}, {2, 3, 4}} | i = 4, q = 7 | {7, {6, 7}} |
| i = 2, q = 3 | {3, {2, 3}, {3, 4}, {2, 3, 4}} | i = 5, q = 7 | {7, {7, 8}} |
| i = 2, q = 4 | {4, {2, 4}, {3, 4}, {2, 3, 4}} | i = 5, q = 8 | {8, {7, 8}} |
| i = 3, q = 4 | {4, {4, 5}} | i = 6, q = 9 | {9} |
| i/j | 1 (q1) | 2 (q2) | 3 (q3) | 4 (q4) | 5 (q5) | 6 (q6) | 7 (q7) | 8 (q8) | 9 (q9) | 10 (q1–2) | 11 (q2–3) | 12 (q2–4) | 13 (q3–4) | 14 (q2–3–4) | 15 (q4–5) | 16 (q6–7) | 17 (q7–8) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| j | 1 (q1) | 2 (q2) | 3 (q3) | 4 (q4) | 5 (q5) | 6 (q6) | 7 (q7) | 8 (q8) | 9 (q9) | 10 (q1–2) | 11 (q2–3) | 12 (q2–4) | 13 (q3–4) | 14 (q2–3–4) | 15 (q4–5) | 16 (q6–7) | 17 (q7–8) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Cj ($) | 20,000 | 500 | 1500 | 2500 | 13,000 | 10,000 | 4000 | 10,000 | 9000 | 20,500 | 2000 | 3000 | 4000 | 4500 | 15,500 | 14,000 | 14,000 |
| i/j | k | 1 (q1) | 2 (q2) | 3 (q3) | 4 (q4) | 5 (q5) | 6 (q6) | 7 (q7) | 8 (q8) | 9 (q9) | 10 (q1–2) | 11 (q2–3) | 12 (q2–4) | 13 (q3–4) | 14 (q2–3–4) | 15 (q4–5) | 16 (q6–7) | 17 (q7–8) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.83 | 0.66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.94 | 0.66 | 0.66 | 0 | 0.66 | 0 | 0 | 0 |
| 2 | 0.17 | 0.34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.06 | 0.34 | 0.34 | 0 | 0.34 | 0 | 0 | 0 | |
| 2 | 1 | 0 | 0.66 | 0.65 | 0.61 | 0 | 0 | 0 | 0 | 0 | 0.66 | 0.87 | 0.85 | 0.83 | 0.966 | 0.61 | 0 | 0 |
| 2 | 0 | 0.34 | 0.35 | 0.39 | 0 | 0 | 0 | 0 | 0 | 0.34 | 0.13 | 0.15 | 0.17 | 0.034 | 0.39 | 0 | 0 | |
| 3 | 1 | 0 | 0 | 0 | 0.61 | 0.72 | 0 | 0 | 0 | 0 | 0 | 0 | 0.61 | 0.61 | 0.61 | 0.92 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0.39 | 0.28 | 0 | 0 | 0 | 0 | 0 | 0 | 0.39 | 0.39 | 0.39 | 0.08 | 0 | 0 | |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0.72 | 0.57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.93 | 0.57 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0.28 | 0.43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.07 | 0.43 | |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.57 | 0.58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.57 | 0.91 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.43 | 0.42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.43 | 0.09 | |
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.78 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i/j | k | 1 (q1) | 2 (q2) | 3 (q3) | 4 (q4) | 5 (q5) | 6 (q6) | 7 (q7) | 8 (q8) | 9 (q9) | 10 (q1–2) | 11 (q2–3) | 12 (q2–4) | 13 (q3–4) | 14 (q2–3–4) | 15 (q4–5) | 16 (q6–7) | 17 (q7–8) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0.0005 | 0.0005 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0005 | 0.0005 | 0.0005 | 0 | 0.0005 | 0 | 0 | 0 |
| 2 | 0.005 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.005 | 0.005 | 0.005 | 0 | 0.005 | 0 | 0 | 0 | |
| 2 | 1 | 0 | 0.0005 | 0.0005 | 0.0005 | 0 | 0 | 0 | 0 | 0 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0.0005 | 0 | 0 |
| 2 | 0 | 0.005 | 0.005 | 0.005 | 0 | 0 | 0 | 0 | 0 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0.005 | 0 | 0 | |
| 3 | 1 | 0 | 0 | 0 | 0.0055 | 0.0055 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0.0055 | 0.0055 | 0.0055 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0.055 | 0.055 | 0 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0.055 | 0.055 | 0.055 | 0 | 0 | |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0.0055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0.0055 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0.055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0.055 | |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0.0055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0.0055 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0.055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0.055 | |
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.0055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0.055 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i/j | k | 1 (q1) | 2 (q2) | 3 (q3) | 4 (q4) | 5 (q5) | 6 (q6) | 7 (q7) | 8 (q8) | 9 (q9) | 10 (q1–2) | 11 (q2–3) | 12 (q2–4) | 13 (q3–4) | 14 (q2–3–4) | 15 (q4–5) | 16 (q6–7) | 17 (q7–8) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 5500 | 0 | 5500 | 0 | 0 | 0 |
| 2 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 5500 | 0 | 5500 | 0 | 0 | 0 | |
| 2 | 1 | 0 | 5500 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 5500 | 5500 | 5500 | 5500 | 0 | 0 |
| 2 | 0 | 5500 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 5500 | 5500 | 5500 | 5500 | 0 | 0 | |
| 3 | 1 | 0 | 0 | 0 | 550 | 550 | 0 | 0 | 0 | 0 | 0 | 0 | 550 | 550 | 550 | 550 | 0 | 0 |
| 2 | 0 | 0 | 0 | 550 | 550 | 0 | 0 | 0 | 0 | 0 | 0 | 550 | 550 | 550 | 550 | 0 | 0 | |
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 |
| 2 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | |
| 5 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 5500 | 5500 | |
| 6 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 550 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 550 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i | k | ρ’ik | L’ik | S’ik |
|---|---|---|---|---|
| 1 | 2 | 0.98 | 0.0055 | 5,500,000 |
| 3 | 0.02 | 0.055 | 5,500,000 | |
| 2 | 2 | 0.98 | 0.0055 | 5,500,000 |
| 3 | 0.02 | 0.055 | 5,500,000 | |
| 3 | 2 | 0.97 | 0.055 | 550,000 |
| 3 | 0.03 | 0.55 | 550,000 | |
| 4 | 2 | 0.95 | 0.055 | 5,500,000 |
| 3 | 0.05 | 0.55 | 5,500,000 | |
| 5 | 2 | 0.96 | 0.055 | 5,500,000 |
| 3 | 0.04 | 0.55 | 5,500,000 | |
| 6 | 2 | 0.97 | 0.055 | 550,000 |
| 3 | 0.03 | 0.55 | 550,000 |
| X(j) | Value | Y (i, q) | Value | V(q) | Value |
|---|---|---|---|---|---|
| j = 1 | 0 | i1, q1 | 0 | q1 | 0 |
| j = 2 | 1 | i1, q2 | 1 | q2 | 1 |
| j = 3 | 0 | i2, q2 | 1 | q3 | 0 |
| j = 4 | 0 | i2, q3 | 0 | q4 | 0 |
| j = 5 | 0 | i2, q4 | 0 | q5 | 0 |
| j = 6 | 0 | i3, q4 | 0 | q6 | 1 |
| j = 7 | 0 | i3, q5 | 0 | q7 | 1 |
| j = 8 | 0 | i4, q6 | 1 | q8 | 0 |
| j = 9 | 0 | i4, q7 | 1 | q9 | 0 |
| j = 10 | 0 | i5, q7 | 1 | ||
| j = 11 | 0 | i5, q8 | 0 | ||
| j = 12 | 0 | i6, q9 | 0 | ||
| j = 13 | 0 | ||||
| j = 14 | 0 | ||||
| j = 15 | 0 | ||||
| j = 16 | 1 | ||||
| j = 17 | 0 | ||||
| Metric | Deterministic Model | Proposed Stochastic Model |
|---|---|---|
| Objective Function Value | 385,575 | 312,523 |
| Total Expected Risk Reduction | 353,925 | 427,977 |
| Total Budget Utilized | 13,500 | 14,500 |
| Expected Risk Reduction per USD 1 | 26.2 | 29.5 |
| Value of Stochastic Solution (VSS) | – | 73,052 |
| Solution Time (seconds) | 0.39 | 0.11 |
| Invested SMs | q2, q7, q9 | q2, q6–7 |
| Impacted Risks | i1, i2, i4, i5, i6 | i1, i2, i4, i5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Özkan, G.; Birgören, B.; Sakallı, Ü.S. A Stochastic Knapsack Model for Sustainable Safety Resource Allocation Under Interdependent Safety Measures. Sustainability 2025, 17, 5242. https://doi.org/10.3390/su17125242
Özkan G, Birgören B, Sakallı ÜS. A Stochastic Knapsack Model for Sustainable Safety Resource Allocation Under Interdependent Safety Measures. Sustainability. 2025; 17(12):5242. https://doi.org/10.3390/su17125242
Chicago/Turabian StyleÖzkan, Gökhan, Burak Birgören, and Ümit Sami Sakallı. 2025. "A Stochastic Knapsack Model for Sustainable Safety Resource Allocation Under Interdependent Safety Measures" Sustainability 17, no. 12: 5242. https://doi.org/10.3390/su17125242
APA StyleÖzkan, G., Birgören, B., & Sakallı, Ü. S. (2025). A Stochastic Knapsack Model for Sustainable Safety Resource Allocation Under Interdependent Safety Measures. Sustainability, 17(12), 5242. https://doi.org/10.3390/su17125242






