Optimizing Subsurface Drainage Pipe Layout Parameters in Southern Xinjiang’s Saline–Alkali Soils: Impacts on Soil Salinity Dynamics and Oil Sunflower Growth Performance
Abstract
1. Introduction
2. Materials and Methods
2.1. Site Description
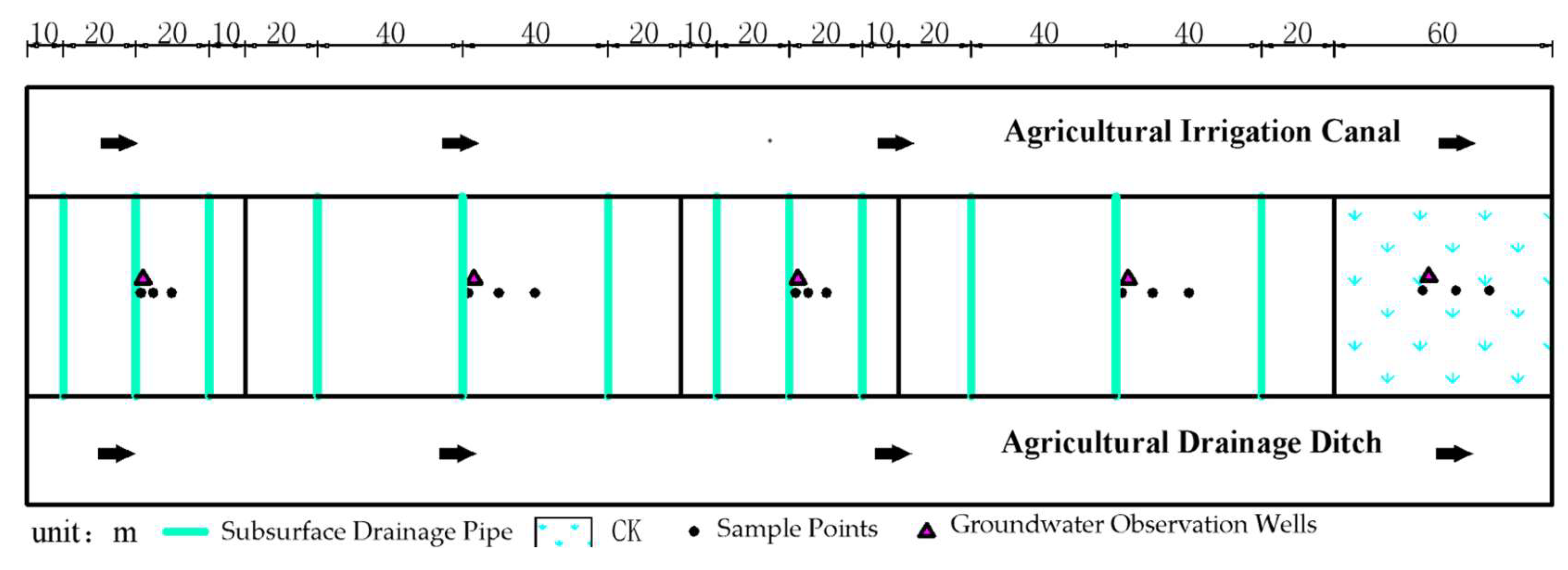
2.2. Experimental Design
2.3. Sample Determination and Processing
2.3.1. Soil Sample Treatment
2.3.2. Crop Growth Index
2.4. Model
2.4.1. Multi-Objective Genetic Algorithm
2.4.2. Entropy Weight TOPSIS
2.5. Statistical Analysis
3. Results
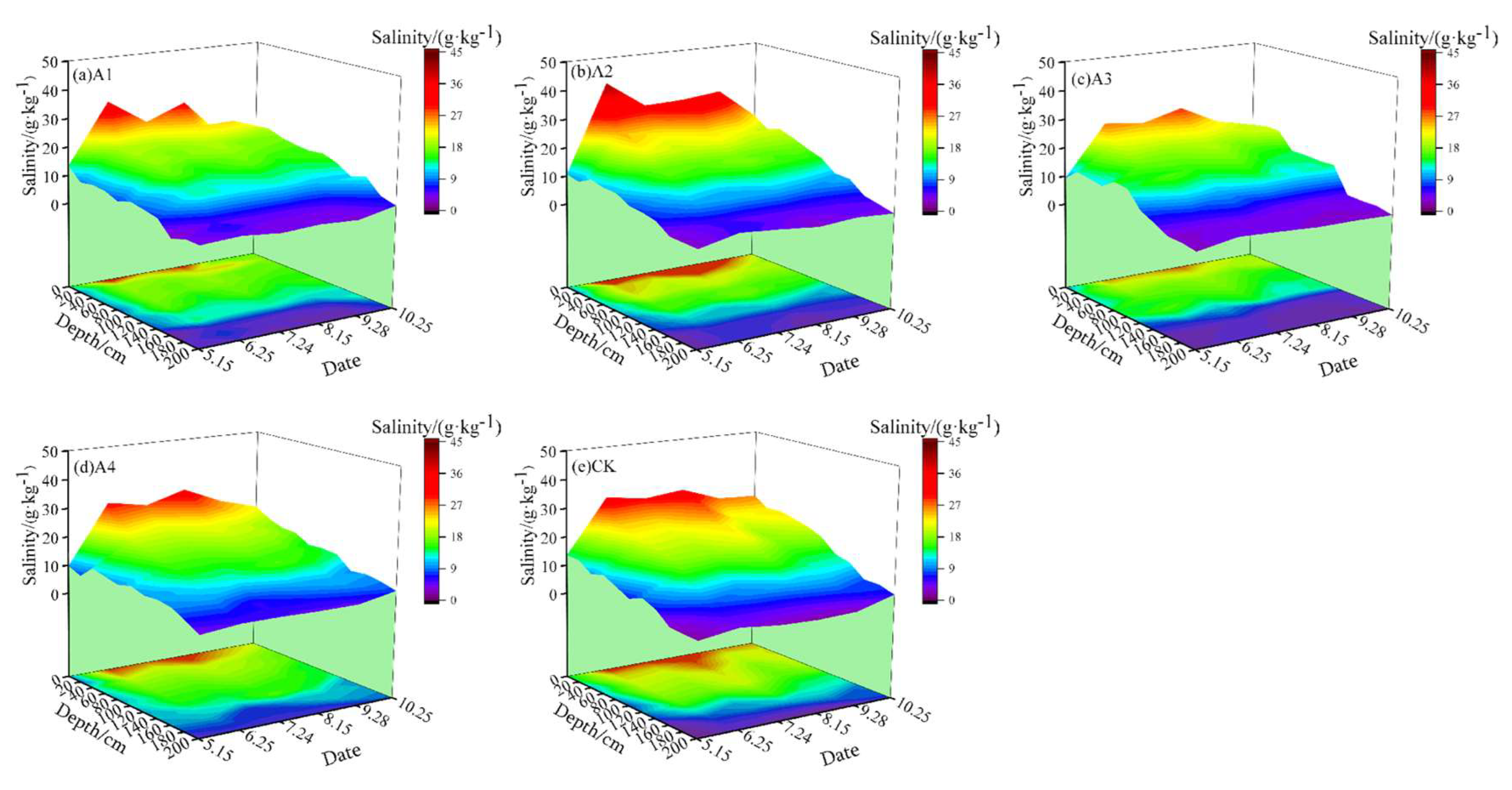
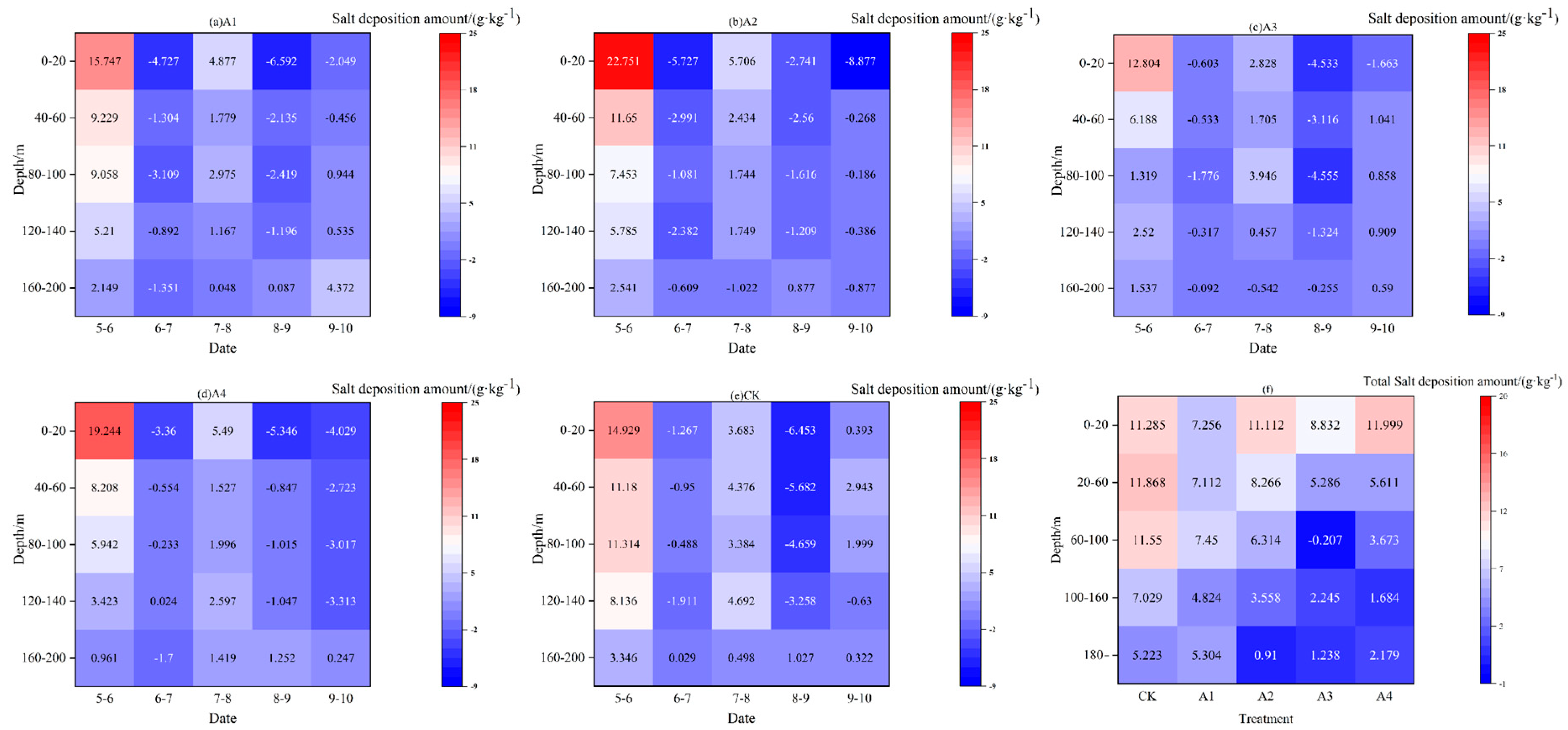
3.1. Change in the Salt Content of the Soil Profile During the Fertility Period
3.2. Coupling Relationship Between Groundwater Depth and Soil Salinity
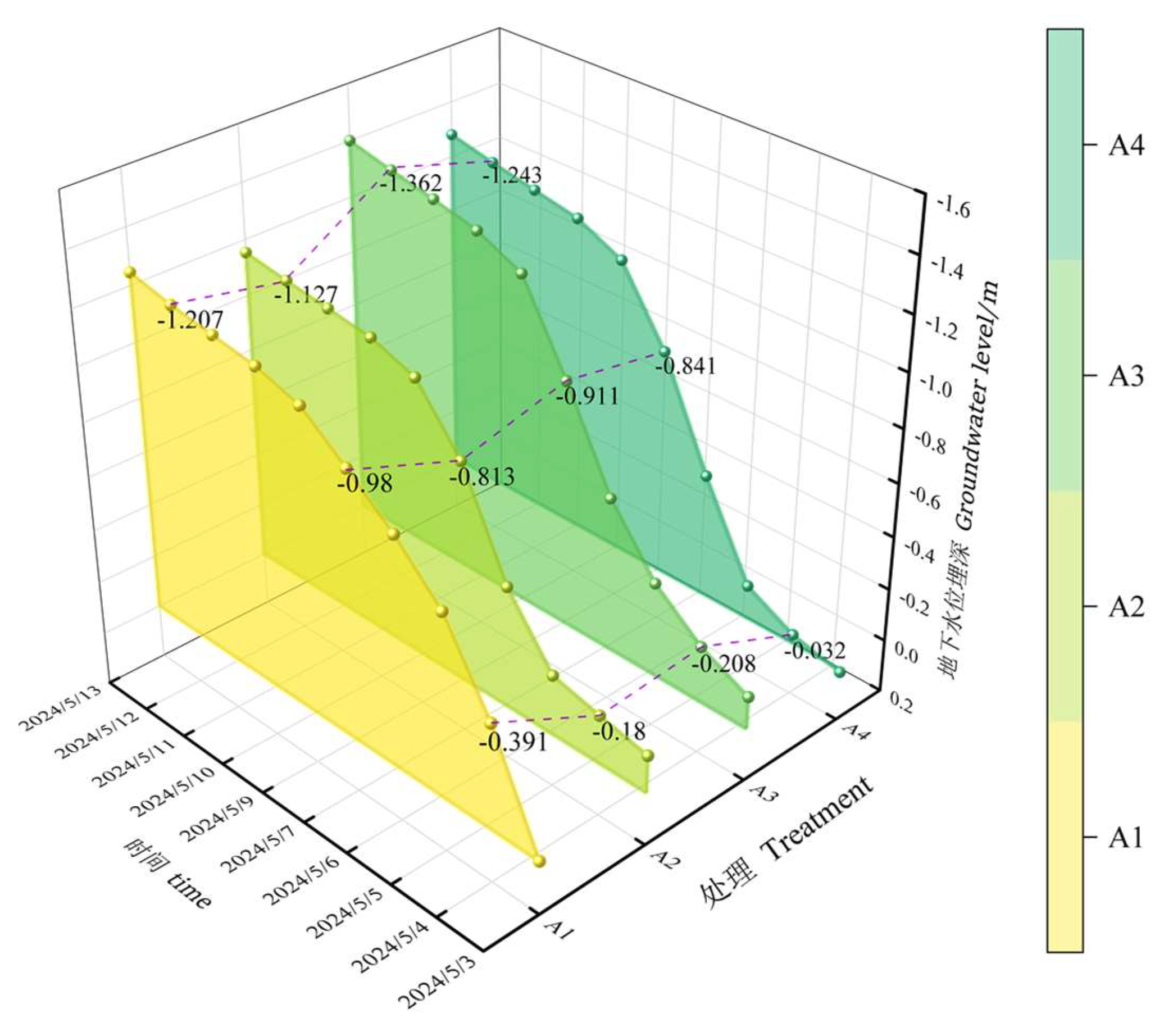
3.2.1. The Effect of the Dark Pipe on the Reduction of the Groundwater Burial Depth
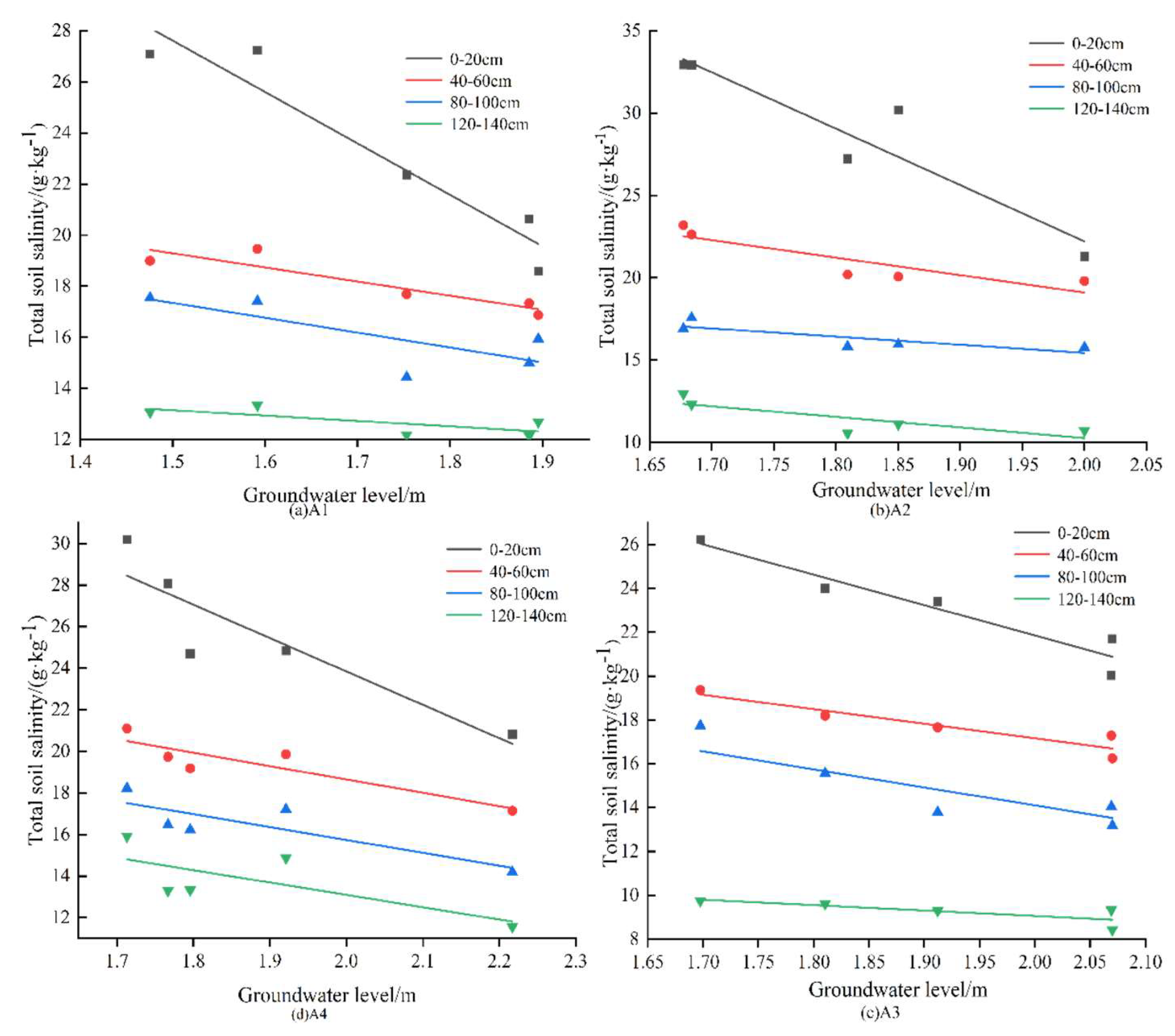
3.2.2. The Relationship Between Groundwater Buried Depth and Soil Salt
3.3. Salt Content Change in Soil Section Area During the Fertility Period
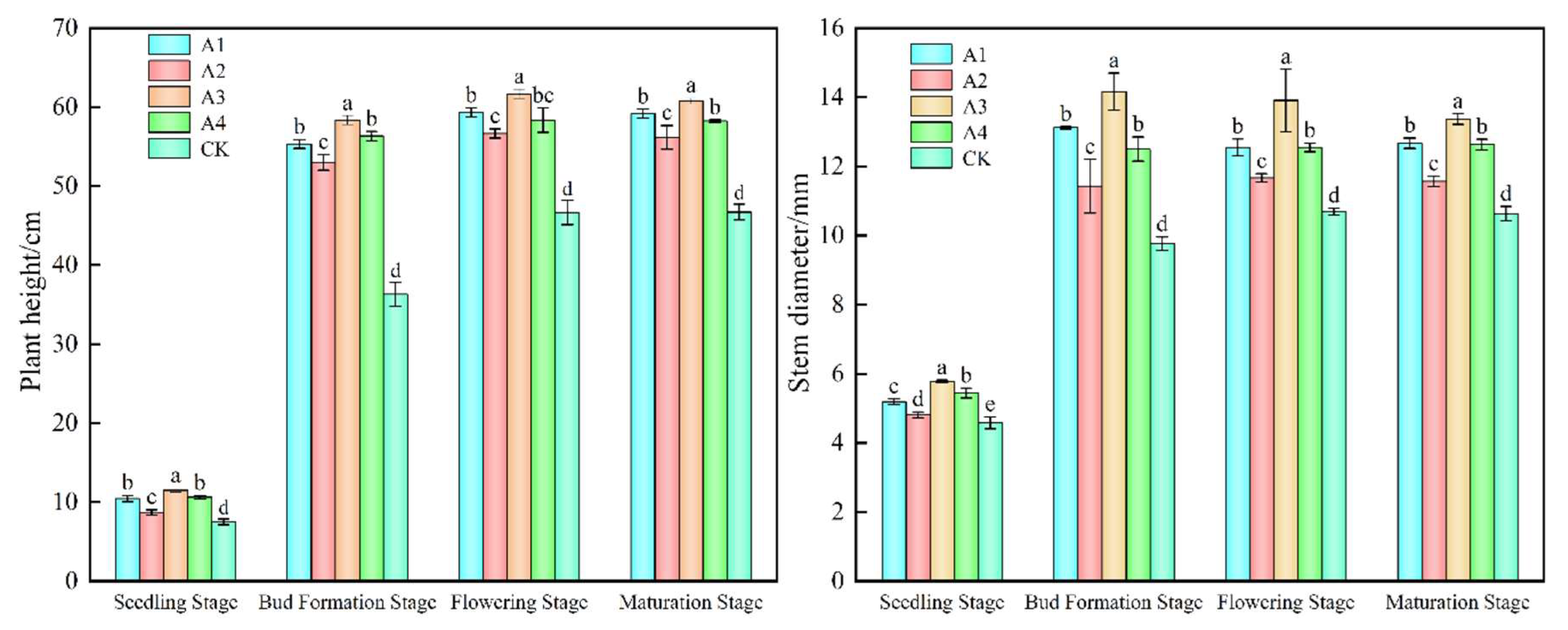
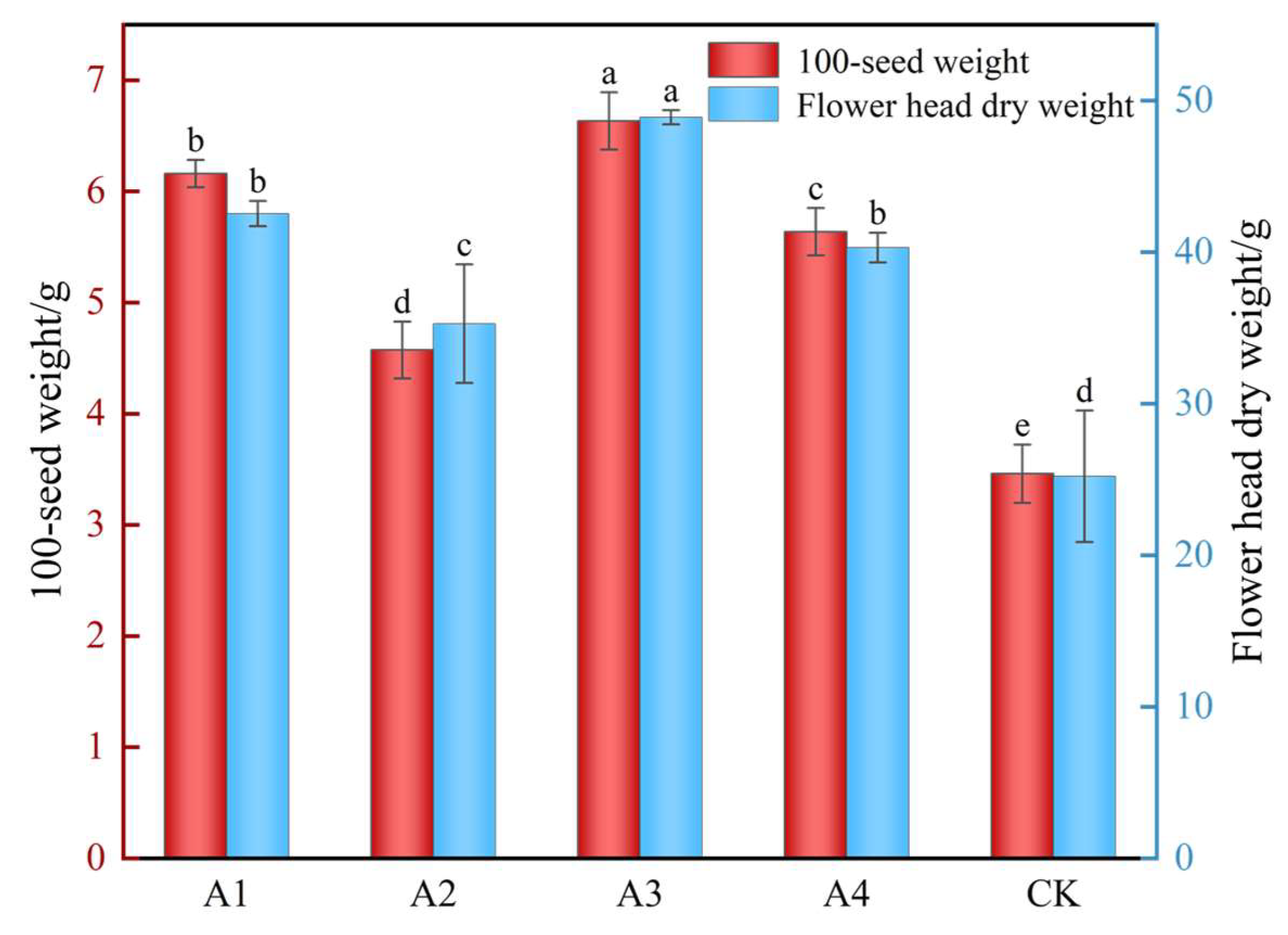
3.4. Effects of Different Treatments on Growth Indexes of Sunflowers
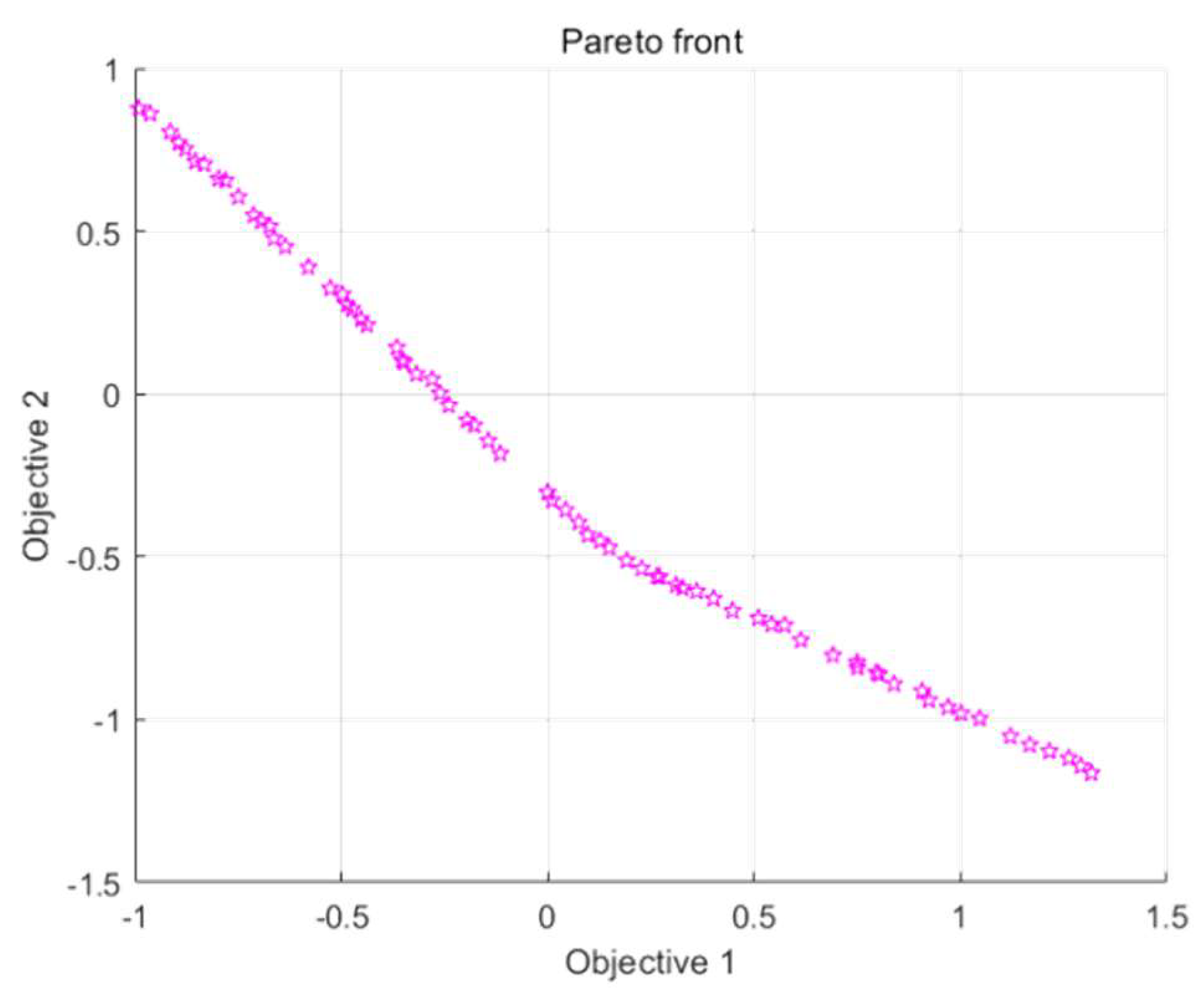
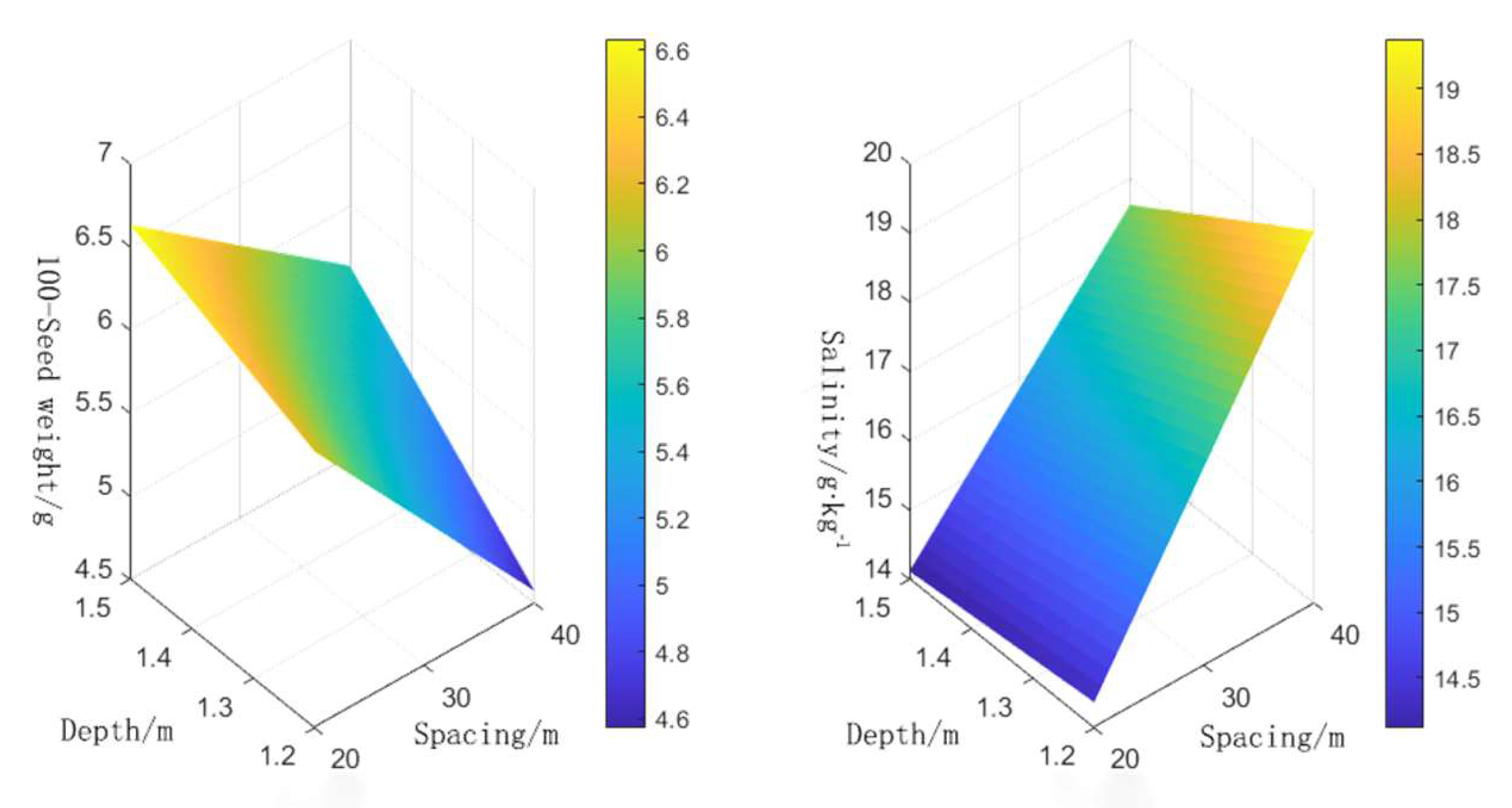
3.5. The Parameters of Dark Pipe Layout Are Optimized by Multi-Objective Genetic Algorithm
4. Discussion
4.1. Effect of Dark Tube on Soil Salt Accumulation
4.2. The Influence of Groundwater Burial Depth on Soil Salinity
4.3. The Influence of Dark Pipe Layout on the Change of Crop Growth Index
4.4. Subsurface Drainage Parameter Optimization
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, S.R.; Huang, Y.X. Research progress on saline-alkali land improvement in Songnen Plain. Soil Crop. 2023, 12, 206–217. [Google Scholar] [CrossRef]
- Guo, B.; Yang, F.; Fan, Y.W.; Han, B.M.; Chen, S.T.; Yang, W.N. Dynamic monitoring of soil salinization in Yellow River Delta utilizing MSAVI–SI feature space models with Landsat images. Environ. Earth Sci. 2019, 78, 308. [Google Scholar] [CrossRef]
- Yang, J.S.; Yao, R.J.; Wang, X.P.; Xie, W.P.; Zhang, X.; Zhu, W.; Zhang, L.; Sun, R.J. Research on salt-affected soils in China: History, status quo and prospect. Acta Petrol. Sin. 2022, 59, 10–27. [Google Scholar] [CrossRef]
- Chang, X.M.; Gao, Z.Y.; Wang, S.L.; Chen, H.R. Modelling long-term soil salinity dynamics using SaltMod in Hetao irrigation District, China. Comput. Electron. Agric. 2019, 156, 447–458. [Google Scholar] [CrossRef]
- Sun, G.F.; Zhu, Y.; Ye, M.; Yang, J.Z.; Qu, Z.Y.; Mao, W.; Wu, J.W. Development and application of long-term root zone salt balance model for predicting soil salinity in arid shallow water table area. Agric. Water Manag. 2019, 213, 486–498. [Google Scholar] [CrossRef]
- Wichelns, D.; Qadir, M. Achieving sustainable irrigation requires effective management of salts, soil salinity, and shallow groundwater. Agric. Water Manag. 2015, 157, 31–38. [Google Scholar] [CrossRef]
- Okur, B.; Örçen, N. Soil salinization and climate change. In Climate Change and Soil Interactions; Elsevier: Amsterdam, The Netherlands, 2020; pp. 331–350. [Google Scholar] [CrossRef]
- Liu, H.J.; Liu, H.J.; Tan, L.M.; Liu, J.-T. Simulating the changes of water table depth in coastal saline land with agro-subsurface drainage system. Chin. J. Eco-Agric. 2012, 20, 1687–1692. [Google Scholar] [CrossRef]
- Liu, Y.G.; Yang, H.C.; Wang, K.Y.; Lu, T.; Zhang, F. Shallow subsurface pipe drainage in Xinjiang lowers soil salinity and improves cotton seed yield. Trans. Chin. Soc. Agric. Eng. 2014, 30, 84–90. [Google Scholar] [CrossRef]
- Jafari-talukolaee, M.; Ritzema, H.; Darzi-naftchali, A. Subsurface drainage to enable the cultivation of winter crops in consolidated paddy fields in Northern Iran. Sustainability 2016, 8, 249. [Google Scholar] [CrossRef]
- Zhang, L.; Jiao, P.J.; Dong, Q.G.; Tao, Y. Effects of spacing and depth of subsurface drain on water and salt transport in the field. J. Irrig. Drain. 2023, 42, 92–101. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, H.J.; Su, T.; Shi, X.-Y.; Song, J.-H.; Zhu, Y.-Q.; Zheng, Q. Research on Salt Discharge Effect of Different Buried Deep Pipes in Salinized Farmland. Xinjiang Agric. Sci. 2018, 55, 1523–1533. [Google Scholar]
- Yang, Y.H.; Zhou, X.G.; Li, D.W.; Ji, Q. The Efficacy of Subsurface Drain in Desalinizing Cotton Field with Shallow Groundwater and Mulched Drip-irrigation in Southern Xinjiang. J. Irrig. Drain. 2021, 40, 137–144. [Google Scholar] [CrossRef]
- Shi, L.; Lv, N.; He, S.; Yin, F.H.; Gao, Z.J.; Tan, X.R. Screening of the water drainage and salt control mode of subsurface pipe and shaft on the secondary salinization soil and its effect evaluation. Xinjiang Agric. Sci. 2022, 59, 716–724. [Google Scholar] [CrossRef]
- Wen, Y.; Wang, Z.H.; Chen, L. Effects of buried depth of subsurface pipe on water and salt transport and oil sunflower yield under drip irrigation. J. Shihezi Univ. 2021, 39, 183–189. [Google Scholar] [CrossRef]
- Ebrahimian, H.; Noory, H. Modeling paddy field subsurface drainage using HYDRUS-2D. Paddy Water Environ. 2015, 13, 477–485. [Google Scholar] [CrossRef]
- Qian, Y.Z.; Zhu, Y.; Huang, J.S.; Jingwei, W.; Chang, A.; Shuai, H. Key parameters for the optimal layout of subsurface drainage pipe in arid areas. Trans. Chin. Soc. Agric. Eng. 2021, 37, 117–126. [Google Scholar] [CrossRef]
- Qi, Q. Response of sunflower growth and water nitrogen transport to different nitrogen fertilizers and field drainage simulation under dark pipe drainage. Inner Mong. Agric. Univ. 2022. [Google Scholar] [CrossRef]
- Zhou, D.W.; Hu, J.; Li, Q.; Huang, Y.X. Research progress of salt-affected land in Songnen Plain. Chin. J. Ecol. 2025, 44, 1671–1677. [Google Scholar]
- Shi, P.J.; Liu, H.G.; He, X.L.; Li, H.; Li, K. The simulation of water and salt transportation under subsurface drainage by HYDRUS model. Agric. Res. Arid Reg. 2019, 37, 224–231. [Google Scholar] [CrossRef]
- Li, X.W.; Zuo, Q.; Shi, J.C.; Bengal, A.; Wang, S. Evaluation of salt discharge by subsurface pipes in the cotton field with film mulched drip irrigation in Xinjiang, China Ⅰ. Calibration to models and parameters. J. Hydraul. Eng. 2016, 47, 537–544. [Google Scholar] [CrossRef]
- Zhang, D.M.; Gao, W.; Zhang, D.X.; Liu, M.X.; Liu, D. Relationship between soil water-soluble total salt content S and electrical conductivity EC5:1. J. Changjiang Veg. 2017, 20, 92–94. [Google Scholar]
- Lv, J.Y.; Jiang, Y.A.; Xu, C.; Liu, Y.J.; Su, Z.H.; Liu, J.C.; He, J.Q. Multi-Objective Winter Wheat Irrigation Strategies Optimization Based on Coupling AquaCrop-OSPy and NSGA-III: A Case Study in Yangling, China. Sci. Total Environ. 2022, 843, 157104. [Google Scholar] [CrossRef]
- Wang, B. Effects and Effectiveness Evaluation of Saline Soil Improvement by Subsurface Drainage in Hetao Irrigation District. Hohhot Inner Mong. Agric. Univ. 2022. [Google Scholar] [CrossRef]
- Long, L.J.; Zheng, G.Y.; Li, Z.Y.; Shi, L.; Li, Y.X.; Yang, G.J. Optimal depth and spacing of subsurface drains for soil desalination in Yanqi basin farmlands. J. Irrig. Drain. 2024, 43, 103–112. [Google Scholar] [CrossRef]
- Shao, X.H.; Hou, M.M.; Chen, L.H.; Chang, T.T.; Wang, W.N. Evaluation of subsurface drainage design based on Projection Pursuit. Energy Procedia. 2012, 16, 747–752. [Google Scholar] [CrossRef]
- Liu, G.M.; Yang, J.S.; Li, D.S. Salt dynamics in soil profiles under condition of different groundwater depths and salinities. J. Soil Sci. 2001, 38, 365–372. [Google Scholar] [CrossRef]
- Liu, M.H. Exploration of appropriate groundwater depth for water saving, salt suppression and optimization of maize irrigation schedule in the Hetao Irrigation District. Hohhot Inner Mong. Agric. Univ. 2021. [Google Scholar] [CrossRef]
- Xu, Y.; Ge, Z.; Wang, J.; Li, W.; Feng, S.Y. Study on the relationship between soil salinization and groundwater depth based on indicator Kriging method. Trans. Chin. Soc. Agric. Eng. 2019, 35, 123–130. [Google Scholar] [CrossRef]
- Jiao, B.Z.; Wu, H.F.; Zhu, X.D.; Shi, S.Q.; Tang, Y. Impact of winter irrigation and dark tube drainage on the water and salt movement in secondary saline soil and maize growth. Soil Fertil. Sci. China. 2024, 11, 173–180. [Google Scholar] [CrossRef]
- Zhu, L.; Tian, S.; Huang, J.X.; Sun, S.; Qiao, H.; Response and Regulation of Plants to Salt Stress: A review. Response and Regulation of Plants to Salt Stress: A review. Mol. Plant Breed. 2022, 2, 1–12. Available online: https://kns.cnki.net/kcms/detail/46.1068.S.20221116.1548.020.html (accessed on 17 November 2022).
- Heng, T.; He, X.L.; Yang, L.L.; Zhao, L.; Gong, P.; Xu, X.; Wang, X. Design and effect evaluation of subsurface pipe and vertical shaft drainage project to improve saline soil in Xinjiang. Trans. Chin. Soc. Agric. Eng. 2022, 38, 111–118. [Google Scholar] [CrossRef]
- Guo, H.; Ma, Y.J.; Wang, G.N.; Ma, L. The impact of different configurations of subsurface drainage pipes on soil water and salt dynamics and the efficacy of salt leaching through drainage during the spring-to-autumn irrigation season in southern Xinjiang. J. Agric. Resour. Environ. 2024, 41, 1422–1432. [Google Scholar] [CrossRef]
- Liu, H.G.; Bai, Z.T.; Li, K.M. Soil salinity changes in cotton field under mulched drip irrigation with subsurface pipes drainage using HYDRUS-2D model. Trans. Chin. Soc. Agric. 2021, 37, 130–141. [Google Scholar] [CrossRef]
- Ding, Y.T.; Cheng, Y.; Zhang, T.B. Modeling of dynamics of deep soil water and root uptake of maize with mulched drip irrigations using HYDRUS-2D. Arid Zone Agric. 2021, 39, 23–32. [Google Scholar] [CrossRef]
| Depth/cm | Bulk Density/(g·cm−3) | Total Porosity/% | Clay/% | Silt/% | Sand/% |
|---|---|---|---|---|---|
| 0–20 | 1.59 | 40.30 | 15.70 | 62.01 | 22.29 |
| 20–40 | 1.54 | 39.06 | 15.69 | 61.12 | 23.19 |
| 40–60 | 1.47 | 40.14 | 14.43 | 59.39 | 26.18 |
| 60–80 | 1.53 | 38.30 | 14.27 | 58.50 | 27.23 |
| 80–100 | 1.62 | 40.65 | 13.06 | 53.06 | 33.88 |
| 100–120 | 1.59 | 38.70 | 12.31 | 52.97 | 34.72 |
| 120–140 | 1.55 | 51.26 | 11.61 | 52.04 | 36.35 |
| 140–160 | 1.61 | 44.24 | 10.00 | 44.99 | 45.01 |
| 160–180 | 1.61 | 45.46 | 9.32 | 43.78 | 46.90 |
| 180–200 | 1.62 | 46.00 | 9.01 | 42.37 | 48.62 |
| Parameter | A1 | A2 | A3 | A4 | CK |
|---|---|---|---|---|---|
| Spacing/m | 20 | 40 | 20 | 40 | - |
| Depth/m | 1.2 | 1.2 | 1.5 | 1.5 | |
| Area/m2 | 3180 | 6360 | 3180 | 6360 | 3180 |
| Error Sum of Square | df | Square | F | p | Partial η2 | |
|---|---|---|---|---|---|---|
| Spacing | 0.001 | 1 | 0.001 | 30.278 | 0.001 ** | 0.791 |
| Depth | 0.001 | 1 | 0.001 | 38.123 | 0.000 ** | 0.827 |
| Spacing × Depth | 0.000 | 1 | 0.000 | 2.358 | 0.163 | 0.228 |
| Residual | 0.000 | 8 | 0.000 |
| MD | SE | t | p | Cohen’s d | |
|---|---|---|---|---|---|
| 20–40 | 0.017 | 0.003 | 5.503 | 0.001 | 3.177 |
| 1.2–1.5 | −0.019 | 0.003 | −6.174 | 0.000 | −3.565 |
| Depth/cm | Fitting Equation | R2 | ||||||
|---|---|---|---|---|---|---|---|---|
| A1 | A2 | A3 | A4 | A1 | A2 | A3 | A4 | |
| 0–20 | y = −20.1284x + 57.80725 | y = −34.24075x + 90.68594 | y = −13.84332x + 49.54053 | y = −16.04791x + 55.93775 | 0.917 | 0.881 | 0.919 | 0.817 |
| 40–60 | y = −5.52997x + 27.58208 | y = −10.6204x + 40.33789 | y = −6.61504x + 30.39591 | y = −6.42782x + 31.50319 | 0.841 | 0.784 | 0.878 | 0.802 |
| 80–100 | y = −5.81952x + 26.07549 | y = −4.95533x + 25.34552 | y = −10.22076x + 34.4067 | y = −6.19247x + 28.11942 | 0.586 | 0.684 | 0.825 | 0.704 |
| 120–140 | y = −2.09952x + 16.29413 | y = −6.43368x + 23.13112 | y = −2.46006x + 13.98265 | y = −5.942x + 24.97841 | 0.529 | 0.671 | 0.604 | 0.516 |
| Error Sum of Square | df | Square | F | p | Partial η2 | |
|---|---|---|---|---|---|---|
| Spacing | 33.260 | 1 | 33.260 | 9.107 | 0.017 * | 0.532 |
| Depth | 40.407 | 1 | 40.407 | 11.064 | 0.010 * | 0.580 |
| Spacing × Depth | 5.661 | 1 | 5.661 | 1.550 | 0.248 | 0.162 |
| Residual | 29.216 | 8 | 3.652 |
| MD | SE | t | p | Cohen’s d | |
|---|---|---|---|---|---|
| 20–40 | −3.330 | 1.103 | −3.018 | 0.017 | −1.742 |
| 1.2–1.5 | 3.670 | 1.103 | 3.326 | 0.010 | 1.920 |
| Spacing (m) | Depth (m) | 100-Seed Weight (g) | Root Zone Salinity (g·kg−1) | Spacing (m) | Depth (m) | 100-Seed Weight (g) | Root Zone Salinity (g·kg−1) |
|---|---|---|---|---|---|---|---|
| 25.158 | 1.4856 | 6.3461 | 15.049 | 23.094 | 1.48 | 6.4413 | 14.691 |
| 20.028 | 1.4969 | 6.6267 | 14.125 | 39.692 | 1.4372 | 5.4316 | 17.921 |
| 39.947 | 1.2025 | 4.5861 | 19.35 | 39.752 | 1.2236 | 4.676 | 19.178 |
| 24.98 | 1.4901 | 6.3646 | 15.008 | 37.811 | 1.4899 | 5.7125 | 17.281 |
| 38.352 | 1.4897 | 5.6843 | 17.379 | 39.822 | 1.3761 | 5.2086 | 18.304 |
| 34.108 | 1.4925 | 5.908 | 16.614 | 30.539 | 1.487 | 6.0741 | 16.004 |
| 39.603 | 1.3982 | 5.2996 | 18.131 | 39.555 | 1.2972 | 4.9488 | 18.705 |
| 39.626 | 1.2091 | 4.6345 | 19.232 | 39.628 | 1.3906 | 5.2716 | 18.179 |
| 23.094 | 1.4878 | 6.456 | 14.678 | 20.21 | 1.4874 | 6.6025 | 14.166 |
| 32.696 | 1.4932 | 5.9815 | 16.362 | 39.948 | 1.4197 | 5.3553 | 18.073 |
| 39.936 | 1.2513 | 4.7597 | 19.061 | 39.937 | 1.4497 | 5.462 | 17.895 |
| 35.503 | 1.4972 | 5.8523 | 16.838 | 37.001 | 1.4892 | 5.7512 | 17.142 |
| 33.357 | 1.4982 | 5.9627 | 16.458 | 39.659 | 1.2642 | 4.8257 | 18.92 |
| 29.694 | 1.4953 | 6.1383 | 15.826 | 39.752 | 1.4809 | 5.582 | 17.678 |
| 39.873 | 1.3576 | 5.1399 | 18.423 | 39.867 | 1.4624 | 5.5108 | 17.807 |
| 39.913 | 1.2392 | 4.7185 | 19.126 | 39.795 | 1.2056 | 4.6089 | 19.294 |
| 39.952 | 1.3219 | 5.0087 | 18.649 | 24.758 | 1.4926 | 6.3809 | 14.964 |
| 39.954 | 1.3442 | 5.0873 | 18.519 | 34.872 | 1.4952 | 5.8778 | 16.737 |
| 39.071 | 1.4947 | 5.665 | 17.478 | 28.751 | 1.4932 | 6.1807 | 15.667 |
| 28.019 | 1.4928 | 6.2167 | 15.539 | 33.946 | 1.4949 | 5.9236 | 16.575 |
| 23.883 | 1.4868 | 6.4138 | 14.82 | 26.179 | 1.4943 | 6.3129 | 15.21 |
| 28.936 | 1.4926 | 6.1698 | 15.701 | 21.017 | 1.4864 | 6.5595 | 14.31 |
| 39.888 | 1.2802 | 4.8653 | 18.88 | 31.43 | 1.4981 | 6.0586 | 16.121 |
| 39.855 | 1.4732 | 5.5496 | 17.742 | 21.792 | 1.4908 | 6.5276 | 14.443 |
| 29.436 | 1.4952 | 6.151 | 15.781 | 39.111 | 1.4878 | 5.6389 | 17.524 |
| 37.505 | 1.494 | 5.7416 | 17.206 | 39.336 | 1.4854 | 5.6192 | 17.578 |
| 22.396 | 1.4956 | 6.5058 | 14.543 | 27.065 | 1.4922 | 6.2635 | 15.372 |
| 39.943 | 1.4538 | 5.4761 | 17.872 | 22.434 | 1.4862 | 6.4868 | 14.563 |
| 39.239 | 1.3757 | 5.2435 | 18.186 | 31.319 | 1.4976 | 6.0628 | 16.103 |
| 28.155 | 1.4849 | 6.1909 | 15.586 | 39.752 | 1.3273 | 5.041 | 18.574 |
| 21.529 | 1.4911 | 6.5414 | 14.396 | 31.898 | 1.4849 | 5.999 | 16.253 |
| 39.882 | 1.2881 | 4.8936 | 18.832 | 25.853 | 1.498 | 6.3371 | 15.145 |
| 39.71 | 1.3281 | 5.0467 | 18.56 | 39.571 | 1.3372 | 5.0878 | 18.477 |
| 39.937 | 1.4653 | 5.5173 | 17.803 | 31.947 | 1.498 | 6.0324 | 16.212 |
| 39.657 | 1.4264 | 5.3956 | 17.977 | 39.976 | 1.3014 | 4.9342 | 18.775 |
| e | d | Weight Coefficient w | |
|---|---|---|---|
| root zone salinity | 0.9950 | 0.0050 | 53.7869% |
| 100-seed weight | 0.9957 | 0.0043 | 46.2131% |
| Spacing (m) | Depth (m) | Relative Proximity C | Sorting Results | Spacing (m) | Depth (m) | Relative Proximity C | Sorting Results |
|---|---|---|---|---|---|---|---|
| 20.028 | 1.4969 | 1 | 1 | 37.811 | 1.4899 | 0.475 | 36 |
| 20.21 | 1.4874 | 0.99 | 2 | 38.352 | 1.4897 | 0.459 | 37 |
| 21.017 | 1.4864 | 0.966 | 3 | 39.071 | 1.4947 | 0.445 | 38 |
| 21.529 | 1.4911 | 0.953 | 4 | 39.111 | 1.4878 | 0.435 | 39 |
| 21.792 | 1.4908 | 0.945 | 5 | 39.336 | 1.4854 | 0.425 | 40 |
| 22.396 | 1.4956 | 0.93 | 6 | 39.752 | 1.4809 | 0.407 | 41 |
| 22.434 | 1.4862 | 0.923 | 7 | 39.855 | 1.4732 | 0.393 | 42 |
| 23.094 | 1.4878 | 0.905 | 8 | 39.937 | 1.4653 | 0.379 | 43 |
| 23.094 | 1.48 | 0.9 | 9 | 39.867 | 1.4624 | 0.377 | 44 |
| 23.883 | 1.4868 | 0.881 | 10 | 39.943 | 1.4538 | 0.363 | 45 |
| 24.758 | 1.4926 | 0.858 | 11 | 39.937 | 1.4497 | 0.357 | 46 |
| 24.98 | 1.4901 | 0.85 | 12 | 39.692 | 1.4372 | 0.347 | 47 |
| 25.158 | 1.4856 | 0.842 | 13 | 39.657 | 1.4264 | 0.333 | 48 |
| 25.853 | 1.498 | 0.83 | 14 | 39.948 | 1.4197 | 0.314 | 49 |
| 26.179 | 1.4943 | 0.818 | 15 | 39.603 | 1.3982 | 0.295 | 50 |
| 27.065 | 1.4922 | 0.79 | 16 | 39.628 | 1.3906 | 0.283 | 51 |
| 28.019 | 1.4928 | 0.762 | 17 | 39.239 | 1.3757 | 0.275 | 52 |
| 28.155 | 1.4849 | 0.752 | 18 | 39.822 | 1.3761 | 0.256 | 53 |
| 28.751 | 1.4932 | 0.741 | 19 | 39.873 | 1.3576 | 0.228 | 54 |
| 28.936 | 1.4926 | 0.735 | 20 | 39.571 | 1.3372 | 0.209 | 55 |
| 29.436 | 1.4952 | 0.723 | 21 | 39.954 | 1.3442 | 0.206 | 56 |
| 29.694 | 1.4953 | 0.716 | 22 | 39.71 | 1.3281 | 0.191 | 57 |
| 30.539 | 1.487 | 0.683 | 23 | 39.752 | 1.3273 | 0.189 | 58 |
| 31.319 | 1.4976 | 0.671 | 24 | 39.952 | 1.3219 | 0.174 | 59 |
| 31.43 | 1.4981 | 0.668 | 25 | 39.555 | 1.2972 | 0.153 | 60 |
| 31.947 | 1.498 | 0.653 | 26 | 39.976 | 1.3014 | 0.143 | 61 |
| 31.898 | 1.4849 | 0.641 | 27 | 39.882 | 1.2881 | 0.127 | 62 |
| 32.696 | 1.4932 | 0.626 | 28 | 39.888 | 1.2802 | 0.115 | 63 |
| 33.357 | 1.4982 | 0.612 | 29 | 39.659 | 1.2642 | 0.101 | 64 |
| 33.946 | 1.4949 | 0.592 | 30 | 39.936 | 1.2513 | 0.072 | 65 |
| 34.108 | 1.4925 | 0.584 | 31 | 39.913 | 1.2392 | 0.055 | 66 |
| 34.872 | 1.4952 | 0.565 | 32 | 39.752 | 1.2236 | 0.039 | 67 |
| 35.503 | 1.4972 | 0.55 | 33 | 39.626 | 1.2091 | 0.023 | 68 |
| 37.001 | 1.4892 | 0.497 | 34 | 39.795 | 1.2056 | 0.011 | 69 |
| 37.505 | 1.494 | 0.489 | 35 | 39.947 | 1.2025 | 0 | 70 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Guo, H.; Zhu, Q.; An, D.; Song, Z.; Ma, L. Optimizing Subsurface Drainage Pipe Layout Parameters in Southern Xinjiang’s Saline–Alkali Soils: Impacts on Soil Salinity Dynamics and Oil Sunflower Growth Performance. Sustainability 2025, 17, 4797. https://doi.org/10.3390/su17114797
Wang G, Guo H, Zhu Q, An D, Song Z, Ma L. Optimizing Subsurface Drainage Pipe Layout Parameters in Southern Xinjiang’s Saline–Alkali Soils: Impacts on Soil Salinity Dynamics and Oil Sunflower Growth Performance. Sustainability. 2025; 17(11):4797. https://doi.org/10.3390/su17114797
Chicago/Turabian StyleWang, Guangning, Han Guo, Qing Zhu, Dong An, Zhenliang Song, and Liang Ma. 2025. "Optimizing Subsurface Drainage Pipe Layout Parameters in Southern Xinjiang’s Saline–Alkali Soils: Impacts on Soil Salinity Dynamics and Oil Sunflower Growth Performance" Sustainability 17, no. 11: 4797. https://doi.org/10.3390/su17114797
APA StyleWang, G., Guo, H., Zhu, Q., An, D., Song, Z., & Ma, L. (2025). Optimizing Subsurface Drainage Pipe Layout Parameters in Southern Xinjiang’s Saline–Alkali Soils: Impacts on Soil Salinity Dynamics and Oil Sunflower Growth Performance. Sustainability, 17(11), 4797. https://doi.org/10.3390/su17114797






