An Evaluation of the Robustness of Length-Based Stock Assessment Approaches for Sustainable Fisheries Management in Data and Capacity Limited Situations

Abstract

To ensure sustainability, the Ecosystem Approach to Fisheries (EAF) requires the evaluation of the impacts of fisheries beyond the main targeted species, to include those on bycaught, endangered, threatened and protected populations and keystone species. However, traditional stock assessments require extensive datasets that are often unavailable for data-limited fisheries, particularly in small-scale settings or in the Global South. This study evaluates the robustness of length-based approaches for fish stock assessment by comparing simple indicators and quantitative methods using an age-structured Operating Model. Simulations were conducted for a range of scenarios, for a range of life-history types and recruitment and natural mortality dynamics. Results reveal that while length-based approaches can effectively track trends in fishing mortality, performance varies significantly depending on species-specific life histories and assumptions about key parameters. Simple indicators often matched or outperformed complex methods, particularly when assumptions about equilibrium conditions or natural mortality were violated. The study highlights the limitations of length-based methods for classifying stock status relative to reference points, but demonstrates their utility when used with historical reference periods or as part of empirical harvest control rules. The findings provide practical guidance for applying length-based approaches in data-limited fisheries management, ensuring sustainability in data and capacity situations.

1. Introduction

The prevention of overfishing and the recovery of overfished stocks is crucial to ensure sustainability. This requires assessments of fishery impacts not only on the primary commercially exploited stocks, for which analytical stock assessments are available, but also on secondary stocks that are retained for the market. In addition, the Ecosystem Approach to Fisheries (EAF) requires an assessment of impacts on the broader ecosystem and mitigation of negative impacts on non-target species to maintain the balance of marine ecosystems. This includes bycatch and discarded stocks, endangered, threatened or protected (ETP) populations, and keystone or hub species [1,2]. The designation of ETP depends on national and international legislation intended to protect highly vulnerable species and may vary by jurisdiction. The Marine Stewardship Council (MSC [3]) also defines primary and secondary species. The former are species of commercial value for which there are management reference points, such as the biomass associated with Maximum Sustainable Yield ($B_{MSY}$). The latter are those that are not ETP nor managed according to reference points and may be retained if they are of market value or discarded if catches are undesired but unavoidable.

Traditional stock assessments conducted for the main commercially valuable stocks require extensive datasets that are often unavailable for small-scale fisheries, fisheries in the Global South, or for discarded species [4]. These limitations have driven significant efforts over the past two decades to develop data-limited approaches, such as biomass-based catch-only methods [5]. Catch-only methods were originally developed to provide a global assessment of stock status [6]. The provision of fisheries management advice also requires the assessment of stock status relative to reference points, the prediction of the response of a stock to management, the validation that the predictions are consistent with reality, and the updating of advice based on feedback about the state of the stock [7]. However, catch-only methods have been shown to exhibit notable biases, which limit their utility in fisheries management.

Effective fisheries management requires more than biomass-based assessments, since setting size limits and monitoring the size structure of fish stocks are critical to preventing overfishing in growth and recruitment [8,9]. Length-based data are often also more readily available than age or time series of catch and effort in data and capacity-limited situations. The analysis of the size distribution of fish in a population can reveal whether juvenile or mature individuals are being harvested disproportionately [10,11]. Growth overfishing occurs when juveniles are harvested before reaching their optimal size, reducing yield. Recruitment overfishing occurs when there are not enough mature individuals remaining to reproduce and replenish the population. Length-based methods and empirical indicators can be used to assess historical and current levels of exploitation using short time series of data and provide advice as part of harvest control rules (HCR) [12,13].

Model-based estimates are attractive because, by incorporating assumptions about stock productivity, they provide estimates of unobservable state variables, such as stock biomass and fishing mortality, along with analytical reference points. Empirical indicators, such as mean size or relative abundance, on the other hand, are easier for managers and stakeholders to understand. However, model-based estimators do not necessarily ensure more robust management, since they require assumptions that, if incorrectly specified, introduce bias.

In data and capacity-limited situations, with limited knowledge about key processes, such as natural mortality, recruitment, and fishery exploitation patterns, the focus is often on generic solutions. Therefore, verification is essential to ensure that the methods are implemented correctly and produce outputs consistent with their intended purpose. Validation is required to ensure that scientific advice is robust and credible [14], by evaluating whether it is plausible that a system equivalent to the model could have generated the observed data [15]. Methodological differences can introduce bias, where fixed parameters are uncertain or priors misspecified; therefore, calibration is necessary to align model estimates or empirical indicators with observed data to classify stocks as being overfished or subject to overfishing.

The use of techniques, such as cross-validation, which involve partitioning data into testing and training subsets, is problematic in data-limited situations with few observations. Therefore, we conduct a simulation using an Operating Model to represent the ‘true’ system. The Operating Model is conditioned on species with a range of life histories, and then an Observation Error Model is used to generate pseudo-data to test candidate length-based approaches.

The objectives of this study are to facilitate comparisons and integration of the results from different assessment approaches and to identify the impact of uncertainties on management advice in order to promote transparency in the scientific advice process and to ensure that management decisions are based on the best available science. The primary research questions are as follows: (i) How do simple indicators compare to complex methods in tracking exploitation trends? (ii) Which assumptions have the greatest impact on performance? (iii) How reliable are proxy reference points and the use of historical reference periods? (iv) What are the implications for implementing length-based methods in data-limited fisheries?

2. Materials and Methods

To ensure sustainability, it is necessary to monitor trends in exploitation and population health relative to reference levels [16]. These can be targets, limits, thresholds, or baselines [17]. Targets are to be achieved on average and limits are to be avoided with high probability, while thresholds trigger management action. Targets, limits, and thresholds are generally based on model-based quantities. Baselines, either based on model estimates or empirical quantities, are derived from historical periods when a stock was considered healthy, and can be used to monitor long-term or recovery plans [18,19].

Size data are potentially available from many fisheries and can provide either long-term trends or snapshots. If time series are unavailable, data from a single year, e.g., recovered from archives or from one-off sampling programmes, can be used to assess fisheries. Length data can also be used to develop community indicators and priors for stock assessment methods.

Various length-based approaches have been developed [20], from simple length-based indicators to sophisticated models that apply Bayesian Markov chain Monte Carlo, mixed-effects and maximum likelihood techniques [21,22]. The more complex methods are capable of integrating biological and fisheries information and estimating fishing mortality and reference points. However, the basic assumptions of all approaches are the same: the proportion of older and larger individuals is determined by the rate at which individuals grow and the level of mortality that determines how quickly they disappear from the population [10]. This requires knowledge of species- or stock-specific life histories.

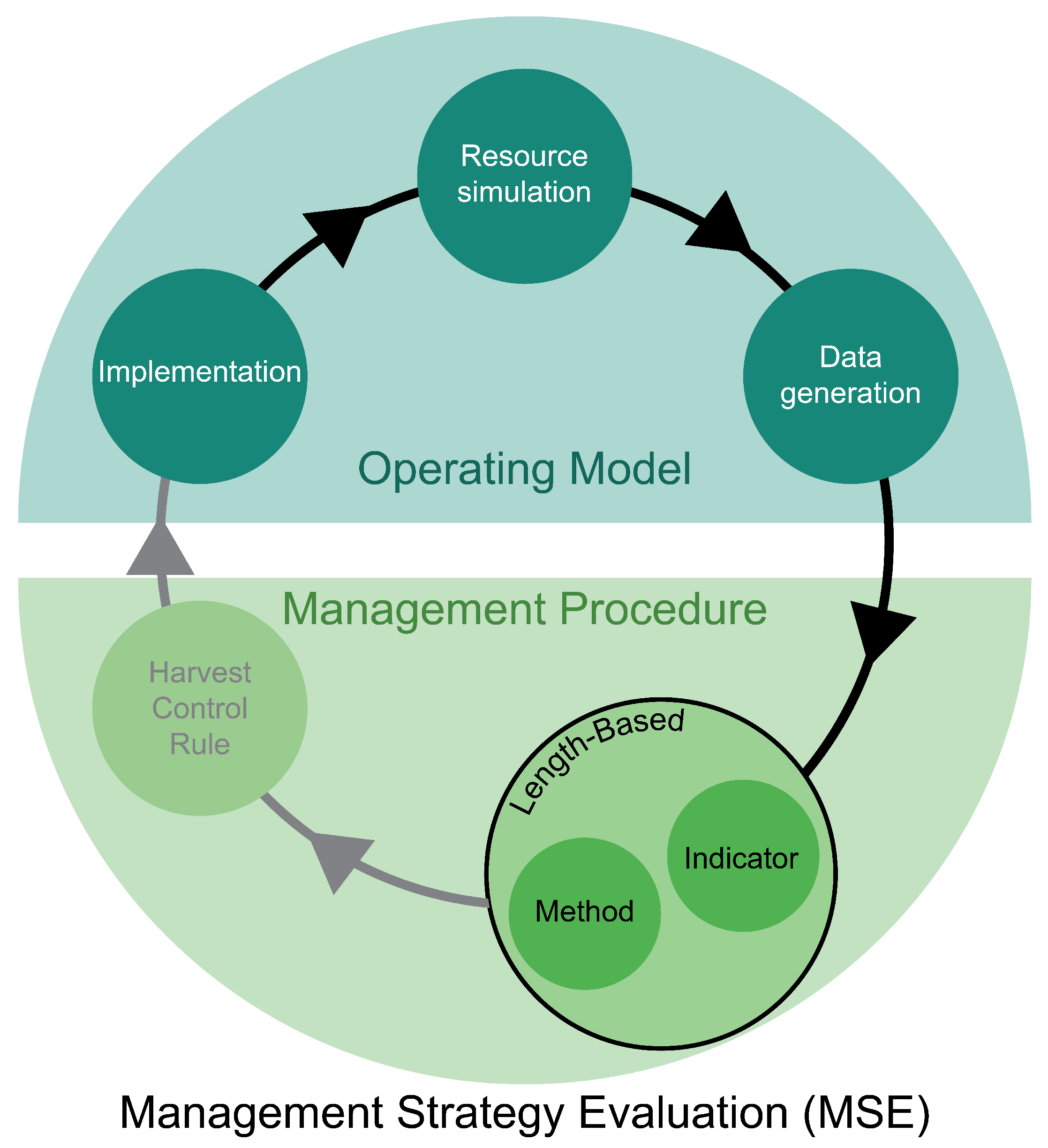
2.1. Simulation Framework

Management Strategy Evaluation is a computationally intensive closed-loop framework that simulates feedback control rules by testing candidate Management Procedures against Operating Models that represent hypotheses about resource dynamics (Figure 1). This study employed open-loop simulations (omitting the harvest control rule and feedback) to screen length-based approaches, using pseudo-data generated by the Observation Error Model to compare their ability to assess fishing mortality relative to reference target fishing mortality reference points based on maximum sustainable yield ($F_{MSY}$).

To establish a theoretical foundation for formulating hypotheses regarding population dynamics, an age-structured Operating Model was implemented using life history theory conditioned on scenarios related to hypotheses about resource dynamics; the Observation Error Model then generates pseudo-data. This enables a sensitivity analysis to be conducted to assess the skill of length-based approaches and determine their robustness for a range of resource dynamics [23,24]. The analysis was performed using R statistical version 4.2.4 software using FLR [25], full details are provided in the (Appendix A).

2.1.1. Operating Model Conditioning

To evaluate robustness, a range of hypothetical but plausible Operating Model scenarios were conditioned that are likely to have major impacts on the performance of the approaches [26].

A reference case was defined and then scenarios representing the primary uncertainties (

Table 1. Parameters used in the Operating Model and their impact on key stock assessment metrics. This table demonstrates how changes in growth, maturity, and mortality parameters affect the assessment outputs. (✔ indicates where a parameter is required by a specific approach).

Category	Parameter	${\mathit{L}}_{\mathit{F}=\mathit{M}}$	${\mathit{L}}_{\mathit{Mean}}$	BH	LCC	LBSPR	LIME
Growth	$L_{\infty }$	✔	-	✔	✔	✔	✔
	k	-	-	✔	✔	✔	✔
	$t_0$	-	-	-	-	-	✔
	$CV\left(L_{\infty }\right)$	-	-	-	-	✔	-
	$CV\left(L\right)$	-	-	-	-	-	✔
Mortality (M)	Mean	-	-	-	-	✔	✔
	Exponent	-	-	-	-	✔	-
Maturity	$L_{50}$	-	-	-	-	-	✔
Selectivity	$S_{50}$	-	-	-	-	✔	✔
	$S_{95}$	-	-	-	-	✔	✔
	Shape	-	-	-	-	Logistic	✔

). The scenarios included the steepness of the stock-recruitment relationship, recruitment variability, natural mortality, selection pattern, and the level of measurement error. In all scenarios, the length-based approaches used the parameters specified in the Reference Case. This was conducted to ensure that the robustness of the methods was evaluated.

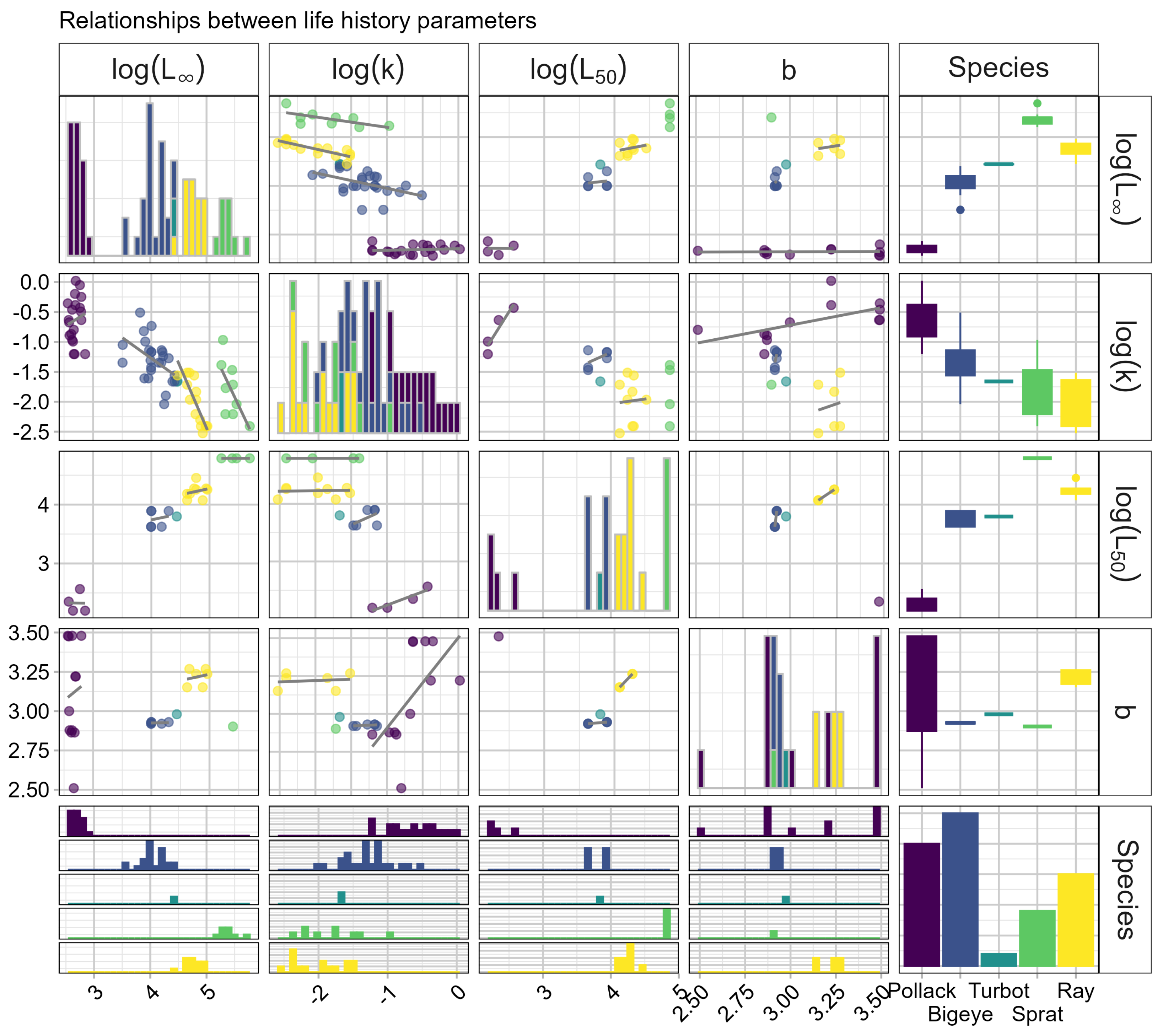
2.1.2. Life Histories

Case study species represent a variety of contrasting life histories, allowing a comparison of length-based approaches across a range of biological and ecological characteristics. Therefore, they exhibit a range of growth rates, maturity patterns, and natural mortality rates, chosen because they are familiar to the authors and are not intended to represent specific stocks. The species were sprat (Prattus sprattus sprattus), turbot (Posetta maxima), pollack (Pollachius pollachius), bigeye tuna (Thunnus obesus), and thornback ray (Raja clavata). Life history parameters were obtained from FishBase (www.fishbase.org), and Figure 2 provides a summary of $L_{\infty }$, k, $L_{50}$, and b; species are organized according to k. The bottom right panel illustrates the relative number of observations. Interspecific and intraspecific relationships are apparent, for example, $L_{\infty }$ shows an inverse correlation with k and $L_{50}$. A significant variation is observed in the condition factor of the length-weight relationship (b) for sprat. There are limited observations for pollack, indicating a high degree of uncertainty attributable to the reliance on FishBase data, which are often characterized by small sample sizes, restricted coverage, and the potential for life history parameters (such as maturity and growth) to be derived from different studies.

Natural mortality by age was based on length [27], and Spawning Stock Biomass (SSB) was used as an indicator of a stock’s reproductive capability [28], assuming that fertilization depends on the mass of sexually mature individuals, regardless of the age structure of the adult population [29], and that factors like sexual maturity are age-dependent and unaffected by sex [30].

2.1.3. Fishery Dynamics

A double normal distribution modeled selectivity, allowing the simulation of asymptotic or dome-shaped selectivity. In the reference scenario, logistic selectivity was designed in accordance with the maturity ogive, ensuring that MSY reference points are consistent across various case studies.

The Operating Model Reference Cases for each species are summarized in Figure 3. The fishing pressure is initially low before increasing to twice $F_{MSY}$, management then reduces the fishing to 70% of $F_{MSY}$; ribbons indicate the 95th percentile range along with the median and example Monte Carlo realizations.

2.2. Observation Error Model

Methods based on length can be biased with low precision due to uncertain life history parameters, time-lags in exploitation rates, shifts in fishery selection patterns, fluctuations in year-class strength, and non-random sampling. An observation error model was, therefore, used to generate pseudo-data with alternative characteristics.

A main source of variability in fish populations is the length at a given age; therefore, length data were generated using a Monte Carlo simulation to allow the evaluation of issues related to bias and the level of sampling. However, there is no consensus on how it should be modeled, e.g., as constant at length (standard deviation) or proportional to length (coefficient of variation), how it changes with age (constant, linear, or functional form), or even the shape of the distribution for a given age [31]. It may also vary by life history, being less variable for fast-growing tuna than for short-lived species such as sprat. The length-based methods tested in this study [21,22] assume a value of 10%, which has also been assumed in previous simulation studies (e.g., [20]). To generate size data, an inverse age-length key was applied to the catch-at-age generated by the Operating Model. Variations in length-at-age were incorporated by applying a normal distribution to the anticipated length-at-age with a coefficient of variation (CV) of 10%. The sampling was carried out proportionally to the appearance of an age class for a specified sample size.

2.3. Length-Based Approaches

Length-based methods range from simple empirical indicators, such as mean length, to more complex models that incorporate biological and fisheries information to estimate fishing mortality and reference points.

2.3.1. Indicators

The length-based indicator considered was $L_{mean}$, the mean length of the individuals greater than the length at 50% of the modal abundance (>$L_{c50}$). The key parameters are $L_c$, the length at which the fish are first vulnerable to capture by the fishing gear and $L_{\infty }$. The population is assumed to be in equilibrium, which means that the recruitment, growth, and mortality rates are constant over time. $L_{mean}$ can be used to evaluate exploitation relative to a proxy for $F_{MSY}$, such as the length at which fishing mortality is equal to natural mortality ($L_{F=M}$).

A single realization of the Reference Case is shown in Figure 4 by species. The length frequencies are pooled by lustrum (5 years); the vertical line is $L_{mean}$ (see below). There are differences in the length frequency distributions before overfishing (year 60), the right-hand limbs contain larger individuals than under overfishing (year 100); although the biomass recovers when fishing pressure is reduced, the size structure does not recover (year 120).

2.3.2. Beverton and Holt Estimator

The Beverton and Holt Z estimator estimates the total instantaneous mortality rate (Z) based on the relationship between the length of fish that have been recruited to the fishery and mortality and assumes that growth follows the von Bertalanffy growth function [32].

$$Z={\displaystyle \frac{k(L_{\infty }-\overline{L})}{(\overline{L}-L^{\prime })}}$$

where Z is the total instantaneous mortality rate, and $\overline{L}$ is the mean length of the fish in the catch above $L^{\prime }$, the length at which the fish are fully recruited into the fishing. It is assumed that the population is in equilibrium, that the selection for the fishery is knife-edged, and that mortality is constant for all fully recruited fish.

2.3.3. Length-Converted Catch Curve (LCC)

Instantaneous total mortality (Z) can be estimated using length-converted catch curve analysis (LCC, [33]). This assumes that as fish age, their growth rate decreases, causing larger size categories to include more age groups compared to smaller ones, a phenomenon referred to as the “stack-up” effect, thereby resulting in broader age ranges in larger size categories than in smaller ones.

2.3.4. Length-Based SPR (LBSPR)

LBSPR is based on equilibrium assumptions, including asymptotic selectivity, the von Bertalanffy growth model, normally distributed length-at-age, constant natural mortality across adult age groups, stable recruitment over time, and unchanging growth rates across different cohorts. LBSPR estimates the selectivity parameters and the ratio of fishing mortality to natural mortality ($F/M$) by maximizing the probability [22]. The method estimates fishing mortality (F), with natural mortality (M) fixed. The spawning potential ratio (SPR) is also estimated and is the fraction of the reproductive potential that remains unfished per recruit, based on a specific F, derived from the length composition of the catch and biological data.

Selectivity is assumed to be logistic, defined by $S_{50}$ and $S_{95}$, the sizes at which 50% and 95% of a population are retained by the fishing gear. The maturity ogive is specified by $L_{50}$ and $L_{95}$. Therefore, the inputs are the selectivity, maturity ogive and life history ratios $M/k$ and $L_m/L_{\infty }$; where k is the von Bertalanffy growth coefficient, $L_{\infty }$ is the asymptotic size and $L_m$ is the size at maturity [34].

2.3.5. Length-Based Integrated Mixed Effects (LIME)

LIME provides estimates of F and SPR from length data and biological information, but does not assume equilibrium conditions. LIME estimates changes in recruitment and fishing mortality over time, using automatic differentiation and Laplace approximations to calculate the marginal likelihood of mixed effects [21]. LIME estimates a single selectivity curve for the entire time series, while LBSPR estimates a selectivity curve for each year, since each time step in LBSPR is independent of the other.

Other assumptions are the same as for LBSPR and the inputs to LIME are $M, k, L_{\infty }, t_0,$$\mathrm{CV}{L}_{\infty }, L_{50}, L_{95}$, steepness (h) and the parameters of the length-weight relationship (a and b). In the simulations, we estimate F and $SPR$ for 3-year blocks to reduce the computation time.

Proxy Reference Points

In data-limited cases, natural mortality (M) is commonly used as a proxy for $F_{MSY}$, the fishing mortality that will achieve the maximum sustainable yield [35]. Alternatively, $L_{opt}$, the length at which a cohort achieves its maximum biomass, approximated by $2/3L_{\infty }$, can be used as a proxy for $F_{MSY}$ [36]. An advantage of using length is that it is an observable quantity, while M is difficult to estimate even in data-rich assessments [37].

Baselines

An alternative to proxy reference points based on assumptions about M is to use a historical reference period. Therefore, the classification skill was evaluated for a reference period, years 79 to 81, when the fishing mortality was at $F_{MSY}$.

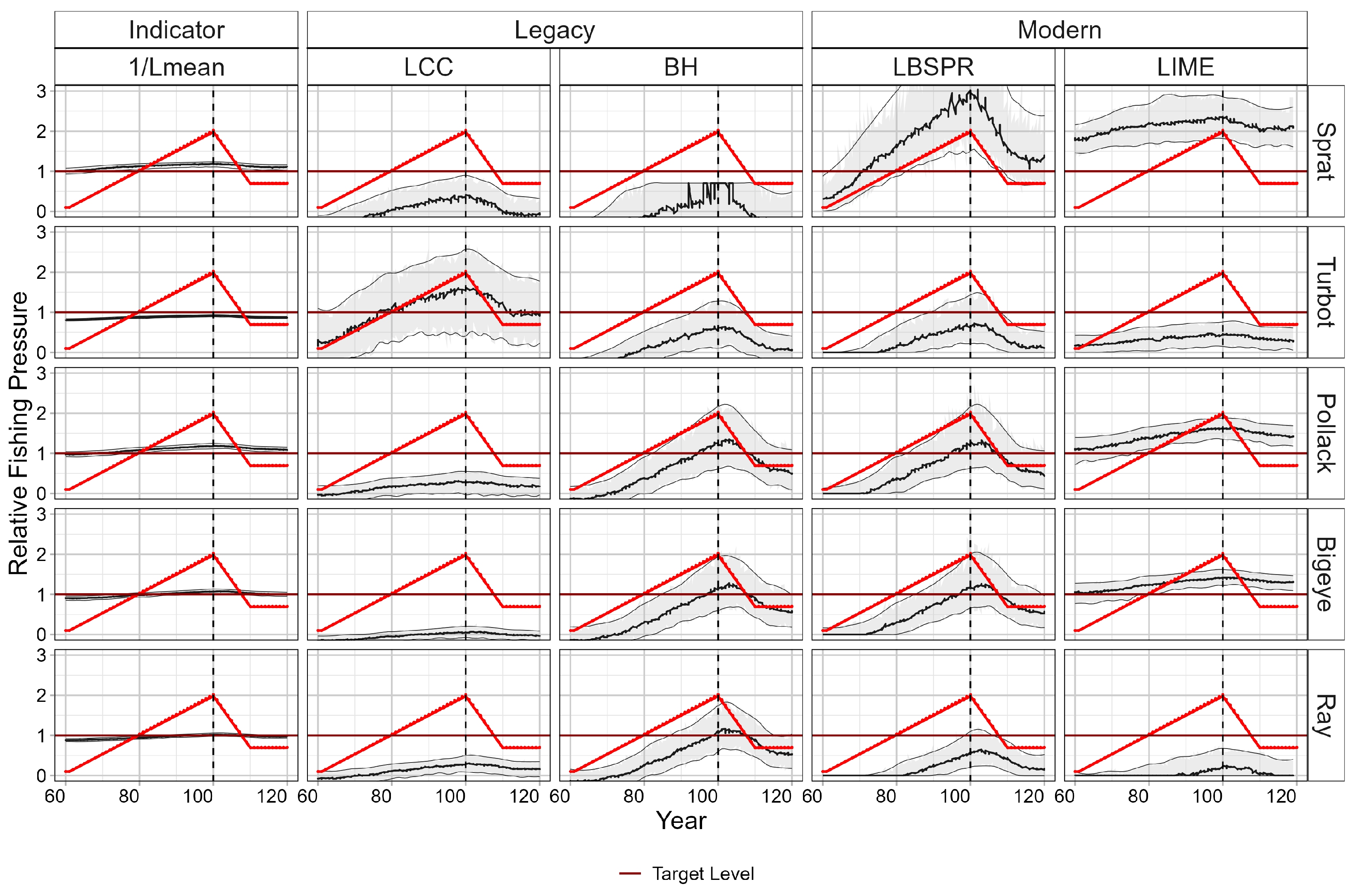
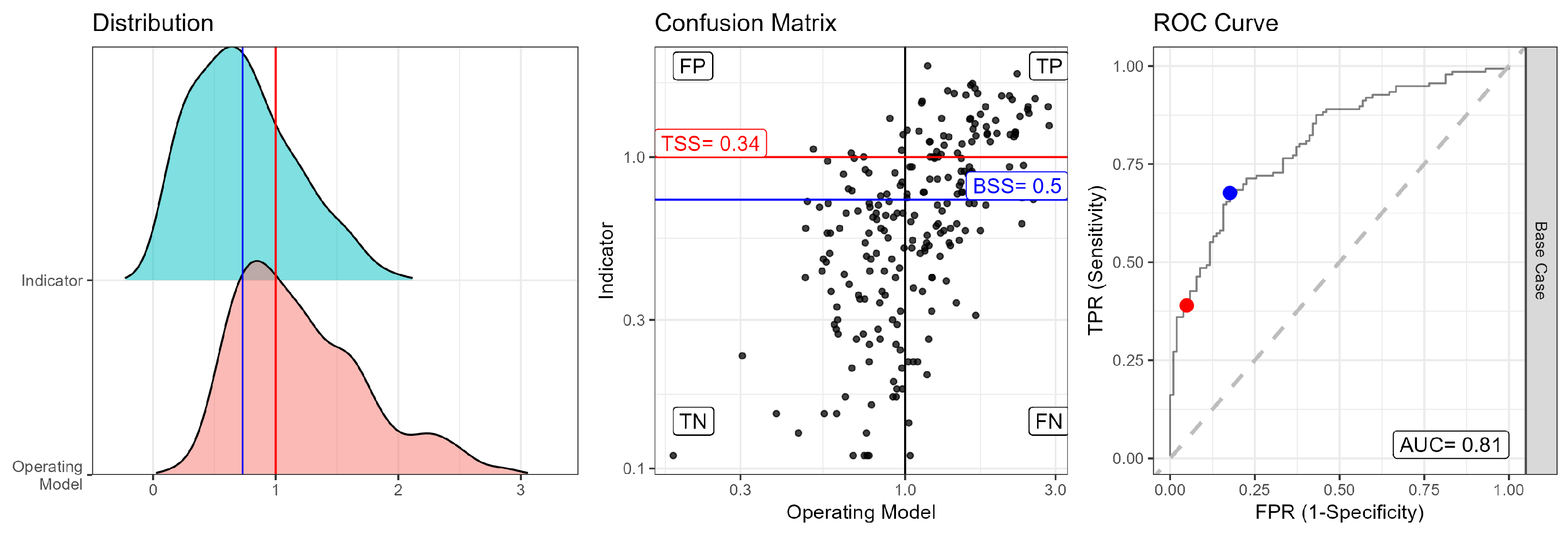
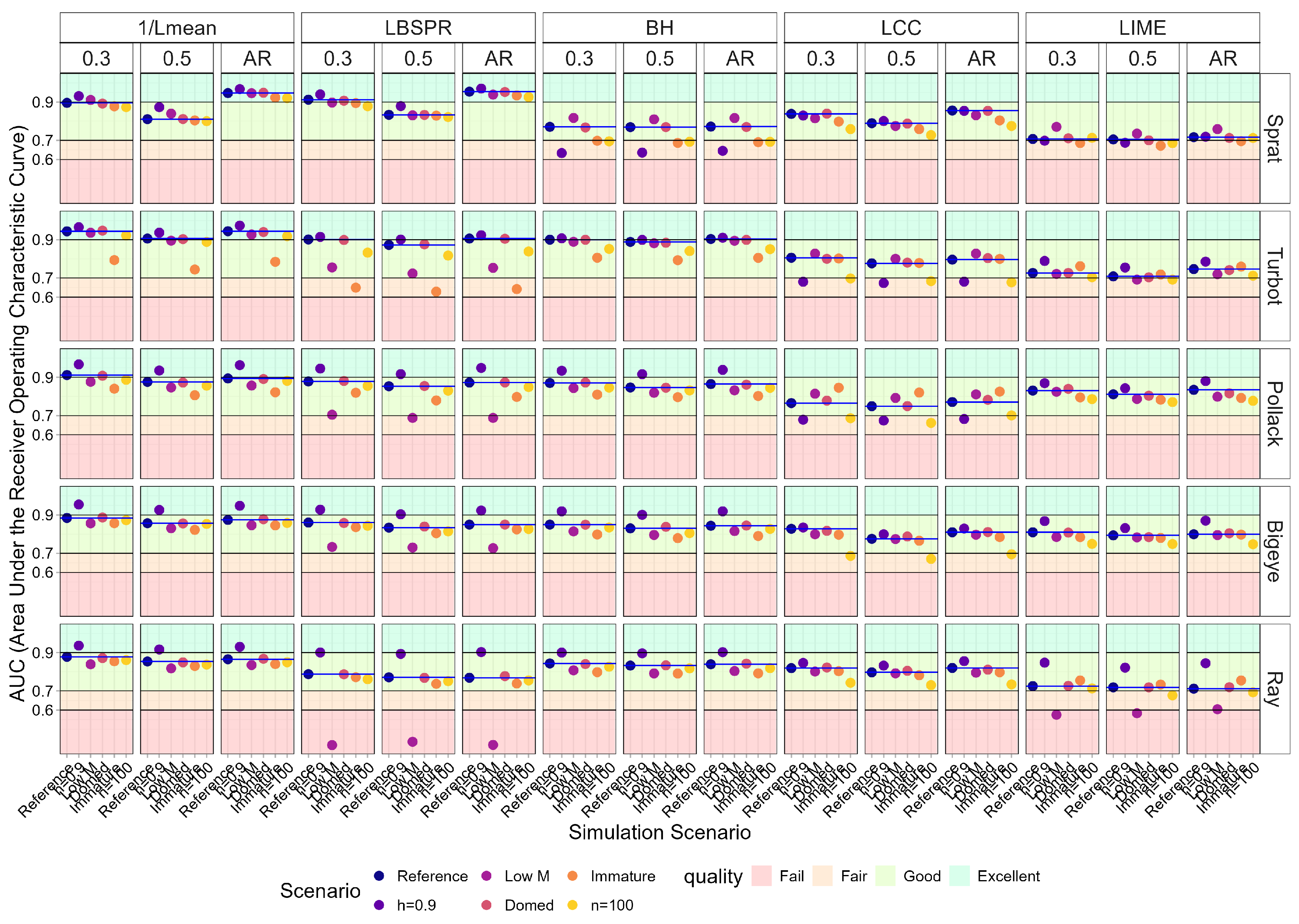
3. Results

The indicator ($L_{mean}$), the two legacy methods (LCC and BH), and the modern, more complex methods (LBSPR and LIME), are compared in Figure 5 for the Reference Case by species; the dashed line is the Operating Model values of $F/F_{MSY}$ and the ribbons the 95th percentiles. All approaches follow trends in F, although species- and method-specific bias is apparent. $L_{mean}$ exhibits hyperstability, not showing the same level of variation as the Operating Model, and BH fails for sprat at higher F levels.

The different length-based approaches were validated by comparing their skill in classifying fishing mortality relative to $F/F\left[MSY\right]$. As an example, the LBSPR estimates from the Reference Case are summarized in Figure 6. The first panel shows the distributions of $F/F_{MSY}$ from LBSPR (i.e., the indicator) and the Operating Model; the indicator is biased as it underestimates the Operating Model values. The classification skill is assessed by comparing the estimates with the Operating Model, in the form of the confusion matrix, which summarizes the number of true positives (TP), false positives (FP), true negatives (TN) and false negatives (FN). The ability to identify positive and negative cases is measured by the indicators sensitivity ($TPR={\displaystyle \frac{TP}{TP+FN}}$) and specificity ($TNR={\displaystyle \frac{TN}{TN+FP}}$), respectively. An ideal indicator would have sensitivity and specificity equal to 1. Receiver operating characteristic (ROC) curves plot the TPR against the false positive rate ($FPR=1-TNR$). A perfect indicator would correctly classify all cases ($TPR=1$ and $FPR=0$). Therefore, the area under the ROC curve (AUC) quantifies the classification skill; a perfect classifier would have an AUC of 1 and a random classifier 0.5. An ROC curve can be used for calibration to correct bias in reference levels, since the best discriminant threshold is the point with the shortest Euclidean distance to $(TPR=1,FPR=0)$; the red dot shows the classification skill of the proxy reference point $F_{MSY}$ and the blue dot the best value obtained by calibration. Calibration improves the best skill score (BSS) from 0.34 to 0.5.

The skill and robustness of the length-based approaches are summarized using the AUCs by approach, species, and scenario in Figure 7. A value of 0.5 is equivalent to a coin toss, and values close to 1 indicate excellent skill (

Table 2. Summary of Operating Model Scenarios with Reference Case values highlighted. This table outlines the key parameters and assumptions used in the Operating Model to simulate different fishery management scenarios.

Parameter	Values
Steepness (H)	0.7 (Reference Case), 0.8, 0.9
Recruitment Variability	Low, Medium, High
Natural Mortality (M)	0.2, 0.25, 0.3
Selectivity	Shifted, Logistic, Domed
Sample Size	50, 100, 150

), and the length-based approaches are ranked (left to right) by their median AUCs. $1/L_{mean}$ and LBSPR performed the best, and LIME the worst. This is particularly true for species with higher individual growth rates (k).

The scenarios represent a robustness test, as the length-based approach settings are based on the Reference Case. High steepness and low M improve performance even when M, a required input assumption for LIME and LBSPR, is misspecified. Although M is used as a proxy for $F_{MSY}$, this changes the reference level, and therefore, does not affect the AUC. Recruitment variability has an impact and increasing the CV reduces it, while auto-correlated errors improve classification skill.

The AUCs were used to screen and select the best-performing approaches. The methods with the best AUCs are $L_{mean}$ and LBSPR and were selected for the following analysis, and their TSS is summarized in Figure 8 and

Table 3. AUC and TSS Categories.

AUC Categories
Quality	Range
Fail	$(0,0.6)$
Fair	$[0.6,0.7)$
Good	$[0.7,0.9)$
Excellent	$[0.9,1.0)$
TSS Categories
Quality	Range
Negative	$(-1.0,0.0)$
None	$[0.0,0.2)$
Low	$[0.2,0.4)$
Moderate	$[0.4,0.6)$
High	$[0.6,1.0)$

). Four options are available to provide advice: (i) use a proxy for $F_{MSY}$ based on M, (ii) calibration by determining the best reference level, (iii) use a reference period where the stock was considered healthy, or (iv) evaluate trends/Trends derived from year-to-year changes in the five-year running mean to identify directional trends while reducing noise.

The performance of the proxies was poor, even when the assumptions were met (i.e., in the Reference Case). For sprat $L_{mean}$ only performed well if M was low, and there were more older individuals in the population; the performance was better for the LBSPR Reference Case. For turbot, $L_{mean}$ had at best moderate skill when immature individuals were caught and LBSPR if the steepness was equal to 0.9. When calibration was used to set the best reference level, performance improved. Performance was scenario-specific and species-specific, and so it is difficult to draw general conclusions about how to choose defaults and specify proxy reference points. The scenario had an effect, and low M and high steepness improved TSS, and fishing on immature individuals reduced TSS. Of the scenarios, fishing on immatures had a negative effect on turbot, but low M only affected ray. Calibration is likely to be difficult for data-poor stocks, where agreeing and weighting the plausibility of scenarios will be difficult. An easier option if historical data are available is to use a reference period, in which case performance across scenarios and life histories is similar to calibration.

An alternative to assessing state (relative to a proxy reference point, a calibrated reference level, or a historical period) is to assess trend, i.e., year-on-year changes. This performs better, is less affected by the choice of scenario, and is robust to uncertainty.

4. Discussion

Stock assessment has been criticized for the use of overly complex models that rely on poorly constrained parameters or arbitrary assumptions [38], and simpler models have been proposed as alternatives [39]. For example, length-based approaches are increasingly being used to assess and manage data- and capacity-limited fisheries. The performance of stock assessment models must be validated against independent observations rather than model outputs alone [7]. Therefore, this study used a simulation framework to validate length-based approaches using an Operating Model. None of the methods provided robust estimates of $F_{MSY}$ for the scenarios evaluated. The classification skill was highest compared to a baseline reference period in which the health of the stock was known. In particular, LIME, even though it did not assume equilibrium conditions, exhibited the least reliable performance. These findings support the argument that an increase in model complexity does not necessarily translate into improved reliability or robustness.

Guidelines for length-based methods often emphasize the importance of ensuring that older fish are vulnerable to capture. However, length frequency distributions are influenced by multiple factors beyond the selection pattern, including the steepness of the stock-recruitment relationship and whether a population is declining or recovering. In depleted populations where recruitment potential is reduced (i.e., for low steepness), the absence of recruits (i.e., smaller fish) can be misinterpreted as reduced exploitation. Even when selection pattern assumptions are violated (is dome-shaped), trends can still be detected relative to a baseline. A challenge lies in accounting for shifts in spatial or temporal distribution that alter vulnerability to capture. Standardizing length-frequency data to mitigate potential biases introduced by such changes is essential for robust assessments.

It is crucial to distinguish between the reference points used for performance evaluation (e.g., $F_{MSY}$ proxies) and control points that define management actions (e.g., as part of a harvest control rule). Proxy reference points based on assumed natural mortality (M) may introduce bias if M is poorly estimated. Instead, using historical reference periods, when stocks were at desirable levels, can provide more reliable benchmarks for management [40]. Empirical harvest control rules based on observable trends (e.g., mean size or relative abundance) are often easier for managers and stakeholders to understand compared to model-based rules. However, both approaches should be rigorously tested as a Management Procedure using Management Strategy Evaluation to ensure robustness under uncertainty.

There are three main components to consider when developing robust harvest control rules, namely state, trend, and variability or entropy. The state component provides an immediate response to current stock conditions, e.g., based on trigger reference points, enabling prompt management action. The trend component measures the rate of change, allowing the incorporation of recruitment trends or environmental changes into management decisions. Entropy reflects how controllable a stock is; for example, stocks with high natural mortality and recruitment variability are inherently less controllable than long-lived species with more stable age structures, and incorporating this component into a harvest control rule allows signal and noise to be balanced. Harvest control rules can integrate these three components based on either model-based estimates or empirical indicators, for instance, by weighting state and trend indicators based on the AUC and calibrating control points by maximizing the True Skill Statistic. This is analogous to PID (Proportional-Integral-Derivative) controllers in control theory, which offer a flexible and adaptive framework for fisheries management [41,42].

5. Conclusions

Length-based approaches offer potential for assessing and managing data-limited fisheries. However, the results of this study demonstrate that these methods face significant challenges in providing robust estimates of fishing mortality F relative to $F_{MSY}$. The use of historical reference periods, where the health of the stock is known, was found to be more reliable than relying on proxies based on uncertain parameters such as natural mortality. Simple indicators, such as the mean length ($L_{mean}$), often outperformed more complex methods like LIME, especially in scenarios where key assumptions about resource dynamics were violated. This highlights that increasing the complexity of the model does not necessarily improve performance, and the careful selection of assessment methods that are tailored to the specific characteristics of each fishery is essential. In particular, a large bias can result from misspecification of M and selection pattern, which were species- and scenario-specific. Therefore, length-frequency data should be standardized to account for potential spatial or temporal shifts in stocks and fisheries.

The validation of length-based methods using Operating Models allows testing for a range of plausible scenarios (i.e., it is probable based on the available evidence and is logically coherent) and uncertainties that have a significant impact on the performance to ensure robustness before real-world application. Integrating length-based approaches with complementary methods, such as catch-only methods, could further improve the performance of data-limited assessments. The Operating Models applied here can also be used to develop harvest control rules, enabling the design and testing of management strategies. Ultimately, the success of length-based methods will depend on their alignment with fishery-specific needs and on maintaining transparency and simplicity in scientific advice. By addressing these considerations, method selection, data standardization, robust validation, and integration with other approaches, length-based methods can play a critical role in achieving sustainable fisheries management in data- and capacity-limited contexts.