Dependency and Risk Spillover of China’s Industrial Structure Under the Environmental, Social, and Governance Sustainable Development Framework
Abstract
1. Introduction
2. Literature Review
3. Materials and Methods
3.1. Study Area and Data Sources
3.2. Data Processing
3.3. Descriptive Statistics
3.4. Methodology
3.4.1. ARMA-eGARCH-Skew t Model
3.4.2. Copula
3.4.3. Vine Copula
3.4.4. Tail Dependence Based on Vine Copula
3.4.5. CoVaR Method for Risk Spillover Analysis
4. Result
4.1. Marginal Distribution
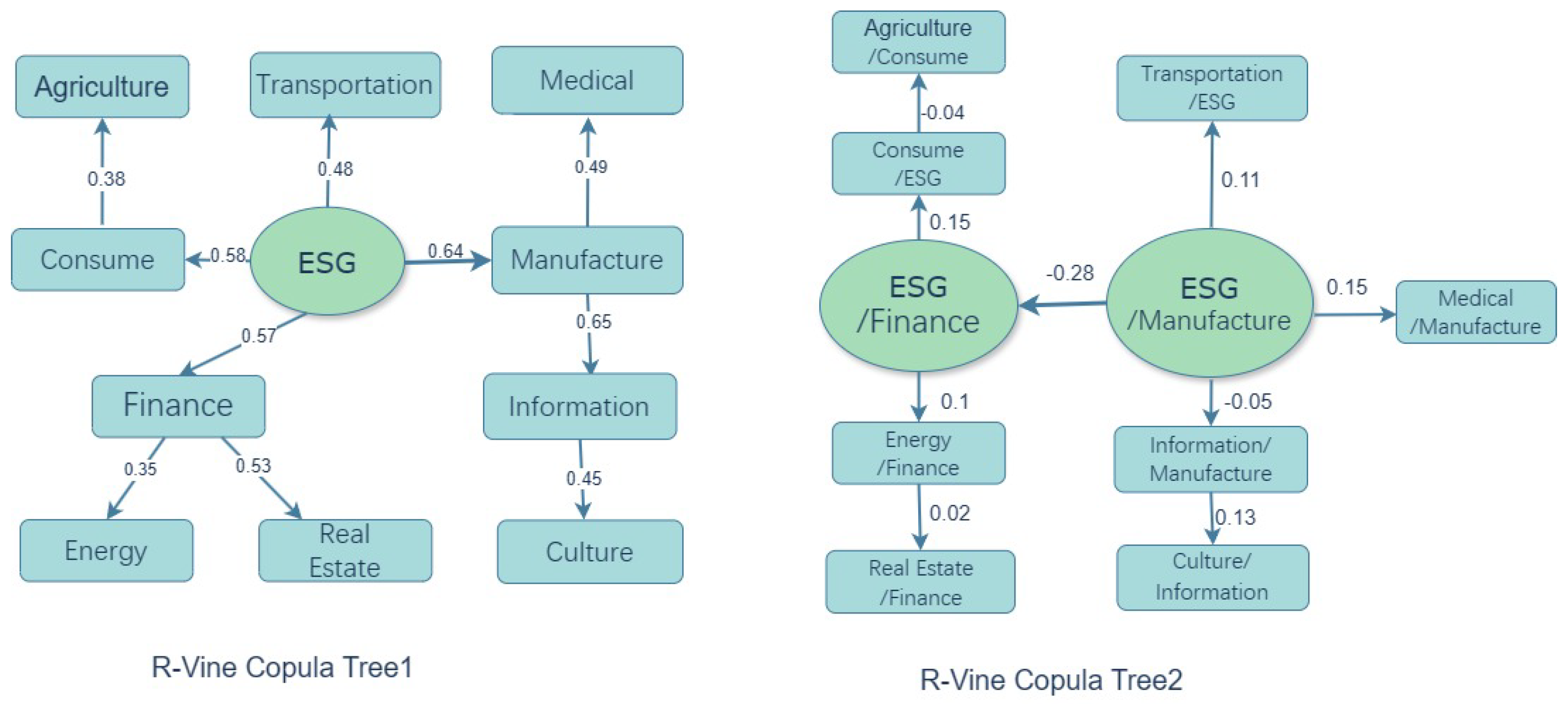
4.2. Vine Copula
4.3. Tail Dependency
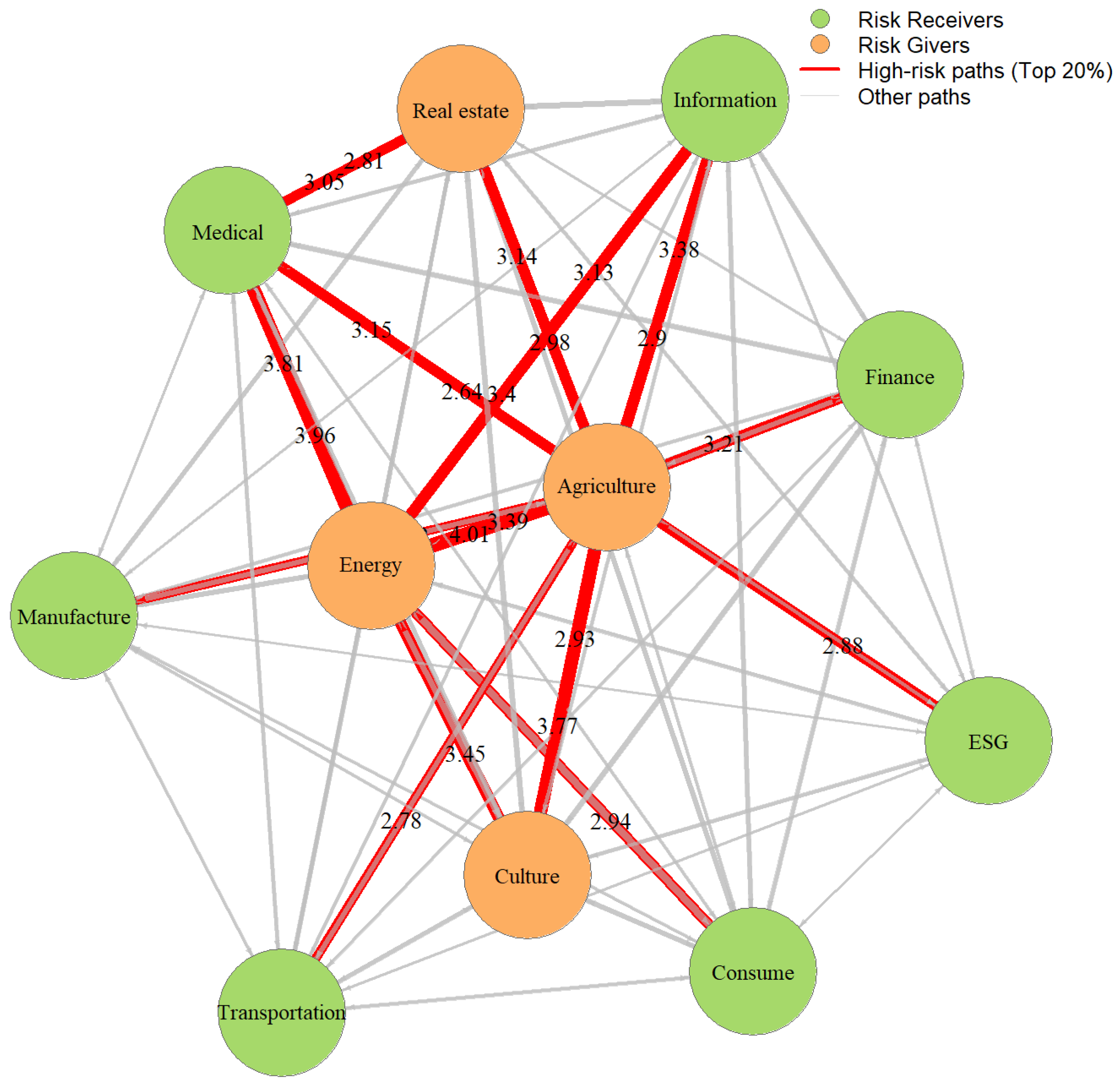
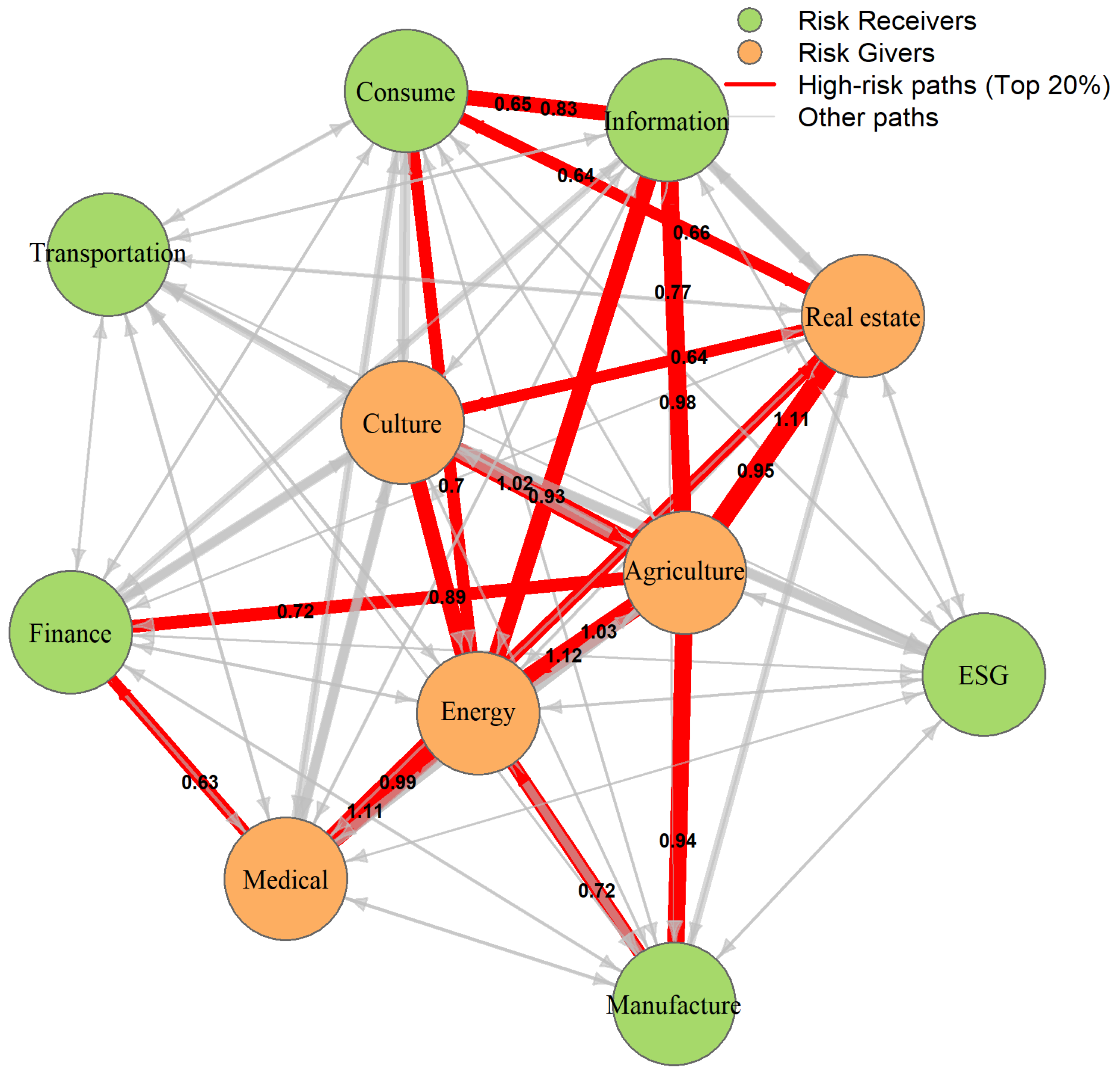
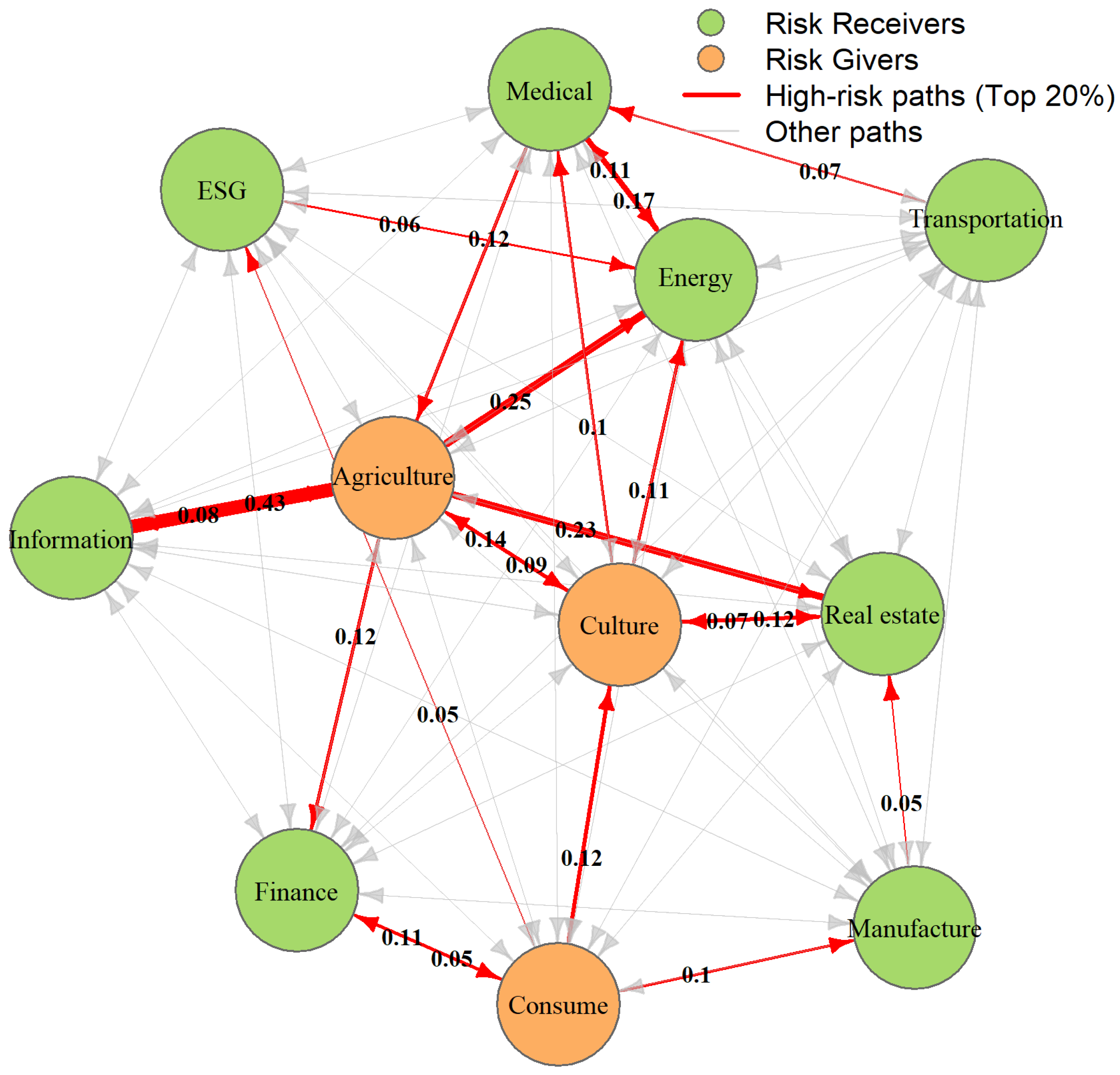
4.4. Risk Spillover Analysis by CoVaR
4.4.1. VaR Analysis
4.4.2. CoVaR Analysis
4.5. Robustness Check Based on Confidence Levels
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Alharbi, F. The Impact of ESG Reforms on Economic Growth in GCC Countries: The Role of Financial Development. Sustainability 2024, 16, 11067. [Google Scholar] [CrossRef]
- Eccles, R.G.; Serafeim, G.; Seth, D.; Ming, C.C.Y. The Performance Frontier: Innovating for a Sustainable Strategy: Interaction. Harv. Bus. Rev. 2013, 91, 17–18. [Google Scholar]
- Wu, Y.; Ivashkovskaya, I.; Besstremyannaya, G.; Liu, C. Unlocking Green Innovation Potential Amidst Digital Transformation Challenges—The Evidence from ESG Transformation in China. Sustainability 2025, 17, 309. [Google Scholar] [CrossRef]
- Liu, Z.; Deng, Z.; He, G.; Wang, H.; Zhang, X.; Lin, J.; Liang, X. Challenges and opportunities for carbon neutrality in China. Nat. Rev. Earth Environ. 2022, 3, 141–155. [Google Scholar] [CrossRef]
- Liu, Z.; Zhou, Q. The Pressure of Carbon Loss in Industrial Upgrading: Pathways and Challenges of Low-Carbon Transition in China’s Manufacturing Sector. Law Econ. 2024, 3, 54–64. [Google Scholar] [CrossRef]
- Traverso, M. ESG and Systemic Risk, the Mitigation Effect of ESG on Systemic Risk Using a Network Approach. 2024. Available online: https://unitesi.unive.it/handle/20.500.14247/23123 (accessed on 21 October 2024).
- Chong, Z.L. Environmental, Social and Governance (ESG) Practices in Construction Supply Chain Organisations: A Comparison of Organisational Practices and Cognitive Perceptions of Industrial Practitioners. Ph.D. Thesis, UTAR, Petaling Jaya, Malaysia, 2024. [Google Scholar]
- Kotsantonis, S.; Serafeim, G. Four things no one will tell you about ESG data. J. Appl. Corp. Financ. 2019, 31, 50–58. [Google Scholar] [CrossRef]
- Scholtens, B. Why finance should care about ecology. Trends Ecol. Evol. 2017, 32, 500–505. [Google Scholar] [CrossRef]
- Cruz, C. The Impact of ESG Policies on Macroeconomic Volatility. Int. Rev. Econ. Financ. 2019, 64, 12–25. [Google Scholar]
- Wei, J.; Hu, R.; Chen, F. The Path to Sustainable Stability: Can ESG Investing Mitigate the Spillover Effects of Risk in China’s Financial Markets? Sustainability 2024, 16, 10316. [Google Scholar] [CrossRef]
- Wang, X.; Wu, H.; Shen, Y.; Wang, T. Towards Sustainable Supply Chains: Evaluating the Role of Supply Chain Diversification in Enhancing Corporate ESG Performance. Systems 2025, 13, 266. [Google Scholar] [CrossRef]
- Fourgon, Y. The Global Impact of Mandatory ESG Disclosure on the Cost of Capital: A Comparative Analysis Across Legal Regimes. 2024. Available online: https://matheo.uliege.be/bitstream/2268.2/19920/4/23%20Master%20Thesis%20-%20Fourgon%20Ysaline.pdf (accessed on 25 July 2024).
- Lins, K.V.; Servaes, H.; Tamayo, A. Social capital, trust, and firm performance: The value of corporate social responsibility during the financial crisis. J. Financ. 2017, 72, 1785–1824. [Google Scholar] [CrossRef]
- Kramer, M.R.; Porter, M. Creating Shared Value; FSG: Boston, MA, USA, 2011; Volume 17. [Google Scholar]
- Liu, L. Impact of firm ESG performance on cost of debt: Insights from the Chinese Bond Market. Macroecon. Financ. Emerg. Mark. Econ. 2024, 1–20. [Google Scholar] [CrossRef]
- Lööf, H.; Sahamkhadam, M.; Stephan, A. Incorporating ESG into optimal stock portfolios for the global timber & forestry industry. J. For. Econ. 2023, 38, 133–157. [Google Scholar]
- Dong, F.; Li, Z.; Huang, Z.; Liu, Y. Extreme weather, policy uncertainty, and risk spillovers between energy, financial, and carbon markets. Energy Econ. 2024, 137, 107761. [Google Scholar] [CrossRef]
- Sklar, M. Fonctions de répartition à n dimensions et leurs marges. Ann. l’ISUP 1959, 8, 229–231. [Google Scholar]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; CRC Press: Boca Raton, FL, USA, 1997. [Google Scholar]
- Embrechts, P. Correlation and Dependence in Risk Management: Properties and Pitfalls. In Risk Management: Value at Risk and Beyond; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Bedford, T.; Cooke, R.M. Probability density decomposition for conditionally dependent random variables modeled by vines. Ann. Math. Artif. Intell. 2001, 32, 245–268. [Google Scholar] [CrossRef]
- Czado, C.; Bax, K.; Sahin, Ö.; Nagler, T.; Min, A.; Paterlini, S. Vine copula based dependence modeling in sustainable finance. J. Financ. Data Sci. 2022, 8, 309–330. [Google Scholar] [CrossRef]
- Tobias, A.; Brunnermeier, M.K. CoVaR. Am. Econ. Rev. 2016, 106, 1705. [Google Scholar]
- Demartis, S.; Rogo, B. The Relationship Between ESG Scores and Value-at-Risk: A Vine Copula–GARCH Based Approach. J. Risk Financ. Manag. 2024, 17, 517. [Google Scholar] [CrossRef]
- Thornqvist, V. Effects of ESG on Market Risk: A Copula and a Regression Approach to CoVaR. 2023. Available online: https://www.diva-portal.org/smash/record.jsf?pid=diva2:1765155 (accessed on 13 June 2023).
- Bollerslev, T. Generalized Autoregressive Conditional Heteroskedasticity. J. Econom. 1986, 31, 307–327. [Google Scholar] [CrossRef]
- Nelson, D.B. Conditional heteroskedasticity in asset returns: A new approach. Econom. J. Econom. Soc. 1991, 59, 347–370. [Google Scholar] [CrossRef]
- Joe, H. Dependence Modeling with Copulas; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Trivedi, P.K.; Zimmer, D.M. Copula modeling: An introduction for practitioners. Found. Trends Econom. 2007, 1, 1–111. [Google Scholar] [CrossRef]
- Genest, C.; MacKay, J. The Joy of Copulas: Bivariate Distributions with Uniform Marginals. Am. Stat. 1986, 40, 280–283. [Google Scholar] [CrossRef]
- Song, Y.; Ori-McKenney, K.M.; Zheng, Y.; Han, C.; Jan, L.Y. Regeneration of Drosophila sensory neuron axons and dendrites is regulated by the Akt pathway involving Pten and microRNA bantam. Genes Dev. 2012, 26, 1612–1625. [Google Scholar] [CrossRef]
- Demarta, S.; McNeil, A.J. The t copula and related copulas. Int. Stat. Rev. 2005, 73, 111–129. [Google Scholar] [CrossRef]
- Gudendorf, G.; Segers, J. Extreme-value copulas. In Copula Theory and Its Applications, Proceedings of the Workshop, Warsaw, Poland, 25–26 September 2009; Springer: Berlin/Heidelberg, Germany, 2010; pp. 127–145. [Google Scholar]
- Salvadori, A.; Gray, L.J. Analytical integrations and SIFs computation in 2D fracture mechanics. Int. J. Numer. Methods Eng. 2007, 70, 445–495. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Nelsen, R.B. An Introduction to Copulas, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Diebold, F.X.; Yilmaz, K. Better to give than to receive: Predictive directional measurement of volatility spillovers. Int. J. Forecast. 2012, 28, 57–66. [Google Scholar] [CrossRef]
- Afzal, F.; Pan, H.; Afzal, F.; Gul, R.F. Analyzing risk contagion and volatility spillover across multi-market capital flow using EVT theory and C-vine Copula. Heliyon 2024, 10, e39918. [Google Scholar] [CrossRef]



| Variable Name | Definition | Construction Method | Code |
|---|---|---|---|
| ESG | CSI 300 ESG Index | Select top 80% companies by ESG score among CSI 300 constituents | 931463 |
| Energy | Energy Sector Index | Free-float market-cap weighted index of energy companies | 399928 |
| Manufacturing | Manufacturing Sector Index | Composite index of industrial and capital goods manufacturers | 399233 |
| Finance | Financial Sector Index | Weighted average of banks (60%), insurers (25%), and securities (15%) | 399934 |
| Real Estate | Real Estate Sector Index | Index of companies in real estate development and operations | 399241 |
| Consumption | Consumer Goods Sector Index | Index tracking consumer discretionary and staple goods sectors | 399932 |
| Agriculture | Agriculture Sector Index | Firms involved in farming, forestry, fisheries, and agribusiness | 399231 |
| Medical | Medical and Healthcare Sector Index | Medical services, pharmaceuticals, biotech, and healthcare equipment | 399989 |
| Transportation | Transportation Sector Index | Logistics, passenger, and freight transportation companies | 399237 |
| Information | Information Technology Sector Index | Software, hardware, telecom, and digital services companies | 399935 |
| Culture | Cultural Media Sector Index | Media, entertainment, publishing, and cultural service companies | 399248 |
| Industries | Mean | SD | Skewness | Kurtosis | JB | ADF | LB |
|---|---|---|---|---|---|---|---|
| ESG | 0.012 | 1.214 | −0.529 | 4.408 | 0.001 | 0.01 | 0.77 |
| Energy | 0.053 | 1.618 | −0.184 | 2.295 | 0.001 | 0.01 | 0.011 |
| Manufacturing | 0.033 | 1.447 | −0.503 | 2.790 | 0.001 | 0.01 | 0.47 |
| Finance | −0.003 | 1.307 | 0.333 | 4.449 | 0.001 | 0.01 | 0.37 |
| Real estate | −0.052 | 1.786 | 0.361 | 2.919 | 0.001 | 0.01 | 0.118 |
| Consumption | 0.037 | 1.541 | −0.157 | 2.046 | 0.001 | 0.01 | 0.963 |
| Agriculture | 0.012 | 1.980 | 0.153 | 1.997 | 0.001 | 0.01 | 0.051 |
| Medical | 0.000 | 1.805 | 0.022 | 1.201 | 0.001 | 0.01 | 0.057 |
| Transportation | 0.001 | 1.487 | −0.061 | 2.422 | 0.001 | 0.01 | 0.204 |
| Information | 0.017 | 1.813 | −0.260 | 1.808 | 0.001 | 0.01 | 0.455 |
| Culture | −0.017 | 2.032 | −0.199 | 1.188 | 0.001 | 0.01 | 0.872 |
| Family | Copula Name | Function | Range |
|---|---|---|---|
| Elliptical | Student-t | ||
| Normal | |||
| Archimedean | Clayton | ||
| Frank | |||
| Joe | |||
| Extreme | Gumbel | ||
| Galambos | |||
| Husler–Reiss |
| Industries | Skew | Shape | LLH | LB | ARCH-LM | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| ESG | −0.010 | 0.009 | −0.033 | 0.966 | 0.160 | 0.980 | 6.315 | −2024.173 | 0.173 | 0.466 |
| Energy | 0.059 | 0.011 | 0.051 | 0.988 | 0.104 | 1.028 | 5.515 | −2391.513 | 0.442 | 0.390 |
| Manufacturing | 0.006 | 0.029 | −0.056 | 0.954 | 0.194 | 0.899 | 9.273 | −2281.310 | 0.068 | 0.899 |
| Finance | −0.007 | 0.020 | 0.010 | 0.961 | 0.126 | 1.143 | 4.239 | −2123.317 | 0.467 | 0.585 |
| Real estate | −0.048 | 0.026 | −0.020 | 0.977 | 0.173 | 1.186 | 4.636 | −2520.924 | 0.089 | 0.109 |
| Consumption | −0.007 | 0.014 | −0.022 | 0.982 | 0.113 | 1.031 | 6.504 | −2391.001 | 0.117 | 0.158 |
| Agriculture | 0.009 | 0.015 | 0.016 | 0.988 | 0.095 | 1.129 | 5.888 | −2696.581 | 0.179 | 0.306 |
| Medical | −0.023 | 0.026 | −0.017 | 0.976 | 0.136 | 1.044 | 12.318 | −2618.876 | 0.123 | 0.526 |
| Transportation | −0.014 | 0.026 | −0.028 | 0.966 | 0.128 | 1.041 | 5.491 | −2333.950 | 0.385 | 0.795 |
| Information | −0.003 | 0.031 | −0.003 | 0.973 | 0.124 | 0.985 | 11.362 | −2625.459 | 0.753 | 0.148 |
| Culture | −0.034 | 0.037 | −0.010 | 0.973 | 0.151 | 0.942 | 12.501 | −2764.208 | 0.262 | 0.454 |
| Vine Copula | Edge | Copula | Para1 | Para2 | tau | Utd | Ltd |
|---|---|---|---|---|---|---|---|
| C-Vine Copula | ESG–Agriculture | SG | 1.4 | - | 0.29 | - | 0.36 |
| ESG–Transportation | SBB1 | 0.22 | 1.75 | 0.48 | 0.16 | 0.51 | |
| ESG–Medical | t | 0.69 | 12.57 | 0.49 | 0.14 | 0.14 | |
| ESG–Real Estate | SBB1 | 0.21 | 1.51 | 0.4 | 0.12 | 0.42 | |
| ESG–Energy | SBB1 | 0.14 | 1.39 | 0.33 | 0.03 | 0.48 | |
| ESG–Information | SBB1 | 0.37 | 1.65 | 0.49 | 0.33 | 0.48 | |
| ESG–Consumption | t | 0.8 | 24.97 | 0.59 | 0.52 | 0.52 | |
| ESG–Finance | BB1 | 0.6 | 1.78 | 0.57 | 0.52 | 0.52 | |
| ESG–Manufacturing | t | 0.85 | 8 | 0.65 | 0.41 | 0.41 | |
| ESG–Culture | SBB1 | 0.12 | 1.53 | 0.38 | 0.02 | 0.43 | |
| D-Vine Copula | Culture–Energy | SG | 1.11 | - | 0.18 | - | 0.23 |
| Energy–Real Estate | t | 0.41 | 5.13 | 0.27 | 0.16 | 0.16 | |
| Real Estate–Finance | SBB1 | 0.31 | 1.86 | 0.53 | 0.3 | 0.55 | |
| Finance–Transportation | SBB1 | 0.17 | 1.44 | 0.36 | 0.06 | 0.38 | |
| Transportation–Medical | t | 0.55 | 9.37 | 0.37 | 0.11 | 0.11 | |
| Medical–Information | SBB1 | 0.2 | 1.48 | 0.39 | 0.1 | 0.4 | |
| Information–Manufacturing | t | 0.85 | 7.24 | 0.65 | 0.44 | 0.44 | |
| Manufacture-ESG | t | 0.85 | 8 | 0.65 | 0.41 | 0.41 | |
| ESG–Consumption | t | 0.8 | 24.97 | 0.59 | 0.1 | 0.1 | |
| Consumption–Agriculture | SBB1 | 0.26 | 1.43 | 0.38 | 0.16 | 0.37 | |
| R-Vine Copula | ESG–Manufacturing | t | 0.85 | 8 | 0.64 | 0.41 | 0.41 |
| ESG–Finance | BB1 | 0.59 | 1.79 | 0.57 | 0.53 | 0.54 | |
| ESG–Consumption | t | 0.79 | 26.62 | 0.58 | 0.09 | 0.09 | |
| ESG–Transportation | Survival BB1 | 0.21 | 1.74 | 0.48 | 0.15 | 0.51 | |
| Manufacture–Information | t | 0.85 | 7.23 | 0.65 | 0.44 | 0.44 | |
| Information–Culture | t | 0.65 | 8 | 0.45 | 0.2 | 0.2 | |
| Manufacture–Medical | t | 0.69 | 11.57 | 0.49 | 0.15 | 0.15 | |
| Finance–Real estate | Survival BB1 | 0.32 | 1.84 | 0.53 | 0.31 | 0.54 | |
| Finance–Energy | Survival BB1 | 0.16 | 1.43 | 0.35 | 0.04 | 0.38 | |
| Consumption–Agriculture | Survival BB1 | 0.26 | 1.43 | 0.38 | 0.15 | 0.37 |
| Industries | 90% | 95% | 99% |
|---|---|---|---|
| ESG | 0.099 | 0.051 | 0.010 |
| Energy | 0.102 | 0.051 | 0.009 |
| Manufacturing | 0.098 | 0.053 | 0.008 |
| Finance | 0.102 | 0.048 | 0.009 |
| Real estate | 0.101 | 0.049 | 0.010 |
| Consumption | 0.101 | 0.049 | 0.010 |
| Agriculture | 0.102 | 0.054 | 0.011 |
| Medical | 0.096 | 0.049 | 0.009 |
| Transportation | 0.103 | 0.050 | 0.011 |
| Information | 0.099 | 0.054 | 0.009 |
| Culture | 0.103 | 0.048 | 0.009 |
| Industries | ESG | Energy | Manufacturing | Finance | Real Estate | Consumption | Agriculture | Medical | Transportation | Information | Culture |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ESG | NA | 1.498 | 1.119 | 1.267 | 1.319 | 1.134 | 2.876 | 1.360 | 1.107 | 1.116 | 1.488 |
| Energy | 1.708 | NA | 1.928 | 1.523 | 1.817 | 2.540 | 4.009 | 3.959 | 1.634 | 3.404 | 2.340 |
| Manufacturing | 0.923 | 1.916 | NA | 1.554 | 1.907 | 1.150 | 2.059 | 1.095 | 1.519 | 0.995 | 1.244 |
| Finance | 0.806 | 1.365 | 1.334 | NA | 1.182 | 1.392 | 2.058 | 1.637 | 1.386 | 1.981 | 2.083 |
| Real estate | 1.371 | 1.700 | 1.746 | 1.150 | NA | 2.137 | 3.145 | 2.809 | 1.285 | 2.464 | 2.503 |
| Consumption | 1.109 | 2.936 | 1.329 | 2.038 | 1.962 | NA | 1.354 | 1.162 | 1.249 | 2.005 | 1.961 |
| Agriculture | 1.899 | 3.394 | 2.716 | 3.206 | 2.976 | 1.242 | NA | 2.639 | 2.134 | 2.905 | 2.932 |
| Medical | 1.081 | 3.806 | 1.089 | 2.236 | 3.049 | 1.373 | 3.148 | NA | 1.497 | 1.430 | 1.613 |
| Transportation | 1.119 | 1.966 | 0.963 | 1.237 | 1.549 | 1.579 | 2.777 | 1.785 | NA | 1.482 | 1.953 |
| Information | 1.366 | 3.128 | 1.127 | 1.698 | 2.368 | 1.817 | 3.382 | 1.585 | 1.307 | NA | 1.528 |
| Culture | 1.822 | 3.450 | 1.532 | 2.198 | 2.066 | 2.071 | 3.767 | 2.068 | 1.751 | 1.383 | NA |
| Industries | ESG | Energy | Manufacturing | Finance | Real Estate | Consumption | Agriculture | Medical | Transportation | Information | Culture |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ESG | NA | 0.350 | 0.377 | 0.246 | 0.273 | 0.417 | 0.427 | 0.248 | 0.236 | 0.331 | 0.486 |
| Energy | 0.303 | NA | 0.477 | 0.351 | 0.422 | 0.695 | 1.121 | 0.989 | 0.372 | 0.928 | 0.888 |
| Manufacturing | 0.352 | 0.722 | NA | 0.303 | 0.468 | 0.313 | 0.938 | 0.365 | 0.290 | 0.180 | 0.330 |
| Finance | 0.294 | 0.330 | 0.414 | NA | 0.247 | 0.377 | 0.719 | 0.410 | 0.356 | 0.292 | 0.451 |
| Real estate | 0.396 | 0.297 | 0.300 | 0.288 | NA | 0.655 | 1.109 | 0.376 | 0.450 | 0.488 | 0.641 |
| Consumption | 0.305 | 0.463 | 0.357 | 0.377 | 0.642 | NA | 0.213 | 0.335 | 0.304 | 0.646 | 0.364 |
| Agriculture | 0.450 | 1.031 | 0.504 | 0.393 | 0.950 | 0.371 | NA | 0.623 | 0.443 | 0.984 | 0.611 |
| Medical | 0.274 | 1.107 | 0.384 | 0.634 | 0.653 | 0.490 | 0.616 | NA | 0.403 | 0.346 | 0.581 |
| Transportation | 0.299 | 0.446 | 0.275 | 0.225 | 0.285 | 0.449 | 0.438 | 0.357 | NA | 0.325 | 0.496 |
| Information | 0.295 | 0.555 | 0.286 | 0.473 | 0.597 | 0.834 | 0.770 | 0.381 | 0.374 | NA | 0.328 |
| Culture | 0.588 | 0.587 | 0.278 | 0.589 | 0.454 | 0.577 | 1.024 | 0.480 | 0.361 | 0.415 | NA |
| Industries | ESG | Energy | Manufacturing | Finance | Real Estate | Consumption | Agriculture | Medical | Transportation | Information | Culture |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ESG | NA | 0.062 | 0.012 | 0.040 | 0.004 | 0.015 | 0.012 | 0.041 | 0.041 | 0.015 | 0.009 |
| Energy | 0.013 | NA | 0.039 | 0.001 | 0.044 | 0.011 | 0.027 | 0.175 | 0.047 | 0.010 | 0.013 |
| Manufacturing | 0.024 | 0.011 | NA | 0.038 | 0.052 | 0.010 | 0.004 | 0.025 | 0.026 | 0.008 | 0.015 |
| Finance | 0.007 | 0.014 | 0.022 | NA | 0.018 | 0.109 | 0.028 | 0.008 | 0.027 | 0.017 | 0.037 |
| Real estate | 0.019 | 0.029 | 0.027 | 0.023 | NA | 0.033 | 0.013 | 0.004 | 0.033 | 0.013 | 0.122 |
| Consumption | 0.054 | 0.050 | 0.097 | 0.052 | 0.046 | NA | 0.008 | 0.018 | 0.006 | 0.031 | 0.121 |
| Agriculture | 0.032 | 0.253 | 0.018 | 0.117 | 0.229 | 0.003 | NA | 0.039 | 0.026 | 0.427 | 0.137 |
| Medical | 0.016 | 0.106 | 0.030 | 0.020 | 0.033 | 0.005 | 0.117 | NA | 0.014 | 0.051 | 0.033 |
| Transportation | 0.015 | 0.031 | 0.014 | 0.034 | 0.013 | 0.019 | 0.014 | 0.068 | NA | 0.008 | 0.026 |
| Information | 0.040 | 0.011 | 0.020 | 0.020 | 0.014 | 0.011 | 0.078 | 0.014 | 0.009 | NA | 0.029 |
| Culture | 0.023 | 0.108 | 0.023 | 0.032 | 0.075 | 0.013 | 0.094 | 0.096 | 0.028 | 0.003 | NA |
| Level | Type | ESG | Energy | Manufacturing | Finance | Real Estate | Consumption | Agriculture | Medical | Transportation | Information | Culture |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 90% | Risk_Out | 0.778 | 0.650 | 1.569 | 1.844 | 0.855 | 1.578 | −1.533 | 2.989 | 0.456 | 1.850 | 0.074 |
| Risk_In | −4.396 | 7.390 | −4.228 | −3.074 | 2.321 | −1.332 | 9.131 | 2.111 | −2.072 | 1.115 | 4.143 | |
| Net | −5.174 | 6.740 | −5.797 | −4.917 | 1.467 | −2.910 | 10.664 | −0.878 | −2.528 | −0.735 | 4.069 | |
| Role | R | G | R | R | G | R | G | R | R | R | G | |
| 95% | Risk_Out | 0.513 | 0.799 | −0.019 | 0.239 | 0.380 | 0.484 | −0.072 | 0.778 | −0.075 | 1.131 | 0.265 |
| Risk_In | −1.140 | 2.218 | −0.208 | −0.581 | 0.623 | −0.359 | 2.269 | 1.031 | −0.875 | 0.437 | 1.008 | |
| Net | −1.653 | 1.419 | −0.189 | −0.820 | 0.243 | −0.843 | 2.341 | 0.252 | −0.800 | −0.694 | 0.744 | |
| Role | R | G | R | R | G | R | G | G | R | R | G | |
| 99% | Risk_Out | 0.034 | 0.270 | 0.075 | 0.046 | 0.144 | 0.107 | 0.194 | 0.167 | −0.008 | 0.444 | 0.232 |
| Risk_In | −0.020 | 0.129 | −0.055 | 0.030 | 0.062 | 0.203 | 1.009 | 0.166 | −0.024 | −0.031 | 0.236 | |
| Net | −0.055 | −0.141 | −0.130 | −0.016 | −0.082 | 0.097 | 0.815 | −0.001 | −0.016 | −0.475 | 0.004 | |
| Role | R | R | R | R | R | G | G | R | R | R | G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Busababodhin, P.; Wichitchan, S. Dependency and Risk Spillover of China’s Industrial Structure Under the Environmental, Social, and Governance Sustainable Development Framework. Sustainability 2025, 17, 4660. https://doi.org/10.3390/su17104660
Li Y, Busababodhin P, Wichitchan S. Dependency and Risk Spillover of China’s Industrial Structure Under the Environmental, Social, and Governance Sustainable Development Framework. Sustainability. 2025; 17(10):4660. https://doi.org/10.3390/su17104660
Chicago/Turabian StyleLi, Yucui, Piyapatr Busababodhin, and Supawadee Wichitchan. 2025. "Dependency and Risk Spillover of China’s Industrial Structure Under the Environmental, Social, and Governance Sustainable Development Framework" Sustainability 17, no. 10: 4660. https://doi.org/10.3390/su17104660
APA StyleLi, Y., Busababodhin, P., & Wichitchan, S. (2025). Dependency and Risk Spillover of China’s Industrial Structure Under the Environmental, Social, and Governance Sustainable Development Framework. Sustainability, 17(10), 4660. https://doi.org/10.3390/su17104660







