Multi-Scale Sponge Capacity Trading and SLSQP for Stormwater Management Optimization

Abstract

Low-impact development (LID) facilities serve as a fundamental approach in urban stormwater management. However, significant variations in land use among different plots lead to discrepancies in runoff reduction demands, frequently leading to either the over- or under-implementation of LID infrastructure. To address this issue, we propose a cost-effective optimization framework grounded in the concept of “Capacity Trading (CT)”. The study area was partitioned into multi-scale grids (CT-100, CT-200, CT-500, and CT-1000) to systematically investigate runoff redistribution across heterogeneous land parcels. Integrated with the Sequential Least Squares Programming (SLSQP) optimization algorithm, LID facilities are allocated according to demand under two independent constraint conditions: runoff coefficient ($\phi$ ≤ 0.49) and runoff control rate ($\eta$ ≥ 70%). A quantitative analysis was conducted to evaluate the construction cost and reduction effectiveness across different trading scales. The key findings include the following: (1) At a constant return period, increasing the trading scale significantly reduces the demand for LID facility construction. Expanding trading scales from CT-100 to CT-1000 reduces LID area requirements by 28.33–142.86 ha under the $\phi$-constraint and 25.5–197.19 ha under the $\eta$-constraint. (2) Systematic evaluations revealed that CT-500 optimized cost-effectiveness by balancing infrastructure investments and hydrological performance. This scale allows for coordinated construction, avoiding the high costs associated with small-scale trading (CT-100 and CT-200) while mitigating the diminishing returns observed in large-scale trading (CT-1000). This study provides a refined and efficient solution for urban stormwater management, overcoming the limitations of traditional approaches and demonstrating significant practical value.

1. Introduction

The rapid pace of urbanization has placed unprecedented pressure on traditional urban water management systems [1,2]. The widespread increase in impervious surfaces has significantly elevated stormwater runoff volumes, exacerbating flood risks and undermining urban sustainability and residents’ quality of life [3,4]. Globally, nature-based solutions (NBSs) have been adopted to tackle these challenges. In the United States, these include LID and Best Management Practices (BMPs) [5]. In the United Kingdom, Sustainable Urban Drainage Systems (SUDSs) have been introduced [6], and Sponge Cities have been introduced in China [7,8,9]. As a component of green infrastructure (GI), LID facilities reduce urban runoff by restoring surface permeability. Empirical studies confirm their effectiveness in stormwater management [10,11]. However, widespread implementation faces ongoing challenges, particularly high capital costs and inefficient spatial configurations [12,13].

Traditional LID deployment strategies prioritize the hydrological characteristics of functional zones (e.g., residential, commercial, industrial, green spaces) [14]. However, this approach amplifies a hydrological paradox: Impervious commercial zones require significant mitigation but lack space for implementation, while underused green areas possess excess capacity [15,16]. As a result, functional zone-based frameworks, though fundamental, have significant limitations. Due to significant differences in land use across functional areas, some regions may face the over-construction of facilities and resource wastage, while others may lack the capacity to handle excessive runoff [17]. Therefore, allocating runoff reduction potential across different regions is essential to achieving the city’s overall runoff control objectives [18]. To address these issues, Dai et al. introduced the concept of CT [19], which aims to meet runoff reduction demands across different regions by “transferring” runoff between them. The core of the CT mechanism enables surplus units, with better permeability, to “transfer” their runoff reduction potential to deficit units under greater runoff management pressure. Previous studies have demonstrated that CT can effectively optimize urban runoff management. For example, Xu et al. explored the effectiveness of two trading scales (neighboring trading and 20 m range trading) and found that the trading scale significantly influences runoff management [20]. Jia et al. confirmed that conducting CT within a spatial range of 500–600 m can halve the cost of LID facilities, and expanding the trading scale to 1200 m can reduce the cost by three-quarters [21]. Zhang et al. determined that the optimal trading scale for multiple cities ranges from 80 to 180 hectares, with the trading area incorporating various complementary functional zones, achieving near-optimal trading effects [22]. Although previous studies have shown that as the trading scale increases, the required intensity of LID construction decreases, excessively large trading scales conflict with the core concept of “local treatment” in Sponge City construction [23]. Thus, identifying the optimal trading scale is essential. Moreover, although CT based on functional areas aligns with urban planning, and the significant differences in area sizes across functional zones make it challenging for surplus units’ reduction potential to meet the needs of deficit units, thereby diminishing the effectiveness of CT. In CT, controlling the trading scale is crucial to balancing resource efficiency with construction benefits. Furthermore, exploring new trading methods can address issues such as mismatched reduction potential and resource waste in functional zone-based transactions. This approach will further enhance the overall benefits of Sponge City construction.

To address these challenges, this study proposes a grid-partitioning method that divides the study area into grids of varying scales to accurately identify runoff reduction needs. This method facilitates the flexible trading of runoff reduction potential across regions, thereby enhancing optimization and enabling more precise adjustments in LID facility configurations [24,25]. Additionally, the SLSQP optimization algorithm is employed to determine the optimal spatial scale for CT while meeting the runoff control targets (runoff coefficient ≤ 0.49 and runoff control rate ≥ 70%). This approach effectively integrates the runoff reduction potential within the region, balancing resource allocation efficiency, runoff control effectiveness, and construction cost minimization.

2. Materials and Methods

The effectiveness of CT depends on spatial heterogeneity and the uniform spatial scale of deficit and surplus units [22]. At smaller scales (100 m and 200 m), it facilitates capturing detailed spatial variations. The 500 m scale is identified as a sensitive scale for landscape diversity, where diversity indices exhibit a ring-like expansion pattern, while at the 1000 m scale, the spatial diversity index gradually stabilizes [20,26]. Therefore, the study area was partitioned into multi-scale grids (100 m, 200 m, 500 m, and 1000 m) to facilitate refined stormwater management. Using data related to the research area (e.g., pipe networks, sub-catchments, rainfall data; data sources are listed in

Table 1. Data sources.

Data Types	Source	Time
Satellite map	Gaode Map	2020
Digital elevation model (DEM)	China Geospatial Data Cloud	2021
Pipe networks	Lianyungang Municipal Bureau of Housing and Urban-Rural Development	2012
Rainfall data	Lianyungang Municipal Bureau of Housing and Urban-Rural Development	2014

), this study employed the SWMM to simulate stormwater runoff in sub-catchments of varying scales, assessing the hydrological characteristics of each region and the demand for LID facilities. The study introduced the CT mechanism by analyzing the reduction potential between surplus and deficit units. Additionally, the SLSQP optimization algorithm was employed to optimize the allocation of LID facilities across different grid units, aiming to minimize the construction area and maximize runoff reduction efficiency. Finally, by simulating and analyzing runoff reduction effects under various trading scales, the configurations of LID facilities and construction requirements were evaluated, and the optimal solution was proposed, as shown in Figure 1.

2.1. Study Area

2.1.1. Area Overview

Lianyungang City is located in the northeastern part of Jiangsu Province, with geographic coordinates ranging from 33°58′55″ N to 35°08′30″ N and 118°24′03″ E to 119°54′51″ E. The region has a temperate monsoon climate, with an annual average precipitation of approximately 982 mm. Precipitation is unevenly distributed spatially and temporally, with summer rainfall accounting for about 60% of the total annual precipitation. Frequent extreme weather events, such as heavy rainfall and storm surges, pose a significant risk of urban flooding in the area.

The study area selected for this research was Haizhou District in Lianyungang City, bordered to the south by Hailian Middle Road and Cangwu Road, to the north by Yudai River, to the west by Dapu River, and to the east by Dongyan River. The area is surrounded by water on three sides, covering a total area of approximately 12.68 km². Longwei River flows through the area, dividing it into eastern and western sections. The western section, which contains the old city, has a lower proportion of green space and reduced runoff reduction potential, while the eastern section, being densely populated, has a higher demand for runoff reduction. The significant land use differences between the eastern and western sections create favorable conditions for the application of the CT mechanism. The impervious surface area in the study area accounts for 80.3%, as shown in Figure 2. The region’s soil types, primarily sandy and clay, exhibit good permeability. However, due to extensive land development, urbanization, and frequent extreme weather events such as storm surges and typhoons along the coast, the traditional drainage system can no longer manage the excessive stormwater runoff, resulting in local flooding. These challenges are widespread in many cities across China. According to the “Technical Guidelines for Sponge City Construction” [27], the annual runoff control rate in Lianyungang City should reach 70%. The “Lianyungang Sponge City Special Plan (2016–2030)” [28] stipulates that the runoff coefficient for urban construction land should be maintained below 0.49 by 2030.

2.1.2. Design Rainfall

Using the revised design storm intensity Formula (1) from the Lianyungang Meteorological Bureau, we set the design rainfall duration to 2 h, with a peak rain factor of r = 0.417. To more accurately represent rainfall scenarios and stormwater response characteristics for different return periods, we employed the Chicago Rainfall Model to generate rainfall processes. The rainfall scenarios for the study area encompassed the 1-year, 2-year, 3-year, and 5-year return periods, as shown in Figure 3.

$$i={\displaystyle \frac{9.5\times (1+0.719\lg T)}{(t+11.2{)}^{0.619}}}$$

(1)

In the formula, i represents the rainfall intensity (mm/min), t represents the rainfall duration (min), and T represents the return period (years).

2.2. Research Methods

2.2.1. SWMM and Sub-Catchment Division

The Storm Water Management Model (SWMM) is extensively used in urban stormwater management and hydrological analysis. It simulates runoff generation, surface flow dynamics, and water quality variations under varying rainfall conditions [29,30]. In the SWMM, sub-catchment delineation, pipe network configuration, and design rainfall data are fundamental elements for model operation. In this study, we utilized the ArcGIS “Create Fishnet” tool to partition the study area into grids of varying scales (CT-100, CT-200, CT-500, and CT-1000), which function as sub-catchments. Compared to traditional methods such as Thiessen polygons, hydrological characteristics, and functional zones [31], grid-based partitioning provides greater flexibility, making it more adaptable for CT at various scales and enhancing resource allocation efficiency and optimization capabilities.

2.2.2. SWMM Parameter Calibration and Validation

Key parameters in the SWMM include impervious surface roughness, pervious surface roughness, maximum infiltration rate, and minimum infiltration rate [32]. The parameter values of the SWMM are usually determined based on the comparison between simulated and observed flow data, using the Nash–Sutcliffe Efficiency (NSE) and the coefficient of determination (R²) as evaluation metrics [33,34]. However, due to the lack of field data for the study area, this research uses the SWMM parameter calibration results from a previous study by Guo for the Xuwei District of Lianyungang City [35]. Based on these results, the comprehensive runoff coefficient method was applied for parameter calibration. This method adjusts the model’s parameters by comparing the simulated runoff coefficient with the empirical runoff coefficient values for urban areas [11,36,37]. The runoff coefficient in the SWMM is calculated as the weighted average for each sub-catchment, while the empirical runoff coefficient for the urban area is determined according to the GB50014-2021 “Outdoor Drainage Design Standards” [38], as presented in

Table 2. Empirical values of the urban composite runoff coefficient.

Region Characteristics	Impervious Area Proportion (%)	Composite Runoff Coefficient
Central Area with High Density	>70	0.6–0.8
Central Area with Moderate Density	50–70	0.5–0.7
Residential Area with Low Density	30–50	0.4–0.6
Residential Area with Very Low Density	<30	0.3–0.5

.

$${\phi }_{\mathrm{total}}={\displaystyle \frac{1}{A_{\mathrm{total}}}}{\displaystyle \sum A_i}{\phi }_i$$

(2)

In the formula, $A_i$ is the area of the i-th unit (km²), ${\phi }_i$ is the runoff coefficient of the i-th unit, $A_{\mathrm{total}}$ is the total area of the study area (km²), and ${\phi }_{\mathrm{total}}$ is the composite runoff coefficient for the entire study area.

According to the visual interpretation of ArcGIS, the impervious area of the study region was 80.3%, categorizing it as a densely built central area. Consequently, the composite runoff coefficient ranged from 0.6 to 0.8. The simulation results revealed a significant negative correlation between the runoff coefficient and scale in the absence of LID facilities (see

Table 3. Runoff coefficients for different return periods.

Scale	1 Years	2 Years	3 Years	5 Years
CT-100	0.725	0.763	0.781	0.800
CT-200	0.703	0.741	0.758	0.777
CT-500	0.657	0.692	0.710	0.729
CT-1000	0.600	0.634	0.652	0.672

). Variations in runoff coefficients exhibited substantial differences in runoff reduction demands and potential across different scales, providing a theoretical foundation for the application of the CT mechanism. Throughout the four simulated design rainfall events, the runoff coefficients remained within the range of 0.6–0.8, complying with the GB50014-2021 “Outdoor Drainage Design Standards” requirements [38], thereby indicating high model stability and reliability. The model’s parameters are presented in

Table 4. Model parameters.

Parameter Name	Value Range	Reference Value	Calibrated Value
N-Imperv	0.01–0.05	0.01	0.023
N-Perv	0.05–0.4	0.25	0.25
D-Imperv (mm)	0–3	2.5	2.5
D-Perv (mm)	2–10	7.0	7
Max. Infil. Rate (mm/h)	10–100	90	76
Min. Infil. Rate (mm/h)	0–10	4	6.6
Decay constant (1/h)	0–7	4	2
Drying Time (days)	1–7	7	7

.

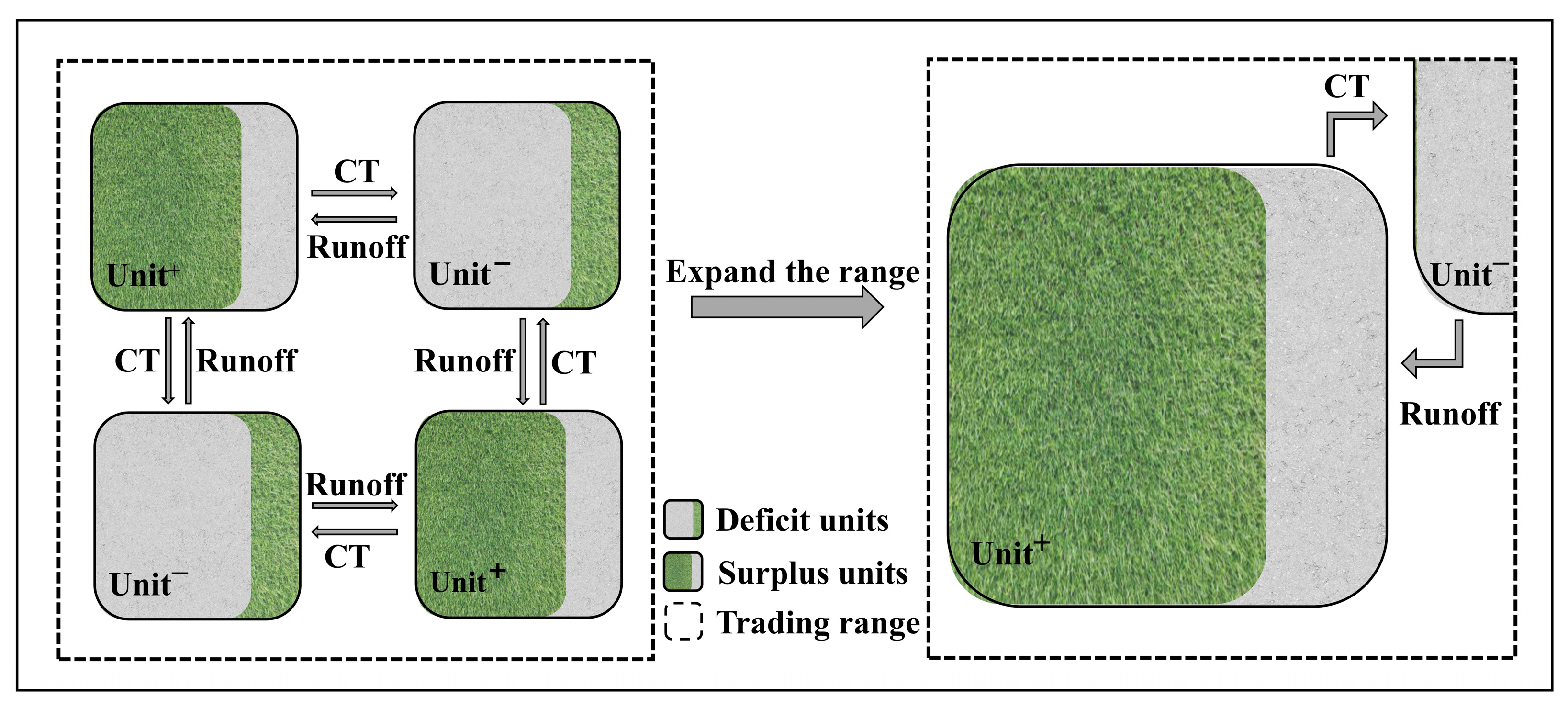
2.2.3. Concept of Capacity Trading

The CT mechanism aims to leverage the linkage between LID facilities and individual units, enabling deficit units (with runoff coefficients > 0.49) to “borrow” from surplus units (with runoff coefficients < 0.49), thereby dynamically allocating runoff reduction potential. The core objective is to optimize resource flow and allocation between units, achieving the most efficient distribution of the reduction potential and preventing the drainage system of deficit units from bearing excessive runoff pressure that could lead to overflow. In practical trading, runoff is first directed from deficit units to surplus units through natural terrain slopes. If the slope is insufficient, powered devices, natural overflow pathways, or slope-oriented LID facilities can be utilized to guide excess runoff toward areas with higher permeability or lower pipe network pressure for treatment. The water flows forward as a pushing flow, contacting the ground surface during the process, which increases infiltration.

As shown in Figure 4, when their own runoff reduction demands cannot be fully met, deficit units “transfer” runoff to surplus units to achieve runoff targets. Surplus units typically have strong rainwater infiltration capacity, while deficit units need to rely on LID facilities or the CT mechanism to achieve their control objectives. Through the “trading” of runoff, the reduction potential of surplus units can be “transferred” to deficit units, thereby optimizing resource allocation, reducing the construction area of LID facilities, and further enhancing overall runoff reduction efficiency.

2.2.4. Capacity Trading Calculation Formula

After the surplus area meets the runoff coefficient constraint ($\phi$ ≤ 0.49), any excess reduction capacity can be used through CT to compensate for deficit areas. The relationship function is as follows:

Compensation Capacity of Surplus Area Calculation:

$$T_{\mathrm{surplus},\mathrm{total}=}{\displaystyle \sum _{i\in \mathrm{surplus}}{Q}_{\left(X_i\right)}\times \frac{{\phi }_{\mathrm{target}}}{{\phi }_{\left(X_i\right)}}}-Q_{\left(X_i\right)}$$

(3)

In the formula, $Q_{\left(X_i\right)}$ is the runoff volume of the i-th unit under a certain construction proportion condition (10³ m³); ${\phi }_{\mathrm{target}}$ is the target runoff coefficient of the unit (0.49); ${\phi }_{\left(X_i\right)}$ is the runoff coefficient of the i-th unit under the specific construction proportion condition; $T_{\mathrm{surplus},\mathrm{total}}$ is the total surplus runoff capacity of the region (10³ m³).

Reduction Demand of the Deficit Area:

$$T_{\mathrm{deficit},\mathrm{total}=}{\displaystyle \sum _{i\in \mathrm{deficit}}{Q}_{\left(X_i\right)}-Q_{\left(X_i\right)}\times \frac{{\phi }_{\mathrm{target}}}{{\phi }_{\left(X_i\right)}}}$$

(4)

In the formula, $T_{\mathrm{deficit},\mathrm{total}}$ is the total deficit runoff capacity of the region (10³ m³).

Remaining Reduction Demand After Theoretical Trading:

$$T_{\mathrm{net}}=T_{\mathrm{surplus},\mathrm{total}}-T_{\mathrm{deficit},\mathrm{total}}$$

(5)

In the formula, $T_{\mathrm{net}}$ is the remaining reduction demand after compensating the deficit area with the surplus area’s reduction capacity, and $T_{\mathrm{net}}$ ≥ 0. After trading, the surplus area fully compensates for the deficit area, and no new LID facilities are required: $T_{\mathrm{net}}$ < 0. The surplus is insufficient to compensate for the deficit, and new LID facilities must be added or further trading needs to be sought.

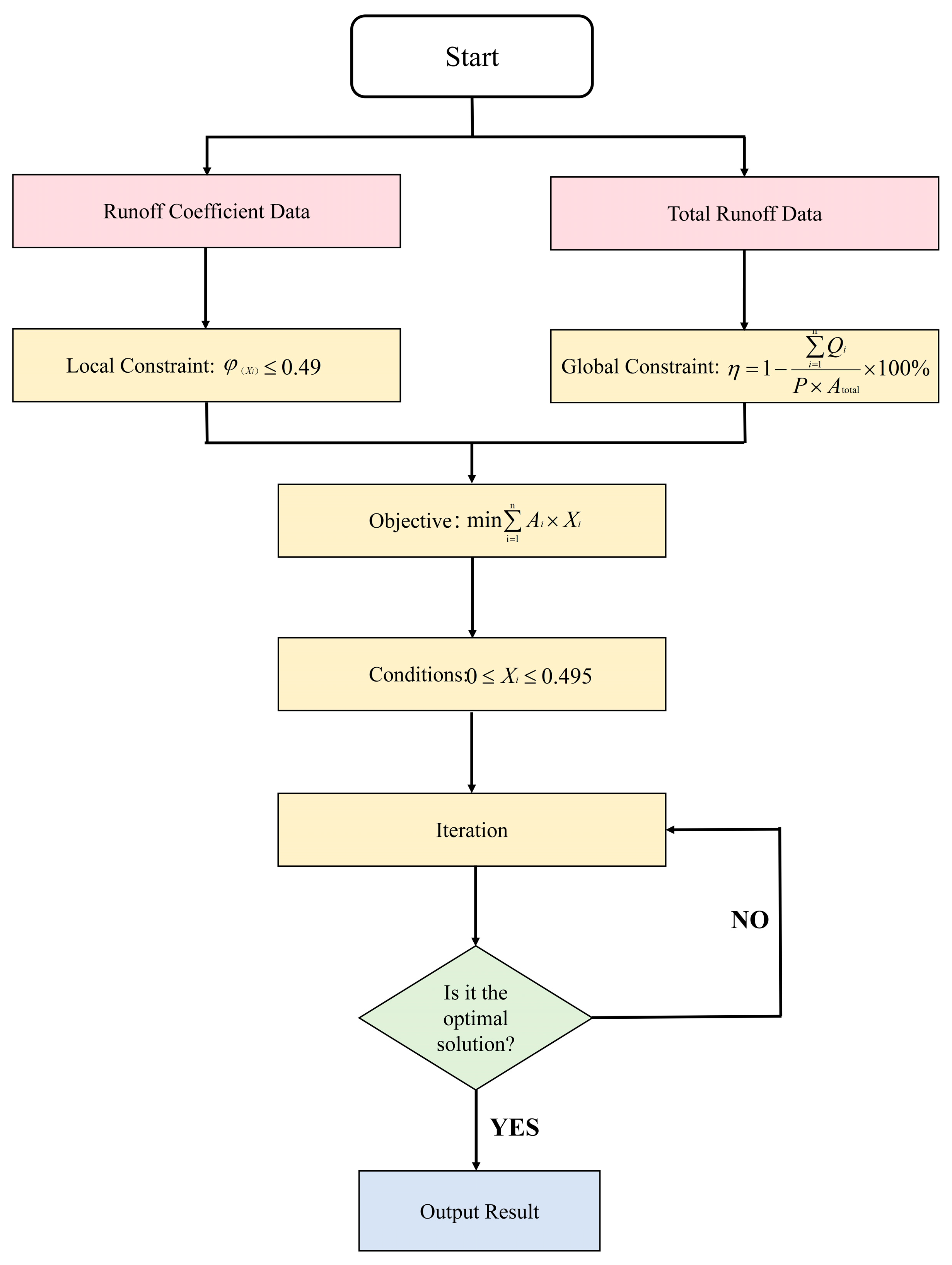
2.2.5. SLSQP Optimization Model

To account for the constructed demand at different trading scales, this study formulates a function to minimize the construction area of LID facilities. SLSQP effectively handles nonlinear and inequality constraints. Through iterative optimization, it mitigates the limitations of local optimal solutions, achieving a global multi-objective optimization balance, including minimizing the construction area of LID facilities and maximizing runoff reduction benefits. This enhances resource allocation efficiency and ensures that the optimal solution is obtained under various constraints, including runoff coefficients and reduction demands. Additionally, compared to Non-Dominated Sorting Genetic Algorithm II (NSGA-II) and Particle Swarm Optimization (PSO), SLSQP demonstrates faster convergence and higher computational efficiency in handling small-scale optimization problems with strict constraints, such as runoff coefficients and runoff control rates. It can directly incorporate multiple constraints without the need for additional penalty functions, making it more suitable for optimizing LID facility configurations under dual constraint conditions [18,39].

In the study area, three types of LID facilities were selected, rain gardens, green roofs, and permeable pavements, to accommodate different land use requirements. Previous studies have demonstrated a significant linear relationship between the proportion of LID facilities, the runoff coefficient, and the total runoff volume [40]. When configuring LID facilities, constraints such as runoff coefficients and runoff control rates are typically expressed as inequalities. SLSQP can directly integrate these inequality constraints into the optimization process and determine the optimal solution while ensuring constraint satisfaction [41]. This feature makes SLSQP particularly suitable for optimizing LID facility configurations under multiple inequality constraints. The SLSQP optimization process is illustrated in Figure 5. The formula is as follows.

Design variables: For each unit in the study area, the construction proportion of LID facilities ranges from 0% to 49.5%.

$$X_{(i+1)}=X_i+\Delta X$$

(6)

In the formula, $\Delta X$ represents the proportion of LID facilities added per iteration; $\Delta X$ is 1.5%, where rain gardens, green roofs, and permeable pavements each account for 0.5%; $X_i$ is the construction proportion of the i-th unit.

Optimization objective: Minimize the construction area of all units.

$$\min {\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}{A}_i}\times X_i$$

(7)

In the formula, $A_i$ is the area of the i-th unit (km²).

Local constraint: The runoff coefficient for each unit must be less than or equal to 0.49.

$${\phi }_{\left(X_i\right)}\le 0.49$$

(8)

In the formula, ${\phi }_{\left(X_i\right)}$ is the runoff coefficient for the i-th unit under the construction proportion $X_i$.

Global constraint: The overall runoff control rate must be greater than 70%.

$$\eta =1-{\displaystyle \frac{{\displaystyle \sum _{i=1}^{\mathrm{n}}Qi}}{P\times A_{\mathrm{total}}}}\times 100\%$$

(9)

In the formula, $\eta$ is the runoff control rate; $Q_i$ is the residual runoff for the i-th unit (10³ m³); $P$ is the rainfall amount (mm); $A_{\mathrm{total}}$ is the total area of the study region (km²).

Boundary Conditions:

$$0\le X_i\le 0.495$$

(10)

2.2.6. Marginal Benefit

Excessive increases in construction intensity result in diminishing returns on construction benefits. To quantify the benefits of various proportions of LID facilities, this study introduces the Marginal Rate (MR) indicator, which measures the reduction in runoff coefficient benefits achieved by increasing the construction proportion by 3%. The calculation formula is presented as follows:

$$MR=\left|{\displaystyle \frac{R_{i+1}-R_i}{P_{i+1}-P_i}}\right|$$

(11)

In the formula, $R_i$ and $R_{i+1}$ are the runoff coefficients at the i-th and (i + 1)-th stages, respectively; $P_i$ and $P_{i+1}$ are the construction proportions at the i-th and (i + 1)-th stages, respectively.

3. Results

3.1. SWMM Simulation Run

3.1.1. Runoff Characteristics at Different Trading Scales

One of the core objectives of Sponge Cities is to reduce urban flooding and runoff pollution through source control and decentralized management measures. The 2-year return period rainfall event, due to its higher frequency, has a particularly significant impact on urban hydrological processes [42]. These frequent rainfall events cause localized water flow concentration, leading to localized flooding issues. Furthermore, according to the GB50014-2021 “Outdoor Drainage Design Standards” [38], the design return period for stormwater drainage networks in medium and small cities is between 2 and 3 years. Therefore, selecting the 2-year return period as the optimization target effectively reflects the regulatory effects of Sponge Cities in managing high-frequency rainfall events. The research results indicate that, in the absence of LID facilities, there is a significant negative correlation between the composite runoff coefficient and the trading scale. The composite runoff coefficients for CT-100, CT-200, CT-500, and CT-1000 are 0.763, 0.741, 0.692, and 0.634, respectively. This indicates that larger trading scales (e.g., CT-500 and CT-1000) enable surplus units’ runoff reduction potential to be more fully traded to deficit units, resulting in better runoff reduction effects. In contrast, smaller trading scales (e.g., CT-100 and CT-200) lead to higher composite runoff coefficients for the study area because surplus units’ reduction potential is not fully traded relative to deficit units. Additionally, a negative correlation exists between the surplus area and trading scale. This is primarily due to the excessive expansion of the trading scale, where more deficit areas are included when trading with local surplus areas. As a result, surplus areas cannot accommodate the needs of the newly included deficit areas, leading to surplus units being overloaded. The surplus areas are presented in

Table 5. Area of each runoff coefficient range at different trading scales (unit: ha).

Runoff Coefficient	CT-100	CT-200	CT-500	CT-1000
0–0.49 (Surplus)	48.51	34.14	24.99	0
0.491–0.6 (Deficit)	60.4	55.05	51.29	209
0.601–0.7 (Deficit)	105.34	149.18	471.25	1023.99
0.701–0.8 (Deficit)	446.48	814.62	720.48	35.02
0.801–0.9 (Deficit)	607.28	215.02	0	0

, and the runoff coefficient distribution map is provided in Figure 6.

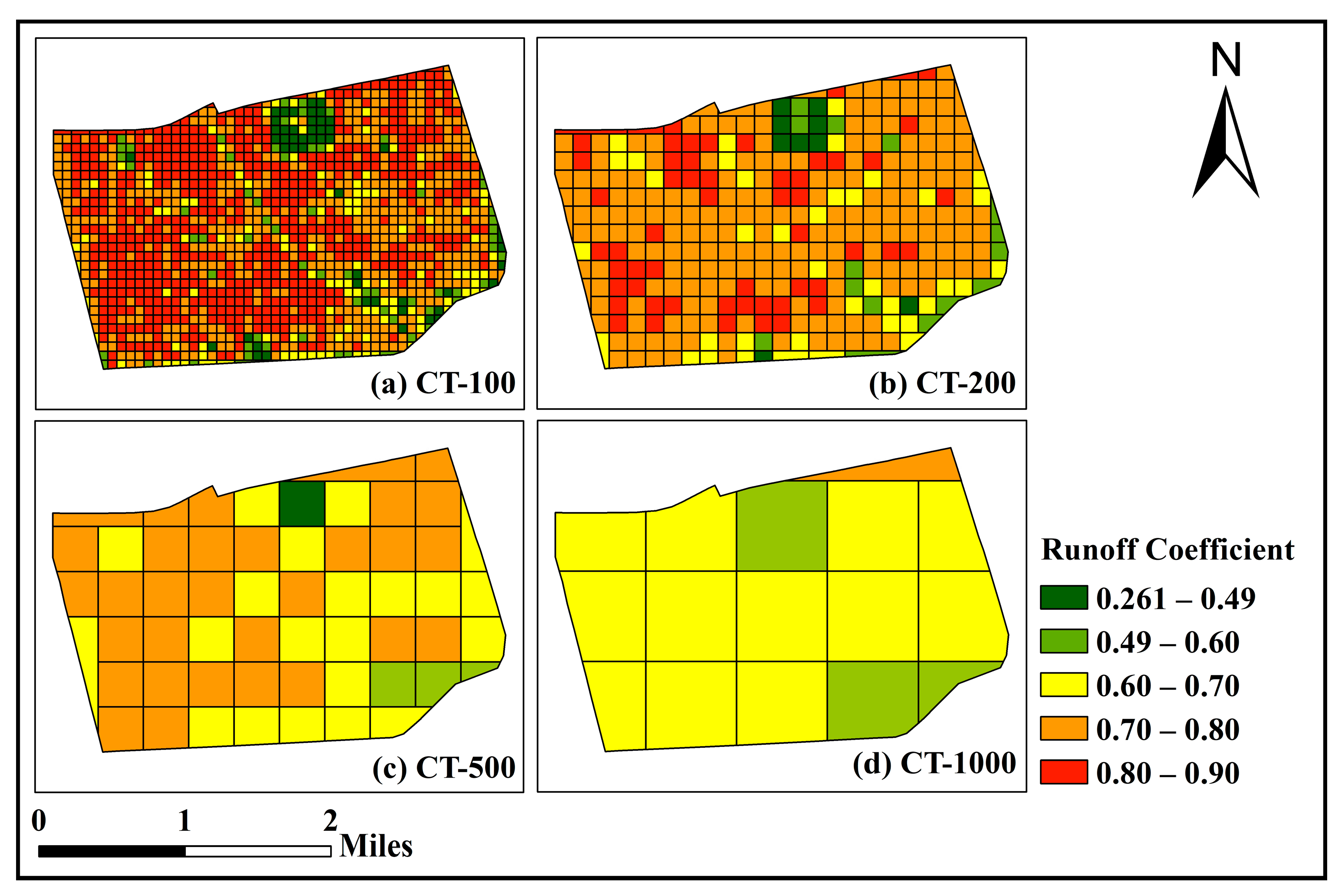
3.1.2. Runoff Coefficient Trend

This study examines the impact of different trading scales and construction proportions on runoff reduction effects by gradually increasing the proportion of LID facilities (0–49.5%) across varying trading scales. The results, shown in Figure 7, indicate a significant decrease in the runoff coefficient as the LID facility construction proportion increases, confirming the effectiveness of LID facilities at different scales [43]. The data show that, in the absence of LID facilities, the initial runoff coefficients for CT-100, CT-200, CT-500, and CT-1000 are 0.763, 0.741, 0.692, and 0.634, respectively. As the LID facility proportion gradually increases to 49.5%, the runoff coefficients decrease to 0.227, 0.213, 0.139, and 0.095, representing a reduction of over 70% for each trading scale. Among these, the runoff coefficient for CT-500 shows the largest reduction, reaching 0.553.

The SWMM simulation results indicate that there are significant differences in marginal benefits across different trading scales. As shown in Figure 8, when the LID facilities are initially constructed, CT-500 demonstrates the highest marginal benefit, reaching 1.44. In contrast, CT-100 shows the lowest marginal benefit at 1.33. As the LID facility construction proportion increases to 48%, the marginal benefit for CT-100 surpasses that of other scales, reaching 0.84, while CT-500 is slightly lower at 0.79. This phenomenon suggests that, compared to other trading scales, CT-500 consistently achieves superior marginal benefits across various construction proportions. Overall, as the construction proportion increases, the marginal benefit decreases. This trend aligns with previous studies [44,45], which also noted that the runoff reduction efficiency tends to stabilize as the construction proportion increases. Therefore, when constructing LID facilities, it is crucial to select a moderate LID proportion to balance runoff reduction benefits with economic efficiency. These results provide data support for subsequent CT and optimization configurations, further validating the effectiveness of LID facility allocation under multi-scale trading conditions.

3.2. Capacity Trading Optimization Effect

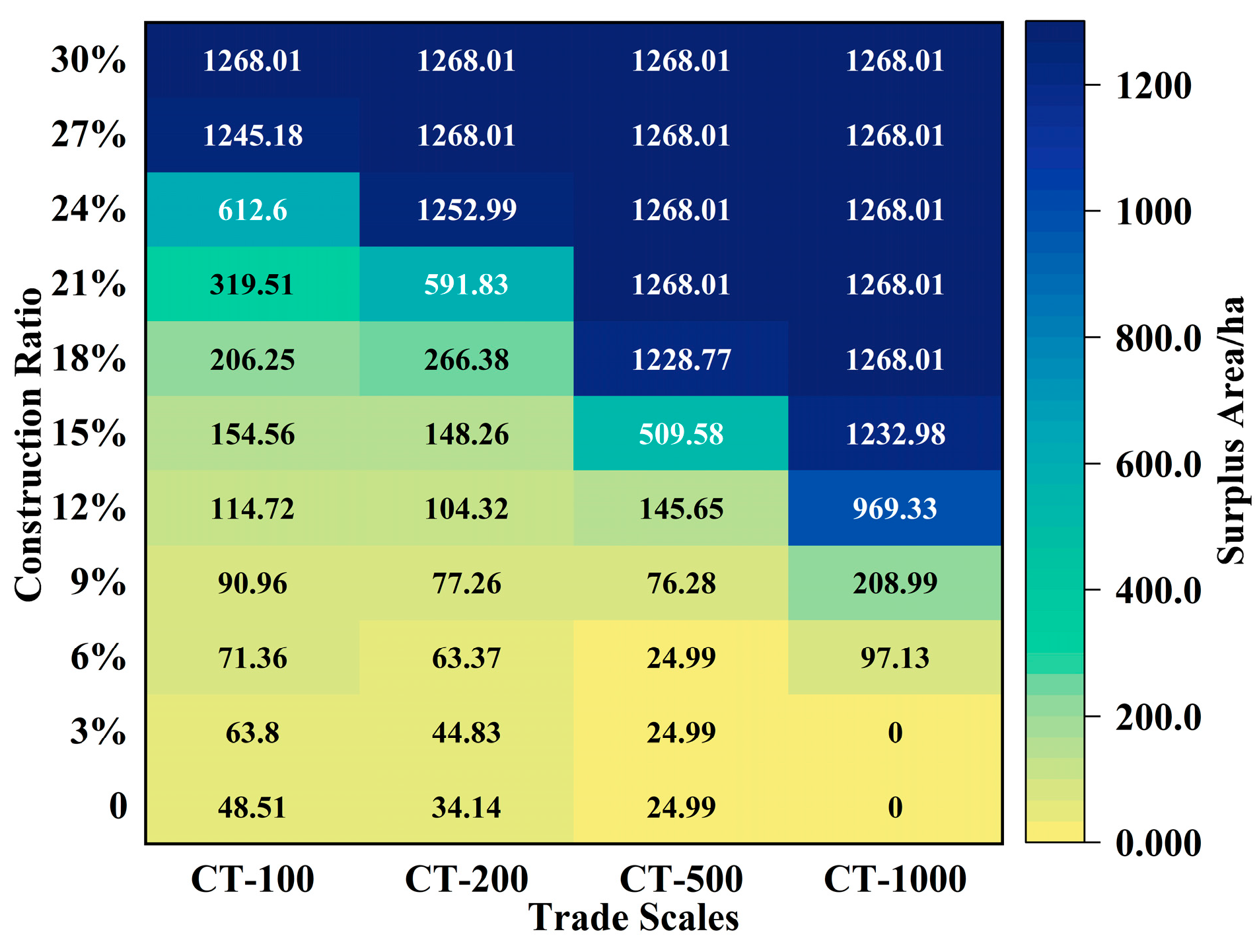
3.2.1. Surplus Area Changes with Trading Scale

As the proportion of LID facilities increases, the relationship between the trading scale and surplus area gradually becomes clearer; however, noticeable differences remain in performance across different trading scales. As shown in Figure 9, when the construction proportion of LID facilities is relatively low (e.g., 0–9%), the increase in surplus area for different trading scales is gradual and does not exhibit a significant upward trend. However, as the construction proportion increases, the impact of trading scale expansion on the surplus area becomes more evident. When the construction proportion reaches 12%, the surplus area for CT-1000 increases significantly; CT-500 begins to show significant growth at 15%, while CT-200 and CT-100 show significant growth only at 21% and 24%, respectively. When the construction proportion reaches 18%, all units in CT-1000 satisfy the runoff coefficient requirement. At this point, the surplus area for CT-100 reaches only 206.25 ha or just 16.27% of the study area, indicating that smaller trading scales at low construction proportions are insufficient on their own to achieve the same results as larger trading scales, which rely on more extensive regional transactions.

From the CT perspective, this trend reflects the differences in resource allocation between surplus and deficit units at varying trading scales. Larger trading scales can more effectively leverage the runoff reduction potential of surplus units, reducing the runoff reduction demand of deficit units. In contrast, smaller trading scales, due to their limited scope, necessitate a higher proportion of LID facilities to meet the runoff reduction needs of deficit units. Overall, appropriately expanding the scale of Sponge City trading helps integrate resource allocation between surplus and deficit units more efficiently, thereby better achieving the overall runoff reduction objectives of the city.

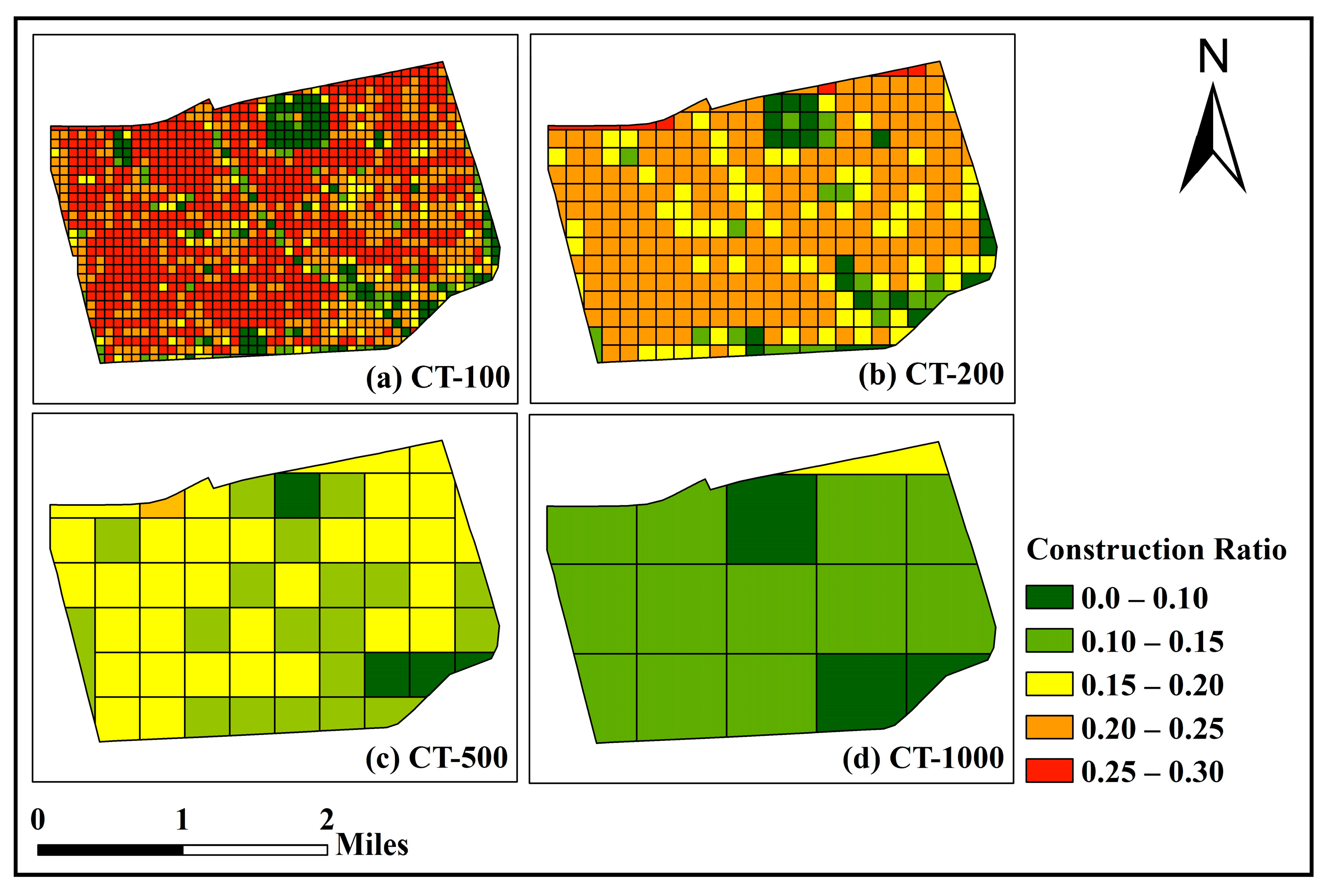
3.2.2. Construction Proportion Distribution Under Local Constraints for Different Trading Scales

Under the condition of meeting local constraints ($\phi$ ≤ 0.49), the distribution of construction proportions varies significantly across different trading scales, as shown in Figure 10. In smaller trading scales (e.g., CT-100), notable differences in construction demand are mainly driven by high-density areas such as built-up zones and transportation hubs. These areas require a higher proportion of LID facilities to meet runoff reduction targets due to their larger runoff volumes. In contrast, permeable areas such as green spaces require fewer facilities, and in some cases, they require none. However, the runoff reduction potential in these permeable areas is not fully utilized by the CT mechanism, leading to surplus resource waste and reduced allocation efficiency. As the trading scale increases (e.g., CT-200 and CT-500), the runoff reduction potential of surplus units is gradually transferred to deficit units. This transfer leads to a more balanced spatial distribution of construction proportions. For example, in CT-500, the construction proportion in high-demand areas significantly decreases, and most units require only 10–20% of LID facilities to meet the runoff coefficient requirement. At the maximum trading scale (CT-1000), the resource integration effect is further optimized, and the construction demand for all units becomes more uniform, with significantly reduced construction proportions. This result aligns with the conclusions drawn from Xu et al. [23], which indicate that construction intensity decreases as the trading area expands. Specifically, the required LID facility areas to address all surplus needs for CT-100, CT-200, CT-500, and CT-1000 are 284.67 ha, 256.34 ha, 195.09 ha, and 141.81 ha, respectively. Correspondingly, the runoff coefficients were reduced by 0.283, 0.261, 0.212, and 0.153. These results indicate that expanding the trading scale can effectively optimize resource allocation, reduce construction demands, and achieve more balanced resource distribution and runoff reduction objectives. Overall, smaller trading scales show more significant variation in construction demands across different units, whereas larger trading scales effectively reduce the construction demand in high-density areas through CT, resulting in a lower degree of dispersion in the construction intensity distribution.

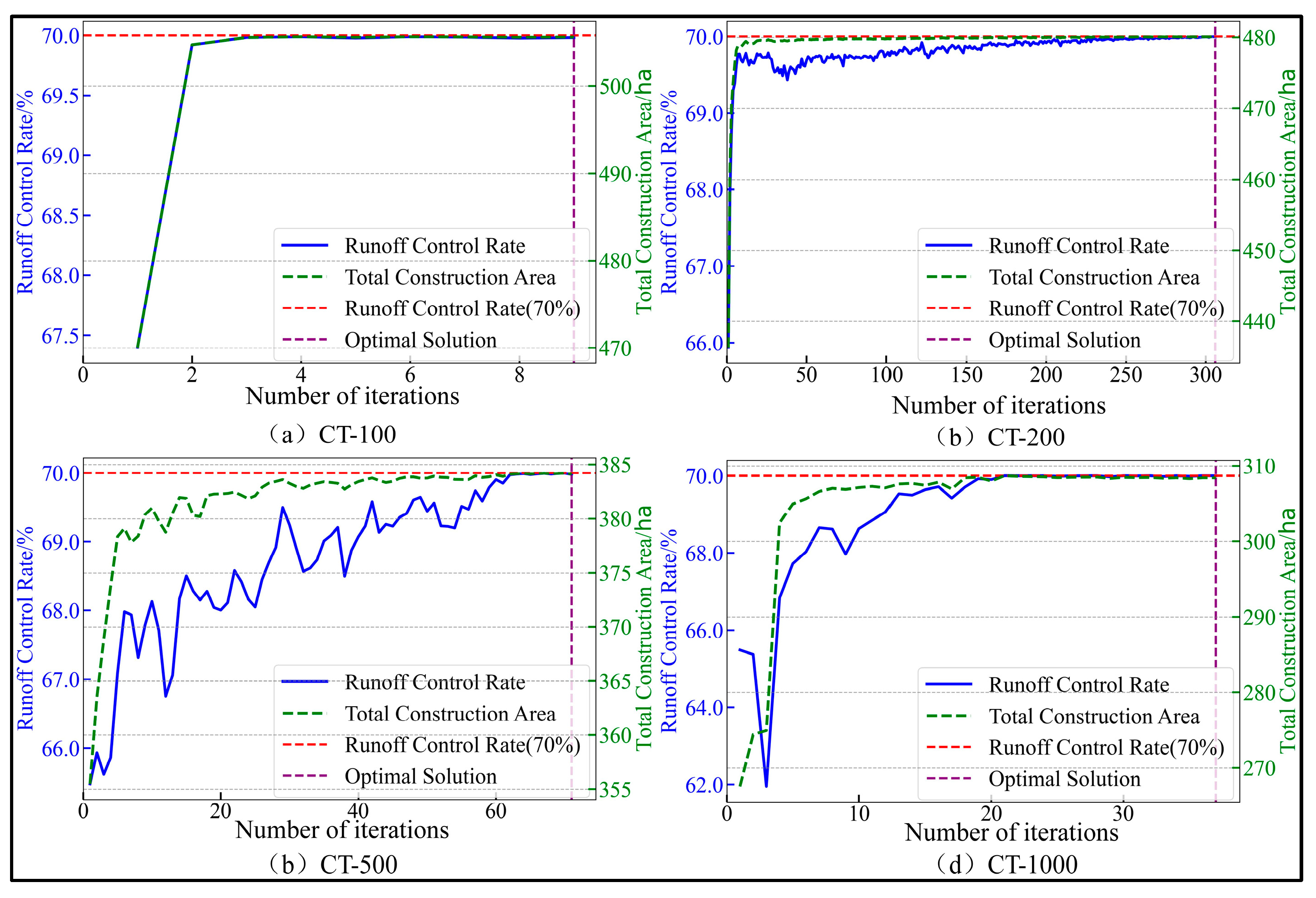
3.2.3. Construction Demand Under Global Constraints for Different Trading Scales

Figure 11 illustrates the iterative optimization process of the runoff control rate and construction area across different trading scales. CT-100 requires only nine iterations to reach the optimal construction plan, mainly due to the tolerance settings of the optimization model. The algorithm terminates when the change in the objective function value (construction area) is less than 0.001. Additionally, CT-100 has more grid units with reduced mutual influence between them, allowing the construction proportion of each unit to be more independent. Therefore, the optimization algorithm can adjust most units simultaneously, rapidly finding the global optimal solution.

The optimization results show that as the trading scale increases, the total construction area for LID facilities gradually decreases. The construction areas for each trading scale are 505.59 ha, 480.09 ha, 384.11 ha, and 308.4 ha, respectively. Compared to CT-100, the construction areas for CT-200, CT-500, and CT-1000 are reduced by 5.04%, 24.03%, and 39%, respectively. However, when the trading scale expands from CT-500 to CT-1000, the construction area decreases by only 19.7%. Zhang et al. similarly noted that as the trading scale increases, the integration benefits of resources tend to saturate, and the increase in benefits slows down [22].

When the optimized construction plan is re-entered into the SWMM for simulation, the runoff control rates for each trading scale are 69.98%, 69.66%, 69.9%, and 69.97%, representing increases of 46.18%, 43.66%, 39%, and 33.67%, respectively, all of which are close to meeting the constraint requirements. To further validate the optimized solution at the 2-year return period, this study applies the optimized plan to higher return periods (3 years and 5 years). As shown in

Table 6. Runoff control rates.

Trading Scales	2 Years	3 Years	5 Years
CT-100	69.98%	66.48%	62.83%
CT-200	69.95%	66.93%	63.98%
CT-500	69.9%	67.57%	65.0%
CT-1000	69.97%	67.95%	65.74%

, the simulation results show that the runoff control rate is maintained at over 60%, and as the trading scale increases under the same return period, the runoff control rate gradually increases, further validating the effectiveness of CT.

4. Discussion

4.1. Surplus Area Changes in Typical Regions

In the absence of LID facilities, the study found that surplus areas were primarily concentrated in the typical regions shown in Figure 12, which were selected for analysis. The analysis indicates that this typical region contains a large permeable area, which serves as the primary source of surplus units in CT-100, CT-200, and CT-500. However, in CT-1000, due to the larger trading scale, the surplus potential is distributed across a broader range of deficit areas, leading to insufficient surplus capacity to fully balance the global deficit. As a result, CT-1000 appears in a deficit state when no LID facilities are present. Further comparisons of the surplus distribution characteristics at different construction proportions and trading scales reveal that larger trading scales often derive their surplus from the local surplus areas of smaller trading scales. This is primarily because, during the expansion of the trading scale, the runoff reduction potential of surplus areas is gradually “transferred” to deficit areas through the CT mechanism. Consequently, larger trading scales exhibit more significant surplus effects.

From the analysis of

Table 7. Surplus amount at different construction proportions.

Trading Scales	Number of Units	${\mathit{T}}_{\mathbf{net}}$
		0	3%	6%	9%	12%	15%	18%	21%	24%	27%	30%
CT-100	98	−12.21	−9.92	−7.64	−5.42	−3.28	−1.20	0.84	2.82	4.79	6.69	8.50
CT-200	25	−10.79	−8.41	−6.09	−3.84	−1.65	0.45	2.52	4.5	6.42	8.28	10.04
CT-500	4	−7.88	−5.35	−2.88	−0.53	1.78	4.05	6.2	8.28	10.28	12.22	14.11
CT-1000	1	−4.68	−2.11	0.33	2.7	5.01	7.28	9.35	11.48	13.44	15.34	17.19

, it can be observed that at construction intensities of 18% and 15%, CT-100 and CT-200 have, respectively, achieved the theoretical surplus balance. Through SWMM simulation, CT-500 requires only 18% of LID facilities to meet all surplus needs in the region, while CT-100 and CT-200 require 30% and 24% of the region’s LID facility area, respectively, to meet the full surplus demand. This indicates that the potential resource waste in smaller trading scales has been effectively utilized in the resource integration process of CT-500.

From a practical application perspective, when planning sponge cities, the distribution characteristics of typical regions (such as parks, which have high permeability, or transportation hubs, which have low permeability) should be identified and addressed in greater detail. It may be necessary to consider using smaller trading scales or assigning higher weights to avoid the scale effect overshadowing their characteristics. This ensures the efficiency and accuracy of resource allocation. Furthermore, it suggests the need for careful evaluation of the overall resource integration capability when expanding trading scales to avoid excessive integration that could lead to local resource waste or the further expansion of deficit areas.

4.2. Limitations and Future Prospects

In existing CT studies, functional zoning has been widely adopted to define trading areas [21,46]. While functional zoning facilitates the clarification of responsibility boundaries for stakeholders (e.g., government departments or developers), its rigid spatial demarcation may lead to resource mismatches—high-density built-up areas face spatial constraints in deploying sufficient LID facilities, while low-demand zones such as green spaces exhibit redundant infiltration potential, resulting in resource underutilization [47]. In contrast, multi-scale grid partitioning enables the flexible adjustment of trading scales, allowing for a more balanced integration of pollution reduction potential across regions. However, grid-based approaches also face practical challenges, including high-resolution data acquisition costs and cross-departmental coordination complexities [24]. To address this, a hybrid “zoning-grid” strategy is proposed for future research: At the macrolevel, functional zoning retains its role in defining accountability boundaries, while at the microlevel, refined grids capture localized demand heterogeneity. Machine learning algorithms could further optimize LID facility allocation [48,49], thereby balancing administrative efficiency with precision in resource optimization.

It is further noted that this study employs the Chicago Rainfall Model to generate precipitation scenarios, which simplifies the spatiotemporal complexity of rainfall patterns. Although this method enables standardized comparisons, it may underestimate the spatial heterogeneity and stochasticity of real rainfall events (e.g., localized extreme rainfall or non-uniform temporal distributions). Natural rainfall variability could significantly alter runoff dynamics and the efficacy of LID configurations. Additionally, while the current analysis focuses on 2-year return period rainfall events (aligned with drainage design standards for small-to-medium cities [38]), the framework’s performance under extreme rainfall scenarios (e.g., 10-year or 50-year return periods) remains unvalidated, despite the increasing frequency and intensity of such events due to climate change. Future research should prioritize the following directions: 1. multi-element synergy optimization: enhance collaborative effects between LID facilities, traditional gray infrastructure (e.g., pipe network expansion), and blue infrastructure (water bodies and wetlands) [50,51], with system resilience quantified through blue-green-gray coupled models; 2. data-driven validation: validate CT threshold robustness under extreme rainfall by integrating observed precipitation data and long-term climate scenarios.

5. Conclusions

This study proposes a new method to optimize urban stormwater runoff control through multi-scale grid partitioning (CT-100, CT-200, CT-500, and CT-1000) and the CT mechanism. Using Lianyungang City as the study area, the research demonstrates that multi-scale grid partitioning effectively adapts to varying reduction demands and achieves more efficient resource allocation and runoff control as the trading area gradually expands. The key conclusions are as follows:

(1)

Small-scale grids (CT-100 and CT-200) identify “hotspot” areas within the region, with the largest runoff coefficient difference reaching 0.6. They capture local runoff reduction demand more accurately. In contrast, large-scale grids (CT-500 and CT-1000), by integrating broader regions, significantly improve runoff reduction efficiency.

(2)

Construction intensity is negatively correlated with runoff reduction benefits. At low construction proportions, CT-500 and CT-1000 exhibit better marginal benefits than other trading scales. At higher construction proportions, CT-100 and CT-500 show superior marginal benefits. In general, CT-500 achieves the best marginal benefits across different construction proportions, offering superior resource allocation and reduction effects, making it highly applicable in practical planning.

(3)

As the trading scale increases, the required LID facility area gradually decreases. The required areas for meeting the Global Constraint for CT-100, CT-200, CT-500, and CT-1000 are 505.59 ha, 480.09 ha, 384.11 ha, and 308.4 ha, respectively, with runoff control rate increases of 46.18%, 43.66%, 39%, and 33.67%. Meanwhile, to address all surplus needs under each trading scale, the required LID facility areas are 284.67 ha, 256.34 ha, 195.09 ha, and 141.81 ha, respectively. Correspondingly, the comprehensive runoff coefficients decreased by 0.283, 0.261, 0.212, and 0.153. However, once the trading scale expands beyond a certain point, the benefits gained from further expansion decrease significantly. In practical applications, the appropriate trading scale should be selected based on factors such as the specific region’s topography, precipitation characteristics, functional zone distribution, and resource allocation needs to achieve optimal resource distribution and runoff reduction effects.

(4)

CT-500 is considered the optimal trading scale for the study area. It effectively integrates the runoff reduction potential of surplus areas and achieves significant runoff reduction effects under different construction intensities. It avoids the high construction costs associated with smaller trading scales and overcomes the diminishing returns of larger scales, ensuring the efficiency and economy of CT.

(5)

Traditional functional zones, which rely on land use characteristics for trading, lack flexibility in resource allocation, and the reduction potential of some surplus units may not meet the needs of deficit units. Multi-scale grid partitioning enables trading under more equitable conditions, and CT in such a context demonstrates higher efficiency in fine-tuned resource allocation.

In summary, compared to traditional functional zone partitioning, multi-scale grid partitioning demonstrates significant flexibility and refined management capabilities. However, traditional functional zones still have irreplaceable advantages in clarifying responsibilities and implementing policies. Therefore, future research and practical applications could combine the macro-management capabilities of functional zone partitioning with the micro-optimization characteristics of grid partitioning, flexibly selecting the best approach for different scenarios and promoting the refined and intelligent development of urban stormwater management.