Prediction of Compressive Strength of Sustainable Concrete Incorporating Waste Glass Powder Using Machine Learning Algorithms
Abstract
1. Introduction
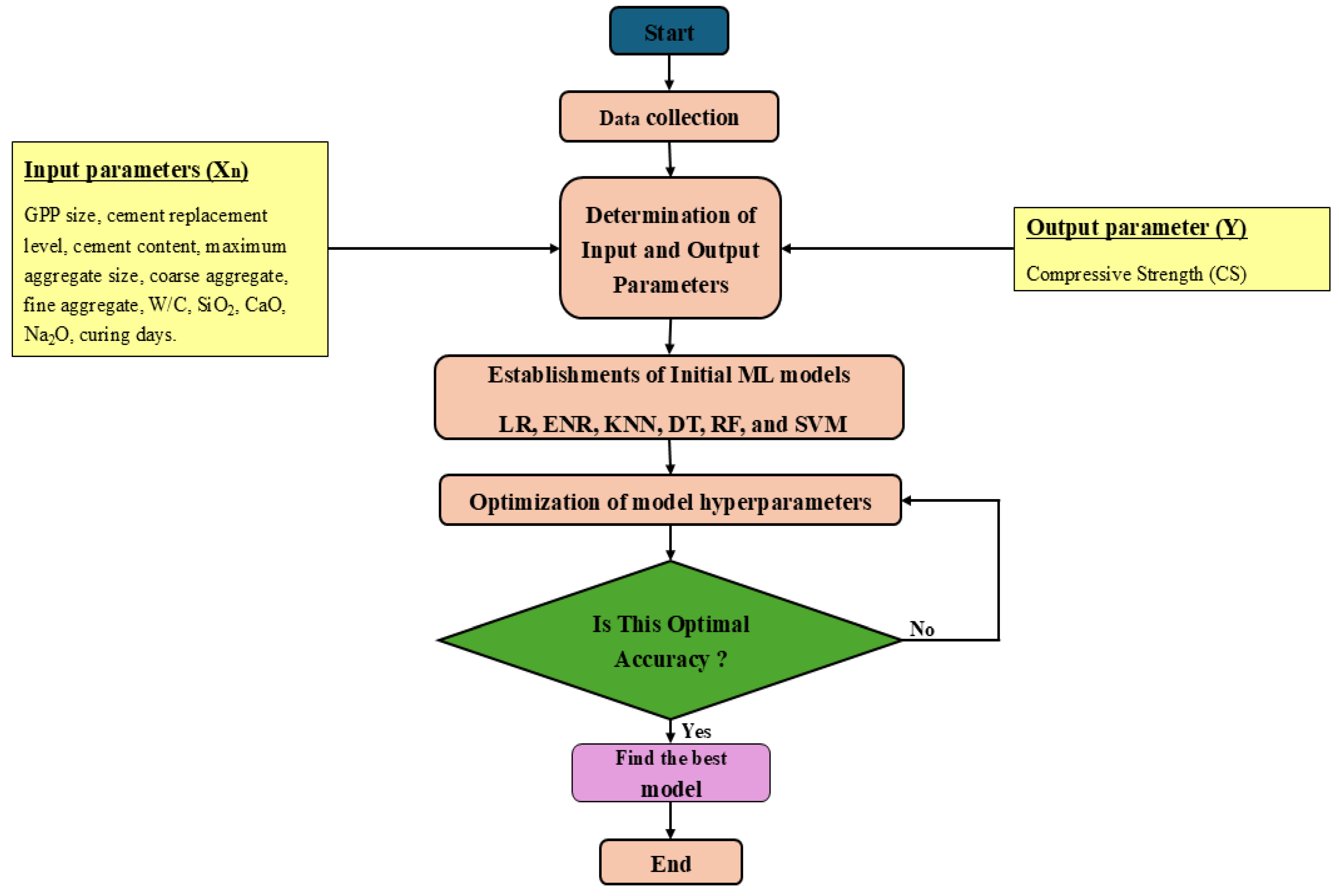
2. Materials and Methods
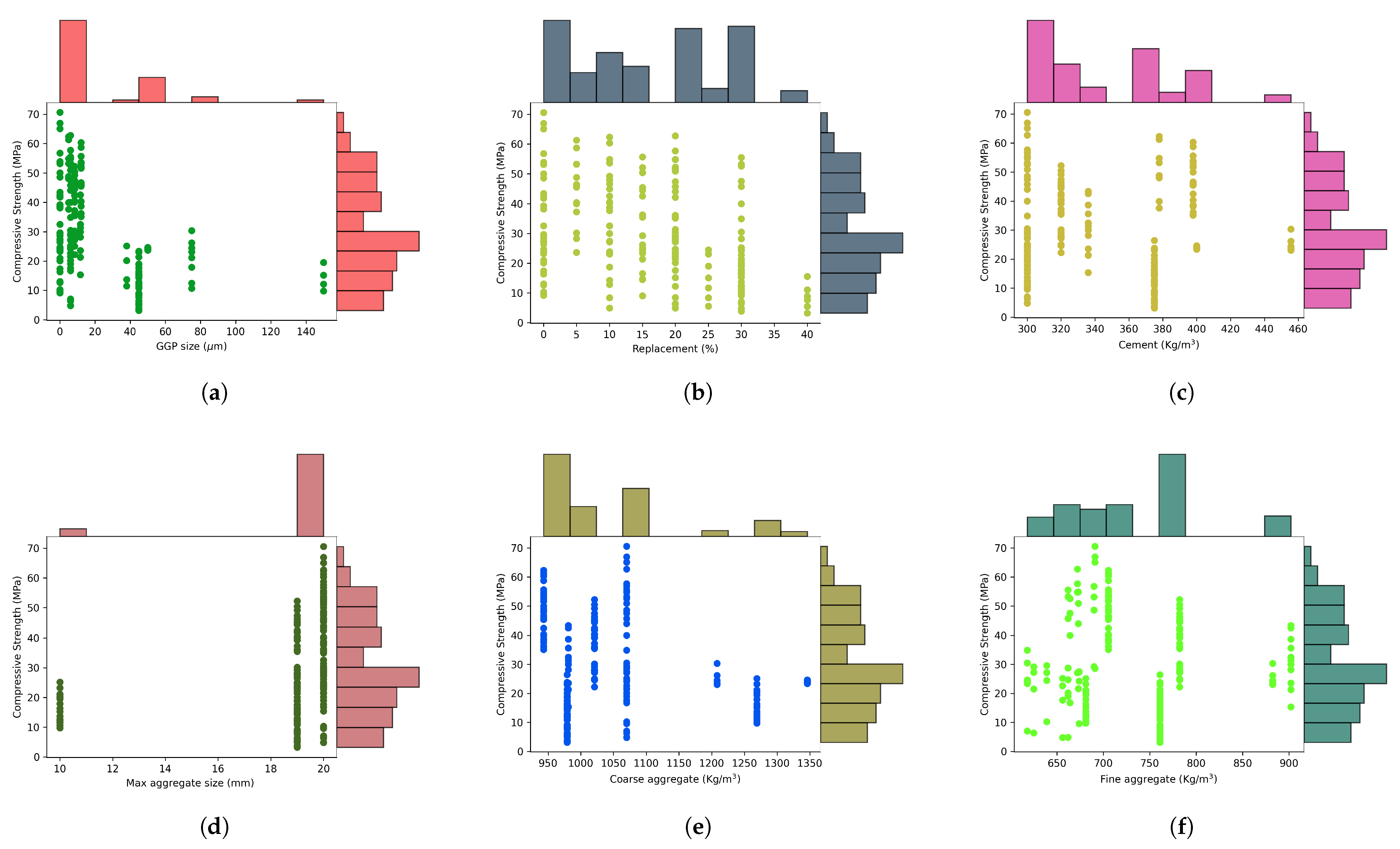
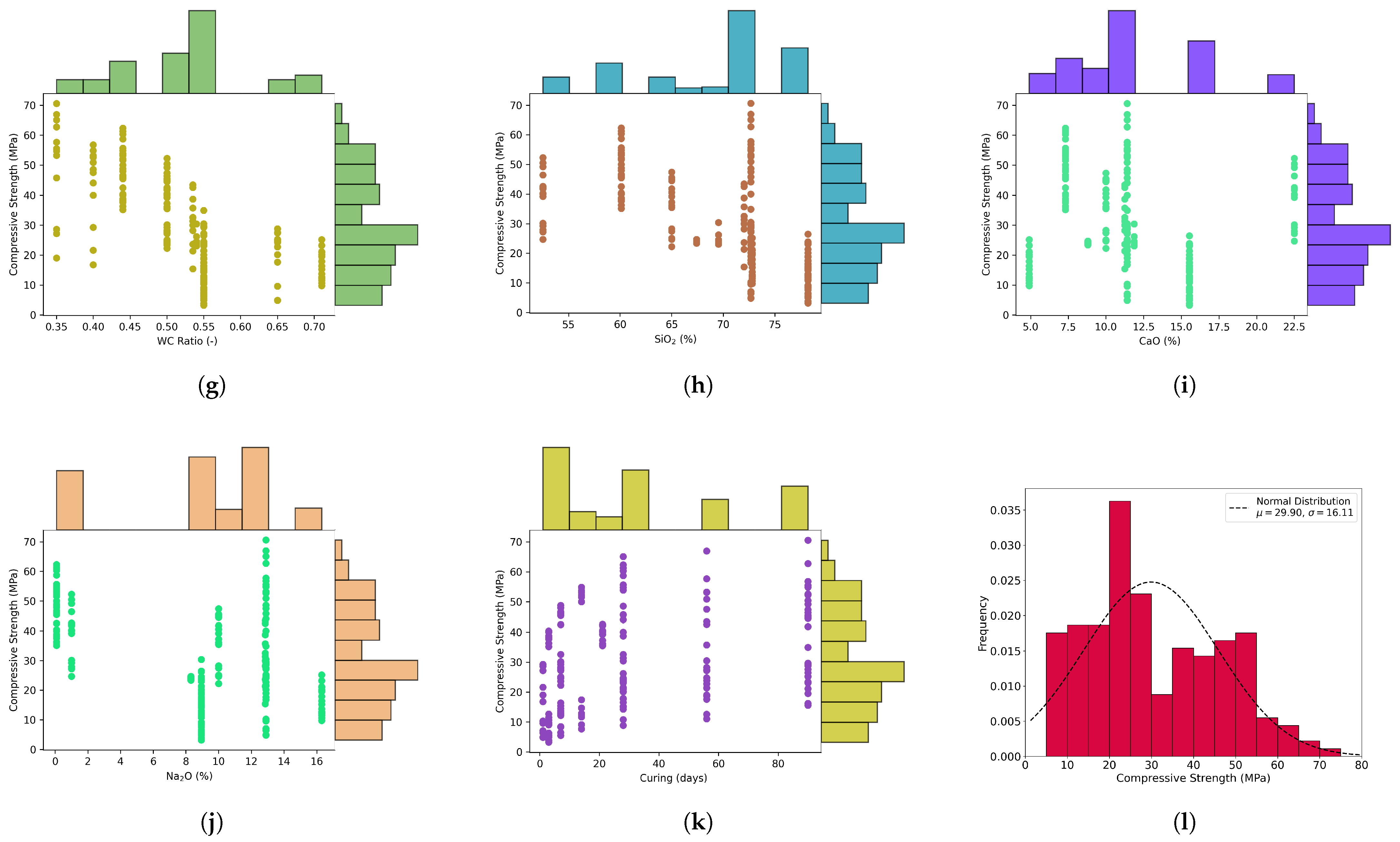
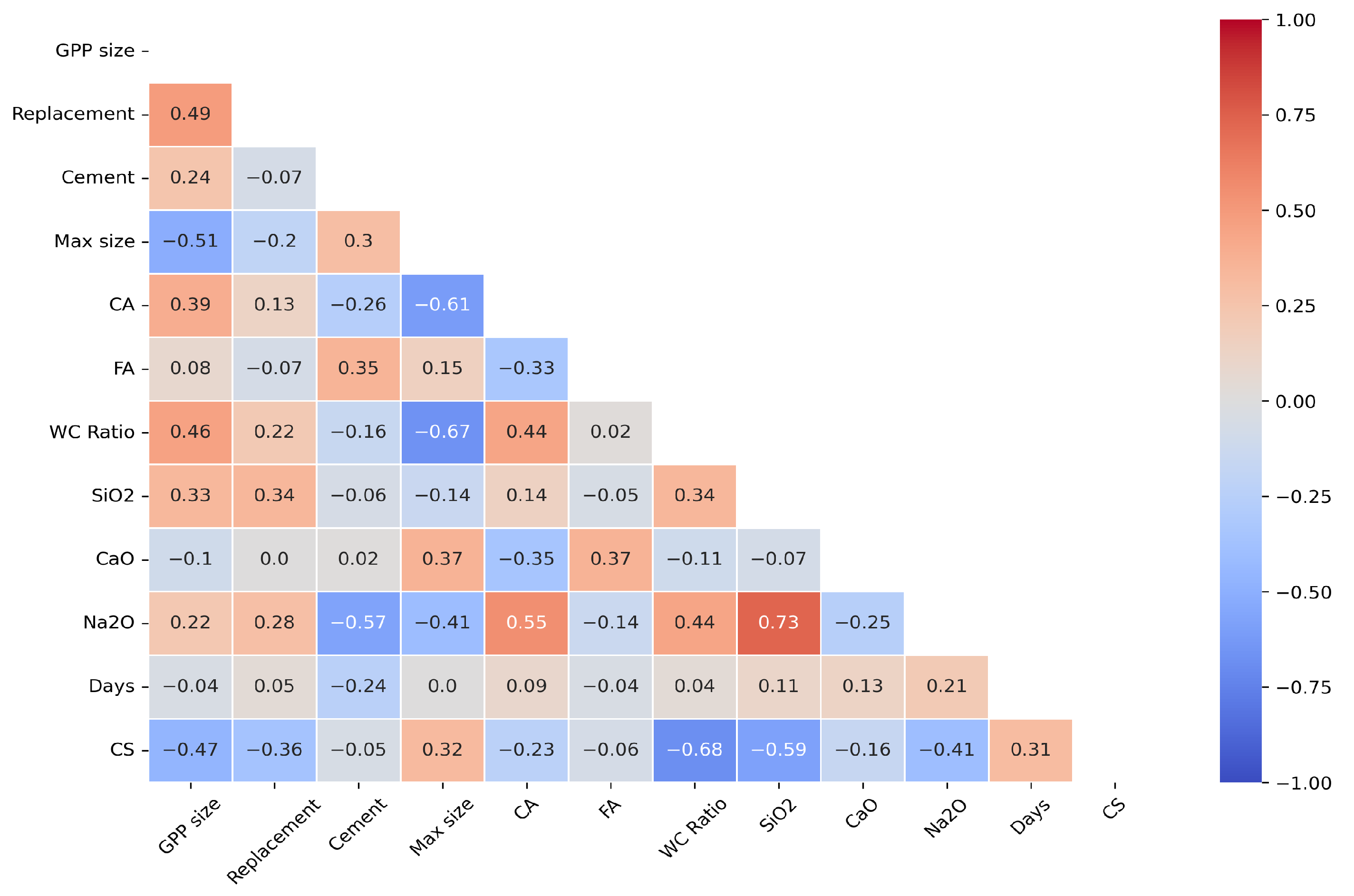
2.1. Data Collection and Preparation
2.2. Machine Learning Models
2.2.1. Linear Regression (LR)
2.2.2. ElasticNet Regression (ENR)
- : overall regularization strength (same as ‘alpha’ in ‘ElasticNet (alpha=…)’).
- : mixing parameter, controlling the balance between L1 and L2 regularization.
- : coefficient for L1 (lasso) regularization, derived from .
- : coefficient for L2 (ridge) regularization, derived from .
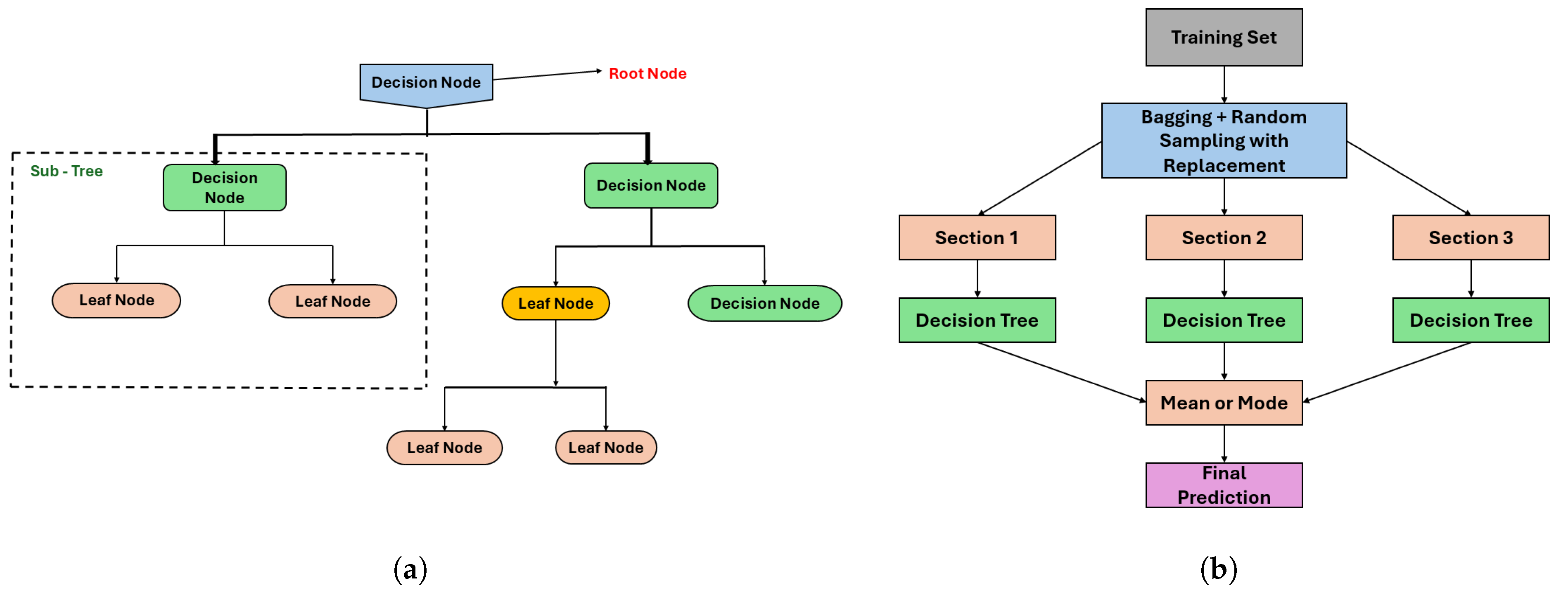
2.2.3. Decision Tree Regressor (DT)
2.2.4. Random Forest Regressor (RF)
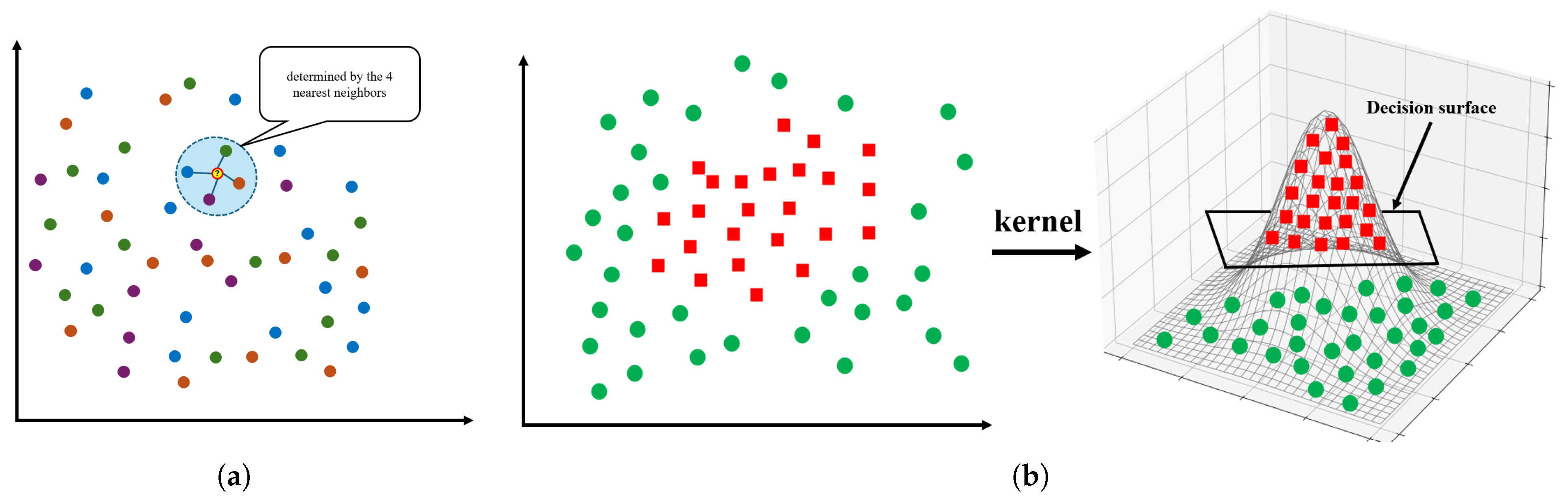
2.2.5. K-Nearest Neighbor Regressor (KNN)
2.2.6. Support Vector Regressor (SVR)
- -
- controls the model complexity.
- -
- C is a hyperparameter that determines the trade-off between margin size and prediction accuracy.
- -
- .
- -
- .
- -
- are the Slack variables that penalize the error if the prediction is outside the margin.
2.3. Error Computation
2.4. Hyperparameter Tuning
3. Results and Discussion
4. Conclusions
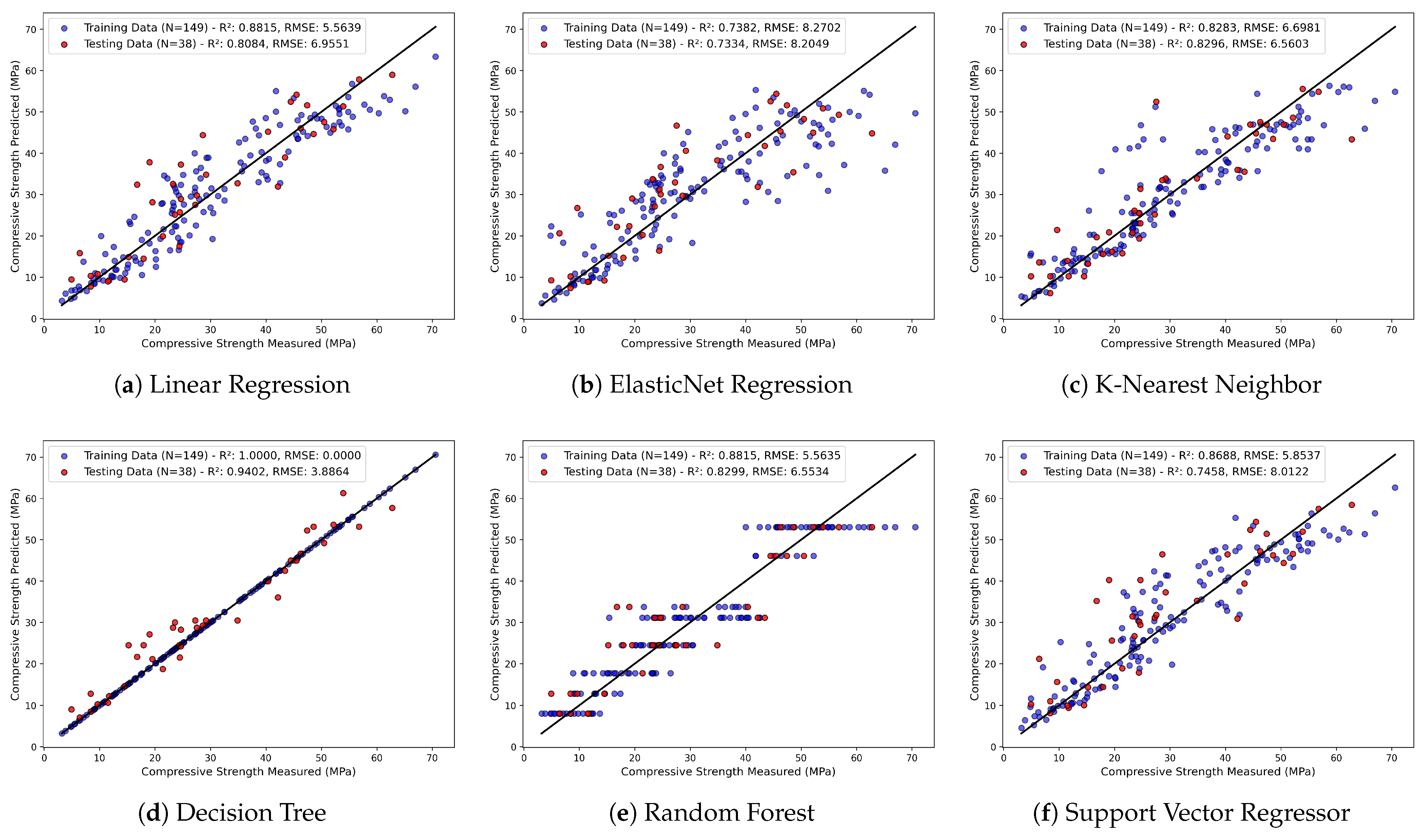
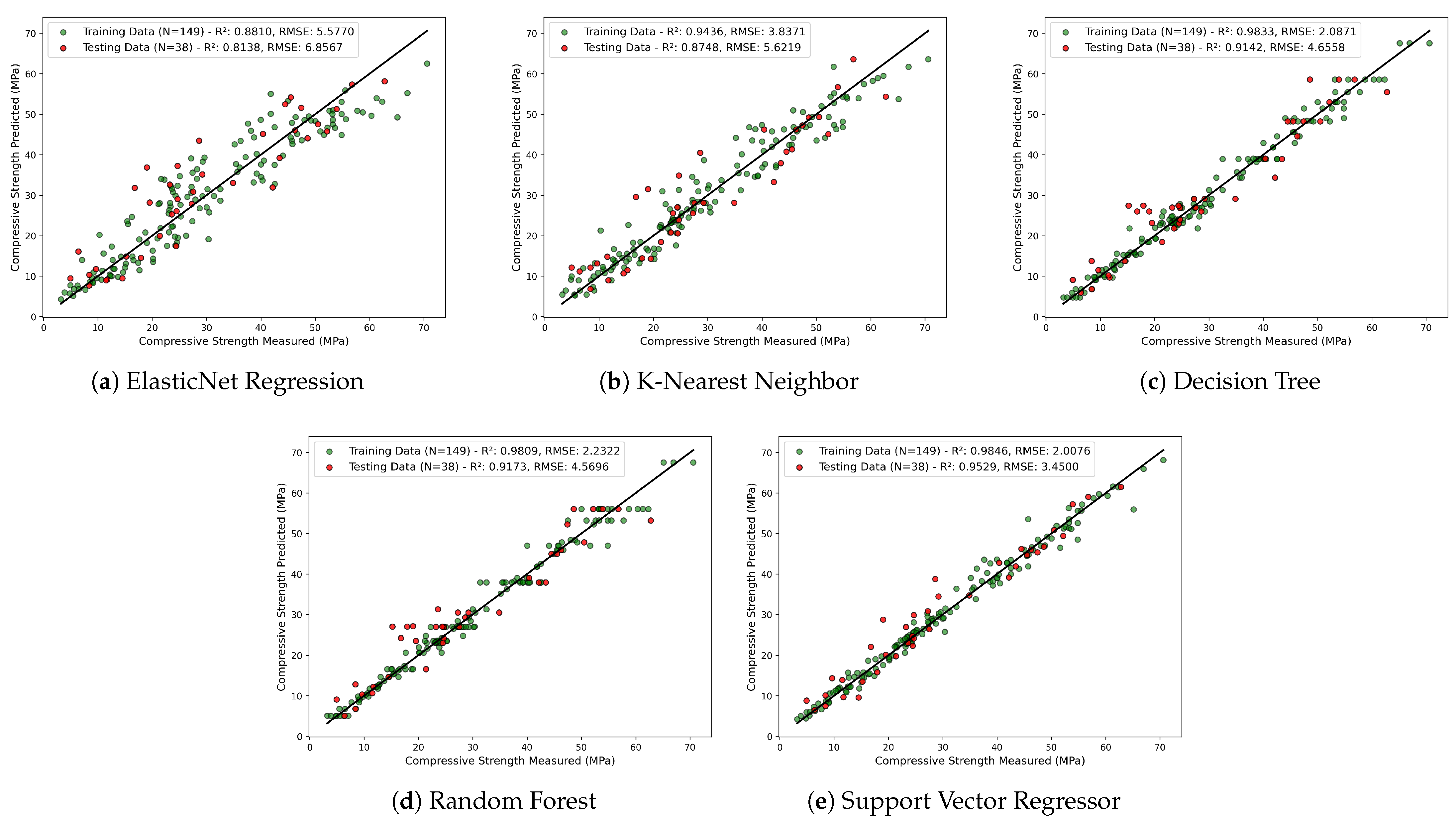
- Linear regression and ElasticNet regression exhibit stable yet moderate performance with similar R2 and RMSE values before hyperparameter tuning. However, ElasticNet regression shows a significant increase in the R2 value from 0.73 to 0.81 with a drop in RMSE value from 8.20 to 6.85 MPa for the test dataset after hyperparameter tuning.
- The K-Nearest Neighbor regressor model shows good prediction with the same R2 value of 0.82 for training and testing before hyperparameter tuning. Furthermore, with hyperparameter tuning, the R2 value increased to 0.87 and RMSE decreased to 5.62 MPa for the test dataset.
- The decision tree regressor demonstrates the highest accuracy (R2 = 1.0 for training, R2 = 0.94 for testing) before hyperparameter tuning due to the creation of deep trees. A reduction in overfitting and better generalization with training and testing datasets was achieved through hyperparameter tuning.
- The random forest regressor model exhibits moderate performance with an R2 of 0.82 and RMSE of 6.55 MPa for the test dataset. However, after hyperparameter tuning, the RMSE decreased to 4.56 MPa from 6.55 MPa and R2 improved to 0.91 from 0.82 for the test dataset. In conclusion, the RF model benefits from hyperparameter tuning, leading to improved generalization.
- Support vector regressor demonstrates lower accuracy with an R2 of 0.74 and RMSE of 8.01 MPa for the test dataset before hyperparameter tuning. However, a significant increase in R2 to 0.95 and a reduction in RMSE to 3.40 MPa show the superior predictive capability of SVR after hyperparameter tuning.
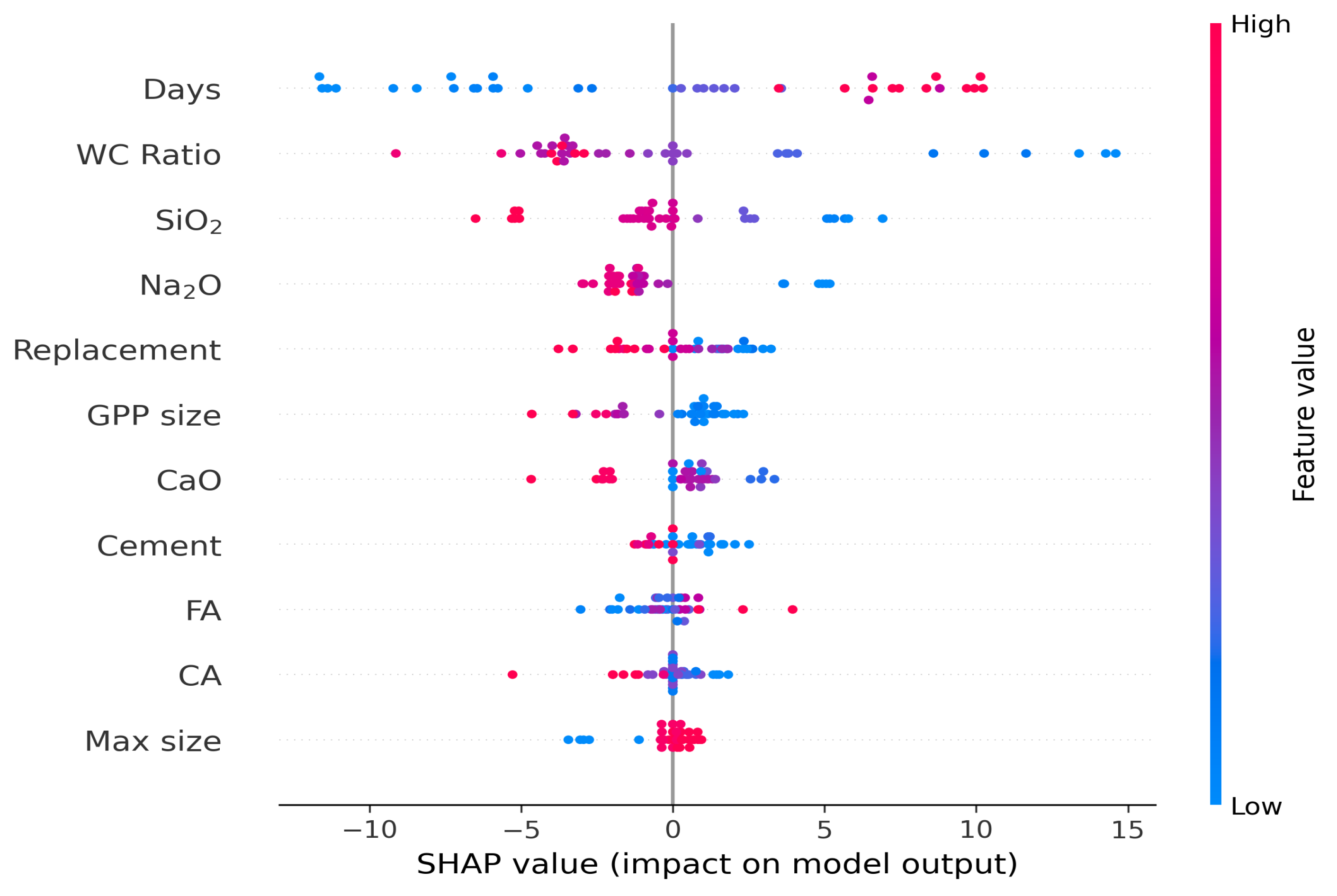
- SHAP analysis shows that curing time has the most significant positive influence, while the W/C ratio has the most significant negative influence on the prediction of CS for the SVR algorithm.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Feng, D.C.; Liu, Z.T.; Wang, X.D.; Chen, Y.; Chang, J.Q.; Wei, D.F.; Jiang, Z.M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Yehia, S.A.; Shahin, R.I.; Fayed, S. Compressive behavior of eco-friendly concrete containing glass waste and recycled concrete aggregate using experimental investigation and machine learning techniques. Constr. Build. Mater. 2024, 436, 137002. [Google Scholar] [CrossRef]
- Chopra, P.; Sharma, R.K.; Kumar, M.; Chopra, T. Comparison of machine learning techniques for the prediction of compressive strength of concrete. Adv. Civ. Eng. 2018, 2018, 5481705. [Google Scholar] [CrossRef]
- Elmikass, A.G.; Makhlouf, M.H.; Mostafa, T.S.; Hamdy, G.A. Experimental Study of the Effect of Partial Replacement of Cement with Glass Powder on Concrete Properties. Key Eng. Mater. 2022, 921, 231–238. [Google Scholar] [CrossRef]
- Abdelli, H.E.; Mokrani, L.; Kennouche, S.; de Aguiar, J.B. Utilization of waste glass in the improvement of concrete performance: A mini review. Waste Manag. Res. 2020, 38, 1204–1213. [Google Scholar] [CrossRef]
- Muhedin, D.A.; Ibrahim, R.K. Effect of waste glass powder as partial replacement of cement & sand in concrete. Case Stud. Constr. Mater. 2023, 19, e02512. [Google Scholar]
- Paul, S.C.; Šavija, B.; Babafemi, A.J. A comprehensive review on mechanical and durability properties of cement-based materials containing waste recycled glass. J. Clean. Prod. 2018, 198, 891–906. [Google Scholar] [CrossRef]
- Khatib, J.; Hibbert, J. Selected engineering properties of concrete incorporating slag and metakaolin. Constr. Build. Mater. 2005, 19, 460–472. [Google Scholar] [CrossRef]
- Siddique, R. Utilization of silica fume in concrete: Review of hardened properties. Resour. Conserv. Recycl. 2011, 55, 923–932. [Google Scholar] [CrossRef]
- Safiuddin, M.; West, J.; Soudki, K. Hardened properties of self-consolidating high performance concrete including rice husk ash. Cem. Concr. Compos. 2010, 32, 708–717. [Google Scholar] [CrossRef]
- Althoey, F.; Ansari, W.S.; Sufian, M.; Deifalla, A.F. Advancements in low-carbon concrete as a construction material for the sustainable built environment. Dev. Built Environ. 2023, 16, 100284. [Google Scholar] [CrossRef]
- Chousidis, N.; Rakanta, E.; Ioannou, I.; Batis, G. Mechanical properties and durability performance of reinforced concrete containing fly ash. Constr. Build. Mater. 2015, 101, 810–817. [Google Scholar] [CrossRef]
- Ramakrishnan, K.; Pugazhmani, G.; Sripragadeesh, R.; Muthu, D.; Venkatasubramanian, C. Experimental study on the mechanical and durability properties of concrete with waste glass powder and ground granulated blast furnace slag as supplementary cementitious materials. Constr. Build. Mater. 2017, 156, 739–749. [Google Scholar] [CrossRef]
- Teng, S.; Lim, T.Y.D.; Divsholi, B.S. Durability and mechanical properties of high strength concrete incorporating ultra fine ground granulated blast-furnace slag. Constr. Build. Mater. 2013, 40, 875–881. [Google Scholar] [CrossRef]
- Alharthai, M.; Onyelowe, K.C.; Ali, T.; Qureshi, M.Z.; Rezzoug, A.; Deifalla, A.; Alharthi, K. Enhancing concrete strength and durability through incorporation of rice husk ash and high recycled aggregate. Case Stud. Constr. Mater. 2025, 22, e04152. [Google Scholar] [CrossRef]
- Banerji, S.; Poudel, S.; Thomas, R.J. Performance of Concrete with Ground Glass Pozzolan as Partial Cement Replacement. In Proceedings of the 10th International Conference on CONcrete Under SEvere Conditions—Environment and Loading 2024, Chennai, India, 25–27 September 2024. [Google Scholar]
- Tural, H.; Ozarisoy, B.; Derogar, S.; Ince, C. Investigating the governing factors influencing the pozzolanic activity through a database approach for the development of sustainable cementitious materials. Constr. Build. Mater. 2024, 411, 134253. [Google Scholar] [CrossRef]
- Olaiya, B.C.; Lawan, M.M.; Olonade, K.A.; Segun, O.O. An overview of the use and process for enhancing the pozzolanic performance of industrial and agricultural wastes in concrete. Discov. Appl. Sci. 2025, 7, 164. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Zhou, S.; Tang, S.; Lu, X. Investigation of microstructure of CSH and micro-mechanics of cement pastes under NH4NO3 dissolution by 29Si MAS NMR and microhardness. Measurement 2021, 185, 110019. [Google Scholar] [CrossRef]
- Geng, Z.; Tang, S.; Wang, Y.; He, Z.; Wu, K.; Wang, L. Stress relaxation properties of calcium silicate hydrate: A molecular dynamics study. J. Zhejiang Univ. Sci. A 2024, 25, 97–115. [Google Scholar] [CrossRef]
- Poudel, S.; Bhetuwal, U.; Kharel, P.; Khatiwada, S.; KC, D.; Dhital, S.; Lamichhane, B.; Yadav, S.K.; Suman, S. Waste Glass as Partial Cement Replacement in Sustainable Concrete: Mechanical and Fresh Properties Review. Buildings 2025, 15, 857. [Google Scholar] [CrossRef]
- Miao, X.; Chen, B.; Zhao, Y. Prediction of compressive strength of glass powder concrete based on artificial intelligence. J. Build. Eng. 2024, 91, 109377. [Google Scholar] [CrossRef]
- Deschamps, J.; Simon, B.; Tagnit-Hamou, A.; Amor, B. Is open-loop recycling the lowest preference in a circular economy? Answering through LCA of glass powder in concrete. J. Clean. Prod. 2018, 185, 14–22. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, X.; Rajabipour, F.; Hendrickson, C.T. Comparative life cycle assessment of conventional, glass powder, and alkali-activated slag concrete and mortar. J. Infrastruct. Syst. 2014, 20, 04014020. [Google Scholar] [CrossRef]
- Mansour, M.A.; Ismail, M.H.B.; Imran Latif, Q.B.a.; Alshalif, A.F.; Milad, A.; Bargi, W.A.A. A systematic review of the concrete durability incorporating recycled glass. Sustainability 2023, 15, 3568. [Google Scholar] [CrossRef]
- Shi, C.; Wu, Y.; Riefler, C.; Wang, H. Characteristics and pozzolanic reactivity of glass powders. Cem. Concr. Res. 2005, 35, 987–993. [Google Scholar] [CrossRef]
- Shayan, A.; Xu, A. Value-added utilisation of waste glass in concrete. Cem. Concr. Res. 2004, 34, 81–89. [Google Scholar] [CrossRef]
- Xiao, R.; Prentice, D.; Collin, M.; Balonis, M.; La Plante, E.; Torabzadegan, M.; Gadt, T.; Sant, G. Calcium nitrate effectively mitigates alkali–silica reaction by surface passivation of reactive aggregates. J. Am. Ceram. Soc. 2024, 107, 7513–7527. [Google Scholar] [CrossRef]
- Song, H.; Ahmad, A.; Farooq, F.; Ostrowski, K.A.; Maślak, M.; Czarnecki, S.; Aslam, F. Predicting the compressive strength of concrete with fly ash admixture using machine learning algorithms. Constr. Build. Mater. 2021, 308, 125021. [Google Scholar] [CrossRef]
- Bhandari, I.; Kumar, R.; Sofi, A.; Nighot, N.S. A systematic study on sustainable low carbon cement – Superplasticizer interaction: Fresh, mechanical, microstructural and durability characteristics. Heliyon 2023, 9, e19176. [Google Scholar] [CrossRef]
- Linderoth, O.; Wadsö, L.; Jansen, D. Long-term cement hydration studies with isothermal calorimetry. Cem. Concr. Res. 2021, 141, 106344. [Google Scholar] [CrossRef]
- Jin, L.; Duan, J.; Jin, Y.; Xue, P.; Zhou, P. Prediction of HPC compressive strength based on machine learning. Sci. Rep. 2024, 14, 16776. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.; Anwar, M.R. The Future of Adaptive Machine Learning Algorithms in High-Dimensional Data Processing. Int. Trans. Artif. Intell. 2024, 3, 97–107. [Google Scholar] [CrossRef]
- Hajkowicz, S.; Sanderson, C.; Karimi, S.; Bratanova, A.; Naughtin, C. Artificial intelligence adoption in the physical sciences, natural sciences, life sciences, social sciences and the arts and humanities: A bibliometric analysis of research publications from 1960–2021. Technol. Soc. 2023, 74, 102260. [Google Scholar] [CrossRef]
- Sarker, I.H. Machine learning: Algorithms, real-world applications and research directions. SN Comput. Sci. 2021, 2, 160. [Google Scholar] [CrossRef]
- Niu, X.; Wang, L.; Yang, X. A comparison study of credit card fraud detection: Supervised versus unsupervised. arXiv 2019, arXiv:1904.10604. [Google Scholar]
- Hamed, A.K.; Elshaarawy, M.K.; Alsaadawi, M.M. Stacked-based machine learning to predict the uniaxial compressive strength of concrete materials. Comput. Struct. 2025, 308, 107644. [Google Scholar] [CrossRef]
- Bentegri, H.; Rabehi, M.; Kherfane, S.; Nahool, T.A.; Rabehi, A.; Guermoui, M.; Alhussan, A.A.; Khafaga, D.S.; Eid, M.M.; El-Kenawy, E.S.M. Assessment of compressive strength of eco-concrete reinforced using machine learning tools. Sci. Rep. 2025, 15, 5017. [Google Scholar] [CrossRef]
- Sathiparan, N. Predicting compressive strength in cement mortar: The impact of fly ash composition through machine learning. Sustain. Chem. Pharm. 2025, 43, 101915. [Google Scholar] [CrossRef]
- Sinkhonde, D.; Bezabih, T.; Mirindi, D.; Mashava, D.; Mirindi, F. Ensemble machine learning algorithms for efficient prediction of compressive strength of concrete containing tyre rubber and brick powder. Clean. Waste Syst. 2025, 10, 100236. [Google Scholar] [CrossRef]
- Abdellatief, M.; Murali, G.; Dixit, S. Leveraging machine learning to evaluate the effect of raw materials on the compressive strength of ultra-high-performance concrete. Results Eng. 2025, 25, 104542. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, J.; Xu, X.; Li, W.; Feng, X.; Lu, C.; Hu, Z.; Liu, J. A new method to evaluate features importance in machine-learning based prediction of concrete compressive strength. J. Build. Eng. 2025, 102, 111874. [Google Scholar] [CrossRef]
- Bypour, M.; Yekrangnia, M.; Kioumarsi, M. Machine Learning-Driven Optimization for Predicting Compressive Strength in Fly Ash Geopolymer Concrete. Clean. Eng. Technol. 2025, 25, 100899. [Google Scholar] [CrossRef]
- Bashir, A.; Gupta, M.; Ghani, S. Machine intelligence models for predicting compressive strength of concrete incorporating fly ash and blast furnace slag. Model. Earth Syst. Environ. 2025, 11, 129. [Google Scholar] [CrossRef]
- Jamal, A.S.; Ahmed, A.N. Estimating compressive strength of high-performance concrete using different machine learning approaches. Alex. Eng. J. 2025, 114, 256–265. [Google Scholar] [CrossRef]
- Khan, A.U.; Asghar, R.; Hassan, N.; Khan, M.; Javed, M.F.; Othman, N.A.; Shomurotova, S. Predictive modeling for compressive strength of blended cement concrete using hybrid machine learning models. Multiscale Multidiscip. Model. Exp. Des. 2025, 8, 25. [Google Scholar] [CrossRef]
- Nikoopayan Tak, M.S.; Feng, Y.; Mahgoub, M. Advanced Machine Learning Techniques for Predicting Concrete Compressive Strength. Infrastructures 2025, 10, 26. [Google Scholar] [CrossRef]
- Sah, A.K.; Hong, Y.M. Performance comparison of machine learning models for concrete compressive strength prediction. Materials 2024, 17, 2075. [Google Scholar] [CrossRef]
- Khan, K.; Ahmad, W.; Amin, M.N.; Rafiq, M.I.; Arab, A.M.A.; Alabdullah, I.A.; Alabduljabbar, H.; Mohamed, A. Evaluating the effectiveness of waste glass powder for the compressive strength improvement of cement mortar using experimental and machine learning methods. Heliyon 2023, 9, e16288. [Google Scholar] [CrossRef]
- Ben Seghier, M.E.A.; Golafshani, E.M.; Jafari-Asl, J.; Arashpour, M. Metaheuristic-based machine learning modeling of the compressive strength of concrete containing waste glass. Struct. Concr. 2023, 24, 5417–5440. [Google Scholar] [CrossRef]
- Alkadhim, H.A.; Amin, M.N.; Ahmad, W.; Khan, K.; Nazar, S.; Faraz, M.I.; Imran, M. Evaluating the strength and impact of raw ingredients of cement mortar incorporating waste glass powder using machine learning and SHapley additive ExPlanations (SHAP) methods. Materials 2022, 15, 7344. [Google Scholar] [CrossRef]
- Qasem, O.A.M.A. The Utilization of Glass Powder as Partial Replacement Material for the Mechanical Properties of Concrete. Ph.D. Thesis, Universitas Islam Indonesia, Yogyakarta, Indonesia, 2024. [Google Scholar]
- Shao, Y.; Lefort, T.; Moras, S.; Rodriguez, D. Studies on concrete containing ground waste glass. Cem. Concr. Res. 2000, 30, 91–100. [Google Scholar] [CrossRef]
- Tamanna, N.; Tuladhar, R. Sustainable use of recycled glass powder as cement replacement in concrete. Open Waste Manag. J. 2020, 13, 1–13. [Google Scholar] [CrossRef]
- Kim, S.K.; Kang, S.T.; Kim, J.K.; Jang, I.Y. Effects of particle size and cement replacement of LCD glass powder in concrete. Adv. Mater. Sci. Eng. 2017, 2017, 3928047. [Google Scholar] [CrossRef]
- Balasubramanian, B.; Krishna, G.G.; Saraswathy, V.; Srinivasan, K. Experimental investigation on concrete partially replaced with waste glass powder and waste E-plastic. Constr. Build. Mater. 2021, 278, 122400. [Google Scholar] [CrossRef]
- Khan, F.A.; Fahad, M.; Shahzada, K.; Alam, H.; Ali, N. Utilization of waste glass powder as a partial replacement of cement in concrete. Magnesium 2015, 2, 181–185. Available online: https://www.researchgate.net/publication/289537481_Utilization_of_waste_glass_powder_as_a_partial_replacement_of_cement_in_concrete (accessed on 7 April 2025).
- Kamali, M.; Ghahremaninezhad, A. Effect of glass powders on the mechanical and durability properties of cementitious materials. Constr. Build. Mater. 2015, 98, 407–416. [Google Scholar] [CrossRef]
- Zidol, A.; Tognonvi, M.T.; Tagnit-Hamou, A. Effect of glass powder on concrete sustainability. New J. Glass Ceram. 2017, 7, 34–47. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]
- Waskom, M.L. Seaborn: Statistical Data Visualization. J. Open Source Softw. 2021, 6, 3021. [Google Scholar] [CrossRef]
- Shrestha, N. Detecting multicollinearity in regression analysis. Am. J. Appl. Math. Stat. 2020, 8, 39–42. [Google Scholar] [CrossRef]
- Garrett, T.D.; Cardenas, H.E.; Lynam, J.G. Sugarcane bagasse and rice husk ash pozzolans: Cement strength and corrosion effects when using saltwater. Curr. Res. Green Sustain. Chem. 2020, 1, 7–13. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Van Rossum, G.; Drake, F.L., Jr. Python Reference Manual; Centrum voor Wiskunde en Informatica: Amsterdam, The Netherlands, 1995. [Google Scholar]
- Khademi, F.; Behfarnia, K. Evaluation of Concrete Compressive Strength Using Artificial Neural Network and Multiple Linear Regression Models. Int. J. Optim. Civil Eng. 2016, 6, 423–432. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. B Stat. Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Kelly, J.W.; Degenhart, A.D.; Siewiorek, D.P.; Smailagic, A.; Wang, W. Sparse linear regression with elastic net regularization for brain-computer interfaces. In Proceedings of the 2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society, San Diego, CA, USA, 28 August–1 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 4275–4278. [Google Scholar]
- Czajkowski, M.; Kretowski, M. The role of decision tree representation in regression problems–An evolutionary perspective. Appl. Soft Comput. 2016, 48, 458–475. [Google Scholar] [CrossRef]
- Pekel, E. Estimation of soil moisture using decision tree regression. Theor. Appl. Climatol. 2020, 139, 1111–1119. [Google Scholar] [CrossRef]
- Biau, G.; Scornet, E. A random forest guided tour. Test 2016, 25, 197–227. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random forests. In Ensemble Machine Learning: Methods and Applications; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar]
- Louppe, G. Understanding Random Forests: From Theory to Practice. Ph.D. Thesis, Universite de Liege, Liège, Belgium, 2014. [Google Scholar]
- Shao, W.; Yue, W.; Zhang, Y.; Zhou, T.; Zhang, Y.; Dang, Y.; Wang, H.; Feng, X.; Chao, Z. The Application of Machine Learning Techniques in Geotechnical Engineering: A Review and Comparison. Mathematics 2023, 11, 3976. [Google Scholar] [CrossRef]
- Rachmawati, D.A.; Ibadurrahman, N.A.; Zeniarja, J.; Hendriyanto, N. Implementation of The Random Forest Algorithm in Classifying The Accuracy of Graduation Time for Computer Engineering Students at Dian Nuswantoro University. J. Tek. Inform. (Jutif) 2023, 4, 565–572. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Azadkia, M. Optimal choice of k for k-nearest neighbor regression. arXiv 2019, arXiv:1909.05495. [Google Scholar]
- Beyer, K.; Goldstein, J.; Ramakrishnan, R.; Shaft, U. When is “nearest neighbor” meaningful? In Proceedings of the 7th International Conference on Database Theory (ICDT’99), Jerusalem, Israel, 10–12 January 1999; Proceedings 7. Springer: Berlin/Heidelberg, Germany, 1999; pp. 217–235. [Google Scholar]
- Jakkula, V. Tutorial on support vector machine (SVM). Sch. EECS Wash. State Univ. 2006, 37, 3. [Google Scholar]
- Valentini, G.; Dietterich, T.G. Bias-variance analysis of support vector machines for the development of SVM-based ensemble methods. J. Mach. Learn. Res. 2004, 5, 725–775. [Google Scholar]
- Blanco, V.; Puerto, J.; Rodriguez-Chia, A.M. On lp-support vector machines and multidimensional kernels. J. Mach. Learn. Res. 2020, 21, 1–29. [Google Scholar]
- Zhao, C.; Song, J.S. Exact heat kernel on a hypersphere and its applications in kernel SVM. Front. Appl. Math. Stat. 2018, 4, 1. [Google Scholar] [CrossRef]
- Maldonado-Romo, A.; Montiel-Pérez, J.Y.; Onofre, V.; Maldonado-Romo, J.; Sossa-Azuela, J.H. Quantum K-Nearest Neighbors: Utilizing QRAM and SWAP-Test Techniques for Enhanced Performance. Mathematics 2024, 12, 1872. [Google Scholar] [CrossRef]
- Ennouri, K.; Smaoui, S.; Gharbi, Y.; Cheffi, M.; Ben Braiek, O.; Ennouri, M.; Triki, M.A. Usage of artificial intelligence and remote sensing as efficient devices to increase agricultural system yields. J. Food Qual. 2021, 2021, 6242288. [Google Scholar] [CrossRef]
- Chicco, D.; Warrens, M.J.; Jurman, G. The coefficient of determination R-squared is more informative than SMAPE, MAE, MAPE, MSE and RMSE in regression analysis evaluation. PeerJ Comput. Sci. 2021, 7, e623. [Google Scholar] [CrossRef]
- Hossain, M.R.; Timmer, D. Machine learning model optimization with hyper parameter tuning approach. Glob. J. Comput. Sci. Technol. D Neural Artif. Intell 2021, 21, 31. [Google Scholar]
- Açikkar, M. Fast grid search: A grid search-inspired algorithm for optimizing hyperparameters of support vector regression. Turk. J. Electr. Eng. Comput. Sci. 2024, 32, 68–92. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.I. A unified approach to interpreting model predictions. Adv. Neural Inf. Process. Syst. 2017, 30. Available online: https://arxiv.org/abs/1705.07874v2 (accessed on 7 April 2025).
- Shamsabadi, E.A.; Roshan, N.; Hadigheh, S.A.; Nehdi, M.L.; Khodabakhshian, A.; Ghalehnovi, M. Machine learning-based compressive strength modelling of concrete incorporating waste marble powder. Constr. Build. Mater. 2022, 324, 126592. [Google Scholar] [CrossRef]
| No. | Algorithm | Predicted | Materials | Sample | Reference |
|---|---|---|---|---|---|
| 1 | RF, XGB, ANN | CS | Ordinary | 1030 | [37] |
| 2 | ET, XGBOOST, GBR, RF, DT, LIGHTGBM, ADA, KNN, BR, RIDGE, LR, LAR, HUBER, OMP, EN, LASSO, LLAR | CS | Fibers | 279 | [38] |
| 3 | KNN, SVR, XGB, ANN | CS | Flyash | 481 | [39] |
| 4 | DT, RF, SVR, ANN | CS | Tyre rubber and brick powder | 86 | [40] |
| 5 | SLR, RF, GB, XGB, GPR | CS | UHPC | 357 | [41] |
| 6 | XGB | CS | Flyash | 419 | [42] |
| 7 | DT, ET, RF, GB, EGB, AdaBoost | CS | Geopolymer | 161 | [43] |
| 8 | DT, RF, GBRT, XGB, AdaBoost | CS | Recycled aggregate | 319 | [2] |
| 9 | DT, RF, GBRT, XGB, AdaBoost | CS | Glass powder | 241 | [2] |
| 10 | SVR, LSSVR, ANFIS, MLP | CS | Glass powder | 830 | [50] |
| 11 | LR, ENR, KNN, DT, RF, SVR | CS | GGP | 187 | This study |
| Parameter | Unit | Minimum | Maximum | Mean | SD | Type |
|---|---|---|---|---|---|---|
| X1: GGP Size | m | 5 | 150 | 27.23 | 29.65 | Input |
| X2: Replacement | - | 5 | 40 | 19.79 | 11.64 | Input |
| X3: W/C | - | 0.35 | 0.71 | 0.5 | 0.09 | Input |
| X4: Cement | kg/m3 | 300 | 455.59 | 343.82 | 42.74 | Input |
| X5: Max size | mm | 10 | 20 | 18.75 | 2.72 | Input |
| X6: Coarse aggregate | kg/m3 | 943.1 | 1346 | 1045.82 | 103.32 | Input |
| X7: Fine aggregate | kg/m3 | 618 | 902 | 732.50 | 72.88 | Input |
| X8: SiO2 | % | 52.5 | 78.21 | 69.52 | 7.70 | Input |
| X9: CaO | % | 4.9 | 22.5 | 11.87 | 4.48 | Input |
| X10: Na2O | % | 0.08 | 16.3 | 8.93 | 5.16 | Input |
| X11: Curing time | days | 1 | 90 | 33.22 | 30.85 | Input |
| Y: Compressive strength | MPa | 3.19 | 70.6 | 29.90 | 16.11 | Output |
| Model | Before Hyperparameter Tuning | After Hyperparameter Tuning | ||||||
|---|---|---|---|---|---|---|---|---|
| Training Data | Testing Data | Training Data | Testing Data | |||||
| RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | |
| Linear Regression | 5.56 | 0.88 | 6.95 | 0.80 | – | – | – | – |
| ElasticNet Regression | 8.27 | 0.73 | 8.20 | 0.73 | 5.57 | 0.88 | 6.85 | 0.81 |
| K-Nearest Neighbor | 6.69 | 0.82 | 6.56 | 0.82 | 3.83 | 0.94 | 5.62 | 0.87 |
| Decision Tree | 0.00 | 1.00 | 3.88 | 0.94 | 2.08 | 0.98 | 4.65 | 0.91 |
| Random Forest | 5.56 | 0.88 | 6.55 | 0.82 | 2.23 | 0.98 | 4.56 | 0.91 |
| Support Vector Regressor | 5.85 | 0.86 | 8.01 | 0.74 | 2.00 | 0.98 | 3.40 | 0.95 |
| ENR | KNN | DT | RF | SVR |
|---|---|---|---|---|
| alpha = 0.01 | Neighbors = 3 | Max depth = 7 | No. of estimators = 79 | C = 100 |
| L1 ratio = 0.987 | p = 2 | criterion = squared error | Minimum samples splits = 2 | Epsilon = 0.1 |
| Weights = uniform | Min samples split = 3 | Minimum samples leaf = 1 | Kernel = rbf | |
| Min samples leaf = 2 | bootstrap = False | Gamma = 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Poudel, S.; Gautam, B.; Bhetuwal, U.; Kharel, P.; Khatiwada, S.; Dhital, S.; Sah, S.; KC, D.; Kim, Y.J. Prediction of Compressive Strength of Sustainable Concrete Incorporating Waste Glass Powder Using Machine Learning Algorithms. Sustainability 2025, 17, 4624. https://doi.org/10.3390/su17104624
Poudel S, Gautam B, Bhetuwal U, Kharel P, Khatiwada S, Dhital S, Sah S, KC D, Kim YJ. Prediction of Compressive Strength of Sustainable Concrete Incorporating Waste Glass Powder Using Machine Learning Algorithms. Sustainability. 2025; 17(10):4624. https://doi.org/10.3390/su17104624
Chicago/Turabian StylePoudel, Sushant, Bibek Gautam, Utkarsha Bhetuwal, Prabin Kharel, Sudip Khatiwada, Subash Dhital, Suba Sah, Diwakar KC, and Yong Je Kim. 2025. "Prediction of Compressive Strength of Sustainable Concrete Incorporating Waste Glass Powder Using Machine Learning Algorithms" Sustainability 17, no. 10: 4624. https://doi.org/10.3390/su17104624
APA StylePoudel, S., Gautam, B., Bhetuwal, U., Kharel, P., Khatiwada, S., Dhital, S., Sah, S., KC, D., & Kim, Y. J. (2025). Prediction of Compressive Strength of Sustainable Concrete Incorporating Waste Glass Powder Using Machine Learning Algorithms. Sustainability, 17(10), 4624. https://doi.org/10.3390/su17104624