Urban Joint Distribution Problem Optimization Model from a Low-Carbon Point of View
Abstract
1. Introduction
2. Literature Review
2.1. Research Status of Low-Carbon Logistics
2.2. Research Status of Route Optimization
3. Model Formulation
3.1. Distribution Vehicle Information
3.2. Model Assumptions
3.3. Model Symbol Description
3.4. Model Representation
4. Optimization and Solution of M Company’s Urban Joint Distribution Model
4.1. Scoring Based Delayed Delivery
4.1.1. Time Series Forecasting
4.1.2. Score Response Mechanism
4.1.3. Main Steps of Delayed Delivery
4.2. Improved Ant Colony Algorithm
4.2.1. Principle of Ant Colony Algorithm
4.2.2. Ant Colony Algorithm Optimization
Elite Ant Strategy
Minimum Energy Consumption and Actual Route Distance
Cluster Point Batch Processing
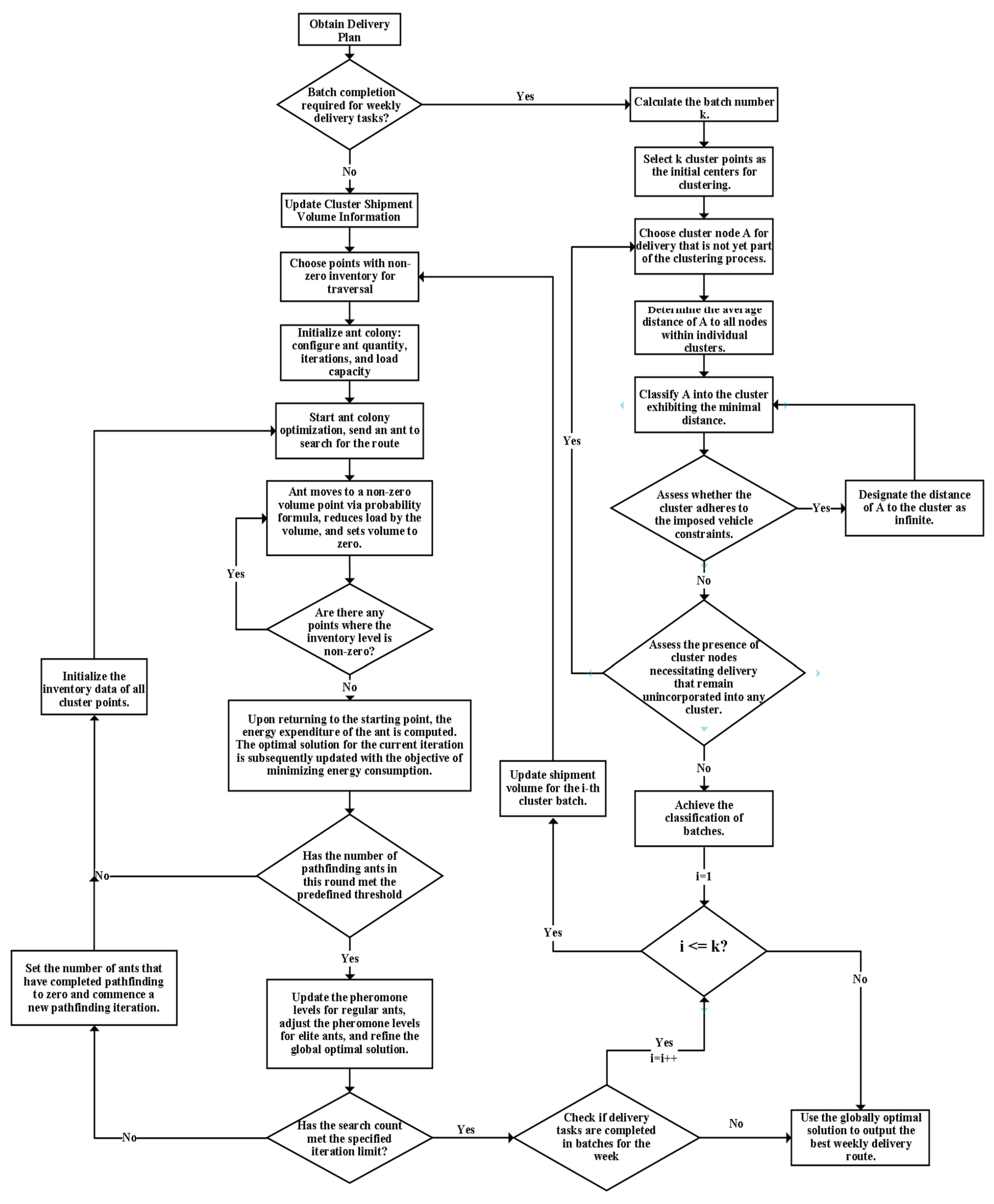
4.2.3. Steps to Improve the Ant Colony Algorithm
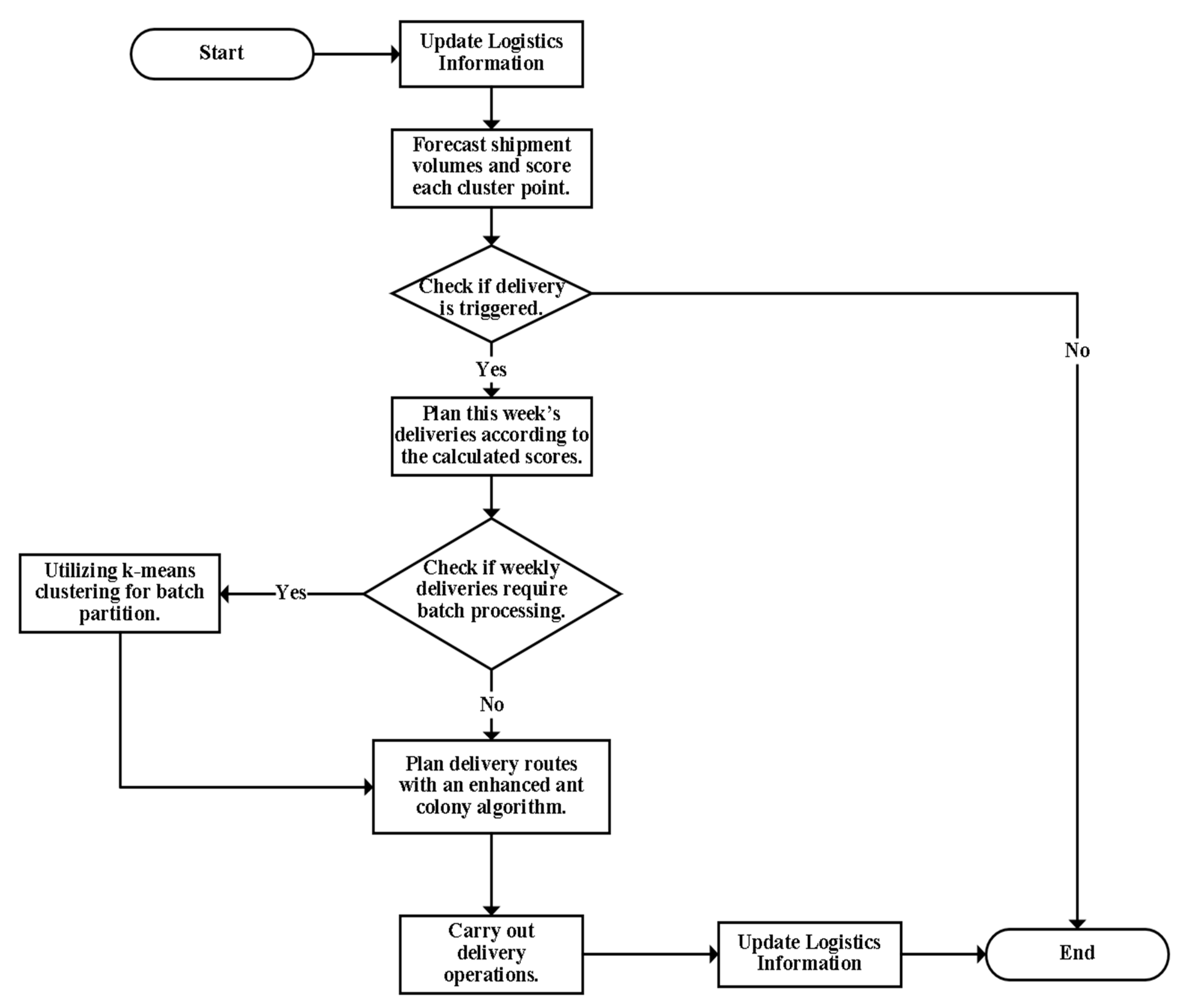
4.3. Flow of Optimized Model
5. Results
5.1. Instance Data and Parameters
5.2. Example Solution
5.2.1. Solution Steps
5.2.2. Final Distribution Route Solution
5.3. Comparative Analysis
5.3.1. Comparison of Distribution Planning
5.3.2. Comparison of Route Optimization
5.4. Summary of Optimization Results
6. Conclusions
6.1. Summary
6.2. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Library/Environment/Software | Version | Library/Environment/Software | Version |
|---|---|---|---|
| Dev-C++ | 6.3 | sympy | 1.6.2 |
| pandas | 1.4.2 | SQLAlchemy | 1.3.20 |
| numpy | 1.22.4 | Pillow | 8.0.1 |
| python-dateutil | 2.8.1 | matplotlib | 3.5.1 |
| scipy | 1.7.3 | openpyxl | 3.0.5 |
Appendix B
References
- Babagolzadeh, M.; Shrestha, A.; Abbasi, B.; Zhang, Y.; Woodhead, A.; Zhang, A. Sustainable cold supply chain management under demand uncertainty and carbon tax regulation. Transp. Res. Part D Transp. Environ. 2020, 80, 102245. [Google Scholar] [CrossRef]
- Cheng, L.D. Vehicle Routing Problem with Fuzzy Timewindows Considering with Carbon Emission. Ph.D. Thesis, Zhejiang University of Technology, Hangzhou, China, 2018. [Google Scholar]
- Lu, M.M. Research on Multi-Objective Path Planning Problem of Cold Chain Logistics with Carbon Emission and Fuzzy Time Windows. Ph.D. Thesis, Shanghai Ocean University, Shanghai, China, 2020. [Google Scholar]
- Dong, J.M. Research on the Vehicle Routing Optimization of Convenience Stores Considering Carbon Emissions and Multi Distribution Centers. Ph.D. Thesis, Nanjing University, Nanjing, China, 2021. [Google Scholar]
- Guo, Z.; Zhang, X.; Zheng, Y.; Rao, R. Exploring the impacts of a carbon tax on the Chinese economy using a CGE model with a detailed disaggregation of energy industrys. Energy Econ. 2014, 45, 455–462. [Google Scholar] [CrossRef]
- Hariga, M.; As’ad, R.; Shamayleh, A. Integrated economic and environmental models for a multi stage cold supply chain under carbon tax regulation. J. Clean. Prod. 2017, 166, 1357–1371. [Google Scholar] [CrossRef]
- Bai, Q.; Gong, Y.; Jin, M.; Xu, X. Effects of carbon emission reduction on supply chain coordination with vendor-managed deteriorating product inventory. Int. J. Prod. Econ. 2019, 208, 83–99. [Google Scholar] [CrossRef]
- Jauhari, W.A.; Cahaya Sakti, C.T.; Hisjam, M.; Hishamuddin, H. A sustainable circular economic supply chain model with green production, delays in payment, and carbon tax regulation. J. Clean. Prod. 2025, 495, 145008. [Google Scholar] [CrossRef]
- Shimizu, Y.; Sakaguchi, T.; Shimada, H. Multi-objective optimization for creating a low-carbon logistics system through community-based action. J. Adv. Mech. Des. Syst. Manuf. 2015, 9, JAMDSM0063. [Google Scholar] [CrossRef]
- Liu, F.; Chen, W.-L.; Fang, D.-B. Optimal coordination strategy of dynamic supply chain based on cooperative stochastic differential game model under uncertain conditions. Appl. Soft Comput. 2017, 56, 669–683. [Google Scholar] [CrossRef]
- Zhang, X.; Jin, F.-Y.; Yuan, X.-M.; Zhang, H.-Y. Low-Carbon Multimodal Transportation Path Optimization under Dual Uncertainty of Demand and Time. Sustainability 2021, 13, 8180. [Google Scholar] [CrossRef]
- Liu, Z.; Niu, Y.; Guo, C.; Jia, S. A Vehicle Routing optimization Model for Community Group Buying Considering Carbon Emissions and Total Distribution Costs. Energies 2023, 16, 931. [Google Scholar] [CrossRef]
- Ma, L.; Li, M. Research on a Joint Distribution Vehicle Routing Problem Considering Simultaneous Pick-Up and Delivery under the Background of Carbon Trading. Sustainability 2024, 16, 1698. [Google Scholar] [CrossRef]
- Dantzig, G.B.; Ramser, J.H. The truck dispatching problem. Manag. Sci. 1959, 6, 80–91. [Google Scholar] [CrossRef]
- Cheng, N.; She, L.; Chen, D. Electric Vehicle Charging Scheduling Optimization Method Based on Improved Ant Colony. J. Phys. Conf. Ser. 2023, 2418, 012112. [Google Scholar] [CrossRef]
- Gao, P.; Zhou, L.; Zhao, X.; Shao, B. Research on ship collision avoidance path planning based on modified potential field ant colony algorithm. Ocean Coast. Manag. 2023, 235, 106482. [Google Scholar] [CrossRef]
- Li, E.; Qi, K. Ant Colony Algorithm for Path Planning Based on Grid Feature Point Extraction. J. Shanghai Jiaotong Univ. (Sci.) 2023, 28, 86–99. [Google Scholar] [CrossRef]
- Luo, Q.; Wang, H.B.; Zheng, Y.; He, J.C. Research on path planning of mobile robot based on improved ant colony algorithm. Neural Comput. Appl. 2020, 32, 1555–1566. [Google Scholar] [CrossRef]
- Liu, J.H.; Yang, J.G.; Liu, H.P.; Tian, X.J.; Gao, M. An improved ant colony algorithm for robot path planning. Soft Comput. 2017, 21, 5829–5839. [Google Scholar] [CrossRef]
- Wei, L.; Zhang, Z.; Zhang, D.; Leung, S.C.H. A simulated annealing algorithm for the capacitated vehicle routing problem with two-dimensional loading constraints. Eur. J. Oper. Res. 2018, 265, 843–859. [Google Scholar] [CrossRef]
- Li, G.; Li, J. An Improved Tabu Search Algorithm for the Stochastic Vehicle Routing Problem With Soft Time Windows. IEEE Access 2020, 8, 158115–158124. [Google Scholar] [CrossRef]
- Xu, J.; Han, Y.; Liu, J.; Pan, N.; Yin, S.; Liang, W.; Han, W.; Lin, C. Investigation of the joint Automated mobile loading systems Two-Stage vehicle routing problem under the consideration of Supply-Demand Imbalance, fair Efficiency, and demand uncertainty. Comput. Oper. Res. 2025, 181, 107108. [Google Scholar] [CrossRef]
- Zhen, L.; Ma, C.; Wang, K.; Xiao, L.; Zhang, W. Multi-depot multi-trip vehicle routing problem with time windows and release dates. Transp. Res. Part E Logist. Transp. Rev. 2020, 135, 101866. [Google Scholar] [CrossRef]
- Zhang, S.; Gajpal, Y.; Appadoo, S.S.; Abdulkader, M.M.S. Electric vehicle routing problem with recharging stations for minimizing energy consumption. Int. J. Prod. Econ. 2018, 203, 404–413. [Google Scholar] [CrossRef]
- Xiong, H.; Xu, Y.; Yan, H.; Guo, H.; Zhang, C. Optimizing electric vehicle routing under traffic congestion: A comprehensive energy consumption model considering drivetrain losses. Comput. Oper. Res. 2024, 168, 106710. [Google Scholar] [CrossRef]
- Jiang, Y.; Hu, W.; Gu, W.; Yu, Y.; Xu, M. A multi-mode hybrid electric vehicle routing problem with time windows. Transp. Res. Part E Logist. Transp. Rev. 2025, 195, 103976. [Google Scholar] [CrossRef]
- Boyack, J.; Choi, J.B.; Jeong, J.; Park, H.; Kim, S. LogPath: Log data based energy consumption analysis enabling electric vehicle path optimization. Transp. Res. Part D Transp. Environ. 2024, 135, 104387. [Google Scholar] [CrossRef]
- Gao, C.H. Study on Optimization of Low-Carbon Distribution Routing of T Company. Ph.D. Thesis, University of Jinan, Shandong, China, 2022. [Google Scholar]
- Ottmar, R.D. Wildland fire emissions, carbon, and climate: Modeling fuel consumption. For. Ecol. Manag. 2014, 317, 41–50. [Google Scholar] [CrossRef]
- Chen, Y.S.; Ma, J.Q.; Ding, Z.S.; Chen, H. Research on life cycle energy conservation and emission reduction performance assessment of power system for pure electric vehicle. Mach. Electron. 2018, 36, 20–23. [Google Scholar]
- Liu, L.L.; Liu, T.L.; Jin, X.X. The discussion of calculation method of electric vehicle carbon emission and tracking evaluation. Intern. Combust. Engine Parts 2022, 196–198. [Google Scholar] [CrossRef]
- Tang, Y.Y.; Mao, B.H.; Zhou, Q.; Gao, Q.Q. Impact analysis on carbon emission factor in operations of electric vehicle. Transp. Energy Conserv. Environ. Prot. 2022, 18, 17–22. [Google Scholar]
- Xiao, Y.; Zhao, Q.; Kaku, I.; Xu, Y. Development of a fuel consumption optimization model for the capacitated vehicle routing problem. Comput. Oper. Res. 2012, 39, 1419–1431. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, D.P.; Zhao, Y. Study on the CO₂ emission evaluation of the provincial logistics operation and low-carbon strategy in china. China Popul. Resour. Environ. 2011, 21, 81–87. [Google Scholar]
- Xue, J.M.; Sun, A.R. Study on logistics service quality evaluation of takeout platform based on SERVPERF Model. J. Hebei Univ. Sci. Technol. (Soc. Sci.) 2021, 21, 35–43. [Google Scholar]
- De Livera, A.M.; Hyndman, R.J.; Snyder, R.D. Forecasting Time Series With Complex Seasonal Patterns Using Exponential Smoothing. J. Am. Stat. Assoc. 2011, 106, 1513–1527. [Google Scholar] [CrossRef]
- Wang, Y.F. Implementation of multiple vehicle routing optimization system based on ant colony clustering algorithm. J. Hubei Univ. Natl. (Nat. Sci. Ed.) 2015, 33, 200–204+209. [Google Scholar]


| Symbol | Symbolic Meaning | Symbol | Symbolic Meaning |
|---|---|---|---|
| Distribution vehicle energy consumption | Represents the distance from node to node | ||
| Expresses a collection of time in weeks | Indicates fuel/electricity consumption per unit distance when the vehicle is unloaded. | ||
| Represents the set of cluster points and distribution centers | Indicates fuel/electricity consumption per unit distance when the vehicle is fully loaded. | ||
| Represents the set of cluster points | Indicates the gross vehicle weight when the vehicle is unloaded | ||
| Represents the set of distribution centers | Indicates the maximum freight capacity of the vehicle | ||
| Represents the set of distribution batches | Indicates the loading capacity from node i to node j in week k | ||
| Represents the node, | Denotes the waiting time for the freight that should be distributed to node i in week k | ||
| indicates the distribution batch. ∈ | Indicates the maximum waiting time for freight that should be distributed to node i in week k | ||
| Indicates the time, | Denotes the freight weight scheduled for distribution to node i in week k | ||
| Indicates the maximum volume of the distribution vehicle | 0-1 variable indicating whether node i in week k is scheduled for distribution in batch b or not | ||
| denotes the volume of freight scheduled for distribution to node i in week k | Indicates the maximum mileage of the distribution vehicle in a single week | ||
| Indicates range of distribution vehicles | |||
| 0-1 variable indicating whether the week k distribution vehicle has traveled from node i to node j in batch b |
| Symbol | Symbolic Meaning | Symbol | Symbolic Meaning |
|---|---|---|---|
| Score of cluster i in week k | Maximum waiting time for cluster point i | ||
| Score presets to prevent negative scores | Maximum waiting time for freight at cluster point i in week k | ||
| Time reference value for cluster point i in week k | Weighting coefficient of freight weight reference value | ||
| Freight weight reference value for cluster point i in week k | Weighting coefficient of forecast value in week j | ||
| Weighting factors for time reference values | Forecasted freight weight in week j after cluster point i in week k | ||
| Natural constant | Distance from cluster point i to cluster point j | ||
| The associated reference value for cluster point i in week k, is influenced by other identified cluster points. | A set of cluster points identified for distribution operations | ||
| Weighting coefficient of associated reference value | |||
| The current weight of deliveries to be made at cluster point i in week k. |
| Symbol | Symbolic Meaning | Symbol | Symbolic Meaning |
|---|---|---|---|
| Probability that ant n chooses to go to point j at point i | Pheromone concentration between current loop nodes i, j | ||
| Pheromone concentration between nodes i, j | Pheromone concentration between the next loop nodes i, j | ||
| visibility coefficient between nodes i, j, numerically equal to | The amount of change in pheromone concentration between nodes i, j | ||
| Distance between nodes i, j | The total amount of pheromones carried by an ant | ||
| Important factors in pheromones, visibility | Horizontal and vertical coordinates of node i | ||
| The set of points that ant n can reach from its current location | Pheromone left by ant n between nodes i, j | ||
| Volatile coefficient of pheromone concentration | |||
| The total length of the path taken by ant n |
| Point Position | Euclidean Distance | Manhattan Distance | Actual Route Distance |
|---|---|---|---|
| Bajia Jiayuan, Beijing Jiaotong University | 7.1 km | 7.3 km | 8.1 km |
| Yuandayuan, Anzhenli community | 10.6 km | 12.6 km | 13 km |
| Beijing Foreign Studies University, Guoaocun community | 8.2 km | 11.6 km | 12 km |
| Serial Number | location | Week 1 | Week 2 | Week 3 | Week 4 |
|---|---|---|---|---|---|
| 1 | Yuanda Park and surrounding areas | 10.2 | 11.9 | 11.1 | 12.8 |
| 2 | Bajiajiayuan and surrounding areas | 9.1 | 9.7 | 8.4 | 9.9 |
| 3 | Beijing Foreign Studies University and surrounding areas | 22.8 | 43.7 | 13.3 | 24.7 |
| 4 | China Agricultural University and surrounding areas | 12.4 | 9.0 | 5.7 | 7.9 |
| 5 | Anxiangli and surrounding areas | 13.9 | 13.1 | 11.3 | 9.6 |
| 6 | China University of Geosciences and surrounding areas | 85.1 | 74.5 | 101.1 | 98.4 |
| 7 | Peony Garden Xili community and surrounding areas | 11.2 | 5.1 | 7.9 | 4.1 |
| 8 | Yilin homeland and surrounding areas | 8.5 | 9.2 | 5.4 | 6.9 |
| 9 | Anzhenli community and surrounding areas | 7.1 | 10.7 | 10.7 | 11.6 |
| 10 | Guoao village community and surrounding areas | 0 | 17.7 | 12.6 | 11.9 |
| 11 | Andedongli and surrounding areas | 15.7 | 18.6 | 12.9 | 21.5 |
| 12 | Huizhong Beili and surrounding areas | 11.5 | 6.6 | 19.7 | 18.0 |
| 13 | Beijing Normal University and surrounding areas | 64.1 | 66.6 | 81.1 | 69.0 |
| 14 | Huixin building and surrounding areas | 8.3 | 7.1 | 4.8 | 8.3 |
| 15 | Beiying community and its surrounding areas | 12.0 | 14.7 | 17.5 | 24.8 |
| 16 | Peking University and surrounding areas | 107.9 | 81.8 | 117.8 | 70.7 |
| 17 | Wanquan business garden and surrounding areas | 10.2 | 11.2 | 15.8 | 11.2 |
| 18 | Beijing Jiaotong University and surrounding areas | 36.5 | 25.7 | 31.1 | 20.3 |
| 19 | Beijing University of Aeronautics and Astronautics and surrounding areas | 55.9 | 31.6 | 20.0 | 41.2 |
| 20 | China University of political science and law and surrounding areas | 22.7 | 12.4 | 13.4 | 15.5 |
| 21 | Capital Institute of physical education and its surrounding areas | 21.3 | 17.0 | 25.6 | 19.9 |
| 22 | Renmin University of China and surrounding areas | 14.9 | 12.9 | 16.8 | 11.9 |
| Symbol | Meaning | Assignment |
|---|---|---|
| Delayed delivery stage: weight coefficient of reference value of cargo volume | 0.1 | |
| Delayed delivery stage: weight coefficient of time reference value | 1.0 | |
| Delayed delivery stage: weight coefficient of associated reference value | 0.5 | |
| Delayed delivery stage: weight coefficient of the forecast value in week j | 0.75, 0.5, 0.25 | |
| Path optimization stage: Volatilization Coefficient of pheromone concentration | 0.5 | |
| Path optimization stage: an important factor of pheromone | 1.0 | |
| Route optimization stage: an important factor of visibility | 2.0 | |
| Path optimization stage: the total amount of pheromones carried by elite ants | 100 | |
| Path optimization stage: the total amount of pheromones carried by ordinary ants | 50 |
| Node Serial Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 129 | 18 | 100 | 41 | 76 | 48 | 81 | 43 | 119 | 58 | 124 | 74 | 96 | 91 |
| 1 | 129 | 0 | 123 | 29 | 120 | 129 | 97 | 102 | 146 | 126 | 145 | 97 | 163 | 79 | 150 |
| 2 | 18 | 123 | 0 | 94 | 23 | 58 | 30 | 63 | 25 | 101 | 40 | 106 | 56 | 78 | 73 |
| 3 | 100 | 29 | 94 | 0 | 91 | 100 | 68 | 73 | 117 | 97 | 116 | 68 | 134 | 50 | 121 |
| 4 | 41 | 120 | 23 | 91 | 0 | 35 | 23 | 40 | 26 | 78 | 25 | 83 | 43 | 55 | 50 |
| 5 | 76 | 129 | 58 | 100 | 35 | 0 | 32 | 27 | 33 | 43 | 18 | 48 | 34 | 50 | 21 |
| 6 | 48 | 97 | 30 | 68 | 23 | 32 | 0 | 33 | 49 | 71 | 48 | 76 | 66 | 48 | 53 |
| 7 | 81 | 102 | 63 | 73 | 40 | 27 | 33 | 0 | 44 | 38 | 43 | 43 | 61 | 23 | 48 |
| 8 | 43 | 146 | 25 | 117 | 26 | 33 | 49 | 44 | 0 | 76 | 15 | 81 | 31 | 67 | 48 |
| 9 | 119 | 126 | 101 | 97 | 78 | 43 | 71 | 38 | 76 | 0 | 61 | 29 | 45 | 47 | 28 |
| 10 | 58 | 145 | 40 | 116 | 25 | 18 | 48 | 43 | 15 | 61 | 0 | 66 | 18 | 66 | 33 |
| 11 | 124 | 97 | 106 | 68 | 83 | 48 | 76 | 43 | 81 | 29 | 66 | 0 | 66 | 28 | 53 |
| 12 | 74 | 163 | 56 | 134 | 43 | 34 | 66 | 61 | 31 | 45 | 18 | 66 | 0 | 84 | 17 |
| 13 | 96 | 79 | 78 | 50 | 55 | 50 | 48 | 23 | 67 | 47 | 66 | 28 | 84 | 0 | 71 |
| 14 | 91 | 150 | 73 | 121 | 50 | 21 | 53 | 48 | 48 | 28 | 33 | 53 | 17 | 71 | 0 |
| 15 | 77 | 88 | 59 | 59 | 36 | 41 | 29 | 14 | 58 | 42 | 57 | 47 | 75 | 19 | 62 |
| 16 | 60 | 69 | 54 | 42 | 51 | 60 | 32 | 65 | 77 | 103 | 76 | 108 | 94 | 80 | 81 |
| 17 | 95 | 34 | 89 | 25 | 86 | 95 | 63 | 68 | 112 | 92 | 111 | 91 | 129 | 63 | 116 |
| 18 | 87 | 50 | 73 | 29 | 70 | 79 | 47 | 52 | 96 | 76 | 95 | 47 | 113 | 29 | 100 |
| Time | Route | Total Road Length (km) | Energy Consumption (Ah) |
|---|---|---|---|
| Week 1 | [0, 4, 6, 16, 22, 18, 20, 21, 19, 7, 5, 14, 0] | 35.6 | 24.45 |
| Week 2 | [0, 16, 3, 18, 19, 13, 11, 10, 0] | 35.6 | 24.87 |
| Week 3 | [0, 16, 17, 1, 3, 18, 20, 21, 19, 2, 0] [0, 6, 15, 13, 9, 12, 8, 0] | 27.4 25.6 | 20.12 17.01 |
| Week 4 | [0, 6, 5, 11, 13, 15, 22, 1, 16, 0] | 38.2 | 26.62 |
| Week 5 | [0, 2, 19, 21, 20, 18, 3, 1, 17, 22, 16, 0] [0, 4, 6, 5, 7, 15, 13, 11, 9, 14, 12, 10, 0] | 29.4 33.2 | 20.82 21.44 |
| Week 6 | [0, 2, 8, 10, 12, 14, 9, 11, 13, 20, 18, 3, 1, 17, 22, 16, 6, 19, 21, 15, 7, 5, 4, 0] | 52.4 | 39.78 |
| Week 7 | [0, 2, 4, 6, 19, 21, 22, 16, 17, 1, 3, 18, 20, 13, 11, 7, 5, 14, 12, 10, 8, 0] | 49.2 | 34.44 |
| Week 8 | [0, 4, 7, 15, 21, 19, 6, 16, 22, 17, 1, 3, 18, 20, 13, 11, 7, 5, 14, 12, 10, 8, 0] | 54.2 | 37.86 |
| Week 9 | [0, 2, 4, 6, 19, 21, 15, 7, 13, 20, 18, 3, 1, 22, 16, 12, 8, 0] | 47 | 32.05 |
| Method Name | Number of Distributions | Access to Cluster Points | Unladen Rate | Distribution Weight (kg) |
|---|---|---|---|---|
| Delayed delivery | 11 | 139 | 6.6% | 4111.3 |
| Fully loaded distribution | 10 | 151 | 0.2% | 3992.5 |
| Instant distribution | 16 | 197 | 34.9% | 4172.1 |
| Time | Route | Total Road Length (km) | Energy Consumption (Ah) |
|---|---|---|---|
| Week 1 | [0, 4, 14, 5, 7, 19, 21, 20, 18, 22, 16, 6, 0] | 34 | 28.39 |
| Week 2 | [0, 19, 16, 3, 18, 13, 11, 10, 0] | 35.2 | 25.25 |
| Week 3 | [0, 16, 17, 1, 3, 18, 20, 21, 19, 2, 0] [0, 8, 12, 9, 13, 15, 6, 0] | 27.4 25.6 | 20.12 21.08 |
| Week 4 | [0, 6, 5, 11, 13, 15, 22, 1, 16, 0] | 38.2 | 26.62 |
| Week 5 | [0, 2, 19, 21, 20, 18, 3, 1, 17, 22, 16, 0] [0, 10, 12, 14, 9, 11, 13, 15, 7, 5, 6, 4, 0] | 29.4 33.2 | 20.82 22.63 |
| Week 6 | [0, 2, 8, 10, 12, 14, 9, 11, 13, 20, 18, 3, 1, 17, 22, 16, 6, 19, 21, 15, 7, 5, 4, 0] | 52.4 | 39.78 |
| Week 7 | [0, 2, 8, 10, 12, 14, 5, 7, 19, 21, 20, 13, 11, 18, 3, 1, 17, 22, 16, 6, 4, 0] | 49.2 | 39.5 |
| Week 8 | [0, 8, 10, 12, 9, 11, 13, 15, 21, 18, 3, 1, 17, 22, 16, 6, 19, 7, 5, 4, 0] | 52.2 | 40.26 |
| Week 9 | [0, 2, 8, 12, 4, 6, 19, 21, 15, 7, 13, 20, 18, 1, 3, 22, 16, 0] | 43.8 | 32.99 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, L.; Cao, L.; Zhang, X.; Wu, Z. Urban Joint Distribution Problem Optimization Model from a Low-Carbon Point of View. Sustainability 2025, 17, 4602. https://doi.org/10.3390/su17104602
Kong L, Cao L, Zhang X, Wu Z. Urban Joint Distribution Problem Optimization Model from a Low-Carbon Point of View. Sustainability. 2025; 17(10):4602. https://doi.org/10.3390/su17104602
Chicago/Turabian StyleKong, Lingjia, Liting Cao, Xiaoyan Zhang, and Zhiguo Wu. 2025. "Urban Joint Distribution Problem Optimization Model from a Low-Carbon Point of View" Sustainability 17, no. 10: 4602. https://doi.org/10.3390/su17104602
APA StyleKong, L., Cao, L., Zhang, X., & Wu, Z. (2025). Urban Joint Distribution Problem Optimization Model from a Low-Carbon Point of View. Sustainability, 17(10), 4602. https://doi.org/10.3390/su17104602





