Factors Impacting Technical Efficiency in Mexican WUOs: A DEA with a Spatial Component
Abstract
1. Introduction
2. Literature Review
3. Methodology
Mathematical Model
- : quantity of input i used by DMU j (where i varies from 1 to m and j to 1 to n).
- : quantity of product r produced by DMU j (where r varies from 1 to 1).
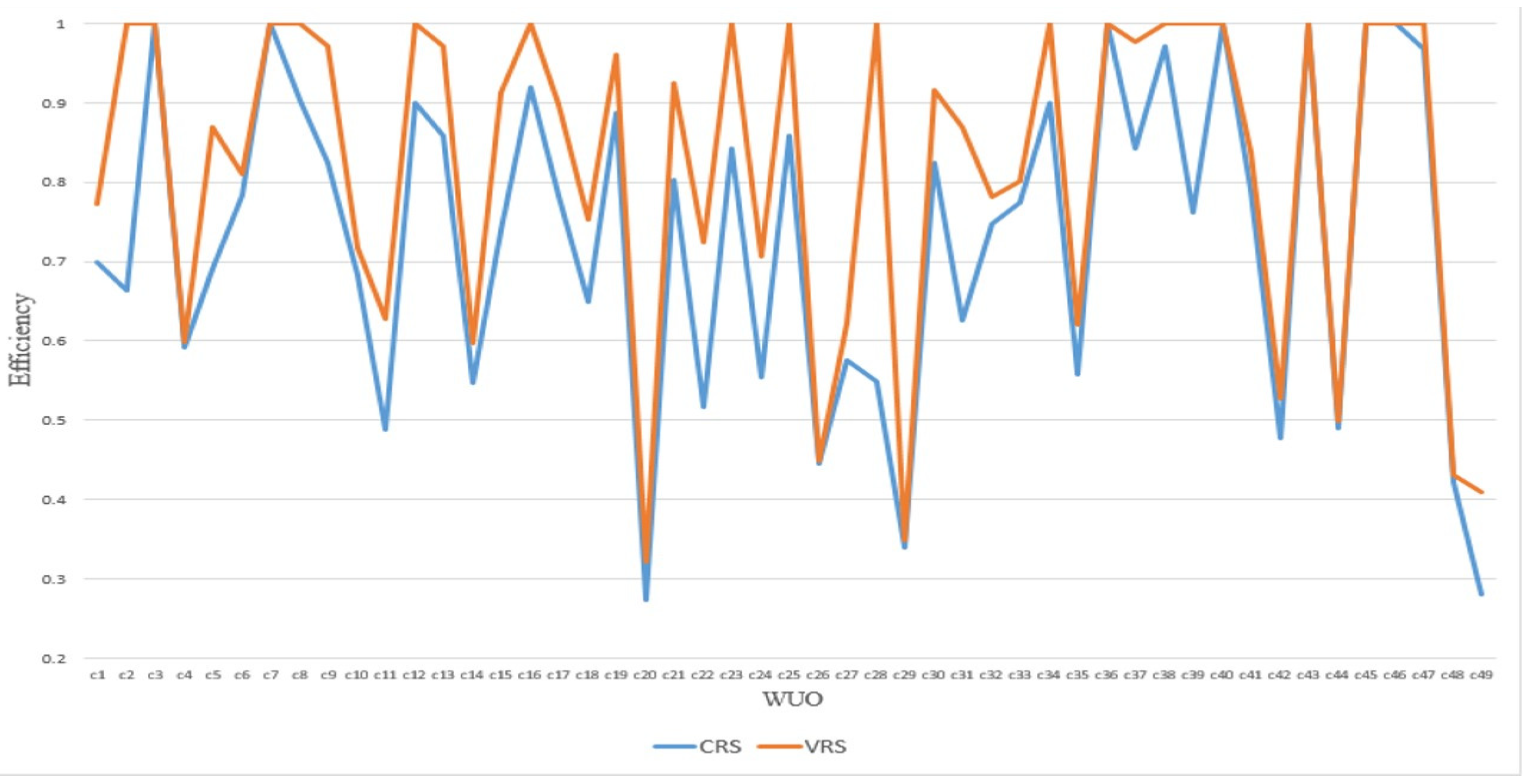
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WUOs | Water Utility Organizations |
| DEA | Data Envelopment Analysis |
| CRS | Constant Returns to Scale |
| VRS | Variable Returns to Scale |
| DMUs | Decision-Making Unit(s) |
| CV | Coefficient of variation |
| SD | Standard Deviation |
| PoblAtend | Population served |
| EmplTotal | Number of employees |
| CostoTotal | Total costs |
| VolProd | Total volume of drinking water |
| PIGOO | Program of Management Indicators of Operating Agencies |
| CONAGUA | National Water Commission |
| WUOs | Water Utility Organizations |
| DEA | Data Envelopment Analysis |
| CRS | Constant Returns to Scale |
| VRS | Variable Returns to Scale |
| DMUs | Decision-Making Unit(s) |
| CV | Coefficient of variation |
| SD | Standard Deviation |
| PoblAtend | Population served |
| EmplTotal | Number of employees |
| CostoTotal | Total costs |
| VolProd | Total volume of drinking water |
| PIGOO | Program of Management Indicators of Operating Agencies |
| CONAGUA | National Water Commission |
References
- Marques, R.C.; Berg, S.; Yane, S. Nonparametric benchmarking of Japanese water utilities: Institutional and environmental factors affecting efficiency. J. Water Resour. Plan. Manag. 2014, 140, 562–571. [Google Scholar] [CrossRef]
- Cetrulo, T.B.; Marques, R.C.; Malheiros, T.F. An analytical review of the efficiency of water and sanitation utilities in developing countries. Water Res. 2019, 161, 372–380. [Google Scholar] [CrossRef]
- Gidion, D.K.; Hong, J.; Adams, M.Z.; Khoveyni, M. Network DEA models for assessing urban water utility efficiency. Util. Policy 2019, 57, 48–58. [Google Scholar] [CrossRef]
- Golder, P.N.; Mitra, D.; Moorman, C. What is quality? An integrative framework of processes and states. J. Mark. 2012, 76, 1–23. [Google Scholar] [CrossRef]
- Carvalho, P.; Marques, R.C. The influence of the operational environment on the efficiency of water utilities. J. Environ. Manag. 2011, 92, 2698–2707. [Google Scholar] [CrossRef] [PubMed]
- Kirkpatrick, C.; Parker, D.; Zhang, Y.F. An empirical analysis of state and private-sector provision of water services in Africa. World Bank Econ. Rev. 2006, 20, 143–163. [Google Scholar] [CrossRef]
- Calabrese, A. Service productivity and service quality: A necessary trade-off? Int. J. Prod. Econ. 2012, 135, 800–812. [Google Scholar] [CrossRef]
- Feng, Y.; Zhu, Q.; Lai, K.H. Corporate social responsibility for supply chain management: A literature review and bibliometric analysis. J. Clean. Prod. 2017, 158, 296–307. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Maziotis, A. Drivers of productivity change in water companies: An empirical approach for England and Wales. Int. J. Water Resour. Dev. 2020, 36, 972–991. [Google Scholar] [CrossRef]
- Amaral, A.L.; Martins, R.; Dias, L.C. Drivers of water utilities’ operational performance–An analysis from the Portuguese case. J. Clean. Prod. 2023, 389, 136004. [Google Scholar] [CrossRef]
- Sharif, O.; Hasan, M.; Kurniasari, F.; Hermawan, A.; Gunardi, A. Productivity and efficiency analysis using DEA: Evidence from financial companies listed in bursa Malaysia. Management Sci. Lett. 2019, 9, 301–312. [Google Scholar] [CrossRef]
- Coelho, B.; Andrade-Campos, A. Efficiency achievement in water supply systems—A review. Renew. Sustain. Energy Rev. 2014, 30, 59–84. [Google Scholar] [CrossRef]
- Mann, P.C.; Mikesell, J.L. Ownership and water system operation 1. JAWRA J. Am. Water Resour. Assoc. 1976, 12, 995–1004. [Google Scholar] [CrossRef]
- Moher, D.; Cook, D.J.; Eastwood, S.; Olkin, I.; Rennie, D.; Stroup, D.F. Improving the quality of reports of meta-analyses of randomised controlled trials: The QUOROM statement. Lancet 1999, 354, 1896–1900. [Google Scholar] [CrossRef] [PubMed]
- Molinos-Senante, M.; Hernández-Sancho, F.; Sala-Garrido, R. Economic feasibility study for wastewater treatment: A cost–benefit analysis. Sci. Total Environ. 2010, 408, 4396–4402. [Google Scholar] [CrossRef]
- Ferro, G.; Romero, C.A.; Covelli, M.P. Regulation and performance: A production frontier estimate for the Latin American water and sanitation sector. Util. Policy 2011, 19, 211–217. [Google Scholar] [CrossRef]
- Romano, G.; Guerrini, A. Measuring and comparing the efficiency of water utility companies: A data envelopment analysis approach. Util. Policy 2011, 19, 202–209. [Google Scholar] [CrossRef]
- Grossman, P.J.; Mavros, P.; Wassmer, R.W. Public sector technical inefficiency in large US cities. J. Urban Econ. 1999, 46, 278–299. [Google Scholar] [CrossRef]
- De Witte, K.; Marques, R.C. Designing performance incentives, an international benchmark study in the water sector. Cent. Eur. J. Oper. Res. 2010, 18, 189–220. [Google Scholar] [CrossRef]
- Byrnes, J.; Crase, L.; Dollery, B.; Villano, R. The relative economic efficiency of urban water utilities in regional New South Wales and Victoria. Resour. Energy Econ. 2010, 32, 439–455. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Estimation and inference in two-stage, semi-parametric models of production processes. J. Econom. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Camanho, A.S.; Silva, M.C.; Piran, F.S.; Lacerda, D.P. A literature review of economic efficiency assessments using Data Envelopment Analysis. Eur. J. Oper. Res. 2024, 315, 1–18. [Google Scholar] [CrossRef]
- Bottasso, A.; Conti, M. Scale economies, technology and technical change in the water industry: Evidence from the English water only sector. Reg. Sci. Urban Econ. 2009, 39, 138–147. [Google Scholar] [CrossRef]
- Daraio, C.; Simar, L. Introducing environmental variables in nonparametric frontier models: A probabilistic approach. J. Product. Análisis 2005, 24, 93–121. [Google Scholar] [CrossRef]
- Sala-Garrido, R.; Mocholí-Arce, M.; Molinos-Senante, M.; Maziotis, A. Comparing operational, environmental and eco-efficiency of water companies in England and Wales. Energies 2021, 14, 3635. [Google Scholar] [CrossRef]
- Cheng, L.; Song, S.; Xie, Y. Evaluation of water resources utilization efficiency in Guangdong Province based on the DEA–Malmquist model. Front. Environ. Sci. 2022, 10, 819693. [Google Scholar] [CrossRef]
- Tourinho, M.; Barbosa, F.; Santos, P.R.; Pinto, F.T.; Camanho, A.S. Productivity change in Brazilian water services: A benchmarking study of national and regional trends. Socio-Econ. Plan. Sci. 2023, 86, 101491. [Google Scholar] [CrossRef]
- Estache, A.; Kouassi, E. Sector Organization, Governance, and the Inefficiency of African Water Utilities; World Bank Policy Research Working Paper 2890; World Bank: Washington, DC, USA, 2002; 21p, Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=636253 (accessed on 10 November 2024).
- Walter, M.; Cullmann, A.; von Hirschhausen, C.; Wand, R.; Zschille, M. Quo vadis efficiency analysis of water distribution? A comparative literature review. Util. Policy 2009, 17, 225–232. [Google Scholar] [CrossRef]
- Levidow, L.; Lindgaard-Jørgensen, P.; Nilsson, Å.; Skenhall, S.A.; Assimacopoulos, D. Process eco-innovation: Assessing meso-level eco-efficiency in industrial water-service systems. J. Clean. Prod. 2016, 110, 54–65. [Google Scholar] [CrossRef]
- Tupper, H.C.; Resende, M. Efficiency and regulatory issues in the Brazilian water and sewage sector: An empirical study. Util. Policy 2004, 12, 29–40. [Google Scholar] [CrossRef]
- Färe, R.; Grosskopf, S.; Norris, M.; Zhang, Z. Productivity growth, technical progress, and efficiency change in industrialized countries. Am. Econ. Rev. 1994, 84, 66–83. Available online: http://www.jstor.org/stable/2117971 (accessed on 12 November 2024).
- Meeusen, W.; van Den Broeck, J. Efficiency estimation from Cobb-Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econom. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Pinto, F.S.; Simões, P.; Marques, R.C. Raising the bar: The role of governance in performance assessments. Util. Policy 2017, 49, 38–47. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Maziotis, A.; Sala-Garrido, R. Assessment of the total factor productivity change in the English and Welsh water industry: A Färe-primont productivity index approach. Water Resour. Manag. 2017, 31, 2389–2405. [Google Scholar] [CrossRef]
- Walker, N.L.; Styles, D.; Gallagher, J.; Williams, A.P. Aligning efficiency benchmarking with sustainable outcomes in the United Kingdom water sector. J. Environ. Manag. 2021, 287, 112317. [Google Scholar] [CrossRef]
- Pineda Pablos, N. Urban water management between opportunism and adaptive development. In Water in Mexico, Actors, Sectors and Paradigms for An Ecological Social Transformation; Denzin, C., Taboada, F., Pacheco-Vega, R., Eds.; Friedrich-Ebert-Stiftung: Mexico City, Mexico, 2017; pp. 171–193. Available online: http://centro.paot.org.mx/documentos/paot/libro/aguaen_mexico.pdf (accessed on 15 November 2024).
- Maziotis, A.; Sala-Garrido, R.; Mocholi-Arce, M.; Molinos-Senante, M. Cost and quality of service performance in the Chilean water industry: A comparison of stochastic approaches. Struct. Change Econ. Dyn. 2023, 67, 211–219. [Google Scholar] [CrossRef]
- García-Rubio, M.A.; González-Gómez, F.; Guardiola, J. Performance and ownership in the governance of urban water. Proc. Inst. Civ. Eng.-Munic. Eng. 2010, 163, 51–58. [Google Scholar] [CrossRef]
- Mugisha, S. Performance assessment and monitoring of water infrastructure: An empirical case study of benchmarking in Uganda. Water Policy 2007, 9, 475–491. [Google Scholar] [CrossRef]
- Villegas, A.; Molinos-Senante, M.; Maziotis, A. Impact of environmental variables on the efficiency of water companies in England and Wales: A double-bootstrap approach. Environ. Sci. Pollut. Res. 2019, 26, 31014–31025. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Maziotis, A. The impact of greenhouse gas emissions on the performance of water companies: A dynamic assessment. Environ. Sci. Pollut. Res. 2021, 28, 48284–48297. [Google Scholar] [CrossRef]
- Mocholi-Arce, M.; Sala-Garrido, R.; Molinos-Senante, M.; Maziotis, A. Performance assessment of water companies: A metafrontier approach accounting for quality of service and group heterogeneities. Socio-Econ. Plan. Sci. 2021, 74, 100948. [Google Scholar] [CrossRef]
- See, K.F. Exploring and analysing sources of technical efficiency in water supply services: Some evidence from Southeast Asian public water utilities. Water Resour. Econ. 2015, 9, 23–44. [Google Scholar] [CrossRef]
- Hana, U. Competitive advantage achievement through innovation and knowledge. J. Compet. 2013, 5, 82–96. [Google Scholar] [CrossRef]
- Pinto, F.S.; Simões, P.; Marques, R.C. Water services performance: Do operational environment and quality factors count? Urban Water J. 2017, 14, 773–781. [Google Scholar] [CrossRef]
- Filippini, M.; Hrovatin, N.; Zoric, J. Cost efficiency of Slovenian water distribution utilities: An application of stochastic frontier methods. J. Prod. Anal. 2008, 29, 169–182. [Google Scholar] [CrossRef]
- Mbuvi, D.; De Witte, K.; Perelman, S. Urban water sector performance in Africa: A step-wise bias-corrected efficiency and effectiveness analysis. Util. Policy 2012, 22, 31–40. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Villegas, A.; Maziotis, A. Are water tariffs sufficient incentives to reduce water leakages? An empirical approach for Chile. Util. Policy 2019, 61, 100971. [Google Scholar] [CrossRef]
- Ferro, G.; Lentini, E.J.; Mercadier, A.C.; Romero, C.A. Efficiency in Brazil’s water and sanitation sector and its relationship with regional provision, property and the independence of operators. Util. Policy 2014, 28, 42–51. [Google Scholar] [CrossRef]
- Rodrigues, M.; Tavares, A.F. The same deep water as you? The impact of alternative governance arrangements of water service delivery on efficiency. J. Strateg. Contract. Negot. 2017, 3, 78–101. [Google Scholar] [CrossRef]
- Nyathikala, S.A.; Jamasb, T.; Llorca, M.; Kulshrestha, M. Utility governance, incentives, and performance: Evidence from India’s urban water sector. Util. Policy 2023, 82, 101534. [Google Scholar] [CrossRef]
- Heather, A.I.J.; Bridgeman, J. Water industry asset management: A proposed service-performance model for investment. Water Environ. J. 2007, 21, 127–132. [Google Scholar] [CrossRef]
- Vilarinho, H.; D’Inverno, G.; Nóvoa, H.; Camanho, A.S. The measurement of asset management performance of water companies. Socio-Econ. Plan. Sci. 2023, 87, 101545. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some models for estimating technical and scale inefficiencies in data envelopment analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Carvalho, P.; Marques, R.C.; Berg, S. A meta-regression analysis of benchmarking studies on water utilities market structure. Util. Policy 2012, 21, 40–49. [Google Scholar] [CrossRef]
- Anwandter, L. Can public sector reforms improve the efficiency of public water utilities? Environ. Dev. Econ. 2002, 7, 687–700. [Google Scholar] [CrossRef]
- Renzetti, S.; Dupont, D.P. Measuring the technical efficiency of municipal water suppliers: The role of environmental factors. Land Econ. 2009, 85, 627–636. [Google Scholar] [CrossRef]
- Saal, D.S.; Parker, D.; Weyman-Jones, T. Determining the contribution of technical change, efficiency change and scale change to productivity growth in the privatized English and Welsh water and sewerage industry: 1985–2000. J. Product. Anal. 2007, 28, 127–139. [Google Scholar] [CrossRef]
- De Witte, K.; Marques, R.C. Influential observations in frontier models, a robust non-oriented approach to the water sector. Ann. Oper. Res. 2010, 181, 377–392. [Google Scholar] [CrossRef]
- Xu, S.; Zhang, X.; Feng, L.; Yang, W. Disruption risks in supply chain management: A literature review based on bibliometric analysis. Int. J. Prod. Res. 2020, 58, 3508–3526. [Google Scholar] [CrossRef]
- Picazo-Tadeo, A.J.; Sáez-Fernández, F.J.; González-Gómez, F. Does service quality matter in measuring the performance of water utilities? Util. Policy 2008, 16, 30–38. [Google Scholar] [CrossRef]
- Marques, R.C.; Simões, P.; Pires, J.S. Performance benchmarking in utility regulation: The worldwide experience. Pol. J. Environ. Stud. 2011, 20, 125–132. Available online: https://www.pjoes.com/Performance-Benchmarking-in-Utility-Regulation-r-nthe-Worldwide-Experience,88538,0,2.html (accessed on 10 November 2024).
- Marques, R.C.; De Witte, K. Towards a benchmarking paradigm in European water utilities. Public Money Manag. 2010, 30, 42–48. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Donoso, G.; Sala-Garrido, R.; Villegas, A. Benchmarking the efficiency of the Chilean water and sewerage companies: A double-bootstrap approach. Environ. Sci. Pollut. Res. 2018, 25, 8432–8440. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Springer: New York, NY, USA, 2007; Volume 2, p. 489. [Google Scholar]
- Worthington, A.C. Efficiency, Technology, and Productivity Change in Australian Urban Water Utilities; Griffith University: Brisbane, Australia, 2011. [Google Scholar] [CrossRef]
- Buendía Hernández, A.; André, F.J.; Santos-Arteaga, F.J. On the Evolution and Determinants of Water Efficiency in the Regions of Spain. Water Resour. Manag. 2024, 38, 3093–3112. [Google Scholar] [CrossRef]
- Zschille, M.; Walter, M. The performance of German water utilities: A (semi)-parametric analysis. Appl. Econ. 2012, 44, 3749–3764. [Google Scholar] [CrossRef]
- Peda, P.; Grossi, G.; Liik, M. Do ownership and size affect the performance of water utilities? Evidence from Estonian municipalities. J. Manag. Gov. 2013, 17, 237–259. [Google Scholar] [CrossRef]
- Lambert, D.K.; Dichev, D.; Raffiee, K. Ownership and sources of inefficiency in the provision of water services. Water Resour. Res. 1993, 29, 1573–1578. [Google Scholar] [CrossRef]
- Berg, S.; Lin, C. Consistency in performance rankings: The Peru water sector. Appl. Econ. 2008, 40, 793–805. [Google Scholar] [CrossRef]
- Suárez-Varela, M.; de los Ángeles García-Valiñas, M.; González-Gómez, F.; Picazo-Tadeo, A.J. Ownership and performance in water services revisited: Does private management really outperform public? Water Resour. Manag. 2017, 31, 2355–2373. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Sala-Garrido, R. The impact of privatization approaches on the productivity growth of the water industry: A case study of Chile. Environ. Sci. Policy 2015, 50, 166–179. [Google Scholar] [CrossRef]
- Chakraborty, K.; Biswas, B.; Lewis, W.C. Measurement of technical efficiency in public education: A stochastic and nonstochastic production function approach. South. Econ. J. 2001, 67, 889–905. [Google Scholar] [CrossRef]
- Rangan, N.; Grabowski, R.; Aly, H.Y.; Pasurka, C. The technical efficiency of US banks. Econ. Lett. 1988, 28, 169–175. [Google Scholar] [CrossRef]
- Ferreira da Cruz, N.; Marques, R.C.; Romano, G.; Guerrini, A. Measuring the efficiency of water utilities: A cross-national comparison between Portugal and Italy. Water Policy 2012, 14, 841–853. [Google Scholar] [CrossRef]
- Maddala, G.S. Limited-Dependent and Qualitative Variables in Econometrics; Cambridge University Press: Cambridge, UK, 1983; Volume 149. [Google Scholar]
- Deng, G.; Li, L.; Song, Y. Provincial water use efficiency measurement and factor analysis in China: Based on SBM-DEA model. Ecol. Indic. 2016, 69, 12–18. [Google Scholar] [CrossRef]
- Abbott, M.; Cohen, B. Productivity and efficiency in the water industry. Util. Policy 2009, 17, 233–244. [Google Scholar] [CrossRef]
- Faraia, R.C.D.; Moreira, T.B.S.; Souza, G.S. Public versus private water utilities: Empirical evidence for Brazilian companies. Econ. Bull. 2005, 8, 1–7. Available online: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=662421 (accessed on 2 November 2024).
- Molinos-Senante, M.; Sala-Garrido, R.; Lafuente, M. The role of environmental variables on the efficiency of water and sewerage companies: A case study of Chile. Environ. Sci. Pollut. Res. 2015, 22, 10242–10253. [Google Scholar] [CrossRef]
- Lannier, A.L.; Porcher, S. Efficiency in the public and private French water utilities: Prospects for benchmarking. Appl. Econ. 2014, 46, 556–572. [Google Scholar] [CrossRef]
- De la Higuera-Molina, E.J.; Campos-Alba, C.M.; López-Pérez, G.; Zafra-Gómez, J.L. Efficiency of water service management alternatives in Spain considering environmental factors. Util. Policy 2023, 84, 101644. [Google Scholar] [CrossRef]
- García-Sánchez, I.M. Efficiency measurement in Spanish local government: The case of municipal water services. Rev. Policy Res. 2006, 23, 355–372. [Google Scholar] [CrossRef]
- Correia, T.; Marques, R.C. Performance of Portuguese water utilities: How do ownership, size, diversification and vertical integration relate to efficiency? Water Policy 2011, 13, 343–361. [Google Scholar] [CrossRef]
- Setiawan, A.R.; Gravitiani, E.; Rahardjo, M. Production cost efficiency analysis of regional water companies in eastern Indonesia. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 724, p. 012012. [Google Scholar] [CrossRef]
- Anh, N.V.; Tran, H.H.T. Evaluation of performance indicators of selected water companies in Viet Nam. Vietnam. J. Sci. Technol. 2020, 58, 42–53. [Google Scholar] [CrossRef]
- Chang, J.; Li, W.; Zhou, Y.; Zhang, P.; Zhang, H. Impact of public service quality on the efficiency of the water industry: Evidence from 147 cities in China. Sustainability 2022, 14, 15160. [Google Scholar] [CrossRef]
- Smithson, M.; Merkle, E.C. Generalized Linear Models for Categorical and Continuous Limited Dependent Variables; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Kleiber, C.; Zeileis, A. Applied Econometrics with R; Springer: New York, NY, USA, 2008. [Google Scholar]
- Bennich, A.; Engwall, M.; Nilsson, D. Operating in the shadowland: Why water utilities fail to manage decaying infrastructure. Util. Policy 2023, 82, 101557. [Google Scholar] [CrossRef]
- Molinos-Senante, M.; Maziotis, A.; Sala-Garrido, R.; Mocholi-Arce, M. Assesing the influence of environmental variables on the performance of water companies: An efficiency analysis tree approach. Expert Syst. Appl. 2023, 212, 118844. [Google Scholar] [CrossRef]
| Variable | Definition |
|---|---|
| Total employees (EmplTotal). | Represents the number of human resources assigned to the production and distribution of drinking water [88]. EmplTotal is used as input. |
| Total Cost (TotalCost). | The variable TotalCost, which includes all operational costs of a water utility (energy, chemicals, maintenance, administration), is used as an input in the DEA to assess efficiency. The objective is to minimize these costs to achieve a given level of production and service [89]. |
| Total volume of drinking water (VolProd). | It represents the total volume of potable water produced by a company, entering the output in the DEA efficiency assessment. This is further justified because production is maximized with the available resources, meaning that higher production with similar inputs highlights greater efficiency [90]. |
| Population served (PoblAtend) | It represents the total number of people who receive drinking water service, it is an outcome used in the DEA to evaluate the efficiency of the result. It is necessary to maximize the coverage capacity in relation to the available resources: a greater number of people served with the same contribution indicates greater efficiency [91]. Several studies, including PoblAtend, have applied it as an indicator of canned service, social impact, and overall capacity of the company on demand. |
| Microregion Category | Grouping Criteria (States Included, Based on Provided List) | Representative WUOs (Examples from Provided List) |
|---|---|---|
| Central (Code 1) | Aguascalientes, Puebla, Guanajuato, Estado de México, San Luis Potosí, Morelos, Hidalgo, Querétaro | Aguascalientes, Celaya, Huixquilucan, León, Pachuca, Puebla (Atlixco), Querétaro, SLP (Cd. Valles), Toluca |
| Center-West (Code 2) | Tamaulipas (Altamira), Jalisco, Guanajuato (Salamanca), Michoacán, Nayarit, Zacatecas (Zacatecas city) | Altamira, Guadalajara, Salamanca, Uruapan, Valle de Banderas, Zacatecas |
| Northeast (Code 3) | Coahuila, Chihuahua (Cuauhtémoc, Juárez), Tamaulipas (Matamoros, Nvo. Laredo, Tampico), Nuevo León | Acuña, Juárez, Matamoros, Monterrey, Nuevo Laredo, Piedras Negras, Saltillo, Tampico, Torreón |
| Northwest (Code 4) | Sonora, Chihuahua (Chihuahua city, Rosales), Sinaloa, Zacatecas (Fresnillo), Baja California | Agua Prieta, Chihuahua, Culiacán, Fresnillo, Hermosillo, Los Mochis, Mexicali, San Luis Río Colorado |
| South-Southeast (Code 5) | Quintana Roo, Campeche, Puebla (Puebla city), Chiapas, Guerrero | Cancún, Ciudad del Carmen, Puebla (H. Puebla), Playa del Carmen, San Cristóbal, San Fco. Campeche, Zihuatanejo |
| Max | Min | Standard Deviation (SD) | Coefficient of Variation (CV) | |
|---|---|---|---|---|
| TotalEmployees (total employees) | 4684.00 | 127.00 | 787.06 | 1.12 |
| CostTotal (total cost) | 478,689,022.10 | 935,663.00 | 85,065,234.75 | 1.28 |
| Vprod (Volume of drinking water production) (m3) | 8,501,117,672.79 | 52,474,136.00 | 1,306,895,758.27 | 1.70 |
| PobAtend (population served) | 4,957,280.00 | 105,201.00 | 931,248.79 | 1.36 |
| EmplTotal | TotalCost | Vprod | PopAtend | |
|---|---|---|---|---|
| EmplTotal | 1 | |||
| TotalCost | 0.95389497 | 1 | ||
| Vprod | 0.93444161 | 0.92170399 | 1 | |
| PopAtend | 0.94560348 | 0.91203689 | 0.95531224 | 1 |
| Dependent Variable | Model 1: CRS Inefficiency | Model 2: VRS Inefficiency |
|---|---|---|
| Model Parameters | ||
| Constant (Base Inefficiency) | 0.731 | 0.871 |
| Center-West (Code 2) | −0.118 (0.096) | −0.165 (0.129) |
| Northeast (Code 3) | −0.093 (0.094) | −0.151 (0.126) |
| Northwest (Code 4) | −0.062 (0.111) | −0.132 (0.148) |
| South-Southeast (Code 5) | −0.040 (0.116) | −0.020 (0.153) |
| Scale Parameter (ln(Sigma)) | −1.466 | −1.215 |
| Joint Significance Test | ||
| Wald Test (Microregions vs. Base) | p = 0.814 | p = 0.794 |
| (Degrees of freedom = 4) | ||
| Model Fit Measures | ||
| Observations (N) | 49 | 49 |
| Log-Likelihood | −5.8379 | −212.935 |
| Pseudo R2 (McKelvey–Zavoina) | ~0.003 | ~0.002 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Niebla Lizárraga, G.; Somoza Ríos, J.A.; Lizárraga Bernal, R.d.C.; Cañedo Raygoza, L.A. Factors Impacting Technical Efficiency in Mexican WUOs: A DEA with a Spatial Component. Sustainability 2025, 17, 4540. https://doi.org/10.3390/su17104540
Niebla Lizárraga G, Somoza Ríos JA, Lizárraga Bernal RdC, Cañedo Raygoza LA. Factors Impacting Technical Efficiency in Mexican WUOs: A DEA with a Spatial Component. Sustainability. 2025; 17(10):4540. https://doi.org/10.3390/su17104540
Chicago/Turabian StyleNiebla Lizárraga, Gilberto, Jesús Alberto Somoza Ríos, Rosa del Carmen Lizárraga Bernal, and Luis Alonso Cañedo Raygoza. 2025. "Factors Impacting Technical Efficiency in Mexican WUOs: A DEA with a Spatial Component" Sustainability 17, no. 10: 4540. https://doi.org/10.3390/su17104540
APA StyleNiebla Lizárraga, G., Somoza Ríos, J. A., Lizárraga Bernal, R. d. C., & Cañedo Raygoza, L. A. (2025). Factors Impacting Technical Efficiency in Mexican WUOs: A DEA with a Spatial Component. Sustainability, 17(10), 4540. https://doi.org/10.3390/su17104540








