Research on Strategy Selection of Power Supply Chain Under Renewable Energy Consumption and Energy Storage Cost Sharing
Abstract
1. Introduction
2. Literature Review
2.1. Environmental Policy Research
2.2. Research on the Current State of Energy Storage
2.3. Research on Enterprise Cost-Allocation Problem
- In contrast to existing studies that focus on power generation companies’ investments in renewable energy electricity, this paper constructs Stackelberg game models under various scenarios to investigate the renewable energy investment strategies of electricity retailers. Furthermore, we incorporate the renewable energy (RE) consumption policy and the green certificate trading market into the decision-making framework of the electricity supply chain.
- In contrast to existing research focusing on cost allocation for energy storage within the same tier of the power supply chain, this paper investigates cost-sharing mechanisms for energy storage between generation companies and electricity retailers. Furthermore, it analyzes the impact of different cost-allocation models on power supply chain members’ decision-making.
- To conduct a comparative analysis of the advantages and disadvantages of the two distinct energy storage cost allocation methods, in the numerical simulation section, we conduct a comparative analysis of decision-making behaviors among power supply chain members under four distinct models, followed by an examination of optimal mode selection strategies for power enterprises.
3. Problem Description and Model Assumptions
- The power supplier and retailer are both rational and share information.
- Electricity price will not only be affected by demand, but also by the reliability of power supply [50]. The inverse demand function of users for electricity is shown in Equation (1).
- The renewable energy input cost of power producers or retailers is , where is the renewable energy input cost coefficient, and represents the amount of renewable energy input [52].
- The power supplier carries out the construction of an energy storage power station, and the construction cost of the energy storage power plant is , where denotes the energy storage cost coefficient, and denotes the stability of power supply [53].
- The generator and retailers share energy storage investment costs. Under the unit power method, the retailer needs to bear the cost per unit of electricity of the power producer (generator decision-making). Under the proportional method, the retailer pays a certain percentage of the energy storage investment cost incurred by the generator, assuming that the proportion is (generator decision-making).
4. Model Construction and Solution
4.1. Model Construction and Solution Under the Unit Power Method
4.1.1. RE-Investment (UK)
4.1.2. No-RE-Investment (UT)
4.2. Model Construction and Solution Under Proportional Method
4.2.1. RE-Investment (YK)
4.2.2. No-RE-Investment (YT)
5. Equilibrium Analysis
- 1.
- ;;;;;
- 2.
- ;;;
- 3.
- ;;;;;
- 4.
- ; ; .
- 1.
- if , then , if , then ;
- 2.
- if , then , if , then ;
- 3.
- if , then ; if , then ;
- 4.
- if , then ; if , then .
- 1.
- ; ; ;
- 2.
- ; ; ;
- 3.
- ; ; ;
- 4.
- ; ; .
- 1.
- if , then ; if , then ;
- 2.
- if , then ; if , then .
- 1.
- When , if , then , if , then ; when , ; ;
- 2.
- When , if , then , if , then ; when , then ; .
- 1.
- When , if , then , if , then ; when , then ;
- 2.
- If , then , if , then ;
- 3.
- When , if , then , if , then ; when , then ;
- 4.
- If , then ; if , then .
6. Analysis of Power Retailer Strategy Selection
6.1. Strategy Selection of Retailer Under Unit Electricity Method
6.2. The Selection of Retailer Strategy Under the Proportional Method
7. Numerical Example
7.1. Electricity Retailers’ Renewable Energy Input Influencing Factors Analysis
7.2. Electricity Price Impacts Factors Analysis
7.3. Analysis of the Factors Affecting the Profit of Power Producers
7.4. Analysis of Influencing Factors of Retailer Profit
7.5. Analysis of Influencing Factors of Supply Chain Profit
7.6. Comparative Analysis of the Four Models
8. Model Extension
- 1.
- When , , ;
- 2.
- When , , .
- 1.
- ; when , , when , ;
- 2.
- ; when , , when , .
- 1.
- ; when , , when , ;
- 2.
- ; when , , when , .
9. Concluding Remarks
9.1. Conclusions
- An increase in the proportion of renewable energy consumption results in a reduction in wholesale electricity price, power stability, renewable energy input, power purchases, electricity sales, and the profits of power companies. However, the impact on electricity prices is influenced by the energy storing cost coefficient. When the coefficient for energy storage expenses is elevated, electricity prices increase as the proportion of renewable energy utilized rises; otherwise, electricity prices decrease.
- An increase in the green certificate price reduces the wholesale price, power stability, and electricity purchases. However, the changes in electricity price, renewable energy input, and electricity sales resulting from a growth in the green certificate price are influenced by both the energy storage cost coefficient and the proportion of renewable energy consumption.
- A higher greater proportion of cost allocation for energy storage can compel electricity retail companies to increase their investment in renewable energy.
- When the energy storage cost is low, a higher proportion of renewable energy consumption can encourage the seller to allocate funds for sustainable energy, and the retailer’s investment in renewable energy will reduce electricity price and improve its own profit, but will damage the benefit of the power producer.
- When the power supplier and the retailer use the proportional method to share the energy storage cost and the retailer chooses to take responsibility for consumption by investing in renewable energy, it can increase the renewable energy input of the retailer and maximize the supply chain profit.
- Under conditions of information asymmetry in demand, when generation companies or electricity retailers exhibit risk-averse behavior, the renewable consumption standards and the trading price of green certificates will not alter their impact on both wholesale electricity price and general electricity pricing.
9.2. Practical Implication
- For governments, it is essential to establish a renewable energy consumption ratio based on regional realities. For instance, regions abundant in hydropower, wind, and solar resources should be assigned higher renewable energy consumption quotas, while those with scarce renewable resources may be subject to lower requirements. Meanwhile, proactive measures must be taken to regulate the green certificate trading market, ensuring prices remain within a reasonable range. Policymakers should facilitate technological collaboration within the power sector, revitalize certificate trading, and stabilize price levels through targeted interventions.
- For the power companies, it is essential to strengthen energy storage research and development to reduce energy storage costs, enhance profitability, and improve total supply chain profit. It should also appropriately increase the proportion of energy storage costs allocated to electricity retail companies, which can compel electricity retail company to invest in renewable energy.
- For the retailer, investing in renewable energy can reduce electricity prices and increase both their own profits and the overall supply chain profits. This approach not only benefits environmental protection but also serves the interests of consumers. In recent years, China has actively promoted the market-oriented reform of its power sector. For electricity retail companies, aligning with policy requirements and proactively investing in renewable energy represents a strategic approach to fostering their own development.
9.3. Limitations and Future Directions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Feng, C.; Liu, Y.-Q.; Yang, J. Do Energy Trade Patterns Affect Renewable Energy Development? The Threshold Role of Digital Economy and Economic Freedom. Technol. Forecast. Soc. Change 2024, 203, 123371. [Google Scholar] [CrossRef]
- Erdoğdu, A.; Dayi, F.; Yanik, A.; Yildiz, F.; Ganji, F. Innovative Solutions for Combating Climate Change: Advancing Sustainable Energy and Consumption Practices for a Greener Future. Sustainability 2025, 17, 2697. [Google Scholar] [CrossRef]
- Maliszewska-Nienartowicz, J. Impact of Russia’s Invasion of Ukraine on Renewable Energy Development in Germany and Italy. Util. Policy 2024, 87, 101731. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, H.; Yuan, Y.; Li, M. Can Renewable Energy Development Facilitate China’s Sustainable Energy Transition? Perspective from Energy Trilemma. Energy 2024, 304, 132160. [Google Scholar] [CrossRef]
- Huang, H.; Mbanyele, W.; Wang, F.; Song, M.; Wang, Y. Climbing the Quality Ladder of Green Innovation: Does Green Finance Matter? Technol. Forecast. Soc. Change 2022, 184, 122007. [Google Scholar] [CrossRef]
- Mbanyele, W.; Huang, H.; Muchenje, L.T.; Zhao, J. How Does Climate Regulatory Risk Influence Labor Employment Decisions? Evidence from a Quasi-Natural Experiment. China Econ. Rev. 2024, 87, 102236. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, H.; Mbanyele, W.; Wei, Z.; Li, X. How Does Green Industrial Policy Affect Corporate Green Innovation? Evidence from the Green Factory Identification in China. Energy Econ. 2025, 141, 108047. [Google Scholar] [CrossRef]
- Huang, H.; Mbanyele, W.; Zhang, L.; Chen, X.-L.; Song, M. Nonnegligible Transition Risks towards Net-Zero Economy: Lessons from Green Finance Initiatives in China. J. Environ. Manag. 2025, 375, 124132. [Google Scholar] [CrossRef]
- Huang, H.; Mbanyele, W.; Wang, F.; Zhang, C.; Zhao, X. Nudging Corporate Environmental Responsibility through Green Finance? Quasi-Natural Experimental Evidence from China. J. Bus. Res. 2023, 167, 114147. [Google Scholar] [CrossRef]
- Dimitriadis, C.N.; Tsimopoulos, E.G.; Georgiadis, M.C. Co-Optimized Trading Strategy of a Renewable Energy Aggregator in Electricity and Green Certificates Markets. Renew. Energy 2024, 236, 121444. [Google Scholar] [CrossRef]
- Karakosta, O.; Petropoulou, D. The EU Electricity Market: Renewables Targets, Tradable Green Certificates and Electricity Trade. Energy Econ. 2022, 111, 106034. [Google Scholar] [CrossRef]
- Yu, X.; Ge, S.; Zhou, D.; Wang, Q.; Chang, C.-T.; Sang, X. Whether Feed-in Tariff Can Be Effectively Replaced or Not? An Integrated Analysis of Renewable Portfolio Standards and Green Certificate Trading. Energy 2022, 245, 123241. [Google Scholar] [CrossRef]
- Ji, C.-Y.; Tan, Z.-K.; Chen, B.-J.; Zhou, D.-C.; Qian, W.-Y. The Impact of Environmental Policies on Renewable Energy Investment Decisions in the Power Supply Chain. Energy Policy 2024, 186, 113987. [Google Scholar] [CrossRef]
- Meng, X.; Yu, Y. Can Renewable Energy Portfolio Standards and Carbon Tax Policies Promote Carbon Emission Reduction in China’s Power Industry? Energy Policy 2023, 174, 113461. [Google Scholar] [CrossRef]
- Bangjun, W.; Yue, W.; Linyu, C.; Kejia, X. Supply Chain Coordination Mechanisms of Coal Power Enterprises under Renewable Energy Quota System: A Perspective of Game Analysis. J. Clean. Prod. 2023, 426, 139108. [Google Scholar] [CrossRef]
- Qu, R.; Kou, R.; Zhang, T. The Impact of Weather Variability on Renewable Energy Consumption: Insights from Explainable Machine Learning Models. Sustainability 2025, 17, 87. [Google Scholar] [CrossRef]
- Chakraborty, N.; Choudhury, N.B.D.; Tiwari, P.K. Profit Maximization of Retailers with Intermittent Renewable Sources and Energy Storage Systems in Deregulated Electricity Market with Modern Optimization Techniques: A Review. Renew. Energy Focus 2023, 47, 100492. [Google Scholar] [CrossRef]
- Radmanesh, H.; Barkam, E. Robust Co-Planning of Transmission Expansion and Merchant Energy Storage Investments Considering Long- and Short-Term Uncertainties. Int. J. Electr. Power Energy Syst. 2024, 160, 110062. [Google Scholar] [CrossRef]
- Nazari, A.; Keypour, R.; Amjady, N. Joint Investment of Community Energy Storage Systems in Distribution Networks Using Modified Nash Bargaining Theory. Appl. Energy 2021, 301, 117475. [Google Scholar] [CrossRef]
- Lin, B.; Xie, Y. How Feed-in-Tariff Subsidies Affect Renewable Energy Investments in China? New Evidence from Firm-Level Data. Energy 2024, 294, 130853. [Google Scholar] [CrossRef]
- Fu, C.; Li, Y.; Giwa, A.S.; Luo, S. Impact Analysis of Renewable Portfolio Standard on Retail Power Market Considering Quota Heterogeneity. Heliyon 2023, 9, e20701. [Google Scholar] [CrossRef]
- Han, R.; Li, J.; Guo, Z. Optimal Quota in China’s Energy Capping Policy in 2030 with Renewable Targets and Sectoral Heterogeneity. Energy 2022, 239, 121971. [Google Scholar] [CrossRef]
- Kilinc-Ata, N.; Proskuryakova, L.N. The Contribution of Energy Policies to Green Energy Transition in the Asia-Pacific Region. Renew. Energy 2024, 237, 121797. [Google Scholar] [CrossRef]
- Guo, S.; Feng, T. Blockchain-Based Smart Trading Mechanism for Renewable Energy Power Consumption Vouchers and Green Certificates: Platform Design and Simulation. Appl. Energy 2024, 369, 123351. [Google Scholar] [CrossRef]
- Liu, W.-J.; Chiu, W.-Y.; Hua, W. Blockchain-Enabled Renewable Energy Certificate Trading: A Secure and Privacy-Preserving Approach. Energy 2024, 290, 130110. [Google Scholar] [CrossRef]
- Li, J.; Hu, Y.; Chi, Y.; Liu, D.; Yang, S.; Gao, Z.; Chen, Y. Analysis on the Synergy between Markets of Electricity, Carbon, and Tradable Green Certificates in China. Energy 2024, 302, 131808. [Google Scholar] [CrossRef]
- Zhen, J.; Zhao, L.; Yi, H.; Cheng, Y.; Wang, K.; Hu, H. Cross-Provincial Collaborative Transaction That Considers Both the Green Electricity and the Green Certificate Markets under a Renewable Portfolio Standard Policy. Appl. Energy 2024, 372, 123787. [Google Scholar] [CrossRef]
- Wang, H.; Feng, T.; Kong, J.; Cui, M.; Xu, M. Grappling with the Trade-Offs of Carbon Emission Trading and Green Certificate: Achieving Carbon Neutrality in China. J. Environ. Manag. 2024, 360, 121101. [Google Scholar] [CrossRef]
- Deng, X.; Lv, T.; Xu, J.; Hou, X.; Liu, F. Assessing the Integration Effect of Inter-Regional Transmission on Variable Power Generation under Renewable Energy Consumption Policy in China. Energy Policy 2022, 170, 113219. [Google Scholar] [CrossRef]
- Zahan, I.; Shuai, C. Towards a Green Economic Policy Framework in China: Role of Green Investment in Fostering Clean Energy Consumption and Environmental Sustainability. Environ. Sci. Pollut. Res. 2021, 28, 43618–43628. [Google Scholar] [CrossRef]
- Wang, K.; Shi, X.; He, Q. Thermodynamic Analysis of Novel Carbon Dioxide Pumped-Thermal Energy Storage System. Appl. Therm. Eng. 2024, 225, 123969. [Google Scholar] [CrossRef]
- Chen, L.; Wang, J.; Lou, J.; Cheng, Z.; Wang, N.; Cheng, S.; Sun, L. Thermo-Economic Analysis of a Pumped Thermal Energy Storage Combining Cooling, Heating and Power System Coupled with Photovoltaic Thermal Collector: Exploration of Low-Grade Thermal Energy Storage. J. Energy Storage 2024, 96, 112718. [Google Scholar] [CrossRef]
- Liao, Y.; Yang, C.; Bai, J.; He, Q.; Wang, H.; Chen, H.; Zhang, Q.; Chen, L. Insights into the Cycling Stability of Manganese-Based Zinc-Ion Batteries: From Energy Storage Mechanisms to Capacity Fluctuation and Optimization Strategies. Chem. Sci. 2024, 15, 7441–7473. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Gu, L.; Li, Y.; Hou, P.; Huang, Q.; Shi, Z.; Liu, Y.; Ma, F.; Zhao, J. Optimization of Guide Plates and Orifice Plates on Thermal Management of Battery Energy Storage System. Appl. Therm. Eng. 2024, 253, 123794. [Google Scholar] [CrossRef]
- Du, B.; Zhu, H.; Bai, Y.; Xu, J.; Pan, Z.; Wang, Q.; Wang, X.; Zhou, J. Multifunction Lignin-Based Carbon Nanofibers with Enhanced Electromagnetic Wave Absorption and Surpercapacitive Energy Storage Capabilities. Int. J. Biol. Macromol. 2022, 199, 201–211. [Google Scholar] [CrossRef]
- Alsalmah, H.A.; Alruqi, A.B.; Nur, O.; Rajeh, A. Developing Polymer Nanocomposite Films of ZnO/NiFe2O4 Nanohybrids, Polyvinyl Pyrrolidone, and Chitosan for Flexible Electromagnetic Applications and Energy Storage Devices. Ceram. Int. 2024, 50, 28794–28804. [Google Scholar] [CrossRef]
- Mao, Y.; Cai, Z.; Jiao, X.; Long, D. Multi-Timescale Optimization Scheduling of Integrated Energy Systems Oriented towards Generalized Energy Storage Services. Sci. Rep. 2025, 15, 8549. [Google Scholar] [CrossRef]
- Zhang, T.; She, X.; Nie, B.; Kildahl, H.; Ding, Y. Integration of Liquid Air Energy Storage with Ammonia Synthesis Process for Resource Efficiency and Cost-Effectiveness. J. Energy Storage 2024, 97, 112637. [Google Scholar] [CrossRef]
- Kurşun, B.; Ökten, K.; Özak, B. Reducing the Cost of Electricity Storage with a Novel Solar Thermal Support Scenario in Pumped Thermal Energy Storage (PTES). Appl. Therm. Eng. 2024, 241, 122317. [Google Scholar] [CrossRef]
- Iñigo Agirre-Muñoz, J.; Lozano, J.; Serrano, A.; Arribalzaga, P.; Martinez, I.; Bielsa, D. Experimental Results and Upscaling Assessment of a Cost-Efficient Macro-Encapsulated Latent Heat Energy Storage System for Heat Pumps. Energy Build. 2024, 319, 114496. [Google Scholar] [CrossRef]
- Rajeevkumar Urs, R.; Mussawar, O.; Zaiter, I.; Mezher, T.; Mayyas, A. Navigating the Cost-Efficiency Frontier: Exploring the Viability of Grid-Connected Energy Storage Systems in Meeting District Load Demand. Energy Convers. Manag. 2024, 299, 117828. [Google Scholar] [CrossRef]
- Ahsan, M.B.F.; Mekhilef, S.; Soon, T.K.; Usama, M.; Binti Mubin, M.; Seyedmahmoudian, M.; Stojcevski, A.; Mokhlis, H.; Shrivastava, P.; Alshammari, O. Optimal Sizing and Cost Analysis of Hybrid Energy Storage System for EVs Using Metaheuristic PSO and Firefly Algorithms. Results Eng. 2024, 23, 102358. [Google Scholar] [CrossRef]
- Ahmad, F.; Ashraf, I.; Iqbal, A.; Bilal, M.; Yadav, D.M. Energy Management Strategies and Cost Benefits Analysis at Electric Vehicle Parking Lots Incorporating Photovoltaic Energy Generation and Energy Storage System. J. Energy Storage 2024, 92, 112105. [Google Scholar] [CrossRef]
- Song, H.; Chu, H.; Yue, H.; Chen, Y. Green Supply Chain Coordination with Substitutable Products under Cost Sharing Contract. Procedia Comput. Sci. 2022, 199, 1112–1119. [Google Scholar] [CrossRef]
- Shen, J.; Yan, H.; Sheng, L.; Zhang, B.; Shi, Y.; Shen, S. Pricing Decision in an Uncertain Green Product Supply Chain under Cost Sharing Contract. Expert Syst. Appl. 2024, 250, 123899. [Google Scholar] [CrossRef]
- Herbon, A.; David, I. Optimal Manufacturer’s Cost Sharing Ratio, Shipping Policy and Production Rate—A Two-Echelon Supply Chain. Oper. Res. Perspect. 2023, 10, 100264. [Google Scholar] [CrossRef]
- Pei, N.; Song, X.; Zhang, Z.; Peña-Mora, F. Optimizing the Operation and Allocating the Cost of Shared Energy Storage for Multiple Renewable Energy Stations in Power Generation Side. Energy Convers. Manag. 2024, 302, 118148. [Google Scholar] [CrossRef]
- Ma, X.; Pan, Y.; Zhang, M.; Ma, J.; Yang, W. A Study of Licensing Strategies for Energy Storage Technologies in the Renewable Electricity Supply Chain under Government Subsidies. J. Clean. Prod. 2023, 420, 138343. [Google Scholar] [CrossRef]
- Mao, Y.; Wan, K.; Xu, D.; Long, D. Collaborative Operation Strategy of Multiple Microenergy Grids Considering Demand-Side Energy-Sharing Behavior. Energy Sci. Eng. 2024, 12, 3663–3680. [Google Scholar] [CrossRef]
- Jamali, M.-B.; Rasti-Barzoki, M. A Game-Theoretic Approach for Examining Government Support Strategies and Licensing Contracts in an Electricity Supply Chain with Technology Spillover: A Case Study of Iran. Energy 2022, 242, 122919. [Google Scholar] [CrossRef]
- Yuan, J.; Wang, L.; Li, Y. Carbon Emission Reduction Dynamic Decision-Making in the Electricity Supply Chain with Different Carbon Emission Allowance Principles. Energy 2024, 312, 133563. [Google Scholar] [CrossRef]
- Menanteau, P.; Finon, D.; Lamy, M.-L. Prices versus Quantities: Choosing Policies for Promoting the Development of Renewable Energy. Energy Policy 2003, 31, 799–812. [Google Scholar] [CrossRef]
- Jamali, M.-B.; Rasti-Barzoki, M. A Game Theoretic Approach for Green and Non-Green Product Pricing in Chain-to-Chain Competitive Sustainable and Regular Dual-Channel Supply Chains. J. Clean. Prod. 2018, 170, 1029–1043. [Google Scholar] [CrossRef]


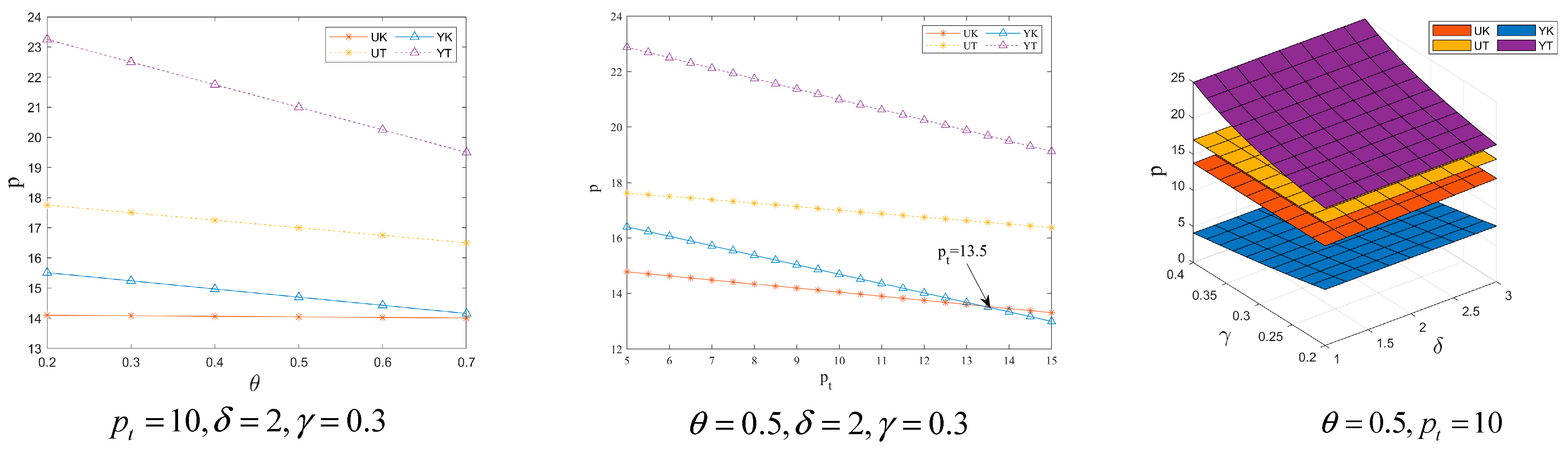


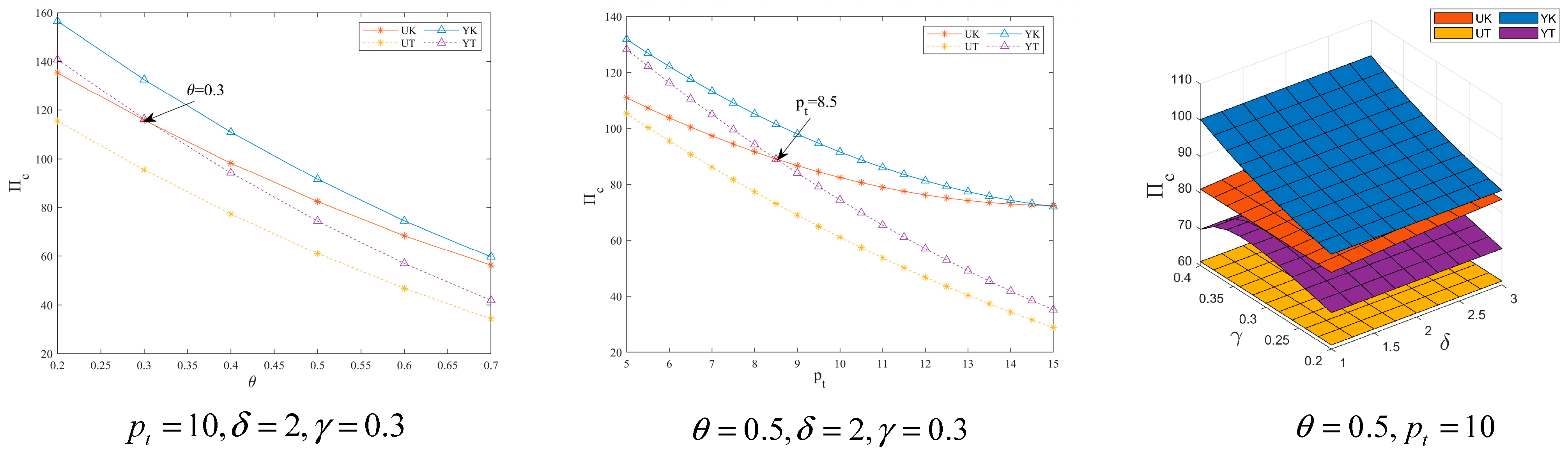
| UK | UT | YK | YT | |
|---|---|---|---|---|
| RE input | Yes | No | Yes | No |
| cost allocation | Unit power | Unit power | Proportion | Proportion |
| Notation | Description |
|---|---|
| Parameters | \ |
| Basic electricity price, . (USD/MWh) | |
| The influence coefficient of power demand on electricity price, . | |
| The influence coefficient of power reliability on electricity price, . | |
| Unit power generation cost of the traditional power producer, . (USD/MWh) | |
| Renewable energy investment cost coefficient of retailer, . (USD/h) | |
| Energy storage cost coefficient, . (USD/h) | |
| When M = UK and M = UT, it represents the unit power energy storage cost charged by the power producer to the retailer, . (USD/MWh) | |
| When M = YK and M = YT, it represents the percentage of energy storage investment cost charged by power supplier to electricity retailer, . | |
| Dependent variables | \ |
| Wholesale price, . (USD/MWh) | |
| Electricity price, . (USD/MWh) | |
| Renewable energy input of retailer, . (MW) | |
| Electricity demand, . (MW) | |
| The electricity purchased by the retailer from the power producer, . (MW) | |
| Electricity reliability, . | |
| The profit of electric power enterprise, .(USD) | |
| Decision variables | \ |
| Green certificate transaction price, . (USD) | |
| Renewable energy consumption ratio, . | |
| Index | \ |
| Subscripts, representing power supplier, electricity retailer and power supply chain, respectively | |
| Superscript, the strategy of electric power enterprise. () |
| UK | UT |
|---|---|
| \ | |
| YK | YT |
|---|---|
| \ | |
| Decisions | Variables | Conditions | High → Low | |||
|---|---|---|---|---|---|---|
| \ | YK | \ | \ | UK | ||
| \ | YT | UT | YK | UK | ||
| YT | UT | YK | UK | |||
| YT | UT | UK | YK | |||
| \ | YT | UT | UK | YK | ||
| \ | YT | UT | UK | YK | ||
| \ | YK | UK | YT = UT | |||
| YK | UK | YT | UT | |||
| YK | UK | UT | YT | |||
| YK | YT | UK | UT | |||
| YK | UK | YT | UT | |||
| YK | YT | UK | UT | |||
| YK | UK | YT | UT | |||
| \ | YK | UK | YT | UT | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, D.; Wu, Q.; Guo, J. Research on Strategy Selection of Power Supply Chain Under Renewable Energy Consumption and Energy Storage Cost Sharing. Sustainability 2025, 17, 4382. https://doi.org/10.3390/su17104382
Wang D, Wu Q, Guo J. Research on Strategy Selection of Power Supply Chain Under Renewable Energy Consumption and Energy Storage Cost Sharing. Sustainability. 2025; 17(10):4382. https://doi.org/10.3390/su17104382
Chicago/Turabian StyleWang, Di, Qiyue Wu, and Junyan Guo. 2025. "Research on Strategy Selection of Power Supply Chain Under Renewable Energy Consumption and Energy Storage Cost Sharing" Sustainability 17, no. 10: 4382. https://doi.org/10.3390/su17104382
APA StyleWang, D., Wu, Q., & Guo, J. (2025). Research on Strategy Selection of Power Supply Chain Under Renewable Energy Consumption and Energy Storage Cost Sharing. Sustainability, 17(10), 4382. https://doi.org/10.3390/su17104382






