Sustainable Dynamic Scheduling Optimization of Shared Batteries in Urban Electric Bicycles: An Integer Programming Approach
Abstract
1. Introduction
- (1)
- We develop an integer programming model for the dynamic scheduling of shared e-bike batteries that minimizes transportation costs and promotes resource balance in a sustainable urban mobility context.
- (2)
- We propose a hybrid solution framework combining an IPM and B&B to improve computational efficiency and guarantee global optimality.
- (3)
- We validate our approach using operational data from 729 Shanghai swap stations, demonstrating enhanced resource utilization, reduced operational costs, and lower carbon emissions.
2. Materials and Methods
2.1. Integer Programming in Resource Allocation
2.2. Algorithmic Approaches for Vehicle Resource Allocation
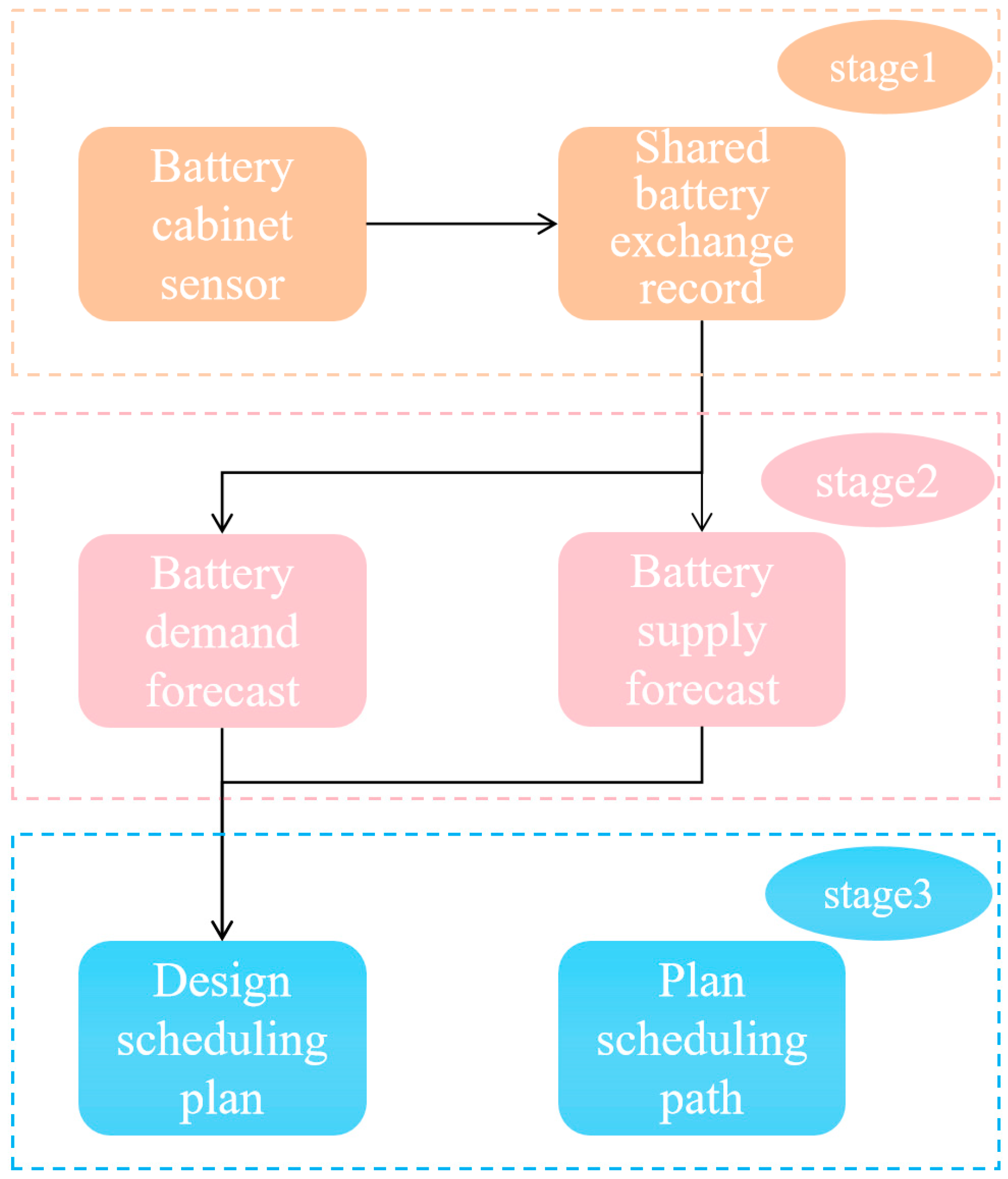
2.3. Integrated Framework for Dynamic Scheduling Optimization
- (1)
- Problem formulation and IP model: We formalize the battery scheduling problem as a multi-constraint integer program (Section 3 and Section 4.1). Key components include decision variables (), the objective function (Equation (5)), and constraints (Equations (6)–(8)).
- (2)
- Synergistic ‘IPM + B&B’ optimization: To solve the model efficiently, we combine (a) the interior-point Method (IPM): handles continuous relaxations of sub-problems, using barrier functions (Equation (9)) and Newton iterations (Equation (13)) to navigate the feasible region; and (b) Branch-and-Bound (B&B)): Enforces integer constraints via variable branching (Equations (10) and (11)) and pruning strategies.
- (3)
- Algorithmic workflow: The step-by-step workflow ensures systematic convergence, including (a) initialization: feasible integer solutions via greedy allocation, (b) iterative optimization: IPM solves relaxed sub-problems; B&B partitions non-integer variables, and (c) convergence: terminates when duality gaps or iteration limits are met.
3. Problem Description
3.1. Fundamental Issues of Battery Resource Allocation
- (1)
- Data Collection and Analysis:
- (2)
- Demand Forecasting and Supply Planning:
- (3)
- Configuration and Scheduling Implementation:
- (1)
- Battery Demand Forecasting at Swap Stations:
- (2)
- Battery Supply Forecasting at Swapping Stations
- (3)
- Battery Configuration Scheme Design
- (4)
- Dispatch Route Planning
3.2. Basic Assumptions for Battery Resource Allocation
- (1)
- Rider demand follows predictable patterns, accurately forecast using one week of historical swapping records (time, location, frequency).
- (2)
- Daily initial battery reserves at each station are fixed, with stable battery performance and no unexpected failures or charging errors.
- (3)
- Dispatch vehicles, station capacities, and labor resources are unlimited, and non-dispatch operational costs are fixed, and thus excluded from the model.
- (4)
- Per-battery dispatch costs are calculated piecewise, with fixed unit distance costs substituted for actual transportation expenses.
- (1)
- The distance between swap cabinets is computed using the Euclidean distance. Consequently, the transfer cost is shown in Equation (4), where and are the geographic coordinates of surplus and deficit stations, respectively, is the Euler distance between the two cabinets, and is a fixed cost coefficient. Thus, the allocation cost is proportional to the distance.
- (2)
- Each station is assumed to be equipped with two swap cabinets, each with a capacity of 24 batteries, resulting in a total initial daily inventory of 48 fully charged batteries per station.
- (3)
- A battery takes 24 h to discharge from full charge to depletion (ignoring the transfer time), meaning that battery transfers are required only once per day.
4. Model Construction and Algorithm Design
4.1. Model Construction
- (1)
- For any deficit station , the total incoming batteries must satisfy its deficit without over-supply:
- (2)
- For any surplus station , the total outgoing batteries must not exceed its supply capacity:
- (3)
- Non-negativity and integrality:
4.2. Interior Point Method
- (1)
- Scalability to Large-Scale Problems: IPM efficiently handles high-dimensional, sparse linear/quadratic programming problems, making it ideal for complex resource allocation scenarios like multi-station battery dispatch.
- (2)
- Numerical Stability: In ill-conditioned or pathological optimization problems, the iteration paths of IPM remain within the feasible region, reducing numerical oscillations compared to simplex methods.
- (3)
- Global Feasibility: By constraining iteration paths via barrier functions, IPM maintains solution feasibility throughout the process, minimizing inefficient searches and accelerating convergence.
4.2.1. Initialization of Feasible Solutions
4.2.2. Construction of the Potential Function
4.2.3. Iterative Optimization for the Optimal Solution
| Algorithm 1 B&B and IPM |
| Input: Model parameters (), termination conditions () |
| Output: Optimal dispatch scheme , minimum transportation |
| 1. Initialize global bounds: |
| 2. add root node to the active node queue |
| 3. while active node queue is non-empty and not timed out: |
| 4. extract a node and solve its relaxation via IPM |
| 5. if the relaxed solution is infeasible or : |
| 6. prune the node |
| 7. elif the relaxed solution is integer-feasible: |
| 8. if : |
| 9. update |
| 10. else: |
| 11. select branching variable () via |
| 12. generate sub-problem 1: , sub−problem 2: |
| 13. for each sub-problem: |
| 14. warm-Start initialization |
| 15. solve sub-problems using the IPM, Obtain |
| 16. if : |
| 17. add sub-problems to the active queue |
| 18. update {active queue’s } |
| 19. if , terminate |
| 20. check convergence criteria (Table 4) |
| 21. return |
4.2.4. Initialization of Feasible Solutions
| Algorithm 2 Model convergence verification |
| Input: , , , ,, parameters {, , ,, , , } |
| Output: True/False |
| 1. update barrier parameter |
| 2. if : stop decay |
| 3. end if |
| 4. if the difference between primal and dual objectives satisfies : |
| 5. return True |
| 6. end if |
| 7. if (For all integer variables in the continuous relaxed solution, check the deviation between their values and rounded counterparts, and apply rounding to variables that meet the criteria to obtain ) |
| 8. if and (verify the rounded solution satisfies all constraints. Then, the algorithm converges) |
| 9. return True |
| 10. end if |
| 11. end if |
| 12. if () or () or () (bounds close/reach maximum iteration count/time limit is exceeded) |
| 13. return True |
| 14. else |
| 15. return False |
| 16. end if |
5. Computing Example
5.1. Data Preprocessing
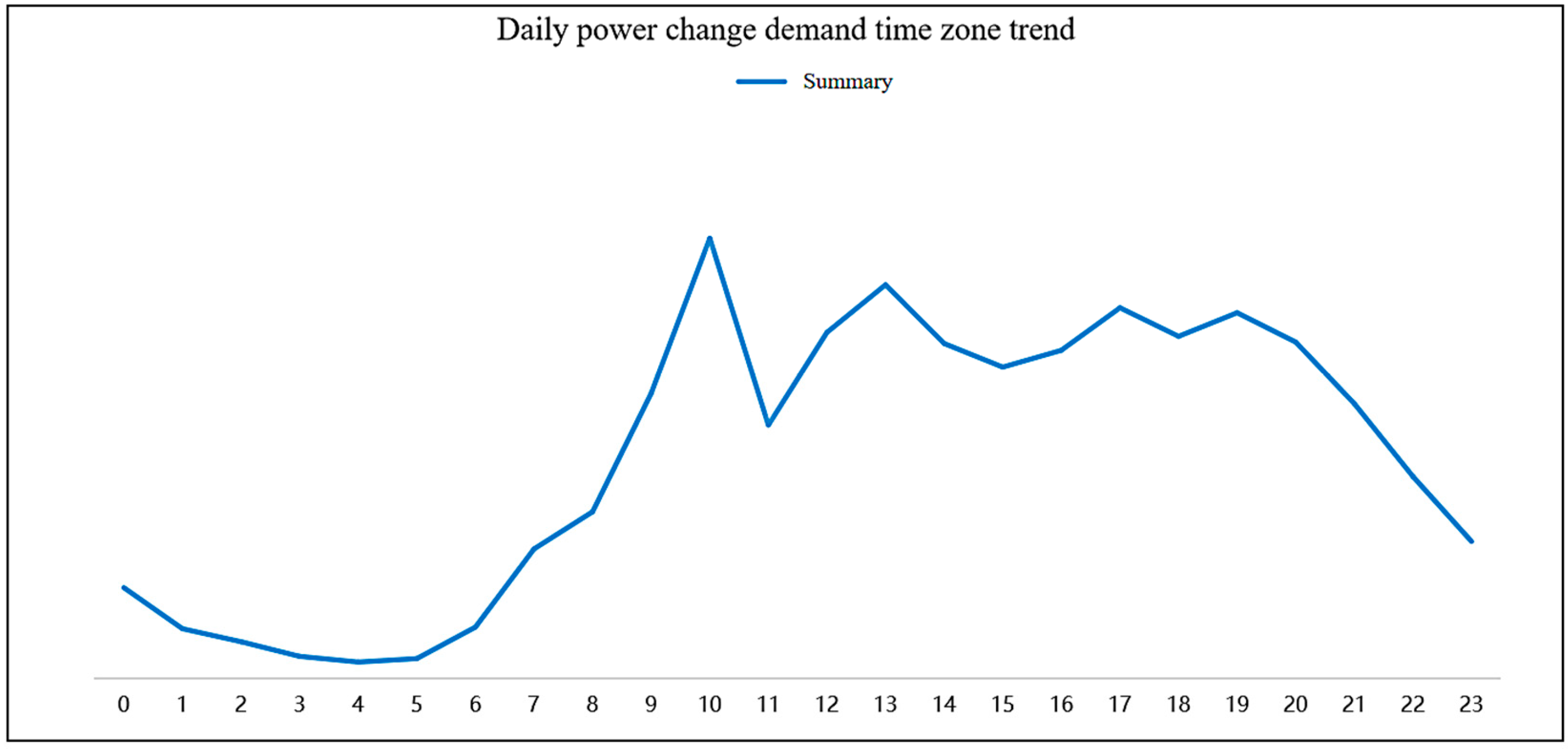
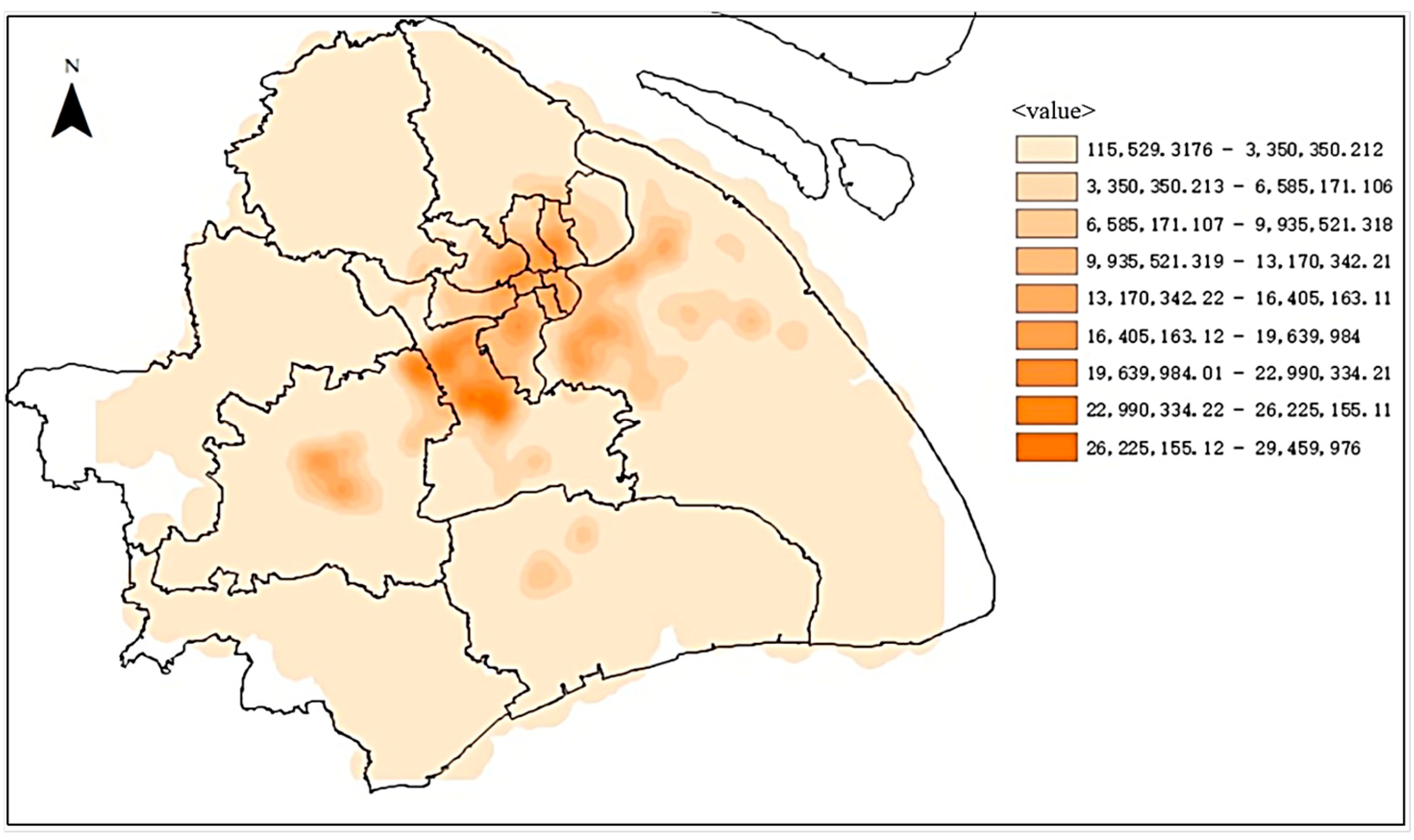
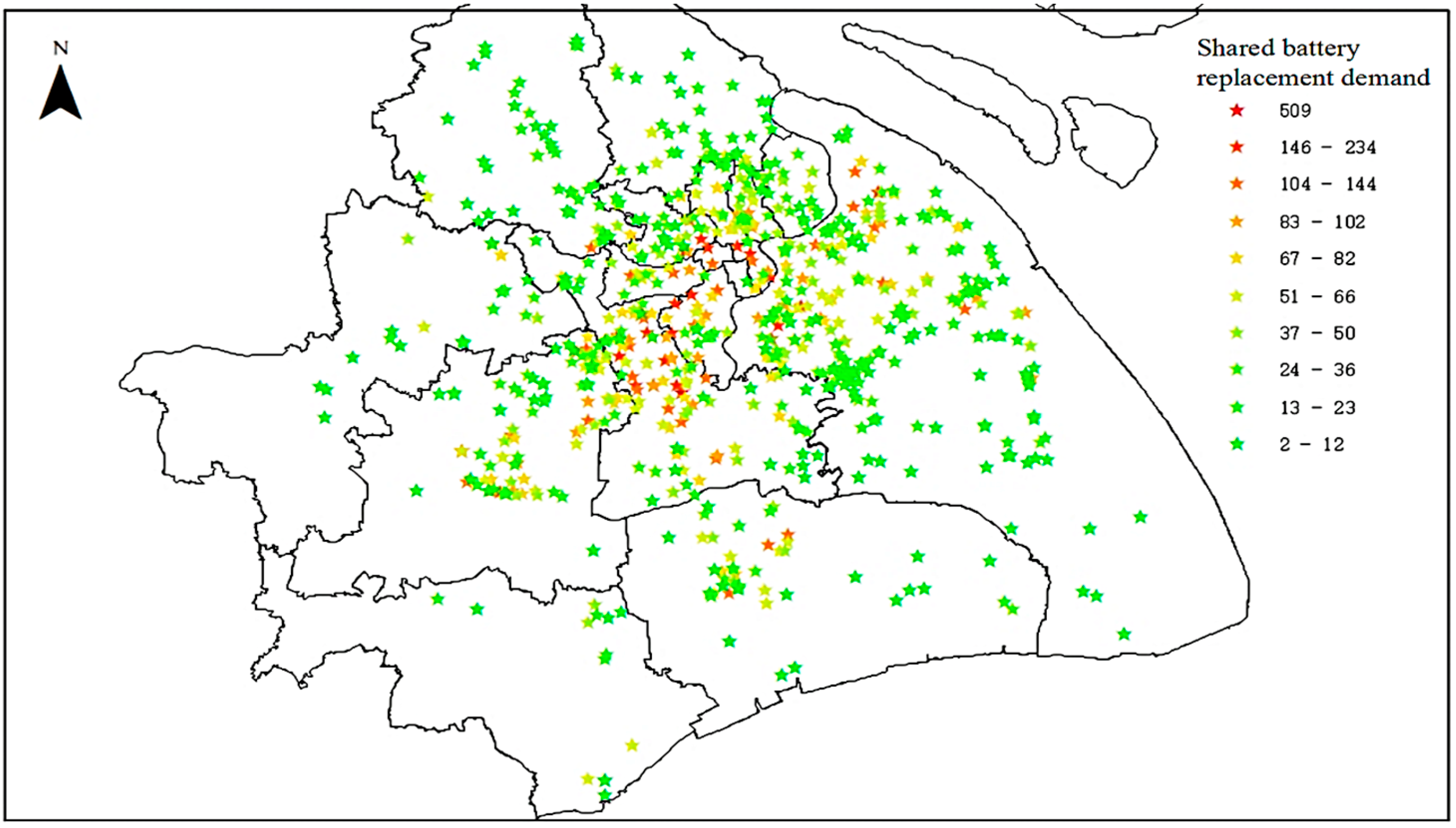
5.2. Swapping Demand Analysis
5.3. Battery Configuration Scheme Analysis
6. Conclusions and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olabi, A.G.; Abdelkareem, M.A. Renewable energy and climate change. Renew. Sustain. Energy Rev. 2022, 158, 112111. [Google Scholar] [CrossRef]
- Bieliński, T.; Kwapisz, A.; Ważna, A. Electric bike-sharing services mode substitution for driving, public transit, and cycling. Transp. Res. Part D Transp. Environ. 2021, 96, 102883. [Google Scholar] [CrossRef]
- Shao, D.; Li, W. New Characteristics and Management Countermeasures of Electric Bicycle Development in Shanghai. Traffic Port Transp. 2020, 7, 16–20. [Google Scholar]
- Kohlrautz, D.; Kuhnimhof, T. E-bike charging infrastructure in the workplace—Should employers provide it? Sustainability 2023, 15, 10540. [Google Scholar] [CrossRef]
- Gao, S. Electric Bicycles Embrace the “Battery Swap Model”. Hebei Dly. 2021, 7, 1–2. [Google Scholar]
- Zhang, S.; Li, X.; Li, Y.; Zheng, Y.; Liu, J. A green-fitting dispatching model of station cluster for battery swapping under charging-discharging mode. Energy 2023, 276, 127600. [Google Scholar] [CrossRef]
- Gwalani, H.; Tiwari, C.; Mikler, A.R. Evaluation of heuristics for the p-median problem: Scale and spatial demand distribution. Comput. Environ. Urban Syst. 2021, 88, 101656. [Google Scholar] [CrossRef]
- Dang, J.; Wang, X.; Xie, Y.; Fu, Z. The location optimization of urban shared new energy vehicles based on P-Median model: The example of Xuzhou City, China. Sustainability 2023, 15, 9553. [Google Scholar] [CrossRef]
- Atta, S.; Mahapatra, P.R.S.; Mukhopadhyay, A. A multi-objective formulation of maximal covering location problem with customers’ preferences: Exploring Pareto optimality-based solutions. Expert Syst. Appl. 2021, 186, 115830. [Google Scholar] [CrossRef]
- Hashim, N.I.M.; Shariff, S.S.R.; Deni, S.M. Allocation of relief centre for flood victims using Location Set Covering Problem (LSCP). In Proceedings of the International Conference on Mathematics, Statistics and Computing Technology 2021 (ICMSCT 2021), Bangkok, Thailand, 27–28 October 2021; Volume 2084, p. 012016. [Google Scholar]
- Wang, W.; Yang, K.; Yang, L.; Gao, Z. Tractable approximations for the distributionally robust conditional vertex p-center problem: Application to the location of high-speed railway emergency rescue stations. J. Oper. Res. Soc. 2022, 73, 525–539. [Google Scholar] [CrossRef]
- Ayudhya, W.S.N. Selecting Temporary Flood Shelter Locations by P-Center Model. In Proceedings of the 2021 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 13–16 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 78–82. [Google Scholar]
- Zou, Z.; Yang, W.; Sheng, S.Y.; Yan, X. Research on the Location Selection Problem of Electric Bicycle Battery Exchange Cabinets Based on an Improved Immune Algorithm. Sustainability 2024, 16, 8394. [Google Scholar] [CrossRef]
- Faghih-Imani, A.; Hampshire, R.; Marla, L.; Eluru, N. An empirical analysis of bike sharing usage and rebalancing: Evidence from Barcelona and Seville. Transp. Res. Part A Policy Pract. 2017, 97, 177–191. [Google Scholar] [CrossRef]
- Shuai, C.; Yang, F.; Ouyang, X.; Xu, G. Data-Driven Prediction of Electric Bicycle Battery Swap Demand. J. Transp. Syst. Eng. Inf. Technol. 2021, 21, 173–179. [Google Scholar]
- Gondzio, J. Interior point methods 25 years later. Eur. J. Oper. Res. 2012, 218, 587–601. [Google Scholar] [CrossRef]
- Chen, X.; Hai, Y.; Lang, M.; Yu, X.; Li, Y. Railway Express Logistics Network Cargo Flow Distribution Based on Multiple Transportation Organization Modes. Railw. Transp. Econ. 2024, 46, 1–9. [Google Scholar]
- Yu, Y.; Bao, X.; Zhang, Y.; Li, Z. Research on Cargo Distribution and Delivery in Airport Logistics Temporary Storage Areas. Mod. Manuf. Eng. 2023, 10, 113–119. [Google Scholar]
- Peng, W.; Chen, X.; Xue, Z. Optimization of Highway Truck Freight under the Trailer Swap Mode. J. Transp. Eng. Inf. 2024, 22, 107–117. [Google Scholar]
- Zoltners, A.A.; Sinha, P. Integer programming models for sales resource allocation. Manag. Sci. 1980, 26, 242–260. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, C.; Jiang, J.; Yang, H.; Shang, H. Reinforcement learning approach for resource allocation in humanitarian logistics. Expert Syst. Appl. 2021, 173, 114663. [Google Scholar] [CrossRef]
- Huang, C.; Lin, Y.; Li, N.; Wu, X.; Han, F.; Zhang, J. Optimal Strategies for Production Order Allocation and Transportation Based on Integer Programming Models. Enterp. Sci. Technol. Dev. 2023, 12, 110–115. [Google Scholar]
- Li, J.; Zhang, X.; Li, H.; Zhang, S. Design and Optimization of Rural Logistics Distribution Schemes: A Case Study of China Post. Logist. Res. 2023, 6, 34–42. [Google Scholar]
- Yücel, E.; Salman, F.S.; Erdoğan, G. Optimizing two-dimensional vehicle loading and dispatching decisions in freight logistics. Eur. J. Oper. Res. 2022, 302, 954–969. [Google Scholar] [CrossRef]
- Sun, X.; Fang, M.; Guo, S.; Yue, H. UAV-rider coordinated dispatching for the on-demand delivery service provider. Transp. Res. Part E Logist. Transp. Rev. 2024, 186, 103571. [Google Scholar] [CrossRef]
- Wu, C.; Mu, X.; Liu, Y.; Gu, X.; Wang, X. Resource allocation in STAR-RIS-aided networks: OMA and NOMA. IEEE Trans. Wirel. Commun. 2022, 21, 7653–7667. [Google Scholar] [CrossRef]
- Xu, Y.; Gui, G.; Gacanin, H.; Adachi, F. A survey on resource allocation for 5G heterogeneous networks: Current research, future trends, and challenges. IEEE Commun. Surv. Tutor. 2021, 23, 668–695. [Google Scholar] [CrossRef]
- Wei, W.; Yang, R.; Gu, H.; Zhao, W.; Chen, C.; Wan, S. Multi-objective optimization for resource allocation in vehicular cloud computing networks. IEEE Trans. Intell. Transp. Syst. 2021, 23, 25536–25545. [Google Scholar] [CrossRef]
- Jia, W.; Ding, T.; Bai, J.; Bai, L.; Yang, Y.; Blaabjerg, F. Hybrid swapped battery charging and logistics dispatch model in continuous time domain. IEEE Trans. Veh. Technol. 2022, 71, 2448–2458. [Google Scholar] [CrossRef]
- Tan, X.; Qu, G.; Sun, B.; Li, N.; Tsang, D.H.K. Optimal scheduling of battery charging station serving electric vehicles based on battery swapping. IEEE Trans. Smart Grid 2017, 10, 1372–1384. [Google Scholar] [CrossRef]
- Lam, E.; Van Hentenryck, P.; Kilby, P. Joint Vehicle and Crew Routing and Scheduling. Transp. Sci. 2020, 54, 488–511. [Google Scholar] [CrossRef]
- Ouahmed, A.A.; Josselin, D.; Zhou, F. Relocation optimization of electric cars in one-way car-sharing systems: Modeling, exact solving and heuristics algorithms. Int. J. Geogr. Inf. Sci. 2017, 32, 367–398. [Google Scholar] [CrossRef]
- Eliyi, D.T.; Ormek, A.; Karakütük, S.S. A vehicle scheduling problem with fixed trips and time limitations. Int. J. Prod. Econ. 2008, 117, 150–161. [Google Scholar] [CrossRef]
- Alfian, G.; Rhee, J.; Ijaz, M.F.; Syafrudin, M.; Fitriyani, N.L. Performance Analysis of a Forecasting Relocation Model for One-Way Carsharing. Appl. Sci. 2017, 7, 598–619. [Google Scholar] [CrossRef]
- Tang, J.; Cao, J. Research on Joint Scheduling Optimization of Shared Cars. J. Syst. Simul. 2021, 33, 1959–1968. [Google Scholar]
- Yang, Y.; Wu, Y.; Yao, Z.; Ren, Z.; Gao, Y. Research and Application of Heuristic Algorithms for Vehicle Routing Problems with Time Windows. Comput. Appl. 2013, 33 (Suppl. S1), 59–61. [Google Scholar]
- Gao, J.; Cui, X.; Zhao, P.; Yao, B. Vehicle Scheduling Method for One-Way Shared Electric Vehicles Based on Demand Forecasting. J. Dalian Univ. Technol. 2019, 59, 648–655. [Google Scholar]
- Xu, M.; Yu, G.; Zhou, X.; Ge, X. Low-Carbon Vehicle Routing Problem with Integrated Cost Minimization and Its Algorithm. Comput. Integr. Manuf. Syst. 2015, 21, 1906–1914. [Google Scholar]
- Li, J.-Q.; Borenstein, D.; Mirchandani, P.B. A decision support system for the single-depot vehicle rescheduling problem. Comput. Oper. Res. 2005, 34, 1008–1032. [Google Scholar] [CrossRef]
- Liu, C.; Wu, L.; Xiao, W.; Li, G.; Xu, D.; Guo, J.; Li, W. An improved heuristic mechanism ant colony optimization algorithm for solving path planning. Knowl.-Based Syst. 2023, 271, 110540. [Google Scholar] [CrossRef]
- Kardoš, J.; Kourounis, D.; Schenk, O.; Zimmerman, R. BELTISTOS: A robust interior point method for large-scale optimal power flow problems. Electr. Power Syst. Res. 2022, 212, 108613. [Google Scholar] [CrossRef]
- Tomazella, C.P.; Nagano, M.S. A comprehensive review of Branch-and-Bound algorithms: Guidelines and directions for further research on the flowshop scheduling problem. Expert Syst. Appl. 2020, 158, 113556. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| Index of surplus swapping station, . | |
| Set of surplus swapping stations. | |
| Index of deficit swapping station, . | |
| Set of deficit swapping stations. | |
| Transportation cost per battery from to . | |
| Daily battery demand at station . | |
| Daily surplus battery supply at station . | |
| Daily battery deficit at station . | |
| Initial daily reserve of fully charged batteries at each station. | |
| Decision variable (number of batteries dispatched). | |
| Fractional deviation of , used for branching variable selection. | |
| Barrier parameter controlling the precision of interior path tracking. | |
| Fixed attenuation factor determining the decay rate of the barrier parameter. | |
| Termination threshold for the barrier parameter. | |
| Convergence threshold for the duality gap. | |
| Tolerance for integer feasibility checks. | |
| Global upper bound (current best integer solution’s objective value). | |
| Global lower bound (minimum relaxed solution across active nodes). |
| Step 1: Initialization | |
| Initialize global bounds: the global upper bound is , and the global lower bound is . Initially, there is no feasible integer solution or relaxed solution information. Then, add the original integer programming problem to the active node queue as the root node. Generate an initial feasible integer solution using the heuristic method in Section 4.2.1 ( followed by greedy allocation) and assign it as the root node’s relaxed solution. | |
| Step 2: Branch Variable Selection and Sub-problem Generation | |
| Step 2.1: Branch Variable Selection: Select the non-integer variable with the greatest impact on the objective function using fractional deviation: | |
| (10) | |
| The variable with the smallest is chosen: | |
| (11) | |
| Step 2.2: Sub-problem Generation: Two sub-problems are created by adding constraints: | |
| Sub-problem 1: , Sub-problem 2: | |
| Step 3: IPM-Based Sub-problem Solving | |
| Step 3.1: Barrier Function Modification: For each sub-problem, a barrier term is incorporated into the objective function (Equation (9)) to implicitly enforce branching constraints. For instance, in sub-problem 1, the modified objective function is as follows: | |
| (12) | |
| Step 3.2: Newton Iteration: Construct Newton direction linear system, where is the constraint matrix and is the right-hand side. (Newton’s method is not applied directly to integer variables. Instead, in our hybrid approach, the interior-point/Newton iterations are used only to solve the continuous barrier sub-problems that arise after relaxing the integrality constraints and adding branch-specific barrier terms. The integrality of decision variables is then enforced by the overarching B&B framework through explicit branching constraints and node-wise bounds.) | |
| (13) | |
| Step 3.3: Warm-Start Strategy: Use the parent node’s solution as the initial point for sub-problems. Adjust the step size via backtracking line search to ensure feasibility. Ensure that the sub-problem solution starts from the region close to the parent node’s solution, accelerating convergence. | |
| (14) | |
| Step 4: Pruning and Bound Updates | |
| Step 4.1: Pruning Rules: (a) Bound Pruning: prune the branch if the sub-problem’s relaxed solution value is greater than the current optimal integer solution (); (b) Infeasibility Pruning: prune if no feasible solution exists; (c) Integer Solution Pruning: update and prune if and the solution is integer-feasible. | |
| Step 4.2: Global Bound Updates: Record the relaxed solution values of all active nodes and update the global lower bound to ensure it always reflects the potential optimum bound of unprocessed branches. | |
| Step 5: Convergence Check and Termination | |
| Terminate if , maximum iterations, or time limit is reached. Otherwise, return to Step 1. | |
| Step 1: Barrier Parameter Decay |
| Reduce the barrier parameter by a fixed ratio () per iteration; decay stops when : (namely ). This avoids numerical oscillations and controls the precision of path tracking. |
| Step 2: Duality Gap Check |
| Convergence is declared if the absolute difference between the primal objective value and the dual objective value is less than 10−6 (namely ). |
| Step 3: Integer Feasibility Check |
| Evaluate the deviation of the continuous relaxed solution from integrality. Round the solution to integers if the maximum deviation is less than 10−3 (namely ) and verify if the rounded solution satisfies the original constraints and . |
| Step 4: Global Termination Conditions |
| Terminate the algorithm if (a) The bounds close: ; the maximum iteration count is reached: ; or the time limit is exceeded: . |
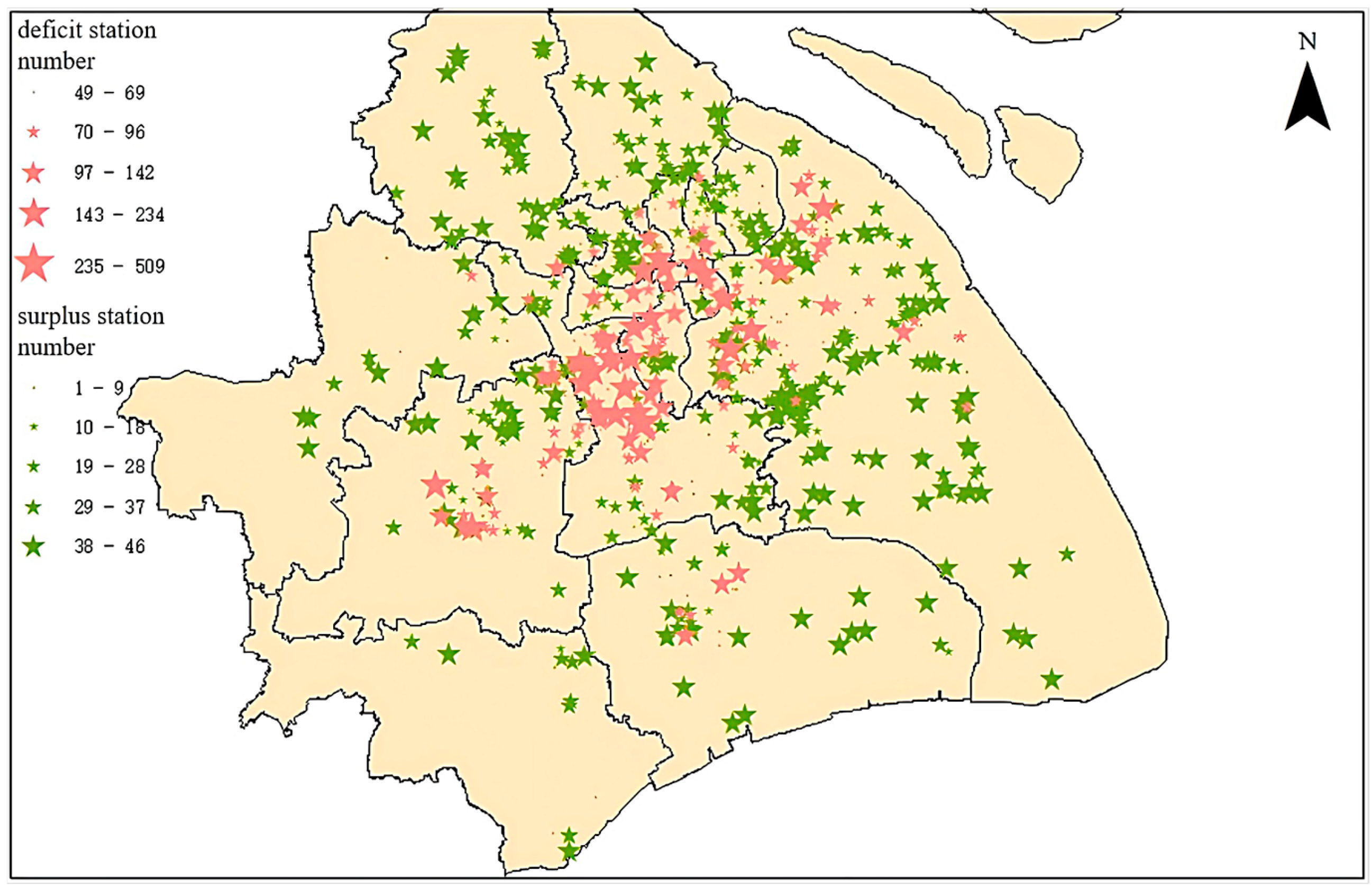
| Station ID | Longitude | Latitude | Daily Demand | Initial Reserve | Incoming Batteries | Outgoing Batteries | Note |
|---|---|---|---|---|---|---|---|
| 9201801796 | 121.401 | 31.134 | 96 | 48 | 48 | 0 | Incoming |
| 9201801837 | 121.760 | 31.114 | 96 | 48 | 48 | 0 | Incoming |
| 9330015974 | 121.401 | 31.133 | 95 | 48 | 47 | 0 | Incoming |
| 9201807446 | 121.477 | 31.244 | 22 | 48 | 0 | 26 | Outgoing |
| 9201801855 | 121.534 | 31.263 | 22 | 48 | 0 | 26 | Outgoing |
| 9330012493 | 121.319 | 31.107 | 21 | 48 | 0 | 27 | Outgoing |
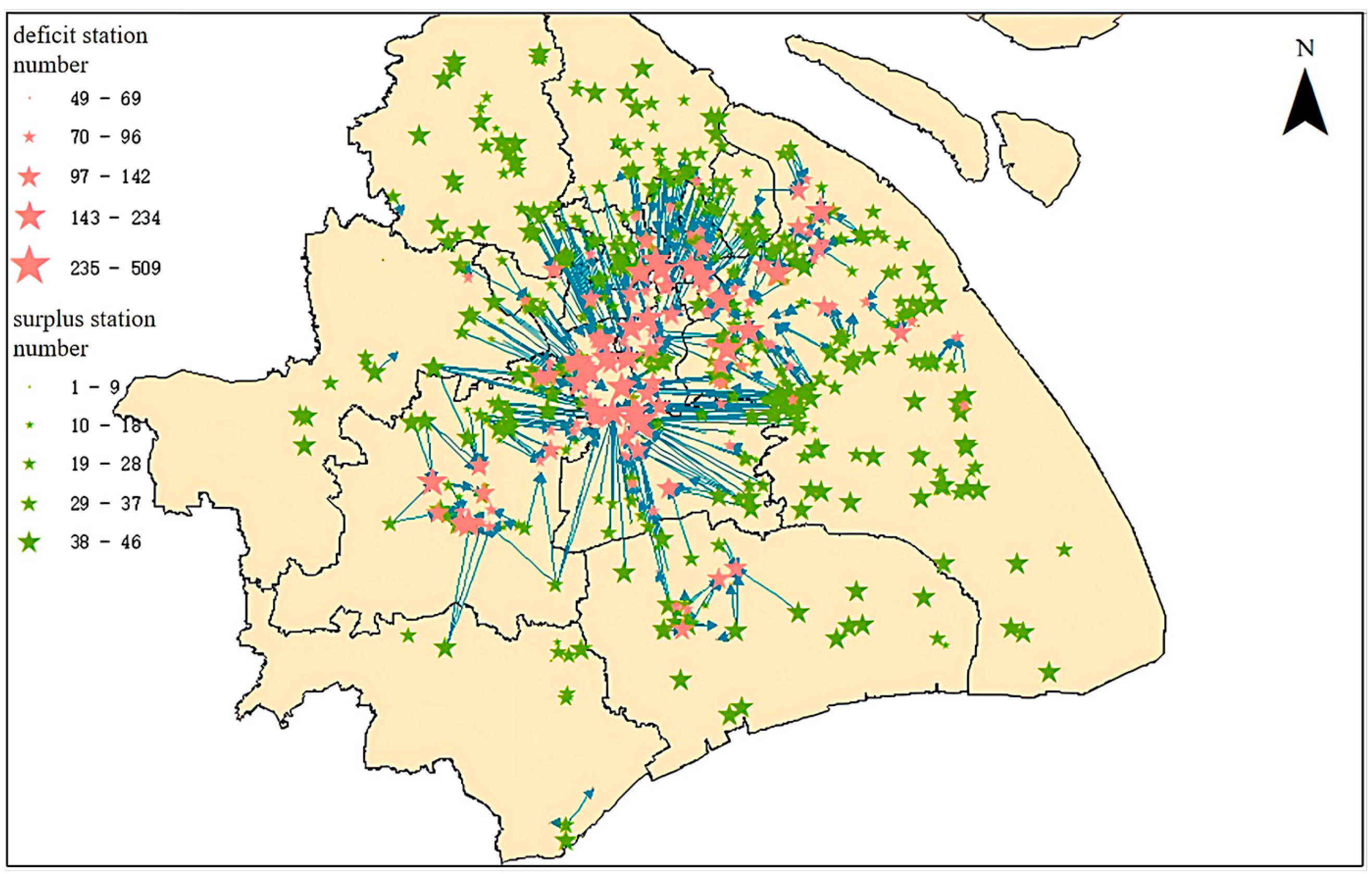
| Origin Station ID | Origin Longitude | Origin Latitude | Destination Station ID | Destination Longitude | Destination Latitude | Dispatch Quantity |
|---|---|---|---|---|---|---|
| 9201801051 | 121.408 | 31.246 | 9201804694 | 121.414 | 31.236 | 8 |
| 9330008636 | 121.506 | 31.172 | 9201801755 | 121.507 | 31.165 | 8 |
| 9201803153 | 121.688 | 31.190 | 9201807403 | 121.693 | 31.180 | 8 |
| 9201801666 | 121.416 | 31.137 | 9201801841 | 121.401 | 31.133 | 9 |
| 9330015149 | 121.470 | 31.306 | 9330015802 | 121.442 | 31.223 | 9 |
| 9330008423 | 121.500 | 31.134 | 9201801131 | 121.497 | 31.134 | 9 |
| 9201801051 | 121.457 | 31.158 | 9201804694 | 121.430 | 31.167 | 7 |
| 9330008636 | 121.457 | 31.158 | 9201801755 | 121.425 | 31.177 | 2 |
| 9201803153 | 121.521 | 31.072 | 9201807403 | 121.510 | 31.077 | 9 |
| 9201801666 | 121.326 | 31.069 | 9201801841 | 121.319 | 31.073 | 9 |
| Demand Density Range | Typical Regions | Coverage Tier | Station Distribution Strategy | Service Optimization Measures |
|---|---|---|---|---|
| 1907.76–55,748.89 | Chongming, Jinshan Districts | Basic Coverage | Uniform distribution at community centers | Standardized facilities, 24/7 availability |
| 55,748.89–109,590.02 | Fengxian, Qingpu Districts | Moderate Coverage | Increased density along major roads | Optimized spacing, reduced wait times |
| 109,590.02–163,431.15 | Pudong Outer Areas (Kangqiao, Zhoupu) | Medium-High Density | Near commercial complexes/subway stations | Fast-charging equipment, extended peak-hour service |
| 163,431.15–217,272.28 | Xuhui, Changning (non-core) | High Density | Star-marked stations | Dynamic inventory allocation to prevent empty cabinets |
| 217,272.28–271,113.41 | Jing’an, Huangpu (office clusters) | Core Coverage | Dynamic density adjustment for rush hours | Real-time dispatch via navigation apps + emergency backup cabinets |
| 271,113.41–324,954.54 | Lujiazui, Nanjing West Road | Ultra-High Demand | Embedded micro-stations in offices/malls | Corporate partnerships for scheduled battery swaps + drone replenishment trials |
| 324,954.54–378,795.68 | Hongqiao Transport Hub | Specialized Hub | Coordinated layout with railway station/airports | Large-capacity reserves for cross-regional dispatch |
| 378,795.68–432,636.81 | Zhangjiang, Lingang New Area | Emerging Regions | Planned per industrial park commuter demand | Customized services (e.g., nighttime swap cabinets) |
| 432,636.81–486,477.94 | People’s Square, The Bund | Experimental Zone | Redundant high-density layout + AI optimization | Real-time monitoring, iterative algorithm updates |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, Z.; Yan, X.; Liu, P.; Yang, W.; Zhang, C. Sustainable Dynamic Scheduling Optimization of Shared Batteries in Urban Electric Bicycles: An Integer Programming Approach. Sustainability 2025, 17, 4379. https://doi.org/10.3390/su17104379
Zou Z, Yan X, Liu P, Yang W, Zhang C. Sustainable Dynamic Scheduling Optimization of Shared Batteries in Urban Electric Bicycles: An Integer Programming Approach. Sustainability. 2025; 17(10):4379. https://doi.org/10.3390/su17104379
Chicago/Turabian StyleZou, Zongfeng, Xin Yan, Pupu Liu, Weihao Yang, and Chao Zhang. 2025. "Sustainable Dynamic Scheduling Optimization of Shared Batteries in Urban Electric Bicycles: An Integer Programming Approach" Sustainability 17, no. 10: 4379. https://doi.org/10.3390/su17104379
APA StyleZou, Z., Yan, X., Liu, P., Yang, W., & Zhang, C. (2025). Sustainable Dynamic Scheduling Optimization of Shared Batteries in Urban Electric Bicycles: An Integer Programming Approach. Sustainability, 17(10), 4379. https://doi.org/10.3390/su17104379






