Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development
Abstract
1. Introduction
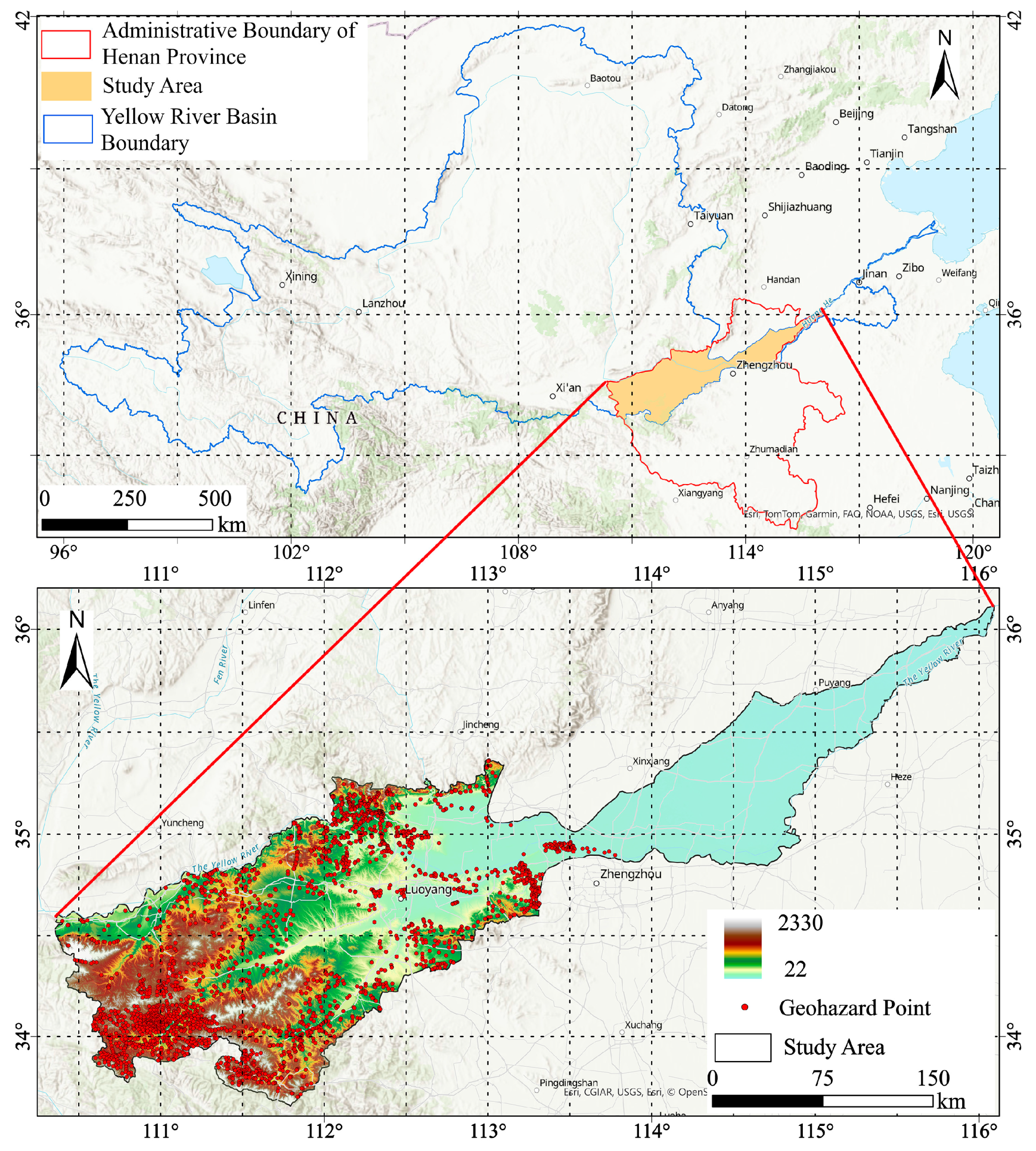
2. Study Area and Data Sources
2.1. Study Area Overview
2.2. Data Used
2.2.1. Selection of Evaluation Factors
2.2.2. Grading of Evaluation Factors
2.3. Data Sources
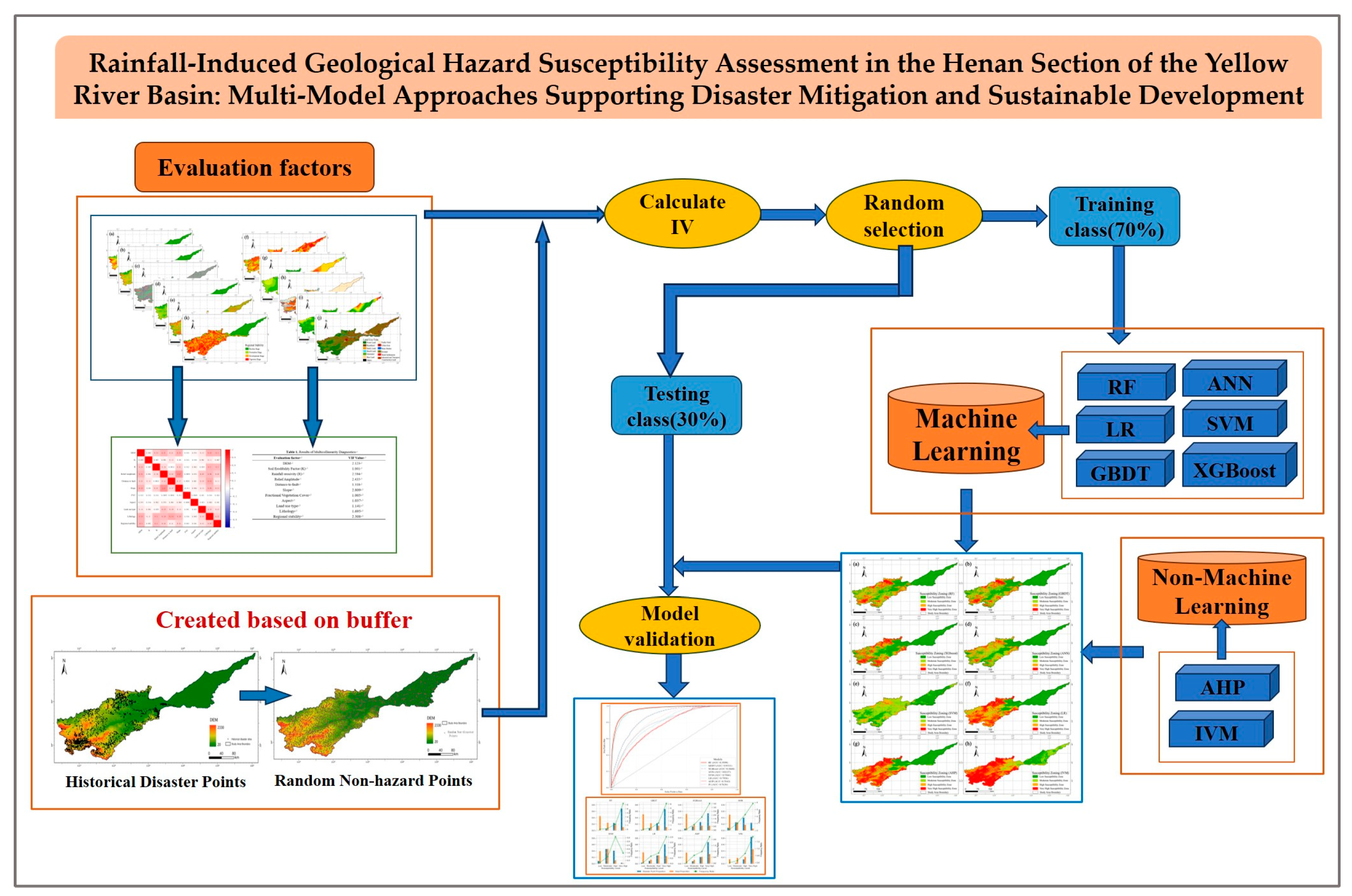
3. Theory and Methods
3.1. Information Value Model (IVM)
3.2. Weighted Information Value Model
3.3. Analytic Hierarchy Process (AHP)
3.4. Logistic Regression (LR) Model
3.5. Gradient Boosting Decision Tree (GBDT) Model
3.6. Extreme Gradient Boosting Decision Tree (XGBoost) Model
3.7. Support Vector Machine (SVM) Model
3.8. Random Forest (RF) Model
3.9. Artificial Neural Network (ANN) Model
3.10. Erosion Cycle Theory
- (1)
- Incubation stage: ∂xP is in the range (0, −0.0131], and N is in the range (0, 0.62];
- (2)
- Development stage: ∂xP is in the range (−0.0131, −0.0979], and N is in the range (0.62, 1.23];
- (3)
- Active stage: ∂xP is in the range (−0.0979, 0), and N is in the range (1.23, 2.0);
- (4)
- Recession stage: ∂xP is in the range [0, 38.85), and N is in the range [2.0, 3.71).
4. Experiments and Results
4.1. Calculation of Information Value
4.2. Collinearity Diagnosis of Evaluation Factors
4.3. The Application of the Model
4.3.1. Information Value Model
4.3.2. Weighted Information Value Model Evaluation Based on AHP
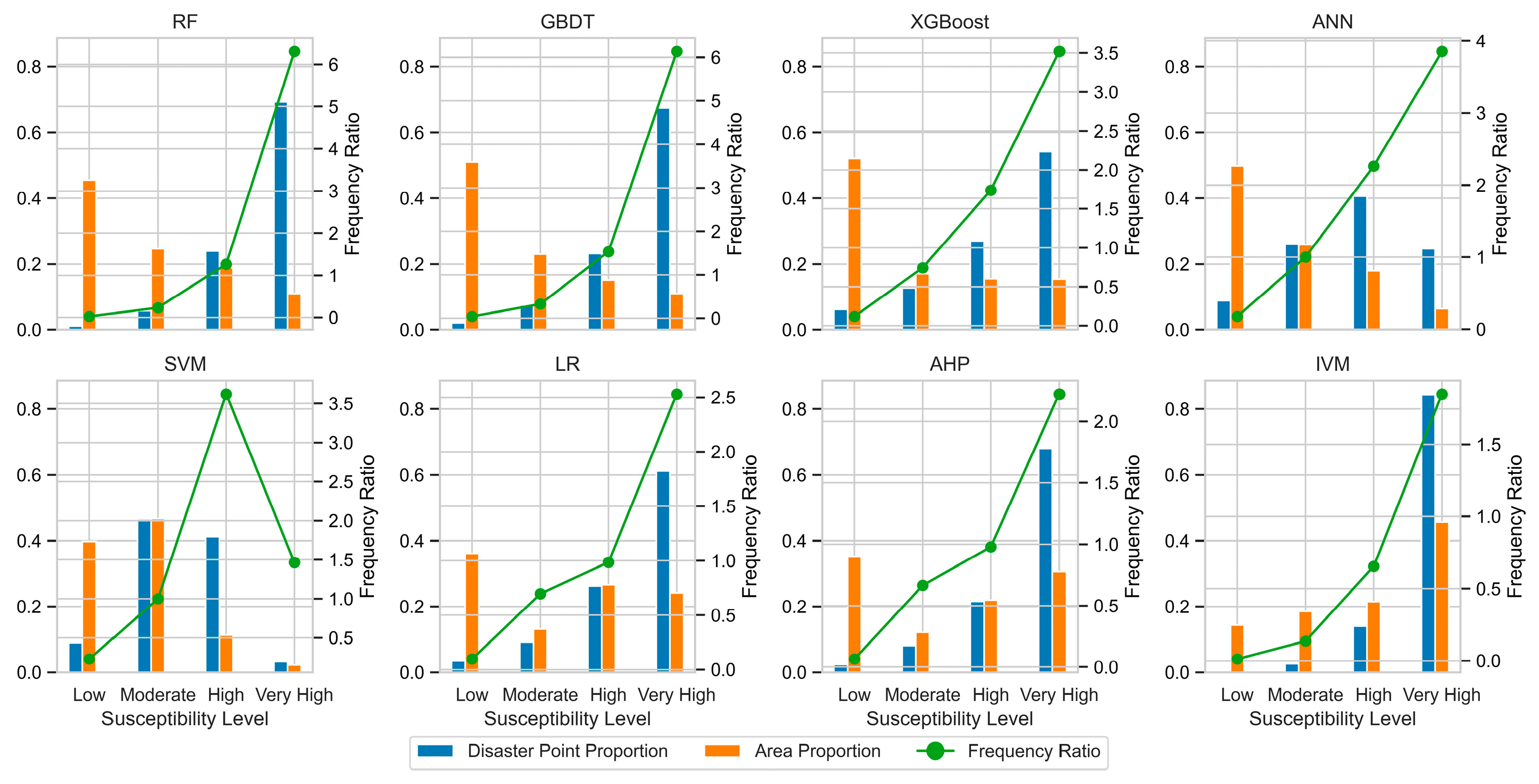
4.3.3. ML Models
5. Discussion
5.1. Model Performance Analysis
5.2. Key Factors Controlling RGH Occurrence in HNYR
5.3. Spatial Analysis of RGH Susceptibility Mapping
5.4. Rationality of Negative Sample Selection
5.5. Implications for Sustainable Development and Disaster Resilience
5.6. Limitations
5.6.1. Regional Transferability Constraints
5.6.2. Incompleteness of Disaster-Inducing Factors
5.6.3. Data Resolution and Overfitting Risks
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| HNYR | Henan section of the Yellow River Basin |
| SVM | Support Vector Machine |
| RGHA | Rainfall-induced geological hazard susceptibility assessment |
| RGH | Rainfall-induced geological hazard |
| ML | Machine learning |
| RF | Random Forest |
| GBDT | Gradient Boosting Decision Tree |
| IVM | Information Value Model |
| ANN | Artificial Neural Network |
| LR | Logistic Regression |
| XGBoost | eXtreme Gradient Boosting |
| AHP | Analytic Hierarchy Process |
| K | Soil erodibility factor |
| R | Rainfall erosivity |
| FVC | Fractional vegetation cover |
| CT | Consistency test |
References
- Henan Provincial Department of Natural Resources. 2023 Henan Provincial Natural Resources Statistical Bulletin. 2024. Available online: https://dnr.henan.gov.cn/2024/12-03/3094375.html (accessed on 15 April 2025).
- Henan Provincial Department of Natural Resources. 2024 Announcement on the Situation of Geological Hazard Risk Points in Henan Province. 2024. Available online: https://dnr.henan.gov.cn/2024/05-11/2989580.html (accessed on 15 April 2025).
- Sajid, T.; Maimoon, S.K.; Waseem, M.; Ahmed, S.; Khan, M.A.; Tränckner, J.; Pasha, G.A.; Hamidifar, H.; Skoulikaris, C. Integrated Risk Assessment of Floods and Landslides in Kohistan, Pakistan. Sustainability 2025, 17, 3331. [Google Scholar] [CrossRef]
- Fan, Z.; Gou, X.; Qin, M.; Fan, Q.; Yu, J.; Zhao, J. Geological Disaster Susceptibility Assessment Based on Coupling of Information Volume Model and Logistic Regression Model. J. Eng. Geol. 2018, 26, 340–347. [Google Scholar] [CrossRef]
- Jin, C.; Fei, W.; Ding, W.; Chen, X.; Du, Y. Geological Disaster Susceptibility Assessment Based on Information Volume Model and Logistic Regression Model—A Case Study of Yunyang District, Shiyan City. Resour. Environ. Eng. 2021, 35, 845–850+886. [Google Scholar] [CrossRef]
- Zhao, P.; Wang, Y.; Xie, Y.; Uddin, M.G.; Xu, Z.; Chang, X.; Zhang, Y. Landslide susceptibility assessment using information quantity and machine learning integrated models: A case study of Sichuan province, southwestern China. Earth Sci. Inform. 2025, 18, 190. [Google Scholar] [CrossRef]
- Guillen, K.A.D.; Mendoza, M.E.; Macías, J.L.; Solis-Castillo, B. Landslide susceptibility analysis based on A semiquantitative method in the sierra-costa region, michoacan, mexico. Phys. Geogr. 2022, 43, 463–486. [Google Scholar] [CrossRef]
- Sur, U.; Singh, P.; Meena, S.R. Landslide susceptibility assessment in a lesser Himalayan road corridor (India) applying fuzzy AHP technique and earth-observation data. Geomat. Nat. Hazards Risk 2020, 11, 2176–2209. [Google Scholar] [CrossRef]
- Do, H.M.; Yin, K.L.; Guo, Z.Z. A comparative study on the integrative ability of the analytical hierarchy process, weights of evidence and logistic regression methods with the Flow-R model for landslide susceptibility assessment. Geomat. Nat. Hazards Risk 2020, 11, 2449–2485. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, Z.; Lin, S. Landslide Susceptibility Assessment in the Ili River Valley Region, Xinjiang Based on Evidence Weight and Logistic Regression Coupling. J. Eng. Geol. 2023, 31, 1350–1363. [Google Scholar] [CrossRef]
- Zhang, S.; Li, C.; Peng, J.; Peng, D.; Xu, Q.; Zhang, Q.; Bate, B. GIS-based soil planar slide susceptibility mapping using logistic regression and neural networks: A typical red mudstone area in southwest China. Geomat. Nat. Hazards Risk 2021, 12, 852–879. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, C. Assessment of Landslide Susceptibility Based on ReliefF Feature Weight Fusion: A Case Study of Wenxian County, Longnan City. Sustainability 2025, 17, 3536. [Google Scholar] [CrossRef]
- Duwal, S.; Liu, D.; Pradhan, P.M. Flood susceptibility modeling of the Karnali river basin of Nepal using different machine learning approaches. Geomat. Nat. Hazards Risk 2023, 14, 2217321. [Google Scholar] [CrossRef]
- Li, Y.; Sheng, Y.; Chai, B.; Zhang, W.; Zhang, T.; Wang, J. Collapse susceptibility assessment using a support vector machine compared with back-propagation and radial basis function neural networks. Geomat. Nat. Hazards Risk 2020, 11, 510–534. [Google Scholar] [CrossRef]
- Basharat, M.u.; Khan, J.A.; Abdo, H.G.; Almohamad, H. An integrated approach based landslide susceptibility mapping: Case of Muzaffarabad region, Pakistan. Geomat. Nat. Hazards Risk 2023, 14, 2210255. [Google Scholar] [CrossRef]
- Mangkhaseum, S.; Bhattarai, Y.; Duwal, S.; Hanazawa, A. Flood susceptibility mapping leveraging open-source remote-sensing data and machine learning approaches in Nam Ngum River Basin (NNRB), Lao PDR. Geomat. Nat. Hazards Risk 2024, 15, 2357650. [Google Scholar] [CrossRef]
- He, Q.; Jiang, Z.; Wang, M.; Liu, K. Landslide and Wildfire Susceptibility Assessment in Southeast Asia Using Ensemble Machine Learning Methods. Remote Sens. 2021, 13, 1572. [Google Scholar] [CrossRef]
- Song, Y.; Song, Y.; Wang, C.; Wu, L.; Wu, W.; Li, Y.; Li, S.; Chen, A. Landslide susceptibility assessment through multi-model stacking and meta-learning in Poyang County, China. Geomat. Nat. Hazards Risk 2024, 15, 2354499. [Google Scholar] [CrossRef]
- Can, R.; Kocaman, S.; Gokceoglu, C. A Comprehensive Assessment of XGBoost Algorithm for Landslide Susceptibility Mapping in the Upper Basin of Ataturk Dam, Turkey. Appl. Sci. 2021, 11, 4993. [Google Scholar] [CrossRef]
- Shen, S.; Deng, L.; Tang, D.; Chen, J.; Fang, R.; Du, P.; Liang, X. Landslide Hazard Assessment Based on Ensemble Learning Model and Bayesian Probability Statistics: Inference from Shaanxi Province, China. Sustainability 2025, 17, 1973. [Google Scholar] [CrossRef]
- Al-Sheriadeh, M.S.; Daqdouq, M.A. Robustness of machine learning algorithms to generate flood susceptibility maps for watersheds in Jordan. Geomat. Nat. Hazards Risk 2024, 15, 2378991. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, Q.; Luan, S.; Gao, M.; Liang, H.; Zheng, J.; Yuan, W.; Ji, X. Landslide susceptibility prediction and mapping in Taihang mountainous area based on optimized machine learning model with genetic algorithm. Earth Sci. Inform. 2024, 17, 5539–5559. [Google Scholar] [CrossRef]
- Lu, M.; Tay, L.T.; Mohamad-Saleh, J. Landslide susceptibility analysis using random forest model with SMOTE-ENN resampling algorithm. Geomat. Nat. Hazards Risk 2024, 15, 2314565. [Google Scholar] [CrossRef]
- Nsengiyumva, J.B.; Valentino, R. Predicting landslide susceptibility and risks using GIS-based machine learning simulations, case of upper Nyabarongo catchment. Geomat. Nat. Hazards Risk 2020, 11, 1250–1277. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, X.; Niu, R.; Wang, Y.; Zhang, K. Using the rotation and random forest models of ensemble learning to predict landslide susceptibility. Geomat. Nat. Hazards Risk 2020, 11, 1542–1564. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, X.; Liu, A. Rainfall-induced Geological Disaster Susceptibility Evaluation Model Based on ArcGIS for Fujian Province. Fujian Geol. 2010, 29, 72–76. [Google Scholar]
- Wang, J. Construction of a Rainfall-induced Geological Disaster Susceptibility Evaluation Model Based on ArcGIS. Water Conserv. Sci. Econ. 2020, 26, 17–22. [Google Scholar]
- Zhou, B.; Xie, H.; Wen, G. Rainfall-Induced Geological Hazard Susceptibility Zoning in Henan Province Based on the Erosion Cycle Theory. J. North China Univ. Water Resour. Electr. Power (Nat. Sci. Ed.) 2024, 45, 92–101. [Google Scholar] [CrossRef]
- Oliveira, S.C.; Zêzere, J.L.; Garcia, R.A.C.; Pereira, S.; Vaz, T.; Melo, R. Landslide susceptibility assessment using different rainfall event-based landslide inventories: Advantages and limitations. Nat. Hazards 2024, 120, 9361–9399. [Google Scholar] [CrossRef]
- Fan, Y. Effectiveness and Practices of Soil and Water Conservation and Ecological Construction in the Yellow River Basin, Henan Province. China Soil Water Conserv. 2016, 10, 24–26. [Google Scholar] [CrossRef]
- Luo, S.; Li, X.; Yang, J.; Li, X. How to Consider Human Footprints to Assess Human Disturbance: Evidence from Urban Agglomeration in the Yellow River Basin. Land 2024, 13, 2163. [Google Scholar] [CrossRef]
- Guo, F.; Wu, D.; Ge, M.; Dong, J.; Fang, H.; Tian, D. Impact of Continuous Variable Factor Classification and Machine Learning Models on Landslide Susceptibility Assessment Accuracy. J. Wuhan Univ. (Inf. Sci. Ed.) 2024, 1–17. [Google Scholar] [CrossRef]
- Network, E.S.S.D.S. 1:4,000,000 China Soil Map (2000). 2006. Available online: https://nnu.geodata.cn/index.html (accessed on 15 April 2025).
- Kayet, N.; Chakrabarty, A.; Pathak, K.; Sahoo, S.; Dutta, T.; Hatai, B.K. Comparative analysis of multi-criteria probabilistic FR and AHP models for forest fire risk (FFR) mapping in Melghat Tiger Reserve (MTR) forest. J. For. Res. 2020, 31, 565–579. [Google Scholar] [CrossRef]
- Nuthammachot, N.; Stratoulias, D. Multi-criteria decision analysis for forest fire risk assessment by coupling AHP and GIS: Method and case study. Environ. Dev. Sustain. 2021, 23, 17443–17458. [Google Scholar] [CrossRef]
- Fell, R.; Corominas, J.; Bonnard, C.; Cascini, L.; Leroi, E.; Savage, W.Z. Guidelines for landslide susceptibility, hazard and risk zoning for land use planning. Eng. Geol. 2008, 102, 85–98. [Google Scholar] [CrossRef]
- Chen, L.; Meng, G.; Zhang, W.; Wang, B. Application of the Information Content Model in the Survey and Zoning of Geological Disasters in Counties and Cities—A Case Study of Xianju County, Zhejiang Province. Hydrogeol. Eng. Geol. 2003, 5, 49–52. [Google Scholar]
- Hu, X.; Ming, L.; Wu, T.; Liu, B.; Pang, D.; Yin, J.; Song, B.; Ke, F. Evaluation of geological hazard vulnerability in Xining city based on InSAR and informativeness-hierarchical analysis coupled modeling. Bull. Surv. Mapp. 2023, 12, 51–56, 75. [Google Scholar]
- Saaty, T. The Analytic Hierarchy Process (AHP) for Decision Making. J. Oper. Res. Soc. 1980, 41, 1073. [Google Scholar]
- Wang, L. Geological Disaster Susceptibility Evaluation Based on GIS Technology—A Case Study of Qujiang District, Guangdong Province. Miner. Explor. 2023, 14, 2492–2501. [Google Scholar] [CrossRef]
- Nelder, J.A.; Wedderburn, R.W.M. Generalized Linear Models. R. Stat. Society J. Ser. A Gen. 2018, 135, 370–384. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A working guide to boosted regression trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Pham, Q.B.; Khedher, K.M.; Dehbozorgi, M.; Rabby, Y.W.; Anh, D.T.; Nguyen, D.H. An ensemble random forest tree with SVM, ANN, NBT, and LMT for landslide susceptibility mapping in the Rangit River watershed, India. Nat. Hazards 2022, 113, 1601–1633. [Google Scholar] [CrossRef]
- Jiang, Z. Super Entropy of Debris Flow Watershed Systems. J. Geol. Hazards Civ. Eng. 1992, 1, 35–42. [Google Scholar]
- Zhang, J.; Qian, J.; Lu, Y.; Li, X.; Song, Z. Study on Landslide Susceptibility Based on Multi-Model Coupling: A Case Study of Sichuan Province, China. Sustainability 2024, 16, 6803. [Google Scholar] [CrossRef]
- Tao, S.; Hu, D.; Zhao, W. Susceptibility assessment of earthquake-triggered landslide in Wenchuan. In Proceedings of the Sixth International Symposium on Digital Earth: Data Processing and Applications, Beijing, China, 9–12 September 2009; SPIE: Bellingham, WA, USA, 2010; Volume 7841, pp. 465–472. [Google Scholar]
- Dai, X.; Zhu, Y.; Sun, K.; Zou, Q.; Zhao, S.; Li, W.; Hu, L.; Wang, S. Examining the spatially varying relationships between landslide susceptibility and conditioning factors using a geographical random forest approach: A case study in Liangshan, China. Remote Sens. 2023, 15, 1513. [Google Scholar] [CrossRef]
- Xiao, X.; Zou, Y.; Huang, J.; Luo, X.; Yang, L.; Li, M.; Yang, P.; Ji, X.; Li, Y. An interpretable model for landslide susceptibility assessment based on Optuna hyperparameter optimization and Random Forest. Geomat. Nat. Hazards Risk 2024, 15, 2347421. [Google Scholar] [CrossRef]
- Zhang, L.; Zeng, T.; Wang, L.; Li, L. Advancing seismic landslide susceptibility modeling: A comparative evaluation of deep learning models through particle swarm optimization. Earth Sci. Inform. 2024, 17, 3547–3566. [Google Scholar] [CrossRef]
- Zhou, H.; Mu, C.; Yang, B.; Huang, G.; Hong, J. Evaluating Landslide Hazard in Western Sichuan: Integrating Rainfall and Geospatial Factors Using a Coupled Information Value–Geographic Logistic Regression Model. Sustainability 2025, 17, 1485. [Google Scholar] [CrossRef]
- Lohan, N.; Kumar, S.; Singh, V.; Gupta, R.P.; Tiwari, G. Analyzing an Extreme Rainfall Event in Himachal Pradesh, India, to Contribute to Sustainable Development. Sustainability 2025, 17, 2115. [Google Scholar] [CrossRef]
- Ali, M.Z.; Chu, H.-J.; Chen, Y.-C.; Ullah, S. Machine learning in earthquake-and typhoon-triggered landslide susceptibility mapping and critical factor identification. Environ. Earth Sci. 2021, 80, 233. [Google Scholar] [CrossRef]
- Günther, A.; Van Den Eeckhaut, M.; Malet, J.-P.; Reichenbach, P.; Hervás, J. Climate-physiographically differentiated Pan-European landslide susceptibility assessment using spatial multi-criteria evaluation and transnational landslide information. Geomorphology 2014, 224, 69–85. [Google Scholar] [CrossRef]
- Wu, B.; Shi, Z.; Zheng, H.; Peng, M.; Meng, S. Impact of sampling for landslide susceptibility assessment using interpretable machine learning models. Bull. Eng. Geol. Environ. 2024, 83, 461. [Google Scholar] [CrossRef]
- Khabiri, S.; Crawford, M.M.; Koch, H.J.; Haneberg, W.C.; Zhu, Y. An assessment of negative samples and model structures in landslide susceptibility characterization based on Bayesian network models. Remote Sens. 2023, 15, 3200. [Google Scholar] [CrossRef]

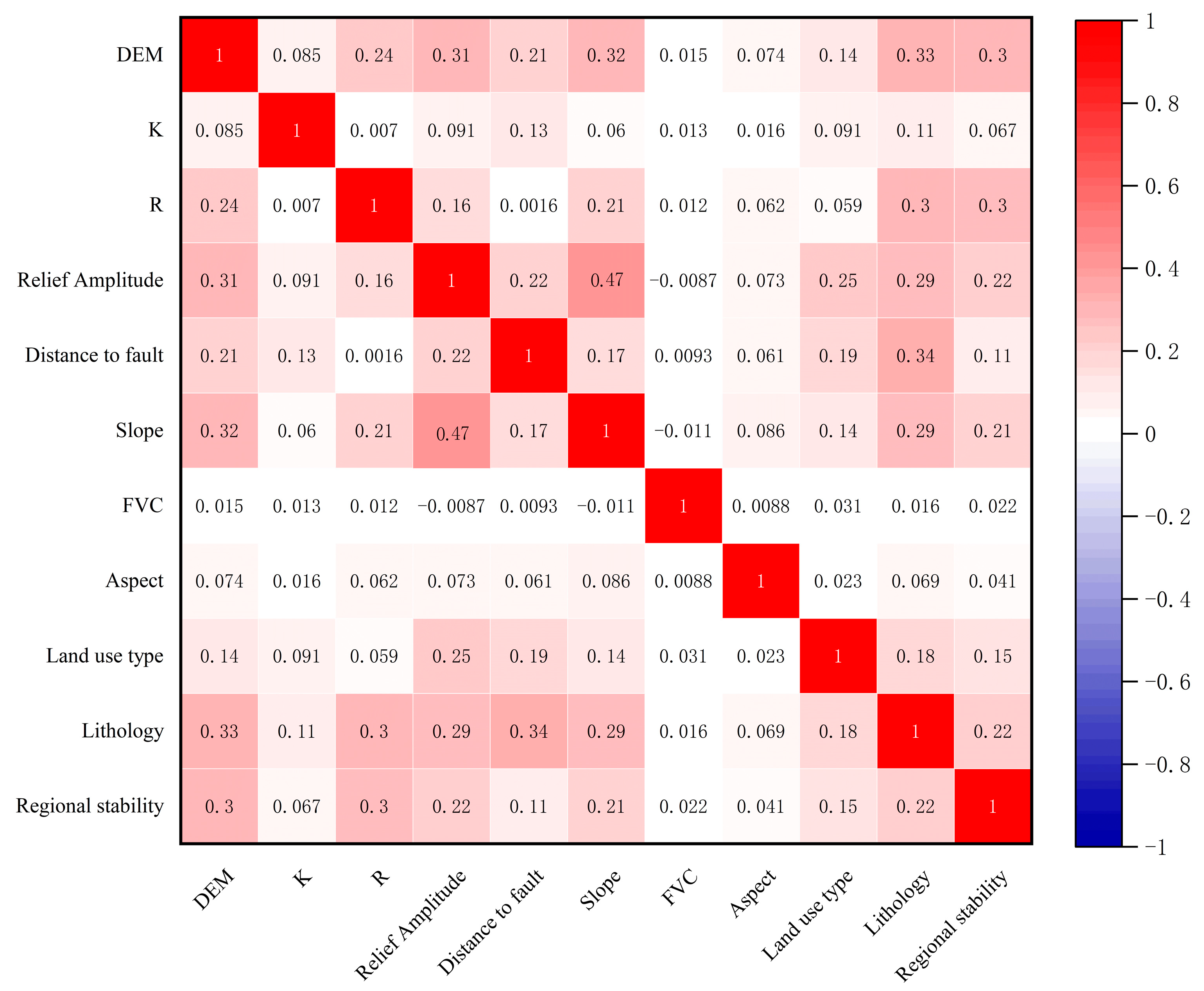

| Evaluation Factor | VIF Value |
|---|---|
| DEM | 2.123 |
| Soil erodibility factor (K) | 1.001 |
| Rainfall erosivity (R) | 2.594 |
| Relief amplitude | 2.435 |
| Distance to fault | 1.318 |
| Slope | 2.809 |
| Fractional vegetation cover | 1.005 |
| Aspect | 1.037 |
| Land use type | 1.141 |
| Lithology | 1.695 |
| Regional stability | 2.308 |
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | S8 | S9 | S10 | S11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| S1 | 1 | 1/2 | 5 | 2 | 2 | 2 | 2 | 2 | 1/2 | 6 | 5 |
| S2 | 2 | 1 | 7 | 3 | 4 | 4 | 4 | 4 | 2 | 8 | 6 |
| S3 | 1/5 | 1/7 | 1 | 1/5 | 1/3 | 1/4 | 1/4 | 1/4 | 1/6 | 2 | 1 |
| S4 | 1/2 | 1/3 | 5 | 1 | 3 | 3 | 2 | 2 | 1/2 | 5 | 4 |
| S5 | 1/2 | 1/4 | 3 | 1/3 | 1 | 1 | 1 | 1/2 | 1/3 | 3 | 3 |
| S6 | 1/2 | 1/4 | 4 | 1/3 | 1 | 1 | 1/2 | 1/3 | 1/4 | 3 | 2 |
| S7 | 2/2 | 1/4 | 4 | 1/2 | 1 | 2 | 1 | 1/2 | 1/3 | 3 | 2 |
| S8 | 1/2 | 1/4 | 4 | 1/2 | 2 | 3 | 2 | 1 | 1/2 | 3 | 2 |
| S9 | 2 | 1/2 | 6 | 2 | 3 | 4 | 3 | 2 | 1 | 6 | 5 |
| S10 | 1/6 | 1/8 | 1/2 | 1/5 | 1/3 | 1/3 | 1/3 | 1/3 | 1/6 | 1 | 1/2 |
| S11 | 1/5 | 1/6 | 1 | 1/4 | 1/3 | 1/2 | 1/2 | 1/2 | 1/5 | 2 | 1 |
| CT | The maximum eigenvalue λmax = 11.4258, and the consistency ratio CR = 0.028 < 0.1, which passes the consistency test | ||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Ci, H.; Yang, H.; Wang, R.; Yan, Z. Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development. Sustainability 2025, 17, 4348. https://doi.org/10.3390/su17104348
Zhang Y, Ci H, Yang H, Wang R, Yan Z. Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development. Sustainability. 2025; 17(10):4348. https://doi.org/10.3390/su17104348
Chicago/Turabian StyleZhang, Yinyuan, Hui Ci, Hui Yang, Ran Wang, and Zhaojin Yan. 2025. "Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development" Sustainability 17, no. 10: 4348. https://doi.org/10.3390/su17104348
APA StyleZhang, Y., Ci, H., Yang, H., Wang, R., & Yan, Z. (2025). Rainfall-Induced Geological Hazard Susceptibility Assessment in the Henan Section of the Yellow River Basin: Multi-Model Approaches Supporting Disaster Mitigation and Sustainable Development. Sustainability, 17(10), 4348. https://doi.org/10.3390/su17104348








