Low-Carbon Optimization Scheduling for Systems Considering Carbon Responsibility Allocation and Electric Vehicle Demand Response

Abstract

To achieve low carbon emissions in the power system and contribute to economic growth, a low-carbon optimization scheduling strategy for a power system, considering carbon responsibility sharing and electric vehicle demand response, is proposed based on the establishment of a flexible-load model guided by carbon potential. Firstly, utilizing the principle of proportional sharing to track carbon emission flow and establish a carbon emission flow model. Secondly, based on the Shapley value carbon responsibility allocation method, the reasonable range of carbon responsibility on each load side is calculated, and a hierarchical carbon price is established. A load aggregator demand response carbon emission model is established using the node carbon potential, and a dual-layer optimization scheduling model for the power system based on the node carbon potential demand response is constructed. The upper layer of the model is the optimal economic dispatch of the power grid operator, and the lower layer is the demand response economic dispatch of the load aggregator. Through numerical verification, the carbon trading model takes into account the system’s carbon emissions and overall operating costs while balancing the system’s low-carbon and economic aspects.

1. Introduction

With the aggravation of environmental problems such as global warming, reducing the use of fossil fuels and increasing the consumption of clean energy are important issues that need to be addressed for the survival and development of human society [1]. Among them, the role of CO₂ in causing climate warming is as high as 77% [2]. The power industry, as a key part of energy system energy conservation and emission reduction, has become one of the necessary stakeholders in achieving carbon emission reduction by improving the system’s economy and low-carbon nature [3,4]. The new round of energy reform in China is moving towards a green and low-carbon direction, and the development of energy conservation and emission reduction in the power industry involves many elements such as the interaction characteristics between sources and loads, carbon trading market mechanisms, and operational strategies [5,6]. Among these, electric vehicles (EVs), as a new type of environmentally friendly transportation, have been increasingly favored and promoted in recent years. Their scheduling flexibility and participation in vehicle-to-grid interaction (V2G) are conducive to energy conservation and carbon emission reductions [7,8].

At present, traditional electricity production still relies on non-renewable resources such as coal mines, leading to significant carbon emission issues [9]. The main source of carbon emissions is from the power sector, and many studies on carbon emission responsibility are focused on the power generation side. References [10,11,12] adopted a full-lifecycle-assessment approach to determine the carbon emission factors of the power generation end from a macro perspective; references [13,14,15] conducted in-depth analyses of the power generation process in the energy system, and effectively reduced the overall carbon emission level by adding optimization goals that include carbon emission costs or setting carbon emission limits. These methods can indeed reduce carbon emissions to a certain extent, but they have not delved into how to influence user behavior, nor have they explored how to reasonably share the responsibility for load-side carbon emissions or developed corresponding low-carbon scheduling strategies.

As an effective analytical tool for developing low-carbon electricity, the theory of carbon emission flow has been further developed and improved. References [16,17,18] provide the basic concept of carbon flow and propose the concept of carbon emissions flowing in the power flow network based on power system’s power flow. References [17,18] provide a basic calculation method for the carbon flow rate. Reference [19] provides a comprehensive method for power flow tracking in the electricity market; references [20,21] propose the basic idea of power flow tracking; and references [22,23] mention the concept of carbon flow tracking and establish a carbon flow tracking model based on active power.

Research on a carbon emission analysis model that takes into account both the operational characteristics of the power system and network features, we can quantitatively analyze carbon emissions during the power transmission process [24,25]. Reference [26] proposes a carbon emission analysis method considering wind power uncertainty, constructs a system injection carbon flow function that includes wind power output and wind speed, and analyzes the trend in the impact of wind power uncertainty on node carbon potential. Based on the energy supply characteristics of the park, reference [27] analyzed the mechanism of multi-energy virtual carbon flow transmission, established a node carbon emission intensity evaluation model, and realized the perception and optimization of the entire process’s carbon footprint. Reference [28] divides user emission intensity levels based on node carbon emission intensity, provides differentiated guidance and focuses on user emission reduction work, and achieves emission reduction goals through demand-side management. Reference [29] uses the average carbon emission factor of regional power grids as a guiding signal to guide user emission reduction work, and analyzes the feasibility and universality of carbon signal guidance for demand-side management to achieve carbon emission reduction.

The above literature considers the impact of source load low-carbon interaction and carbon trading on the low-carbon economy of the power system. By combining carbon emission flow with the power network, it analyzes the real-time flow of carbon emissions from the generation side to the demand side in the power grid. However, most of the current related research explores low-carbon potential from the perspective of the source side, limited to the analysis of carbon emission flows, and there are few studies based on carbon flow tracking to guide the demand response of multi-dimensional flexible loads guided by the node carbon potential.

Based on the above research, this paper proposes a low-carbon optimization scheduling strategy that considers carbon responsibility allocation and electric vehicle demand response. This strategy is based on the principle of proportional sharing, and tracks and analyzes the carbon emission flow in the power network in both the time and space dimensions. The carbon emission responsibility of the power system is transferred from the generation side to the load side for calculation. On the load side, the carbon responsibility of each load node is reasonably allocated based on the Shapley value. A stepped carbon price setting method is proposed, and an optimal economic scheduling model for power grid operators is constructed. On this basis, fully considering the demand elasticity of flexible loads containing electric vehicles within the scope of different load aggregators (LAs), the carbon potential and electricity price signals are effectively combined with the demand response of multiple flexible loads, and a two-layer optimization scheduling model for demand response guided by the node carbon potential and time-of-use electricity price is established. This realizes the refinement of low-carbon economic benefits for diversified flexible loads, promotes the development of low-carbon economy in the power system, and provides theoretical support for the subsequent participation of load-side resources in low-carbon emission reduction strategies.

2. Load Demand Response Model Based on Carbon Flow Tracking

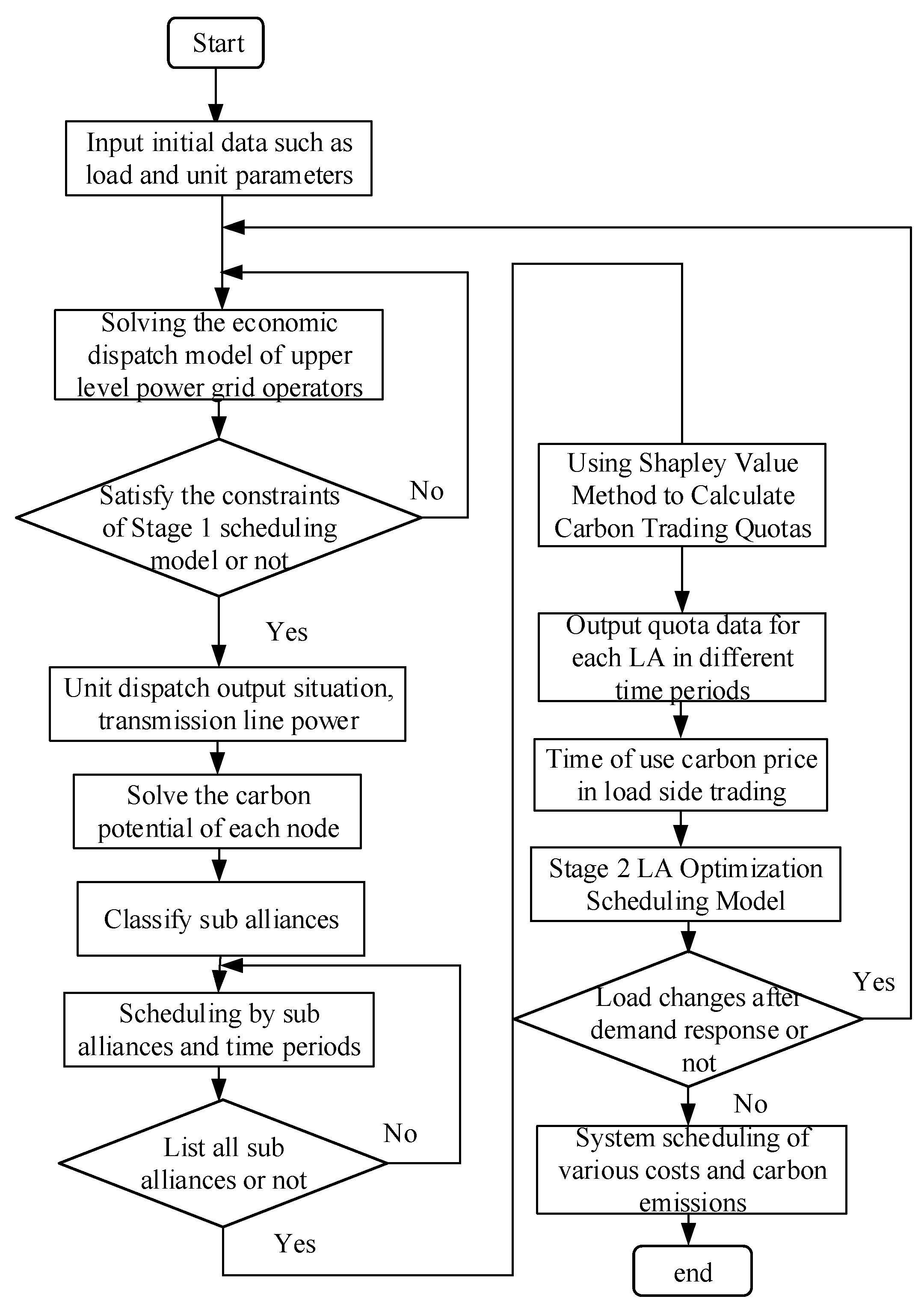
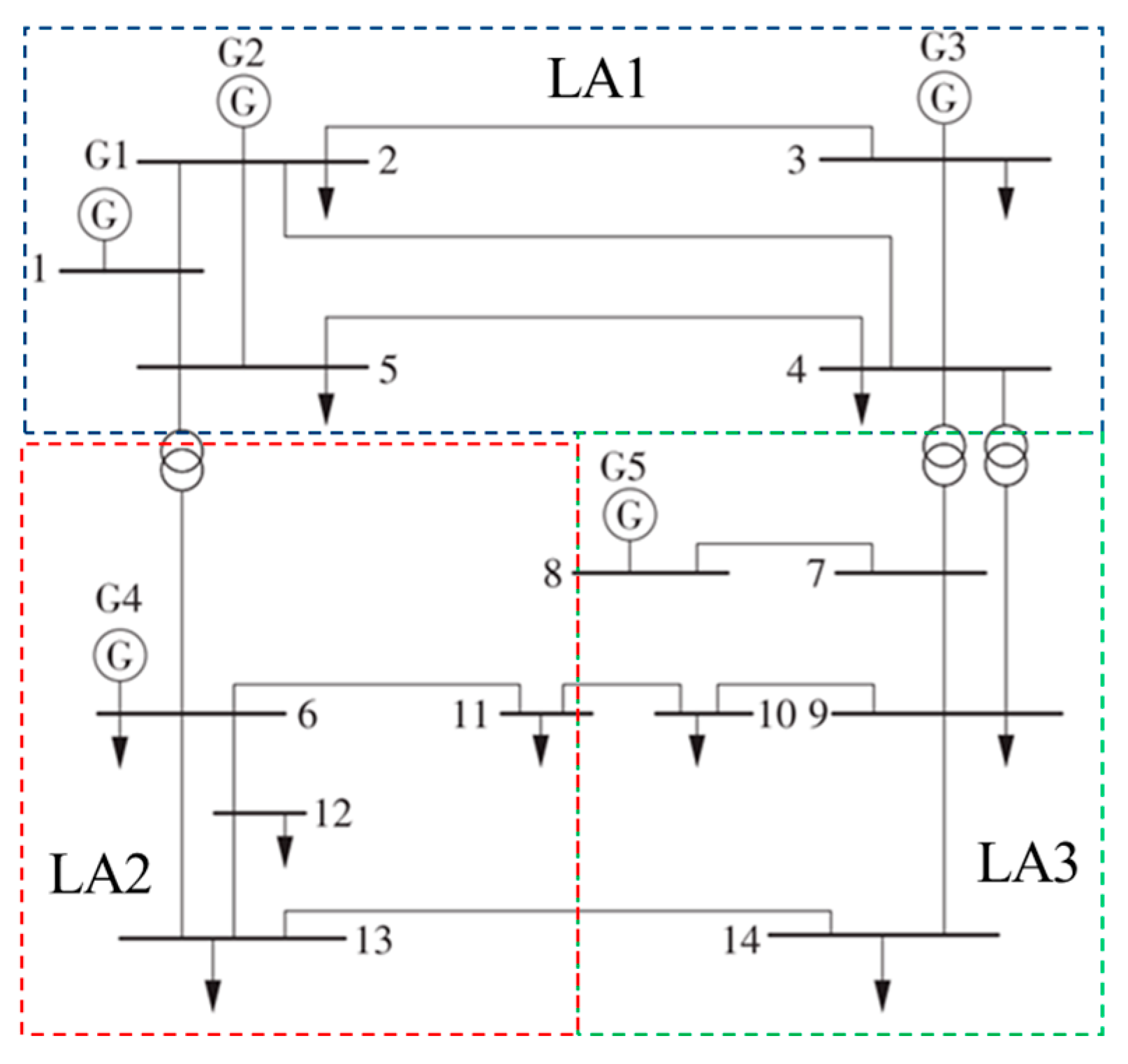
2.1. Carbon Emission Stream Model Based on Proportional Sharing Principle

Most of the carbon dioxide comes from the source side of the energy industry, but the key factor determining carbon emissions is in the end-use stage. A carbon emission flow model constructed using the principle of proportional distribution can measure the total carbon emissions of various energy products from production to consumption. At present, the calculation method of this carbon emission flow theory is gradually improving, and the carbon emission flow situation at each time period and node can be calculated based on the known trend distribution.

When calculating carbon flow, the carbon potential of a node is only affected by the injected current, so the sum of the active current of the node is

$$P_m={\displaystyle \sum _{s\in S^{+}}{P}_s^B+P_i^G}$$

(1)

In the formula, $P_m$ is the sum of active power flows flowing into the node $m$; $P_s^B$ is the active power of the branch $s$; $S^{+}$ is the set of branches representing node $m$ with flowing currents; and $P_i^G$ is the output of the connected generator $i$.

(1)

Carbon flow rate

The carbon flow rate represents the carbon emissions corresponding to the energy flow through network nodes or branches per unit time. It can be represented by $R$, in seconds, as shown in Equation (2).

$$R=\frac{\mathit{dF}}{\mathit{dt}}$$

(2)

In the formula, $F$ represents the inflow of carbon emissions and $t$ represents time.

(2)

Carbon flow density

The carbon flow density represents the carbon emissions per unit of electricity, including three concepts: generator carbon emission intensity, branch carbon flow density, and node carbon potential, all measured in t/MWh. The carbon intensity of a generator represents the real-time carbon emission intensity of a power plant based on its power generation characteristics, denoted as $e_G$.

Branch carbon intensity refers to the carbon emissions on the generation side caused by unit electricity consumption in branch transmission, which is the ratio of branch carbon flow to active power flow. The calculation formula is

$$\rho =\frac{R}{P}$$

(3)

In the formula, $R$ is the carbon flow rate, and $P$ is the power of the transmission line.

(3)

Node carbon potential

The carbon potential of a node represents the equivalent carbon emissions generated on the power generation side per unit of electricity consumed by the node. This value is equal to the weighted average of the carbon flow density of all branches flowing into the node relative to the active power flow. For node n, the carbon potential of node n is

$$e_n=\frac{{\displaystyle \sum _{i=1}^{I_i}}(P_i{\rho }_i)+P_{\mathit{Gn}}{e}_{\mathit{Gn}}}{{\displaystyle \sum _{i=1}^{I_i}}{P}_i+P_{\mathit{Gn}}}$$

(4)

In the formula, $e_n$ is the carbon potential of the node $n$; $e_{G_n}$ is the carbon emission intensity of the generator $G_n$; $P_i$ is the injection power of node i in the branch; $P_{G_n}$ is the generated power of the generator $G_n$ at the node $n$; ${\rho }_i$ is the carbon flow density of branch i injected into the node; and $I_i$ is the number of injected power branches connected to the node.

After obtaining the carbon potential of the node, the carbon emissions of the node load can be calculated:

$$E_n=e_n{L}_n$$

(5)

In the formula, $E_n$ represents the carbon emissions of node n; and $L_n$ is the load capacity of node n.

2.2. Load Carbon Emission Model Guided by Node Carbon Potential

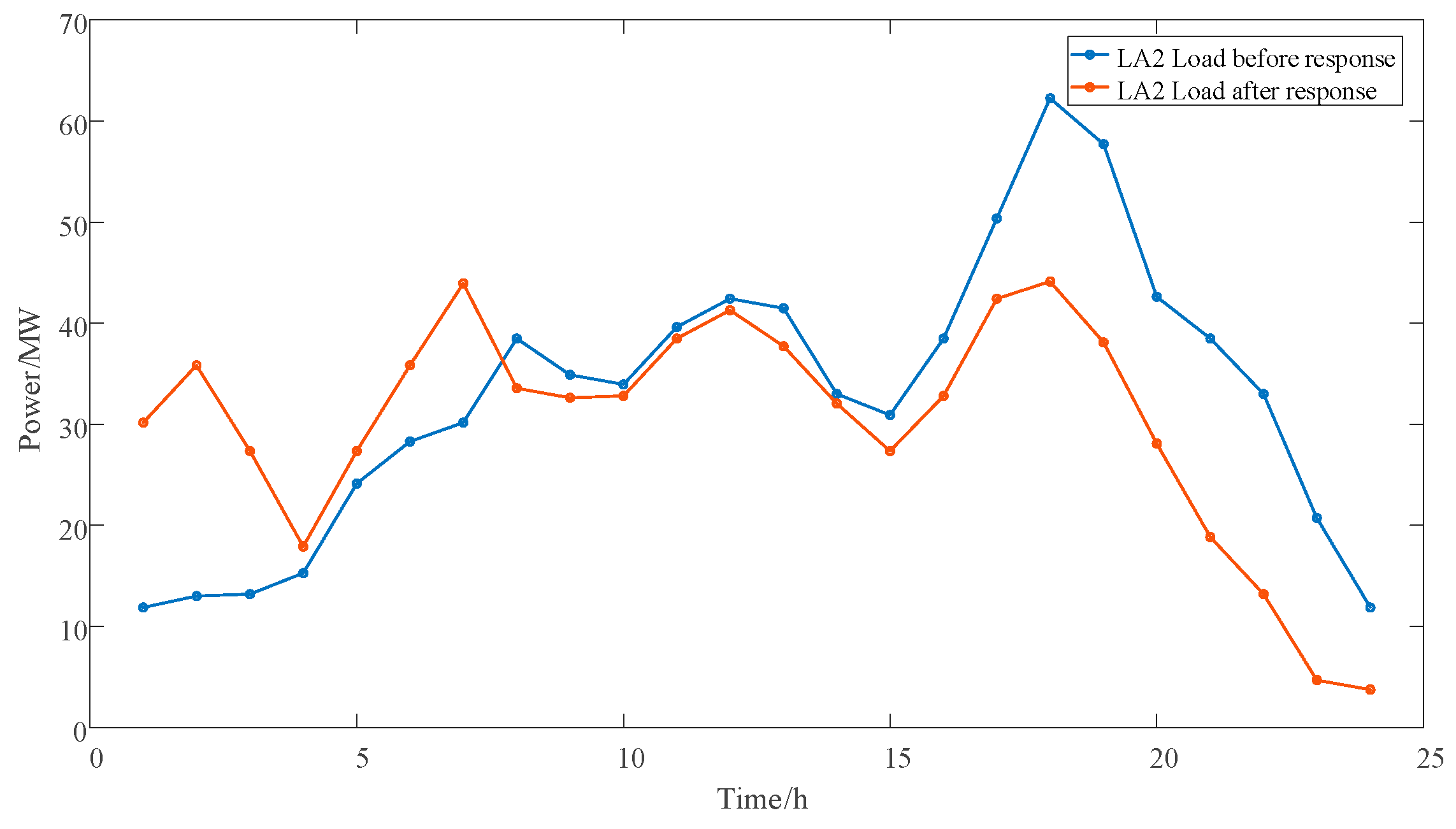
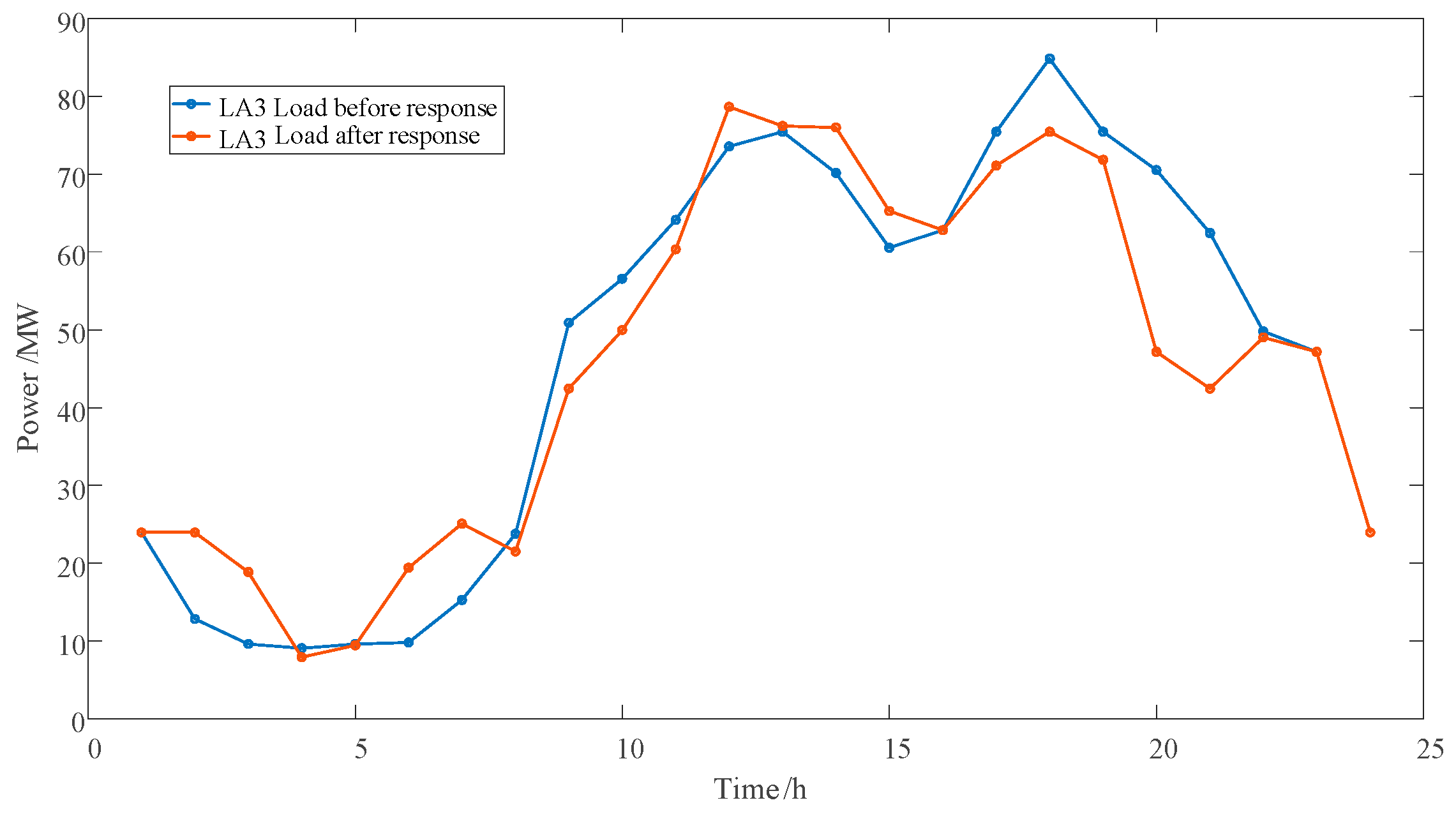
After calculating the carbon potential of each node through the carbon flow tracking method, each LA receives the node carbon potential signal and uses incentive contracts to guide flexible loads to respond to it. A flexible load carbon emission model based on node carbon potential is constructed to obtain the carbon emissions of flexible loads after demand response. This article divides flexible loads in residential LA, commercial LA, and industrial LA areas into electric vehicles, reducible loads (CLs), and transferable loads (TLs). The carbon emission model of flexible loads guided by the node carbon potential is shown below.

(1)

EV carbon emission model

After an EV signs an agreement with an LA, the EV grants the LA the right to charge and discharge, and the LA can freely schedule authorized EVs within the agreed time and limitations. This article uses the Monte Carlo method to simulate the uncertainty of EV daily mileage, access time, departure time, initial access power, and target power.

The carbon emissions $D_t^{EV}$ of an EV are the carbon emissions generated by charging the EV at time t minus the carbon emissions reduced by discharging:

$$\left\{\begin{array}{l}{D}_t^{EV}=e_{m,t}{P}_t^{EV}\Delta t\\ P_t^{EV}={\displaystyle \sum _{n=1}^{N_{ev}}(P_{n,t}^{evc}-P_{n,t}^{evd})}\end{array}\right.$$

(6)

In the formula, $P_t^{EV}$ is the total charge and discharge amount of all connected EVs at time t; $e_{m,t}$ is the carbon potential of node m; $N_{ev}$ is the number of EVs; and $P_{n,t}^{evc}$ and $P_{n,t}^{evd}$ represent the charging and discharging power of the $n$th EV at time t.

(2)

CL and TL carbon emission models

The incentive contract specifies the load response amount, load response compensation fee, and response time of users of CLs and TLs. A CL refers to a load that cannot be transferred, but can be reduced by a certain proportion within a certain period of time. The TL operating period is relatively flexible, allowing interruptions with an indefinite duration while ensuring the same cumulative operating time, and keeping the total amount of load input and output unchanged.

The flexible load of the new energy microgrid in the park can respond to the demand of the power system, adjust the electricity consumption and power load according to the actual situation, and assist the new energy generation system in power dispatching, thereby improving the stability of the power system.

The carbon emissions $D_t^{flex}$ after demand response by the CL and TL are as follows:

$$D_t^{flex}=e_{m,t}^R(P_t^{tra,in}-P_t^{tra,out}-P_t^{cut})$$

(7)

$$\left\{\begin{array}{l}0⩽y_t^{cut}{P}_t^{cut}⩽P_{\mathit{max}}^{cut}\hspace{1em}t\in [t_{sta}^{cut},t_{end}^{cut}]\\ {\displaystyle \sum _{t=1}^{N_t}{y}_t^{cut}=t_{\mathit{max}}^{cut}\hspace{1em}\hspace{1em} t\in [t_{sta}^{cut},t_{end}^{cut}]}\\ 0⩽y_t^{tra,in}{P}_t^{tra,in}⩽P_{\mathit{max}}^{tra,in}\hspace{1em}t\in [t_{sta}^{tra,in},t_{end}^{tra,in}]\\ 0⩽y_t^{tra,out}{P}_t^{tra,out}⩽P_{\mathit{max}}^{tra,out}\hspace{1em}t\in [t_{sta}^{tra,out},t_{end}^{tra,out}]\\ 0⩽y_t^{tra,out}+y_t^{tra,in}⩽1\\ {\displaystyle \sum _{t=1}^{N_t}{y}_t^{tra,in}{P}_t^{tra,in}\Delta t={\displaystyle \sum _{t=1}^{N_t}{y}_t^{tra,out}{P}_t^{tra,out}\Delta t}}\end{array}\right.$$

(8)

In the formula, $e_{m,t}^R$ represents the node carbon potential after the load participates in the demand response at node m at time t; $P_t^{tra,in}$ and $P_t^{tra,out}$ represent the power input and output of the TL at time t, respectively; $P_t^{cut}$ is the reduction in the load at time t; $y_t^{cut}$ is the 0–1 state variable of the CL at time t; $P_{\mathit{max}}^{cut}$ is the upper limit value of the CL; $t_{sta}^{cut}$ and $t_{end}^{cut}$ are the starting and ending moments of the CL response, respectively; $t_{\mathit{max}}^{cut}$ is the upper limit of the CL response period; $y_t^{tra,in}$ and $y_t^{tra,out}$ represent the response status of the transfer in and transfer out of the TL at time t, represented by 0–1 variables; $P_{\mathit{max}}^{tra,in}$ and $P_{\mathit{max}}^{tra,out}$ are the upper limits of the TL input and output power, respectively; $t_{sta}^{tra,in}$ and $t_{end}^{tra,in}$ are the starting and ending times of the TL transfer in and transfer out, respectively. By combining Equations (7) and (8), the actual carbon emissions $D^{\mathrm{LA}}$ in the LA can be obtained, which is the sum of the initial load, CL, TL response, and carbon emissions generated by EV charging and discharging:

$$D^{\mathrm{LA}}=\sum _{t=1}^{N_t}{e}_{m,t}^{\mathrm{R}}{P}_t^{\mathrm{load}}\Delta t+D_t^{\mathrm{EV}}+D_t^{\mathrm{flex}}$$

(9)

In the formula, $P_t^{\mathrm{load}}$ is the initial load of the LA at time t.

(3)

Price-based demand response model

According to consumer psychology theory, price-based demand response aims to change users’ charging load and habitual electricity usage patterns, and to develop reasonable electricity prices to guide user load distribution. Taking electricity load as an example, the impact of electricity price changes on electricity load is represented by the demand elasticity matrix E, as follows:

$${[{\displaystyle \frac{\Delta q_1}{q_1}}\dots {\displaystyle \frac{\Delta q_t}{q_t}}\dots {\displaystyle \frac{\Delta q_T}{q_T}}]}^T=E{[{\displaystyle \frac{\Delta p_1}{p_1}}\dots {\displaystyle \frac{\Delta p_t}{p_t}}\dots {\displaystyle \frac{\Delta p_T}{p_T}}]}^T$$

(10)

$$P_{DR,t}=P_t\Delta q_t$$

(11)

$${\displaystyle \sum _{t=1}^T{P}_{DR,t}}={\displaystyle \sum _{t=1}^T{P}_{YC,t}}$$

(12)

In the formula, the values of electricity load and user electricity value at time t are $q_t$ and $p_t$, respectively, and their changes from time $t-1$ to time $t$ are represented by $\Delta q_t$ and $\Delta p_t$. The ratio between the two is the load change rate and electricity price change rate at time t, represented by ${\displaystyle \frac{\Delta q_t}{q_t}}$ and ${\displaystyle \frac{\Delta p_t}{p_t}}$, respectively. The main diagonal of the demand elasticity matrix $E$ is the self-elasticity coefficient. The sub-diagonal is the mutual elasticity coefficient, with values of −0.2 and 0.033, respectively, in this paper. The total load remains unchanged before and after demand response. The load forecast value at time t is represented by $P_{DR,t}$. The load forecast value before demand response is represented by $P_{YC,t}$. $T$ represents the entire scheduling cycle.

3. Load-Side Carbon Responsibility Allocation and Tiered Carbon Price Interval Calculation Method Based on Shapley Value

The load side carbon responsibility allocation and segmented carbon price range calculation method are based on Shapley values method. The carbon emission flow theory tracks the carbon responsibility of the source side to the load side for calculation. However, due to the differences in the location of each node in the power system, power consumption levels, and grid congestion, the corresponding carbon emission responsibilities of each node are different, and the carbon emission responsibility costs they bear also vary. In order to enable load-side users to fairly and reasonably share the carbon emission responsibilities of each load node and solve the shortcomings of the traditional segmented carbon price range calculation method, this paper adopts the Shapley value allocation method. By sharing the responsibility for carbon emissions to calculate the reasonable range of carbon emissions in each region, a tiered carbon pricing method with interval differences is proposed. This provides more reasonable allocation of carbon emission responsibilities and calculation of load-side carbon emission costs.

The Shapley value method is a mathematical approach used to solve cooperative game problems involving multiple players. Its advantage is that it distributes the benefits according to the marginal contributions of members, and the benefits obtained by participants are equal to their average marginal contributions to the alliance. Therefore, it is very suitable for the allocation of carbon emission responsibility quotas.

3.1. Carbon Responsibility Allocation Theory Based on Shapley Value

For the issue of how to allocate the carbon emission responsibility on the load side, the Shapley value allocation method is adopted, considering the marginal effect of each sub-alliance on the overall alliance. According to the Shapley value allocation principle, the carbon emission responsibility of each sub-alliance is calculated based on its average marginal effect, as shown in Formula (13):

$$x_i={\displaystyle \sum _{S\subseteq N/i}P(S)(c(S\cup \left\{i\right\})-c(S))}$$

(13)

$x_i$ is the carbon emission responsibility corresponding to member $i$ of the alliance; $S$ is a sub-alliance composed of other members that is not included; $P(S)$ is the probability of the sub-alliance $S$ occurring; $S\cup \left\{i\right\}$ is a new alliance formed by merging alliance member $i$ into alliance $S$; $c(S\cup \{i\})-c(S)$ represents the marginal impact generated when alliance member $i$ joins sub-alliance $S$.

$$P(S)={\displaystyle \frac{n_s!(n_N-n_s-1)!}{n_N!}}$$

(14)

The carbon emission responsibility borne by members of a sub-alliance should be within a certain range, not greater than the maximum marginal effect of the sub-alliance member, $x_{\mathit{max}}(i)=\mathit{max}(c(S\cup \left\{i\right\})-c(S))$, nor less than the minimum marginal effect of the sub-alliance member, $x_{\mathit{min}}(i)=\mathit{min}(c(S\cup \left\{i\right\})-c(S))$, that is,

$$x_{\mathit{min}}(i)\le x(i)\le x_{\mathit{max}}(i)$$

(15)

3.2. Calculation Method for Tiered Carbon Price Range

According to the theory in the previous section, calculating the carbon emission quotas corresponding to different alliances, forming each LA quota interval, respectively, 0~$x_{\mathit{min}}$, $x_{\mathit{min}}$~$x_{ave}$, $x_{ave}$~$x_{\mathit{max}}$, and $x_{\mathit{max}}$~∞, and corresponding to four carbon price intervals, free, low, medium, and high, would result in the following:

$$\lambda =\left\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\le E_{i,t}<x_{\mathit{min}}(i)\\ {\lambda }_1 \hspace{1em}\hspace{1em}\hspace{1em}{x}_{\mathit{min}}(i)\le E_{i,t}<x_{eva}(i)\\ {\lambda }_2=(1+\alpha ){\lambda }_1\hspace{1em}{x}_{eva}(i)\le E_{i,t}<x_{\mathit{max}}(i) \\ {\lambda }_3=(1+2\alpha ){\lambda }_2\hspace{1em}{x}_{\mathit{max}}(i) \le E_{i,t} \end{array}\right.$$

(16)

Among these, $\lambda$ is the tiered carbon emission cost. $E_{i,t}$ is the total carbon emissions per unit time load node.

The total cost of carbon emissions based on the tiered carbon price can be calculated as follows:

$$C_{emi,i,t}=\left\{\begin{array}{l}0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0\le E_{i,t}<x_{\mathit{min}}(i)\\ {\lambda }_1(E_{i,t}-x_{\mathit{min}}(i))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_{\mathit{min}}(i)\le E_{i,t}<x_{eva}(i)\\ {\lambda }_1(x_{eva}(i)-x_{\mathit{min}}(i))\\ +{\lambda }_2(E_{i,t}-x_{eva}(i))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{x}_{eva}(i)\le E_{i,t}<x_{\mathit{max}}(i) \\ {\lambda }_1(x_{eva}(i)-x_{\mathit{min}}(i))\\ +{\lambda }_2(E_{\mathit{max}}-x_{eva}(i))+{\lambda }_3(E_{i,t}-x_{\mathit{max}}(i))\\ \hspace{1em}\hspace{1em}\hspace{1em} x_{\mathit{max}}(i) \le E_{i,t} \end{array}\right.$$

(17)

4. Dual-Layer Optimization Scheduling for Low-Carbon Demand Response

4.1. Dual-Layer Optimization Scheduling Framework for Low-Carbon Demand Response

The low-carbon demand response is coupled between the upper and lower levels through the node carbon potential, time-of-use electricity price, and load electricity demand.

Both upper-level grid operators and lower-level LAs participate in carbon market trading. The upper-level power grid operator receives the carbon quota coefficient transmitted by the carbon trading platform and adjusts the unit output plan by calculating the generation cost and carbon trading cost. Based on the carbon flow tracking calculation, the node carbon potential is obtained, and the Shapley value carbon emission allocation method is used to reasonably allocate the load-side node carbon responsibility. By utilizing node carbon potential and time of use pricing strategies, the carbon quota responsibility value is transferred to the lower level LA of different nodes.

This section establishes a demand response low-carbon optimization scheduling model with carbon price as the price signal. The power of the generator set and the line power are calculated in the first stage of the model. The data are sent to the second stage of the model. The current node carbon emissions and the total carbon emission cost of the system are calculated through carbon emission flow theory. And based on the Shapley value carbon emission responsibility allocation method, the reasonable range of carbon emission responsibilities for each load node is calculated. In the second stage of the model, the carbon price is used as the price signal for demand response, and the actual node load after response is re-inputted into the first stage. The carbon emissions of each load node and the system’s carbon emission responsibility cost are calculated. The objective function of the two-stage demand response low-carbon optimization scheduling model is to minimize the sum of the carbon emission responsibility cost and demand response cost.

The lower-level LAs include residential LAs, commercial LAs, and industrial LAs, each of which aggregates the dispersed flexible loads within the park. In the following text, they are represented by LA1, LA2, and LA3, respectively. After receiving the node carbon potential signal, the lower-level LA assumes the corresponding carbon emission responsibility. By invoking flexible loads through incentive contracts to change electricity usage plans, and providing feedback on electricity purchase demand to upper-level grid operators. After receiving the updated power purchase demand from the lower layer, the upper layer adjusts the unit output again, updates the node carbon potential, and iteratively optimizes the cycle.

4.2. Dual-Layer Optimization Scheduling Model for Low-Carbon Demand Response

4.2.1. Economic Dispatch Model for Upper-Level Power Grid Operators

The upper-level power grid operator trades with the external carbon market. The unit output plan is adjusted with the goal of minimizing the total cost., The carbon trading cost is the product of the unit’s carbon emission coefficient and its power generation. According to the constraint of node power balance, the amount of electricity generated by the generator set is equal to the sum of load electricity consumption and line transmission electricity. The power generation of the unit already includes the network loss. Therefore, the carbon emissions from the network loss are attributed to the power generation side.

(1)

Objective function

The optimization goal of power grid operators is to minimize the total cost, including the coal consumption cost $C^G$ of thermal power, wind power generation cost $C^W$, and carbon trading cost $C_{grid}^{C{O}_2}$ of power grid operators. The objective function F of the power grid operator is

$$\mathit{min}F=C^G+C^W+C_{grid}^{C{O}_2}$$

(18)

$$\left\{\begin{array}{l}{C}^G={\displaystyle \sum _{t=1}^{N_t}{\displaystyle \sum _{i=1}^{N_G}[a_i{(P_{i,t}^G)}^2+b_i{P}_{i,t}^G+c_i] \Delta t}}\\ C^W={\displaystyle \sum _{t=1}^{N_t}{\displaystyle \sum _{k=1}^K{\displaystyle \sum _{g=1}^{N_W}{q}^W{P}_{g,t}^W+{\epsilon }_k{q}^{Wq}(P_{k,g,t}^{Wy}-P_{g,t}^W)\Delta t}}}\\ C_{grid}^{C{O}_2}={\displaystyle \sum _{t=1}^{N_t}{\displaystyle \sum _{i=1}^{N_G}(e_i^G-\kappa )P_{i,t}^G\Delta t}}\end{array}\right.$$

(19)

In the formula, $N_G$ is the number of generator sets; $a_i$, $b_i$, and $c_i$ are the coal consumption cost coefficients of the $i$-th thermal power unit; $P_{i,t}^G$ is the output of the $i$-th thermal power unit at time t; $K$ is the number of wind farms; $N_W$ is the number of wind turbines; $q^W$ is the cost coefficient of wind power generation; $P_{g,t}^W$ is the actual output of the $g$-th wind turbine unit at time t; ${\epsilon }_k$ is the probability of the k-th wind power scenario; $q^{Wq}$ is the penalty coefficient for wind power curtailment; $P_{k,g,t}^{Wy}$ is the predicted output of the $k$-th wind turbine unit at time t in the $g$-th wind power scenario; $e_i^G$, $\kappa$ represents the carbon emission coefficient and initial carbon quota coefficient corresponding to the unit power generation of the generator set.

(2)

Constraint conditions

Power generation unit output constraints:

$$P_i^{G,min}\le P_i^G\le P_i^{G,max}$$

(20)

In the formula, $P_i^{G,max}$ and $P_i^{G,min}$ represent the maximum and minimum output values of the i-th thermal power unit.

Climbing constraints for thermal power units:

$$\left\{\begin{array}{l}{P}_{i,t}^G-P_{i,t-1}^G\le R_i^U{P}_i^{G,max}\\ P_{i,t-1}^G-P_{i,t}^G\le R_i^D{P}_i^{G,max}\end{array}\right.$$

(21)

In the formula, $P_{i,t-1}^G$ is the output of the i-th thermal power unit at time t; $R_i^U$ and $R_i^D$ represent the maximum climbing rate and maximum landslide rate of the i-th thermal power unit.

Start stop constraints for thermal power units:

$$\left\{\begin{array}{l}(T_{i,t-1}^{on}-T_i^{on,\mathit{min}})(u_{i,t-1}-u_{i,t})\ge 0\\ (T_{i,t-1}^{off}-T_i^{off,\mathit{min}})(u_{i,t}-u_{i,t-1})\ge 0\end{array}\right.$$

(22)

In the formula, $T_{i,t-1}^{on}$ and $T_{i,t-1}^{off}$ represent the running and stopping times of the i-th thermal power unit at time t, respectively; $T_i^{on,\mathit{min}}$ and $T_i^{off,\mathit{min}}$ represent the shortest operation and shutdown time of the i-th thermal power unit; $u_{i,t}$ and $u_{i,t-1}$ represent the start–stop status of the i-th thermal power unit at times t and t − 1.

$$0\le P_{g,t}^W\le P_g^{W,max}$$

(23)

In the formula, $P_g^{W,max}$ is the maximum output value of the g-th wind turbine unit.

Line transmission capacity constraint:

$$P_{zj}^{min}\le P_{zj,t}\le P_{zj}^{\mathit{max}}$$

(24)

In the formula, $P_{zj,t}$ is the active power flow of the line $zj$ at time t; $P_{zj}^{\mathit{max}}$ and $P_{zj}^{min}$ represent the upper and lower limits of the transmission power between line $zj$.

Balance node constraints:

$${\theta }_t^{ref}=0$$

(25)

In the formula, ${\theta }_t^{ref}$ is the phase angle of the balanced node voltage at time t.

Node power balance constraint:

$${\displaystyle \sum _{i\in V_{G,j}}{P}_{i,t}^G}+{\displaystyle \sum _{g\in V_{W,j}}{P}_{g,t}^W}-{\displaystyle \sum _{zj\in V_{F,j}}{P}_{zj,t}}=P_{j,t}^{buy}$$

(26)

In the formula, $V_{G,j}$ is the set of thermal power units at node j. $V_{W,j}$ is the set of wind turbines at node j; $V_{F,j}$ is the set of lines connected to node j; and $P_{j,t}^{buy}$ is the power load of node j at time t.

Line flow equation constraint:

$$\left\{\begin{array}{l}{P}_{zj,t}-{\beta }_{zj}({\theta }_{z,t}-{\theta }_{j,t})=0\\ -{\displaystyle \frac{\pi }{2}}\le {\theta }_{j,t}\le {\displaystyle \frac{\pi }{2}}\end{array}\right.$$

(27)

In the formula, ${\beta }_{zj}$ is the reactance of line $zj$. ${\theta }_{z,t}$ and ${\theta }_{j,t}$ are the voltage phase angles of node z and node j at time t.

4.2.2. Lower-Level LA Optimization Scheduling Model

The lower-level LA responds to the carbon potential signal of the upper-level nodes with the goal of minimizing the total cost, adjusts the flexible load electricity consumption strategy, and reduces the carbon emissions and total cost of the LA.

(1)

Objective function

Based on user electricity demand, the LA guides users to participate in low-carbon response through price incentives. The LA provides users with a certain degree of economic subsidies, and the total cost $f$ is shown in Equation (26), including the cost of purchasing electricity from superiors $C^{buy}$, carbon trading costs $C_{LA}^{C{O}_2}$, TL demand response subsidy costs $C^{ct}$, and EV discharge subsidy costs $C^{evd}$. The cost of LA carbon trading is shown in Equation (15).

$$minf=C^{buy}+C_{LA}^{C{O}_2}+C^{ct}+C^{evd}$$

(28)

$$\left\{\begin{array}{l}{C}_{buy}={\displaystyle \sum _{t=1}^{N_t}{q}_t{P}_t^{buy}\Delta t}\\ C^{ct}={\displaystyle \sum _{t=1}^{N_t}(q^{cut}{P}_t^{cut}+q^{tra,in}{P}_t^{tra,in}}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em} +q^{tra,out}{P}_t^{tra,out})\Delta t\\ C^{evd}={\displaystyle \sum _{t=1}^{N_t}{\displaystyle \sum _{n=1}^{N_{ev}}\varphi P_{n,t}^{evd}\Delta t}}\end{array}\right.$$

(29)

In the formula, $P_t^{buy}$ is the power purchased by the LA from the grid operator at time t. $q_t$ is the time-of-use electricity purchase price. $q^{cut}$ is the unit CL compensation coefficient. $q^{tra,in}$ and $q^{tra,out}$ are the compensation coefficients for unit TL transfer in and transfer out. A is the EV discharge subsidy coefficient.

(2)

Constraint conditions

Power balance constraint:

$$P_t^{buy}+{\displaystyle \sum _{n=1}^{N_{ev}}{P}_{n,t}^{evd}}=P_t^{load}+{\displaystyle \sum _{n=1}^{N_{ev}}{P}_{n,t}^{cut}}-P_t^{cut}+P_t^{tra,in}-P_t^{tra,out}$$

(30)

EV charging and discharging constraints:

$$\left\{\begin{array}{l}0\le y_{n,t}^c{P}_{n,t}^{evc}\le P^{evc,max}\\ 0\le y_{n,t}^d{P}_{n,t}^{evd}\le P^{evd,max}\\ 0\le y_{n,t}^c+y_{n,t}^d\le 1\end{array}\right.$$

(31)

In the formula, $y_{n,t}^c$ and $y_{n,t}^d$ represent the charging and discharging states of the n-th EV at time t. When charging an EV, $y_{n,t}^c$ is 1, and when discharging an EV, $y_{n,t}^d$ is 1. $P^{evc,max}$ and $P^{evd,max}$ represent the maximum charging and discharging power of the EV.

EV battery power constraint:

$$\left\{\begin{array}{l}{E}_n^{in}+{\displaystyle \sum _{t=t_{in}}^{t_{out}}{\eta }^c{P}_{n,t}^{evc}\Delta t-\frac{P_{n,t}^{evd}\Delta t}{{\eta }^d}}\ge E_n^{out}\\ S_{n,t}=S_{n,t-1}+{\displaystyle \frac{{\eta }^c{P}_{n,t}^{evc}\Delta t}{E^{es}}}-{\displaystyle \frac{P_{n,t}^{evd}\Delta t}{{\eta }^d{E}^{es}}}\\ S^{\mathit{min}}\le {\displaystyle \frac{E_n^{in}+{\displaystyle \sum _{t=t^{in}}^{t^{out}}{\eta }^c{P}_{n,t}^{evc}\Delta t-P_{n,t}^{evd}\Delta t/{\eta }^d}}{E^{es}}}\le S^{max}\end{array}\right.$$

(32)

In the formula, $E_n^{in}$ and $E_n^{out}$ represent the initial arrival energy and target energy of the n-th EV. $t^{in}$ and $t^{out}$ represent the entry time and departure time of the EV. ${\eta }^c$ and ${\eta }^d$ represent the EV charging and discharging efficiency. $S_{n,t}$ and $S_{n,t-1}$ represent the battery state of charge of the n-th EV at times t and t − 1, respectively. $E^{es}$ is the rated capacity of the EV battery. $S^{max}$ and $S^{\mathit{min}}$ represent the upper and lower limits of the EV battery’s state of charge.

4.3. Solution Flowchart of Dual-Layer Low-Carbon Optimization Scheduling Model

This study establishes a dual-layer optimization scheduling model for power systems based on collaborative guidance of demand response through node carbon potential and time-of-use electricity pricing. The solution process is shown in Figure 1. The specific steps for obtaining the solution are as follows:

Step 1: Enter the initial load curve, as well as EV-related parameters, unit parameters, line parameters, etc.

Step 2: Solve the optimal economic dispatch model of the upper-level power grid operator, output the output of each unit, and use the carbon emission flow model to calculate the node carbon potential.

Step 3: Schedule each sub-alliance and time period, use the Shapley value method to calculate carbon trading quotas, and output quota data for each load aggregator in each time period.

Step 4: Use the carbon potential and electricity price as signals to guide the lower-level LA to respond to demand, establish an optimization scheduling model based on node carbon potential demand response, and output the load demand of each LA after stimulating demand response.

Step 5: Substitute the LA load demand data into the upper-level model, re-solve the economic dispatch model of the power grid operator, and output the updated node carbon potential to be transmitted to the lower-level LA.

Step 6: When the load demand of each LA iteration meets the convergence judgment condition $|P_{\phi ,t}^{buy}-P_{\phi -1,t}^{buy}|<\epsilon$, $\epsilon$ takes 0.05 MW, this ends the solving process, and outputs the optimized scheduling result. If the load does not meet the convergence condition, continue to repeat steps 2–5. To prevent oscillation, the line is constrained using a binary method.

5. Example Analysis

5.1. Basic Data

This study analyzes a typical residential, industrial, and commercial LA coupled with an improved IEEE 14 node power grid, and its topology structure is shown in Figure 2. In the figure, the division of industrial LA1, residential LA2, and commercial LA3 includes different regional nodes.

Unit 1, unit 2, and unit 4 are set as thermal power units, with the relevant parameters shown in

Table 1. Generator set parameters.

Unit	1	2	4
Output limit (MW)	455	130	165
Lower output limit (MW)	200	25	45
Carbon emission coefficient (t/MW)	0.875	0.52	0.52
Coal consumption cost coefficient ai (CNY 10,000)	0.00366	0.014	0.02788
Coal consumption cost coefficient bi (CNY 10,000)	113.40	115.50	137.90
Coal consumption cost coefficient ci (CNY/MWh)	7000	4900	2450

, and the time-of-use electricity purchase price shown in

Table 2. Table of time-of-use electricity prices.

Name	Period of Time	Time-of-Use Electricity Price (CNY/(kW·h))
Peak period	08:00–12:00, 18:00–23:00	0.92
Regular period	12:00–18:00	0.62
Valley period	00:00–08:00, 23:00–24:00	0.31

. Unit 3 is a wind turbine generator, and unit 5 is a hydroelectric generator. The Monte Carlo method generates 1000 wind power scenarios and 4 scenarios after reduction, and the wind power output curve is taken from reference [30]. The probabilities for each scenario are 0.281, 0.239, 0.221, and 0.259, respectively. The cost coefficient of wind power generation is 60 CNY/MW; the penalty coefficient for wind power curtailment is 250 CNY/MW; and the carbon emission coefficient of wind power is 0.043 t/MW. The carbon emission quota coefficient for the LA unit’s electricity purchase is set to 0.728 t/MW, the carbon trading benchmark price to 290 CNY/t, and the price growth coefficient to 0.25. Assuming all EVs are of the same model, the EV-related parameters are shown in

Table 3. Parameters of electric vehicle.

Parameter	Data
Rated capacity of battery (kW·h)	57
EV discharge subsidy coefficient (CNY/(MW·h))	100
LA maximum charging power (kW)	15
Maximum discharge power of LA (kW)	7
Maximum and minimum values of state of charge (%)	90, 10

. The number of EVs in each LA is set to 1000, 1500, and 600, respectively. The parameters of the TL and CL contracts are shown in

Table 4. Incentive contract parameters of transferable load.

Parameter	LA1	LA2	LA3
Unit transfer compensation coefficient (CNY·(MW·h)−1)	45	38	40
Compensation coefficient for unit transfer out (CNY·(MW·h)−1)	35	28	30
Transfer to upper limit value (MW·h)	5.5	2.5	10
Transfer limit value (MW·h)	7.5	3	15
Transfer start time (h)	1	1	1
Transfer end time (h)	17	16	16
Starting time of transfer out (h)	18	17	17
Transfer end time (h)	22	22	21

and

Table 5. Incentive contract parameters of curtailable load.

Parameter	LA1	LA2	LA3
Unit reduction compensation coefficient (CNY/(MW·h))	250	233	260
Reduce starting time (h)	12	12	12
Reduce end time (h)	21	20	20
Upper limit of response time period (h)	5	5	5
Reduce power upper limit value (MW·h)	2	1	3

. The scheduling cycle is set to 24 h; Δt = 1 h. MATLAB R2019b is used to call Cplex for the solution.

To verify the effectiveness of the model and method proposed in this article, the collaborative guidance of the node carbon potential and time-of-use electricity price on demand response of various LA flexible loads is analyzed. The following five scenarios are set up:

Scenario 1: Consider fixed electricity prices, load not participating in optimization scheduling, and not considering carbon trading;

Scenario 2: Consider a dual-layer optimization scheduling strategy guided by time-of-use electricity prices for flexible load adjustment, without considering carbon trading;

Scenario 3: Consider time-of-use electricity pricing and tiered carbon trading, with flexible loads not participating in optimization scheduling;

Scenario 4: Consider a dual-layer optimization scheduling strategy of fixed electricity prices, tiered carbon trading, and node carbon potential-guided flexible load adjustment;

Scenario 5: Consider a dual-layer optimization scheduling strategy that incorporates time-of-use electricity pricing, tiered carbon trading, and node carbon potential-guided flexible load adjustment.

5.2. Carbon Quota Calculation and Analysis

The Shapley value method is used to measure the carbon emissions of each LA. According to the improved IEEE 14 node system topology diagram, there are a total of three LAs in the quota calculation system, divided into regions LA1, LA2, and LA3. So, N = {LA1, LA2, LA3}. And there are six non-empty sub-alliances in the entire alliance. They are {LA1}, {LA2}, {LA3}, {LA1, LA2}, {LA1, LA3}, and {LA2, LA3}.

Taking scenario 5 as an example, consider the dual-layer optimization scheduling strategy of time-of-use electricity pricing, tiered carbon trading, and node carbon potential-guided flexible load adjustment. At time t = 1, the carbon emissions results of each sub-alliance are shown in

Table 6. Comparison of carbon emissions and costs of LA in different scenarios.

Union	System Carbon Emissions (t)
{LA1}	175.9
{LA2}	30.5
{LA3}	41.4
{LA1, LA2}	230.4
{LA1, LA3}	240.7
{LA2, LA3}	49.6
{LA1, LA2, LA3}	290.3

.

Taking sub-alliance LA1 as an example. When t = 1 h, according to Equation (13), the carbon emissions of sub-alliance {LA1} consist of four parts. They are $E_{CO2}\left\{\mathrm{LA}1\right\}$, $E_{CO2}\{\mathrm{LA}1,\mathrm{LA}2\}-E_{CO2}\left\{\mathrm{LA}2\right\}$, $E_{CO2}\{\mathrm{LA}1,\mathrm{LA}3\}-E_{CO2}\left\{\mathrm{LA}3\right\}$, and $E_{CO2}\{\mathrm{LA}1,\mathrm{LA}$$2,\mathrm{LA}3\}-E_{CO2}\{\mathrm{LA}1,\mathrm{LA}2\}$. The minimum value is 175.9 tons and the maximum value is 240.7 tons. According to Equations (14) and (15), carbon emission responsibility quota is calculated to be 219.5 t. According to Equation (15), when t = 1 h, the carbon emission quota ranges for LA1 are [0, 175.9], [175.9, 219.5], [219.5, 240.7], [240.7, ∞], respectively. The carbon emission quotas for each LA in 24 h are shown in the figure.

From Figure 3, Figure 4 and Figure 5, it can be seen that the carbon emission quotas for LA1 are relatively high in each period, while the quotas for LA2 and LA3 are relatively similar and at a moderate level. Because LA1 is an industrial zone with high overall carbon potential and electricity consumption, the corresponding carbon emission quota for LA1 is relatively high. From 8:00 to 20:00, the position of each LA carbon emission quota interval is relatively high. And the position is lower from 00:00 to 07:00. This is because the electricity load in the LA accounts for the main part, mainly distributed during the daytime, so the changes in carbon quota values are similar to the changes in load. This also validates the rationality of the carbon emission flow tracking model for the changes in carbon emissions on both sides of the source load, achieving the tracking of the carbon footprint. It also proves the effectiveness of using Shapley values for carbon responsibility allocation.

5.3. Comparison of LA Carbon Emissions and Costs in Different Scenarios

The upper-level power grid operator trades with the external carbon market to adjust the unit output plan, and its carbon trading cost is the product of the unit’s carbon emission coefficient and its power generation. The carbon emissions of the system all come from the upper-level generator units. Part of the electricity used by the lower-level load comes from thermal power units G1, G2, and G4. Although the use of electricity itself does not generate additional carbon emissions, the source of electricity generates carbon emissions, so carbon responsibility allocation is required.

The carbon emissions and cost comparison of each LA under five scenarios are shown in

Table 7. Comparison of LA1 carbon emissions and costs in different scenarios.

Scene	1	2	3	4	5
Carbon emissions (t)	5509.53	5471.47	5509.53	5473.59	5450.66
Total cost (CNY 10,000)	403.46	395.73	450.62	415.74	441.01
Electricity purchase cost (CNY 10,000)	403.46	394.07	403.46	368.38	394.07
Carbon trading cost (CNY 10,000)	0	0	47.15	46.66	45.28
EV discharge subsidy (CNY 10,000)	0	0.34	0	0.02	0.34
CT and TL subsidies (CNY 10,000)	0	1.3	0	0.69	1.3

,

Table 8. Comparison of LA2 carbon emissions and costs in different scenarios.

Scene	1	2	3	4	5
Carbon emissions (t)	611.45	579.49	611.45	579.71	573.76
Total cost (CNY 10,000)	52.06	48.04	56.24	48.15	50.24
Electricity purchase cost (CNY 10,000)	52.06	47.26	52.07	44.96	47.28
Carbon trading cost (CNY 10,000)	0	0	4.16	2.48	2.07
EV discharge subsidy (CNY 10,000)	0	0.39	0	0.37	0.51
CT and TL subsidies (CNY 10,000)	0	0.37	0	0.37	0.38

and

Table 9. Comparison of LA3 carbon emissions and costs in different scenarios.

Scene	1	2	3	4	5
Carbon emissions (t)	1025.1	1001.71	1025.1	1004.47	1001.41
Total cost (CNY 10,000)	84.93	81.14	91.78	78.73	87.36
Electricity purchase cost (CNY 10,000)	84.93	80.06	84.93	71.54	80.06
Carbon trading cost (CNY 10,000)	0	0	6.87	6.41	6.22
EV discharge subsidy (CNY 10,000)	0	0.25	0	0.02	0.25
CT and TL subsidies (CNY 10,000)	0	0.83	0	0.78	0.83

. When scenarios 1 and 3 do not consider time-of-use electricity prices or node carbon potential to guide demand response, the carbon emissions are highest, and scenario 3 has the highest total cost. Scenario 2 guides flexible loads to respond to demand through time-of-use electricity pricing. Scenario 4 guides demand response on the load side through the node carbon potential. Both scenarios result in a decrease in carbon emissions. Scenario 5 combines scenario 2 and scenario 4, while considering time-of-use electricity prices and the node carbon potential to guide the LA’s demand response. Compared to scenario 1, the cost of purchasing electricity in the LA decreases and the total cost increases, with the main increase being carbon trading costs. The carbon emissions of each LA are reduced by 58.87, 37.69, and 23.69 tons, respectively, balancing the low-carbon and economic aspects of the LA.

In addition, after incorporating carbon trading in scenario 5 based on scenario 2, under the influence of time-of-use electricity prices and node carbon potential, the carbon trading costs and purchase costs of each LA are reduced, and the carbon emissions are significantly reduced, with reductions of 20.81, 5.73, and 0.3 tons, respectively. This indicates that the use of time-of-use electricity prices and node carbon potential to guide flexible loads in this study can effectively improve the low-carbon and economic performance of the system.

Comparing scenario 4 and scenario 5, it can be clearly seen that compared to fixed electricity prices, scenario 5 considers time-of-use electricity prices, and the responsiveness of flexible loads in demand response is improved. The carbon emissions of each LA decrease by 22.93, 5.95, and 3.06 tons, respectively, compared to scenario 4, and the carbon trading cost also decreases accordingly.

However, due to the limitations of EV access time and departure time, charging may be carried out during peak time-of-use electricity pricing periods to meet EV charging needs. This leads to an increase in the purchase cost of electricity in scenario 5 compared to scenario 4.

Therefore, although the model proposed in this article has increased some costs to a certain extent, by increasing the response of flexible loads, the dependence on the source side is reduced. The reduction in the carbon emissions is greater, thereby improving the low-carbon nature of the system.

5.4. Analysis of Optimization Scheduling Results for Scenario 5

The node carbon potential can reflect the carbon emission level of each node in the power system. Figure 6 shows the distribution of the carbon potential at different nodes at different times. Node 1 is connected to the thermal power unit, and the carbon potential is at a relatively high level. The carbon potential of nodes 2 and 6 is higher than the carbon emission factor of the generator at that node because the unit at node 1 injects power into nodes 2 and 6 through the line. Node 8 is a clean energy unit and there are no other units injected; it has a carbon potential of 0. The higher the carbon potential of a node, the more electricity flows from coal-fired units in the electricity source, and the less electricity flows from clean energy units. So, guiding electric vehicles to charge at nodes with lower carbon potential in the region is beneficial for achieving carbon reduction in the system.

The carbon emissions generated by the basic load of each node are mainly concentrated in nodes 2–4. The reason is that these nodes are relatively close to unit 1, which has the highest power generation and carbon emission factor, so the carbon emissions generated by the unit account for a significant proportion. The closer the node branch is to unit 1, the higher the carbon flow rate, the higher the carbon potential, and the higher the carbon emissions.

Figure 7 shows the average carbon potential size of each LA. It can be seen that the trend in carbon potential is basically the same, with a sudden increase in carbon potential between 16:00 and 23:00. This is because this time period is the peak-load period, and the clean energy output of the LA equipment decreases. Mainly powered by thermal power units, the carbon emission intensity of the units is much higher than that of gas-fired units and clean energy units. As a result, there is an increase in carbon potential during this period. The average carbon potential of LA1 is greater than that of LA2 and LA3. This is also a phenomenon caused by LA1 being in an industrial zone with high carbon emissions. Therefore, the carbon emission flow model can accurately reflect the carbon emission situation of the system and track the carbon emission footprint.

The load changes before and after the demand response of LA1, LA2, and LA3 are shown in Figure 8, Figure 9 and Figure 10, respectively. The pre-response load includes the original load curve and the EV unordered charging load. Due to the lack of optimized scheduling, EVs start charging immediately after being connected, resulting in a significant peak load. The peak–valley difference of the original load is relatively large. After the LA stimulates and schedules the flexible load, the EV is scheduled for orderly charging and discharging. This leads to load reduction and transfer, transferring the peak load of electricity consumption to the low-load period, reducing the electricity pressure during the peak-load period.

5.5. The Impact of EV Response Ratio on LA Carbon Emissions and Costs

To further analyze the impact of EV participation in demand response on LA carbon emissions and costs, the response ratios were set to 1.0, 0.8, 0.6, and 0.4. The remaining vehicles that did not participate in the response were charged randomly, and the carbon emissions and costs of each LA are shown in the table.

As shown in

Table 10. Changes in carbon emission and cost of LA1 with different response ratios of EV.

Number of EVs per Vehicle	Carbon Emissions (t)	Cost (CNY 10,000)	Electricity Purchase Cost (CNY 10,000)	Carbon Trading Cost (CNY 10,000)	EV Discharge Subsidy (CNY 10,000)
1000	5450.66	441.01	394.07	45.28	0.34
800	5447.34	441.21	394.43	45.22	0.27
600	5446.68	441.62	394.83	45.28	0.2
400	5445.54	442.01	395.03	45.32	0.14

,

Table 11. Changes in carbon emission and cost of LA2 with different response ratios of EV.

Number of EVs per Vehicle	Carbon Emissions (t)	Cost (CNY 10,000)	Electricity Purchase Cost (CNY 10,000)	Carbon Trading Cost (CNY 10,000)	EV Discharge Subsidy (CNY 10,000)
1500	573.76	50.24	47.28	2.07	0.51
1200	569.82	50.44	47.52	1.99	0.55
900	571.79	51.01	47.08	2.31	0.42
600	574.66	52.21	49.62	2.61	0.28

and

Table 12. Changes in carbon emission and cost of LA3 with different response ratios of EV.

Number of EVs per Vehicle	Carbon Emissions (t)	Cost (CNY 10,000)	Electricity Purchase Cost (CNY 10,000)	Carbon Trading Cost (CNY 10,000)	EV Discharge Subsidy (CNY 10,000)
600	1001.41	87.36	80.06	6.22	0.25
480	999.53	87.57	80.16	6.18	0.21
360	997.81	87.76	80.42	6.16	0.16
240	997.13	87.9	80.58	6.14	0.14

, with the increase in EV response ratio, the number of EVs participating in discharge increases, and the cost of discharge subsidies increases. The overall LA2 carbon emissions show an upward trend, leading to an increase in carbon trading costs. The cost of purchasing electricity slightly decreases as the proportion increases.

As the proportion of electric vehicles participating in demand response increases, the cost of participating in carbon trading also increases, but the purchase price of electricity will decrease. Therefore, the total cost of charging is reduced, which is more profitable for electric vehicle users. Not only does this facilitate the participation of electric vehicle users in demand response, but it also basically ensures low levels of carbon emissions. Therefore, increasing the response ratio of EVs appropriately is beneficial for improving the economy and low-carbon nature of LAs.

6. Conclusions

This article proposes a system low-carbon optimization scheduling model that considers carbon responsibility allocation and electric vehicle demand response. A study was conducted on an optimization strategy for low-carbon economic operation of multiple LAs with electric vehicles using a carbon emission quota allocation method based on Shapley values. The main conclusions are as follows:

(1)

The carbon responsibility allocation method based on Shapley values reflects the carbon emission responsibility of the load. Compared to traditional carbon trading models, the model proposed in this article has a better emission reduction effect. Compared with the situation without considering carbon trading, the carbon emissions of each LA decreased by 20.81, 5.73, and 0.3 tons, respectively.

(2)

Time-of-use electricity pricing and node carbon potential should be considered to guide LA in demand response. Compared with not considering carbon trading and flexible load adjustment, the purchasing costs of each LA decreased, and the carbon emissions decreased by 58.87, 37.69, and 23.69 tons, respectively, balancing the low-carbon and economic aspects of scheduling strategies.

(3)

Time-of-use electricity pricing and node carbon potential synergy should be used to guide LA in demand response. Scheduling orderly charging and discharging of EVs, as well as load reduction and transfer, alleviated the electricity pressure during peak periods.