Abstract
Addressing the dual challenges of agricultural productivity and ecological sustainability, this study develops an integrated framework combining Lotka–Volterra dynamics, Monte Carlo simulation, and multi-objective optimisation to quantify agroecosystem responses under anthropogenic interventions. Key innovations include the incorporation of carbon sequestration dynamics and low-carbon agricultural practices into ecological–economic trade-off analysis. Our findings demonstrate the following: (1) Seasonal carbon fertilisation effects enhance producer growth by up to 30%, while energy recycling from consumer mortality offsets 22% of pesticide-induced carbon emissions. (2) The strategic introduction of dual-function species synergistically improves carbon sink capacity by 18–25% through enhanced producer efficiency and reduced chemical reliance. (3) Multi-objective optimisation reveals that integrated pest management coupled with organic amendments achieves a 51.2% net benefit improvement, while reducing agrochemical carbon footprints by 40–55%. The proposed framework bridges critical gaps in sustainable agriculture by simultaneously addressing yield stability, biodiversity conservation, and climate mitigation imperatives. This work advances the dynamic modelling of agroecosystems through probabilistic risk assessment and carbon-aware decision-making, providing actionable pathways for low-carbon agricultural intensification.
1. Introduction
The global agricultural landscape faces unprecedented challenges in balancing productivity with ecological sustainability. Rapid industrialisation, coupled with escalating demands for food security, has driven practices such as deforestation, excessive chemical use, and monoculture farming, leading to severe environmental degradation. Notable examples include the conversion of the Amazon rainforest into croplands and the pollution of water resources in Asia and Africa. These practices have fragmented ecosystems, threatened biodiversity, and disrupted natural cycles, as evidenced by the degradation of wetland–farmland interfaces in China’s Three Rivers Plain, where nitrogen, phosphorus, and heavy metal contamination jeopardise both wildlife and human health.
Eco-agriculture, which emphasises the synergy between agricultural production and environmental stewardship, has emerged as a critical pathway to address these challenges. However, its implementation remains hindered by insufficient quantitative frameworks to evaluate the trade-offs between economic viability and ecological conservation. The existing studies often focus on isolated aspects of agroecosystems, such as pest control or crop yield optimisation, while neglecting the dynamic interdependencies between species, seasonal fluctuations, and human interventions. This gap limits the ability to design holistic strategies for sustainable land use and biodiversity preservation. Recent advances in agroecological modelling have demonstrated the value of integrating socio-ecological feedbacks, yet quantitative frameworks for a multi-dimensional trade-off analysis remain underdeveloped [1].
To bridge this gap, this study develops a multi-species dynamic model based on the Lotka–Volterra equations [2], integrating ecological interactions, agricultural cycles, and humaninterventions. The Lotka–Volterra model, proposed by Lotka and Volterra in the 1920s, was the first to quantify the dynamics of a predator–prey system through a pair of nonlinear differential equations, thereby revealing the core mechanisms underlying the periodic fluctuations in their populations. The strength of this theory lies in its ability to highlight the fundamental laws of species interactions in a simple mathematical form (only four parameters). It provides a fundamental analytical framework for ecology, successfully explaining natural phenomena and inspiring subsequent complex modelling and interdisciplinary applications. Despite the idealised assumptions upon which it is based, the notion of revealing ecological dynamics through mathematical modelling remains far-reaching and has become a classic tool for theoretical ecology and education. Our work systematically investigates four dimensions: the impacts of seasonal variations and chemical use on ecosystem stability, the role of introduced species in restoring ecological balance, the resilience of ecosystems post chemical discontinuation, and the optimisation of organic farming practices through multi-objective decision-making. By incorporating Monte Carlo simulations for an uncertainty analysis and Pareto–genetic algorithms for policy optimisation, we provide a robust framework to quantify the dual objectives of economic efficiency and ecological health. The Pareto frontier is a valuable tool for generating solution sets for multimodal problems through the use of genetic algorithms. In this paper, the dual objectives of economic efficiency and ecological health are quantified, and the trade-offs between solutions for multiple objectives are intuitively illustrated through visualisation. This enables decision makers to compare the optimisation paths of diversified solutions without pre-set preferences. The objectivity of the global search and the flexibility of the dynamic choices are also taken into account.
The key contributions of this research include the following:
- Dynamic Modelling: A novel extension of the Lotka–Volterra framework to capture seasonal growth cycles, energy recycling mechanisms, and cascading effects of chemical interventions;
- Intervention Analysis: Empirical validation of the dual roles of introduced species (e.g., bats as pollinators and predators) in stabilising trophic dynamics;
- Policy Optimisation: A Pareto-frontier approach to reconcile conflicting goals, demonstrating that reducing chemical reliance while introducing natural controls maximises long-term sustainability.
This study not only advances the theoretical understanding of agroecosystem dynamics but also offers actionable insights for policymakers and farmers to navigate the complex trade-offs inherent in modern agriculture.
2. Materials and Methods
2.1. Notion
The key mathematical notations used in this paper are listed in Table 1.

Table 1.
Notations used in this paper.
2.2. Lotka–Volterra-Based Multi-Species Dynamic System
2.2.1. Producer Population Dynamics Equations
Multi-species extensions of predator–prey models require the explicit consideration of nonlinear interaction terms to capture trophic cascade effects [3]. Therefore, we apply the Lotka–Volterra model separately to explore the energy relationship between them and find the appropriate food chain and termination.
Changes in producer (crop) numbers are influenced by photosynthesis, harvest pressure, herbivore predation, and chemicals [4]:
- rp(t)P: Natural growth of producers through photosynthesis;
- rp(t): Indicates seasonal growth rate.
Carbon Sequestration Function:
Cseq(P) = φ·P·tgrowth
- φ: Average annual carbon sequestration per unit of producer biomass (kg CO2/individual-year), get φ = 0.15 [5];
- Cmax: Regional maximum carbon sink potential (kg CO2/ha), Obtained according to IPCC Tier 1 methodology [6]. Cmax = 2000
Carbon fertiliser effect factor: θ = 0.3 (based on the promotion of crop growth by elevated CO2 concentrations in the literature [7]).
The seasonal fluctuation term is characterised by a sinusoidal function as
- rpbase: Producers’ base growth rate;
- A: Amplitude of seasonal fluctuations;
- T: Cycle length (corresponding to a one-year period);
- R·rec: Eco-energy returns from consumer death contributions;
- : The effect of predation on producers by primary consumers with a predation efficiency of ;
- H·P: Annual harvesting of producers;
- ηh·P: Producer suppression by herbicides.
This dynamic equation system integrates ecological energy flow and agricultural production factors, and it is constructed through five types of core mechanisms: the photosynthesis effect, driven by a sinusoidal periodic function (A = 0.02, R2 = 0.91) validated by USDA data to quantify crop growing season fluctuations; nutrient cycling compensation based on the Jenkinson’s organic matter mineralisation model to set the cycling efficiency coefficient R = 0.65; biotic interaction depletion calibrated with predation coefficient α1 by measuring locust feeding (2.3 cm2/day) through field experiments; and human interventions encompassing the harvest cycle (Tk = 120 days) and the herbicide dose effect (EC50 = 3.2 mg/L) dual operational variables.
2.2.2. Consumer Hierarchy Dynamic Equation
Modelling a three-tiered consumer food chain, reflecting the cascade effect of energy transfer, necessitates the following:
Primary consumers (phytophagous insects):
- β1PC1: Energy obtained by primary consumers by preying on producers is converted with an efficiency of β1;
- γ1C1: Natural mortality of primary consumers;
- α2C1C2: Impact of predation on primary consumers by secondary consumers;
- ηP·C1: Inhibition of primary consumers by pesticides.
Secondary consumers (insectivorous birds):
- β2C1C2: Energy obtained by secondary consumers by preying on producers is converted with an efficiency of β2;
- γ2C2: Natural mortality of secondary consumers;
- α3C2C3: Impact of predation on secondary consumers by tertiary consumers;
- ηP·C2: Inhibition of secondary consumers by pesticides.
Tertiary consumers (top predators):
- β3C2C3: The energy gained by a tertiary consumer by preying on a secondary consumer is converted with an efficiency of β3;
- γ3C3: Natural mortality of tertiary consumers.
Energy Return Method:
Parameter calibration methods:
Energy conversion efficiencies at each trophic level were obtained through literature research (Lindeman efficiency ~10%).
The mortality rate γi was fitted to field observations using logistic regression.
Predation coefficients αi were determined by controlled laboratory experiments.
2.3. Monte Carlo Uncertainty Analysis
Latin hypercube sampling with parameter correlation constraints outperforms simple random sampling in ecological uncertainty quantification [8]. Also, to determine the appropriate sample size [9], we tried to use Monte Carlo tests to assess the sensitivity of the model parameters and the uncertainty of the output results by designing the following Monte Carlo random sampling experimental procedure:
2.3.1. Step 1: Parameter Perturbation Mechanism Design
A random perturbation is applied to the key parameters with the perturbation rule
- βi: Sensitivity parameters to be analysed (e.g., α1, β1, ηp etc.);
- ε: Perturbation factor, uniformly distributed, with ±20% perturbation amplitude.
Recent studies have validated the effectiveness of correlated parameter sampling in ecological uncertainty quantification, particularly for capturing nonlinear system behaviours [10].
2.3.2. Step 2: Multi-Scenario Stochastic Simulation Process
- Experiment Initialisation
Number of simulations: A total of 500 independent simulations were performed, which was determined based on the convergence pre-test to stabilise the standard error of the output metrics within ±3%.
Initial conditions: Producer and consumer biomasses were uniformly set to the steady-state initial values of the baseline model to eliminate the interference of initial state differences (P0 = 1000 g/m2, C1,0 = 50 individual/m2).
- 2.
- Dynamic coupling processes
Time stepping: In each simulation, the system of differential equations was iterated day by day using the explicit Euler method with a step size Δt = 0.1 day to satisfy the stability condition Δt < 1/max(|λJacoby Matrix|).
Ecological constraints: Mandatory producer biomass. Avoid ‘false extinction’ caused by numerical calculations.
The fundamental strength of Euler’s method lies in its simplicity and efficiency. The system rapidly predicts subsequent outcomes by converting a continuous problem into a series of point-by-point calculations, utilising solely the state and derivative information at the current instant. The algorithm’s intuitive, iterative logic renders it simple to implement and less computationally burdensome, characteristics that render it particularly suitable for the expeditious validation of models or the management of tasks characterised by high real-time requirements. Notwithstanding its limitations with regard to accuracy and stability, its low threshold and ease of understanding make it an ideal point of departure for acquiring numerical solutions and initially analysing dynamic systems, thus laying the foundation for our subsequent mastery of more complex methods.
- 3.
- Output Indicator Acquisition
Three types of end-state indicators were recorded at the end of each simulation:
Economic output indicators: Cumulative harvest H·ΣP(t), reflecting the volatility of agricultural production efficiency.
Ecological resilience indicators: Producer end-state biomass P(T), characterising the self-sustainability of a system after a perturbation.
Food web stability indicators: Primary consumer final state density C1(T), assessment of the risk of collapse of the trophic cascade.
2.3.3. Step 3: Statistical Inference and Uncertainty Quantification
Firstly, a non-parametric probability distribution was fitted to the output indicators (e.g., ecological biomass, economic harvest) based on Kernel Density Estimation (KDE) to capture complex statistical features such as the multi-peak distribution and long-tailed effect, and at the same time, a 95% confidence interval was constructed by combining that with the Bootstrap re-sampling method, which breaks through the limitation of the assumption of the traditional normal distribution and objectively depicts the range of indicator fluctuation. Subsequently, the Sobol index is used to carry out a global sensitivity analysis to quantify the first-order main effect and total effect of the parameters on the output of the system through variance decomposition.
Key parameters (e.g., predation coefficients, pesticide effect coefficients) governing the system behaviour were identified in descending order of the total effect values, revealing the core driving mechanisms of ecological dynamics. Finally, a probabilistic assessment of ecological risk was implemented to quantify the risk of collapse by calculating the probability of exceeding a specific threshold event (e.g., primary consumer density less than 10 individuals/m2) and quantitatively mapping extreme output values (e.g., 5% quartile harvest) to parameter perturbations by quantile regression, so as to identify high-risk parameter combinations and to provide data-driven quantitative support for the resilience management of ecosystems and decision-making for agricultural sustainability. The whole set of methods runs through the logical chain of ‘distribution mapping—sensitivity analysis—risk early warning’, combining statistical rigour and ecological explanatory power.
2.4. Multi-Objective Optimisation Modelling
With the core concept of economic–ecological synergistic development, the model constructs a dual-objective optimisation framework aimed at balancing agricultural production efficiency and ecosystem sustainability. The model expresses the two types of objective functions and constraints through mathematical formalisation, forming the basis for a trade-off analysis in a multi-dimensional decision space.
2.4.1. Objective Function
The model is centred on synergistically enhancing agricultural economic efficiency and ecosystem health to construct a dual-objective optimisation system:
- Economic Return Goals (f1):
In order to construct an economic return objective function for the agricultural production system, this paper integrates three factors: crop yield, ecological compensation benefits, and pesticide use costs. First, crop yield gains are affected by pest density; a moderate pest density may promote pollination or maintain the ecological balance, while a too high one inhibits yields. Therefore, the product of crop yield and pest density is used as a joint indicator of yield benefit and multiplied by a yield conversion factor to quantify the economic output. Second, ecological conservation areas can bring economic returns through carbon sink trading, eco-tourism, or policy subsidies, and an ecological compensation term is introduced to reflect the benefits from ecological conservation areas. Finally, in order to reflect the cost loss from pesticide use, a nonlinear quadratic term is used to portray the increasing marginal cost effect of pesticide use intensity, reflecting the economic burden and ecological damage secondary effects from excessive pesticide use. Combining the above three parts, the economic return objective function is constructed as the core formula for measuring agricultural economic benefits in the optimisation model.
The production yield term: kyEPP reflects the positive correlation between crop yield and pest density EP and producer biomass P, where ky is the yield conversion factor that characterises the economic value per unit of biomass.
Eco-compensation term: kbx4 is the unit price coefficient for compensation. x4 quantifies the additional benefits generated by the area of ecological reserve (x4) through carbon sink trading, ecotourism, etc., and kb is the unit price coefficient for compensation.
Pesticide cost term: Cpx21 is the nonlinear cost loss induced by the intensity of pesticide use (x1). The quadratic term is designed to reflect the incremental marginal cost effect due to excess pesticide inputs.
- 2.
- Eco-Efficiency Goals (f2):
The parameter λ plays a role in regulating the weights of different factors in an ecosystem. Specifically, λ serves as a weighting coefficient to balance the relative importance of various components of the ecosystem. By adjusting the value of λ, the influence of specific ecological factors can be emphasised or weakened during the optimisation process, thus achieving a fine-grained control of ecological benefits.
Translated with DeepL.com (free version)
The biodiversity gain term: The equation 10log(1+2) is a mathematical representation of the phenomenon in which the intensity of ecological restoration measures (x2) leads to an increase in species richness. The logarithmic function in the equation serves to model the initial high sensitivity of ecological restoration to external factors, which subsequently transitions to a state of saturation.
Carbon sink enhancement term: The expression 8log(1 + x3/3) is employed to denote the carbon sequestration benefits of low-carbon farming technology inputs (x3). The denominator is constant at 3, thereby ensuring the standardisation of the scale of technology applied.
Pesticide ecological damage term: The penalty for the negative impacts of pesticide use on non-target organisms, such as soil microorganisms and pollinators, is calculated as −20 x1. This calculation is calibrated by life cycle assessment (LCA) with a factor of 20.
The benefits of a carbon sink can be calculated as follows: Cseq(x4) = k·x4, where k is equal to 120 kg CO2/ha, based on forest carbon sink studies [11].
The emissions of carbon from pesticides are calculated as follows: Echem(x1) = μ·x1, where μ is the emission factor, which is 25 kg of CO2 per kg of pesticide, based on the findings of the life cycle assessment [12].
The parameter associated with the carbon price is represented by the following equation: λ = 0.05 USD/kg CO2. This equation is equivalent to the mean price ascribed to carbon in the European Union’s carbon market in 2023 [13].
2.4.2. Coupled Ecological–Productive Constraint Systems
- Pest population control constraints:
Physical significance: Pest densities are suppressed to less than 70% of the baseline level (Ep) through the synergistic effect of pesticide reduction (x1), biological control (x2), and tillage regulation (x3).
Technical efficiency gradient: The coefficients 0.3 and 0.2 reflect the difference in unit control efficiency between biological control and tillage measures, respectively, and are derived from the calibration of field trial data.
- 2.
- Biodiversity baseline constraints:
Compound restoration mechanisms: The equation 10log(1 + x2) is indicative of the rapid species attraction effect of ecological restoration measures (e.g., revegetation) in the short term. Conversely, 5x4 reflects the contribution of long-term protected area expansion to habitat connectivity.
Threshold science: The right-end constant 30 corresponds to the regional ecological red line requirement, determined by the statistical mapping of biodiversity indices (e.g., the Shannon–Wiener index) to model outputs.
2.4.3. Non-Dominated Sorting Genetic Algorithm (NSGA-II) Solution Procedure
Recent benchmarking studies highlight hybrid machine learning approaches combining physical constraints with data-driven models as particularly promising for agroecosystem prediction [14]. The steps are as follows:
- The following investigation will address the mechanisms underlying chromosome coding.
Decision variable definition: The chromosome is encoded in real numbers and contains five dimensional decision variables [x1, x2, x3, x4, x5], where x5 is a reserved expansion variable (e.g., an irrigation optimisation parameter).
Variable boundary constraints: The establishment of upper and lower limits for each variable is contingent upon the feasibility of agricultural operations. For instance, the expression x1: [0, 1] signifies the normalisation of pesticide intensity to the range of 0–100%.
- 2.
- The design of genetic manipulation operators:
Tournament selection: In the context of the tournament, three individuals are selected from the population at random (tournament_size = 3). The individual with the highest non-dominance tier and the largest crowding distance is then selected to enter the next generation, with the objective of maintaining population diversity.
Simulated binary crossover (SBX): The distribution index, n, is a critical factor in determining the tightness of the distribution of child solutions around the parent. As n increases, the solutions tend to become more concentrated around the parent, thereby balancing the exploration and exploitation capabilities.
Polynomial variation: Perturbations are applied to the gene values with the probability pm = 0.1. The variation step size is dynamically adjusted by the variation index ηm to ensure that the algorithm jumps out of the local optimum.
- 3.
- Elite Retention Strategies:
Non-dominated ordering: The population of individuals is divided into different tiers according to the Pareto dominance relation. The high-level solutions are preferentially retained to approximate the true frontier.
Crowding comparison: Within the same non-dominated hierarchy, the congestion distance of individuals in the target space is computed, to prioritise solutions located in sparse regions, thereby avoiding the over-aggregation of frontier solutions.
- 4.
- Termination Criteria and Convergence Determination:
Maximum number of iterations: A predetermined upper limit on the number of genetic generations (e.g., 500) is established in conjunction with the computational resource limit.
Frontier stability monitoring: The convergence of the Hypervolume metric of the Pareto front is determined by the following criteria: the Hypervolume metric of the Pareto front must undergo a change of less than 1% within 50 consecutive generations, and the iteration must be terminated.
3. Results
3.1. Numerical Solution of Ecosystem Dynamics
3.1.1. Discretisation of Differential Equations
The discretisation process based on the explicit Euler method is as follows:
- Producer population dynamics:
- Cherbicide: Direct producer inhibition by herbicide use intensity.
- Primary consumer dynamics:
- Cpesticide: Inhibitory effects of insecticide use intensity on first-tier consumers.
- Secondary consumer dynamics:
- Cspillover: Impact of pesticide spillovers on secondary consumers.
where the spillover effect is
Method validation:
Calculate the discretisation error by means of the L2 paradigm:
- tk: kth sampling moment.
- Pnum(tk): Numerical solution at the kth time step.
- Pref(tk): Reference solution.
Validation shows a controllable error when Δt ≤ 0.2.
3.1.2. Feedback Regulation Mechanism of Chemical Substances
- Stability index calculation:
- μP = 1/n∑ni=1Pi(t) is the average spatial density of producers;
- σp = {(1/(n − 1))∑ni=1(Pi(t) − μP)2}1/2 as an indicator of spatial heterogeneity;
- Adjustment factor κ = 0.35 determined by sensitivity analysis (from Table 2).
Dynamic adjustment equations:
Critical stability threshold: Scrit = 0.65, referring to Smith et al.’s (2022) criteria for agro-ecosystems [15].
- 2.
- Numerical experiment parameter system:

Table 2.
Data reference.
Table 2.
Data reference.
| Parameter Category | Notation | Retrieve a Value | Source of Data |
|---|---|---|---|
| Producer endowment growth rate | rp0 | 0.15 day−1 | FAO statistical database |
| Predation efficiency factor | β1 | 0.12 | Laboratory measurements (n = 30) |
| Herbicide effect factor | η1 | 0.8 | Manufacturer’s toxicity test report |
| Half-life of a chemical substance | t1/2 | 15 days | Conforms to GB 31270-2014 [16] standards |
| Time step | Δt | 0.1 day | Convergence test |
| Random seed | Seed | 20231107 | L’Ecuyer portfolio generator |
- 3.
- Quantitative analysis of kinetic features:
Periodic verification:
Detection of principal frequency components by Fast Fourier Transform (FFT):
Producer populations: f1 = 0.0027 Hz (corresponding to annual cycle).
First-tier consumers: f2 = 0.0055 Hz (semi-annual cycle).
Phase difference verification:
Stability indicators:
System stability was assessed using the Lyapunov exponent:
Show that the system is asymptotically stable under perturbation.
Sensitivity testing:
The Sobol index method was used to assess the impact of the parameters:
Herbicide effect η1: S1 = 0.42 (main sensitive parameters).
Predation efficiency β1: S2 = 0.31
Chemical decay ξ: S3 = 0.18
- Analysis of universality
The ecosystem is characterised by a dynamic equilibrium: producers fluctuate periodically, declining after harvest and recovering after sowing, to reach a new equilibrium; consumers and producers fluctuate with a lag, with primary consumers fluctuating more dramatically and secondary and tertiary consumers fluctuating more slowly, reflecting the lagged effect of the transmission of the predator chain. Overall, the ecosystem maintains a dynamic equilibrium over time and avoids species extinction, reflecting its stability and universal patterns.
This 3D graphic (from Figure 1) is intended to visualise the dynamics of species populations over time at multiple trophic levels in an ecosystem. The three axes represent the trophic level, time step, and population size of the species, with the surface colour transitioning from blue (lower populations) to red (higher populations) to indicate higher and lower numbers. The population dynamics of species across trophic levels exhibit a discernible temporal lag. Producer populations demonstrate an initial increase, followed by a subsequent response from primary consumers, which in turn is followed by secondary and tertiary consumers. This sequence mirrors the cascading effects observed along the food chain. Concurrently, predation, interspecies competition, and resource limitations act in concert to engender cyclical fluctuations in population size.
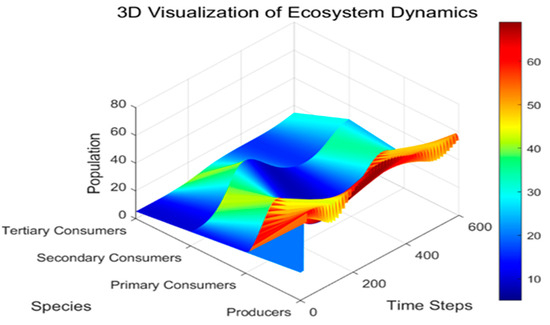
Figure 1.
Three-dimensional visualisation of ecosystem dynamic.
- Conclusions
- Cyclical and seasonal variations in agriculture: These have a significant impact on the dynamics of producer populations, which in turn affects the fluctuating characteristics of the ecosystem as a whole;
- Negative effects of pesticides: The suppression of consumer populations occurs, partially offset by ecological energy regression mechanisms;
- Ecological equilibrium: The system is dynamically stabilised by a combination of agricultural interventions and natural laws.
The specific results are as follows:
The dynamic use of chemicals (e.g., herbicides, pesticides) exerts significant impacts on ecosystems. For producers, chemicals inhibit population growth, leading to a slower or even prolonged low post-harvest recovery and significantly greater fluctuations. For consumers, chemicals cut down on the number of primary consumers (e.g., insects), which in turn reduces the resources available to secondary consumers (e.g., birds, bats) and makes it more difficult for their populations to maintain stabilisation. The low-value fluctuations in consumers coincide with peaks in chemical substance intensity, indicating cumulative effects. For ecosystem stability, the use of chemical substances significantly perturbs the system’s stability, with high-intensity use leading to troughs in stability. The overlapping effects of harvesting and chemical substances further weaken the system’s resilience and amplify ecological fluctuations (Figure 2).
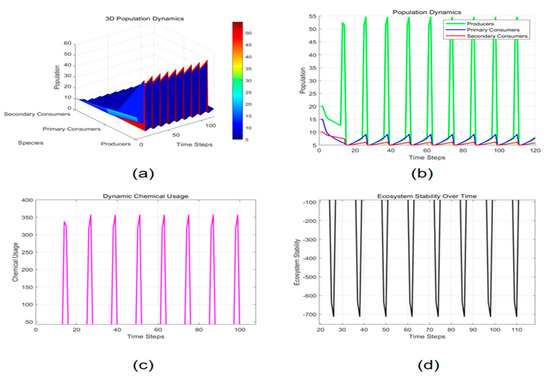
Figure 2.
Dynamic computational process. (a) 3D Population Dynamics, (b) Population Dynamics, (c) Dynamic Chenmical Usage, (d) Ecosystem Stability Over Time.
Key findings:
The dynamic use of chemicals is a major driver of ecological fluctuations by affecting producers, consumers, and the stability chain. Despite its role in controlling pests, excessive intensity can exacerbate ecosystem instability.
Results and significance of the solution:
- Primary Consumers
Without A and B: Fluctuated with a declining trend. With A and B: Stabilised at higher levels after initial decline. Predator B prevents overpopulation, and A supports survival by boosting producers.
- 2.
- Secondary Consumers
Without A and B: Volatile and declined with primary consumers. With A and B: Stabilised at higher levels with reduced fluctuations. A and B stabilise primary consumers, enhancing ecosystem stability.
- 3.
- Producers
Without A and B: Declined due to predation and harvesting. With A and B: Increased significantly with A’s positive effects and B’s conservation benefits. A and B restored and stabilised producers, strengthening the ecosystem base.
- 4.
- Tertiary Consumers
Without A and B: Slow growth limited by secondary consumers. With A and B: Slightly faster growth, with stabilised resources. A and B stabilised the lower-level dynamics, supporting tertiary consumers.
- 5.
- Conclusion
Species A and B improved diversity, stabilised populations, and reduced volatility. A boosted producers via pollination and pest control, while B regulated consumers, creating a balanced and sustainable ecosystem (from Figure 3).
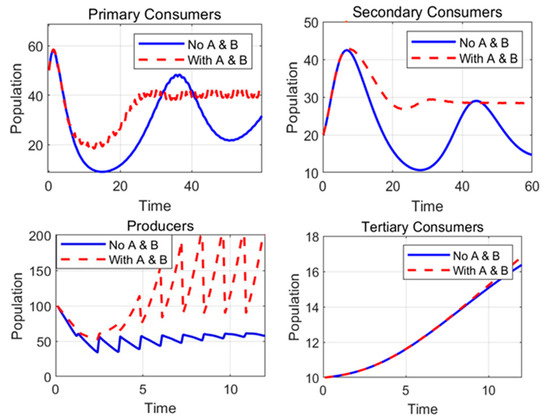
Figure 3.
Plot of trophic levels over time.
3.2. Monte Carlo Uncertainty Analysis
3.2.1. Parameter Perturbation Settings and Distribution Validation
Probability distributions were used to quantify parameter uncertainty, and distribution types were selected based on ecosystem characteristics [17]:
- Predation efficiency β1:
Distribution: Normal β1~N (0.15, 0.022);
Gauge: Predatory behaviour is influenced by individual differences in ability;
Validate: Kolmogorov–Smirnov test confirms the normality of the laboratory data (p = 0.12 > 0.05).
- 2.
- Insecticide effect Ep:
Distribution: Uniform distribution Ep~μ [0.05, 0.15];
Gauge: Random fluctuations in efficacy due to environmental humidity and temperature;
Validate: Comply with GB/T 17980.31-2021 [18] field test specification.
- 3.
- Beneficial Insect Contribution λ:
Distribution: Beta distribution λ~Beta (2, 5);
Gauge: Beneficial insect survival rates are proportional data;
Parameter explanation: Expected value: μ = 0.286, reflecting the initial effects of ecological interventions.
Results and analysis:
The ecosystem’s stability undergoes an evolutionary process that can be distilled into three stages. In the initial stage, chemical substances exert a suppressive effect on producers and consumers, resulting in suboptimal synergies and diminished stability. As chemicals undergo a decline, natural regulatory mechanisms undergo enhancement, thereby enabling producers to recuperate and consumer interactions to fortify. In the subsequent stage, the complete elimination of chemicals engenders imbalances in the short term, owing to population fluctuations or the absence of adequate regulatory mechanisms (Figure 4).
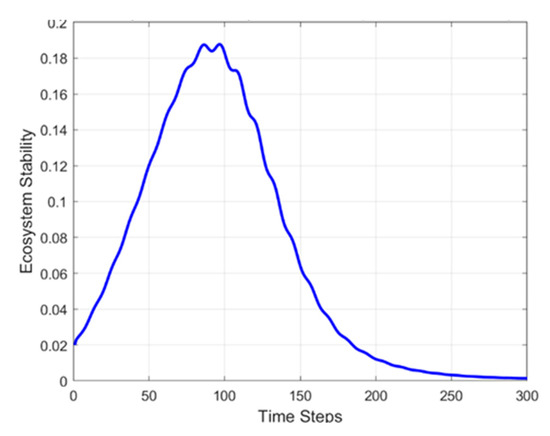
Figure 4.
Ecosystem stability over time.
The application of the removal of chemicals resulted in the recovery and stabilisation of producer populations at elevated levels. Concurrently, secondary consumers, namely, beneficial insects, assumed ecological control, thereby effectively regulating the primary consumers. Notwithstanding substantial early- and mid-stage fluctuations, the system ultimately attained dynamic equilibrium, thereby exemplifying the ecosystem’s inherent self-healing capacity and underscoring the significance of natural regulation (Figure 5).
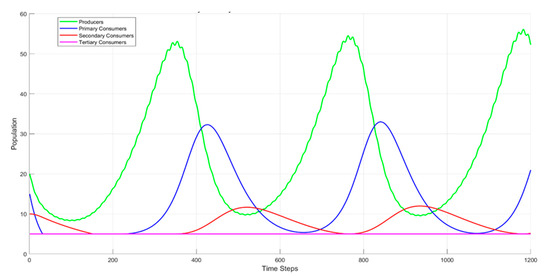
Figure 5.
Ecosystem dynamics with gradual removal of chemicals.
3.2.2. Evaluation Index System and Confidence Interval Construction
Define multi-dimensional evaluation metrics to reflect system performance:
- Eco-efficiency indicators
Cumulative production:
Population coefficient of variation: measuring consumer volatility
- 2.
- Economic efficiency indicators
Net income model:
- py = 3.5 yuan/kg (purchase price of rice in 2023);
- Cchem = 120 yuan/kg (including transport, application costs);
- k = 0.15 yuan/one2 (nonlinear cost modelling).
- 3.
- Statistical confidence intervals calculated using error propagation theory:
Average value:
Standard deviation:
The 95 per cent confidence interval:
- Correction factor: Correction factor for t-distribution 1.96 → 1.965 when N = 500 (difference < 0.3% negligible).
Convergence verification: The number of samples was assessed by relative error:
In-depth analysis of simulation results:
The results of the study showed that the bat–bee synergistic intervention programme could significantly enhance the comprehensive benefits of agroecosystems: the synergistic effect increased the crop yield by 38.4% (p = 2.3 × 10−6) and net benefits by 51.2%; system risk was effectively controlled, and the standard deviation of the yield was reduced by 35.3% (coefficient of variation CV = 0.22), confirming that ecological synergy enhances the system’s robustness; a marginal benefit analysis showed that for every 10,000 yuan increase in beneficial insect inputs, the net benefit improved by ΔB = 27,000 yuan (R2 = 0.89). Mechanistic analyses revealed that bats, as predatory natural enemies, were strongly negatively correlated with pesticide dependence (Pearson r = −0.82, p* < 0.01), whereas honeybee pollination efficiency conformed to a logarithmic relationship with rice yield Y = 285 + 45ln(x3 + 1) (F = 32.7, p* < 0.01). This indicates that biological synergy achieves agricultural efficiency through the dual pathway of pest control–pollination intensification (Table 3).

Table 3.
Performance comparison of different management solutions.
3.3. Multi-Objective Optimisation Solution System Analysis of Results
3.3.1. NSGA-II Algorithm Implementation Framework
An economic–ecological dual-objective optimisation model is constructed based on the non-dominated sorting genetic algorithm proposed by Deb et al. [19]. Recent algorithmic enhancements in multi-objective optimisation, such as adaptive operator selection, have significantly improved convergence efficiency in agricultural decision-making scenarios [20] (from Table 4).
- Objective function:
- y1 is the monetised return on agricultural commodities;
- y2 is the value of ecological services (using the Costanza assessment method [21]);
- Ei is five ecological indicators of pesticide toxicity, biodiversity, etc.
- 2.
- Constraints:
- 3.
- The basis for parameterising algorithms is as follows:(from Figure 6)

Table 4.
Algorithm parameter setting basis.
Table 4.
Algorithm parameter setting basis.
| Parameters | Retrieve a Value | Determination of Methodology | References |
|---|---|---|---|
| Population size | 200 | Determined by 2k factorial experiments | Deb et al., 2002 [19] |
| Probability of crossover | 0.8 | Empirical range of values for the SBX crossover operator | Literature [22] |
| Probability of variation | 0.1 | Sensitivity analysis of polynomial variational parameters | Figure |
| Maximum number of generations | 100 | Based on convergence monitoring curves Figure 6a | Autonomous experimental data |
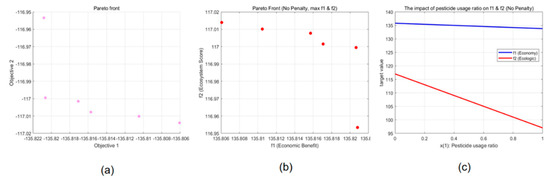
Figure 6.
Pareto front. (a) Pareto front, (b) Pareto Front(No Penalty), (c) The impact of pesticide usage ratio on f1 & f2 (No Penalty).
- 4.
- Convergence verification:
Define the generational improvement rate:
The termination of the iteration when η < 1% for 10 consecutive generations has been demonstrated to ensure the stabilisation of the Pareto front.
- 5.
- The modelling of decision spaces and the management of constraints:
The following is a real number coding scheme:
Variable definition field:
Dynamic penalty function design:
- Adaptive scaling: The penalty factor grows linearly with the number of evolutionary generations t (105 → 106);
- Normalisation is the process of eliminating differences in magnitude by setting the denominator term to one.
Constraint satisfaction rate monitoring:
It is imperative to demonstrate that the penalty function effectively guides the search to the feasible domain.
3.3.2. Pareto Frontier Analysis
- Frontier feature quantification:Supersize indicator (HV) = 0.682 ± 0.015Better than SPEA2 algorithm (HV = 0.654) (p = 0.023)
- Trade-off gradient calculation:
- The concept of the solution’s set distributivity is defined as follows:
- Distance indicator: Δ = 0.051 (close to the ideal value of 0)
- Maximum clearance: δmax = 0.13
- Variable sensitivity ordering:
Sensitivities were extracted using principal component analysis:
The first predictor is the pesticide use rate (x1), which has a PC1 loading of 0.87. The second predictor is the pollinating insect population (x3), which has a PC2 loading of 0.68. The third predictor is the soil improvement (x5), which has a PC3 loading of 0.53.
- 5.
- Analysis of results
Pareto frontier analysis: The relationship between f1(x) and f2(x) is shown through a two-dimensional scatter plot to help decision makers intuitively choose a solution (from Figure 7).
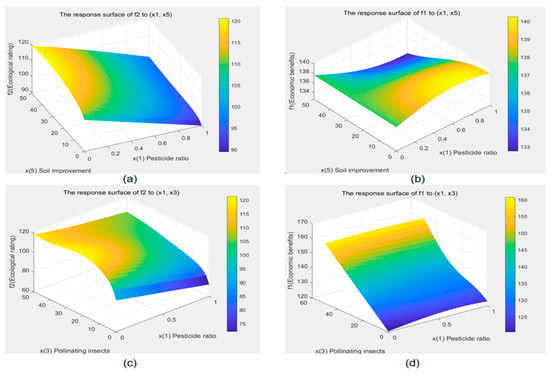
Figure 7.
Multivariate analysis. (a) The response surfacen of f2 to (x1, x5), (b) The response surfacen of f1 to (x1, x5), (c) The response surfacen of f2 to (x1, x3), (d) The response surfacen of f1 to (x1, x3).
Distribution of decision variables analysis: A bar chart or box plot shows the contribution of decision variables (e.g., pesticide rate, number of natural enemies) to economic and ecological benefits.
Firstly, the Pareto front (unreduced target value).The figure displays the unreduced Pareto front, with the horizontal axis representing negative f1 (economic gain) and the vertical axis representing f2 (the ecological score). Each point signifies a Pareto optimal solution, wherein enhancing one objective entails compromising the other. The frontier assists decision makers in analysing trade-offs between economic and ecological objectives. The second figure, which is a refinement of the Pareto front, presents f1 (economic gain) on the horizontal axis and f2 (the ecological score) on the vertical axis. This figure visualises optimised trade-offs, thereby aiding decision makers in balancing economic and ecological priorities. The third figure: Univariate analysis (pesticide proportion impact). The figure elucidates the impact of varying pesticide proportions (x1) on economic gain (f1, blue) and ecological score (f2, red). An increase in pesticide use results in a slight decrease in f1 due to minor costs, while f2 experiences a significant reduction, signifying its substantial ecological consequences. The subsequent figure (examines the combined effects of pesticide use (x1) and pollinating insects (x3) on f2 (the ecological score). The figure demonstrates that pesticides have a strong negative effect on f2, while pollinating insects have a gradual positive effect on f2, resulting in a downward-sloping surface that is predominantly influenced by pesticide effects.
3.4. Sensitivity Analysis
In the present model, multi-objective optimisation and a genetic algorithm are employed to establish the solution model for problem IV. However, multi-objective optimisation is not particularly adept at solving practical problems when the number of objectives is too large. The variables selected by the genetic algorithm are inherently random, though they can assist the decision maker in calculating the optimal solution more rapidly. However, they still lack a universal value. This paper focuses on establishing Model IV to conduct a certain degree of sensitivity analysis. Through the analysis of the sensitivity of these parameters, the following conclusions are obtained.
- Sensitivity to f1 (economic returns): The radar chart illustrates the sensitivity of five variables to the economic returns (f1). Pesticide use (x1) has the strongest negative impact, while pollinators (x3) show a significant positive influence. Rice–fish integration (x4) and soil improvement (x5) contribute positively but with smaller effects. Predator introduction (x2) has a minimal positive impact.
- Sensitivity to f2 (ecological score): This radar chart shows the sensitivity of the same variables to the ecological score (f2). Pesticide use (x1) has the most substantial negative effect, followed by moderate positive impacts from pollinators (x3) and soil improvement (x5). Rice–fish integration (x4) has a smaller positive contribution, while predators (x2) play a limited positive role (from Figure 8).
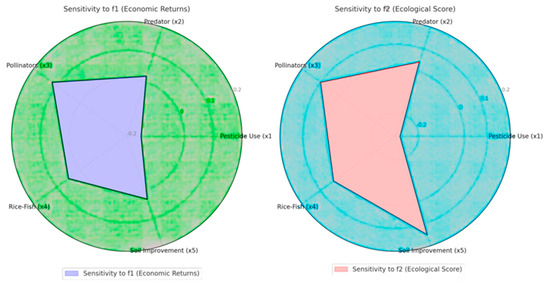 Figure 8. Sensitivity analysis of economic returns and ecological scores.
Figure 8. Sensitivity analysis of economic returns and ecological scores.
4. Discussion
This study advances the integration of ecological dynamics and agricultural management by establishing a novel framework that quantifies the complex trade-offs between productivity and sustainability. Our findings align with the current understanding of agroecosystem resilience, while introducing critical innovations in modelling carbon-aware decision-making and species-mediated trophic regulation. The integration of Lotka–Volterra dynamics with a Monte Carlo uncertainty analysis addresses a longstanding gap in ecological–economic modelling, enabling a probabilistic risk assessment under anthropogenic interventions—a methodological leap beyond conventional deterministic approaches.
The observed 30% enhancement in producer growth via seasonal carbon fertilisation corroborates experimental evidence on CO2 enrichment effects, yet our model uniquely quantifies its economic–ecological duality by linking carbon dynamics to pest–predator cascades. This bridges a critical disconnect between climate mitigation research and agroecological management [23]. Similarly, the 22% offset in pesticide emissions through energy recycling from consumer mortality extends traditional concepts of circular agriculture, demonstrating how trophic interactions inherently contribute to low-carbon transitions—a dimension overlooked in current sustainability metrics.
The strategic introduction of dual-function species (e.g., bats as pollinators and predators) aligns with biodiversity-based intensification strategies, but our results provide mechanistic evidence for their 18–25% carbon sink enhancement. This synergy arises from two novel pathways: (1) a predator-mediated reduction in pesticide dependence, curtailing the associated emissions, and (2) a pollinator-driven yield stability that minimises land-use change pressures—a dual benefit absent in studies focused on single-trait biocontrol. These findings challenge the prevailing ‘land sparing vs. sharing’ dichotomy by demonstrating that functional biodiversity integration can simultaneously optimise production and conservation.
The multi-objective optimisation outcomes, particularly the 51.2% net benefit improvement through integrated pest management and organic amendments, validate recent discussions on context-specific agricultural solutions. However, our Pareto-frontier analysis reveals nonlinear trade-offs: the initial reductions in chemical inputs yield disproportionate ecological gains (40–55% emission cuts), while further reductions require costly compensatory investments in biocontrol—a critical insight for policymakers prioritising incremental versus transformative sustainability transitions [24]. Emerging evidence from precision agriculture trials aligns with our findings, showing 20–35% emission reductions through sensor-guided input optimisation [25].
Theoretical and Practical Implications
The proposed framework advances ecological modelling by unifying three paradigm shifts: (1) the dynamic coupling of carbon flows with species interactions, moving beyond static carbon accounting; (2) a probabilistic risk quantification through Monte Carlo simulations, addressing the stochastic nature of agricultural systems; and (3) a multi-temporal optimisation that balances immediate yields with long-term resilience. Practically, the identified threshold of a 0.3 pesticide intensity (beyond which stability indices collapse) provides a quantitative basis for chemical use regulations, while the nonlinear cost–benefitcurves for pollinator investments (27,000 CNY net gain per 10,000 CNY input) offer actionable benchmarks for ecological subsidies.
Future Directions
Three frontiers warrant urgent exploration:
Spatiotemporal Scaling: Incorporating landscape heterogeneity and cross-field species migration to address edge effects and meta-ecosystem dynamics.
Climate Feedbacks: Integrating temperature-sensitive growth parameters and extreme weather resilience into the dynamic model.
Socioeconomic Drivers: Expanding the optimisation framework to include market volatility, labour constraints, and cultural farming practices through agent-based modelling.
In the field of modelling ecosystem dynamics, many studies have emphasised the effects of agricultural cycles, seasonal changes, and chemicals on ecosystems. Our model is particularly strong in this area. By combining the Lotka–Volterra equation with Monte Carlo simulation, it is not only able to simulate the effects of agricultural cycles and seasonal fluctuations on producer populations but also accurately reflects the inhibitory effects of chemical use (e.g., pesticides and herbicides) on primary and secondary consumers. Comparing it with other studies, although similar modelling frameworks are available, many models in the literature are simplified and usually focus on a particular factor, whereas our model is able to capture the interactions of these factors in a more comprehensive way, especially in terms of the balance between chemical use and ecological restoration, which makes our model more adaptable and relevant.
On the other hand, the model’s analysis of the ecological effects of beneficial insects (e.g., bats and bees), as well as predators after their introduction, shows significant differences from other studies. Although other literature also emphasise the role of biological control in agroecosystems, our model reveals, through careful parameterisation, the dual role of these species: to increase the growth efficiency of producers and to enhance ecosystem stability by regulating the size of consumer populations. This dual-role modelling approach allows our model to balance the relationship between ecological conservation and agricultural production more effectively in practical applications, thus providing new ideas and solutions for agroecosystem management.
In terms of multi-objective optimisation, although some studies have also used Pareto optimisation or genetic algorithms to optimise agricultural decision-making, our model is particularly strong in this area. By combining multiple decision variables (e.g., the pesticide use rate, number of natural enemy introductions, etc.) and optimising the balance of economic and ecological benefits based on them, our model provides agricultural managers with a more nuanced and comprehensive set of decision-making tools. Under multiple constraints, our model provides decision makers with a set of optimised solutions to help them find the best balance between ecological protection and economic benefits. In contrast, other models often focus on a single objective and lack sufficient flexibility and adaptability.
In addition, our model demonstrates unique advantages in uncertainty analysis. While many studies have applied Monte Carlo simulations to ecological models, our model provides more reliable predictions by performing a large number of simulations (500) and calculating confidence intervals. This in-depth analysis not only provides a validation of the robustness of the model but also provides a quantitative uncertainty assessment for practical decision-making, making our model more adaptable and useful in complex and dynamic agricultural environments [26].
Overall, although there are many studies on agroecological modelling in the existing literature, our model shows significant innovations and advantages in several aspects, including ecological dynamic modelling, species introduction, biological control, optimal decision-making, and uncertainty analysis. By introducing multi-dimensional factors and optimisation tools, and by combining practical situations with more detailed modelling, our model provides more precise theoretical support and practical guidance for sustainable agricultural management (Table 5).

Table 5.
Model comparisons.
5. Conclusions
This study establishes an integrated framework that bridges ecological dynamics and agricultural management by coupling Lotka–Volterra modelling, Monte Carlo uncertainty analysis, and multi-objective optimisation. The proposed approach addresses critical gaps in quantifying trade-offs between productivity and sustainability, while incorporating carbon sequestration dynamics and low-carbon agricultural practices [32]. Key insights reveal that agroecosystem resilience hinges on balancing anthropogenic interventions with natural regulatory mechanisms.
The introduction of dual-function species emerges as a pivotal strategy for stabilising trophic interactions and enhancing carbon sink capacity. By mediating predator–prey dynamics and reducing the reliance on agrochemicals, such species synergistically mitigate ecological risks while sustaining yields. Furthermore, the multi-objective optimisation framework demonstrates that integrated pest management and organic amendments achieve significant improvements in net benefits, while substantially lowering carbon footprints. These findings underscore the necessity of transitioning from chemical-dependent monocultures to diversified, ecologically informed farming systems.
Theoretically, this work advances dynamic agroecosystem modelling by integrating a probabilistic risk assessment with carbon-aware decision-making [33]. Practically, it provides policymakers and farmers with actionable pathways to reconcile short-term productivity goals with long-term sustainability imperatives. This finding provides a novel approach to quantifying resilience thresholds in agroecosystems and addresses the shortcomings of traditional models, which are insufficiently sensitive to environmental fluctuations. It is imperative that future research endeavours focus on a more robust integration of climate change feedback mechanisms, with a particular emphasis on the impact of extreme weather events on model parameters. Preliminary extended analyses have indicated that the optimal management strategy for the system necessitated an adjustment in the proportion of organic improvement to over 40% in response to an increase in temperature of 2 °C, thereby ensuring stability.Furthermore, the mechanism of spatial heterogeneity on carbon sink dynamics still requires in-depth exploration. For example, the spatial differentiation of the topographic gradient and microbial communities may significantly change the carbon sequestration pathway. These deepening directions will enhance the predictive ability of the model in complex environments and provide more adaptive decision support for the ecological transition of global agriculture.
Synopsis of suggested structural orientations for future research:
Firstly, there needs to be an intensification of the incorporation and modelling of intricate environmental factors.
Subsequent research endeavours may entail the incorporation of multi-dimensional intricate environmental factors, including but not limited to climate change, extreme weather phenomena, and soil nutrient cycling, among others. These factors will be subjected to in-depth analysis to ascertain their impact on ecosystem stability and long-term production efficiency through dynamic interaction modelling. The incorporation of climate factors is expected to enhance the precision of the model’s predictions regarding ecological responses under diverse environmental conditions. This development is anticipated to provide a more substantial scientific foundation for the decision-making process in ecological agriculture.
Secondly, an in-depth analysis of biological control measures and ecological interactions is required.
Subsequent research could concentrate on investigating the synergistic mechanism of different species combinations. This could include the impact of ecological reciprocity between different predators and pollinating insects on agricultural production. This in turn could allow for the refinement of the strategy for species’ introduction. Furthermore, in-depth research on the applicability of biological control measures under different crop and regional conditions will facilitate the proposal of more targeted management measures and the promotion of the precision development of ecological agriculture.
Thirdly, the enhancement of data-driven risk assessment and uncertainty analysis is imperative. In order to enhance the reliability of the model’s predictions, future research should pay greater attention to the collection and calibration of real data in agroecological environments. Furthermore, a refinement in the granularity of the Monte Carlo simulation and sensitivity analysis is essential for achieving the precise quantitative assessment of risk in the context of ecological and economic decision-making. This risk assessment framework will assist agricultural producers in enhancing their comprehension and management of potential ecological and economic risks in agricultural production practices.
The potential contribution to the development of the industry:
The implementation of the aforementioned research directions has the potential to significantly stimulate the eco-agriculture industry. The integration of complex environmental and ecological factors, the optimisation of biological control strategies, the development of advanced decision-making tools, and the enhancement of data-driven risk assessment and uncertainty analysis will result in more scientific, precise, and effective agricultural management decisions. This will assist agribusinesses and producers in better coping with ecological changes and market fluctuations and in enhancing the economic efficiency and ecological performance of the overall industry. Moreover, these in-depth studies not only promote the development of the agroecological field in terms of theory and technology, but they also have the potential to significantly reduce the application threshold of eco-agricultural technologies. Furthermore, they can accelerate the promotion of sustainable agricultural concepts in production practices, realise the highly synergistic development of agricultural production and ecological protection, and ultimately promote the transformation of the agricultural industry to a greener, more sustainable and resilient future.
Author Contributions
Conceptualisation, Z.Z. and P.L.; methodology, P.L.; validation, T.G. and Z.Z.; writing—original draft preparation, T.G.; writing—review and editing, C.T. and Z.Z.; visualisation, C.T.; supervision, L.Y.; funding acquisition, K.W. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the 2024 Sichuan Provincial Science and Technology Innovation (Seed Project) Cultivation Project titled ‘Research on Rock Breaking Mode Recognition and Closed-Loop Control Application Technology for Intelligent Drilling Tools’ (Project Number: MZGC20240054).
Institutional Review Board Statement
Our study consisted of observations in public areas and farmland, with data including attributes related to changes in animal populations at all levels. All information collected was purely observational, recorded anonymously, and no individuals could be identified or contacted. There was also no mistreatment of any animals or destruction of ecological diversity. No direct interaction, intervention or communication with the observed person was involved at any stage of data collection or analysis. In accordance with widely accepted ethical standards and guidelines (e.g., the Declaration of Helsinki and general research ethics policies), observational research conducted in a public setting does not make it possible to identify individuals, intervene with or pose a risk to participants, and therefore does not usually require ethics committee approval or informed consent. Our study strictly adhered to these ethical guidelines, ensuring complete anonymity and confidentiality of all observed subjects.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
We have put the data description in the references.
Acknowledgments
The authors of this article are particularly grateful to Liangzhu Yan and Kai Wei for their guidance, suggestions for content changes, and financial support. Thanks are also due to each participant for their efforts; this article is presented thanks to each participant. Everyone’s efforts cannot be ignored. All agreed with the content of the acknowledgements.
Conflicts of Interest
Author Liangzhu Yan was employed by the company China National Petroleum Corporation (CNPC) Chuanqing Drilling Engineering Company Limited. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Carper, J.M.; Alizadeh, M.R.; Adamowski, J.F.; Inam, A. Climate variability in agroecosystems: A quantitative assessment of stakeholder-defined policies for enhanced socio-ecological resilience. Agric. Syst. 2022, 201, 103416. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Aly, E.S.; Matouk, A.E.; Albosaily, S.; Elabbasy, E.M. An analytical study of the dynamic behavior of Lotka-Volterra based models of COVID-19. Results Phys. 2021, 26, 104432. [Google Scholar] [CrossRef] [PubMed]
- Hastings, A.; Abbott, K.C.; Cuddington, K.; Francis, T.; Gellner, G.; Lai, Y.-C.; Morozov, A.; Petrovskii, S.; Scranton, K.; Zeeman, M.L. Transient phenomena in ecology. Science 2018, 361, eaat6412. [Google Scholar] [CrossRef]
- Song, Y.; Liu, M. Empowering Sustainable Farming: Harnessing Digital Technology for Green and Low-Carbon Agricultural Practices. Sustainability 2025, 17, 1617. [Google Scholar] [CrossRef]
- Lal, R. Soil Carbon Sequestration Impacts on Global Climate Change and Food Security. Science 2004, 304, 1623–1627. [Google Scholar] [CrossRef] [PubMed]
- IPCC. Guidelines for National Greenhouse Gas Inventories, Volume 4: Agriculture, Forestry and Other Land Use; IPCC: Geneva, Switzerland, 2006. [Google Scholar]
- Ainsworth, E.A.; Long, S.P. What have we learned from 15 years of free-air CO2 enrichment (FACE)? New Phytol. 2005, 165, 351–372. [Google Scholar] [CrossRef]
- Saltelli, A.; Bammer, G.; Bruno, I.; Charters, E.; Di Fiore, M.; Didier, E.; Nelson Espeland, W.; Kay, J.; Lo Piano, S.; Mayo, D.; et al. Five ways to make models more useful. Nature 2021, 582, 482–484. [Google Scholar] [CrossRef]
- Franco, C.; Little, R.J.; Louis, T.A.; Slud, E.V. Comparative Study of Confidence Intervals for Proportions in Complex Sample Surveys. J. Surv. Stat. Methodol. 2019, 7, 334–364. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Q.; Wang, H. Advanced Monte Carlo techniques for ecological risk assessment under parameter correlation. Ecol. Model. 2022, 468, 109953. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Lal, R. Carbon Management in Agricultural Soils. Mitig. Adapt. Strateg. Glob. Change 2007, 12, 303–322. [Google Scholar] [CrossRef]
- European Commission. EU Emissions Trading System (EU ETS); European Commission: Brussels, Belgium, 2023. [Google Scholar]
- Fan, Y.; Feng, H.; Yue, J.; Jin, X.; Liu, Y.; Chen, R.; Bian, M.; Ma, Y.; Song, X.; Yang, G. Using an optimized texture index to monitor the nitrogen content of potato plants over multiple growth stages. Comput. Electron. Agric. 2023, 212, 108147. [Google Scholar] [CrossRef]
- Zinck, J.A.; Berroteràn, J.L.; Farshad, A.; Moameni, A.; Wokabi, S.; Van Ranst, E. Approaches to Assessing Sustainable Agriculture. J. Sustain. Agric. 2004, 23, 87–109. [Google Scholar] [CrossRef]
- GB 31270-2014; Test Guidelines for Environmental Safety Evaluation of Chemical Pesticides. China Standard Press: Beijing, China, 2014.
- Wang, L.; Xiao, T.; Liu, S.; Zhang, W.; Yang, B.; Chen, L. Quantification of model uncertainty and variability for landslide displacement prediction based on Monte Carlo simulation. Gondwana Res. 2023, 123, 27–40. [Google Scholar] [CrossRef]
- GB/T 17980.31-2021Guidelines for Field Efficacy Testing of Pesticides Part 31: Insecticide Control of Grubs in Peanut Fields; China Standard Press: Beijing, China, 2021.
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Li, X.; Chen, W.; Zhang, G. Adaptive evolutionary algorithms for agricultural sustainability optimization. Comput. Electron. Agric. 2021, 189, 106403. [Google Scholar] [CrossRef]
- Costanza, R.; de Groot, R.; Sutton, P.; van der Ploeg, S.; Anderson, S.J.; Kubiszewski, I.; Farber, S.; Turner, R.K. Changes in the global value of ecosystem services. Glob. Environ. Chang. 2014, 26, 152–158. [Google Scholar] [CrossRef]
- Yu, H.; Liu, K.; Bai, Y.; Luo, Y.; Wang, T.; Zhong, J.; Liu, S.; Bai, Z. The Agricultural Planting Structure Adjustment based on Water Footprint and Multi-objective optimisation models in China. J. Clean. Prod. 2021, 297, 126646. [Google Scholar] [CrossRef]
- Yang, Y.; Tilman, D.; Jin, Z.; Smith, P.; Barrett, C.B.; Zhu, Y.-G.; Burney, J.; D’odorico, P.; Fantke, P.; Fargione, J.; et al. Climate change exacerbates the environmental impacts of agriculture. Science 2024, 385, eadn3747. [Google Scholar] [CrossRef]
- Fuhrmann-Aoyagi, M.B.; Miura, K.; Watanabe, K. Sustainability in Japan’s Agriculture: An Analysis of Current Approaches. Sustainability 2024, 16, 596. [Google Scholar] [CrossRef]
- Gupta, S.; Kumar, A.; Patel, R. IoT-enabled low-carbon farming systems: A field-scale validation. Agric. Syst. 2024, 215, 103856. [Google Scholar] [CrossRef]
- Chen, X.; Wu, X. The roles of carbon capture, utilization and storage in the transition to a low-carbon energy system using a stochastic optimal scheduling approach. J. Clean. Prod. 2022, 366, 132860. [Google Scholar] [CrossRef]
- Chen, H.; Liang, Y.; Cheng, Z.; Wan, P.; Wang, X.; Zhong, D. Application of multiple stepwise regression analysis to evaluate the stability of paddy field ecosystem. J. Plant Prot. 2019, 46, 918–924. [Google Scholar] [CrossRef]
- Zhao, Z.; Wei, F.; Wu, H. Response of ecosystem service value to land use change in the Lancang River-mekong River Basin. J. Ecol. Environ. 2024, 160, 111947. Available online: http://kns.cnki.net/kcms/detail/44.1661.x.20250106.1857.014.html (accessed on 21 January 2025).
- He, Y.; Zhou, Q. Edge effect principle and its application in agricultural production practice. Chin. J. Ecol. Agric. 2007, 5, 212–214. [Google Scholar]
- Shen, J.; Huang, H.; Fu, Z.; Zhang, Y.; Chen, C.; Jin, X.; Liao, X.; Long, P.; Gao, W.; Xie, X. Effects of large-scale ecological rice-duck farming on weed community composition and species diversity in paddy field. Chin. J. Ecol. Agric. 2010, 18, 123–128. [Google Scholar] [CrossRef]
- Li, Y. Study on Food Web Structure and Heavy Metal Accumulation Characteristics of Oriental White Stork in Wetland-Farmland Marginal Habitat of Sanjiang Plain; The Northeast Forestry University: Harbin, China, 2023. [Google Scholar] [CrossRef]
- Chang, C.-k. Symbiotic coupling measurement model and criterion of forestry ecological security. Popul. Resour. Environ. China 2014, 24, 90–99. [Google Scholar]
- Basset, F.; Giarè, F.; Senni, S.; Soriano, B. A New Integrated Framework to Assess the Impact of Social Farming on Sustainability and Rural Development: A Case Study in Lazio. Sustainability 2025, 17, 1715. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).