Influence of Regional Temperature Anomalies on Strawberry Yield: A Study Using Multivariate Copula Analysis
Abstract
1. Introduction
2. Materials and Methods
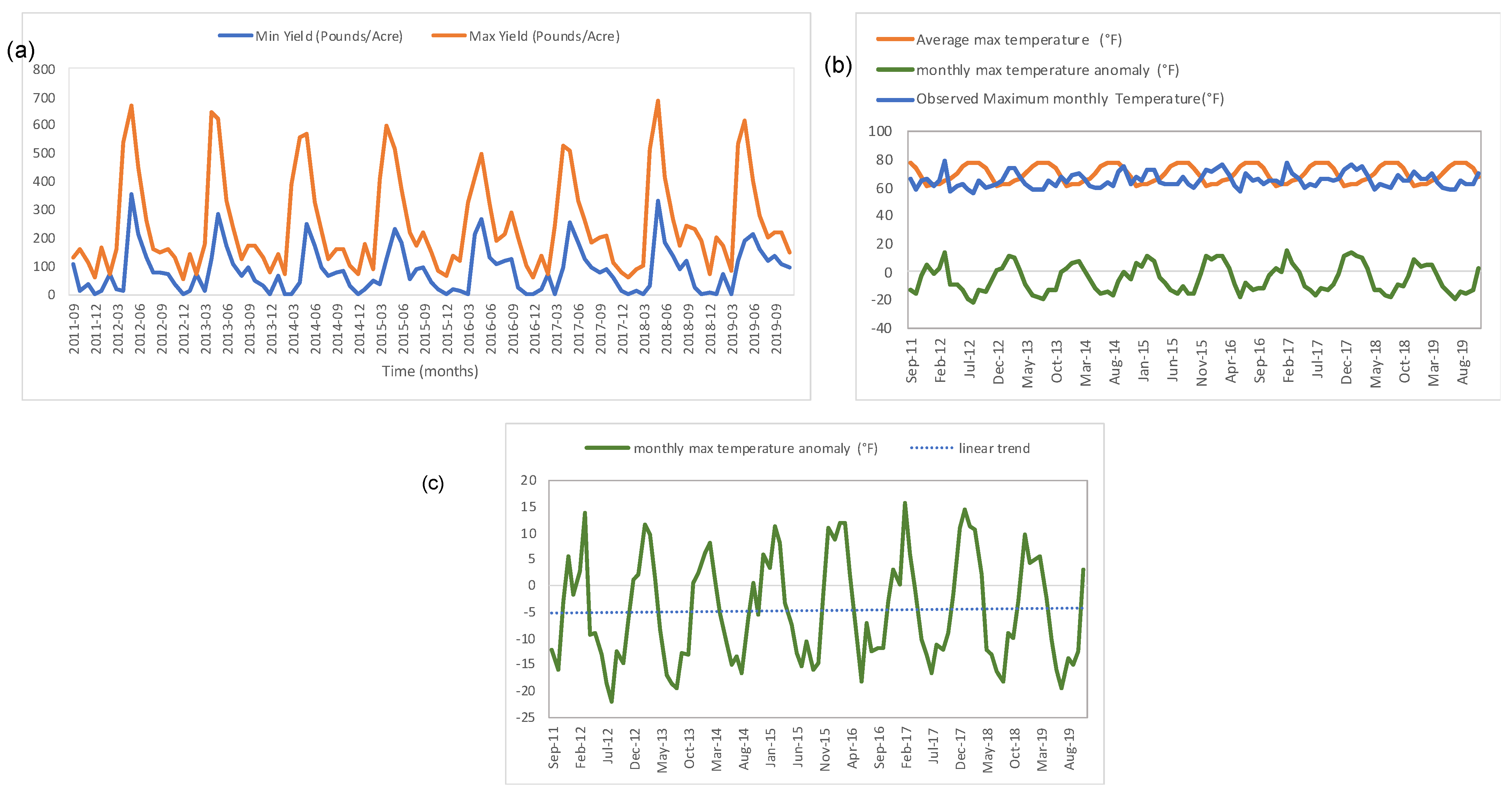
2.1. Data
2.2. Copula Analysis
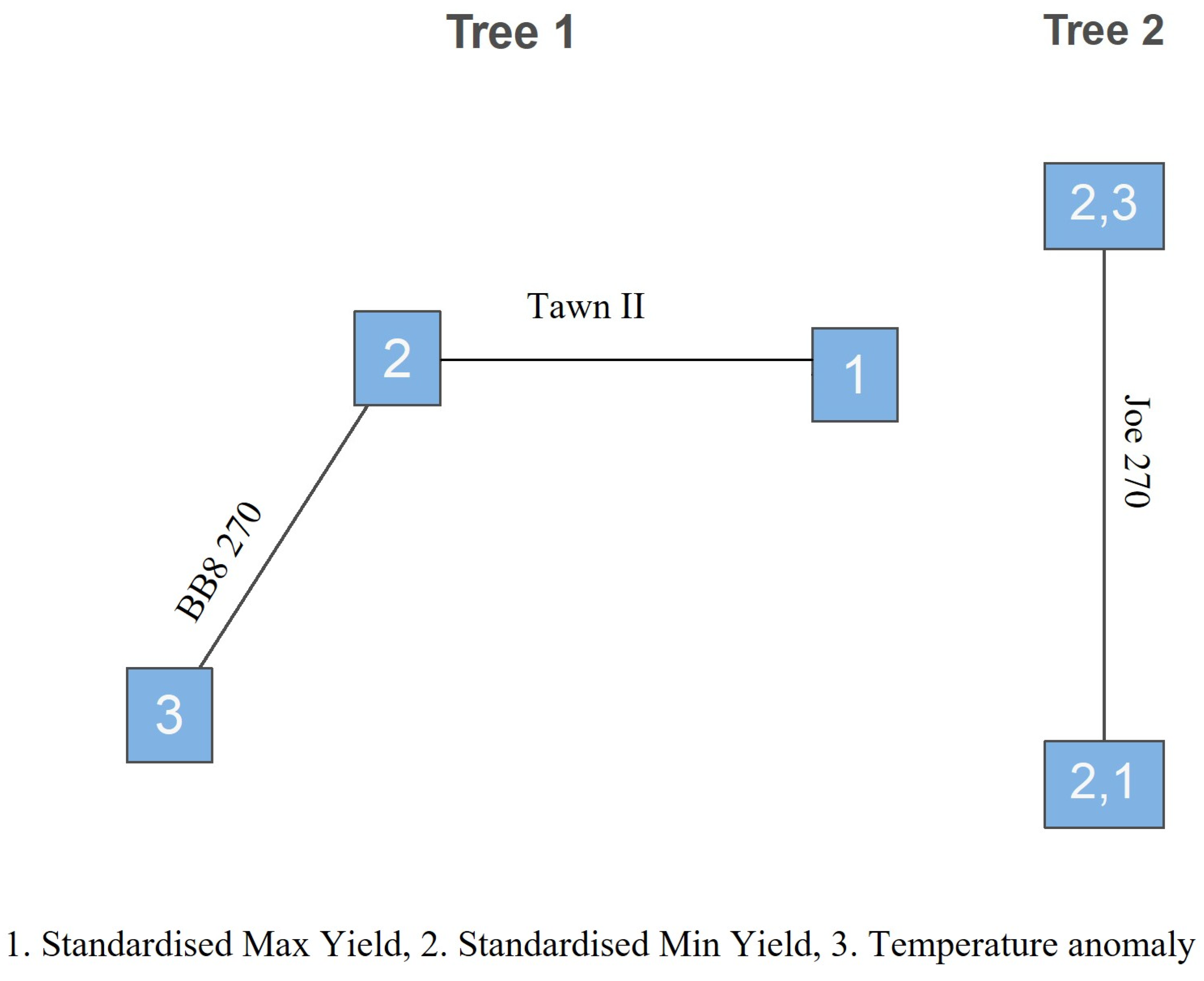
2.3. Construction of a 3-Dimensional Vine Copula
2.4. Calculation of Joint Probability of Occurrence of Events Using Copula
2.4.1. Univariate Probability
2.4.2. Joint Probability for Tri-Variate Events
2.4.3. Conditional Probability of Tri-Variate Events
3. Preliminary Data Analysis
4. Results and Discussion
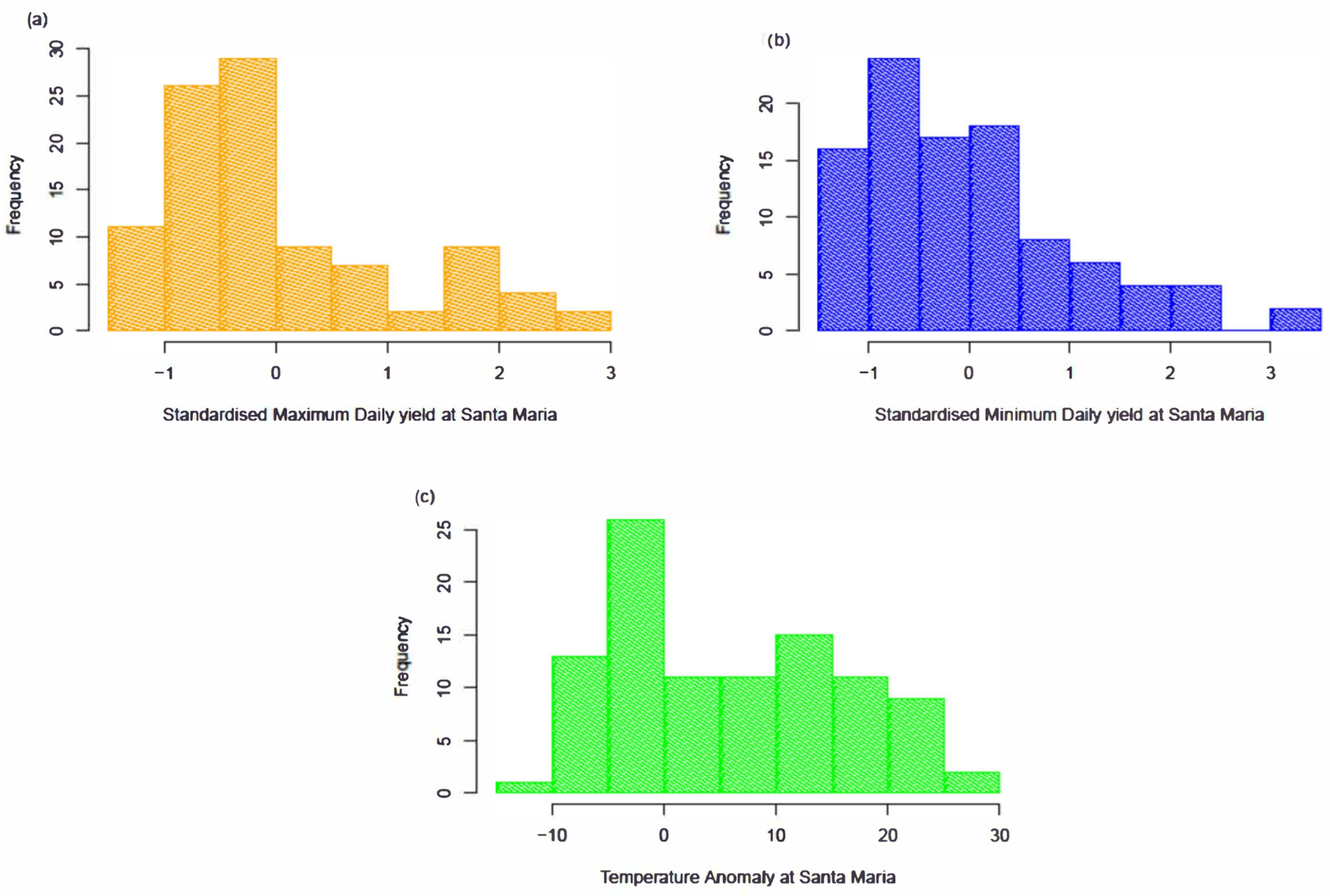
4.1. Univariate Analysis
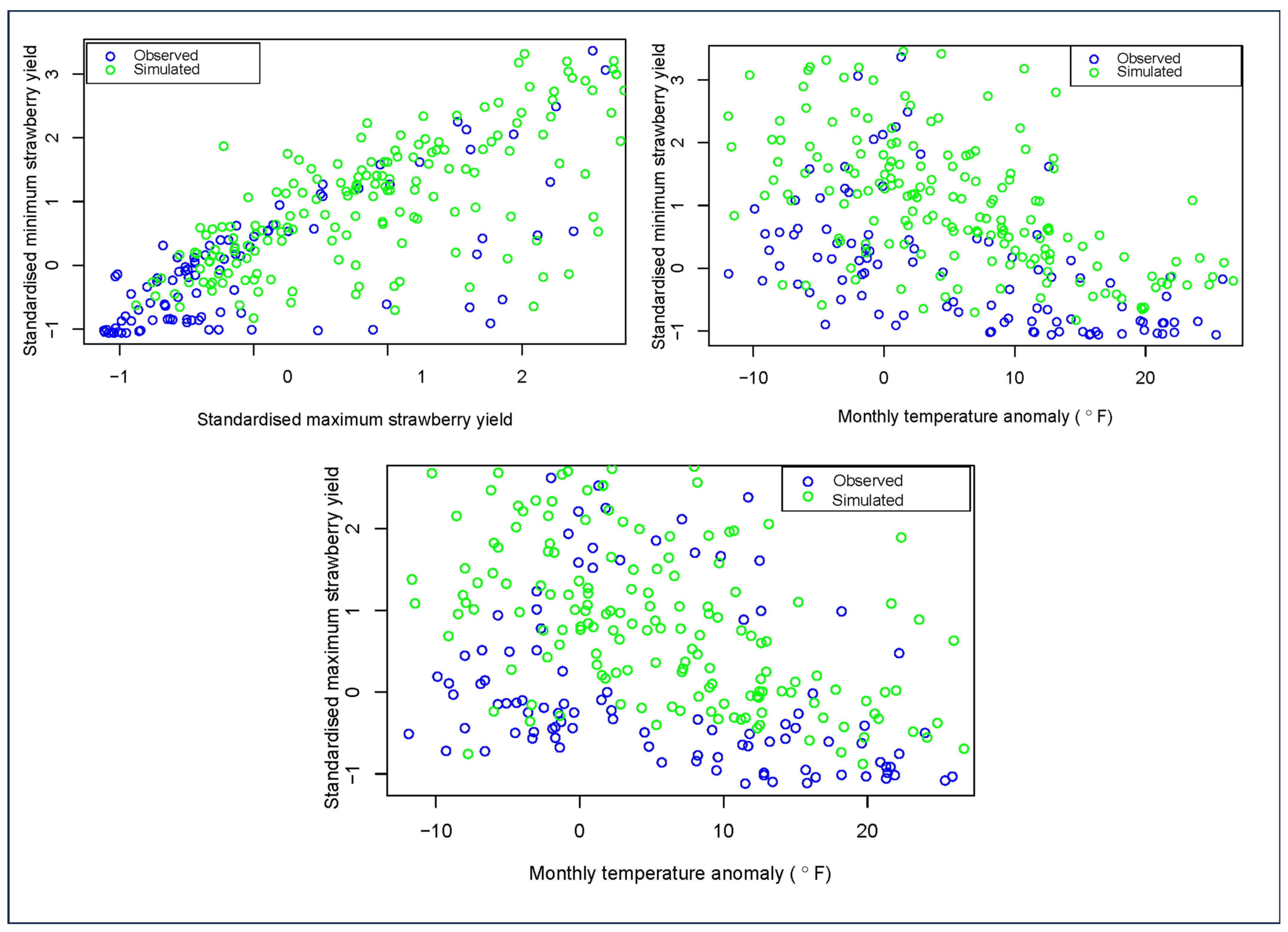
4.2. Multivariate Copula Analysis Using Vine Copula
5. Limitations of This Study
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kumari, A.; Lakshmi, G.A.; Krishna, G.K.; Patni, B.; Prakash, S.; Bhattacharyya, M.; Singh, S.K.; Verma, K.K. Climate Change and Its Impact on Crops: A Comprehensive Investigation for Sustainable Agriculture. Agronomy 2022, 12, 3008. [Google Scholar] [CrossRef]
- Elias, E.H.; Flynn, R.; Idowu, O.J.; Reyes, J.; Sanogo, S.; Schutte, B.J.; Smith, R.; Steele, C.; Sutherland, C. Crop Vulnerability to Weather and Climate Risk: Analysis of Interacting Systems and Adaptation Efficacy for Sustainable Crop Production. Sustainability 2019, 11, 6619. [Google Scholar] [CrossRef]
- Malhi, G.S.; Kaur, M.; Kaushik, P. Impact of Climate Change on Agriculture and Its Mitigation Strategies: A Review. Sustainability 2021, 13, 1318. [Google Scholar] [CrossRef]
- Talib, M.N.A.; Ahmed, M.; Naseer, M.M.; Slusarczyk, B.; Popp, J. The Long-Run Impacts of Temperature and Rainfall on Agricultural Growth in Sub-Saharan Africa. Sustainability 2021, 13, 595. [Google Scholar] [CrossRef]
- Eck, M.A.; Murray, A.R.; Ward, A.R.; Konrad, C.E. Influence of Growing Season Temperature and Precipitation Anomalies on Crop Yield in the Southeastern United States. Agric. For. Meteorol. 2020, 291, 108053. [Google Scholar] [CrossRef]
- John, R.P.; Megan, G. Temperatures and the Growth and Development of Wheat: A Review. Eur. J. Agron. 1999, 10, 23–36. [Google Scholar]
- Ottman, M.J.; Kimball, B.A.; White, J.W.; Wall, G.W. Wheat Growth Response to Increased Temperature from Varied Planting Dates and Supplemental Infrared Heating. Agron. J. 2012, 104, 7–16. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Piao, S.; Wang, X.; Lobell, D.B.; Huang, Y.; Huang, M.; Yao, Y.; Bassu, S.; Ciais, P.; et al. Temperature Increase Reduces Global Yields of Major Crops in Four Independent Estimates. Proc. Natl. Acad. Sci. USA 2017, 114, 9326–9331. [Google Scholar] [CrossRef]
- Asseng, S.; Ewert, F.; Martre, P.; Rötter, R.P.; Lobell, D.B.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising Temperatures Reduce Global Wheat Production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
- Challinor, A.J.; Wheeler, T.R.; Craufurd, P.Q.; Slingo, J.M. Simulation of the Impact of High Temperature Stress on Annual Crop Yields. Agric. For. Meteorol. 2005, 135, 180–189. [Google Scholar] [CrossRef]
- Ferris, R.; Ellis, R.H.; Wheeler, T.R.; Hadley, P. Effect of High Temperature Stress at Anthesis on Grain Yield and Biomass of Field-Grown Crops of Wheat. Ann. Bot. 1998, 82, 631–639. [Google Scholar] [CrossRef]
- Matsui, T.; Omasa, K.; Horie, T. The Difference in Sterility Due to High Temperatures during the Flowering Period among Japonica-Rice Varieties. Plant Prod. Sci. 2001, 4, 90–93. [Google Scholar] [CrossRef]
- Vara Prasad, P.V.; Craufurd, P.Q.; Summerfield, R.J.; Wheeler, T.R. Effects of Short Episodes of Heat Stress on Flower Production and Fruit-set of Groundnut (Arachis hypogaea L.). J. Exp. Bot. 2000, 51, 777–784. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Peng, L.; Zhang, X.; Yin, G.; Zhao, C.; Piao, S. Divergence of Climate Impacts on Maize Yield in Northeast China. Agric. Ecosyst. Environ. 2014, 196, 51–58. [Google Scholar] [CrossRef]
- Karimzadeh Soureshjani, H.; Ghorbani Dehkordi, A.; Bahador, M. Temperature Effect on Yield of Winter and Spring Irrigated Crops. Agric. For. Meteorol. 2019, 279, 107664. [Google Scholar] [CrossRef]
- Grace, J. Temperature as a Determinant of Plant Productivity. Symp. Soc. Exp. Biol. 1988, 42, 91–107. [Google Scholar] [PubMed]
- Goulart, H.M.D.; van der Wiel, K.; Folberth, C.; Balkovic, J.; van den Hurk, B. Storylines of Weather-Induced Crop Failure Events under Climate Change. Earth Syst. Dyn. 2021, 12, 1503–1527. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, S.; Liu, D.; Piao, S. Susceptibility of Vegetation Low-Growth to Climate Extremes on Tibetan Plateau. Agric For Meteorol. 2023, 331, 109323. [Google Scholar] [CrossRef]
- Feng, S.; Hao, Z.; Zhang, X.; Hao, F. Changes in Climate-Crop Yield Relationships Affect Risks of Crop Yield Reduction. Agric. For. Meteorol. 2021, 304–305, 108401. [Google Scholar] [CrossRef]
- Powell, J.P.; Reinhard, S. Measuring the Effects of Extreme Weather Events on Yields. Weather Clim. Extrem. 2015, 12, 69–79. [Google Scholar] [CrossRef]
- Shayanmehr, S.; Rastegari Henneberry, S.; Sabouhi Sabouni, M.; Shahnoushi Foroushani, N. Climate Change and Sustainability of Crop Yield in Dry Regions Food Insecurity. Sustainability 2020, 12, 9890. [Google Scholar] [CrossRef]
- Schmitt, J.; Offermann, F.; Söder, M.; Frühauf, C.; Finger, R. Extreme Weather Events Cause Significant Crop Yield Losses at the Farm Level in German Agriculture. Food Policy 2022, 112, 102359. [Google Scholar] [CrossRef]
- Zipper, S.C.; Qiu, J.; Kucharik, C.J. Drought Effects on US Maize and Soybean Production: Spatiotemporal Patterns and Historical Changes. Environ. Res. Lett. 2016, 11, 094021. [Google Scholar] [CrossRef]
- Toreti, A.; Cronie, O.; Zampieri, M. Concurrent Climate Extremes in the Key Wheat Producing Regions of the World. Sci Rep 2019, 9, 5493. [Google Scholar] [CrossRef]
- Lobell, D.B.; Cahill, K.N.; Field, C.B. Weather-Based Yield Forecasts Developed for 12 California Crops. Calif. Agric. 2006, 60, 211–215. [Google Scholar] [CrossRef]
- Nassar, L.; Okwuchi, I.E.; Saad, M.; Karray, F.; Ponnambalam, K.; Agrawal, P. Prediction of Strawberry Yield and Farm Price Utilizing Deep Learning. In Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN), Glasgow, UK, 19–24 July 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
- Newlands, N.K.; Zamar, D.S.; Kouadio, L.A.; Zhang, Y.; Chipanshi, A.; Potgieter, A.; Toure, S.; Hill, H.S.J. An Integrated, Probabilistic Model for Improved Seasonal Forecasting of Agricultural Crop Yield under Environmental Uncertainty. Front. Environ. Sci. 2014, 2, 17. [Google Scholar] [CrossRef]
- California Department of Food and Agriculture (CDFA)—Statistics. Available online: https://www.cdfa.ca.gov/statistics/ (accessed on 9 October 2022).
- Li, H.; Li, T.; Gordon, R.J.; Asiedu, S.K.; Hu, K. Strawberry Plant Fruiting Efficiency and Its Correlation with Solar Irradiance, Temperature and Reflectance Water Index Variation. Environ. Exp. Bot. 2010, 68, 165–174. [Google Scholar] [CrossRef]
- Palencia, P.; Martínez, F.; Medina, J.J.; López-Medina, J. Strawberry Yield Efficiency and Its Correlation with Temperature and Solar Radiation. Hortic. Bras. 2013, 31, 93–99. [Google Scholar] [CrossRef][Green Version]
- Waister, P.D. Wind as a Limitation on the Growth and Yield of Strawberries. J. Hortic. Sci. 1972, 47, 411–418. [Google Scholar] [CrossRef]
- Casierra-Posada, F.; Peña-Olmos, J.E.; Ulrichs, C. Basic Growth Analysis in Strawberry Plants (Fragaria sp.) Exposed to Different Radiation Environments. Agron. Colomb. 2012, 30, 25–33. [Google Scholar]
- Ganmore-Neumann, R.; Kafkafi, U. The Effect of Root Temperature and Nitrate/Ammonium Ratio on Straw-berry Plants. II. Nitrogen Uptake, Mineral Ions, and Carboxylate Concentrations. Agron J. 1985, 77, 835–840. [Google Scholar] [CrossRef]
- Heide, O.M. Photoperiod and Temperature Interactions in Growth and Flowering of Strawberry. Physiol. Plant. 1977, 40, 21–26. [Google Scholar] [CrossRef]
- Webber, H.; Ewert, F.; Olesen, J.E.; Müller, C.; Fronzek, S.; Ruane, A.C.; Bourgault, M.; Martre, P.; Ababaei, B.; Bindi, M.; et al. Diverging Importance of Drought Stress for Maize and Winter Wheat in Europe. Nat. Commun. 2018, 9, 4249. [Google Scholar] [CrossRef] [PubMed]
- Asseng, S.; Foster, I.; Turner, N.C. The Impact of Temperature Variability on Wheat Yields. Glob. Chang. Biol. 2011, 17, 997–1012. [Google Scholar] [CrossRef]
- Zabel, F.; Müller, C.; Elliott, J.; Minoli, S.; Jägermeyr, J.; Schneider, J.M.; Franke, J.A.; Moyer, E.; Dury, M.; Francois, L.; et al. Large Potential for Crop Production Adaptation Depends on Available Future Varieties. Glob. Chang. Biol. 2021, 27, 3870–3882. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Zhang, T.Q.; Tan, C.S.; Xue, L.; Bukovsky, M.; Qi, Z.M. Modeling Impacts of Climate Change on Crop Yield and Phosphorus Loss in a Subsurface Drained Field of Lake Erie Region, Canada. Agric. Syst. 2021, 190, 103110. [Google Scholar] [CrossRef]
- Eyshi Rezaei, E.; Webber, H.; Gaiser, T.; Naab, J.; Ewert, F. Heat Stress in Cereals: Mechanisms and Modelling. Eur. J. Agron. 2015, 64, 98–113. [Google Scholar] [CrossRef]
- United States Department of Agriculture. National Agricultural Statistics Service. Available online: https://www.nass.usda.gov/ (accessed on 9 April 2024).
- Hanson, B.; Bendixen, W. Drip Irrigation Evaluated in Santa Maria Valley Strawberries. Calif. Agric. 2004, 58, 48–53. [Google Scholar] [CrossRef][Green Version]
- The California Strawberry Commission. Available online: https://www.calstrawberry.com/en-us/ (accessed on 9 January 2022).
- The California Irrigation Management Information System. Available online: http://www.cimis.water.ca.gov/ (accessed on 10 January 2022).
- Santa Maria Climate. Available online: https://en.climate-data.org/north-america/united-states-of-america/california/santa-maria-1488/ (accessed on 7 June 2022).
- Sklar, A. Fonctions de Repartition à n Dimensionls et Leurs Marges; Publications de l’Institut Statistique de l’Université de Paris: Paris, France, 1959; pp. 229–231. [Google Scholar]
- Ponnambalam, K.; Seifi, A.; Vlach, J. Yield Optimization with Correlated Design Parameters and Non-Symmetrical Marginal Distributions. In Proceedings of the 2003 International Symposium on Circuits and Systems, ISCAS ’03, Bangkok, Thailand, 25–28 May 2003; IEEE: Piscataway, NJ, USA, 2020; Volume 4, pp. IV-736–IV-739. [Google Scholar]
- Hofert, M.; Kojadinovic, I.; Machler, M.; Yan, J. Elements of Copula Modeling with R; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 9783319896342. [Google Scholar]
- Nelson, R.B. An Introduction to Copulas, 2nd ed.; Bickel, P., Diggle, P., Fienberg, S., Gather, U., Olkin, I., Zeger, S., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 13:978-0387-28659-4. [Google Scholar]
- Zhang, L.; Singh, V.P. Copulas and Their Applications in Water Resources Engineering; Cambridge University Press: Cambridge, UK, 2019; ISBN 9781108565103. [Google Scholar]
- Latif, S.; Mustafa, F. Bivariate Flood Distribution Analysis under Parametric Copula Framework: A Case Study for Kelantan River Basin in Malaysia. Acta Geophys. 2020, 68, 821–859. [Google Scholar] [CrossRef]
- Roch, O.; Alegre, A. Testing the Bivariate Distribution of Daily Equity Returns Using Copulas. An Application to the Spanish Stock Market. Comput. Stat. Data Anal. 2006, 51, 1312–1329. [Google Scholar] [CrossRef]
- Vaz de Melo Mendes, B.; Mendes Semeraro, M.; Câmara Leal, R.P. Pair-Copulas Modeling in Finance. Financ. Mark. Portf. Manag. 2010, 24, 193–213. [Google Scholar] [CrossRef]
- Righi, M.B.; Ceretta, P.S. Analyzing the Dependence Structure of Various Sectors in the Brazilian Market: A Pair Copula Construction Approach. Econ. Model 2013, 35, 199–206. [Google Scholar] [CrossRef]
- Hu, L. Dependence Patterns Across Financial Markets: A Mixed Copula Approach. Appl. Financ. Econ. 2006, 16, 717–729. [Google Scholar] [CrossRef]
- Okhrin, O.; Ristig, A.; Xu, Y.-F. Copulae in High Dimensions: An Introduction. In Applied Quantitative Finance; Härdle, W., Chen, C.H., Overbeck, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783662544860. [Google Scholar]
- Zhang, M.; Bedford, T. Vine Copula Approximation: A Generic Method for Coping with Conditional Dependence. Stat. Comput. 2018, 28, 219–237. [Google Scholar] [CrossRef]
- Joe, H. Multivariate Models and Multivariate Dependence Concepts; Chapman and Hall/CRC: Boca Raton, FL, USA, 1997; ISBN 9780367803896. [Google Scholar]
- Nazir, H.M.; Hussain, I.; Faisal, M.; Mohamd Shoukry, A.; Abdel Wahab Sharkawy, M.; Fawzi Al-Deek, F.; Ismail, M. Dependence Structure Analysis of Multisite River Inflow Data Using Vine Copula-CEEMDAN Based Hybrid Model. PeerJ 2020, 8, e10285. [Google Scholar] [CrossRef] [PubMed]
- Spanhel, F.; Kurz, M.S. Simplified Vine Copula Models: Approximations Based on the Simplifying Assumption. Electron. J. Stat. 2019, 13, 1254–1291. [Google Scholar] [CrossRef]
- Latif, S.; Mustafa, F. Parametric Vine Copula Construction for Flood Analysis for Kelantan River Basin in Malaysia. Civ. Eng. J. 2020, 6, 1470–1491. [Google Scholar] [CrossRef]
- El Hannoun, W.; el Adlouni, S.-E.; Zoglat, A. Vine-Copula-Based Quantile Regression for Cascade Reservoirs Management. Water 2021, 13, 964. [Google Scholar] [CrossRef]
- Xu, P.; Wang, D.; Wang, Y.; Singh, V.P. A Stepwise and Dynamic C-Vine Copula–Based Approach for Nonstationary Monthly Streamflow Forecasts. J. Hydrol. Eng. 2022, 27, 04021043. [Google Scholar] [CrossRef]
- Chen, L.; Singh, V.P.; Shenglian, G.; Hao, Z.; Li, T. Flood Coincidence Risk Analysis Using Multivariate Copula Functions. J. Hydrol. Eng. 2012, 17, 742–755. [Google Scholar] [CrossRef]
- Bedford, T.; Cooke, R.M. Vines: A New Graphical Model for Dependent Random Variables. Ann. Stat. 2002, 30, 1031–1068. [Google Scholar] [CrossRef]
- Gräler, B.; van den Berg, M.J.; Vandenberghe, S.; Petroselli, A.; Grimaldi, S.; de Baets, B.; Verhoest, N.E.C. Multivariate Return Periods in Hydrology: A Critical and Practical Review Focusing on Synthetic Design Hydrograph Estimation. Hydrol. Earth Syst. Sci. 2013, 17, 1281–1296. [Google Scholar] [CrossRef]
- Aas, K.; Czado, C.; Frigessi, A.; Bakken, H. Pair-Copula Constructions of Multiple Dependence. Insur. Math. Econ. 2009, 44, 182–198. [Google Scholar] [CrossRef]
- Dißmann, J.; Brechmann, E.C.; Czado, C.; Kurowicka, D. Selecting and Estimating Regular Vine Copulae and Application to Financial Returns. Comput. Stat. Data Anal. 2013, 59, 52–69. [Google Scholar] [CrossRef]
- Nagler, T.; Schepsmeier, U.; Stoeber, J.; Brechmann, E.C.; Graeler, B.; Erhardt, T. VineCopula: Statistical Inference of Vine Copulas. Available online: https://github.com/tnagler/VineCopula (accessed on 11 January 2022).
- Rigby, R.; Stasinopoulos, M.; Heller, G.; De Bastiani, F. Distributions for Modelling Location, Scale and Shape: Using GAMLSS in R; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Stasinopoulos, D.M.; Rigby, R.A. Generalized Additive Models for Location Scale and Shape (GAMLSS) in R. J. Stat. Softw. 2007, 23, 1–46. [Google Scholar] [CrossRef]
- Jane, R.; Dalla Valle, L.; Simmonds, D.; Raby, A. A Copula-Based Approach for the Estimation of Wave Height Records Through Spatial Correlation. Coast. Eng. 2016, 117, 1–18. [Google Scholar] [CrossRef]
- Eschenburg, P. Properties of Extreme-Value Copulas; Universitat Munchen: München, Germany, 2013. [Google Scholar]
- Tawn, J.A. Bivariate Extreme Value Theory: Models and Estimation. Biometrika 1988, 75, 397–415. [Google Scholar] [CrossRef]
| Statistics | Max Yield (Pounds/Acre) | Min Yield (Pounds/Acre) | Max Temp Anomaly (°F) |
|---|---|---|---|
| Min. | 57.94 | 1 | −11.9 |
| 1st Qu. | 128.5 | 17.72 | −2.6 |
| Median | 185 | 73.74 | 4.5 |
| Mean | 245.66 | 86.21 | 5.839 |
| 3rd Qu | 327.67 | 123.15 | 13.85 |
| Max. | 686 | 356.32 | 25.9 |
| Events | Probability of Occurrence | Remarks |
|---|---|---|
| Std. Ymax , Std. Ymin | 0.004 | Yield loss |
| Std. Ymax , Std. Ymin | 0.0001 | Moderate or high yield loss |
| Std. Ymax , Std. Ymin | 0.25 × 10−6 | High yield loss |
| TA TA | 0.036 | Temperature anomaly is between the range of 1 °F and 2 °F |
| TA TA | 0.042 | Temperature anomaly is between the range of 2 °F and 3 °F |
| TA | 0.61 | Temperature anomaly greater than 3 °F |
| Variables | Std. Max Yield | Std. Min Yield | Temperature Anomaly | Sum |
|---|---|---|---|---|
| Standardised maximum yield | 1 | 0.55 | −0.29 | 1.84 |
| Standardised minimum yield | 0.55 | 1 | −0.417 | 1.967 |
| Temperature anomaly | −0.29 | −0.417 | 1 | 1.707 |
| No | Events | Conditional Probability of Occurrence of Events Given the Following TA (°F) | Remarks | ||
|---|---|---|---|---|---|
| 1 | |TA | 0.584 | 0.56 | 0.8 | Yield loss |
| 2 | |TA | 0.039 | 0.037 | 0.66 | Moderate or high yield loss |
| 3 | |TA | 0.0006 | 0.0005 | 0.63 | High yield loss |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unnikrishnan, P.; Ponnambalam, K.; Karray, F. Influence of Regional Temperature Anomalies on Strawberry Yield: A Study Using Multivariate Copula Analysis. Sustainability 2024, 16, 3523. https://doi.org/10.3390/su16093523
Unnikrishnan P, Ponnambalam K, Karray F. Influence of Regional Temperature Anomalies on Strawberry Yield: A Study Using Multivariate Copula Analysis. Sustainability. 2024; 16(9):3523. https://doi.org/10.3390/su16093523
Chicago/Turabian StyleUnnikrishnan, Poornima, Kumaraswamy Ponnambalam, and Fakhri Karray. 2024. "Influence of Regional Temperature Anomalies on Strawberry Yield: A Study Using Multivariate Copula Analysis" Sustainability 16, no. 9: 3523. https://doi.org/10.3390/su16093523
APA StyleUnnikrishnan, P., Ponnambalam, K., & Karray, F. (2024). Influence of Regional Temperature Anomalies on Strawberry Yield: A Study Using Multivariate Copula Analysis. Sustainability, 16(9), 3523. https://doi.org/10.3390/su16093523








