Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters
Abstract
1. Introduction
2. Vibration Control Mechanisms
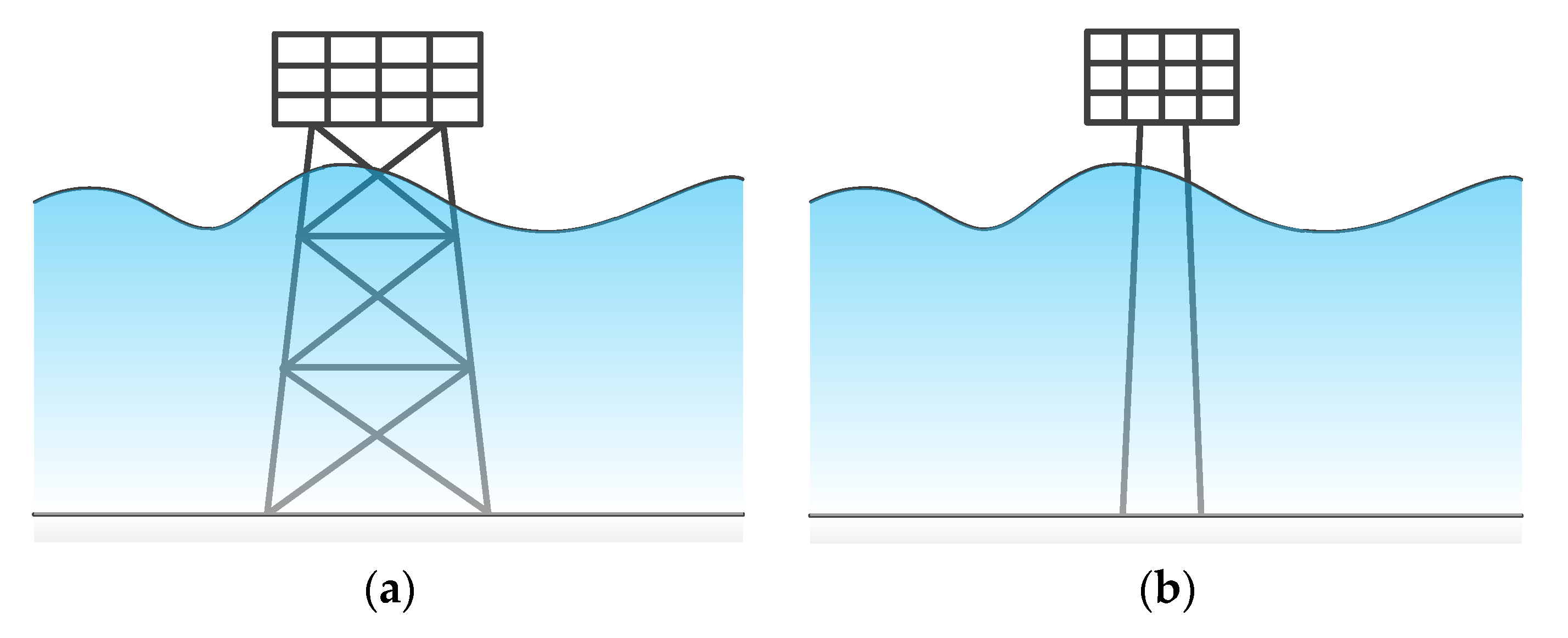
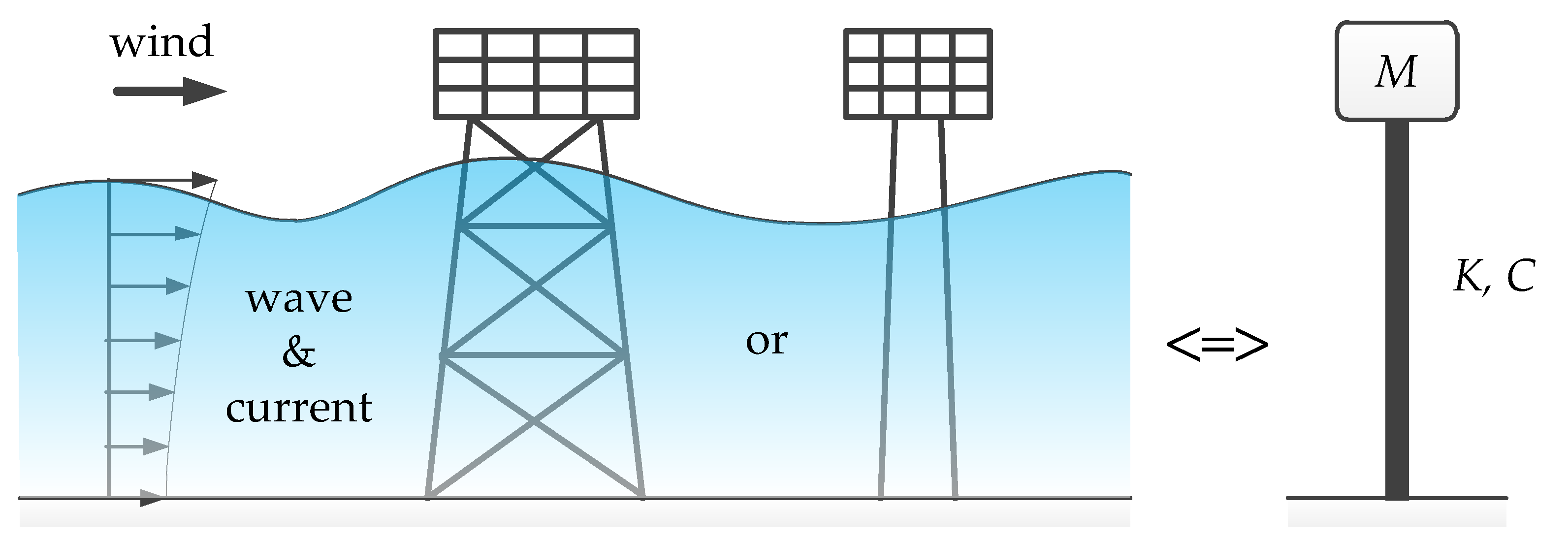
2.1. Primary Offshore Substation Structure without Control
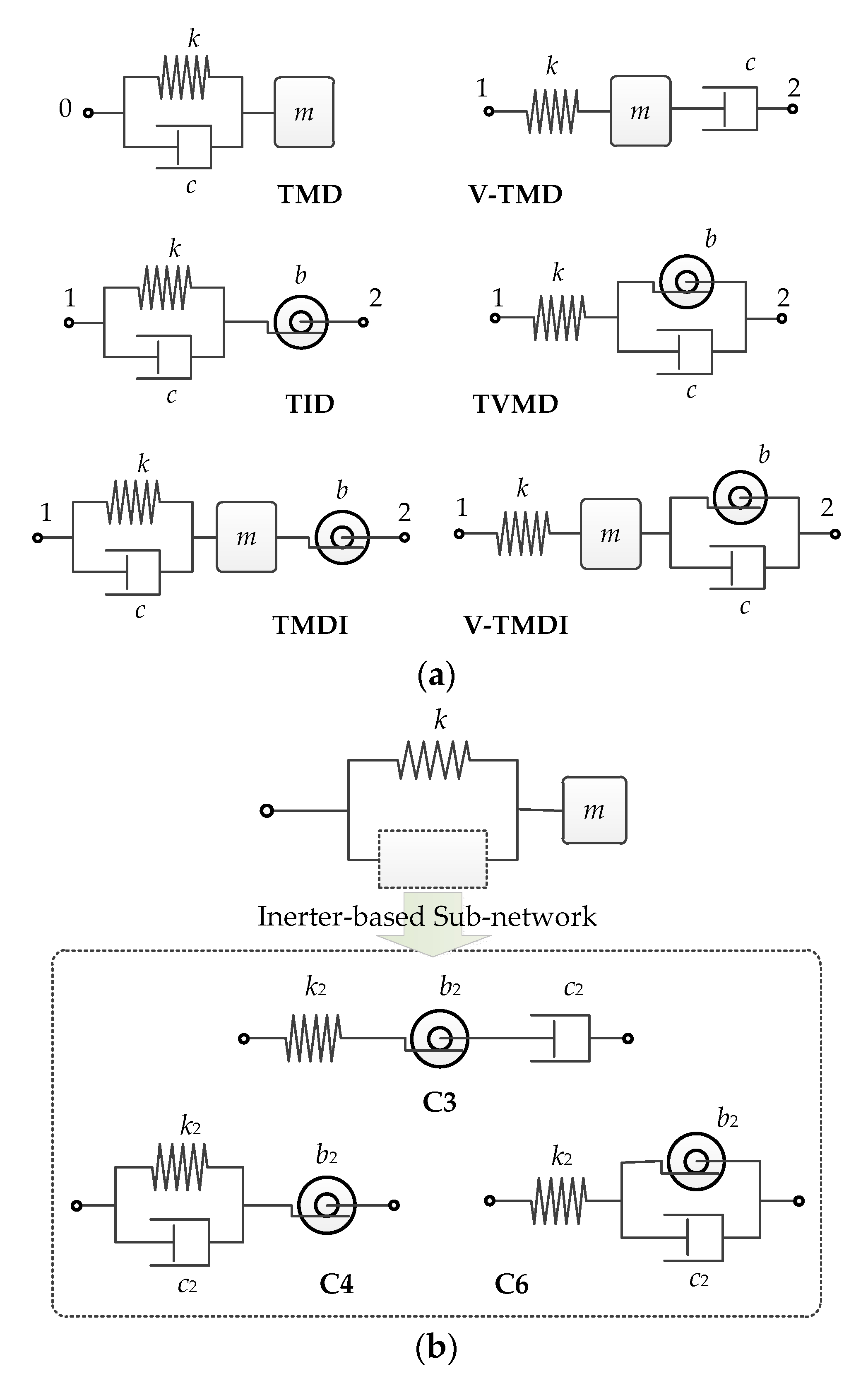
2.2. Vibration Control with Conventional TMD
2.3. Single-Tuned Vibration Control Devices
2.3.1. Conventional Type (TMDI)
2.3.2. Variant Type (V-TMDI)
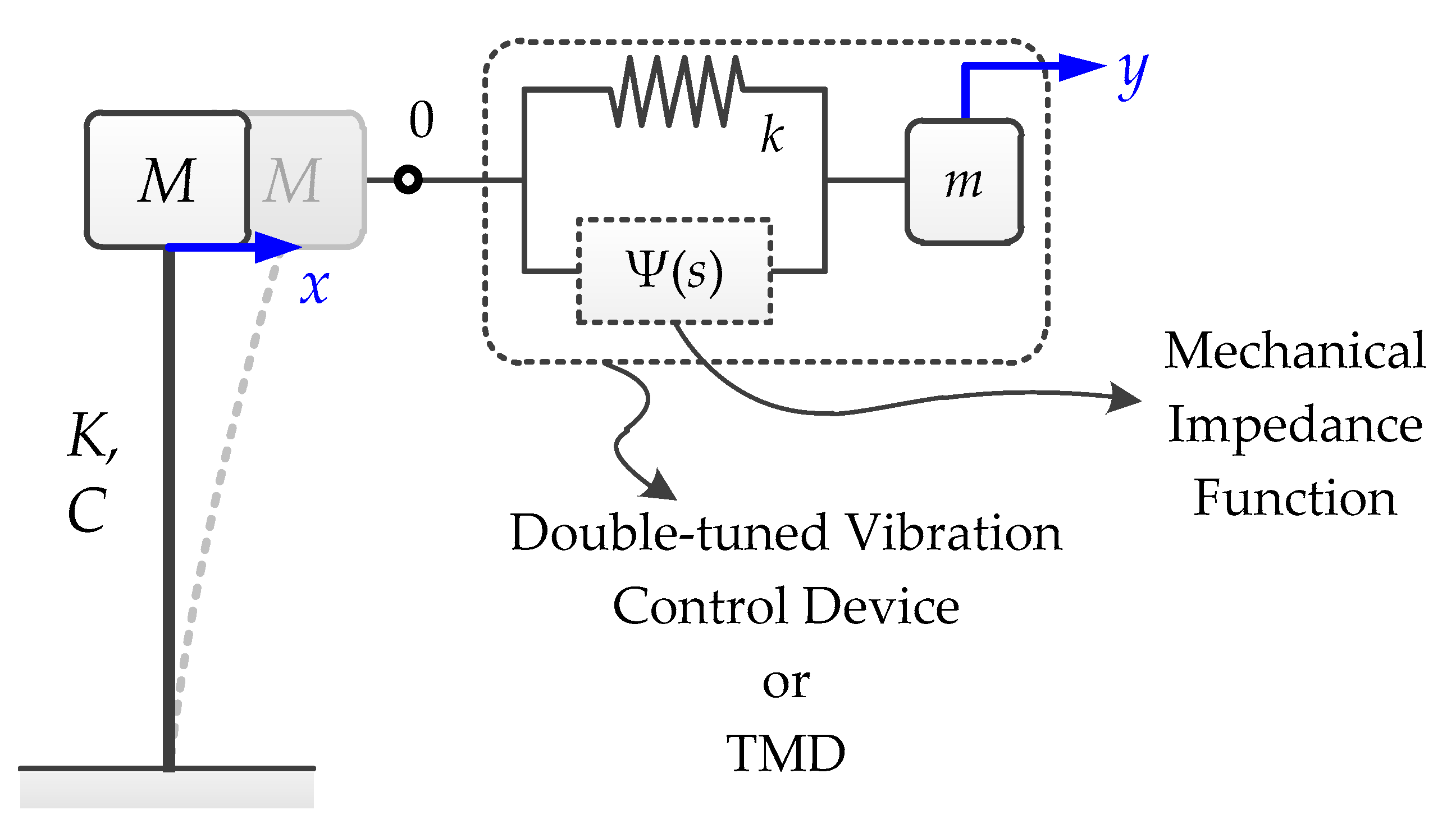
2.4. Double-Tuned Vibration Control Devices
2.4.1. C6 Type (RIDTMD)
2.4.2. C4 Type
2.4.3. C3 Type
2.4.4. Mechanical Impedance Function
3. Determination of Optimal Parameters of Vibration Control Devices
3.1. Parametric Optimization Method
3.1.1. Dynamic Amplification Function
3.1.2. H-Norm-Based Optimization
3.2. Single-Tuned Vibration Control Devices
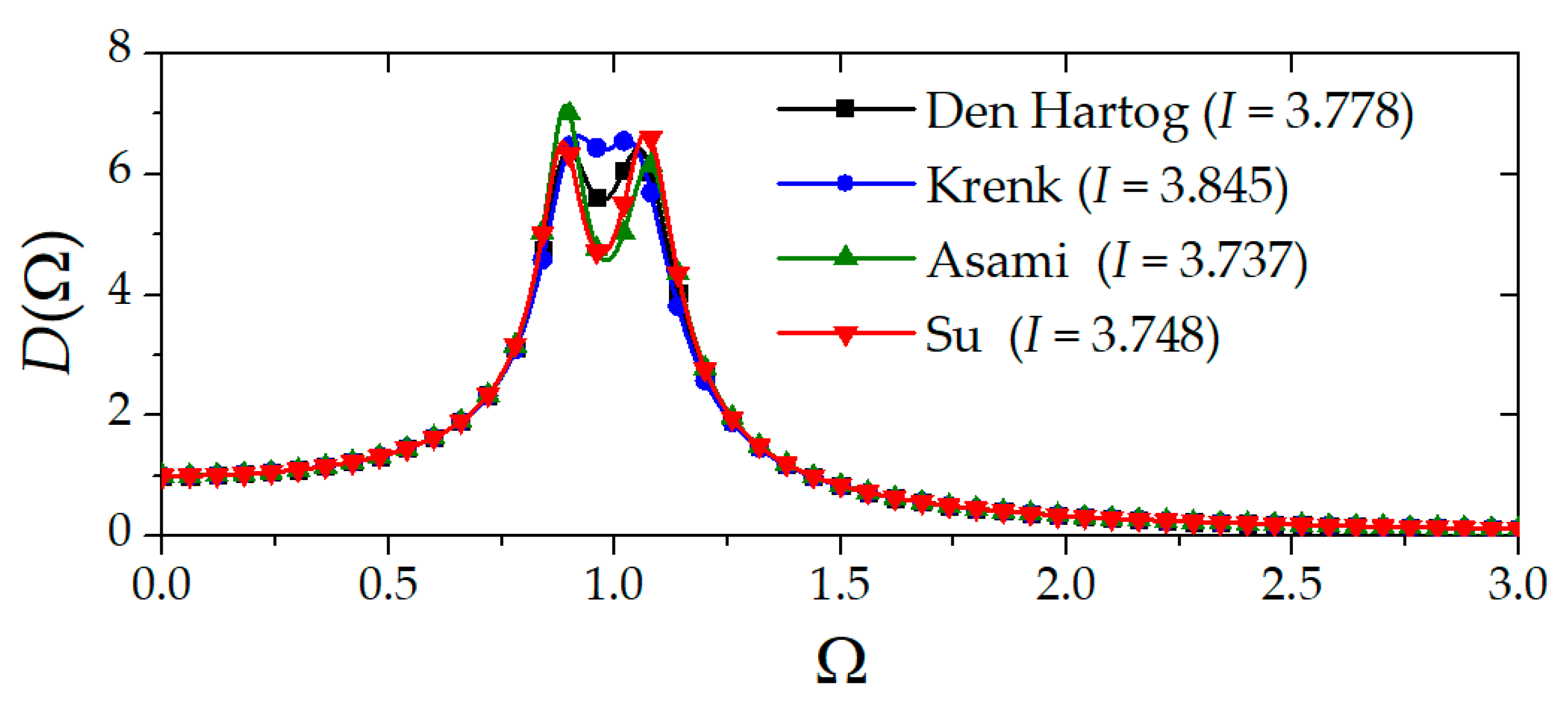
3.2.1. Conventional TMD
3.2.2. Ground Connected Single-Tuned Vibration Control Devices
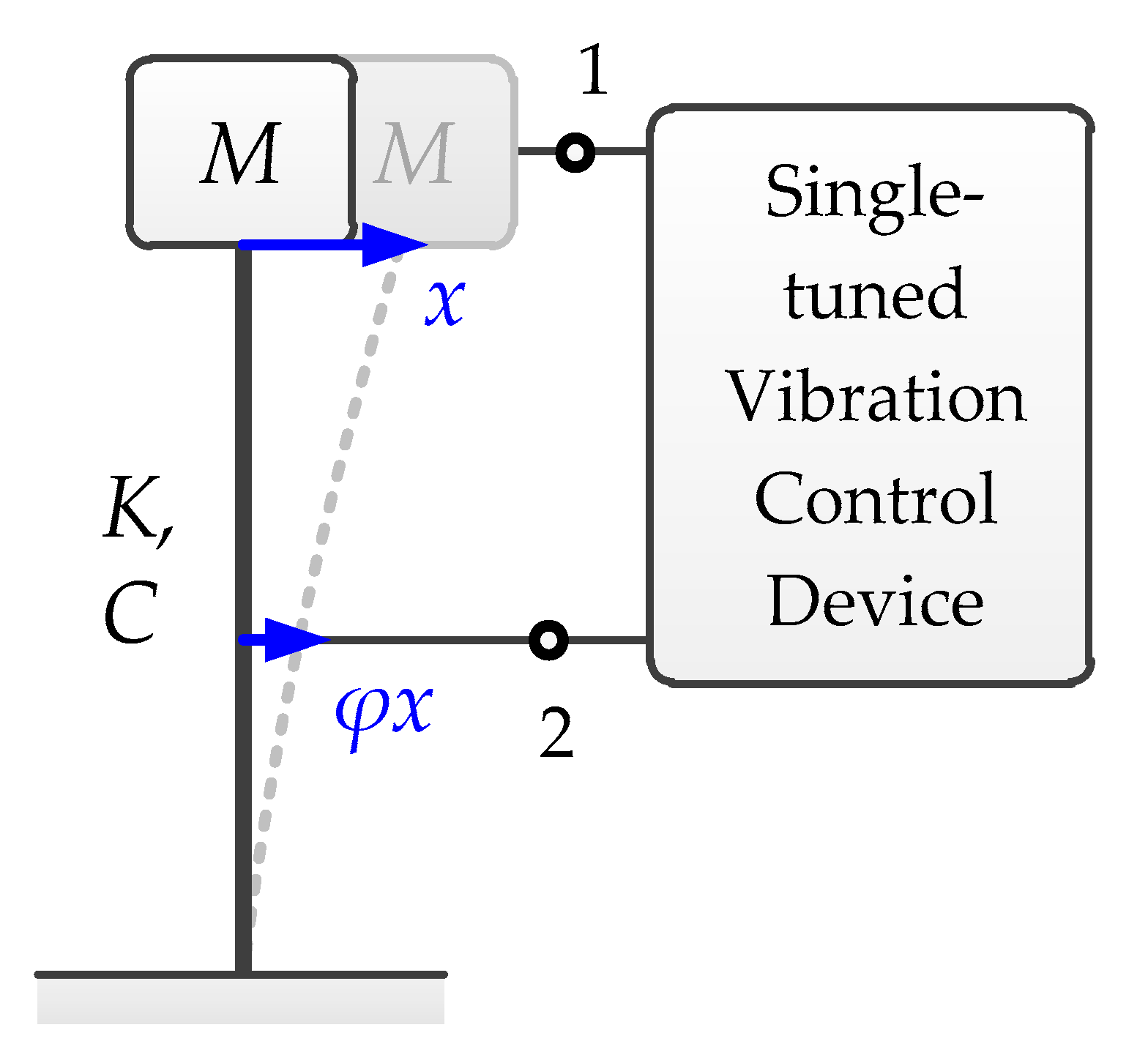
3.2.3. Equivalent Mass Ratio Approach to Address the Installation Location
3.3. Double-Tuned Vibration Control Devices
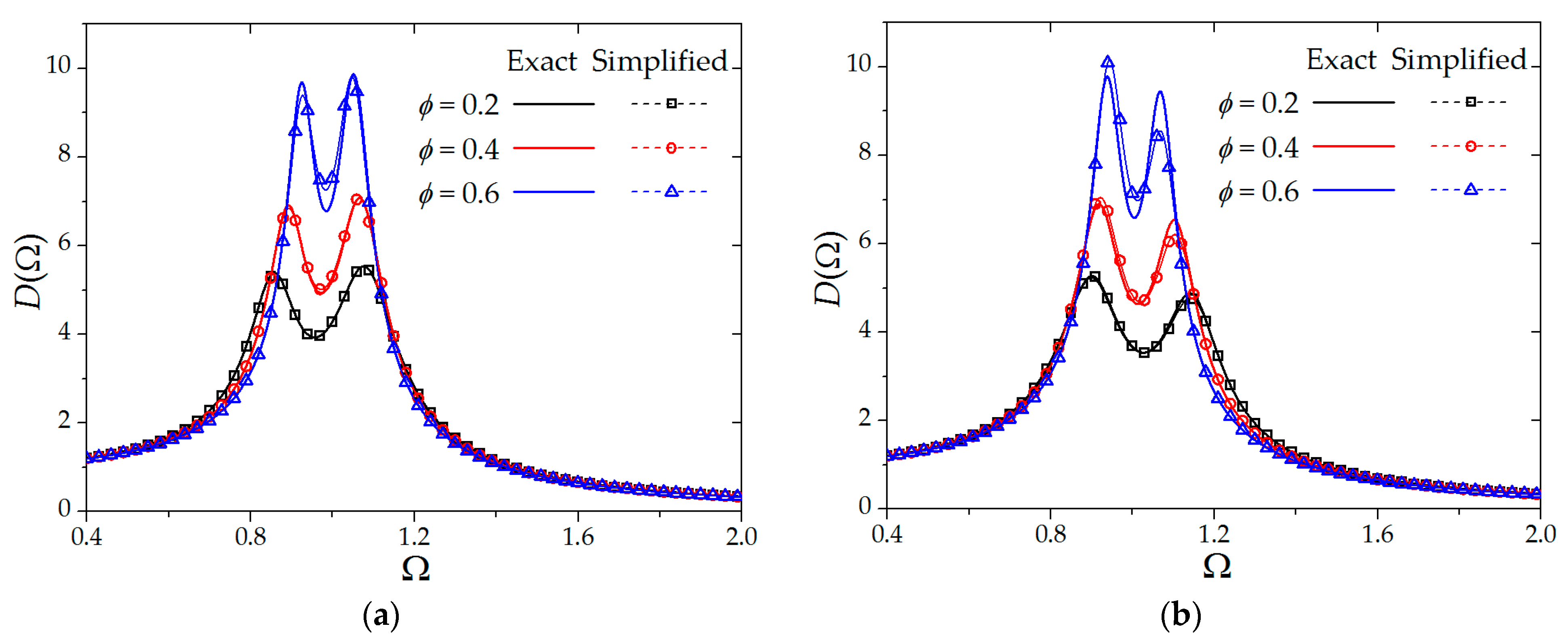
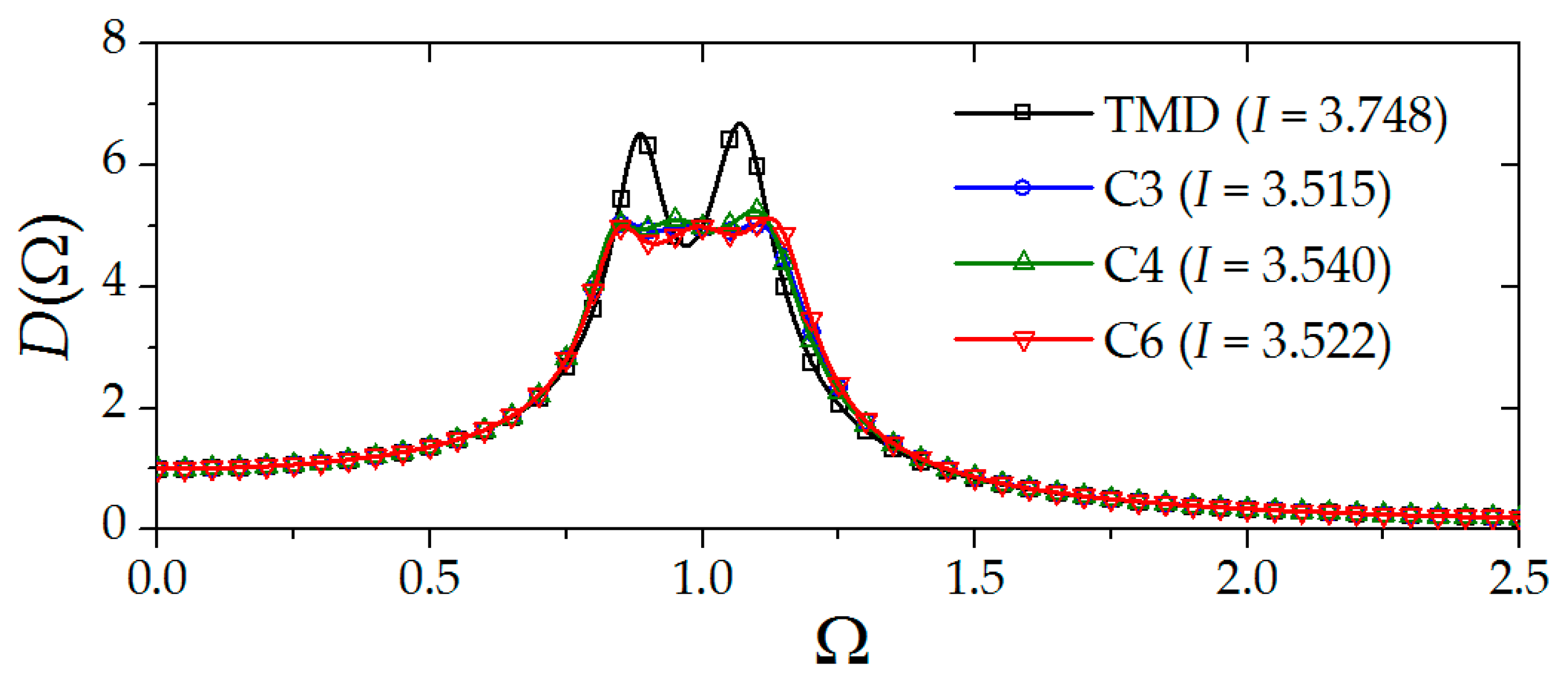
3.3.1. Optimal Parameters
3.3.2. Equivalent Mass Ratio
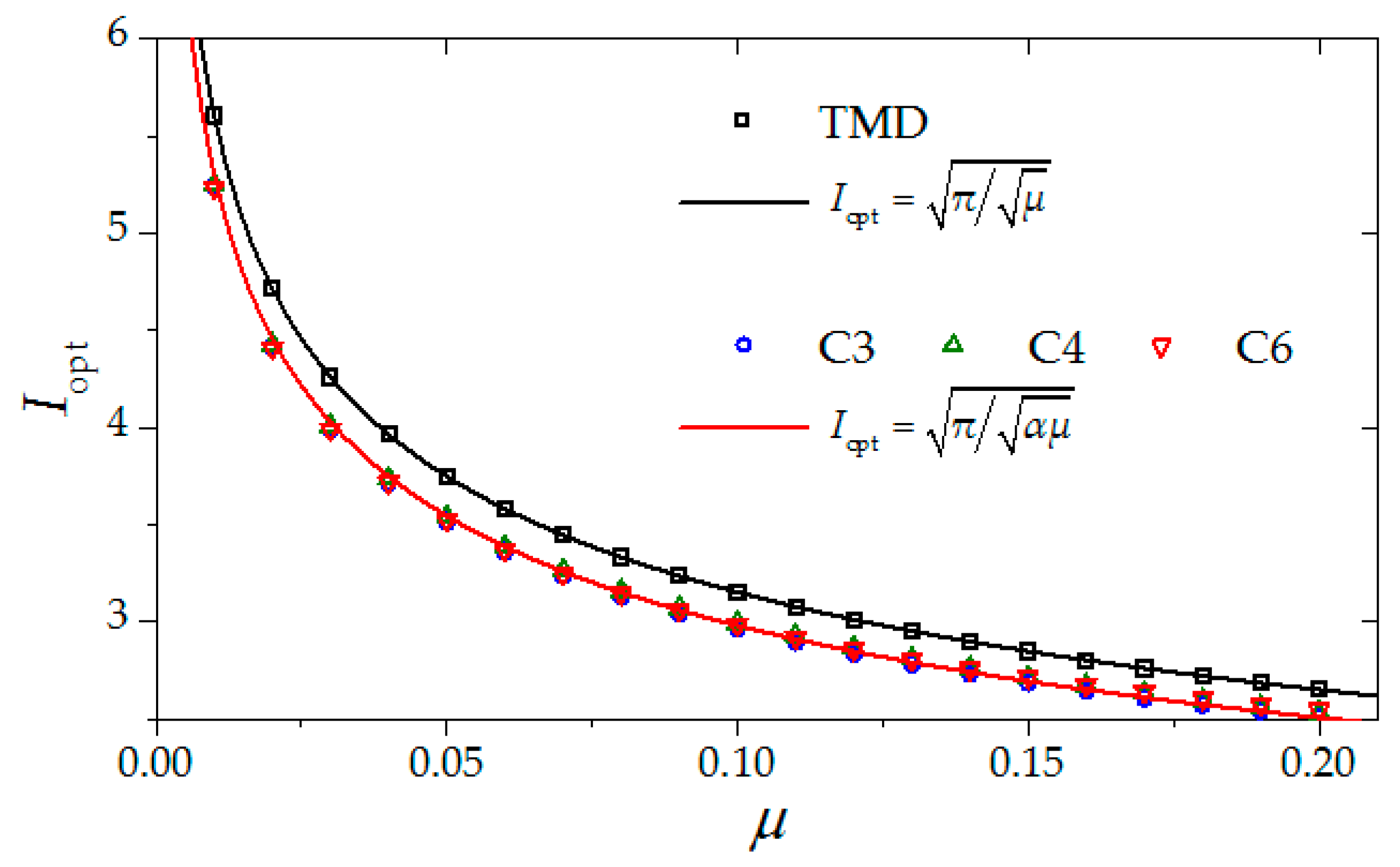
- In order to further quantify the lightweight vibration control performance, with the formant of the conventional TMD in Equation (27), an equivalent mass ratio for double-tuned vibration control devices is defined as μeq = αμ, with α being a mass magnification effect factor. The factor α is determined by equalizing the optimal H2-norms of double-tuned vibration control devices with those of the conventional TMD, as per Equation (36), via a least square technique.
- The optimal H2-norms of double-tuned vibration control devices and the conventional TMD are plotted in Figure 10. It is noticed that Equation (36) can fit well with the data, indicating the effectiveness of the equivalent mass approach. The resulting factor α is determined as 1.25, which indicates that the optimally designed double-tuned vibration control device may save 25% of the mass compared to a conventional TMD.
4. Vibration Control on a Practical Offshore Substation
4.1. Vibration Response Analysis
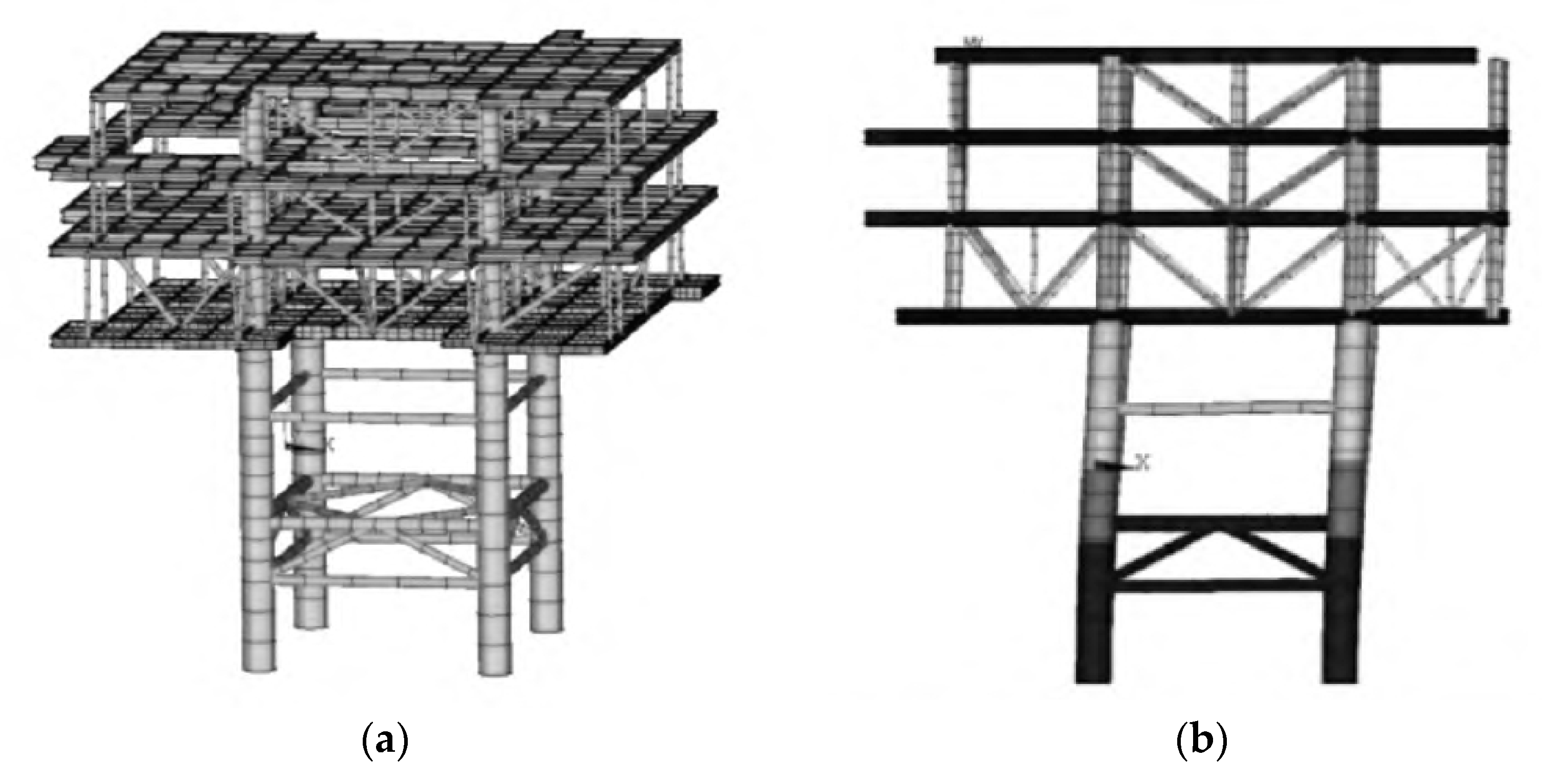
4.1.1. Finite Element Model of the Offshore Substation
4.1.2. Environmental Excitations
- (1)
- Wind load
- (2)
- Wave and current loads
4.2. Vibration Control Performance
4.2.1. Vibration Control Devices
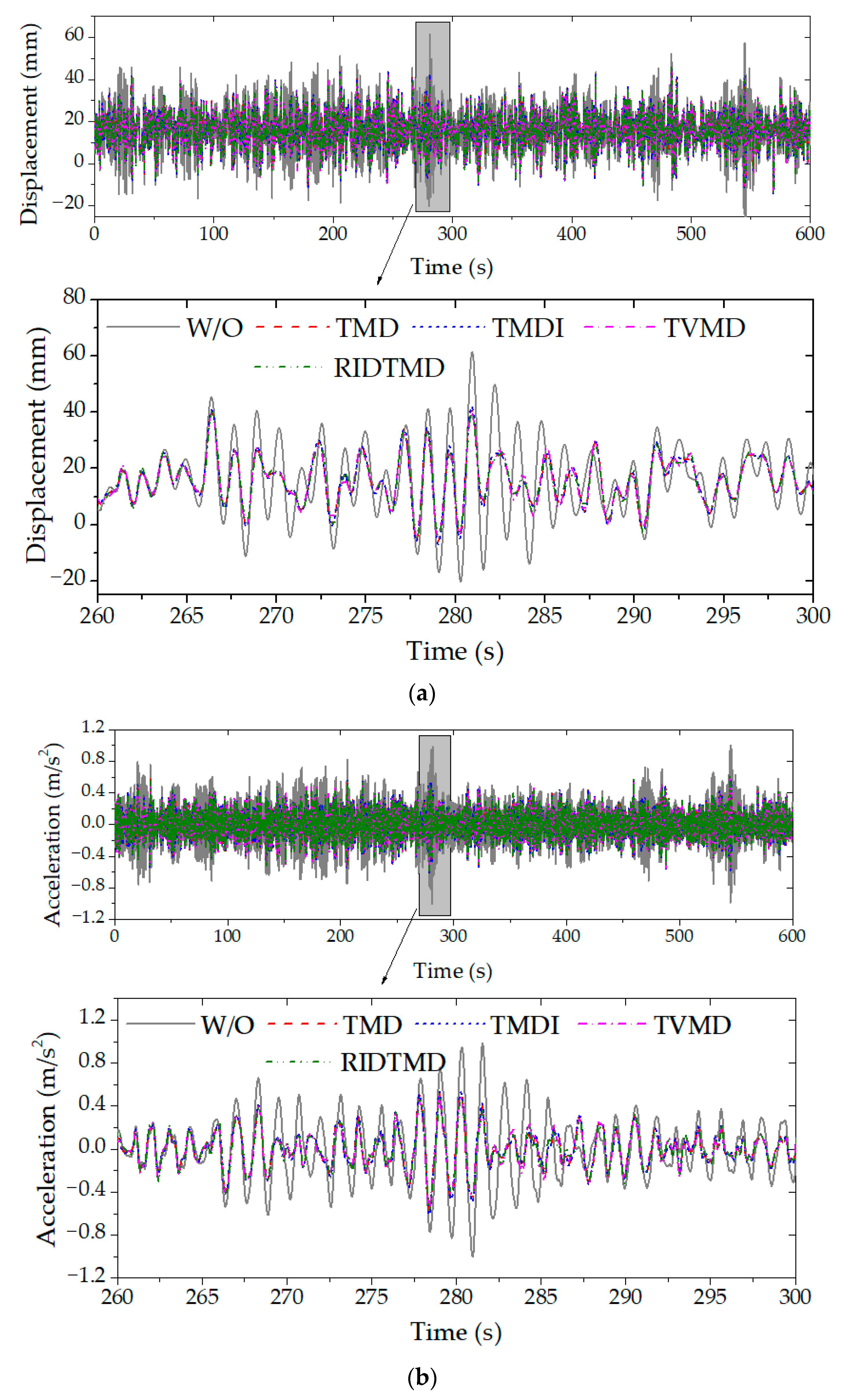
4.2.2. Vibration Responses and Control Rates
4.3. Comparisons of Different Vibration Control Devices
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Faraggiana, E.; Ghigo, A.; Sirigu, M.; Petracca, E.; Giorgi, G.; Mattiazzo, G.; Bracco, G. Optimal floating offshore wind farms for Mediterranean islands. Renew. Energy 2024, 221, 119785. [Google Scholar] [CrossRef]
- Wang, H.J.; Liu, C.; Guo, Y.H.; Zhao, Y.; Li, X.Y.; Lian, J.J. Experimental and numerical research on the wet-towing of wide-shallow bucket jacket foundation for offshore substation. Ocean Eng. 2023, 275, 114126. [Google Scholar] [CrossRef]
- Elobeid, M.; Pillai, A.C.; Tao, L.; Ingram, D.; Hanssen, J.E.; Mayorga, P. Implications of wave–current interaction on the dynamic responses of a floating offshore wind turbine. Ocean Eng. 2024, 292, 116571. [Google Scholar] [CrossRef]
- Townsend, J.F.; Xu, G.J.; Jin, Y.J.; Yu, E.B.; Wei, H.; Han, Y. On the development of a generalized atmospheric boundary layer velocity profile for offshore engineering applications considering wind–wave interaction. Ocean Eng. 2023, 286, 115621. [Google Scholar] [CrossRef]
- Kikuchi, Y.; Ishihara, T. Assessment of capital expenditure for fixed-bottom offshore wind farms using probabilistic engineering cost model. Appl. Energy 2023, 341, 120912. [Google Scholar] [CrossRef]
- Sykes, V.; Collu, M.; Coraddu, A. A Review and Analysis of the Uncertainty Within Cost Models for Floating Offshore Wind Farms. Renew. Sustain. Energy Rev. 2023, 186, 113634. [Google Scholar] [CrossRef]
- Danovaro, R.; Bianchelli, S.; Brambilla, P.; Brussa, G.; Corinaldesi, C.; Del Borghi, A.; Dell’Anno, A.; Fraschetti, S.; Greco, S.; Grosso, M.; et al. Making eco-sustainable floating offshore wind farms: Siting, mitigations, and compensations. Renew. Sustain. Energy Rev. 2024, 197, 114386. [Google Scholar] [CrossRef]
- Machado, M.R.; Dutkiewicz, M.; Colherinhas, G.B. Metamaterial-based vibration control for offshore wind turbines operating under multiple hazard excitation forces. Renew. Energy 2024, 223, 120056. [Google Scholar] [CrossRef]
- Rezaei, F.; Contestabile, P.; Vicinanza, D.; Azzellino, A. Towards understanding environmental and cumulative impacts of floating wind farms: Lessons learned from the fixed-bottom offshore wind farms. Ocean Coast. Manag. 2023, 243, 106772. [Google Scholar] [CrossRef]
- Díaz-Motta, A.; Díaz-González, F.; Villa-Arrieta, M. Energy sustainability assessment of offshore wind-powered ammonia. J. Clean. Prod. 2023, 420, 138419. [Google Scholar] [CrossRef]
- Ormondroyd, J.; Den Hartog, J.P. The theory of the dynamic vibration absorber. Trans. ASME 1928, 50, 9–22. [Google Scholar] [CrossRef]
- Krenk, S.; Høgsberg, J. Tuned mass absorbers on damped structures under random load. Probabilistic Eng. Mech. 2008, 23, 408–415. [Google Scholar] [CrossRef]
- Asami, T.; Nishihara, O.; Baz, A.M. Analytical solutions to H∞ and H2 optimization of dynamic vibration absorbers attached to damped linear systems. J. Vib. Acoust. 2002, 124, 284–295. [Google Scholar] [CrossRef]
- Bisegna, P.; Caruso, G. Closed-form formulas for the optimal pole-based design of tuned mass dampers. J. Sound Vib. 2012, 331, 2291–2314. [Google Scholar] [CrossRef]
- Krenk, S.; Høgsberg, J. Tuned mass absorber on a flexible structure. J. Sound Vib. 2014, 333, 1577–1595. [Google Scholar] [CrossRef]
- Argenziano, M.; Faiella, D.; Carotenuto, A.R.; Mele, E.; Fraldi, M. Generalization of the Den Hartog model and rule-of-thumb formulas for optimal tuned mass dampers. J. Sound Vib. 2022, 538, 117213. [Google Scholar] [CrossRef]
- Sun, X.; Wu, H.; Wu, Y.; Su, N. Wind-induced responses and control of a Kilometer skyscraper with mass and viscous dampers. J. Build. Eng. 2021, 43, 102552. [Google Scholar] [CrossRef]
- Kaveh, A.; Javadi, S.M.; Moghanni, R.M. Optimal structural control of tall buildings using tuned mass dampers via chaotic optimization algorithm. Structures 2020, 28, 2704–2713. [Google Scholar] [CrossRef]
- Domizio, M.; Garrido, H.; Ambrosini, D. Single and multiple TMD optimization to control seismic response of nonlinear structures. Eng. Struct. 2022, 252, 113667. [Google Scholar] [CrossRef]
- Lin, Y.Y.; Cheng, C.M.; Lee, C.H. A tuned mass damper for suppressing the coupled flexural and torsional buffeting response of long-span bridges. Eng. Struct. 2000, 22, 1195–1204. [Google Scholar] [CrossRef]
- Labbafi, S.F.; Shooshtari, A.; Mohtashami, E. Optimal design of friction tuned mass damper for seismic control of an integral bridge. Structures 2023, 58, 105200. [Google Scholar] [CrossRef]
- Wang, J.W.; Liang, X.; Wang, L.Z.; Wang, B.X.; Wang, L.L. The influence of tuned mass dampers on vibration control of monopile offshore wind turbines under wind-wave loadings. Ocean Eng. 2023, 278, 114394. [Google Scholar]
- Jahangiri, V.; Sun, C.; Kong, F. Study on a 3D pounding pendulum TMD for mitigating bi-directional vibration of offshore wind turbines. Eng. Struct. 2021, 241, 112383. [Google Scholar] [CrossRef]
- Elias, S. Vibration improvement of offshore wind turbines under multiple hazards. Structures 2024, 59, 105800. [Google Scholar] [CrossRef]
- Smith, M.C. Synthesis of mechanical networks: The inerter. IEEE Trans. Autom. Control 2002, 47, 1648–1662. [Google Scholar] [CrossRef]
- Ma, R.S.; Bi, K.M.; Hao, H. Inerter-based structural vibration control: A state-of-the-art review. Eng. Struct. 2021, 243, 112655. [Google Scholar] [CrossRef]
- Sun, L.; Hong, D.; Chen, L. Cables interconnected with tuned inerter damper for vibration mitigation. Eng. Struct. 2017, 151, 57–67. [Google Scholar] [CrossRef]
- Papageorgiou, C.; Houghton, N.E.; Smith, M.C. Experimental testing and analysis of inerter devices. J. Dyn. Syst. Meas. Control 2009, 131, 101–116. [Google Scholar] [CrossRef]
- John, E.D.A.; Wagg, D.J. Design and testing of a frictionless mechanical inerter device using living-hinges. J. Frankl. Inst. 2019, 356, 7650–7668. [Google Scholar] [CrossRef]
- De Domenico, D.; Deastra, P.; Ricciardi, G.; Sims, N.D.; Wagg, D.J. Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Frankl. Inst. 2019, 356, 7626–7649. [Google Scholar] [CrossRef]
- Ikago, K.; Saito, K.; Inoue, N. Seismic control of single-degree-of-freedom structure using tuned viscous mass damper. Earthq. Eng. Struct. Dyn. 2012, 41, 453–474. [Google Scholar] [CrossRef]
- Ikago, K.; Sugimura, Y.; Saito, K.; Inoue, N. Modal response characteristics of a multiple-degree-of-freedom structure incorporated with tuned viscous mass dampers. J. Asian Arch. Build. Eng. 2012, 11, 375–382. [Google Scholar] [CrossRef]
- Zhang, R.F.; Zhao, Z.P.; Pan, C.; Ikago, K.; Xue, S.T. Damping enhancement principle of inerter system. Struct. Control Health Monit. 2020, 27, e2523. [Google Scholar] [CrossRef]
- Su, N.; Bian, J.; Peng, S.T.; Xia, Y. Impulsive resistant optimization design of tuned viscous mass damper (TVMD) based on stability maximization. Int. J. Mech. Sci. 2023, 239, 107876. [Google Scholar] [CrossRef]
- Mustapha, A.; Zhang, X.; Atroshchenko, E.; Jaroon, R. Vibration control of inerter-enhanced mega sub-controlled structure system (MSCSS) and the reliability analysis of the structure under seismic action. Eng. Struct. 2024, 241, 117508. [Google Scholar]
- Marian, L.; Giaralis, A. Optimal design of a novel tuned mass-damper-inerter (TMDI) passive vibration control configuration for stochastically support-excited structural systems. Probabilistic Eng. Mech. 2014, 38, 156–164. [Google Scholar] [CrossRef]
- Lazar, I.F.; Neild, S.A.; Wagg, D.J. Using an inerter-based device for structural vibration suppression. Earthq. Eng. Struct. Dyn. 2014, 43, 1129–1147. [Google Scholar] [CrossRef]
- Deastra, P.; Wagg, D.; Sims, N.; Akbar, M. Tuned inerter dampers with linear hysteretic damping. Earthq. Eng. Struct. Dyn. 2020, 49, 1216–1235. [Google Scholar] [CrossRef]
- Alotta, G.; Failla, G. Improved inerter-based vibration absorbers. Int. J. Mech. Sci. 2021, 192, 106087. [Google Scholar] [CrossRef]
- Su, N.; Peng, S.T.; Xia, Y. Filter-based inerter location dependence analysis approach of Tuned mass damper inerter (TMDI) and optimal design. Eng. Struct. 2022, 250, 113459. [Google Scholar] [CrossRef]
- Islam, N.U.; Jangid, R.S. Optimum parameters of tuned inerter damper for damped structures. J. Sound Vib. 2022, 537, 117218. [Google Scholar] [CrossRef]
- Fitzgerald, B.; McAuliffe, J.; Baisthakur, S.; Sarkar, S. Enhancing the reliability of floating offshore wind turbine towers subjected to misaligned wind-wave loading using tuned mass damper inerters (TMDIs). Renew. Energy 2023, 221, 522–538. [Google Scholar] [CrossRef]
- Ren, M.Z. A variant design of the dynamic vibration absorber. J. Sound Vib. 2001, 245, 762–770. [Google Scholar] [CrossRef]
- Masnata, C.; Matteo, A.D.; Adam, C.; Pirrotta, A. Smart structures through nontraditional design of Tuned Mass Damper Inerter for higher control of base isolated systems. Mech. Res. Commun. 2020, 105, 103513. [Google Scholar] [CrossRef]
- Su, N.; Bian, J.; Peng, S.T.; Xia, Y. Generic optimal design approach for inerter-based tuned mass systems. Int. J. Mech. Sci. 2022, 233, 107654. [Google Scholar] [CrossRef]
- Su, N.; Chen, Z.Q.; Xia, Y.; Bian, J. Hybrid analytical H-norm optimization approach for dynamic vibration absorbers. Int. J. Mech. Sci. 2024, 264, 108796. [Google Scholar] [CrossRef]
- Garrido, H.; Curadelli, O.; Ambrosini, D. Improvement of tuned mass damper by using rotational inertia through tuned viscous mass damper. Eng. Struct. 2013, 56, 2149–2153. [Google Scholar] [CrossRef]
- Zhang, L.; Xue, S.T.; Zhang, R.F.; Xie, L.Y.; Hao, L.F. Simplified multimode control of seismic response of high-rise chimneys using distributed tuned mass inerter systems (TMIS). Eng. Struct. 2021, 228, 111550. [Google Scholar] [CrossRef]
- Hu, Y.L.; Chen, M.Z.Q.; Shu, Z.; Huang, L.X. Analysis and optimisation for inerter-based isolators via fixed-point theory and algebraic solution. J. Sound Vib. 2015, 346, 17–36. [Google Scholar] [CrossRef]
- Barredo, E.; Blanco, A.; Colín, J.; Penagos, V.M.; Abúndez, A.; Luis, G.V.; Meza, V.; Cruz, R.H.; Mayen, J. Closed-form solutions for the optimal design of inerter-based dynamic vibration absorbers. Int. J. Mech. Sci. 2018, 144, 41–53. [Google Scholar] [CrossRef]
- Barredo, E.; Mendoza Larios, J.G.; Colín, J.; Mayen, J.; Flores-Hernandez, A.A.; Arias-Montiel, M. A novel high-performance passive non-traditional inerter-based dynamic vibration absorber. J. Sound Vib. 2020, 485, 115583. [Google Scholar] [CrossRef]
- Barredo, E.; Rojas, G.L.; May´en, J.; Flores-Hernandez, A.A. Innovative negative-stiffness inerter-based mechanical networks. Int. J. Mech. Sci. 2021, 205, 106597. [Google Scholar] [CrossRef]
- Su, N.; Peng, S.T.; Hong, N.N.; Xia, Y. Wind-induced vibration absorption using inerter-based double tuned mass dampers on slender structures. J. Build. Eng. 2022, 58, 104993. [Google Scholar] [CrossRef]
- Melaku, A.F.; Bitsuamlak, G.T. A divergence-free inflow turbulence generator using spectral representation method for large-eddy simulation of ABL flows. J. Wind. Eng. Ind. Aerodyn 2021, 212, 104580. [Google Scholar] [CrossRef]
- Mazzaretto, O.M.; Menéndez, M.; Lobeto, H. A global evaluation of the JONSWAP spectra suitability on coastal areas. Ocean Eng. 2022, 266, 112756. [Google Scholar] [CrossRef]

| Symbol | Expression | Physical Meaning |
|---|---|---|
| The natural frequency of the primary offshore substation structure. | ||
| The damping ratio of the primary offshore substation structure. | ||
| The tuning mass ratio of the vibration control device. | ||
| The tuning inertance ratio of the vibration control device. Note that for a single-tuned vibration control device, b2 = 0, whereas for a double-tuned vibration control device, b = 0. | ||
| The nominal frequency of the vibration control device. Note that for a double-tuned vibration control device, b = 0. | ||
| The tuning frequency ratio of the vibration control device. | ||
| The secondary nominal frequency of the sub-network of the double-tuned vibration control device. | ||
| The secondary tuning frequency ratio of the double-tuned vibration control device. | ||
| The nominal damping ratio of the vibration control device. Note that for a double-tuned vibration control device, b = 0. | ||
| The dimensionless Laplace complex frequency. |
| Case # | Device | Predetermined Parameter | Underdetermined Parameter |
|---|---|---|---|
| 0 | None | — | — |
| 1 | TMD | μ = 0.05 | ν = 0.9524, ζd = 0.1118 |
| 2 | TMDI | μ = 0.01, β = 0.16, φ = 0.5 | ν = 0.9524, ζd = 0.1118 |
| 3 | TVMD | β = 0.20, φ = 0.5 | ν = 1.0260, ζd = 0.1147 |
| 4 | RIDTMD | μ = 0.04 | β = 0.0046, ν = 0.9259, γ = 1.1200, ζd = 0.0234 |
| Response | Case # | Device | SD[q(t)] | Jdyn (%) | Max[q(t)] | Jtot (%) |
|---|---|---|---|---|---|---|
| Displacement (mm) | 0 | None | 11.1 | — | 61.5 | — |
| 1 | TMD | 8.4 | 24.4 | 46.2 | 24.9 | |
| 2 | TMDI | 8.5 | 24.0 | 46.3 | 24.7 | |
| 3 | TVMD | 8.1 | 26.9 | 46.2 | 24.8 | |
| 4 | RIDTMD | 8.2 | 26.7 | 46.3 | 24.8 | |
| Acceleration (m/s2) | 0 | None | 0.253 | — | 1.000 | — |
| 1 | TMD | 0.167 | 33.9 | 0.603 | 39.7 | |
| 2 | TMDI | 0.168 | 33.5 | 0.606 | 39.4 | |
| 3 | TVMD | 0.164 | 35.1 | 0.615 | 38.5 | |
| 4 | RIDTMD | 0.163 | 35.7 | 0.630 | 37.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, C.; Yu, M.; Huang, Z. Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters. Sustainability 2024, 16, 3385. https://doi.org/10.3390/su16083385
Wang Y, Xu C, Yu M, Huang Z. Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters. Sustainability. 2024; 16(8):3385. https://doi.org/10.3390/su16083385
Chicago/Turabian StyleWang, Yanfeng, Chenghao Xu, Mengze Yu, and Zhicong Huang. 2024. "Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters" Sustainability 16, no. 8: 3385. https://doi.org/10.3390/su16083385
APA StyleWang, Y., Xu, C., Yu, M., & Huang, Z. (2024). Lightweight Design of Vibration Control Devices for Offshore Substations Based on Inerters. Sustainability, 16(8), 3385. https://doi.org/10.3390/su16083385









