Zero-Energy Purification of Ambient Particulate Matter Using a Novel Double-Skin Façade System Integrated with Porous Materials

Abstract

This study introduces an innovative double-skin façade system integrated with porous materials (DSF-PM) designed to combat air pollution by purifying atmospheric particulate matter without energy consumption. By evaluating three installation strategies—vertical, horizontal, and cross placement—and examining porous materials with pore sizes of 0.5 mm, 1 mm, and 2 mm through a validated computational fluid dynamics (CFD) model, we optimized the DSF-PM system for enhanced particulate matter purification. Our findings reveal that positioning the porous material on both airflow sides with a pore size of 1 mm yields the best purification performance. The seasonal performance analysis demonstrates that the DSF-PM system achieves an average annual purification efficiency of 26.24% for particles larger than 5 µm, surpassing 20% efficiency, comparable to primary filters in global standards, with zero energy input. This passive double-skin façade system, leveraging solar-driven natural convection, emerges as a sustainable solution for ambient air purification in urban environments.

1. Introduction

Urban environmental pollution governance in China has achieved remarkable results in the past decade. However, it still faces the pollution pressure caused by atmospheric particulate matter [1]. In 2022, 25.4% of the country’s cities had excessive particulate matter in urban ambient air [2]. Compared to the emission environment of industrial pollution sources, particulate matter pollution in the external environment of buildings in urban environments is characterized by low concentrations and large space, which also leads to serious indoor particulate matter pollution [3,4,5]. So far, the use of professional purification equipment with a fan to purify particulate matter has led to good progress, but it will also lead to a significant increase in energy consumption. Therefore, the zero-energy control of particulate matter is an important subject to improve air quality and simultaneously realize the synergy of pollution reduction and carbon reduction.

Porous materials with the advantages of high porosity and high specific area (e.g., polyurethane sponges or ceramic foam material) are increasingly used as purifiers in particulate matter under low-pressure-drop conditions [6,7,8], which play an important role in the field of environmental governance, such as in filtration and in the separation of particulate matter. This is because particulate matter can be retained through mechanisms such as diffusion, interception, adsorption, and sedimentation [9] when air with particulate matter flows through porous materials. Due to the remarkable performance of porous materials in purifying particulate matter, in the context of pollution reduction and carbon reduction, researchers are investigating how to make full use of the natural flow of airflow to achieve the zero-energy purification of particulate matter. For example, Liu et al. [10] used nanofiber composite window screens to purify the particulate matter in indoor and outdoor air. Zanoletti et al. [11] synthesized silica fume and alginate into a new porous hybrid material called SUNSPACE, which can be used in an open environment to actively adsorb [12], and the material can be recycled by washing. Ma et al. [13] used machine learning for the first time to study the effects of the pore structure and chemical properties of porous carbon on CO₂ adsorption performance and predicted the CO₂ adsorption capacity. The use of plant canopy [14,15,16] in removing particulate matter naturally through dry deposition (including diffusion, interception, and adsorption) can also be considered as a typical case of porous materials purifying particulate matter. However, the space structures and environments of urban underlying surfaces are complex, especially in the street canyon, where the flow field is unstable.

Although the above methods do not require energy consumption, the polluted airflow around the porous material is affected by the combined effects of wind, light, and heat in the regional environment when the porous material is directly used to capture particulate matter in an open environment. Multi-directional airflow movements occur on the surfaces of porous materials, and they tend to move irregularly, resulting in low actual capture efficiency in particulate matter. Therefore, how to form a stable and controllable flow field environment, for realizing the stable delivery of particulate matter in the external environment of a building, has become a key step in the efficient purification of particulate matter.

The double-skin façade system, as the building envelope, is in direct contact with the external environment of the building [17]. A heating channel is spontaneously formed in the cavity of the double-skin façade system under solar radiation, and the airflow in the channel is restricted from the bottom to the top, which provides layout space for placing porous materials [18]. In recent years, researchers [19,20,21,22] have begun to integrate various functional materials with the micro-environment inside the double-skin façade system for solving various urgent problems. The concept mentioned in the above studies is also consistent with the research concept of the present study, i.e., the full use of the airflow movement inside the double-skin façade system to realize the zero-energy control of particulate matter. The circulating ventilation volume in the double-skin façade system can reach 150~450 m³/h [23]. Therefore, the characteristics of high urban building density and large total area of glass curtain walls can be transformed into available resources, providing favorable conditions for the in situ purification of particulate matter in the external environment of a building.

The aim of the present study is to identify the design principle of a novel double-skin façade system integrated with porous materials (DSF-PM) for maximizing the purification of particulate matter. Therefore, the differences in purification performance between different placement strategies for porous materials in one typical double-skin façade system were first investigated by analyzing the particle movement law inside the porous material. Next, the effects of porous materials with different pore sizes on particle capture efficiency were studied after the optimal placement was determined. Finally, the variation of the capture efficiency of the DSF-PM system for particulate matter during different seasons was evaluated to test the stability of the system. The conclusions obtained regarding the DSF-PM system in this study can provide technical support and a theoretical basis for realizing the zero-energy control of particulate matter.

The DSF-PM system represents a significant innovation in the integration of building envelope design and in situ purification technology. Its dynamic ventilation is uniquely driven by solar energy, eliminating the need for mechanical equipment. This integration of a double-skin façade with functional materials not only enhances architectural aesthetics but also contributes to environmental sustainability. The system’s purification process is entirely eco-friendly, positioning it as an effective, zero-energy consumption method for in situ treatment. This innovative approach underscores the DSF-PM system’s potential to revolutionize the way buildings manage air quality, emphasizing sustainability and energy efficiency.

2. Methodology

2.1. Physical Model

The porous material, sandwiched by external and internal glass panes, is considered as a purification device in the novel DSF-PM system. The parameters of the DSF-PM system comply with the design criteria of conventional double-skin façades. Su et al. [24] presented the optimal external design parameters of DSF according to different climate regions, while the optimization of internal parameters inside the DSF-PM system is a concern in the present study. Figure 1 depicts a 3D sketch of the DSF-PM system installed on a south-facing façade.

As shown in Figure 1, it is recommended that the installation range of the porous material (h) does not exceed 0.4 m from the ground to facilitate later maintenance, which is also the range of activities that human arms can encompass. The structural parameters of the DSF-PM system are listed in

Table 1. Structural parameters of DSF-PM system.

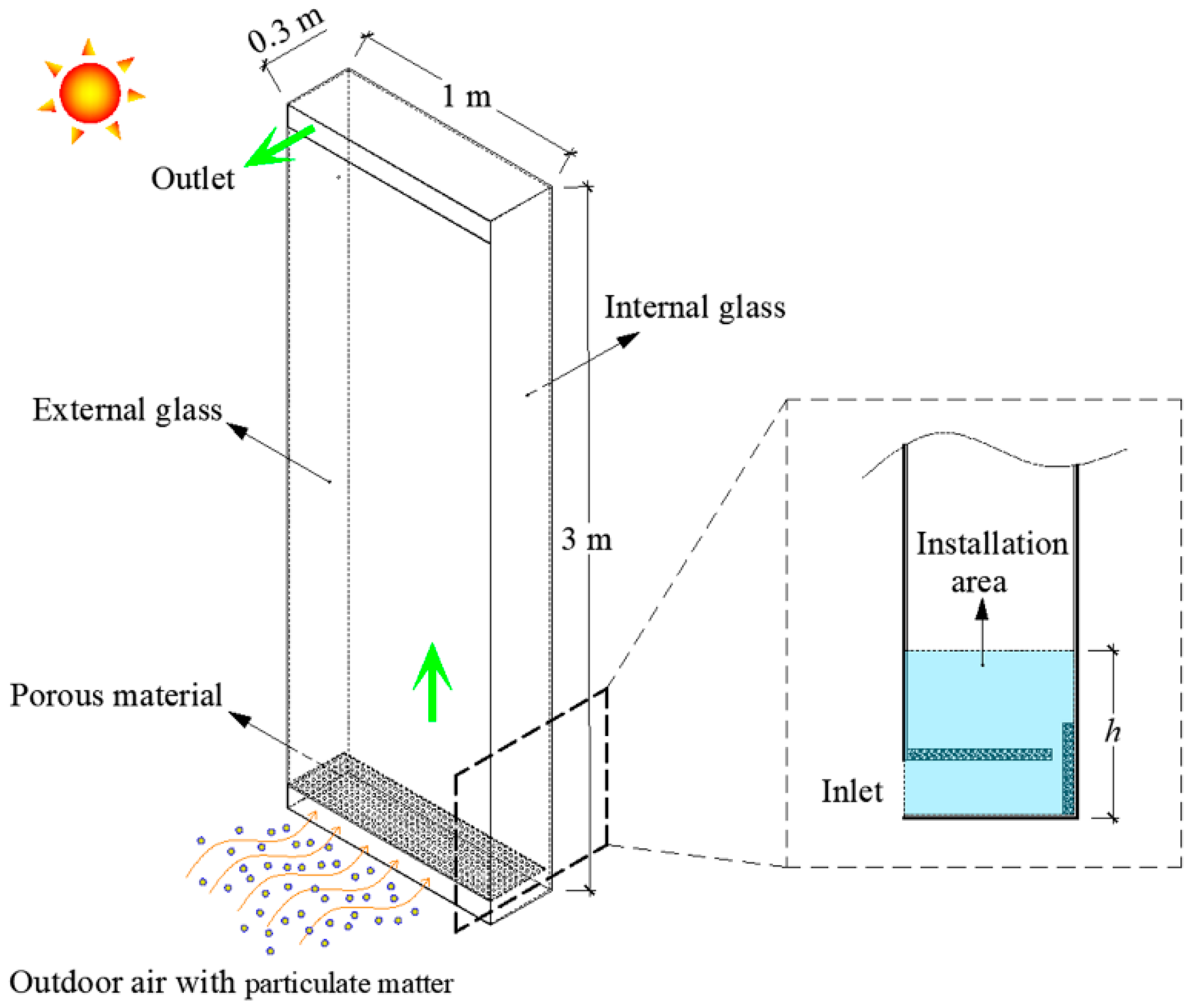
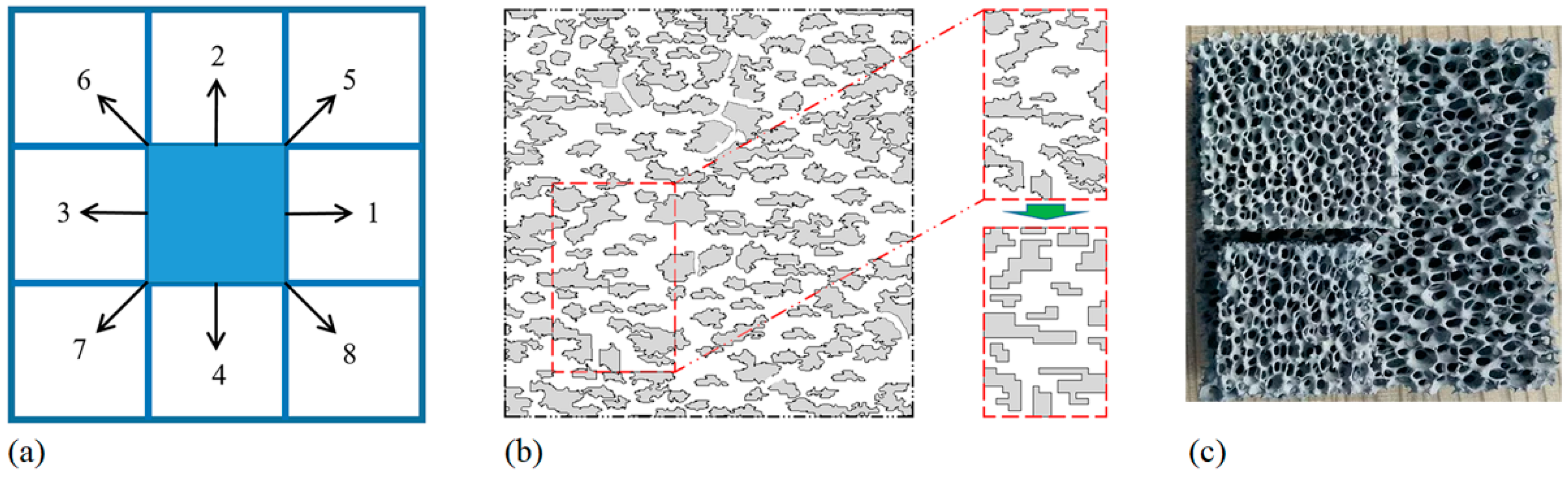
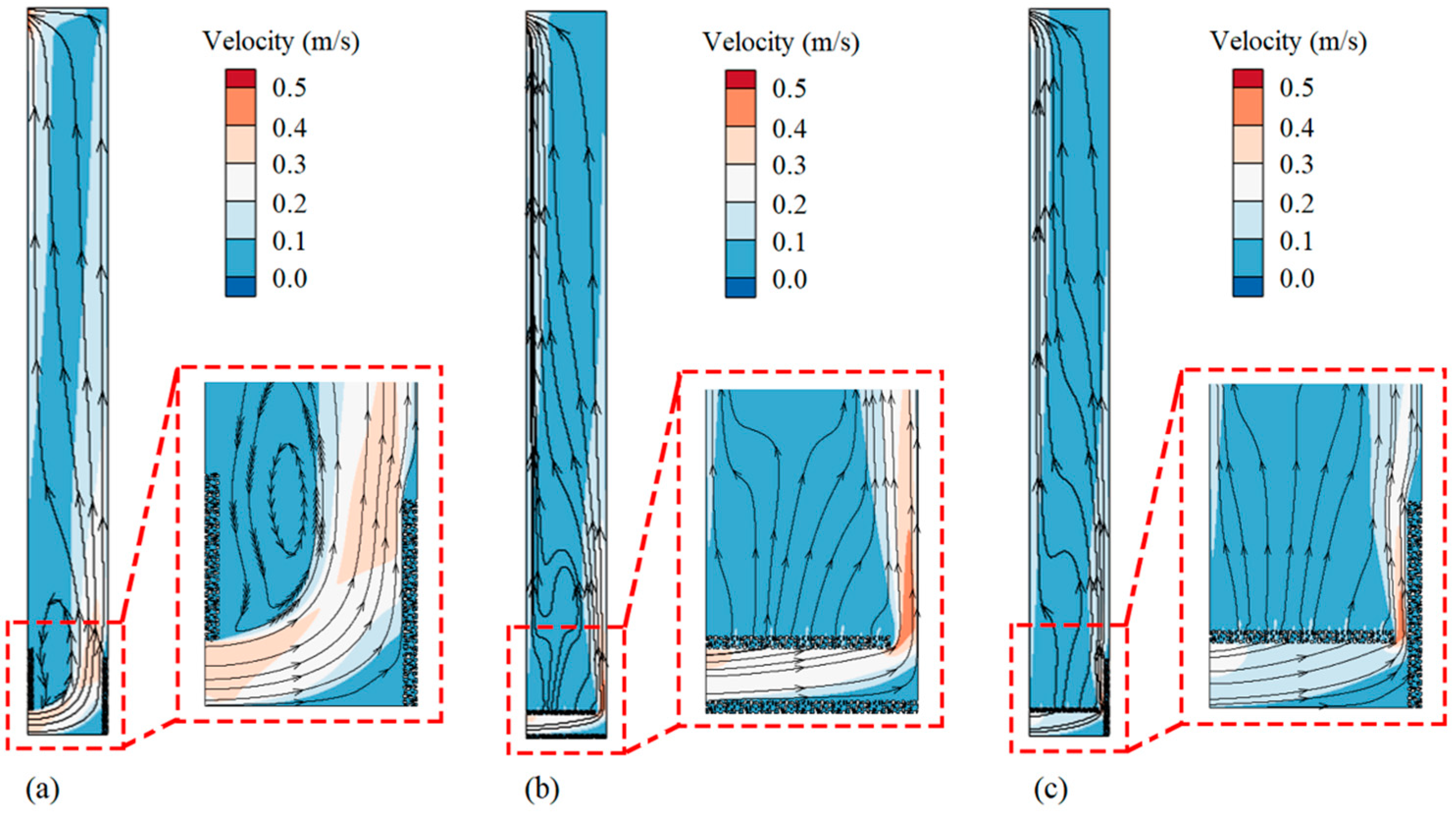
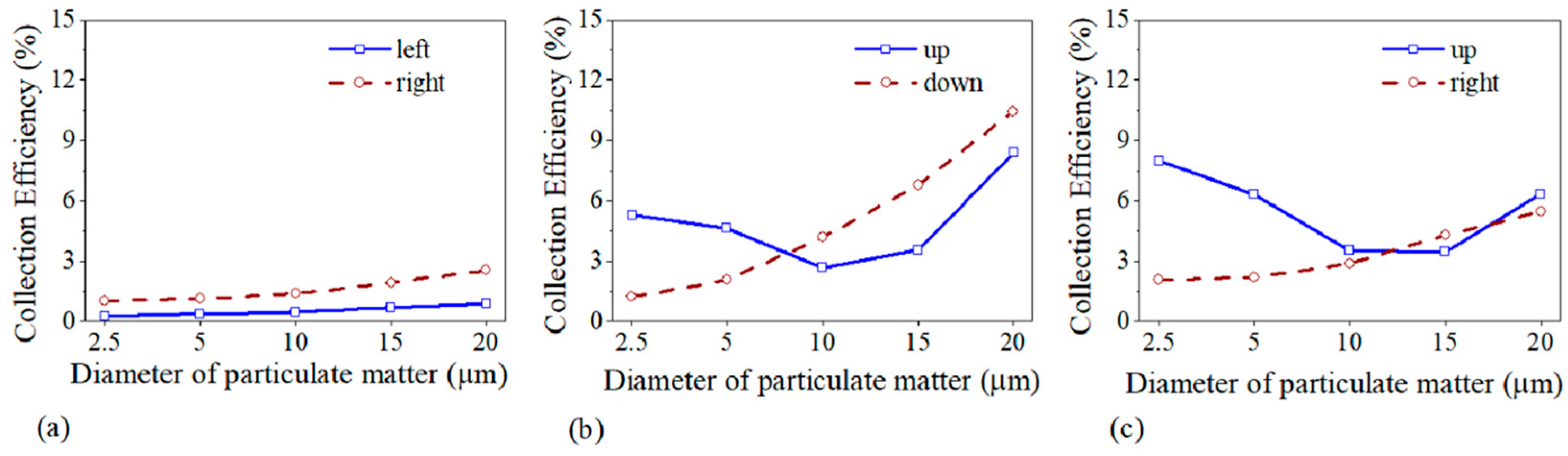
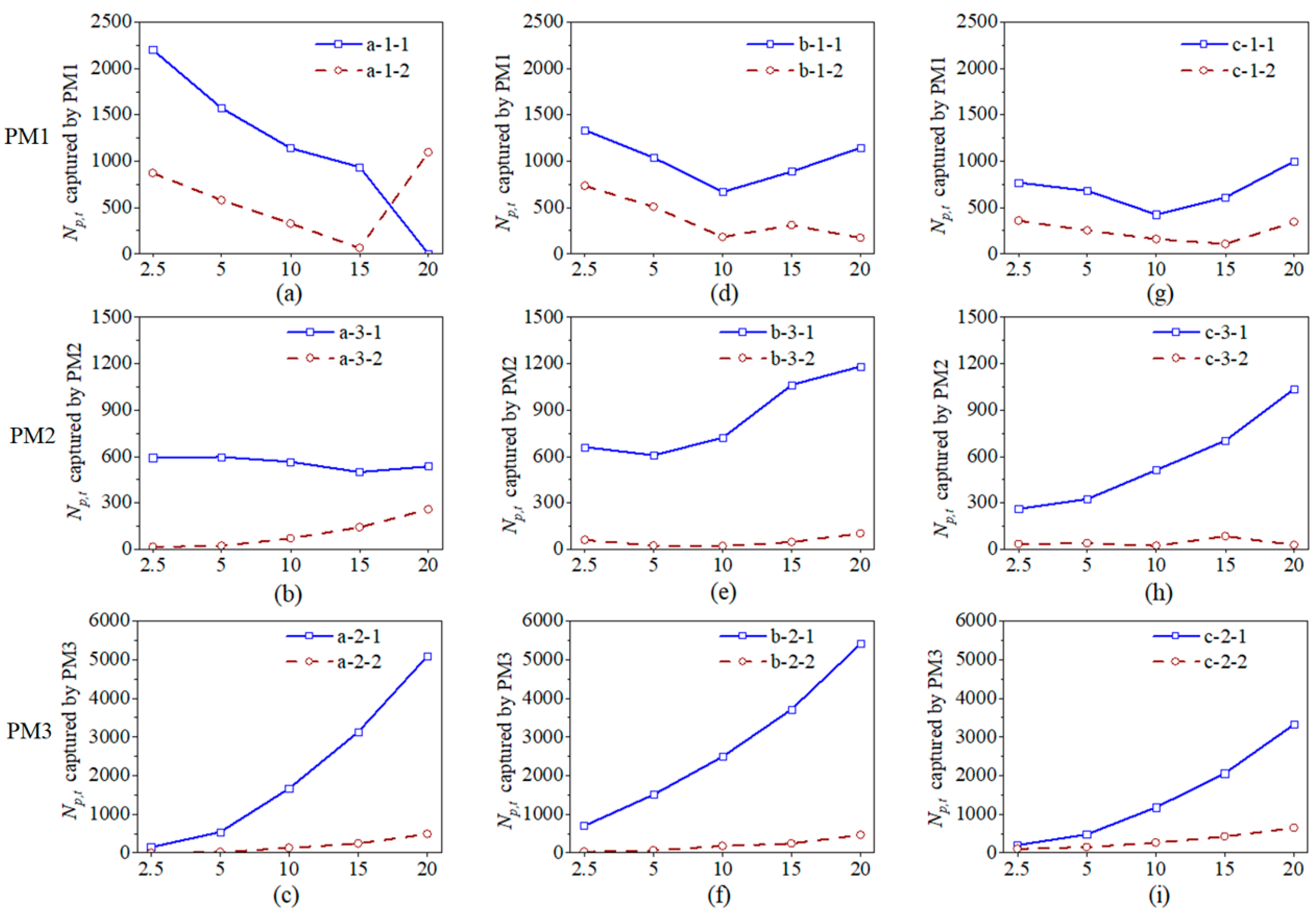
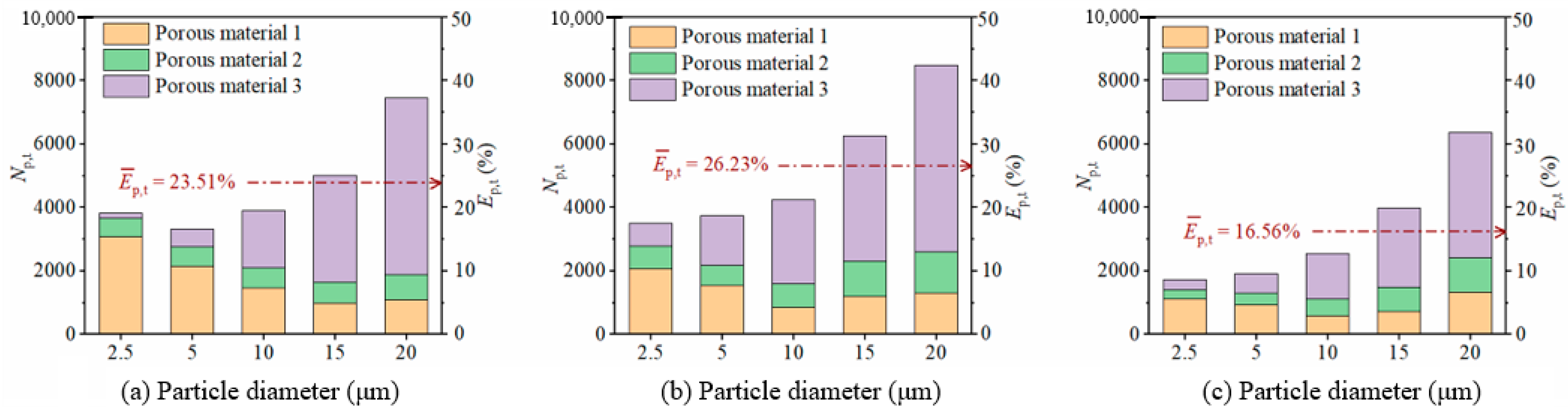
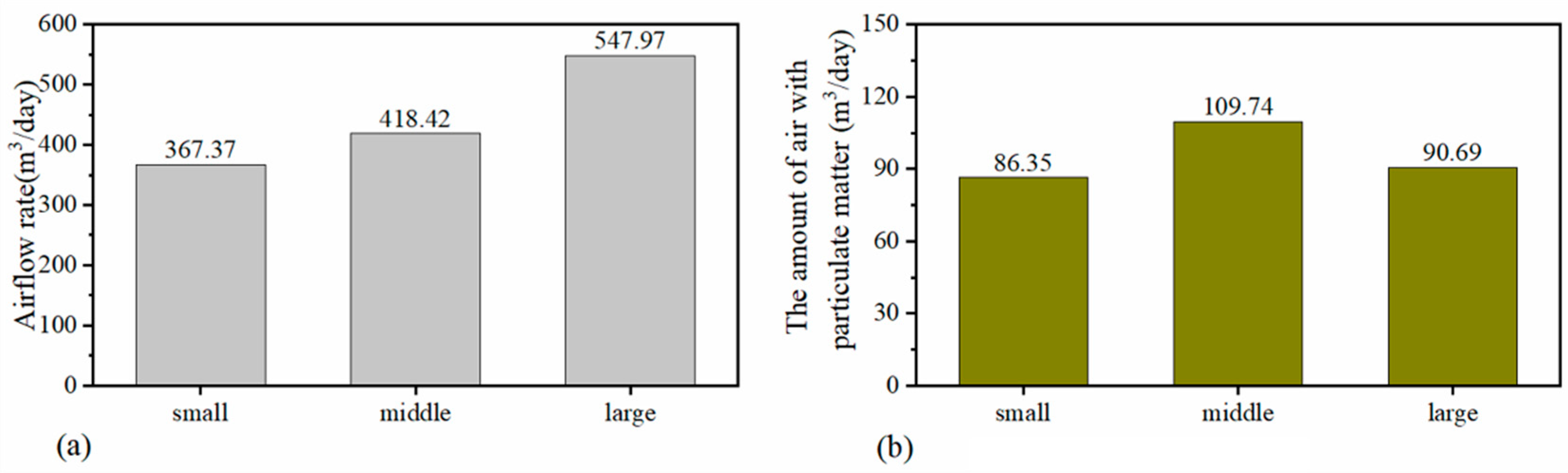
Parameters	Values
Height of DSF-PM	3.0 m
Depth of DSF-PM	0.3 m
Height of external glass	2.8 m
Height of internal glass	3.0 m
Thickness of external and internal glass	0.006 m
Height of air inlet and outlet	0.1 m
Glass density	2500 kg/m3
Specific heat of glass	840 J/(kg·K)
Thermal conductivity of glass	1.5 W/(kg·K)

.

The DSF-PM system has a height of 3 m and a width of 1 m, with a gap of 0.3 m separating its two sides. A height of 3 m was chosen to fit environments with floor heights of 3 m. The 0.3 m distance between the two sides is based on the construction standard (DG/TJ08-56-2019) [25], which stipulates that the air-layer thickness of a double-skin façade should not be less than 0.12 m. Additionally, the width of the DSF-PM was designed to be 1 m to facilitate subsequent modular arrangement.

2.2. Numerical Generation of Stochastic Porous Material

The reasonable organization and control of the airflow in the double-layer curtain wall cavity converts random airflow movement into an orderly and stable airflow movement, which can stabilize the movement characteristics of fine particles and improve the capture efficiency of porous media. However, the interior of porous material is microscopic and complex, and the capture efficiency of porous material for particles with different sizes is thus difficult to determine experimentally. Therefore, investigation using numerical simulations is the focus of the considered methods.

The advantages of numerical methods for analyzing particles captured by porous materials in the flow field have been reported by Cornelio et al. [26] and Wu et al. [27]. In particular, Wang et al. [28] and Guan et al. [29] concluded that the predictions obtained by numerical methods were applied to evaluate the purification performance at the design stage. Moreover, numerical solutions to ventilation-related issues can be generated quickly and accurately from simulations and in agreement with experimental results [30]. Therefore, numerical simulations are considered important approaches to predicting the properties of porous materials. The complex pore structures of porous materials lead to extremely complicated internal physical processes [31].

Traditionally, the continuum model, which is equivalent to the black box model, is mostly used in analyzing and solving physical issues of porous media. This model can only reflect the overall properties of the material and cannot clarify the specific internal conditions [32]. Therefore, the overall trapping law of porous materials cannot reveal the relationship between microstructural and macroscopic properties. Many studies have proposed various structural models, such as stochastic models [33], granular models [34], etc. Therefore, the structure of porous media is described using mathematical methods in the present study. A porous material model was constructed by a stochastic model, and then modeling and simulation investigation were performed using ANSYS Fluent 19.2.

The microstructures of porous media can be constituted using the fractional Brownian motion method [35], grain sedimentation method [36], hard-sphere Monte Carlo technique [37], quartet structure generation set (QSGS) method [38,39], etc. Among these, the QSGS method can generate porous morphological features closely resembling the formation progress of porous materials. The generation process using the QSGS method is controlled by three parameters, i.e., the volume fraction of the generation phase (ε), core distribution probability (c_d), and directional growth probability (D_i). The edge profiles generated directly by the QSGS method are mostly curved, which causes great difficulties in mesh generation in simulations. To reduce the simulation cost, regularization corrections are performed by controlling the same specific surface area and porosity based on the edge contours generated by the QSGS method. The modeling process of the modified QSGS method is shown in Figure 2.

Porous materials consist of two phases, including the matrix material and the air surrounding the matrix material. In the structure growing process, the core of the growing phase grows around its eight surrounding directions according to the given value of D_i, where i = 1, 2, …, 8 denotes the ith growing direction, as shown in Figure 3a. Figure 3b demonstrates the generated microstructures with D_i = 4, c_d = 0.01, and ε = 0.6. The gray area represents the matrix material and the white area stands for the air channel.

The stochastic characteristics are depicted rather realistically (see Figure 3b), and the generated structures are similar to the cross-sectional area shown in Figure 3c. Furthermore, the physical meaning of each parameter is explicit and unambiguous. Therefore, the generated structure was utilized to investigate their particulate filtration performance.

2.3. Mathematical Method

The purpose of this study is to explore the filtration efficiency of particulate matter under natural light irradiation in a special double-skin façade. A 2D incompressible flow model is assumed to simplify the simulation of the DSF-PM system [40].

The foundational equations governing the fluid domain are derived from the Navier–Stokes equations, and the buoyancy effect in air is modeled through the Boussinesq approximation, as referenced in [41,42].

$$\frac{\partial \left(\rho \phi \right)}{\partial t_0}+\nabla \left(\rho U\phi \right)=\nabla \left({\Gamma }_{\phi }gra\phi \right)+S_{\phi }$$

(1)

where ρ is the air density in kg/m³; φ is a common variable that refers to the continuity equation, temperature, and velocity; t₀ is the time in seconds; U is velocity vector; Γ_φ is the diffusion coefficient; S_φ is the user-defined source term. The solar load model in ANSYS Fluent 19.2 is effectively simulated the heat gain of the solar radiation to DSF-PM, while this model can only be used in the 3D model. Therefore, in order to accurately assess the thermal force inside DSF-PM caused by solar radiation, the thermal boundary conditions for the 2D model are first determined by the 3D general model using the solar load model, where wall temperatures at different locations are the information exchanged between the two models.

Equations (2a)–(2d), which regulate the solid phase (i.e., a single particle), are as follows [43]:

$$m_{p}d{v}_p\overrightarrow{v_p}/dt=\overrightarrow{F_D}+m_p\left({\rho }_p-\rho \right)\overrightarrow{g}/{\rho }_p$$

(2a)

$$\overrightarrow{F}=\pi d_p^2{C}_D\left(\overrightarrow{v}-\overrightarrow{v_p}\right)\left|\overrightarrow{v}-\overrightarrow{v_p}\right|/8$$

(2b)

$$C_D=a_1/{\mathrm{Re}}_p+a_2/{\mathrm{Re}}_p^2+a_3$$

(2c)

$${\mathrm{Re}}_p=\rho \left|v-v_p\right|D_p/\mu$$

(2d)

where drag force, gravity, and buoyancy are considered. The $\overrightarrow{F_D}$ is the drag force acting on the particle in N; the second term on the right side of Equation (2a) represents gravity and buoyancy; mp is the mass of the particle in kg; $\overrightarrow{v_p}$ is the velocity vector of the particle in m/s; ρ_p is the particle density in kg/m³; v is the air velocity in m/s; v_p is the particle velocity in m/s; D_p is the particle diameter in m; μ is dynamic viscosity in N·s/m²; a₁, a₂, and a₃ are coefficients determined by Re_p.

2.4. Grid Sensitivity Analysis and Verification of the Numerical Model

Three grid resolutions were used to simulate the velocity field inside the DSF-PM, i.e., I (1,000,000), II (2,000,000), and III (4,000,000). The inlet velocity under thermal force was compared using the three grids’ simulation results. As listed in

Table 2. Calculation and comparison of GCI.

Item	GCI
Criteria value	≤2.2%
II–III	0.27%
I–II	5.9%

, the grid convergence index (GCI) [44,45,46] comparing the II-grid with the III-grid was lower than the criterion values, indicating that the resolution of the medium grid was adequate to obtain accurate results. The computational domain utilized for all the simulations had roughly 4,000,000 grid cells in total, of which finer grids were set aside for the porous materials. The smallest and largest cell sizes were 0.1 mm × 0.1 mm and 0.5 mm × 0.5 mm, respectively.

To ensure the reliability of the numerical method, experimental data were employed to verify the airflow in the DSF-PM induced by thermal force under solar radiation. The velocities at different locations in the DSF-PM system were tested and simulated to validate the present model. The experiments were performed using a double-skin-façade full-scale outdoor test facility (1.0 m × 0.5 m × 0.15 m) located in Shanghai, China (31.2° E, 121.4° N), on 5th March 2023 (see Figure 4). The double-skin façade, which had a single-glazed outer layer and an internal double-glazed layer, faced south. In order to reduce the heat room gained from solar radiation in summer, as shown in Figure 4b, a heat insulation film, which can block 75% of solar radiation, was stuck on the internal glass of DSF-PM.

The specific numerical model was generated for comparing the cavity velocities obtained at different locations. Among the measured points, Point 1 and Point 3 were set at the inlet and outlet of the DSF-PM system, respectively. Point 2 was set in the middle of the DSF-PM system. A hot-wire anemometer (TSI-9535, TSI Inc., Shoreview, MN, USA) with an accuracy of ±0.015 m/s was utilized to test the velocity at the measured points. The simulated results were compared with the measured values for the velocity profiles, as shown in Figure 5.

The results in Figure 5 indicate that the simulated velocities at the measured points obtained from the present model agree well with the measurements, where uniform temperature conditions are imposed on all glazed surfaces of the façades and its ground and ceiling. Since there was a small fraction of particles, a thin phase can be considered, assuming that the particles are spherical. The momentum transfer from the particles to the turbulence has little impact on the flow because of the low particle concentration [47]. Thus, it can be argued that the velocity field (and, consequently, the dispersion of contaminants) in the DSF-PM system may be accurately simulated by the simulation method used in this study.

3. Case Study Description

The porous material arranged inside the DSF-PM significantly affects the airflow movement, including the airflow velocity and the airflow channel formed between the porous material and the curtain wall. In particular, the airflow channel affects the contact area between the contaminated airflow mixed with particulate matter and the porous material, while the airflow velocity affects the inertial motion of particulate matter. Therefore, both the airflow channel and the airflow velocity have a significant influence on the active purification performance of the porous material. Therefore, the porous material placement is a key factor affecting the active purification performance of porous material. In summary, three installation strategies for porous materials (as listed in

Table 3. Parameter settings of the simulation cases.

Case	Term	Parameters
1	Installation strategies	Horizontal placement
2		Vertical placement
3		Horizontal and vertical cross placement
4	Pore size of porous material	2.0 mm
5		1.0 mm
6		0.5 mm

, horizontal placement, vertical placement, and horizontal and vertical cross placement) were explored and simulated in this study.

The numerical generation of the porous materials for all the cases was performed according to Section 2.2. The porous material had a porosity of 0.65, a thickness of 20 mm, and a total length of 560 mm (300 mm + 260 mm), as shown in Figure 6.

The ANSYS Fluent 19.2, a commercial software solver, was utilized for simulating all the scenarios. To model the airflow dynamics influenced by the thermal pressure, the RNG k-ε turbulence model was employed [48]. This is because the RNG k-ε model is more accurate for the analysis of heat transfer compared to the k-ω model [49]. Moreover, the RNG k-ε model includes the effect of the swirl on the turbulence. The particle simulation was based on the assumption of monodispersed non-interacting spherical particles. The airflow was barely affected by the momentum transfer from the particles to the air turbulence. The particles were tracked using ANSYS Fluent’s discrete particle model (CFD-DPM). The release conditions of particle are listed in

Table 4. Release conditions of particle.

Variable	Values
Aerodynamic diameter of particle	2.5 μm, 5 μm, 10 μm, 15 μm, 20 μm
Density of particle	1000 kg/m3

.

The particulate matter capture efficiency for different particle sizes (η_i) is written as:

$${\eta }_i=N_{\mathrm{Trap},i}/N_{\mathrm{Total},i}$$

(3)

where i represents particles of different sizes, i = 2.5, 10, and 20 μm; N_trap is the amount of particulate matter with a particle diameter of i μm trapped by the porous material, and N_total is the total amount of particulate matter with a particle diameter of i μm entering from the inlet.

The average purification efficiency is written as:

$$\overline{\eta }={\displaystyle \sum _{i=1}^n{\eta }_i}/n$$

(4)

The equivalent of the air purified throughout the day is expressed:

$$V_{\mathrm{Total}}=V_{\mathrm{hour}}\times \overline{\eta }\times 8$$

(5)

The climatic data for typical summer days in Shanghai (31.2° N, 121.5° E) were used as the outdoor climate conditions, which included the average outdoor air temperature and the average solar radiation intensity during these summer days. The key inputs of the model are listed in

Table 5. Key inputs of model.

Parameters	Values
Wind pressure	0 Pa (buoyancy analysis only)
Outdoor air temperature	30.4 °C
Indoor air reference temperature	26 °C
Solar radiation intensity in summer	647.22 W/m2
Heat-transfer coefficient of outer surface	23 W/(m2·°C)
Heat-transfer coefficient of inner surface	8.7 W/(m2·°C)
Transmittance of the glass shell	0.85
Transmittance of the heat insulation film	0.25

.

4. Results and Discussion

As mentioned in the above sections, the placement and porosity of porous materials are key parameters affecting the purification efficiency of particulate matter. In the following discussion, the influence of the placement and porosity of the porous material on the purification efficiency of the particulate matter are investigated, respectively.

4.1. Placement of Porous Materials inside the Double-Skin Façade

Different installation strategies for porous materials change the airflow channel and flow field inside the double-skin façade system, affecting the movement trajectory of the particles. Figure 7 shows the flow field for three installation strategies (i.e., vertical placement, horizontal placement, and horizontal and vertical cross placement).

It can be observed in Figure 7 that the flow field inside the DSF-PM was significantly different for the three installation strategies. For the vertical placement, the flow field inside the DSF-PM was similar to the flow field inside a typical double-skin façade system. The airflow near the inlet was located close to the internal glass, while the airflow near the outlet was located close to the external glass (Figure 7a). For the horizontal placement, the airflow velocity was fastest at the throat, and some of the airflow passed through the porous material (Figure 7b). Compared to the horizontal placement, the airflow velocity was further accelerated at the throat for the horizontal and vertical cross placement due to the reduced throat size.

According to the characteristics of the flow field, 20,000 particles with five different particle sizes (i.e., 2.5 μm, 5 μm, 10 μm, 15 μm, and 20 μm) were tracked using the discrete particle model (DPM) in the simulations. The number of particles captured by each porous material was counted, and the capture efficiency of the porous material in different positions for five particle sizes was obtained according to Equation (3), using three installation strategies (see Figure 8).

It can be seen in Figure 8a that the capture efficiency of the porous material increased with the particle size for the vertical placement. Notably, the capture efficiency on the right side was higher than that on the left side. This is because the particles entrained by the airflow were more likely to be captured by the right porous material located on the windward side of the mainstream area.

For the horizontal placement, the capture efficiency on the lower side increased with the particle size under the effect of the gravitational force (see Figure 8b). Furthermore, the porous material on the upper side had a higher capture efficiency for smaller or larger particles, meaning that the process of the airflow passing through the porous material was similar to the principle of the filter. The capture efficiency was lowest when the particle size was around 10 μm, corresponding to the most penetrating particle size (MPPS).

Compared to the vertical placement, the capture efficiency for different particle sizes was improved for the horizontal and vertical cross placement (i.e., staggered placement), and only for smaller particle sizes compared to the horizontal placement (see Figure 8c). This is because the staggered placement altered the airflow path and reduced the size of the throat.

Figure 9 presents the overall purification efficiency using three installation strategies. It can be observed that the vertical placement had the lowest overall purification efficiency among the three placement strategies. However, the horizontal and staggered placements had their own advantages and disadvantages. The horizontal placement had a higher overall efficiency with particles larger than 10 μm, while the staggered placement had a higher overall efficiency with particles less than 10 μm. With a particle size of 10 μm, the overall purification efficiency was almost the same for both. To capture more particulate matter, a combination of horizontal and staggered placements is used for the following detailed analysis.

4.2. Effects of Porous Materials with Different Pore Sizes on Particle Capture Efficiency

According to the results in Section 4.1, two installation strategies were combined to improve the overall purification efficiency with different particle sizes, i.e., the porous materials were installed on the upper side (porous material 1, PM1), lower side (porous material 2, PM2), and right side (porous material 3, PM3), respectively.

Figure 10 shows the structure of the combined installation strategy inside the DSF-PM. Moreover, the porous material was divided into two parts (defined as Part 1 and Part 2), and the thickness of each part was half that of the original porous material (i.e., 10 mm), as shown in Figure 10b.

Meanwhile, the pore sizes of the porous material are also taken into consideration in the combined installation strategy given in Figure 10. The capture efficiency of the three porous materials with different pore sizes (i.e., 0.5 mm, 1 mm, 2 mm) was investigated according to the combined installation strategy.

Figure 11 gives the velocity distributions near the porous materials with different pore sizes. It is shown in Figure 11 that the airflow passing through porous material increased with the pore size of porous material. This is because the airflow resistance of the porous material decreased as the pore size increased. When the pore size was sufficiently small, it was difficult for the airflow to pass through the porous material; hence, most of the air traveled upward through the throat (see Figure 11a).

Figure 12 presents the statistical results of the particle numbers trapped by the porous materials versus the particle diameters in different locations and partitions (i.e., Part 1 and Part 2). According to the results shown in Figure 12, the number of particles captured by Part 1 was larger than that of Part 2 for three porous materials. For the PM1 installed in the mainstream region, particle diameters of 2.5 μm and 20 μm were more easily captured than those with a diameter of 10 μm (see Figure 12a,d,g). This is because PM1 was similar to a filter with a maximum penetrating particle size (MPPS) of 10 μm, and the airflow could pass directly through PM1. For the PM2 installed in the airflow-diversion area, the number of captured particles increased with particle diameter due to the inertial force, as shown in Figure 12b,e,h. Moreover, since the gravitational effect increased with the particle diameter, the number of captured particles increased for the PM3 installed on the bottom (see Figure 12c,f,i). In summary, the porous materials had different mechanisms for capturing particles in these three placements.

In order to investigate the effect of the pore size of the porous material on the overall purification efficiency (E_p,t), the variations of the E_p,t with particle diameters for three pore sizes of porous material are summarized in Figure 13 (i.e., 0.5 mm, 1 mm, and 2 mm).

It can be observed in Figure 13 that the E_p,t increased with the increase in the particle diameter. In particular, the purification efficiency for the particle diameter of 20 μm reached 42% in the porous materials with a pore size of 1 mm. Moreover, the average purification efficiency ($\overline{E_{\mathrm{p},\mathrm{t}}}$) was significantly influenced by the different pore sizes of the porous materials. The results in Figure 13b indicate that the $\overline{E_{\mathrm{p},\mathrm{t}}}$ reached a maximum value of 26.23% for the porous materials with a pore size of 1 mm compared to that for the pore sizes of 0.5 mm or 2 mm. For particles larger than 5 μm, the purification efficiency exceeded 20%, which is equivalent to a primary filter in the Chinese standard GB/T14295-2019 [50] (i.e., G2 in the European standard EN779-2012 or MERV 5 in the American standard ASHRAE 52.2-2017 [51,52]) running continuously during the day.

The airflow rate inside the DSF-PM system is another factor that affects the purification performance of particulate matter. To specify the optimum pore size in porous materials, it is necessary to analyze the volume of air purified by porous materials per day. Figure 14 depicts the airflow rate through the DSF-PM system and the amount of air with particulate matter purified per day, and the values are calculated using Equation (5).

It can be observed in Figure 14a that the total airflow rate increased with the increases in the pore size of the porous material. This was due to the reduced resistance of the DSF-PM system at larger pore sizes. However, although the airflow rate in the porous material with pore sizes of 2 mm was greater than that of the pore size of 1 mm, and the amount of air with particulate matter purified per day (90.69 m³/day) was smaller than that in the material with a pore size of 1 mm (109.74 m³/day) (see Figure 14b). This is consistent with the previous analysis and confirms that porous materials with a pore size of 1 mm exhibit the highest purification efficiency, which also indicates the better purification performance of DSF-PM system in this situation.

4.3. Annual Performance Evaluation

The obtained results in Section 4.1 and Section 4.2 show that the staggered placement of porous materials with 1-millimeter pore sizes in the DSF-PM system is more favorable for particle capture. In fact, the variations in solar radiation and indoor–outdoor temperature differences throughout the year have a significant influence on the purification performance of the DSF-PM system. Therefore, the purification performance of the DSF-PM system in different seasons, including the solar radiation intensity, indoor temperature, and outdoor temperature, are investigated in the present study. The climatic parameters for different seasons are recorded in

Table 6. Average daytime radiation intensity and temperature under three season conditions.

	Season	Winter	Spring/Autumn	Summer
Parameters
Direct solar radiation intensity (W/m2)		195.17	444.05	556.26
Diffuse solar radiation intensity (W/m2)		32.92	72.62	90.96
Outdoor temperature (°C)		6.9	18.3	30.4
Indoor temperature (°C)		18	18.3	26
Indoor–outdoor temperature difference (°C)		11.1	0	−4.4

.

According to the staggered placement of the porous material with a pore size of 1 mm and the climate conditions listed in Table 6, three simulation cases were analyzed for different seasons to evaluate the purification performance. Figure 15 presents the predicted performance of the DSF-PM system in purifying particulate matter.

The results in Figure 15a show that the purification efficiency in different seasons tended to be consistent with increases in the particle diameter, which fully exhibits the stability of the DSF-PM system throughout the year. The purification efficiency (E_p,t) was almost stable between 17.5% and 21.5% for particle diameters less than or equal to 10 μm. When the particle diameter was larger than 10 μm, the E_p,t increased with the increase in the particle diameter and reached 45%. The average annual purification efficiency of the DSF-PM system was 26.24%. In addition, it is worth noting that there was no positive correlation between the amount of air with particulate matter purified per day and the solar radiation intensity (see Figure 15b). The temperature difference between indoors and outdoors also had a significant impact on the ventilation in the cavity [53].

In winter, the indoor temperature (T_in) was higher than the outdoor temperature (T_out) because of the space heating. The positive temperature difference (T_in − T_out) also contributed to the chimney effect. In summer, the room was air-conditioned, the indoor temperature was lower than the outdoor temperature, and the temperature distribution almost offset the effect of the thermal pressure in the cavity caused by the solar radiation, resulting in a significant decrease in the ventilation rate.

4.4. Discussion and Prospects

According to the Shanghai Ecological and Environmental Bulletin (2021), the average annual concentrations of PM_2.5 and PM₁₀ in Shanghai are 27 μg/m³ and 43 μg/m³, respectively. Moreover, the average concentration of road dust recorded with mobile monitoring in all the districts in Shanghai ranges from 76 to 89 µg/m³, with an average value of 81 µg/m³. After the purification of the DSF-PM system, the values of PM_2.5, PM₁₀, and PM₂₀ reduced to 22.41 μg/m³, 34.4 μg/m³, and 46.98 μg/m³, respectively, all of which reached the first class of the National Ambient Air Quality Standard.

In summary, the double-skin façade system integrated with porous materials (DSF-PM) can effectively purify particulate matter in ambient air. It is estimated that a 12-story commercial building with a south façade of 50 m × 40 m could purify approximately 82,671 m³ of ambient air per day if equipped with the DSF-PM system on half of the façade. This is equivalent to 0.26 ACH cleaning capacity (within 8 h) for a building with a volume of 20 m × 50 m. The DSF-PM system has great potential to reduce contaminants because it can operate in the natural environment without energy consumption by buildings. Whether used for outdoor or indoor air purification, it can provide a practical reference for reducing carbon emissions and purifying ambient air in buildings.

According to the experimental calculation, the cost of a single DSF-PM system unit (1 m × 3 m × 0.3 m) is CNY 3000. For a representative room measuring 9 m × 8 m × 3 m, using one IAM-KJ780F-A1 model purifier, with a clean air delivery rate (CADR) for solid pollutants of 800 m³/h, and considering the residential electricity price of CNY 0.617/(kW·h), the operating cost of using the IAM purifier over 5 years is CNY 9707.656. In contrast, the cost of operating the DSF-PM system for 5 years is CNY 24,000 (based on the installation of eight such DSF-PM systems). Ignoring the time value of money, the investment recovery period (IRP) is 2.5 years.

Our work contributes to the broader scientific discourse on environmental sustainability and public health by demonstrating the DSF-PM system’s potential for widespread application in urban settings. The cost-effectiveness analysis, comparing the DSF-PM system with traditional air purifiers, highlights the economic viability and efficiency of our system, making a compelling case for its adoption in both new and existing buildings. This comparison not only emphasizes the system’s lower operating costs but also its shorter investment recovery period (IRP), further advocating for its practicality and financial accessibility.

In essence, the DSF-PM system represents a significant advancement in the integration of building design and air purification technology. By offering a solution that leverages natural environmental forces, this system sets a new standard for sustainable urban development and indoor air quality management. Our research not only fills a gap in the existing knowledge on building-integrated air purification strategies but also encourages a shift towards more environmentally friendly and health-conscious architectural practices.

5. Conclusions

The study introduces a novel double-skin façade system (DSF-PM) integrated with porous materials for purifying particulate matter in urban environments. This system utilizes solar energy to generate airflow, making it an energy-efficient and environmentally friendly solution. Three installation strategies for porous materials were examined—vertical, horizontal, and cross placement—to optimize particulate matter capture. The results indicate that the porous materials with a 1-millimeter pore size exhibited the best performance, achieving a maximum purification efficiency of 45% for particles larger than 10 µm and an average annual efficiency of 26.24%. This efficiency is comparable to primary filters in various international standards. The DSF-PM system’s effectiveness varies with the particle size and is influenced by seasonal changes in solar radiation and temperature. This approach offers a zero-energy, pollution-free method for in situ particulate matter purification, which can be integrated seamlessly with building exteriors.