1. Introduction
Modern electrical power systems encounter substantial difficulties in ensuring a consistent and dependable electricity supply when faced with extreme weather events and other disruptions characterized by High-Impact Low-Probability (HILP) [
1,
2]. These occurrences can result in severe repercussions, causing widespread power outages and incurring significant financial burdens. To illustrate, Winter Storm Uri in Texas, United States, in February 2021 led to extensive power disruptions, affecting 4.5 million customers without electricity [
3]. Additionally, in the year 2023 alone, the United States experienced 28 weather-related disasters, each with costs exceeding USD 1 billion [
4]. The influence of extreme events extends beyond the United States, as demonstrated by incidents such as a severe storm in Australia in 2016, a windstorm in Canada in 2015, and the 2016 tornado in Jiangsu Province, China [
5]. These occurrences emphasize the critical necessity for tools to gauge resilience and strategic planning approaches based on such metrics, ultimately leading to strategies to invest in grid capacity to endure and recover from these challenging events expediently [
6]. In the broader context, incorporating energy sustainability principles into these strategies becomes imperative for creating resilient and environmentally conscious power systems.
In recent years, there has been a notable surge in interest regarding strategies to enhance the resilience of electric power supply, driven by the growing dependence on electricity access and the increasing occurrence and severity of extreme weather events [
7]. These strategies aim to strengthen the resilience of power systems, incorporating both planning-based and operation-based approaches. Operation-based strategies are centered on optimizing the efficient utilization of existing resources to mitigate the impact of extreme events and the subsequent outages [
8]. Conversely, planning-based strategies focus on expanding electricity infrastructures to fortify them against potential future events, with a key emphasis on selecting investments that ensure a dependable and resilient power supply to end-use customers [
9]. Examples of planning-based strategies may encompass the installation of underground cables, planning for energy storage, and other relevant measures [
10,
11,
12].
Previous studies have investigated different planning strategies for boosting the resilience of power systems. In the work of Nazemi et al. [
13], an optimization problem was devised through linear programming to strategically deploy energy storage for earthquake resilience. The researchers introduced a new metric that measures the resilience of distribution networks, taking into account uncertainties such as the location, duration, and intensity of potential extreme events. A resilient transmission expansion planning model that optimizes the configuration of the transmission network was presented in [
14], minimizing cascading outage effects and enhancing resilience by considering security and
security criterion, utilizing an iterative algorithm to estimate cascading outages, and employing a multistage solution procedure based on Benders decomposition algorithm for the efficient handling of investment decisions and resilience requirements. In [
15], a resilience-oriented distribution system planning strategy was introduced, utilizing a multistage hybrid–stochastic–robust formulation with a progressive hedging algorithm, aiming to enhance power system resilience by addressing the challenges of multiple extreme weather events in the context of increasing renewable penetration and climate change uncertainties. The study presented in [
11] introduced a planning strategy focused on resilience for the optimal setup of urban multienergy systems. This strategy conducted a thorough analysis of impacts originating from the supply, network, and demand aspects. An impactful planning approach utilizing mobile energy storage systems to enhance distribution system resilience during disasters was presented in [
16], focusing on postdisaster restoration in conjunction with photovoltaic-powered electric vehicle parking lots, distributed generation, and network reconfiguration. The study outlined in [
17] introduced a resilience assessment framework oriented towards planning. This framework was designed to evaluate the power system’s resilience in the face of typhoon disasters and identify its vulnerabilities. Through a detailed analysis of the potential impacts of various typhoon disasters on each transmission corridor, a comprehensive investigation of the power system’s resilience was conducted, pinpointing its weak points. Moreover, the framework could guide measures aimed at enhancing resilience by addressing these weaknesses, such as expanding or upgrading vulnerable transmission corridors. A multistage optimization framework for resilient distribution system expansion planning was proposed in [
18], focusing on nonutility DER bidding strategies in external shock conditions to enhance system resilience and reduce costs. A planning-targeted resilience assessment framework for electric power transmission systems in coastal areas was presented in [
19], leveraging data-driven schemes and the analytic hierarchy process to identify weak links and select optimal resilience improvement strategies against typhoon disasters. A robust mixed-integer optimization model for integrated planning of a power network and electric vehicle charging infrastructure was introduced in [
20], enhancing power system resilience by determining optimal joint expansion decisions under various extreme weather scenarios, validated through case studies on IEEE 30-bus and IEEE 118-bus power systems. In [
21], a comprehensive model for planning the joint transmission system and DER was introduced with the aim of enhancing the resiliency of the power system, taking into account both regular and emergency operating conditions, along with the duration of each situation. Additionally, the emergency condition was characterized by a series of damage scenarios, categorizing transmission system components into three damage states: moderate damage, severe damage, and complete damage. Although these studies have substantially contributed to the domain of power system resilience planning, there exists a noticeable gap in research. Specifically, there is a requirement for a comprehensive framework that not only identifies weak points in the system but also quantifies resilience and recommends investment in assets to improve resilience. Such a framework should facilitate Integrated Resource Planning to attain predefined resilience levels.
In this article, we present a resilient Integrated Resource Planning (IRP) framework designed specifically for transmission systems, with a focus on the analysis and evaluation of HILP events. Our framework is developed to gauge and improve the resilience of transmission networks, employing the proximity of outage lines to generators as a metric for selecting HILP events. Through the generation of numerous random line outage scenarios, we selectively examine HILP events to assess the system’s foundational resilience. Furthermore, we integrate additional generating resources into the framework and re-evaluate system resilience after the proposed investment according to desired levels. By quantifying load curtailment and introducing the resilience metric Expected Load Curtailment (ELC), our framework provides a comprehensive evaluation of system resilience. To showcase the effectiveness of our proposed framework, we conduct case studies on the IEEE 24-bus system, highlighting its capabilities and potential for optimizing resource placement and planning decisions. Through the advancement of resilient power system planning, our research contributes to the development of more robust and resilient transmission networks capable of withstanding and recovering from disruptive events. Importantly, our approach aligns with energy sustainability principles, ensuring the development of resilient power systems that are environmentally conscious and sustainable. The main contributions of this article are summarized as follows:
Introduction of a resilient IRP framework for the transmission system, incorporating analysis, evaluation, and optimization considering HILP events.
Proposal of the proximity index, a metric based on the closeness of outage lines to generators, facilitating the selection of HILP events from a broad array of randomly generated multiple-line outage scenarios.
Development of a methodology for conducting power flows on islands formed due to multiple-line outages and calculating the total load curtailment in the outage scenario.
Introduction of the resilience metric ELC to quantify the anticipated load curtailment in all HILP scenarios, serving as a measure for resilience planning.
Proposal of the strategic placement of DER investments to achieve a desired level of resilience.
The remainder of this article is organized as follows:
Section 2 describes the proposed IRP framework and solution approach, along with the proposed metrics and optimization problem formulation for reassessing the system resilience.
Section 3 presents the analysis of results and validates the proposed work through case studies on the IEEE 24-bus system.
Section 4 provides the concluding remarks along with potential future works.
2. Proposed Framework
In this section, we introduce the proposed framework designed for the IRP of resilient transmission systems. The framework adopts a comprehensive approach to tackle the specific challenges presented by HILP events. The proposed framework establishes a systematic process for assessing the base case resilience of the system, identifying network configurations that yield HILP events, and reassessing resilience with the incorporation of new resources. By providing a holistic understanding of the system’s resilience, the proposed framework facilitates well-informed decision making in the realm of IRP.
The transmission network is depicted as a graph using graph theory methods, where generators, loads, buses, transmission lines, and transformers are components. Buses are nodes, while lines and transformers are edges in this graph. This representation eliminates the necessity of separately modeling generators and loads in the graph by connecting their information to the respective buses. Node information includes all connected generator and load details linked to a specific bus.
Figure 1b illustrates the graph theory representation of a hypothetical six-bus transmission network, as shown in
Figure 1a.
The transmission network is illustrated as an undirected graph,
, where
denotes the nodes (or vertices), and
represents the edges (or branches). This graphical model offers a distinct visual and mathematical depiction of the interconnected parts of the transmission system [
22].
Additionally, this work utilizes the concept of connected components from graph theory. In an undirected graph, a connected component is defined as the largest set of nodes where each pair of nodes is connected by a path [
23]. Essentially, within a connected component, every pair of nodes is linked by either a direct or an indirect path. Connected components are crucial for understanding the behavior and resilience of the system, as they represent distinct networks within the transmission system. By identifying and analyzing these connected components, valuable insights can be gained into the structural integrity, load distribution, and susceptibility to disruptions of the system.
Figure 1d illustrates the creation of two connected components in the hypothetical transmission network following the outage of lines 4–5 and 4–6 (depicted in
Figure 1c). The first connected component (CC-1) consists of nodes 2 and 4, while the second connected component (CC-2) comprises nodes 1, 3, 5, and 6.
Connected components form a partition of the set of graph vertices, meaning they are nonempty, pairwise disjoint, and their union encompasses all the vertices in the graph [
23]. Another way to conceptualize connected components is by understanding the relationship between nodes. The relation that associates two nodes if and only if they belong to the same connected component is an equivalence relation. This equivalence relation is reflexive, symmetric, and transitive, allowing for the identification and classification of distinct networks within the transmission system.
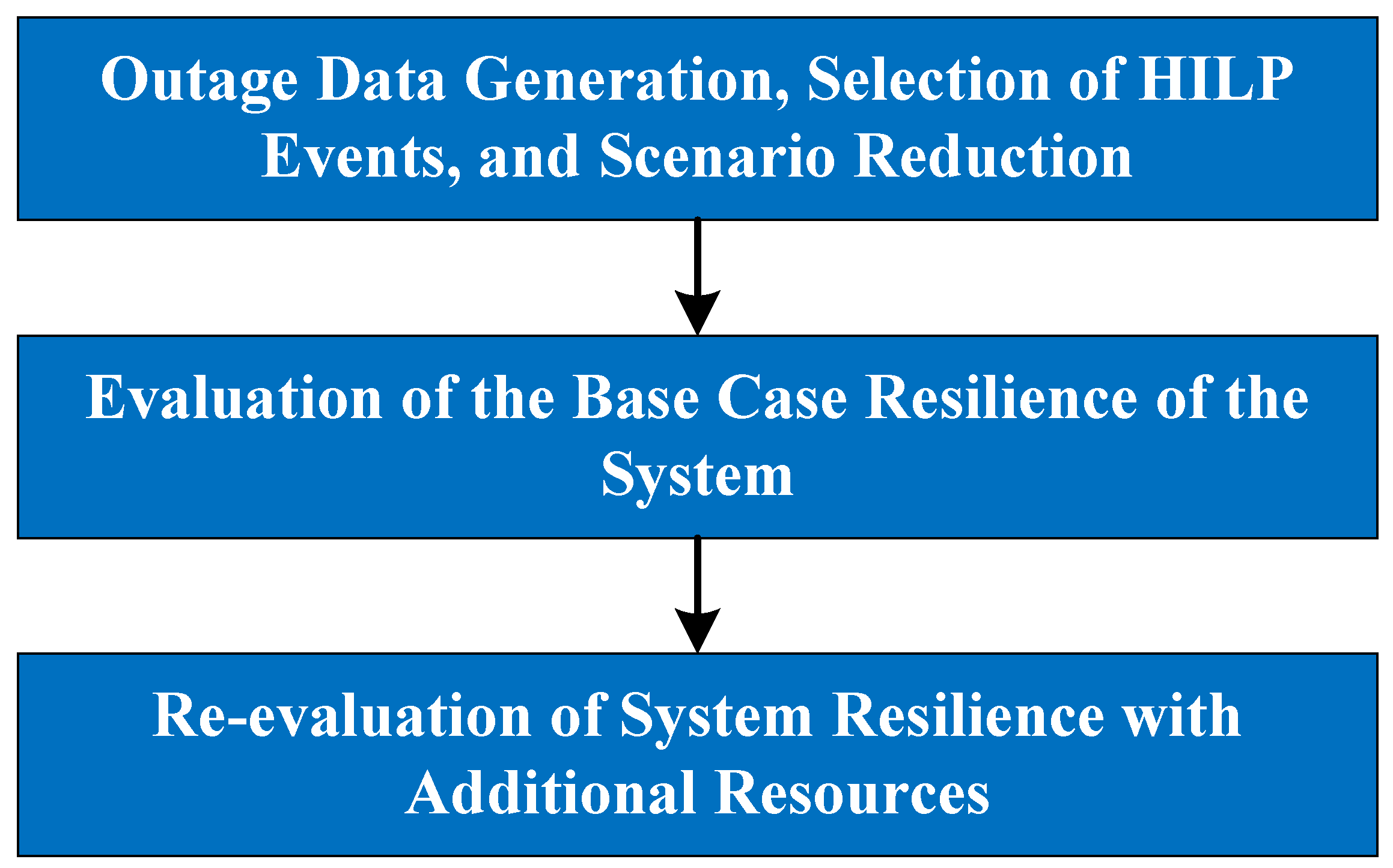
Utilizing graph theory modeling and the concept of connected components, the proposed framework establishes a strong analytical basis for evaluating and improving the resilience of transmission systems. This framework is structured into three primary stages, as depicted in
Figure 2. The following subsections elaborate on each stage, detailing their aims, approaches, and contributions to a thorough grasp of the system’s resilience.
2.1. Outage Data Generation, Selection of HILP Events, and Scenario Reduction
In the first stage of the proposed framework, outage data are generated, HILP events are selected, and scenario reduction is performed. To thoroughly evaluate the resilience of the transmission system, numerous line outage scenarios are randomly generated from a uniform distribution. These scenarios represent a broad array of potential disruptions that the system might face. By incorporating a diverse set of outage scenarios, the framework aims to encompass the entire range of potential multiple-line outages that could affect the system’s resilience [
24].
To select HILP events from the randomly generated line outage scenarios, a metric known as the proximity index (PI) is utilized. The PI is based on the proximity or closeness of the outage lines to the generators. This metric is based on the understanding that outages occurring near generators are more likely to result in higher load curtailments within the system. By evaluating the proximity of outage lines to generators, the framework identifies events that have a higher likelihood of causing significant disruptions and load curtailments. The mathematical expression for the PI of the
ith scenario is as follows:
where
represents the total number of outaged lines in the
ith scenario, and
is a binary variable indicating whether the
kth line of the
ith scenario is connected to a generator (1 if connected, 0 if not).
A threshold is established to determine the qualification of an event as a HILP event. This threshold ensures that the number of line outages exceeds a certain level, indicating a significant impact on the system. By setting an appropriate threshold, the framework concentrates on events with high impact. This approach is in line with a resilience-oriented perspective, enabling a focused analysis of events that are most likely to test the system’s resilience. The binary condition in Equation (
2) is utilized for selecting a HILP event.
where
denotes the threshold value of the PI, which is established at six for this particular study.
Through this stage, the framework selectively narrows down the set of outage scenarios to specifically focus on HILP events. By prioritizing events with a high potential for severe consequences, the framework ensures that the subsequent analysis and evaluation are concentrated on the most critical disruptions. This approach provides a more refined understanding of the system’s vulnerabilities and aids in the development of effective resilience enhancement strategies.
The final phase of this stage involves scenario reduction. While leveraging a diverse set of HILP scenarios can undoubtedly improve the accuracy of the approach, managing such an extensive dataset can pose computational challenges and consume a significant amount of time [
25]. This is where the scenario reduction technique becomes crucial. In this study, scenario reduction (or clustering) based on load curtailment (LC) is employed. Scenarios are grouped into specific clusters based on the similarity in LC values of those scenarios. Algorithm 1 presents the LC-based scenario reduction adopted in this work.
| Algorithm 1: Load Curtailment (LC)-based Scenario Reduction |
![Sustainability 16 02449 i001]() |
The overall load curtailment for each outage scenario is calculated by aggregating the load curtailment across all islands. Mathematically, the total load curtailment for the
jth scenario is expressed as follows:
where
is the load curtailment of the
kth island of the
jth outage scenario, and
is the number of islands in the
jth outage scenario.
The power flow is solved to compute the load curtailment in (
3). The power balance equations for an AC power flow are as follows [
26]:
where
,
,
, and
represent active power generation, reactive power generation, active load, and reactive load, respectively, for bus
x;
is the voltage magnitude of bus
y;
is the number of buses;
is the difference between voltage angles of buses
x and
y; and
and
, respectively, are the real and imaginary parts of the element of the bus admittance matrix corresponding to the
xth row and the
ythe column.
2.2. Evaluation of the Base Case Resilience of the System
The second phase of the provided framework centers on assessing the base case resilience of the transmission system. This assessment occurs without the introduction of extra generating resources into the system. Instead, the analysis revolves around harnessing the intrinsic capabilities of the existing system, such as the establishment of stable sustainable grid segments or microgrids, to bolster resilience.
In the event of a HILP outage event, the transmission system can be segmented into several interconnected components or islands, with some islands featuring generators and others not. This stage employs graph-theoretic techniques to pinpoint these connected components within the system. By discerning the separate networks of connected components, it becomes feasible to evaluate the outage’s impact on each network and quantify the ensuing load curtailment.
The evaluation of base case resilience involves calculating the LC for each network of connected components. This assessment provides valuable insights into the system’s ability to withstand and recover from disruptive events. By quantifying the amount of load curtailment, a realistic picture of the system’s performance under various HILP outage scenarios can be obtained.
A key resilience metric is introduced in this stage: Expected Load Curtailment (ELC). ELC signifies the expected value of total load curtailments across all HILP outage scenarios under consideration. This metric offers a comprehensive gauge of the system’s resilience, factoring in both the probability and magnitude of curtailed loads in the reduced HILP scenarios. The calculation of ELC is as follows:
where
is the total of reduced HILP scenarios;
represents the probability of the
ith reduced HILP scenario; and
is the amount of load curtailed in case of the
ith reduced HILP scenario.
2.3. Re-Evaluation of System Resilience with Additional Resources
In the first and second stages, the framework generated outage scenarios and evaluated the system’s initial resilience. Building on these assessments, the third and final stage of the framework shifts to reassessing the system’s resilience after integrating extra resources. This stage evaluates how these resources affect the system’s capacity to endure and rebound from HILP events.
In this stage, different resources are introduced into the system to achieve the desired resilience level. These resources can be a mix of renewable energy sources, energy storage systems, microreactors, or other options like reclosers, microgrids, and infrastructure reinforcement. Their selection and positioning are informed by the findings from the earlier stages of the framework. The framework seeks to enhance the system’s resilience by strategically integrating extra generation resources, aiming to decrease load curtailment and improve demand coverage during HILP events. These resources are placed considering the system’s vulnerabilities and critical failure points, with the aim of optimizing their allocation and use to attain the desired resilience level. After the integration of extra generating resources, the system’s resilience is reassessed by repeating the earlier analyses with the updated configuration. This reassessment evaluates the system’s performance during HILP outage scenarios, considering the advantages and capabilities of the newly added generating resources.
In this study, an optimization problem concerning the optimal placement of DERs is addressed to reassess system resilience. The objective of the problem is to determine the optimal locations and sizes of DERs that achieve the target Expected Load Curtailment (ELC) while minimizing the total DER capacity, subject to constraints imposed by power balance equations and the maximum capacities of DERs. The considered optimization problem is formulated as follows:
subject to
where
is the Expected Load Curtailment calculated similarly to (
6) but with the system consisting of DERs;
is the target ELC;
is the capacity of DER at candidate bus
k;
is the penalty factor empirically determined; and
is the maximum allowable capacity of each DER. The candidate buses and
are the decision variables of the problem.
The optimization problem presented above is characterized as nonlinear due to the incorporation of a large number of HILP outage scenarios during the determination of ELC. This nonlinearity makes the problem challenging to address using conventional optimization techniques. Consequently, this study employs graph theory and a genetic algorithm (GA), which is a population-based evolutionary search technique [
27]. The GA implementation in this research involves considering crossover, mutation, and elitist-based selection strategies to enhance the optimization process [
28]. These approaches enable the exploration of a diverse solution space and contribute to the effectiveness of the optimization algorithm in handling the complexity introduced by the multitude of outage scenarios. Since the objective function of the optimization problem under consideration is of minimization type, the fitness function for the GA is calculated using the following expression:
where
represents the minimization-type objective function in Equation (
7).
3. Case Studies and Discussion
In this section, we present a comprehensive exploration of case studies conducted on the IEEE 24-bus system, widely recognized as the Reliability Test System (RTS) [
29]. The primary objective is to provide a detailed demonstration of the functionality and efficacy of the proposed resilient IRP framework. By examining a wide range of outage scenarios on the RTS, we aim to illustrate the practical application and impact of the framework. Through these case studies, we delve into the analysis of HILP outages, the base case resilience level, and the optimal placement of DERs to achieve the desired value of system resilience facilitated by the proposed framework.
3.1. Simulation Setup
The IEEE 24-bus system is commonly utilized as a benchmark in power system analysis, consisting of 24 interconnected buses connected by transmission lines and transformers. This configuration provides a simplified yet realistic representation of an actual power system. Within this system, there are 11 generator buses (including the slack bus), 13 load buses, 5 transformers, and 29 lines (including 4 double-circuit lines treated as single lines). The detailed system data are provided in
Appendix A. We construct an undirected graph, considering buses as vertices and branches (lines and transformers) as edges in the graph. This graph-theory-based approach aids in visually understanding and studying the system’s structure and connections, forming the foundation of our case studies. The Python package “pandapower” [
30] is employed to conduct power flow analyses within both the primary network and isolated network segments. In this work, the DC approximation [
31] to the AC power flow is considered, where bus voltage magnitudes are assumed to be unity and reactive power flow is neglected, along with other assumptions.
3.2. Analysis of the Outage Scenarios
To showcase the effectiveness of the framework, we systematically examine a diverse set of 10,000 randomly generated multiple-line outage scenarios within the IEEE 24-bus system. Each scenario undergoes evaluation to determine its classification as a HILP event, based on the criteria established by our proposed proximity index. This index calculates the proximity of outage lines to generator buses, enabling the identification of scenarios with the potential for significant disruptions. Our focus is then directed towards the HILP events, as they offer valuable insights into the system’s resilience. Leveraging the introduced resilience metric, we conduct a quantitative assessment of the system’s response to these HILP scenarios.
Illustrative figures play a crucial role in communicating the specifics of our case study findings.
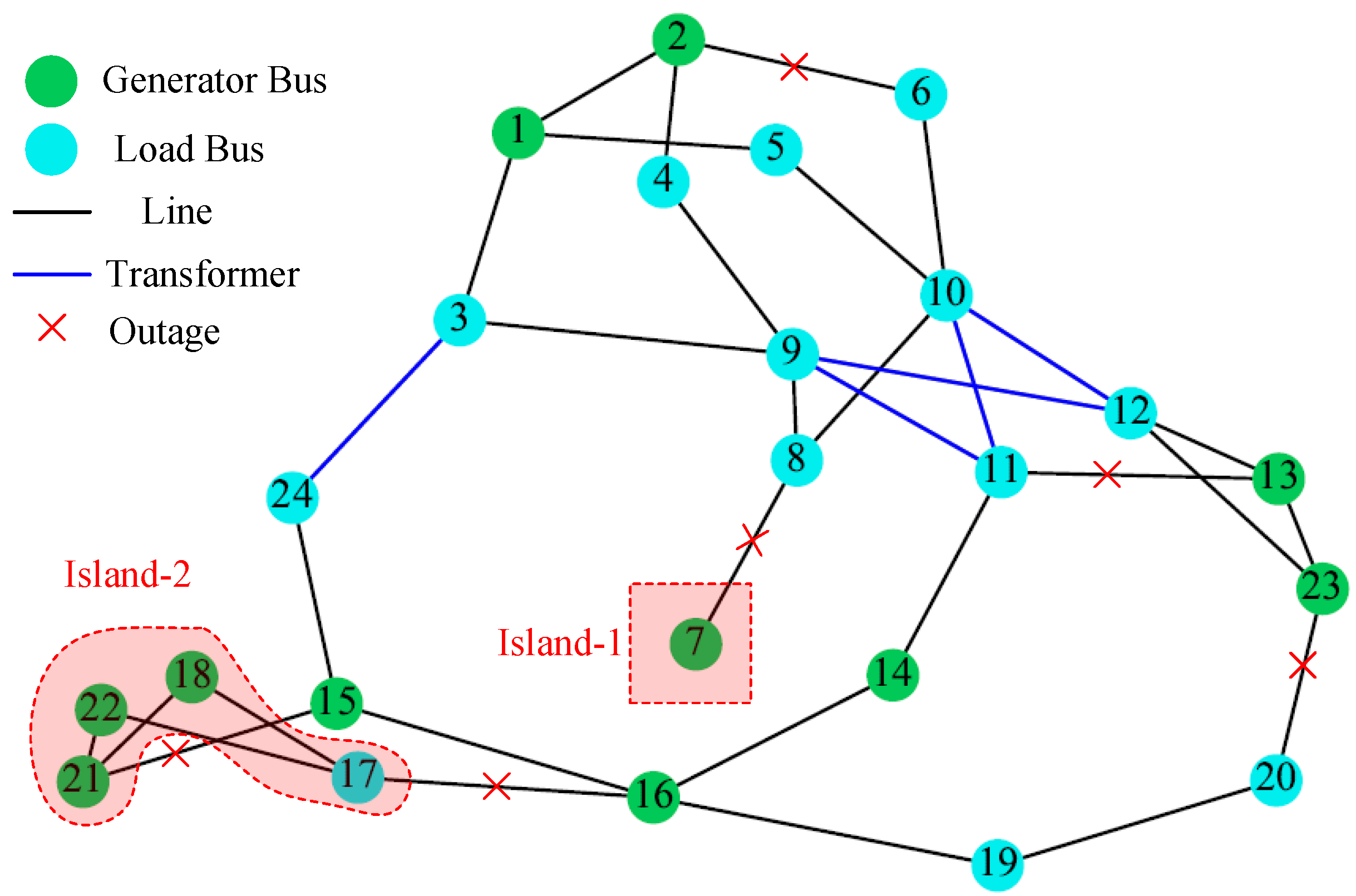
Figure 3 and
Figure 4 showcase two representative outage scenarios selected from the pool of 10,000 randomly generated instances. In scenario 1, the outage affects six transmission lines: 2–6, 3–9, 7–8, 11–13, 16–17, and 20–23. Conversely, scenario 2 involves the outage of lines 2–6, 7–8, 11–13, 15–21, 16–17, and 20–23, with the only distinction being the substitution of lines 3–9 from scenario 1 with lines 15–21. Despite both scenarios featuring six line outages, only the latter, scenario 2, is classified as a HILP event. This classification is determined by the proximity index (PI), which assesses the direct connections between the outaged lines and generator buses. It is noteworthy that the PI for scenario 2 is six, surpassing the PI threshold of six, while the PI for scenario 1 is five, falling just below the PI threshold.
Delving into a more in-depth analysis of each line outage scenario, we focus on the computation of the total load curtailment.
Figure 5 provides a detailed examination of Scenario 1. In this scenario, bus 7 becomes isolated, leading to the creation of an isolated island. Notably, within Island-1, consisting of bus 7, the total load of 125 MW is less than the total available generation of 300 MW, resulting in no load curtailment. Similarly, the remainder of the primary network exhibits a total available generation of 3105 MW, exceeding the total load of 2725 MW, thereby eliminating the need for load curtailment. Consequently, Scenario 1 is characterized by zero total load curtailment.
Similarly,
Figure 6 provides the analysis of Scenario 2. In contrast to Scenario 1, Scenario 2 introduces a more intricate situation where two islands are formed. Island-1, resembling the isolated island from Scenario 1, once again experiences no load curtailment. Island-2 consists of three generator buses (buses 18, 21, and 22) and a load bus (bus 17). With a total generation capacity of 1100 MW exceeding the load demand of 333 MW, Island-2 remains free from curtailment. However, the disconnection of these islands from the primary network results in load curtailment. The total load of the primary network is 2392 MW, but the available capacity remains confined to 2005 MW, leading to a load curtailment of 387 MW. Therefore, the total load curtailment is 387 MW in Scenario 2.
The examination of these scenarios underscores the justification for choosing HILP events, as demonstrated by Scenario 2, which exhibits a more significant disruption attributable to its higher load curtailment. This further substantiates the HILP classification approach relying on the proximity index.
3.3. Scenario Reduction and Evaluation of the Base Case Resilience
Expanding on the preceding analysis, we progress to the second stage, which involves a comprehensive examination of the system’s base case resilience. Within the pool of 10,000 randomly generated multiple-line outage scenarios, a total of 5237 scenarios were identified as HILP events. The distribution of load curtailment (LC) in the original set of HILP scenarios is visually depicted in
Figure 7.
Recognizing the computational challenges associated with evaluating ELC using the full set of 5237 HILP scenarios, we implement a scenario reduction approach based on load curtailment values. This reduction involves clustering the original HILP scenarios into 100 reduced HILP scenarios, grouping them based on the similarity of LC values.
Figure 8 illustrates the distribution of load curtailment in these reduced HILP scenarios.
As a result of LC-based scenario reduction in this work, the computation time to calculate the ELC on a 64-bit 12th-generation Intel i5 1.6 GHz 16 GB RAM PC running the Windows 10 platform is 4 s, compared with 360 s when all 5237 HILP scenarios were considered. Despite the time reduction benefit, there is a compromise in the accuracy of the ELC metric. The ELC calculated using 5237 HILP scenarios is 304.326 MW, whereas with 100 reduced scenarios, an ELC of 256.125 MW was obtained. Thus, the accuracy is reduced by 15.8% as a result of scenario reduction. There is a trade-off between computation time and accuracy resulting from scenario reduction. Based on the desired level of accuracy, scenario reduction can be performed.
The proposed approach not only addresses computational efficiency concerns but also provides a meaningful representation of the system’s base case resilience, considering a condensed yet representative set of scenarios. The subsequent sections delve into the implications of these findings and explore strategies for enhancing system resilience considering the optimal placement of DERs.
3.4. Resilience Enhancement through Optimal Placement of DERs
The third stage of the study unfolds a systematic approach involving the re-evaluation of resilience metrics through the optimal placement of DERs utilizing a genetic algorithm (GA). In this stage, a population size of 10 is considered, where the size of individual chromosomes is contingent on the maximum limit of DER capacity, the assumed granularity of DERs, and the number of candidate DER locations. All load buses are considered as candidate DER locations, with an arbitrary maximum limit of DER size set at 150 MW and a granularity of 10 MW. The individual chromosomes are represented in binary form, employing a three-point crossover, and incorporating a randomized multipoint mutation. The simulation is halted when the maximum, minimum, and average fitness values converge.
For a thorough exploration, the simulation is iteratively performed with ELC reduction values ranging from 10 MW to 100 MW at intervals of 10 MW.
Figure 9 illustrates the evolution of maximum, minimum, and average fitness, along with the ELC error, as the GA generation progresses toward convergence in the case of an ELC reduction of 10 MW.
The ELC error, as calculated in Equation (
10), measures the percentage deviation from the target ELC from the ELC obtained from the GA:
In the case of an ELC reduction of 10 MW, the maximum, minimum, and average fitness values converge after 58 generations, as shown in
Figure 9. The continuous decrease and stabilization of the ELC error after convergence indicate a consistent and satisfactory solution. As can be seen from the figure, the simulation is allowed to run for an additional 10 generations post convergence to assess if the problem is stuck in a local optimum.
Similarly,
Figure 10 portrays the progression of maximum, minimum, and average fitness, along with the ELC error, as the GA generation advances toward convergence in the case of an ELC reduction of 20 MW. The convergence pattern remains similar to the earlier scenario, but the notable distinction lies in the convergence generation. In this instance, convergence is achieved at the 120th generation. As before, the simulation is continued for an extra 10 generations post convergence.
While similar plots can be generated for higher values of ELC reduction, they are omitted here for the sake of brevity.
Table 1 provides a comprehensive overview of the outcomes derived from the optimal placement of DERs for diverse target ELC values, ranging from an ELC reduction of 10 MW to 100 MW. The table outlines the optimal configurations of DERs, offering insights into the optimal locations and capacities required for achieving specific levels of resilience improvement.
Furthermore,
Figure 11 complements the tabulated results by providing a graphical representation of the correlation between ELC reduction and total DER capacity. This visual representation highlights the increase in total DER capacity as the desired ELC reduction grows. The observed trend indicates that aiming for higher levels of resilience enhancement leads to the deployment of increased DER capacities.
The overarching implication derived from these findings is that decisions regarding the desired level of resilience should be informed by comprehensive technoeconomic analyses. However, it is important to note that detailed technoeconomic analyses are beyond the scope of this article.
3.5. Comparison of HILP-Based Planning with Traditional Reliability-Based Planning
Traditional reliability-based planning methods typically focus on the average value of all events, encompassing both low-impact and high-impact events [
32].
Figure 12 illustrates the distribution of load curtailment in the original 10,000 randomly generated multiple-line outage scenarios. In comparison with
Figure 7, which includes only 1400 outage scenarios with load curtailment ranging from 0 to 143 MW,
Figure 12 reveals that more than 5000 outage scenarios have load curtailment within the same range. This abundance of lower-impact scenarios would lead to a decreased value of ELC in the reliability-based planning approach. The ELC computed based on the original scenarios is 178.79 MW, which is lower than the ELC obtained from the HILP scenarios. This difference arises because traditional reliability-based analysis tends to average out scenarios, often overlooking high-impact events. Resilience planning, on the other hand, emphasizes a higher risk level and investment, as reflected by the higher values of ELC.
3.6. Scalability Challenges
The proposed framework for the resilient IRP of transmission systems itself does not pose any scalability challenges and can be easily adopted or implemented in larger transmission systems. However, scalability challenges may arise due to the use of GA for the optimal placement of DERs for enhanced resilience. It is important to note that the proposed resilient IRP is a planning problem that does not require frequent execution. Consequently, high-speed computation is not a primary concern in this context. Modern computers are capable of handling this task for most practical-sized systems. However, in situations where resources are limited or specific needs arise, the framework remains flexible. It can accommodate simpler and approximate optimization methods for the optimal placement of DERs. This flexibility ensures that the proposed framework remains a reliable and practical solution, even when resources are scarce.
4. Conclusions and Future Work
In this article, we introduced a resilient IRP framework tailored for transmission systems, specifically designed to tackle the challenges posed by HILP events. The framework unfolds across three distinct stages: (a) outage data generation, selection of HILP events, and scenario reduction; (b) evaluation of base case resilience; and (c) re-evaluation of system resilience with additional resources, incorporating the use of a GA. Employing graph-theoretic modeling and strategically considering connected components, the framework provides a systematic methodology for assessing, enhancing, and optimizing the resilience of the transmission system.
The application of our proposed framework, including the utilization of a GA, yields valuable insights into the vulnerabilities and behavior of the transmission system when subjected to HILP events. The evaluation of base case resilience establishes a benchmark for gauging system performance, while the selection of HILP events concentrates on disruptive incidents with substantial impacts. Subsequently, the re-evaluation stage enables the assessment of the effectiveness of additional resources, particularly demonstrated through the optimal placement of DERs using the GA, to achieve the desired values of ELC reduction. By quantifying the resilience metric ELC, our framework, enhanced by the GA, facilitates informed decision making for investment in resource allocation, ultimately enhancing the system’s ability to withstand and recover from disruptions. Furthermore, this approach contributes to the broader goal of advancing energy sustainability by promoting efficient resource utilization and resilient power system planning.
In future research endeavors, a promising avenue to explore involves conducting a technoeconomic analysis. This analysis aims to determine the optimal sizes of DERs, considering both the benefits derived from increased resiliency, as indicated by ELC reduction, and the associated costs arising from the augmentation of DER capacity for resilience enhancement. This integrated approach ensures a comprehensive understanding of the trade-offs between resiliency benefits and economic considerations, contributing to the development of more robust and economically viable transmission systems. Additionally, incorporating the outage probability of generators into the proposed resilience planning framework could be a potential future avenue, further enhancing the framework’s capability to address system vulnerabilities.