Impact of Probabilistic Modeling Alternatives on the Seismic Fragility Analysis of Reinforced Concrete Dual Wall–Frame Buildings towards Resilient Designs
Abstract
1. Introduction
2. Alternative PDFs to Generate Fragility Functions
2.1. Lognormal Distribution
2.2. Weibull Distribution
2.3. Gumbel Distribution
2.4. Gamma Distribution
2.5. Cauchy Distribution
2.6. Inverse Weibull Distribution
2.7. Inverse Gamma Distribution
3. Development of Fragility Functions of RC Buildings
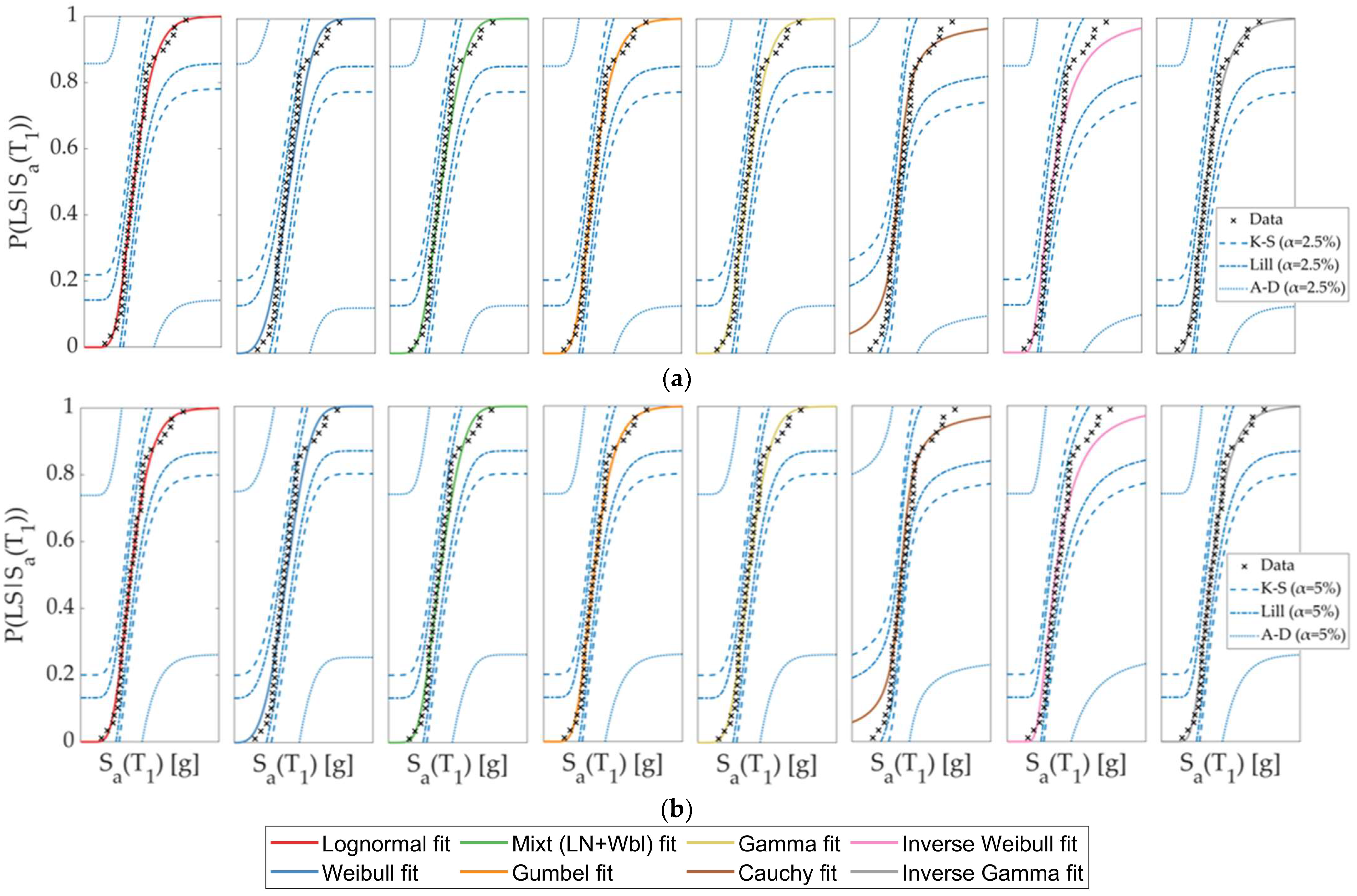
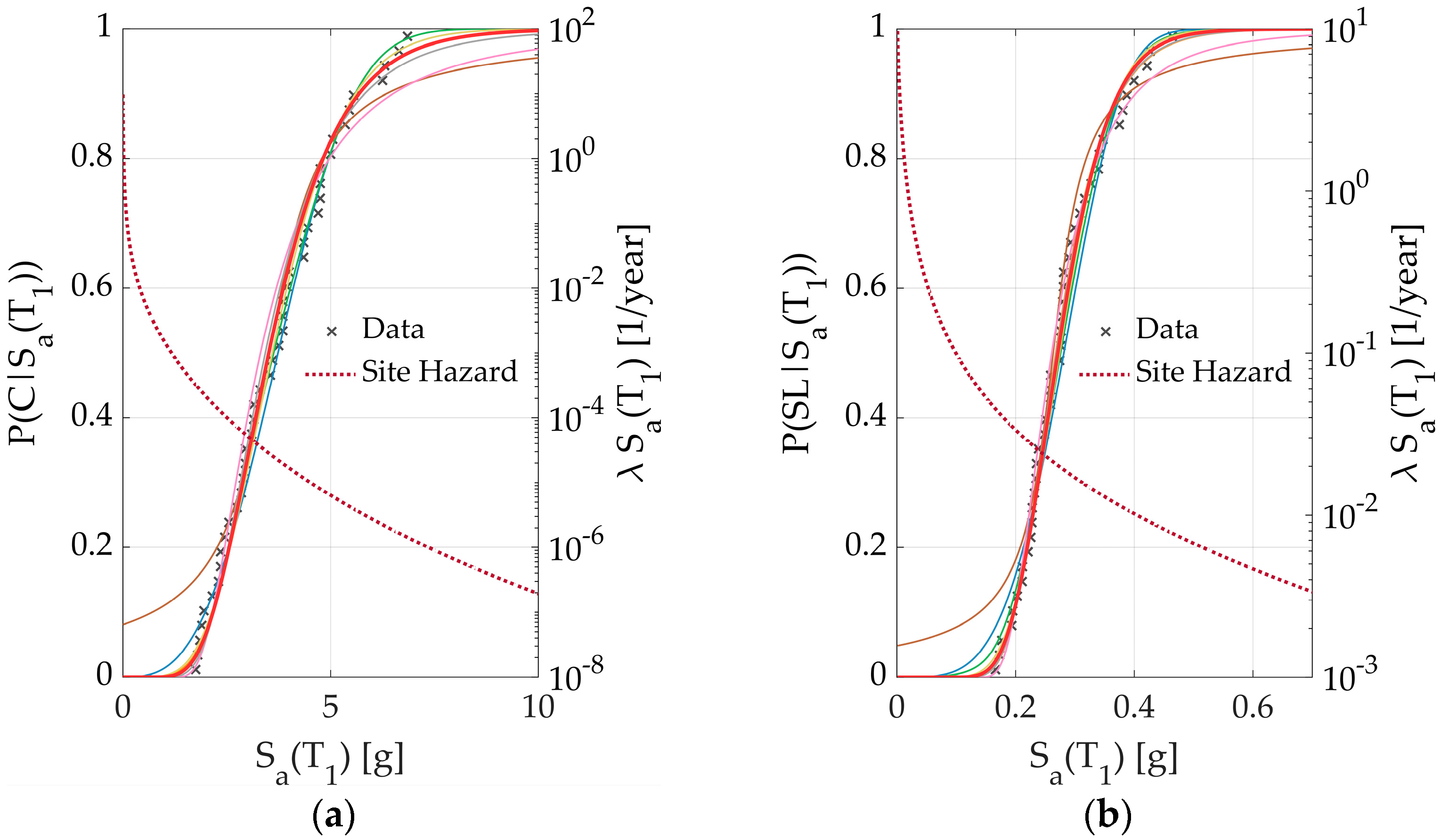
3.1. Fitting of Fragility Functions Procedure
3.2. Assessment of the Quality of the Fragility Functions
3.2.1. Goodness-of-Fit Tests
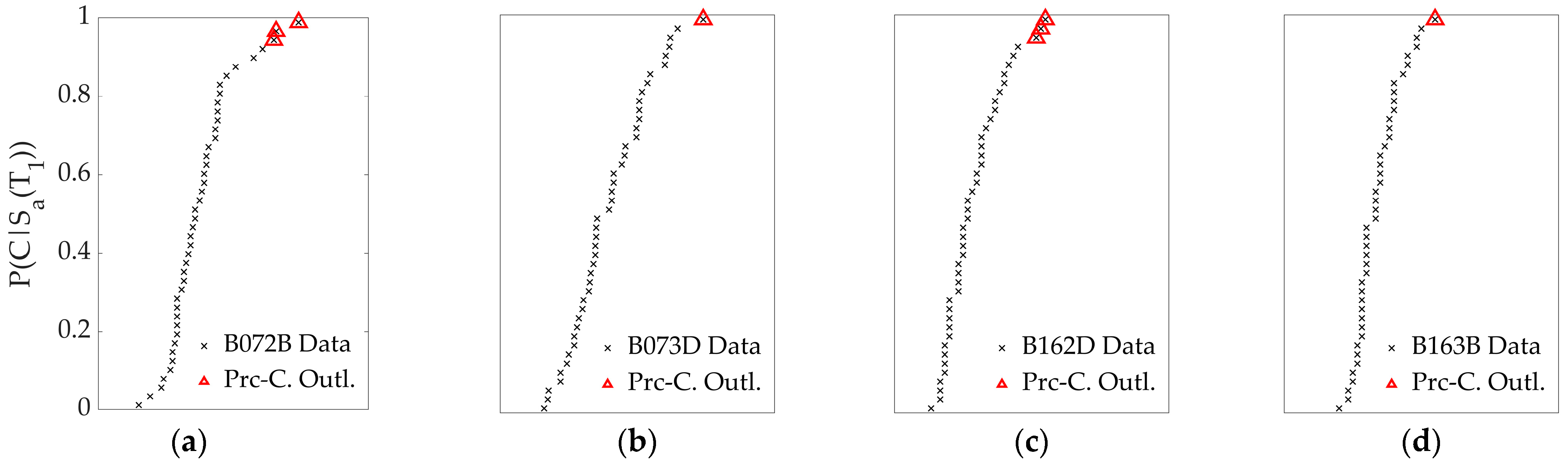
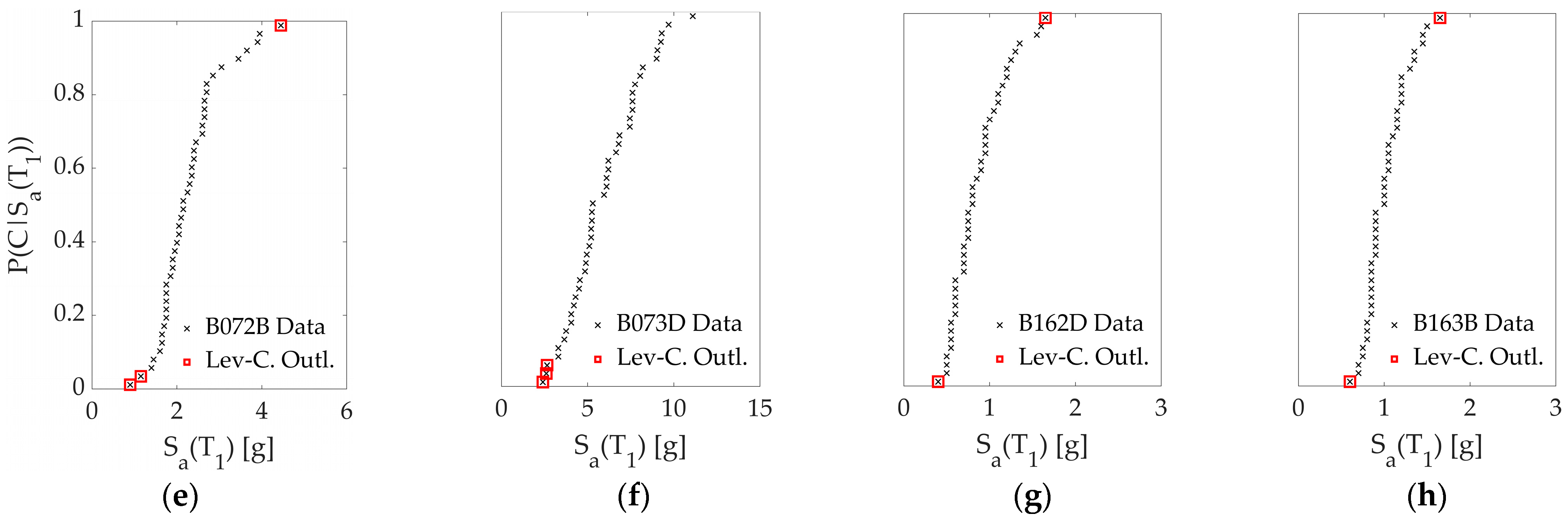
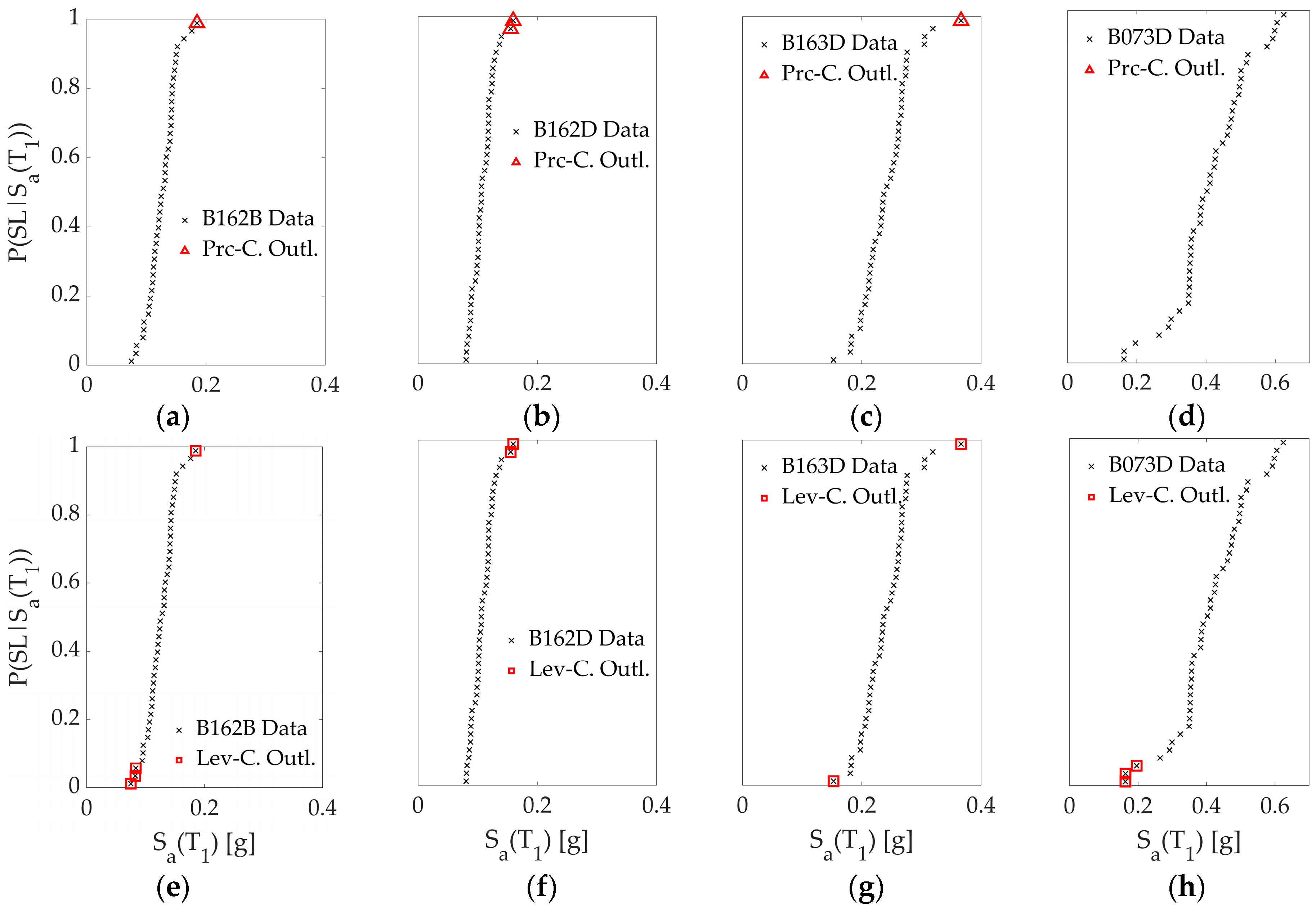
3.2.2. Identification of Data Outliers
3.2.3. Comparison of Estimated Parameters
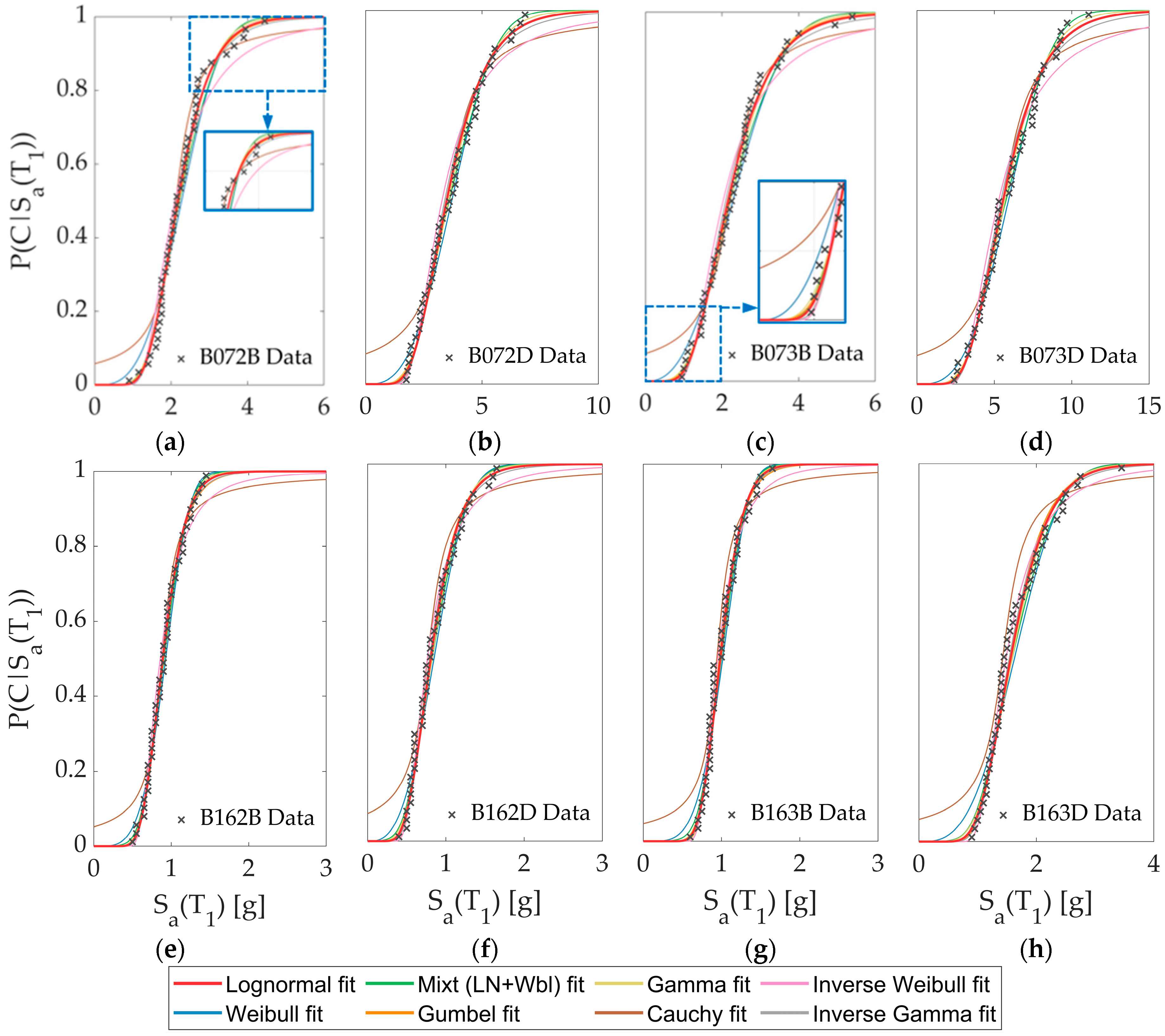
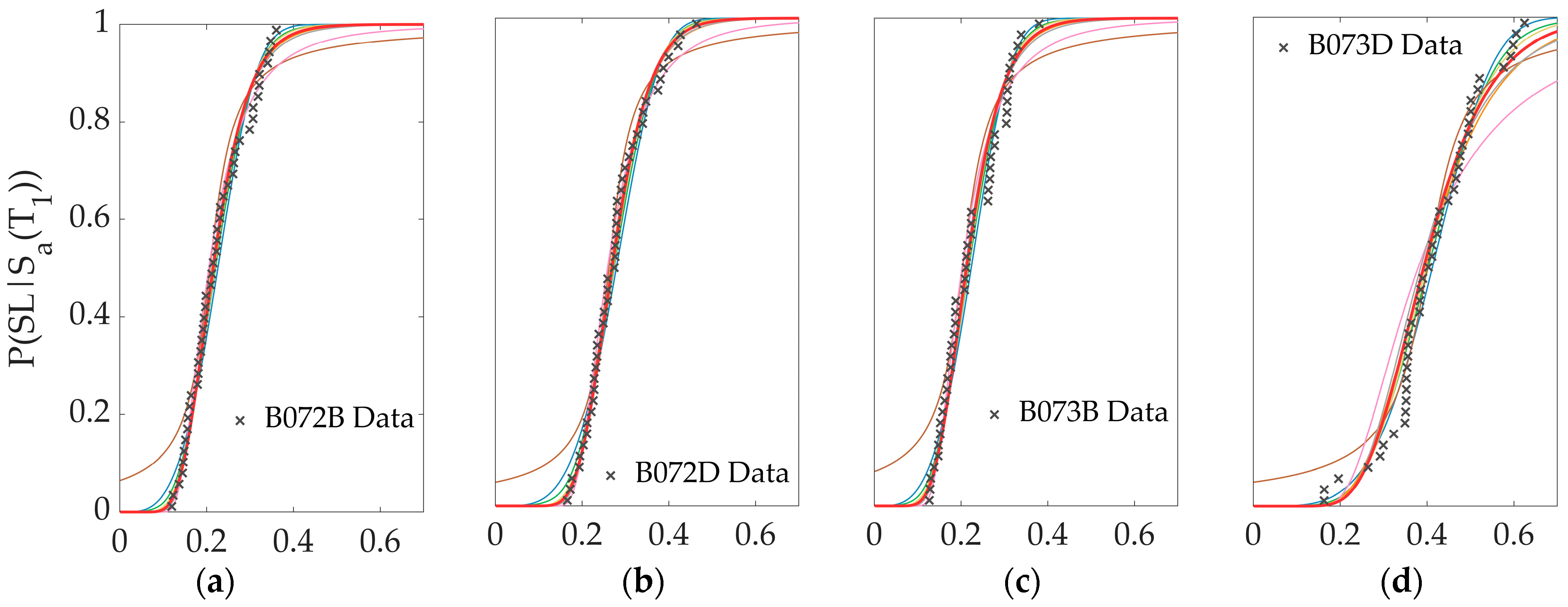
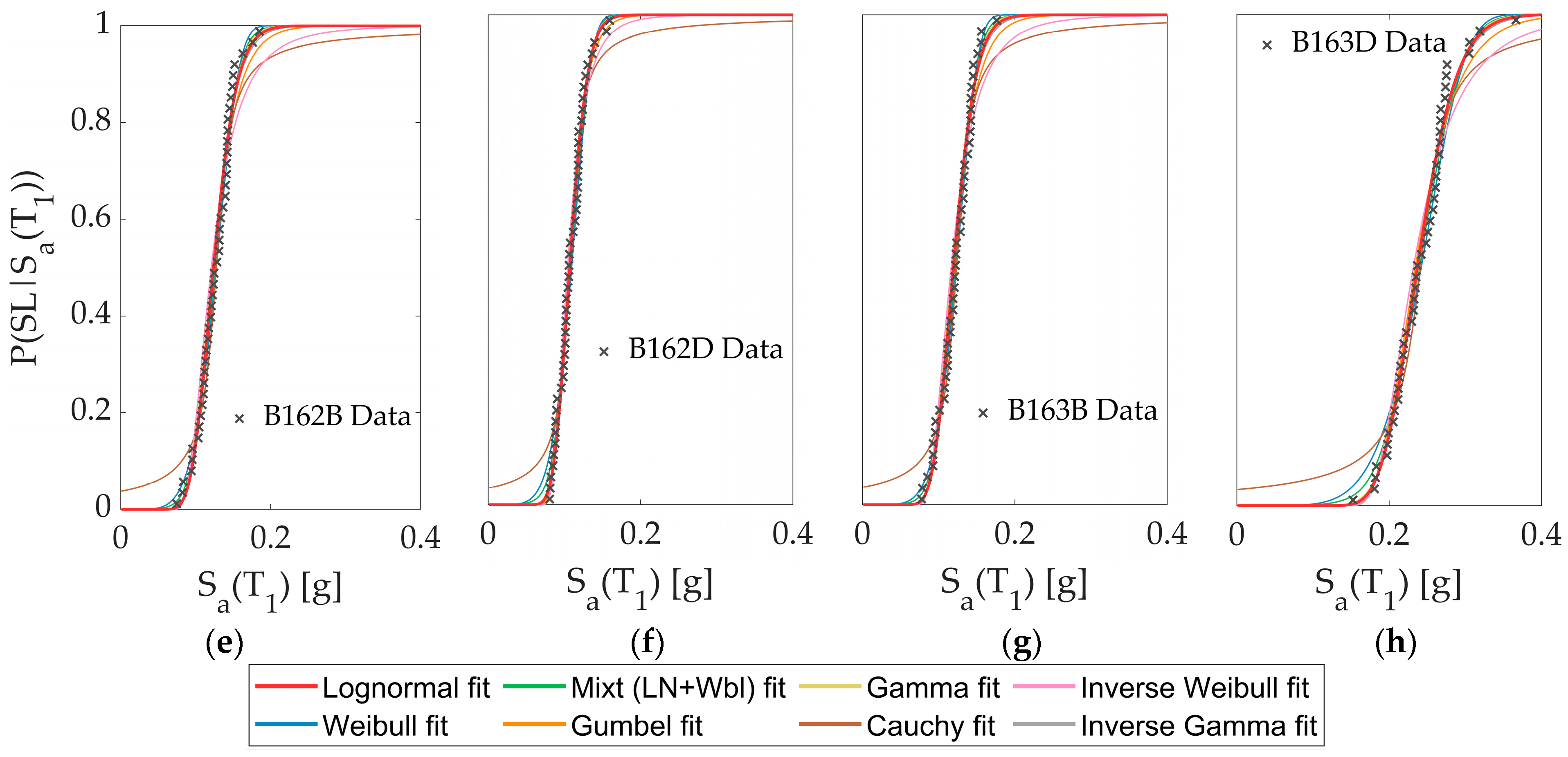
3.2.4. Comparison of Alternative PDFs
4. Impact of Alternative Fragility Functions on Annualized Performance-Based Metrics
Metrics Variability
5. Conclusions
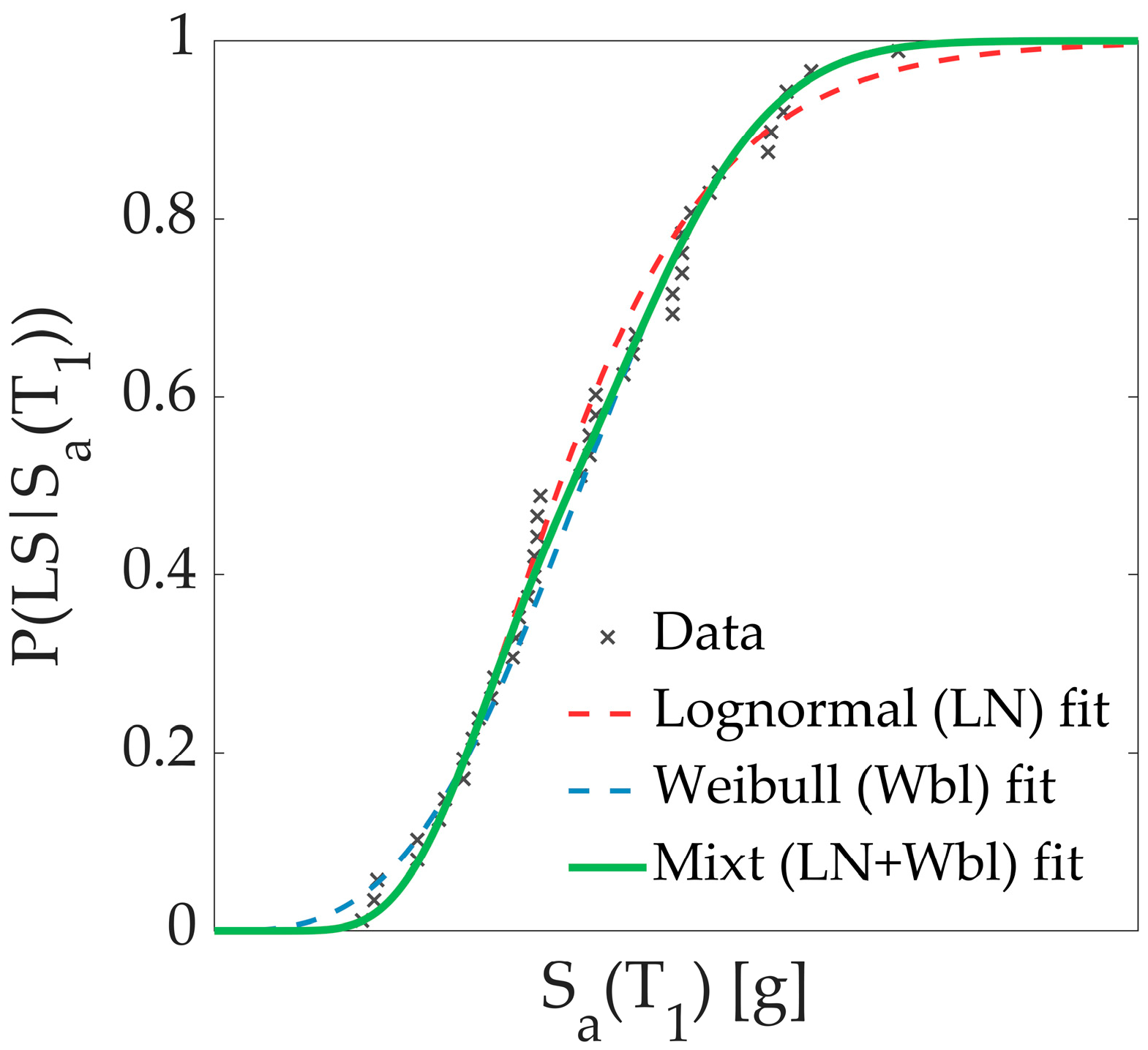
- Even though the Lognormal PDF is, by far, the most widely used PDF within Performance-Based Earthquake Engineering (PBEE), there are other PDFs, such as Weibull or Gamma, that are technically valid (e.g., positive-skewed distribution) to represent fragility functions, that pass goodness-of-fit tests, but that provide significantly different adjustments in some part of the fragility functions (e.g., the Lognormal PDF usually adjusts better to the data in the lower part of the fragility function, whereas the Weibull PDF often adjusts better to the data in the upper part of the fragility function. Actually, a Lognormal PDF is not always the best representation of the data).
- Even though the simulated data used in this study passed all alternative goodness-of-fit tests, the Lilliefors test always resulted in the stricter test for the same confidence level when compared with the Kolmogorov–Smirnov (K–S) and Anderson–Darling (A–D) tests. It is worth noting that several studies have addressed PBEE use of the K–S, which is a more relaxed test that might lead to fragility functions that the Lilliefors test could have rejected.
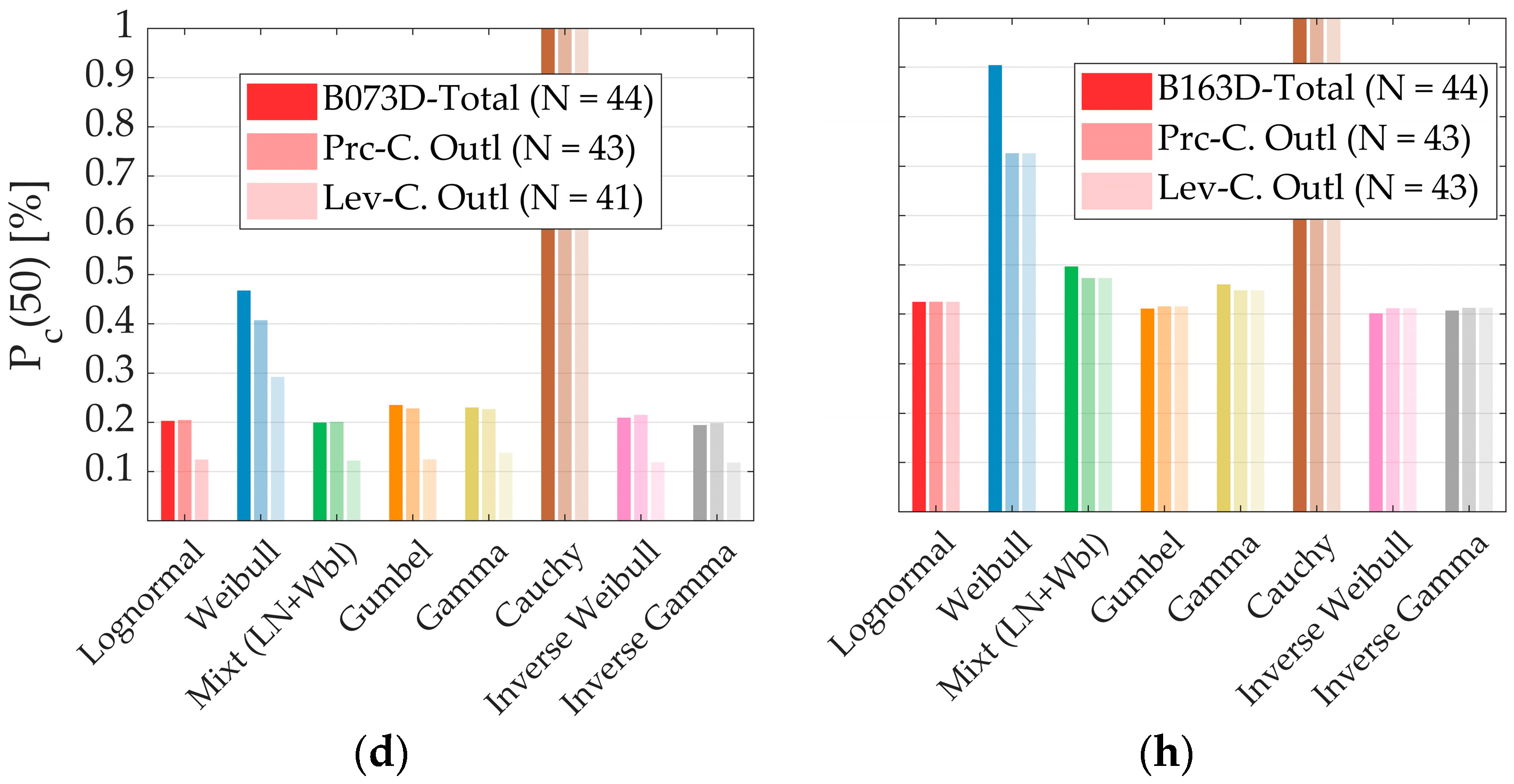
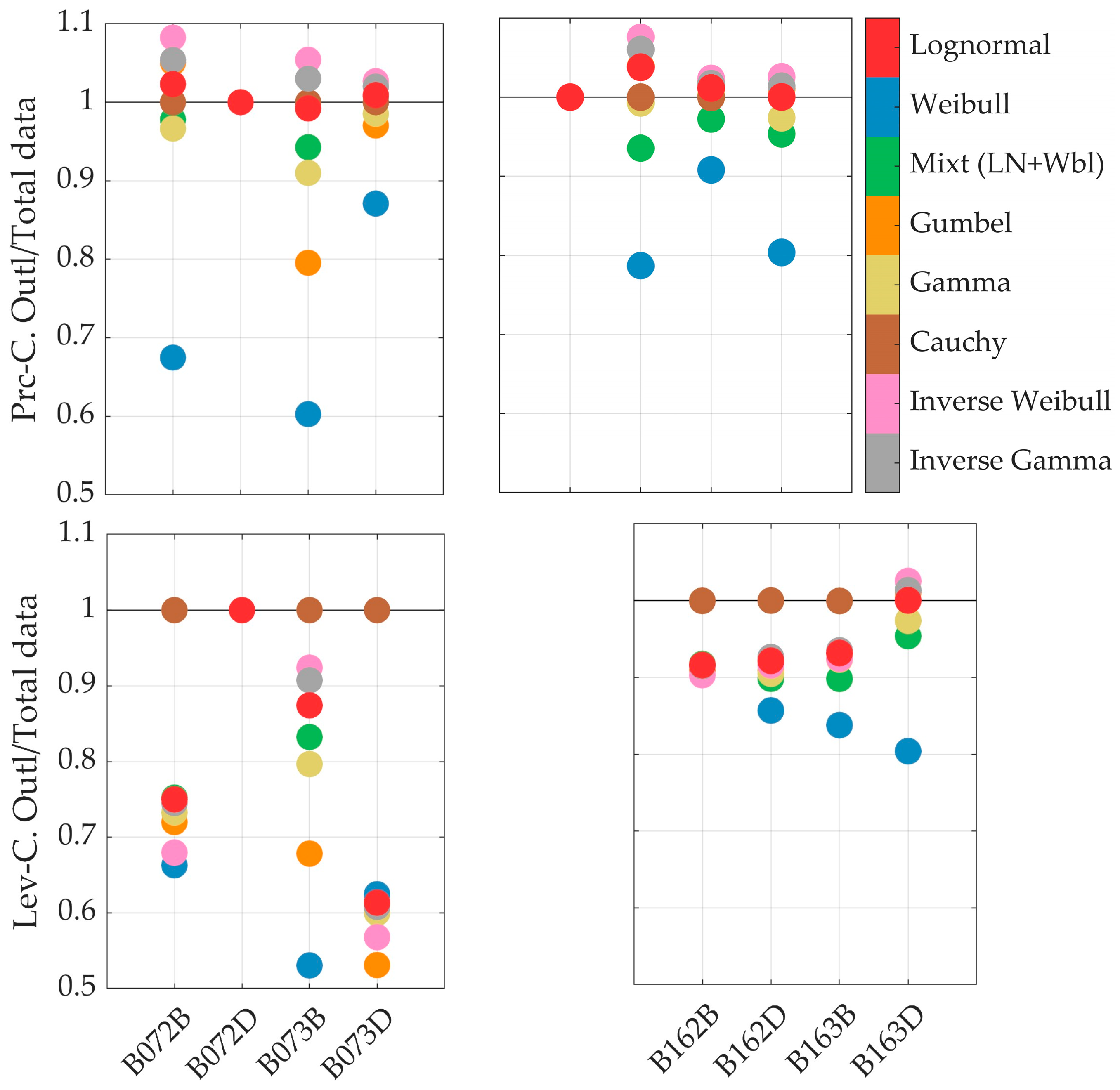
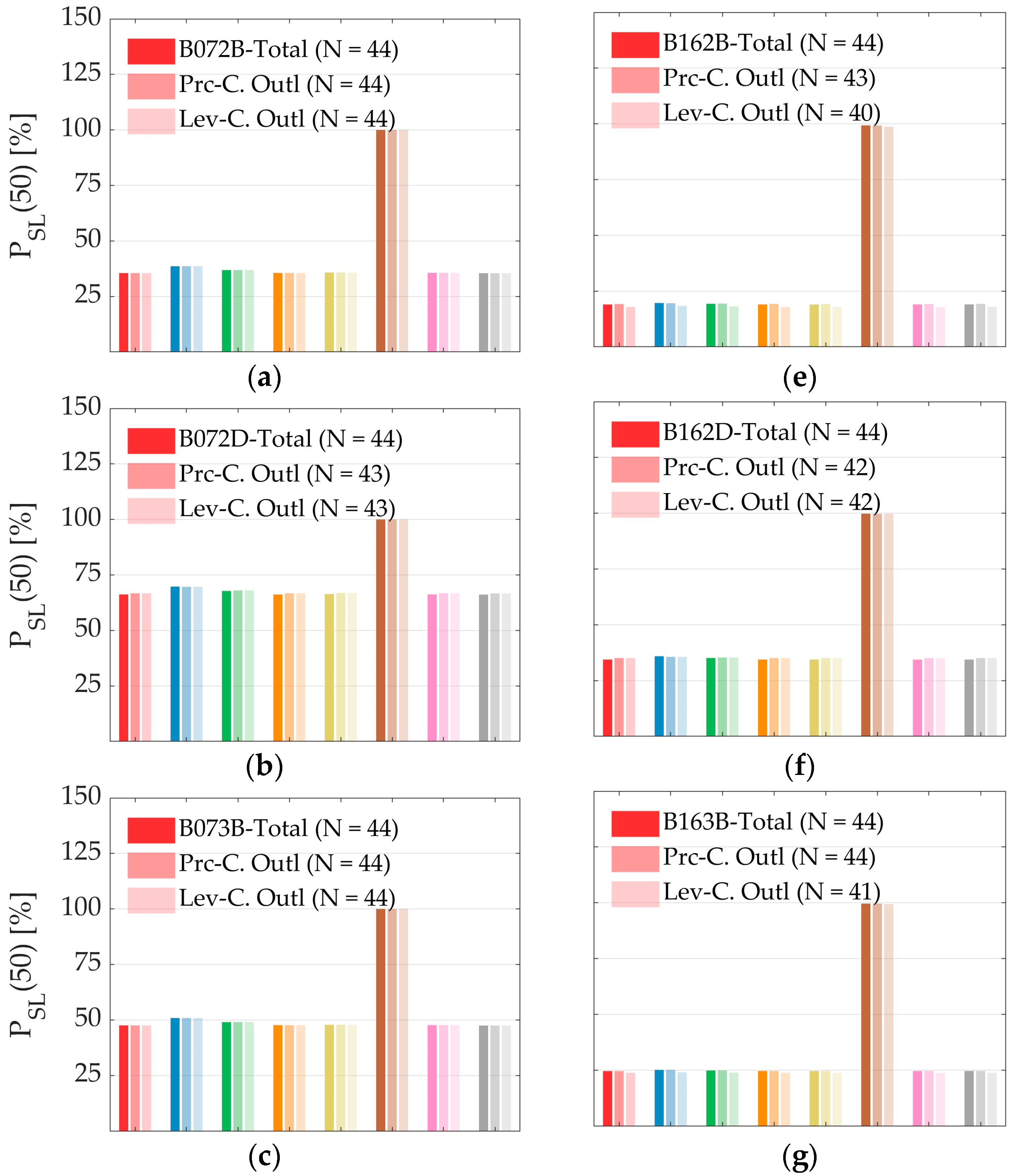
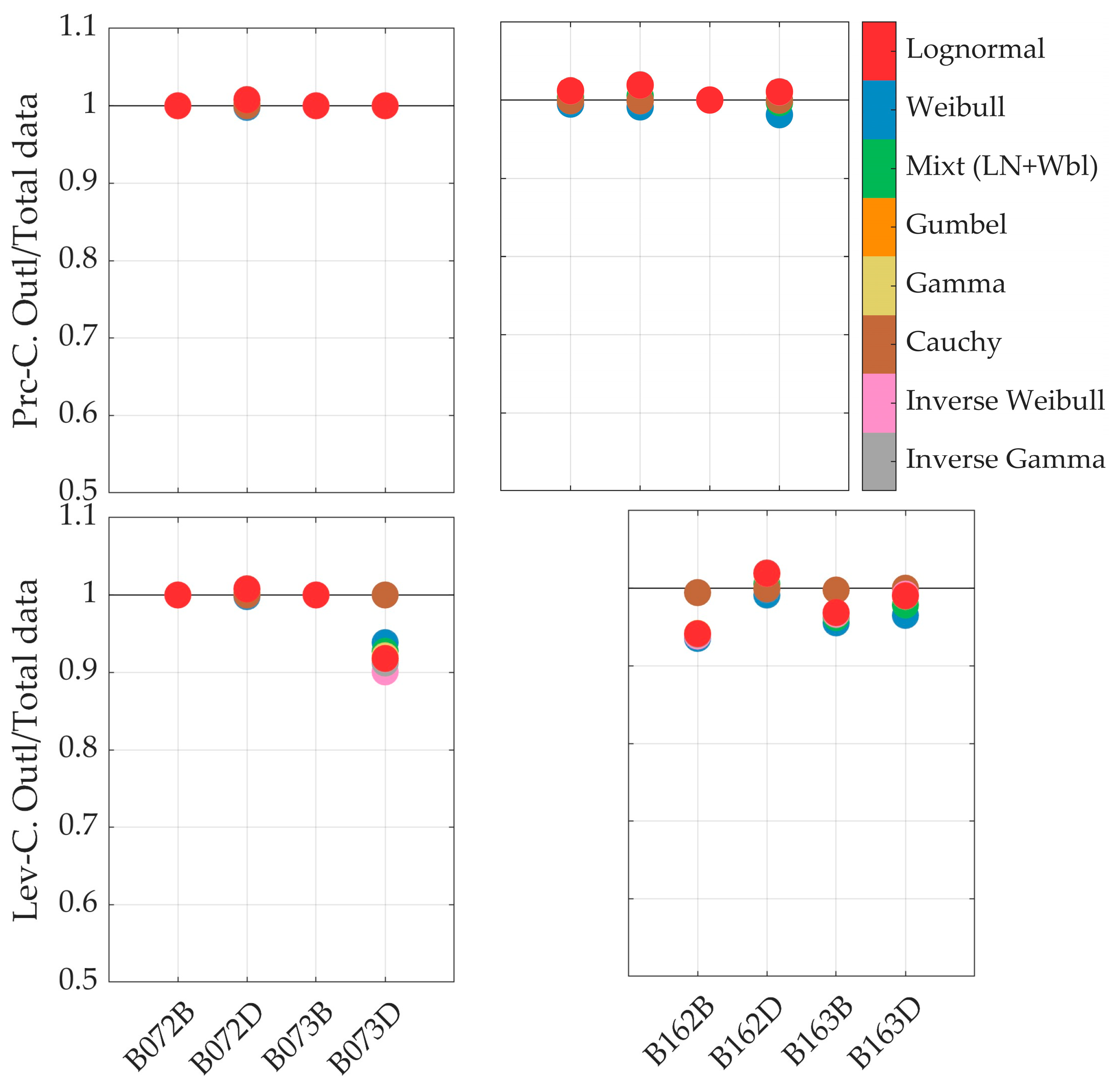
- Nevertheless, the use of outlier detection methods to remove unusual data and the subsequent estimation of new parameters (when the difference between previous and posterior parameters differs by more than 20%) is recommended by FEMA P-58; several studies within PBEE do not even mention the application of this process. In this study, several PDFs presented differences larger than 20% (never the Lognormal PDF, but still showed a −19.21% difference in one case), highlighting the need to implement these outlier detection methods. When comparing past and new estimated parameters after the elimination of data outliers, there is no correlation between which PDF is the one that exhibits the lower or higher variability. This variability is also not explained by a correlation between the leverage or Peirce’s criteria.
- The leverage criterion tends to be more sensitive to the suspicious data of the lower tails of the fragility functions. In contrast, Peirce’s criterion tends to be more sensitive to the upper tail of the fragility functions. The latter effects might generate significant differences, since lower values (located at the lower tail of the fragility functions) tend to affect more annualized metrics associated with intensity measures that occur more often. The latter explains why applying the leverage criterion exhibits the most variability in the assessment measures.
- The use of information criteria allows the quantitative evaluation of alternative PDF based on their adjustment to data, and there is no correlation between best-ranked fitted functions for the eight buildings used in this study. In particular, the Cauchy PDF is always the worst function. At the same time, the Inverse Gamma and Inverse Weibull usually fit better after eliminating the data outlier for the case of collapse LS. However, the Mixture PDF proposed in this study (a combination of a Lognormal PDF and Weibull PDF from 0 to 50% and from 50% to 100%, respectively) tends to fit better for mid-rise RC buildings for Service-Level LS.
- Finally, it is essential to highlight that even though there have been several efforts to advance to more accurate experimental and numerical methods within PBEE to better predict the performance of our built environment (in terms of casualties, environmental impacts, economic losses, and downtime) fewer efforts have been placed on assessing alternative probabilistic methods, whose impacts can be even more significant than some differences generated by some, for instance, structural modeling methods. Consequently, this study recommends the use of multi-comparative analyses for probabilistic model selection (including the alternative outlier detection methods, the PDFs, and the information criteria analyses proposed in this study, except the Cauchy PDF) on a case-to-case basis for extreme LS, such as collapse. These extreme LSs are characterized by large variability (high nonlinear behavior), and significant differences are detected when applying alternative probabilistic methods. Thus, the implementation of these computationally very low-cost intensive probabilistic methods, when compared with other computational methods used in PBEE (e.g., finite element models or IDAs), is recommended to provide the best fitting to each particular building-specific data set to obtain more accurate PBEE estimations. In the case of the SL LS, since the differences obtained from applying these alternative probabilistic methods have significantly lower impacts, the step of multi-comparative analysis for model-selection assessment could be skipped compared with the collapse LS.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| A–D | Anderson–Darling |
| AIC | Akaike Information Criteria |
| BIC | Bayesian Information Criteria |
| B072B | 7-story building located in seismic zone 2 on soil type B |
| B072D | 7-story building located in seismic zone 2 on soil type D |
| B073B | 7-story building located in seismic zone 3 on soil type B |
| B073D | 7-story building located in seismic zone 3 on soil type D |
| B162B | 16-story building located in seismic zone 2 on soil type B |
| B162D | 16-story building located in seismic zone 2 on soil type D |
| B163B | 16-story building located in seismic zone 3 on soil type B |
| B163D | 16-story building located in seismic zone 3 on soil type D |
| CDF | Cumulative Distribution Function |
| DS | Damage State |
| EDP | Engineering Demand Parameter |
| IDA | Incremental Dynamic Analysis |
| IM | Intensity Measure |
| K–S | Kolmogorov–Smirnov goodness-of-fit test |
| Lev-C. | Leverage criterion for data outlier |
| Lill. | Lilliefors goodness-of-fit test |
| LS | Limit State |
| MLM | Maximum Likelihood Method |
| SL | Service Level |
| PBEE | Performance-Based Earthquake Engineering |
| Prc-C. | Peirce’s criterion for data outlier |
| Probability Distribution Function | |
| PFA | Peak Floor Acceleration |
| PSDR | Peak Story Drift Ratio |
| RC | Reinforced Concrete |
| RDR | Roof Drift Ratio |
| Notation list | |
| Spectral acceleration ordinate at the fundamental period of the structure | |
| Probability of a specific limit state conditioned on the spectral pseudo acceleration | |
| Mean annual frequency of a specific limit state | |
| Probability of exceeding a specific limit state in a time of 50 years |
References
- Krawinkler, H.; Miranda, E. Performance-Based Earthquake Engineering. In Earthquake Engineering: From Engineering Seismology to Performance-Based Engineering; Bozorgnia, Y., Bertero, V.V., Eds.; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Deierlein, G.G. Overview of a Comprehensive Framework for Earthquake Performance Assessment. In Proceedings of the International Workshop on Performance-Based Seismic Design—Concepts and Implementation, Bled, Slovenia, 28 June–1 July 2004; pp. 15–26. [Google Scholar]
- Özsoy Özbay, A.E. A Decision Tree-Based Damage Estimation Approach for Preliminary Seismic Assessment of Reinforced Concrete Buildings. Rev. De La Construcción 2023, 22, 5–15. [Google Scholar] [CrossRef]
- FEMA (Federal Emergency Management Agency). Seismic Performance Assessment of Buildings; FEMA P-58-1; FEMA: Washington, DC, USA, 2018.
- Calderón, S.; Vargas, L.; Sandoval, C.; Araya-Letelier, G.; Milani, G. Shear Design Equation and Updated Fragility Functions for Partially Grouted Reinforced Masonry Shear Walls. J. Build. Eng. 2022, 50, 104097. [Google Scholar] [CrossRef]
- Zhang, Z.; Murcia-Delso, J.; Sandoval, C.; Araya-Letelier, G.; Wang, F. In-Plane Shear Strength and Damage Fragility Functions for Partially-Grouted Reinforced Masonry Walls with Bond-Beam Reinforcement. Eng. Struct. 2021, 242, 112569. [Google Scholar] [CrossRef]
- Gallegos, M.; Araya-Letelier, G.; Lopez-Garcia, D. Influence of statistical approaches on structural collapse potential assessment. In Proceedings of the 12th National Conference in Earthquake Engineering, Salt Lake City, UT, USA, 27 June–1 July 2022; Earthquake Engineering Research Institute: Salt Lake City, UT, USA, 2022. [Google Scholar]
- Araya-Letelier, G.; Parra, P.F.; Lopez-Garcia, D.; Garcia-Valdes, A.; Candia, G.; Lagos, R. Collapse Risk Assessment of a Chilean Dual Wall-Frame Reinforced Concrete Office Building. Eng. Struct. 2019, 183, 770–779. [Google Scholar] [CrossRef]
- Pan, J.-X.; Fang, K.-T. Maximum Likelihood Estimation. In Growth Curve Models and Statistical Diagnostics; Pan, J.-X., Fang, K.-T., Eds.; Springer: New York, NY, USA, 2002; pp. 77–158. [Google Scholar]
- Lilliefors, H.W. On the Kolmogorov–Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Massey, F.J. The Kolmogorov–Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Ruggieri, S.; Calò, M.; Cardellicchio, A.; Uva, G. Analytical-Mechanical Based Framework for Seismic Overall Fragility Analysis of Existing RC Buildings in Town Compartments. Bull. Earthq. Eng. 2022, 20, 8179–8216. [Google Scholar] [CrossRef]
- Ruggieri, S.; Liguori, F.S.; Leggieri, V.; Bilotta, A.; Madeo, A.; Casolo, S.; Uva, G. An Archetype-Based Automated Procedure to Derive Global-Local Seismic Fragility of Masonry Building Aggregates: META-FORMA-XL. Int. J. Disaster Risk Reduct. 2023, 95, 103903. [Google Scholar] [CrossRef]
- Devore, J. Probability and Statistics for Engineering and the Sciences, 9th ed.; Cengage Learning: San Luis Obispo, CA, USA, 2014. [Google Scholar]
- Ibarra, L. Global Collapse of Frame Structures under Seismic Excitations. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Shome, N. Probabilistic Seismic Demand Analysis of Nonlinear Structures. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1999. [Google Scholar]
- Song, J. Seismic Reliability Evaluation of Steel Frames with Damaged Welded Connections. Ph.D. Thesis, The Johns Hopkins University, Baltimore, MD, USA, 1998. [Google Scholar]
- Araya-Letelier, G.; Calderón, S.; Sandoval, C.; Sanhueza, M.; Murcia-Delso, J. Fragility Functions for Partially-Grouted Masonry Shear Walls with Bed-Joint Reinforcement. Eng. Struct. 2019, 191, 206–218. [Google Scholar] [CrossRef]
- Ermeydan, I.; Akgönen, A.İ. Investigation on Behavior and Seismic Performance of Reduced Beam Sections. Rev. De La Construcción 2022, 21, 427–446. [Google Scholar] [CrossRef]
- Sayin, B.; Cosgun, T.; Gunes, B. A Methodological Approach for Seismic Performance of Existing Single-Storey Industrial RC Precast Facilities. Rev. De La Construcción 2022, 21, 167–183. [Google Scholar] [CrossRef]
- Baker, J.; Bradley, B.; Stafford, P. Seismic Hazard and Risk Analysis; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Alfredo, H.S.-A.; Tang, W.H. Probability Concepts in Engineering Planning and Design; John Wiley & Sons. Inc.: New York, NY, USA, 2006; Volume 2. [Google Scholar]
- Luko, S.N. A Review of the Weibull Distribution and Selected Engineering Applications. J. Commer. Veh. 1999, 15, 398–412. [Google Scholar]
- Ghanaat, Y.; Patev, R.; Chudgar, A. Seismic Fragility Analysis of Concrete Gravity Dams. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Yahyaabadi, A.; Talebkhah, R.; Adibi, M. Development of Seismic Fragility Curves for Precast Concrete Frames with Cast-in-Situ Concrete Shear-Walls. Earthq. Eng. Eng. Vib. 2022, 21, 149–167. [Google Scholar] [CrossRef]
- Mandal, T.K.; Ghosh, S.; Pujari, N.N. Seismic Fragility Analysis of a Typical Indian PHWR Containment: Comparison of Fragility Models. Struct. Saf. 2016, 58, 11–19. [Google Scholar] [CrossRef]
- Keller, A.Z.; Giblin, M.T.; Farnworth, N.R. Reliability Analysis of Commercial Vehicle Engines. Reliab. Eng. 1985, 10, 15–25. [Google Scholar] [CrossRef]
- Mann, N.R. Simplified Expressions for Obtaining Approximately Optimum System- Reliability Confidence Bounds from Exponential Subsystem Data. J. Am. Stat. Assoc. 1974, 69, 492. [Google Scholar]
- Fisher, R.A.; Tippett, L.H.C. Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Jazi, M.A.; Lai, C.-D.; Alamatsaz, M.H. A Discrete Inverse Weibull Distribution and Estimation of Its Parameters. Stat. Methodol. 2010, 7, 121–132. [Google Scholar] [CrossRef]
- Furman, E.; Zitikis, R. A Monotonicity Property of the Composition of Regularized and Inverted-Regularized Gamma Functions with Applications. J. Math. Anal. Appl. 2008, 348, 971–976. [Google Scholar] [CrossRef]
- Pedersen, H.L. Inverses of Gamma Functions. Constr. Approx. 2015, 41, 251–267. [Google Scholar] [CrossRef]
- Gallegos, M.F.; Araya-Letelier, G.; Lopez-Garcia, D.; Parra, P.F. Collapse Assessment of Mid-Rise RC Dual Wall-Frame Buildings Subjected to Subduction Earthquakes. Buildings 2023, 13, 880. [Google Scholar] [CrossRef]
- Gallegos, M.F.; Araya-Letelier, G.; Lopez-Garcia, D.; Parra, P.F. Seismic Collapse Performance of High-Rise RC Dual System Buildings in Subduction Zones. Case Stud. Constr. Mater. 2023, 18, e02042. [Google Scholar] [CrossRef]
- NCh433:1996 Mod 2009; INN Norma Chilena Oficial NCh433 Of. 1996 Mod. 2009 Diseño Sismico de Edificios. Instituto Nacional de Normalización: Santiago, Chile, 2009.
- MINVU DS 61—Diseño Sismico de Edificios; Ministerio de Vivienda y Urbanismo: Santiago, Chile, 2011.
- Vose, D. Risk Analysis, a Quantitative Guide, 3rd ed.; John Wiley & Sons, Ltd.: Chischester, UK, 2000. [Google Scholar]
- Baker, J.W. Efficient Analytical Fragility Function Fitting Using Dynamic Structural Analysis. Earthq. Spectra 2015, 31, 579–599. [Google Scholar] [CrossRef]
- Cunnane, C. Unbiased Plotting Positions—A Review. J. Hydrol. (Amst.) 1978, 37, 205–222. [Google Scholar] [CrossRef]
- Araya-Letelier, G. Design of Building Structural Systems and Enhanced Partition Walls to Improve Life Cycle Costs Associated with Risk of Earthquake Damage. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2014. [Google Scholar]
- Campbell, N.A. Mixture Models and Atypical Values. J. Int. Assoc. Math. Geol. 1984, 16, 465–477. [Google Scholar] [CrossRef]
- Albabtain, A.A.; Shrahili, M.; Al-Shehri, M.A.; Kayid, M. Stochastic Comparisons of Weighted Distributions and Their Mixtures. Entropy 2020, 22, 843. [Google Scholar] [CrossRef] [PubMed]
- Ross, S.M. Peirce’s Criterion for the Elimination of Suspect Experimental Data. J. Eng. Technol. 2003. Available online: https://classes.engineering.wustl.edu/2009/fall/che473/handouts/OutlierRejection.pdf (accessed on 9 February 2024).
- Lglewicz, B.; Hoaglin, D.C. How to Detect and Handle Outliers; Mykytka, E.F., Ed.; American Society for Quality Control, Statistics Division: Milwaukee, WI, USA, 1993; Volume 16. [Google Scholar]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer New York: New York, NY, USA, 2013; Volume 103. [Google Scholar]
- Zentner, I. A General Framework for the Estimation of Analytical Fragility Functions Based on Multivariate Probability Distributions. Struct. Saf. 2017, 64, 54–61. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the Dimension of a Model. Ann. Stat. 1978, 2, 461–464. [Google Scholar] [CrossRef]
- ASCE (American Association of Civil Engineers). Minimum Design Loads and Associated Criteria for Buildings and Other Structures ASCE/SEI 7-22; American Association of Civil Engineers: Reston, VA, USA, 2022. [Google Scholar]


| Name | 1st Parameter | 2nd Parameter | Equation | |
|---|---|---|---|---|
| Lognormal ✓ | median | logarithmic standard deviation | (1) | |
| Weibull ✓ | shape | scale | (2) | |
| Gumbel ✓ | location | scale | (3) | |
| Gamma ✓ | shape | rate | (4) | |
| Cauchy ✓✓ | location | scale | (5) | |
| Inverse Weibull ✓✓ | shape | scale | (6) | |
| Inverse Gamma ✓✓ | shape | scale | (7) |
| Requirement | FEMA P58-1 (Lognormal PDF only) | This Study (All PDFs) |
|---|---|---|
| Peer reviewed | Yes | Yes |
| Number of specimens | ≥5 | 44 |
| Goodness-of-fitness | Lilliefors test (α = 5%) 1 | Lill. test (α = 2.5%, α = 5%) K–S test (α = 2.5%, α = 5%) A–D (α = 2.5%, α = 5%) |
| Elimination of outliers | Peirce’s criterion | Peirce’s criterion Leverage criterion |
| Re-estimation of PDF parameters after removal of outliers |
|
|
| Outliers Criteria | B072B | B072D | B073B | B073D | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | ||
| Peirce | Lognormal | −4.51% | −13.01% | 0.00% | 0.00% | −4.03% | −9.48% | −1.58% | −2.94% |
| Weibull | 26.23% | −7.01% | 0.00% | 0.00% | 23.36% | −6.42% | 6.02% | −2.22% | |
| Mixt (LN + Wbl) | −4.51% | −13.01% | 0.00% | 0.00% | −4.03% | −9.48% | −1.58% | −2.94% | |
| Gumbel | −12.08% | −3.64% | 0.00% | 0.00% | −10.74% | −3.50% | −3.77% | −1.40% | |
| Gamma | 37.02% | 45.44% | 0.00% | 0.00% | 26.40% | 34.00% | 6.80% | 8.97% | |
| Cauchy | −1.58% | −10.24% | 0.00% | 0.00% | −0.91% | −6.40% | −0.97% | −3.70% | |
| Inverse Weibull | 5.90% | −3.05% | 0.00% | 0.00% | 5.39% | −2.63% | 1.89% | −1.13% | |
| Inverse Gamma | 26.43% | 22.03% | 0.00% | 0.00% | 17.45% | 14.13% | 5.30% | 4.02% | |
| Leverage | Lognormal | 1.99% | −19.21% | 0.00% | 0.00% | −2.17% | −13.73% | 5.94% | −15.46% |
| Weibull | 16.38% | −0.54% | 0.00% | 0.00% | 27.64% | −5.30% | 11.12% | 3.57% | |
| Mixt (LN + Wbl) | 1.99% | −19.21% | 0.00% | 0.00% | −2.17% | −13.73% | 5.94% | −15.46% | |
| Gumbel | −21.74% | 3.29% | 0.00% | 0.00% | −13.25% | −1.39% | −11.76% | 6.81% | |
| Gamma | 46.35% | 45.77% | 0.00% | 0.00% | 37.79% | 44.07% | 33.56% | 28.18% | |
| Cauchy | 0.83% | −8.25% | 0.00% | 0.00% | 0.21% | −9.10% | 3.20% | −5.17% | |
| Inverse Weibull | 52.59% | 5.90% | 0.00% | 0.00% | 11.24% | 0.22% | 30.42% | 9.66% | |
| Inverse Gamma | 60.66% | 67.05% | 0.00% | 0.00% | 29.85% | 29.51% | 44.94% | 57.04% | |
| Outliers Criteria | B162B | B162D | B163B | B163D | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | ||
| Peirce | Lognormal | 0.00% | 0.00% | −4.79% | −11.78% | −1.17% | −5.00% | −1.80% | −6.50% |
| Weibull | 0.00% | 0.00% | 20.29% | −7.00% | 8.56% | −1.84% | 13.25% | −3.01% | |
| Mixt (LN + Wbl) | 0.00% | 0.00% | −4.79% | −11.78% | −1.17% | −5.00% | −1.80% | −6.50% | |
| Gumbel | 0.00% | 0.00% | −14.12% | −4.01% | −4.54% | −0.87% | −6.78% | −1.38% | |
| Gamma | 0.00% | 0.00% | 30.65% | 39.21% | 11.64% | 13.27% | 16.31% | 19.29% | |
| Cauchy | 0.00% | 0.00% | −2.25% | −11.15% | −0.62% | −4.01% | −0.46% | −4.68% | |
| Inverse Weibull | 0.00% | 0.00% | 8.85% | −3.13% | 2.94% | −0.73% | 4.00% | −1.04% | |
| Inverse Gamma | 0.00% | 0.00% | 25.15% | 20.59% | 9.84% | 8.79% | 12.32% | 10.87% | |
| Leverage | Lognormal | 1.35% | −4.97% | 0.03% | −7.91% | −0.01% | −10.15% | −1.80% | −6.50% |
| Weibull | 3.10% | 0.85% | 7.67% | −1.27% | 11.81% | −1.11% | 13.25% | −3.01% | |
| Mixt (LN + Wbl) | 1.35% | −4.97% | 0.03% | −7.91% | −0.01% | −10.15% | −1.80% | −6.50% | |
| Gumbel | −4.92% | 1.69% | −8.45% | 0.53% | −11.96% | 0.67% | −6.78% | −1.38% | |
| Gamma | 9.54% | 8.39% | 16.90% | 17.90% | 23.25% | 23.86% | 16.31% | 19.29% | |
| Cauchy | 0.61% | −2.66% | 0.20% | −5.52% | −0.04% | −5.64% | −0.46% | −4.68% | |
| Inverse Weibull | 9.12% | 2.16% | 13.25% | 1.50% | 18.48% | 1.22% | 4.00% | −1.04% | |
| Inverse Gamma | 11.79% | 13.70% | 18.31% | 19.44% | 24.30% | 24.91% | 12.32% | 10.87% | |
| Outliers Criteria | B072B | B072D | B073B | B073D | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | ||
| Peirce | Lognormal | 0.00% | 0.00% | −1.24% | −4.44% | 0.00% | 0.00% | 0.00% | 0.00% |
| Weibull | 0.00% | 0.00% | 6.85% | −1.88% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Mixt (LN + Wbl) | 0.00% | 0.00% | −1.24% | −4.44% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Gumbel | 0.00% | 0.00% | −4.45% | −0.95% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Gamma | 0.00% | 0.00% | 10.14% | 11.86% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Cauchy | 0.00% | 0.00% | −0.37% | −3.52% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Inverse Weibull | 0.00% | 0.00% | 2.90% | −0.79% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Inverse Gamma | 0.00% | 0.00% | 8.65% | 7.56% | 0.00% | 0.00% | 0.00% | 0.00% | |
| Leverage | Lognormal | 0.00% | 0.00% | −1.24% | −4.44% | 0.00% | 0.00% | 6.21% | −30.94% |
| Weibull | 0.00% | 0.00% | 6.85% | −1.88% | 0.00% | 0.00% | 17.60% | 3.08% | |
| Mixt (LN + Wbl) | 0.00% | 0.00% | −1.24% | −4.44% | 0.00% | 0.00% | 6.21% | −30.94% | |
| Gumbel | 0.00% | 0.00% | −4.45% | −0.95% | 0.00% | 0.00% | −31.74% | 8.30% | |
| Gamma | 0.00% | 0.00% | 10.14% | 11.86% | 0.00% | 0.00% | 86.63% | 79.06% | |
| Cauchy | 0.00% | 0.00% | −0.37% | −3.52% | 0.00% | 0.00% | 1.13% | −7.92% | |
| Inverse Weibull | 0.00% | 0.00% | 2.90% | −0.79% | 0.00% | 0.00% | 89.46% | 13.04% | |
| Inverse Gamma | 0.00% | 0.00% | 8.65% | 7.56% | 0.00% | 0.00% | 135.59% | 157.71% | |
| Outliers Criteria | B162B | B162D | B163B | B163D | |||||
|---|---|---|---|---|---|---|---|---|---|
| 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | 1st P | 2nd P | ||
| Peirce | Lognormal | −0.93% | −4.04% | −1.79% | −11.37% | 0.00% | 0.00% | −0.99% | −6.99% |
| Weibull | 10.54% | −1.46% | 27.82% | −2.98% | 0.00% | 0.00% | 22.27% | −1.82% | |
| Mixt (LN + Wbl) | −0.93% | −4.04% | −1.79% | −11.37% | 0.00% | 0.00% | −0.99% | −6.99% | |
| Gumbel | −3.00% | −0.72% | −8.69% | −1.26% | 0.00% | 0.00% | −4.07% | −0.68% | |
| Gamma | 9.52% | 10.73% | 29.67% | 32.45% | 0.00% | 0.00% | 17.64% | 19.07% | |
| Cauchy | −0.38% | −2.80% | −0.71% | −6.64% | 0.00% | 0.00% | −0.27% | −2.82% | |
| Inverse Weibull | 1.92% | −0.64% | 6.95% | −1.09% | 0.00% | 0.00% | 2.66% | −0.60% | |
| Inverse Gamma | 7.65% | 6.80% | 24.93% | 23.03% | 0.00% | 0.00% | 13.73% | 12.79% | |
| Leverage | Lognormal | 2.29% | −23.09% | −1.79% | −11.37% | 1.19% | −16.08% | 0.04% | −15.28% |
| Weibull | 24.52% | 0.34% | 27.82% | −2.98% | 23.59% | −0.23% | 27.67% | −1.26% | |
| Mixt (LN + Wbl) | 2.29% | −23.09% | −1.79% | −11.37% | 1.19% | −16.08% | 0.04% | −15.28% | |
| Gumbel | −24.20% | 3.83% | −8.69% | −1.26% | −15.07% | 2.16% | −16.57% | 0.87% | |
| Gamma | 64.95% | 62.41% | 29.67% | 32.45% | 40.80% | 39.84% | 39.33% | 39.83% | |
| Cauchy | 1.16% | −11.44% | −0.71% | −6.64% | 0.42% | −8.81% | 0.18% | −5.78% | |
| Inverse Weibull | 44.26% | 4.93% | 6.95% | −1.09% | 22.72% | 2.82% | 26.26% | 1.36% | |
| Inverse Gamma | 72.77% | 78.17% | 24.93% | 23.03% | 42.80% | 45.26% | 39.42% | 40.04% | |
| Case | Total Data | Prc-C. Outl. | Lev-C. Outl. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | ||||
| B072B | Gumbel | 95.67 | 99.23 | Gamma | 72.93 | 76.36 | Gumbel | 72.38 | 75.81 |
| Lognormal | 95.85 | 99.42 | Lognormal | 74.38 | 77.81 | Inverse Gamma | 72.54 | 75.96 | |
| Gamma | 96.28 | 99.85 | Mixt (LN + Wbl) | 74.64 | 78.07 | Inverse Weibull | 72.60 | 76.02 | |
| Inverse Gamma | 97.23 | 100.80 | Weibull | 74.78 | 78.20 | Lognormal | 73.72 | 77.15 | |
| Mixt (LN + Wbl) | 99.95 | 103.52 | Gumbel | 75.54 | 78.97 | Gamma | 75.57 | 79.00 | |
| Weibull | 102.29 | 105.86 | Inverse Gamma | 77.18 | 80.61 | Mixt (LN + Wbl) | 80.10 | 83.53 | |
| Inverse Weibull | 106.07 | 109.63 | Cauchy | 87.46 | 90.89 | Weibull | 83.85 | 87.28 | |
| Cauchy | 108.74 | 112.31 | Inverse Weibull | 88.97 | 92.40 | Cauchy | 91.33 | 94.76 | |
| B072D | Gamma | 153.02 | 156.59 | Gamma | 153.02 | 156.59 | Gamma | 153.02 | 156.59 |
| Lognormal | 153.27 | 156.84 | Lognormal | 153.27 | 156.84 | Lognormal | 153.27 | 156.84 | |
| Gumbel | 153.78 | 157.35 | Gumbel | 153.78 | 157.35 | Gumbel | 153.78 | 157.35 | |
| Mixt (LN + Wbl) | 154.37 | 157.94 | Mixt (LN + Wbl) | 154.37 | 157.94 | Mixt (LN + Wbl) | 154.37 | 157.94 | |
| Inverse Gamma | 154.59 | 158.16 | Inverse Gamma | 154.59 | 158.16 | Inverse Gamma | 154.59 | 158.16 | |
| Weibull | 154.96 | 158.53 | Weibull | 154.96 | 158.53 | Weibull | 154.96 | 158.53 | |
| Inverse Weibull | 158.87 | 162.43 | Inverse Weibull | 158.87 | 162.43 | Inverse Weibull | 158.87 | 162.43 | |
| Cauchy | 176.94 | 180.51 | Cauchy | 176.94 | 180.51 | Cauchy | 176.94 | 180.51 | |
| B073B | Lognormal | 117.74 | 121.30 | Gamma | 99.43 | 102.91 | Gamma | 95.07 | 98.49 |
| Gumbel | 118.06 | 121.63 | Weibull | 100.01 | 103.49 | Lognormal | 96.07 | 99.50 | |
| Gamma | 118.39 | 121.96 | Mixt (LN + Wbl) | 100.27 | 103.74 | Mixt (LN + Wbl) | 96.10 | 99.53 | |
| Inverse Gamma | 119.06 | 122.63 | Lognormal | 100.74 | 104.22 | Weibull | 96.12 | 99.55 | |
| Mixt (LN + Wbl) | 121.14 | 124.71 | Gumbel | 100.86 | 104.33 | Gumbel | 96.35 | 99.77 | |
| Weibull | 123.09 | 126.66 | Inverse Gamma | 103.29 | 106.76 | Inverse Gamma | 98.21 | 101.63 | |
| Inverse Weibull | 124.09 | 127.66 | Inverse Weibull | 109.85 | 113.33 | Inverse Weibull | 104.55 | 107.98 | |
| Cauchy | 134.85 | 138.42 | Cauchy | 118.81 | 122.29 | Cauchy | 113.88 | 117.31 | |
| B073D | Gamma | 191.70 | 195.27 | Weibull | 182.70 | 186.22 | Lognormal | 171.10 | 174.52 |
| Weibull | 192.37 | 195.94 | Gamma | 183.13 | 186.65 | Gamma | 171.31 | 174.74 | |
| Mixt (LN + Wbl) | 192.61 | 196.18 | Mixt (LN + Wbl) | 183.47 | 186.99 | Gumbel | 171.48 | 174.91 | |
| Lognormal | 193.02 | 196.59 | Lognormal | 184.79 | 188.31 | Inverse Gamma | 171.59 | 175.02 | |
| Gumbel | 193.04 | 196.61 | Gumbel | 184.88 | 188.40 | Mixt (LN + Wbl) | 172.99 | 176.42 | |
| Inverse Gamma | 195.74 | 199.31 | Inverse Gamma | 187.70 | 191.22 | Weibull | 174.23 | 177.65 | |
| Inverse Weibull | 202.91 | 206.48 | Inverse Weibull | 195.19 | 198.71 | Inverse Weibull | 175.10 | 178.52 | |
| Cauchy | 213.66 | 217.23 | Cauchy | 205.01 | 208.53 | Cauchy | 193.84 | 197.26 | |
| Case | Total Data | Prc-C. Outl. | Lev-C. Outl. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | ||||
| B162B | Gamma | −0.93 | 2.64 | Gamma | −0.93 | 2.64 | Lognormal | −3.98 | −0.45 |
| Lognormal | −0.86 | 2.71 | Lognormal | −0.86 | 2.71 | Inverse Gamma | −3.74 | −0.22 | |
| Inverse Gamma | −0.10 | 3.47 | Inverse Gamma | −0.10 | 3.47 | Gamma | −3.66 | −0.14 | |
| Gumbel | −0.09 | 3.47 | Gumbel | −0.09 | 3.47 | Gumbel | −3.60 | −0.08 | |
| Mixt (LN + Wbl) | 1.38 | 4.95 | Mixt (LN + Wbl) | 1.38 | 4.95 | Mixt (LN + Wbl) | −0.88 | 2.64 | |
| Weibull | 2.33 | 5.90 | Weibull | 2.33 | 5.90 | Weibull | 0.45 | 3.98 | |
| Inverse Weibull | 5.81 | 9.37 | Inverse Weibull | 5.81 | 9.37 | Inverse Weibull | 0.50 | 4.02 | |
| Cauchy | 18.78 | 22.34 | Cauchy | 18.78 | 22.34 | Cauchy | 16.16 | 19.68 | |
| B162D | Inverse Gamma | 17.52 | 21.09 | Lognormal | 2.60 | 6.03 | Inverse Gamma | 9.63 | 13.10 |
| Lognormal | 17.85 | 21.42 | Gamma | 2.83 | 6.25 | Inverse Weibull | 10.30 | 13.77 | |
| Gumbel | 18.13 | 21.70 | Gumbel | 2.94 | 6.37 | Gumbel | 10.32 | 13.79 | |
| Gamma | 19.23 | 22.80 | Inverse Gamma | 3.07 | 6.49 | Lognormal | 10.33 | 13.80 | |
| Inverse Weibull | 19.83 | 23.40 | Mixt (LN + Wbl) | 4.84 | 8.26 | Gamma | 11.77 | 15.24 | |
| Mixt (LN + Wbl) | 22.62 | 26.19 | Weibull | 5.62 | 9.05 | Mixt (LN + Wbl) | 15.29 | 18.76 | |
| Weibull | 24.41 | 27.98 | Inverse Weibull | 6.78 | 10.21 | Weibull | 17.15 | 20.62 | |
| Cauchy | 40.35 | 43.92 | Cauchy | 24.84 | 28.26 | Cauchy | 32.81 | 36.29 | |
| B163B | Gumbel | −3.38 | 0.19 | Inverse Gamma | −8.26 | −4.74 | Gumbel | −12.76 | −9.28 |
| Inverse Gamma | −3.32 | 0.25 | Lognormal | −8.19 | −4.67 | Inverse Gamma | −12.26 | −8.79 | |
| Lognormal | −2.92 | 0.65 | Gumbel | −8.06 | −4.54 | Inverse Weibull | −11.88 | −8.40 | |
| Gamma | −1.97 | 1.59 | Gamma | −7.66 | −4.14 | Lognormal | −11.60 | −8.13 | |
| Inverse Weibull | −0.19 | 3.38 | Mixt (LN + Wbl) | −4.27 | −0.75 | Gamma | −10.63 | −7.15 | |
| Mixt (LN + Wbl) | 2.23 | 5.80 | Inverse Weibull | −4.18 | −0.65 | Mixt (LN + Wbl) | −6.65 | −3.18 | |
| Weibull | 4.78 | 8.34 | Weibull | −2.36 | 1.16 | Weibull | −4.20 | −0.73 | |
| Cauchy | 16.99 | 20.56 | Cauchy | 12.07 | 15.59 | Cauchy | 9.74 | 13.22 | |
| B163D | Inverse Gamma | 65.28 | 68.85 | Inverse Gamma | 57.20 | 60.72 | Inverse Gamma | 57.20 | 60.72 |
| Inverse Weibull | 65.40 | 68.97 | Gumbel | 57.48 | 61.00 | Gumbel | 57.48 | 61.00 | |
| Gumbel | 66.09 | 69.65 | Lognormal | 57.89 | 61.42 | Lognormal | 57.89 | 61.42 | |
| Lognormal | 66.66 | 70.22 | Inverse Weibull | 58.42 | 61.94 | Inverse Weibull | 58.42 | 61.94 | |
| Gamma | 68.99 | 72.56 | Gamma | 59.26 | 62.78 | Gamma | 59.26 | 62.78 | |
| Mixt (LN + Wbl) | 72.79 | 76.36 | Mixt (LN + Wbl) | 62.14 | 65.66 | Mixt (LN + Wbl) | 62.14 | 65.66 | |
| Weibull | 76.80 | 80.37 | Weibull | 64.83 | 68.35 | Weibull | 64.83 | 68.35 | |
| Cauchy | 85.55 | 89.11 | Cauchy | 77.76 | 81.28 | Cauchy | 77.76 | 81.28 | |
| Case | Total Data | Case | Total Data | Lev-C. Outl. | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | |||||
| B072B | Mixt (LN + Wbl) | −112.84 | −111.06 | B073B | Mixt (LN + Wbl) | −112.67 | −110.88 | |||
| Lognormal | −112.37 | −108.81 | Lognormal | −111.97 | −108.40 | |||||
| Gamma | −112.07 | −108.50 | Gamma | −111.71 | −108.14 | |||||
| Gumbel | −112.04 | −108.48 | Inverse Gamma | −111.69 | −108.12 | |||||
| Inverse Gamma | −112.02 | −108.45 | Gumbel | −111.56 | −107.99 | |||||
| Weibull | −109.06 | −105.49 | Weibull | −109.16 | −105.59 | |||||
| Inverse Weibull | −108.53 | −104.96 | Inverse Weibull | −108.99 | −105.42 | |||||
| Cauchy | −89.23 | −85.66 | Cauchy | −85.35 | −81.78 | |||||
| B072D | Inverse Gamma | −108.32 | −104.75 | B073D | Weibull | −67.33 | −63.76 | Mixt (LN + Wbl) | −81.93 | −80.22 |
| Gumbel | −108.30 | −104.74 | Gamma | −62.77 | −59.20 | Lognormal | −79.69 | −76.26 | ||
| Lognormal | −108.06 | −104.49 | Mixt (LN + Wbl) | −60.64 | −58.86 | Inverse Gamma | −79.62 | −76.19 | ||
| Mixt (LN + Wbl) | −107.82 | −106.04 | Lognormal | −58.55 | −54.98 | Gamma | −79.37 | −75.94 | ||
| Gamma | −107.16 | −103.59 | Gumbel | −57.76 | −54.19 | Gumbel | −79.24 | −75.81 | ||
| Inverse Weibull | −105.26 | −101.69 | Cauchy | −53.22 | −49.65 | Inverse Weibull | −75.42 | −71.99 | ||
| Weibull | −101.12 | −97.55 | Inverse Gamma | −52.49 | −48.92 | Weibull | −74.90 | −71.48 | ||
| Cauchy | −89.94 | −86.37 | Inverse Weibull | −37.33 | −33.76 | Cauchy | −59.70 | −56.27 | ||
| Case | Total Data | Prc-C. Outl. | Lev-C. Outl. | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AIC | BIC | AIC | BIC | AIC | BIC | ||||
| B162B | Mixt (LN + Wbl) | −201.74 | −199.96 | Mixt (LN + Wbl) | −203.69 | −201.93 | Gamma | −200.60 | −197.22 |
| Gamma | −200.83 | −197.26 | Weibull | −202.68 | −199.16 | Mixt (LN + Wbl) | −200.49 | −198.80 | |
| Weibull | −199.75 | −196.18 | Gamma | −200.93 | −197.41 | Lognormal | −200.39 | −197.01 | |
| Lognormal | −199.72 | −196.15 | Lognormal | −199.44 | −195.91 | Inverse Gamma | −199.98 | −196.61 | |
| Inverse Gamma | −198.08 | −194.51 | Inverse Gamma | −197.50 | −193.97 | Gumbel | −197.93 | −194.55 | |
| Gumbel | −195.88 | −192.31 | Gumbel | −194.70 | −191.18 | Weibull | −197.61 | −194.23 | |
| Inverse Weibull | −187.18 | −183.61 | Inverse Weibull | −185.70 | −182.18 | Inverse Weibull | −194.34 | −190.96 | |
| Cauchy | −184.88 | −181.31 | Cauchy | −184.31 | −180.79 | Cauchy | −180.83 | −177.45 | |
| B162D | Inverse Gamma | −225.81 | −222.24 | Mixt (LN + Wbl) | −227.67 | −225.93 | Mixt (LN + Wbl) | −227.67 | −225.93 |
| Lognormal | −225.50 | −221.93 | Gamma | −226.98 | −223.51 | Gamma | −226.98 | −223.51 | |
| Gumbel | −225.49 | −221.92 | Lognormal | −226.72 | −223.25 | Lognormal | −226.72 | −223.25 | |
| Gamma | −224.87 | −221.31 | Inverse Gamma | −226.30 | −222.82 | Inverse Gamma | −226.30 | −222.82 | |
| Inverse Weibull | −223.24 | −219.67 | Weibull | −225.29 | −221.81 | Weibull | −225.29 | −221.81 | |
| Mixt (LN + Wbl) | −221.35 | −219.57 | Gumbel | −224.32 | −220.84 | Gumbel | −224.32 | −220.84 | |
| Weibull | −217.08 | −213.52 | Inverse Weibull | −221.12 | −217.64 | Inverse Weibull | −221.12 | −217.64 | |
| Cauchy | −206.69 | −203.13 | Cauchy | −205.56 | −202.09 | Cauchy | −205.56 | −202.09 | |
| B163B | Mixt (LN + Wbl) | −208.47 | −206.68 | Mixt (LN + Wbl) | −208.47 | −206.68 | Mixt (LN + Wbl) | −208.37 | −206.66 |
| Weibull | −206.95 | −203.39 | Weibull | −206.95 | −203.39 | Weibull | −207.20 | −203.77 | |
| Gamma | −206.51 | −202.94 | Gamma | −206.51 | −202.94 | Gamma | −205.36 | −201.93 | |
| Lognormal | −205.34 | −201.77 | Lognormal | −205.34 | −201.77 | Lognormal | −204.48 | −201.05 | |
| Inverse Gamma | −203.77 | −200.20 | Inverse Gamma | −203.77 | −200.20 | Inverse Gamma | −203.40 | −199.97 | |
| Gumbel | −201.31 | −197.74 | Gumbel | −201.31 | −197.74 | Gumbel | −200.29 | −196.86 | |
| Inverse Weibull | −193.68 | −190.11 | Inverse Weibull | −193.68 | −190.11 | Inverse Weibull | −195.03 | −191.60 | |
| Cauchy | −189.40 | −185.83 | Cauchy | −189.40 | −185.83 | Cauchy | −186.18 | −182.75 | |
| B163D | Gamma | −155.15 | −151.58 | Mixt (LN + Wbl) | −160.75 | −158.99 | Mixt (LN + Wbl) | −162.64 | −160.91 |
| Lognormal | −155.06 | −151.50 | Gamma | −159.42 | −155.90 | Gamma | −161.93 | −158.45 | |
| Inverse Gamma | −154.51 | −150.94 | Weibull | −159.06 | −155.54 | Lognormal | −161.72 | −158.25 | |
| Mixt (LN + Wbl) | −154.44 | −152.66 | Lognormal | −158.54 | −155.02 | Inverse Gamma | −161.34 | −157.86 | |
| Gumbel | −152.19 | −148.62 | Inverse Gamma | −157.34 | −153.82 | Gumbel | −159.09 | −155.62 | |
| Weibull | −148.56 | −144.99 | Gumbel | −153.60 | −150.07 | Weibull | −159.05 | −155.57 | |
| Inverse Weibull | −145.58 | −142.01 | Inverse Weibull | −146.19 | −142.66 | Inverse Weibull | −155.56 | −152.08 | |
| Cauchy | −139.60 | −136.04 | Cauchy | −141.04 | −137.52 | Cauchy | −141.29 | −137.81 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martinez, I.; Gallegos, M.F.; Araya-Letelier, G.; Lopez-Garcia, D. Impact of Probabilistic Modeling Alternatives on the Seismic Fragility Analysis of Reinforced Concrete Dual Wall–Frame Buildings towards Resilient Designs. Sustainability 2024, 16, 1668. https://doi.org/10.3390/su16041668
Martinez I, Gallegos MF, Araya-Letelier G, Lopez-Garcia D. Impact of Probabilistic Modeling Alternatives on the Seismic Fragility Analysis of Reinforced Concrete Dual Wall–Frame Buildings towards Resilient Designs. Sustainability. 2024; 16(4):1668. https://doi.org/10.3390/su16041668
Chicago/Turabian StyleMartinez, Ivanna, Marco F. Gallegos, Gerardo Araya-Letelier, and Diego Lopez-Garcia. 2024. "Impact of Probabilistic Modeling Alternatives on the Seismic Fragility Analysis of Reinforced Concrete Dual Wall–Frame Buildings towards Resilient Designs" Sustainability 16, no. 4: 1668. https://doi.org/10.3390/su16041668
APA StyleMartinez, I., Gallegos, M. F., Araya-Letelier, G., & Lopez-Garcia, D. (2024). Impact of Probabilistic Modeling Alternatives on the Seismic Fragility Analysis of Reinforced Concrete Dual Wall–Frame Buildings towards Resilient Designs. Sustainability, 16(4), 1668. https://doi.org/10.3390/su16041668









