Optimal Scheduling of Networked Microgrids Considering the Temporal Equilibrium Allocation of Annual Carbon Emission Allowance
Abstract
1. Introduction
- (1)
- A CEA temporal decomposition model is proposed. It allocates allowance to individual microgrids and further decomposes them temporally using the entropy method, thus providing a basis for daily scheduling.
- (2)
- A Lyapunov-optimization-based low-carbon scheduling model is proposed. It breaks down the annual CEA targets into each dispatch interval for management, avoiding penalties due to excessive emissions during annual settlement and ensuring both annual CEA compliance and daily economic efficiency.
- (3)
- A Stackelberg game-based energy–-carbon coupling trading model is presented. Moreover, it fully considers the uncertainty caused by external electricity and carbon price fluctuations, coordinating the electric–carbon coupling trading of the networked microgrids.
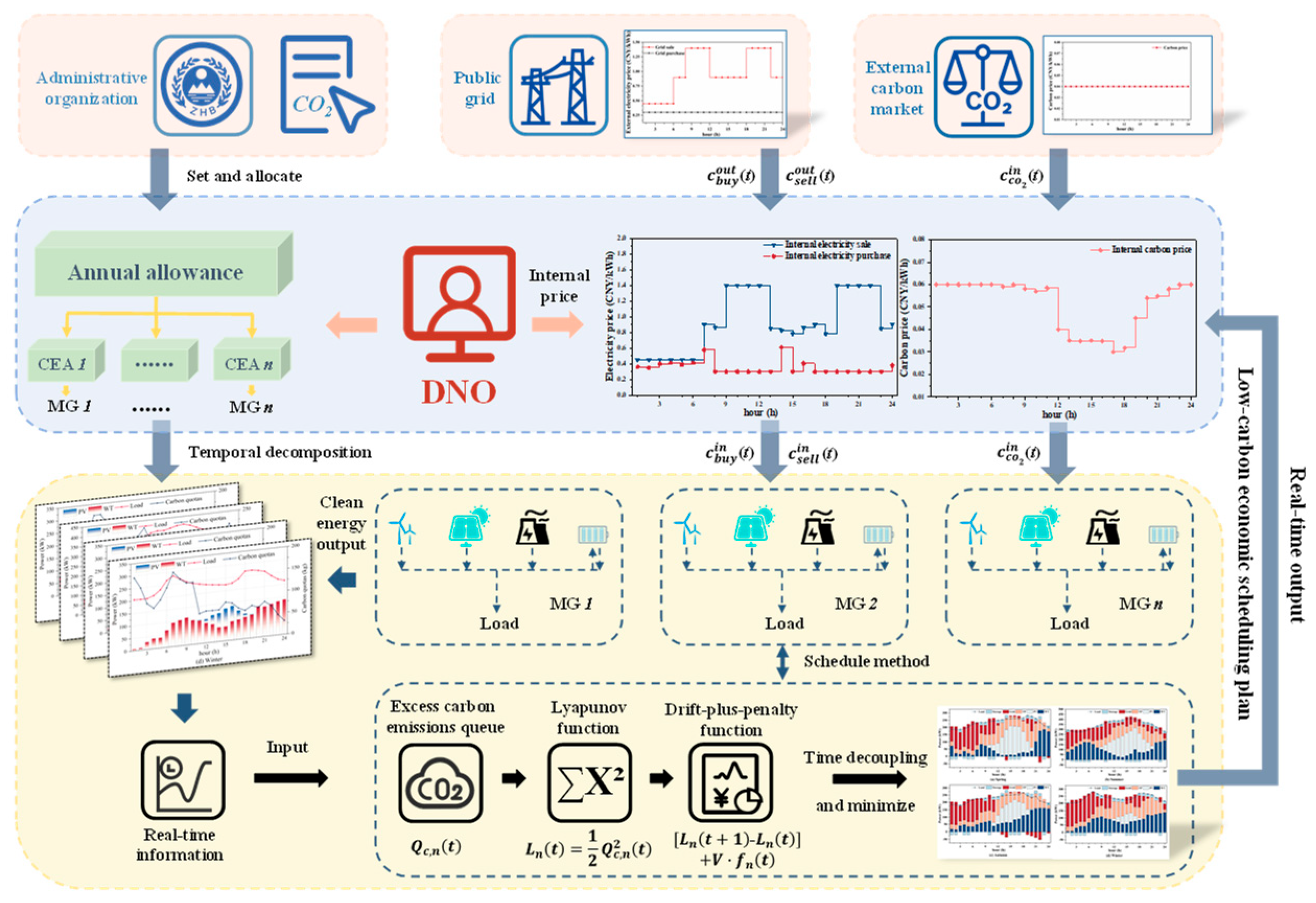
2. Carbon Emission Allowance Temporal Decomposition Model
2.1. Framework for Carbon Emission Management
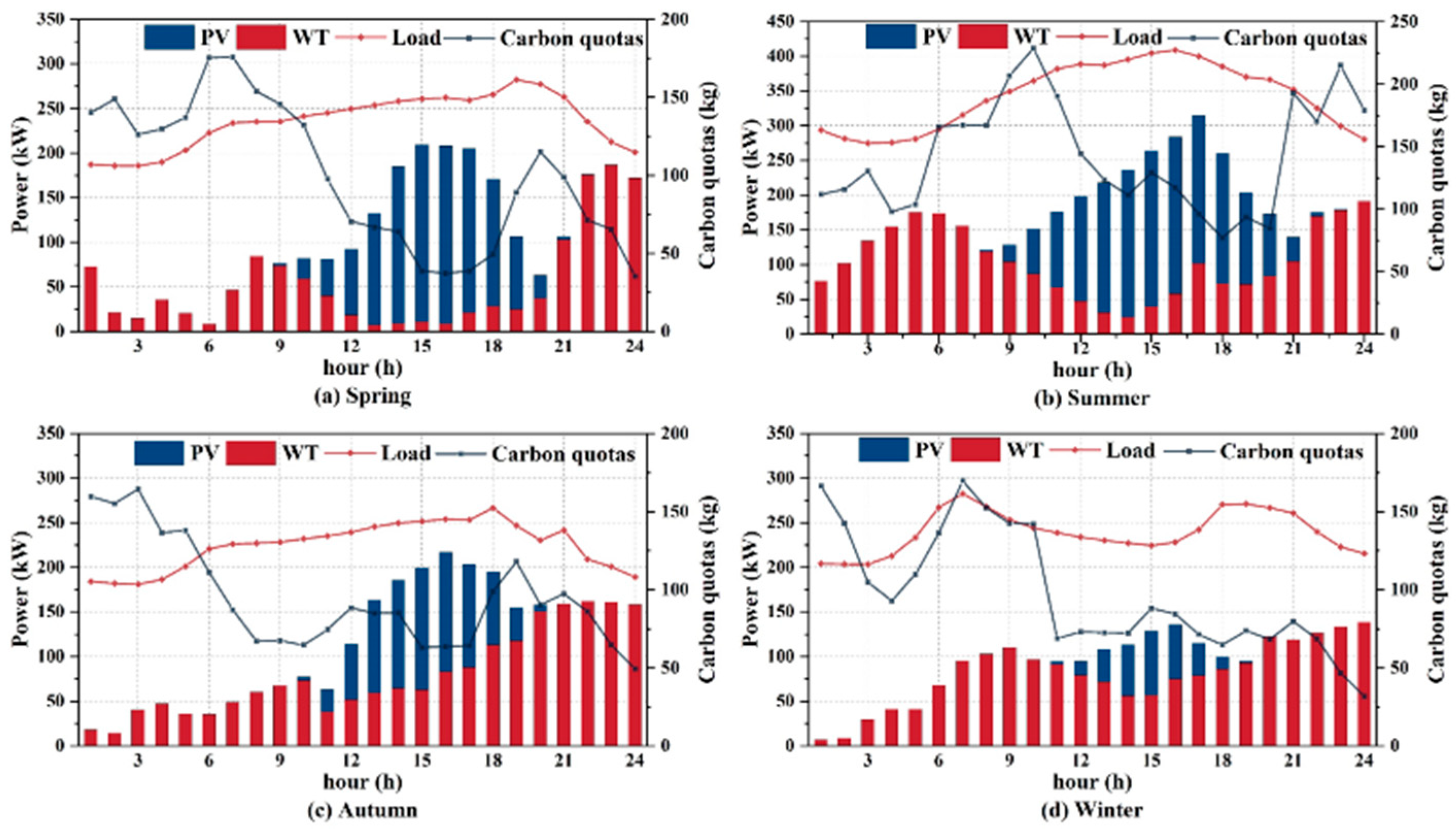
2.2. Temporal Decomposition of Carbon Emission Allowances
3. Lyapunov Optimization-Based Low-Carbon Scheduling of the Microgrid
3.1. Actual Carbon Emissions
3.2. Lyapunov Optimization-Based Low-Carbon Economic Scheduling Model
- (1)
- Energy storage equipment constraints:
- (2)
- Thermal power units and electricity trading constraints:
- (3)
- Load balance constraint:
4. Stackelberg Game-Based Energy–Carbon Coupling Trading Among the Microgrids
4.1. The Framework of the Stackelberg Game
- (1)
- Participants: the DNO and MGs form a Stackelberg game as leaders and followers, respectively.
- (2)
- Strategies: the DNO’s strategy is to set the internal electricity and carbon prices, and the MGs’ strategy is electricity and allowances transaction strategies.
- (3)
- Utility function: the DNO’s utility function is to maximize profit, and MGs’ utility function is to minimize the drift-plus-penalty function as a Formula (23).
4.2. The Revenue Model of DNO
4.3. Formulation and Solution of Stackelberg Game Model
- Step 1: The parameters of the DNO and MGs, k = 0, are initialized; the number of populations m is set to 10, the number of iterations to 30, the population variation rate to 5%, and the crossover probability to 70%. The choice of these parameters is based on previous studies, particularly [34], where similar settings have been found to provide effective results for optimization problems of this nature.
- Step 2: A genetic algorithm is used to randomly generate m sets of acceptable internal electricity prices and carbon prices for the MGs, the DNO calculates optimal revenue and sends the corresponding prices to the MGs.
- Step 3: k = k + 1.
- Step 4: If k = 30, the iteration is ended, and the optimal prices and scheduling plan are output; otherwise, step 5 is initialized.
- Step 5: MGs receive the optimal internal prices, using the Gurobi solver to solve the scheduling model. It calculates and retains the current operating cost and returns its moment-by-moment electricity and allowance transaction strategy to the DNO.
- Step 6: The DNO calculates its current revenue based on the electricity and allowance transaction information returned by MGs.
- Step 7: If convergence conditions are met, the iteration is ended and the optimal prices and scheduling plan are output; otherwise, step 8 is initialized.
- Step 8: The genetic algorithm’s selection and mutation are used to generate new internal prices and calculate the DNO’s revenue based on new prices.
- Step 9: If > , internal prices are updated and step 3 is resumed; otherwise, step 8 is resumed.
5. Case Analysis
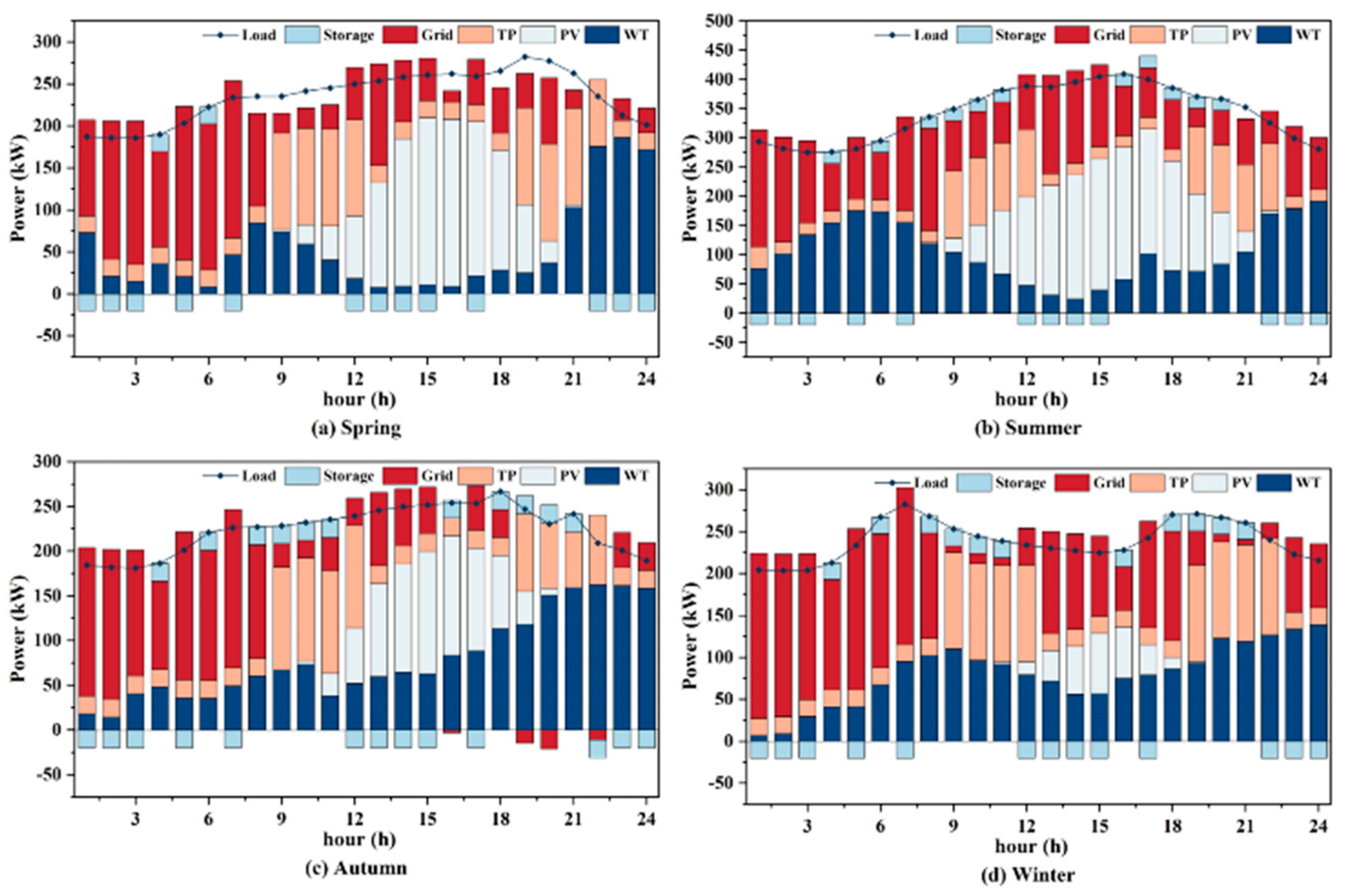
5.1. Comparison of Different CEA Allocation Scheme and Scheduling Methods
5.2. Analysis of Long-Term Economic Benefits
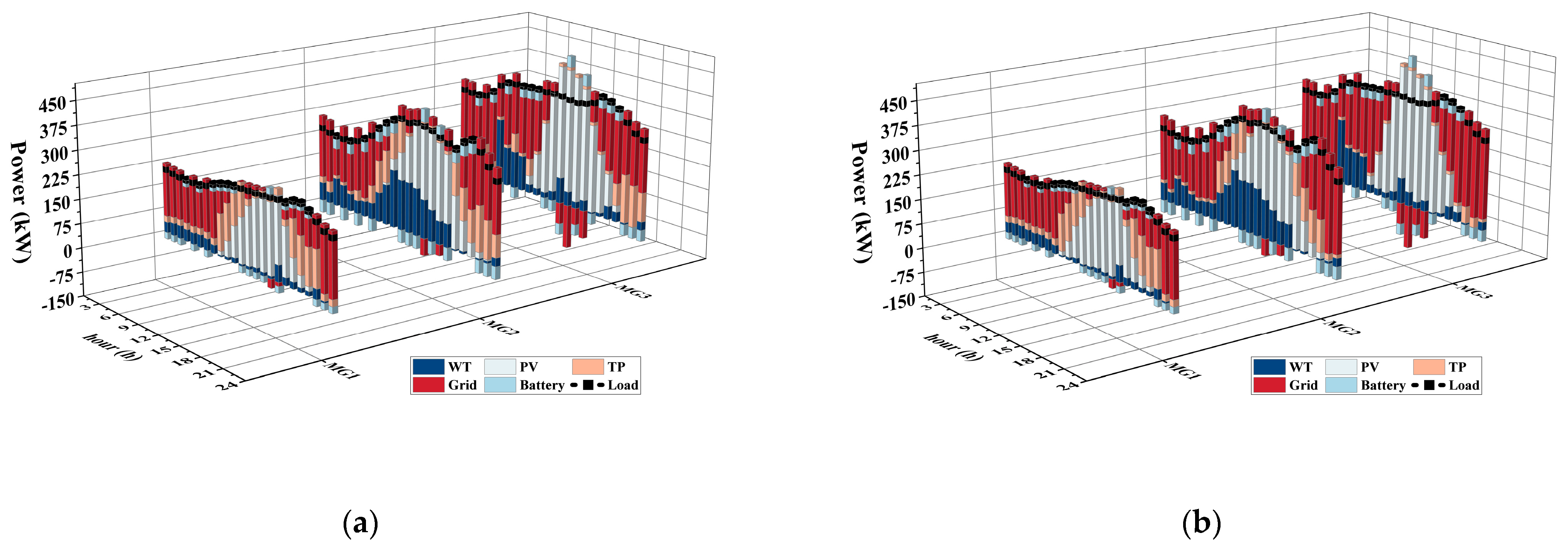
5.3. Analysis of Energy–Carbon Coupling Trading
6. Conclusions
- (1)
- Compared with the annual averaging allocation of CEA, the proposed temporal decomposition model can better allocate CEA, and a decrease in operating costs and carbon emissions is observed with the same CEA, which verifies the effectiveness of the proposed model.
- (2)
- The proposed Lyapunov optimization-based low-carbon scheduling model can manage carbon emissions within each dispatch interval and be solved online. The CO2 over-emissions are reduced by at least 16% and show an excellent long-term economic benefit.
- (3)
- The overall costs of networked microgrids are reduced by 7.3% through the energy–carbon coupling trading, while the overall CO2 over-emissions of the MGs are reduced by 4.4%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Proof of Theorem 1
Appendix B. Proof of Stackelberg Game Equilibrium
- (1)
- The utility function of the game leader is a non-empty and continuous function of its strategy space.
- (2)
- The utility function of the game follower is a continuous convex/concave function of its strategy space.
References
- An, I. Special Report on the Impacts of Global Warming of 1.5 C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change. Sustain. Dev. Efforts Eradicate Poverty 2018, 32. [Google Scholar]
- Liu, R.; Ding, M.; Wang, S. International net zero emission route and its implications for China’s dual carbon strategy. Reform Strategy 2022, 38, 1–12. [Google Scholar]
- He, B.; Zheng, H.; Zhang, Q.; Zhao, A.; Tang, H.; Xi, P.; Wei, L.; Li, M.; Guan, Q. Toward a Comprehensive Economic Comparison Framework for Solar Projects: A Case Study of Utility and Residential Scales. Sustainability 2024, 16, 10320. [Google Scholar] [CrossRef]
- Han, H.; Xu, Y.; Wu, C.; Jiang, X.; Cao, S.; Zang, H.; Chen, S.; Wei, Z. Nash Equilibrium-Based Two-Stage Cooperative Operation Strategy for Multi-Microgrids Considering Uncertainty. Prot. Control Mod. Power Syst. 2024, 9, 42–57. [Google Scholar] [CrossRef]
- Wang, T.; Huang, Z.; Ying, R.; Valencia-Cabrera, L. A Low-Carbon Operation Optimization Method of ETG-RIES Based on Adaptive Optimization Spiking Neural P Systems. Prot. Control Mod. Power Syst. 2024, 9, 162–177. [Google Scholar] [CrossRef]
- Vásquez, L.O.P.; Redondo, J.L.; Hervás, J.D.Á.; Ramírez, V.M.; Torres, J.L. Balancing CO2 emissions and economic cost in a microgrid through an energy management system using MPC and multi-objective optimization. Appl. Energy 2023, 347, 120998. [Google Scholar] [CrossRef]
- Zhong, X.; Zhong, W.; Liu, Y.; Yang, C.; Xie, S. Optimal energy management for multi-energy multi-microgrid networks considering carbon emission limitations. Energy 2022, 246, 123428. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, H.; Tan, H.; Qi, H.; Li, Z.; Weng, H. Optimization Configuration of Hydrogen Storage in Park Integrated Energy System Considering Photovoltaic Photothermal and Stepped Carbon Trading. South. Power Syst. Technol. 2024, 1–12. [Google Scholar]
- Qin, M.; Yang, Y.; Zhao, X.; Xu, Q.; Yuan, L. Low-carbon economic multi-objective dispatch of integrated energy system considering the price fluctuation of natural gas and carbon emission accounting. Prot. Control Mod. Power Syst. 2023, 8, 61. [Google Scholar] [CrossRef]
- Qi, X.; Jiang, Z.; Zhang, J. Low-carbon joint dispatch of integrated energy systems based on differentiated dynamic pricing mechanisms. Int. J. Electr. Power Energy Syst. 2024, 156, 109774. [Google Scholar] [CrossRef]
- Ma, S.; Mi, Y.; Shi, S.; Li, D.; Xing, H.; Wang, P. Low-carbon economic operation of energy hub integrated with linearization model and nodal energy-carbon price. Energy 2024, 294, 130754. [Google Scholar] [CrossRef]
- Li, J.; Ge, S.; Liu, H.; Yu, Q.; Zhang, S.; Wang, C.; Gu, C. An electricity and carbon trading mechanism integrated with TSO-DSO-prosumer coordination. Appl. Energy 2024, 356, 122328. [Google Scholar] [CrossRef]
- Yang, P.; Yang, X.; Yang, L.; Wu, C.; Yang, Z. Low-Carbon Economic Dispatch of Source and Load Based on Carbon Market and Green Certificate Allocation System. South. Power Syst. Technol. 2024, 1–9. [Google Scholar]
- Feng, H.; Hu, Y.-J.; Li, C.; Wang, H. Rolling horizon optimisation strategy and initial carbon allowance allocation model to reduce carbon emissions in the power industry: Case of China. Energy 2023, 277, 127659. [Google Scholar] [CrossRef]
- Shi, W.; Li, W.; Qiao, F.; Wang, W.; An, Y.; Zhang, G. An inter-provincial carbon quota study in China based on the contribution of clean energy to carbon reduction. Energy Policy 2023, 182, 113770. [Google Scholar] [CrossRef]
- Yan, N.; Ma, G.; Li, X.; Guerrero, J.M. Low-carbon economic dispatch method for integrated energy system considering seasonal carbon flow dynamic balance. IEEE Trans. Sustain. Energy 2022, 14, 576–586. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, Y.; Xu, Q.; Wu, C.; Hua, K. A low-carbon economic dispatch for integrated energy systems with CCUS considering multi-time-scale allocation of carbon allowance. Appl. Energy 2023, 351, 121841. [Google Scholar] [CrossRef]
- Chen, S.; Shroff, N.B.; Sinha, P. Heterogeneous delay tolerant task scheduling and energy management in the smart grid with renewable energy. IEEE J. Sel. Areas Commun. 2013, 31, 1258–1267. [Google Scholar] [CrossRef]
- Grillo, S.; Marinelli, M.; Massucco, S.; Silvestro, F. Optimal management strategy of a battery-based storage system to improve renewable energy integration in distribution networks. IEEE Trans. Smart Grid 2012, 3, 950–958. [Google Scholar] [CrossRef]
- Li, J.; Ge, S.; Xu, Z.; Liu, H.; Li, J.; Wang, C.; Cheng, X. A network-secure peer-to-peer trading framework for electricity-carbon integrated market among local prosumers. Appl. Energy 2023, 335, 120420. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Liu, N. Low-carbon economic dispatch and energy sharing method of multiple Integrated Energy Systems from the perspective of System of Systems. Energy 2022, 244, 122717. [Google Scholar] [CrossRef]
- Xu, X.; Qiu, Z.; Zhang, T.; Gao, H. Distributed Source-Load-Storage Cooperative Low-Carbon Scheduling Strategy Considering Vehicle-to-Grid Aggregators. J. Mod. Power Syst. Clean Energy 2024, 12, 440–453. [Google Scholar] [CrossRef]
- Fu, M.; Wu, W.; Tian, L.; Zhen, Z.; Ye, J. Analysis of Emission Reduction Mechanism of High-Tiered Carbon Tax under Green and Low Carbon Behavior. Energies 2023, 16, 7555. [Google Scholar] [CrossRef]
- Liu, L.; Jiang, K.; Liu, N.; Zhang, Y. Multi-agent Energy-carbon Sharing Mechanism for MGs Based on Stackelberg Game. Proc. CSEE 2024, 44, 2119–2131. [Google Scholar]
- Cui, X.; Zhao, T.; Wang, J. Allocation of carbon emission quotas in China’s provincial power sector based on entropy method and ZSG-DEA. J. Clean. Prod. 2021, 284, 124683. [Google Scholar] [CrossRef]
- Yang, M.; Liu, Y. Research on multi-energy collaborative operation optimization of integrated energy system considering carbon trading and demand response. Energy 2023, 283, 129117. [Google Scholar] [CrossRef]
- Shi, J.; Ye, Z.; Gao, H.O.; Yu, N. Lyapunov optimization in online battery energy storage system control for commercial buildings. IEEE Trans. Smart Grid 2022, 14, 328–340. [Google Scholar] [CrossRef]
- Neely, M. Stochastic Network Optimization with Application to Communication and Queueing Systems; Springer Nature: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Lakshminarayana, S.; Quek, T.Q.; Poor, H.V. Cooperation and storage tradeoffs in power grids with renewable energy resources. IEEE J. Sel. Areas Commun. 2014, 32, 1386–1397. [Google Scholar] [CrossRef]
- Xiong, S.; Liu, D.; Chen, Y.; Zhang, Y.; Cai, X. A deep reinforcement learning approach based energy management strategy for home energy system considering the time-of-use price and real-time control of energy storage system. Energy Rep. 2024, 11, 3501–3508. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Xu, C.; Wang, D. The Competition Between Taxi Services and On-Demand Ride-Sharing Services: A Service Quality Perspective. Sustainability 2024, 16, 9877. [Google Scholar] [CrossRef]
- Zhu, P.; Lv, X.; Shao, Q.; Kuang, C.; Chen, W. Optimization of Green Multimodal Transport Schemes Considering Order Consolidation under Uncertainty Conditions. Sustainability 2024, 16, 6704. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, Y. Research on Location and Routing for Cold Chain Logistics in Health Resorts Considering Carbon Emissions. Sustainability 2024, 16, 6362. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Zhang, F.; Li, Y. A Stackelberg game-based approach to load aggregator bidding strategies in electricity spot markets. J. Energy Storage 2024, 95, 112509. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Z.; Wang, J.; Du, B.; Qin, Y.; Liu, X.; Liu, L. A Stackelberg game-based approach to transaction optimization for distributed integrated energy system. Energy 2023, 283, 128475. [Google Scholar] [CrossRef]
- Wang, Y.; Hu, J.; Liu, N. Energy management in integrated energy system using energy–carbon integrated pricing method. IEEE Trans. Sustain. Energy 2023, 14, 1992–2005. [Google Scholar] [CrossRef]
- Maharjan, S.; Zhu, Q.; Zhang, Y.; Gjessing, S.; Basar, T. Dependable demand response management in the smart grid: A Stackelberg game approach. IEEE Trans. Smart Grid 2013, 4, 120–132. [Google Scholar] [CrossRef]




| Indicator | Explanation | Attribute |
|---|---|---|
| Historical carbon emissions | Ensure sufficient allowances during periods of high carbon emissions | + |
| Historical clean energy generation | Reduce the use of CEA during periods of abundant clean energy | − |
| Seasonal adjustment factor | Adjust the usage of CEA according to the seasonal characteristics of the load | + |
| Equipment | Parameter | Value |
|---|---|---|
| TP1 | a1 (CNY/(kW2·h)) | 0.00475 |
| b1 (CNY/(kW·h)) | 0.3 | |
| c1 (CNY/h) | 12 | |
| (kW) | 20 | |
| (kW) | 400 | |
| TP2 | a2 (CNY/(kW2·h)) | 0.00515 |
| b2 (CNY/(kW·h)) | 0.38 | |
| c2 (CNY/h) | 16 | |
| (kW) | 10 | |
| (kW) | 375 | |
| TP3 | a3 (CNY/(kW2·h)) | 0.00515 |
| b3 (CNY/(kW·h)) | 0.4 | |
| c3 (CNY/h) | 18 | |
| (kW) | 10 | |
| (kW) | 425 | |
| EES1 | (kW) | 20 |
| (kW) | 20 | |
| EES2 | (kW) | 40 |
| (kW) | 60 | |
| EES3 | (kW) | 35 |
| (kW) | 40 | |
| Grid | (kW) | 200 |
| Scenario | Spring | Summer | Autumn | Winter | Total | |
|---|---|---|---|---|---|---|
| 1 | Operating costs (¥) | 2802.4 | 3819.5 | 2412.3 | 3203.7 | 12,237.9 |
| CO2 over-emissions (kg) | 720.1 | 706.2 | 534.8 | 1397.6 | 3358.7 | |
| 2 | Operating costs (¥) | 2834.8 | 3701.4 | 2361.7 | 3130.8 | 12,028.7 |
| CO2 over-emissions (kg) | 756.4 | 500.2 | 479.2 | 1278.9 | 3014.7 | |
| 3 | Operating costs (¥) | 2526.8 | 3336.8 | 2029.8 | 2849.4 | 10,742.8 |
| CO2 over-emissions (kg) | 913.4 | 607.9 | 694.5 | 1372.3 | 3588.1 | |
| Scenario | Spring | Summer | Autumn | Winter | Total | |
|---|---|---|---|---|---|---|
| 4 | Operating costs (¥) | 14,523.8 | 44,544 | 20,720.8 | 22,600.7 | 102,389.3 |
| CO2 over-emissions (kg) | 1560.1 | 11,606.5 | 2091.5 | 5081.9 | 20,340 | |
| 5 | Operating costs (¥) | 12,934.1 | 42,874.7 | 18,957.5 | 21,590.8 | 96,357.1 |
| CO2 over-emissions (kg) | 2283.1 | 13,092.8 | 3416.9 | 5697.7 | 24,490.5 | |
| Scenario | Costs of MG 1 (CNY) | Costs of MG 2 (CNY) | Costs of MG 3 (CNY) | Total Costs (CNY) | Profits of DNO (CNY) | CO2 Over-Emissions (kg) |
|---|---|---|---|---|---|---|
| 6 | 3018.9 | 4096.7 | 5088.6 | 12,204.2 | / | 3216.5 |
| 7 | 3028.8 | 3871.8 | 4411.8 | 11,312.4 | 37.8 | 3073.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Bai, H.; Li, W.; Xie, K.; Liu, Y.; Liu, T.; Shao, C. Optimal Scheduling of Networked Microgrids Considering the Temporal Equilibrium Allocation of Annual Carbon Emission Allowance. Sustainability 2024, 16, 10986. https://doi.org/10.3390/su162410986
Hu C, Bai H, Li W, Xie K, Liu Y, Liu T, Shao C. Optimal Scheduling of Networked Microgrids Considering the Temporal Equilibrium Allocation of Annual Carbon Emission Allowance. Sustainability. 2024; 16(24):10986. https://doi.org/10.3390/su162410986
Chicago/Turabian StyleHu, Chengling, Hao Bai, Wei Li, Kaigui Xie, Yipeng Liu, Tong Liu, and Changzheng Shao. 2024. "Optimal Scheduling of Networked Microgrids Considering the Temporal Equilibrium Allocation of Annual Carbon Emission Allowance" Sustainability 16, no. 24: 10986. https://doi.org/10.3390/su162410986
APA StyleHu, C., Bai, H., Li, W., Xie, K., Liu, Y., Liu, T., & Shao, C. (2024). Optimal Scheduling of Networked Microgrids Considering the Temporal Equilibrium Allocation of Annual Carbon Emission Allowance. Sustainability, 16(24), 10986. https://doi.org/10.3390/su162410986







