Research on the Mechanism of Coal-Wall Spalling and Flexible Reinforcement in Soft-Coal Seams Based on the Mogi–Coulomb Criterion

Abstract

The problem of soft coal-seam wall spalling is more prominent in the deep mining process, which seriously restricts the safety and sustainability of mining. The horizontal ground stress is usually ignored in the analysis of the coal-wall spalling mechanism. In this paper, based on the Mogi–Coulomb criterion and limit-equilibrium analysis, it is found that the traces of coal siding can be approximated as linear. The safety-stability coefficient of a soft-coal wall under the limit-equilibrium condition is obtained by applying the Mogi–Coulomb criterion. The coal stability of different positions is quite different. The coal with greater cohesion is more stable. In this regard, the cohesion of the coal can be improved through flexible reinforcement so as to improve the stability of the coal body. The control mechanism of the grouting and flexible rope reinforcing technology for the coal-wall spalling in the soft-coal seam is revealed. The safety-stability coefficient of the reinforced coal wall and the limit-stability coefficient are deduced. The reinforcement effect is related to the aperture ratio, the ultimate tensile force of the flexible rope, and the layout spacing. Reasonable aperture ratio, layout spacing, and flexible rope selection are key to reinforcement. This study has important guiding significance for the sustainability and safety of mining by revealing the mechanism of coal-wall spalling and reinforcement.

1. Introduction

Underground mining is accompanied by many disasters, such as rock bursts, coal and gas outbursts, and coal-wall spalling. Among them, coal-wall spalling occurs frequently, especially in large mining height and thick coal seams [1,2,3]. As the mining height increases, the problem of coal-wall spalling at the working face becomes more serious [4,5]. In addition, the increase in mining depth makes the mine pressure more severe, which further increases the possibility and danger of coal-wall spalling [6,7]. Coal-wall spalling seriously restricts the safety and sustainability of mining. During the mining process, the stress on coal seams will increase rapidly under the influence of mining [8,9]. The sudden increase in stress will further increase the possibility of coal-wall spalling. Due to its low cohesion and low strength, soft coal has a higher probability of being unstable under high stress [10]. The research on the mechanism and prevention of coal-wall spalling has become one of the focuses of research.

In order to explore the mechanism of coal-wall spalling, scholars have conducted many studies. The compression-rod theory simplifies the coal wall as a “compression rod”, and, in this context, the position of maximum deflection of the coal wall is the most dangerous [7,11,12,13]. The theory of the sliding body draws on the research results in slope engineering. In the process of studying the spalling of soft-coal seams, the coal-wall failure is regarded as compression and shear failure, and the spalling trace is simplified to an oblique straight line or arc shape [14,15,16,17]. In the mining of thick coal seams, the phenomenon of coal seam intercalation is common. The large difference between the hardness of the gangue and coal will also affect the stability of the coal wall [18]. On this basis, the instability theory considers the intercalation of the gangue formed. It can be considered as an extension of the sliding theory. It is found that the self-weight of coal also has a greater impact on coal-wall spalling in the large mining height of the coal seam, and the thick coal seam is more prone to spalling [19]. The studies are usually based on the Mohr–Coulomb criterion, ignoring the influence of the self-weight of the coal on the coal-wall spalling [20,21,22,23,24]. The horizontal in situ stress in the coal-seam tectonic area is usually unequal and is in a true triaxial stress state, which is more obvious in deep coal seams [25,26,27,28]. The research shows that the intermediate principal stress also has a certain effect on the strength of coal [25,26]. However, few relevant studies have focused on the differences in horizontal ground stress and the self-weight of coal on coal-wall spalling. Mogi et al. considered the effect of intermediate principal stresses on the coal mass and proposed a new criterion applicable to the true triaxial stress state based on the Coulomb criterion [29]. This criterion has been recognized by the vast majority of people and has good applicability in the theory of rock mechanics. Therefore, it is necessary to study the mechanism of soft coal-wall spalling while considering the differences in horizontal ground stress and the weight of the coal.

Due to the differences in coal properties, the type and position of coal-wall spalling present various states [4,30]. At present, it has been found that coal seams with different hardness exhibit significant differences in their failure modes. The cohesion of soft-coal seams is relatively small, and it is first destroyed when the coal wall is subjected to periodic stress from the roof. Therefore, a plastic zone is formed in the coal seams. As the deformation continues to increase, the coal slides toward the working face under the action of its own gravity. This spalling is caused by the shear failure of the coal [31,32]. The spalling traces are mainly oblique straight lines and arcs, among which the oblique straight lines account for the largest proportion [33,34]. Therefore, in the study of the coal-wall spalling of soft-coal seams, the stability of the coal can be judged by the relationship between the shear moment and the shear-resistance moment on the sliding surface.

The coal wall with severe spalling urgently needs to be provided with reinforcement measures. Combining grouting and flexible rope reinforcement technology can change the mechanical properties of the coal and rock mass and improve the strength and stability of coal and rock [19,35,36,37]. It has been widely used in spalling prevention and control. The effect of flexible reinforcement is mainly related to factors such as its slurry properties, drilling flexible rope diameter, drilling length, and flexible rope properties [38]. Jiao studied the role of grouting–flexible rope reinforcement technology under different parameters in combination with the Mohr–Coulomb criterion and achieved results in improving spalling. However, the research on the technical mechanism of flexible reinforcement, which is also based on the Mohr–Coulomb criterion, does not consider the difference in horizontal in situ stress and the influence of coal self-weight on the stability of the coal wall. Therefore, it is necessary to consider the difference in actual horizontal stress and the self-weight of the coal body to study the flexible reinforcement mechanism.

In this paper, based on the condition of the 91–105 working face in the Lu’an Wangzhuang coal mine, which is located in Changzhi City, Shanxi Province, China, the true triaxial three-dimensional stress and the coal gravity are considered. To reveal the spalling mechanism of the coal wall in the soft-coal seam, based on the Mogi–Coulomb criterion and limit-equilibrium stability analysis, the safety-stability coefficient of the coal-wall sliding surface before and after reinforcement is established. The calculation formula of the limit stability width is deduced. The reasonable reinforcement parameters are determined. The research results can provide theoretical support for the stability control of the soft-coal seam and have important guiding significance for the sustainability and safety of mining.

2. Materials and Methods

2.1. Project Overview of 91–105 Working Face of Lu’an Wangzhuang Coal Mine

The coal in the 91–105 working face of Lu’an Wangzhuang coal mine is stored in the middle and lower parts of the Shanxi Formation of the Permian System. The coal seam of this working face is low phosphorus, low sulfur, medium ash, viscous, has high calorific value, and is a high-quality power coal. The ground elevation is 905–932 m. The working face elevation is 397–463 m. Within the working face, the coal seam thickness is stable, with a coal thickness of 6.15 m. The Pugh hardness of the coal seam is 1–3, with an average value of 1.2. The geographical location diagram of the Lu’an Wangzhuang coal mine is shown in Figure 1. It is a typical soft-coal seam. As a whole, the working face is an anticline structure with local undulations. The coal seam is nearly horizontal, with a coal-seam dip of 2–6°. The working face has an inclination length of 2998 m and a strike length of 266 m. The working-face mining adopts the strike longwall, retreat-type, comprehensive, mechanized, low-level caving, top-coal, one-time mining, full-height, and full-caving mining method, with a mining height of 3.3 ± 0.1 m and a circulation progress of 0.8 m.

The characteristics of the surrounding rock of this working face are shown in

Table 1. The characteristics of the surrounding rock of this working face.

The Surrounding Rock	The Lithology	Average Thickness/m
Main roof	Mudstone	4.10
	Medium-grained sandstone	5.60
Immediate roof	Mudstone	7.08
Immediate floor	Mudstone	2.56
Hard floor	Medium-grained sandstone	3.35

. There is a direct roof composed of mudstone above the 3# coal seam in the 91–105 working face, with an average thickness of 7.08 m and a Pugh hardness of 3 to 8. The direct roof is relatively thick compared to the 5.6 m thick medium-grained sandstone above the direct roof. The basic roof is thick and hard, and the stress is strong when it collapses. The first weighting distance of the old roof in the 91–105 working face is within the range of 30 to 40 m, and the periodic pressure distance is within the range of 11 to 15 m. According to the statistics of coal-wall spalling in the Lu’an Wangzhuang mining area, it is found that most of the coal-wall caving positions were located in the upper area. The schematic diagram of the spalling at the Lu’an Wangzhuang coal mine is shown in Figure 2. It can be seen that there is an obvious shear surface in the coal-wall spalling, and the failure trace is regarded as a straight line or an arc.

2.2. Research Methods

In this study, the mechanical model of the soft-coal seam is established under the condition of the 91–105 working face of the Lu’an Wangzhuang coal mine. Based on the mechanical model and the limit-equilibrium analysis method, the differential equation on the slip surface of the coal wall is established and solved. The stability of the coal wall is judged by the established safety-stability coefficient of the coal wall. When the safety-stability coefficient is greater than 1, the anti-slip moment is greater than the sliding moment, indicating the coal wall is stable. When the safety-stability coefficient is less than 1, the sliding moment exceeds the anti-slip moment, indicating the coal wall is unstable. When the safety-stability coefficient is 1, it indicates that the coal wall is in a state of limit stability. The established model needs to meet the following assumptions: (1) The coal wall of the working face is soft coal, and the failure mode is shear. (2) The sliding coal body is vertically divided into a plurality of vertical coal strips, and the vertical shear force on the side of any coal strip is the same. (3) The sliding coal body is vertically divided into a plurality of vertical coal strips, and the anti-slip safety factor on the sliding surface at the bottom of any coal strip is the same. (4) The coal body does not contain special geological conditions such as large faults.

3. Results and Analysis

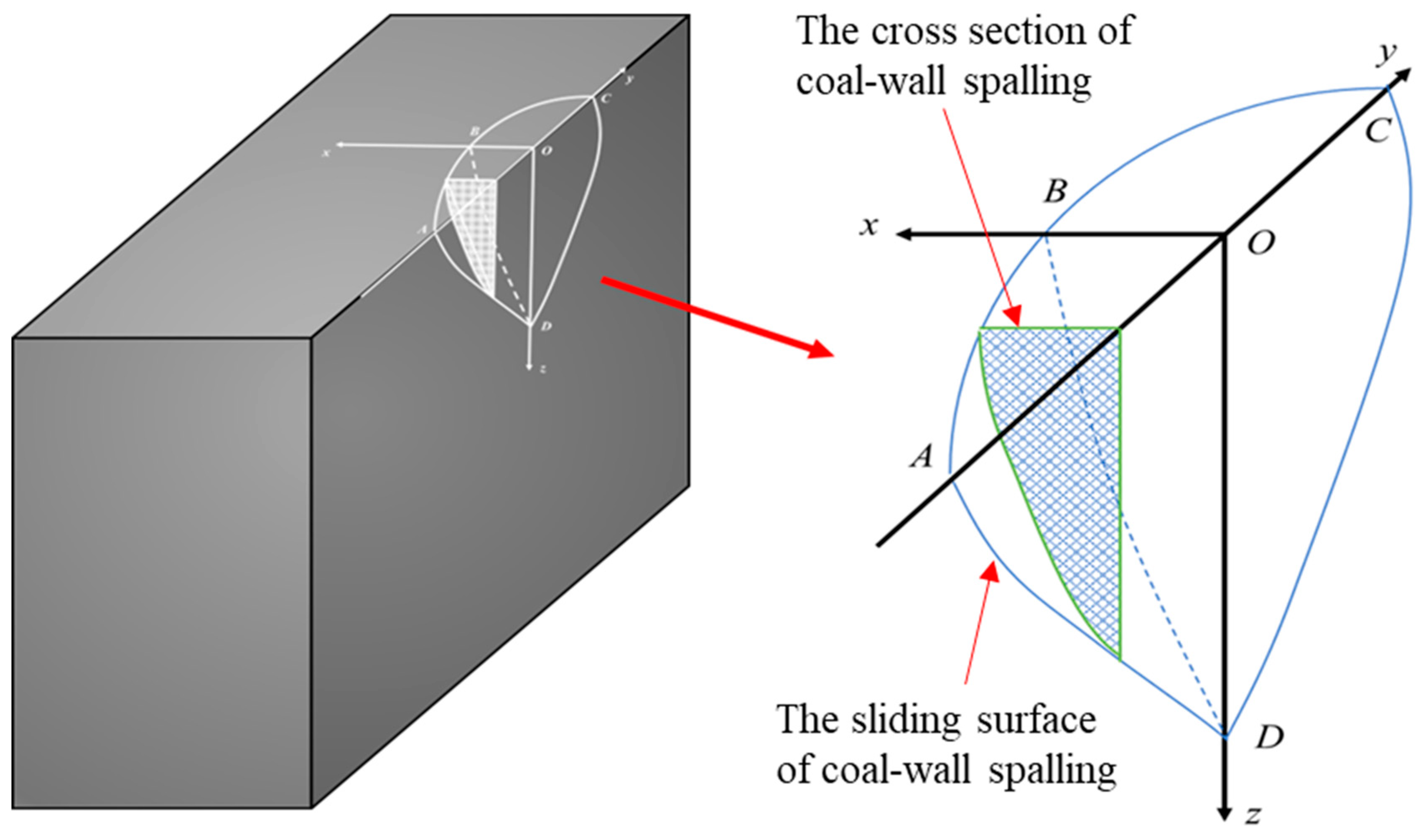
3.1. Determination of the Spalling Shape of the Soft-Coal Seam

Considering the shear failure in the working face and coal properties, the shape of the coal-wall spalling is geometrically simplified into a three-dimensional model, as shown in Figure 3. The vertical section shown in Figure 3 is taken as the research object, and the established mechanical model is shown in Figure 4. The horizontal direction perpendicular to the coal wall plane is selected as the x direction (minimum principal-stress direction), the horizontal direction along the coal-wall plane is selected as the y direction (intermediate principal-stress direction), and the vertical direction is selected as the z direction (maximum principal-stress direction).

Taking the vertical strips of coal wall as the research object, the equation is:

$${\sigma }_z\mathrm{d}x+\left({\tau }_x+\mathrm{d}{\tau }_x\right)\mathrm{d}x=\tau \sin \theta \mathrm{d}s+{\sigma }_{\mathrm{n}xz}\cos \theta \mathrm{d}s+{\tau }_x\mathrm{d}x$$

(1)

Ignoring the high-order terms in Equation (1), we can simplify Equation (1) to obtain Equation (2):

$${\sigma }_z\mathrm{d}x=\tau \sin \theta \mathrm{d}s+{\sigma }_{\mathrm{n}xz}\cos \theta \mathrm{d}s$$

(2)

where σ_z is the vertical stress, τ_x is the shear stress between vertical strips, σ_nxz is the component of the normal stress on the xOz plane, and θ is the angle between a differential unit and the x direction.

According to geometric relationships, we can state the following:

$$\left\{\begin{array}{l}\sin \theta =\mathrm{d}z/\mathrm{d}s\\ \cos \theta =\mathrm{d}x/\mathrm{d}s\\ \sin {\beta }_y={\sigma }_{\mathrm{n}xz}/{\sigma }_{\mathrm{n}}\end{array}\right.$$

(3)

where σ_n is the normal stress of the sliding surface on the vertical strips.

Then, Equation (2) can be further converted into:

$${\displaystyle \frac{\mathrm{d}z}{\mathrm{d}x}}={\displaystyle \frac{{\sigma }_z-{\sigma }_{\mathrm{n}}\sin {\beta }_y}{\tau }}$$

(4)

A. M. Al-Ajmi et al. found that the Mogi–Coulomb criterion, taking into account the effect of the intermediate principal stress, has better applicability than the Mohr–Coulomb criterion and can better reflect the actual situation [29]. Mogi–Coulomb can be regarded as the generalization of the Mohr–Coulomb criterion under true triaxial stress. Similar to the Mohr–Coulomb criterion, the Mogi–Coulomb criterion is essentially a shear-failure criterion, and its expression is:

$${\tau }_{\mathrm{oct}}=a+b{\sigma }_{\mathrm{m},2}$$

(5)

where τ_oct is the octahedral shear stress, σ_m,2 is the mean effective stress, and a and b are fitting parameters. These parameters can be calculated according to the following equation:

$$\left\{\begin{array}{l}a={\displaystyle \frac{2\sqrt{2}}{3}}c\cos \phi \\ b={\displaystyle \frac{2\sqrt{2}}{3}}\sin \phi \\ {\tau }_{\mathrm{oct}}={\displaystyle \frac{1}{3}}\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2}\\ {\sigma }_{\mathrm{m},2}={\displaystyle \frac{1}{2}}\left({\sigma }_1+{\sigma }_3\right)\end{array}\right.$$

(6)

where c is the cohesion of the coal, φ is the friction angle in the coal, and σ₁, σ₂, and σ₃ are the maximum principal stress, the intermediate principal stress, and the minimum principal stress, respectively.

Xu [39] conducted a mechanical analysis of the coal in front of the large mining height working face and obtained the distribution law of the advanced support pressure in front of the coal wall, which is expressed as follows:

$$\left\{\begin{array}{l}{\sigma }_z=K_1{e}^{dx}+K_0\\ K_1=\left(\gamma H+c_{\mathrm{m}}\cot {\phi }_{\mathrm{m}}\right)e^{{\displaystyle \frac{\tan {\phi }_{\mathrm{m}}}{\lambda L}}\left(L+x^{\prime }\right)}\\ K_0=-c_{\mathrm{m}}\cot {\phi }_{\mathrm{m}}\\ d={\displaystyle \frac{\tan {\phi }_{\mathrm{m}}}{\lambda L}}\end{array}\right.$$

(7)

where γ is the weight of the rock; H is the burial depth; c_m and φ_m are the cohesion and internal friction angle between the coal-rock interface, respectively; L is the thickness of the coal seam; x’ is the length of the accumulated gangue along the surface of the protective beam; and μ is the friction coefficient between the coal seam and the roof. After the roof is damaged, the vertical load on the coal body will rapidly increase several times. Therefore:

$${\sigma }_{z\mathrm{m}}=k_1{\gamma }_{\mathrm{r}}H$$

(8)

where σ_zm is the peak stress, and k₁ is the peak stress coefficient.

The width of the plastic zone is:

$$x_0={\displaystyle \frac{1}{d}}\ln {\displaystyle \frac{k_2{\gamma }_{\mathrm{r}}H-K_0}{K_1}}$$

(9)

According to the Mogi–Coulomb criterion, Equation (4) can be transformed into:

$${\displaystyle \frac{\mathrm{d}z}{\mathrm{d}x}}={\displaystyle \frac{{\sigma }_z-\frac{1}{3}\left({\sigma }_z+{\sigma }_y+{\sigma }_x\right)\sin {\beta }_y}{a+\frac{b}{2}\left({\sigma }_z+{\sigma }_x\right)}}$$

(10)

Integrating Equation (10) yields:

$$z=A_1\ln \left(B_{1}x+D_1\right)+E_{1}x+C_1$$

(11)

Each coefficient can be represented by the following equation:

$$\left\{\begin{array}{l}{A}_1={\displaystyle \frac{6-2\sin {\beta }_y}{3db}}-{\displaystyle \frac{6K_0-2\sin {\beta }_y\left(K_0+{\sigma }_x+{\sigma }_y\right)}{6ad+3bd\left(K_0+{\sigma }_x\right)}}\\ B_1={\displaystyle \frac{K_{1}b}{2}}\\ D_1=a+{\displaystyle \frac{b\left(K_0+{\sigma }_x\right)}{2}}\\ E_1={\displaystyle \frac{6K_0-2\sin {\beta }_y\left(K_0+{\sigma }_x+{\sigma }_y\right)}{6a+3b\left(K_0+{\sigma }_x\right)}}-{\displaystyle \frac{6-2\sin {\beta }_y}{3b}}+\\ \hspace{1em} {\displaystyle \frac{2}{b}}\left(1-{\displaystyle \frac{\sin {\beta }_y}{3}}\right)\end{array}\right.$$

(12)

According to the Taylor expansion, Equation (11) can be approximated as a linear function:

$$\begin{array}{c}z=A_1\left(B_{1}x+D_1-1\right)+E_{1}x+C_1\\ =\left(A_1{B}_1+E_1\right)x+A_1{D}_1-A_1+C_1\end{array}$$

(13)

According to the above analysis, the soft-coal seam coal-body failure trace is finally determined to be a straight line.

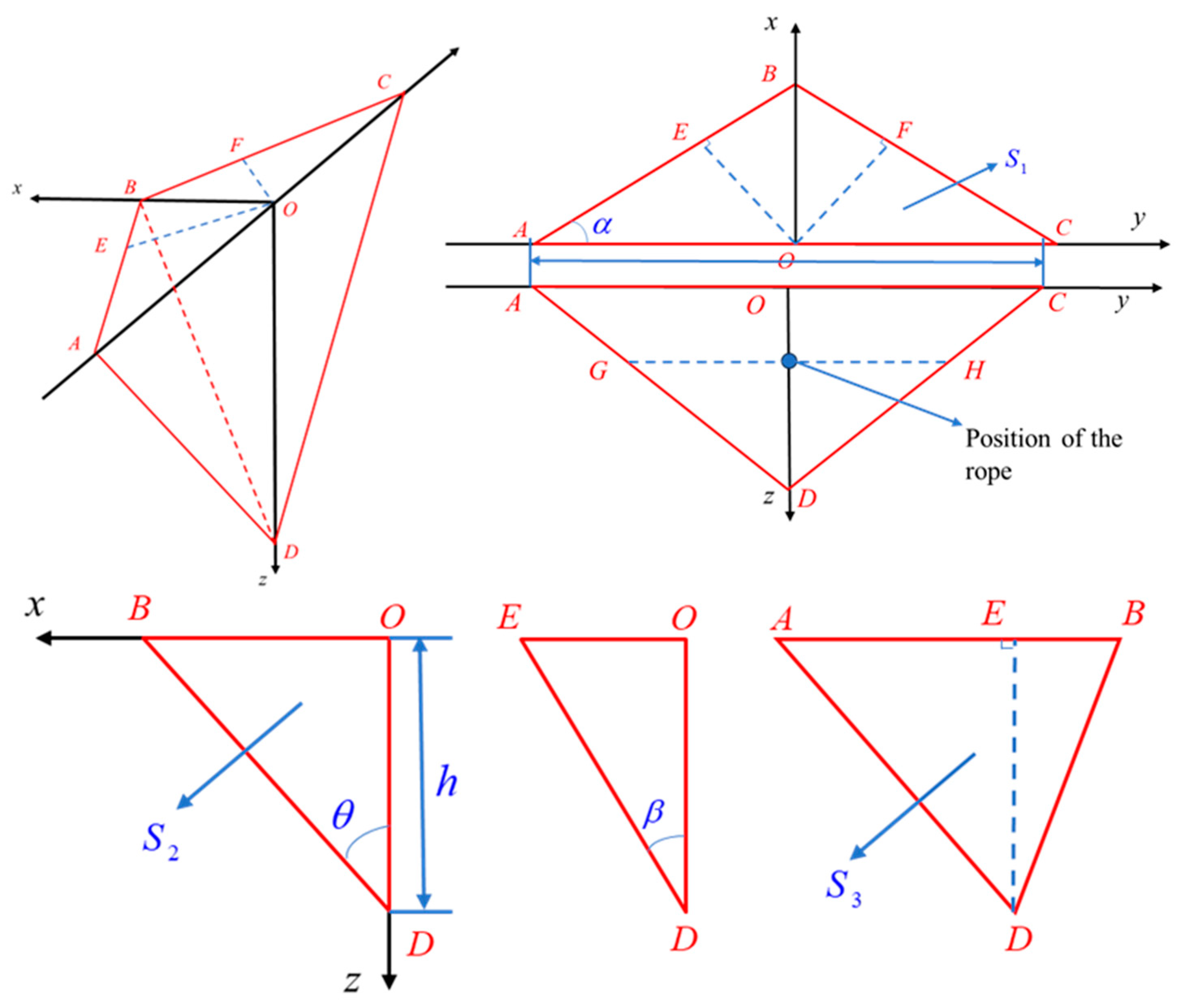
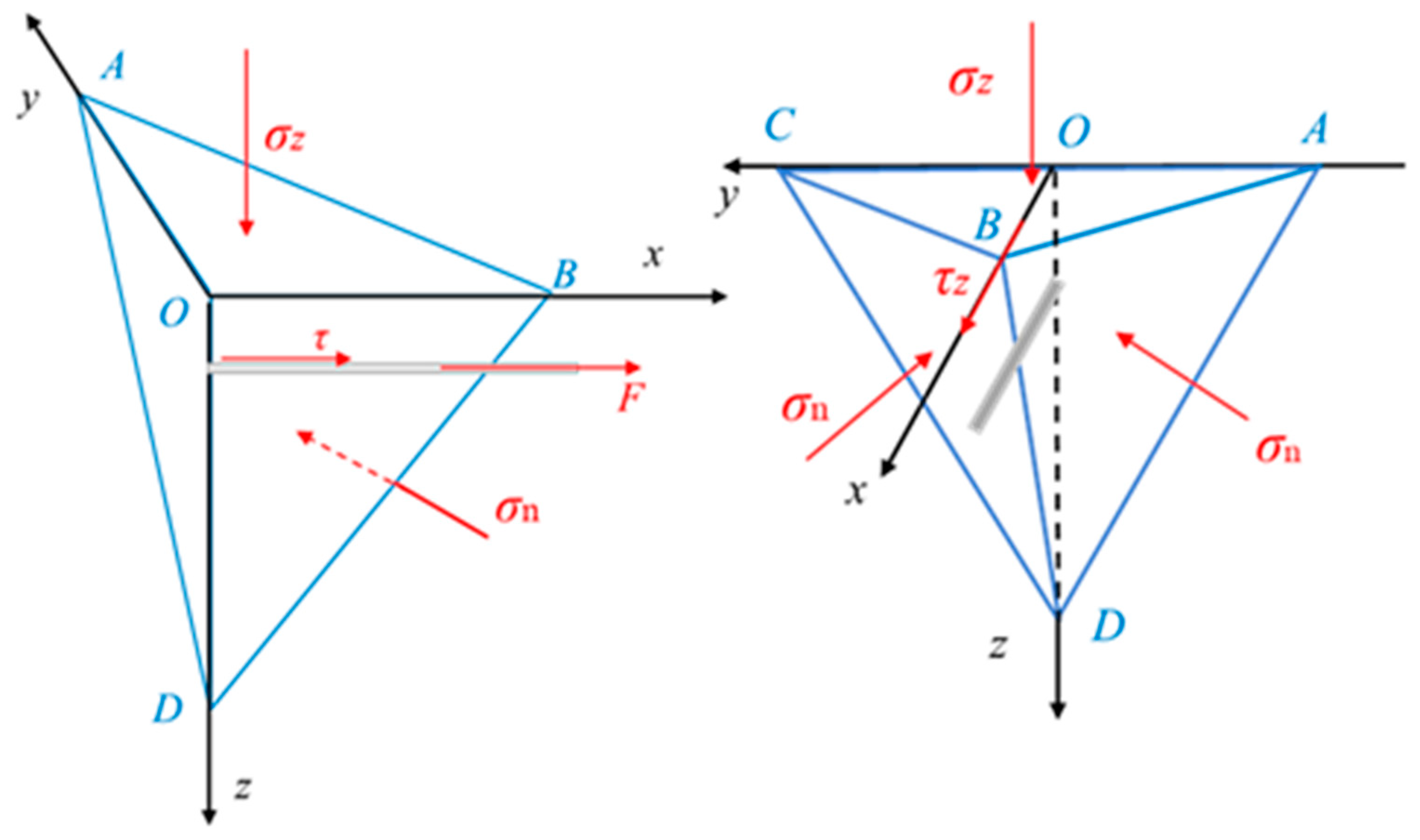
3.2. Determination of the Safety-Stability Coefficient of the Coal-Wall Sliding Face

The limit-equilibrium analysis is the most basic and commonly used method to study the failure mechanism of the coal-wall spalling [18,40,41]. The safety stability of coal walls is defined as the ratio of the anti-sliding moment to the sliding moment to judge the safety stability of coal walls. According to the sliding-body theory and the limit-equilibrium analysis, the safety-stability coefficient of the coal-wall sliding surface is obtained as:

$$K={\displaystyle \frac{{\displaystyle \int F\left(x,y\right)\mathrm{d}s}}{{\displaystyle \int G\left(x,y\right)\mathrm{d}s}}}$$

(14)

where F(x, y) is a function related to the anti-slip force, and G(x, y) is a function related to the sliding force. According to the Mogi–Coulomb criterion, the safety-stability coefficient can be expressed as follows:

$$K={\displaystyle \frac{{\displaystyle \int \left(a+b{\sigma }_{\mathrm{m},2}\right)\mathrm{d}}s}{{\displaystyle \int \mathrm{d}\tau }}}$$

(15)

According to the mechanical model shown in Figure 3, we have the following equation:

$$\left(a+b{\sigma }_{\mathrm{m},2}\right)\mathrm{d}s={\displaystyle \frac{2\sqrt{2}c\cos \phi \mathrm{d}s}{3}}+{\displaystyle \frac{\sqrt{2}\sin \phi \left({\sigma }_z+\gamma z+{\sigma }_x\right)\mathrm{d}s}{3}}$$

(16)

$$\mathrm{d}\tau =\left({\sigma }_z\sin \theta +\gamma z\sin \theta -{\tau }_z\cos \theta -\tau \right)\mathrm{d}s$$

(17)

where γ is the weight of coal, and z is the height of the differential strip.

The safety-stability coefficient can be further expressed as:

$$K={\displaystyle \frac{{\displaystyle \int \left[\frac{2\sqrt{2}c\cos \phi }{3}+\frac{\sqrt{2}\sin \phi }{3}\left({\sigma }_z+\gamma z+{\sigma }_x\right)\right]\mathrm{d}s}}{{\displaystyle \int \left({\sigma }_z\sin \theta +\gamma z\sin \theta -{\tau }_z\cos \theta -\tau \right)\mathrm{d}s}}}$$

(18)

For the convenience of calculation, the safety-stability coefficient of the coal wall is expressed as a function of I₁, I₂, I₃, and I₄:

$$K={\displaystyle \frac{I_1+I_2}{I_3-I_4}}$$

(19)

$$\begin{array}{l}{I}_1={\displaystyle \int \frac{\sqrt{2}\sin \phi \left({\sigma }_z+\gamma z\right)}{3}}\mathrm{d}s\\ ={\displaystyle \int \frac{\sqrt{2}\sin \phi \left(K_1{e}^{dx}+K_0+\gamma \left(h-x\tan \theta \right)\right)}{3}}\mathrm{d}s\\ ={\displaystyle \frac{\sqrt{2}\sin \phi }{3}}\sqrt{1+{\tan }^2\theta }\left(\begin{array}{l}{\displaystyle \frac{K_1}{d}}{e}^{d{x}_0}+K_0{x}_0+\\ \gamma h{x}_0-{\displaystyle \frac{\gamma x_0^2\tan \theta }{2}}\end{array}\right)\\ I_2={\displaystyle \int \left[\frac{2\sqrt{2}}{3}c\cos \phi +\frac{\sqrt{2}\sin \phi }{3}{\sigma }_x\right]}\mathrm{d}s\\ =\left[{\displaystyle \frac{2\sqrt{2}}{3}}c\cos \phi +{\displaystyle \frac{\sqrt{2}\sin \phi }{3}}{\sigma }_x\right]x_0\sqrt{1+{\tan }^2\theta }\end{array}$$

$$\begin{array}{l}{I}_3={\displaystyle \int \left({\sigma }_z\sin \theta +\gamma z\sin \theta \right)\mathrm{d}}s\\ ={\displaystyle \int \left[K_1{e}^{dx}+K_0+\gamma \left(h-x\tan \theta \right)\right]\sin \theta \sqrt{1+{\tan }^2\theta }\mathrm{d}x}\\ =\left({\displaystyle \frac{K_1}{d}}{e}^{d{x}_0}+K_0{x}_0+\gamma h{x}_0-{\displaystyle \frac{\gamma x_0^2\tan \theta }{2}}\right)\tan \theta \\ I_4={\displaystyle \int \left({\tau }_z\cos \theta +\tau \right)\mathrm{d}s}\\ ={\displaystyle \int \left[\begin{array}{l}\frac{2\sqrt{2}\left(1+\cos \theta \right)c\cos \phi }{3\cos \theta }+\gamma \left(h-x\tan \theta \right)+\\ \frac{\sqrt{2}\left(1+\cos \theta \right)\left(K_1{e}^{dx}+K_0+{\sigma }_x\right)\sin \phi }{3\cos \theta }\end{array}\right]}\mathrm{d}x\\ ={\displaystyle \frac{\sqrt{2}\left(1+\cos \theta \right)}{3\cos \theta }}\left({\displaystyle \frac{K_1}{d}}{e}^{d{x}_0}+K_0{x}_0+{\sigma }_x{x}_0\right)\sin \phi +\\ {\displaystyle \frac{2\sqrt{2}\left(1+\cos \theta \right)}{3\cos \theta }}{x}_{0}c\cos \phi +\gamma h{x}_0-{\displaystyle \frac{\gamma x_0^2\tan \theta }{2}}\end{array}$$

(20)

When disturbed by mining, stress is redistributed. Therefore, it is necessary to reconfirm the stress distribution under the limit-stability state. The coal body deforms and migrates toward the coal wall under the stress. When the deformation of the coal body along the x direction exceeds the maximum strain of the coal body, we have the following equation:

$${\sigma }_x-\mu \left({\sigma }_y+{\sigma }_z\right)={\sigma }_{\mathrm{c}}$$

(21)

where σ_c is tensile strength. In the y direction, due to the constraint of the adjacent coal body, ε_y = 0. According to the generalized Hooke’s law:

$${\epsilon }_y={\displaystyle \frac{{\sigma }_y-\mu \left({\sigma }_x+{\sigma }_z\right)}{E}}=0$$

(22)

Based on the Equations (20) and (21), we can get the following:

$${\sigma }_x={\sigma }_{\mathrm{c}}+{\displaystyle \frac{{\mu }^2{\sigma }_{\mathrm{c}}}{1-{\mu }^2}}+{\displaystyle \frac{\mu {\sigma }_z}{1-\mu }}$$

(23)

$${\sigma }_y={\displaystyle \frac{\mu {\sigma }_{\mathrm{c}}}{1-{\mu }^2}}+{\displaystyle \frac{\mu {\sigma }_z}{1-\mu }}$$

(24)

3.3. Analysis of Mechanism of Grouting–Flexible Rope Reinforcement

The effect of flexible reinforcement on the coal wall is to form a whole through the bite force between the slurry and the flexible rope and between the slurry and coal. When the coal body is deformed laterally under stress, the reinforcement system is also deformed accordingly, which has a certain inhibitory effect on the lateral deformation caused by the roof stress. The slurry and the flexible rope increase the cohesive force of the coal, thereby increasing the safety-stability coefficient of the coal. Therefore, this can effectively prevent the occurrence of spalling. In addition, with the use of flexible reinforcement technology, when coal-wall spalling occurs, the flexible rope can suspend the fallen coal body to prevent it from falling. At this time, the friction between the slurry and the coal body must be greater than the gravity of the fallen coal body. Otherwise, the flexible rope and the slurry will fall off.

Continuing to perform mechanical analyses on the strip in the vertical section passed through the flexible rope, the mechanical model is established, as shown in Figure 5. The shear stress between the slurry and the coal body in the flexible reinforcement system is:

$${\tau }_{\mathrm{r}}=a_m+{\displaystyle \frac{b_m}{2}}\left({\sigma }_z+{\sigma }_x\right)$$

(25)

The tension on the flexible rope is:

$$F=E_{\mathrm{r}}{\epsilon }_x$$

(26)

where E_r is the deformation modulus of the flexible rope, and ε_x is the coal strain in the x direction. The safety-stability coefficient of the coal wall after flexible reinforcement is:

$$K^{\prime }={\displaystyle \frac{{\displaystyle \int \left[\frac{2\sqrt{2}}{3}c\cos \phi +\frac{\sqrt{2}}{3}\sin \phi \left({\sigma }_z+{\gamma }_{\mathrm{c}}z+{\sigma }_x\right)+\frac{1}{s_{\mathrm{r}}}\left(F+{\tau }_{\mathrm{r}}\right)\sin \theta \right]}\mathrm{d}s}{{\displaystyle \int \left[\left({\sigma }_z+\gamma z\right)\cos \theta -{\tau }_z\cos \theta -\tau \right]}\mathrm{d}s}}$$

(27)

where s_r is the drilling spacing.

The safety-stability coefficient K’ at this time is a function of I₁, I₃, I₄, and I₅, and we can formulate the following:

$$K^{\prime }={\displaystyle \frac{I_1+I_5}{I_3-I_4}}$$

(28)

$$\begin{array}{l}{I}_5={\displaystyle \int \left[\frac{2\sqrt{2}}{3}c\cos \phi +\frac{\sqrt{2}\sin \phi {\sigma }_x}{3}+\frac{\left({\tau }_{\mathrm{r}}+F\right)\cos \theta }{s_{\mathrm{r}}}\right]}\mathrm{d}s\\ ={\displaystyle \frac{2\sqrt{2}c\cos \phi }{3\cos \theta }}+{\displaystyle \frac{\sqrt{2}{x}_0{\sigma }_x\sin \phi }{3\cos \theta }}+{\displaystyle \frac{\left({\tau }_{\mathrm{r}}+F\right)x_0}{s_{\mathrm{r}}}}\end{array}$$

(29)

After the coal body is flexibly reinforced, the safety-stability coefficient increases. In addition, the suspension effect of the flexible rope can be used to prevent the coal body from sliding into the working-face space. From the analysis in Section 2.2 and the situation of coal-wall spalling, it can be seen that the failure curve of coal-wall spalling is a nearly-straight line. For further in-depth research, the shape of the coal body spalling is simplified to a wedge block. The wedge-block model is shown in Figure 6, and the mechanical model is shown in Figure 7. The limit stability width L_y (the length of the side AC) is introduced. If the coal body is to be prevented from falling, L_GH ≥ s_r is required, and:

$$L_{\mathrm{GH}}={\displaystyle \frac{h_{\mathrm{b}}{L}_y}{M}}$$

(30)

The equation of surface ABD is:

$${\displaystyle \frac{x}{\tan \theta }}+{\displaystyle \frac{y}{\cot \alpha }}+z-h=0$$

(31)

The normal vector of the surface ABD is $\overrightarrow{n}=\left\{\cot \theta ,\tan \alpha ,1\right\}$, and the cosine of the angles between it and the three coordinate axes is:

$$\left\{\begin{array}{l}\cos {\alpha }_x={\displaystyle \frac{\cot \gamma }{\sqrt{1+{\tan }^2\alpha +{\cot }^2\theta }}}\\ \cos {\beta }_y={\displaystyle \frac{\tan \alpha }{\sqrt{1+{\tan }^2\alpha +{\cot }^2\theta }}}\\ \cos {\gamma }_z={\displaystyle \frac{1}{\sqrt{1+{\tan }^2\alpha +{\cot }^2\theta }}}\end{array}\right.$$

(32)

For a wedge in the limit stability state, we have the following:

$$\left\{\begin{array}{l}{\sigma }_{\mathrm{n}}=\sqrt{{\sigma }_z^2+{\sigma }_x^2+{\sigma }_y^2}\\ \cos {\gamma }_z={\displaystyle \frac{{\sigma }_z}{{\sigma }_{\mathrm{n}}}}\end{array}\right.$$

(33)

According to Equation (33), we can get:

$$\tan \alpha =\sqrt{{\displaystyle \frac{{\sigma }_{\mathrm{n}}^2}{{\sigma }_z^2}}-{\cot }^2\theta -1}$$

(34)

Therefore:

$$L_{\mathrm{AC}}={\displaystyle \frac{2L_{\mathrm{OB}}}{\tan \alpha }}={\displaystyle \frac{2{\sigma }_z{L}_{\mathrm{OB}}}{\sqrt{{\sigma }_{\mathrm{n}}^2-{\sigma }_z^2{\cot }^2\theta -{\sigma }_z^2}}}$$

(35)

The above equation determines the limit stability width of the coal wall. If the coal wall still has spalling after the reinforcement, the coal body can also be prevented from falling by the hanging effect of the flexible rope. To prevent the spalling of the coal body, it is also necessary to ensure that the maximum shear stress between the slurry and the coal body and between the slurry and the flexible rope is greater than the weight of the maximum spalling coal body; that is:

$$\left\{\begin{array}{l}12\pi {\varphi }_b\left(x_{\mathrm{k}}-x_0\right)\left(c_{\mathrm{m}2}+P_1\tan {\psi }_1\right)\ge \rho gh{x}_0{L}_{\mathrm{AC}}\tan \theta \\ 12\pi {\varphi }_a\left(x_{\mathrm{k}}-x_0\right)\left(c_{\mathrm{m}3}+P_2\tan {\psi }_2\right)\ge \rho gh{x}_0{L}_{\mathrm{AC}}\tan \theta \end{array}\right.$$

(36)

where ϕ_a is the borehole radius; c_m2, P_1, and ψ₁ are the cohesive force, normal stress, and internal friction angle between the coal and slurry, respectively; ϕ_b is the flexible rope radius; c_m3, P₂, and ψ₂ are the cohesive force, normal stress and internal friction angle between the slurry and flexible rope, respectively; and x_k is the borehole depth.

According to the research [42,43], the stress between the coal and the slurry and between the slurry and the flexible rope is:

$$\left\{\begin{array}{l}{P}_1={\displaystyle \frac{{\varphi }_b\left({\varphi }_a+{\varphi }_b\right)\beta }{{\varphi }_a\left({\varphi }_a+{\varphi }_b\right)x_{\omega }+{\left({\varphi }_a+{\varphi }_b\right)}^2{x}_{\mathrm{s}1}-{\varphi }_a{\varphi }_b{x}_{\mathrm{s}2}+{\varphi }_b\left({\varphi }_a+{\varphi }_b\right)x_{\mathrm{m}}}}\\ P_2={\displaystyle \frac{{\varphi }_a\left({\varphi }_a+{\varphi }_b\right)\beta }{{\varphi }_a\left({\varphi }_a+{\varphi }_b\right)x_{\omega }+{\left({\varphi }_a+{\varphi }_b\right)}^2{x}_{\mathrm{s}1}-{\varphi }_a{\varphi }_b{x}_{\mathrm{s}2}+{\varphi }_b\left({\varphi }_a+{\varphi }_b\right)x_{\mathrm{m}}}}\end{array}\right.$$

(37)

$$\left\{\begin{array}{l}{x}_{\omega }={\displaystyle \frac{1+{\mu }_{\omega }}{E_{\omega }}}\\ x_{\mathrm{s}1}={\displaystyle \frac{1+{\mu }_{\mathrm{s}}}{E_{\mathrm{s}}}}\\ x_{\mathrm{s}2}={\displaystyle \frac{4{\mu }_{\mathrm{s}}\left(1+{\mu }_{\mathrm{s}}\right)}{E_{\mathrm{s}}}}\\ x_{\mathrm{m}}={\displaystyle \frac{\left(1+{\mu }_{\mathrm{m}}\right)\left(1-2{\mu }_{\mathrm{m}}\right)}{E_{\mathrm{m}}}}\end{array}\right.$$

(38)

where β is the expansion coefficient of the slurry; μ_ω and E_ω are the Poisson’s ratio and elastic modulus of the coal; μ_s and E_s are the Poisson’s ratio and elastic modulus of the slurry; μ_m and E_m are the Poisson’s ratio and deformation modulus of the flexible rope; and ϕ_b/ϕ_a is defined as the aperture ratio.

4. Discussion

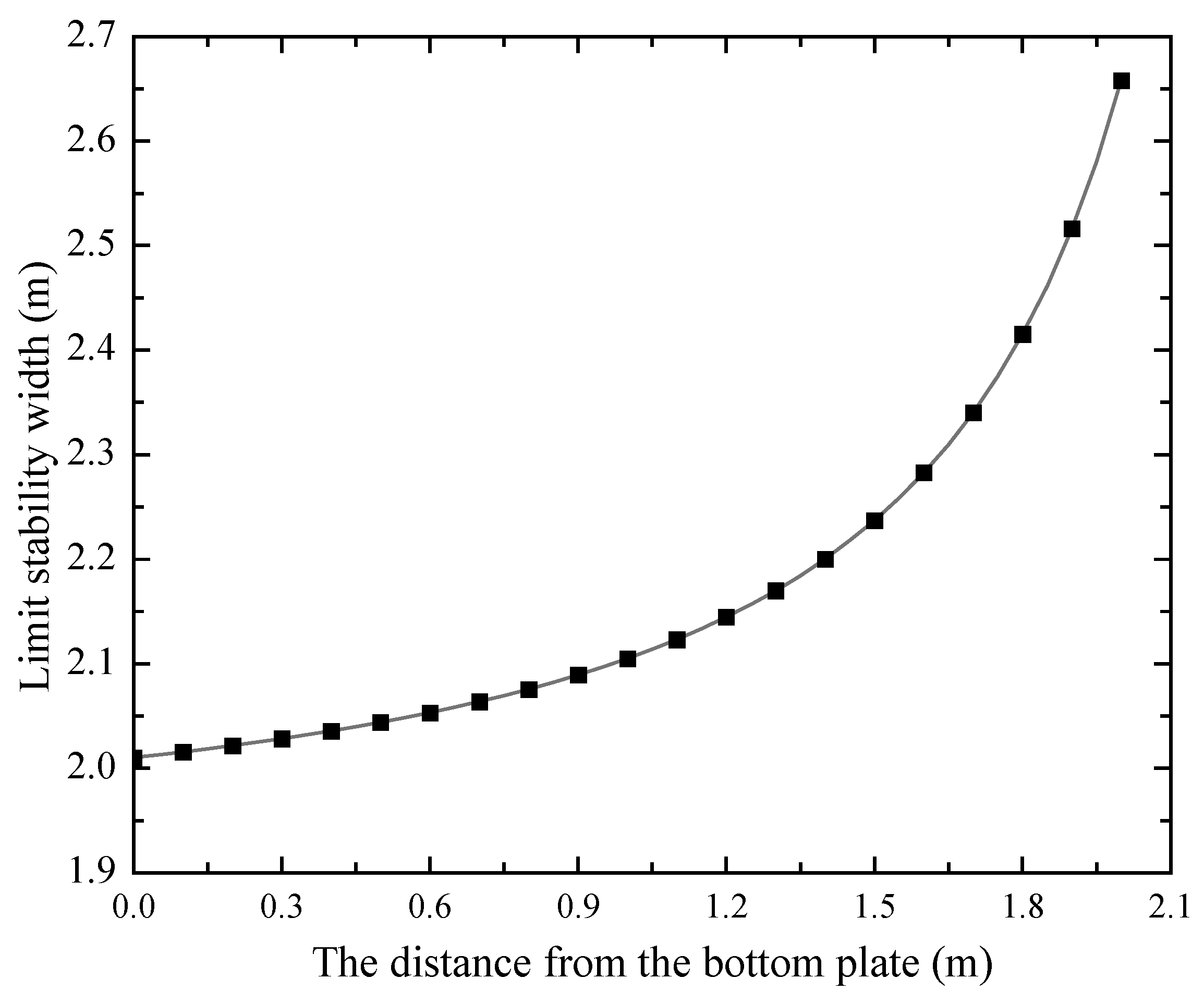
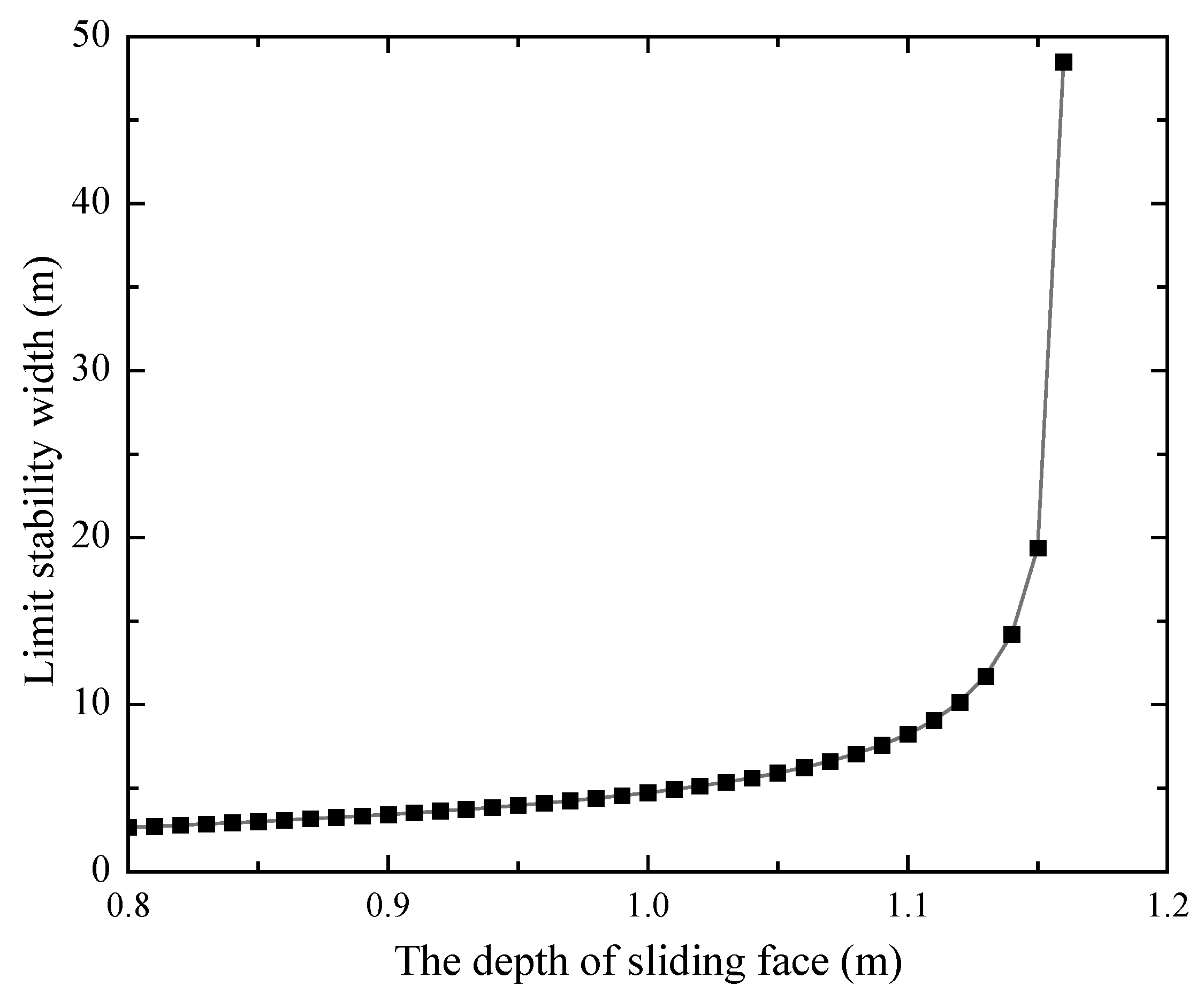
4.1. The Effect of Parameters Affecting Stability of Coal Wall

(1)

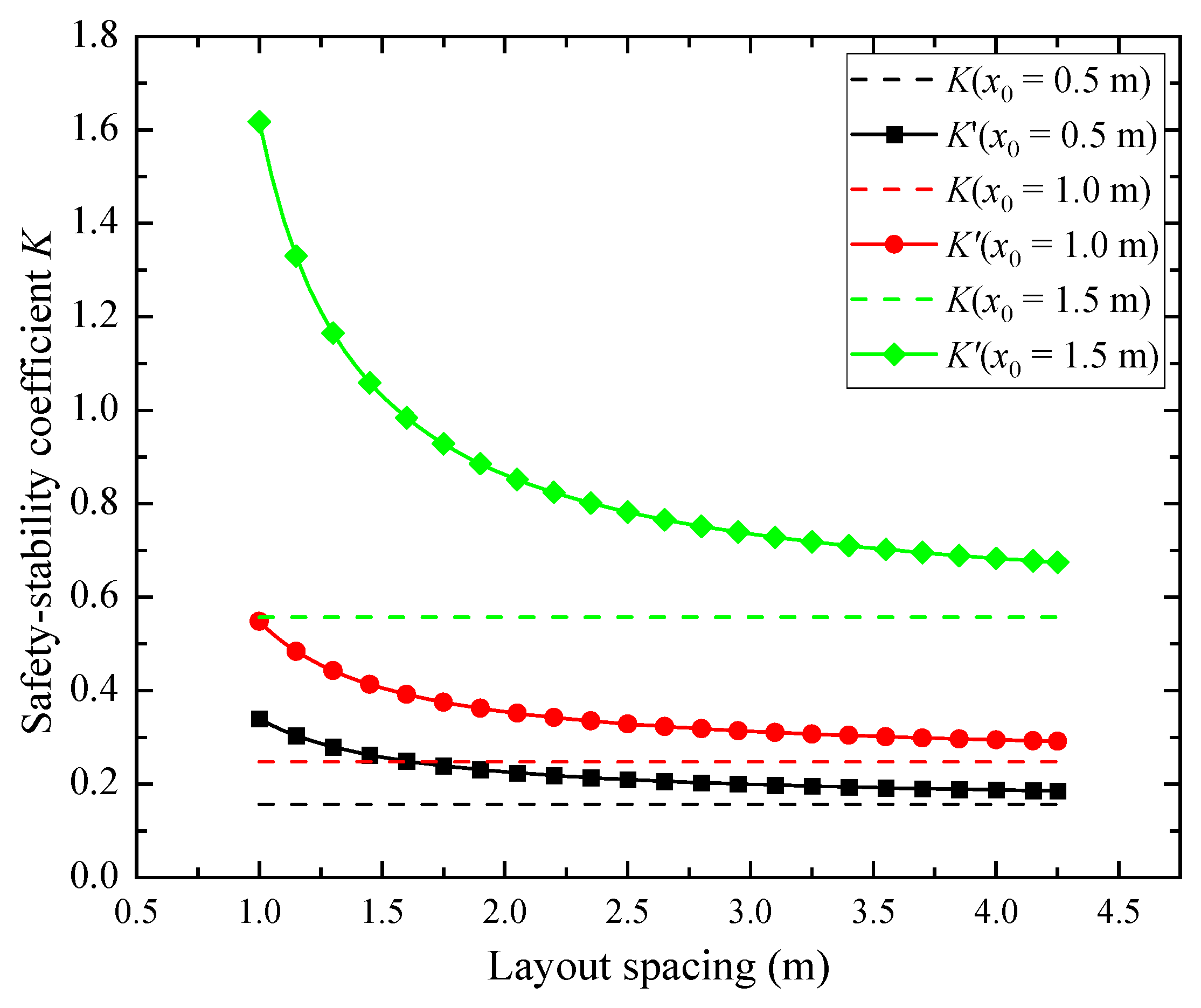
Safety-stability coefficient at different sliding face positions

The mechanical parameters of coal in the Wangzhuang Coal Mine, Lu’an, Shanxi Province, are summarized as shown in

Table 2. Mechanical parameters of coal rock [44].

Weight kN/m3	Elastic Modulus /GPa	Cohesion/MPa	Internal Friction Angle/°	Poisson’s Ratio	Tensile Strength/MPa	Compressive Strength /MPa	Cohesion of Direct Roof/MPa	Internal Friction Angle of Direct Roof/°
14.11	2.87	1.32	27.38	0.36	0.88	13.56	3.46	23.77

[44]. Coal-wall spalling generally occurs within the plastic zone [44]. According to the mechanical parameters of coal and Equation (9), the maximum width of the plastic zone is 2.5 m. For sliding surfaces of different depths (0.5 m, 1.0 m, 1.5 m, 2.0 m, and 2.5 m), the variation trend of the safety-stability coefficient with the distance from the bottom plate is shown in Figure 8. As can be seen from Figure 8, firstly, the safety-stability coefficient increases slowly with the increase of the distance from the bottom plate. Then, the safety-stability coefficient increases rapidly after reaching a certain position. This is mainly due to the self-weight of the coal body in the thick coal seam, and the coal body below is subjected to greater stress because of the high mining face. Under the action of high stress, the safety-stability coefficient of the coal wall decreases rapidly. In addition, from Equations (18) and (20), it can be seen that the greater the vertical stress, the lower the stability of the coal wall. For the sliding surface with a maximum depth of 0.5 m, the safety-stability coefficient increases rapidly after the distance from the bottom plate exceeds 2.5 m. The safety-stability coefficient of the sliding surface below this position remains almost unchanged. For the sliding surface with a maximum depth of 2.5 m, the safety-stability coefficient increases rapidly after the distance from the bottom plate exceeds 2.0 m. From the perspective of the safety-stability coefficient, the most dangerous position is determined to be 0.5 m deep and 2.0 m from the bottom plate on the coal wall (0.6 times the mining height).

(2)

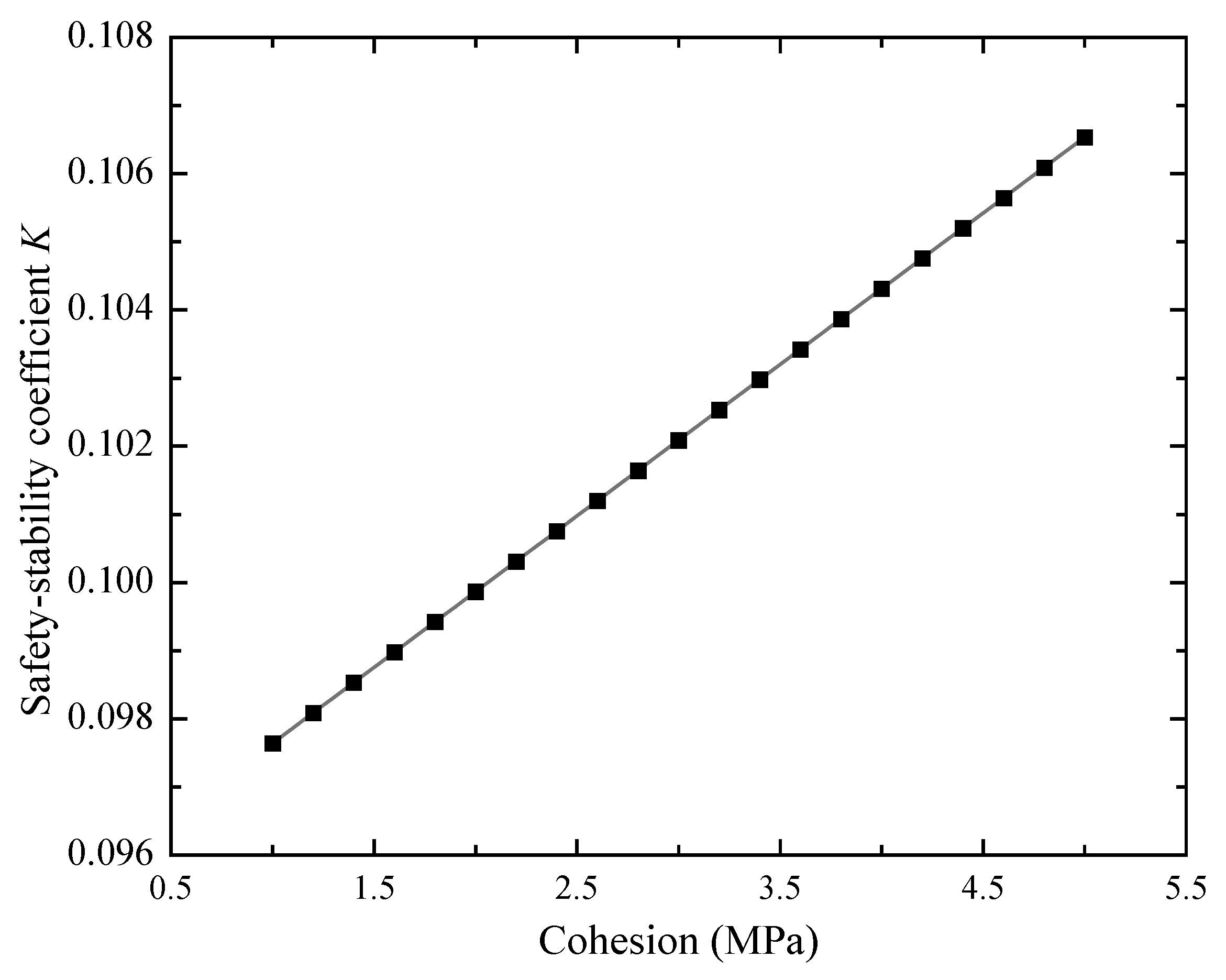
Influence of cohesion and internal friction angle on safety-stability coefficient

For the sliding face with a distance of 2 m from the bottom plate and a depth of 0.5 m from the coal surface, the variation trend of the safety-stability coefficient of the coal from 1 MPa to 5 MPa is shown in Figure 9. As shown in Figure 9, the safety-stability coefficient of the coal wall increases with the increase of the cohesion of the coal. This is mainly due to the fact that the cohesion of the coal body is first destroyed when the soft coal is damaged, resulting in coal failure. For a certain stress, the damage in the coal body is smaller when the cohesion is larger, and the stability of the coal body is also higher. When the cohesion is 1.32 MPa, and the other parameters remain unchanged, the variation trend of the safety-stability coefficient of the coal wall with the internal friction angle is shown in Figure 10. As shown in Figure 10, the safety-stability coefficient of the coal wall increases with the increase of the internal friction angle. The larger the internal friction angle, the smaller the shear stress, and the higher the stability of the coal wall.

(3)

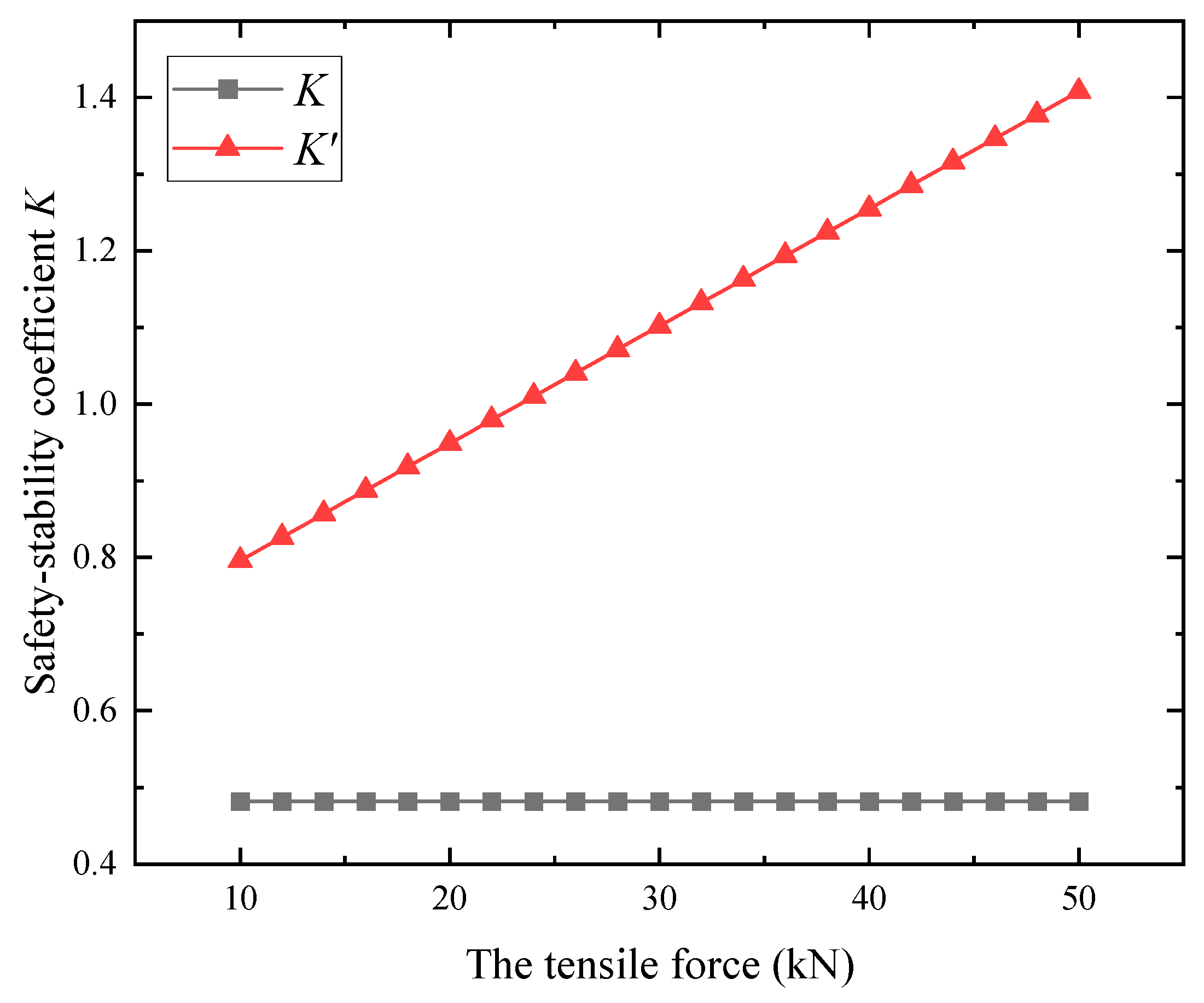
Influence of the maximum tension of the flexible rope on the safety-stability coefficient

For the sliding face corresponding to the distance of 2 m from the bottom plate and the maximum depth of 0.5 m, when the maximum tension of the flexible rope changes from 10 kN to 50 kN, the variation trend between the safety-stability coefficient before and after reinforcement and the maximum tension of the flexible rope is shown in Figure 11.

As shown in Figure 11, as the maximum tension that the flexible rope can withstand increases, the safety-stability coefficient also increases. This is mainly due to the fact that the higher the strength and deformation modulus of the flexible reinforcement system, the smaller the deformation and the higher the stability of the coal–slurry–flexible rope system under the same stress conditions. For the same slip surface, the other parameters remain unchanged, and the variation trend of the safety-stability coefficient with the flexible rope layout spacing is shown in Figure 12. As shown in Figure 12, with the increase of the layout spacing, the safety-stability coefficient gradually decreases, and for the same layout spacing, the grouting–flexible rope reinforcement technology has a better reinforcement effect on deep spalling. The smaller the spacing between ropes, the better the effect of the flexible reinforcement system on improving the strength of the coal body and the higher the safety and stability. However, smaller spacing can quickly increase the costs and is not conducive to the sustainable production of coal mines. Therefore, it is necessary to adopt a reasonable layout spacing to ensure the dual benefits of safety, sustainability, and economy. With a 1.5 m layout spacing, when the maximum depth is greater than 1.5 m, the safety-stability coefficient is greater than 1.

According to the actual conditions of the working face, when the maximum tension of the flexible rope is 30 kN, the changing trend of the limit stability width L_AC after flexible reinforcement with the distance from the bottom plate is shown in Figure 13. As shown in Figure 13, as the distance from the bottom plate increases, the limit stability width increases nonlinearly, and the growth trend gradually increases. This is mainly caused by the self-weight of the coal body. When the distance from the bottom plate is 2 m, and the other parameters remain unchanged, the variation trend of the limit stability width with the depth of the slip surface is shown in Figure 14. As shown in Figure 14, the limit stability width gradually increases with the increase of the slip surface depth.

4.2. The Effect of Parameters on the Normal Stress of the Flexible Reinforcement System

Under the condition of a certain grouting pressure, the variation trend of the normal stress between the coal body and the slurry and the normal stress between the slurry and the flexible rope with the aperture ratio is shown in Figure 15. It can be seen from the figure that P₁ increases with the increase of the aperture ratio, and P₂ decreases with the increase of the aperture ratio. When the aperture ratio gradually increases beyond a certain range, the coal body that falls after the spalling is greater than the friction between the flexible rope and the slurry due to the low normal stress, causing the flexible rope to fall off. Therefore, the selection of the aperture ratio must meet certain requirements. For a certain drilling radius, the larger the radius of the flexible rope is not necessarily the better. This is caused by the combination of the friction between the slurry and the rope and between the slurry and the coal.

4.3. Methods and Measures for Preventing Spalling

The most commonly used grouting material in flexible reinforcement technology is Marisan, but its extensive use greatly increases the cost. The use of flexible ropes can reduce costs to a certain extent.

As mentioned above, the maximum load that the flexible rope can withstand has a great influence on the effect of the flexible reinforcement technology. For parameters such as a certain row of drilling-hole spacing and drilling-hole size, the larger the deformation modulus of the flexible rope, the higher the safety-stability coefficient. When the deformation modulus of the flexible rope is constant, the smaller the layout spacing, that is, the greater the drilling density, the higher the safety-stability coefficient. If the coal wall still spalls after flexible reinforcement, a larger maximum load of the flexible rope can also prevent the flexible rope from being broken, thereby preventing the spalled coal body from falling. In addition, the diameter of the flexible rope also has a certain influence on its maximum load. Studies have shown that when the diameter of the coir rope is 14–20 mm, the tension that the flexible rope can withstand can reach its maximum value [39]. The safety-stability coefficient can be increased by selecting a flexible rope with a large deformation modulus and a large limit tensile force, thereby increasing the stability of the coal body. In addition, it is necessary to select a suitable aperture ratio and drilling radius to maximize the normal stress, thereby increasing the shear stress between the coal–slurry–flexible rope and the tensile strength of the flexible rope and making the limit stability width greater than the layout spacing, thereby effectively preventing the spalled coal body from falling.

4.4. Application Examples

The 91–105 working face of the Lu’an Wangzhuang Coal Mine in Changzhi City, Shanxi Province, is selected as an example. The mechanical parameters of the coal rock mass are shown in Table 2. According to the analysis in 4.1, the most dangerous sliding surface is determined to be 0.6 times the mining height.

It is found that when the diameter of the flexible rope is 24 mm, and the aperture ratio is 1.6–1.9, the maximum tensile force that the flexible rope can withstand is 30 kN, and the tensile strength is 61.3 MPa [42]. Therefore, the diameter of the flexible rope is determined to be 24 mm, the borehole diameter is 40 mm, and the aperture ratio is 1.67. According to Figure 15 and Equation (37), the shear stress between the slurry and the flexible rope is determined to be 3 MPa. As shown in Figure 12, the flexible reinforcement technology has a better reinforcement effect for deep spalling. When the layout spacing is 1.5 m, the safety-stability coefficient of the sliding surface at a depth of 1.5 m is 1.03 > 1. At this time, the flexible reinforcement with a layout spacing of 1.5 m can prevent spalling with a depth greater than 1.5 m; for spalling with a depth smaller than 1.5 m, the suspension effect of the flexible rope is required to prevent the coal body from sliding down. According to Equations (30) and (35), the layout height is determined to be 2.5 m. At this time, the normal stress between the flexible reinforcement system and the obtained limit stability width can meet L_GH > s_r and Equation (36) after inspection and can also play a role in preventing spalling. Therefore, the layout spacing of grouting–flexible rope is determined to be 1.5 m. According to the previous working experience of the mine, the drilling angle is determined to be 5°, and the grouting pressure is determined to be 2 MPa. According to the width of the plastic zone obtained by Equations (9) and (36), the hole depth is determined to be 4 m. In summary, the key parameters of flexible reinforcement are obtained, as shown in

Table 3. The key parameters of flexible reinforcement.

Drilling Diameter/mm	Depth of Drilling/m	Angle of Drilling/°	Diameter of Rope/mm	Layout Spacing/m	Aperture Ratio	Grouting Pressure/MPa	Installation Height/m
40	4	5	24	1.5	1.67	2	2.5

. After the flexible reinforcement measures are adopted, the safety-stability coefficient at 0.6 times the mining height increases from 0.09 to 1.03. The reinforcement system can improve the coal body characteristics and the suspension effect of the flexible rope to ensure that the coal wall will not spall, thus ensuring the safe production of the working face. After flexible reinforcement, the coal wall is well improved, and the reinforcement effect was verified by Song [45].

4.5. Model Applicability and Scalability

In order to study the mechanism of soft coal-wall spalling, combined with the influence of horizontal stress and coal self-weight, the mechanical model of the slip surface of the coal wall was established, and the safety-stability coefficient before and after flexible reinforcement was obtained. The stability of the coal body can be judged by the safety and stability factors of the coal wall. In contrast to previous research, the stability of the coal before and after reinforcement is analyzed by combining the differences in horizontal stress. The model is not only applicable to uniaxial and conventional triaxial stress but also to the true triaxial stress state. According to the basic assumptions of this study, there are still some limitations in this study. The model is based on the shear-failure mode of the coal wall, and the instability of hard coal includes other failure modes, such as tensile failure, which is not applicable in this case. In the process of establishing the model, the influence of gangue faults and other factors on the stability of the coal body was not considered. When there are geological conditions such as faults, the applicability of the model is insufficient. In the future, we will continue to improve the model, make up for the shortcomings of faults and other coal failure modes, and carry out numerical research to verify the effect.

Anchors and other support means are limited in the reinforcement of mine coal walls because they are not easy to cut. The grouting technology solves the difficulty of not being easy to cut, but the cost of the slurry is high (25,000–32,000 yuan/t). The cost of flexible rope is low, far less than the cost of slurry, and this highly reduces the cost of grouting. The flexible rope also has the characteristic of not being easy to break. The tensile capacity is much greater than the tensile stress borne by the coal body and has a good reinforcement effect. In addition, in the coal wall sheet with large deformation, it has a better reinforcement effect than the flexible reinforcement technology of bolt support.

5. Conclusions

Coal-wall spalling is a common disaster in mines. In order to ensure the sustainability of coal mining, the mechanism of coal-wall spalling and flexible reinforcement are studied. In this paper, the sliding-body theory and the limit-equilibrium analysis method are combined to analyze the stability of coal walls before and after reinforcement. The main conclusions are as follows:

(1)

Based on the Mogi–Coulomb criterion and the ultimate equilibrium condition of the mechanical model, the differential equation of the coal-wall slip surface is formulated. The functional relationship of the slip surface is obtained, and the soft coal-wall slip surface can be approximated as a straight line. Therefore, traces of coal-wall spalling can be approximated as linear.

(2)

Based on the Mogi–Coulomb criterion, combined with the limit-equilibrium analysis method, the mechanical model of the coal wall is created. The calculation formula of the safety-stability coefficient of the coal wall is obtained. It is found that the stability of the coal wall is related to the properties of the coal body (cohesion and internal friction angle). The higher the cohesion and internal friction angle of the coal body, the better the safety and stability of the coal wall. The larger cohesion of coal can effectively stop coal-wall spalling. Therefore, the cohesion of the coal can be improved through flexible reinforcement so as to improve the stability of the coal body. It was determined that the most dangerous sliding surface of the 91–105 working face of the Lu’an Wangzhuang coal mine was located at 0.6 times the mining height.

(3)

The influencing mechanism of the safety -factor, the ultimate stability width, and the key reinforcement parameters of the sliding surface of the coal wall after flexible reinforcement were analyzed. After flexible reinforcement, the occurrence of spalling can be effectively prevented through the action of the flexible reinforcement system. The reinforcement effect is mainly related to the strength of the flexible rope, the aperture ratio, the laying spacing, and the selection of the reinforcement materials. Flexible ropes with strong load-bearing capacity can enhance the reinforcement effect. The flexible reinforcement effect is mainly affected by the tensile force generated by the flexible rope and the friction between the slurry and coal and between the flexible rope and coal. The opposite trend between the two friction forces makes it necessary to select a certain value of the aperture ratio to ensure the reinforcement effect. Smaller laying spacing can quickly enhance reinforcement, but it can also increase costs. It is necessary to reasonably select the reinforcement material and determine the reinforcement parameters, such as aperture ratio and layout spacing. This paper proposes an alternative method for determining the layout spacing. With a layout spacing of 1.5 m, the safety-stability factor at 0.6 times the mining height increases from 0.09 to 1.03.