Identifying Non-Perennial River Reaches: A Hybrid Model Combining WEP-L and Random Forest
Abstract
1. Introduction
2. Methods
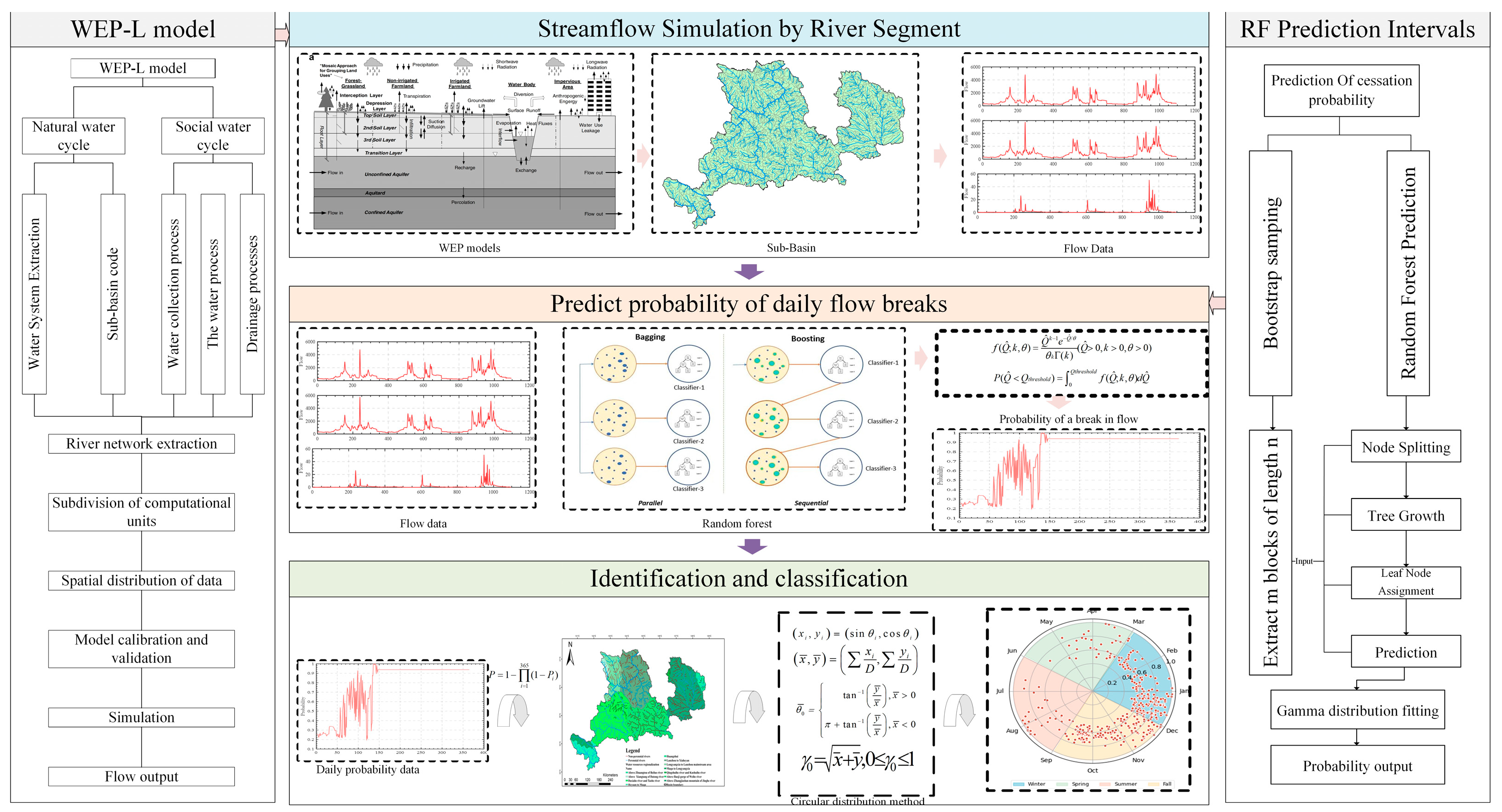
2.1. Technological Framework
2.2. WEP-L Model Implementation
2.3. RF Prediction
2.4. Identification and Classification of Non-Perennial Rivers
2.4.1. Identification
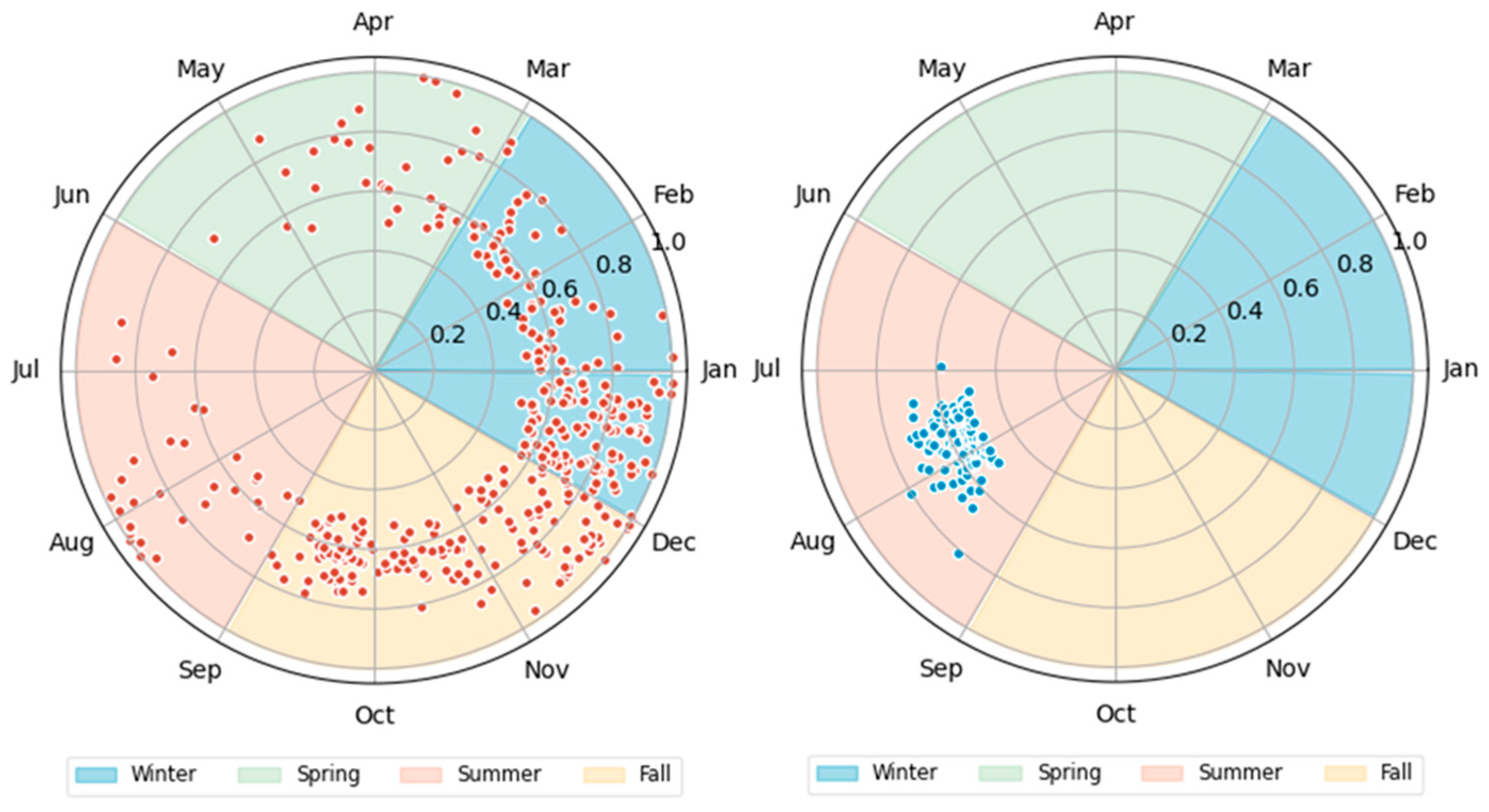
2.4.2. Classification
3. Study Area and Data
3.1. Study Area
3.2. Data Analysis
4. Results and Discussion
4.1. Flow Simulation
4.2. Identification of Non-Perennial Rivers
4.3. Classification of Non-Perennial Rivers
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Levick, L.R.; Goodrich, D.C.; Hernandez, M.; Fonseca, J.; Semmens, D.J.; Stromberg, J.C.; Tluczek, M.; Leidy, R.A.; Scianni, M.; Guertin, D.P. The Ecological and Hydrological Significance of Ephemeral and Intermittent Streams in the Arid and Semi-Arid American Southwest; US Environmental Protection Agency, Office of Research and Development: Washington, DC, USA, 2008. [Google Scholar]
- Snelder, T.H.; Datry, T.; Lamouroux, N.; Larned, S.T.; Sauquet, E.; Pella, H.; Catalogne, C. Regionalization of Patterns of Flow Intermittence from Gauging Station Records. Hydrol. Earth Syst. Sci. 2013, 17, 2685–2699. [Google Scholar] [CrossRef]
- Messager, M.L.; Lehner, B.; Cockburn, C.; Lamouroux, N.; Pella, H.; Snelder, T.; Tockner, K.; Trautmann, T.; Watt, C.; Datry, T. Global Prevalence of Non-Perennial Rivers and Streams. Nature 2021, 594, 391–397. [Google Scholar] [CrossRef] [PubMed]
- De Girolamo, A.M.; Barca, E.; Leone, M.; Lo Porto, A. Impact of Long-Term Climate Change on Flow Regime in a Mediterranean Basin. J. Hydrol. Reg. Stud. 2022, 41, 101061. [Google Scholar] [CrossRef]
- Benstead, J.P.; Leigh, D.S. An Expanded Role for River Networks. Nat. Geosci. 2012, 5, 678–679. [Google Scholar] [CrossRef]
- Larned, S.T.; Datry, T.; Arscott, D.B.; Tockner, K. Emerging Concepts in Temporary-river Ecology. Freshw. Biol. 2010, 55, 717–738. [Google Scholar] [CrossRef]
- Cid, N.; Erős, T.; Heino, J.; Singer, G.; Jähnig, S.C.; Cañedo-Argüelles, M.; Bonada, N.; Sarremejane, R.; Mykrä, H.; Sandin, L. From Meta-system Theory to the Sustainable Management of Rivers in the Anthropocene. Front. Ecol. Environ. 2022, 20, 49–57. [Google Scholar] [CrossRef]
- Leigh, C.; Datry, T. Drying as a Primary Hydrological Determinant of Biodiversity in River Systems: A Broad-scale Analysis. Ecography 2017, 40, 487–499. [Google Scholar] [CrossRef]
- Bogan, M.T.; Chester, E.T.; Datry, T.; Murphy, A.L.; Robson, B.J.; Ruhi, A.; Stubbington, R.; Whitney, J.E. Resistance, Resilience, and Community Recovery in Intermittent Rivers and Ephemeral Streams. In Intermittent Rivers and Ephemeral Streams; Elsevier: Amsterdam, The Netherlands, 2017; pp. 349–376. [Google Scholar]
- Pineda-Morante, D.; Fernández-Calero, J.M.; Pölsterl, S.; Cunillera-Montcusí, D.; Bonada, N.; Cañedo-Argüelles, M. Local Hydrological Conditions and Spatial Connectivity Shape Invertebrate Communities after Rewetting in Temporary Rivers. Hydrobiologia 2022, 849, 1511–1530. [Google Scholar] [CrossRef]
- Leone, M.; Gentile, F.; Lo Porto, A.; Ricci, G.F.; De Girolamo, A.M. Ecological Flow in Southern Europe: Status and Trends in Non-Perennial Rivers. J. Environ. Manag. 2023, 342, 118097. [Google Scholar] [CrossRef] [PubMed]
- Leone, M.; Gentile, F.; Lo Porto, A.; Ricci, G.F.; Schürz, C.; Strauch, M.; Volk, M.; De Girolamo, A.M. Setting an Environmental Flow Regime under Climate Change in a Data-Limited Mediterranean Basin with Temporary River. J. Hydrol. Reg. Stud. 2024, 52, 101698. [Google Scholar] [CrossRef]
- Busch, M.H.; Costigan, K.H.; Fritz, K.M.; Datry, T.; Krabbenhoft, C.A.; Hammond, J.C.; Zimmer, M.; Olden, J.D.; Burrows, R.M.; Dodds, W.K.; et al. What’s in a Name? Patterns, Trends, and Suggestions for Defining Non-Perennial Rivers and Streams. Water 2020, 12, 1980. [Google Scholar] [CrossRef]
- Smakhtin, V.U. Low Flow Hydrology: A Review. J. Hydrol. 2001, 240, 147–186. [Google Scholar] [CrossRef]
- Jaeger, K.L.; Sando, R.; McShane, R.R.; Dunham, J.B.; Hockman-Wert, D.P.; Kaiser, K.E.; Hafen, K.; Risley, J.C.; Blasch, K.W. Probability of Streamflow Permanence Model (PROSPER): A Spatially Continuous Model of Annual Streamflow Permanence throughout the Pacific Northwest. J. Hydrol. X 2019, 2, 100005. [Google Scholar] [CrossRef]
- Costigan, K.H.; Kennard, M.J.; Leigh, C.; Sauquet, E.; Datry, T.; Boulton, A.J. Flow Regimes in Intermittent Rivers and Ephemeral Streams. In Intermittent Rivers and Ephemeral Streams; Elsevier: Amsterdam, The Netherlands, 2017; pp. 51–78. [Google Scholar]
- Eng, K.; Wolock, D.M.; Dettinger, M.D. Sensitivity of Intermittent Streams to Climate Variations in the USA. River Res. Apps 2016, 32, 885–895. [Google Scholar] [CrossRef]
- Poff, N. A Hydrogeography of Unregulated Streams in the United States and an Examination of Scale-dependence in Some Hydrological Descriptors. Freshw. Biol. 1996, 36, 71–79. [Google Scholar] [CrossRef]
- Kennard, M.J.; Pusey, B.J.; Olden, J.D.; Mackay, S.J.; Stein, J.L.; Marsh, N. Classification of Natural Flow Regimes in Australia to Support Environmental Flow Management. Freshw. Biol. 2010, 55, 171–193. [Google Scholar] [CrossRef]
- Yu, S.; Bond, N.R.; Bunn, S.E.; Kennard, M.J. Development and Application of Predictive Models of Surface Water Extent to Identify Aquatic Refuges in Eastern Australian Temporary Stream Networks. Water Resour. Res. 2019, 55, 9639–9655. [Google Scholar] [CrossRef]
- Buttle, J.M.; Boon, S.; Peters, D.L.; Spence, C.; Van Meerveld, H.J.; Whitfield, P.H. An Overview of Temporary Stream Hydrology in Canada. Can. Water Resour. J. Rev. Can. Des Ressour. Hydr. 2012, 37, 279–310. [Google Scholar] [CrossRef]
- Hamada, Y.; O’Connor, B.L.; Orr, A.B.; Wuthrich, K.K. Mapping Ephemeral Stream Networks in Desert Environments Using Very-High-Spatial-Resolution Multispectral Remote Sensing. J. Arid Environ. 2016, 130, 40–48. [Google Scholar] [CrossRef]
- Jia, Y.; Ding, X.; Wang, H.; Zhou, Z.; Qiu, Y.; Niu, C. Attribution of Water Resources Evolution in the Highly Water-Stressed Hai River Basin of China. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Xu, F.; Zhao, L.; Jia, Y.; Niu, C.; Liu, X.; Liu, H. Evaluation of Water Conservation Function of Beijiang River Basin in Nanling Mountains, China, Based on WEP-L Model. Ecol. Indic. 2022, 134, 108383. [Google Scholar] [CrossRef]
- Wang, H.; Jiao, Y.; Hu, B.X.; Li, F.; Li, D. Study on Interaction between Surface Water and Groundwater in Typical Reach of Xiaoqing River Based on WEP-L Model. Water 2023, 15, 492. [Google Scholar] [CrossRef]
- Jia, Y.; Wang, H.; Zhou, Z.; Qiu, Y.; Luo, X.; Wang, J.; Yan, D.; Qin, D. Development of the WEP-L Distributed Hydrological Model and Dynamic Assessment of Water Resources in the Yellow River Basin. J. Hydrol. 2006, 331, 606–629. [Google Scholar] [CrossRef]
- Zhou, Z.; Liu, J.; Yan, Z.; Wang, H.; Jia, Y. Attribution Analysis of the Natural Runoff Evolution in the Yellow River Basin. Adv. Water Sci. 2022, 33, 27–37. [Google Scholar]
- Liu, J.J. Distributed Simulation and Evolution Law of Water Cycle in the Weihe River Basin Under Changing Environment; China Institute of Water Resources and Hydropower Research: Beijing, China, 2013. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Ilinca, C.; Anghel, C.G. Flood Frequency Analysis Using the Gamma Family Probability Distributions. Water 2023, 15, 1389. [Google Scholar] [CrossRef]
- Sabzevari, T. Runoff Prediction in Ungauged Catchments Using the Gamma Dimensionless Time-Area Method. Arab. J. Geosci. 2017, 10, 131. [Google Scholar] [CrossRef]
- Zimmer, M.A.; Kaiser, K.E.; Blaszczak, J.R.; Zipper, S.C.; Hammond, J.C.; Fritz, K.M.; Costigan, K.H.; Hosen, J.; Godsey, S.E.; Allen, G.H.; et al. Zero or Not? Causes and Consequences of Zero-flow Stream Gage Readings. WIREs Water 2020, 7, e1436. [Google Scholar] [CrossRef] [PubMed]
- Burn, D.H. Catchment Similarity for Regional Flood Frequency Analysis Using Seasonality Measures. J. Hydrol. 1997, 202, 212–230. [Google Scholar] [CrossRef]
- Castellarin, A.; Burn, D.H.; Brath, A. Assessing the Effectiveness of Hydrological Similarity Measures for Flood Frequency Analysis. J. Hydrol. 2001, 241, 270–285. [Google Scholar] [CrossRef]
- Harrigan, S.; Prudhomme, C.; Parry, S.; Smith, K.; Tanguy, M. Benchmarking Ensemble Streamflow Prediction Skill in the UK. Hydrol. Earth Syst. Sci. 2018, 22, 2023–2039. [Google Scholar] [CrossRef]
- Sauquet, E.; Shanafield, M.; Hammond, J.C.; Sefton, C.; Leigh, C.; Datry, T. Classification and Trends in Intermittent River Flow Regimes in Australia, Northwestern Europe and USA: A Global Perspective. J. Hydrol. 2021, 597, 126170. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]



| Station | RE (%) | NSE | ||||
|---|---|---|---|---|---|---|
| 1956–1980 | 1981–2016 | 1956–2016 | 1956–1980 | 1981–2016 | 1956–2016 | |
| Machu | −7.1 | −1.2 | −3.7 | 0.788 | 0.754 | 0.768 |
| Zheqiao | −7.6 | 10.2 | 1.4 | 0.834 | 0.697 | 0.796 |
| Hongqi | 7.4 | −2.5 | 2.1 | 0.706 | 0.688 | 0.707 |
| Xiaochuan | −2.4 | 5.2 | 2.0 | 0.864 | 0.667 | 0.788 |
| Lanzhou | −2.3 | 0.9 | −0.4 | 0.878 | 0.701 | 0.809 |
| Beidao | −2.3 | 5.8 | 1.3 | 0.144 | 0.255 | 0.249 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, K.; Chu, J.; Zhou, Z.; Liu, J.; Chen, Y.; Wang, Y.; Tang, Z. Identifying Non-Perennial River Reaches: A Hybrid Model Combining WEP-L and Random Forest. Sustainability 2024, 16, 10543. https://doi.org/10.3390/su162310543
Yuan K, Chu J, Zhou Z, Liu J, Chen Y, Wang Y, Tang Z. Identifying Non-Perennial River Reaches: A Hybrid Model Combining WEP-L and Random Forest. Sustainability. 2024; 16(23):10543. https://doi.org/10.3390/su162310543
Chicago/Turabian StyleYuan, Kangqi, Junying Chu, Zuhao Zhou, Jiajia Liu, Yuwei Chen, Ying Wang, and Zuohuai Tang. 2024. "Identifying Non-Perennial River Reaches: A Hybrid Model Combining WEP-L and Random Forest" Sustainability 16, no. 23: 10543. https://doi.org/10.3390/su162310543
APA StyleYuan, K., Chu, J., Zhou, Z., Liu, J., Chen, Y., Wang, Y., & Tang, Z. (2024). Identifying Non-Perennial River Reaches: A Hybrid Model Combining WEP-L and Random Forest. Sustainability, 16(23), 10543. https://doi.org/10.3390/su162310543






