Double-Layer Optimization and Benefit Analysis of Shared Energy Storage Investment Considering Life-Cycle Carbon Emission
Abstract
1. Introduction
1.1. Literature Review
1.2. Previous Work on SESS and Research Gap
- (1)
- The concept of life-cycle carbon emission has not been considered in the optimization configuration of SES;
- (2)
- The amount of research that discusses the economy of SESS from multiple perspectives and considers different types of energy storage is relatively low.
1.3. Aims and Contributions
- (1)
- The concept of life-cycle carbon emission is first introduced into the investment of SESS, which considers the carbon emission of the manufacturing, operations, and recycling processes of SESS. This idea enhances the practicability and accuracy of investment strategies for energy storage;
- (2)
- The economy of SESS investment and the energy expenditure of electricity and heat users are considered in the double-layer optimization model, with the uncertainty of supply and demand, which contributes to the realization of a win–win situation for both sides;
- (3)
- The economy of SESS investment is analyzed from multiple perspectives, including net benefits, payback years, and return on investment (ROI). Moreover, the impact of considering the life-cycle carbon emission and types of energy storage on its investment is also analyzed quantitatively.
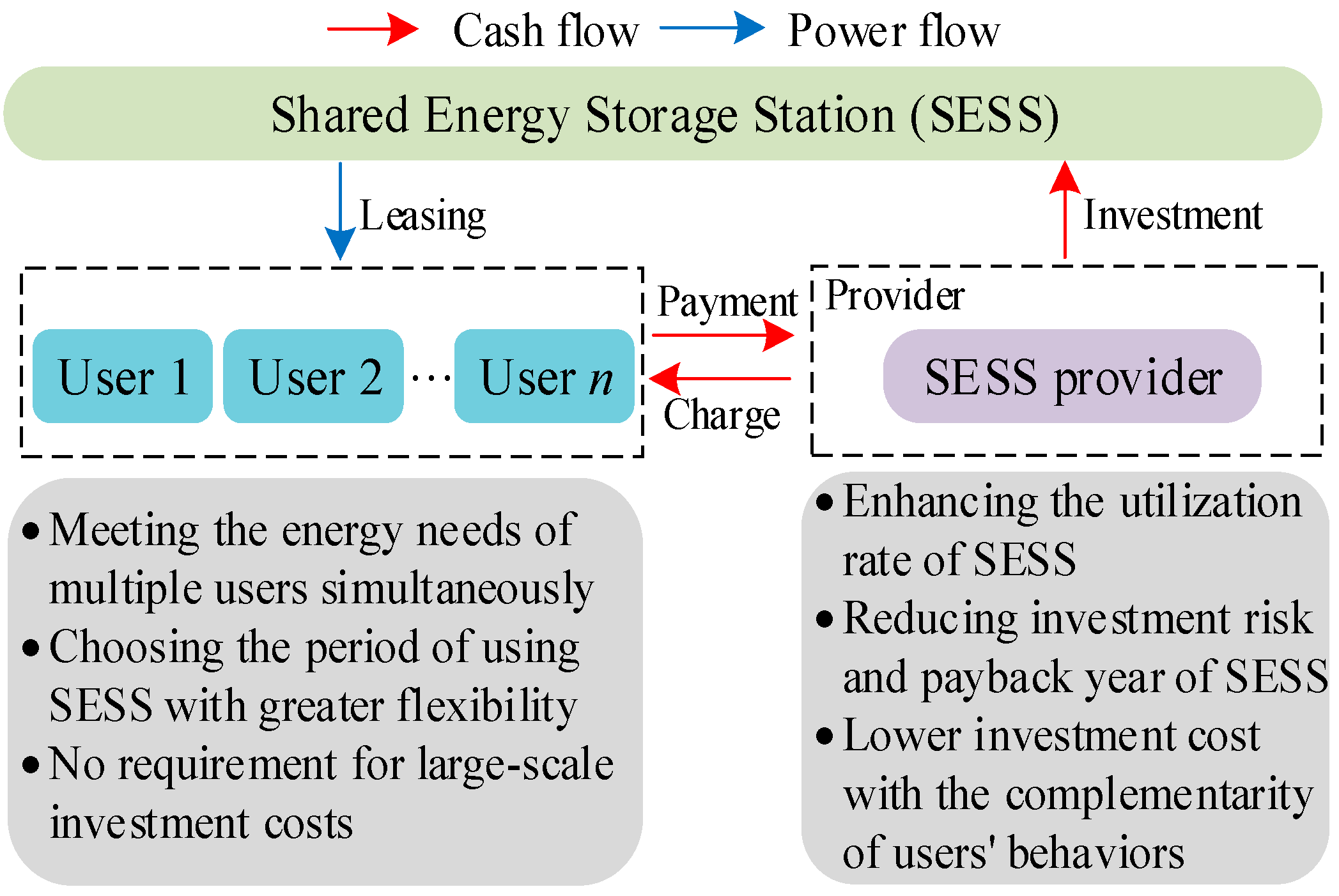
2. Shared Energy Storage Station
2.1. Service Mode of SESS
2.2. Settlement Method and Profit Mechanism of SESS
2.3. Application Scenario of SESS
3. Life-Cycle Carbon Emission Modeling of SESS and Uncertainty of Supply and Demand
3.1. Life-Cycle Carbon Emission Modeling of SESS
3.2. Uncertainty of Supply and Demand
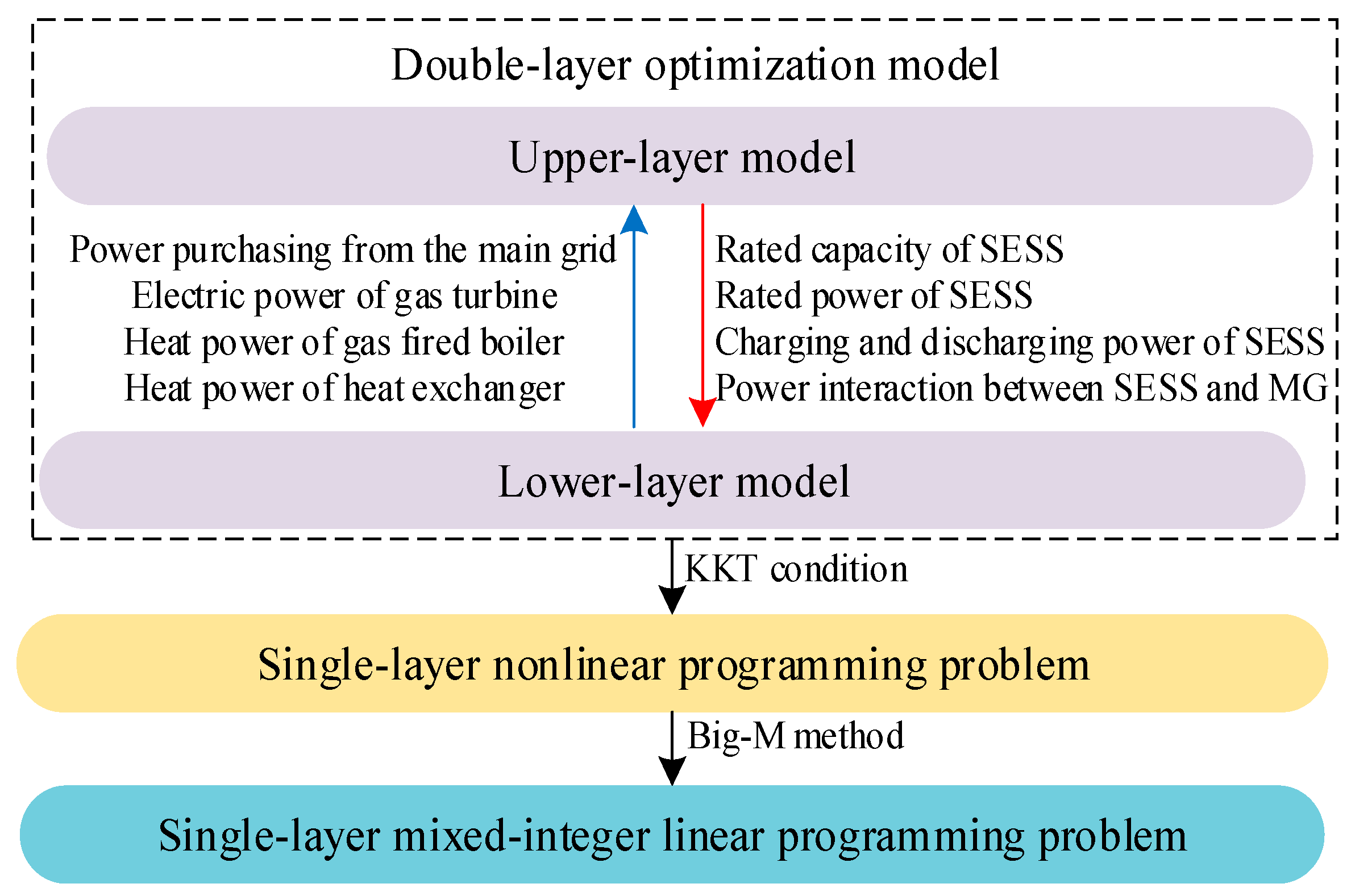
4. Double-Layer Optimization Model Considering Life-Cycle Carbon Emission of SESS
4.1. Upper Layer: Optimal Configuration of SESS
- (1)
- Daily investment cost of SESS
- (2)
- Daily operation and maintenance cost of the SESS
- (3)
- Daily interactive power cost of the SESS [30]
- (4)
- Daily service revenue of the SESS [30]
- (1)
- Capacity/power ratio constraint [33]
- (2)
- State constraints [30]
- (3)
- Power output constraints [30]
4.2. Lower Layer: Optimization Scheduling of CHP Multi-Microgrid System
- (1)
- Daily power cost of microgrid purchasing from the main grid [29]
- (2)
- Daily gas-purchasing cost of the microgrid [29]
- (1)
- Electric power balance constraint
- (2)
- Heat power balance constraint
- (3)
- Heat power balance constraint of the waste heat boiler [29]
- (4)
- Charging and discharging power balance constraint of SESS [30]
- (5)
- Output constraints of equipment in the CHP multi-microgrid system [29]
- (6)
- Purchasing power of the microgrid from the main grid [29]
- (7)
- Interactive power between the CHP multi-microgrid system and the SESS [29]
4.3. Model Solution Strategy
5. Case Study
5.1. Case Description
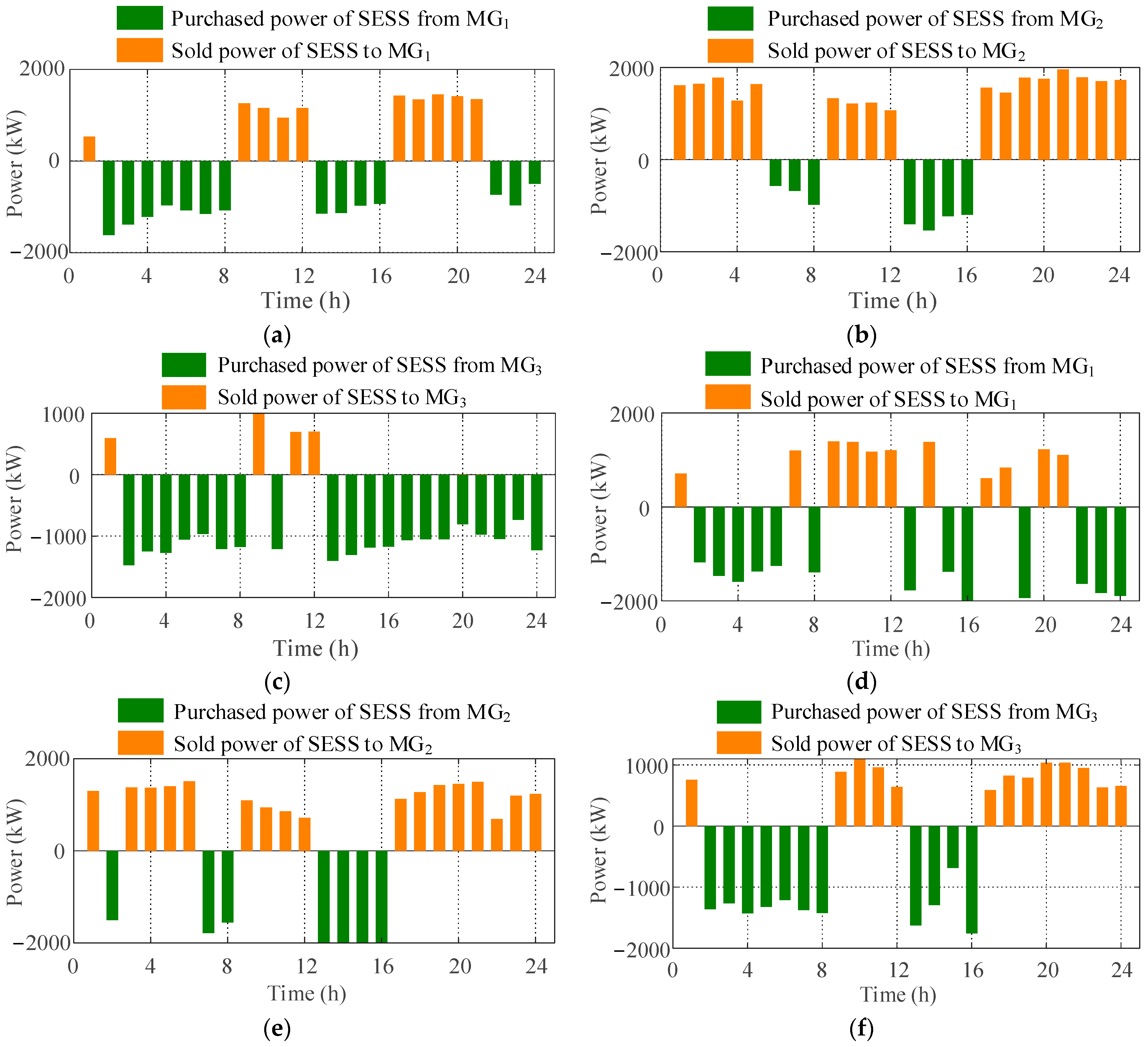
5.2. Results and Analysis
5.3. Economic Evaluation of SESS Investment and Impact of Life-Cycle Carbon Emission on SESS Investment
- (1)
- Net benefits of the SESS
- (2)
- Payback years of the SESS
- (3)
- ROI of the SESS
6. Conclusions
- (1)
- The annual service charge revenue of THE SESS is positively related with the service price. When the service charge price is 0.15 CNY/kWh, the SESS can obtain an annual service charge of 474.19 ten thousand CNY, which is the main source of annual revenue of the SESS;
- (2)
- The neglect of life-cycle carbon emission will introduce errors into the key indicators of the SESS, including the net benefits and payback years. As the load demand and rated capacity of the SESS increases, considering the life-cycle carbon emission of SESS becomes increasingly necessary.
7. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency (IEA). Renewables 2021, Paris. 2021. Available online: https://www.iea.org/reports/renewables-2021 (accessed on 22 October 2024).
- Zhu, H.; Li, H.; Liu, G.; Ge, Y.; Shi, J.; Li, H.; Zhang, N. Energy storage in high variable renewable energy penetration power systems: Technologies and applications. CSEE J. Power Energy Syst. 2023, 9, 2099–2108. [Google Scholar]
- Zhang, J.; Zhang, N.; Ge, Y. Energy storage placements for renewable energy fluctuations: A practical study. IEEE Trans. Power Syst. 2023, 38, 4916–4927. [Google Scholar] [CrossRef]
- Liu, X.; Zhao, T.; Deng, H.; Wang, P.; Liu, J.; Blaabjerg, F. Microgrid energy management with energy storage systems: A review. CSEE J. Power Energy Syst. 2023, 9, 483–504. [Google Scholar]
- Guo, Z.; Wei, W.; Shahidehpour, M.; Chen, L.; Mei, S. Two-timescale dynamic energy and reserve dispatch with wind power and energy storage. IEEE Trans. Sustain. Energy 2023, 14, 490–503. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, L. Optimal operation and economic value of energy storage at consumer locations. IEEE Trans. Autom. Control 2017, 62, 792–807. [Google Scholar] [CrossRef]
- Kalathil, D.; Wu, C.; Poolla, K.; Varaiya, P. The sharing economy for the electricity storage. IEEE Trans. Smart Grid 2019, 10, 556–567. [Google Scholar] [CrossRef]
- Wang, K.; Yu, Y.; Wu, C. Optimal electricity storage sharing mechanism for single peaked time-of-use pricing scheme. Electr. Power Syst. Res. 2021, 195, 107176. [Google Scholar] [CrossRef]
- Tushar, W.; Chai, B.; Yuen, C.; Huang, S.; Smith, D.; Poor, H.; Yang, Z. Energy storage sharing in smart grid: A modified auction based approach. IEEE Trans. Smart Grid 2016, 7, 1462–1475. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, C.; Li, F.; Bale, P.; Sun, H. Active demand response using shared energy storage for household energy management. IEEE Trans. Smart Grid 2013, 4, 1888–1897. [Google Scholar] [CrossRef]
- Wang, Z.; Gu, C.; Li, F. Flexible operation of shared energy storage at households to facilitate PV penetration. Renew. Energy 2018, 116, 438–446. [Google Scholar] [CrossRef]
- Li, X.; Chen, L.; Sun, F.; Hao, Y.; Du, X.; Mei, S. Share or not share, the analysis of energy storage interaction of multiple renewable energy stations based on the evolution game. Renew. Energy 2023, 208, 679–692. [Google Scholar] [CrossRef]
- He, X.; Xiao, J.; Cui, S.; Liu, X.; Wang, Y. A new cooperation framework with a fair clearing scheme for energy storage sharing. IEEE Trans. Ind. Inform. 2022, 18, 5893–5904. [Google Scholar] [CrossRef]
- Li, J.; Fang, Z.; Wang, Q.; Zhang, M.; Li, Y.; Zhang, W. Optimal operation with dynamic partitioning strategy for centralized shared energy storage station with integration of large-scale renewable energy. J. Mod. Power Syst. Clean Energy 2024, 12, 359–370. [Google Scholar] [CrossRef]
- Chang, C.; Ghaddar, B.; Nathwani, J. Shared community energy storage allocation and optimization. Appl. Energy 2022, 318, 119160. [Google Scholar] [CrossRef]
- Yang, Y.; Hu, G.; Spanos, J. Optimal sharing and fair cost allocation of community energy storage. IEEE Trans. Smart Grid 2021, 12, 4185–4194. [Google Scholar] [CrossRef]
- Hafiz, F.; Queiroz, A.; Fajri, P.; Husain, I. Energy management and optimal storage sizing for a shared community: A multi-stage stochastic programming approach. Appl. Energy 2019, 236, 42–54. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Sun, H. Bi-level optimal configuration of intelligent buildings based on shared energy storage services. Proc. CSEE 2024. Available online: https://kns.cnki.net/kcms/detail/11.2107.TM.20240402.1440.024.html (accessed on 22 October 2024).
- Odeh, N.; Cockerill, T. Life cycle GHG assessment of fossil fuel power plants with carbon capture and storage. Energy Policy 2008, 36, 367–380. [Google Scholar] [CrossRef]
- Hou, G.; Ma, X.; Yang, Z.; Chen, Q.; Liu, W.; Zhang, Y.; Zhang, D. Calculation and analysis of carbon emissions in the whole life cycle of pumped storage power stations. China Environ. Sci. 2023, 43, 326–335. [Google Scholar]
- Li, Y.; Zhang, N.; Du, E.; Liu, Y.; Cai, X.; He, D. Mechanism study and benefit analysis on power system low carbon demand response based on carbon emission flow. Proc. CSEE 2022, 42, 2830–2841. [Google Scholar]
- Zhao, W.; Xiong, Z.; Pan, Y.; Li, F.; Xu, P.; Lai, X. Low-carbon planning of power system considering carbon emission flow. Autom. Electr. Power Syst. 2023, 47, 23–33. [Google Scholar]
- Chen, L.; Tang, W.; Wang, Z.; Zhang, L.; Xie, F. Low-carbon oriented planning of shared photovoltaics and energy storage systems in distribution networks via carbon emission flow tracing. Int. J. Electr. Power Energy Syst. 2024, 160, 110126. [Google Scholar] [CrossRef]
- Hu, J.; Wang, Y.; Dong, L. Low carbon-oriented planning of shared energy storage station for multiple integrated energy systems considering energy-carbon flow and carbon emission reduction. Energy 2024, 290, 130139. [Google Scholar] [CrossRef]
- Marsh, E.; Allen, S.; Hattam, L. Tackling uncertainty in life cycle assessments for the built environment: A review. Build. Environ. 2023, 231, 109941. [Google Scholar] [CrossRef]
- Wang, R.; Wen, X.; Wang, X.; Fu, Y.; Zhang, Y. Low carbon optimal operation of integrated energy system based on carbon capture technology, LCA carbon emissions and ladder-type carbon trading. Appl. Energy 2022, 311, 118664. [Google Scholar] [CrossRef]
- Han, X.; Li, Y.; Nie, L.; Huang, X.; Deng, Y.; Yan, J.; Kourkoumpas, D.; Karellas, S. Comparative life cycle greenhouse gas emissions assessment of battery energy storage technologies for grid applications. J. Clean. Prod. 2023, 392, 136251. [Google Scholar] [CrossRef]
- Jiao, Y.; Månsson, D. Greenhouse gas emissions from hybrid energy storage systems in future 100% renewable power systems—A Swedish case based on consequential life cycle assessment. J. Energy Storage 2023, 57, 106167. [Google Scholar] [CrossRef]
- Wu, S.; Liu, J.; Zhou, Q.; Wang, C.; Chen, Z. Optimal economic scheduling for combined cooling heating and power multi-microgrids considering energy storage station service. Autom. Electr. Power Syst. 2019, 43, 10–18. [Google Scholar]
- Li, L.; Xu, Q.; Wang, X.; Lin, J.; Sun, H. Optimal economic scheduling of industrial customers on the basis of sharing energy storage station. Electr. Power Constr. 2020, 41, 100–107. [Google Scholar]
- Ma, Y.; Fan, Z.; Liu, W.; Zhao, S. Environmental and economic dispatch considering carbon trading credit and randomicity of wind power and load forecast error. Power Syst. Technol. 2016, 40, 412–418. [Google Scholar]
- Cui, Y.; Zhang, H.; Zhong, W.; Zhao, Y.; Wang, Z.; Xu, B. Day-ahead scheduling considering the participation of price-based demand response and CSP plant in wind power consumption. Power Syst. Technol. 2020, 44, 183–191. [Google Scholar]
- Chen, L.; Wu, T.; Liu, H.; Huang, G.; Xu, X. Demand management based two-stage optimal storage model for large users. Autom. Electr. Power Syst. 2019, 43, 194–200. [Google Scholar]
- Guo, L.; Ding, Y.; Bao, M.; Zeng, D. An optimal power purchase model of inter-provincial traders in two-level electricity market considering risk management. Power Syst. Technol. 2019, 43, 2726–2733. [Google Scholar]
- Chen, C.; Zhang, Q.; Huang, Y.; Wang, X.; Wang, D.; Yang, L.; Lin, Z. Optimal configuration method of park-level integrated energy system considering optimal construction time sequence and cloud energy storage. Autom. Electr. Power Syst. 2022, 46, 24–32. [Google Scholar]
- Meng, F.; Zeng, X.; Zhang, Y.; Dent, C.; Gong, D. An integrated optimization and learning approach to optimal dynamic pricing for the retailer with multi-type customers in smart grids. Inf. Sci. 2018, 448–449, 215–232. [Google Scholar] [CrossRef]
- Ding, T.; Bo, R.; Gu, W.; Sun, H. Big-M based MIQP method for economic dispatch with disjoint prohibited zones. IEEE Trans. Power Syst. 2014, 29, 976–977. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Xiang, Y. Optimal sizing and investment benefit analysis for energy storage of electricity retailers under market mechanisms considering shared mode. Power Syst. Technol. 2020, 44, 1740–1749. [Google Scholar]
- Chen, L.; Wen, T.; Lin, Y.; Liu, Y.; Qin, Y.; Wu, Q.H. Two-stage expanding boundary algorithm to estimate domains of attraction of large-scale power systems with induction motors. IEEE Trans. Power Syst. 2024. [Google Scholar] [CrossRef]








| Battery Type | cP (CNY/kW) | cE (CNY/kWh) | cMain (CNY/kW) | ηC/ηD | m/Year | Μ (kgCO2/kWh) |
|---|---|---|---|---|---|---|
| Lithium battery | 2234 | 1173 | 97 | 0.9/0.8 | 15 | 136.76 |
| Lead-acid battery | 650 | 1200 | 25 | 0.8/0.9 | 10 | 85.53 |
| Vanadium-redox battery | 3720 | 1085 | 186 | 0.7/0.8 | 20 | 148.45 |
| Items | Scenario 1 | Scenario 2 |
|---|---|---|
| Annual revenue of SESS (ten thousand CNY) | 232.65 | 236.79 |
| Annual investment cost SESS (ten thousand CNY) | 208.37 | 214.06 |
| Annual operation and maintenance cost SESS(ten thousand CNY) | 56.55 | 58.10 |
| Annual purchasing power cost of SESS from multi-microgrid system (ten thousand CNY) | 704.95 | 714.82 |
| Annual carbon emission cost of SESS (ten thousand CNY) | 1.42 | 0 |
| Annual revenue of electricity sale of SESS (ten thousand CNY) | 1045.33 | 1062.85 |
| Annual service revenue charged by SESS (ten thousand CNY) | 158.61 | 160.92 |
| Items | Scenario 1 | Scenario 2 |
|---|---|---|
| Annual operation cost of multi-microgrid system (ten thousand CNY) | 2445.58 | 2475.02 |
| Annual purchasing power cost of multi-microgrid system from main grid (ten thousand CNY) | 1493.47 | 1507.62 |
| Annual gas-purchasing cost of multi-microgrid system (ten thousand CNY) | 453.12 | 458.46 |
| Annual purchasing power cost of multi-microgrid system from SESS (ten thousand CNY) | 1045.33 | 1062.85 |
| Annual revenue of electricity sale of multi-microgrid system (ten thousand CNY) | 704.95 | 714.82 |
| Annual service charge paid by multi-microgrid system(ten thousand CNY) | 158.61 | 160.92 |
| Battery Type | BT (Ten Thousand CNY) | NY (Years) | RO | PEss,rate (kW) | EEss,rate (kWh) |
|---|---|---|---|---|---|
| Lithium battery | 3489.74 | 17.08 | 0.88 | 7420.04 | 19,780.35 |
| Lead-acid battery | 3018.72 | 10.91 | 0.92 | 8994.20 | 23,976.74 |
| Vanadium-redox battery | 2981.66 | 7.90 | 2.53 | 1949.77 | 5197.69 |
| Battery Type | BT (Ten Thousand CNY) | NY (Years) | RO | PEss,rate (kW) | EEss,rate (kWh) |
|---|---|---|---|---|---|
| Lithium battery | 3551.87 | 17.24 | 0.87 | 7886.13 | 21,022.85 |
| Lead-acid battery | 3055.53 | 10.94 | 0.91 | 9038.35 | 24,094.44 |
| Vanadium-redox battery | 2973.86 | 9.25 | 2.16 | 2040.41 | 5439.32 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, S.; Ye, Z. Double-Layer Optimization and Benefit Analysis of Shared Energy Storage Investment Considering Life-Cycle Carbon Emission. Sustainability 2024, 16, 10403. https://doi.org/10.3390/su162310403
Chen S, Ye Z. Double-Layer Optimization and Benefit Analysis of Shared Energy Storage Investment Considering Life-Cycle Carbon Emission. Sustainability. 2024; 16(23):10403. https://doi.org/10.3390/su162310403
Chicago/Turabian StyleChen, Shijia, and Ze Ye. 2024. "Double-Layer Optimization and Benefit Analysis of Shared Energy Storage Investment Considering Life-Cycle Carbon Emission" Sustainability 16, no. 23: 10403. https://doi.org/10.3390/su162310403
APA StyleChen, S., & Ye, Z. (2024). Double-Layer Optimization and Benefit Analysis of Shared Energy Storage Investment Considering Life-Cycle Carbon Emission. Sustainability, 16(23), 10403. https://doi.org/10.3390/su162310403





