Next Article in Journal
Valuing Sustainability Impacts and Food Security Effects of Local Mariculture
Previous Article in Journal
Overview of the Special Issue: Embracing the Messiness of Transdisciplinarity
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Sustainability
Volume 16
Issue 22
10.3390/su16229623
sustainability-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics

by
Longfei Li
1,
Lei Xue
2,3,4,*,
Tong Jiang
1,*,
Kun Huang
1 and
Zhuan Li
1
1
College of Geosciences and Engineering, North China University of Water Resources and Electric Power, Zhengzhou 450046, China
2
State Key Laboratory of Lithospheric and Environmental Coevolution, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
3
Key Laboratory of Shale Gas and Geoengineering, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China
4
Innovation Academy for Earth Science, Chinese Academy of Sciences, Beijing 100029, China
*
Authors to whom correspondence should be addressed.
Sustainability 2024, 16(22), 9623; https://doi.org/10.3390/su16229623
Submission received: 21 September 2024 / Revised: 25 October 2024 / Accepted: 31 October 2024 / Published: 5 November 2024
Browse Figures
Versions Notes

Abstract

:
The long-term stability of slopes in areas with strong earthquakes not only is very important for people’s lives and the safety of property, but also it enables restoration of the ecological environment in the landslide areas, which is very important for sustainable development. The most commonly used seismic-support method, anti-slide piles, provides outstanding seismic performance. However, piles still deform and fail during earthquakes, which can lead to instability of the slope. The dynamic response of a slope reinforced with anti-slide piles is crucial for maintaining the long-term stability of the slope in a strong-earthquake area and, thus, for promoting its sustainable development. However, current research is focused mainly on the stability of the slope, and there have been few studies on the dynamic response of anti-slide piles. For this reason, we have undertaken the present study of a bedding-rock slope supported by a single row of anti-slide piles. By changing the frequency, amplitude, and duration of the input seismic waves, we have systematically explored the influence of their spectral characteristics on the dynamic response of the anti-slide piles and the slope using numerical simulations combined with the wavelet-transform method. Our results show that the spectral characteristics of the seismic waves significantly affect the deformations of the anti-slide piles. Low-frequency and high-amplitude seismic waves have stronger destructive effects on slopes, and high-amplitude seismic waves can generate multi-level sliding surfaces that extend to deeper levels. The low-frequency component of the seismic wave controls the overall deformation of the slope, and the high-frequency component controls the local deformations. An increase in the proportion and duration of low frequencies in seismic waves is the main cause of slope deformation and failure. The present work, thus, provides a useful reference for the design of a slope supported by anti-slide piles in an area with strong earthquakes, as well as for the maintenance of the long-term stability of such a slope, therefore, encouraging the sustainable development of related areas.

1. Introduction

The indirect hazards caused by earthquake-induced landslides are often no less than those caused directly by the earthquakes [1,2,3]. Many large structures are located in strong-earthquake areas, and the potential risk of earthquake-induced landslides becomes a significant safety hazard for them [4,5], seriously restricting the economic and social development of those areas [6,7,8]. The 2008 Wenchuan earthquake in China, for example, generated roughly 50,000 landslides totaling between 5 and 15 billion m3 [9,10]. Large numbers of structures were severely damaged by these earthquake-induced landslides, causing significant losses to the economic and social development of the area. In addition, vegetation on the slopes was seriously damaged by the landslides, with obvious destructive effects on the ecological environment [11,12]. The long-term stability of a slope in a strong-earthquake area is consequently of great significance for the sustainable development of the local economy and society.
Great emphasis has been placed on research focused on the design of seismic supports for slopes subject to earthquakes, and several seismic-support methods have been proposed [13,14,15,16]. In particular, the support and anti-seismic performance provided by anti-slide piles—along with the benefits of their simple construction process and minimal disturbance to the slope—have been extensively acknowledged [17,18]. Consequently, anti-slide piles have become the most commonly used engineering measures in seismic-support projects for slopes [19,20]. The dynamic response and seismic performance of a slope supported by anti-slide piles has, therefore, become a research hotspot. Even with the excellent seismic performance of anti-slide piles, however, failure and deformation still occur during earthquakes, which can lead to slope instability. Although these failures may be related to the parameters and arrangements of the anti-slide piles, the influence of the ground-motion parameters on the dynamic response of the anti-slide piles should not be neglected.
Considerable research has been carried out on the seismic reinforcement of slopes with anti-slide piles. For example, using shaking-table tests, Mao et al. [21] studied the seismic performance of different configurations of anti-slide piles during the earthquake-liquefaction process. They found that the bending moment of a pile is greatly influenced by the pile arrangement. Xu and Huang [22] combined a dynamic finite-element method and Newmark’s permanent-displacement method to study the effect of pile diameter on the seismic performance of an anti-slide pile. They found that the optimal pile diameter was about 1.5–2.0 m. Using a kinematic-limit analysis approach, Wang et al. [23] evaluated the effects of suction, pile location, and pile spacing on the stability of a slope, and they proposed a semi-analytical method for assessing the seismic performance of an unsaturated soil slope supported by anti-slide piles. Ma et al. [24] performed shaking-table tests of a soil slope restrained by anti-slide piles to analyze the seismic performance of two types of anti-slide piles. Xue et al. [25] employed numerical simulations to study the seismic performance of anti-slide piles, and they found that anti-slide piles arranged in the middle and upper parts of a slope had a better seismic effect than those placed in other areas and that there was an optimal value for the number of anti-slide piles. These studies are very important for improving the seismic reinforcement effect of anti-slide piles, but they focus mainly on the parameters and arrangements of the anti-slide piles and do not consider the influence of the ground-motion parameters.
Different earthquake areas have experienced landslides with varying numbers, frequencies, and levels of harm. In addition to the local geological structures and geotechnical characteristics, ground-motion parameters are crucial elements that should not be disregarded [26,27]. Using the finite-element method, Maheshwari et al. [28] studied the seismic performance of anti-slide piles under harmonic and transient excitation, and they found that the seismic-wave frequency significantly influences the dynamic response of both the slope and the anti-slide piles. Chatterjee et al. [29] investigated the bending moment and displacement response of anti-slide piles in saturated sand subjected to different forms of seismic waves. They discovered that the liquefaction of saturated sand under seismic action increased the load on the anti-slide piles as well as their bending moments. Wang et al. [30] investigated the impact of the duration of seismic waves on the dynamic response of the slope, and they discovered that the duration had a significant impact on the permanent displacements. Pai et al. [31] compared the seismic performance of a traditional pile and a new ESP pile using shaking-table tests, and they analyzed the spectral characteristics of the acceleration of anti-slide piles using fast Fourier transforms. The ground-motion parameters of seismic waves include many factors, such as their frequency, amplitude, and duration. Although the investigations highlighted above considered the influence of ground-motion parameters on the seismic-reinforcement effect of anti-slide piles, most considered only a single parameter, and the research was not very systematic.
In summary, the majority of current research is concentrated on optimizing the design of anti-slide piles, with particular emphasis on their physical properties and arrangements. However, there is a dearth of research on the way the spectral characteristics of seismic waves affect the seismic performance of anti-slide piles. Consequently, more emphasis needs to be placed on studying the instability mechanism and the deformation process of anti-slide piles and slopes subjected to different ground-motion parameters. We have, therefore, carried out systematic numerical simulations of a single row of anti-slide piles supported by a bedding-rock slope, varying the frequency, amplitude, and duration of the seismic waves. In addition, we have utilized continuous wavelet transforms to investigate the influence of the spectral characteristics of the seismic waves on the dynamic response of the anti-slide piles and slopes. Our goal is to provide a reference for maintaining the long-term stability of slopes and encouraging sustainable development in areas with strong earthquakes.

2. Numerical Simulation Scheme

2.1. Establishing the Numerical Model

The area we have studied is located in Yunnan Province, southwest China, near the north–south Xiaojiang fault zone of the Sichuan–Yunnan tectonic block, which has complex geological conditions and experiences frequent earthquakes. It belongs to a low–middle mountain landform of tectonic erosion. The microgeomorphology is mountainous and sloped, and the terrain is undulating. The specific geographical location is shown in Figure 1. A 6.5 magnitude earthquake occurred in this area on 8 August 2014, causing 617 deaths and affecting nearly 1.1 million people. The elevation of the prototype slope lies between 1600 m and 1630 m, with a slope of about 45°, and a site investigation has determined that it is a bedding-rock slope. The rock is soft, and it is composed—from top to bottom—of fully weathered siltstone, strongly weathered siltstone and weakly weathered siltstone. The rock strata have a dip angle of 15–20° and a volume of roughly 8000 m3. The geological profile and topography of the slope are shown in Figure 2.
We established a geological model of the bedding slope (Figure 3) to resemble the prototype slope shown in Figure 2. The slope angle was 45°, and the dip angle of the rock strata was 20°. We determined the mesh size Δl following the guidelines proposed by Kuhlemeyer and Lysmer [32] to ensure the accuracy of the simulation. It is given by
Δ l ≤ 1 10 λ   to   1 8 λ
where Δl is the mesh size, and λ is the wavelength corresponding to the highest frequency of the input wave. The bottom layer is bedrock, with a mesh size between 1.0 m and 2.0 m, and we divided the upper part into six layers, each 6 m thick and with a 1.0 m mesh size. We constructed a total of 106,848 grid nodes and 99,860 surface-strain elements. We obtained the detailed parameters of the rock mass from field data and laboratory tests (Table 1). We considered all of the rock types to be elastic–plastic materials, and we employed the Mohr–Coulomb constitutive model in the dynamic analysis. To minimize the influence of boundary effects and to satisfy the computational-accuracy requirements under dynamic conditions, we extended the model as recommended by the Itasca Consulting Group [33] and a previous study [34]. The dimensions of the model are as follows: the distance from the foot of the slope to the right boundary is 1.5 times the height of the slope; the distance from the top to the left boundary is 2.5 times the slope height, and the distance from the top to the bottom of the model is twice the height of the slope.

2.2. Boundary Conditions

Boundary conditions are essential for a dynamic analysis of the slope [35]. To address boundary problems in a dynamics analysis, FLAC3D 3.0 version provides viscous and free-field boundaries. The setting of the boundary conditions is shown in Figure 4: we utilized a viscous boundary at the bottom of the model to reduce the reflection of the seismic waves, and we employed a free-field boundary at each side to simulate a semi-infinite space. We coupled the free-field mesh with the side boundaries of the model through dampers, thus, achieving the effect of a semi-infinite space and ensuring that the input seismic waves were not being distorted. Rayleigh damping and local damping are the two damping mechanisms used most commonly in dynamic calculations with FLAC3D. Although the results of calculations using Rayleigh damping are quite good, this greatly increases the burden of the calculations. In contrast, local damping is more efficient, and—for rock materials—local damping also yields realistic calculational results. We, therefore, adopted local damping in this dynamic analysis. We used the local damping coefficient αL = πD, where D refers to the critical damping ratio. Following the “Code for Seismic Design of Railway Engineering” (GB 50111-2006) of China [36], we fixed D to be 5% [37]; the local damping coefficient was, thus, αL = 0.157. To avoid the influence of gravity, we performed a stress balance.

2.3. Numerical Simulation Conditions

To investigate systematically the influence of ground-motion parameters on the dynamic responses of the anti-slide piles and the slope deformations, in this study we selected three fundamental ground-motion parameters: the amplitude amax, the frequency f, and the duration t. We utilized 18 distinct sinusoidal seismic waves for the dynamic analysis (Table 2), and we applied them as boundary conditions to the bottom of the above numerical model to simulate the conditions of an earthquake. The horizontal distance from a pile to the top of the slope was Lx = 18 m, the spacing between piles was S = 4 m, the side length of each square anti-slide pile was D = 2 m, and the length of each pile was Lp = 30 m (Figure 5). For each anti-slide pile, we adopted the pile structural unit embedded in FLAC3D, and its physical and mechanical parameters are shown in Table 3.

3. Results

3.1. Analysis of the Dynamic Response of an Anti-Slide Pile

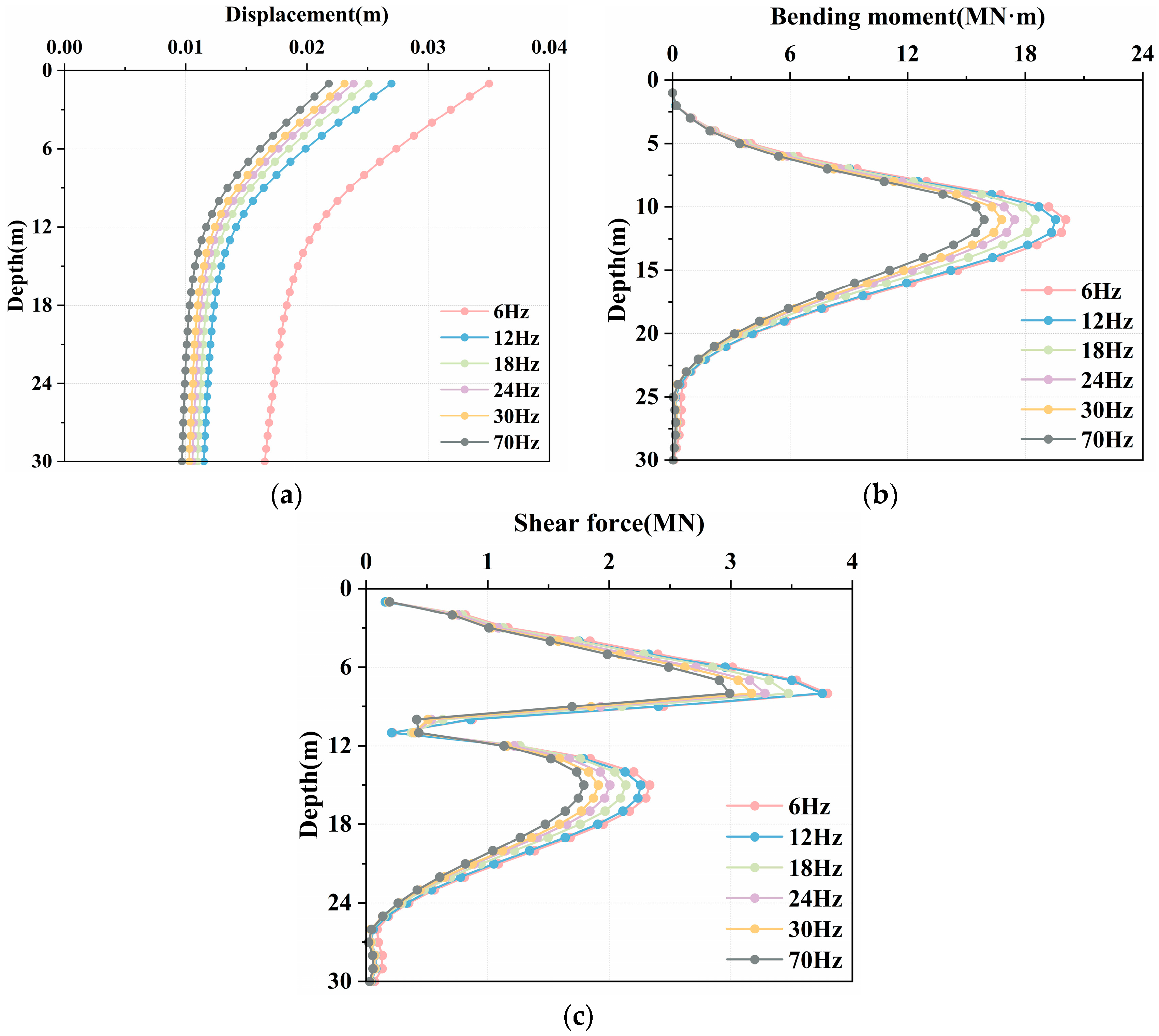
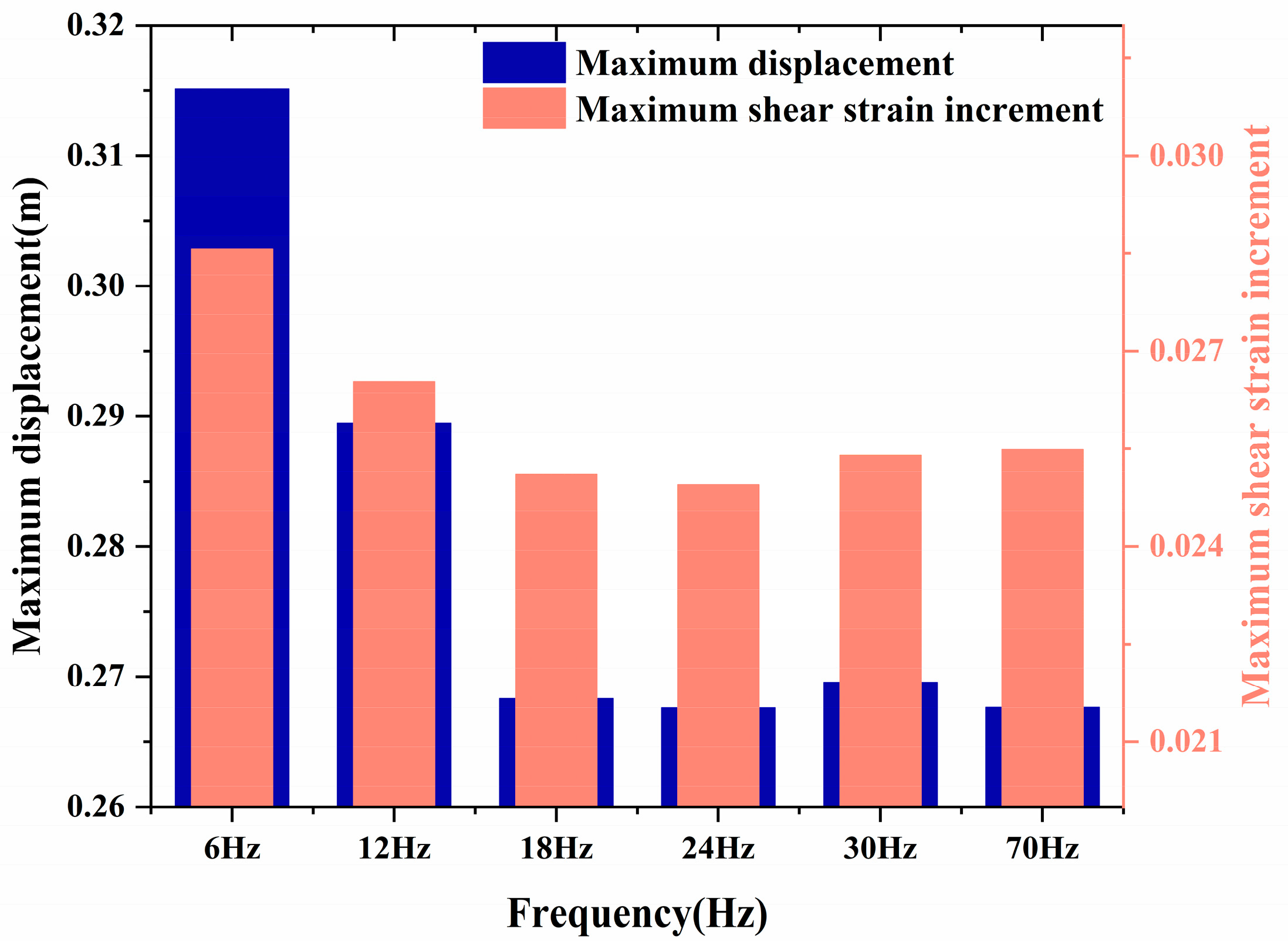
3.1.1. Effect of Seismic-Wave Frequency on the Dynamic Response of an Anti-Slide Pile

We first analyzed working conditions 1–6 in Table 2, i.e., for each sinusoidal seismic wave, we fixed the amplitude to be 0.1 g, where g is the acceleration due to gravity, and the duration to be 6 s. To study the dynamic response of the anti-slide piles under different seismic-wave frequencies, we fixed the frequencies of the sinusoidal seismic waves to be either 6, 12, 18, 24, 30, or 70 Hz. As shown in Figure 6, the displacement, bending moment, and shear force on each pile decreased—and the decrease in amplitude became slower—as the seismic-wave frequency increased. Additionally, the displacement, bending moment, and shear force on the pile were much greater at 6 Hz than at 70 Hz, demonstrating that low-frequency waves are more seriously destructive for anti-slide piles. Using shaking-table tests, Pai et al. [38] have also concluded that low-frequency seismic waves have a greater impact on a structure. It is, therefore, necessary to pay special attention to the strongly destructive effect of low-frequency waves on anti-slide piles. In particular, the amplifying effect of resonances can be avoided by choosing anti-slide piles with higher self-resonance frequencies, thus, ensuring their safety.

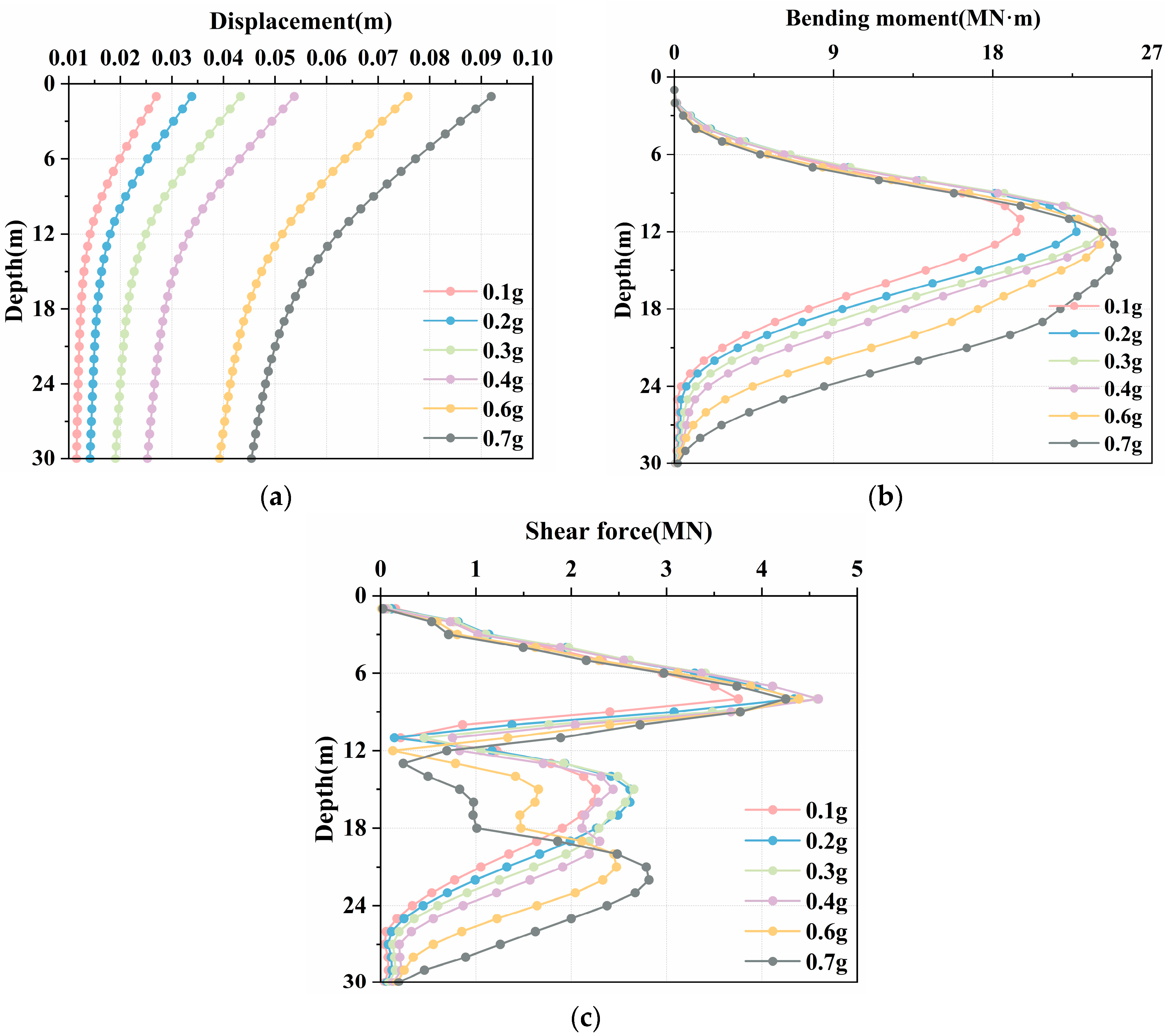
3.1.2. Effect of Seismic-Wave Amplitude on the Dynamic Response of an Anti-Slide Pile

Next, we analyzed working conditions 7–12 in Table 2, i.e., we employed a sinusoidal seismic-wave with a frequency of 12 Hz and a duration of 6 s. To study the dynamic response of the anti-slide pile under different seismic-wave amplitudes, we set the wave amplitudes to be either 0.1, 0.2, 0.3, 0.4, 0.6, or 0.7 g. Figure 7 shows that the pile displacement, bending moment, and shear force all increase—and the growth rates increase—as the amplitude increases. This finding is consistent with the conclusion from shaking-table tests of bedding-rock slopes [39,40]. At higher amplitudes, all the anti-slide piles exhibit significant displacements (Figure 7a), and they are at risk of toppling. Furthermore, the position of the maximum bending moment of an anti-slide pile deepens as the amplitude increases, indicating that the most dangerous position in a pile shifts to greater depths below the surface. Consequently, when using anti-slide piles to reinforce a slope in a high-intensity seismic area, it is necessary to be alert to the possible occurrence of a deep sliding surface. Additionally, the embedding depth and diameter of the anti-slide piles must be increased appropriately to prevent toppling.

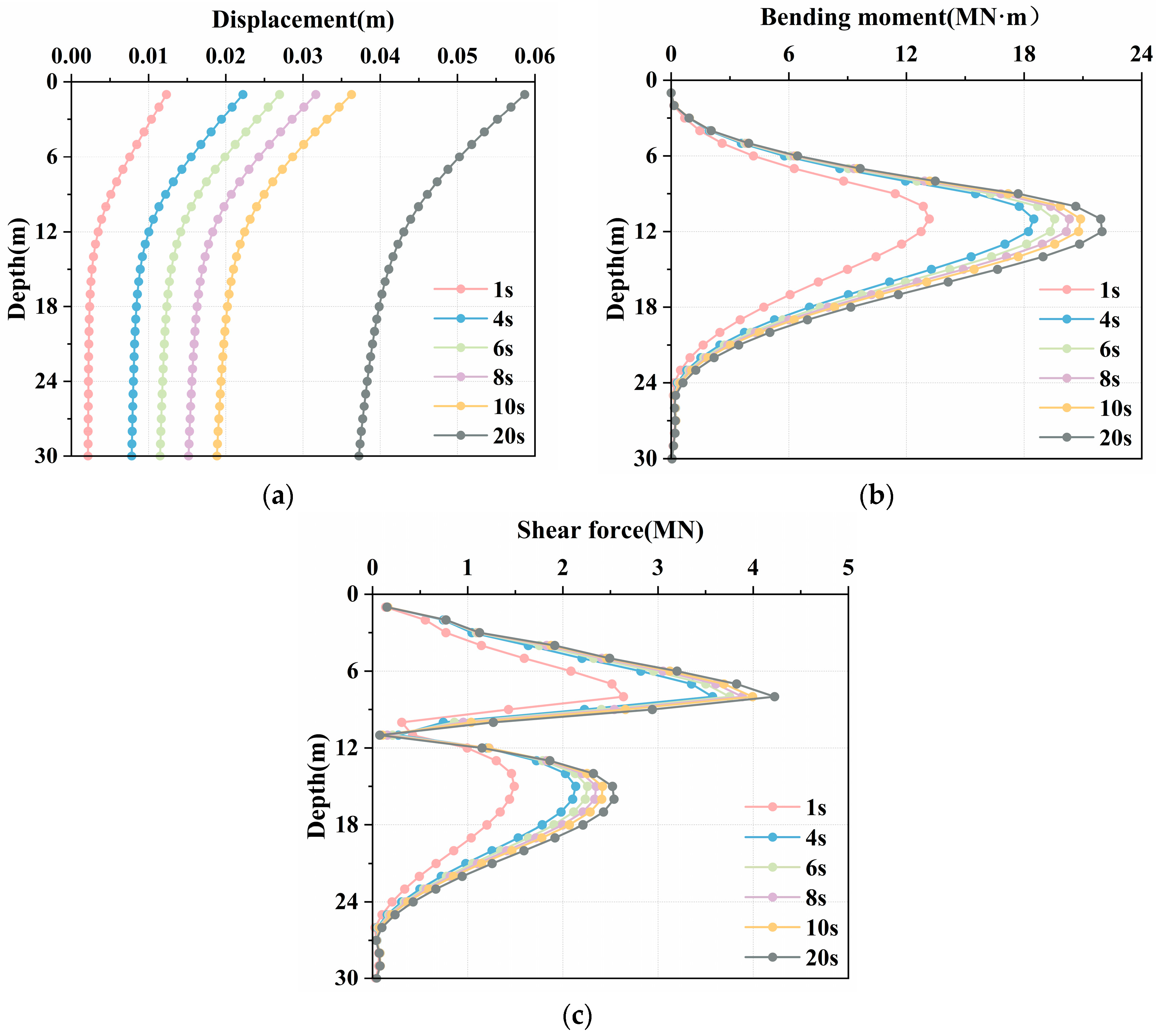
3.1.3. Effect of Seismic-Wave Duration on the Dynamic Response of an Anti-Slide Pile

To study the dynamic response of the anti-slide piles to seismic waves of different durations, we analyzed working conditions 13–18 in Table 2, i.e., we fixed the frequency of the sinusoidal seismic wave to be 12 Hz and the amplitude to be 0.1 g. We set the wave duration to be either 1, 4, 6, 8, 10, or 20 s. Figure 8 shows that the locations of the maximum bending moment and of the shear force of the anti-slide piles remain unchanged as the seismic-wave duration increases, indicating that the duration has little effect on the location of greatest danger. However, when the duration is longer, the anti-slide piles have more obvious deep displacements, and there is a risk of them tipping over. Thus, an increased duration can lead to an increase in the cumulative deformation, which in turn threatens the safety of an anti-slide pile, even though it has a minimal effect on the position of maximum danger.
To sum up, the spectral characteristics of a seismic wave seriously affect the dynamic response of anti-slide piles. In order to guarantee that they provide adequate safety, their seismic performance must be taken into account when they are used to support slopes in an area with strong earthquakes.

3.2. Analysis of the Dynamic Response of the Slope

3.2.1. Effect of Seismic-Wave Frequency on the Dynamic Response of the Slope

Figure 9 shows the location of the sliding surface for seismic waves with different frequencies. As the frequency increases, the shear band narrows slightly, and the deep extension of the sliding surface’s range gradually decreases, but the critical sliding surface is highly overlapping, indicating that the frequency has a minimal effect on the critical sliding surface. Further analysis shows that the maximum displacement and maximum shear strain increments of the slopes under low-frequency seismic waves (6 Hz, 12 Hz) are significantly larger than those produced by high-frequency seismic waves (18 Hz, 24 Hz, 30 Hz, 70 Hz), indicating that the low-frequency waves have stronger destructive effects on the slope (Figure 10). The maximum displacement and maximum shear strain increment of the slope increase slightly for seismic-wave frequencies that exceed 24 Hz. This occurs because the range of extension of the deep sliding surface becomes significantly smaller above 24 Hz (Figure 9d–f), and the slope changes from an overall deformation to a local deformation. The upper part of the slope is then subjected to more intense shear, which leads to this phenomenon. Thus, the slope is more severely damaged by low-frequency seismic waves, but it tends to experience local deformations when the frequency of the seismic wave is higher, as demonstrated in the study by Song et al. [41].

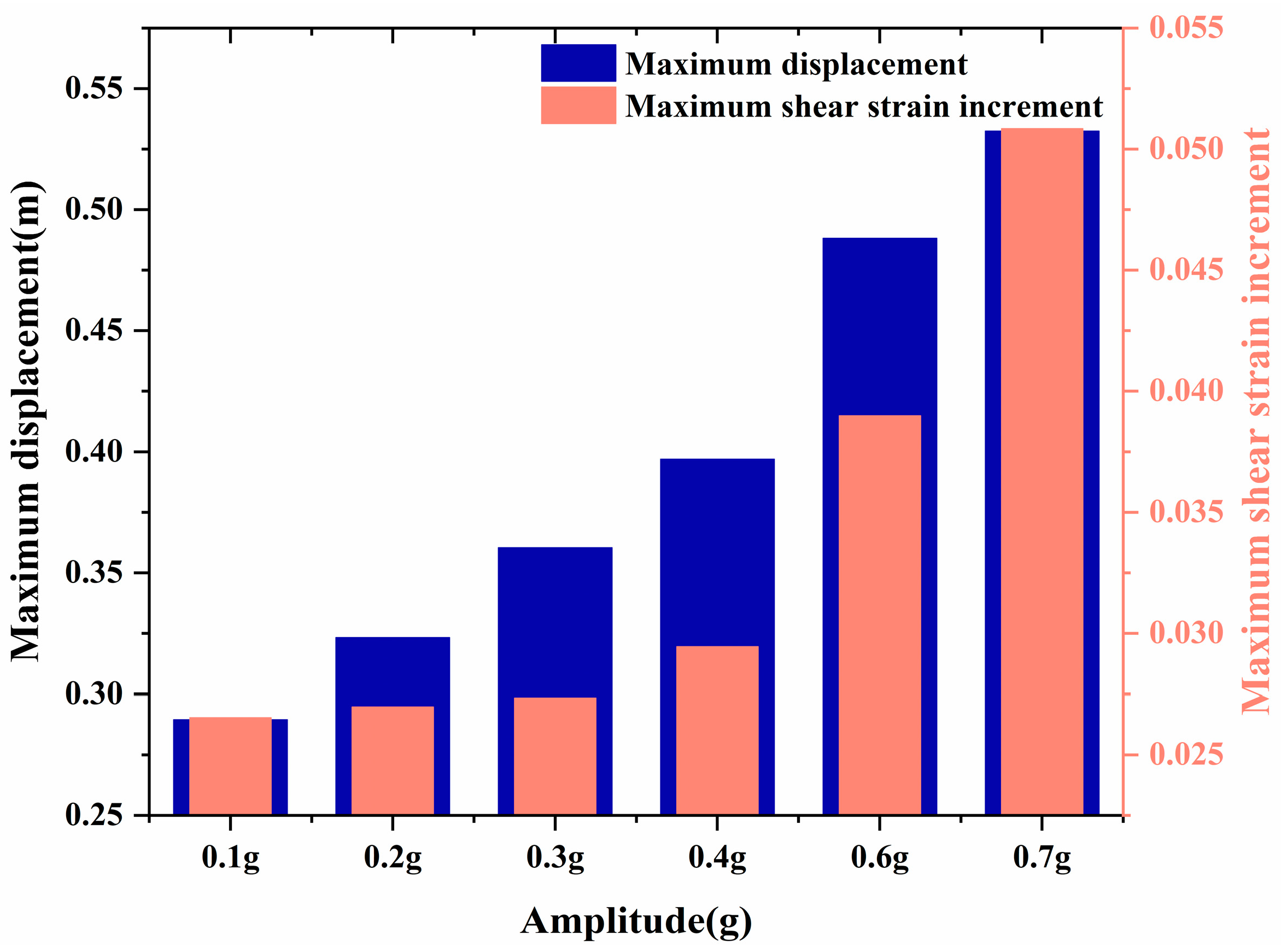
3.2.2. Effect of Seismic-Wave Amplitude on the Dynamic Response of the Slope

Figure 11 shows the sliding surface of the slope for seismic waves with different amplitudes. The amplitude clearly has a significant effect on the position and shape of the sliding surface. As the amplitude increases, a deep sliding surface appears and gradually penetrates, and the slope is at risk of deep sliding. Similar phenomena have been found in previous studies [42]. Under the action of high-amplitude seismic waves, a single sliding surface may change into a multi-stage sliding surface. In addition, as the amplitude increases, the maximum displacement and maximum shear strain increments of the slope both tend to increase (Figure 12), indicating that the destructive effect of high-amplitude seismic waves is more intense. In conclusion, when using anti-slide piles to support slopes in strong-earthquake areas, one must consider increasing their diameters and embedding depths to deal with deep sliding surfaces. Furthermore, one must also consider the possibility that slopes may develop multi-level sliding surfaces under the action of high-amplitude seismic waves, and the possible positions of such new sliding surfaces should be reinforced in advance using methods such as anchoring.

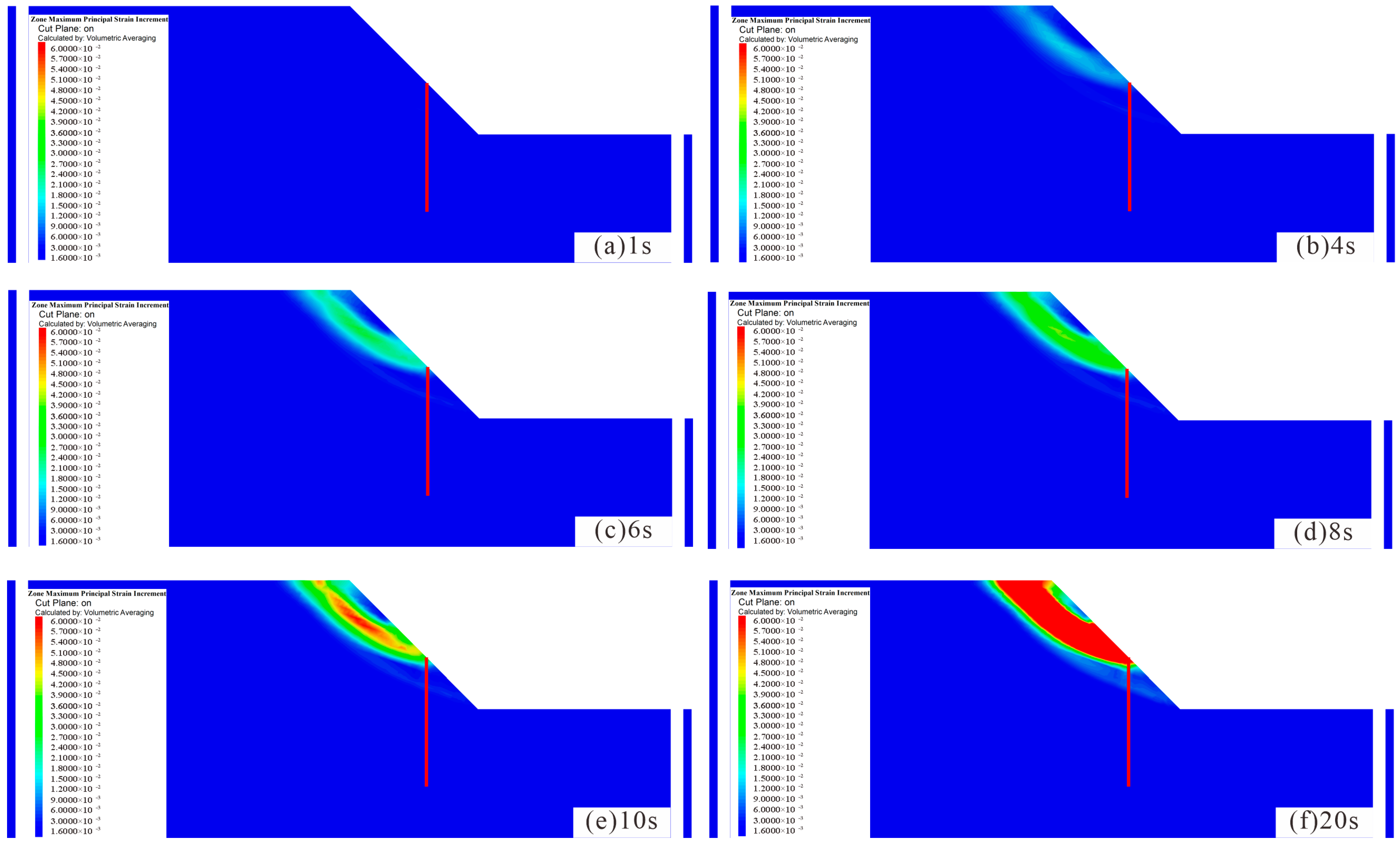
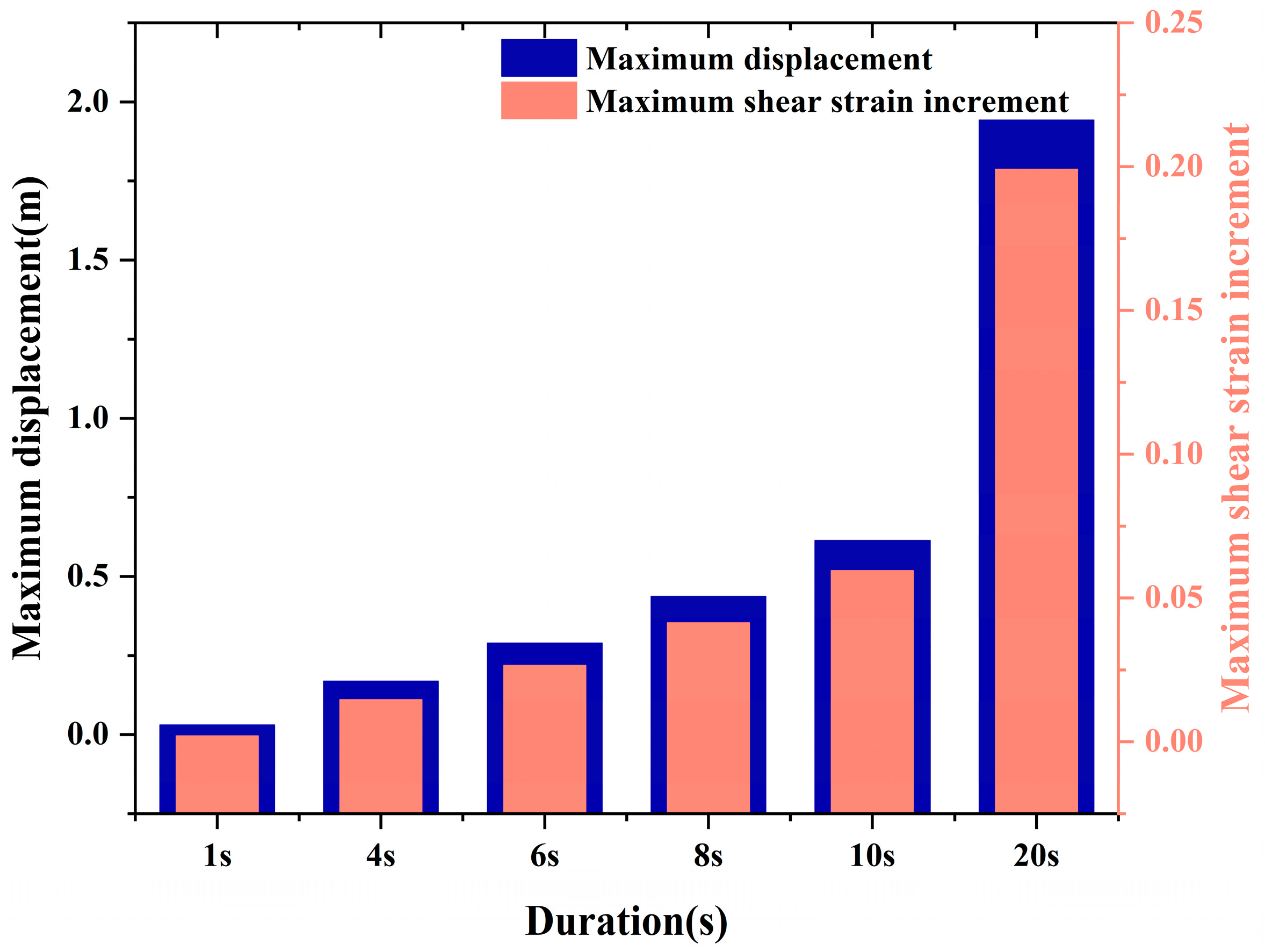
3.2.3. Effect of Seismic-Wave Duration on the Dynamic Response of the Slope

Figure 13 shows the sliding surface of a slope subjected to seismic waves of different durations. An increase in duration results in a notable expansion of the shear band, accompanied by the appearance of a deep sliding surface (Figure 13). Furthermore, for long durations, the upper part of the slope is subjected to a more pronounced shear force; we, therefore, recommend that the upper part of the slope be reinforced by supporting methods such as anchors. In addition, both the slope displacement and the maximum shear strain increment increased with an increase in the seismic-wave duration (Figure 14). To counteract this, measures such as increasing the diameters and embedding depths of the anti-slide piles can be utilized to address the cumulative deformation caused by long-duration seismic waves.

4. Discussion

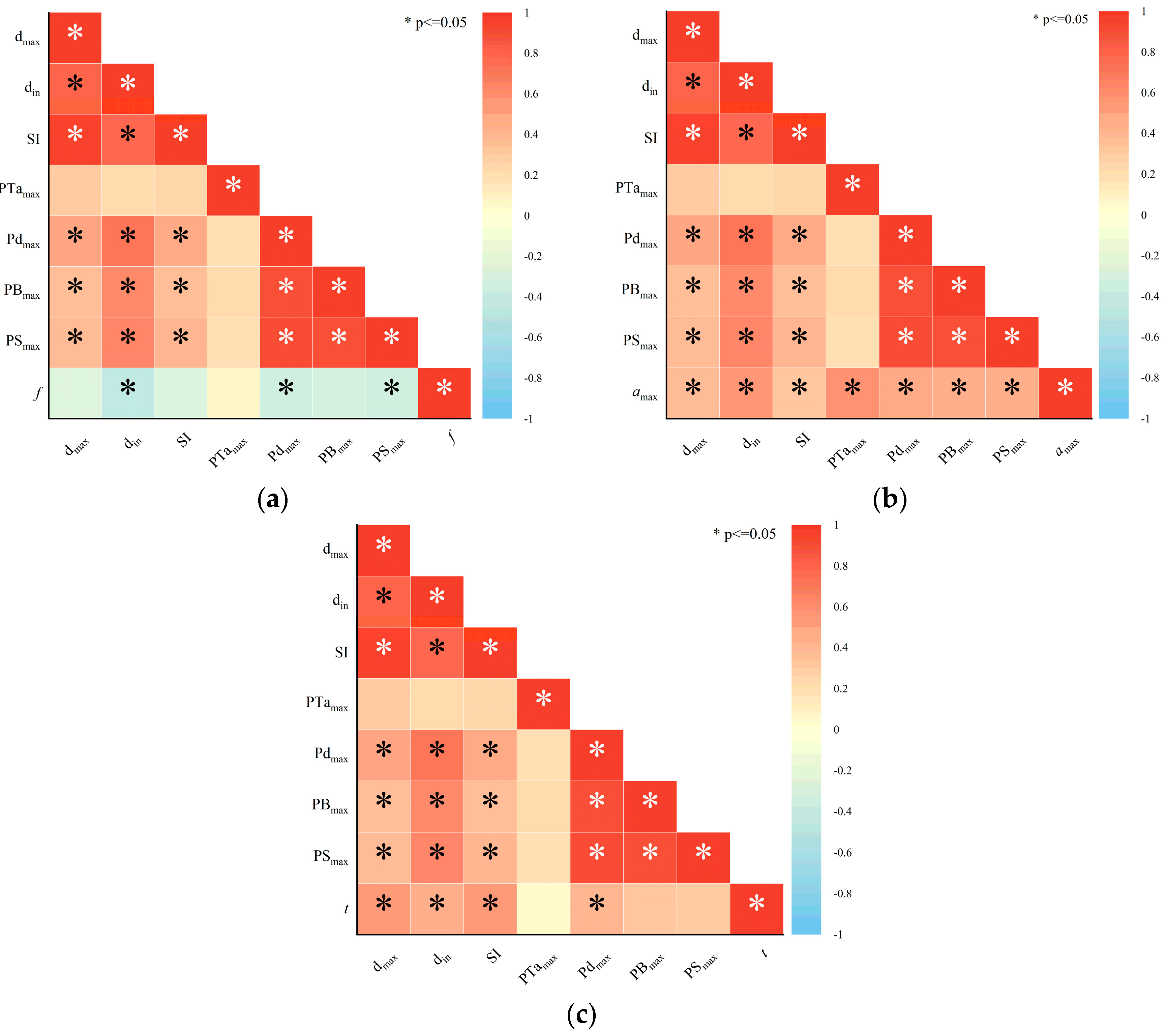
4.1. Correlation Analysis of the Dynamic Response of the Anti-Slide Pile–Slope System

In order to analyze further the influence of the frequency, amplitude, and duration of the seismic waves on the dynamic response of a pile–slope system and identify the key parameters that affect its deformation and failure characteristics during an earthquake, we extracted seven indicators and investigated their correlations with the frequency f, amplitude amax, and duration t of the seismic waves (Figure 15). As the seven indicators, we chose the maximum slope displacement dmax, the deep slope displacement din (i.e., the displacement of monitoring point Pin; see Figure 4), the maximum shear strain increment SI, the maximum acceleration at the top of the slope PTamax, the maximum pile displacement Pdmax, the maximum pile bending moment PBmax, and the maximum pile shear force PSmax.
An evident negative correlation exists between din, Pdmax, PSmax, and the seismic-wave frequency, further indicating that a low-frequency wave has a stronger destructive effect on the pile–slope system than does a high-frequency wave. In contrast, the amplitude of the seismic wave is positively correlated with the above seven indexes, particularly with din and PTamax, indicating that the amplitude significantly affects the depth of the sliding surface and the dynamic response of the slope. We also observed a positive correlation between the wave duration and dmax, din, and Pdmax. This indicates that the duration has great influence on the displacements in the pile–slope system, which may result in the toppling of the anti-slide piles. However, there is no significant correlation between the wave duration and either PBmax or PSmax, indicating that the duration has little effect on the bending and shear of the anti-slide piles. Thus, an increase in the wave duration will not increase the shearing risk of the anti-slide piles.
To sum up, the amplitude of a seismic wave has great influence on the dynamic response of the anti-slide piles and the slope. This was also demonstrated by Xu et al. [43] through a shaking-table experiment. On the other hand, the seismic-wave frequency mainly affects the range of deformation of the slope and the shear of the anti-slide piles. The duration of the seismic wave has little effect on the forces on the anti-slide piles, but it can change the range of the shear in the slope, which in turn affects the deformation of the anti-slide piles and the slope.

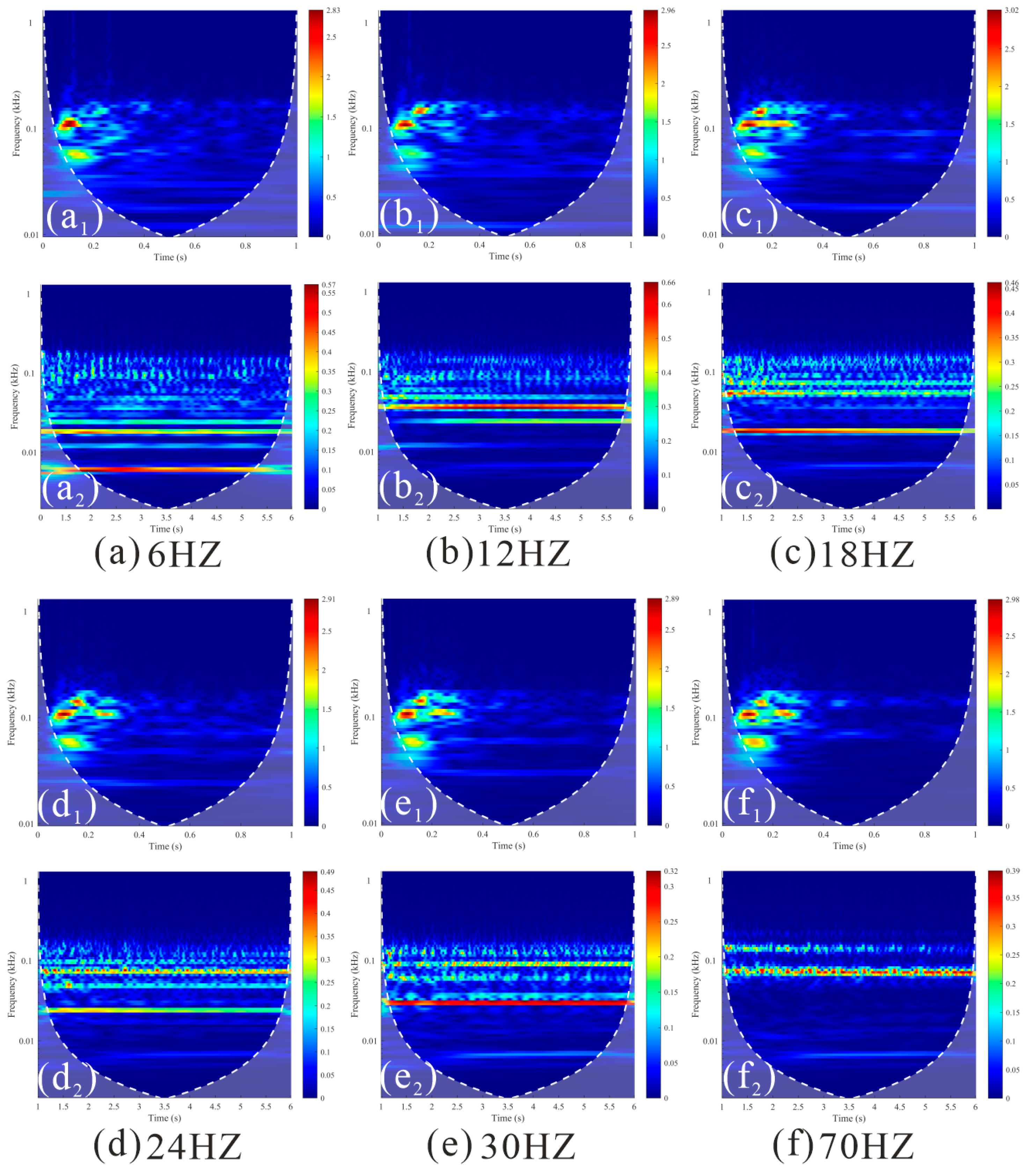
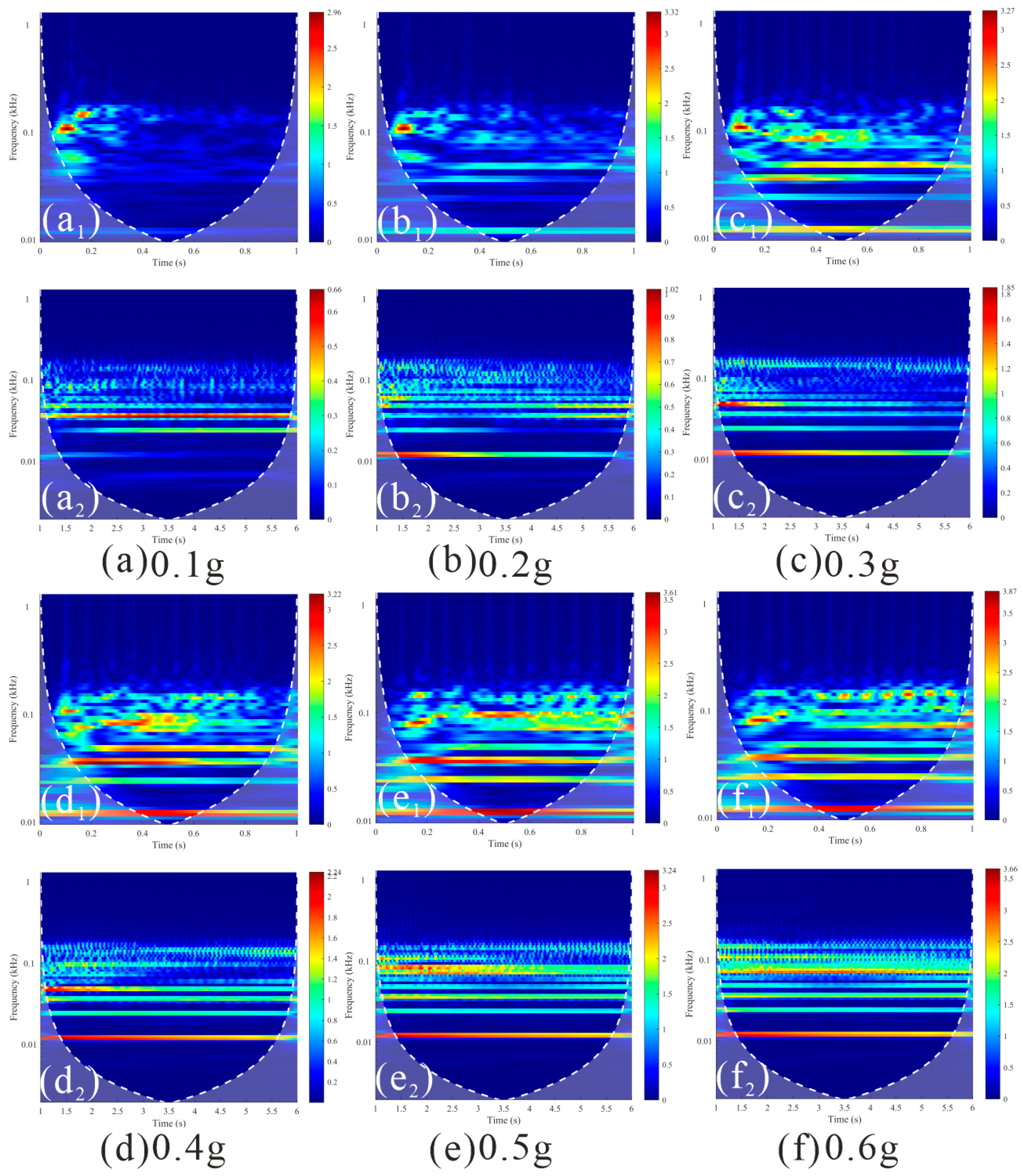
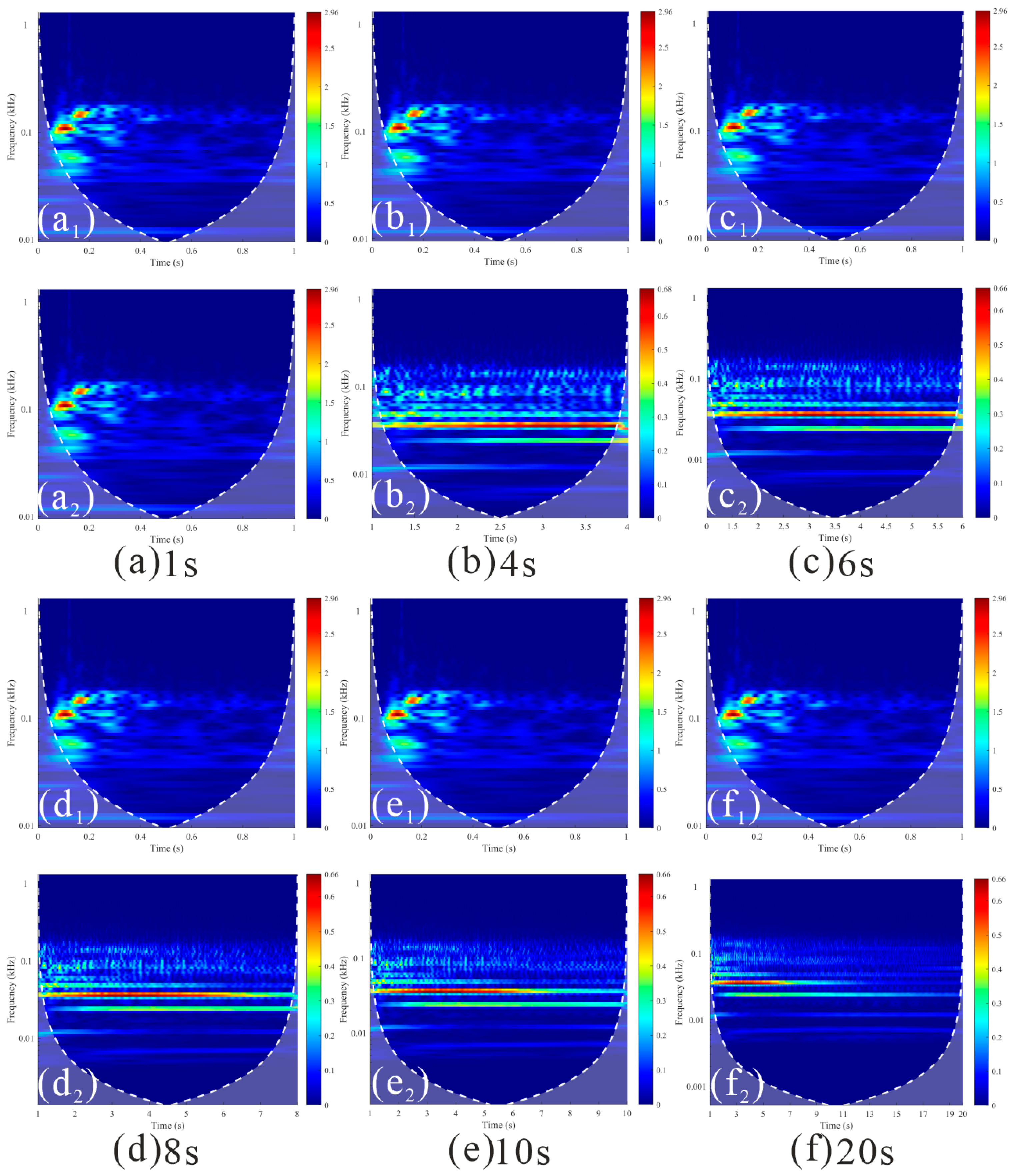
4.2. Time–Frequency Analysis of the Dynamic Response of the Slope

Continuous wavelet transforms are the methods used most commonly in the time–frequency analysis of signals. They deal with signals in both the time and frequency domains, and—because they have good resolution for low-frequency signals—they are ideal for processing earthquake signals [44,45]. The fundamental principle is that the wavelet coefficients are obtained by convolving wavelets of different scales, window by window. In the frequency domain, the frequency of the wavelet is altered by stretching or compressing its length. In the time domain, the wavelets are displaced in time, and the wavelet coefficients at different frequencies are aggregated to create a transformed time–frequency wavelet-coefficient map by sequentially contrasting the window signals at different times.
In this section, we perform a continuous wavelet transform of the x-direction acceleration of the slope-top monitoring point under different working conditions. Our objective is to analyze the influence of the spectral characteristics of the seismic waves on the dynamic response of the slope from the perspectives of both the time and frequency domains. Figure 16 shows the influence of the seismic-wave frequency on the time–frequency characteristics of the slope acceleration. Note that the amplitude of the acceleration remains relatively unchanged as the frequency of the seismic wave increases, while the main frequency increases significantly, and the low-frequency component decreases. Because the deformation of the slope is more intense under the action of a low-frequency wave, as shown in Section 3.2.1, we conclude that the low-frequency component plays a leading role in the deformation and failure of the slope, which is consistent with previous research [46].
Figure 17 shows the effect of the seismic-wave amplitude on the time–frequency characteristics. As the seismic-wave amplitude increases, the amplitudes of both the low- and high-frequency parts of the acceleration data increase, and their durations become significantly longer, indicating more severe slope damage. This is consistent with the findings of Chen et al. [42]. At low seismic-wave amplitudes (0.1–0.3 g), the changes occur mainly in the low-frequency part of the spectrum, and the low-frequency component of the slope acceleration increases significantly. In contrast, at high seismic-wave amplitudes (0.4–0.6 g), the changes occur mainly in the high-frequency part of the spectrum, the high-frequency component of the slope acceleration increases further and its duration continues to extend. This means that the low-frequency component of the slope acceleration increases first as the seismic-wave amplitude increases, causing the sliding surface of the slope to deepen and producing greater overall displacement. Subsequently, a continuing increase in the amplitude of the seismic waves leads to a significant increase in the high-frequency components of the slope acceleration, resulting in greater local displacements in the upper part of the slope.
Figure 18 shows the impact of the seismic-wave duration on the time–frequency characteristics of the slope acceleration. We observe that the duration has no obvious impact on the spectral characteristics of the acceleration data, and the main effect is to weaken the stability of the slope by extending the vibration time.
In summary, the spectral characteristics of seismic waves have great influence on the dynamic response of a slope, and the low-frequency components in particular play a leading role in the deformation of the slope. The spectral characteristics of the seismic wave mainly affect the stability of the slope by changing the proportion, amplitude, and duration of the low-frequency components of the slope acceleration. By increasing the pile diameter and the embedding depth of the anti-slide piles, the influence of the spectral characteristics of the seismic wave on the slope can be mitigated, helping to maintain its long-term stability, effectively enhancing its ecological environment and contributing to the sustainability of development of the local area.

5. Conclusions

In this paper, we have established a numerical model for a single row of anti-slide piles that are reinforcing a bedding-rock slope, and we have studied systematically the influence of the spectral characteristics of seismic waves on the dynamic response of the anti-slide piles and the slope. We have analyzed in detail the deformation characteristics of both the anti-slide piles and the slope when subjected to seismic waves of different frequencies, amplitudes, and durations. We obtained the following findings:
(1) A decreasing frequency of the seismic waves—as well as an increasing amplitude or duration—causes the bending moment, displacement, and shear force of an anti-slide pile to increase. The damage to an anti-slide pile from low-frequency waves is greater than that from high-frequency waves. With increasing seismic-wave amplitude, the most dangerous position in an anti-slide pile moves downward, increasing the possibility of the overall toppling of the pile. An increase in the seismic-wave duration leads to the displacement of a deeper part of an anti-slide pile. Therefore, when using anti-slide piles for slope support in areas with strong earthquakes, the seismic performance of the anti-slide piles must be considered in order to cope with the damage caused by seismic waves.
(2) As the frequency of a seismic wave decreases, the shear band of the slope widens, and the range of extension of the deep sliding surface increases, making the deformation of the slope more serious. The position and shape of the sliding surface changes with an increase in the seismic-wave amplitude. A shallow sliding surface may transform into a deep sliding surface, and a single-stage sliding surface may transform into a multi-stage sliding surface. It is, therefore, necessary to pay attention to the possible need for advanced support at the positions of the new sliding surfaces.
(3) The dynamic responses of the anti-slide piles and the slope are very sensitive to changes in the seismic-wave amplitude. In addition, the position of the deep sliding surface is sensitive to changes in the seismic-wave frequency, which then influences the deformations of the anti-slide piles. The range of the shear band of the slope is sensitive to the seismic-wave duration, which affects the deformations of both the anti-slide piles and the slope.
(4) The spectral characteristics of the seismic waves also have great influence on the dynamic response of the slope. Low-frequency seismic waves have a stronger destructive effect on the slope and control its overall deformation, whereas high-frequency seismic waves have a greater impact on the local deformation of the slope. The main reason for the slope deformation is an increase in the proportion of low-frequency and high-amplitude components in the slope acceleration.
In this paper, we have undertaken a preliminary study of the influence of the spectral characteristics of seismic waves on the dynamic response of a slope supported by anti-slide piles in an area with strong earthquakes. This study provides theoretical guidance for the seismic reinforcement of slopes in different earthquake areas. However, the arrangement of anti-slide piles and the interaction between the anti-slide piles and the slope have still not been fully considered. Further research on these aspects of the problem can provide additional useful information to help guide the optimal design of anti-slide piles for the seismic reinforcement of a given slope. Furthermore, the environmentally friendly slope-protection method has developed rapidly in recent years. In future studies, we, therefore, plan to study the synergistic effects of combined anti-slide pile support and ecological slope-protection methods to provide assistance for the sustainable development of strong-earthquake areas.

Author Contributions

Conceptualization, L.L. and T.J.; methodology, L.X.; software, L.L.; validation, Z.L. and K.H.; formal analysis, L.L.; investigation, L.L. and L.X.; data curation, K.H. and Z.L.; writing—original draft preparation, L.L.; writing—review and editing, L.L. and L.X.; project administration, T.J.; funding acquisition, L.X. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China under Grant Nos. 42090052 and 41977249, and the National Key Research and Development Program of China under Grant No. 2019YFC1509701.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Yin, Y.; Zhang, Y.; Ma, Y.; Hu, D.; Zhang, Z. Research on major characteristics of geohazards induced by the Yushu Ms 7.1 earthquake. J. Eng. Geol. 2010, 18, 289–296. [Google Scholar] [CrossRef]
  2. Li, Y.; Cui, P.; Ye, C.; Junior, J.M.; Zhang, Z.; Guo, J.; Li, J. Accurate Prediction of Earthquake-Induced Landslides Based on Deep Learning Considering Landslide Source Area. Remote Sens. 2021, 13, 3436. [Google Scholar] [CrossRef]
  3. Xiong, M.; Huang, Y. Stochastic seismic response and dynamic reliability analysis of slopes: A review. Soil. Dyn. Earthq. Eng. 2017, 100, 458–464. [Google Scholar] [CrossRef]
  4. Wu, H.G.; Pai, L.F. Shaking table test for reinforcement of soil slope with multiple sliding surfaces by reinforced double-row anti-slide piles. J. Mt. Sci. 2022, 19, 1419–1436. [Google Scholar] [CrossRef]
  5. Li, D.Q.; Jiang, S.H.; Cao, Z.J.; Zhou, C.B.; Li, X.Y.; Zhang, L.M. Efficient 3-D reliability analysis of the 530 m high abutment slope at Jinping I Hydropower Station during construction. Eng. Geol. 2015, 195, 269–281. [Google Scholar] [CrossRef]
  6. Chen, H.R.; Qin, S.Q.; Xue, L.; Yang, B.C.; Zhang, K. Universal precursor seismicity pattern before locked-segment rupture and evolutionary rule for landmark earthquakes. Geosci. Front. 2022, 13, 101314. [Google Scholar] [CrossRef]
  7. Jiang, X.; Fu, Y.; Jiang, J.; Li, J. Spatial distribution of the earthquake in Mainland China. Physica A. 2019, 530, 120941. [Google Scholar] [CrossRef]
  8. Wu, G.; Tan, H.; Zou, Z.; Yang, G.; Shen, C. Gravity distribution characteristics and their relationship with the distribution of earthquakes and tectonic units in the North–South seismic belt, China. Geod. Geodyn. 2015, 6, 194–208. [Google Scholar] [CrossRef]
  9. Gorum, T.; Fan, X.; van Westen, C.J.; Huang, R.Q.; Xu, Q.; Tang, C.; Wang, G. Distribution pattern of earthquake-induced landslides triggered by the 12 May 2008 Wenchuan earthquake. Geomorphology 2010, 133, 152–167. [Google Scholar] [CrossRef]
  10. Tang, C.; Zhu, J.; Qi, X.; Ding, J. Landslides induced by the Wenchuan earthquake and the subsequent strong rainfall event: A case study in the Beichuan area of China. Eng. Geol. 2011, 122, 22–33. [Google Scholar] [CrossRef]
  11. Chen, S.; Hua, J.; Liu, W.; Yang, S.; Wang, X.; Ji, W. Effects of Artificial Restoration and Natural Recovery on Plant Communities and Soil Properties across Different Temporal Gradients after Landslides. Forests 2023, 14, 1974. [Google Scholar] [CrossRef]
  12. Duan, C.S.; Zhang, Q.J.; Gong, X.; Zhang, Y.B. Evaluation of plant community and soil recovery in earthquake landslide. Act. Ecol. Siica 2020, 40, 6584–6596. [Google Scholar] [CrossRef]
  13. Xu, M.; Tang, Y.; Liu, X.; Yang, H.; Luo, B. A shaking table model test on a rock slope anchored with adaptive anchor cables. Int. J. Rock. Mech. Min. 2018, 112, 201–208. [Google Scholar] [CrossRef]
  14. Shi, K.; Wu, X.; Liu, Z.; Dai, S. Coupled calculation model for anchoring force loss in a slope reinforced by a frame beam and anchor cables. Eng. Geol. 2019, 260, 105245. [Google Scholar] [CrossRef]
  15. Faiz, H.; Ng, S.; Rahman, M. A state-of-the-art review on the advancement of sustainable vegetation concrete in slope stability. Constr. Build. Mater. 2022, 326, 126502. [Google Scholar] [CrossRef]
  16. Pushkarev, A.; Sokolov, N.; Mihailov, A. Methods and technology of reinforcing a leaning slope. Transp. Res. Proce. 2021, 57, 538–546. [Google Scholar] [CrossRef]
  17. Xu, C.; Xue, L.; Cui, Y.; Guo, S.; Zhai, M.; Bu, F. A New Multi-Objective Comprehensive Optimization Model for Homogeneous Slope Reinforced by Anti-Slide Piles: Insights from Numerical Simulation. Lithosphere 2022, 2022, 6499724. [Google Scholar] [CrossRef]
  18. Tang, H.; Gong, W.; Wang, L.; Juang, C.H.; Martin, J.R.; Li, C.D. Multi-objective optimization-based design of stabilizing piles in earth slopes. Int. J. Numer. Anal. Met. 2019, 43, 1516–1536. [Google Scholar] [CrossRef]
  19. Lian, J.; Ding, X.; Wen, H.; Tong, X.; Qu, L. Dynamic responses and evolution characteristics of bedrock and overburden layer slope with space anchor cable anti-slide piles based on large-scale shaking table test. Soil. Dyn. Earthq. Eng. 2023, 175, 108245. [Google Scholar] [CrossRef]
  20. Liu, X.; Cai, G.; Liu, L.; Zhou, Z. Investigation of internal force of anti-slide pile on landslides considering the actual distribution of soil resistance acting on anti-slide piles. Nat. Hazards. 2020, 102, 1369–1392. [Google Scholar] [CrossRef]
  21. Mao, W.; Liu, B.; Rasouli, R.; Aoyama, S.; Towhata, I. Performance of piles with different configurations subjected to slope deformation induced by seismic liquefaction. Eng. Geol. 2019, 263, 105355. [Google Scholar] [CrossRef]
  22. Xu, X.; Huang, Y. Parametric study of structural parameters affecting seismic stability in slopes reinforced by pile-anchor structures. Soil. Dyn. Earthq. Eng. 2021, 147, 106789. [Google Scholar] [CrossRef]
  23. Wang, L.; Sun, D.; Yao, Y.; Tan, Y. Seismic stability of 3D piled unsaturated earth slopes using kinematic limit analysis. Soil. Dyn. Earthq. Eng. 2019, 126, 105821. [Google Scholar] [CrossRef]
  24. Ma, N.; Wu, H.; Ma, H.; Wu, X.; Wang, G. Examining dynamic soil pressures and the effectiveness of different pile structures inside reinforced slopes using shaking table tests. Soil. Dyn. Earthq. Eng. 2019, 116, 293–303. [Google Scholar] [CrossRef]
  25. Xue, L.; Li, L.; Xu, C.; Cui, Y.; Ding, H.; Huang, K.; Li, Z. A multi-objective optimization evaluation model for seismic performance of slopes reinforced by pile-anchor system. Sci. Rep. 2024, 14, 5044. [Google Scholar] [CrossRef]
  26. Qi, S.; He, J.; Zhan, Z. A single surface slope effects on seismic response based on shaking table test and numerical simulation. Eng. Geol. 2022, 306, 106762. [Google Scholar] [CrossRef]
  27. Wu, M.; Liu, F.; Yang, J. Seismic response of stratified rock slopes due to incident P and SV waves using a semi-analytical approach. Eng. Geol. 2022, 301, 106594. [Google Scholar] [CrossRef]
  28. Maheshwari, B.K.; Truman, K.Z.; Naggar, M.H.E.; Gould, P.L. Three-dimensional finite element nonlinear dynamic analysis of pile groups for lateral transient and seismic excitations. Can. Geotech. J. 2004, 41, 118–133. [Google Scholar] [CrossRef]
  29. Chatterjee, K.; Choudhury, D.; Poulos, H.G. Seismic analysis of laterally loaded pile under influence of vertical loading using finite element method. Comput. Geotech. 2015, 67, 172–186. [Google Scholar] [CrossRef]
  30. Wang, W.; Li, D.Q.; Liu, Y.; Du, W. Influence of ground motion duration on the seismic performance of earth slopes based on numerical analysis. Soil. Dyn. Earthq. Eng. 2021, 143, 106595. [Google Scholar] [CrossRef]
  31. Pai, L.F.; Wu, H.G.; Guan, W.; Wei, H.; Tang, L. Shaking table test for seismic optimization of soil slope reinforced by new EPS pile under earthquake. Soil. Dyn. Earthq. Eng. 2022, 154, 107140. [Google Scholar] [CrossRef]
  32. Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. ASCE Soil. Mech. Found. Div. J. 1973, 99, 421–427. [Google Scholar] [CrossRef]
  33. Itasca Consulting Group. FLAC3D 6.0 Modelling; Itasca Consulting Group: Minneapolis, MN, USA, 2017; 405p. [Google Scholar]
  34. Ma, Z.; Liao, H.; Dang, F.; Cheng, Y. Seismic slope stability and failure process analysis using explicit finite element method. Bull. Eng. Geol. Environ. 2021, 80, 1287–1301. [Google Scholar] [CrossRef]
  35. Buah, P.A.; Zhang, Y.; He, J.; Yu, P.; Xiang, C.; Fu, H.; He, Y.; Liu, J. Evaluating the dynamic response and failure process of a rock slope under pulse-like ground motions. Geomat. Nat. Haz Risk. 2023, 14, 1. [Google Scholar] [CrossRef]
  36. GB 50111-2006; Code for Seismic Design of Railway Engineering. China Planning Press: Beijing, China, 2009.
  37. Lin, Y.L.; Cheng, X.M.; Yang, G.L. Shaking table test and numerical simulation on a combined retaining structure response to earthquake loading. Soil. Dyn. Earthq. Eng. 2018, 108, 29–45. [Google Scholar] [CrossRef]
  38. Pai, L.F.; Wu, H.G. Shaking table test of comparison and optimization of seismic performance of slope reinforcement with multi-anchor piles. Soil. Dyn. Earthq. Eng. 2021, 145, 106737. [Google Scholar] [CrossRef]
  39. Dong, J.; Wang, C.; Huang, Z.; Yang, J.; Xue, L. Shaking Table Model Test to Determine Dynamic Response Characteristics and Failure Modes of Steep Bedding Rock Slope. Rock. Mech. Rock. Eng. 2022, 55, 3645–3658. [Google Scholar] [CrossRef]
  40. Zang, M.; Yang, G.; Dong, J.; Qi, S.; He, J.; Liang, N. Experimental study on seismic response and progressive failure characteristics of bedding rock slopes. J. Rock. Mech. Geotech. 2022, 14, 1394–1405. [Google Scholar] [CrossRef]
  41. Song, D.; Chen, Z.; Chao, H.; Ke, Y.; Nie, W. Numerical study on seismic response of a rock slope with discontinuities based on the time-frequency joint analysis method. Soil. Dyn. Earthq. Eng. 2020, 133, 106112. [Google Scholar] [CrossRef]
  42. Chen, G.; Yang, C.; Qu, L.; Tong, X.; Zhang, K.; Zhang, L. Shaking table test and numerical analysis of dynamic response and damage mechanism of a deposit slope with a weak interlayer reinforced by a pile–anchor structure. Structures 2024, 59, 105728. [Google Scholar] [CrossRef]
  43. Xu, B.; Liu, X.; Zhou, X.; Liang, Y.; Cai, P.; Han, Y.; Huang, J. Investigation of the Dynamic Response Pattern and Instability Mechanism of a Bedding Rock Slope Subjected to Frequent Seismic Loads. Int. J. Geomech. 2024, 24, 04024117. [Google Scholar] [CrossRef]
  44. Wang, L.; Shi, W.; Zhou, Y. Adaptive-passive tuned mass damper for structural aseismic protection including soil–structure interaction. Soil. Dyn. Earthq. Eng. 2022, 158, 107298. [Google Scholar] [CrossRef]
  45. Wang, L.; Shi, W.; Li, X.; Zhang, Q.; Zhou, Y. An adaptive-passive retuning device for a pendulum tuned mass damper considering mass uncertainty and optimum frequency. Struct. Control Hlth. 2019, 26, e2377. [Google Scholar] [CrossRef]
  46. Song, D.; Chen, Z.; Ke, Y.; Nie, W. Seismic response analysis of a bedding rock slope based on the time-frequency joint analysis method: A case study from the middle reach of the Jinsha River, China. Eng. Geol. 2020, 274, 105731. [Google Scholar] [CrossRef]
Sustainability 16 09623 g001
Figure 1. Location of the study area. (a) Topographic map of Yunnan Province. (b) Satellite image of the study area. (We generated this map using QGIS 3.28.1 software; https://qgis.org/en/site/ (accessed on 18 November 2022)).
Figure 1. Location of the study area. (a) Topographic map of Yunnan Province. (b) Satellite image of the study area. (We generated this map using QGIS 3.28.1 software; https://qgis.org/en/site/ (accessed on 18 November 2022)).
Sustainability 16 09623 g001
Sustainability 16 09623 g002
Figure 2. Geological profile and topography of the slope. (a) Geological profile. (b) Topography of the slope.
Figure 2. Geological profile and topography of the slope. (a) Geological profile. (b) Topography of the slope.
Sustainability 16 09623 g002
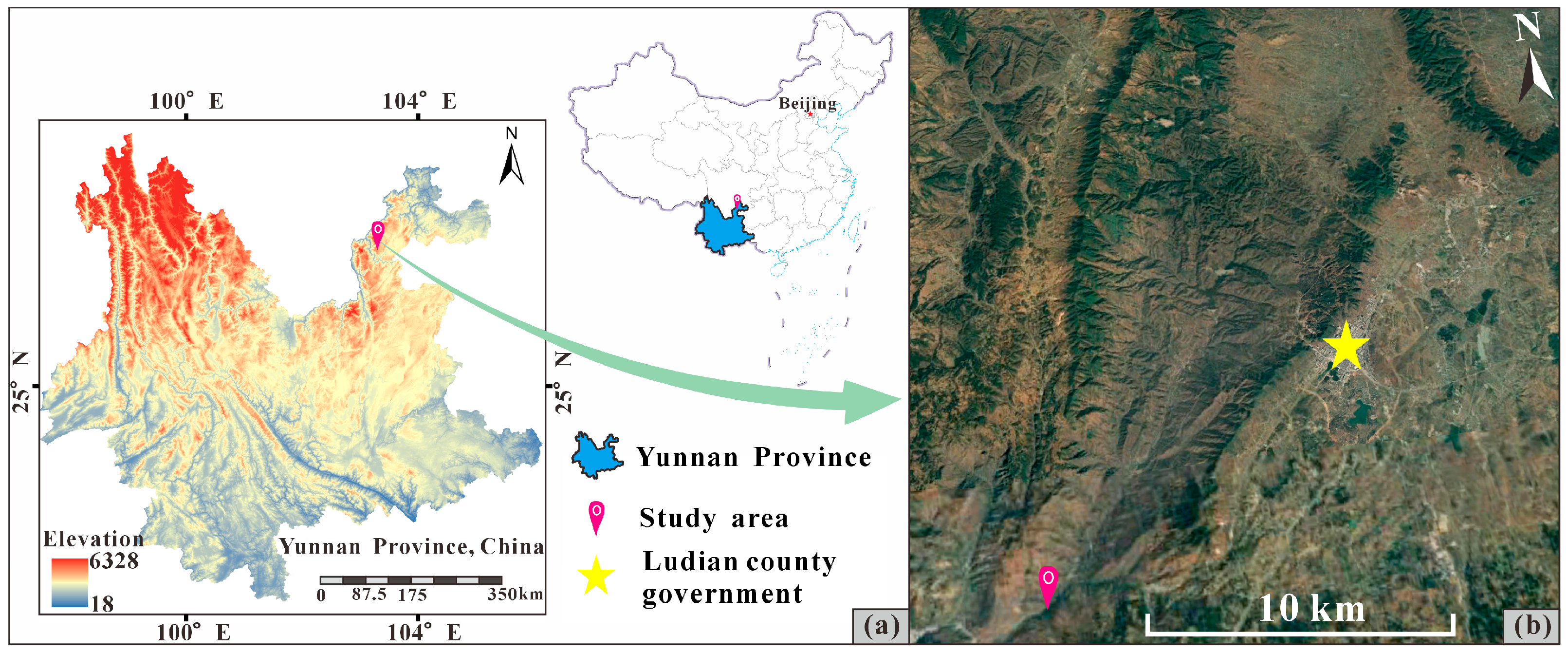
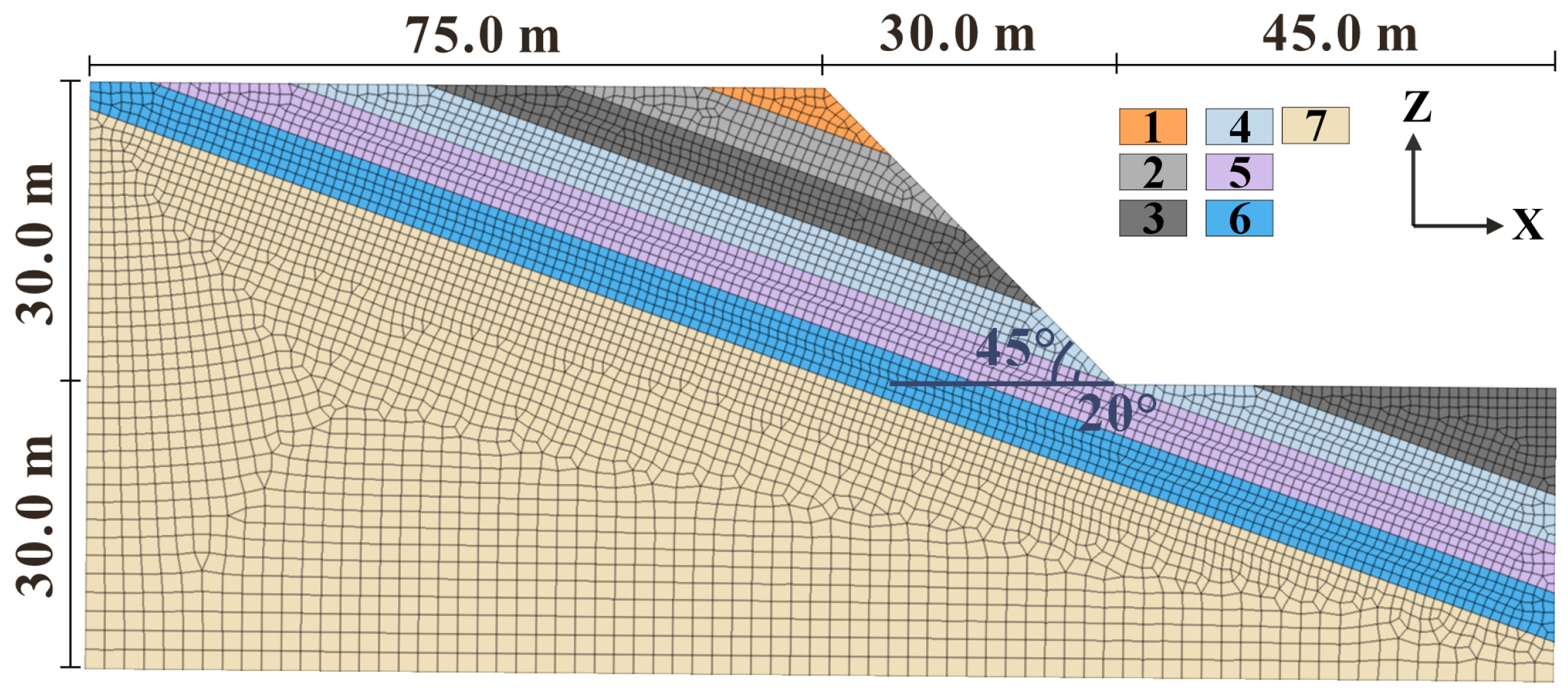
Sustainability 16 09623 g003
Figure 3. Numerical model of the slope.
Figure 3. Numerical model of the slope.
Sustainability 16 09623 g003
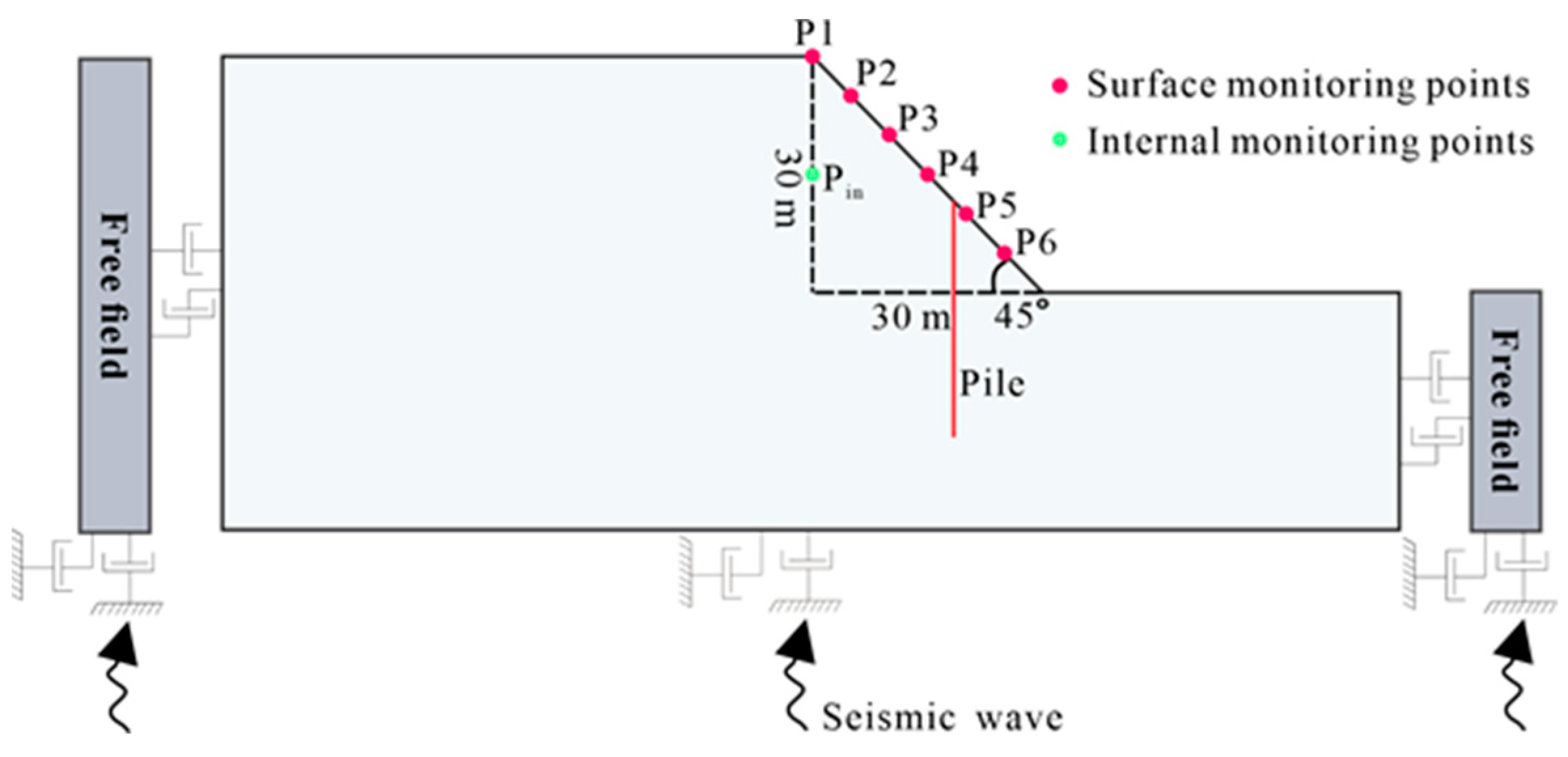
Sustainability 16 09623 g004
Figure 4. Diagram illustrating the boundary conditions.
Figure 4. Diagram illustrating the boundary conditions.
Sustainability 16 09623 g004
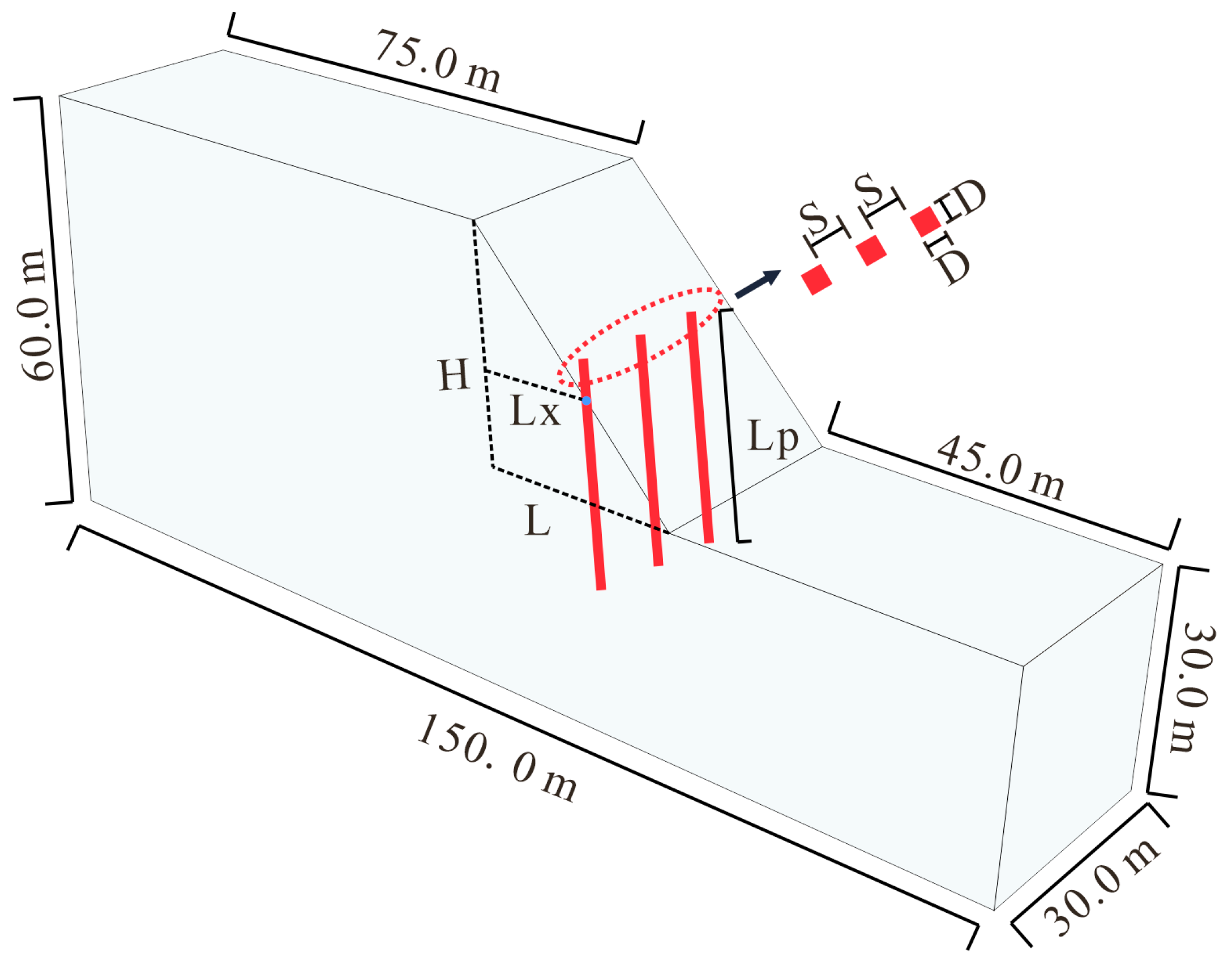
Sustainability 16 09623 g005
Figure 5. Numerical model of a slope supported by anti-slide piles.
Figure 5. Numerical model of a slope supported by anti-slide piles.
Sustainability 16 09623 g005
Sustainability 16 09623 g006
Figure 6. Influence of frequency on the dynamic response of anti-slide piles. (a) Displacement. (b) Bending moment. (c) Shear force.
Figure 6. Influence of frequency on the dynamic response of anti-slide piles. (a) Displacement. (b) Bending moment. (c) Shear force.
Sustainability 16 09623 g006
Sustainability 16 09623 g007
Figure 7. Influence of amplitude on the dynamic response of an anti-slide pile. (a) Displacement. (b) Bending moment. (c) Shear force.
Figure 7. Influence of amplitude on the dynamic response of an anti-slide pile. (a) Displacement. (b) Bending moment. (c) Shear force.
Sustainability 16 09623 g007
Sustainability 16 09623 g008
Figure 8. Influence of duration on the dynamic response of anti-slide piles. (a) Displacement. (b) Bending moment. (c) Shear force.
Figure 8. Influence of duration on the dynamic response of anti-slide piles. (a) Displacement. (b) Bending moment. (c) Shear force.
Sustainability 16 09623 g008
Sustainability 16 09623 g009
Figure 9. Influence of frequency on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the seismic-wave frequency is 6, 12, 18, 24, 30, and 70 Hz, respectively.
Figure 9. Influence of frequency on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the seismic-wave frequency is 6, 12, 18, 24, 30, and 70 Hz, respectively.
Sustainability 16 09623 g009
Sustainability 16 09623 g010
Figure 10. Influence of frequency on the slope deformation.
Figure 10. Influence of frequency on the slope deformation.
Sustainability 16 09623 g010
Sustainability 16 09623 g011
Figure 11. Influence of seismic-wave amplitude on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the amplitude is 0.1, 0.2, 0.3, 0.4, 0.6, and 0.7 g, respectively.
Figure 11. Influence of seismic-wave amplitude on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the amplitude is 0.1, 0.2, 0.3, 0.4, 0.6, and 0.7 g, respectively.
Sustainability 16 09623 g011
Sustainability 16 09623 g012
Figure 12. Influence of amplitude on the slope deformation.
Figure 12. Influence of amplitude on the slope deformation.
Sustainability 16 09623 g012
Sustainability 16 09623 g013
Figure 13. Influence of duration on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the seismic-wave duration is 1, 4, 6, 8, 10, and 20 s, respectively.
Figure 13. Influence of duration on the critical sliding surface. Panels (a–f) represent the critical sliding surface of the slope when the seismic-wave duration is 1, 4, 6, 8, 10, and 20 s, respectively.
Sustainability 16 09623 g013
Sustainability 16 09623 g014
Figure 14. Influence of the duration on the slope deformation.
Figure 14. Influence of the duration on the slope deformation.
Sustainability 16 09623 g014
Sustainability 16 09623 g015
Figure 15. Correlation analysis of multiple key indicators. (a) Frequency, (b) amplitude, and (c) duration. A white asterisk (*) indicates a strong correlation between the two variables on the vertical and horizontal axes, and a black asterisk indicates a less−strong correlation. No asterisk indicates a weak correlation.
Figure 15. Correlation analysis of multiple key indicators. (a) Frequency, (b) amplitude, and (c) duration. A white asterisk (*) indicates a strong correlation between the two variables on the vertical and horizontal axes, and a black asterisk indicates a less−strong correlation. No asterisk indicates a weak correlation.
Sustainability 16 09623 g015
Sustainability 16 09623 g016
Figure 16. The effect of frequency on the spectral characteristics of acceleration at the slope-top monitoring points. (a) 6 Hz, (b) 12 Hz, (c) 18 Hz, (d) 24 Hz, (e) 30 Hz, (f) 70 Hz. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Figure 16. The effect of frequency on the spectral characteristics of acceleration at the slope-top monitoring points. (a) 6 Hz, (b) 12 Hz, (c) 18 Hz, (d) 24 Hz, (e) 30 Hz, (f) 70 Hz. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Sustainability 16 09623 g016
Sustainability 16 09623 g017
Figure 17. The effect of amplitude on the spectral characteristics of the acceleration at the slope-top monitoring points. (a) 0.1 g, (b) 0.2 g, (c) 0.3 g, (d) 0.4 g, (e) 0.5 g, (f) 0.6 g. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Figure 17. The effect of amplitude on the spectral characteristics of the acceleration at the slope-top monitoring points. (a) 0.1 g, (b) 0.2 g, (c) 0.3 g, (d) 0.4 g, (e) 0.5 g, (f) 0.6 g. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Sustainability 16 09623 g017
Sustainability 16 09623 g018
Figure 18. The effect of duration on the spectral characteristics of acceleration at the slope-top monitoring points. (a) 1 s, (b) 4 s, (c) 6 s, (d) 8 s, (e) 10 s, (f) 20 s. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Figure 18. The effect of duration on the spectral characteristics of acceleration at the slope-top monitoring points. (a) 1 s, (b) 4 s, (c) 6 s, (d) 8 s, (e) 10 s, (f) 20 s. The continuous wavelet transforms of the first 1s are a1, b1, etc., and those of the first 1–6 s are a2, b2, etc.
Sustainability 16 09623 g018
Table 1. Physical-property indices of the slope strata.
Table 1. Physical-property indices of the slope strata.
Stratum NumberBulk Modulus
K (MPa)		Shear Modulus
G (MPa)		Unit Weight
Γ (kN/m3)		Cohesion
C (kPa)		Friction Angle
φ (°)
125616920.019.821
235620920.821.023
340424721.022.926
444631721.223.828
555636721.5120.033
664642721.8140.034
7384063823.5160.038
Table 2. Sinusoidal seismic-wave parameters.
Table 2. Sinusoidal seismic-wave parameters.
Serial Numberamax (g)f (Hz)t (s)Serial Numberamax (g)f (Hz)t (s)
10.166100.4126
20.1126110.6126
30.1186120.7126
40.1246130.1121
50.1306140.1124
60.1706150.1126
70.1126160.1128
80.2126170.11210
90.3126180.11220
Table 3. Parameters of anti-slide piles.
Table 3. Parameters of anti-slide piles.
ParameterValueParameterValueParameterValue
Young modulus30 GPaCoupling-cohesion: shear1.9 × 107 PaCoupling-cohesion: normal1.9 × 107 Pa
Poisson ratio0.21Coupling-stiffness: shear1.0 × 109 N/m2Coupling-stiffness: normal1.0 × 109 N/m2
Moi-z2.0 m4Coupling-friction-shear22°Coupling-friction: normal22°
Moi-y4.5 m4Density2500 kg/m3Coupling-gap: normalon
Moi-polar6.5 m4Cross-sectional area4.0 m2Perimeter8.0 m
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Li, L.; Xue, L.; Jiang, T.; Huang, K.; Li, Z. A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics. Sustainability 2024, 16, 9623. https://doi.org/10.3390/su16229623

AMA Style

Li L, Xue L, Jiang T, Huang K, Li Z. A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics. Sustainability. 2024; 16(22):9623. https://doi.org/10.3390/su16229623

Chicago/Turabian Style

Li, Longfei, Lei Xue, Tong Jiang, Kun Huang, and Zhuan Li. 2024. "A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics" Sustainability 16, no. 22: 9623. https://doi.org/10.3390/su16229623

APA Style

Li, L., Xue, L., Jiang, T., Huang, K., & Li, Z. (2024). A Study on the Dynamic Response and Deformation of Slopes Supported by Anti-Slide Piles Subjected to Seismic Waves with Different Spectral Characteristics. Sustainability, 16(22), 9623. https://doi.org/10.3390/su16229623

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop