Multi-Energy Coupling Load Forecasting in Integrated Energy System with Improved Variational Mode Decomposition-Temporal Convolutional Network-Bidirectional Long Short-Term Memory Model
Abstract
1. Introduction
2. Load Decomposition Model Based on VMD-PE-SCSO
2.1. Variational Mode Decomposition (VMD)
- (1)
- Construct the constrained variation problem as follows:
- (2)
- Lagrange Multiplier λ(t) and the penalty factor α are introduced to turn the constrained variational problem into an unconstrained problem; the extended Lagrangian function is expressed in Equation (2):
- (3)
- The IMF component {uk(t)} and the central frequency {ωk} are updated based on the alternating direction multiplier method, this results in generating the final decomposition.
2.2. VMD Parameter Optimization Model Based on Minimum Average Permutation Entropy
- (1)
- Suppose a time series containing L observations x(1), x(2), …, x(L), with given embedding dimension m and delay time τ, the new sequence is represented by Equation (3).
- (2)
- To determine the correlation degree among the data, each vector in x*(i) is rearranged in an ascending order. The process is shown in Equation (4).
- (3)
- Introduce P1, P2, …, PN to represent the occurrence frequency of each vector in x*(i) using the rearrangement order, where N ≤ m!. Moreover, the PE of the time series x(1), x(2), …, x(L) can be determined by calculating Shannon entropy as follows:
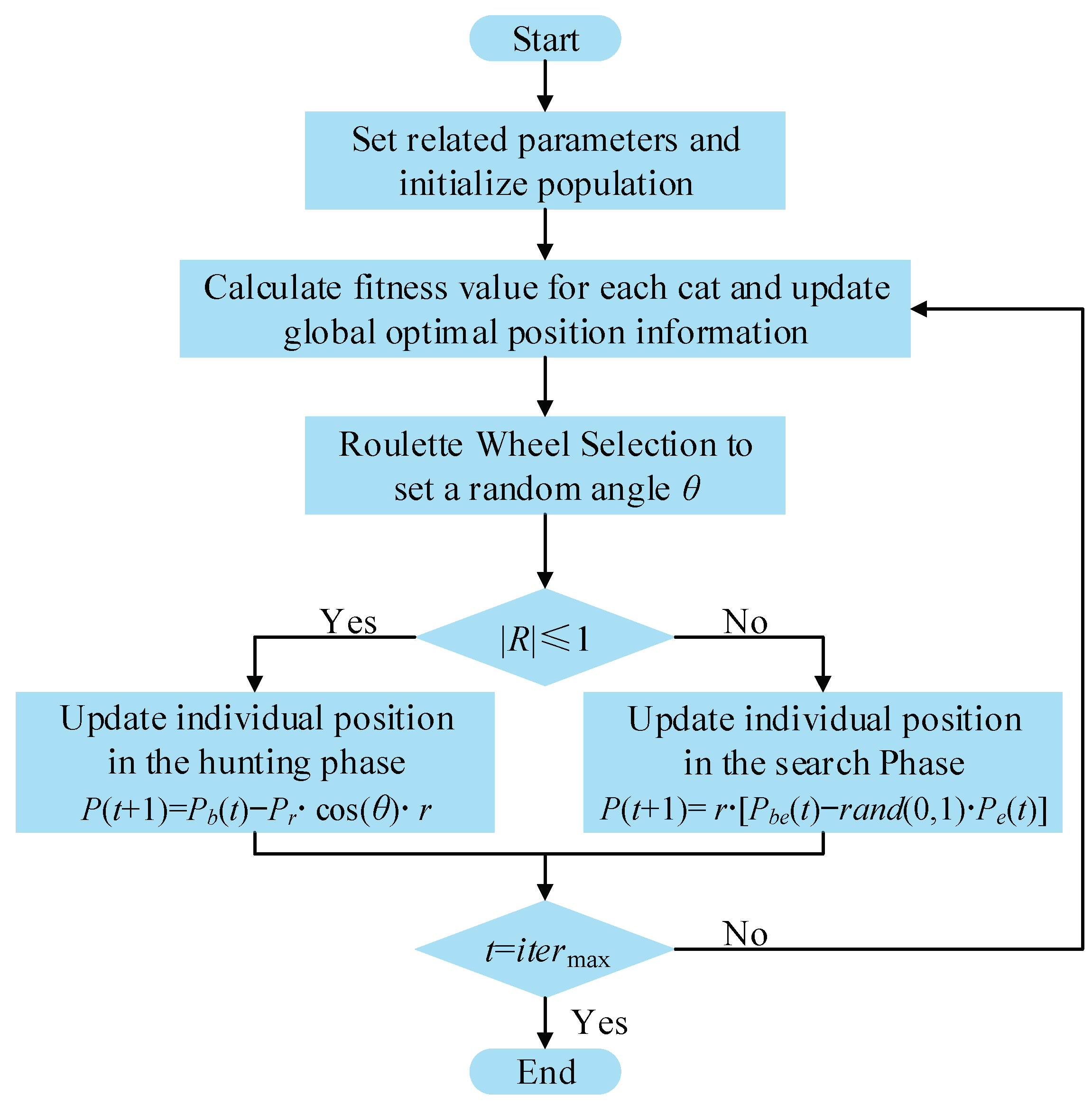
2.3. Optimizing VMD Parameters Using SCSO Algorithm
3. Load Forecasting Model Combining TCN and BiLSTM
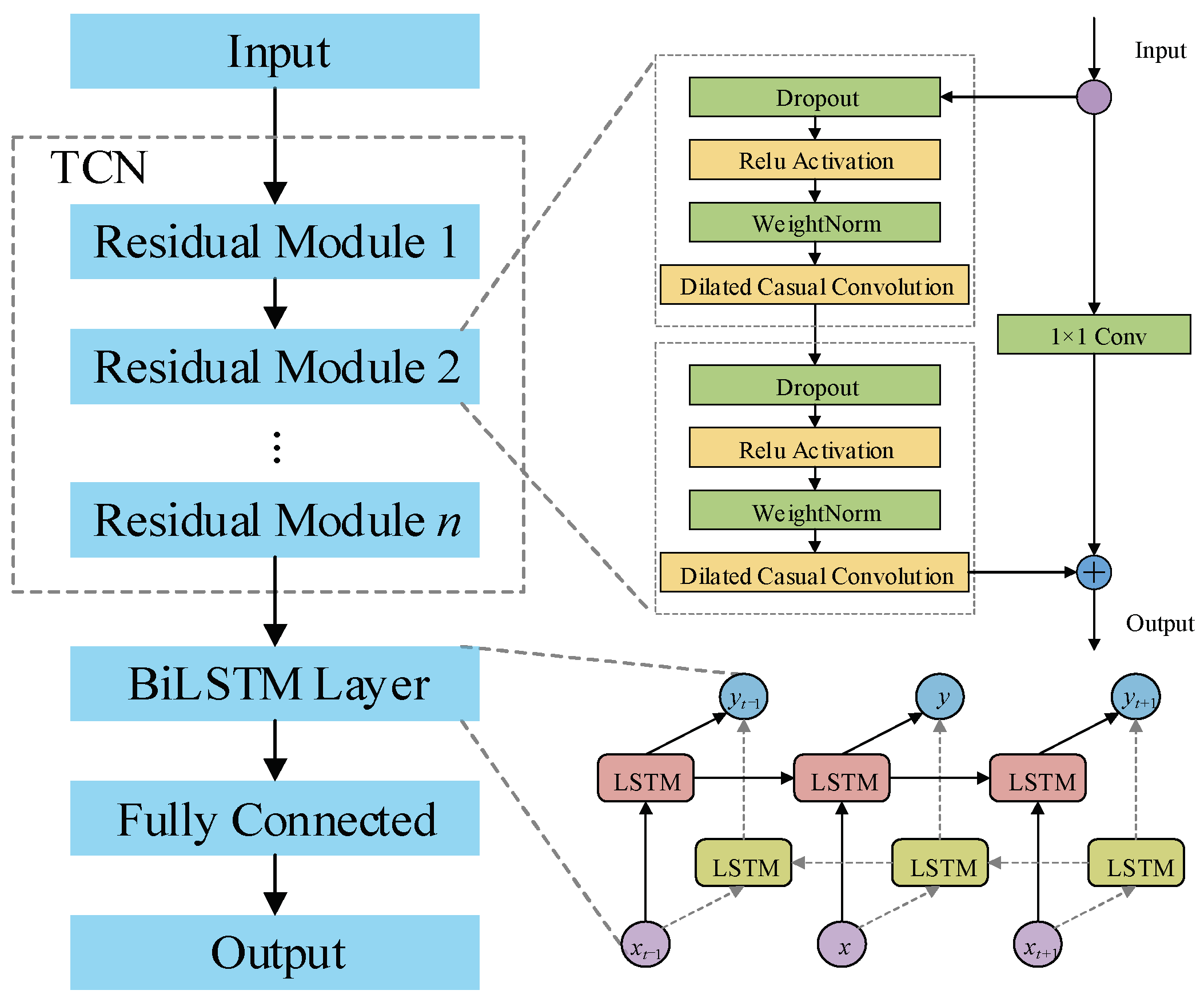
3.1. Temporal Convolutional Network (TCN)
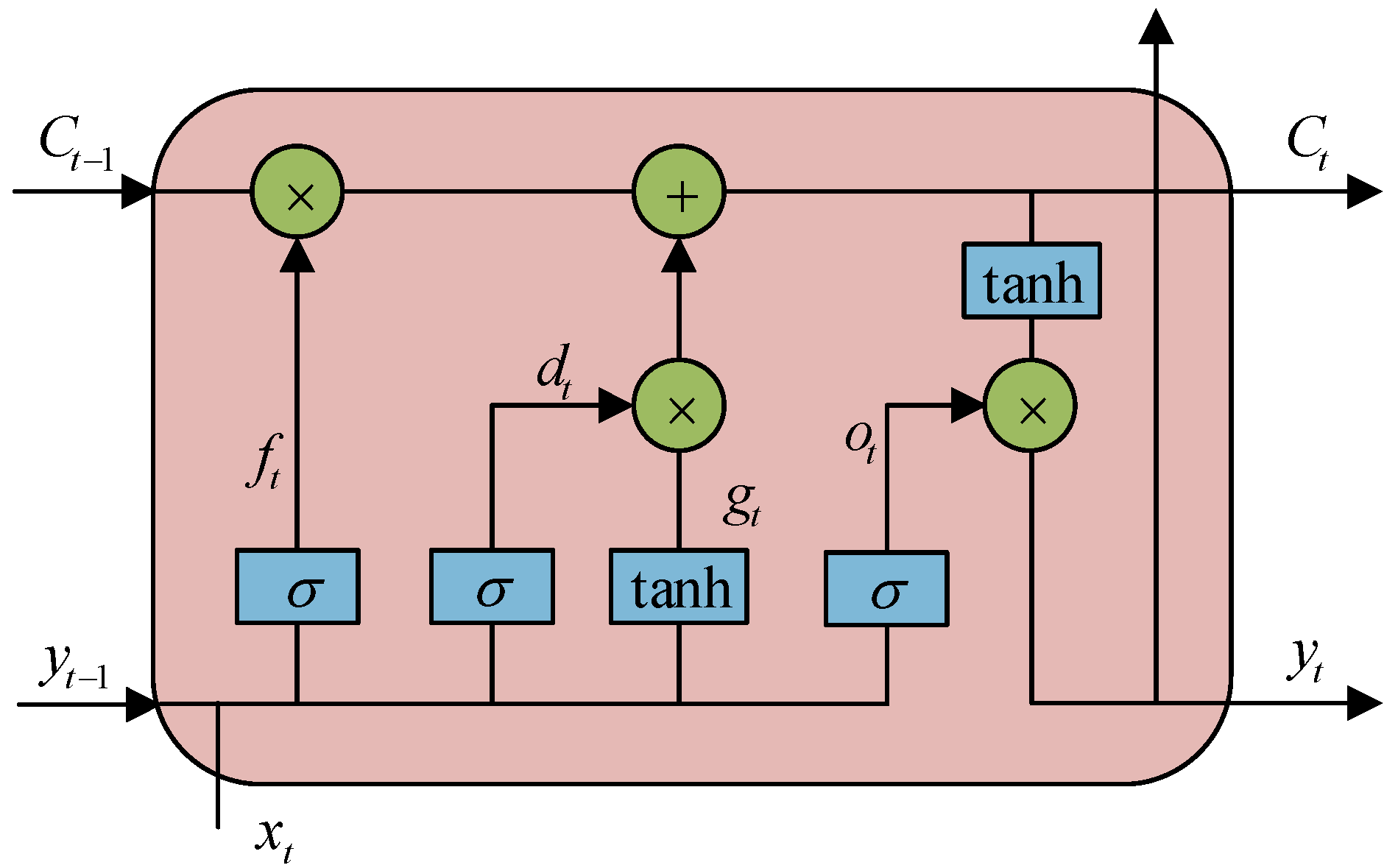
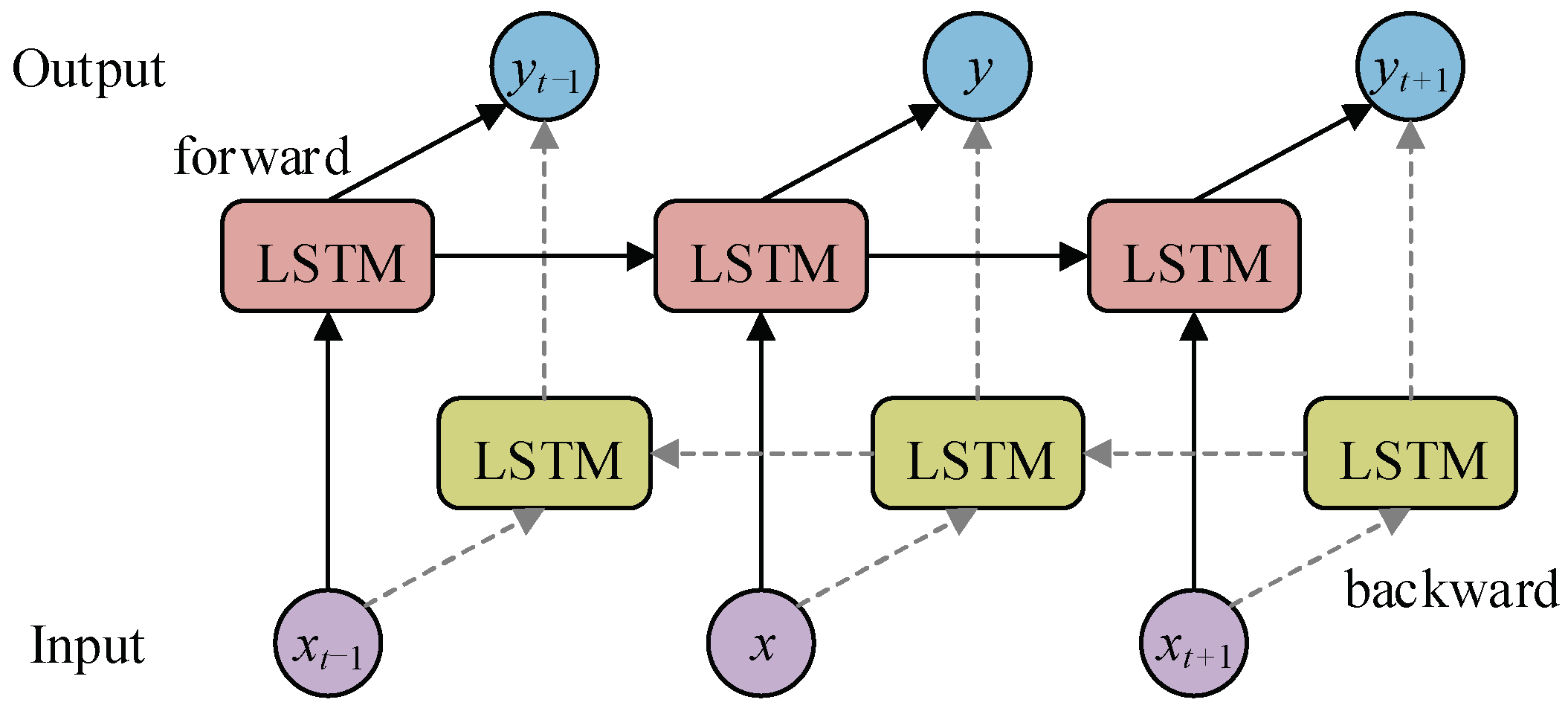
3.2. Bidirectional Long Short-Term Memory Network
3.3. TCN-BiLSTM Neural Network
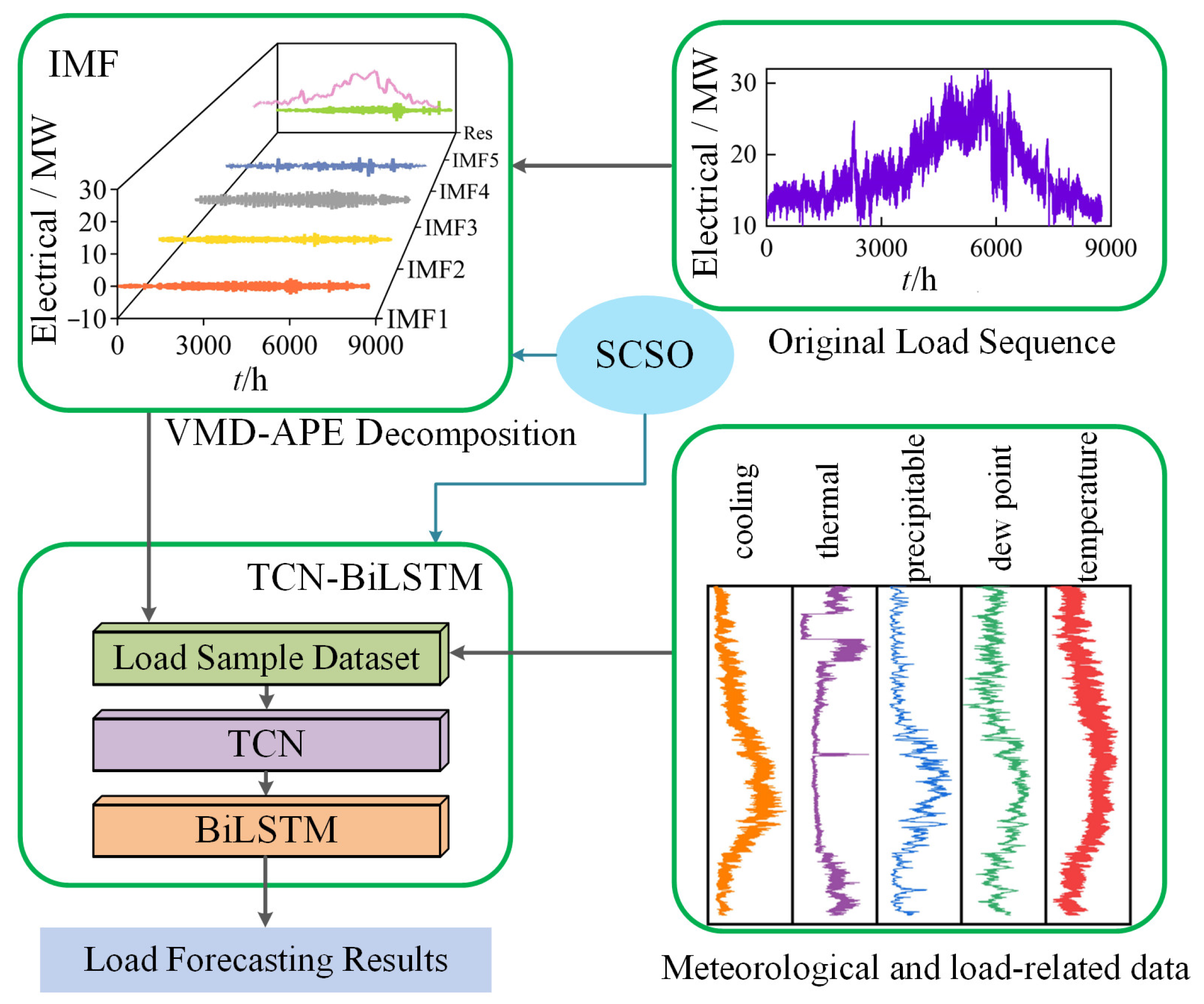
4. Multi-Energy Load Forecasting Method Using VMD-TCN-BiLSTM
4.1. Forecasting Process
- (1)
- To address the non-stationary characteristics of the multi-variate load sequence, this study builds a VMD optimization model based on the minimum average permutation entropy (VMD-APE). The SCSO algorithm is employed to solve this model, generating the IMF sets as well as the residues for electrical, thermal, and cooling loads. Therefore, it facilitates the effective decomposition of the multivariate loads;
- (2)
- The preprocessed multi-variate load IMF sets are combined with the meteorological information and related load data to build the input and output samples for electrical, thermal, and cooling loads;
- (3)
- The TCN-BiLSTM models are constructed for different types of loads and used to learn and train the sample sequences. Parameters’ optimization is achieved using the SCSO algorithm;
- (4)
- Trained models are then used for multi-variate load forecasting. Evaluation metrics are developed to assess forecasting accuracy.
4.2. Evaluation Metrics
5. Empirical Studies
5.1. Load Series Decomposition
5.2. Input and Output Feature Selection
5.3. Hyper-Parameters Description of TCN-BiLSTM
5.4. Comparison of Different Decomposition Methods
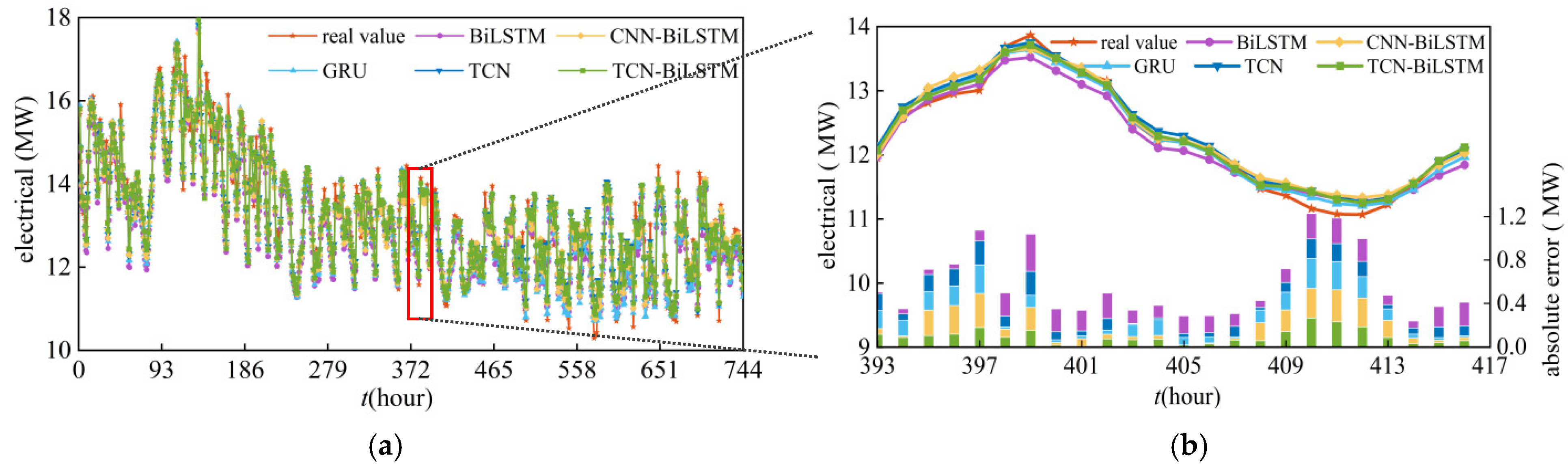
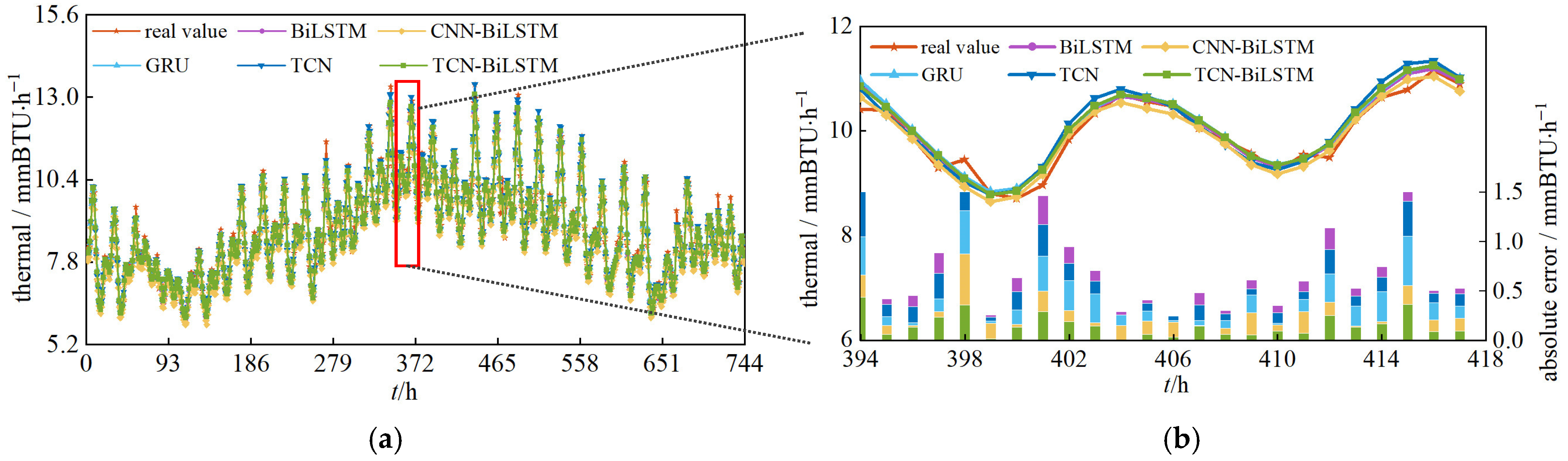
5.5. Comparison of Different Forecasting Models
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ji, L.; Zhang, B.B.; Huang, G.H.; Xie, Y.L.; Niu, D.X. GHG-mitigation oriented and coal-consumption constrained inexact robust model for regional energy structure adjustment-A case study for Jiangsu Province, China. Renew. Energy 2018, 123, 549–562. [Google Scholar] [CrossRef]
- Xie, B.C.; Zhang, R.Y.; Chen, X.P. China’s optimal development pathway of intermittent renewable power towards carbon neutrality. J. Clean. Prod. 2023, 406, 136903. [Google Scholar] [CrossRef]
- Xu, M.K.; Liao, C.P.; Huang, Y.; Gao, X.Q.; Dong, G.L.; Liu, Z. LEAP model-based analysis to low-carbon transformation path in the power sector: A case study of Guangdong-Hong Kong-Macao Greater Bay Area. Sci. Rep. 2024, 14, 7405. [Google Scholar] [CrossRef] [PubMed]
- Niu, D.X.; Yu, M.; Sun, L.J.; Gao, T.; Wang, K.K. Short-term multi-energy load forecasting for integrated energy systems based on CNN-BiGRU optimized by attention mechanism. Appl. Energy 2022, 313, 118801. [Google Scholar] [CrossRef]
- Talaat, M.; Tayseer, M.; Farahat, M.A.; Song, D.R. Artificial intelligence strategies for simulating the integrated energy systems. Artif. Intell. Rev. 2024, 57, 106. [Google Scholar] [CrossRef]
- Wang, J.X.; Zhong, H.W.; Ma, Z.M.; Xia, Q.; Kang, C.Q. Review and prospect of integrated demand response in the multi-energy system. Appl. Energy 2017, 202, 772–782. [Google Scholar] [CrossRef]
- Dal Cin, E.; Carraro, G.; Lazzaretto, A.; Tsatsaronis, G. Optimizing the retrofit design and operation of multi-energy systems integrated with energy networks. J. Energy Resour. Technol. 2024, 146, 042102. [Google Scholar] [CrossRef]
- Wang, Y.L.; Qin, Y.M.; Ma, Z.B.; Wang, Y.N.; Li, Y. Operation optimisation of integrated energy systems based on cooperative game with hydrogen energy storage systems. Int. J. Hydrogen Energy 2023, 48, 37335–37354. [Google Scholar] [CrossRef]
- Li, K.; Mu, Y.C.; Yang, F.; Wang, H.Y.; Yan, Y.; Zhang, C.H. A novel short-term multi-energy load forecasting method for integrated energy system based on feature separation-fusion technology and improved CNN. Appl. Energy 2023, 351, 121823. [Google Scholar] [CrossRef]
- Liu, B.D.; Nowotarski, J.; Hong, T.; Weron, R. Probabilistic load forecasting via quantile regression averaging on sister forecasts. IEEE Trans. Smart Grid 2017, 8, 730–737. [Google Scholar] [CrossRef]
- Laouafi, A.; Mordjaoui, M.; Laouafi, F.; Boukelia, T.E. Daily peak electricity demand forecasting based on an adaptive hybrid two-stage methodology. Int. J. Electr. Power Energy Syst. 2016, 77, 136–144. [Google Scholar] [CrossRef]
- Tarmanini, C.; Sarma, N.; Gezegin, C.; Ozgonenel, O. Short term load forecasting based on ARIMA and ANN approaches. Energy Rep. 2023, 9, 550–557. [Google Scholar] [CrossRef]
- Fang, P.; Fu, W.L.; Wang, K.; Xiong, D.Z.; Zhang, K. A compositive architecture coupling outlier correction, EWT, nonlinear Volterra multi-model fusion with multi-objective optimization for short-term wind speed forecasting. Appl. Energy 2022, 307, 118191. [Google Scholar] [CrossRef]
- Jahani, A.; Zare, K.; Khanli, L.M. Short-term load forecasting for microgrid energy management system using hybrid SPM-LSTM. Sustain. Cities Soc. 2023, 98, 104775. [Google Scholar] [CrossRef]
- Eskandari, H.; Imani, M.; Moghaddam, M.P. Best-tree wavelet packet transform bidirectional GRU for short-term load forecasting. J. Supercomput. 2023, 79, 13545–13577. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Chen, J.; Chen, X.Q.; Zeng, X.J.; Kong, Y.; Sun, S.F.; Guo, Y.S.; Liu, Y. Short-term load forecasting for industrial customers based on TCN-LightGBM. IEEE Trans. Power Syst. 2021, 36, 1984–1997. [Google Scholar] [CrossRef]
- Cai, C.C.; Li, Y.J.; Su, Z.H.; Zhu, T.Q.; He, Y.Y. Short-term electrical load forecasting based on VMD and GRU-TCN hybrid network. Appl. Sci. 2022, 12, 6647. [Google Scholar] [CrossRef]
- Sulandari, W.; Subanar; Lee, M.H.; Rodrigues, P.C. Indonesian electricity load forecasting using singular spectrum analysis, fuzzy systems and neural networks. Energy 2020, 190, 116408. [Google Scholar] [CrossRef]
- Wang, L.Y.; Zhou, X.; Xu, H.L.; Tian, T.; Tong, H.M. Short-term electrical load forecasting model based on multi-dimensional meteorological information spatio-temporal fusion and optimized variational mode decomposition. IET Gener. Transm. Distrib. 2023, 17, 4647–4663. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Bedi, J.; Toshniwal, D. Energy load time-series forecast using decomposition and autoencoder integrated memory network. Appl. Soft Comput. 2020, 93, 106390. [Google Scholar] [CrossRef]
- Hu, X.; Li, K.Y.; Li, J.F.; Zhong, T.T.; Wu, W.N.; Zhang, X.; Feng, W.J. Load forecasting model consisting of data mining based orthogonal greedy algorithm and long short-term memory network. Energy Rep. 2022, 8, 235–242. [Google Scholar] [CrossRef]
- Sekhar, C.; Dahiya, R. Robust framework based on hybrid deep learning approach for short term load forecasting of building electricity demand. Energy 2023, 268, 126660. [Google Scholar] [CrossRef]
- Ma, S.J.; Ning, J.; Mao, N.; Liu, J.; Shi, R.F. Research on Machine Learning-Based method for predicting industrial park electric vehicle charging load. Sustainability 2024, 16, 7258. [Google Scholar] [CrossRef]
- Xiao, Z.C.; Yu, L.J.; Zhang, H.J.; Zhang, X.T.; Su, Y.X. HVAC load forecasting based on the CEEMDAN-Conv1D-BiLSTM-AM model. Mathematics 2023, 11, 4630. [Google Scholar] [CrossRef]
- Liu, M.P.; Sun, X.H.; Wang, Q.N.; Deng, S.H. Short-term load forecasting using EMD with feature selection and TCN-based deep learning model. Energies 2022, 15, 7170. [Google Scholar] [CrossRef]
- Hong, Y.; Wang, D.; Su, J.M.; Ren, M.W.; Xu, W.Q.; Wei, Y.H.; Yang, Z. Short-Term Power Load Forecasting in Three Stages Based on CEEMDAN-TGA Model. Sustainability 2023, 15, 11123. [Google Scholar] [CrossRef]
- Jia, T.R.; Yao, L.X.; Yang, G.Q.; He, Q. A short-term power load forecasting method of based on the CEEMDAN-MVO-GRU. Sustainability 2022, 14, 16460. [Google Scholar] [CrossRef]
- Li, K.; Huang, W.; Hu, G.Y.; Li, J. Ultra-short term power load forecasting based on CEEMDAN-SE and LSTM neural network. Energy Build. 2023, 279, 112666. [Google Scholar] [CrossRef]
- Wen, Y.; Pan, S.; Li, X.X.; Li, Z.B. Highly fluctuating short-term load forecasting based on improved secondary decomposition and optimized VMD. Sustain. Energy Grids Netw. 2024, 37, 101270. [Google Scholar] [CrossRef]
- Li, W.W.; Shi, Q.; Sibtain, M.; Li, D.; Mbanze, D.E. A hybrid forecasting model for short-term power load based on sample entropy, two-phase decomposition and whale algorithm optimized support vector regression. IEEE Access 2020, 8, 166907–166921. [Google Scholar] [CrossRef]
- Chen, G.; Ma, X.F.; Lin, W. Multifeature-based Variational Mode Decomposition-Temporal Convolutional Network-Long Short-Term Memory for short-term forecasting of the load of port power systems. Sustainability 2024, 164, 5321. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Keller, K.; Mangold, T.; Stolz, I.; Werner, J. Permutation entropy: New ideas and challenges. Entropy 2017, 19, 134. [Google Scholar] [CrossRef]
- Seyyedabbasi, A.; Kiani, F. Sand Cat swarm optimization: A nature-inspired algorithm to solve global optimization problems. Eng. Comput. 2023, 39, 2627–2651. [Google Scholar] [CrossRef]
- Lin, Q.Y.; Yang, Z.P.; Huang, J.; Deng, J.; Chen, L.; Zhang, Y.R. A Landslide Displacement Prediction Model Based on the ICEEMDAN Method and the TCN-BiLSTM Combined Neural Network. Water 2023, 15, 4247. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Xia, T.B.; Song, Y.; Zheng, Y.; Pan, E.S.; Xi, L.F. An ensemble framework based on convolutional bi-directional LSTM with multiple time windows for remaining useful life estimation. Comput. Ind. 2020, 115, 103182. [Google Scholar] [CrossRef]
- AUS. Campus Metabolism. Available online: https://www.asu.edu/ (accessed on 5 January 2023).
- Fan, J.L.; Zhuang, W.; Xia, M.; Fang, W.X.; Liu, J. Optimizing attention in a Transformer for multihorizon, multienergy load forecasting in integrated energy systems. IEEE Trans. Ind. Inform. 2024, 20, 10238–10248. [Google Scholar] [CrossRef]
- NSRDB. Data Viewer. Available online: https://nsrdb.nrel.gov/data-viewer (accessed on 6 January 2023).
- Wang, C.; Wang, Y.; Ding, Z.T.; Zheng, T.; Hu, J.Y.; Zhang, K.F. A transformer-based method of multienergy load forecasting in integrated energy system. IEEE Trans. Smart Grid 2022, 13, 2703–2714. [Google Scholar] [CrossRef]
- Guo, Y.X.; Li, Y.; Qiao, X.B.; Zhang, Z.Y.; Zhou, W.F.; Mei, Y.J.; Lin, J.J.; Zhou, Y.C.; Nakanishi, Y. BiLSTM multitask learning-based combined load forecasting considering the loads coupling relationship for multienergy system. IEEE Trans. Smart Grid 2022, 13, 3481–3492. [Google Scholar] [CrossRef]




| K = 2 | K = 3 | K = 4 | K = 5 | K = 6 | K = 7 | K = 8 | |
|---|---|---|---|---|---|---|---|
| α = 100 | 0.984 | 0.979 | 0.924 | 0.927 | 0.939 | 0.921 | 0.906 |
| α = 500 | 0.973 | 0.938 | 0.910 | 0.933 | 0.923 | 0.903 | 0.916 |
| α = 1000 | 0.938 | 0.938 | 0.917 | 0.903 | 0.906 | 0.890 | 0.899 |
| α = 2000 | 0.911 | 0.889 | 0.904 | 0.870 | 0.894 | 0.900 | 0.922 |
| α = 2724 | 0.920 | 0.932 | 0.911 | 0.859 | 0.879 | 0.929 | 0.916 |
| α = 3000 | 0.924 | 0.928 | 0.908 | 0.880 | 0.876 | 0.921 | 0.926 |
| Input Feature | Output Feature |
|---|---|
| Electrical load IMFs in the previous five hours | Electricity load to be forecast at the moment |
| Thermal and cooling load in the previous five hours | |
| Temperature, dew point, precipitable |
| Parameter | Value Range |
|---|---|
| Convolution layer kernel size | 3 |
| Dilation factors | 1/2/4 |
| Number of convolution layer kernels | [8, 64] |
| Hidden layer units in BiLSTM layer | [10, 100] |
| Learning rate | [1 × 10−4, 1 × 10−1] |
| Regularization coefficient | [1 × 10−4, 1 × 10−1] |
| Load Type | Decomposition Methods | R2 | EMAPE/% |
|---|---|---|---|
| Electrical | No decomposition | 0.742 | 4.145 |
| CEEMDAN | 0.952 | 1.833 | |
| VMD-APE | 0.963 | 1.462 | |
| Thermal | No decomposition | 0.880 | 4.153 |
| CEEMDAN | 0.889 | 4.888 | |
| VMD-APE | 0.985 | 1.563 | |
| Cooling | No decomposition | 0.935 | 5.739 |
| CEEMDAN | 0.987 | 2.525 | |
| VMD-APE | 0.993 | 1.830 |
| Load Type | Prediction Model | R2 | EMAPE/% |
|---|---|---|---|
| Electrical | BiLSTM | 0.944 | 1.939 |
| TCN | 0.961 | 1.551 | |
| GRU | 0.960 | 1.544 | |
| CNN-BiLSM | 0.959 | 1.533 | |
| TCN-BiLSM | 0.963 | 1.462 | |
| Thermal | BiLSTM | 0.983 | 1.637 |
| TCN | 0.979 | 1.883 | |
| GRU | 0.983 | 1.655 | |
| CNN-BiLSM | 0.971 | 2.269 | |
| TCN-BiLSM | 0.985 | 1.563 | |
| Cooling | BiLSTM | 0.986 | 2.648 |
| TCN | 0.992 | 1.838 | |
| GRU | 0.989 | 2.317 | |
| CNN-BiLSM | 0.988 | 2.289 | |
| TCN-BiLSM | 0.993 | 1.830 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, W.; Zhou, W.; Cao, Y.; Wang, M.; Hu, W.; Liu, C.; Liu, P.; Liu, G. Multi-Energy Coupling Load Forecasting in Integrated Energy System with Improved Variational Mode Decomposition-Temporal Convolutional Network-Bidirectional Long Short-Term Memory Model. Sustainability 2024, 16, 10082. https://doi.org/10.3390/su162210082
Liu X, Liu W, Zhou W, Cao Y, Wang M, Hu W, Liu C, Liu P, Liu G. Multi-Energy Coupling Load Forecasting in Integrated Energy System with Improved Variational Mode Decomposition-Temporal Convolutional Network-Bidirectional Long Short-Term Memory Model. Sustainability. 2024; 16(22):10082. https://doi.org/10.3390/su162210082
Chicago/Turabian StyleLiu, Xinfu, Wei Liu, Wei Zhou, Yanfeng Cao, Mengxiao Wang, Wenhao Hu, Chunhua Liu, Peng Liu, and Guoliang Liu. 2024. "Multi-Energy Coupling Load Forecasting in Integrated Energy System with Improved Variational Mode Decomposition-Temporal Convolutional Network-Bidirectional Long Short-Term Memory Model" Sustainability 16, no. 22: 10082. https://doi.org/10.3390/su162210082
APA StyleLiu, X., Liu, W., Zhou, W., Cao, Y., Wang, M., Hu, W., Liu, C., Liu, P., & Liu, G. (2024). Multi-Energy Coupling Load Forecasting in Integrated Energy System with Improved Variational Mode Decomposition-Temporal Convolutional Network-Bidirectional Long Short-Term Memory Model. Sustainability, 16(22), 10082. https://doi.org/10.3390/su162210082







