The Spatial Impact of Innovative Human Capital on Green Total Factor Productivity in Chinese Regions Based on Quantity and Quality Dimensions
Abstract
1. Introduction
2. Literature Review
2.1. TFP and GTFP
2.2. The Influence of Human Capital on GTFP
2.3. The Measuring Methods of Innovative Human Capital
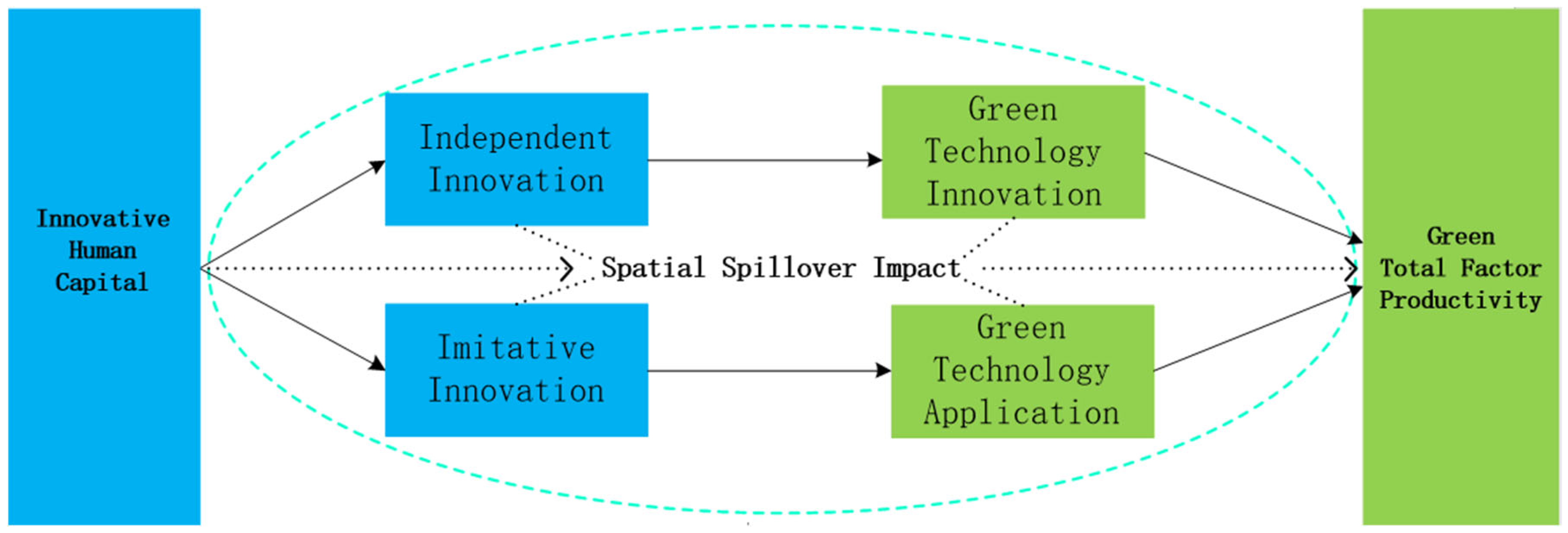
3. Theoretical Mechanisms and Research Hypotheses
3.1. Analysis of the Direct Mechanism of IHC’s Effects on GTFP
3.2. Analyzing the Indirect Mechanism of IHC Influencing GTFP
3.3. Spatial Spillover Mechanism of IHC Affecting GTFP
4. Model Construction and Variables Description
4.1. Building a Calculation Model for GTFP
4.2. GTFP Measurement and Evaluation System
4.3. Empirical Model Construction and Variable Data
4.3.1. Spatial Durbin Model
4.3.2. Selection and Description of Variables
- (a)
- The first control variable is foreign investment size, which is calculated as the ratio of foreign direct investment to GDP and expressed as FDI. FDI is considered as it has a potential influence on the regional economy and environment. It can bring advanced technologies and management experience, which may impact GTFP [25]. FDI is converted through the average exchange rate of the US dollar and Yuan every year.
- (b)
- The second one is the government’s size, which is calculated as the ratio of government spending to GDP and expressed as GOV. The function of government in an economy is essential as it can allocate resources and affect economic activities. The proportion of government expenditure in GDP impacts GTFP based on the specific use of the expenditure. Spending on scientific research and environmental protection may have a positive influence on GTFP, while general fiscal expenditure might have a negative effect [26].
- (c)
- The third one is the urbanization level, which is calculated as the ratio of the urban population to the whole population and expressed as URB. Urbanization is a complex process that affects resource use and environmental quality. As mentioned by Wang et al. (2024) [27], the ratio of urban population to the whole population can indicate the degree of urbanization and its potential effect on GTFP.
- (d)
- The fourth one is international trade which is calculated by the ratio of total imports and exports to GDP and expressed as EX. International trade can impact a region’s industrial structure and technological progress, subsequently affecting GTFP [28]. The total amount of imports and exports is converted from US dollars to RMB based on the average exchange rate per year.
- (e)
- The fifth one is the infrastructure level, which is calculated as the ratio of the sum of road kilometers and railway kilometers in various places to the area of land in the region and expressed as INFRA. Infrastructure is of great importance for connecting markets, lowering transportation costs, and promoting economic growth [29].
- (f)
- The sixth one is environmental regulation and is expressed as REG. Strict environmental regulations can drive innovation and the adoption of cleaner production methods, thus affecting GTFP [30]. This article considers the availability and continuity of data and uses the comprehensive indexes of pollutant emissions calculated from SO2 emissions, solid waste generation, wastewater emissions, and regional GDP as specific measurement indicators.
5. Results
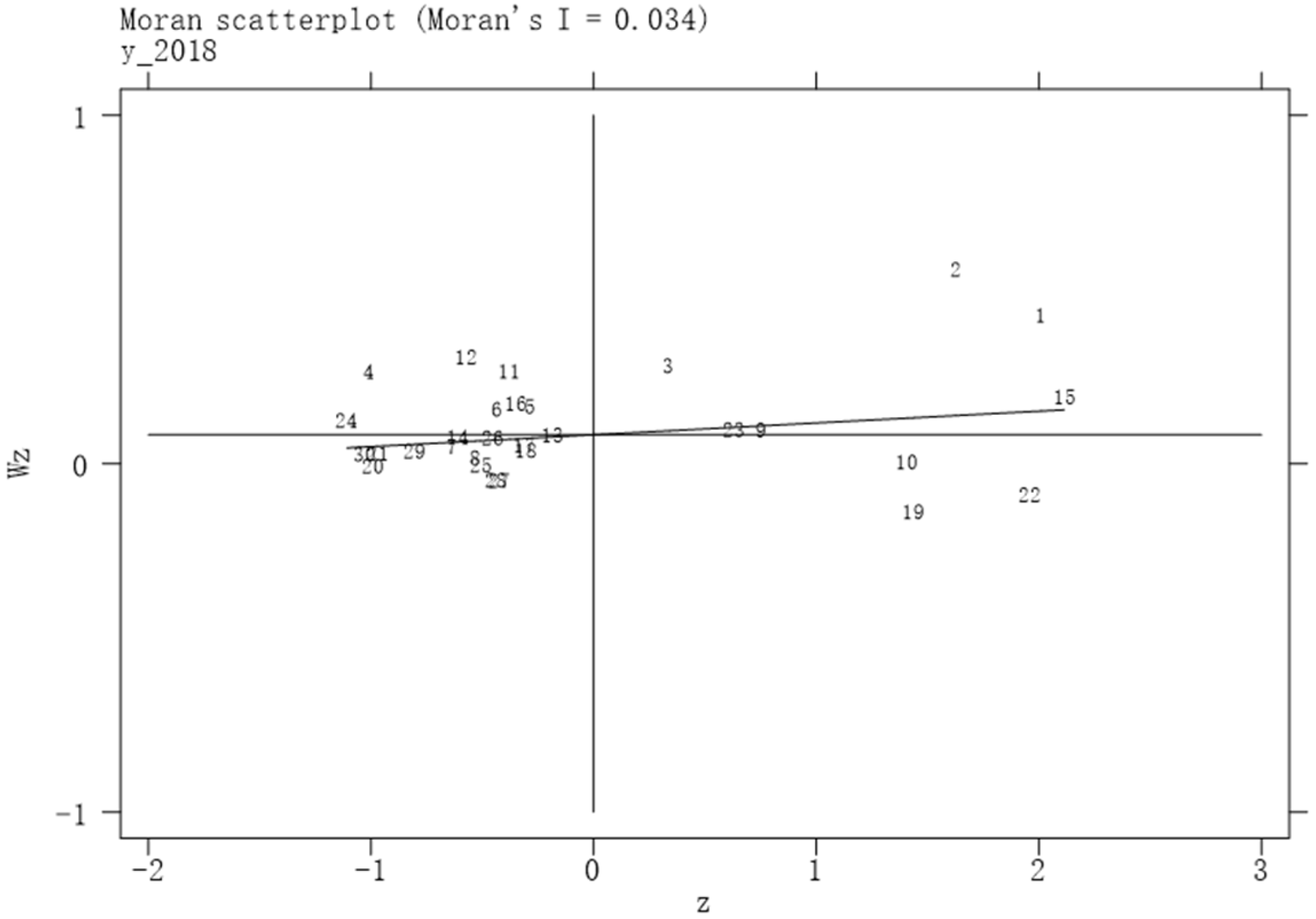
5.1. Spatial Correlation Test
5.2. Test of the Direct Mechanism of IHC Promoting GTFP
5.3. Test of the Indirect Mechanism of IHC Promoting GTFP
5.4. The Mechanism Test of Spatial Spillover Effect
5.5. Robustness Test
5.6. Analyzing Heterogeneity for Both the Eastern and the Middle-Western Regions
6. Discussion
6.1. Direct Influence of IHC on GTFP
6.2. Indirect Impact of IHC on GTFP Through Technological Progress
6.3. Spatial Spillover Effect of IHC on GTFP
7. Conclusions and Policies
7.1. Conclusions
7.2. Policies
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Luo, Y.; Mensah, C.N.; Lu, Z.; Wu, C. Environmental Regulation and Green Total Factor Productivity in China: A Perspective of Porter’s and Compliance Hypothesis. Ecol. Indic. 2022, 145, 109744. [Google Scholar] [CrossRef]
- Liu, S.; Hou, P.; Gao, Y.; Tan, Y. Innovation and Green Total Factor Productivity in China: A Linear and Nonlinear Investigation. Environ. Sci. Pollut. Res. 2022, 29, 12810–12831. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Cui, H.; Zhao, Q. Effect of Green Technology Innovation on Green Total Factor Productivity in China: Evidence from Spatial Durbin Model Analysis. J. Clean. Prod. 2021, 288, 125624. [Google Scholar] [CrossRef]
- Zhou, R.; Zhang, Y. Measurement of Urban Green Total Factor Productivity and Analysis of Its Temporal and Spatial Evolution in China. Sustainability 2023, 15, 9435. [Google Scholar] [CrossRef]
- Zhou, Y.; Xu, Y.; Liu, C.; Fang, Z.; Fu, X.; He, M. The Threshold Effect of China’s Financial Development on Green Total Factor Productivity. Sustainability 2019, 11, 3776. [Google Scholar] [CrossRef]
- Jiakui, C.; Abbas, J.; Najam, H.; Liu, J.; Abbas, J. Green Technological Innovation, Green Finance, and Financial Development and Their Role in Green Total Factor Productivity: Empirical Insights from China. J. Clean. Prod. 2023, 382, 135131. [Google Scholar] [CrossRef]
- McGuirk, H.; Lenihan, H.; Hart, M. Measuring the Impact of Innovative Human Capital on Small Firms’ Propensity to Innovate. Res. Policy 2015, 44, 965–976. [Google Scholar] [CrossRef]
- Xu, Y.; Li, A. The Relationship between Innovative Human Capital and Interprovincial Economic Growth Based on Panel Data Model and Spatial Econometrics. J. Comput. Appl. Math. 2020, 365, 112381. [Google Scholar] [CrossRef]
- Hang, X.; You, J. The Heterogeneous Impacts of Human Capital on Green Total Factor Productivity: Regional Diversity Perspective. Front. Environ. Sci. 2021, 9, 713562. [Google Scholar] [CrossRef]
- Mannasoo, K.; Hein, H.; Ruubel, R. The Contributions of Human Capital, R&D Spending and Convergence to Total Factor Productivity Growth. Reg. Stud. 2018, 52, 1598–1611. [Google Scholar] [CrossRef]
- Cheng, C.; Yu, X.; Hu, H.; Su, Z.; Zhang, S. Measurement of China’s Green Total Factor Productivity Introducing Human Capital Composition. Int. J. Environ. Res. Public Health 2022, 19, 13563. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Sun, C.; Wang, S.; Zhang, Z.; Zou, W. Going Green or Going Away? A Spatial Empirical Examination of the Relationship between Environmental Regulations, Biased Technological Progress, and Green Total Factor Productivity. Int. J. Environ. Res. Public Health 2018, 15, 1917. [Google Scholar] [CrossRef] [PubMed]
- Jin, W.; Gao, S.; Pan, S. Research on the Impact Mechanism of Environmental Regulation on Green Total Factor Productivity from the Perspective of Innovative Human Capital. Environ. Sci. Pollut. Res. 2022, 30, 352–370. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Deng, H. Green Total Factor Productivity in Chinese Cities: Measurement and Causal Analysis within a New Structural Economics Framework. J. Innov. Knowl. 2022, 7, 100235. [Google Scholar] [CrossRef]
- Wang, F.; Wu, M. Does Air Pollution Affect the Accumulation of Technological Innovative Human Capital? Empirical Evidence from China and India. J. Clean. Prod. 2021, 285, 124818. [Google Scholar] [CrossRef]
- Zhang, R.; Ying, W.; Wu, K.; Sun, H. The Impact of Innovative Human Capital Agglomeration on Urban Green Development Efficiency: Based on Panel Data of 278 Cities in China. Sustain. Cities Soc. 2024, 111, 105566. [Google Scholar] [CrossRef]
- Zhang, G.; Chen, C.; Cao, Y.; Xie, L. An Empirical Study on the Impact of Innovative Human Capital on Economic Growth from the Perspective of Stock and Level. Sci. Technol. Prog. Policy 2010, 27, 137–141. [Google Scholar]
- Liu, T.; Mao, Y.; Tian, X. The Role of Human Capital: Evidence from Corporate Innovation. J. Empir. Financ. 2023, 74, 101435. [Google Scholar] [CrossRef]
- Huang, S.-Z.; Chien, F.; Sadiq, M. A Gateway towards a Sustainable Environment in Emerging Countries: The Nexus between Green Energy and Human Capital. Ekon. Istraz. 2022, 35, 4159–4176. [Google Scholar] [CrossRef]
- Sarkodie, S.A.; Adams, S.; Owusu, P.A.; Leirvik, T.; Ozturk, I. Mitigating Degradation and Emissions in China: The Role of Environmental Sustainability, Human Capital and Renewable Energy. Sci. Total Environ. 2020, 719, 137530. [Google Scholar] [CrossRef]
- Yao, H.; Gu, X.; Yu, Q. Impact of Graduate Student Expansion and Innovative Human Capital on Green Total Factor Productivity. Sustainability 2023, 15, 1721. [Google Scholar] [CrossRef]
- Feng, F.; Zhang, S. The Measurement of China’s Provincial Green Total Factor Productivity Based on DEA Method: Does the Choice of DEA Model Make Difference. Acta Sci. Nat. Univ. Pekin. 2017, 53, 151–159. [Google Scholar]
- Zhang, X.; Li, R.; Zhang, J. Understanding the Green Total Factor Productivity of Manufacturing Industry in China: Analysis Based on the Super-SBM Model with Undesirable Outputs. Sustainability 2022, 14, 9310. [Google Scholar] [CrossRef]
- Zhong, S.; Fang, Y. The Impact of Electricity Consumption on Green Total Factor Productivity: Evidence from Chinese Provinces. J. Knowl. Econ. 2024. [Google Scholar] [CrossRef]
- Wang, C.; Wang, L. Green Credit and Industrial Green Total Factor Productivity: The Impact Mechanism and Threshold Effect Tests. J. Environ. Manag. 2023, 331, 117266. [Google Scholar] [CrossRef]
- Niu, B. Government Environmental Protection Expenditure and National ESG Performance: Global Evidence. Innov. Green Dev. 2024, 3, 100117. [Google Scholar] [CrossRef]
- Wang, C.; Wang, J.; Ai, W. Do Urbanization, Environmental Regulation and GDP Affect Agricultural Land Use Efficiency? Implications for Just Transition. Environ. Impact Assess. Rev. 2024, 105, 107421. [Google Scholar] [CrossRef]
- Li, L.; Du, F. The Impact of Postgraduate Education on Economic Growth in China: An Empirical Analysis on a Provincial Panel Data from 1996 to 2016. Tsing Hua J. Educ. 2019, 56–65. [Google Scholar]
- Tan, R.; Pan, L.; Xu, M.; He, X. Transportation Infrastructure, Economic Agglomeration and Non-Linearities of Green Total Factor Productivity Growth in China: Evidence from Partially Linear Functional Coefficient Model. Transp. Policy 2022, 129, 1–13. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, Z.; Geng, S. How Do Environmental Regulation and Foreign Investment Behavior Affect Green Productivity Growth in the Industrial Sector? An Empirical Test Based on Chinese Provincial Panel Data. J. Environ. Manag. 2021, 287, 112282. [Google Scholar] [CrossRef]
- Anselin, L.; Le Gallo, J.; Jayet, H. Spatial Panel Econometrics; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- LeSage, J.P.; Pace, R.K. Introduction to Spatial Econometrics; Chapman & Hall CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Islam, R.; Ang, J.; Madsen, J. Quality-Adjusted Human Capital and Productivity Growth. Econ. Inq. 2014, 52, 757–777. [Google Scholar] [CrossRef]

| Items | Indexes | Specific Indexes | Unit | Indicator Attribute |
|---|---|---|---|---|
| Input | Labor input | Number of employed personnel in each province at the end of the year | 10,000 persons | Positive |
| Capital input | Fixed capital stock | 100 million Yuan | Positive | |
| Energy input | Energy consumption of provinces, municipalities and autonomous regions | 10,000 tons of standard coal | Positive | |
| Output | Economic output | Real GDP | 100 million Yuan | Positive |
| Environmental output | COD discharge in industrial wastewater | Tons | Negative | |
| Industrial SO2 emissions | 10,000 tons | Negative |
| Variables | Sample Size | Mean | Standard Deviation | Minimum Value | Maximum Value |
|---|---|---|---|---|---|
| Employed personnel (10,000 people) | 450 | 2610.450 | 1727.572 | 290.420 | 7132.990 |
| Fixed capital stock (100 million Yuan) | 450 | 32,611.803 | 29,295.264 | 1291.540 | 158,047.050 |
| Energy consumption (10,000 tons of standard coal) | 450 | 12,800.585 | 8176.127 | 742.000 | 40,581.000 |
| Real GDP (100 million Yuan) | 450 | 12,732.286 | 11,910.422 | 460.350 | 64,866.199 |
| COD discharge in industrial wastewater (Tons) | 450 | 121,042.300 | 114,886.630 | 1463.000 | 975,456.000 |
| Industrial SO2 emission (10,000 tons) | 450 | 55.468 | 39.413 | 0.105 | 171.600 |
| Variable Names | Data Sources |
|---|---|
| IHC including IHCA and IHCQ | China Statistical Yearbook China Population and Employment Statistical Yearbook |
| The mechanism variable: TEC | China Science and Technology Statistical Yearbook Statistical yearbooks of various provinces, autonomous regions, and municipalities |
| Control variable: FDI | China Trade and External Economic Statistical Yearbook |
| Control variables: GOV, URB, EX | China Statistical Yearbook Website of National Bureau of Statistics |
| Control variable: INFRA | Statistical yearbooks of various provinces, autonomous regions, and municipalities EPS database |
| Control variable: REG | China Environmental Statistical Yearbook |
| Variables | Number of Observations | Mean Value | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|---|
| 450 | 1.435 | 0.825 | 0.307 | 4.757 | |
| 450 | 5.064 | 4.032 | 0.274 | 21.855 | |
| 450 | 0.946 | 0.867 | 0.054 | 10.314 | |
| 450 | 0.405 | 0.503 | 0.048 | 5.705 | |
| 450 | 0.215 | 0.096 | 0.079 | 0.627 | |
| 450 | 0.533 | 0.143 | 0.256 | 0.896 | |
| 450 | 0.313 | 0.382 | 0.017 | 1.722 | |
| 450 | 0.838 | 0.498 | 0.040 | 2.188 | |
| 450 | 694.426 | 540.612 | 95.073 | 4930.431 |
| Year | ||||
|---|---|---|---|---|
| Value | Value | |||
| 2005 | −0.04 | −0.232 | −0.079 | −0.551 |
| 2006 | −0.038 | −0.123 | −0.08 | −0.507 |
| 2007 | −0.036 | −0.056 | −0.074 | −0.419 |
| 2008 | −0.024 | 0.403 | −0.043 | −0.091 |
| 2009 | −0.019 | 0.523 | −0.038 | −0.03 |
| 2010 | −0.015 | 0.609 | −0.028 | 0.062 |
| 2011 | −0.014 | 0.718 | −0.019 | 0.167 |
| 2012 | −0.009 | 0.822 | −0.005 | 0.294 |
| 2013 | −0.012 | 0.747 | −0.001 | 0.335 |
| 2014 | −0.012 | 0.741 | 0.013 | 0.474 |
| 2015 | −0.011 | 0.770 | 0.023 | 0.563 |
| 2016 | 0.038 ** | 2.088 | 0.108 * | 1.534 |
| 2017 | 0.033 ** | 1.884 | 0.103 * | 1.660 |
| 2018 | 0.034 ** | 1.893 | 0.117 * | 1.662 |
| Variables | ||||
|---|---|---|---|---|
| 0.051 *** (0.01) | / | 0.055 *** (0.011) | / | |
| / | 0.071 ** (0.029) | / | 0.061 ** (0.03) | |
| 0.037 (0.044) | 0.086 * (0.045) | 0.066 (0.045) | 0.107 ** (0.046) | |
| −0.072 (0.573) | −0.833 (0.558) | −0.100 (0.557) | −0.921 * (0.543) | |
| 0.075 (0.707) | −0.635 (0.738) | 0.967 (0.698) | 0.692 (0.705) | |
| −53.767 *** (15.618) | −70.708 *** (15.472) | −60.948 *** (15.886) | −79.103 *** (15.545) | |
| 0.569 *** (0.116) | 0.717 *** (0.119) | 0.572 *** (0.11) | 0.621 *** (0.113) | |
| 0.0001 *** (0.000) | 0.0002 *** (0.000) | 0.0002 *** (0.000) | 0.0002 *** (0.000) | |
| −3.150 *** (0.716) | −0.751 (0.495) | −0.982 ** (0.387) | −0.787 ** (0.319) | |
| −0.216 *** (0.041) | / | −0.166 *** (0.066) | / | |
| / | 0.076 (0.103) | / | 0.0211 (0.056) | |
| −0.249 (0.214) | 0.026 (0.209) | 0.057 (0.092) | −0.001 (0.094) | |
| −6.873 *** (2.083) | −4.271 ** (2.060) | −3.459 *** (0.995) | −2.382 ** (0.981) | |
| 14.482 *** (2.470) | 6.497 *** (1.401) | 4.924 ** (1.141) | 4.493 *** (0.907) | |
| −1.747 *** (0.604) | −0.441 (0.526) | −0.501 (0.321) | −0.136 (0.288) | |
| −0.829 *** (0.204) | −0.812 *** (0.214) | −0.633 *** (0.154) | −0.727 *** (0.163) | |
| −0.001 *** (0.0001) | −0.0001 (0.0002) | −0.0006 (0.0001) | −0.0001 (0.0001) | |
| 0.311 *** (0.108) | 0.177 *** (0.061) | 0.252 ** (0.113) | 0.164 *** (0.061) | |
| 0.077 *** (0.005) | 0.083 *** (0.006) | 0.083 *** (0.006) | 0.087 *** (0.006) | |
| Log-likehood | 125.438 | 142.542 | 143.234 | 155.815 |
| LR test Spatial lag p Value | 0.001 | 0.001 | 0.001 | 0.001 |
| LR test Spatial error p Value | 0.003 | 0.002 | 0.002 | 0.002 |
| Hausman test p Value | 0.000 | 0.000 | 0.000 | 0.000 |
| R2 | 0.621 | 0.593 | 0.596 | 0.572 |
| Sample size | 450 | 450 | 450 | 450 |
| Variables | ||||
|---|---|---|---|---|
| −0.090 (0.062) | −0.084 (0.0629) | / | / | |
| / | / | −1.116 *** (0.209) | −1.076 *** (0.216) | |
| 0.011 ** (0.005) | 0.011 ** (0.005) | / | / | |
| / | / | 0.109 *** (0.020) | 0.105 *** (0.196) | |
| 0.097 * (0.005) | 0.138 *** (0.051) | 0.007 (0.06) | 0.022 (0.055) | |
| 0.046 (0.427) | 0.065 (0.044) | 0.633 (0.434) | 0.088 ** (0.044) | |
| −0.355 (0.0427) | −0.001 (0.560) | −0.05 (0.558) | −0.260 (0.548) | |
| −0.422 (0.752) | 0.153 (0.733) | −0.886 (0.741) | 0.319 (0.728) | |
| −0.447 *** (0.161) | −0.464 *** (0.163) | −0.333 ** (0.164) | −0.407 *** (0.166) | |
| 0.491 *** (0.117) | 0.432 *** (0.113) | 0.637 *** (0.118) | 0.538 *** (0.112) | |
| 0.000 *** (0.001) | 0.000 *** (0.000) | 0.000 *** (0.000) | 0.000 *** (0.000) | |
| −6.105 *** (1.110) | −1.647 (0.518) | −0.1735 (1.142) | −0.525 (0.545) | |
| 0.723 *** (0.005) | 0.080 *** (0.006) | 0.077 *** (0.005) | 0.082 *** (0.006) | |
| 114.047 | 134.152 | 126.236 | 139.725 | |
| Hausman test p Value | 0.000 | 0.000 | 0.000 | 0.000 |
| R2 | 0.640 | 0.608 | 0.625 | 0.598 |
| Sample size | 450 | 450 | 450 | 450 |
| Effect | Variables | ||||
|---|---|---|---|---|---|
| Spatial spillover effect | −0.287 *** (0.071) | −0.065 *** (0.019) | / | / | |
| / | / | 0.136 (0.139) | 0.042 (0.065) | ||
| −0.326 (0.321) | 0.088 (0.105) | 0.073 (0.274) | 0.025 (0.106) | ||
| −9.842 *** (2.949) | −4.145 *** (1.144) | −5.962 ** (2.632) | −2.983 *** (1.11) | ||
| 20.798 *** (3.983) | 6.007 *** (1.27) | 8.380 *** (1.464) | 5.370 *** (0.957) | ||
| −2.731 *** (91.13) | −0.718 ** (36.429) | −0.846 (70.38) | −0.322 (33.49) | ||
| −0.946 *** (0.293) | −0.631 *** (0.181) | −0.847 *** (0.28) | −0.735 *** (0.19) | ||
| −0.001 *** (0.000) | 0.0001 (0.0001) | 0.0001 (0.0001) | 0.0001 (0.0001) |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| 0.030 *** (0.008) | 0.031 *** (0.008) | / | / | |
| / | / | 0.032 * (0.020) | 0.026 (0.021) | |
| 0.0257 (0.030) | 0.046 (0.031) | 0.615 * (0.031) | 0.069 ** (0.031) | |
| −0.091 (0.426) | −0.078 (0.427) | −0.585 (0.420) | −0.613 (0.409) | |
| 1.368 ** (0.598) | 2.038 *** (0.597) | 0.623 (0.616) | 1.863 *** (0.585) | |
| −0.562 *** (0.115) | −0.642 *** (0.119) | −0.637 *** (0.116) | −0.741 *** (0.116) | |
| 0.199 * (0.103) | 0.303 *** (0.097) | 0.344 *** (0.105) | 0.335 ** (0.099) | |
| 0.000 * (0.000) | 0.000 ** (0.000) | 0.000 *** (0.000) | 0.000 ** (0.000) | |
| −0.200 *** (−0.031) | −0.038 *** (−0.014) | / | / | |
| / | / | −0.032 (−0.072) | −0.024 (−0.039) | |
| −0.017 (−0.143) | 0.066 (−0.063) | 0.240 (−0.148) | 0.037 (−0.066) | |
| −3.864 *** (−1.457) | −2.053 *** (−0.791) | −0.851 (−1.499) | −1.356 * (−0.753) | |
| 13.63 *** (−2.026) | 3.516 *** (−1.029) | 4.234 *** (−1.202) | 2.820 *** (−0.752) | |
| −80.43 * (−41.780) | −4.853 (−24.190) | 33.160 (−39.820) | 15.260 (−21.320) | |
| −0.615 *** (−0.160) | −0.584 *** (−0.133) | −0.611 *** (−0.173) | −0.583 *** (−0.138) | |
| −0.0005 *** (0.000) | 0.000 (0.000) | 0.000 (0.000) | 0.000 (0.000) | |
| 0.311 *** (0.107) | 0.177 *** (0.061) | 0.252 ** (0.113) | 0.164 *** (0.061) | |
| −3.616 *** (0.615) | −0.827 *** (0.343) | −1.128 *** (0.398) | −0.737 *** (0.268) | |
| 0.033 *** (0.002) | 0.037 *** (0.003) | 0.036 ** (0.003) | 0.038 *** (0.003) | |
| 35.130 | 12.108 | 14.843 | 4.9045 | |
| Hausman test p Value | 0.000 | 0.000 | 0.000 | 0.000 |
| R2 | 0.668 | 0.622 | 0.6329 | 0.6094 |
| Sample size | 390 | 390 | 390 | 390 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| 0.057 *** (2.82) | 0.045 * (2.01) | / | / | |
| / | / | 0.054 (1.23) | 0.087 * (1.92) | |
| 0.048 (0.74) | 0.052 (0.76) | 0.072 (1.13) | 0.063 (0.95) | |
| −1.691 (−0.81) | −4.283 (−1.64) | −3.819 * (−1.88) | −6.666 *** (−2.87) | |
| −1.155 (−0.80) | −1.482 (−0.99) | −0.881 (−0.59) | −1.066 (−0.75) | |
| −0.392 (−1.25) | −0.396 (−1.29) | −0.482 (−1.52) | −0.446 (−1.53) | |
| 0.301 (0.98) | 0.368 (1.28) | 0.306 (0.98) | 0.204 (0.71) | |
| 0.0001 (1.46) | 0.0002 * (1.94) | 0.0002 * (−0.11) | 0.0002 ** (2.24) | |
| 0.135 ** (0.056) | 0.0666 * (0.037) | / | / | |
| / | / | −0.110 (0.087) | −0.116 (0.074) | |
| 0.326 * (0.173) | 0.188 (0.147) | 0.340 * (0.178) | 0.244 (0.151) | |
| 6.576 (6.316) | 4.616 (4.373) | 12.39 * (6.421) | 3.937 (3.910) | |
| −13.23 *** (4.568) | −5.230 ** (2.362) | −0.635 (2.873) | 3.201 * (1.760) | |
| 100.2 (67.36) | 8.537 (45.00) | 47.22 (59.81) | −75.61 * (39.99) | |
| 0.663 (0.495) | 0.322 (0.405) | 0.136 (0.467) | 0.545 (0.395) | |
| 0.0002 (0.0001) | 0.0001 (0.0001) | −0.0001 (0.0001) | −0.0002 (0.0001) | |
| 0.395 *** (0.101) | 0.200 *** (0.075) | 0.413 ** (0.098) | 0.258 *** (0.073) | |
| 2.504 (1.30) | 0.879 (0.94) | −0.153 (−0.11) | 0.145 (0.22) | |
| 0.150 *** (8.49) | 0.169 *** (8.19) | 0.156 *** (8.56) | 0.169 *** (8.44) | |
| −100.4409 | −106.9532 | −104.3168 | −106.9758 | |
| Hausman test p Value | 0.000 | 0.000 | 0.000 | 0.000 |
| R2 | 0.5866 | 0.5556 | 0.5427 | 0.5369 |
| Sample size | 165 | 165 | 165 | 165 |
| Variables | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| 0.027 ** (0.011) | 0.038 *** (0.000) | / | / | |
| / | / | −0.013 (0.069) | −0.0375 (0.069) | |
| −0.305 * (0.186) | −0.098 (0.170) | −0.225 (0.187) | −0.419 (0.177) | |
| 0.955 ** (0.475) | 1.115 ** (0.454) | 0.359 (0.449) | 0.367 (0.441) | |
| 1.823 *** (0.694) | 2.204 *** (0.642) | 1.762 ** (0.702) | 2.019 *** (0.664) | |
| 0.948 *** (0.348) | 0.931 *** (0.325) | 1.152 *** (0.352) | 1.222 *** (0.345) | |
| 0.352 *** (0.096) | 0.266 *** (0.000) | 0.392 *** (0.097) | 0.352 *** (0.092) | |
| 0.001 *** (0.000) | 0.001 *** (0.000) | 0.001 ** (0.000) | 0.001 *** (0.000) | |
| −0.086 ** (−0.037) | −0.067 *** (−0.018) | / | / | |
| / | / | 0.441 ** (−0.203) | 0.086 (−0.134) | |
| −0.199 (−0.491) | 0.419 (−0.274) | −0.307 (−0.498) | 0.291 (−0.286) | |
| −3.84 *** (−1.325) | −1.725 ** (−0.741) | −3.468 ** (−1.348) | −1.401 * (−0.756) | |
| 5.586 *** (−1.988) | 1.058 (−0.982) | 2.759 ** (−1.257) | 0.834 (−0.829) | |
| −188.1 * (−108.000) | −17.330 (−52.280) | −224.7 ** (−112.500) | −95.92 * (−55.100) | |
| −0.798 *** (−0.198) | −0.497 *** (−0.119) | −0.806 *** (−0.187) | −0.548 *** (−0.126) | |
| 0.000 (0.000) | −0.0004 * (0.000) | 0.000 (0.000) | 0.000 (0.000) | |
| 0.220 * (0.129) | 0.352 *** (0.063) | 0.129 (0.137) | 0.271 *** (0.067) | |
| −0.981 ** (0.446) | −0.655 *** (0.245) | −0.062 (0.240) | −0.334 * (0.192) | |
| 0.030 *** (0.003) | 0.027 *** (0.002) | 0.030 *** (0.003) | 0.030 *** (0.003) | |
| 57.827 | 63.757 | 54.711 | 53.974 | |
| Hausman test p Value | 0.000 | 0.000 | 0.000 | 0.000 |
| R2 | 0.679 | 0.671 | 0.674 | 0.656 |
| Sample size | 285 | 285 | 285 | 285 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X. The Spatial Impact of Innovative Human Capital on Green Total Factor Productivity in Chinese Regions Based on Quantity and Quality Dimensions. Sustainability 2024, 16, 9358. https://doi.org/10.3390/su16219358
Lin X. The Spatial Impact of Innovative Human Capital on Green Total Factor Productivity in Chinese Regions Based on Quantity and Quality Dimensions. Sustainability. 2024; 16(21):9358. https://doi.org/10.3390/su16219358
Chicago/Turabian StyleLin, Xi. 2024. "The Spatial Impact of Innovative Human Capital on Green Total Factor Productivity in Chinese Regions Based on Quantity and Quality Dimensions" Sustainability 16, no. 21: 9358. https://doi.org/10.3390/su16219358
APA StyleLin, X. (2024). The Spatial Impact of Innovative Human Capital on Green Total Factor Productivity in Chinese Regions Based on Quantity and Quality Dimensions. Sustainability, 16(21), 9358. https://doi.org/10.3390/su16219358








