Enhancing Sustainability in Watershed Management: Spatiotemporal Assessment of Baseflow Alpha Factor in SWAT
Abstract
1. Introduction
2. Materials and Methods
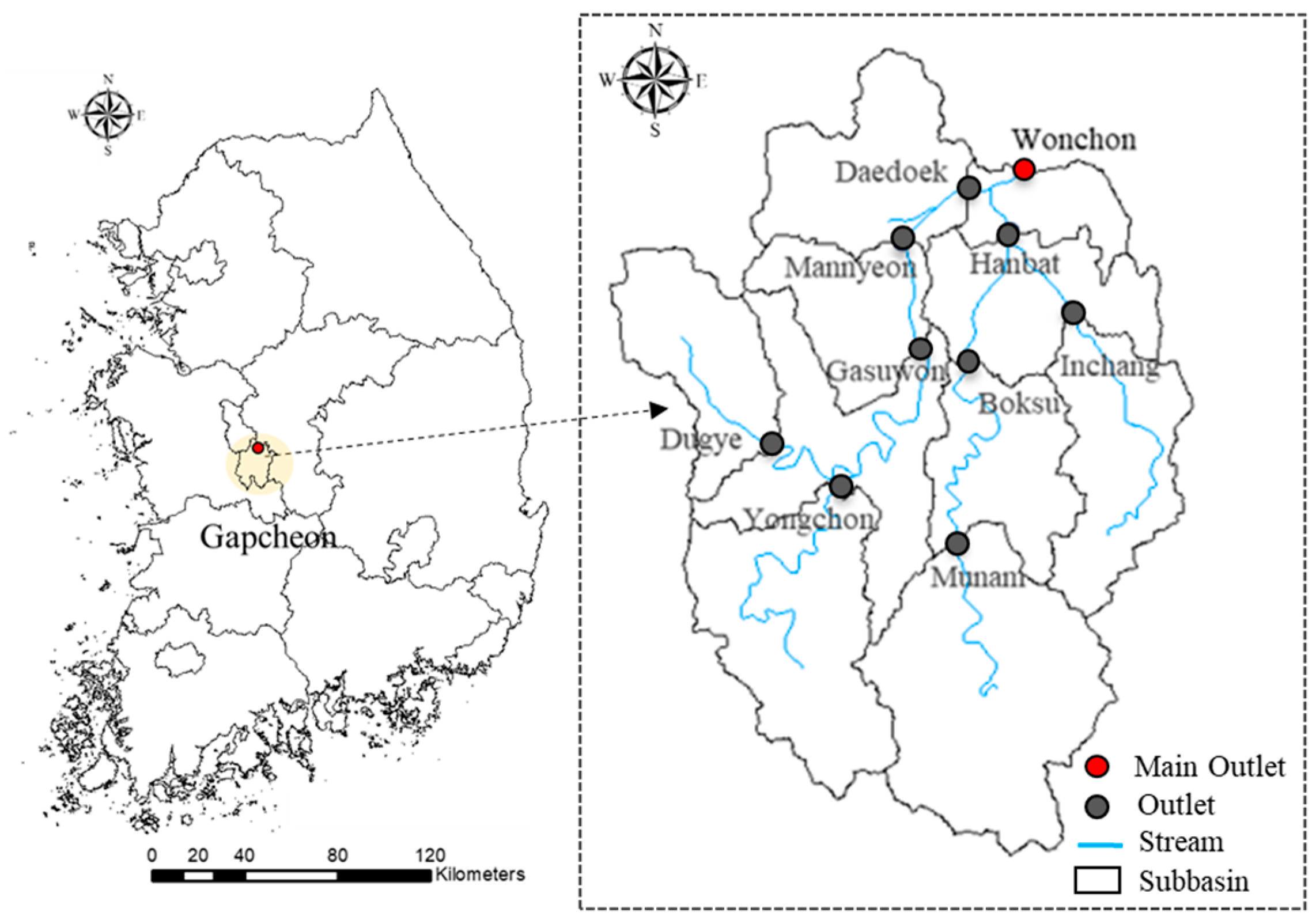
2.1. Study Watershed
2.2. SWAT Overview and Input Data
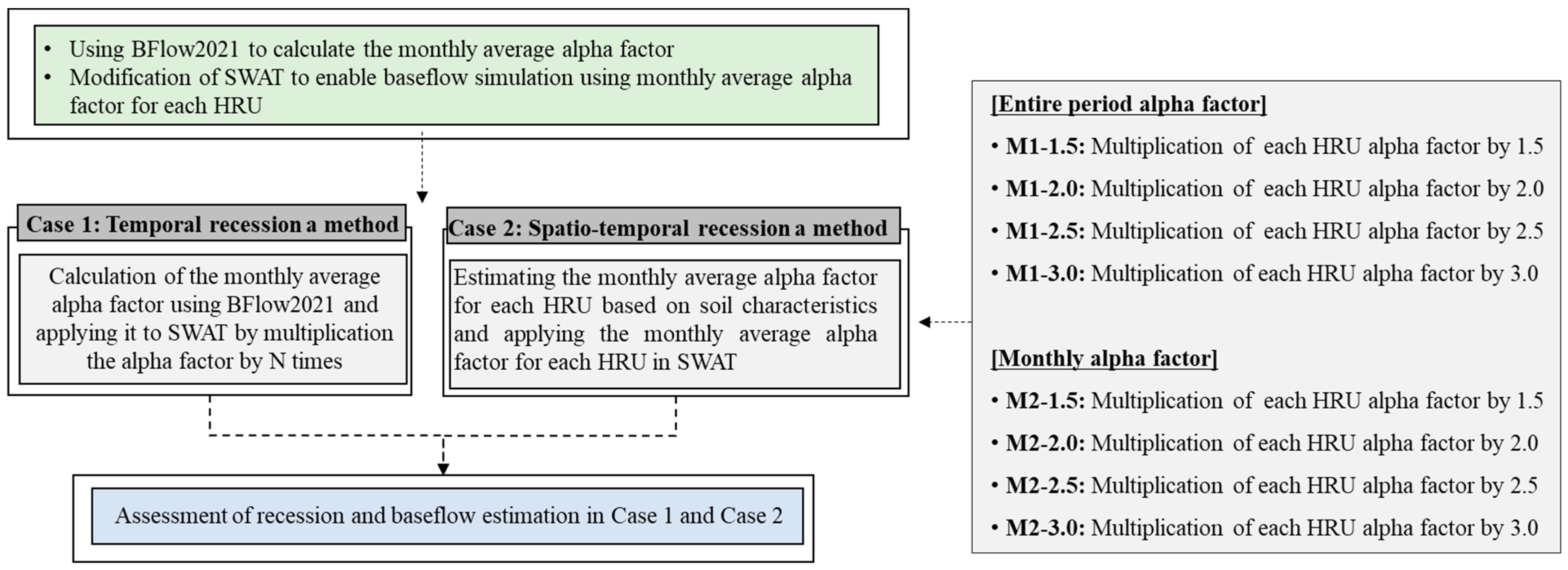
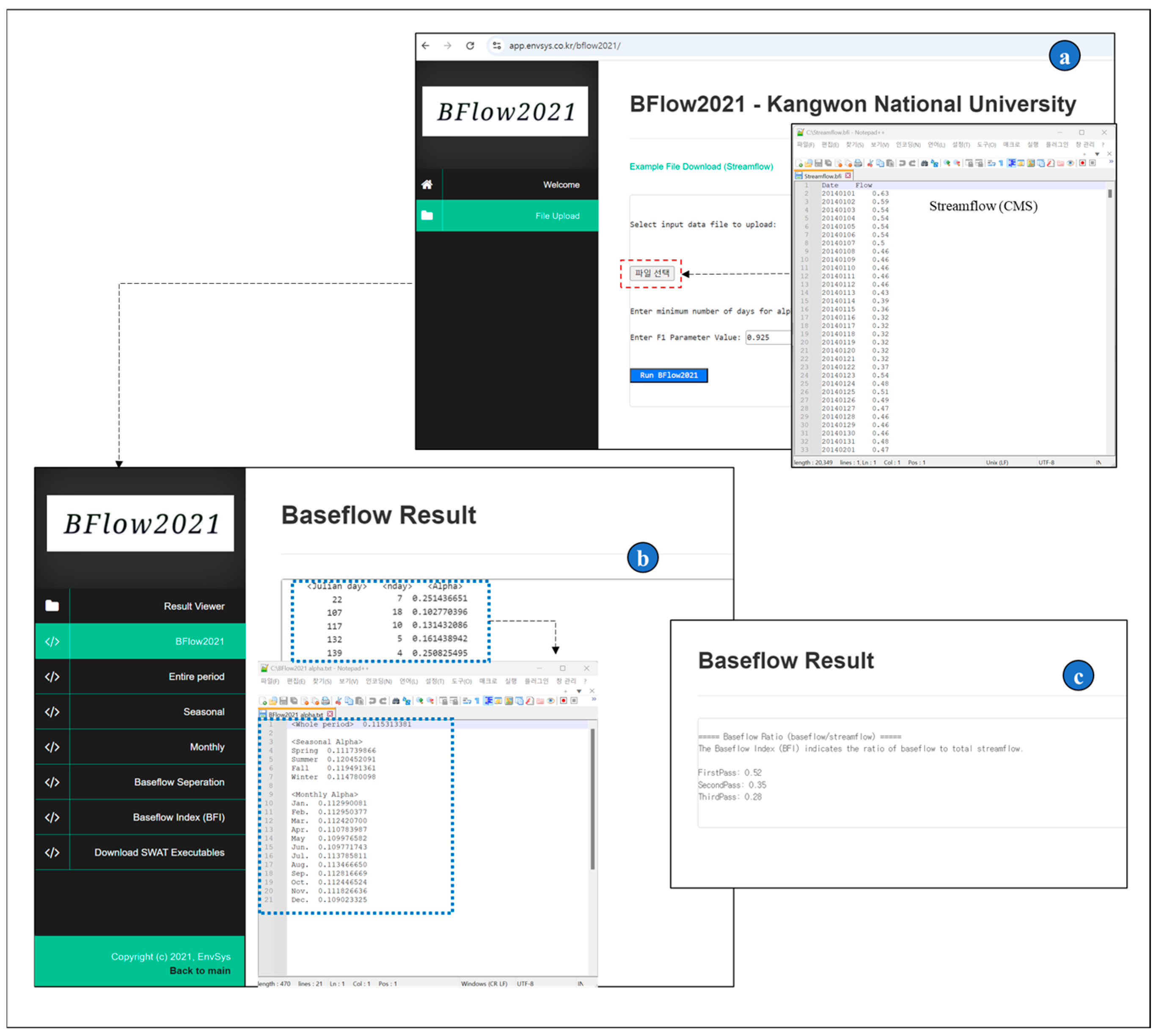
2.3. Calculating the Alpha Factor Considering Temporal and Spatial Variations
2.4. Validation of the Effect of the Spatial and Temporal Alpha Factors on Recession Simulation
2.5. Assessment of Recession and Baseflow Estimation in Case 1 and Case 2
3. Results and Discussion
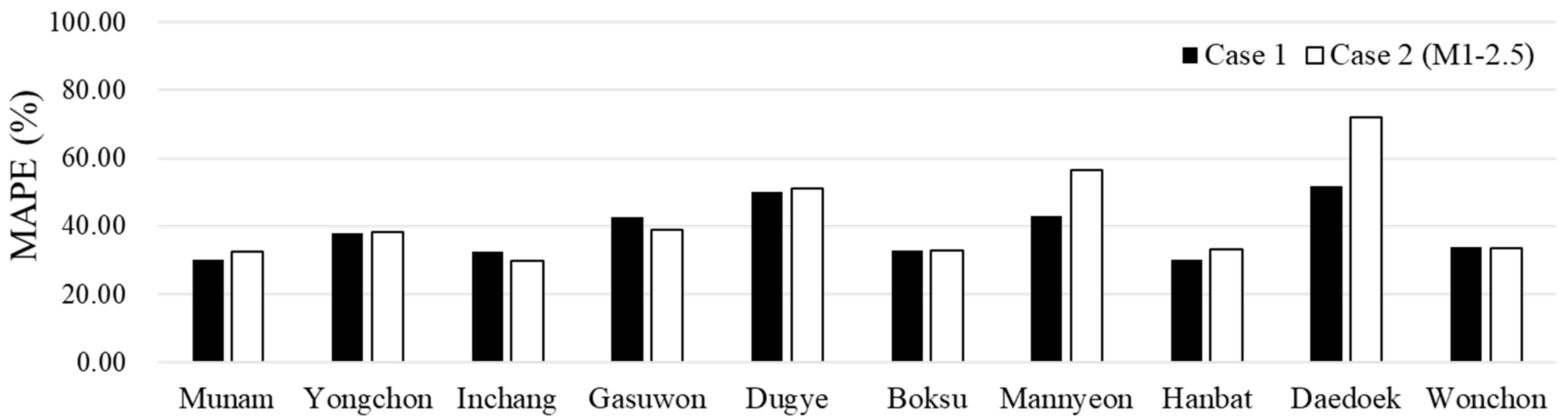
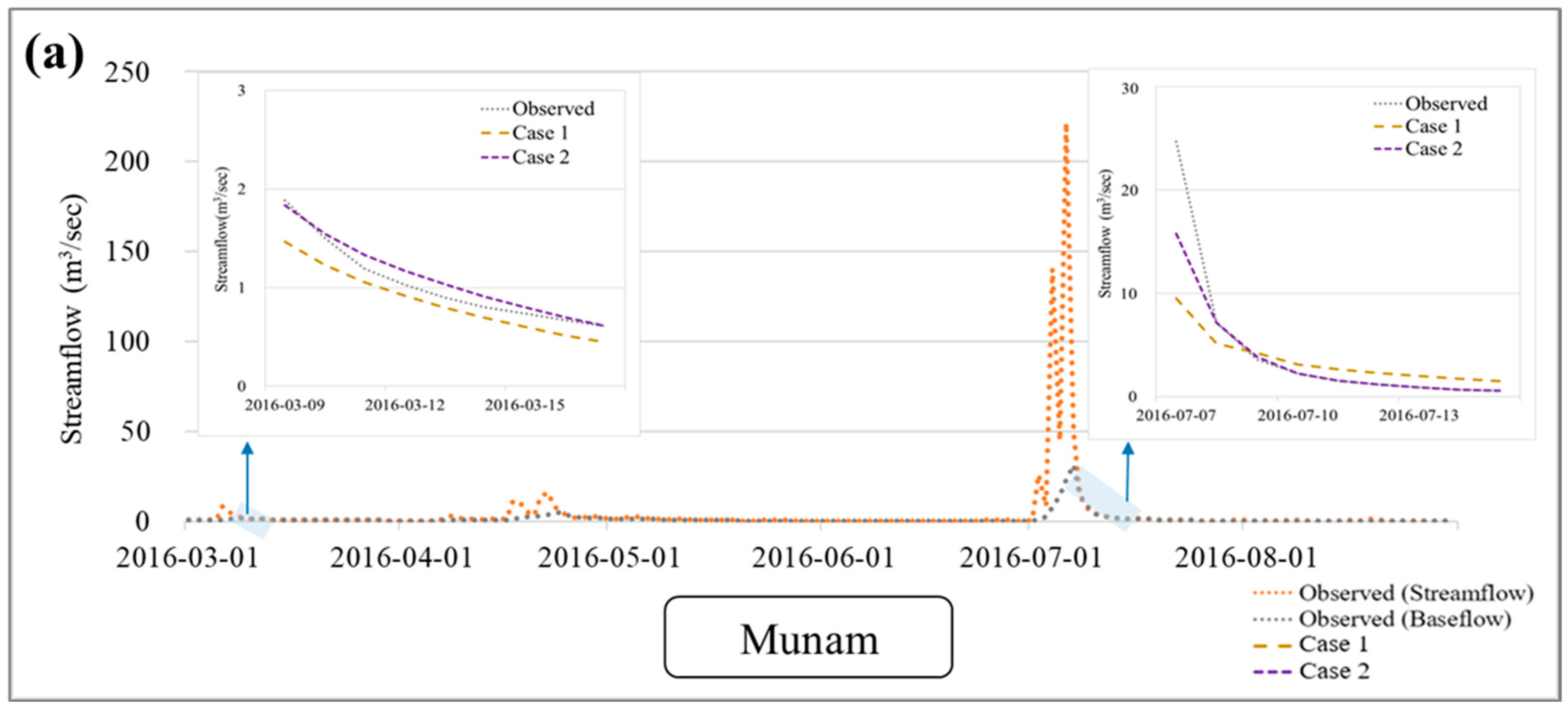
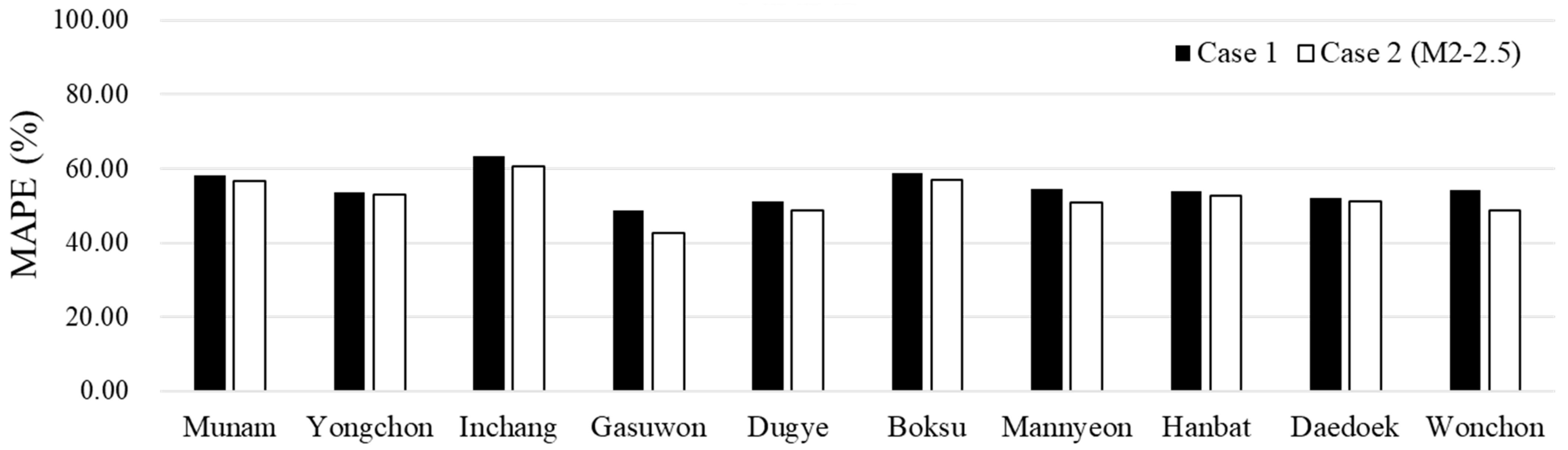
3.1. Comparison of Recession Estimation in Case 1 and Case2
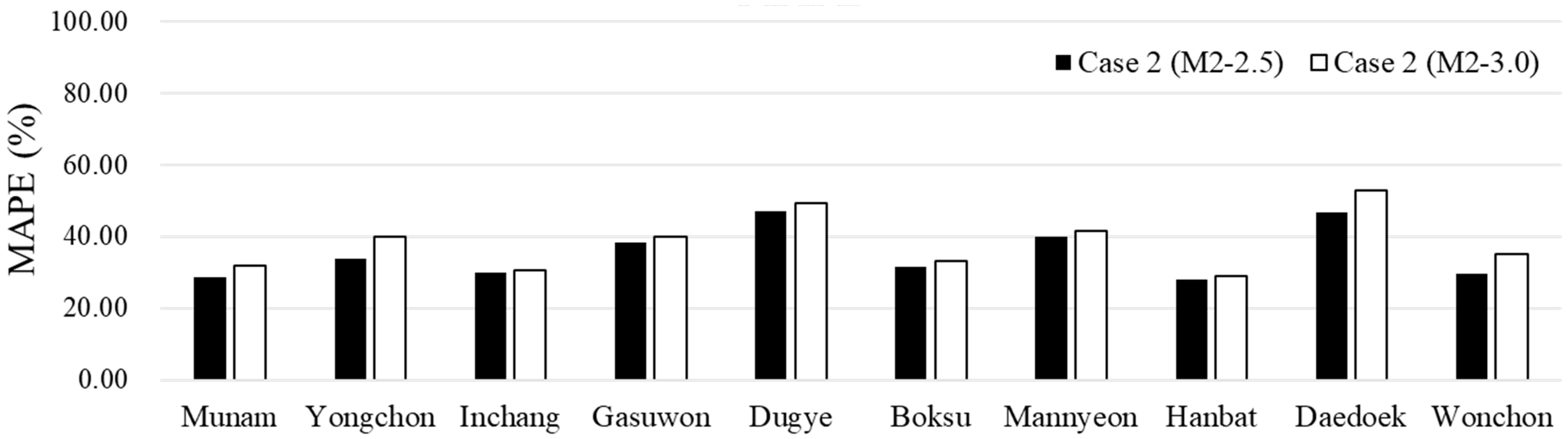
3.2. Comparison of Baseflow Estimation in Case 1 and Case 2
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, W.; Wang, S. Sustainable Stormwater Management for Different Types of Water-Scarce Cities: Environmental Policy Effect of Sponge City Projects in China. Sustainability 2024, 16, 5685. [Google Scholar] [CrossRef]
- Lee, G.J.; Park, K.W.; Jung, Y.H.; Jung, I.K.; Jung, K.W.; Jeon, J.H.; Lee, J.M.; Lim, K.J. Analysis of flood control effects of heightening of agricultural reservoir dam. J. Korean Soc. Agric. Eng. 2013, 55, 83–93. [Google Scholar]
- Miller, O.L.; Miller, M.P.; Longley, P.C.; Alder, J.R.; Bearup, L.A.; Pruitt, T.; Jones, D.K.; Putman, A.L.; Rumsey, C.A.; McKinney, T. How Will Baseflow Respond to Climate Change in the Upper Colorado River Basin? Geophys. Res. Lett. 2021, 48, e2021GL095085. [Google Scholar] [CrossRef]
- Wu, G.; Zhang, J.; Li, Y.; Liu, Y.; Ren, H.; Yang, M. Revealing Temporal Variation of Baseflow and Its Underlying Causes in the Source Region of the Yangtze River (China). Hydrol. Res. 2024, 55, 392–411. [Google Scholar] [CrossRef]
- Bicknell, B.R.; Imhoff, J.C.; Kittle, J.L., Jr.; Donigian, A.S., Jr.; Johanson, R.C. Hydrological Simulation Program—FORTRAN, User’s Manual for Version 11; U.S. Environmental Protection Agency, National Exposure Research Laboratory: Athens, GA, USA, 1997. [Google Scholar]
- Gironás, J.; Roesner, L.A.; Rossman, L.A.; Davis, J. A new applications manual for the Storm Water Management Model(SWMM). Environ. Model. Softw. 2010, 25, 813–814. [Google Scholar] [CrossRef]
- Tufekcioglu, M.; Yavuz, M.; Zaimes, G.N.; Dinc, M.; Koutalakis, P.; Tufekcioglu, A. Application of Soil Water Assessment Tool (SWAT) to suppress wildfire at Bayam Forest, Turkey. J. Environ. Biol. 2017, 38, 719–726. [Google Scholar] [CrossRef]
- Koutalakis, P.; Vlachopoulou, A.; Emmanouloudis, D.; Zaimes, G.N. Simulation of torrent discharge using SWAT and evaluation by field survey in Thasos Island. J. Eng. Sci. Technol. Rev. 2017, 10, 7–10. [Google Scholar] [CrossRef]
- Koutalakis, P.; Zaimes, G.N.; Loannou, K.; Lakovoglou, V. Application of the SWAT model on torrents of the Menoikio, Greece. Fresenius Environ. Bull. 2017, 26, 1210–1215. [Google Scholar]
- Pushpalatha, R.; Perrin, C.; Le Moine, N.; Andréassian, V. A Review of Efficiency Criteria Suitable for Evaluating Low-Flow Simulations. Journal of Hydrology 2012, 420–421, 171–182. [Google Scholar] [CrossRef]
- Parra, V.; Arumí, J.L.; Muñoz, E. Identifying a Suitable Model for Low-Flow Simulation in Watersheds of South-Central Chile: A Study Based on a Sensitivity Analysis. Water 2019, 11, 1506. [Google Scholar] [CrossRef]
- Price, K.; Jackson, C.R.; Parker, A.J.; Reitan, T.; Dowd, J.; Cyterski, M. Effects of Watershed Land Use and Geomorphology on Stream Low Flows during Severe Drought Conditions in the Southern Blue Ridge Mountains, Georgia and North Carolina, United States. Water Resour. Res. 2011, 47, 1–19. [Google Scholar] [CrossRef]
- Lei, Y.; Jiang, X.; Geng, W.; Zhang, J.; Zhao, H.; Ren, L. The Variation Characteristics and Influencing Factors of Base Flow of the Hexi Inland Rivers. Atmosphere 2021, 12, 356. [Google Scholar] [CrossRef]
- Kang, H.; Hyun, Y.J.; Jun, S.M. Regional estimation of baseflow index in Korea and analysis of baseflow effects according to urbanization. J. Korea Water Resour. Assoc. 2019, 52, 97–105. [Google Scholar]
- Choi, S.-H.; Kim, S.-H.; Kim, K. Assessment for the Possibility of Water-Ecosystem Restoration Applying LID Techniques in the Deokjin Park Area, Jeonju City. Econ. Environ. Geol. 2015, 48, 477–490. [Google Scholar] [CrossRef]
- Lamichhane, M.; Phuyal, S.; Mahato, R.; Shrestha, A.; Pudasaini, U.; Lama, S.D.; Chapagain, A.R.; Mehan, S.; Neupane, D. Assessing Climate Change Impacts on Streamflow and Baseflow in the Karnali River Basin, Nepal: A CMIP6 Multi-Model Ensemble Approach Using SWAT and Web-Based Hydrograph Analysis Tool. Sustainability 2024, 16, 3262. [Google Scholar] [CrossRef]
- Biagi, K.M.; Ross, C.A.; Oswald, C.J.; Sorichetti, R.J.; Thomas, J.L.; Wellen, C.C. Novel Predictors Related to Hysteresis and Baseflow Improve Predictions of Watershed Nutrient Loads: An Example from Ontario’s Lower Great Lakes Basin. Sci. Total Environ. 2022, 826, 154023. [Google Scholar] [CrossRef]
- Cao, W.; Li, Q.; Xu, H.; Zhang, Z. Vegetation Dynamics Regulate Baseflow Seasonal Patterns of the Chaohe Watershed in North China. J. Hydrol. Reg. Stud. 2024, 53, 101797. [Google Scholar] [CrossRef]
- Anderson, M.G.; Burt, T.P. Interpretation of Recession Flow. J. Hydrol. 1980, 46, 89–101. [Google Scholar] [CrossRef]
- Rutledge, A. Computer Programs for Describing the Recession of Ground-Water Discharge and for Estimating Mean Ground-Water Recharge and Discharge from Streamflow Records: Update No. 98; U.S. Geological Survey: Reston, VA, USA, 1998. [Google Scholar]
- Arnold, J.G.; Allen, P.M. Automated Methods for Estimating Baseflow and Ground Water Recharge from Streamflow Records. JAWRA J. Am. Water Resour. Assoc. 1999, 35, 411–424. [Google Scholar] [CrossRef]
- Sloto, R.A.; Crouse, M.Y.; Eaton, G.P. HYSEP: A Computer Program for Streamflow Hydrograph Separation and Analysis; U.S. Geological Survey: Reston, VA, USA, 1996. [Google Scholar]
- Kyoung, J.L.; Engel, B.A.; Tang, Z.; Choi, J.; Kim, K.S.; Muthukrishnan, S.; Tripathy, D. Automated Web GIS Based Hydrograph Analysis Tool, WHAT. JAWRA J. Am. Water Resour. Assoc. 2005, 41, 1407–1416. [Google Scholar] [CrossRef]
- Luo, Z.; Shao, Q. A Modified Hydrologic Model for Examining the Capability of Global Gridded PET Products in Improving Hydrological Simulation Accuracy of Surface Runoff, Streamflow and Baseflow. J. Hydrol. 2022, 610, 127960. [Google Scholar] [CrossRef]
- Duan, H.; Li, L.; Kong, Z.; Ye, X. Combining the Digital Filtering Method with the SWAT Model to Simulate Spatiotemporal Variations of Baseflow in a Mountainous River Basin. J. Hydrol. Reg. Stud. 2024, 56, 101972. [Google Scholar] [CrossRef]
- Lee, J.; Kim, J.; Jang, W.S.; Lim, K.J.; Engel, B.A. Assessment of Baseflow Estimates Considering Recession Characteristics in SWAT. Water 2018, 10, 371. [Google Scholar] [CrossRef]
- Lee, J.; Park, M.; Min, J.H.; Na, E.H. Integrated Assessment of the Land Use Change and Climate Change Impact on Baseflow by Using Hydrologic Model. Sustainability 2023, 15, 12465. [Google Scholar] [CrossRef]
- Lee, J. Assessment of Baseflow Estimation Reflecting Spatio-Temporal Distribution of Alpha Factor in SWAT; Kangwon National University: Chuncheon, Republic of Korea, 2024. [Google Scholar]
- Arnold, J. Spatial Scale Variability in Model Development and Parameterization. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1992. [Google Scholar]
- Arnold, J.; Srinivasan, R.; Muttiah, R.; Williams, J. Large Area Hydrologic Modeling and Assessment, Part I: Model Development. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- Jiang, Z.; Lu, B.; Zhou, Z.; Zhao, Y. Comparison of Process-Driven SWAT Model and Data-Driven Machine Learning Techniques in Simulating Streamflow: A Case Study in the Fenhe River Basin. Sustainability 2024, 16, 6074. [Google Scholar] [CrossRef]
- Arnold, J.; Allen, P.; Bernhardt, G. A Comprehensive Surface-Groundwater Flow Model. J. Hydrol. 1993, 142, 47–69. [Google Scholar] [CrossRef]
- Ahiablame, L.; Chaubey, I.; Engel, B.; Cherkauer, K.; Merwade, V. Estimation of Annual Baseflow at Ungauged Sites in Indiana USA. J. Hydrol. 2013, 476, 13–27. [Google Scholar] [CrossRef]
- Rumsey, C.A.; Miller, M.P.; Susong, D.D.; Tillman, F.D.; Anning, D.W. Regional Scale Estimates of Baseflow and Factors Influencing Baseflow in the Upper Colorado River Basin. J. Hydrol. Reg. Stud. 2015, 4, 91–107. [Google Scholar] [CrossRef]
- Abbaspour, K.C. SWAT-CUP: SWAT Calibration and Uncertainty Programs—A User Manual. Eawag; Swiss Federal Institute of Aquatic Science and Technology: Dubendorf, Switzerland, 2015; pp. 1–100. [Google Scholar]
- Wei, C.; Dong, X.; Ma, Y.; Zhao, W.; Yu, D.; Tayyab, M.; Bo, H. Impacts of land use types, soil properties, and topography on baseflow recharge and prediction in an agricultural watershed. Land 2023, 12, 109. [Google Scholar] [CrossRef]
- Trotter, L.; Saft, M.; Peel, M.C.; Fowler, K.J.A. Recession constants are non-stationary: Impacts of multi-annual drought on catchment recession behaviour and storage dynamics. J. Hydrol. 2024, 630, 130707. [Google Scholar] [CrossRef]
- Arnold, J.G.; Muttiah, R.S.; Srinivasan, R.; Allen, P.M. Regional estimation of baseflow and groundwater recharge in the upper Mississippi river basin. J. Hydrol. 2000, 227, 21–40. [Google Scholar] [CrossRef]
- Zomlot, Z.; Verbeiren, B.; Huysmans, M.; Batelaan, O. Spatial distribution of groundwater recharge and baseflow: Assessment of controlling factors. J. Hydrol. Reg. Stud. 2015, 4, 349–368. [Google Scholar] [CrossRef]
- Jameel, Y.; Stahl, M.; Michael, H.; Bostick, B.C.; Steckler, M.S.; Schlosser, P.; Geen, A.V.; Harvey, C. Shift in groundwater recharge of the Bengal Basin from rainfall to surface water. Commun. Earth Environ. 2023, 4, 14. [Google Scholar] [CrossRef]
- Hong, S.Y.; Minasny, B.; Han, K.H.; Kim, Y. Lee; K. Predicting and mapping soil available water capacity in Korea. PeerJ 2013, 1, e71. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]


| Year | Annual Precipitation (mm) | Annual Temperature (°C) | |
|---|---|---|---|
| Maximum | Minimum | ||
| 2008 | 1037.6 | 24.7 | 2.1 |
| 2009 | 1090.4 | 25.0 | 2.5 |
| 2010 | 1419.7 | 24.7 | 1.3 |
| 2011 | 1943.4 | 23.4 | 2.4 |
| 2012 | 1409.5 | 24.2 | 2.3 |
| 2013 | 1120.2 | 25.9 | 2.0 |
| 2014 | 1117.7 | 24.8 | 3.1 |
| 2015 | 822.7 | 25.4 | 2.7 |
| 2016 | 1228.4 | 26.4 | 2.6 |
| 2017 | 1127.5 | 25.3 | 2.3 |
| Ave. | 1231.7 | 25.0 | 2.3 |
| Data Type | Name | Source |
|---|---|---|
| Meteorological data | Precipitation, wind speed, maximum and minimum temperature, relative humidity, and solar radiation | Korea Meteorological Administration (https://data.kma.go.kr/data/rmt/rmtList.do?code=400&pgmNo=570) (accessed on 15 October 2024) |
| Hydrological data | Daily streamflow | Water resource Management Information System (http://www.wamis.go.kr/wkw/flw_dubobsif.do) (accessed on 15 October 2024) |
| Spatial data | DEM | National Geographic Information Institute (https://www.ngii.go.kr/kor/content.do?sq=204) (accessed on 15 October 2024) |
| Land use | Korea Ministry of Environment (https://egis.me.go.kr/req/intro.do) (accessed on 15 October 2024) | |
| Soil type | Korea Rural Development Administration (https://soil.rda.go.kr/soil/index.jsp) (accessed on 15 October 2024) |
| Section | Method | Temporal Extent | Spatial Extent | Multiplier |
|---|---|---|---|---|
| Case 1 | Baseline | Monthly | Subbasin | 2.0–3.0 |
| Case 2 | M1–1.5 | Entire | HRU | 1.5 |
| M1–2.0 | Entire | HRU | 2.0 | |
| M1–2.5 | Entire | HRU | 2.5 | |
| M1–3.0 | Entire | HRU | 3.0 | |
| M2–1.5 | Monthly | HRU | 1.5 | |
| M2–2.0 | Monthly | HRU | 2.0 | |
| M2–2.5 | Monthly | HRU | 2.5 | |
| M2–3.0 | Monthly | HRU | 3.0 |
| Study Watershed | NSE | R2 | IOA | PBIAS (%) | MAPE (%) |
|---|---|---|---|---|---|
| Munam | 0.56 | 0.56 | 0.84 | 9.51 | 68.97 |
| Yongchon | 0.57 | 0.58 | 0.83 | 21.54 | 66.17 |
| Inchang | 0.56 | 0.57 | 0.82 | 9.66 | 72.51 |
| Gasuwon | 0.62 | 0.63 | 0.88 | −8.36 | 57.71 |
| Dugye | 0.73 | 0.78 | 0.93 | 35.26 | 65.47 |
| Boksu | 0.62 | 0.66 | 0.90 | −8.82 | 68.63 |
| Mannyeon | 0.64 | 0.66 | 0.86 | 7.25 | 65.16 |
| Hanbat | 0.58 | 0.57 | 0.86 | 12.92 | 63.02 |
| Daedoek | 0.57 | 0.64 | 0.83 | 43.98 | 76.63 |
| Wonchon | 0.53 | 0.54 | 0.84 | −0.63 | 67.32 |
| Study Watershed | NSE | R2 | IOA | PBIAS (%) | MAPE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 (M1–2.5) | Case 1 | Case 2 (M1–2.5) | Case 1 | Case 2 (M1–2.5) | Case 1 | Case 2 (M1–2.5) | Case 1 | Case 2 (M1–2.5) | |
| Munam | 0.58 | 0.58 | 0.70 | 0.74 | 0.82 | 0.81 | 23.22 | 22.75 | 30.22 | 32.38 |
| Yongchon | 0.61 | 0.58 | 0.66 | 0.68 | 0.86 | 0.84 | 20.27 | 22.11 | 37.98 | 38.24 |
| Inchang | 0.64 | 0.64 | 0.87 | 0.87 | 0.84 | 0.83 | 23.52 | 21.95 | 32.38 | 29.89 |
| Gasuwon | 0.63 | 0.73 | 0.71 | 0.79 | 0.88 | 0.91 | -28.19 | -17.07 | 42.65 | 38.96 |
| Dugye | 0.57 | 0.52 | 0.58 | 0.54 | 0.85 | 0.86 | -4.72 | 0.31 | 49.92 | 50.98 |
| Boksu | 0.66 | 0.64 | 0.86 | 0.86 | 0.85 | 0.83 | 19.01 | 18.92 | 32.94 | 32.73 |
| Mannyeon | 0.56 | 0.54 | 0.66 | 0.68 | 0.80 | 0.77 | -8.53 | -2.82 | 42.93 | 56.34 |
| Hanbat | 0.70 | 0.69 | 0.77 | 0.77 | 0.89 | 0.88 | 13.33 | 14.63 | 30.06 | 33.15 |
| Daedoek | 0.50 | 0.45 | 0.53 | 0.61 | 0.75 | 0.72 | -47.10 | -24.09 | 51.61 | 61.88 |
| Wonchon | 0.70 | 0.69 | 0.79 | 0.87 | 0.87 | 0.86 | -3.50 | -0.50 | 33.85 | 33.39 |
| Study Watershed | NSE | R2 | IOA | PBIAS (%) | MAPE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | |
| Munam | 0.58 | 0.58 | 0.70 | 0.72 | 0.82 | 0.82 | 23.22 | 23.16 | 30.22 | 28.66 |
| Yongchon | 0.61 | 0.61 | 0.66 | 0.70 | 0.86 | 0.85 | 20.27 | 17.00 | 37.98 | 33.68 |
| Inchang | 0.64 | 0.65 | 0.87 | 0.87 | 0.84 | 0.84 | 23.52 | 22.20 | 32.38 | 29.88 |
| Gasuwon | 0.63 | 0.69 | 0.71 | 0.76 | 0.88 | 0.90 | −28.19 | −22.62 | 42.65 | 38.51 |
| Dugye | 0.57 | 0.60 | 0.58 | 0.68 | 0.85 | 0.88 | −4.72 | −18.40 | 49.92 | 46.94 |
| Boksu | 0.66 | 0.66 | 0.86 | 0.86 | 0.85 | 0.85 | 19.01 | 18.31 | 32.94 | 31.69 |
| Mannyeon | 0.56 | 0.57 | 0.66 | 0.68 | 0.80 | 0.80 | −8.53 | −8.05 | 42.93 | 40.08 |
| Hanbat | 0.70 | 0.72 | 0.77 | 0.78 | 0.89 | 0.89 | 13.33 | 10.79 | 30.06 | 27.88 |
| Daedoek | 0.50 | 0.53 | 0.53 | 0.53 | 0.75 | 0.75 | −47.10 | −36.78 | 51.61 | 46.88 |
| Wonchon | 0.70 | 0.74 | 0.79 | 0.84 | 0.87 | 0.90 | −3.50 | −8.47 | 33.85 | 29.48 |
| Study Watershed | NSE | R2 | IOA | PBIAS (%) | MAPE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| M2–2.5 | M2–3.0 | M2–2.5 | M2–3.0 | M2–2.5 | M2–3.0 | M2–2.5 | M2–3.0 | M2–2.5 | M2–3.0 | |
| Munam | 0.58 | 0.54 | 0.72 | 0.62 | 0.82 | 0.80 | 23.16 | 13.93 | 28.66 | 31.82 |
| Yongchon | 0.61 | 0.58 | 0.70 | 0.64 | 0.85 | 0.86 | 17.00 | 13.59 | 33.68 | 39.94 |
| Inchang | 0.65 | 0.59 | 0.87 | 0.69 | 0.84 | 0.83 | 22.20 | 16.28 | 29.88 | 30.75 |
| Gasuwon | 0.69 | 0.52 | 0.76 | 0.66 | 0.90 | 0.86 | −22.62 | −26.51 | 38.51 | 40.05 |
| Dugye | 0.60 | 0.52 | 0.68 | 0.56 | 0.88 | 0.77 | −18.40 | 6.30 | 46.94 | 49.41 |
| Boksu | 0.66 | 0.57 | 0.86 | 0.60 | 0.85 | 0.83 | 18.31 | 6.34 | 31.69 | 33.21 |
| Mannyeon | 0.57 | 0.63 | 0.68 | 0.73 | 0.80 | 0.84 | −8.05 | −21.04 | 40.08 | 41.57 |
| Hanbat | 0.72 | 0.52 | 0.78 | 0.53 | 0.89 | 0.84 | 10.79 | 8.77 | 27.88 | 29.12 |
| Daedoek | 0.53 | 0.50 | 0.53 | 0.68 | 0.75 | 0.79 | −36.78 | −55.47 | 46.88 | 52.94 |
| Wonchon | 0.74 | 0.65 | 0.84 | 0.70 | 0.90 | 0.87 | −8.47 | −10.32 | 29.48 | 35.17 |
| Study Watershed | NSE | R2 | IOA | PBIAS (%) | MAPE (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2 (M2–2.5) | Case 1 | Case 2(M2–2.5) | Case 1 | Case 2 (M2–2.5) | |
| Munam | 0.65 | 0.65 | 0.67 | 0.67 | 0.87 | 0.87 | 23.80 | 23.11 | 58.10 | 56.72 |
| Yongchon | 0.55 | 0.57 | 0.61 | 0.62 | 0.87 | 0.87 | 25.01 | 23.06 | 53.69 | 52.86 |
| Inchang | 0.64 | 0.64 | 0.68 | 0.68 | 0.88 | 0.89 | 31.31 | 31.12 | 63.35 | 60.68 |
| Gasuwon | 0.54 | 0.54 | 0.67 | 0.67 | 0.90 | 0.90 | −4.61 | −5.51 | 48.59 | 42.50 |
| Dugye | 0.53 | 0.54 | 0.57 | 0.57 | 0.85 | 0.86 | 17.49 | 17.44 | 51.31 | 57.06 |
| Boksu | 0.64 | 0.64 | 0.65 | 0.65 | 0.89 | 0.89 | 16.70 | 16.22 | 58.70 | 50.96 |
| Mannyeon | 0.62 | 0.61 | 0.63 | 0.62 | 0.88 | 0.88 | −0.41 | −1.13 | 54.64 | 52.77 |
| Hanbat | 0.53 | 0.54 | 0.60 | 0.60 | 0.87 | 0.87 | 27.32 | 27.14 | 53.78 | 51.10 |
| Daedoek | 0.52 | 0.52 | 0.54 | 0.54 | 0.83 | 0.83 | 20.93 | 20.07 | 52.07 | 51.10 |
| Wonchon | 0.67 | 0.68 | 0.67 | 0.68 | 0.89 | 0.90 | 4.80 | 1.41 | 54.26 | 48.69 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Han, J.; Lee, S.; Kim, J.; Na, E.H.; Engel, B.; Lim, K.J. Enhancing Sustainability in Watershed Management: Spatiotemporal Assessment of Baseflow Alpha Factor in SWAT. Sustainability 2024, 16, 9189. https://doi.org/10.3390/su16219189
Lee J, Han J, Lee S, Kim J, Na EH, Engel B, Lim KJ. Enhancing Sustainability in Watershed Management: Spatiotemporal Assessment of Baseflow Alpha Factor in SWAT. Sustainability. 2024; 16(21):9189. https://doi.org/10.3390/su16219189
Chicago/Turabian StyleLee, Jimin, Jeongho Han, Seoro Lee, Jonggun Kim, Eun Hye Na, Bernard Engel, and Kyoung Jae Lim. 2024. "Enhancing Sustainability in Watershed Management: Spatiotemporal Assessment of Baseflow Alpha Factor in SWAT" Sustainability 16, no. 21: 9189. https://doi.org/10.3390/su16219189
APA StyleLee, J., Han, J., Lee, S., Kim, J., Na, E. H., Engel, B., & Lim, K. J. (2024). Enhancing Sustainability in Watershed Management: Spatiotemporal Assessment of Baseflow Alpha Factor in SWAT. Sustainability, 16(21), 9189. https://doi.org/10.3390/su16219189









