Coupling and Coordination Analysis of High-Quality Agricultural Development and Rural Revitalization: Spatio-Temporal Evolution, Spatial Disparities, and Convergence
Abstract
1. Introduction
2. Theoretical Analysis
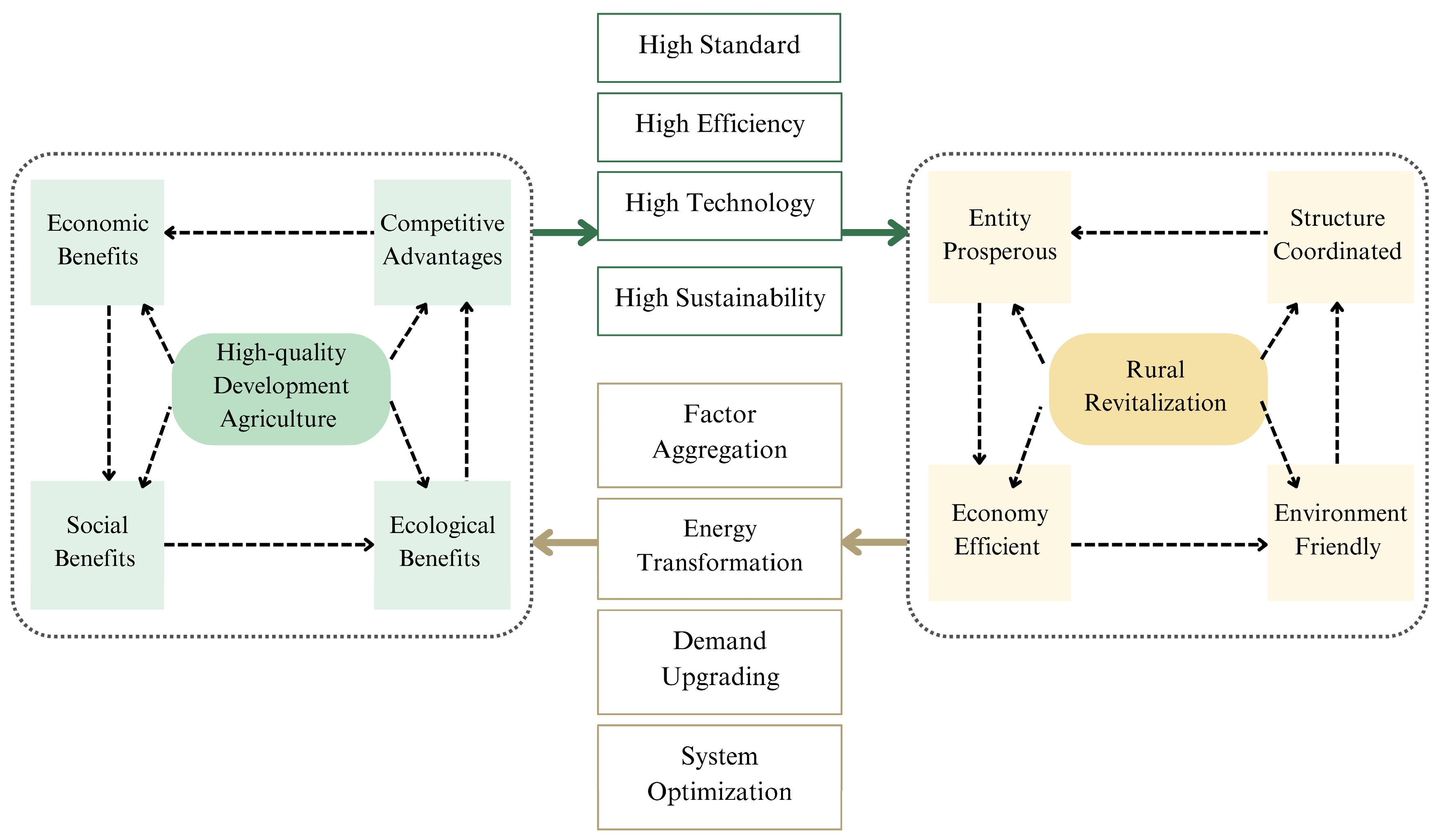
2.1. Connotations and Composition of Rural Revitalization
2.2. Connotations and Composition of HQAD
2.3. Mechanism of Mutual Reinforcement between HQAD and Rural Revitalization
3. Methodology
3.1. Improved AHP–Entropy Weight Method
3.1.1. Analytical Hierarchy Process (AHP)
3.1.2. Improved Entropy Method
3.1.3. Combined Weighted Model Based on the AHP and Improved Entropy
3.2. Coupling Coordination Degree Model
3.3. Kernel Density Estimation
3.4. Dagum Gini Coefficient
3.5. Convergence Model
3.5.1. σ Convergence Method
3.5.2. Spatial β Convergence Method
4. Spatiotemporal Evolutionary Characteristics of CCD
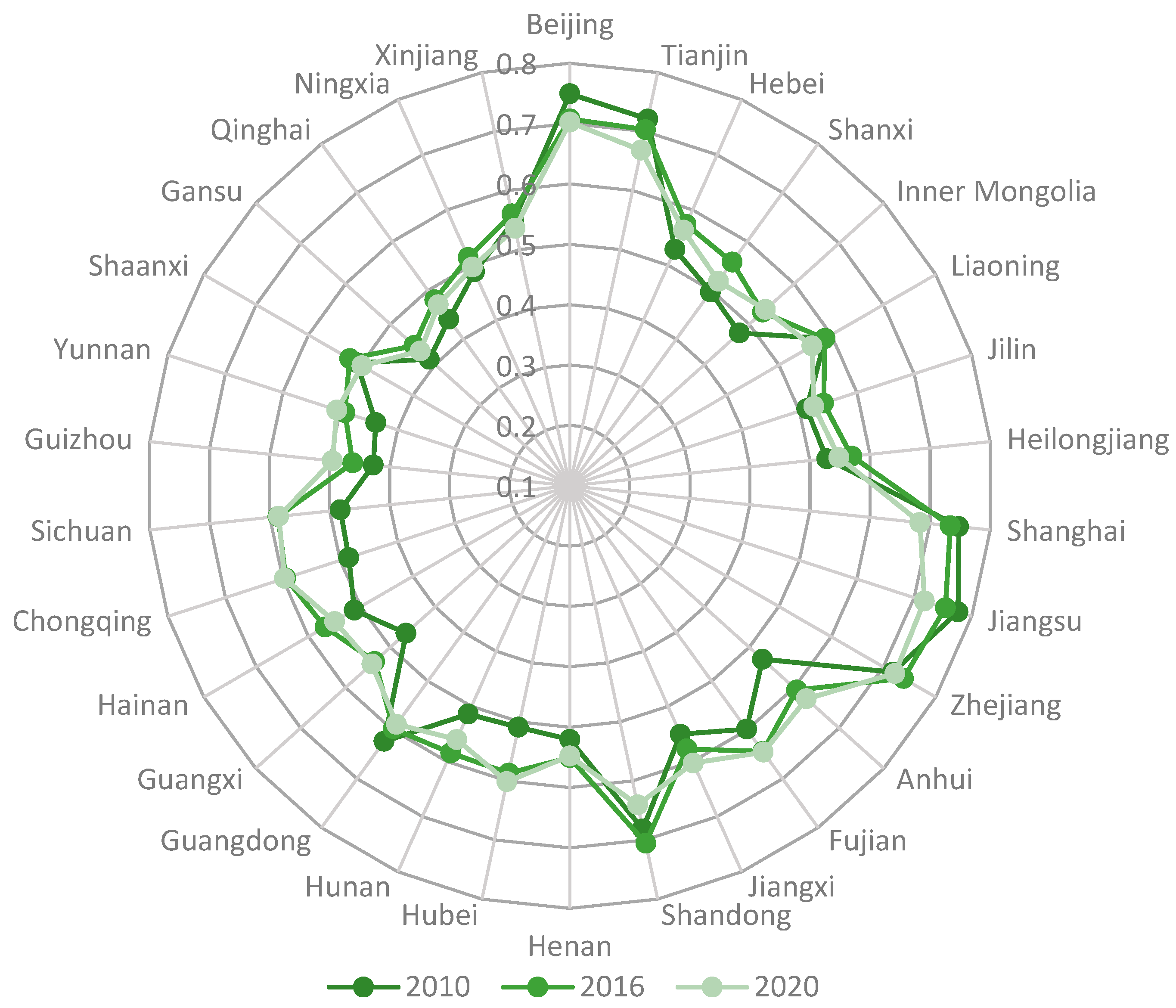
4.1. Temporal Evolution Characteristics of CCD
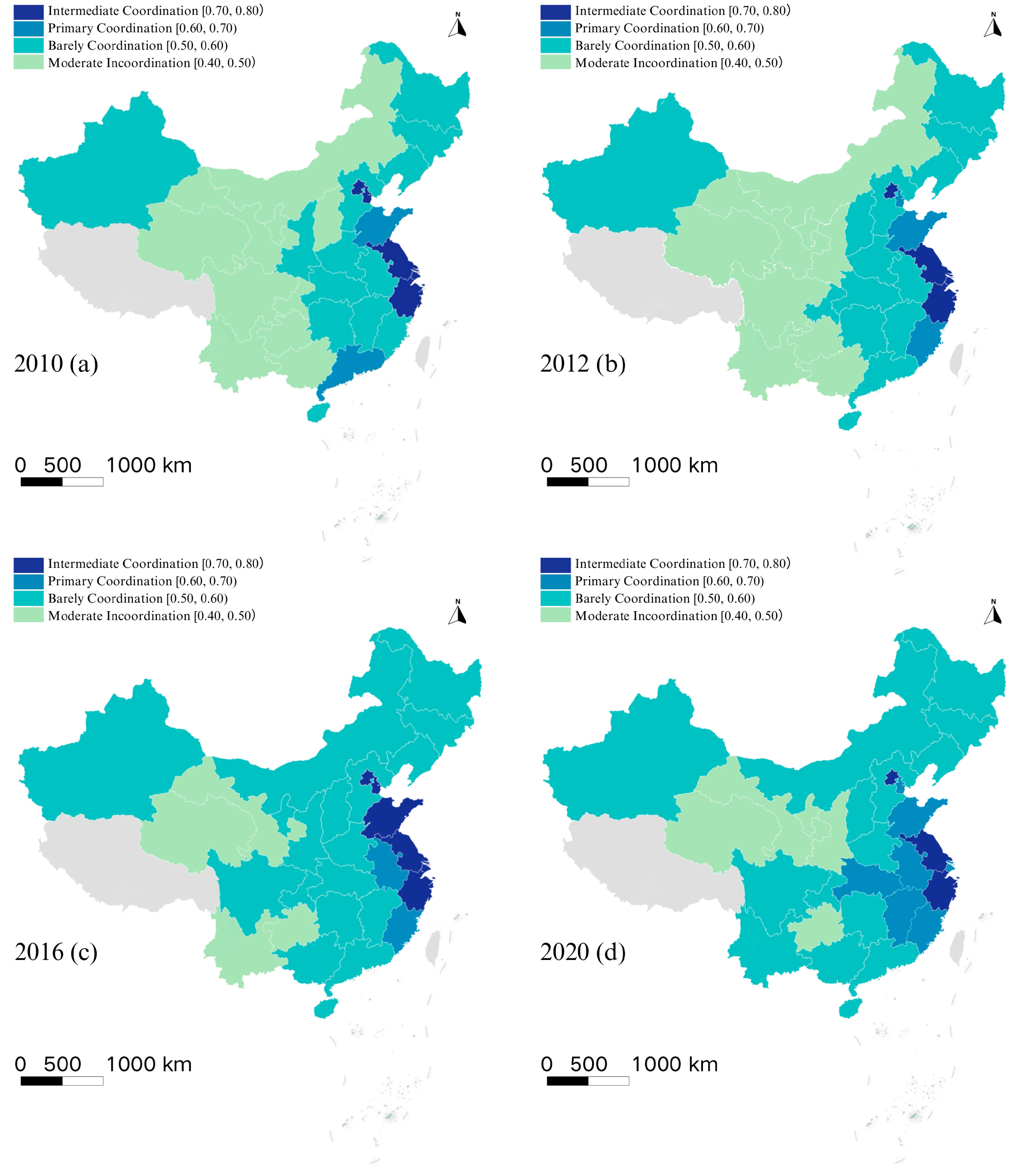
4.2. Spatial Evolutionary Characteristics of CCD
4.2.1. Evolutionary Trends of CCD
4.2.2. Spatial Differentiation of CCD
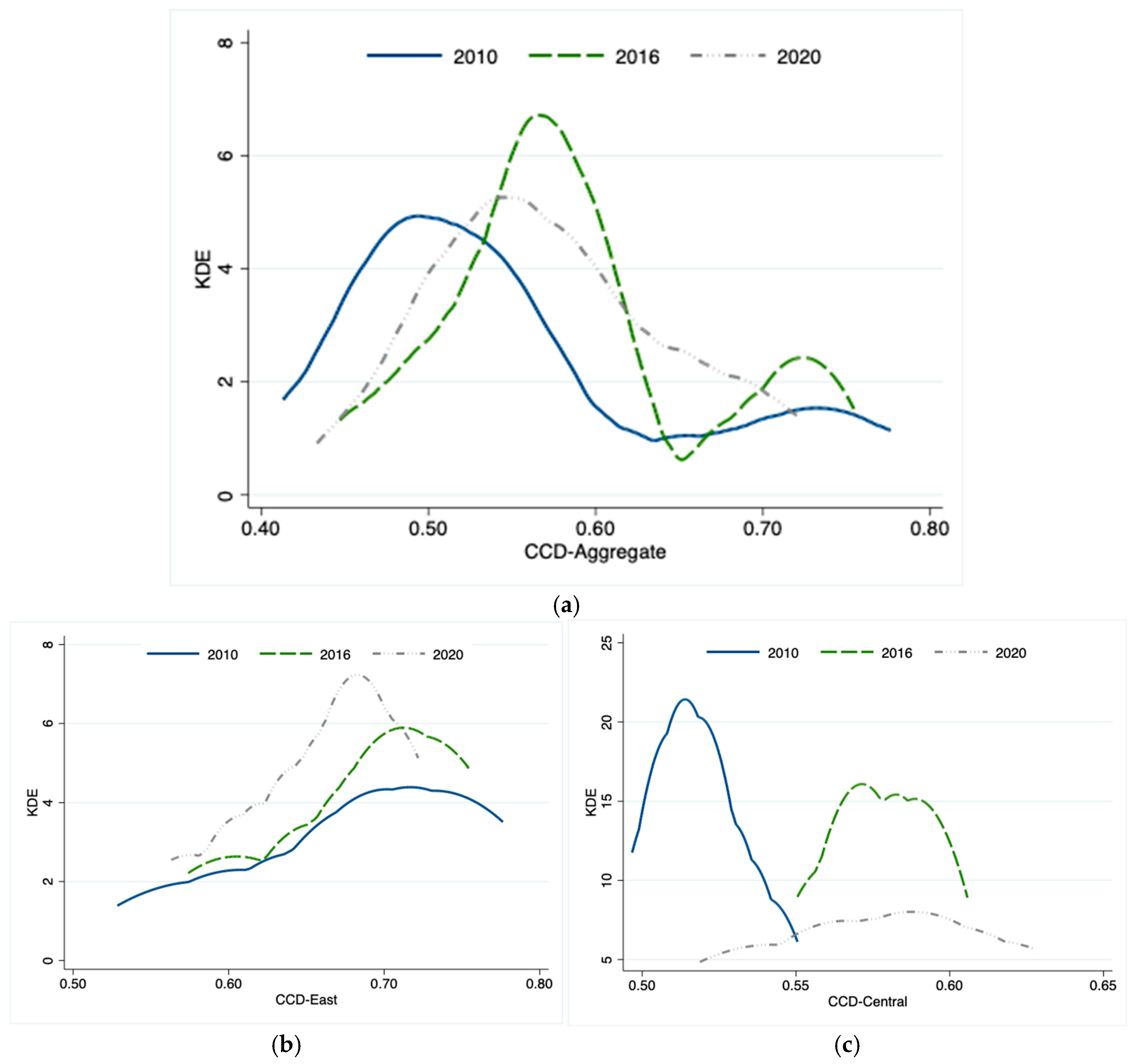
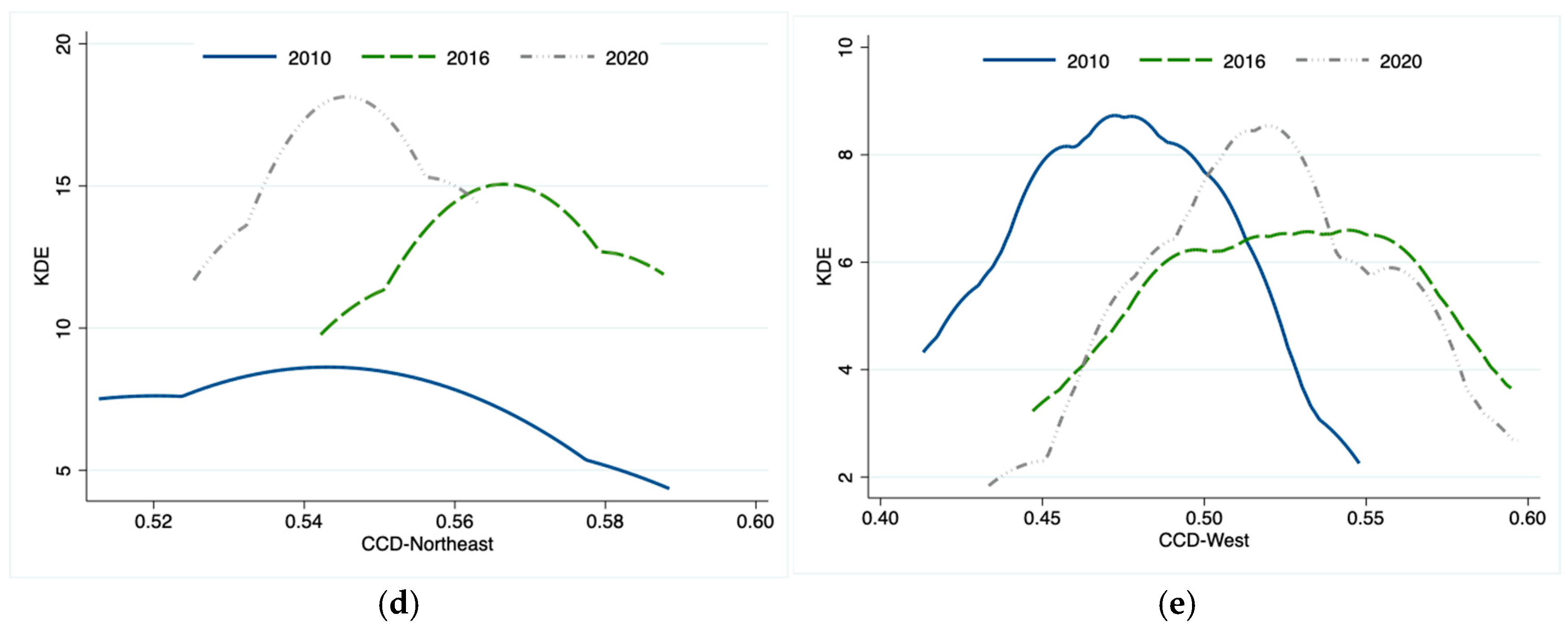
5. Kernel Density Analysis of CCD
6. Regional Disparities and Sources of CCD
6.1. Aggregate Regional Disparities and Intra-Region Disparities of CCD
6.2. Inter-Regional Disparities of CCD
6.3. Sources of Regional Disparities and Contributions of CCD
7. Convergence Analysis of CCD
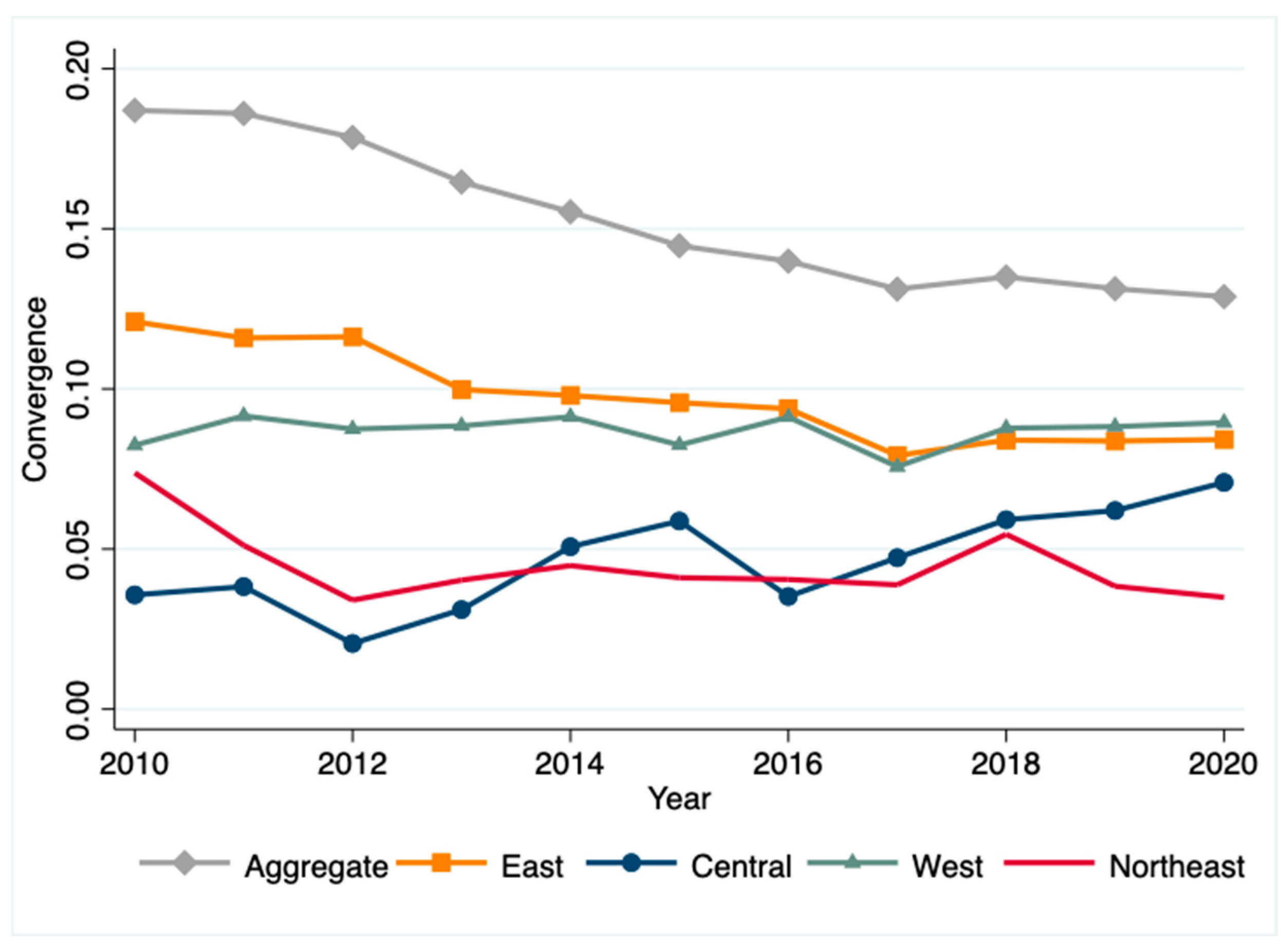
7.1. σ Convergence Test
7.2. Spatial β Convergence Test
8. Conclusions and Recommendations
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Matlovič, R.; Matlovičová, K. Polycrisis in the Anthropocene as a Key Research Agenda for Geography: Ontological Delineation and the Shift to a Postdisciplinary Approach. Folia Geogr. 2024, 66, 5–33. [Google Scholar]
- Onitsuka, K.; Hoshino, S. Inter-community Networks of Rural Leaders and Key People: Case Study on a Rural Revitalization Program in Kyoto Prefecture, Japan. J. Rural Stud. 2018, 61, 123–136. [Google Scholar] [CrossRef]
- Bai, X.; Shi, P.; Liu, Y. Society: Realizing China’s Urban Dream. Nature 2014, 509, 158–160. [Google Scholar] [CrossRef]
- Rigg, J.; Ritchie, M. Production, Consumption, and Imagination in Rural Thailand. J. Rural Stud. 2002, 18, 359–371. [Google Scholar] [CrossRef]
- Zhang, J.; Zeng, Z.; Li, G. Theoretical Interpretation and Logical Mechanism of High-Quality Agricultural Economic Development in the New Era. Agric. Econ. 2023, 4, 3–5. [Google Scholar]
- Li, K.; Yang, N.; Feng, L. Problems and Development Strategies in the Process of High-Quality Agricultural Development in China. Agric. Econ. 2023, 3, 32–33. [Google Scholar]
- Xin, L.; An, X. Construction and Empirical Analysis of Agricultural High-quality Development Evaluation System in China. Econ. Rev. 2019, 5, 109–118. [Google Scholar]
- Feng, L.; Chen, Z.; Ma, Y. Research on the Impact of Land Transfer Policy on High-Quality Agricultural Development. Stat. Decis. 2022, 19, 76–79. [Google Scholar]
- Wang, H.; Tang, Y. Spatiotemporal Distribution and Influencing Factors of Coupling Coordination between Digital Village and Green and High-Quality Agricultural Development—Evidence from China. Sustainability 2023, 15, 8079. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, L.; Zhang, Y.; Wang, C.; Yu, K. Does FDI Promote or Inhibit the High-Quality Development of Agriculture in China? An Agricultural GTFP Perspective. Sustainability 2019, 11, 4620. [Google Scholar] [CrossRef]
- Cui, X.C.; Cai, T.; Deng, W.; Zheng, R.; Jiang, Y.; Bao, H. Indicators for Evaluating High-Quality Agricultural Development: Empirical Study from Yangtze River Economic Belt, China. Soc. Indic Res. 2022, 164, 1101–1127. [Google Scholar] [CrossRef]
- Ye, X. Enhancing the Inclusiveness of Rural Revitalization to Promote Common Prosperity among Farmers and Rural Areas. China Rural Econ. 2022, 2, 2–14. [Google Scholar]
- Chen, M.; Zhou, Y.; Huang, X.; Ye, C. The Integration of New-Type Urbanization and Rural Revitalization Strategies in China: Origin, Reality, and Future Trends. Land 2021, 10, 207. [Google Scholar] [CrossRef]
- Chen, J.; Shi, H.; Lin, Y. Research on the Evaluation System and Method of Rural Revitalization Level: A Case Study of Six Provinces in East China. East China Econ. Manag. 2021, 35, 91–99. [Google Scholar]
- Mao, J.; Wang, L. Construction of the Evaluation Index System of Rural Revitalization: An Empirical Study Based on the Provincial Level. Stat. Decis. 2020, 19, 181–184. [Google Scholar]
- Zhang, T.; Li, M.; Xu, Y. Construction and Empirical Research on the Evaluation Index System of Rural Revitalization. Manag. World 2018, 34, 99–105. [Google Scholar]
- Zha, Q.; Liu, Z.; Song, Z.; Wang, J. A Study on Dynamic Evolution, Regional Differences, and Convergence of High-Quality Economic Development in Urban Agglomerations: A Case Study of Three Major Urban Agglomerations in the Yangtze River Economic Belt. Front. Environ. Sci. 2022, 10, 1012304. [Google Scholar] [CrossRef]
- Lu, F.; Pang, Z.; Deng, G. Measurement of Regional Differences and Formation Mechanisms of Rural Revitalization Development in China. Explor. Econ. Issues 2022, 4, 19–36. [Google Scholar]
- Haiyirete, X.; Xu, Q.; Wang, J.; Liu, X.; Zeng, K. Comprehensive Evaluation of the Development Level of China’s Characteristic Towns under the Perspective of an Urban–Rural Integration Development Strategy. Land 2024, 13, 1069. [Google Scholar] [CrossRef]
- Chen, D.; Hu, W. Temporal and Spatial Effects of Heavy Metal-Contaminated Cultivated Land Treatment on Agricultural Development Resilience. Land 2023, 12, 945. [Google Scholar] [CrossRef]
- Sun, P.; Ge, D.; Yuan, Z.; Lu, Y. Rural Revitalization Mechanism Based on Spatial Governance in China: A Perspective on Development Rights. Habitat Int. 2024, 147, 103068. [Google Scholar] [CrossRef]
- Diedrich, A.; Benham, C.; Pandihau, L.; Sheaves, M. Social Capital Plays a Central Role in Transitions to Sportfishing Tourism in Small-Scale Fishing Communities in Papua New Guinea. Ambio 2019, 48, 385–396. [Google Scholar] [CrossRef]
- Jing, Z.; Yu, Y.; Wang, Y.; Su, X.; Qiu, X.; Yang, X.; Xu, Y. Study on the Mechanism of Livelihood Behavior Decision of Rural Residents in Ethnic Tourism Villages in Western Sichuan. Ecol. Indic. 2024, 166, 112250. [Google Scholar] [CrossRef]
- Jia, X. Digital Economy Factor Allocation and Sustainable Agricultural Development: The Perspective of Labor and Capital Misallocation. Sustainability 2023, 15, 4418. [Google Scholar] [CrossRef]
- Dong, Z.; Zhao, C. Path Selection for High-Quality Agricultural and Rural Development under the Background of Rural Revitalization. J. Party Sch. Cent. Comm. CPC 2022, 26, 80–88. [Google Scholar]
- Yang, X.; Liang, Y. The Logical Foundation, Restrictive Factors, and Institutional Supply of High-Quality Industrial Development from the Perspective of Rural Revitalization. Hubei Soc. Sci. 2023, 4, 87–93. [Google Scholar]
- Xie, Y.; Qi, C. Mechanism and Countermeasures for the Linkage between High-Quality Agricultural Development and Rural Revitalization. Zhongzhou Acad. J. 2020, 2, 33–37. [Google Scholar]
- Yang, S.; Jiang, L. Study on the Spatial and Temporal Effects of High-Quality Agricultural Development on Rural Revitalization. Stat. Decis. 2023, 39, 116–120. [Google Scholar]
- Meng, F.; Ding, S. Research on the Coupling and Coordination Relationship between Rural Revitalization and High-Quality Agricultural Development. Stat. Decis. 2024, 40, 79–83. [Google Scholar]
- Qi, C.; Liu, X.; Wu, W.; Yuan, J. Spatial Correlation and Coupling Coordination Evaluation between High-Quality Development and Rural Revitalization in the Yellow River Basin. Stat. Decis. 2024, 40, 124–128. [Google Scholar]
- Lu, P.; Yu, S. Research on the Coordinated Development Trend of New Urbanization and Rural Revitalization in China. Econ. Perspect. 2021, 11, 76–82. [Google Scholar]
- Wei, C.; Zhang, Z.; Ye, S.; Hong, M.; Wang, W. Spatial-Temporal Divergence and Driving Mechanisms of Urban-Rural Sustainable Development: An Empirical Study Based on Provincial Panel Data in China. Land 2021, 10, 1027. [Google Scholar] [CrossRef]
- Ding, C.; Yang, F.; Guo, Q. Research on the Coupling and Coordinated Development of New Industrialization, New Urbanization, and Rural Revitalization. Stat. Decis. 2020, 36, 71–75. [Google Scholar]
- Du, M.; Huang, Y.; Dong, H.; Zhou, X.; Wang, Y. The Measurement, Sources of Variation, and Factors Influencing the Coupled and Coordinated Development of Rural Revitalization and Digital Economy in China. PLoS ONE 2022, 17, e0277910. [Google Scholar] [CrossRef]
- Wu, R. Measurement Evolution and Spatial Effect of Coupling Coordination between Tourism High-Quality Development and Rural Revitalization. Ph.D. Thesis, Jiangxi University of Finance and Economics, Nanchang, China, 2022. [Google Scholar]
- Lu, Y. Issues of Agricultural and Rural Modernization in Rural Revitalization. J. China Agric. Univ. (Soc. Sci. Ed.) 2018, 3, 48–56. [Google Scholar]
- Yang, J.; Yang, R.; Chen, M.H.; Su, C.H.J.; Zhi, Y.; Xi, J. Effects of Rural Revitalization on Rural Tourism. J. Hosp. Tour. Manag. 2021, 47, 35–45. [Google Scholar] [CrossRef]
- Yang, X.; Li, W.; Zhang, P.; Chen, H.; Lai, M.; Zhao, S. The Dynamics and Driving Mechanisms of Rural Revitalization in Western China. Agriculture 2023, 13, 1448. [Google Scholar] [CrossRef]
- Rao, Y.; Zou, Y.; Yi, C.; Luo, F.; Song, Y.; Wu, P. Optimization of Rural Settlements Based on Rural Revitalization Elements and Rural Residents’ Social Mobility: A Case Study of a Township in Western China. Habitat Int. 2023, 137, 102851. [Google Scholar] [CrossRef]
- Ma, M.; Tang, J.; Dombrosky, J.M. Coupling Relationship of Tourism Urbanization and Rural Revitalization: A Case Study of Zhangjiajie, China. Asia Pac. J. Tour. Res. 2022, 27, 673–691. [Google Scholar] [CrossRef]
- Wang, Y.; Kuang, Y. Evaluation, Regional Disparities, and Driving Mechanisms of High-Quality Agricultural Development in China. Sustainability 2023, 15, 6328. [Google Scholar] [CrossRef]
- Xie, C.; Dong, D.; Hua, S.; Xin, X.; Chen, Y. Safety Evaluation of Smart Grid Based on AHP-Entropy Method. Syst. Eng. Procedia 2012, 4, 203–209. [Google Scholar]
- Bai, L.; Wang, H.; Huang, N.; Du, Q.; Huang, Y. An Environmental Management Maturity Model of Construction Programs Using the AHP-Entropy Approach. Int. J. Environ. Res. Public Health 2018, 15, 1317. [Google Scholar] [CrossRef]
- Wu, G.; Duan, K.; Zuo, J.; Zhao, X.; Tang, D. Integrated Sustainability Assessment of Public Rental Housing Community Based on a Hybrid Method of AHP-Entropy Weight and Cloud Model. Sustainability 2017, 9, 603. [Google Scholar] [CrossRef]
- Yang, C.; Zeng, W.; Yang, X. Coupling Coordination Evaluation and Sustainable Development Pattern of Geo-Ecological Environment and Urbanization in Chongqing Municipality, China. Sustain. Cities Soc. 2020, 61, 102271. [Google Scholar] [CrossRef]
- Shi, T.; Yang, S.; Zhang, W.; Zhou, Q. Coupling Coordination Degree Measurement and Spatiotemporal Heterogeneity between Economic Development and Ecological Environment—Empirical Evidence from Tropical and Subtropical Regions of China. J. Clean. Prod. 2020, 244, 118739. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X. Coupling and Coordination Analysis of Digital Economy and Green Agricultural Development: Evidence from Major Grain Producing Areas in China. Sustainability 2024, 16, 4533. [Google Scholar] [CrossRef]
- Zhang, Y.; Khan, S.U.; Swallow, B.; Liu, W.; Zhao, M. Coupling Coordination Analysis of China’s Water Resources Utilization Efficiency and Economic Development Level. J. Clean. Prod. 2022, 373, 133874. [Google Scholar] [CrossRef]
- Deng, M.; Chen, J.; Tao, F.; Zhu, J.; Wang, M. On the Coupling and Coordination Development between Environment and Economy: A Case Study in the Yangtze River Delta of China. Int. J. Environ. Res. Public Health 2022, 19, 586. [Google Scholar] [CrossRef]
- Liu, J.; Ma, Y. Research on the Coupled Growth Evolution and Driving Mechanisms of Tourism Flow and Destination Supply and Demand Based on Phylogenetics and System Theory: A Case Study of Xi’an City. Geogr. Res. 2017, 36, 1583–1600. [Google Scholar]
- Zhong, S.; Shao, J. Research on the Distribution Dynamics, Spatial Differences, and Convergence of Innovation Development in the Yellow River Basin. J. Quant. Tech. Econ. 2022, 39, 25–46. [Google Scholar]
- Senga Kiesse, T.; Corson, M.S. The Utility of Less-Common Statistical Methods for Analyzing Agricultural Systems: Focus on Kernel Density Estimation, Copula Modeling, and Extreme Value Theory. Behaviormetrika 2023, 50, 491–508. [Google Scholar] [CrossRef]
- Yang, Y.D.; Sun, C.Z. Assessment of Land–Sea Coordination in the Bohai Sea Ring Area and Spatial–Temporal Differences. Resour. Sci. 2014, 36, 691–701. [Google Scholar]
- Zhou, R.; Jin, J.; Cui, Y.; Ning, S.; Zhou, L.; Zhang, L.; Wu, C.; Zhou, Y. Spatial Equilibrium Evaluation of Regional Water Resources Carrying Capacity Based on Dynamic Weight Method and Dagum Gini Coefficient. Front. Earth Sci. 2022, 9, 1342. [Google Scholar] [CrossRef]
- Xiao, W.; He, M. Characteristics, Regional Differences, and Influencing Factors of China’s Water-Energy-Food (WEF) Pressure: Evidence from Dagum Gini Coefficient Decomposition and PGTWR Model. Environ. Sci. Pollut. Res. 2023, 30, 66062–66079. [Google Scholar] [CrossRef]
- Dagum, C. A New Approach to the Decomposition of the Gini Income Inequality Ratio. Empir. Econ. 1997, 22, 515–531. [Google Scholar] [CrossRef]
- Bao, H.; Liu, X.; Xu, X.; Shan, L.; Ma, Y.; Qu, X.; He, X. Spatial-Temporal Evolution and Convergence Analysis of Agricultural Green Total Factor Productivity—Evidence from the Yangtze River Delta Region of China. PLoS ONE 2023, 18, e0271642. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Zhu, X. Balanced Growth of Sustainable Economic Welfare Structure under the Goal of Common Prosperity. Quant. Econ. Tech. Econ. Res. 2022, 39, 3–24. [Google Scholar]
- Zhang, Z.; Zhang, T.; Feng, D. Research on Regional Differences, Dynamic Evolution, and Convergence of Carbon Emission Intensity in China. J. Quant. Tech. Econ. 2022, 39, 67–87. [Google Scholar]
- Avdic, A.; Avdic, B. Center and Periphery in Bosnia and Herzegovina—Social and Spatial Indicators of Regional Disparities. Folia Geogr. 2023, 65, 103–126. [Google Scholar]

| Dimension Index | Factor Index | Basic Index | Attribute | Weight |
|---|---|---|---|---|
| Rural Revitalization | Industrial Prosperity | Land Productivity | + | 0.0526 |
| Labor Productivity | + | 0.0416 | ||
| Per Capita Agricultural Output Value | + | 0.0441 | ||
| Level of Agricultural Mechanization | + | 0.0316 | ||
| Ratio of Agricultural Product Processing Industry Value | + | 0.0673 | ||
| Ratio of Effective Irrigated Area to Cultivated Land Area | + | 0.0417 | ||
| Ratio of Leisure Agriculture to Agricultural Output Value | + | 0.0548 | ||
| Ecological Livability | Density of Rural Drainage Channels | + | 0.0315 | |
| Rural Greening Coverage Rate | + | 0.0340 | ||
| Proportion of Villages with Centralized Garbage Disposal | + | 0.0441 | ||
| Penetration Rate of Harmless Sanitary Toilets | + | 0.0382 | ||
| Number of National Beautiful Village Demonstration Sites | + | 0.0778 | ||
| Civilized Civilization | Coverage Rate of Rural Cultural Institutions | + | 0.0291 | |
| Number of National Civilized Villages and Towns | + | 0.0302 | ||
| Proportion of Full-time Teachers in Rural Compulsory Education Schools with Bachelor’s Degree or Above | + | 0.0324 | ||
| Proportion of Rural Residents’ Education, Culture, and Entertainment Expenditure | + | 0.0313 | ||
| Effective Governance | Voter Turnout in Village Elections | + | 0.0229 | |
| Proportion of Village Committee Chairpersons and Secretaries with Dual Roles | + | 0.0312 | ||
| Proportion of Village Committee Chairpersons with University Degree or Above | + | 0.0462 | ||
| Proportion of Rural Population Receiving Minimum Living Security | − | 0.0231 | ||
| Prosperous Life | Rural Residents’ Income Level | + | 0.0508 | |
| Rural Tap Water Penetration Rate | + | 0.0311 | ||
| Gas Penetration Rate | + | 0.0371 | ||
| Per Capita Rural Road Area | + | 0.0362 | ||
| Per Capita Rural Housing Level | + | 0.0390 |
| Level of Importance | Same Importance | Slightly More Important | Obviously More Important | Strongly More Important | Extremely More Important | Middle Values |
|---|---|---|---|---|---|---|
| Scale () | 1 | 3 | 5 | 7 | 9 | 2, 4, 6, 8 |
| Matrix Order (n) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| RI | 0 | 0 | 0.58 | 0.90 | 1.12 | 1.24 | 1.32 | 1.41 | 1.45 |
| Index Levels | Coupling (C) | Coupling Coordination (CCD) |
|---|---|---|
| 0.00~0.39 | Extremely Decoupling | Extremely Incoordination |
| 0.40~0.49 | Moderate Decoupling | Moderate Incoordination |
| 0.50~0.59 | Barely Coupling | Barely Coordination |
| 060~0.69 | Primary Coupling | Primary Coordination |
| 0.70~0.79 | Intermediate Coupling | Intermediate Coordination |
| 0.80~0.90 | Favorable Coupling | Favorable Coordination |
| 0.90~1.0 | Quality Coupling | Quality Coordination |
| Year | Coupling (C) | CDL * | CCD | Coordination Types |
|---|---|---|---|---|
| 2010 | 0.9925 | 0.3179 | 0.5526 | Barely Coordinated |
| 2011 | 0.9934 | 0.3166 | 0.5519 | Barely Coordinated |
| 2012 | 0.9911 | 0.3093 | 0.5453 | Barely Coordinated |
| 2013 | 0.9922 | 0.3468 | 0.5795 | Barely Coordinated |
| 2014 | 0.9928 | 0.3480 | 0.5813 | Barely Coordinated |
| 2015 | 0.9933 | 0.3465 | 0.5810 | Barely Coordinated |
| 2016 | 0.9931 | 0.3533 | 0.5870 | Barely Coordinated |
| 2017 | 0.9936 | 0.3504 | 0.5853 | Barely Coordinated |
| 2018 | 0.9929 | 0.3487 | 0.5835 | Barely Coordinated |
| 2019 | 0.9939 | 0.3489 | 0.5842 | Barely Coordinated |
| 2020 | 0.9943 | 0.3386 | 0.5757 | Barely Coordinated |
| Year | East | Central | West | Northeast | East–Central | East–West | Northeast–East | Northeast–Central | West–Central | Northeast–West |
|---|---|---|---|---|---|---|---|---|---|---|
| 2010 | 0.0627 | 0.0180 | 0.0444 | 0.0310 | 0.136 | 0.181 | 0.117 | 0.0308 | 0.0521 | 0.0712 |
| 2011 | 0.0615 | 0.0193 | 0.0495 | 0.0215 | 0.134 | 0.181 | 0.108 | 0.0314 | 0.0535 | 0.0769 |
| 2012 | 0.0615 | 0.0094 | 0.0467 | 0.0138 | 0.132 | 0.172 | 0.105 | 0.0285 | 0.0454 | 0.0691 |
| 2013 | 0.0524 | 0.0152 | 0.0476 | 0.0161 | 0.119 | 0.162 | 0.0917 | 0.0311 | 0.0485 | 0.0732 |
| 2014 | 0.0503 | 0.0248 | 0.0491 | 0.0173 | 0.100 | 0.151 | 0.0932 | 0.0236 | 0.0565 | 0.0613 |
| 2015 | 0.0498 | 0.0291 | 0.0447 | 0.0171 | 0.0959 | 0.139 | 0.0941 | 0.0258 | 0.0538 | 0.0521 |
| 2016 | 0.0479 | 0.0179 | 0.0500 | 0.0179 | 0.0869 | 0.133 | 0.0949 | 0.0202 | 0.0540 | 0.0485 |
| 2017 | 0.0407 | 0.0241 | 0.0410 | 0.0154 | 0.0859 | 0.129 | 0.0922 | 0.0233 | 0.0514 | 0.0455 |
| 2018 | 0.0427 | 0.0295 | 0.0476 | 0.0242 | 0.0803 | 0.129 | 0.0894 | 0.0304 | 0.0602 | 0.0512 |
| 2019 | 0.0434 | 0.0318 | 0.0476 | 0.0170 | 0.0759 | 0.124 | 0.0939 | 0.0332 | 0.0605 | 0.0439 |
| 2020 | 0.0444 | 0.0361 | 0.0478 | 0.0154 | 0.0732 | 0.119 | 0.0941 | 0.0373 | 0.0608 | 0.0412 |
| Mean | 0.0507 | 0.0232 | 0.0469 | 0.0188 | 0.1017 | 0.1473 | 0.0976 | 0.0287 | 0.0542 | 0.0576 |
| Intra-Regional Disparity | Inter-Regional Disparities | Hyper Variance | |||||
|---|---|---|---|---|---|---|---|
| Year | Aggregate | Contribution Value | Contribution Rate % | Contribution Value | Contribution Rate % | Contribution Value | Contribution Rate % |
| 2010 | 0.0990 | 0.0140 | 14.19 | 0.0831 | 84.01 | 0.0018 | 1.80 |
| 2011 | 0.0992 | 0.0145 | 14.66 | 0.0837 | 84.35 | 0.0010 | 0.99 |
| 2012 | 0.0938 | 0.0137 | 14.63 | 0.0794 | 84.58 | 0.0007 | 0.79 |
| 2013 | 0.0885 | 0.0130 | 14.74 | 0.0746 | 84.24 | 0.0009 | 1.02 |
| 2014 | 0.0837 | 0.0134 | 15.99 | 0.0688 | 82.19 | 0.0015 | 1.81 |
| 2015 | 0.0786 | 0.0129 | 16.45 | 0.0625 | 79.55 | 0.0031 | 4.00 |
| 2016 | 0.0757 | 0.0130 | 17.24 | 0.0602 | 79.52 | 0.0024 | 3.24 |
| 2017 | 0.0720 | 0.0112 | 15.6 | 0.0582 | 80.82 | 0.0026 | 3.58 |
| 2018 | 0.0746 | 0.0127 | 16.97 | 0.0587 | 78.66 | 0.0033 | 4.37 |
| 2019 | 0.0727 | 0.0128 | 17.57 | 0.0564 | 77.64 | 0.0035 | 4.79 |
| 2020 | 0.0713 | 0.0131 | 18.33 | 0.0540 | 75.77 | 0.0042 | 5.90 |
| Mean | 0.0826 | 0.0131 | 16.03 | 0.0672 | 81.03 | 0.0023 | 2.93 |
| China | East | Central | West | Northeast | |
|---|---|---|---|---|---|
| (Space-Fixed SDM) | (OLS) | (Space-Fixed SDM) | (Space-Fixed SDM) | (OLS) | |
| β | −0.370 *** | −0.074 *** | −0.682 *** | −0.493 *** | −0.314 *** |
| (−8.966) | (−2.766) | (−5.998) | (−6.766) | (−3.005) | |
| θ | 0.273 *** | 0.593 *** | 0.373 *** | ||
| (4.845) | (4.774) | (4.828) | |||
| ρ | 0.625 *** | 0.588 *** | 0.546 *** | ||
| (11.823) | (6.680) | (7.233) | |||
| N | 300 | 90 | 60 | 120 | 30 |
| r2 | 0.072 | 0.071 | 0.034 | 0.031 | 0.209 |
| Spatial Effect | YES | NO | YES | YES | NO |
| Time Effect | YES | NO | YES | YES | NO |
| Hausman | 43.46 *** | 10.48 ** | 20.72 *** | ||
| LM Spatial Error | 2.801 * | 1.290 | 0.155 | 0.391 | 0.763 |
| Robust LM Spatial Error | 13.368 *** | 0.893 | 5.278 ** | 7.318 *** | 0.864 |
| LM Spatial Lag | 6.094 *** | 0.629 | 1.038 | 1.221 | 3.486 * |
| Robust LM Spatial Lag | 16.661 *** | 0.233 | 6.161 ** | 8.148 *** | 3.587 * |
| Wald Test Spatial Error | 3.33 * | 3.49 * | 2.13 | ||
| LR Test Spatial Error | 2.91 * | 6.95 *** | 4.43 ** | ||
| Wald Test Spatial Lag | 12.79 *** | 21.29 *** | 21.17 *** | ||
| LR Test Spatial Lag | 9.68 *** | 18.22 *** | 20.65 *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Lei, Y.; Shah, M.H. Coupling and Coordination Analysis of High-Quality Agricultural Development and Rural Revitalization: Spatio-Temporal Evolution, Spatial Disparities, and Convergence. Sustainability 2024, 16, 9007. https://doi.org/10.3390/su16209007
Wang Y, Lei Y, Shah MH. Coupling and Coordination Analysis of High-Quality Agricultural Development and Rural Revitalization: Spatio-Temporal Evolution, Spatial Disparities, and Convergence. Sustainability. 2024; 16(20):9007. https://doi.org/10.3390/su16209007
Chicago/Turabian StyleWang, Yaoyao, Yifan Lei, and Muhammad Haroon Shah. 2024. "Coupling and Coordination Analysis of High-Quality Agricultural Development and Rural Revitalization: Spatio-Temporal Evolution, Spatial Disparities, and Convergence" Sustainability 16, no. 20: 9007. https://doi.org/10.3390/su16209007
APA StyleWang, Y., Lei, Y., & Shah, M. H. (2024). Coupling and Coordination Analysis of High-Quality Agricultural Development and Rural Revitalization: Spatio-Temporal Evolution, Spatial Disparities, and Convergence. Sustainability, 16(20), 9007. https://doi.org/10.3390/su16209007






