Abstract
With the increasing share of renewable energy in the power system, traditional power flow calculation methods are facing challenges of complexity and efficiency. To address these issues, this paper proposes a new framework for AC optimal power flow analysis based on a physics-informed convolutional neural network (PICNN) approach, which enables the neural network to learn solutions that follow physical laws by embedding the power flow equations and other physical constraints into the loss function of the network. Compared with the traditional power flow calculation method, the calculation speed of this method is improved by 10–30 times. Compared to traditional neural network models, the method provides higher accuracy, with an average increase in accuracy of up to 2.5–10 times. In addition, this paper introduces a methodology to extract worst-case guarantees for violations of the neural network’s predicted power generation constraints, determining the worst possible violation that could result from any neural network output across the entire input domain, and taking appropriate measures to reduce the violation. The method is experimentally shown to be highly accurate and reliable for the AC optimal power flow (AC-OPF) analysis problem, while reducing the dependence on a large amount of labelled data.
1. Introduction
A physics-informed neural network (PINN) is an approach that combines physics equations with artificial intelligence techniques. A PINN exploits the nonlinear modelling capabilities of neural networks in order to solve complex problems in engineering [1]. By embedding the physical equations into the loss function of the neural network, a PINN is able to use the physical constraints to guide the network learning process, thus improving the accuracy and reliability of the problem solution. The PINN has a wide range of applications in several fields [2] such as fluid mechanics [3], structural mechanics [4], and power systems [5]. Its advantage lies in its ability to automatically extract features and discover patterns, thus improving the efficiency of problem solving. However, when facing large-scale problems, the PINN needs to overcome challenges such as high dimensional space and computational resource consumption. Compared with traditional numerical methods, the PINN can better adapt to data-driven environments, but its performance may not be as robust as traditional methods when the amount of data is small or noisy.
In recent years, the increasing share of renewable energy sources in high-capacity power systems has intensified the need for stability, reliability, and most planning solutions for power system operators, power market operators, and other participants [6]. Optimal power flow (OPF) allows us to determine the optimal configuration and operation strategy of the system by taking into account constraints such as load demand, generator output limits, and line capacity [7]. This strategy not only improves the operational efficiency of the power system, but also promotes the green transformation of the energy system, thus realising the intelligent optimisation of the power system and the goal of sustainable development. Traditional optimisation methods such as linear programming [8], the Newton–Raphson method [9], and interior point method [10] require the re-establishment of mathematical models according to the changes in the network structure, which is time-consuming especially when dealing with large-scale systems and lacks a certain degree of generalisation capability.
To address the problem of reconstructing mathematical models due to changes in network structure, many studies have proposed data-driven approaches. In optimal power flow analysis, various data-driven approaches, such as neural networks (NNs) and machine learning (ML), are broadly classified into two categories: hybrid model reconstruction [11,12,13] and end-to-end solver learning [14,15,16]. The core of hybrid model reconstruction lies in rediscovering the model parameters (e.g., line parameters, bus conductance matrix, PF Jacobi matrix) using historical operational data, so as to calibrate or reconstruct the PF model, which is then solved using conventional numerical methods. Some studies [17,18] use machine learning methods to improve the computational speed of OPF by learning historical data to find better starting solutions before the traditional iterative algorithms. However, these methods are still not detached from the traditional iterative solution methods, which have the disadvantages of higher computational cost, error accumulation, and computational complexity.
The end-to-end solver learning approach, on the other hand, focuses more on the mapping relationship between inputs and outputs, and circumvents the problem of model reconstruction by learning the mapping rules from historical data to generate optimal solutions directly. Linear regression (LR) [15,19] and support vector regression (SVR) [14,20] using support vector regression with polynomial kernel are used to learn the mutual mapping relationship between bus voltage and bus power, but the LR model is too simplified, which may lead to the loss of the solution accuracy, and the same computational cost and high scalability problem of SVR. It has also been studied to generate optimal solutions directly through a Deep Neural Network (DNN): [21] used a DNN to generate all optimal solutions directly. Ref. [22] generated DNN models to predict some of the optimal solutions and calculated the remaining solutions based on the AC power flow. However, the neural network methods have high requirements for hyperparameters, and they are only designed for OPF computation in specific operation modes, and their computational accuracy and efficiency decrease when the operation status of the transmission line changes.
To cope with the problem of hyperparameter dependence, refs. [23,24] proposed the Stacked Extreme Learning Machine (SELM) approach. It randomly generates the input weights of the hidden layer neurons and determines the output weights by a simple matrix computation parse. This greatly improves the training speed while requiring fewer hyperparameters for tuning. However, due to the process of random generation of input weights and analytical determination of output weights, the learning capability of SELM is limited. Inspired by the literature [25,26,27,28], ref. [29] developed a new framework using a known physical model of OPF to reduce the learning complexity of SELM by including its physical properties. However, as with most machine learning methods, the method has large requirements on the quality and quantity of the training dataset, which needs to include a large number of data points for both normal and abnormal situations. Such datasets usually do not exist or are often difficult to generate. Therefore, there is a need to find a way to reduce the dependence on data to solve the OPF problem.
In this paper, we address the above problem through a PICNN approach by reformulating the OPF as a Lagrangian dual function of the constraint violation minimisation problem and integrating the physical and engineering constraints in a Lagrangian framework into a deep neural network via the violation term in the loss function, yielding a more accurate and efficient solution with low dependence on data.
The main contributions of this paper are as follows:
- (1)
- An end-to-end learning-based model, PICNN, is proposed, which accurately predicts AC-OPF solutions under different network structures without repeated modelling;
- (2)
- PICNN introduces physical a priori knowledge of optimal power flow, which makes it easier to tune the parameters and reduces the dependence on the size and quality of the training dataset;
- (3)
- The model achieves higher accuracy and lower constraint violations compared to traditional data-driven approaches, improving model reliability.
2. Formulation of the Optimal Power Flow Analysis Problem
2.1. Description of the AC-OPF Problem
The objective of the AC-OPF problem is to minimise a certain metric, such as total cost, power loss, or line loading, by adjusting the generator output and load distribution at each node of the power system, where constraints such as voltage limitations at each bus, power flow balancing, generator limitations, and branch circuit currents are also considered to limit. As an example, the mathematical description of the AC-OPF problem for minimising generation cost is as follows:
Minimising the objective function:
where and are the active and reactive power of the generating node, f is the objective function, i.e., minimising the cost of generation, and and are the linear cost terms for the active power and reactive power .
Constraints:
- a.
- Power balance bus constraints
- b.
- Generation of bus constraints
- c.
- Load bus constraints
- d.
- Busbar voltage constraints
- e.
- Branch flow constraints
Tributary flow forms:
where is the set of branches; is the conductance on branch l; and are the minimum and maximum values of the branch current on branch l; and is the branch transmission limit on branch l.
The constraints of the AC-OPF problem are collapsed into a Lagrangian function framework and a binary problem associated with the original non-convex optimisation problem is induced by using the Karush–Kuhn–Tucker (KKT) conditions to obtain a lower bound on the original problem and help verify the validity of the solution to the original problem. Since non-convex functions have multiple local minima and only one global minimum, the introduction of the KKT conditions ensures that a globally optimal solution satisfying the constraints is found.
First, the above constraints are integrated into a functional form and simplified as follows.
where, when S represents the current, , and when S represents other variables, . The equality constraints (2)–(5) can be expressed uniformly in terms of (15) and (16). Similarly, the inequality constraints (6)–(13) can be represented uniformly by (17).
The objective function (14) as well as the equation constraints (15) and (16) and inequality constraints (17) of the above AC-OPF problem are converted into Lagrangian functional form as follows.
Thus, the KKT conditions for the original Langeranger function L can be expressed as
In the above constraints, (19)–(21) are the original problem feasibility conditions, the complementary relaxation conditions of (22), and (23) and (24) are the pairwise feasibility conditions. For the AC-OPF problem, these KKT conditions serve as necessary conditions for optimality for the AC-OPF problem.
2.2. Physical Information Architecture
Optimisation of deep neural networks is nonlinear and non-convex, so the choice of initial solutions is crucial. Good initial weights can accelerate convergence and prevent falling into local minima [30]. One approach is to use physical information to guide parameter initialisation, e.g., in this paper, we incorporate electrical physical information such as the power flow equations and various state variable constraints into the neural network framework by assigning specific physical meanings to the outputs of the hidden layer neurons or imposing physical constraints on the weights. This mitigates the black-box nature of the network and improves the interpretability of the network, which helps debugging and users of the neural network to interpret the output of the neural network. In addition, the search space for weight parameter and bias parameter b is significantly reduced, thereby reducing the dependence on the number of training samples.
In order to make the neural network generate physically consistent solutions, we need to introduce a physical information loss function. Implementing a physically informative loss function requires two core steps: firstly, the variables in the output or hidden layer of the neural network need to be given a physical meaning; secondly, the control equations containing these physical variables need to be extended to a loss function through regularisation.The expression for the loss function L of a PINN is given by
where Z represents the ordinary loss function, which measures the error between the predicted output and the target output (i.e., prediction error) in a supervised learning manner, and is its regularisation hyperparameter; R represents the parameter regularisation term imposed on the neural network weights and bias b, e.g., L1 and L2 paradigm regularisation; and P is the Physical Regularization Term (PRT) based on the physical principle equation as its regularisation hyperparameter. The Regularisation Term (PRT) is for its regularisation hyperparameters.
3. Formulation of the Optimal Power Flow Analysis Problem
3.1. Data Preprocessing
In this section, we describe in detail the steps involved in preprocessing the data generated using the Matpower tool. These data include nodal voltages, currents, load active and reactive power, and generator active and reactive power in four systems with different number of nodes (e.g., case 39). The node voltage as well as generator node active and reactive power data for the AC optimal power flow of the corresponding systems were generated, 10,000 sets of load data were generated within the load range of the corresponding nodes using the Latin Hypercubic Sampling method, and the optimal power flow corresponding to each set of data was calculated by the Matpower tool, in order to ensure the quality and availability of the data for use in subsequent AC-OPF analysis. Raw data cleaning is also required to remove possible noise, outliers, and non-optimal power flow results of computational failures. And, for model training and evaluation, the dataset is divided into a validation set, training set, and test set in the ratio of 5:2:3 for model training and testing. By checking the completeness and consistency of the data, we can ensure the accuracy of the subsequent analyses.
3.2. Network Architecture Design
This section describes a PICNN architecture for predicting the optimal generating power setpoints of AC-OPF. Active and reactive loads are vectors (for the number of load nodes), which are converted into diagonal arrays and used as inputs to the neural network. The structure of the CNN is shown in Figure 1 (as an example of the IEEE case 39), and there are 6 hidden layers between the inputs and the outputs consisting of 2 convolutional layers, 1 pooling layer, and 3 fully connected layers.
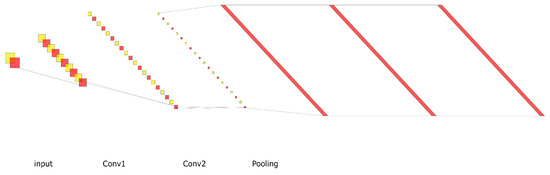
Figure 1.
Schematic of neural network architecture for active power demand D as input to predict optimal generation output G.
Considering the balance of a large number of training samples and reducing overfitting, we set up 2 convolutional layers. For a single feature, we set the size of the convolution kernel. Convolution operations on the input data for each layer will generate a new feature map. Each element of this new feature map can be computed by weighted summation.
where denotes the output of the neuron in row i, column j of the feature mapping of the convolutional layer, and is the output of the neuron in the previous layer, row i, column j, feature mapping w. represents the weights at different locations in the convolution kernel, and b represents the bias. Since the size of the convolution kernel is usually smaller than the size of the input data (), a 3D region of size is sampled at a time and the elements of the new feature mapping are obtained by summing the weights.
The convolution kernel then moves to the next 3D region of until all input data have been scanned. convolution kernels are set up and a feature mapping of is generated. The function of multi-feature mapping is to extract enough features from the input data to achieve an accurate function fit.
The pooling layer is used to reduce the size and number of parameters of the feature map while retaining important feature information. The pooling layer divides the feature graph into non-overlapping regions and performs Max Pooling on each region to obtain the pooled feature graph.
The fully connected layer consists of a set of interconnected nodes connecting the input layer to the output layer, each of its neurons is connected to all the neurons in the previous layer, and its weights and bias terms are learned through training. The fully connected layer consists of a set of interconnected nodes connecting the input and output layers.
In our framework, the convolutional layer has a convolutional kernel size of 3×3 with a step size of 1, Same Padding is used for padding, and the pooling layer has a pooling window of 2×2. The input is load power D and the dimension is {, , 2}. The dimensions of output layer , , , and are {2·, 1}, {2·, 1}, {2·, 1}, and {2·, 1}, where , , , and are the number of load bus nodes of the current test system, the number of total bus nodes, the number of power generation bus nodes, and the number of system branches.
The neural network contains k hidden layers and neurons in each hidden layer k. Each neuron is connected to a nonlinear activation function, the ReLU function, and is connected to the other neurons through edges with weights and biases b. The neural network is connected to the other neurons through edges with weights and biases b. By adjusting the weights and biases, the neural network carries out the task of predicting the optimal generation power and . The fully connected layer’s ReLU activation function and its output can be formulated as
The ReLU activation function returns the input if the input is positive and zero if the input is negative or zero. The choice of ReLU as a nonlinear activation function accelerates the training of the neural network.
3.3. Loss Function
In PICNN, the constraints of the physical equations will be incorporated into the neural network loss function, along with our previous work in power system applications. For the AC-OPF problem, the KKT conditions given in Equations (19)–(24) serve as a set of sufficiently necessary conditions that the optimum should satisfy. In order to incorporate the KKT conditions into the CNN training (and present it as a PINN), we denote the difference between constraints (19)–(24) and zero by , as shown in (29)–(32).
where the smoothness conditional error in the KKT condition is denoted as and the complementary slackness conditional error is denoted as . In Equation (31), the ReLU activation function is denoted by . If the neural network prediction is optimal, the error calculated in Equations (29)–(32) is zero. Considering that we also have the KKT conditions to measure the accuracy of the neural network prediction, we can isolate a portion of the training set as a validation set. Like the neural network training data points, the validation data points are a set of random input values from the input domain. However, unlike the training data points, we do not need to determine the optimal generation scheduling values, voltage setpoints, etc., prior to training, and the error computed from the validation set in Equations (29)–(32) will be used to measure the prediction accuracy and train the neural network to improve the generalisation performance of the neural network. The PICNN loss function is used to modify the shared parameters of the three neural networks, as shown in Equation (33).
where is the number of data points in the training set and is the number of data points in the validation set. The mean absolute error of the predicted values of active and reactive generation relative to the actual values is denoted by as the ordinary loss function. , , and denote the mean absolute error of the voltage, branch power, and dyadic value predictions, and is the mean absolute error of the conditional violation of KKT given in (29)–(32) as the Physical Regularisation Term. , , , , and are the weights corresponding to each loss function. The performance of PICNN depends heavily on these weights. Therefore, they must be appropriately selected and tuned to reduce the average error or the maximum constraint violation. Since the fully connected neural networks for the four different variables are independent of each other, the neural network will be trained to minimise the corresponding as well as . For the validation set of data points, as mentioned above, the optimal generation scheduling values and voltage settings are not computed, so that the generation capacity, voltage, etc., are all set to 0, and only the error of the KKT conditions, for example, is taken into account in the training.
As shown in Figure 2 for the above PICNN structure, the voltage V, the branch flow , and the dyadic variables required to compute the error in the KKT conditions are predicted using a separate set of hidden layers.
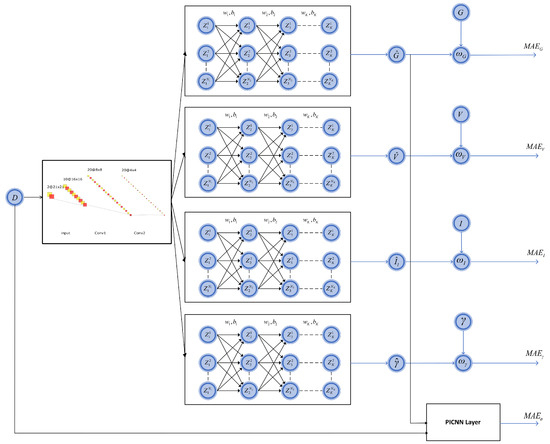
Figure 2.
Schematic diagram of PICNN architecture for prediction of each variable using load power D as input.
3.4. Worst-Case Guarantees
To ensure the stability of the system’s PICNN system, this section describes, in addition to the discussion of the average performance, the worst-case guarantee used to evaluate the minimum performance of the system in terms of constraint violations, sub-optimality, the maximum distance between the optimal generation and the PINN forecast as the worst-case guarantees. In order to determine these worst-case guarantees, it is necessary to reformulate the trained neural network as a Mixed-Integer Linear Programming (MILP) problem using the method proposed in [31]. Since the ReLU activation function in the NN is nonlinear, it needs to be reformulated as a Mixed-Integer Linear Programming problem as follows.
where y is the output value of ReLU; x is the input value of ReLU; z is a binary variable, when , otherwise ; M is a constant large enough to ensure that when .
- (1)
- Worst-case guarantee of constraint violation
Under the above MILP problem, we evaluate the worst-case guarantee of constraint violation in terms of the maximum constraint violation of the generation active power in the prediction results of PICNN. The maximum constraint violation of the generation active power can be expressed as
where and are the maximum and minimum values of the active power generated by each generator, where is not the maximum constraint violation for a single generator but corresponds to the maximum constraint violation for all generators in the entire input domain.
- (2)
- Worst-Case Guarantees of Sub-Optimality
Under the MILP problem, the predicted sub-optimality of the generation active power of the PCINN can be expressed as
where is the optimal generation active power of each generator and is the active power of the given load.
- (3)
- Worst-case guarantee of maximum distance between optimal generation and PICNN prediction
Similarly, for the entire input domain, the maximum distance between the optimal generation and the PICNN prediction is expressed as follows:
where is the maximum distance between the optimal generation active power G and the PICNN prediction .
The above MILP planning limits the constraint violation , sub-optimality , and the distance between the predicted value and the optimal value, and also ensures that the system meets the worst-case guarantees in all cases, thus improving the reliability and robustness of the system.
4. Results
In this study, we evaluate the performance of the proposed PICNN training framework, which is tested on five different test systems to verify its accuracy and scalability. The parameters of each test system are detailed in Table 1. Case 14–case 300 are taken from the literature [30]. In these test cases, we assume that the active and reactive load demands of each node are independent and are set from 60% to 100% of its maximum load as shown in the following equations.
where max loading represents the sum of the maximum load on all nodes in each system.

Table 1.
The parameters of each test system.
In order to generate stochastic active and reactive inputs, a Latin hypercubic sampling method was used, which resulted in 10,000 datasets in the range of Equation (48). Out of these data, half of them are used as a validation dataset, which is not required to compute and provide a solution for the AC-OPF. Of the remaining data, 20% was used for the training set, while the remaining 30% was used as an unknown test set.
The AC-OPF model in the version 7.1 MATPOWER toolbox was used to determine the optimal active and reactive power generation and voltage setpoints for the input data points in the training and test sets, and the corresponding dyadic variables were determined based on Equations (19)–(24).
Table 2 shows the characteristics of the standard neural network and the PINN for subsequent analysis and comparison. The training of the neural network was performed through TensorFlow 2.10.0 and Python 3.10.14, and during the training process, we set the number of iterative training rounds to 1000 and divided the data into 200 batches for processing.

Table 2.
The training time of the neural networks.
An Intel(R) Core(TM) i7-7700HQ CPU was used to train the neural networks. Table 2 demonstrates the comparison of the time taken in the training phase for the Long Short-Term Memory Network (LSTM), Attention Mechanism Network (Attention), PINN, and PICNN. The experimental results show that the training time for the PINN is similar to that of Attention, while the training time for the PICNN is about twice as long as that for the PINN, and the training time for LSTM is up to about 3–10 times longer than that for the PINN. In Table 3, taking case 39 and case 118 as examples, the real computation time of each network model is compared with the computation time of Matpower using the Newton–Raphson method (N-R method), and the time used is less than the computation time of the N-R method, which can meet the requirements of practical applications. Overall, PINN and PICNN have significant advantages in computational efficiency.

Table 3.
The real time of the neural networks.
This section investigates the performance of the PICNN versus standard neural networks, considering the most common performance metric for neural networks/mean absolute error on an unseen test dataset. The metrics used to compare the average performance are shown below in Table 4.

Table 4.
Average Performance.
- Average absolute error percentage;
- Average generation active power constraint violation percentage;
- Average distance from forecast to optimal generation power percentage;
- Average sub-optimality percentage.
During training, both the standard neural network and the physically informed neural network are optimised to minimise the MAE. However, we observe that the average performance of the physically informed neural network in the dataset during training depends on the weight initialisation method and the weight hyperparameters in Equation (28). In Table 5, using case 14 for training and comparing the four weight initialisation strategies. The MAE performance under the Uniform Distribution Initialisation and Glorot Distribution Initialisation methods is not significantly different and better than the other two strategies, so this experiment uses the Glorot Distribution Initialisation for weight initialisation. The search space for the loss function weights hyperparameters , , , , and is {0.1, 0.5, 1.0}, and the final combination is set to {0.5, 1.0, 0.1, 0.1, 0.1}. The same configurations are used for all the following four neural networks, and the results are shown in Table 4.

Table 5.
Weight Initialisation.
In Table 4, we show the average performance of the trained neural networks on the test dataset samples. Except case 162, the average absolute error (MAE) of each neural network in predicting power generation is less than 5%, while the error of PICNN is less than 1%, which shows that it has better generalisation ability. And the MAE of PICNN is also 20–80% lower than that of PINN, which shows that PICNN can achieve higher prediction accuracy using neural networks with the same amount of data with physical information. The average maximum violation of active generators is less than 0.3% of the total maximum system load. The average maximum distance between the PICNN’s predicted values and the optimal generator dispatch range was less than 0.3% in four of the five test cases, rising to 2.25% only in case 162. The average sub-optimality of the predicted solutions is also better than that of the other neural networks, noting that the sub-optimality measure can be negative if constraints are violated. The average performance on the test set indicates that the PICNN performs satisfactorily. The PICNN also shows significant performance improvement in terms of average sub-optimality and average distance from predicted value to optimal generation power. This shows that we can achieve higher prediction accuracy using PICNN with the same amount of data.
In Table 6, in order to verify the reduction of the model’s dependence on the dataset, the experimental dataset is reduced to 50% and 20% of the original, the validation dataset, and the change of their MAE indexes is compared to the three systems with different numbers of nodes in case 14, case 39, and case 118 with a decrease in the number of datasets. When the data volume is 50% of the original, the MAE of the PINN and PICNN models with physical information embedded increases by 0.04–0.24%, while the MAE of the other two models increases by 0.17–1.84%; when the data volume is 20% of the original, the MAE of the PINN and PICNN models increases by 0.15–4.1%, and the MAE of the other two models increases 0.38–13.53%, and the MAE of PICNN was always less than 1.3%. This indicates that PICNN has improved in reducing the dependency of data.

Table 6.
Performance under reduced data sets.
We tested different hyperparameters with weight combinations set to {0.1, 1.0, 0.1, 0.1, 0.1} to produce the lowest worst-case generation constraint violations. In Table 7, the mixed-integer linear reconstruction of the trained neural network is used to solve for MILP in Equations (39)–(41) and compute the corresponding worst-case guarantees. Table 7 shows the generation constraint violations and the percentage of the maximum system load they account for. In percentage terms, the maximum generation violation cases range from 0.01% to 35% of the maximum system load as shown in Table 1 (case 162). We can infer that the PICNN significantly reduces worst-case generation constraint violations compared to other neural networks in all test cases, i.e., the PICNN provides better generalisation and lower worst-case guarantees with the same training data compared to standard neural networks. However, when we adjusted the hyperparameters of the PICNN to improve the worst-case guarantees instead of the goal of minimising the average absolute error, the worst-case generation constraint violations were additionally reduced by 10 to 30%. This suggests that we can further tighten the worst-case guarantees by optimising the hyperparameters to minimise worst-case constraint violations.

Table 7.
Worst-Case guarantee for constraint violations.
5. Conclusions
The main contributions of this paper are twofold. Firstly, this study presents for the first time a convolutional neural network training framework that incorporates the physical equations of the AC-OPF, which improves all the performances in optimising the power flow problem compared to other data-driven methods. It is shown how incorporating the KKT conditions enables the PICNN to achieve higher prediction accuracy even when using fewer data points. Secondly, this study also develops a method to extract and minimise the worst-case generation constraint violations for the PICNN. And the worst-case constraint violations of the PICNN are reduced compared to conventional neural networks. Future work will explore multilevel optimisation algorithms to identify and tune PICNN hyperparameters that are critical for maximum constraint violations in order to optimise average performance and maximum case guarantees. These algorithms will be used to identify and tune those PICNN hyperparameters that are critical for reducing worst-case constraint violations.
Author Contributions
Methodology, C.L.; Writing—original draft, C.L.; Writing—review & editing, Y.L. and T.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Natural Science Foundation of China under Grant 62062068, and Young Academic and Technical Leaders Program of Yunnan Province under Grant 202305AC160077.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Willard, J.; Jia, X.; Xu, S.; Steinbach, M.; Kumar, V. Integrating scientific knowledge with machine learning for engineering and environmental systems. ACM Comput. Surv. 2022, 55, 1–37. [Google Scholar] [CrossRef]
- Cai, S.; Mao, Z.; Wang, Z.; Yin, M.; Karniadakis, G.E. Physics-informed neural networks for fluid mechanics: A review. Acta Mech. Sin. 2021, 37, 1727–1738. [Google Scholar] [CrossRef]
- Zhang, E.; Dao, M.; Karniadakis, G.E.; Suresh, S. Analyses of internal structures and defects in materials using physics-informed neural networks. Sci. Adv. 2022, 8, eabk0644. [Google Scholar] [CrossRef]
- Misyris, G.S.; Venzke, A.; Chatzivasileiadis, S. Physics-informed neural networks for power systems. In Proceedings of the 2020 IEEE Power & Energy Society General Meeting (PESGM), Montreal, QC, Canada, 2–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–5. [Google Scholar]
- Siano, P. Demand response and smart grids—A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Frank, S.; Steponavice, I.; Rebennack, S. Optimal power flow: A bibliographic survey II: Non-deterministic and hybrid methods. Energy Syst. 2012, 3, 259–289. [Google Scholar] [CrossRef]
- Alsac, O.; Bright, J.; Prais, M.; Stott, B. Further developments in LP-based optimal power flow. IEEE Trans. Power Syst. 1990, 5, 697–711. [Google Scholar] [CrossRef]
- Rashed, A.M.H.; Kelly, D.H. Optimal load flow solution using lagrangian multipliers and the Hessian matrix. IEEE Trans. Power App. Syst. 1974, 5, 1292–1297. [Google Scholar] [CrossRef]
- Wei, H.; Sasaki, H.; Kubokawa, J.; Yokoyama, R. An interior point nonlinear programming for optimal power flow problems with a novel data structure. IEEE Trans. Power Syst. 1997, 13, 134–141. [Google Scholar] [CrossRef]
- Yuan, Y.; Low, S.; Ardakanian, O.; Tomlin, C. Inverse power flow problem. arXiv 2016, arXiv:1610.06631. [Google Scholar] [CrossRef]
- Yu, J.; Weng, Y.; Rajagopal, R. Patopa: A data-driven parameter and topology joint estimation framework in distribution grids. IEEE Trans. Power Syst. 2017, 33, 4335–4347. [Google Scholar] [CrossRef]
- Chen, Y.C.; Wang, J.; Domínguez-García, A.D.; Sauer, P.W. Measurement-based estimation of the power flow Jacobian matrix. IEEE Trans. Smart Grid 2016, 7, 2507–2515. [Google Scholar] [CrossRef]
- Yu, J.; Weng, Y.; Rajagopal, R. Mapping rule estimation for power flow analysis in distribution grids. arXiv 2017, arXiv:1702.07948. [Google Scholar]
- Liu, Y.; Zhang, N.; Wang, Y.; Yang, J.; Kang, C. Data-driven power flow linearization: A regression approach. IEEE Trans. Smart Grid 2018, 10, 2569–2580. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Threephase ac/dc power-flow for balanced/unbalanced microgrids including wind/solar, droop-controlled and electronically-coupled distributed energy resources using radial basis function neural networks. IET Power Electron. 2017, 10, 313–328. [Google Scholar] [CrossRef]
- Baker, K. Learning warm-start points for AC optimal power flow. In Proceedings of the 2019 IEEE 29th International Workshop on Machine Learning for Signal Processing, Pittsburgh, PA, USA, 13–16 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Dong, W.; Xie, Z.; Kestor, G.; Li, D. Smart-PGSim: Using neural network to accelerate AC-OPF power grid simulation. In Proceedings of the SC20: International Conference for High Performance Computing, Networking, Storage and Analysis, Atlanta, GA, USA, 9–19 November 2020; pp. 1–15. [Google Scholar] [CrossRef]
- Long, J.; Jiang, W.; Jin, L.; Zhang, T.; Jiang, H.; Xu, T. A Combination of Linear Power Flow Models to Reduce Linearization Error. In Proceedings of the 2020 IEEE 3rd International Conference of Safe Production and Informatization (IICSPI), Chongqing, China, 28–30 November 2020; pp. 256–260. [Google Scholar] [CrossRef]
- Vrablecová, P.; Ezzeddine, A.B.; Rozinajová, V.; Šárik, S.; Sangaiah, A.K. Smart grid load forecasting using online support vector regression. Comput. Electr. Eng. 2018, 65, 102–117. [Google Scholar] [CrossRef]
- Guha, N.; Wang, Z.; Wytock, M.; Majumdar, A. Machine learning for AC optimal power flow. arXiv 2019, arXiv:1910.08842v1. [Google Scholar]
- Pan, X.; Chen, M.; Zhao, T.; Low, S.H. DeepOPF: A feasibilityoptimized deep neural network approach for AC optimal power flow problems. arXiv 2021, arXiv:2007.01002v5. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Zhou, H.; Huang, G.; Lin, Z.; Wang, H.; Soh, Y.C. Stacked extreme learning machines. IEEE Trans. Cybern. 2015, 45, 2013–2025. [Google Scholar] [CrossRef] [PubMed]
- Luo, X.; Sun, J.; Wang, L.; Wang, W.; Zhao, W.; Wu, J.; Wang, J.-H.; Zhang, Z. Short-term wind speed forecasting via stacked extreme learning machine with generalized correntropy. IEEE Trans. Ind. Inform. 2018, 14, 4963–4971. [Google Scholar] [CrossRef]
- Zhou, Y.; Wei, Y. Learning hierarchical spectral–spatial features for hyperspectral image classification. IEEE Trans. Cybern. 2016, 46, 1667–1678. [Google Scholar] [CrossRef] [PubMed]
- Lv, F.; Han, M.; Qiu, T. Remote sensing image classification based on ensemble extreme learning machine with stacked autoencoder. IEEE Access 2017, 5, 9021–9031. [Google Scholar] [CrossRef]
- Wong, C.M.; Vong, C.M.; Wong, P.K.; Cao, J. Kernel-based multilayer extreme learning machines for representation learning. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 757–762. [Google Scholar] [CrossRef]
- Babaeinejadsarookolaee, S.; Birchfield, A.; Christie, R.D.; Coffrin, C.; DeMarco, C.; Diao, R.; Ferris, M.; Fliscounakis, S.; Greene, S.; Huang, R.; et al. The power grid library for benchmarking AC optimal power flow algorithms. arXiv 2019, arXiv:1908.02788. [Google Scholar]
- Karpatne, A.; Atluri, G.; Faghmous, J.H.; Steinbach, M.; Banerjee, A.; Ganguly, A.; Shekhar, S.; Samatova, N.; Kumar, V. Theory-guided data science: A new paradigm for scientific discovery from data. IEEE Trans. Knowl. Data Eng. 2017, 29, 2318–2331. [Google Scholar] [CrossRef]
- Venzke, A.; Qu, G.; Low, S.; Chatzivasileiadis, S. Learning optimal power flow: Worst-case guarantees for neural networks. In Proceedings of the 2020 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids, (SmartGridComm), Tempe, AZ, USA, 11–13 November 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).