Modular Open Chamber Stand for Biomass Densification Using the Example of Miscanthus × Giganteus Greef Et Deu

Abstract

This article presents a modular open chamber stand which simulates the densification process that occurs in a single channel of a pelletising die. The results of the verification tests confirmed the suitability of this stand for determining the optimal geometry of the channel. The test material was the biomass of Miscanthus × giganteus which is considered to be a difficult material for pressure densification; therefore, it was decided that it would be a good material for verifying the stand. The stand consists of four modules: an introductory section with a diameter of D = 12 and 10 mm, a conical part with an angle of α = 10°, 20°, 30°, 40°, a cylindrical part with lengths L = 5, 15, 25, 35, 45 mm and diameter d= 8 mm and a pellet receiving module. The stand is able to heat the densification channel. Individual modules can be assembled into test combinations; this results in a change in channel geometry without the necessity to manufacture many singular channels. The optimum geometry of the channel for miscanthus with a moisture content of 13%, densified at 100 °C was determined. It should be a channel with D = 10 mm, α = 40° and L = 18 mm.

1. Introduction

Pressure densification is a process that is applicable in many industries. It can be observed in the pharmaceutical, feed, food and biofuel industries, among others [1,2]. This process increases the contact surface area between the material particles and reduces the free space between them, enabling the production of granules with a uniform shape.

The process offers numerous benefits including reduced material volume, maximised density, uniform particle size, uniform raw material composition, reduced storage costs and easier storage, reduced transport costs, reduced dust and easier handling [3,4]. Another advantage is that the raw materials, often in the form of dust or pulp, are homogeneous in shape [5].

The process itself is sophisticated because it depends on densification pressure, which is the causal factor of this process, and other factors that can be divided into three groups. The first group includes material parameters such as moisture content, particle size composition, chemical composition or raw material composition [6]. The second group of factors is technological. These include the already mentioned densification pressure, the temperature at which the process is carried out, the speed of densification and the time. The last group consists of structural parameters [7]; in other words, the geometry of the chamber in which the process takes place.

These factors can be divided into those over which we have no control (e.g., the specific properties of the raw material) and those that we can change according to the needs of the process. Generally speaking, it is the process and structural parameters that must be matched to the raw material parameters in order to obtain pellets of the desired quality with the lowest possible energy input, which in most cases means minimising the densification pressure of the process. The main quality parameters are usually the specific density of the pellets and their durability.

The pressure densification process is widely used in the processing of biomass into solid biofuels in the form of briquettes and pellets. This process can be carried out in technical systems where the pellets are formed in a closed or open chamber. In the first case, the material is placed in a cylindrical or cuboidal chamber. One of the bases of the cylinder or cuboid is closed at the bottom during densification. The other is closed by the face of a piston moving through the chamber. The movement of the piston reduces the volume of the chamber and the pressure compacts the material; when the set pressure is reached, the process is stopped, the bottom of the chamber is opened and the granulate produced is pushed out of the chamber by the movement of the piston. The solid biofuel thus produced takes on a cylindrical or cuboidal shape—in this case, the structural parameters (chamber geometry) determine not only the shape of the granules but also, for example, their density [8]. The process pressure must be selected according to the parameters of the material to be compacted so that the required levels for the quality parameters can be achieved. An example of this type of densification process is the production of RUF-type briquettes.

Briquetting can also take place in an open chamber. In this case, the chamber is usually a sleeve and its outlet is a tapered channel [9,10,11]. The piston moves the material towards the channel where the resistance of the material and the pressure exerted by the piston on the material increases due to external friction. When the required pressure level is reached, the sleeve clamping mechanism is released and the piston pushes the briquette, in the form of a cylinder, towards the outlet of the sleeve [9,10]. In this case, the main factors in achieving the required pressure are the raw material parameters (coefficient of friction) and the degree of clamping the sleeve [11,12].

Another type of open chamber is used to densify biomass into pellets. In this case, the material is pressed into the chamber by rollers instead of a piston. The individual dose of material injected is small (the volume of the layer of material is limited by the diameter of the channel opening). The densification channels of the pelletising dies have no bottom or constriction whose function is to stop the flow of the material and thus initiate the densification process. The size of the die is relatively small, so the geometry of the densification channel must be chosen so that the material to be compacted does not leave the densification channel in the form of loose biomass but is densified into pellets in the absence of the aforementioned constriction. Biomass for pellet production is characterised by a low bulk density, which further reduces the dose of densified material. To counteract this, densification cones are used to facilitate the introduction of the material into the channel and its initial densification [13,14]. Thus, such a channel consists of two sections—a conical section and a cylindrical section.

During densification, a layer of material is forced into the channel by a roller. In the conical section, the layer of material is pre-compacted as it passes through an increasingly narrow channel (cone). Overflow of material through the die channel is prevented by the previous layers of material forced into the channel. After passing through the conical section, the material enters the cylindrical section where final shaping and densification takes place. The conical section is formed by a truncated cone, the ratio of the cone’s base diameter (the material input diameter) and the truncation diameter (the diameter of the cylindrical section and therefore the diameter of the pellet formed) can be selected. An increase in the volume of the conical section can also be achieved by reducing the apex angle of the cone. The cylindrical section of the channel is formed by a cylinder with a diameter equal to the diameter of the cone truncation. Increasing the length of this section causes the pellet to remain in the channel longer. The ratio of the length of the densification channel to its diameter (L/D) is called the compression ratio. The choice of the overall channel geometry determines the quality of the pellet obtained. An increase in the inlet diameter, an increase in the volume of the conical section and an increase in the length of the cylindrical section results in an increase in the quality parameters (specific density and mechanical durability of the pellet). At the same time, the pressure required to force the material through the channel increases, which directly translates into an increase in the energy input on the process. A properly selected channel geometry makes it possible to obtain pellets with the required level of quality parameters at minimum pressure. Due to variability in the materials’ characteristics (friction coefficient, moisture content, specific density, porosity, etc.), the channel geometry should be selected to suit the material.

It can therefore be concluded that the densification process is determined by the material to be densified and the whole process, and in particular the geometry of the channel, must be adapted to this. As mentioned above, most tests of the densification process are carried out in closed chamber test stands [6,15]. It is therefore not possible to ascertain from them what the geometry of the channel should be.

Research on stations simulating the real process of densification is being carried out, but the numbers are small compared to studies of the process in a closed chamber [1,16]. These tests provide very important data, but are more difficult to conduct, because the material flows freely through the channel and is not stopped by any supporting element [13,17]. A key issue in this type of testing is the selection of the geometry of the densification channel to suit the requirements of the material to be tested, as it will be responsible for holding the material in the chamber and densifying it [18,19]. Tests in a closed chamber provide only the answer to the question of whether the material can be densified to the required level and what pressure is required. However, only tests in an open chamber give an answer as to how the chamber geometry should be in practice in order for this process to occur at the lowest pressure and allow the required pellet quality to be achieved.

In a study on the densification of woody biomass, Nielsen [14] analysed the energy consumption during the densification process using angle densification cones of 60°. The highest energy consumption was observed during beech densification at 74%, while pine densification required 66% more energy compared to the test procedure carried out in a bushing without variable geometry. Križan, on the other hand, in his study [20], addressed the impact of the geometry of the densification chamber with angles of 1°; 4°; 6°; 9°; 11° on pellet quality. The test material was woody biomass. The study presented a geometry optimisation and resulted in the determination of the ratio of material contact area to densification chamber volume. As the compaction cone changes, this ratio changes—as the angle increases, the ratio of the surface area to the volume of the densification chamber decreases. Winter chose RDF as the object of his research [21]. He identified the impact of angles of 0°; 4°; 14°; 28° on the production of individual granules. His results showed that the lowest pressure of the densification process could be observed when densification took place with a cone with an angle of 28°, and the pellet it produced then achieved the best quality among the variants tested. The parameter to be assessed qualitatively was its resistance to cracking. The densification of wheat straw at the stand was carried out by Mišljenović and his team [22]. Tests were carried out on a single stand, but also using a flat die with a compaction cone characterised by an opening angle of 37.6°. The results showed that the pellets produced on the single stand achieved greater durability in the individual pellets.

Hu et al. [23] determined the level of energy consumption during the densification process, where the test material was rice grass. The test was carried out for a combination of five angles in the range of α = 29.5°–60.5°. The lowest energy consumption was recorded for the combination with angle α = 60.5°. Wu et al. [24] simulated the densification process using angles of α falling within the range of α = 15°–120°. It was observed that as the value of the angle α decreased, the granulation force decreased and, consequently, so did the friction.

The compression ratio, i.e., the ratio of the length of the densification channel L to its diameter D, can take values in the range 4 to 7.5. Its value mainly depends on the material to be compacted, as each material has its own individual characteristics [25].

As the length of the densification channel increases, an increase in the pressure of the densification process can be observed, whereas if the diameter of the channel is increased at the same time, a decrease in the force required to push the material through the densification channel can be expected. Taking these observations into account, it can be concluded that the geometry of the die channel has a significant influence on the operating conditions of a given densification system [26]. Studies on the influence of die channel geometry on durability have been carried out by, among others, Heffiner and Pfost [27]. Their study showed that the most durable granules were those that were compacted using dies with the smallest thickness (length of the densification channel). Butler and McColly [28] in their study proved that, given a constant dosage by means of a specific pressure, the density as well as the length of the resulting pellets was higher for smaller densification chambers (characterised by smaller volume). A comparison of the durability of pellets produced using dies with different densification hole geometries was carried out by Tumuluru et al. [29]. Biomass densification results showed that pellets compacted using a 7.2 mm hole diameter die had lower durability than those produced using a 6.4 mm hole diameter die. The process of the densification of alfalfa was also carried out by Hill and Pulkinen [30]. Their research showed that the highest durability was achieved for pellets produced using a die with a compression ratio of 8–10.

The above examples only give a partial answer to the question of how the geometry of the densification channel influences the densification process for a given type of biomass. In addition, these studies are carried out on different types of test stands and, therefore, the results obtained are difficult to compare. They do not provide information on how to methodically conduct research in order to, regardless of the material being tested, determine the optimal chamber geometry for it, or indicate when the process pressure is lowest, or when the required product quality levels are achieved, or what material moisture content is desirable, or what the process temperature should be, etc.

The difficulty is that there are no test stands for open chamber densification studies, where it is possible to vary the geometry of the chamber, i.e., the length of the cylindrical section, the opening angle of the compaction cone and the diameter of the channel entrance, as well as taking into account temperature, for example. The development of such a stand was the main objective of the article.

Therefore, in order to study the influence of the above-mentioned group of parameters on the process, a test stand was developed to simulate the real course of the densification process in an open chamber with the possibility of changing individual geometrical parameters of the chamber (channel length, entrance angle, diameter of the inlet hole).

This paper presents the construction of a modular test stand for determining the effect of the geometry of the densification channel on the biomass densification process. In order to verify the suitability of the stand, tests were carried out on the course of the densification process of giant miscanthus biomass as a representative of herbaceous biomass (according to EN ISO 17225-1:2021, classification solid biofuels—fuel specifications and grades—Part 1: General requirements) [31]. The choice of miscanthus was made for a number of reasons. It is a species intentionally grown as a source of biomass for energy purposes [32,33]. The technology of cultivation and harvesting is well developed and the biomass yield is high [34,35]. Miscanthus can be grown on marginal soils and the composition of biomass can depend on the soil site. Some limitations to the use of miscanthus for energy purposes may be the high content of silicate [36,37]. This shortcoming can be overcome by the addition of biomasses of less problematic composition, such as woody biomass. Herbaceous biomass, including miscanthus, is considered to be a biomass that is difficult to densify, so this predisposes it to studies verifying the test stand [38,39].

2. Materials and Methods

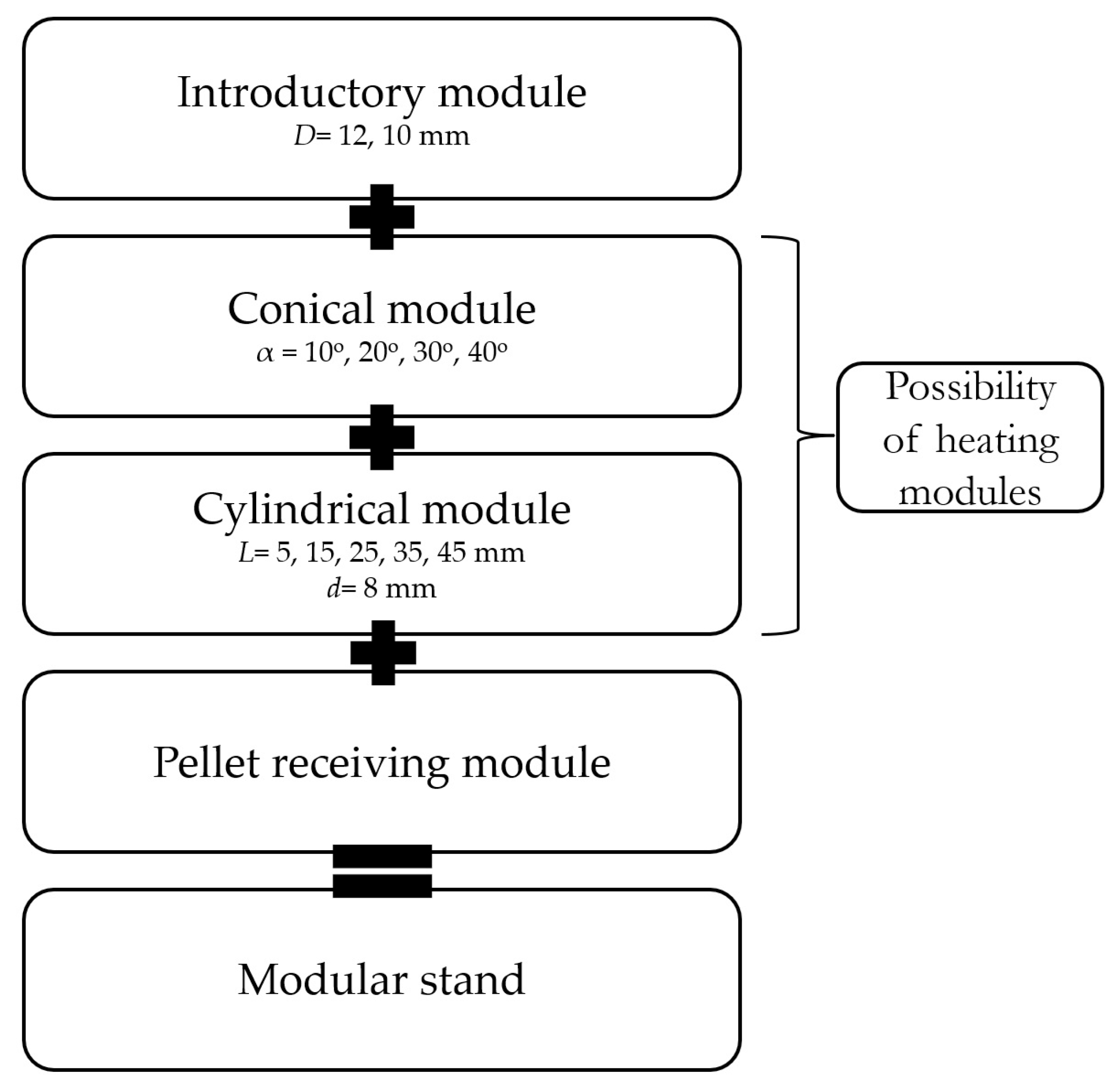
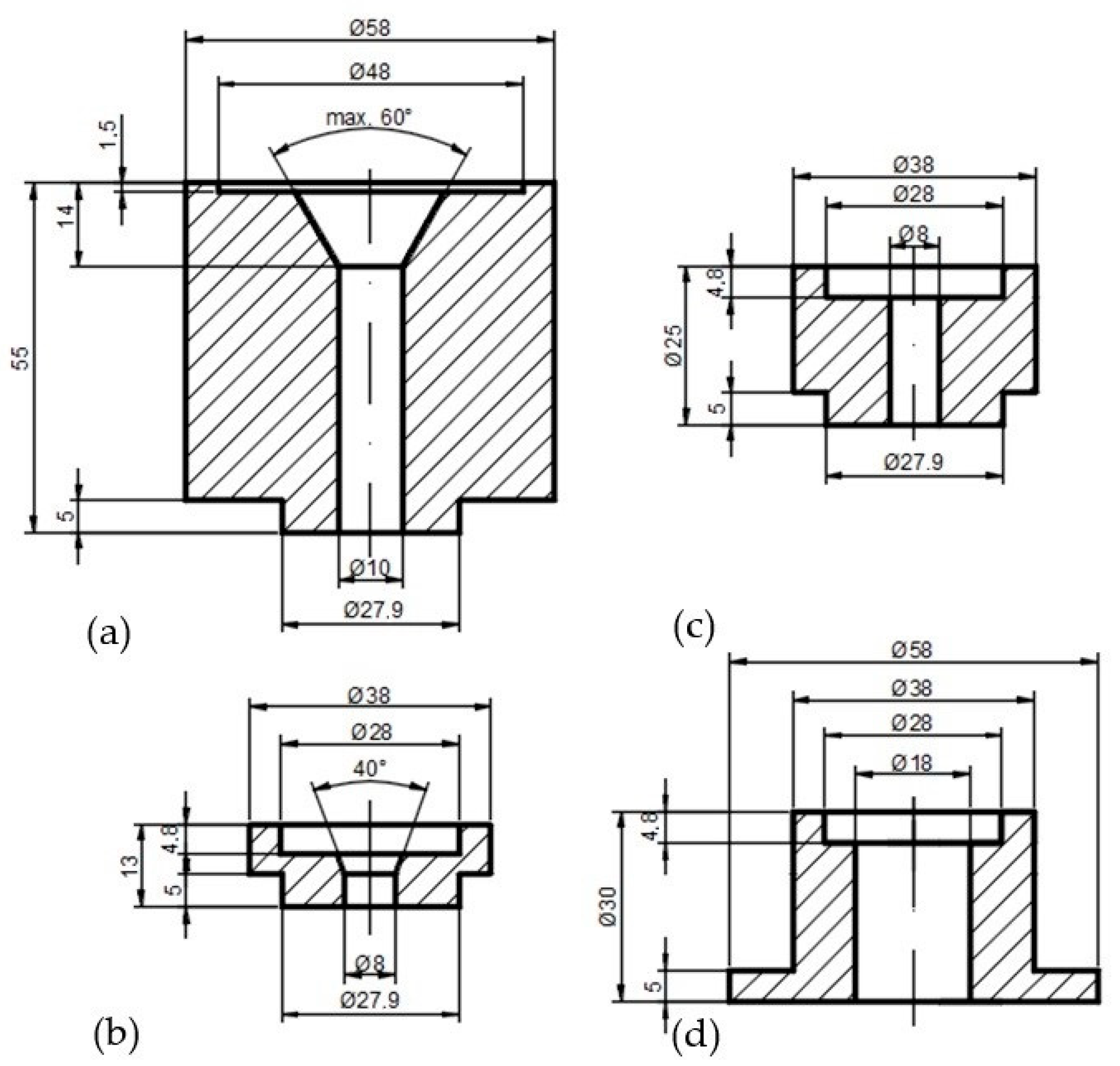
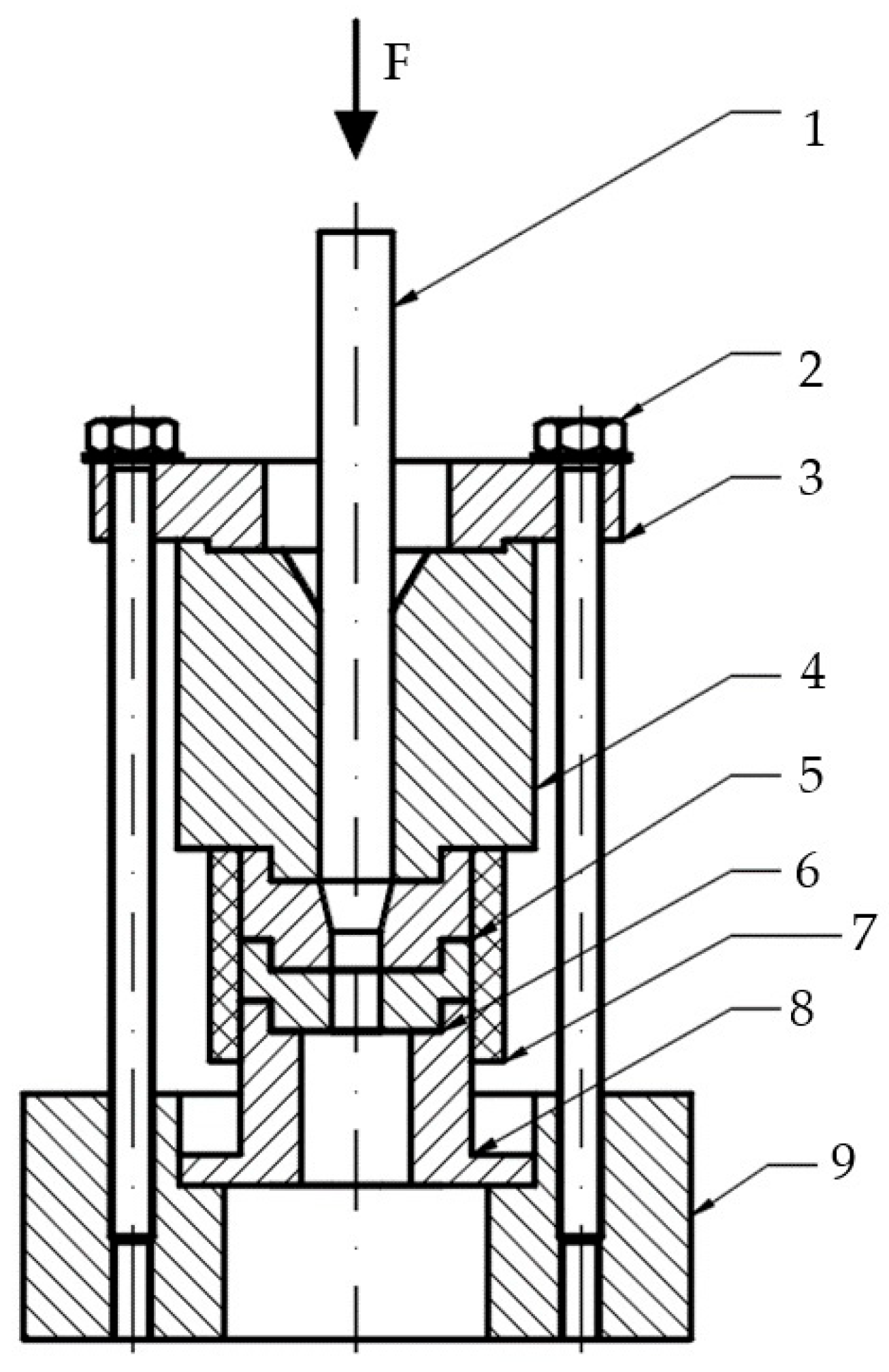
2.1. Conception of Open Chamber Test Stand

The main consideration in the design of the open chamber biomass densification test stand was that the densification process should be as similar as possible to the densification process in the single channel of a pelletiser die. Therefore, in contrast to the widely available studies on biomass densification for energy purposes (including those cited above), it was assumed that the process had to be carried out using a stand that replicated an open densification chamber. This chamber, according to the recommendations for the design of dies for pellet mills producing fuel pellets, should consist of two sections: a cylindrical and a conical section. The main geometric parameters of such a chamber are the diameter of the cylinder d, the length of the cylindrical section L, the diameter of the base of the conical section D and the apex angle of the conical section α° (Figure 1).

As defined in EN ISO 16559, a pellet is a densified biofuel produced from biomass with or without additives, in the form of a cylinder with a maximum diameter of 25 mm and a length of up to 40 mm [40]. Depending on the raw material used, pellets can be divided into wood and non-wood pellets. Following this division, the required quality parameters for pellets are contained in EN ISO 17225-2 [41] and EN ISO 17225-6 [42]. These standards divide pellets into quality classes A and B. According to the quality guideline for non-wood pellets (EN ISO 17225-6) to be included in quality classes A and B, it must have a diameter in the range 6–25 mm, in addition to meeting other requirements. For wood pellets (EN ISO 17225-2), quality classes A1, A2, and B only allow a diameter of 6 and 8 mm. Based on this assumption, it was assumed that the stand must provide the possibility of producing pellets with a diameter of d = 8 mm. This choice was motivated by several considerations. Firstly, this requires a smaller die size than for the production of larger diameter pellets and probably lower densification forces. Second, pellets with diameters of 6 and 8 mm are those mainly available on the market. Thirdly, the choice of an 8 mm rather than 6 mm channel diameter was made so that the material crushed to a nominal top size of < 1 mm would have less impact on the process than would be the case with a 6 mm channel diameter. In addition, the manufacture of the stand elements themselves is technologically easier with an 8 mm diameter than with a 6 mm diameter. Of course, in the case of a positive verification of the test stand and confirmation of its suitability for testing the process of biomass densification into pellets, it will be possible to produce and test channels with other diameters.

It was also assumed that the test lengths of the cylindrical section L would be 5; 15; 25; 35 and 45 mm. For the conical section, based on information obtained from die manufacturers as well as data available in the literature [1,8,11,13,20,43,44], the cone to be located in the stand was assumed to have an apex angle α of 10°; 20°; 30° and 40°. A further assumption was that the diameter of the cone base D was 12 and 10 mm. This would make it possible to determine whether and how, for a given angle α, the course of the process depends on the diameter D and thus on the volume of the conical section, which increases with increasing values of D.

In both cases, the diameter of the cone section is equal to the diameter of the cylindrical section d and is 8 mm.

Another important process factor, without which the pellet production process cannot be realised, is temperature. It was assumed that the stand should be able to heat the channel to a temperature of approximately 130 °C. According to the literature [14,45,46], [46,47], in the temperature range of 90–130 °C, the lignin, which is the main binding factor of the material particles to be compacted, becomes plasticised. Consideration of this factor is therefore necessary.

Analysis of the above data, and the assumptions made, allowed the bench concept shown in Figure 2 to be implemented.

The concept is that the stand will be modular. Depending on the geometry variant to be investigated, the densification channel can be composed of cylindrical and conical modules.

In addition to the pellet forming modules, the stand consists of the following parts:

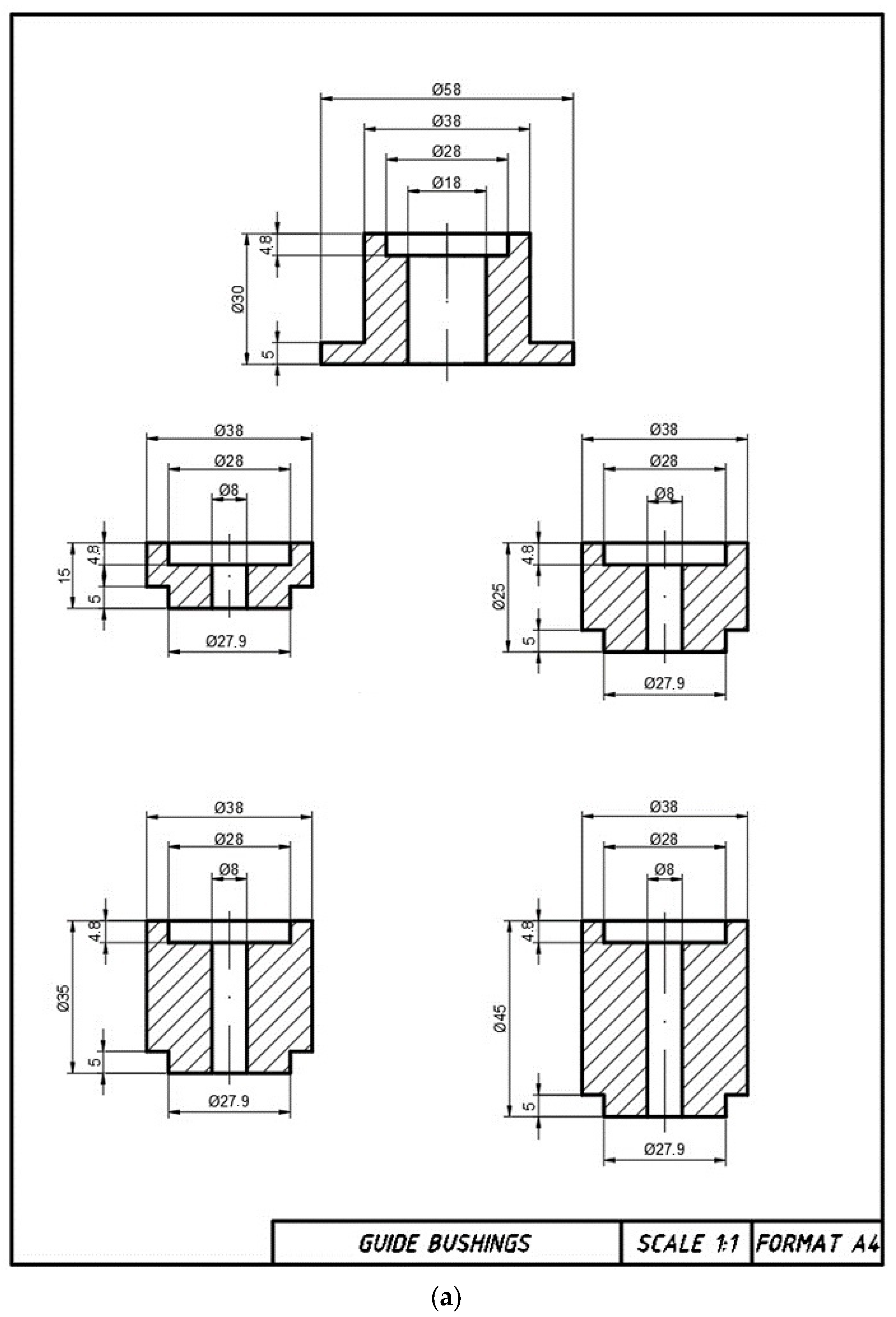
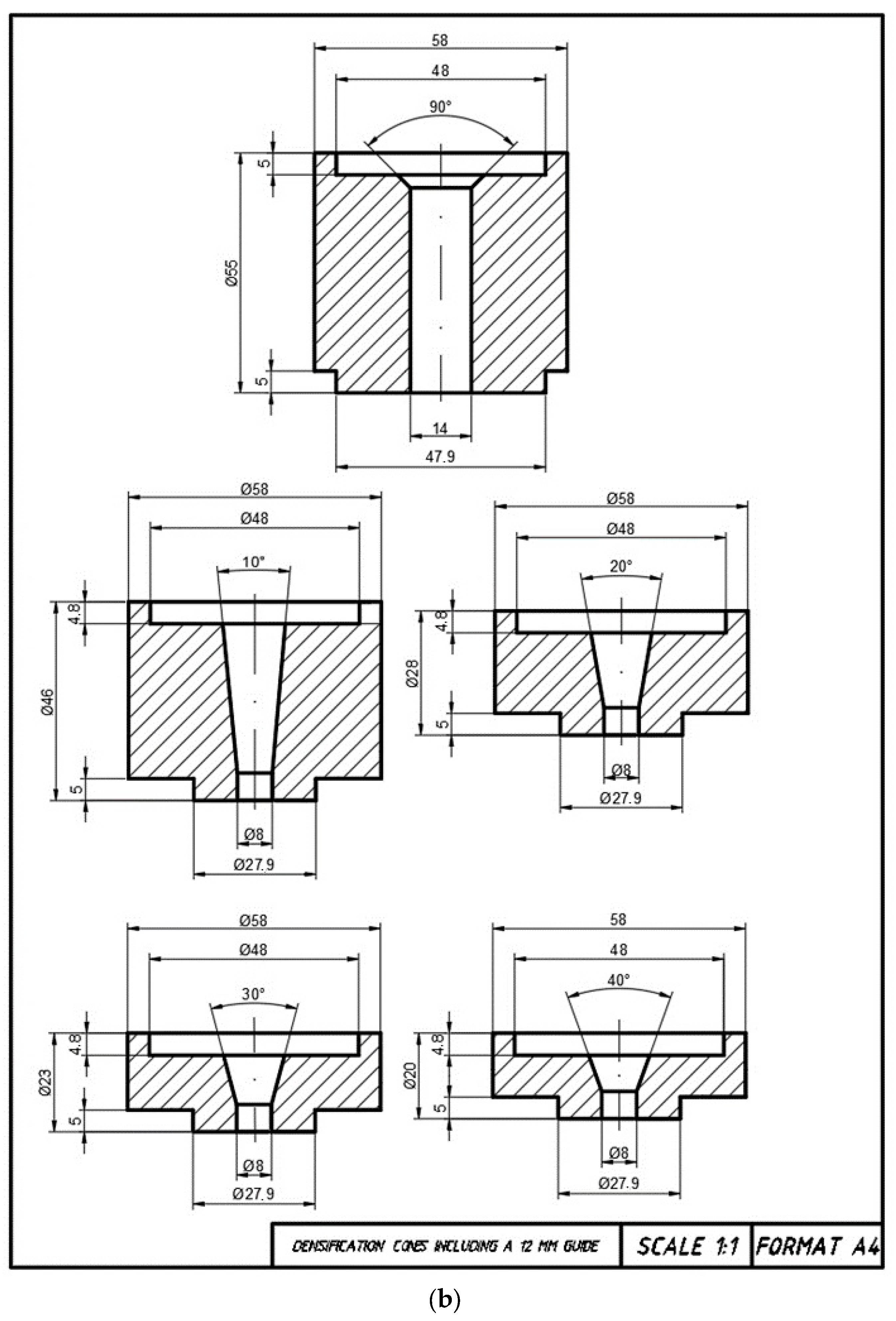
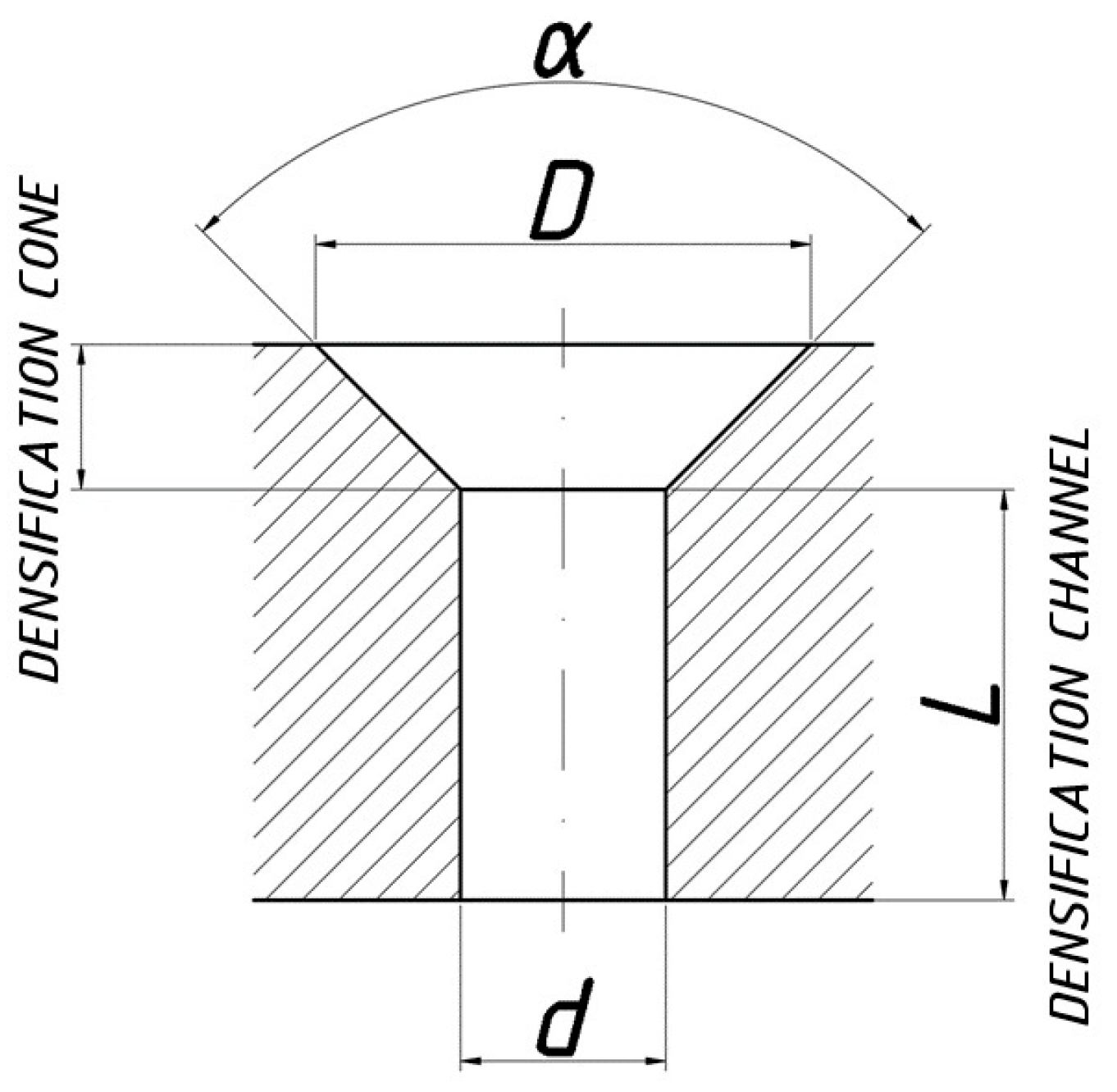
• An introduction module—a bushing into which a dose of material is introduced and in which a piston moves. The piston movement is caused by a testing machine. During densification of the material dose, the piston reaches the lower surface of the insertion bushing without entering the conical section (this approximates the real conditions of the pelletizing process, where the roller rolls on the die surface and forces the material dose into the conical sections of the densification channels). This bush has an inner diameter equal to the diameter D of the conical section;
• A pellet receiving module—a bushing with an inside diameter larger than the cylindrical section of the densification channel d, which is located directly below. The pellet exiting the channel undergoes a partial spring back and can be collected, described and forwarded for further testing;
• The case, which connects the above modules and is also mounted in the tester’s holder;
• A heater, thermocouple and temperature control module for the thickening channel.

One of the combinations of modules that make up the complete system is shown in Figure 3. Cross sections of the other components are shown in Appendix A (Figure A1a–c).

The combination of modules that form the exemplary test variant is shown in the section below (Figure 4). The movement of the piston is caused by the head of the testing machine. In this case, it is a Wance TestStar. (TSE255D, Shenzhen Wance Testing Machine CO., LTD, Shenzhen, China). During densification, the force associated with the process is recorded rather than applied. It is the geometry of the channel that determines how much force is needed to densify and move a portion of the material within the channel. This is a different approach to investigating the densification process of biomass. The optimum channel geometry is one that ensures that the required pellet quality parameters (e.g., specific gravity) are achieved with the minimum densification force.

The set of modules selected for a given test variant was placed in a case and this was mounted on the handle of a Wance TestStar test machine (Figure 5).

2.2. Testing

A preliminary study was carried out to check the suitability of the test stand.

2.2.1. Material

The research material was Miscanthus × giganteus which was obtained from the university’s energy crop plantation after the growing season, which falls in November. The choice of the plant was not random, as it is well known in the literature [32,48,49,50,51], It was also the subject of preliminary tests carried out in a closed chamber [38,39]. Miscanthus is a representative of grasses and is a low-densification material with a low bulk density. In addition, it is a species characterised by rapid growth, high resistance to weather conditions, disease and pests [52,53] which predisposes it as a good source of biomass for solid biofuel production. The material was carefully prepared according to the method described in the Wróbel’s research [54]. Preliminary results show that miscanthus itself is not an easily compactable material [38,39]. As a result, it was concluded that this material would be a good indicator material with which to determine if and how the densification process is affected by the channel geometry of the test stand.

Miscanthus is a species of perennial bunch grass, native to Southeast Asia (Japan, China, Korea) [55]. It was formed by the natural crossbreeding of Chinese miscanthus (Miscanthus sinensis Anders.) with Sugar miscanthus (Miscanthus sacchariflorus Maxim.) [56].

As a hybrid, Miscanthus giganteus is a sterile species and does not produce seeds. Reproduction is possible by dividing the carpel [32,33].

As for soil requirements, Miscanthus is not a demanding plant and can be grown on marginal soils [49,57,58]. In addition, Miscanthus is a prospective plant because of its ability to clean up wastewater from heavy metals such as cadmium, lead, copper and zinc. Ash from its combustion may find use in the fertilizer industry as a source of potassium. [36,37].

Productivity of a Miscanthus plantation is estimated at around 15 years [59]. Due to the predisposition of the seedlings to bushiness, they are grown at a spacing of 1 × 1 m.

The raw material for the production of solid biofuels are shoots that dry out after the growing season. In the first year of cultivation, the plants are not harvested, while in the second year, it is possible to obtain a yield of 8–10 t·ha⁻¹, and in the following years even 20–30 t·ha⁻¹ of dry matter [34,35].

2.2.2. Test Parameters

At this stage, miscanthus biomass with a uniform grain composition in the dry state was moistened to a moisture content of 13%. These parameters were adopted on the basis of the results obtained from preliminary tests as well as with the help of data from the literature [38,39]. In addition, based on the literature data, it was assumed that the channel temperature in the test variant would be 100 °C [13,18,45,60,61]. The constant parameters of the pressure densification process were a piston displacement speed of 300 mm·min⁻¹ and a material dose rate of 0.2 g. The dose rate was taken from the works [13,43,62] and observations of the biomass densification process on actual pellet production stations. The dosage corresponds to a layer of material injected once by the roll of the pelletiser into the die channel.

Two test variants were tested for densification of miscanthus biomass into 8 mm diameter pellets:

• 13% material moisture content, 100 °C process temperature, 12 mm inlet diameter conical section,
• 13% material moisture content, 100 °C process temperature, 10 mm inlet diameter conical section,

This allowed verification of how the process forces and specific density of the pellet change when the conical section changes in volume. Four values of the cone section apex angle were tested in each variant (10°, 20°, 30°, 40°). Because the diameters of the conical section are constant (12 and 8 and 10 and 8 mm), as the angle α changes, the height of the conical section changes and so does its volume (see Section 3). To ensure safety during the test series, critical criteria were introduced using the safety features of the testing machine in the form of limit switches. These were designed to stop the test at the point where the piston would begin to enter the conical section of the channel and cause damage. Some combinations required high densification forces, so a force of 120,000 N was set as another critical criterion that would interrupt the test. Exceeding this criterion would have resulted in irreparable damage to the test stand; moreover, these are force values that are unprecedented and undesirable in real life during the densification process, and their presence could have resulted in the destruction of the die.

As mentioned above, the software of the tester allowed us to record the curve of the force change in relation to the piston displacement. The value of the maximum force was taken as the value of the force causing densification of the test specimen. From this, the pressure exerted on the surface of the compacted material (base of the inlet cone) was determined. The force as well as the pressure exerted is a parameter that was not set during the measurement, but only recorded. It was the channel geometry, material properties, moisture content and temperature that determined the force to be applied during densification. In other words, the force generated by the test specimen was recorded (Figure 6).

2.2.3. Determination of the Specific Density of the Test Pellet

Under the conditions of each test variant, a batch of 6–7 test pellets was made (an example of the pellets obtained is shown in Figure 7). The produced pellets were placed in sealed containers for a period of 24 h. After this time, the quality parameter, the specific density DE of the pellet, was determined. During the stand verification tests, this DE was chosen as a measure of the influence of the densification channel geometry on the quality of the pellets obtained. In the case of regular pellet shapes, DE can be measured based on the pellet geometry. In the case studied, the pellets were characterised by irregular shaped faces, which is a typical shape for pellets obtained on industrial lines. In this case, a precise determination of the pellet volume is possible by using 3D scanners [63], or by dipping methods.

In this study, a quasi-liquid pycnometer (GeoPyc 1360, Micromeritics Instrument Corp., Norcross, GA, USA) was used to determine DE. The pellets produced were placed in a graduated cylinder filled with powder. The nominal particle size of the test powder was 250 µm. A characteristic of this powder is that it does not penetrate the pores of the test material or wet it, as would be the case if a liquid were used. The test method has been described in detail in previous publications [38].

2.2.4. Selection of Particle Size Composition PSD

Particle size composition has an impact on the biomass densification process. Studies confirming the importance of grain composition have been presented, among others, by Jewiarz [18,19,54,64,65,66]. For the verification study, the PSD proposed by Wróbel [54] was taken.

Preparation of the material with the assumed PSD was carried out as follows. Material was ground in a laboratory grinder with a knife grinding system and a sieve with 2 mm hole diameter. The obtained material was divided into 4 sieve classes: C₁: 0.1; C₂: 0.25; C₃: 0.5 and C₄: 1. They were then used to compose a mixture with the particle size composition shown in

Table 1. PSD of test material.

Sieve Classes	C1	C2	C3	C4
Share in the mixture (%)	20	32	14.4	33.6

).

2.2.5. Moisturisation and Moisture Content Measurement

In order to achieve and maintain a material moisture content of 13%, a climate chamber was used (KBF-S 115, BINDER GmbH, Tuttlingen, Germany). This device provides the ability to precisely moisten the material to the desired level, which is important for the accuracy of the results. To confirm the required moisture content of the material, before densification, its moisture content was determined according to EN ISO 18134-3:2015-1 [67].

3. Results

As the cone modules were manufactured in two geometrical variants—entrance diameter D = 12 mm and 10 mm—it was decided to check how the volume of the conical part would change. The course of these changes is shown in the graph in Figure 8. For the conical part with an entrance diameter of D = 12 mm, the volume will be greater for each variant than for D = 10 mm. Comparable volumes can be achieved with a cone module of α = 10° for D = 10 mm and α = 20° for D = 12 mm. Observing this relationship, it could be expected that higher densification pressures would be observed with conical modules with a hole diameter of D = 12 mm than with D = 10 mm. This would be due to the fact that cones with a larger volume would contain a greater amount of material and therefore a greater amount of material will need to be pre-compacted in the cone section than is the case with densification cones with a diameter of D = 10 mm. Also, the sidewall area of the conical section increases which, according to the observations of Križan [20], causes an increase in pressure

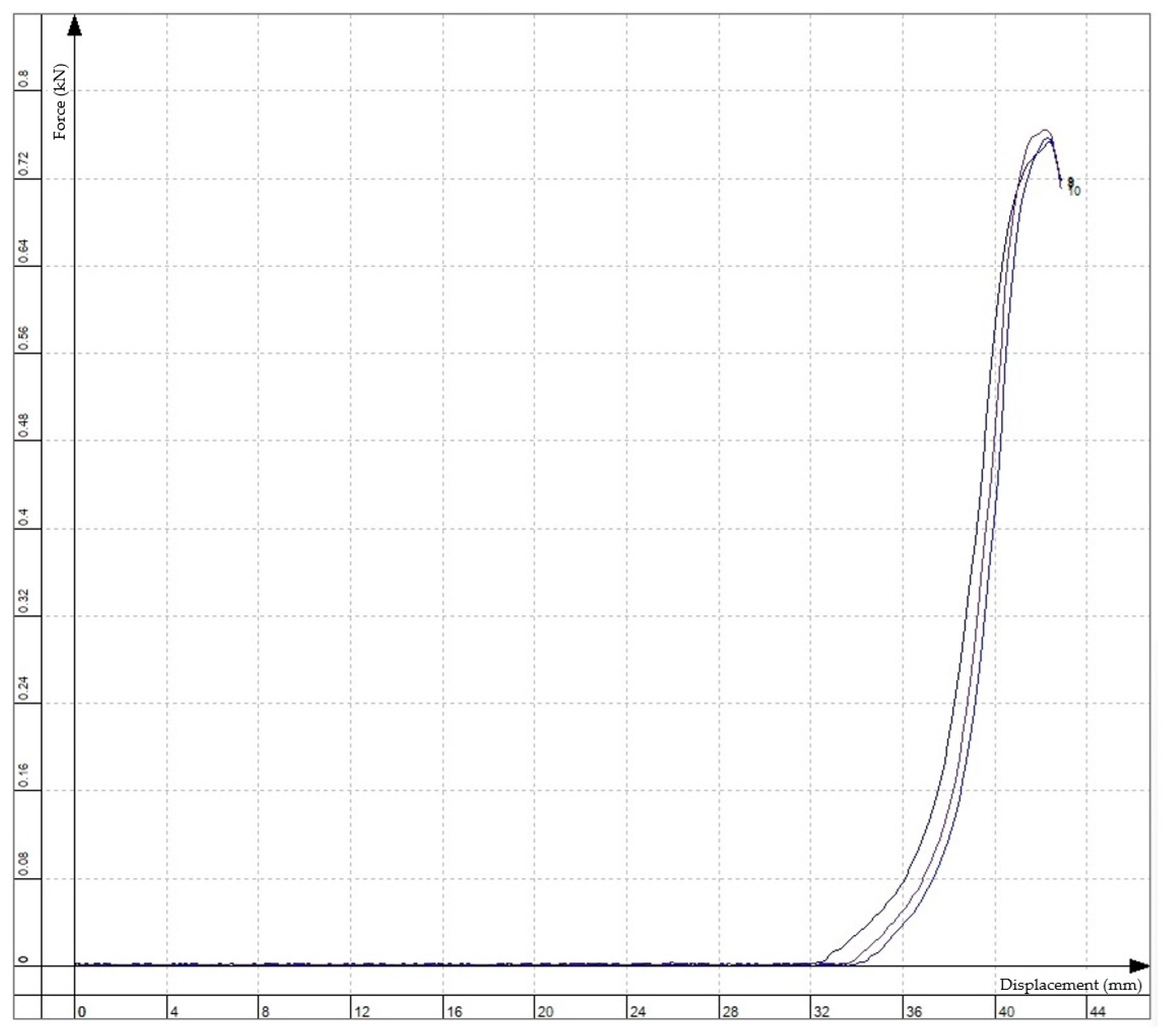
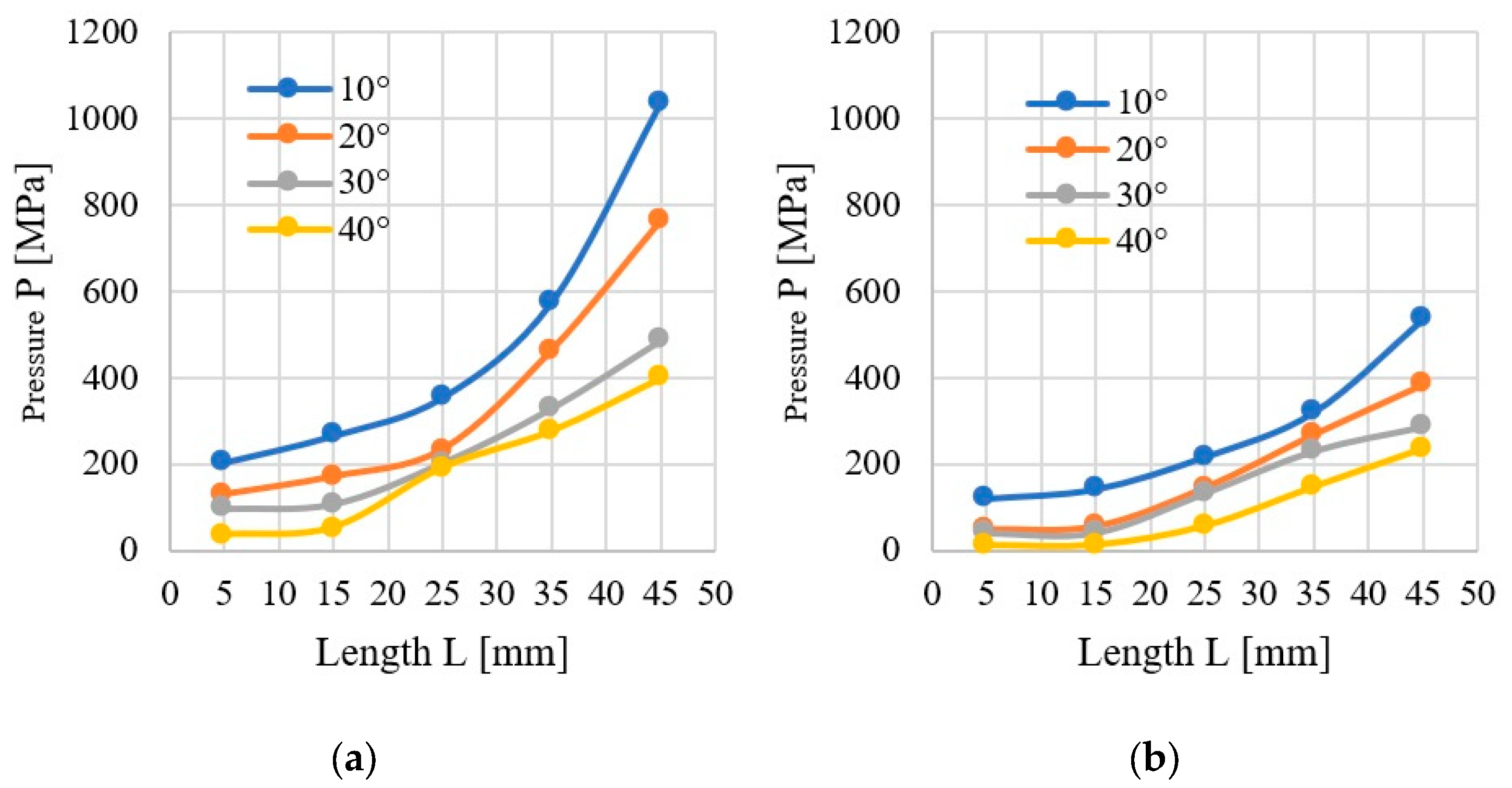
3.1. Pressure

The test apparatus allowed the current recording of the force value, which was necessary to push the material through the cone module and further through the cylindrical module. In order to make it easier to refer to the results of basic or literature tests, the results obtained in the form of force values F were converted into pressure P.

The first relationship to be determined from the results was that between process pressure and the length of the cylindrical section L for four values of cone angle α = 10°; 20°; 30° and 40°. For each variant of angle α, the length of the cylindrical module was L = 5, 15, 25, 35, 45 mm. In each case, the conical and cylindrical modules were heated to a temperature of 100 °C. A material with a moisture content of 13% was used for the test. The obtained relationships are presented in the form of graphs.

Figure 9 shows the dependence of the process pressure on the length of the densification channel L (cylindrical module) for each of the conical modules. As can be seen, the assumption is confirmed that higher pressure accompanies the process carried out on a stand equipped with conical modules of diameter D = 12 mm compared to modules with D = 10 mm. Križhan’s research contains a similar conclusion [20].

It was observed that the highest pressure accompanied the variant α = 10°, L= 45 mm (1037.54 MPa). When using a conical module with an angle of α = 20°, it can be seen that the greatest increase in pressure accompanied the use of a cylindrical module longer than L= 25 mm. A cylindrical module with an angle of α = 30° is characterised by lower pressure than α = 20°, but it can also be seen that the use of cylindrical modules longer than L = 25 mm does not lead to the same pressure increase as with α = 10° and 20°. The lowest pressure for a diameter of D = 12 mm was achieved using a conical module with α = 40° and L = 5 mm. The pressure associated with this variant was only 36.5 MPa. It can be observed on the graph that, for a given length L, the value of the densification pressure increased as the angle α decreased from 40 to 10°.

Noticeably lower pressure values were recorded for the densification process carried out on a stand equipped with conical modules with an inlet hole diameter of D = 10 mm. The dynamics of the pressure increase after the length of the densification module L = 25 mm was also lower here. As in the case of D = 12 mm, the conical module with an angle α = 10° had the highest pressure accompanying the process, and as the angle value increased, the pressure decreased. The highest pressure accompanying the process was 536.6 MPa for the variant α = 10°, L= 45 mm. The lowest pressure value was observed for densification of the material using the combination of α = 40° and L = 5 mm, (12.01 MPa).

The results obtained regarding the geometry of the densification channel are different from the trends obtained in their study by Wu et al. [24]. They simulated the densification process using densification cones with opening angles ranging from α = 15°–120°. They observed that decreasing values of angle α decreased the granulation force. However, in their study, the change in angle was not accompanied by a change in cone volume. Unlike in the case presented here, where the volume of the cone, and thus the volume of the compacted material, increased as the angle value decreased. This is most likely the reason that, in all the cases studied, the pressure value increases with an increase in cone volume caused by a decrease in the angle α from 40° to 10°.

It can also be seen that the L-dependent pressure increase has less dynamics when using modules with D = 10 mm than when using D = 12 mm. It was also shown that both L and angle α cause changes in the readings of the densification pressure accompanying the process. From an economic point of view, we care that the channel geometry generates the lowest possible process pressure, but from a process quality point of view, we care that the geometry produces a pellet with the desired DE density. Thus, the right geometry is one that, at a minimal pressure, achieves the required threshold quality parameter (in this case, a specific density of 1 g·cm⁻³). Thus, in order to determine which channel geometry variant is appropriate, the DE of the pellets obtained was determined.

Winter [21], by densifying RDF, showed that the pellets were of high quality when using a cone α = 28°, while also recording the lowest pressure among the tested variants. In the present study, it should be noted that the lowest pressure accompanying the configuration guarantees the production of pellets with parameters that meet the normative criteria of α = 40° for D = 10 and 12 mm. However, pellets of the required quality can be produced in a channel with α = 30°, but this requires higher pressure. Thus, one can consider whether a single universal die could be used to densify miscanthus and RDF to produce high-quality pellets. An interesting observation was reported by Hu et al. [23] as they showed that the lowest energy consumption occurred when rice grass was compacted using α = 60.5° cones. Despite being herbaceous biomass, one can see a big difference between rice grass and miscanthus, as the lowest pressure, and thus force, was registered for miscanthus by α = 40°. Compared to preliminary studies [38], it should be noted that the specific construction of the stand made it possible to produce pellets that meet the normative criteria. The preliminary studies took place using a closed chamber and different compaction pressures (130.8; 196.2; 261.6; 327 MPa), but for none of the tested variants, with moisture content close to 13%, did miscanthus reach a density that would meet the quality requirements. Thus, it should be noted that the specific construction and properly selected channel geometry have a significant effect on pellet density.

3.2. Density

The specific density DE of the pellets obtained is the only quality parameter analysed at this stage. The influence of channel geometry on the value of this parameter is shown in the graphs in the same arrangement as for pressure. The specific density of the pellets was determined for the pellets obtained from each test batch. The minimal value that a pellet must achieve to meet the quality criterion is 1 g·cm⁻³. Standard EN ISO 17225-1:2021 [31] for quality class A, requires the bulk density of the pellet to be at least 600 kg·m⁻³. Due to the number of test pellets obtained, it was not possible to determine the bulk density. However, it was assumed [54] that a pellet with a bulk density of 600 kg·m⁻³ is simultaneously characterised by a specific density of DE pellets above 1 g·cm⁻³.

A pair of graphs (Figure 10a,b) show the course of the densification process carried out for the four measurement variants discussed above. Additionally, a horizontal green line is placed on the graph, indicating the value of 1 g·cm⁻³. This is the minimum value which allows the pellet to be considered as meeting the quality requirements set out in the standard. With it, the results obtained can be easily interpreted.

Figure 10a shows the data obtained for the densification process carried out with a cone modulus of D = 12 mm. It can be observed that for a conical module with an angle α = 10°, each cylindrical module used makes it possible to obtain a pellet with the required density, and the highest value (1.31 g·cm⁻³) was obtained using a cylindrical module of length L = 45 mm. For α = 20°, it can be seen that by using a cylindrical module of L = 5 mm, the pellet does not reach the desired density level. At this angle, elongation of the cylindrical module makes it possible to produce a pellet with the correct density when using a cylindrical module of length L = 7–8 mm (based on the theoretical curve in Figure 10a). It should also be noted that the maximum density can be obtained using L = 25 mm, a longer cylindrical section does not result in a greater increase in density values. For α = 30°, as in the previous case, only the shortest cylindrical module did not achieve the desired pellet density. Each successive module causes an increase in this value, which is within the range that guarantees the achievement of a pellet with DE > 1 g·cm⁻³; according to the curve, this is possible already at approx. L = 10 mm.

A conical module with an angle of α = 40° only in combination with a cylindrical module of length L = 25 mm makes it possible to produce pellets with the density required by the norm. The use of a shorter module results in a lower value than required. Pellets meeting the normative requirements can be produced for α = 10° at a pressure P of approximately 204 MPa; α = 20°, P = 136 MPa; α = 30°, P = 105 MPa; α = 40°, P = 186 MPa. Thus, four variations of channel geometry are available to achieve the required pellet density, but the lowest densification pressure (105 MPa) and therefore the lowest labour input will be required for the configuration α = 30°, L = 7–8 mm, D = 12 mm.

Figure 10b shows the data obtained from the densification process carried out using a cone module of D = 10 mm. It can be seen that the batch made with a conical module of α = 10°, irrespective of the length of the cylindrical module used, achieved a density of DE > 1 g·cm⁻³ in every configuration. The highest density was recorded for the combination of α = 10° and L = 45 mm and was 1.34 g·cm⁻³. As for α = 10° and α = 20°, they also achieved the normatively required density for all combinations used, irrespective of the length of the cylindrical module. For α = 30°, on the other hand, it was noted that the configuration with the shortest cylindrical modulus, L = 5 mm, did not guarantee a pellet density above 1 g·cm⁻³, but following the curve of L = 7 mm did. The α = 40° module had the fewest combinations of cylindrical modules to guarantee the desired pellet density, as two configurations do not achieve the required densities. Both L = 5 mm and L = 15 mm achieved densities that did not meet the normative requirements. Extending the cylindrical module positively influenced the densification process, as each successive combination from L = 25 mm to L = 45 mm increased its density, allowing the production of pellets with the desired density. In theory, the length to obtain the highest quality pellet for α = 40° would be L = 18 mm.

The pressure associated with the process in the case of D = 10 mm for the combinations enabling the production of pellets with a density DE > 1 g·m⁻³ is for α = 10°, P = 121 MPa; α = 20°, P = 51 MPa; α = 30°, P = 39 MPa; α = 40°, P = 27 MPa. This means that, despite the few configurations that guarantee the production of pellets with the desired density, the configuration with a module with α = 40° requires the lowest pressure among the configurations with D = 10 mm to produce a pellet DE = 1 g·m⁻³. Comparing the pressure values for the input cone diameter D = 10 mm to D = 12 mm, it should be noted that they are significantly lower.

Therefore, it can be concluded that the presented stand makes it possible to carry out tests of the biomass densification process that simulate the pelleting process with a wide range of parameters (the set of these parameters may be wider than in the presented tests). At this stage of the research, we can also indicate which variants will be promising and should be continued, e.g., on real objects (pelleting machines equipped with dies with the geometry of the channel determined at the stage of the presented research), and which variants should be rejected because they do not guarantee that the required quality of pellet will be achieved or generate high values of densification pressure.

Butler and McColly [28] in their study showed that changing the volume of the densification chamber affects pellet quality parameters. Using the same dosage and pressure, they achieved a higher pellet density for a chamber with a smaller volume. A similar observation was noted in the research presented here. The study also showed that an angle of 40° is the optimal angle for miscanthus biomass, and a similar angle of 37.6° was found to be optimal for the rice straw studied by Mišljenović [22]. 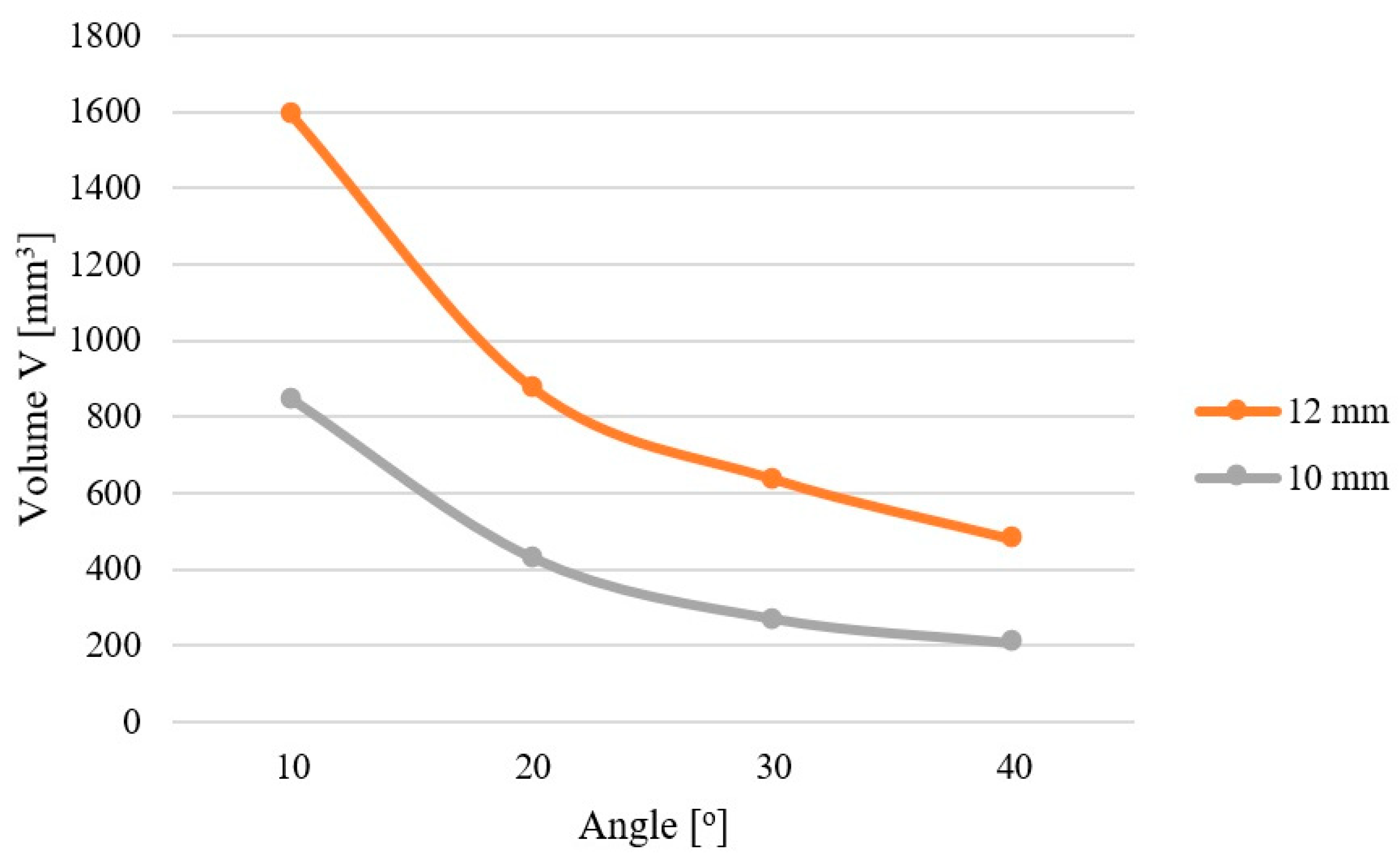Miscanthus and rice straw as grass shoots can therefore be compacted in a channel of similar geometry.

4. Discussion and Conclusions

The presented solution is innovative in terms of its multifunctionality and facilitates the solution of the problem of selecting the appropriate geometry of the densification chamber in the production of solid biofuels. Obviously, the results obtained should still be verified on real dies, but the tests on the presented stand considerably extend the scope of tests on real matrices, which will significantly reduce the costs of tests and their duration. Due to its universal nature, the solution can also be used in other industrial sectors that deal with the densification of bulk materials.

The specific characteristics of the materials tested (density, porosity, structural design, roughness, friction coefficient, etc.), significantly determine the densification process. These characteristics are beyond our control and their effect on the process is difficult to determine. Therefore, obtaining high quality pellets requires a densification channel geometry adapted to the biomass of the plant species concerned.

Most of the research relating to biomass densification concerns materials that are of woody biomass [11,13,14,20], which is a more easily densified material. The current study presents the results of an experiment in which a more difficult material was used—herbaceous biomass—which was not supplemented in any way with binders or other materials and despite this, a channel geometry was found to produce a pellet of the desired density.

The results obtained from the presented study show how complex a process the pressure densification of biomass is and how many factors can have a significant impact on the quality of the pellets produced. The study shows that the geometry of the densification chamber, the pressure, the process temperature and the moisture content of the material have a visible effect on the DE of the pellets.

The aim of the research was to show whether the presented stand allowed research into whether there is an effect from the geometry of the densification channel on the quality parameters of solid biofuels and, if there is, to determine what this effect is—favourable or not. Parameters such as grain composition, time and speed of densification have been standardised to neglect their influence and focus fully on the geometry, but of course the stand allows these relationships to be investigated as well.

The results obtained and their comparison with literature data indicate that the geo-metrics of the densification channel is a factor that has a key influence on the quality parameters of the pellets obtained, and its proper selection results in a decrease in the pressure necessary for the process, and thus a reduction in production costs.

Analyzing the results obtained with the results from the literature, it should be stated that the geometry of the channels must be selected according to the material and its parameters. The analyzed literature studies consider different materials and the geometry for each of them is different. The relationship that appears in the literature that the compaction pressure decreases with an increase in the angle of the conical section (under the condition that with an increase in the angle, the volume of this section decreases, which takes place when a change in the angle does not cause a change in the diameter of the entrance to this section) was confirmed. The cylindrical section is responsible for holding the material in the chamber during densification. An increase in its length always results in an increase in pressure. The advantage of the presented stand is that we can determine not only the trends of the changes in the pressure and density of the pellet, but also indicate which geometry for the tested material and other factors affecting the process will allow us to obtain the required quality of pellet at the minimum pressure. Often, several variants of the geometry allow us to obtain the required quality and then we can choose the one with the lowest pressure, or in the case of testing several materials, we can choose a variant common to them, if there is one. This, in turn, will make it possible to produce densification matrixes that are universal for the material groups, which will reduce the cost of pellet production.