Performance Improvement of Wireless Power Transfer System for Sustainable EV Charging Using Dead-Time Integrated Pulse Density Modulation Approach
Abstract
1. Introduction
- Insertion of dead time in the PDM control technique for HF inverters in WPT EV chargers.
- Effect of dead time in PDM is analyzed; variation in dead time leads to a reduction in the current ripple.
- Dead time and pulse redistribution to reduce current fluctuations, promoting efficient output voltage regulation and enabling zero voltage switching operation in inverters.
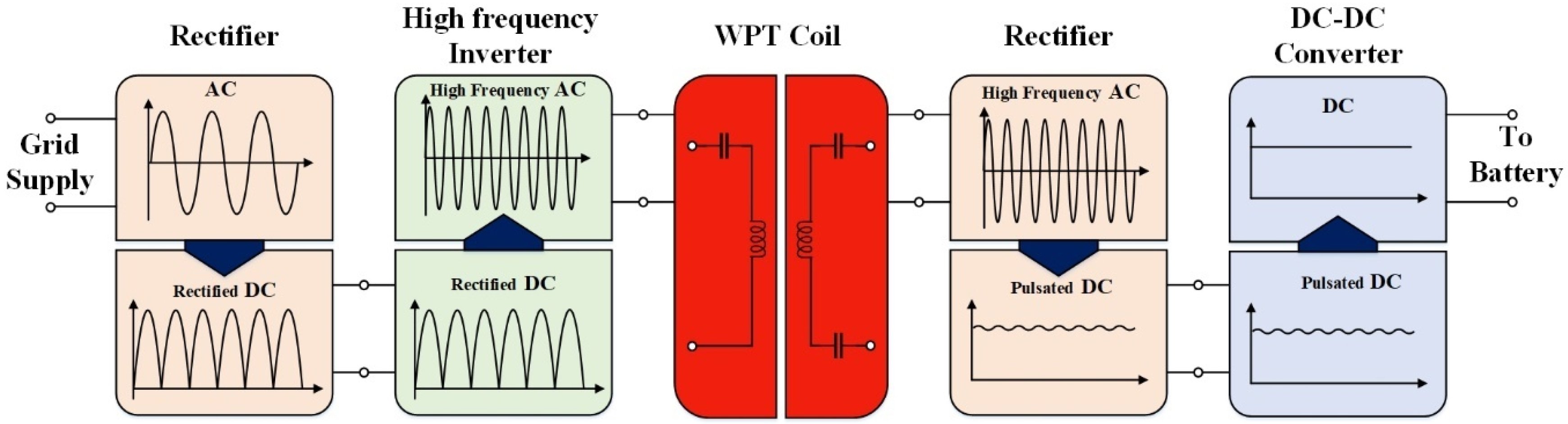
2. Switching Characteristics of a WPT HF Inverter
2.1. Pulse Density Modulation
2.2. Characteristics of Switching with Zero Dead-Time
2.3. Characteristics of Switching with Dead Time
3. Effects of Dead Time on the Fundamental Components
3.1. Theoretical Derivation of the HF Inverter Output Voltage in WPT
3.2. Modeling of Resonance Compensation Network for WPT
4. Dead-Time Effects in WPT System via Simulation and Experimental
5. Analysis of Simulation and Experimental Results
5.1. Simulation Results and Discussions
5.2. Expermental Results and Discussions
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kwilinski, A.; Lyulyov, O.; Pimonenko, T. Environmental Sustainability within Attaining Sustainable Development Goals: The Role of Digitalization and the Transport Sector. Sustainability 2023, 15, 11282. [Google Scholar] [CrossRef]
- Shanmugam, Y.; Narayanamoorthi, R.; Vishnuram, P.; Bajaj, M.; Aboras, K.M.; Thakur, P. A Systematic Review of Dynamic Wireless Charging System for Electric Transportation. IEEE Access 2022, 10, 133617–133642. [Google Scholar] [CrossRef]
- Zhang, W.; Fang, X.; Sun, C. The Alternative Path for Fossil Oil: Electric Vehicles or Hydrogen Fuel Cell Vehicles? J. Environ. Manag. 2023, 341, 118019. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Basset, M.; Gamal, A.; Hezam, I.M.; Sallam, K.M. Sustainability assessment of optimal location of electric vehicle charge stations: A conceptual framework for green energy into smart cities. Environ. Dev. Sustain. 2024, 26, 11475–11513. [Google Scholar] [CrossRef]
- Su, F.; He, X.; Dai, M.; Yang, J.; Hamanaka, A.; Yu, Y.; Li, J. Estimation of the cavity volume in the gasification zone for underground coal gasification under different oxygen flow conditions. Energy 2023, 285, 129309. [Google Scholar] [CrossRef]
- Dimitriadou, K.; Rigogiannis, N.; Fountoukidis, S.; Kotarela, F.; Kyritsis, A.; Papanikolaou, N. Current Trends in Electric Vehicle Charging Infrastructure; Opportunities and Challenges in Wireless Charging Integration. Energies 2023, 16, 2057. [Google Scholar] [CrossRef]
- Sagar, A.; Kashyap, A.; Nasab, M.A.; Padmanaban, S.; Bertoluzzo, M.; Kumar, A.; Blaabjerg, F. A Comprehensive Review of the Recent Development of Wireless Power Transfer Technologies for Electric Vehicle Charging Systems. IEEE Access 2023, 11, 83703–83751. [Google Scholar] [CrossRef]
- Liu, W.; Chau, K.; Tian, X.; Wang, H.; Hua, Z. Smart wireless power transfer—opportunities and challenges. Renew. Sustain. Energy Rev. 2023, 180, 113298. [Google Scholar] [CrossRef]
- Sari, V. Design and Implementation of a Wireless Power Transfer System for Electric Vehicles. World Electr. Veh. J. 2024, 15, 110. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, Y.; Zang, J.; Liu, Z.; Zhou, J.; Wang, J.; Shi, G. An Embedded DC Power Flow Controller Based on Full-Bridge Modular Multilevel Converter. IEEE Trans. Ind. Electron. 2024, 71, 2556–2566. [Google Scholar] [CrossRef]
- Vishnuram, P.; Panchanathan, S.; Rajamanickam, N.; Krishnasamy, V.; Bajaj, M.; Piecha, M.; Blazek, V.; Prokop, L. Review of Wireless Charging System: Magnetic Materials, Coil Configurations, Challenges, and Future Perspectives. Energies 2023, 16, 4020. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Z.; Guan, Y.; Xu, D. Overview of Megahertz Wireless Power Transfer. Proc. IEEE 2023, 111, 528–554. [Google Scholar] [CrossRef]
- Rayan, B.A.; Subramaniam, U.; Balamurugan, S. Wireless Power Transfer in Electric Vehicles: A Review on Compensation Topologies, Coil Structures, and Safety Aspects. Energies 2023, 16, 3084. [Google Scholar] [CrossRef]
- Yin, Y.; Xiao, Y.; Wang, C.; Yang, Q.; Jia, Y.; Liao, Z. A Design Methodology for EV-WPT Systems to Resonate at Arbitrary Given Bands. Energies 2022, 15, 213. [Google Scholar] [CrossRef]
- Zhang, J.; Feng, X.; Zhou, J.; Zang, J.; Wang, J.; Shi, G.; Li, Y. Series-Shunt Multiport Soft Normally Open Points. IEEE Trans. Ind. Electron. 2023, 70, 10811–10821. [Google Scholar] [CrossRef]
- Ahire, D.B.; Gond, V.J.; Chopade, J.J. Compensation topologies for wireless power transmission system in medical implant applications: A review. Biosens. Bioelectron. 2022, 11, 100180. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Dominic Savio, A.; Balaji, C.; Rajamanickam, N.; Kotb, H.; Elrashidi, A.; Nureldeen, W. A Comprehensive Review on Efficiency Enhancement of Wireless Charging System for the Electric Vehicles Applications. IEEE Access 2024, 12, 46967–46994. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Y.; Liu, Z. Joint impact of service efficiency and salvage value on the manufacturer’s shared vehicle-type strategies. RAIRO-Oper. Res. 2024, 58, 2261–2287. [Google Scholar] [CrossRef]
- Ju, Y.; Liu, W.; Zhang, Z.; Zhang, R. Distributed Three-Phase Power Flow for AC/DC Hybrid Networked Microgrids Considering Converter Limiting Constraints. IEEE Trans. Smart Grid 2022, 13, 1691–1708. [Google Scholar] [CrossRef]
- Poornima, P.U.; Elanthirayan, R.; Pongiannan, R.K.; Pravin, A.R.; Franklin, J.; Brindha, R. A Single Phase Cascaded H Bridge PV Inverter’s Harmonic Compensation Strategy in an Unbalanced Condition. In Proceedings of the 2023 International Conference on System, Computation, Automation and Networking, Puducherry, India, 17–18 November 2023. [Google Scholar]
- Aretxabaleta, I.; De Alegria, I.M.; Andreu, J.; Kortabarria, I.; Robles, E. High-Voltage Stations for Electric Vehicle Fast-Charging: Trends, Standards, Charging Modes and Comparison of Unity Power-Factor Rectifiers. IEEE Access 2021, 9, 102177–102194. [Google Scholar] [CrossRef]
- Li, S.; Yu, X.; Yuan, Y.; Lu, S.; Li, T. A Novel High-Voltage Power Supply with MHz WPT Techniques: Achieving High-Efficiency, High-Isolation, and High-Power-Density. IEEE Trans. Power Electron. 2023, 38, 14794–14805. [Google Scholar] [CrossRef]
- Liu, C.; Guan, Y.; Wang, Y.; Xu, D. Optimal Impedance Design for Dual-Branch High-Frequency Inverter Based on Active Regulation and Passive Projection. IEEE Trans. Power Electron. 2023, 38, 11183–11192. [Google Scholar] [CrossRef]
- Viqar, S.; Ahmad, A.; Kirmani, S.; Rafat, Y.; Hussan, M.R.; Alam, M.S. Modelling, Simulation and Hardware Analysis of Misalignment and Compensation Topologies of Wireless Power Transfer for Electric Vehicle Charging Application. Sustain. Energy Grids Netw. 2024, 38, 101285. [Google Scholar] [CrossRef]
- Ding, Z.; Huang, Z.; Pang, M.; Han, B. Design of Bi-Planar Coil for Acquiring Near-Zero Magnetic Environment. IEEE Trans. Instrum. Meas. 2022, 71, 6001310. [Google Scholar] [CrossRef]
- Marques, E.G.; Costa, V.S.; Mendes, A.M.S.; Perdigao, M.S. Inductive Power Transfer in Electric Vehicles: Past and Future Trends. IEEE Veh. Technol. Mag. 2023, 18, 111–122. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, K.; Li, S.; Yang, F.; Cheng, S.; Eldeeb, H.H.; Kang, J.; Xu, G. Shielding Optimization of IPT System Based on Genetic Algorithm for Efficiency Promotion in EV Wireless Charging Applications. IEEE Trans. Ind. Appl. 2022, 58, 1190–1200. [Google Scholar] [CrossRef]
- Pongiannan, R.K.; Yadaiah, N. FPGA Based Space Vector PWM Control IC for Three Phase Induction Motor Drive. In Proceedings of the 2006 IEEE International Conference on Industrial Technology, Mumbai, India, 15–17 December 2006. [Google Scholar]
- Zhou, J.; Guidi, G.; Chen, S.; Tang, Y.; Suul, J.A. Conditional Pulse Density Modulation for Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2024, 39, 88–93. [Google Scholar] [CrossRef]
- Cetin, S.; Yenil, V. High Efficiency Constant Voltage Control of LC/S Compensated Wireless Power Transfer Converter Based on Pulse Density Modulation Control. Int. J. Electron. 2023, 110, 54–72. [Google Scholar] [CrossRef]
- Pongiannan, R.K.; Sathiyanathan, M.; Vinothkumar, U.; Junaid, K.M.; Prakash, A.; Yadaiah, N. FPGA—Realization of Digital PWM Controller Using Q-Format-Based Signal Processing. JVC J. Vib. Control. 2015, 21, 938–948. [Google Scholar] [CrossRef]
- Franklin, J.; Richard Pravin, A.; Pongiannan, R.K. The Performance Analysis of Single Phase PWM Inverter with Various Delay Times. In Proceedings of the 2023 International Conference on Circuit Power and Computing Technologies (ICCPCT), Kollam, India, 10–11 August 2023. [Google Scholar]
- Suresh Kumar, A.; Pongiannan, R.K.; Bharatiraja, C.; Yusuf, A.; Yadaiah, N. A Magnetically Coupled Converter Connected Three Phase Voltage Source Inverter for EV Applications. Int. J. Power Electron. Drive Syst. 2019, 10, 645–652. [Google Scholar] [CrossRef]
- Schettino, G.; Di Tommaso, A.O.; Miceli, R.; Nevoloso, C.; Scaglione, G.; Viola, F. Dead-Time Impact on the Harmonic Distortion and Conversion Efficiency in a Three-Phase Five-Level Cascaded H-Bridge Inverter: Mathematical Formulation and Experimental Analysis. IEEE Access 2023, 11, 32399–32426. [Google Scholar] [CrossRef]
- Vemula, N.K.; Parida, S.K. Impact of Time Delay on Performance and Stability of Inverter-Fed Islanded MG Utilizing Internal Model Controller. Int. J. Electr. Power Energy Syst. 2023, 146, 108713. [Google Scholar] [CrossRef]
- Arrozy, J.; Retianza, D.V.; Duarte, J.L.; Caarls, E.I.; Huisman, H. Influence of Dead-Time on the Input Current Ripple of Three-Phase Voltage Source Inverter. Energies 2023, 16, 688. [Google Scholar] [CrossRef]
- Kavimandan, U.D.; Galigekere, V.P.; Onar, O.; Ozpineci, B.; Mahajan, S.M. Comparison of Dead-Time Effects in a WPT System Inverter for Different Fixed-Frequency Modulation Techniques. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Chicago, IL, USA, 23–26 June 2020; pp. 277–283. [Google Scholar] [CrossRef]
- Chatterjee, D.; Chakraborty, C.; Mukherjee, K.; Dalapati, S. Current-Zero-Crossing Shift for Compensation of Dead-Time Distortion in Pulse-Width-Modulated Voltage Source Inverter. Power Electron. Drives 2023, 8, 84–99. [Google Scholar] [CrossRef]
- Jo, C.H.; Kim, D.H. Reconfigurable LLC Resonant Converter for Bidirectional Electric-Vehicle Chargers. IEEE Trans. Power Electron. 2023, 38, 15168–15172. [Google Scholar] [CrossRef]
- Liu, X.; Gao, F.; Zhang, Y.; Khan, M.M.; Zhang, Y.; Wang, T.; Rogers, D.J. A Multi-Inverter High-Power Wireless Power Transfer System with Wide ZVS Operation Range. IEEE Trans. Power Electron. 2022, 37, 14082–14095. [Google Scholar] [CrossRef]
- Bathala, K.; Kishan, D.; Harischandrappa, N. High-frequency Isolated Bidirectional Dual Active Bridge DC-DC Converters and Its Application to Distributed Energy Systems: An Overview. Int. J. Power Electron. Drive Syst. 2023, 14, 969–991. [Google Scholar] [CrossRef]
- Rashid, M.H.; Hui, S.Y.; Chung, H.S.H.; Madichetty, S.; Kumar, N.B.S.; Krishna, B.M. Resonant and Soft-Switching Converters. In Power Electronics Handbook; Butterworth-Heinemann: Oxford, UK, 2023. [Google Scholar]
- Yang, Y. A Passive Augmented Circuit for EMI Reductions of Full-Bridge Inverters with Conventional Phase Shift Control in Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2023, 38, 13286–13297. [Google Scholar] [CrossRef]
- Acharige, S.S.G.; Haque, M.E.; Arif, M.T.; Hosseinzadeh, N.; Hasan, K.N.; Oo, A.M.T. Review of Electric Vehicle Charging Technologies, Standards, Architectures, and Converter Configurations. IEEE Access 2023, 11, 41218–41255. [Google Scholar] [CrossRef]
- Van Mulders, J.; Delabie, D.; Lecluyse, C.; Buyle, C.; Callebaut, G.; Van der Perre, L.; De Strycker, L. Wireless Power Transfer: Systems, Circuits, Standards, and Use Cases. Sensors 2022, 22, 5573. [Google Scholar] [CrossRef]





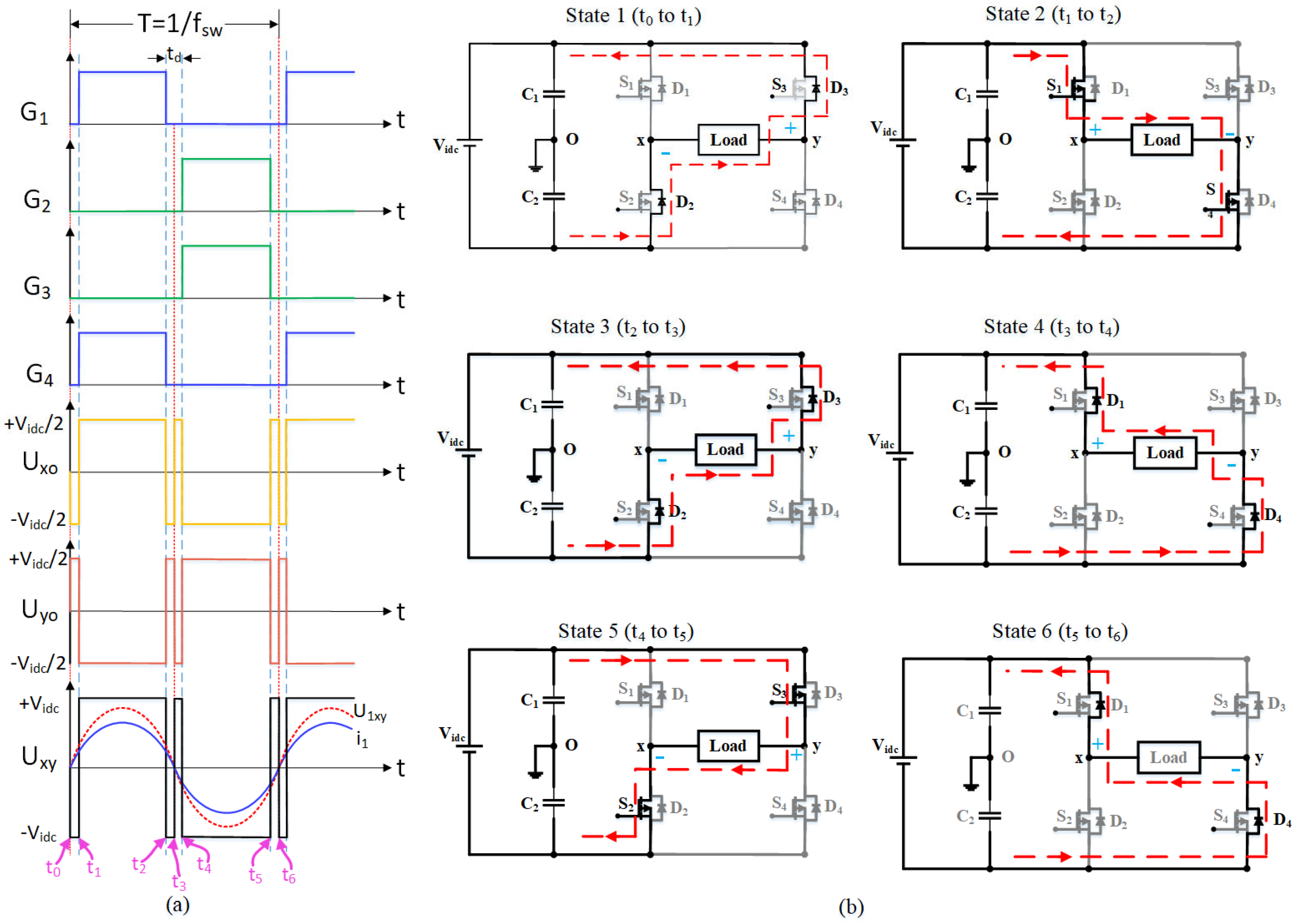

















| Transition State | Switch Condition | Current Flow | Output Voltage |
|---|---|---|---|
| State 1 (t0–t1) | S1, S4-ON & S2, S3-OFF | (+) Vidc-S1-Loadx-Loady-S4-(−) Vidc | Uxy = +Vidc. |
| State 2 (t1–t2) | S1, S4-OFF & S2, S3-OFF | (+) Vidc-S3-Loady-Loadx-S2-(−) Vidc | Uxy = −Vidc. |
| Transition State | Switch Condition | Current Flow | Output Voltage |
|---|---|---|---|
| State 1 (t0–t1) | S1, S2, S3, S4-OFF | (−) Vidc-D2-Loadx-Loady-D3-(+) Vidc | Uxy = −Vidc. |
| State 2 (t1–t2) | S1, S4-ON & S2, S3-OFF | (+) Vidc-S1-Loadx-Loady-S4-(−) Vidc | Uxy = +Vidc. |
| State 3 (t2–t3) | S1, S2, S3, S4-OFF | (−) Vidc-D2-Loadx-Loady-D3-(+) Vidc | Uxy = −Vidc. |
| State 4 (t3–t4) | S1, S2, S3, S4-OFF | (−) Vidc-D4-Loady-Loadx-D1-(+) Vidc | Uxy = +Vidc. |
| State 5 (t4–t5) | S1, S4-OFF & S2, S3-ON | (+) Vidc-S3-Loady-Loadx-S2-(−) Vidc | Uxy = −Vidc. |
| State 6 (t5–t6) | S1, S2, S3, S4-OFF | (−) Vidc-D4-Loady-Loadx-D1-(+) Vidc | Uxy = +Vidc. |
| Symbol | Designed Value |
|---|---|
| Lt | 74.56 µH |
| Ct1 | 5.05 nF |
| Ct2 | 6.26 nF |
| Lr | 36.3 µH |
| Cr | 10.05 nF |
| Parameter | Label | Value |
|---|---|---|
| Input DC voltage Primary coil | Vidc | 325 V |
| Transmitter coil self-Inductance | L1 | 74.56 µH |
| Mutual inductance | LM | 15.95 µH |
| Receiver coil self-inductance | L2 | 85.45 µH |
| Output equivalent resistance | Rload | 22 Ω |
| Output filter capacitance | Co | 22 µF |
| Operating switching frequency | fsw | 85,000 Hz |
| Coupling coefficient | k | 0.2 |
| Distance between transmitter to receiver coil | d | 180 mm |
| Parameters | Control Technique | Without Dead Time | Dead Time in (%) | ||||
|---|---|---|---|---|---|---|---|
| 1 | 5 | 10 | 15 | 20 | |||
| Power dissipation | PWM | 0.400 | 0.955 | 1.145 | 1.395 | 1.500 | 1.555 |
| PDM (D = 0.5) | 0.342 | 0.481 | 1.130 | 1.365 | 1.425 | 1.470 | |
| PDM (D = 0.8) | 0.300 | 0.700 | 1.245 | 1.220 | 1.325 | 1.540 | |
| Transfer efficiency | PWM | 86.1% | 84.3% | 89.7% | 93.8% | 95.5% | 96.8% |
| PDM (D = 0.5) | 86.7% | 84.4% | 89.2% | 92.7% | 94.1% | 98.4% | |
| PDM (D = 0.8) | 80.7% | 81.3% | 82.2% | 82.8% | 84.2% | 84.4% | |
| Overall efficiency | PWM | 88.4% | 85.5% | 62.2% | 50.8% | 46.4% | 30.3% |
| PDM (D = 0.5) | 90.2% | 88.3% | 63.6% | 55.8% | 52.3% | 37.6% | |
| PDM (D = 0.8) | 92.2% | 89.4% | 66.3% | 64.2% | 61.1% | 50.4% | |
| Color scale | Lowest | - | - | - | - | Highest | |
| Control Technique | HF Inverter Voltage Gain | Current Ripple Ratio | HF Inverter Efficiency | |
|---|---|---|---|---|
| Without dead time | PWM [36] | 1.25 | 2.50 | 89.5 |
| PDM [42] | 1.30 | 1.80 | 90.2 | |
| With dead time (1 µs) | PWM | 1.06 | 2.05 | 86.5 |
| PDM (0.5) | 1.19 | 1.96 | 86.7 | |
| PDM (0.8) | 1.25 | 1.95 | 89.5 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
John, F.; Komarasamy, P.R.G.; Rajamanickam, N.; Vavra, L.; Petrov, J.; Kral, V. Performance Improvement of Wireless Power Transfer System for Sustainable EV Charging Using Dead-Time Integrated Pulse Density Modulation Approach. Sustainability 2024, 16, 7045. https://doi.org/10.3390/su16167045
John F, Komarasamy PRG, Rajamanickam N, Vavra L, Petrov J, Kral V. Performance Improvement of Wireless Power Transfer System for Sustainable EV Charging Using Dead-Time Integrated Pulse Density Modulation Approach. Sustainability. 2024; 16(16):7045. https://doi.org/10.3390/su16167045
Chicago/Turabian StyleJohn, Franklin, Pongiannan Rakkiya Goundar Komarasamy, Narayanamoorthi Rajamanickam, Lukas Vavra, Jan Petrov, and Vladimir Kral. 2024. "Performance Improvement of Wireless Power Transfer System for Sustainable EV Charging Using Dead-Time Integrated Pulse Density Modulation Approach" Sustainability 16, no. 16: 7045. https://doi.org/10.3390/su16167045
APA StyleJohn, F., Komarasamy, P. R. G., Rajamanickam, N., Vavra, L., Petrov, J., & Kral, V. (2024). Performance Improvement of Wireless Power Transfer System for Sustainable EV Charging Using Dead-Time Integrated Pulse Density Modulation Approach. Sustainability, 16(16), 7045. https://doi.org/10.3390/su16167045






