Water Resource Regulation and Evaluation Method Based on Optimization of Drought-Limited Water Level in Reservoir Group

Abstract

Reservoirs, as critical nodes in regional water management, play an increasingly important role in drought mitigation. This study aims to optimize the drought-limited water level in the reservoir group and propose an evaluation method for selecting the optimal regulation scheme during drought periods. The reservoir water supply module within the Water Allocation and Simulation (WAS) model was enhanced to optimize the drought-limited water level of the reservoir group. A comprehensive adaptation index (CAI) was developed to quantitatively evaluate the effectiveness of water resource regulation under various drought scenarios. This methodology was applied to large and medium-sized reservoirs in the central Yunnan Province, China. The results show that the optimized drought-limited water level significantly improved the water supply performance of the reservoir group during drought years. Specifically, the optimized drought-limited water level notably reduced severe water shortage for water users in the long series and typical drought years, effectively mitigating the impacts of drought. Additionally, the most suitable water resource regulation strategies for different drought scenarios were identified. These research findings can provide technical references for reservoir management departments and drought operations authorities to formulate drought-limited level for the reservoir group and implement regional drought early warning and defense decision-making.

1. Introduction

With rapid economic development and population growth, human activities have significantly increased the release of greenhouse gases, leading to more frequent and severe extreme drought events. Drought has become one of the most common and severe natural disasters in the world [1]. According to the Intergovernmental Panel on Climate Change (IPCC) report, global warming is an indisputable fact [2]. As the climate warms, it intensifies the natural water cycle, leading to increased evaporation and reduced soil moisture. This process exacerbates drought conditions, as warmer air holds more moisture and draws water away from the soil [3]. Consequently, the frequency of extreme droughts characterized by prolonged duration, widespread impact, and high intensity is expected to rise significantly in the future. Some regions may even experience once-in-a-century droughts or unprecedented records [4]. Reservoirs, as key storage nodes in the water resource system, play an important role in regional water resource regulation and drought alleviation [5]. Therefore, how to use the reservoir group to develop a scientific and reasonable drought resistance scheduling strategy, give full play to the comprehensive benefits of the reservoir group, and form an effective water resource regulation scheme have become urgent tasks to achieve regional sustainable development. This is also a critical research focus in the field of drought resistance.

Compared with the flood-limited water level of the reservoir, the research on the drought-limited water level of the reservoir is still in the early stages and relatively scarce [6]. In 2011, the National Flood Control and Drought Relief Headquarters Office of China introduced a method for determining the drought-limited water level. This method, which first established the concept, has since become a crucial indicator for guiding the drought-resistant operation of reservoirs. Recently, some scholars have explored various methods for calculating the drought-limited water level from different perspectives. These studies contribute to a growing body of research aimed at enhancing our understanding and management of water resources under drought conditions. By integrating hydrological models, statistical analyses, and optimization techniques, these methods offer new insights and tools for setting appropriate water levels in reservoirs to mitigate drought impacts. Li et al. adopted a monthly sliding method to calculate the drought-limited water level of the reservoir [7]. Zhang et al. used a bimonthly sliding method to determine the drought warning level based on the different water supply tasks of the reservoir [8,9]. Cao et al. noted that the static drought-limited water level ignored the water transfer relationship between different drought periods. They proposed modifying the water series month by month according to the actual incoming water. The initial drought-limited water level is expressed as a combination of an early warning period and a corresponding drought-limited water level, enabling dynamic control of the drought-limited water level [10,11]. WU et al. considered limiting the total water demand of users during the drought period and determined the drought-limited water level of the reservoir based on the difference between the early warning period and the amount of water stored at the end of the flood season [12,13]. Utilizing the hedging theory widely applied in reservoir operation [14,15], Wei et al. accounted for differences in the annual water demand processes across various drought levels and industries, using a reverse order recursive algorithm to determine the graded and staged drought-limited water level of the reservoir [16]. Yan et al. introduced a double-layer sliding algorithm to determine the drought-limited water level of the reservoir with multi-year regulation, annual regulation, and seasonal regulation by incorporating the two-layer control period, such as the scheduling period and guarantee period [17].

With in-depth research on the determination method for the drought-limited water level, some scholars have begun to optimize the drought-limited water level. Peng et al. developed an optimal control model with automatic optimization based on optimal control theory and adaptive technology for the drought-limited water level of the multi-year regulation reservoir [18]. Chang et al. adopted a particle swarm optimization algorithm to optimize the reservoir storage and discharge process, selecting the water level in a typical drought year as the drought-limited level for the cascade reservoirs of the Yellow River mainstream [19]. Zhang et al. introduced an improved artificial fish swarm algorithm that addresses the weak balance problem between global and local search, enabling the calculation of the drought-limited water level for the multi-year regulation reservoir [20]. Wei et al. proposed an optimization method for the drought-limited water level of the reservoir based on the principle of shallow and wide damage, addressing the fact that the supply limitation coefficients of various industries are too dependent on empirical values in the process of calculating the drought-limited water level [21]. Luo et al. optimized the drought-limited water level of the reservoir by comprehensively considering the requirements of water users for the depth of damage and the guaranteed rate of water supply [22]. Zhang et al. studied the bilateral regulation of supply and demand by taking the graded and staged drought-limited water level of the reservoir as the optimization variable [23].

However, most of the above studies focus on a single reservoir, and it is still a technical difficulty to determine the drought-limited water level for the reservoir group within a complex regional water system. Existing methods mostly use the rigid water demand of various industries during the drought period as the boundary to calculate the drought-limit water level of the reservoir. In practice, there are complex configurational relationships between individual reservoirs, calculation units, and various industries within the reservoir group. These industries, including urban domestic, rural domestic, industry, agricultural irrigation, and urban ecology, have distinct water demand and interact with the reservoir. Due to the mutual supplementation and regulation among reservoirs, the water demand of different industries allocated to a specific reservoir during a certain period is uncertain. Consequently, it is difficult to ascertain the rigidity of the water demand for each calculation unit and industry and its stable corresponding relationship with the reservoir. For the reservoir management department, the amount of water currently available in the reservoir is relatively clear. Therefore, based on the concept of bidirectional regulation of water supply and demand during the drought period, the available water supply of reservoirs is regulated. The supply-side regulation strategy of “fine water and long flow” is adopted to optimize the drought-limited water level of the reservoir group.

In this study, the primary objectives are summarized as follows: (1) To address the issue that the reservoir water supply module in the Water Allocation and Simulation (WAS) model lacks drought characteristic indicators, which makes it impossible to reasonably and effectively allocate the reservoir water supply during drought and water shortage, the drought-resistant water supply rule of the WAS model is improved. (2) Considering that many reservoirs in the water supply system are often neglected when using the existing methods to determine the drought-limited water level, an optimization method for the drought-limited water level under reservoir group conditions is proposed based on the principle of shallow and wide damage. (3) By establishing a comprehensive adaptation index (CAI), an evaluation method is proposed to compare the optimal regulation scheme, providing a practical analytical tool for quantitative research on water resource regulation under different drought scenarios. Eventually, the optimization and evaluation methods were validated for large and medium-sized reservoirs in the central Yunnan Province, providing a scientific basis and technical support for implementing drought-resistant operation for the regional reservoir group.

2. Materials and Methods

2.1. Overview of the Study Area and Model Construction

2.1.1. Study Area

The central Yunnan Province region is located at the southern end of the longitudinal axis of the Baokun Corridor in China’s Two Horizontals and Three Verticals urbanization strategy, as shown in Figure 1. It is one of the eighteen national key development areas identified in the “China Main Functional Zone Plan”. As the core area of the central Yunnan Province, the water-receiving area of the central Yunnan water diversion project occupies only 9.4% of the province’s land but hosts 26.4% of its population and contributes 56.4% of its industrial added value. This region is the most populous and economically active area in Yunnan Province. It is situated in the watershed zone of the four major water systems of the “Three Rivers and One River”, with an average altitude of 1300 to 2500 m, and a relative altitude difference of 150 to 500 m. The region experiences low precipitation, high evaporation, and frequent droughts. The natural endowment conditions of water resources are extremely incompatible with the layout of social and economic development, making it the area with the most prominent water resource supply and demand contradiction in Yunnan Province.

2.1.2. Model Construction and Verification

This study comprehensively considers the regional terrain characteristics, river basin, administrative division, and water supply system. A model was constructed for the five major cities involved in the water-receiving area of the central Yunnan water diversion project, including Dali, Chuxiong, Kunming, Yuxi, and Honghe. The study area was divided into 102 calculation units, with the Jinsha River, Nanpan River, Red River, and Lancang River systems comprising 51, 33, 12, and 6 calculation units, respectively. The model includes a total of 174 reservoirs, comprising 71 large and medium-sized reservoirs and 103 small reservoirs.

The simulation period of the model is from 1980 to 2020, and 2019 is set as the base year. This study collected extensive reservoir inflow data, water intake data, and related planning data. The characteristic parameters and inflow data of the reservoir were sourced from the Yunnan Survey and Design Institute of Water Conservancy and Hydropower. The water consumption data were obtained from the special report on water resource allocation and project scale for the second phase of the central Yunnan water diversion project. Figure 2 compares the water supply simulated by the WAS model in the base year of the water-receiving area of the central Yunnan water diversion project with the actual water supply. The results show that the relative error of the water supply simulation in each city is of less than 3.2%. The largest simulation error occurs in Dali city, with a relative error of 3.15%. The smallest simulation error occurs in Chuxiong city, with a relative error of 1.04%. According to the water supply of each water industry, the relative error of the water supply simulation is of less than 3.5% for each water industry. The largest error in the water supply simulation is agricultural irrigation, with a relative error of 3.48%. The smallest error in the water supply simulation is rural domestic, with a relative error of 0.09%. These results indicate that the simulation results of the water resource allocation model for the water-receiving area of the central Yunnan water diversion project have relatively small errors and are generally consistent with the actual water supply pattern.

2.1.3. Water Resource Regulation Scheme Setting

According to the characteristics of the central Yunnan Province region, the scenarios of normal dry year and extremely dry year are analyzed. Firstly, encountering drought necessitates changes in reservoir water supply rules, which will inevitably affect the water consumption system. Secondly, the proportion of water allocated to different industries will be compressed, impacting the overall water consumption system. Therefore, to determine the impact of reservoir operation rules, water compression objects, and water compression ratios on the water supply and consumption system, the simulation scenarios were set up. These scenarios provide a reference for formulating water resource allocation schemes when the drought is encountered in the central Yunnan region.

In this study, three types of reservoir operation rules were set up, namely, standard operation policy (SOP); adjustment water supply policy (AWSP), based on the reverse order recursive algorithm [16]; and optimization water supply policy (OWSP), determined by the optimization algorithm. Additionally, considering the adjustment of water demand, five water compression objects were identified: urban domestic, rural domestic, industry, agricultural irrigation, and urban ecology. According to the hierarchy of needs theory [24], the water compression ratio was set to vary between 10% and 60%. The samples were categorized into five groups according to the number of compressed water objects. The analysis involved six simulated scenarios, derived from a combination of two drought scenarios and three reservoir operation rules. Specifically, there are 6 samples where water objects are not compressed, and 100,836 samples where water objects are compressed. In total, the dataset comprises 100,842 samples. The specific scenario of the sample-setting process is shown in Figure 3.

2.2. Research Methods

The flowchart below illustrates the methodology of this study (Figure 4). Firstly, the basic concept is that when the water level falls below the drought-limited water level, the available water supply of the reservoir is allocated to various water users according to a certain compression ratio. This approach aims to achieve an appropriate supply limitation and ensure that the reservoir continues to retain stored water during the drought period, thereby extending the effective water supply period. Secondly, the drought-resistant water supply rules for the reservoir water supply module of the WAS were improved, and the drought limit water level constraint and water allocation coefficient of different industries were added. Then, for the complex water resource allocation system, the non-dominated sorting genetic algorithm (NSGA-II) was used for optimization to determine the drought-limited water levels for each reservoir within the system. Finally, a comprehensive adaptation index (CAI) was then developed to quantitatively assess the effectiveness of water resource regulation under various drought scenarios. The following sections discuss the specifics of the methodology.

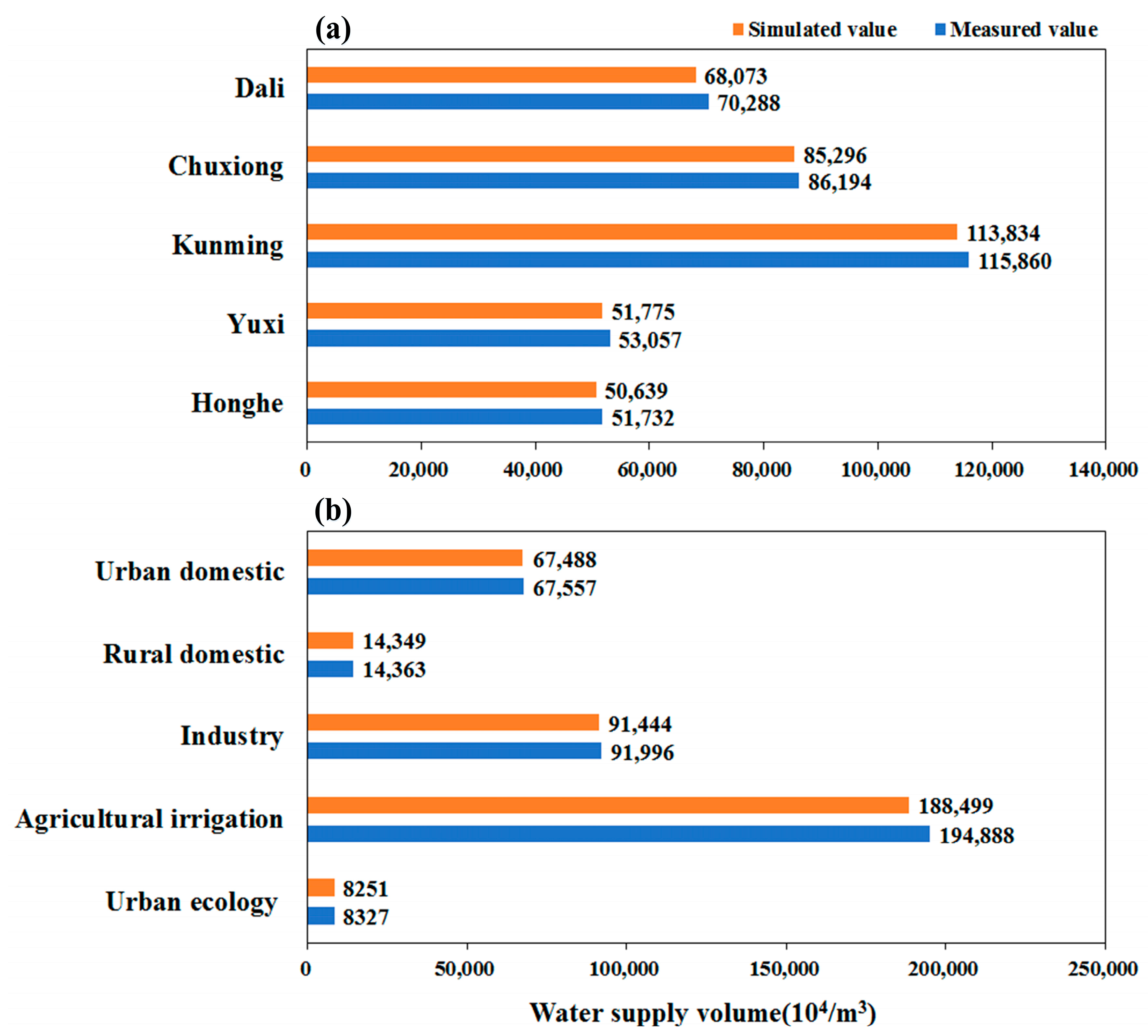
2.2.1. Improvement of Drought-Resistant Water Supply Rules in WAS Model

The WAS model [25] is based on the theory of the natural–social dualistic water cycle and employs the dynamic feedback simulation method of the water cycle time sequence. This method closely couples the production and convergence process of the natural water cycle with the intake, consumption, and discharge process of the artificial water cycle. The WAS model addresses the mutual feedback and linkage simulation between the natural and social water cycle within a regional complex water resource system [26,27]. The current study extends and improves the drought-resistant module of the WAS model based on the supply-side regulation. The concept of supply regulation implies that when the water volume of the reservoir is low in the dry year, and it is difficult to meet the water demand of various industries with the water storage volume, the water allocation of the reservoir to various industries is limited according to a certain proportion coefficient. This approach ensures that the reservoir maintains a certain amount of water during prolonged drought conditions. This principle not only ensures that a certain amount of water can be stored in the reservoir at the beginning stage of the drought but also reserves enough water for the duration or intensification stage of the drought to ensure basic water needs by reducing the initial water supply to various industries. Compared to demand regulation, which directly limits the water demand of various industries, supply regulation is more practical and flexible in complex situations where multiple reservoirs supply water to the same calculation unit, allowing for more effective allocation of the water supply quota to each reservoir [28,29]. The improved part of the WAS model reservoir water supply module is shown in Figure 5.

According to the above principles, two grades of the drought-limited water level were set for each reservoir in the model: the drought warning water level (DWWL) for normal drought (P = 75%), and the drought guarantee water level (DGWL) for extreme drought (P = 95%). Additionally, drought control parameters such as the limiting coefficient of the available water supply of the reservoir were established. The available water supply $S$ of the reservoir in the water balance calculation was finely divided into layers and various industries. The specific improvement calculation formula is as follows:

$$\left\{\begin{array}{l}{S_{i,t}=W}_{i,t}-W_d,W_{i,t}\ge W_{dwwl,t}\\ S_{i,t}=\left(W_{i,t}-W_d\right)\ast {\beta }_{i,1},W_{dgwl,t}<W_{i,t}\le W_{dwwl,t}\\ S_{i,t}=\left(W_{i,t}-W_d\right)\ast {\beta }_{i,2},W_d<W_{i,t}\le W_{dgwl,t}\\ S_{i,t}=0,W_{i,t}\le W_d\\ W_{i,t}=W_t-\sum _{j=0}^{i-1}{s}_j,s_0=0\end{array}\right.$$

(1)

where $S_{i,t}$ is the available water supply of the reservoir to the industry $i$ at the time $t$, which is the upper limit of the water supply from the reservoir to the industry $i$ at the time $t$; $W_t$ is the total water storage capacity of the reservoir at the time $t$, including the initial storage capacity and the incoming water volume of the reservoir at the time $t$; $W_{i,t}$ is the total water storage capacity of the reservoir for the industry $i$ at the time $t$; $s_i$ is the $i$ industry water supply; $s_0$ is no industry water supply; $W_d$ is the dead storage capacity of the reservoir; $W_{dwwl,t}$ and $W_{dgwl,t}$ are the water storage corresponding to the DWWL and the DGWL of the reservoir at the time $t$, respectively; ${\beta }_{i,1}$ and ${\beta }_{i,2}$ are the limiting coefficient of drought warning water supply and the limiting coefficient of drought guarantee water supply of reservoir to industry $i$, respectively; $i=\mathrm{1,2},3\cdots n$, indicating the order of industry water supply, where $n$ is the number of industries.

2.2.2. Optimization of Drought-Limited Water Level in Reservoir Group

The guiding principle for determining the drought-limited water level of the reservoir is to limit the water supply from the reservoir by a certain compression ratio when the water level falls below the drought-limited thresholds for different levels. Only the basic water needs of various industries are guaranteed, and part of the water supply is reserved for future use to ensure that serious water shortage does not occur during the dry season. This strategy aims to reduce the depth of damage caused by water shortages in various industries, mitigate the irreversible negative impact of drought, and effectively alleviate the social and economic losses caused by drought and water shortage. Based on this principle, an optimal calculation model for the drought-limited water level of the reservoir group within a complex water supply system comprising multiple reservoirs and industries was established. The optimization objective function, decision variables, and constraints are as follows:

(1)

Objective function

① Minimum average water shortage rate. The average water shortage rate is used to measure the severity of water shortage; the smaller the better, and the less severe the damage caused by water shortage. The calculation formula is as follows:

$$minF={\sum }_{r=1}^R{\sum }_{u=1}^U{SW}_u$$

(2)

$${SW}_u={\displaystyle \frac{1}{T}}{\sum }_{t=1}^T\left({\sum }_{i=1}^n{N}_{i,t}-{\sum }_{i=1}^n{s}_{i,t}\right)/{\sum }_{i=1}^n{N}_{i,t}$$

(3)

where $N_{i,t}$ is the water demand of the $i$ industry in the $t\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$ during the calculation period; $s_{i,t}$ is the water supply of the $i$ industry in the $t\mathrm{y}\mathrm{e}\mathrm{a}\mathrm{r}$ during the calculation period; ${SW}_u$ is the average water shortage rate of the $u$ calculating unit during the calculation period; $T$ is the number of years in the calculation period; $R$ is the number of optimized reservoirs; $U$ is the number of calculating units; $F$ is the sum of the average water shortage rate of each industry in the corresponding calculation unit for each optimized reservoir during the calculation period.

② Maximum equilibrium rate. The equilibrium rate reflects the temporal differences in the water shortage rate in the region. A larger equilibrium rate indicates a smaller fluctuation in the water shortage process for each unit, resulting in a more stable water shortage process. The formula for calculating the equilibrium rate of each calculation unit during the calculation period is as follows:

$$maxY={\displaystyle \frac{1}{U}}{\sum }_{u=1}^U(1-\sqrt{{\displaystyle \frac{{\sum }_{t=1}^T{\left({SW}_{u,t}-{\overline{SW}}_t\right)}^2}{T-1}}})$$

(4)

where ${SW}_{u,t}$ is the water shortage rate of the $u$ calculation unit in the $t$ calculation period; ${\overline{SW}}_t$ is the regional average water shortage rate during the $t$ calculation period; $Y$ is the equilibrium rate of the corresponding calculation unit of each optimized reservoir during the calculation period.

③ Maximum ecological guarantee rate. The guarantee rate represents the probability that the system meets the water supply demand, and the higher the guarantee rate, the better. The formula for calculating the ecological guarantee rate of each optimized reservoir during the calculation period is as follows:

$$maxZ={\displaystyle \frac{1}{T\ast M}}{\sum }_{m=1}^M{\sum }_{t=1}^T{R}_{t,m}$$

(5)

where $M$ is the optimal number of reservoirs; $R_{t,m}$ is the condition that the discharge of the $m$ optimized reservoir meets the ecological base flow during the $t$ calculation period. If the ecological flow demand is met in this period, then $R_{t,m}=1$; otherwise, $R_{t,m}=0$. $Z$ is the ecological guarantee rate of each optimized reservoir during the calculation period.

(2)

Decision vriable

Based on the operation process and management requirements of reservoir operation, the decision variables are set as the DWWL, DGWL, drought warning water supply limiting coefficient, and drought guarantee water supply limiting coefficient for each industry. The range of values for each decision variable is as follows:

$$0\le {\beta }_{i,1},{\beta }_{i,2}\le 1$$

(6)

$$Z_{min,t}\le Z_{dgwl,t}\le Z_{dwwl,t}\le Z_{max,t}$$

(7)

where $Z_{dgwl,t}$ is the DWWL of reservoir during the $t$ calculation period; $Z_{dwwl,t}$ is the DGWL of reservoir during the $t$ calculation period; $Z_{min,t}$ is the lowest allowable water level of reservoir during the $t$ calculation period; $Z_{max,t}$ is the maximum allowable water level of reservoir during the $t$ calculation period.

(3)

Constraint condition

① Reservoir water balance constraint.

$$W_{k,t+1}=W_{k,t}+W_{kc,t}+W_{kin,t}+W_{kd,t}-s_{k,t}-E_{k,t}-R_{k,t}-Q_{kq,t}$$

(8)

where $W_{k,t}$ and $W_{k,t+1}$ are the water storage capacity of reservoir $k$ at the beginning and end of the time period $t$, respectively; $W_{kc,t}$ is the water production of reservoir $k$ during the time period $t$; $W_{kin,t}$ is the upstream river inflow of reservoir $k$ during the time period $t$; $W_{kd,t}$ is the amount of water transferred into reservoir $k$ during the time period $t$; $s_{k,t}$ is the sum of water supply of all industries in reservoir $k$ during the time period $t$; $E_{k,t}$ and $R_{k,t}$ are the evaporation and leakage losses of reservoir $k$ during the time period $t$, respectively; $Q_{kq,t}$ is the discharge amount of reservoir during the time period $t$.

② Calculation of unit water balance constraint.

$$Q_{i,t}=Q_{ihd,t}+Q_{isk,t}+Q_{idx,t}+Q_{irain,t}+Q_{irew,t}+Q_{ioth,t}$$

(9)

where $Q_{i,t}$ is the water supply of industry $i$ during the time period $t$; $Q_{ihd,t}$ is the water supply of the river channel during the time period $t$; $Q_{isk,t}$ is the water supply of the reservoir during the time period $t$; $Q_{idx,t}$ is the groundwater supply of the reservoir during the time period $t$; $Q_{irain,t}$ is the amount of rainwater supply during the time period $t$; $Q_{irew,t}$ is the amount of reclaimed water supply during the time period $t$; $Q_{ioth,t}$ is the amount of other unconventional water supply during the time period $t$.

③ Reservoir characteristic water level constraint.

$$Z_{kmin,t}\le Z_{k,t}\le Z_{kmax,t}$$

(10)

where $Z_{k,t}$ is the water level of reservoir $k$ during the time period $t$; $Z_{kmin,t}$ is the lowest allowable water level or dead water level from reservoir $k$ during the time period $t$; $Z_{kmax,t}$ is the upper allowable water level of reservoir $k$ during the time period $t$, which is the flood limit water level in flood season and the normal storage level in the non-flood season.

④ Other constraints.

Other constraints include water supply strategy constraints of the reservoir, decision-making variable value range constraints, water demand constraints of various industries, non-negative constraints of other parameters, etc.

(4)

Optimization calculation

The optimization of the drought-limited water level is a three-dimensional, non-linear, and complex large-scale system optimization problem. In this study, the NSGA-II is chosen to solve this problem. The NSGA-II is widely used in various engineering and scientific contexts and has been effectively implemented to address numerous water resource management issues [30,31,32]. The calculation process for optimizing the drought-limited water level of the reservoir group is illustrated in Figure 6. The specific steps are as follows:

Step 1: Establish the WAS model for the reservoir group in the study area and initialize the decision variable parameter file;

Step 2: Run the WAS model and output configuration results;

Step 3: Check if the number of iterations meets the preset termination condition. If not, proceed to Step 4. Otherwise, end the optimization process;

Step 4: Calculate the objective function value based on the result file and assign this value to the population;

Step 5: Generate the next generation subpopulation through selection, crossover, and mutation operations using the NSGA-II optimizer. Update the decision variable parameter file and return to Step 1 until the termination condition is met.

2.2.3. Evaluation of Water Resource Regulation Schemes

1. Determination of Evaluation Index System

The selection of the evaluation index is a crucial step in water resource regulation and evaluation. This study aims to develop an evaluation index system that meets the following needs. Firstly, it can accurately reflect the drought effect of water resource regulation in the study area, aligned with the core concept of water resource regulation. Secondly, as a comprehensive evaluation system, it should reveal the adaptive relationships among water resource, social economy, and ecological environment. Lastly, the evaluation index system can provide a computational framework, enabling the performance comparisons of water resource regulation across different regions. In addition, the evaluation indexes should adhere to the principles of representativeness, comprehensiveness, sensitivity, objectivity, accessibility, and quantifiability. Based on the characteristics of the water resource in the study area and referencing the existing research, 12 evaluation indexes were selected from three aspects: water resource, social economy, and ecological environment. The evaluation index system is presented in

Table 1. Index system for water resource regulation and evaluation.

Field	Index	Unit	Type	Number
Water resource	Reservoir water supply	104 m3	+	I1
	Water deficiency rate	%	_	I2
	Abandonment of water from reservoirs	104 m3	_	I3
	Equilibrium rate	%	+	I4
Social economy	Proportion of population with difficulty in attaining drinking water	%	_	I5
	Per capita water consumption	m3/person	_	I6
	Water satisfaction rate	%	+	I7
	Per capita domestic water consumption	L/(person/day)	+	I8
Ecological environment	River ecological water volume	104 m3	+	I9
	Ecological environment water consumption rate	%	+	I10
	Groundwater-mining output	104 m3	_	I11
	Urban ecological water deficiency rate	%	_	I12

.

2. Determination of Weight

Currently, weight determination methods are categorized into two types: subjective and objective assignment methods. Subjective assignment methods rely on human judgment and experience, mainly including the Analytic Hierarchy Process (AHP) [33,34], the subjective weighting method, and the expert survey method, etc. In contrast, the objective assignment method determines the weight based on the statistical characteristics of the data itself. These methods include the coefficient of variation method [35], the entropy weighting method [36], the Criteria Importance Though Intercriteria Correlation (CRITIC) weighting method [37], the principal component analysis method, and the mean squared deviation method, etc. Among these, the CRITIC weighting method is particularly effective for comprehensive evaluations involving multiple indexes and objects. It can eliminate the influence of highly correlated indexes and reduce information overlap, thus providing more reliable evaluation results. In this study, the CRITIC weight method is adopted to calculate the weight of each index. This method objectively determines the importance of each index by analyzing the differences and correlations between the indexes. The calculation process of the CRITIC weight method is as follows:

(1)

Constructing the original data matrix

$$X=\left(\begin{array}{ccc}{x}_{11}& \dots & x_{1n}\\ ⋮& \ddots & ⋮\\ x_{m1}& \dots & x_{mn}\end{array}\right)$$

(11)

where $X$ is the original data matrix; $m$ is the number of evaluation objects; $n$ is the number of evaluation indexes.

(2)

Standardization of evaluation indexes

The original data matrix $X$ was normalized by Max–Min normalization method.

① Positive indexes:

$$x_i^{\prime }={\displaystyle \frac{x_i-\min \left(x_i\right)}{\max \left(x_i\right)-\min \left(x_i\right)}}$$

(12)

② Negative indexes:

$$x_i^{\prime }={\displaystyle \frac{\max \left(x_i\right)-x_i}{\max \left(x_i\right)-\min \left(x_i\right)}}$$

(13)

where $x_i^{\prime }$ is the normalized value of the $i$-th data after normalization; $x_i$ is the value of the $i$-th data before normalization; $\max \left(x_i\right)$ is the maximum value of the $i$-th data before normalization; $\mathrm{m}\mathrm{i}\mathrm{n}\left(x_i\right)$ is the minimum value of the $i$-th data before normalization.

(3)

Calculation of index variability

$$\left\{\begin{array}{c}\overline{x_j}={\displaystyle \frac{1}{m}}\sum _{j=1}^m{x}_{ij}\\ S_j=\sqrt{{\displaystyle \frac{\sum _{i=1}^m{(x_{ij}-\overline{x_j})}^2}{m-1}}}\end{array}\right.$$

(14)

where $\overline{x_j}$ is the average value of the $j$-th index; $S_j$ is the standard deviation of the $j$-th index; $i$ and $j$ are the rows and columns of the original data matrix, respectively.

(4)

Calculation of index conflict heterogeneity

$$R_j={\sum }_{i=1}^n\left(1-r_{ij}\right)$$

(15)

where $r_{ij}$ is the correlation coefficient between the $i$-th and $j$-th indexes.

(5)

Calculation of information quantity

$$C_j=S_j\times R_j$$

(16)

(6)

Calculation of weight

$$W_j={\displaystyle \frac{C_j}{\sum _{j=1}^n{C}_j}}$$

(17)

where $W_j$ is the target weight of the $j$-th index.

3. Calculation of Evaluation Schemes

Facing various scenarios of water resource regulation, each combination scenario has a water resource regulation scheme suitable for the entire system. However, for different combination scenarios, how to evaluate the advantages and disadvantages of these schemes is of great significance for future regional drought resistance decision-making and the scientific and reasonable regulation of water resource. This study referred to the construction method of the water resource Sustainability Index (SI) proposed by Loucks [38]. Aiming at the target of water resource regulation, the CAI was constructed through three performance indexes: coordination, reliability, and resilience. The CAI is a new index that can comprehensively quantify the water resource regulation of the entire system. The calculation formula for each evaluation index is as follows:

(1)

Coordination

The coordination reflects the degree to which the water resource system responds and adjusts to changes in the internal and external environment. By using the calculation results of the water resource regulation simulation model, different indexes in three fields can be obtained. Firstly, the Max–Min standardization method is used to normalize the indexes in each field to ensure comparability in the subsequent evaluation and analysis. Then, the weight of each index is determined by the CRITIC method, and the comprehensive evaluation results of each field are obtained by the comprehensive evaluation function. Finally, based on the calculation formula of coupling degree and the comprehensive evaluation results, the overall coordination of the water resource system can be calculated. The formula for calculating the comprehensive evaluation function is as follows:

$$\left\{\begin{array}{c}{F}_1\left(x^{\prime }\right)=\sum _{j=1}^n{a}_j\times x_{ij}^{\prime }\\ F_2\left(y^{\prime }\right)=\sum _{j=1}^m{b}_j\times y_{ij}^{\prime }\\ F_3\left(z^{\prime }\right)=\sum _{j=1}^p{c}_j\times z_{ij}^{\prime }\end{array}\right.$$

(18)

where $F_1$, $F_2$, and $F_3$ are the comprehensive evaluation indexes of water resource, social economy, and ecological environment, respectively; $a_j$, $b_j$, and $c_j$ are the weights of different indexes in each field, respectively; $x_{ij}^{\prime }$, $y_{ij}^{\prime }$, and $z_{ij}^{\prime }$ are the standardized values for the different indexes in each field, respectively; $n$, $m$, and $p$ are the number of indexes in each field, respectively.

The coupling degree $C$ reflects the coupling adaptation effect between the water resource, socio-economic, and ecological environment fields. The calculation formula is as follows:

$$C={\displaystyle \frac{3\times \sqrt[3]{F_1\times F_2\times F_3}}{F_1+F_2+F_3}}$$

(19)

The overall comprehensive evaluation result $D$ is based on the coupling degree $C$. The total comprehensive evaluation score is obtained by the arithmetic average of the three fields. The calculation formula is as follows:

$$D={\displaystyle \frac{F_1+F_2+F_3}{3}}$$

(20)

The coordination $A$ takes into account the coupling between different fields and the overall adaptation of the system. The calculation formula is as follows:

$$A=\sqrt{C\times D}$$

(21)

(2)

Reliability

Reliability reflects the degree of safety assurance of the entire water supply system. The higher the index, the greater the reliability and the stronger the ability to resist risks. When the reliability is taken to the maximum value of 1, it indicates that the water supply system can fully meet the requirements of water demand. The calculation formula for reliability is as follows:

$$R={\displaystyle \frac{1}{N}}{\sum }_{t=1}^N{Z}_t$$

(22)

where $R$ is the reliability of the system; $N$ is the total number of statistical analysis periods; $Z_t$ is the water supply status during the time period $t$; if the current time period meets the water supply demand, then $Z_t$= 1; if the current time period does not meet the water supply demand, it means that the water supply is disrupted, and $Z_t$ = 0.

(3)

Resilience

Resilience is used to characterize the rate of recovery after a system failure, or the duration of drought and water shortage. The greater the resilience of the water supply system, the faster the recovery, meaning the shorter the duration of damage. In this study, the resilience index $\gamma$ is expressed as the ratio of the total number of independent recovery events to the total number of failures. The calculation formula is as follows:

$$\gamma ={\displaystyle \frac{\sum _{t=1}^N{W}_t}{\sum _{t=1}^N{Z}_t}}$$

(23)

$$W_t=\left\{\begin{array}{c}1,if{Z}_t=1and{Z}_{t+1}=0\\ 0,otherwies\end{array}\right.$$

(24)

where $W_t$ is used to record the continuous failures that occur during the total simulation period; $Z_t$= 1 and $Z_{t+1}$ = 0 represent the beginning of a continuous failure.

(4)

Comprehensive Adaptation Index

Due to the positive performance indexes of coordination, reliability, and resilience, the geometric average processing is adopted for these three indexes to obtain the CAI when comparing and selecting multiple scenarios. The calculation formula is as follows:

$$\mathrm{C}\mathrm{A}\mathrm{I}=\sqrt[3]{A\times R\times \gamma }$$

(25)

The CAI is an index for evaluating water resource regulation scenarios, which reflects the reliability and adaptability capacity of the water resource system under various drought scenarios. A higher CAI value indicates the greater reliability and improved adaptability of the water resource system under the drought scenario. Among the multiple scenarios compared, the one with the highest CAI is chosen as the optimal scenario. This selection aims to provide better guidance for the decision-making and implementation of water resource regulation during drought scenarios, ensuring the effective utilization and management of water resource.

3. Results

3.1. Optimization Results of Drought-Limited Water Level

For the analysis and modeling presented in this study, we employed the General Water Allocation and Simulation Software (GWAS 2.1) for modeling and Python 3.8 software for data processing, optimization, and evaluation. Based on the relationship between the water supply of large and medium-sized reservoirs and calculation units, Dali (primarily focused on agricultural irrigation) and Kunming (primarily focused on urban domestic and industry water supply) are selected as the case analysis objects. The reservoirs and water supply targets that need to be optimized in the two regions are shown in

Table 2. Selection of optimized reservoirs and water supply target statistics.

Region	Optimized Reservoir	Water Supply Target
Dali	Haishao, Dayindian, Huaqiao, Erhai	Xizhou, Wase, Fengyi, Xiaguan, Qiaodian, Binju, Daying, Jinniu, Pingshan
Kunming	Qingshuihai, Songhuaba, Dianchi, Yunlong	Zhucheng, Kongxiang, Haikou, Longcheng, Jinmapu, Kunyang, Xizhu

.

On the basis of constructing the WAS model for the water-receiving area of the central Yunnan water diversion project, the objective function aims to minimize the sum of the average values of the water shortage rate (WSR) and maximize the equilibrium rate (ER) and the ecological guarantee rate (EGR) for each optimized reservoir corresponding to the calculation unit and industry. The NSGA-II algorithm was employed to optimize the drought-limited water level of the reservoirs in the two regions and the limiting coefficient of water supply by different industries. The number of iterations was set to 500, and the population was set to 100. The CRITIC method was used to determine the weight of each optimization objective, and the optimization scheme for the drought-limited water level of the reservoirs in the two regions that meet the Pareto-frontier optimality was obtained, as shown in Figure 7. The drought-limited water level of each reservoir corresponding to the optimal solution and the limiting coefficients of available water supply in various industries are shown in

Table 3. Drought-limited water level of large reservoirs and lakes (m).

Month	Qingshuihai		Songhuaba		Yunlong		Erhai		Dianchi
	DWWL	DGWL	DWWL	DGWL	DWWL	DGWL	DWWL	DGWL	DWWL	DGWL
Jan	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76
Feb	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76
Mar	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76
Apr	2162.01	2160.05	1962.82	1959.02	2070.20	2060.59	1964.91	1962.89	1884.78	1884.78
May	2162.01	2160.05	1962.82	1959.02	2070.20	2060.59	1964.91	1962.89	1884.78	1884.78
Jun	2164.26	2163.58	1962.70	1961.02	2090.04	2089.62	1967.37	1963.26	1884.79	1884.77
Jul	2164.26	2163.58	1962.70	1961.02	2090.04	2089.62	1967.37	1963.26	1884.79	1884.77
Aug	2164.26	2163.58	1962.70	1961.02	2090.04	2089.62	1967.37	1963.26	1884.79	1884.77
Sep	2164.26	2163.58	1962.70	1961.02	2090.04	2089.62	1967.37	1963.26	1884.79	1884.77
Oct	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76
Nov	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76
Dec	2162.99	2162.04	1944.54	1943.86	2079.79	2078.00	1968.39	1966.30	1884.76	1884.76

and

Table 4. Limiting coefficients of available water supply in different industries of large reservoirs and lakes.

Reservoir	Grade	Urban Domestic	Rural Domestic	Industry	Agricultural Irrigation	Urban Ecology
Qingshuihai	DWWL	0.741	/	0.935	/	0.985
	DGWL	0.313	/	0.289	/	0.701
Songhuaba	DWWL	0.631	/	0.508	/	0.744
	DGWL	0.107	/	0.148	/	0.284
Yunlong	DWWL	0.845	/	0.683	/	0.949
	DGWL	0.811	/	0.547	/	0.453
Erhai	DWWL	0.534	0.450	0.805	0.421	0.578
	DGWL	0.580	0.263	0.903	0.391	0.626
Dianchi	DWWL	/	/	0.559	0.924	0.841
	DGWL	/	/	0.428	0.326	0.392

.

3.2. Analysis of the Application Effect of Drought-Limited Water Level

3.2.1. Analysis of Total Water Shortage

To verify the rationality of the proposed optimization calculation method of the drought-limited water level, three scenarios were set up for comparative analysis: scenario I, SOP without drought-limited water level; scenario II, AWSP based on the reverse order recursive algorithm; and scenario III, OWSP determined by the optimization algorithm. Using the long-term inflow process of the reservoir and historical drought data during the calculation period, the total water shortage in two regions was analyzed for the annual average, normal dry year, and extremely dry year. The statistical results are shown in Figure 8.

As can be seen from Figure 8, the total water shortage in the two regions varied under different reservoir operation rules. Compared with scenario I, the water shortage in scenario II was reduced in different typical years, but the improvement was not substantial. Conversely, scenario III demonstrated a significant reduction in water shortage in different typical years, and the water shortage situation was significantly improved. Specifically, in the extremely dry year, the reduction in total water shortage in scenario III was larger than that in the annual average and normal dry year when compared to scenario I. This indicates that with increasing drought severity in two regions, the drought-limited water level determined by the optimization algorithm is more effective for drought-resistant reservoir operations.

3.2.2. Analysis of Severe Water Shortage Months

According to the “National Flood Control and Drought Relief Emergency Plans” [39], and the actual situation in the central Yunnan region, the threshold values of severe water shortage rates for urban domestic, rural domestic, industry, agricultural irrigation, and urban ecology water use were determined to be 10%, 10%, 20%, 50%, and 50%, respectively. A month in which the water shortage rate of each industry exceeds its threshold is regarded as a severe water shortage month. The number of severe water shortage months during the calculation period under the three scenarios was statistically analyzed, and the results are shown in Figure 9. Compared with scenario I, the number of severe water shortage months in different industries decreased in both scenario II and scenario III. However, the reduction was more significant in scenario III, indicating that the drought-limited water level determined by the optimization algorithm was better applied to the drought-resistant reservoir operations. This highlights the important role of refined water resource management in mitigating the risk of water shortage.

From the two regions, scenario III significantly reduced the number of severe water shortage months in different industries, particularly in specific industries. The situation in Kunming further emphasizes the variability in effects among the different industries. It can be seen in Figure 8b that the number of severe water shortage months decreased the most for urban domestic and industrial. Specifically, the number of severe water shortage months in urban domestic decreased from 197 to 177, and the number of severe water shortage months in industrial decreased from 53 to 32. This demonstrates the importance of the OWSP to secure water use in key industries. However, the smallest reduction was observed in rural domestic, where the number of severe water shortage months decreased from 66 to 57. Although the reduction in rural domestic is smaller, it still contributes to mitigating the risk of water shortage.

3.2.3. Analysis of Water Supply Effect in Typical Drought Events

According to the historical drought data, a severe consecutive drought occurred in Yunnan Province from 2009 to 2012, affecting a wide area, lasting for a long time, and causing deep damage. Therefore, the period from 2009 to 2012 was selected as a typical continuous dry year. The water supply situation of reservoirs in two regions was statistically analyzed, as shown in Figure 10. In a typical continuous dry year, the total water supply of the reservoir group in scenario I is low. In scenario II, the total water supply of the reservoir group is higher than that of scenario I, but the increase in total water supply is small and the effect is not obvious. However, the total water supply of the reservoir group in scenario III is significantly higher than that in scenarios I and II. This reveals that the optimization algorithm can effectively guarantee the water supply during continuous dry years and alleviate drought conditions.

3.3. Evaluation of Water Resource Regulation Scheme and Analysis of Water Supply Effect

3.3.1. Analysis of Weight Calculation Results

To ensure that the evaluation results accurately reflect the actual situation and needs of each region, formulating more refined regulatory policies or measures will be helpful. In this study, the CRITIC weight method is adopted to determine the weight of 12 indexes in the three fields of water resource, social economy, and ecological environment in Dali and Kunming. The weighting statistics for indexes in two regions are shown in

Table 5. The weighting statistics for indexes in two regions.

Field	Index Number	Weight
		Dali	Kunming
Water resource	I1	0.078	0.062
	I2	0.062	0.054
	I3	0.124	0.142
	I4	0.064	0.065
Social economy	I5	0.069	0.106
	I6	0.099	0.068
	I7	0.061	0.064
	I8	0.069	0.104
Ecological environment	I9	0.131	0.087
	I10	0.063	0.058
	I11	0.099	0.108
	I12	0.081	0.083

.

It can be seen in Table 5 that the weights for water resource, social economy, and ecological environment in Dali are 0.328, 0.298, and 0.374, respectively. In the field of water resource, the weight of I₃ is the largest at 0.124. In the field of social economy, the weight of I₆ is the largest at 0.099. In the field of ecological environment, the weight of I₉ is the largest at 0.131. In contrast, the weights for water resource, social economy, and ecological environment in Kunming are 0.322, 0.342, and 0.336, respectively. In the field of water resource, the weight of I₃ is the largest at 0.142. In the field of social economy, the weight of I₅ is the largest at 0.106. In the field of ecological environment, the weight of I₁₁ is the largest at 0.108. The results show that Dali prioritizes the ecological environment over the other two fields, while Kunming prioritizes the social economy indexes. These indexes reflect the priorities of water resource management in each region and provide a reference for developing targeted water resource management and conservation strategies.

3.3.2. Analysis of the Impact of Reservoir Water Supply Rules on Water Supply and Consumption Systems

Reservoir water supply rules determine the timing and quantity of reservoir water supply, which directly impacts the water supply capacity of the water supply system. Adjusting these rules under different drought scenarios can help manage water resource fluctuations, ensuring effective utilization and allocation of water resource. Therefore, it is necessary to establish experimental samples to analyze the impact of different reservoir water supply rules on water supply systems. This analysis will provide targeted recommendations for designing water supply systems tailored to various regions and drought scenarios.

Figure 11 shows the variation trend of the CAI in uncompressed samples during a normal dry year. The horizontal axis represents different regions, the vertical axis represents the CAI, and the colors represent different reservoir water supply rules. As detailed in Figure 11, the CAI value of the AWSP is the highest, followed by that of OWSP. Compared with the SOP, the CAI value of the AWSP in the Dali region increased from 0.455 to 0.553, an increase of 21.54%. The CAI value of the OWSP increased from 0.455 to 0.541, an increase of 18.90%. Similarly, the CAI value of the AWSP in the Kunming region increased from 0.544 to 0.623, an increase of 14.52%. The CAI value of the OWSP increased from 0.544 to 0.605, an increase of 11.21%. These results indicate that the variation in reservoir water supply rules has a significant impact on the CAI value, particularly in the Dali region.

Figure 12 shows the variation trend of CAI in different reservoir water supply rules during a normal dry year. The top horizontal line segment represents the confidence interval upper limit of the CAI distribution, the upper-, middle-, and lower-line segments of the box represent the upper quartile, median, and lower quartile of the CAI distribution, and the bottom horizontal line segment represents the confidence interval lower limit of the CAI distribution. The dots represent the mean value of the CAI distribution. Among them, the sample of Group I were compressed with one water object, which belonged to mild compression. The samples of Group II and Group III were compressed with two and three water objects, respectively, which belonged to moderate compression. The samples of Group IV and Group V are compressed with 4 and 5 water objects, respectively, which belonged to enhanced compression. This stratification allows for a detailed analysis of how different levels of compression impact the CAI, revealing the effectiveness of reservoir water supply rules under varying degrees of water resource constraints.

As can be seen from Figure 12, the mean and maximum CAI values of AWSP and OWSP are better than those of SOP. Compared with the OWSP, the mean and maximum CAI values of AWSP are higher, which indicates that the effect of AWSP is better. However, the CAI changes in the three types of reservoir operation rules are different in two regions and under different compression degrees. Specifically, the highest mean and maximum values of CAI are AWSP in the Dali region under mild compression. Under moderate compression, the highest mean value of CAI is AWSP, while the highest maximum value of CAI is OWSP. Under enhanced compression, the highest mean and maximum values of CAI become the OWSP. These results show that the OWSP is more effective in the Dali region as the compression strength increases. Moreover, under mild compression and moderate compression in the Kunming region, the highest mean and maximum values of CAI are AWSP. Under enhanced compression, the mean and maximum CAI values of AWSP and OWSP are similar. These findings indicate that the AWSP performs better in the Kunming region as the compression strength increases.

Figure 13 shows the variation trend of the CAI in uncompressed samples during an extremely dry year. Under the condition of a constant water consumption system, changing the rules of the reservoir water supply has different effects on CAI in different regions. It can be seen in Figure 13 that the CAI value of the OWSP is the highest, followed by the AWSP. Compared with the SOP, the CAI value of the AWSP in the Dali region increased from 0.406 to 0.484, an increase of 19.21%. The CAI value of the OWSP increased from 0.406 to 0.519, an increase of 27.83%; this indicates that OWSP has a significant impact on CAI in the Dali region. However, the CAI value of the AWSP in the Kunming region increased from 0.525 to 0.530, an increase of 0.95%. The CAI value of the OWSP increased from 0.525 to 0.546, an increase of 4.00%. The results show that OWSP has no significant impact on CAI in the Kunming region. In summary, while the OWSP has a significant impact on improving CAI in the Dali region during an extremely dry year, it has a limited impact in the Kunming region.

Figure 14 details the variation trend of CAI in different compressed samples during an extremely dry year. The observed trends are similar to those in Figure 12. The mean and maximum CAI values of AWSP and OWSP are better than those of SOP. As the compression strength increases, the highest mean and maximum values of CAI are OWSP in the Dali and Kunming regions. This reveals that the OWSP effect is better in the Dali and Kunming regions.

To sum up, by comparing Figure 11, Figure 12, Figure 13 and Figure 14, it can be seen that the reservoir water supply rules exhibit different trends in three compression intensities under different regions and drought scenarios. Under the normal dry year scenario, the CAI values of AWSP for mild and moderate compression are the highest in the Dali region. Moreover, the CAI values of OWSP are the highest in enhanced compression. For the Kunming region, the CAI values of AWSP are the highest in three compression intensities. Under the extremely dry year scenario, the CAI values of OWSP in the Dali and Kunming regions are the highest in three compression intensities. Therefore, it is better to choose AWSP as the drought resistance scheduling rule for reservoirs during a normal dry year. The OWSP is chosen as the best drought resistance scheduling rule for reservoirs during an extremely dry year.

3.3.3. Analysis of the Impact of Water Compression Object on Water Supply and Consumption Systems

Under specific drought conditions, water compression for different water users such as urban domestic, industry, and agricultural irrigation can optimize water resource utilization and mitigate the negative impacts of drought. This provides a scientific basis for developing more reasonable, efficient, and sustainable water resource management strategies. Therefore, to determine the optimal water compression objects for the Dali and Kunming regions to cope with droughts, different water users were compressed based on the optimal reservoir water supply rules.

Table 6. Scenario setting of water compression ratio for each water user in the sample group I.

Sample Number	Urban Domestic	Rural Domestic	Industry	Agricultural Irrigation	Urban Ecology
M1	10%	/	/	/	/
M2	20%	/	/	/	/
M3	30%	/	/	/	/
M4	40%	/	/	/	/
M5	50%	/	/	/	/
M6	60%	/	/	/	/
M7	/	10%	/	/	/
M8	/	20%	/	/	/
M9	/	30%	/	/	/
M10	/	40%	/	/	/
M11	/	50%	/	/	/
M12	/	60%	/	/	/
M13	/	/	10%	/	/
M14	/	/	20%	/	/
M15	/	/	30%	/	/
M16	/	/	40%	/	/
M17	/	/	50%	/	/
M18	/	/	60%	/	/
M19	/	/	/	10%	/
M20	/	/	/	20%	/
M21	/	/	/	30%	/
M22	/	/	/	40%	/
M23	/	/	/	50%	/
M24	/	/	/	60%	/
M25	/	/	/	/	10%
M26	/	/	/	/	20%
M27	/	/	/	/	30%
M28	/	/	/	/	40%
M29	/	/	/	/	50%
M30	/	/	/	/	60%

describes the scenario settings for the water compression ratio when compressing one water object.

The variation in CAI values for different water user compression ratios in the Dali and Kunming regions under normal dry year scenarios is shown in Figure 15. Overall, the CAI values under the AWSP are higher than those of the SOP. As can be seen from Figure 15a, the mean value of CAI for the Group I samples in the Dali region is 0.559 under the AWSP. The CAI values for compression urban domestic and urban ecology are below the mean, while the CAI values for compression rural domestic, industry, and agriculture irrigation are above the mean. The maximum CAI value is 0.580 in the M24 scenario. This indicates that agricultural irrigation is the optimal compression object during a normal drought year.

As detailed in Figure 15b, the mean value of CAI for the Group I samples in the Kunming region is 0.616 under the AWSP. The CAI values for compression urban ecology are below the mean, and some of the CAI values for compression urban domestic are also below the mean. However, the CAI values for compression rural domestic, industry, and agriculture irrigation are above the mean. The maximum CAI value is 0.639 in the M19 scenario. This reveals that agricultural irrigation is also the optimal compression object during a normal drought year.

Figure 16 shows the variation trend of CAI values in compressing different water users during a normal dry year. The variation trends of CAI values are similar in both the Dali and Kunming regions. It can be seen in Figure 16 that the CAI value in both regions decreases as the proportion of compression on urban domestic water use increases, with the Kunming region experiencing a more significant decrease. In the Dali region, the CAI value increases slightly with the proportion of compression on rural domestic water use, while in the Kunming region, it remains nearly unchanged. Both regions see a slow increase in CAI values with the compression of industrial water use, with CAI values second only to those for agricultural irrigation compression. The CAI values in both regions increase the most with the proportion of compression on agricultural irrigation. Conversely, the CAI values decrease slightly with the proportion of compression on urban ecology water use. Therefore, for water resource managers in the Dali and Kunming regions, the AWSP is the optimal reservoir water supply rule, and agricultural irrigation is the optimal compression object during a normal drought.

The variation in CAI values for different water user compression ratios in the Dali and Kunming regions under extremely dry year scenarios is illustrated in Figure 17. Overall, the CAI values of different water user compression ratios under the OWSP are higher than those of the SOP. As detailed in Figure 17a, the mean value of CAI for the Group I samples in the Dali region is 0.537 under the OWSP. The CAI values for compression urban domestic and urban ecology are below the mean, while some of the CAI values for compression rural domestic and industry are also below the mean. In contrast, the CAI values for compression agriculture irrigation are above the mean. The maximum CAI value is 0.618 in the M24 scenario. This indicates that agricultural irrigation is the optimal compression object during an extremely dry year.

As can be seen in Figure 17b, the mean value of CAI for the Group I samples in the Kunming region is 0.581 under the OWSP. The CAI values for compression rural domestic, agriculture irrigation, and urban ecology are below the mean, while some of the CAI values for compression urban domestic and industry are also below the mean. The maximum CAI value is 0.701 in the M18 scenario. This shows that the optimal compression object is industry during an extremely dry year.

Figure 18 shows the variation trend of CAI values in compressing different water users during an extremely dry year. As detailed in Figure 18, the CAI value in the Dali region decreases with an increased proportion of compression on urban domestic and urban ecology. Conversely, the CAI value in the Dali region increases with a higher proportion of compression on rural domestic, agricultural irrigation, and urban ecology, among which the CAI value of the agricultural irrigation is the largest increase. Similarly, the CAI value in the Kunming region decreases with an increased proportion of compression on urban ecology. Moreover, the CAI value in the Kunming region increases with a higher proportion of compression urban domestic, industry, and agricultural irrigation, among which the CAI value of the industry shows the largest increase.

In summary, by comparing Figure 17 and Figure 18, under the extremely dry year scenario, the optimal compression object in the Dali region is agricultural irrigation, followed by industry and rural domestic. In contrast, the optimal compression object in the Kunming region is industry, followed by urban domestic and agricultural irrigation. Therefore, to improve regional drought resilience, the optimal reservoir water supply rule can be adopted when encountering extremely dry years. For the Dali region, the optimal compression object is agricultural irrigation, while for the Kunming region, the optimal compression object is industry.

3.3.4. Analysis of the Impact of Water Compression Ratio on Water Supply and Consumption Systems

The adjustment of the water compression ratio is a crucial strategy to cope with water shortage and drought scenarios. This approach aims to balance supply and demand by reducing water consumption while maintaining the stable operation of the water supply and consumption system. Water compression helps to reduce the burden on the water supply system, ensures water supply during critical periods and to important water users, and improves the reliability and safety of the water supply. By adjusting the water compression ratio, the limited water resource can be allocated more flexibly and the rational allocation of the water resource can be realized.

Figure 19 presents the simulation results in different groups during a normal dry year. It can be seen in Figure 19 that the CAI value of the Dali and Kunming regions initially increases and then stabilizes as the number of compression water objects rises. For the SOP, the CAI value is maximized when the number of compression water objects is four. Conversely, for the AWSP, the CAI value is maximized when the number of compression water objects is three, and the maximum CAI value of the AWSP is higher than that of the SOP. This indicates that the AWSP has a better drought resistance effect.

To determine the optimal compression ratio for each water user in a normal dry year scenario, different compression ratios were analyzed for each water user in the Group III sample. The simulation results are shown in Figure 20. As can be seen from Figure 20, the maximum CAI value of 0.651 was reached in the Dali region when the compression ratios for agricultural irrigation, industry, and rural domestic were 60%, 40%, and 60%, respectively. According to actual regulation requirements, the water supply guarantee rate for urban domestic, rural domestic, industry, and agricultural irrigation is 95%, 95%, 95%, and 75%, respectively. Through simulation regulation, when the compression ratios for agricultural irrigation, industry, and rural domestic are 50%, 20%, and 10%, respectively, the water supply guarantee rate of each water user can meet the requirements. However, the maximum CAI value of 0.768 was reached in the Kunming region when the compression ratios for agricultural irrigation, industry, and rural domestic were 60%, 30%, and 60%, respectively. Through simulation regulation, when the compression ratios for agricultural irrigation, industry, and rural domestic are 40%, 30%, and 10%, respectively, the water supply guarantee rate of each water user can meet the requirements. Therefore, under the normal dry year scenarios, the optimal compression objects of each water user in the Dali region are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 50%, 20%, and 10%, respectively. In the Kunming region, the optimal compression objects are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 40%, 30%, and 10%, respectively.

To evaluate the water supply effect of water resource regulation, this study carried out a comparative analysis of the water shortage rate and index changes for each water user under different regulation strategies. The analysis results are shown in Figure 21 and

Table 7. The regulation index statistics during normal dry year.

Region	Status	Reservoir Water Supply (104 m3)	Abandonment of Water from Reservoirs (104 m3)	Equilibrium Rate (%)	Coordination	Reliability	Resilience
Dali	pre-regulation	11,603	6360	43.3	0.309	0.769	0.396
	post-regulation	14,760	116	69.7	0.426	0.898	0.633
Kunming	pre-regulation	42,776	17,589	82.7	0.397	0.924	0.438
	post-regulation	44,232	11,236	96.3	0.480	0.969	0.539

. As detailed in Figure 21 and Table 7, the water shortage rate of each water user decreased, which indicates that the regulation measures are effective in alleviating the water shortage. Through the comparative analysis before and after regulation, the water supply of the reservoir in the Dali and Kunming regions increased, while the amount of abandonment water significantly decreased. This shows that the operation efficiency of the reservoir was improved. The equilibrium rate and water use efficiency were significantly improved, indicating that there was a balance between supply and demand. The enhancements in coordination, reliability, and resilience demonstrate that the regulation measures improved the overall adaptability and drought resistance of the water resource system.

Figure 22 illustrates the simulation results in different groups during an extremely dry year. The simulation results are similar to those from Figure 19. For the OWSP, the CAI value is maximized when the number of compression water objects is three, and the maximum CAI value of the OWSP is higher than that of the SOP. This reveals that the OWSP has a better drought resistance effect.

Figure 23 shows the simulation results of CAI values for Group III samples during an extremely dry year. As can be seen from Figure 23, the maximum CAI value of 0.782 was reached in the Dali region when the compression ratios for agricultural irrigation, industry, and rural domestic were all 60%. According to actual regulation requirements, when the compression ratios for agricultural irrigation, industry, and rural domestic are 60%, 30%, and 10%, respectively, the water supply guarantee rate of each water user can meet the requirements. In the Kunming region, the maximum CAI value of 0.784 was reached when the compression ratios for industry, agricultural irrigation, and urban domestic were 60%, 60%, and 40%, respectively. Through simulation regulation, when the compression ratios for industry, agricultural irrigation, and urban domestic are 50%, 60%, and 20%, respectively, the water supply guarantee rate of each water user can meet the requirements. Therefore, under the extremely dry year scenarios, the optimal compression objects of each water user in the Dali region are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 60%, 30%, and 10%, respectively. In the Kunming region, the optimal compression objects of each water user are industry, agricultural irrigation, and rural domestic, with the most suitable compression ratios being 50%, 60%, and 20%, respectively.

Figure 24 and

Table 8. The regulation index statistics during extremely dry year.

Region	Status	Reservoir Water Supply (104 m3)	Abandonment of Water from Reservoirs (104 m3)	Equilibrium Rate (%)	Coordination	Reliability	Resilience
Dali	pre-regulation	10,776	7011	43.4	0.281	0.727	0.328
	post-regulation	13,445	68	83.2	0.464	0.927	0.571
Kunming	pre-regulation	28,382	9032	48.1	0.342	0.848	0.500
	post-regulation	33,009	5064	95.5	0.449	0.967	0.643

show the comparison of regulation effects between the Dali and Kunming regions under an extremely dry year. The regulation effect is similar to Figure 21 and Table 7. Compared with pre-regulation, post-regulation was better than pre-regulation in all indexes. The results show that the regulation measures effectively improved the overall management efficiency and drought resistance of the water resource.

4. Discussion

The acceleration of climate change and urbanization has resulted in more frequent and intense climate events, particularly in regions prone to droughts [40,41,42]. The central Yunnan Province region is located in the basin area of the East Yunnan Plateau, which is a drought-prone region. The central Yunnan Province region, including Dali and Kunming, serves as the study area due to its high susceptibility to drought caused by dry hot river valleys and a subtropical monsoon climate. Our analysis indicates that optimizing the drought-limited water level for the reservoir group substantially improves water supply performance during drought years by allowing for more efficient allocation of water resource and reducing severe water shortage. This suggests that the enhanced WAS model, which includes improved drought-resistant water supply rules, provides a more rational allocation of reservoir water supply, especially under drought and water shortage conditions. In addition, the CAI effectively quantified the benefits of optimized water regulation strategies, providing a comprehensive evaluation of water resource management under different drought scenarios.

Domestic and foreign scholars have conducted a lot of research on the optimization of reservoir drought-limited water level, and achieved fruitful results [18,19,43,44,45]. This study introduces a novel methodology that optimizes the drought-limited water level across the reservoir group, diverging from previous research that primarily targeted individual reservoirs. This shift offers a more holistic approach to drought management within complex water resource systems. Moreover, while the existing literature often emphasizes the general impacts of global warming and urban expansion on drought frequency, our study offers a detailed methodology for mitigating these impacts through water resource management. This approach includes the enhancement of the WAS model and the development of a CAI to evaluate the effectiveness of water resource regulation strategies. By comparing these studies, it becomes evident that while there is a broad consensus on the increasing threat of droughts, our research provides a novel contribution by addressing the complex interactions within a group of reservoirs and proposing actionable strategies for drought mitigation.

The results of this study have significant practical implications for reservoir management and drought mitigation, particularly in the central Yunnan Province. The findings offer critical scientific and technical support to regional water resource management and drought operation authorities, facilitating informed policy-making and operational decisions regarding reservoir management and drought mitigation.

Despite the achievements in optimizing the drought-limited water level, there are some limitations to this study. Firstly, the focus on specific reservoirs in central Yunnan may limit the generalizability of the findings to other regions with different hydrological and socio-economic conditions. The assumptions regarding drought scenarios also introduce a degree of uncertainty. Additionally, the methods used in this study, including the optimization algorithms, may have simplifications that affect the accuracy of the results. Future research could expand on this study by incorporating additional variables, such as climate change projections, land-use changes, and socio-economic factors. Exploring the application of these methods to other regions with different hydrological and socio-economic contexts would help test their robustness and adaptability. Furthermore, developing more sophisticated optimization techniques or incorporating machine learning methods could enhance predictive accuracy and decision-making support.

In summary, the optimized drought-limited water levels play a crucial role in improving water supply management for the reservoir group, offering valuable insights and tools for future research and policy development in drought management.

5. Conclusions

The drought-limited water level of the reservoir group is a crucial reference indicator for regional drought management. This study improved the drought-resistant water supply module in the WAS model and proposed the CAI index to evaluate optimal regulation scheme. The application of these methods in central Yunnan Province, China, leads to the following conclusions:

(1)

The proposed drought-limited water level rules under the reservoir group conditions enhance the ability to manage water supplies during droughts.

(2)

The optimization method provides a better water supply effect during consecutive dry years compared to traditional methods, significantly reducing severe water shortages.

(3)

AWSP is preferred for normal dry years, while OWSP is optimal for extremely dry years in the Dali and Kunming regions.

(4)

Under the normal dry year scenario, the optimal compression objects of each water user in the Dali region are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 50%, 20%, and 10%, respectively. In the Kunming region, the optimal compression objects of each water user are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 40%, 30%, and 10%. Under the extremely dry year scenario, the optimal compression objects of each water user in the Dali region are agricultural irrigation, industry, and rural domestic, with the most suitable compression ratios being 60%, 30%, and 10%, respectively. In the Kunming region, the optimal compression objects of each water user are industry, agricultural irrigation, and rural domestic, with the most suitable compression ratios being 50%, 60%, and 20%, respectively.