Intra-Day and Seasonal Peak Shaving Oriented Operation Strategies for Electric–Hydrogen Hybrid Energy Storage in Isolated Energy Systems
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Literature Review
1.3. Research Gaps and Contributions
- (1)
- Operation Model: Contrary to arranging a single BESS, the EH-HESS framework, relying on the complementary characteristics of BESS and HSS, can usefully solve the intra-day and seasonal peaking challenges of the isolated energy systems to improve the energy consumption level and achieve the self-sufficiency of the energy in the off-grid situation, thus contributing to the sustainable and stable operation.
- (2)
- Energy Operation Strategy: Different from the current operation strategy, the novel operation strategy adds the energy interaction between the ESSs to expand the working interval for clarifying intra-day and seasonal peak demands while retaining the ability to rapidly return to the desired operation interval to ensure the regulation capacity of the energy storage system. In addition, an optimization model for the working states of the HSS is designed, which effectively improves the utilization of HESS.
- (3)
- Scenario Uncertainty: Opposite to the scenario uncertainty approach of previous articles, this paper constructs four different seasonal proportion scenarios and three different load types, which validly analyze the EH-HESS configuration and the limitations on the number of HSS states to influence the operation strategy under the seasonal and intra-day perspectives, so as to improve the generalizability of the operation strategy and provide powerful suggestions for related industry agents.
| Refs. | Objectives | HESS | Regulating Demand | ESS Allocation | Off Grid | ||
|---|---|---|---|---|---|---|---|
| Short Time Scale | Seasonal Scale | Short-Term ESS | Long-Term ESS | ||||
| [1] | Cost Energy excess rate Load loss rate | × | √ | × | BESS | × | √ |
| [7] | Profit | × | √ | × | BESS | × | × |
| [8] | Cost | × | √ | × | BESS | × | × |
| [9] | Profit | × | × | √ | × | Pumped storage | × |
| [10] | Cost | × | × | √ | × | Pumped storage | × |
| [11] | Cost | × | × | √ | × | Compressed air ESS | × |
| [12] | Cost | × | × | √ | × | HSS | × |
| [13] | Commercialization viability | × | √ | √ | BESS | HSS | × |
| [14] | Cost | × | × | √ | × | Electricity to methane | × |
| [15] | Cost | × | × | √ | × | HSS | × |
| [17] | Levelized cost of energy | √ | √ | √ | BESS Flywheel–battery | HSS | × |
| [18] | Cost | √ | √ | √ | BESS | HSS | × |
| [19] | Cost Renewable energy penetration | √ | √ | √ | BESS | HSS | × |
| This work | Cost Energy excess rate Load loss rate | √ | √ | √ | BESS | HSS | √ |
| Refs. | Objectives | Prevents over Charge/Discharge | Energy Interaction | ESS State Change Interval | HSS State Limitations | Dynamic Number of State Limits | |
|---|---|---|---|---|---|---|---|
| BESS | HSS | ||||||
| [20] | Stability | √ | × | 1 h | 1 h | × | × |
| [21] | Cost Stability | √ | × | 1 h | 1 h | × | × |
| [22] | Carbon emission reductions Investment costs Operating costs | √ | × | 1 h | 1 h | × | × |
| [23] | Cost | √ | × | 1 h | 24 h | √ | × |
| [24] | Profit | √ | × | 1 h | 24 h | √ | × |
| [25] | Profit Stability | √ | √ | 1 h | 1 h | × | × |
| [26] | Profit Renewable energy utilization | √ | × | 1 h | 1 h | × | × |
| This work | Cost Energy excess rate Load loss rate | √ | √ | 1 h | (1 h, 24 h) | √ | √ |
2. Operation Model of EH-HESS
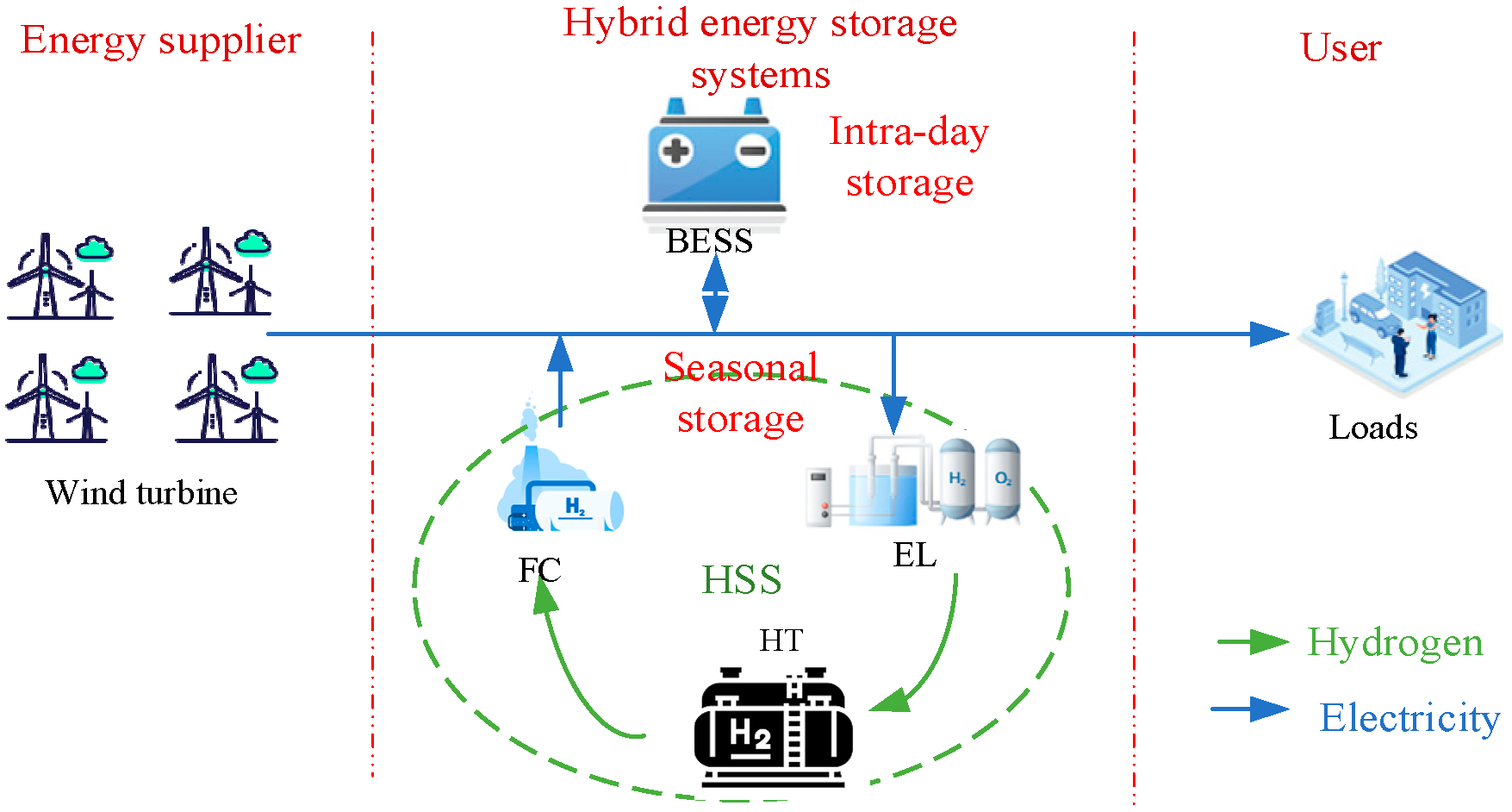
2.1. Framework of EH-HESS
2.2. Model of the EH-HESS
2.2.1. Hierarchical Time Discretization Model
2.2.2. Model of Intra-Day Storage
2.2.3. Model of Seasonal Hydrogen Storage System
- Electrolyze
- Fuel Cell
- Hydrogen Tank
3. The Energy Operation Strategy of EH-HESS
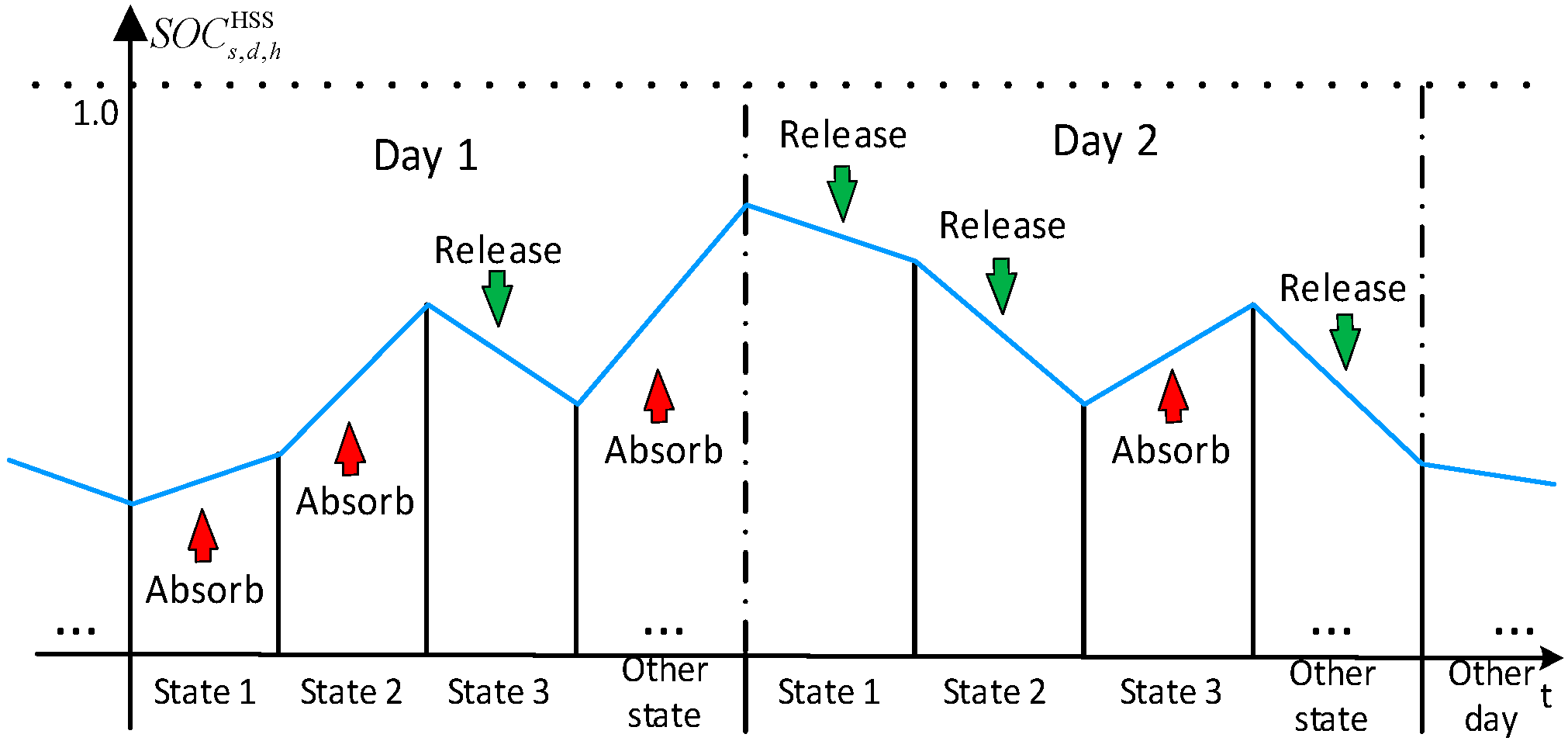
3.1. HSS Optimal State Transition Interval Model
3.2. Interactive Energy Operation Strategies
- (1)
- The complementary mechanism of traditional strategy is simple superposition, which requires high ESS configuration requirements. The deep coupling of intraday and seasonal peak demands is laborious to clarify, making it difficult to actualize the effective configuration of HESS.
- (2)
- In the case of fixed ESS allocation, the complementary charge state has to be adjusted in real-time owing to the high fluctuation of RES to retain maximum adjustability.
- (3)
- Seasonal and intra-day peak demands are mixed in the net load demand, making it hard for a single ESS to fulfill peak demand at a certain moment.
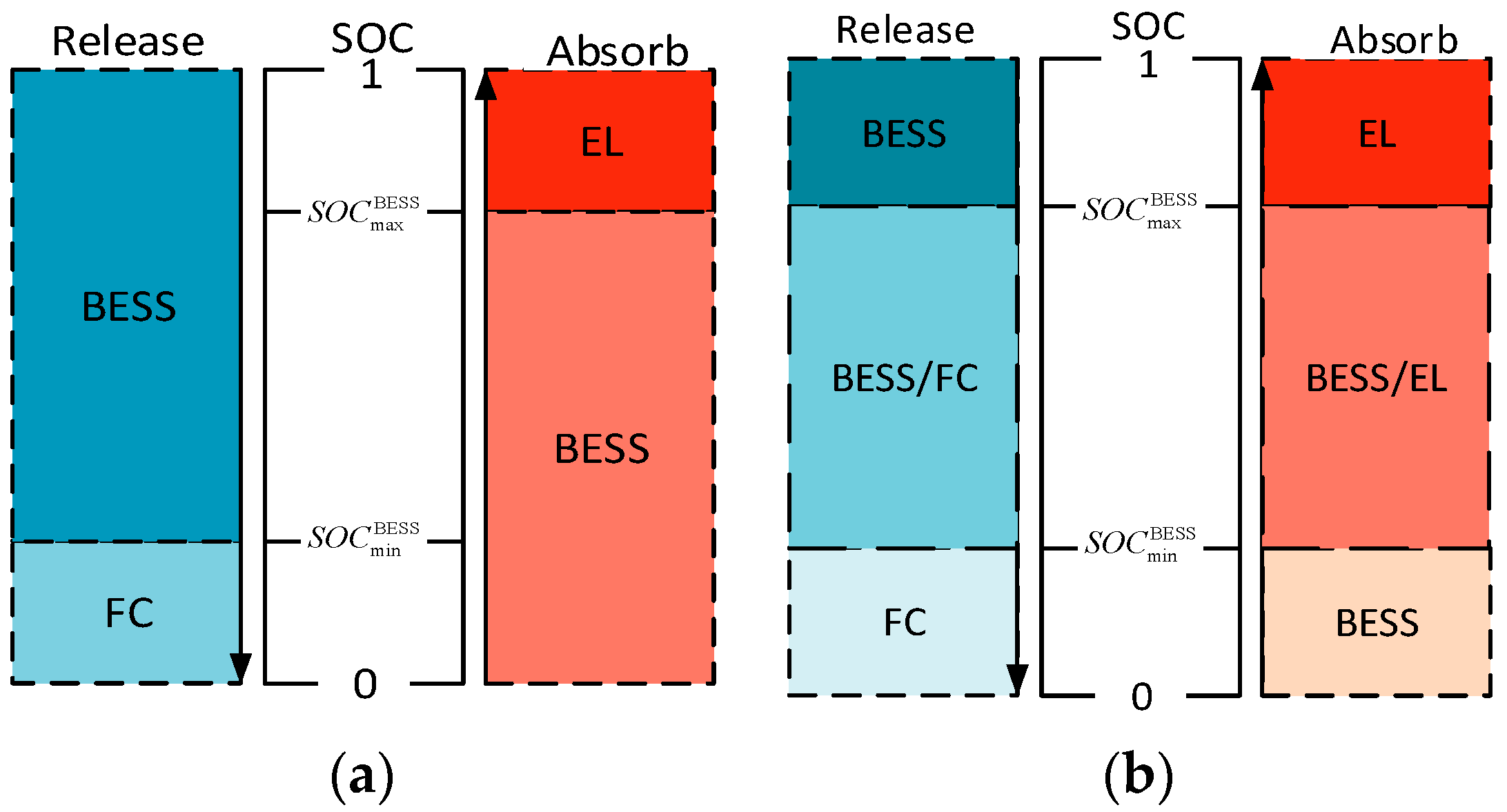
- (1)
- : HSS and BESS working together. All ESSs can both supply or absorb energy at the same time, or HSS can charge to BESS or absorb BESS released. Due to the different energy conversion efficiencies of different ESSs, in order to improve the energy utilization of the system and reduce the energy loss and cost loss, the article optimizes the allocation of energy with the goal of minimizing the operating cost, as described in Section 4;
- (2)
- : If a system requires ESS to absorb energy, BESS works, and, conversely, HSS works;
- (3)
- : If a system requires ESS to deliver energy, BESS works, and, conversely, HSS works.
- (1)
- The novel strategy takes into account the energy interactions between the ESS and the existence of a zone in which the two ESSs work together. It expands the operating range of HSS to increase the utilization of HSS. Moreover, it can reduce the high requirement for energy storage configuration avoiding the inability to meet the regulation demand due to the irrational energy storage configuration under the fixed zoning.
- (2)
- The novel strategy retains the alone operation state to avoid overcharge/discharge of BESS, while rapidly returning to the desired operation interval.
- (3)
- The energy interaction intervals provide a buffer region. Compared to other literature which characterizes uncertainty through real-time scheduling [32] and robust optimization [33], to derive an optimal strategy, this article proposes a solution to uncertainty, namely, a model that sets up buffer intervals to cope with uncertainty, which can be better applied in practice. The two ESSs can work together in this interval with a regulation capability equal to the sum of the maximum charging and discharging power to improve the ability to cope with uncertainty.
4. Optimization and Solution of EH-HESS Operation Model
4.1. Objective Function
4.2. Constraint
4.3. Linearization
4.4. Evaluation Indicators
5. Case Study
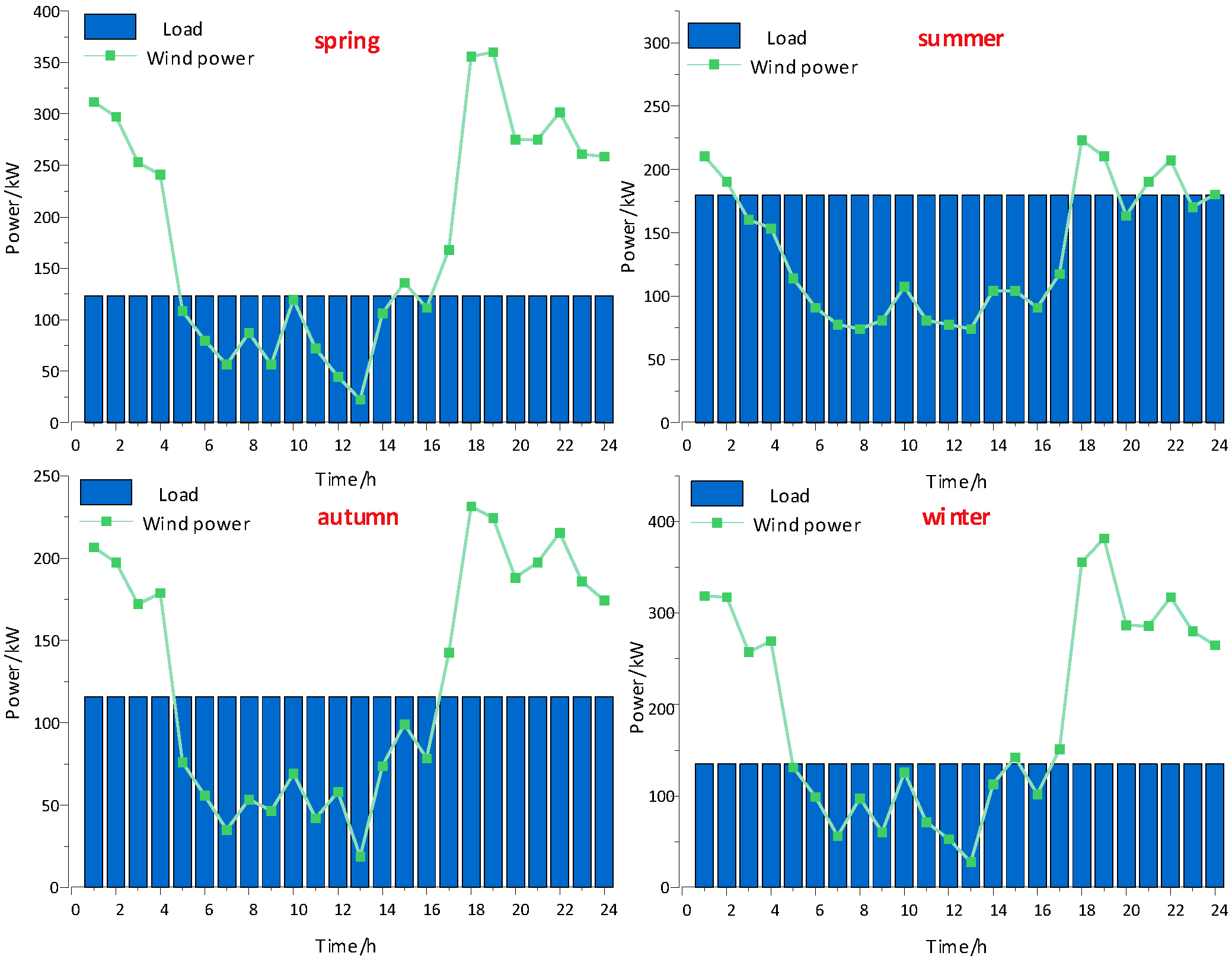
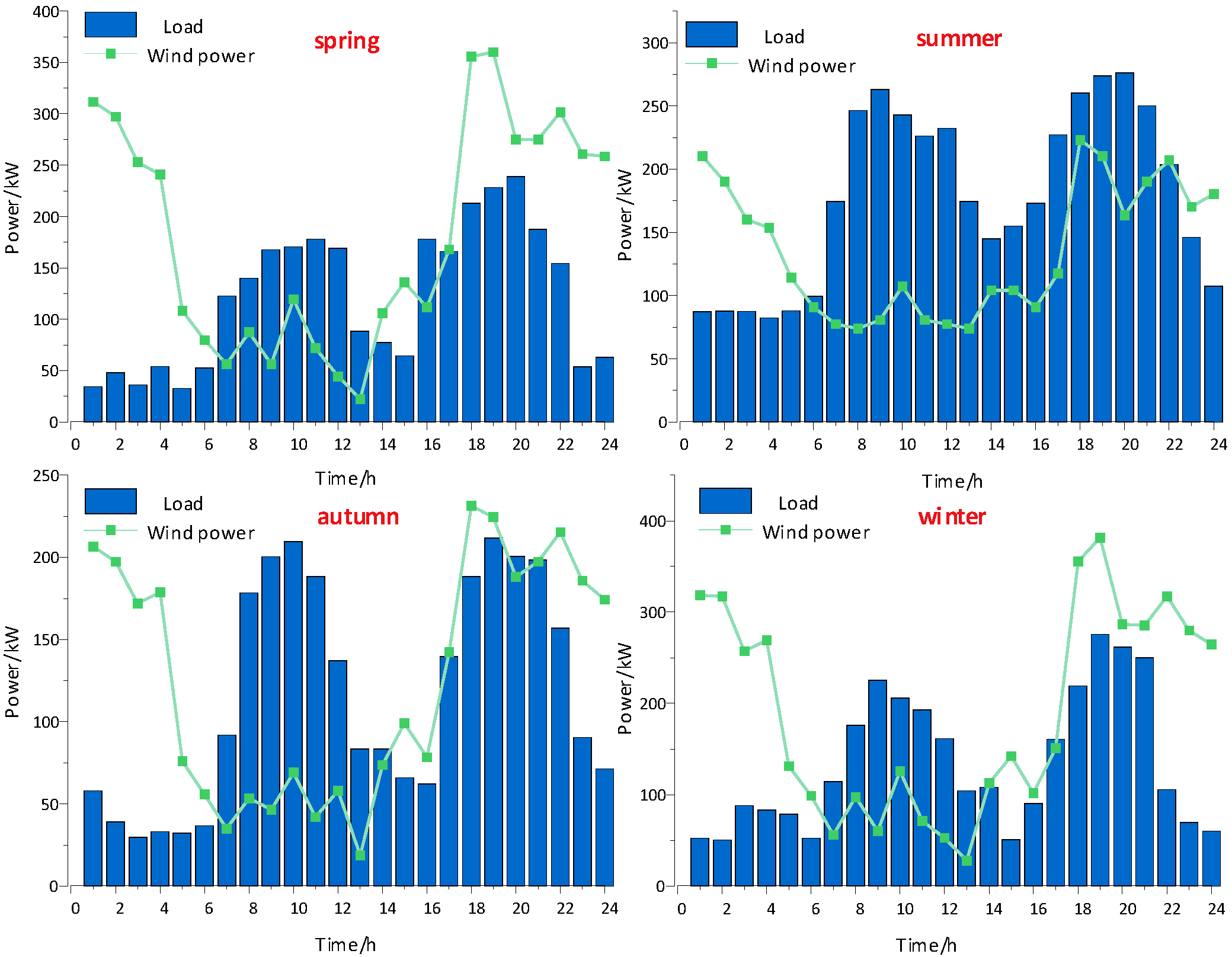
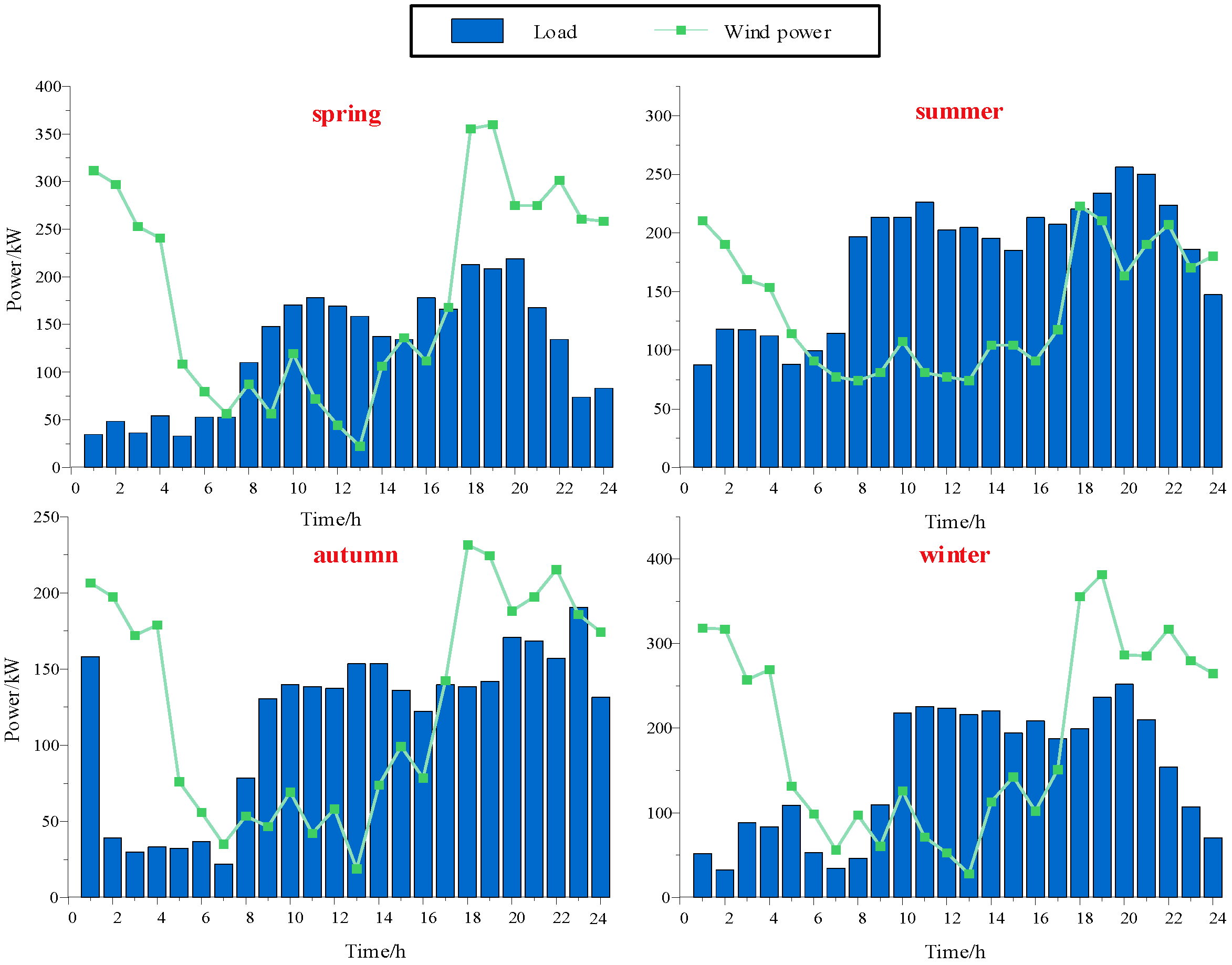
5.1. Initial Parameters and Data
- Case 1: A single BESS model without HSS is presented.
- Case 2: An EH-HESS model with a traditional operation strategy is examined.
- Case 3: An EH-HESS model with a proposed operation strategy is evaluated.
5.2. Benefit of EH-HESS Modeling
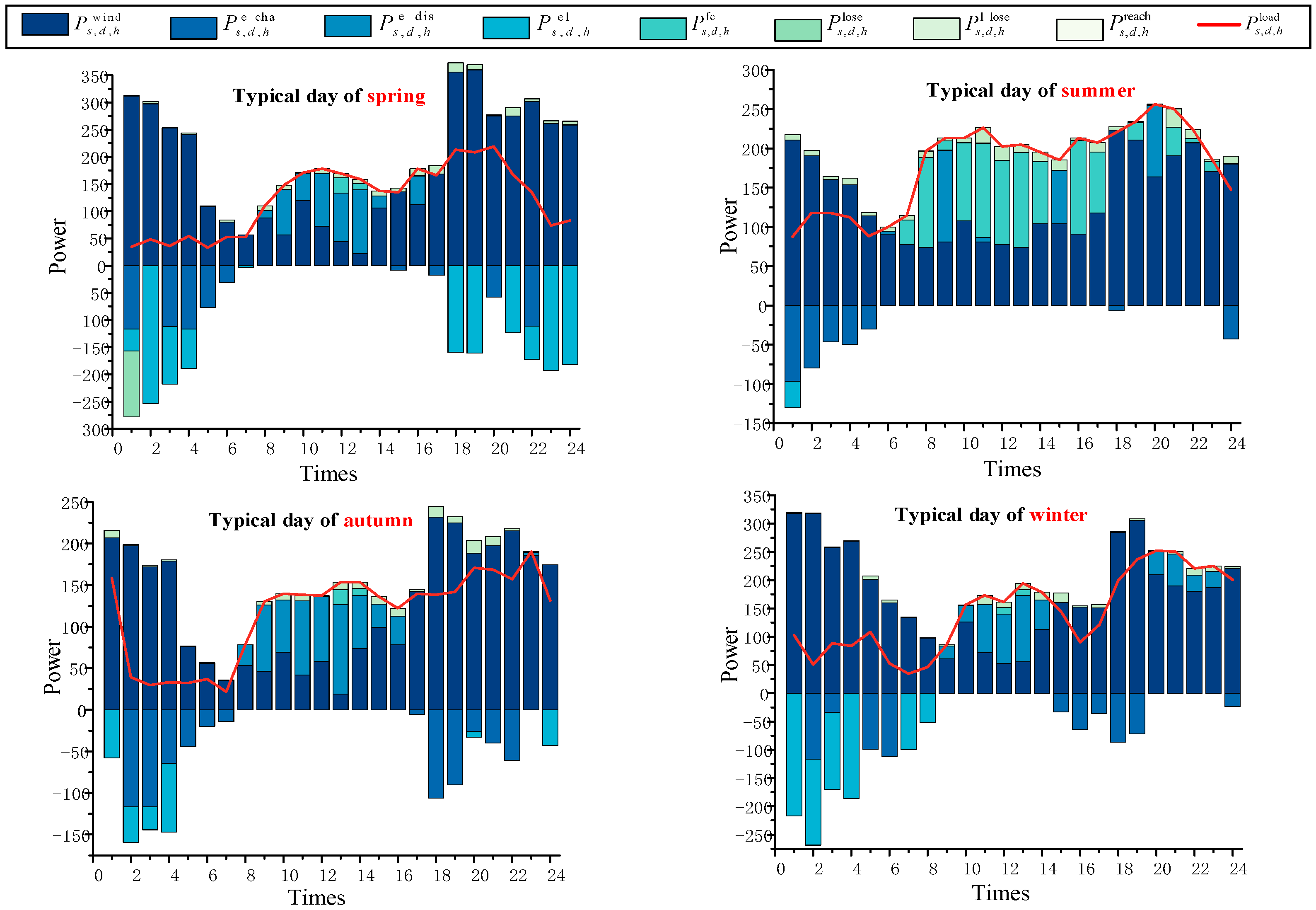
5.3. Benefits of Energy Operation Strategies
5.3.1. Wind Abandonment and Curtailment of Load
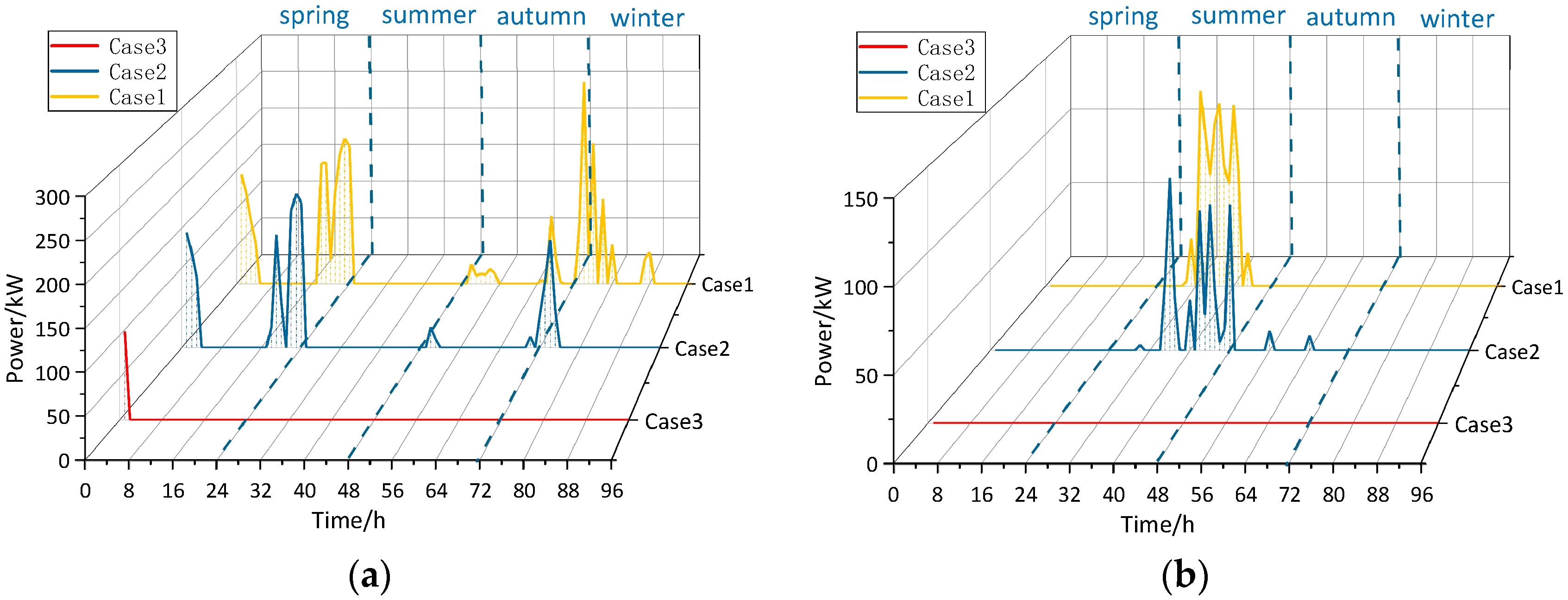
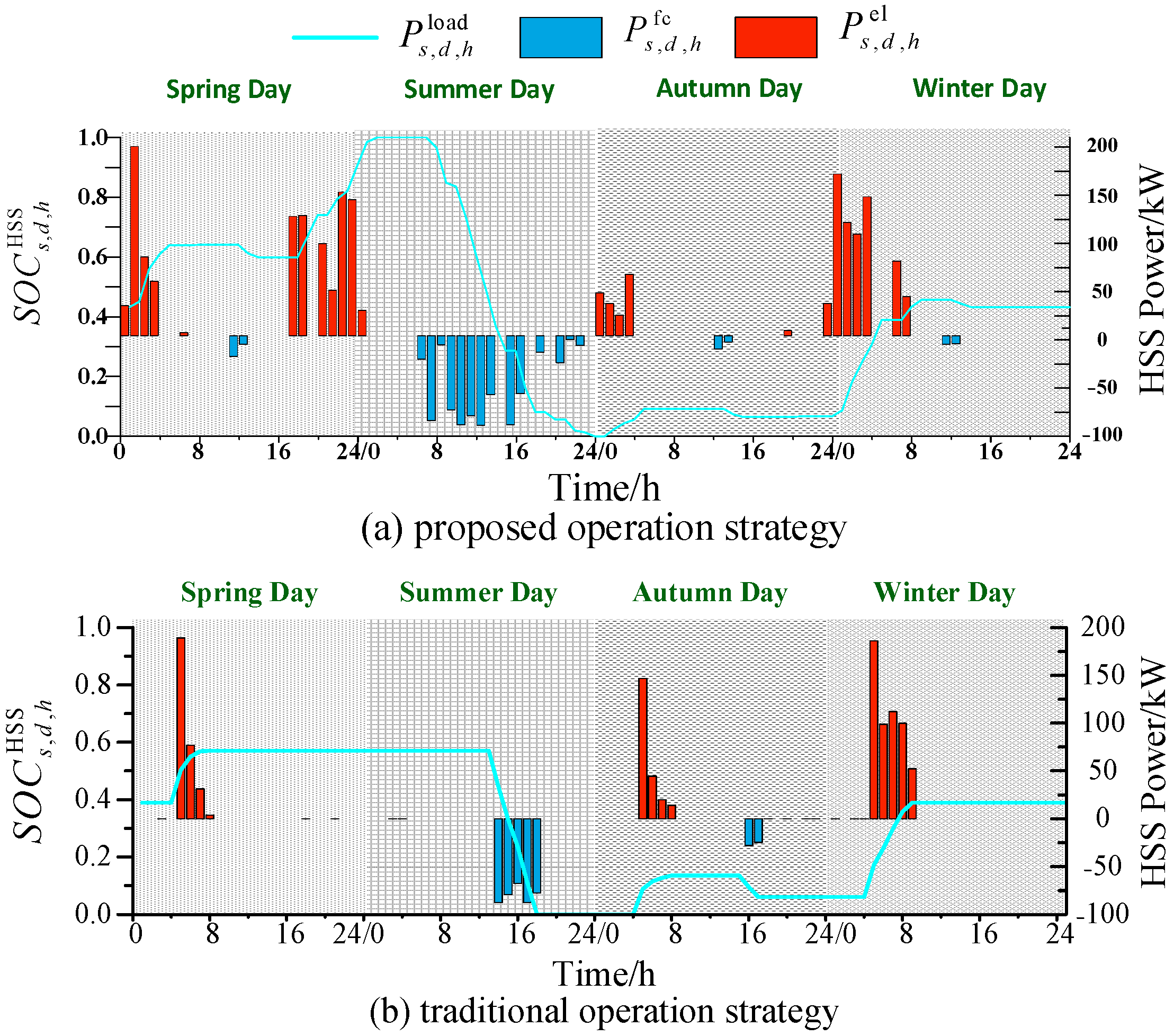
5.3.2. Energy Storage Utilization
5.4. Sensitivity Analysis
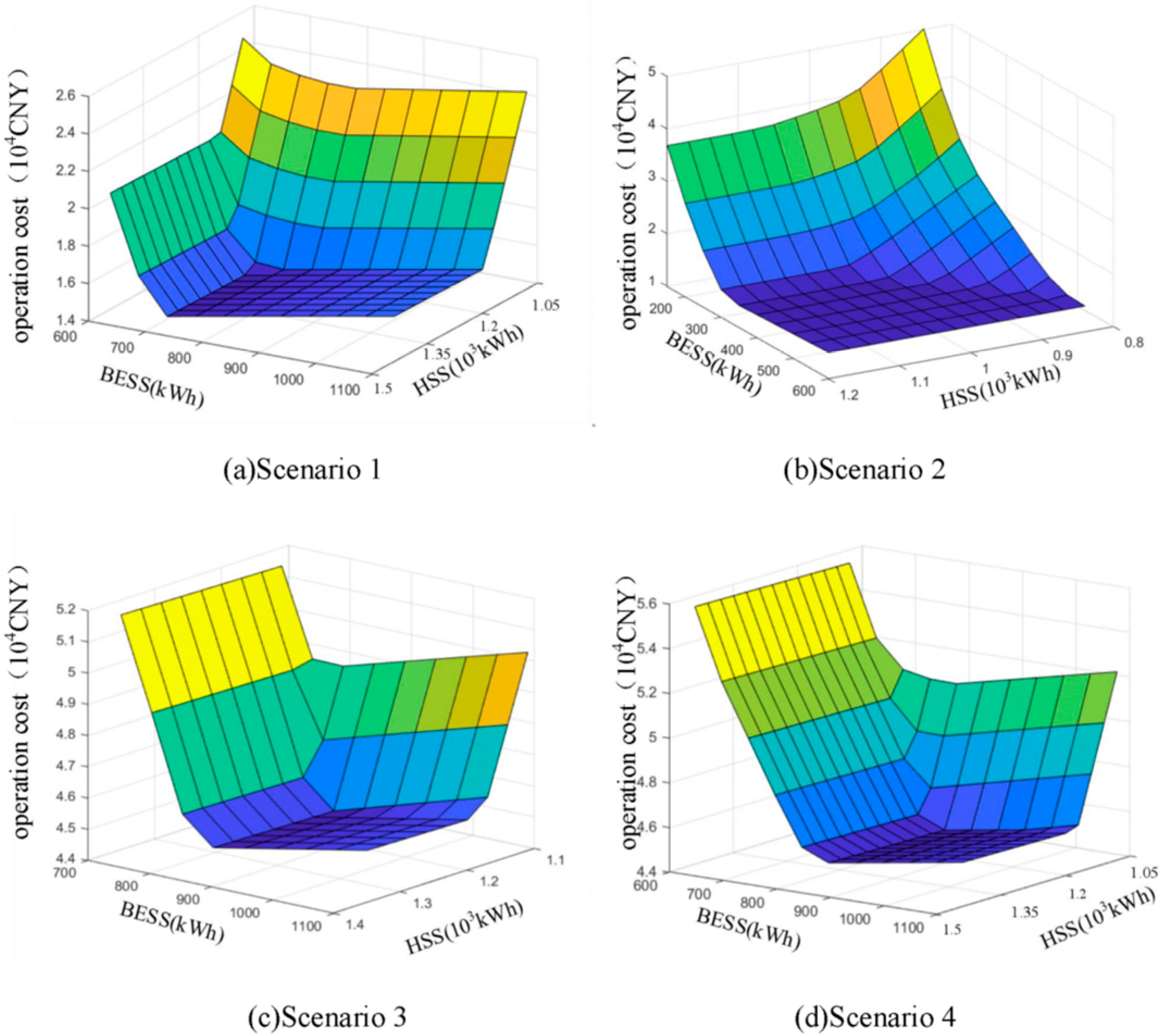
5.4.1. EH-HESS Allocation
5.4.2. Limit on the Times of HSS State Transitions
6. Conclusions
- (1)
- The EH-HESS can effectively cope with the intraday and seasonal peak demands. The EH-HESS greatly diminishes the load loss and curtailment associated with the complementary energy storage characteristics, reducing the load loss rate to 1.06% and the energy excess rate to 0%.
- (2)
- The new operation strategy increases the number of HSS working times by 2.1 times by increasing the interaction interval. It avoids the low utilization rate of HSS due to the irrational division of fixed zones. Additionally, the appearance of the interaction interval allows HESS to jointly respond to the high power demand.
- (3)
- As the ESS allocation increases, the operating cost decreases and increases later. The allocation of optimal seasonal complementary shall prevail as a reference in the face of different seasonal ratios. The increase in the number of state limits facilitates HSS higher utilization three times, decreasing the operating cost by 4.6% after it has no further effect. The three state limits are the most reasonable limits by comparing different load types. These results can assist investors in better decision-making.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Zhou, J.; Weng, Z.; Song, X. Capacity Configuration Method of Islanded Microgrid with Photovoltaic and Energy Storage System Considering Reliability and Economy. Autom. Electr. Power Syst. 2021, 45, 166–174. [Google Scholar]
- Zhou, X.; Chen, S.; Lu, Z.; Huang, Y.; Ma, S.; Zhao, Q. Technology Features of the New Generation Power System in China. Proc. CSEE 2018, 38, 1893–1904. [Google Scholar]
- Ren, D.; Hou, J.; Xiao, J.; Jin, Y.; Jin, C.; Hui, D. Exploration of Key Technologies for Energy Storage in the Cleansing Transformation of Energy and Power. High Volt. Eng. 2021, 47, 2751–2759. [Google Scholar] [CrossRef]
- Jiang, P.; Zhang, H.; Li, M.; Zhang, Y.; Gong, X.; He, D.; Liu, L. Research on the Structural Optimization of the Clean Energy Industry in the Context of Dual Carbon Strategy—A Case Study of Sichuan Province, China. Sustainability 2023, 15, 2993. [Google Scholar] [CrossRef]
- Twitchell, J.; DeSomber, K.; Bhatnagar, D. Defining Long Duration Energy Storage. J. Energy Storage 2023, 60, 105787. [Google Scholar] [CrossRef]
- Jiang, H.; Du, E.; Zhu, G.; Huang, J.; Qian, M.; Zhang, N. Review and Prospect of Seasonal Energy Storage for Power System with High Proportion of Renewable Energy. Autom. Electr. Power Syst. 2020, 44, 194–207. [Google Scholar]
- Khani, H.; Farag, H.E.Z. Joint Arbitrage and Operating Reserve Scheduling of Energy Storage through Optimal Adaptive Allocation of the State of Charge. IEEE Trans. Sustain. Energy 2018, 10, 1705–1717. [Google Scholar] [CrossRef]
- Sun, C.; Chen, L.; Qiu, X.; Zheng, T.; Mei, S. A Generation-Side Shared Energy Storage Planning Model Based on Cooperative Game. J. Global Energy Interconnect. 2019, 2, 360–366. [Google Scholar]
- Yang, Y.; Qin, C.; Zeng, Y.; Wang, C. Optimal Coordinated Bidding Strategy of Wind and Solar System with Energy Storage in Day-ahead Market. J. Mod. Power Syst. Clean Energy 2022, 10, 192–203. [Google Scholar] [CrossRef]
- Hunt, J.D.; Falchetta, G.; Parkinson, S.; Vinca, A.; Zakeri, B.; Byers, E.; Jurasz, J.; Quaranta, E.; Grenier, E.; Junior, A.O.P.; et al. Hydropower and seasonal pumped hydropower storage in the Indus basin:pros and cons. J. Energy Storage 2021, 41, 102916. [Google Scholar] [CrossRef]
- Hunt, J.D.; Zakeri, B.; Nascimento, A.; Gazoli, J.R.; Bindemann, F.T.; Wada, Y.; Riahi, K. Compressed Air Seesaw Energy Storage: A Solution for Long-Term Electricity Storage. J. Energy Storage 2023, 60, 106638. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E.Z. Optimal Energy Management of Hydrogen Energy Facility Using Integrated Battery Energy Storage and Solar Photovoltaic Systems. IEEE Trans. Sustain. Energy 2022, 13, 1457–1468. [Google Scholar] [CrossRef]
- Shu, X.; Kumar, R.; Saha, R.K.; Dev, N.; Stević, Ž.; Sharma, S.; Rafighi, M. Sustainability Assessment of Energy Storage Technologies Based on Commercialization Viability: MCDM Model. Sustainability 2023, 15, 4707. [Google Scholar] [CrossRef]
- Kummer, K.; Imre, A.R. Seasonal and Multi-Seasonal Energy Storage by Power-to-Methane Technology. Energies 2021, 14, 3265. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Li, J. Carbon dioxide recycling in hydrogen-based energy systems using power-to-gas facility and stochastic multi-objective optimization. J. Clean. Prod. 2023, 387, 13582. [Google Scholar] [CrossRef]
- Zhou, Y. Transition towards carbon-neutral districts based on storage techniques and spatiotemporal energy sharing with electrification and hydrogenation. Renew. Sustain. Energy Rev. 2022, 162, 112444. [Google Scholar] [CrossRef]
- Pelosi, D.; Baldinelli, A.; Cinti, G.; Ciupageanu, D.-A.; Ottaviano, A.; Santori, F.; Carere, F.; Barelli, L. Battery-hydrogen vs. flywheel-battery hybrid storage systems for renewable energy integration in mini-grid: A techno-economic comparison. J. Energy Storage 2023, 63, 106968. [Google Scholar] [CrossRef]
- Ji, M.; Zhang, W.; Xu, Y.; Liao, Q.; Klemeš, J.J.; Wang, B. Optimisation of multi-period renewable energy systems with hydrogen and battery energy storage: A P-graph approach. Energy Convers. Manag. 2023, 281, 116826. [Google Scholar] [CrossRef]
- Le, T.S.; Nguyen, T.N.; Bui, D.-K.; Ngo, T.D. Optimal sizing of renewable energy storage: A techno-economic analysis of hydrogen, battery and hybrid systems considering degradation and seasonal storage. Appl. Energy 2023, 336, 120817. [Google Scholar] [CrossRef]
- Li, Q.; Li, R.; Pu, Y.; Li, S.; Sun, C.; Chen, W. Coordinated control of electric-hydrogen hybrid energy storage for multi-microgrid with fuel cell/electrolyzer/PV/battery. J. Energy Storage 2021, 42, 103110. [Google Scholar] [CrossRef]
- Luo, L.; Han, Y.; Li, Q.; Chen, X.; Pu, Y.; Chen, W. Economic droop control strategy of a hybrid electric-hydrogen DC microgrid considering efficiency characteristics. Power Syst. Prot. Control 2022, 50, 69–80. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Z.; Pu, L.; Ren, Z.; Zhang, Y.; Tan, Z. Energy management strategy of hybrid energy storage based on Pareto optimality. Appl. Energy 2022, 327, 120095. [Google Scholar] [CrossRef]
- Pan, G.; Gu, W.; Lu, Y.; Qiu, H.; Lu, S.; Yao, S. Optimal Planning for Electricity-Hydrogen Integrated Energy System Considering Power to Hydrogen and Heat and Seasonal Storage. IEEE Trans. Sustain. Energy 2020, 11, 2662–2676. [Google Scholar] [CrossRef]
- Xu, Y.C.; Liu, H.Q.; Sun, S.H.; Mi, L. The Bi-Level Mixed Integer Programming of Multi-Microgrid System Considering the Hybrid Energy Sharing Station. Proc. CSEE 2022, 59, 1–14. [Google Scholar]
- Li, R.R.; Li, Q.; Pu, Y.C.; Li, S.; Sun, C.; Chen, W.R. Optimal Configuration of an Electric-Hydrogen Hybrid Energy Storage Multi-Microgrid System Considering Power Interaction Constraints. Power Syst. Prot. Control 2022, 50, 53–64. [Google Scholar]
- Chen, M.; Shen, Z.; Wang, L.; Zhang, G. Intelligent Energy Scheduling in Renewable Integrated Microgrid with Bidirectional Electricity-to-Hydrogen Conversion. IEEE Trans. Netw. Sci. Eng. 2022, 9, 2212–2223. [Google Scholar] [CrossRef]
- Samsatli, S.; Samsatli, N.J. A general spatio-temporal model of energy systems with a detailed account of transport and storage. Comput. Chem. Eng. 2015, 80, 155–176. [Google Scholar] [CrossRef]
- Xiao, J.; Hou, J.; Du, E.; Jin, C.; Zhou, Y.; Kang, C. Quantitative Model and Case Study of Energy Storage Demand Supporting Clean Transition of Electric Power System. Autom. Electr. Power Syst. 2021, 45, 9–17. [Google Scholar]
- Xiong, Y.; Chen, L.; Zheng, T.; Si, Y.; Mei, S. Optimal Configuration of Hydrogen Energy Storage in Low-Carbon Park Integrated Energy System Considering Electricity-Heat-Gas Coupling Characteristics. Electr. Power Autom. Equip. 2021, 41, 31–38. [Google Scholar]
- Yuan, T.; Cao, J. Capacity Optimization Allocation of Wind Hydrogen Low-Carbon Energy System Considering Wind Power-Load Uncertainty. High Volt. Eng. 2022, 48, 2037–2044. [Google Scholar]
- Reuß, M.; Grube, T.; Robinius, M.; Preuster, P.; Wasserscheid, P.; Stolten, D. Seasonal Storage and Alternative Carriers: A Flexible Hydrogen Supply Chain Model. Appl. Energy 2017, 200, 290–302. [Google Scholar] [CrossRef]
- Liu, X.; Zu, L.; Li, X.; Wu, H.; Ha, R.; Wang, P. Day-Ahead and Intra-Day Economic Dispatch of Electricity Hydrogen Integrated Energy System with Virtual Energy Storage. IEEE Access 2023, 11, 104428–104440. [Google Scholar] [CrossRef]
- Jiang, Y.; Ren, Z.; Li, W. Committed Carbon Emission Operation Region for Integrated Energy Systems: Concepts and Analyses. IEEE Trans. Sustain. Energy 2023, 15, 1194–1209. [Google Scholar] [CrossRef]
- García-Triviño, P.; Fernández-Ramírez, L.M.; Gil-Mena, A.J.; Llorens-Iborra, F.; García-Vázquez, C.A.; Jurado, F. Optimized operation combining costs, efficiency and lifetime of a hybrid renewable energy system with energy storage by battery and hydrogen in grid-connected applications. Int. J. Hydrogen Energy 2016, 41, 23132–23144. [Google Scholar] [CrossRef]
| Parameters | Value | Parameters | Value |
|---|---|---|---|
| /% | 0.6 | /(CNY/kW) | 14.1 |
| /% | 0.7 | /(CNY/kW) | 100 |
| /% | 0.9 | /(CNY/kW) | 47 |
| /(CNY/kW) | 18.8 | /(CNY/kW) | 4.7 |
| m (year) | 20 | (time) | 250 |
| (hour) | 131,400 | (hour) | 52,560 |
| Case | BESS | HSS | ||||
|---|---|---|---|---|---|---|
| (kW h) | (kW) | (kW) | (kW h) | (kW) | (kW) | |
| 1 | 800 | 133 | 133 | - | - | - |
| 2 | 126,000 | 292 | 123 | |||
| 3 | 126,000 | 292 | 123 | |||
| Cost (CNY) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Case 1 | 7035 | - | - | - | 10,566 | 84,630 | 16.57% | 6.89% | 102,231 |
| Case 2 | 7222 | 2090 | 1054 | 507 | 6356 | 53,394 | 3.93% | 4.34% | 70,624 |
| Case 3 | 5664 | 5218 | 2356 | 507 | 673 | 0 | 1.06% | 0% | 14,418 |
| Load Type | (CNY) | (CNY) | (CNY) | (CNY) | |
|---|---|---|---|---|---|
| Load 1 | 1 | 13,779 | 11,502 | 2277 | 0 |
| 2 | 13,718 | 11,645 | 2073 | 0 | |
| 3 | 13,144 | 13,006 | 138 | 0 | |
| 4 | 13,144 | 13,006 | 138 | 0 | |
| Load 2 | 1 | 16,993 | 13,091 | 1006 | 2896 |
| 2 | 15,085 | 13,221 | 768 | 1096 | |
| 3 | 14,418 | 13,745 | 673 | 0 | |
| 4 | 14,418 | 13,745 | 673 | 0 | |
| Load 3 | 1 | 30,367 | 14,222 | 2251 | 13,930 |
| 2 | 23,479 | 14,715 | 1332 | 7432 | |
| 3 | 16,403 | 15,170 | 513 | 720 | |
| 4 | 16,403 | 15,170 | 513 | 720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, C.; Li, X.; Chen, L.; Mei, S. Intra-Day and Seasonal Peak Shaving Oriented Operation Strategies for Electric–Hydrogen Hybrid Energy Storage in Isolated Energy Systems. Sustainability 2024, 16, 7010. https://doi.org/10.3390/su16167010
Yang C, Li X, Chen L, Mei S. Intra-Day and Seasonal Peak Shaving Oriented Operation Strategies for Electric–Hydrogen Hybrid Energy Storage in Isolated Energy Systems. Sustainability. 2024; 16(16):7010. https://doi.org/10.3390/su16167010
Chicago/Turabian StyleYang, Changxing, Xiaozhu Li, Laijun Chen, and Shengwei Mei. 2024. "Intra-Day and Seasonal Peak Shaving Oriented Operation Strategies for Electric–Hydrogen Hybrid Energy Storage in Isolated Energy Systems" Sustainability 16, no. 16: 7010. https://doi.org/10.3390/su16167010
APA StyleYang, C., Li, X., Chen, L., & Mei, S. (2024). Intra-Day and Seasonal Peak Shaving Oriented Operation Strategies for Electric–Hydrogen Hybrid Energy Storage in Isolated Energy Systems. Sustainability, 16(16), 7010. https://doi.org/10.3390/su16167010







