Applications of the Separation of Variables Method and Duhamel’s Principle to Instantaneously Released Point-Source Solute Model in Water Environmental Flow
Abstract
1. Introduction
2. Basic Model and Mathematical Techniques
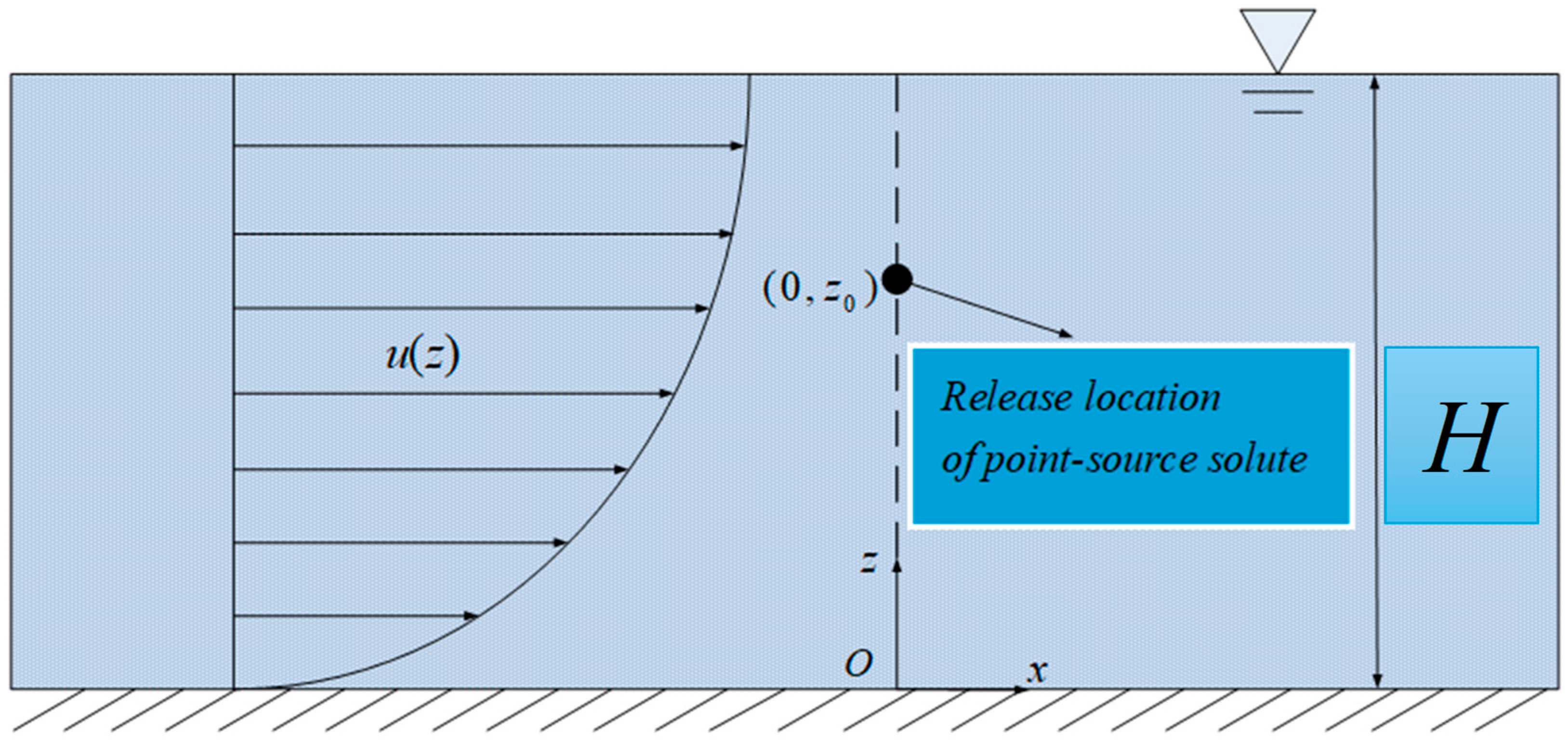
2.1. Review of the Case for Single-Point-Source Solute Instantaneous Release
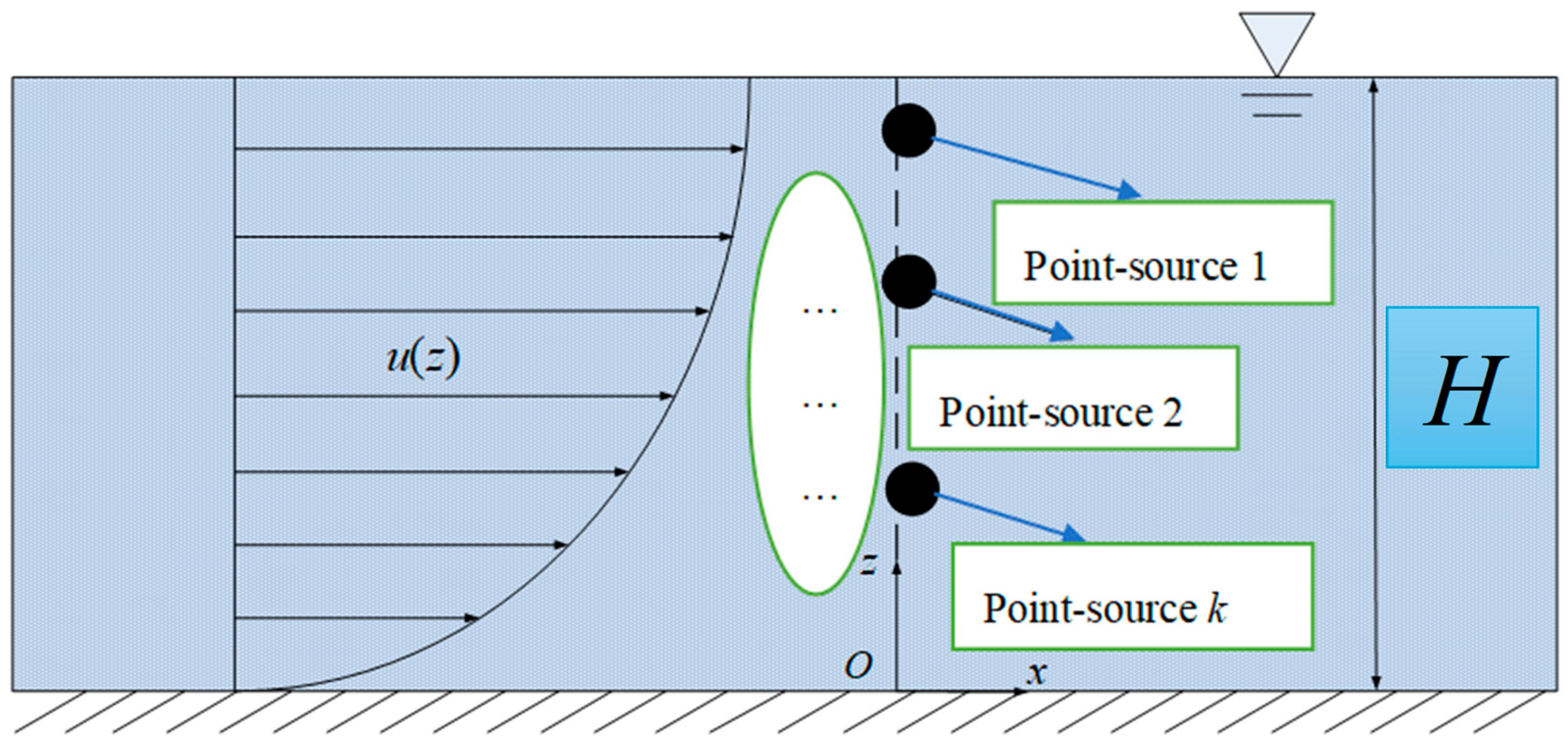
2.2. Generalization of Instantaneous Release of Multi-Point-Source Solute
3. Solving the Solute Concentration Moment Equation Using the Separation of Variables Method
3.1. Zeroth-Order Concentration Moment Solution
3.2. First-Order Concentration Moment Solution
3.3. P-Order Concentration Moment Solution
4. Typical Numerical Examples
5. Summary
- On the basis of a comprehensive review of previous studies, a model for the instantaneous release of solute from multi-point sources is proposed by modifying the initial conditions. For the case of single-point-source release, the analytical solution of the zeroth-order concentration moment was obtained using the separation of variables method. The analytical solution obtained is consistent with the solution derived using integral transformation methods in relevant literature, and satisfies the requirement of solute mass conservation, thereby further validating the accuracy of the results presented in this paper.
- On the basis of the partial differential equation and initial-boundary value conditions of the first-order concentration moment , which holds significant theoretical value for estimating the cross-sectional average concentration, Duhamel’s principle was applied in homogeneous processing. The analytical solution of was obtained through the separation of variables method. The motion of the solute centroid under a uniform flow-velocity distribution was discussed, and a recursive solution for the higher-order concentration moment was derived.
- Under the specified engineering parameters, the movement pattern of the instantaneously released point-source solute centroid was determined. This reveals that the time needed for the released point-source solute to have a downstream environmental–ecological impact on the river is dependent on the initial release location. This finding not only aligns with the conclusions drawn in the relevant literature but also offers a more extensive range of numerical results.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, H. Logic mechanism and key path of developing new quality productivity to enhance water security capacity. China Water Resour. 2024, 8, 1–5. (In Chinese) [Google Scholar]
- Gao, J. Water conservancy construction and sustainable economic and social development. J. China Inst. Water Resour. Hydropower Res. 2004, 2, 81–87. (In Chinese) [Google Scholar]
- Peng, Q. Analysis of key problems in ecological environment monitoring. Leather Prod. Environ. Prot. Sci. Technol. 2023, 4, 38–40. (In Chinese) [Google Scholar]
- Liu, Y. 2022 China’s Modern Ecological Development Index 70.1 Water Pollution as the Biggest Concern. Xiaokang 2022, 16, 44–45. (In Chinese) [Google Scholar]
- Taylor, G. Dispersion of soluble matter flowing slowly through a tube. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1953, 219, 186–203. [Google Scholar]
- Pan, M.; Meng, X. Monitoring of the relationship between water quality and point source pollution in watersheds. Environ. Sci. Res. 2000, 13, 61–64. (In Chinese) [Google Scholar]
- Chen, Y.; Pang, Y.; Li, C.; Cui, X. Simulation study on the influence of buildings on the diffusion of atmospheric pollutants from elevated point sources. J. Environ. Eng. 2010, 4, 147–150. (In Chinese) [Google Scholar]
- Gao, R.; Fu, X.; Wu, Z. Indicators for evaluating uncertainties of solute concentration prediction in wetland flows. Ecol. Indic. 2019, 105, 688–699. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, L.; Chen, H.; Huang, Z. Instantaneous point source and continuous source transport and diffusion with the stream. China Navig. 2020, 43, 97–100. (In Chinese) [Google Scholar]
- Whitaker, S. The Method of Volume Averaging, Theory and Application of Transport in Porous Media; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Liu, S.; Masliyah, H. Dispersion in Porous Media, Handbook of Porous Media; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Zeng, L. Analytical Study on Environmental Dispersion in Wetland Flow. Ph.D. Thesis, Peking University, Beijing, China, 2010. (In Chinese). [Google Scholar]
- Wu, Z. Two-Scale Perturbation Analysis of Typical Taylor Dispersion Process. Ph.D. Thesis, Peking University, Beijing, China, 2014. (In Chinese). [Google Scholar]
- Chen, G.; Zeng, L.; Wu, Z. An ecological risk assessment model for a pulsed contaminant emission into a wetland channel flow. Ecol. Model. 2010, 221, 2927–2937. [Google Scholar] [CrossRef]
- Aris, R. On the dispersion of a solute in a fluid flowing through a tube. Proc. Roy. Soc. Lond. Ser. A-Math. Phys 1956, 235, 67–77. [Google Scholar]
- Barton, N. On the method of moments for solute dispersion. J. Fluid Mech. 1983, 126, 205–218. [Google Scholar] [CrossRef]
- Fu, X.; Gao, R.; Wu, Z. Additional longitudinal displacement for contaminant dispersion in wetland flow. J. Hydrol. 2016, 532, 37–45. [Google Scholar] [CrossRef]
- Gao, R.; Fu, X.; Wu, Z.; Wang, P. Effect of release location on solute dispersion characteristics of point source in open channel wetland flow. J. Appl. Basic Eng. Sci. 2018, 26, 455–470. (In Chinese) [Google Scholar]
- Zhou, M. Mathematical Methods for Physics; Higher Education Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Gu, Q. Mathematical Methods for Physics; Science Press: Beijing, China, 2012. (In Chinese) [Google Scholar]
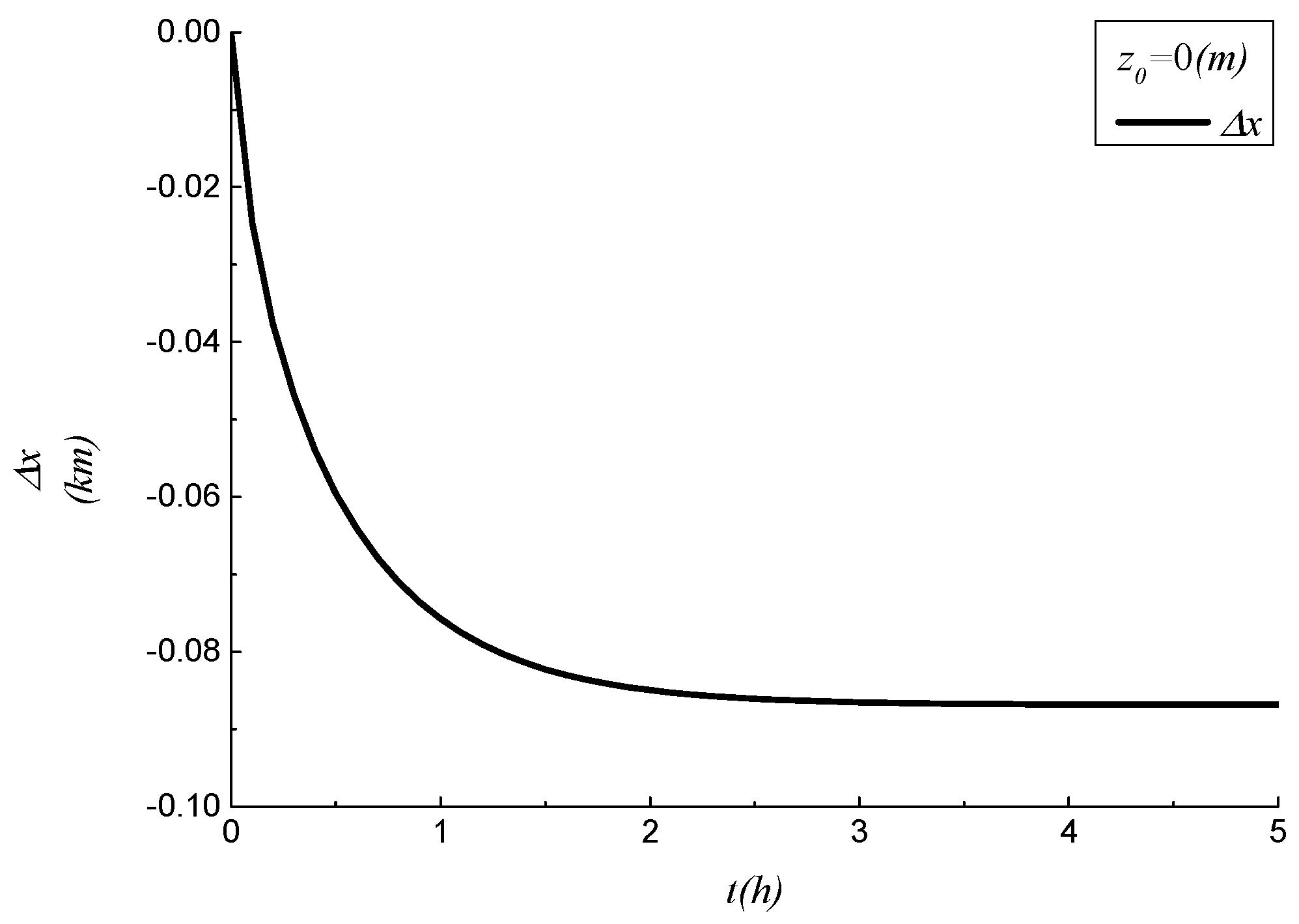
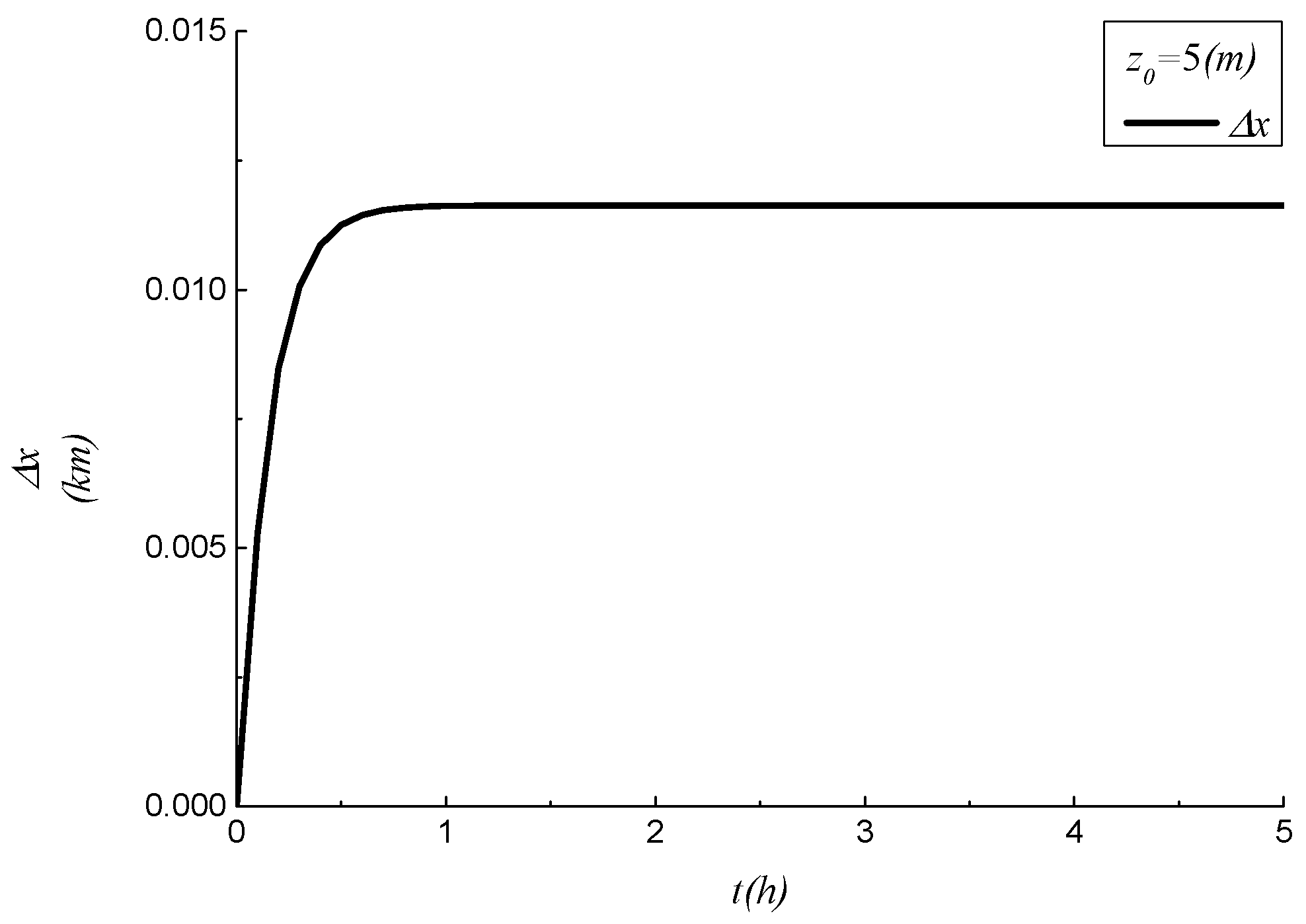

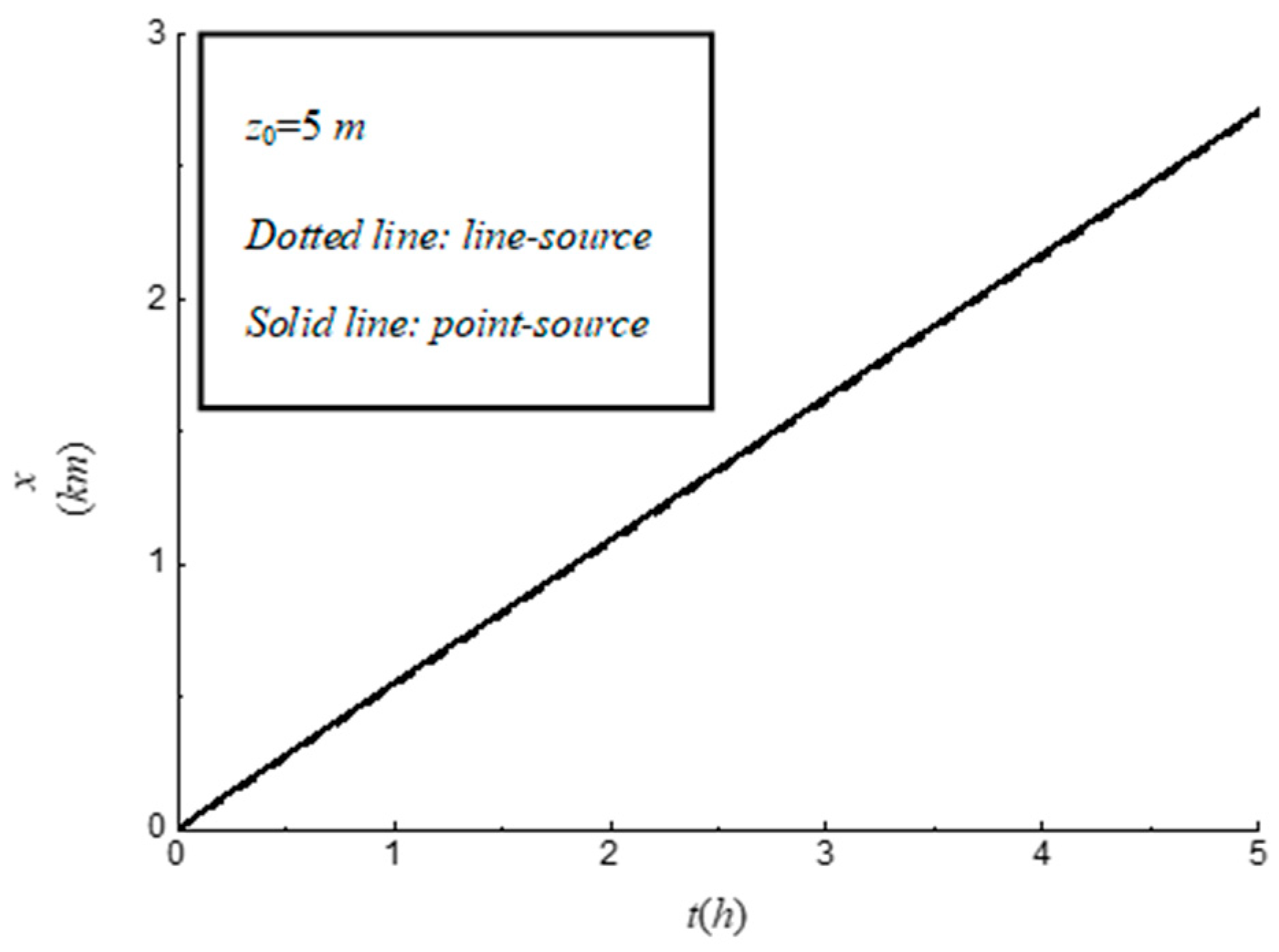
| Time Variable t (Unit: h) | Additional Longitudinal Displacement of Released Solute Centroid Δx (Unit: km) | ||
|---|---|---|---|
| z0 = 0 m | z0 = 5 m | z0 = 10 m | |
| 0 | 0 | 0 | 0 |
| 0.5 | −0.0595 | 0.0113 | 0.0288 |
| 1.0 | −0.0757 | 0.0116 | 0.0443 |
| 1.5 | −0.0823 | 0.0116 | 0.0508 |
| 2.0 | −0.0850 | 0.0116 | 0.0535 |
| 2.5 | −0.0861 | 0.0116 | 0.0546 |
| 3.0 | −0.0865 | 0.0116 | 0.0551 |
| 3.5 | −0.0867 | 0.0116 | 0.0553 |
| 4.0 | −0.0868 | 0.0116 | 0.0553 |
| 4.5 | −0.0868 | 0.0116 | 0.0554 |
| 5.0 | −0.0868 | 0.0116 | 0.0554 |
| Time Variable t (Unit: h) | Total Displacement of Solute Centroid x (Unit: km) | ||
|---|---|---|---|
| z0 = 0 m | z0 = 5 m | z0 = 10 m | |
| 0 | 0 | 0 | 0 |
| 0.5 | 0.21 | 0.28 | 0.30 |
| 1.0 | 0.46 | 0.55 | 0.58 |
| 1.5 | 0.73 | 0.82 | 0.86 |
| 2.0 | 1.00 | 1.09 | 1.13 |
| 2.5 | 1.26 | 1.36 | 1.40 |
| 3.0 | 1.53 | 1.63 | 1.68 |
| 3.5 | 1.80 | 1.90 | 1.95 |
| 4.0 | 2.07 | 2.17 | 2.22 |
| 4.5 | 2.34 | 2.44 | 2.49 |
| 5.0 | 2.61 | 2.71 | 2.76 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, R.; Gao, J.; Chu, L. Applications of the Separation of Variables Method and Duhamel’s Principle to Instantaneously Released Point-Source Solute Model in Water Environmental Flow. Sustainability 2024, 16, 6912. https://doi.org/10.3390/su16166912
Gao R, Gao J, Chu L. Applications of the Separation of Variables Method and Duhamel’s Principle to Instantaneously Released Point-Source Solute Model in Water Environmental Flow. Sustainability. 2024; 16(16):6912. https://doi.org/10.3390/su16166912
Chicago/Turabian StyleGao, Ran, Juncai Gao, and Linlin Chu. 2024. "Applications of the Separation of Variables Method and Duhamel’s Principle to Instantaneously Released Point-Source Solute Model in Water Environmental Flow" Sustainability 16, no. 16: 6912. https://doi.org/10.3390/su16166912
APA StyleGao, R., Gao, J., & Chu, L. (2024). Applications of the Separation of Variables Method and Duhamel’s Principle to Instantaneously Released Point-Source Solute Model in Water Environmental Flow. Sustainability, 16(16), 6912. https://doi.org/10.3390/su16166912





