Probabilistic Prediction Model for Expressway Traffic Noise Based on Short-Term Monitoring Data
Abstract
:1. Introduction
2. Methodology
2.1. Data Collection
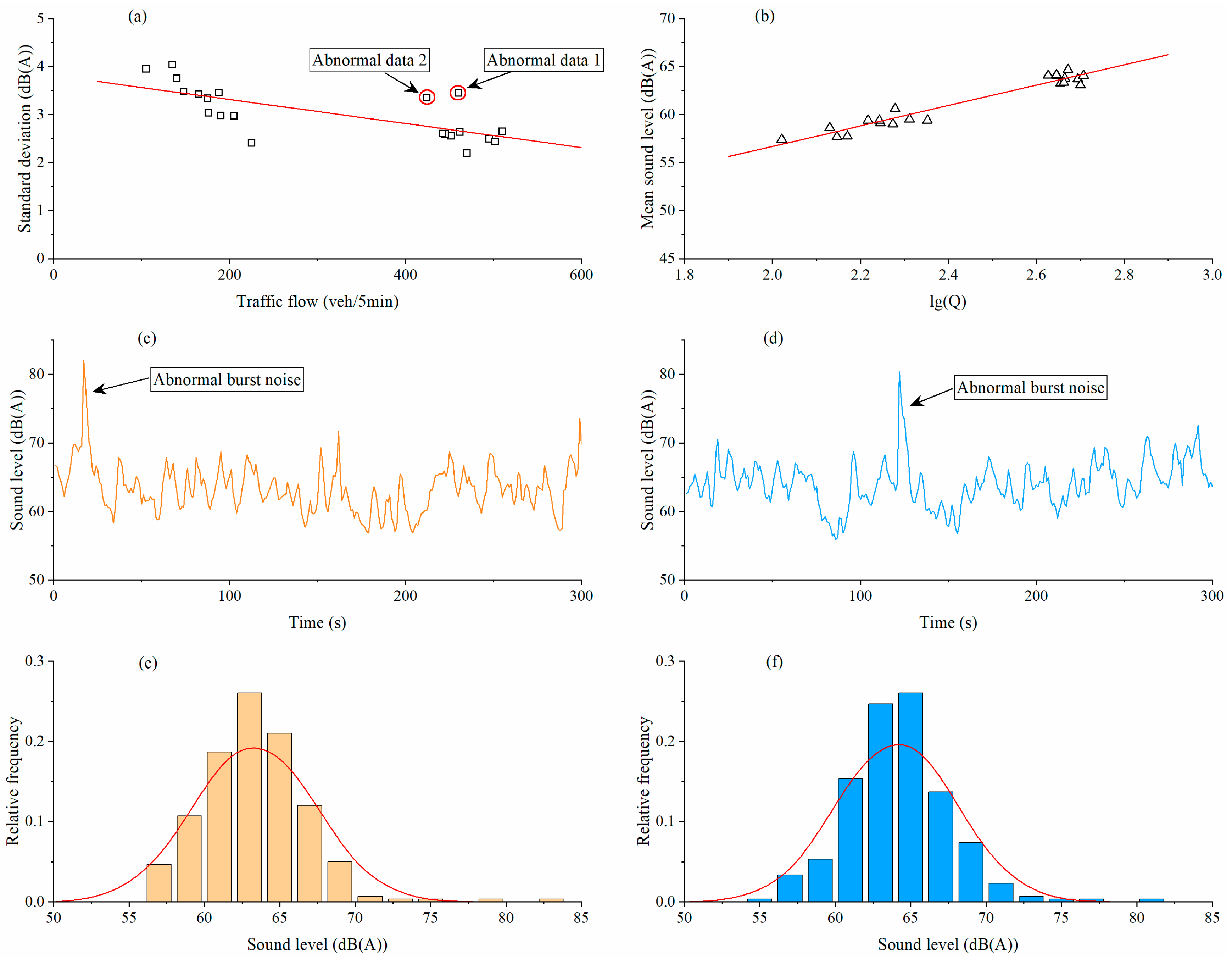
2.2. Data Analysis
2.3. Model Development
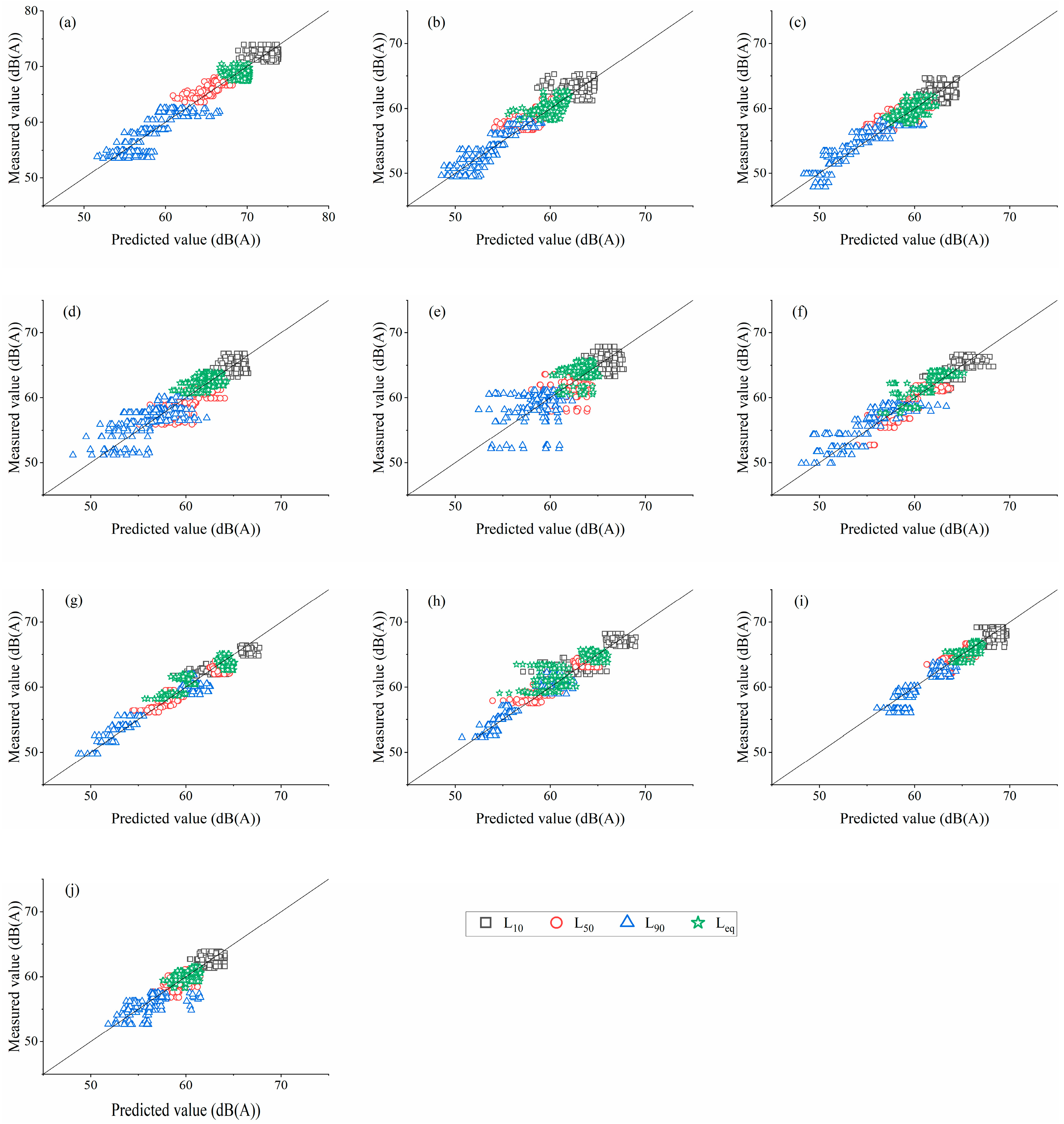
3. Model Validation
4. Discussion
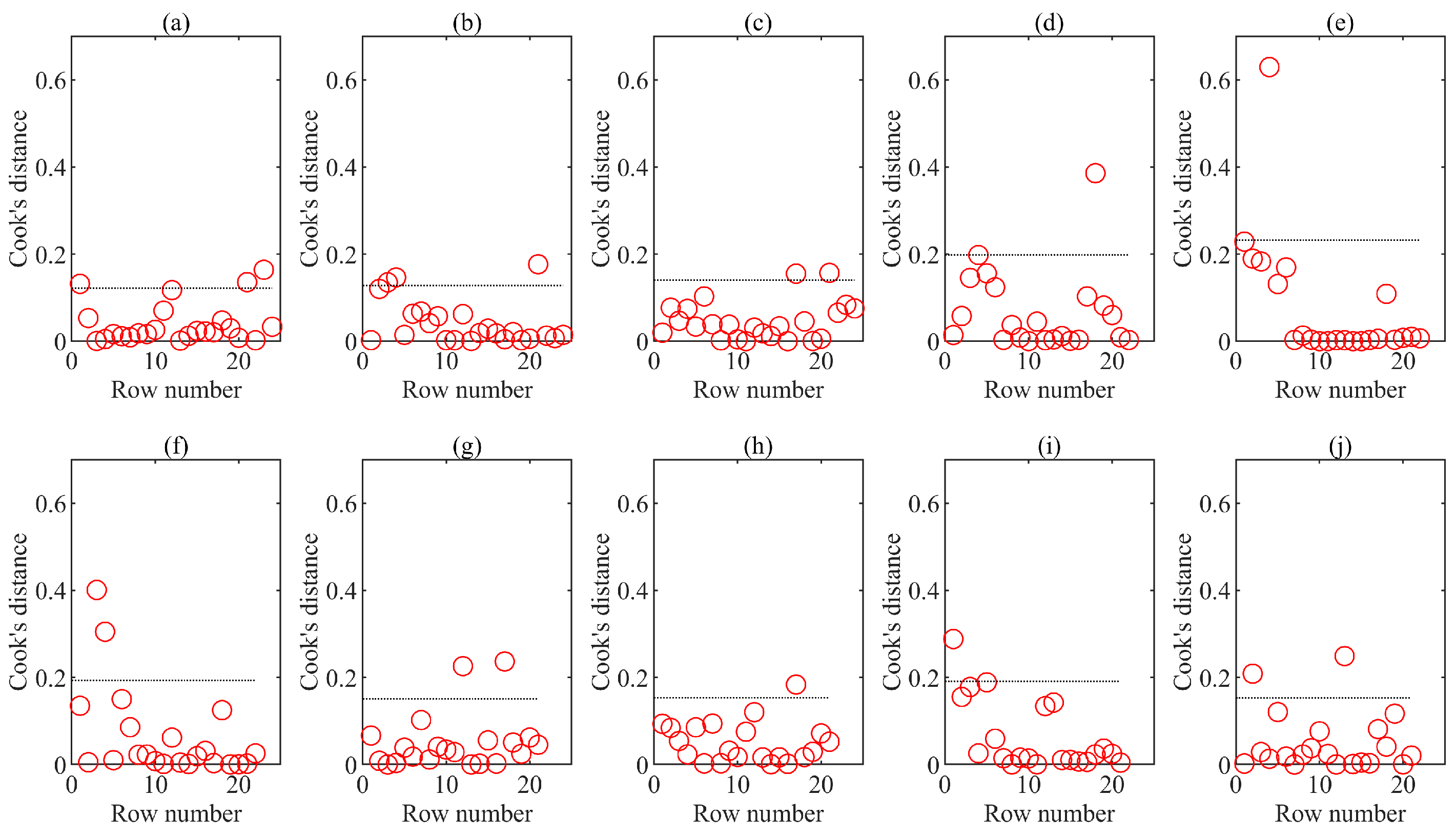
4.1. The Influence of Modeling Samples on Model Accuracy
4.2. Applicability and Limitations of the Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cole-Hunter, T.; So, R.; Amini, H.; Backalarz, C.; Brandt, J.; Bräuner, E.V.; Hertel, O.; Jensen, S.S.; Jørgensen, J.T.; Ketzel, M.; et al. Long-term exposure to road traffic noise and all-cause and cause-specific mortality: A Danish Nurse Cohort study. Sci. Total Environ. 2022, 820, 153057. [Google Scholar] [CrossRef] [PubMed]
- Gu, T.; Yang, T.; Wang, J.; Hu, X.; Xu, Z.; Wang, Y.; Jin, J.; Zhang, J.; He, T.; Li, G.; et al. Modification of green space on the associations between long-term road traffic noise exposure and incident intracerebral hemorrhage: A prospective cohort study. Environ. Res. 2023, 231, 116189. [Google Scholar] [CrossRef]
- Smith, M.G.; Younes, M.; Aeschbach, D.; Elmenhorst, E.M.; Müller, U.; Basner, M. Traffic noise-induced changes in wake-propensity measured with the Odds-Ratio Product (ORP). Sci. Total Environ. 2022, 805, 150191. [Google Scholar] [CrossRef] [PubMed]
- Natarajan, N.; Batts, S.; Stankovic, K.M. Noise-Induced Hearing Loss. J. Clin. Med. 2023, 12, 2347. [Google Scholar] [CrossRef] [PubMed]
- Klompmaker, J.O.; Hoek, G.; Bloemsma, L.D.; Wijga, A.H.; van den Brink, C.; Brunekreef, B.; Lebret, E.; Gehring, U.; Janssen, N.A.H. Associations of combined exposures to surrounding green, air pollution and traffic noise on mental health. Environ. Int. 2019, 129, 525–537. [Google Scholar] [CrossRef]
- Li, H.; Xie, H. Noise exposure of the residential areas close to urban expressways in a high-rise mountainous city. Environ. Plan. B: Urban Anal. City Sci. 2021, 48, 1414–1429. [Google Scholar] [CrossRef]
- Halim, H.; Abdullah, R. Equivalent noise level response to number of vehicles: A comparison between a high traffic flow and low traffic flow highway in Klang Valley, Malaysia. Front. Environ. Sci. 2014, 2, 13. [Google Scholar] [CrossRef]
- Fleming, G.; Rapoza, A.; Lee, C. Development of national reference energy mean emission levels for the FHWA Traffic Noise Model. In Report No FHWA-PD-96-008 and DOT- VNTSC-96-2; John A. Volpe National Transportation Systems Center: Cambridge, MA, USA, 1995. [Google Scholar]
- Givargis, S.; Mahmoodi, M. Converting the UK calculation of road traffic noise (CORTN) to a model capable of calculating LAeq,1h for the Tehran’s roads. Appl. Acoust. 2008, 69, 1108–1113. [Google Scholar] [CrossRef]
- Bartolomaeus, W. Guidelines for noise protection at roads—rls19. Larmbekampfung 2019, 14, 203–207. [Google Scholar] [CrossRef]
- Sakamoto, S. Road traffic noise prediction model “ASJ RTN-Model 2018”: Report of the research committee on road traffic noise. Acoust. Sci. Technol. 2020, 41, 529–589. [Google Scholar] [CrossRef]
- Lokhande, S.K.; Pathak, S.S.; Kokate, P.K.; Bodhe, G.L. Evaluation and forecasting of highway traffic noise in the city of Nagpur, India. Int. J. Earth Sci. Eng. 2016, 9, 1529–1535. [Google Scholar]
- Lodico, D.; Donavan, P. Using onboard sound intensity measurements to interpret results of traffic noise modeling. Transp. Res. Rec. 2013, 2362, 9–15. [Google Scholar] [CrossRef]
- Cook, M.; Gee, K.; Transtrum, M.; Lympany, S. An app for nationwide dynamic traffic noise prediction. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; NOISE-CON22; Institute of Noise Control Engineering: Grand Rapids, MI, USA, 2023; Volume 266. [Google Scholar] [CrossRef]
- Rochat, J.; Cubick, K. Acoustically soft ground as a highway traffic noise reduction strategy. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; Institute of Noise Control Engineering: Lexington, KY, USA, 2022; Volume 264. [Google Scholar] [CrossRef]
- Ibili, F.; Owolabi, A.O.; Ackaah, W.; Massaquoi, A.B. Statistical modelling for urban roads traffic noise levels. Sci. Afr. 2022, 15, e01131. [Google Scholar] [CrossRef]
- Pamanikabud, P.; Tansatcha, M. Simulation of highway traffic noise with utilization of equivalent sound level of pass-by vehicle. J. Acoust. Soc. Am. 2008, 123 (Suppl. S5), 3824. [Google Scholar] [CrossRef]
- Pamanikabud, P.; Tansatcha, M.; Brown, A.L. Development of a highway noise prediction model using an Leq20 s measure of basic vehicular noise. J. Sound Vib. 2008, 316, 317–330. [Google Scholar] [CrossRef]
- Zhao, J.; Ding, Z.; Hu, B.; Chen, Y.; Yang, W. Assessment and improvement of a highway traffic noise prediction model with Leq(20 s) as the basic vehicular noise. Appl. Acoust. 2015, 97, 78–83. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Pradhan, B.; Chakraborty, S.; Alamri, A. Developing vehicular traffic noise prediction model through ensemble machine learning algorithms with GIS. Arab. J. Geosci. 2021, 14, 1564. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Pradhan, B.; Chakraborty, S.; Alamri, A.; Lee, C.W. An Optimized Deep Neural Network Approach for Vehicular Traffic Noise Trend Modeling. IEEE Access 2021, 9, 107375–107386. [Google Scholar] [CrossRef]
- Huang, B.; Pan, Z.; Liu, Z.; Hou, G.; Yang, H. Acoustic amenity analysis for high-rise building along urban expressway: Modeling traffic noise vertical propagation using neural networks. Transp. Res. Part D Transp. Environ. 2017, 53, 63–77. [Google Scholar] [CrossRef]
- Kumar, P.; Nigam, S.P.; Kumar, N. Vehicular traffic noise modeling using artificial neural network approach. Transp. Res. Part C Emerg. Technol. 2014, 40, 111–122. [Google Scholar] [CrossRef]
- Rassafi, A.A.; Ghassempour, J. Highway traffic noise modeling and estimation based on vehicles volume and speed. Adv. Environ. Res. 2015, 4, 211–218. [Google Scholar] [CrossRef]
- Cai, M.; Li, F.; Liu, J.-K. Dynamic simulation and characteristics analysis of traffic noise at signal-controlled pedestrian crossing junction. Noise Control Eng. J. 2011, 59, 549–555. [Google Scholar] [CrossRef]
- Can, A.; Chevallier, E.; Nadji, M.; Leclercq, L. Dynamic traffic modeling for noise impact assessment of traffic strategies. Acta Acust. United Acust. 2010, 96, 482–493. [Google Scholar] [CrossRef]
- Estévez-Mauriz, L.; Forssén, J. Dynamic traffic noise assessment tool: A comparative study between a roundabout and a signalised intersection. Appl. Acoust. 2018, 130, 71–86. [Google Scholar] [CrossRef]
- Li, F.; Cai, M.; Liu, J.K.; Yu, Z. Dynamic traffic noise simulation at a signalized intersection among buildings. Noise Control. Eng. J. 2011, 59, 202–210. [Google Scholar] [CrossRef]
- Li, F.; Lin, Y.; Cai, M.; Du, C. Dynamic simulation and characteristics analysis of traffic noise at roundabout and signalized intersections. Appl. Acoust. 2017, 121, 14–24. [Google Scholar] [CrossRef]
- Du, C.; Qiu, X.; Li, F.; Cai, M. A simulation of traffic noise emissions at a roundabout based on a cellular automaton model. Acta Acust. 2021, 5, 42. [Google Scholar] [CrossRef]
- Li, F.; Liao, S.S.; Cai, M. A new probability statistical model for traffic noise prediction on free flow roads and control flow roads. Transp. Res. Part D Transp. Environ. 2016, 49, 313–322. [Google Scholar] [CrossRef]
- Li, F.; Xue, W.; Rong, Y.; Du, C.; Tang, J.; Zhao, Y. A probability distribution prediction method for expressway traffic noise. Transp. Res. Part D Transp. Environ. 2022, 103, 103175. [Google Scholar] [CrossRef]
- Cho, D.S.; Mun, S. Development of a highway traffic noise prediction model that considers various road surface types. Appl. Acoust. 2008, 69, 1120–1128. [Google Scholar] [CrossRef]
- Cubick, K.; Rochat, J. Solid safety barriers as a highway traffic noise reduction strategy. In INTER-NOISE and NOISE-CON Congress and Conference Proceedings; NOISE-CON22; Institute of Noise Control Engineering: Lexington, KY, USA, 2022; Volume 264. [Google Scholar] [CrossRef]
- Fujiwara, T.; Meiarashi, S.; Namikawa, Y.; Hasebe, M. Reduction of equivalent continuous A-weighted sound pressure levels by porous elastic road surfaces. Appl. Acoust. 2005, 66, 766–778. [Google Scholar] [CrossRef]
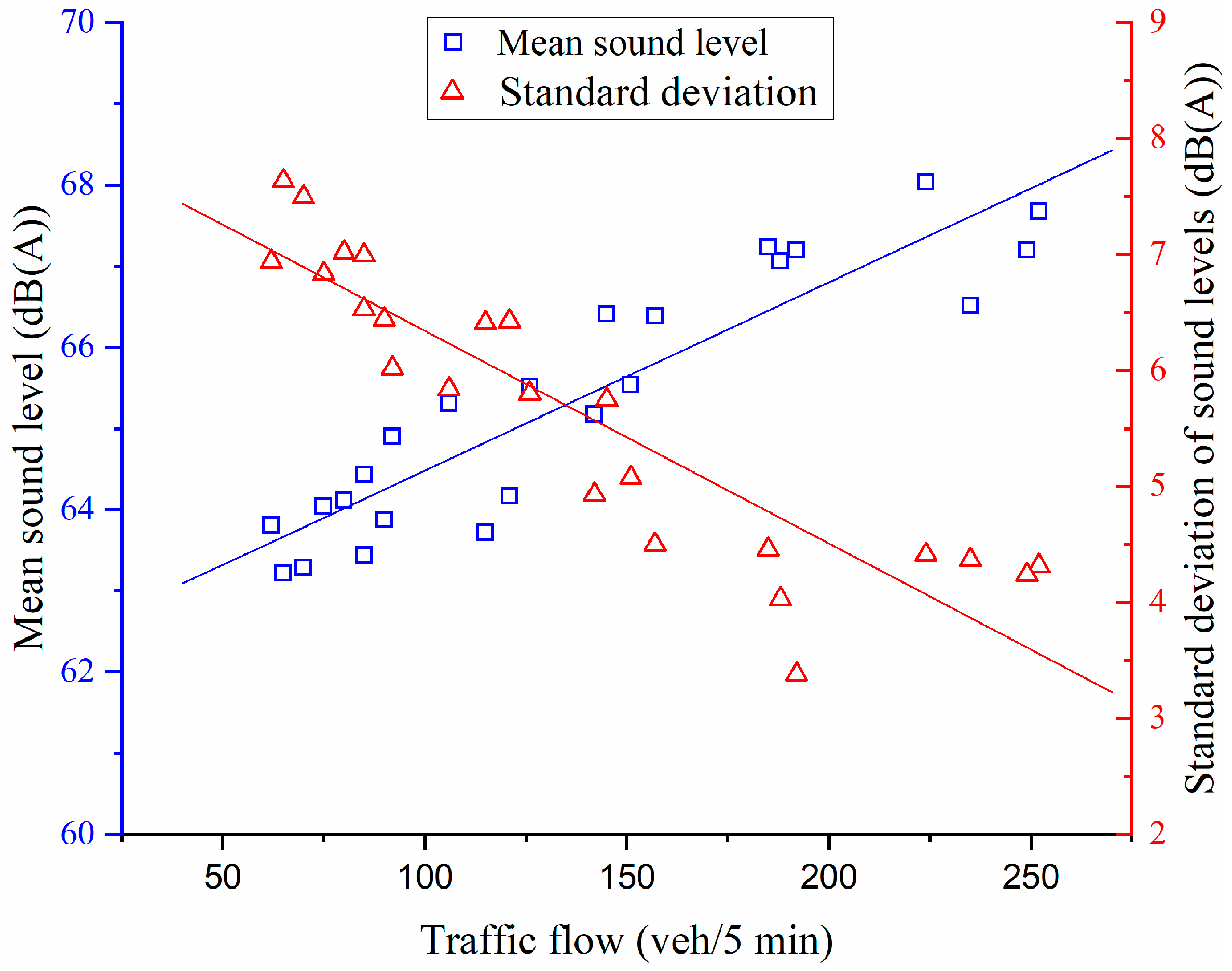





| Monitoring Point Number | Roads | Monitoring Time | Distance to the Road Edge | Sound Obstacle |
|---|---|---|---|---|
| P1 | Guanghe Expressway | 24 × 5 min | 10 m | None |
| P2 | Guanghe Expressway | 24 × 5 min | 50 m | Sparse vegetation |
| P3 | Guanghe Expressway | 24 × 5 min | 100 m | None |
| P4 | Huanzhou Road | 22 × 5 min | 20 m | None |
| P5 | Huanzhou Road | 22 × 5 min | 5 m | None |
| P6 | Huanzhou Road | 22 × 5 min | 10 m | Sparse vegetation |
| P7 | Xuguang Expressway | 21 × 5 min | 100 m | None |
| P8 | Xuguang Expressway | 21 × 5 min | 50 m | None |
| P9 | Xuguang Expressway | 21 × 5 min | 20 m | 0.5 m high noise barrier |
| P10 | Xuguang Expressway | 21 × 5 min | 15 m | 3 m high noise barrier |
| Time | Traffic (veh) | P1 | P2 | P3 | |||
|---|---|---|---|---|---|---|---|
| μ | σ | μ | σ | μ | σ | ||
| 8:00–8:05 | 62 | 63.8 | 6.94 | 56.5 | 5.11 | 56.3 | 4.87 |
| 8:05–8:10 | 85 | 63.4 | 6.53 | 58.7 | 3.60 | 58.0 | 3.37 |
| 8:10–8:15 | 65 | 63.2 | 7.63 | 57.5 | 4.81 | 56.7 | 5.02 |
| 8:15–8:20 | 80 | 64.1 | 7.02 | 56.0 | 4.65 | 55.9 | 4.30 |
| 8:20–8:25 | 75 | 64.0 | 6.83 | 56.7 | 5.16 | 56.1 | 4.90 |
| 8:25–8:30 | 85 | 64.4 | 6.99 | 58.3 | 4.25 | 58.2 | 3.97 |
| 8:30–8:35 | 70 | 63.3 | 7.49 | 57.5 | 4.74 | 55.8 | 5.25 |
| 8:35–8:40 | 90 | 63.9 | 6.44 | 56.9 | 4.53 | 57.0 | 3.68 |
| 8:40–8:45 | 106 | 65.3 | 5.84 | 57.1 | 4.11 | 56.9 | 3.65 |
| 8:45–8:50 | 92 | 64.9 | 6.02 | 57.9 | 3.89 | 57.0 | 4.14 |
| 8:50–8:55 | 121 | 64.2 | 6.42 | 58.4 | 3.82 | 58.1 | 2.96 |
| 8:55–9:00 | 115 | 63.7 | 6.41 | 57.3 | 3.25 | 57.2 | 3.01 |
| 9:00–9:05 | 126 | 65.5 | 5.80 | 58.8 | 4.27 | 59.0 | 4.32 |
| 9:05–9:10 | 151 | 65.5 | 5.07 | 58.7 | 3.25 | 58.4 | 2.76 |
| 9:10–9:15 | 145 | 66.4 | 5.75 | 59.9 | 3.30 | 59.6 | 3.07 |
| 9:15–9:20 | 142 | 65.2 | 4.93 | 58.5 | 3.00 | 58.7 | 3.17 |
| 9:20–9:25 | 188 | 67.1 | 4.03 | 59.8 | 2.69 | 58.3 | 2.50 |
| 9:25–9:30 | 185 | 67.2 | 4.46 | 59.5 | 3.28 | 60.3 | 2.60 |
| 9:30–9:35 | 192 | 67.2 | 3.38 | 60.2 | 2.13 | 59.6 | 2.39 |
| 9:35–9:40 | 157 | 66.4 | 4.50 | 59.7 | 2.79 | 59.4 | 3.25 |
| 9:40–9:45 | 224 | 68.0 | 4.41 | 61.7 | 2.78 | 61.3 | 2.49 |
| 9:45–9:50 | 252 | 67.7 | 4.31 | 61.2 | 2.77 | 60.0 | 2.09 |
| 9:50–9:55 | 235 | 66.5 | 4.37 | 60.5 | 2.82 | 61.1 | 2.55 |
| 9:55–10:00 | 249 | 67.2 | 4.24 | 61.2 | 2.63 | 59.9 | 2.03 |
| Time | Traffic (veh) | P4 | P5 | P6 | |||
|---|---|---|---|---|---|---|---|
| μ | σ | μ | σ | μ | σ | ||
| 7:30–7:35 | 80 | 58.7 | 4.10 | 63.8 | 2.31 | 57.6 | 3.45 |
| 7:35–7:40 | 70 | 59.8 | 3.78 | 62.8 | 2.55 | 58.3 | 4.15 |
| 7:40–7:45 | 56 | 59.4 | 4.29 | 61.7 | 3.61 | 54.3 | 4.65 |
| 7:45–7:50 | 45 | 56.8 | 5.10 | 58.3 | 4.30 | 57.0 | 4.58 |
| 7:50–7:55 | 60 | 57.2 | 4.50 | 58.1 | 4.39 | 56.0 | 4.08 |
| 7:55–8:00 | 73 | 57.6 | 4.93 | 60.4 | 3.24 | 56.6 | 3.57 |
| 8:00–8:05 | 80 | 59.5 | 3.67 | 62.9 | 2.63 | 58.9 | 3.20 |
| 8:05–8:10 | 128 | 61.6 | 3.66 | 61.9 | 3.96 | 58.2 | 4.06 |
| 8:10–8:15 | 105 | 60.5 | 4.12 | 61.9 | 3.33 | 60.3 | 3.14 |
| 8:15–8:20 | 125 | 60.5 | 4.04 | 61.1 | 3.99 | 58.6 | 4.59 |
| 8:20–8:25 | 99 | 61.0 | 3.56 | 62.1 | 2.66 | 62.2 | 3.34 |
| 8:25–8:30 | 165 | 60.8 | 2.55 | 61.9 | 3.39 | 61.0 | 3.50 |
| 8:30–8:35 | 155 | 60.6 | 3.04 | 62.5 | 2.62 | 61.2 | 3.32 |
| 8:35–8:40 | 168 | 61.7 | 3.01 | 62.3 | 3.15 | 61.6 | 3.48 |
| 8:40–8:45 | 162 | 60.9 | 2.88 | 63.5 | 2.48 | 61.5 | 3.26 |
| 8:45–8:50 | 225 | 62.1 | 3.31 | 63.0 | 2.39 | 62.3 | 2.92 |
| 8:50–8:55 | 240 | 60.9 | 2.91 | 62.0 | 2.31 | 61.7 | 2.67 |
| 8:55–9:00 | 260 | 60.3 | 3.02 | 63.2 | 2.94 | 61.7 | 3.34 |
| 9:00–9:05 | 195 | 62.6 | 2.67 | 63.7 | 2.97 | 62.0 | 2.83 |
| 9:05–9:10 | 220 | 62.8 | 2.49 | 62.4 | 2.35 | 62.0 | 3.03 |
| 9:10–9:15 | 205 | 61.2 | 3.24 | 63.5 | 2.92 | 62.4 | 3.03 |
| 9:15–9:20 | 203 | 61.8 | 2.94 | 61.8 | 2.94 | 61.8 | 2.94 |
| Time | Traffic (veh) | P7 | P8 | P9 | P10 | ||||
|---|---|---|---|---|---|---|---|---|---|
| μ | σ | μ | σ | μ | σ | μ | σ | ||
| 6:30–6:35 | 105 | 55.9 | 4.61 | 57.4 | 3.95 | 63.2 | 4.65 | 57.8 | 3.74 |
| 6:35–6:40 | 135 | 56.8 | 3.83 | 58.6 | 4.03 | 62.0 | 3.94 | 57.2 | 3.01 |
| 6:40–6:45 | 140 | 56.9 | 4.22 | 57.7 | 3.75 | 62.0 | 3.83 | 57.9 | 2.95 |
| 6:45–6:50 | 165 | 57.9 | 3.63 | 59.4 | 3.43 | 63.8 | 3.82 | 58.9 | 3.31 |
| 6:50–6:55 | 148 | 56.8 | 4.05 | 57.8 | 3.48 | 62.0 | 4.38 | 57.5 | 3.52 |
| 6:55–7:00 | 176 | 57.7 | 3.13 | 59.1 | 3.03 | 64.2 | 3.36 | 59.1 | 3.09 |
| 7:00–7:05 | 190 | 59.5 | 3.31 | 60.6 | 2.98 | 64.0 | 3.22 | 58.7 | 2.56 |
| 7:05–7:10 | 175 | 58.4 | 3.72 | 59.4 | 3.34 | 63.5 | 3.67 | 59.1 | 3.16 |
| 7:10–7:15 | 188 | 57.8 | 3.94 | 59.0 | 3.45 | 64.0 | 3.29 | 59.4 | 2.53 |
| 7:15–7:20 | 205 | 58.2 | 3.53 | 59.5 | 2.97 | 64.2 | 3.54 | 59.9 | 3.12 |
| 7:20–7:25 | 225 | 58.7 | 2.92 | 59.4 | 2.41 | 64.1 | 3.31 | 59.6 | 2.63 |
| 15:00–15:05 | 470 | 64.2 | 1.94 | 64.7 | 2.20 | 66.6 | 2.07 | 59.9 | 2.51 |
| 15:05–15:10 | 452 | 62.8 | 2.01 | 63.3 | 2.56 | 64.5 | 2.27 | 58.4 | 2.74 |
| 15:10–15:15 | 462 | 63.0 | 2.25 | 63.8 | 2.64 | 65.3 | 2.68 | 60.1 | 2.47 |
| 15:15–15:20 | 495 | 62.7 | 1.98 | 63.7 | 2.49 | 66.0 | 2.35 | 59.9 | 2.61 |
| 15:20–15:25 | 510 | 63.3 | 2.17 | 64.1 | 2.65 | 66.0 | 2.18 | 60.0 | 2.41 |
| 15:25–15:30 | 502 | 62.1 | 2.07 | 63.1 | 2.44 | 66.0 | 2.54 | 60.8 | 2.55 |
| 15:30–15:35 | 460 | 62.2 | 3.18 | 63.3 | 3.45 | 66.0 | 2.57 | 60.5 | 2.52 |
| 15:35–15:40 | 445 | 63.0 | 2.39 | 64.0 | 2.60 | 65.0 | 2.30 | 58.9 | 2.70 |
| 15:40–15:45 | 424 | 63.2 | 2.78 | 64.1 | 3.35 | 65.0 | 2.73 | 59.8 | 2.80 |
| 15:45–15:50 | 442 | 63.2 | 2.31 | 64.1 | 2.60 | 65.3 | 2.25 | 60.3 | 2.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Wang, H.; Du, C.; Lan, Z.; Yu, F.; Rong, Y. Probabilistic Prediction Model for Expressway Traffic Noise Based on Short-Term Monitoring Data. Sustainability 2024, 16, 6841. https://doi.org/10.3390/su16166841
Li F, Wang H, Du C, Lan Z, Yu F, Rong Y. Probabilistic Prediction Model for Expressway Traffic Noise Based on Short-Term Monitoring Data. Sustainability. 2024; 16(16):6841. https://doi.org/10.3390/su16166841
Chicago/Turabian StyleLi, Feng, Haibo Wang, Canyi Du, Ziqin Lan, Feifei Yu, and Ying Rong. 2024. "Probabilistic Prediction Model for Expressway Traffic Noise Based on Short-Term Monitoring Data" Sustainability 16, no. 16: 6841. https://doi.org/10.3390/su16166841
APA StyleLi, F., Wang, H., Du, C., Lan, Z., Yu, F., & Rong, Y. (2024). Probabilistic Prediction Model for Expressway Traffic Noise Based on Short-Term Monitoring Data. Sustainability, 16(16), 6841. https://doi.org/10.3390/su16166841







