Voltage Hierarchical Control Strategy for Distribution Networks Based on Regional Autonomy and Photovoltaic-Storage Coordination
Abstract
1. Introduction
- (i)
- Propose a voltage hierarchical control strategy that integrates PV and ESS resources. This strategy combines voltage region division with a dual-layer optimization model, coordinating PV reactive power output and ESS active power absorption to enhance the voltage autonomy of the distribution network during the voltage improvement process.
- (ii)
- Propose a voltage partitioning strategy for distribution networks that considers PV reactive power margin. By refining the modularity function to partition voltage regions, this strategy classifies regions based on their internal regulation capabilities and identifies voltage weak points, allowing for precise management of voltage areas.
- (iii)
- Establish a dual-layer optimization configuration model for ESSs that accounts for voltage regulation. The upper-layer model focuses on planning configurations that minimize operational costs for an ESS, while the lower-layer model optimizes scheduling to achieve the best regional voltage quality. This model defines voltage regulation constraints based on regional division, enabling optimization from regional to global levels.
- (iv)
- Compare the economic and voltage regulation effects across four scenarios to demonstrate the effectiveness and advantages of the proposed control strategy within the IEEE 33-node distribution network. This analysis also evaluates the rationality of voltage region division and the photovoltaic energy consumption rate.
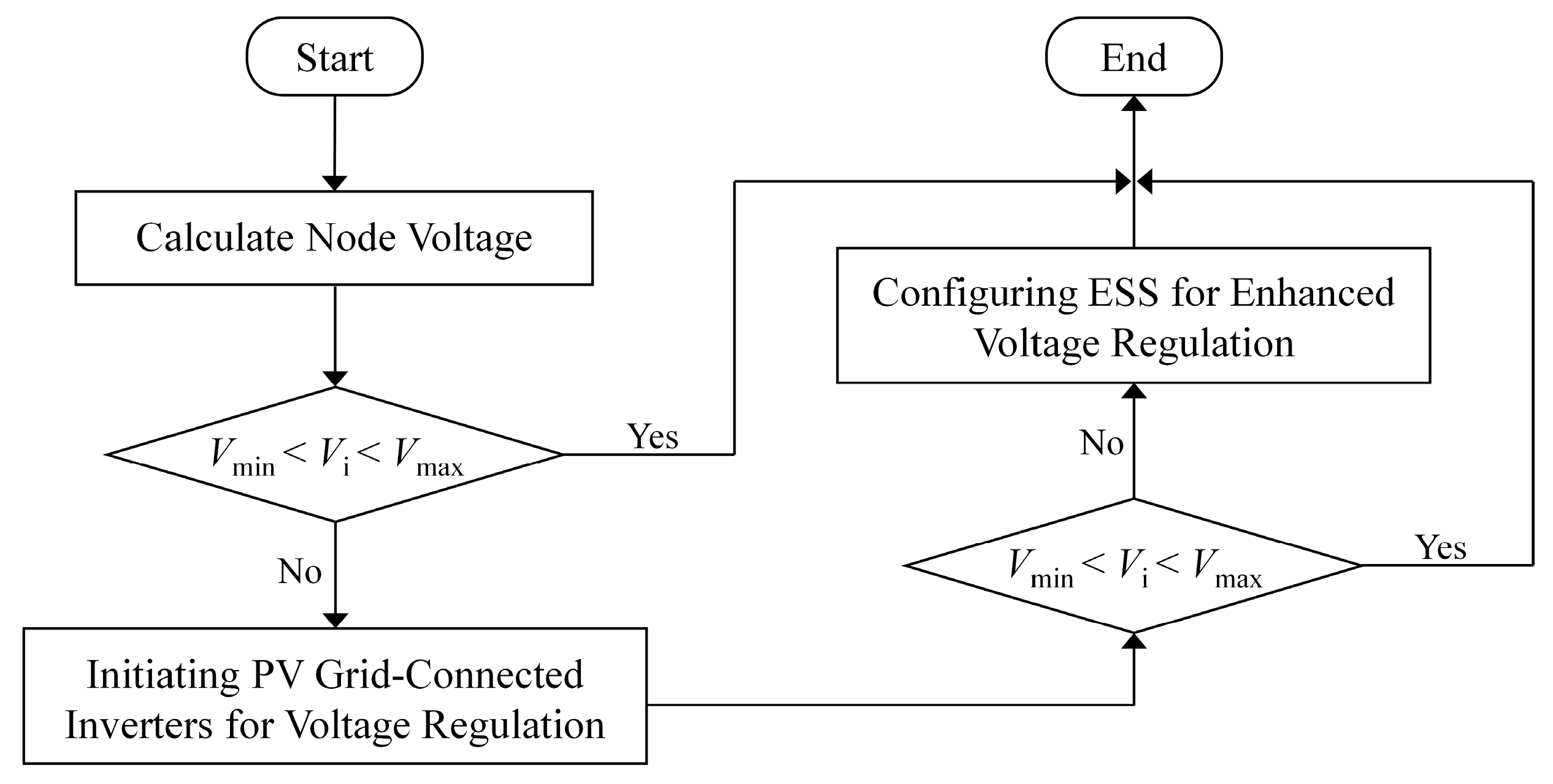
2. Voltage Hierarchical Control of Distribution Networks Considering Photovoltaic and ESS Participation
2.1. Impact of Photovoltaic and ESS Integration on Distribution Network Voltage
2.2. Assessment of Voltage Regulation Resources for Distributed Photovoltaics
2.3. Hierarchical Voltage Control Based on Active and Reactive Power Coordination
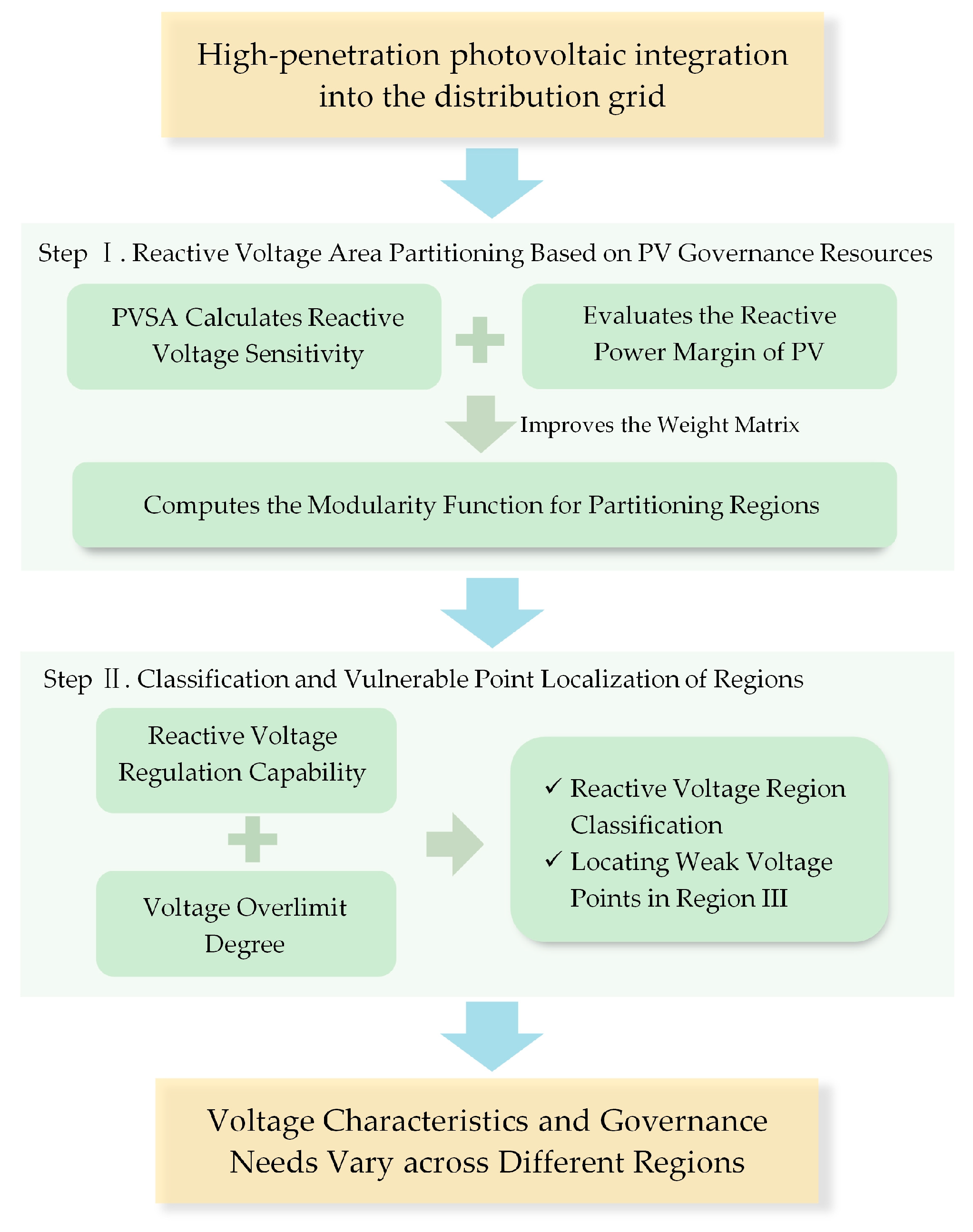
3. Voltage Zoning Strategy for Distribution Networks Considering Photovoltaic Management Resources
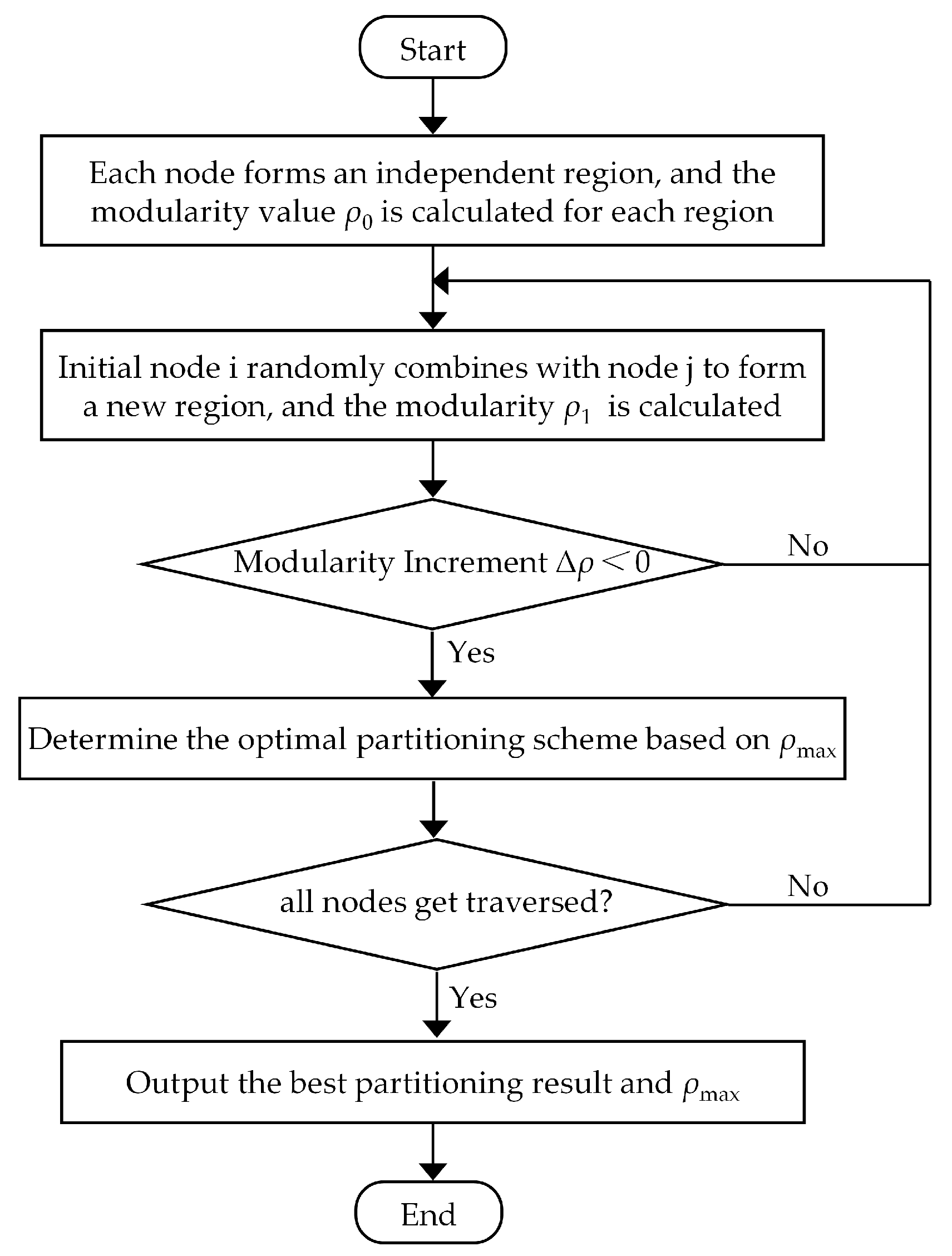
3.1. Modular Function Based on Photovoltaic Reactive Power Margin
3.2. Classification and Weak Point Localization of Distribution Network Regions
3.2.1. Division of Distribution Network Reactive Power Voltage Regions
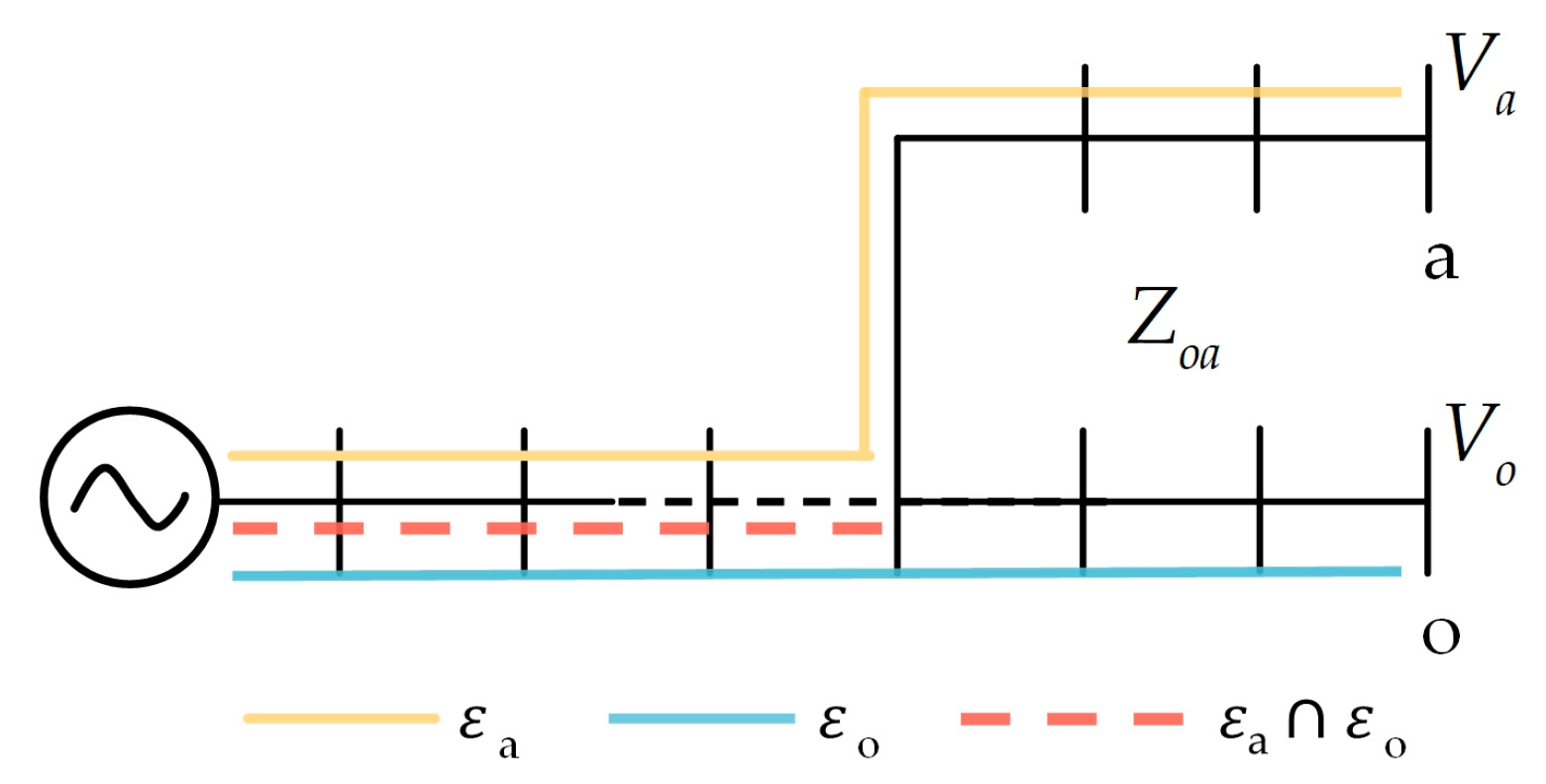
3.2.2. Localization and Evaluation of Voltage Weak Points
4. Considering Regional Voltage Regulation in Energy Storage System Dual-Layer Optimization Configuration Model
4.1. Upper-Layer Energy Storage System Planning Model
4.1.1. Objective Function of Upper-Layer Model
- (1)
- The mean daily expenditure for investment and maintenance of the ESS [30] is
- (2)
- The electricity purchase and sale revenue of the ESS for each typical day is
- (3)
- The service fee collected by the ESS from the distribution network on each typical day is
4.1.2. Constraints of Upper-Layer Model
- (1)
- Constraints on the charging and discharging power of ESSs are imposed. These constraints are subject to economic costs, node voltage limitations, and branch current restrictions. They include limitations on the upper bounds of electric power capacity bought and sold by each ESS, ensuring that its energy capacity exceeds its power capacity.
- (2)
- ESS rate constraints are governed by a direct proportionality between the system’s capacity and its rated power [25].
- (3)
- ESS state-of-charge constraints entail maintaining the storage energy operating range within 10% to 90%. The initial stored energy is set at 20%, and a 10% difference in the state of charge between the beginning and the end is upheld to ensure the continuity and reliability of its long-term operation.
4.2. Lower-Layer Regional Voltage Optimization Model
4.2.1. Objective Function of Lower-Layer Model
4.2.2. Constraints of Lower-Layer Model
- (1)
- Power balance constraint
- (2)
- Power flow constraint
- (3)
- Node voltage and branch current constraints
- (4)
- ESS charging and discharging power balance constraint
- (5)
- Purchase and sale power constraints between the distribution network and ESSs
- (6)
- Constraints on voltage regulation resources within the region
- (7)
- Constraints on interregional voltage differences
4.3. Solution of Dual-Layer Configuration Model
5. Case Study
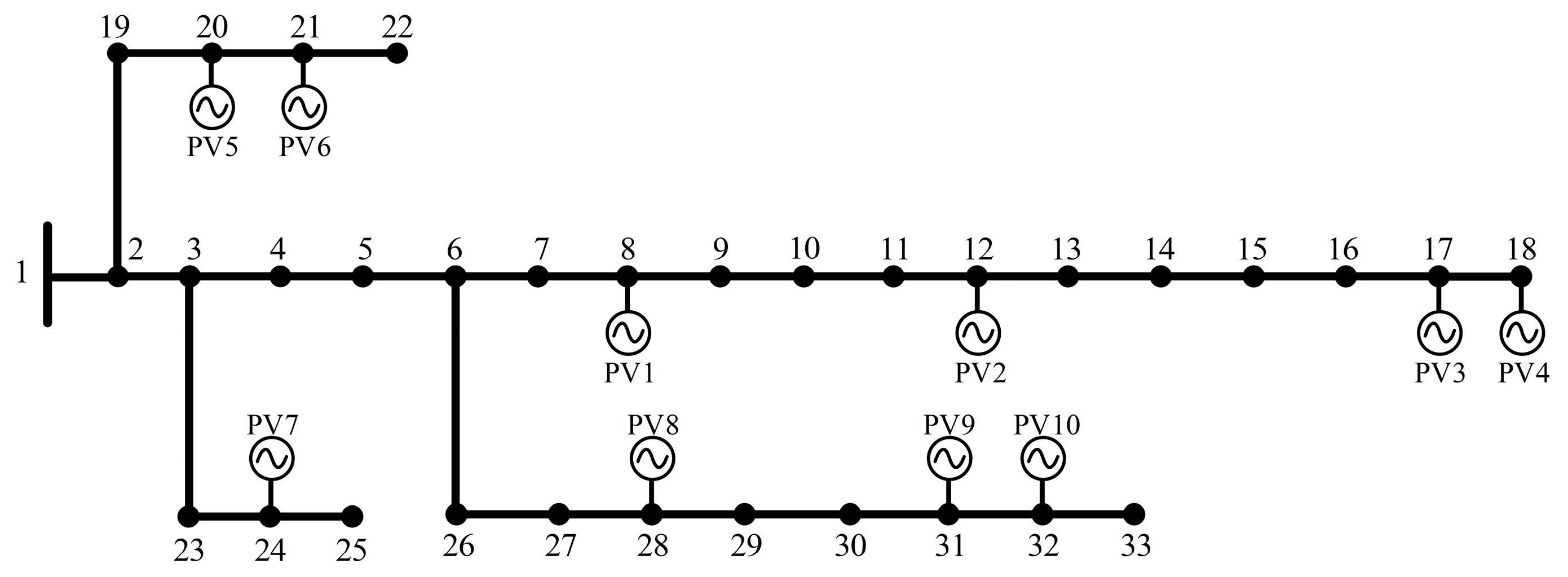
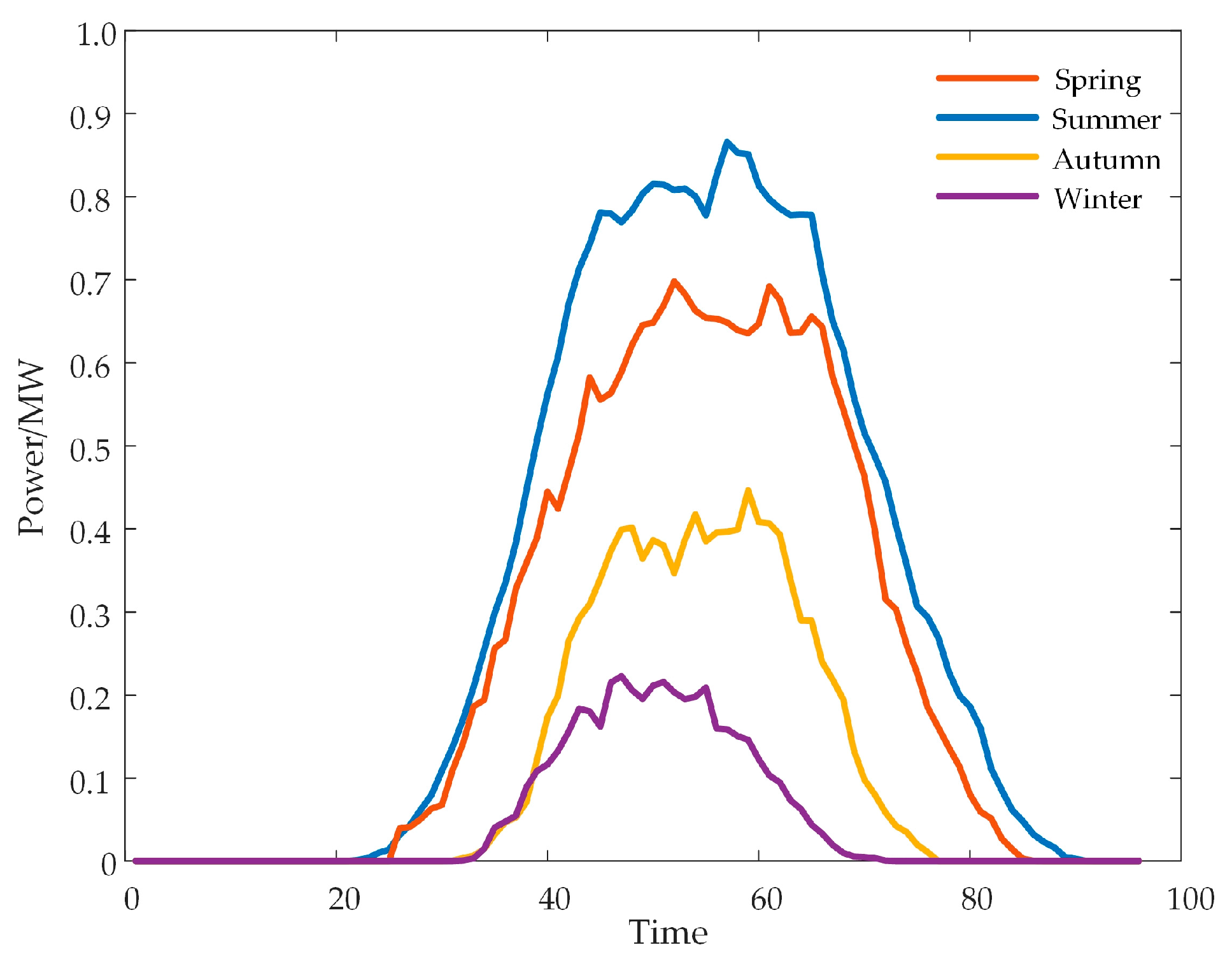
5.1. Case Introduction
5.2. Case Analysis
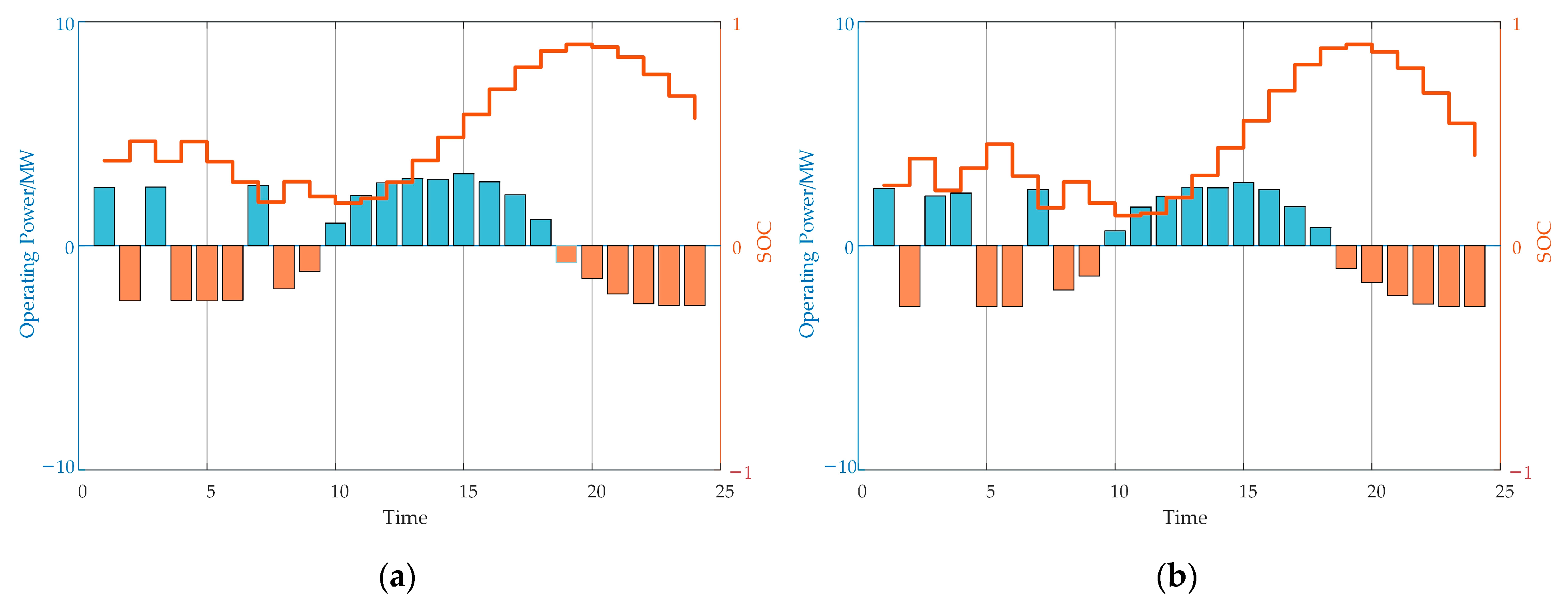
5.2.1. Economic Analysis of Energy Storage Operation
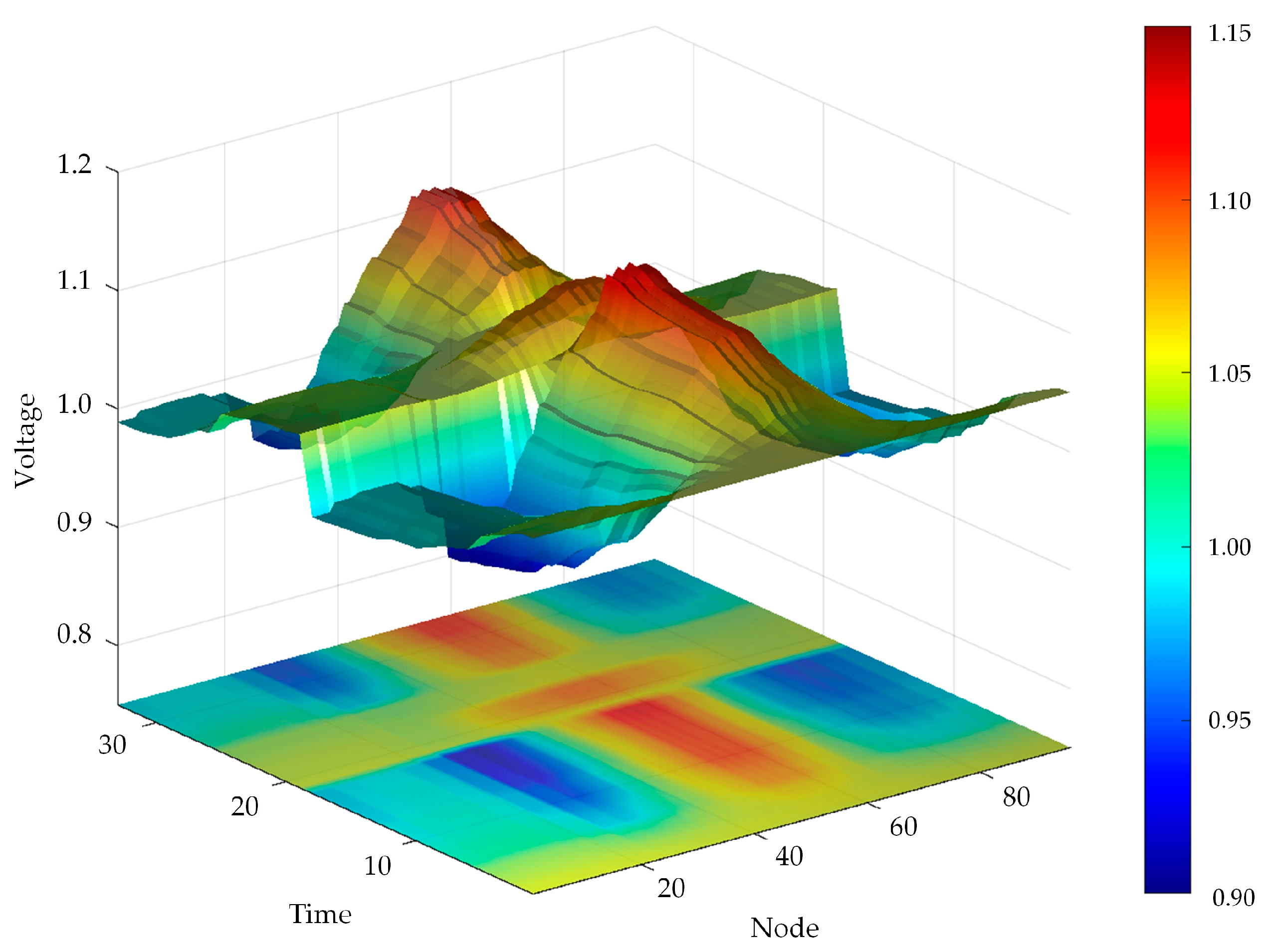
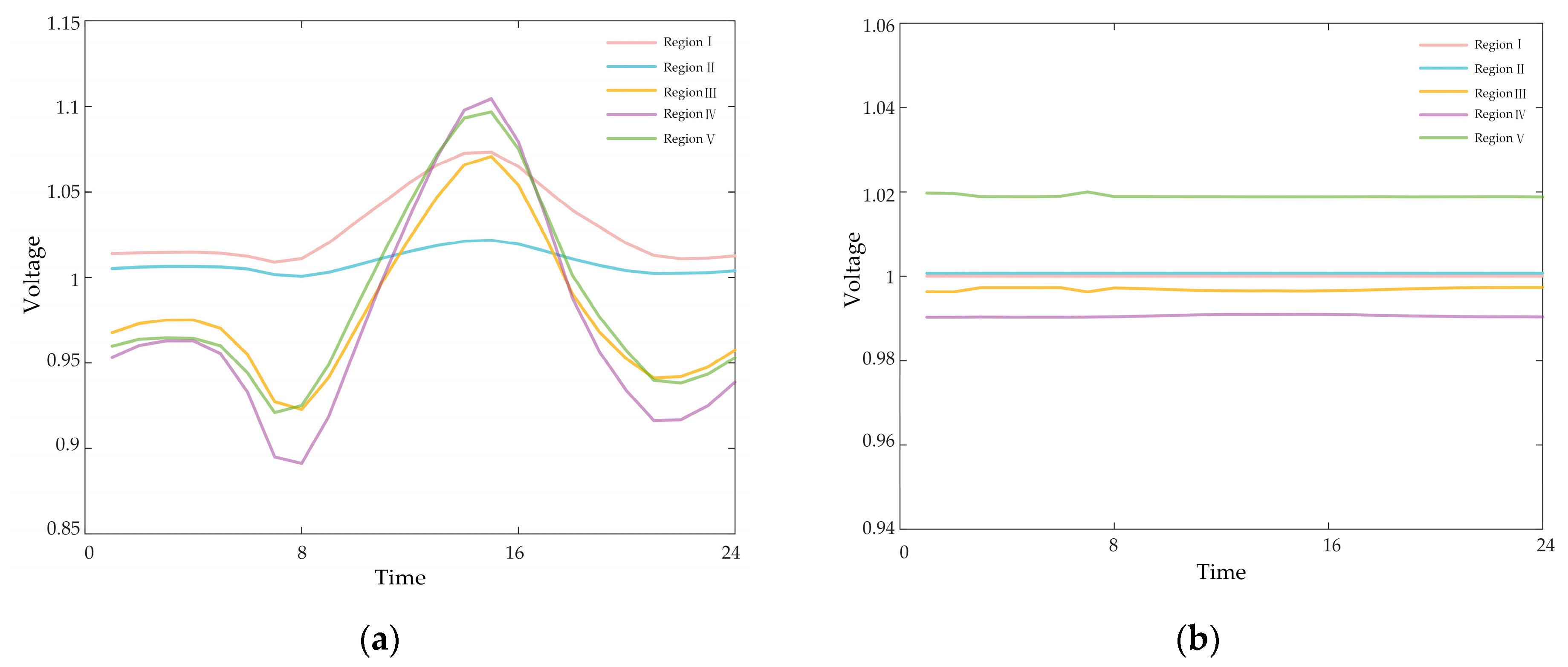
5.2.2. Analysis of Voltage Regulation Effect
6. Conclusions
- (i)
- The proposed voltage zoning strategy determines the optimal number of reactive areas in the distribution network as five, which are categorized into three types based on reactive power and voltage control capabilities. The algorithm proposed in this paper enhances reactive power modularity by 12.05%, resulting in a more rational voltage region division.
- (ii)
- The proposed energy storage system configuration model achieves static investment recovery in 5.2 years, indicating that investment in shared ESSs can yield significant profit margins. Compared to scenarios neglecting voltage zoning, its comprehensive costs decrease by 8.49%, while total revenue increases by 19.36%. This optimized configuration strategy notably enhances economic efficiency.
- (iii)
- The proposed voltage-tiered control strategy improves voltage deviation and daily average voltage fluctuation across distribution network regions under various operating scenarios, thus better serving regional voltage control and enabling 100% local consumption of photovoltaic power.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Wang, S.; Cheng, Y.; Zhao, Q.; Dong, Y. Multi-stage local-distributed voltage control strategy of distribution network considering photovoltaic-energy storage coordination. Electr. Power Autom. Equip. 2024, 44, 1–9. [Google Scholar]
- Leite, R.; Oleskkovicz, M. The Joint Application of Photovoltaic Generation and Distributed or Concentrated Energy Storage Systems in A Low Voltage Distribution Network: A Case Study. IEEE Lat. Am. Trans. 2023, 21, 1122–1131. [Google Scholar] [CrossRef]
- Lin, Z.Y.; Jiang, F.; Tu, C.M.; Xiao, Z.K. Distributed Coordinated Voltage Control of Photovoltaic and Energy Storage System Based on Dynamic Consensus Algorithm. In Proceedings of the IEEE IAS Conference on Industrial and Commercial Power System Asia (IEEE I and CPS Asia), Chengdu, China, 18–21 July 2021; pp. 1223–1228. [Google Scholar]
- Wang, C.Y.; Zhang, L.; Zhang, K.; Song, S.J.; Liu, Y.T. Distributed energy storage planning considering reactive power output of energy storage and photovoltaic. Energy Rep. 2022, 8, 562–569. [Google Scholar] [CrossRef]
- He, X.; Hashimoto, S.; Jiang, W.; Liu, J.C.; Kawaguchi, T. Design and Implementation of a Low-Voltage Photovoltaic System Integrated with Battery Energy Storage. Energies 2023, 16, 3057. [Google Scholar] [CrossRef]
- Zou, Y.Y.; Xu, Y.; Feng, X.; Naayagi, R.T.; Soong, B.H. Transactive Energy Systems in Active Distribution Networks: A Comprehensive Review. CSEE J. Power Energy Syst. 2022, 8, 1302–1317. [Google Scholar]
- Yu, P.; Wan, C.; Song, Y.H.; Jiang, Y.B. Distributed Control of Multi-Energy Storage Systems for Voltage Regulation in Distribution Networks: A Back-and-Forth Communication Framework. IEEE Trans. Smart Grid 2021, 12, 1964–1977. [Google Scholar] [CrossRef]
- Wang, G.; Wu, X.; Li, L.; Zhang, M.; Li, X.; Cheng, K.; Zhang, J. Optimization method of reactive power and harmonic for photovoltaic multi-function grid-connected inverter under different output states. Electr. Power Autom. Equip. 2024, 44, 80–87. [Google Scholar]
- Vidhya, K.; Krishnamoorthi, K. A hybrid technique for optimal power quality enhancement in grid-connected photovoltaic interleaved inverter. Energy Environ. 2024, 35, 244–274. [Google Scholar] [CrossRef]
- Wang, J.; Qin, L.; Xiang, Y.; Ren, P.; Tang, X.; Ruan, J.; Liu, K. A Collaborative Governance Strategy for Power Quality in AC/DC Distribution Networks Considering the Coupling Characteristics of Both Sides. Sensors 2023, 23, 7868. [Google Scholar] [CrossRef]
- Ge, J.; Liu, Y.; Pang, D.; Wang, C.; Wang, Z.; Liu, Z. Cluster Division Voltage Control Strategy of Photovoltaic Distribution Network with High Permeability. High Volt. Eng. 2024, 50, 74–82. [Google Scholar]
- Wang, J.J.; Yao, L.Z.; Liu, K.Y.; Xu, J.; Wang, J. Dynamic Regional Division Method of Distribution Network with Regional Autonomy. Power Syst. Technol. 2024, 8, 1–12. [Google Scholar] [CrossRef]
- Liang, W.; Zhao, Y.; Liu, B.; Wang, Y. Research on Distributed Photovoltaic Low Voltage Ride Through Control Strategy Considering Distribution Network Protection. In Proceedings of the 3rd International Conference on Electrical Engineering and Mechatronics Technology, ICEEMT 2023, Hybrid, Nanjing, China, 21–23 July 2023; pp. 550–555. [Google Scholar]
- Huang, W.; Liu, S.; Yi, Y.; Wu, Z.; Zhang, Y. Multi-time-scale Slack Optimal Control in Distribution Network Based on Voltage Optimization for Point of Common Coupling of PV. Autom. Electr. Power Syst. 2019, 43, 92–100. [Google Scholar]
- Zhao, B.; Xu, Z.C.; Xu, C.; Wang, C.S.; Lin, F. Network Partition-Based Zonal Voltage Control for Distribution Networks with Distributed PV Systems. IEEE Trans. Smart Grid 2018, 9, 4087–4098. [Google Scholar] [CrossRef]
- Lin, Z.; Hu, Z.C.; Zhang, H.C.; Song, Y.H. Optimal ESS allocation in distribution network using accelerated generalised Benders decomposition. IET Gener. Transm. Distrib. 2019, 13, 2738–2746. [Google Scholar] [CrossRef]
- Liu, J.K.; Zhang, N.; Kang, C.Q.; Kirschen, D.; Xia, Q. Cloud energy storage for residential and small commercial consumers: A business case study. Appl. Energy 2017, 188, 226–236. [Google Scholar] [CrossRef]
- Liu, J.K.; Zhang, N.; Kang, C.; Kirschen, D.S.; Xia, Q. Decision-Making Models for the Participants in Cloud Energy Storage. IEEE Trans. Smart Grid 2018, 9, 5512–5521. [Google Scholar] [CrossRef]
- Wu, S.; Li, Q.; Liu, J.; Zhou, Q.; Wang, C. Bi-level Optimal Configuration for Combined Cooling Heating and Power Multi-microgrids Based on Energy Storage Station Service. Power Syst. Technol. 2021, 45, 3822–3829. [Google Scholar]
- Wang, Y.; Tan, K.T.; Peng, X.Y.; So, P.L. Coordinated Control of Distributed Energy-Storage Systems for Voltage Regulation in Distribution Networks. IEEE Trans. Power Deliv. 2016, 31, 1132–1141. [Google Scholar] [CrossRef]
- Li, J.; Sun, D.; Zhu, X.; Yu, H.; Li, C.; Dong, Z. Voltage Regulation Strategy for Distributed Energy Storage Considering Coordination Among Clusters with High Penetration of Photovoltaics. Autom. Electr. Power Syst. 2023, 47, 47–56. [Google Scholar]
- Hen, Z.; Tai, N.; Hu, Y.; Huang, W.; Li, L. A multi-objective joint planning of transmission channel and energy storage system considering economy and flexibility. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission, ACDC 2020, Virtual, Online, 2–3 July 2020; pp. 65–72. [Google Scholar]
- Li, Y.; Yao, T.; Qiao, X.; Xiao, J.; Cao, Y. Optimal Configuration of Distributed Photovoltaic and Energy Storage System Based on Joint Sequential Scenario and Source-Network-Load Coordination. Trans. China Electrotech. Soc. 2022, 37, 3289–3303. [Google Scholar]
- Hao, M.; Lan, J.; Wang, L.; Lin, Y.; Wang, J.; Qin, L. Optimized Dual-Layer Distributed Energy Storage Configuration for Voltage Over-Limit Zoning Governance in Distribution Networks. Energies 2024, 17, 1847. [Google Scholar] [CrossRef]
- Sun, H.P.; Ding, X.H.; Wu, Z.; Wang, K. Voltage Regulation Strategy of Distribution Network Considering Optimization Adjustment of Automatic Voltage Control System Limits. Autom. Electr. Power Syst. 2024, 1, 1–13. [Google Scholar]
- Li, S.; Wang, Z.; Han, W. A Multi-Objective Current Compensation Strategy for Photovoltaic Grid-Connected Inverter. J. Circuits Syst. Comput. 2022, 31, 2250230. [Google Scholar] [CrossRef]
- Tian, F.; Huang, L.; Zhou, C.-G. Photovoltaic power generation and charging load prediction research of integrated photovoltaic storage and charging station. Energy Rep. 2023, 9, 861–871. [Google Scholar] [CrossRef]
- Liao, K.; Pang, B.; Yang, J.; He, Z. Output Current Quality Improvement for VSC with Capability of Compensating Voltage Harmonics. IEEE Trans. Ind. Electron. 2024, 71, 9087–9097. [Google Scholar] [CrossRef]
- Zhao, P.; Ma, K.; Yang, J.; Yang, B.; Guerrero, J.M.; Dou, C.; Guan, X. Distributed Power Sharing Control Based on Adaptive Virtual Impedance in Seaport Microgrids with Cold Ironing. IEEE Trans. Transp. Electrif. 2023, 9, 2472–2485. [Google Scholar] [CrossRef]
- Dehghani, N.L.; Shafieezadeh, A. Multi-stage Resilience Management of Smart Power Distribution Systems: A Stochastic Robust Optimization Model. IEEE Trans. Smart Grid 2022, 13, 3452–3467. [Google Scholar] [CrossRef]
- Jhala, K.; Natarajan, B.; Pahwa, A. Probabilistic Voltage Sensitivity Analysis (PVSA)-A Novel Approach to Quantify Impact of Active Consumers. IEEE Trans. Power Syst. 2018, 33, 2518–2527. [Google Scholar] [CrossRef]
- Cheng, W.; Gong, G.; Huang, J.; Xu, J.; Chen, K. Decentralized Model Predictive Voltage Control for Distributed Generation Clusters of Power Systems. In Proceedings of the 2023 IEEE IAS Industrial and Commercial Power System Asia, I and CPS Asia 2023, Chongqing, China, 7–9 July 2023; pp. 1615–1619. [Google Scholar]
- Wand, Z.; Jia, Y.; Li, Y.; Han, X. Optimal Capacity Configuration of Photovoltaic and Energy Storage System in Active Distribution Network Considering Influence of Power Quality. Power Syst. Technol. 2024, 48, 607–617. [Google Scholar]
- Wu, S.; Liu, J.; Zhou, Q.; Wang, C.; Chen, Z. Optimal Economic Scheduling for Multi-microgrid System with Combined Cooling, Heating and Power Considering Service of Energy Storage Station. Autom. Electr. Power Syst. 2019, 43, 10–18. [Google Scholar]
- Wen, C.; Mo, J.; Li, J.; Zhou, J.; Wang, P. Coordinate the Optimal Configuration of Double-Layer Hybrid Energy Storage Systems for Wind Farms Participating in Power System Frequency Regulation. In Proceedings of the 10th Frontier Academic Forum of Electrical Engineering, FAFEE 2022, Xian, China, 7–8 December 2022; pp. 97–105. [Google Scholar]
- Han, R.; Hu, Q.; Cui, H.; Chen, T.; Quan, X.; Wu, Z. An optimal bidding and scheduling method for load service entities considering demand response uncertainty. Appl. Energy 2022, 328, 120167. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, J.; Yu, Z.; Liu, W.; Wang, Z.; Kong, W.; Chen, H. Research on Hierarchical Optimization Modeling and Scheduling Technology of Distributed Photovoltaic Cluster. In Proceedings of the 5th Asia Energy and Electrical Engineering Symposium, AEEES 2023, Chengdu, China, 23–26 March 2023; pp. 1438–1443. [Google Scholar]





| Period | Electricity Price/(yuan/kWh) | |||
|---|---|---|---|---|
| Purchased from the Grid | Purchased from ESS | Sold to ESS | ||
| Peak | 08:00—12:00 | 1.36 | 1.15 | 0.95 |
| 17:00—22:00 | ||||
| Off-peak | 12:00—17:00 | 0.82 | 0.75 | 0.55 |
| 22:00—24:00 | ||||
| Valley | 00:00—08:00 | 0.37 | 0.40 | 0.20 |
| Parameters | Parameter Values | Unit |
|---|---|---|
| 0.05 | yuan/kWh | |
| 1000 | yuan/kWh | |
| 1897 | yuan/kWh | |
| Operation and maintenance cost Mess | 72 | yuan/(year·kW) |
| Lifecycle | 8 | year |
| 0.95/0.95 | / | |
| Initial stored energy SOC0 | 0.2 | / |
| SOCmax/SOCmin | 0.9/0.1 | / |
| Algorithm | Number of Regions | Modularity |
|---|---|---|
| Fast Newman | 6 | 0.671 |
| Ref. [21] | 6 | 0.755 |
| Proposed Algorithm | 5 | 0.846 |
| Region | Type | Reactive Power and Voltage Control Capability | Voltage Weak Points |
|---|---|---|---|
| R1 | II | 1 | — |
| R2 | I | 1 | — |
| R3 | II | 1 | — |
| R4 | III | 0.39 | 17 |
| R5 | III | 0.46 | 31 |
| Node | Power Capacity/MW | Energy Capacity/MWh |
|---|---|---|
| 17 | 3.217 | 8.576 |
| 31 | 2.824 | 7.528 |
| Scenario | Annual Comprehensive Operating Cost/kUSD | Annual Revenue of the Energy Storage System/kUSD | Photovoltaic Energy Consumption Rate/% |
|---|---|---|---|
| 1 | 28.776 | — | 75.36 |
| 2 | 32.144 | — | 75.36 |
| 3 | 402.526 | 60.6035 | 100 |
| 4 | 368.353 | 75.155 | 100 |
| Scenario | Node 17 | Node 31 | ||
|---|---|---|---|---|
| Voltage Deviation | Daily Average Voltage Fluctuation | Voltage Deviation | Daily Average Voltage Fluctuation | |
| 1 | 9.821% | 5.846% | 9.719% | 5.337% |
| 2 | 8.849% | 5.271% | 8.365% | 4.856% |
| 3 | 2.487% | 0.462% | 2.967% | 0.055% |
| 4 | 0.282% | 0.251% | 1.861% | 0.037% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Lan, J.; Wang, L.; Lin, Y.; Hao, M.; Zhang, Y.; Xiang, Y.; Qin, L. Voltage Hierarchical Control Strategy for Distribution Networks Based on Regional Autonomy and Photovoltaic-Storage Coordination. Sustainability 2024, 16, 6758. https://doi.org/10.3390/su16166758
Wang J, Lan J, Wang L, Lin Y, Hao M, Zhang Y, Xiang Y, Qin L. Voltage Hierarchical Control Strategy for Distribution Networks Based on Regional Autonomy and Photovoltaic-Storage Coordination. Sustainability. 2024; 16(16):6758. https://doi.org/10.3390/su16166758
Chicago/Turabian StyleWang, Jiang, Jinchen Lan, Lianhui Wang, Yan Lin, Meimei Hao, Yan Zhang, Yang Xiang, and Liang Qin. 2024. "Voltage Hierarchical Control Strategy for Distribution Networks Based on Regional Autonomy and Photovoltaic-Storage Coordination" Sustainability 16, no. 16: 6758. https://doi.org/10.3390/su16166758
APA StyleWang, J., Lan, J., Wang, L., Lin, Y., Hao, M., Zhang, Y., Xiang, Y., & Qin, L. (2024). Voltage Hierarchical Control Strategy for Distribution Networks Based on Regional Autonomy and Photovoltaic-Storage Coordination. Sustainability, 16(16), 6758. https://doi.org/10.3390/su16166758






