The Emission-Reduction Effect of Green Demand Preference in Carbon Market and Macro-Environmental Policy: A DSGE Approach
Abstract
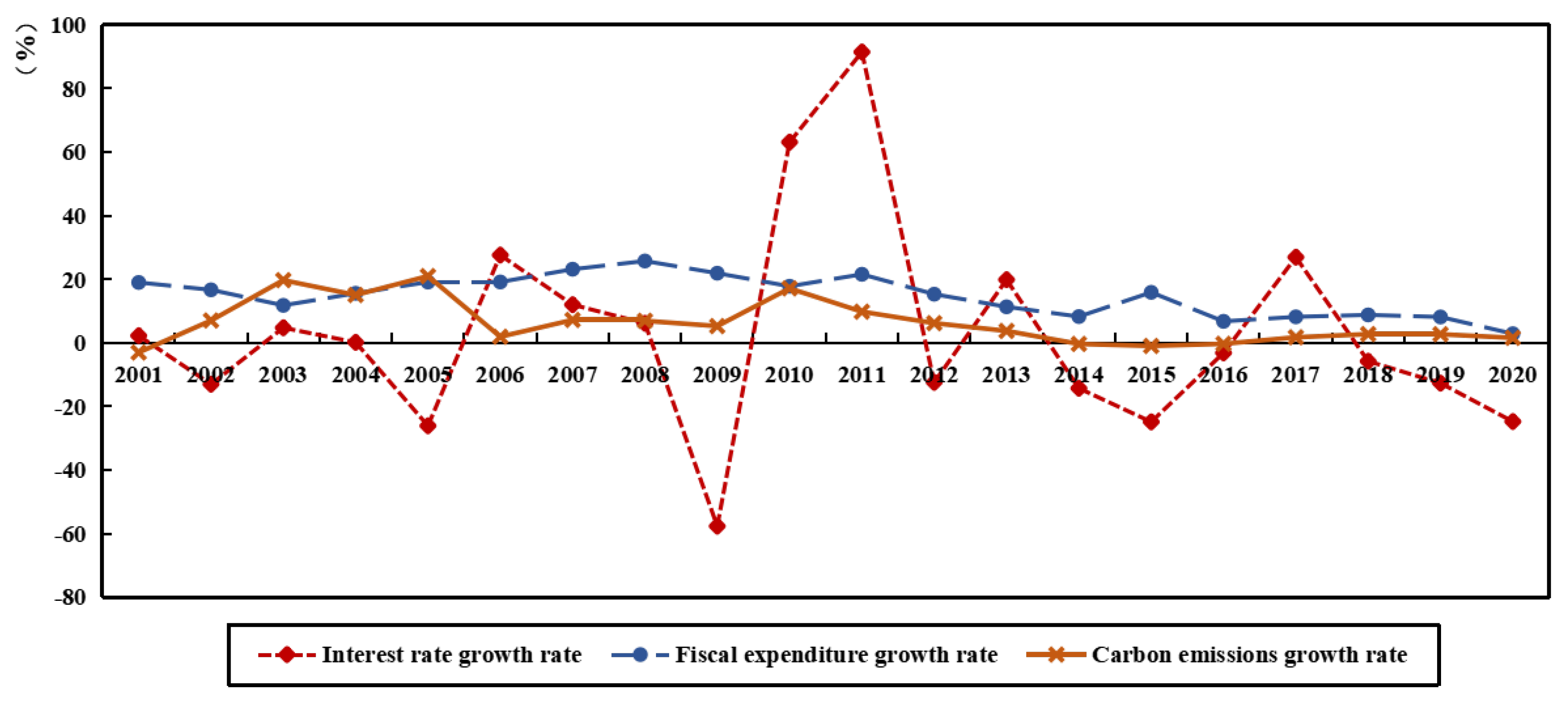
1. Introduction
2. Literature Review
2.1. Research Progress on Emission-Reduction Effects of Carbon Markets
2.2. Emission-Reduction Effects of Carbon Markets under Non-Homothetic Preferences
2.3. Emission-Reduction Effects of Macroeconomic Policies
3. The Model
3.1. Households
3.2. Producers
3.3. Carbon Markets
3.4. Central Banks
3.5. Government
4. Calibration and Estimation
4.1. Calibration
4.2. Bayesian
5. Dynamic Analysis and Mechanisms
5.1. Analysis of the Transmission Path of Carbon Price Shocks
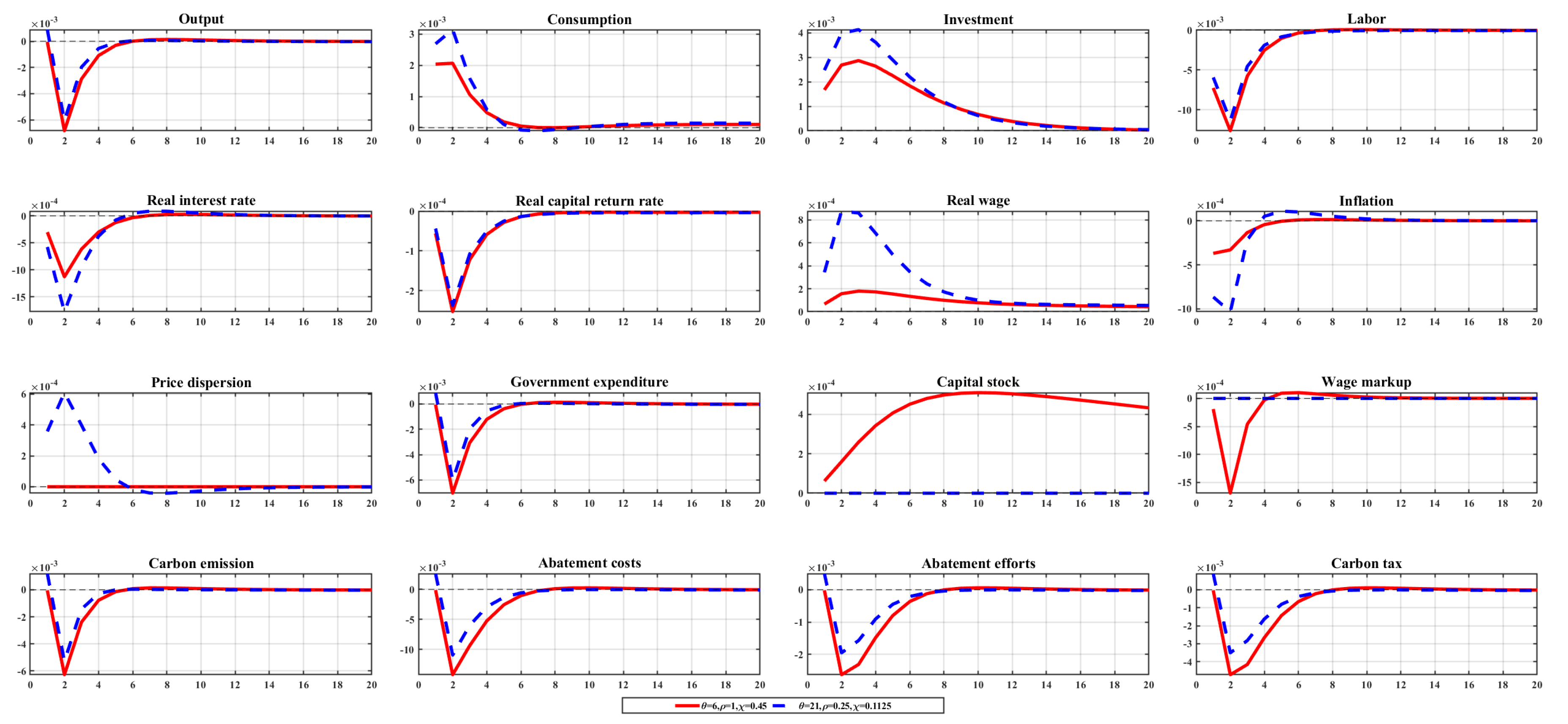
5.1.1. Impact of Carbon Price Shocks
5.1.2. Impact Cycle of Carbon Price Shocks
5.1.3. Impact of Carbon Price Shocks under Low Non-Homothetic Preferences
5.2. Analysis of the Transmission Path of COVID-19 Shocks
5.3. Analysis of the Transmission Path of Monetary Policy Shocks
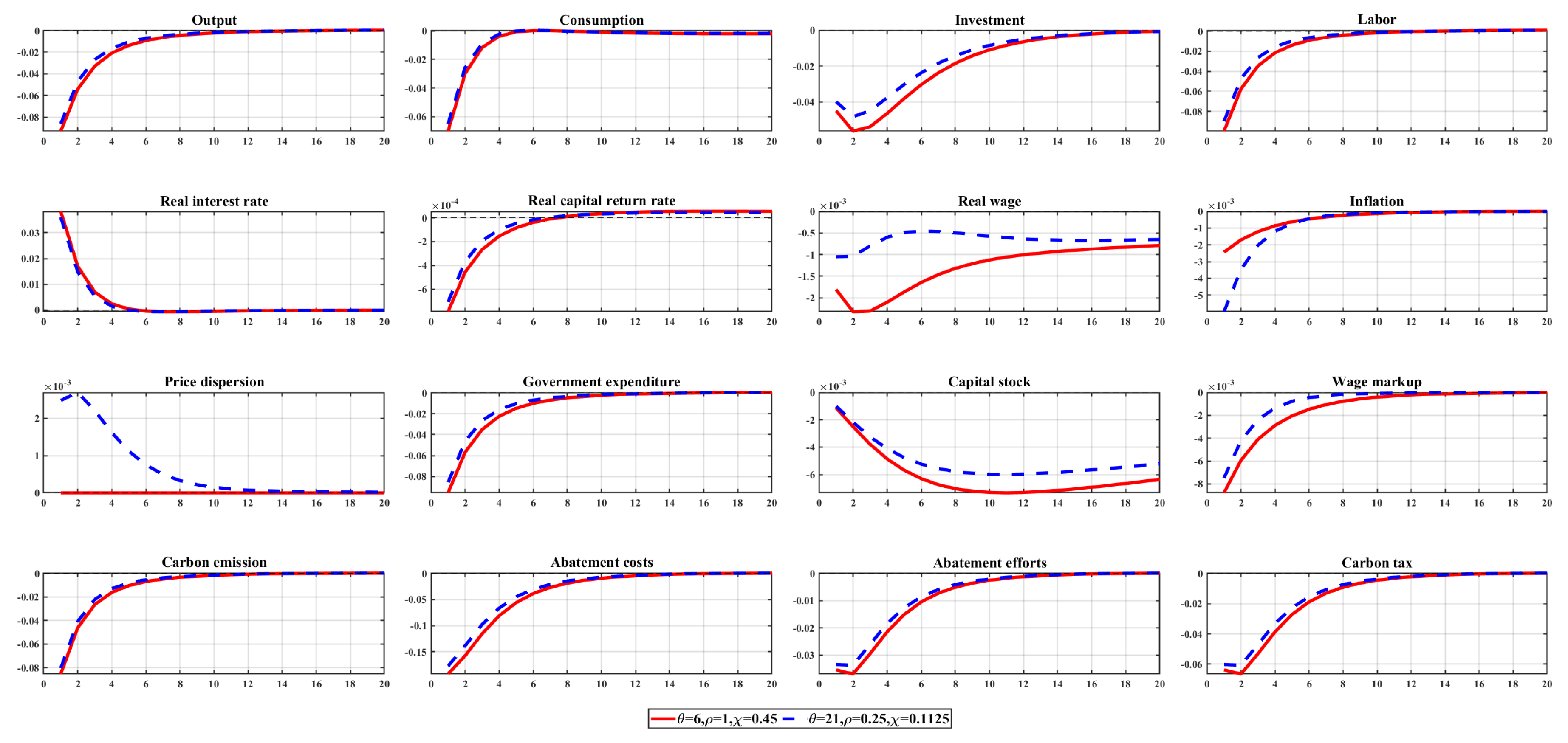
5.3.1. The Impact and Cycle of Monetary Policy Shocks
5.3.2. Impact of Monetary Policy Shocks under Low Non-Homothetic Preferences
5.4. Analysis of the Transmission Path of Fiscal Policy Shocks
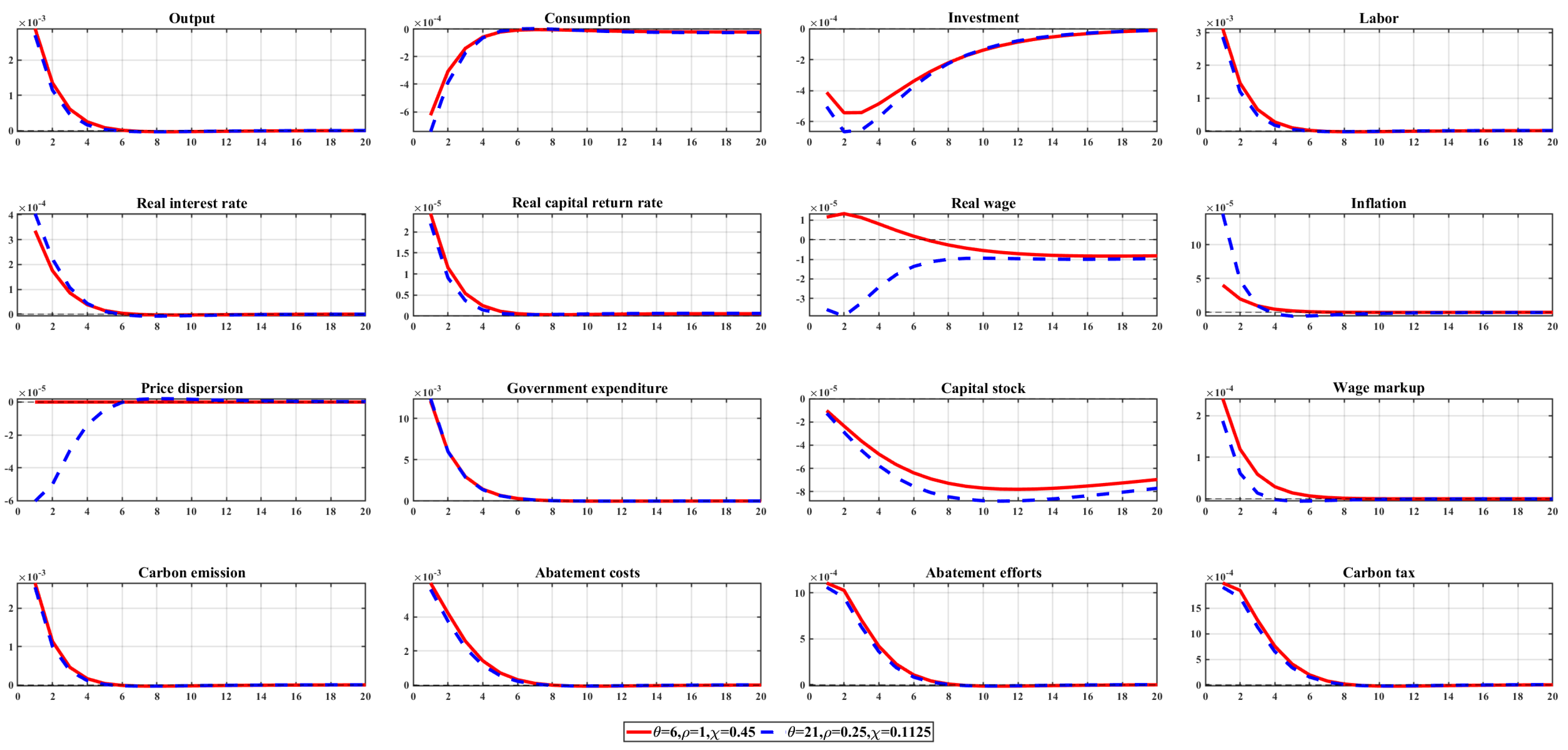
5.4.1. The Impact and Cycle of Fiscal Policy Shocks
5.4.2. Impact of Fiscal Policy Shocks under Low Non-Homothetic Preferences
5.5. Analysis of the Dynamic Impacts and Transmission Paths of the Mix of Policies
5.5.1. The Impact and Cycle of the Mix of Policies
5.5.2. Impact of the Mix of Policies under Low Non-Homothetic Preferences
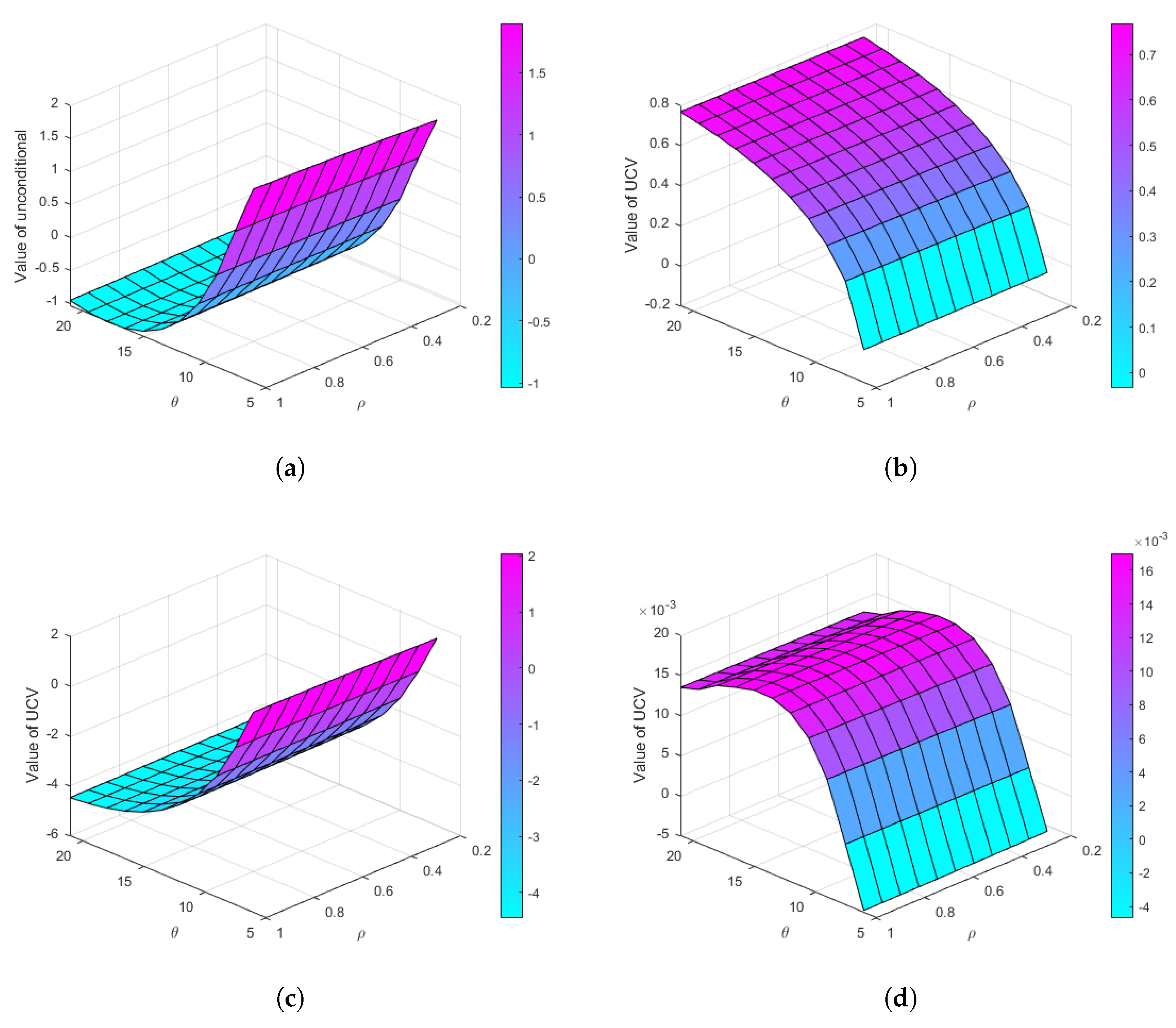
6. Welfare Analysis
7. Conclusions and Policy Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Bank. State and Trends of Carbon Pricing 2021; The World Bank: Washington, DC, USA, 2021. [Google Scholar] [CrossRef]
- Lightfoot, S.; Burchell, J. Green hope or greenwash? The actions of the European Union at the World Summit on sustainable development. Glob. Environ. Chang. 2004, 14, 337–344. [Google Scholar] [CrossRef]
- Honma, S.; Ushifusa, Y.; Okamura, S.; Vandercamme, L. Measuring carbon emissions performance of Japan’s metal industry: Energy inputs, agglomeration, and the potential for green recovery reduction. Resour. Policy 2023, 82, 103519. [Google Scholar] [CrossRef]
- Yu, D.J.; Li, J. Evaluating the employment effect of China’s carbon emission trading policy: Based on the perspective of spatial spillover. J. Clean. Prod. 2021, 292, 126052. [Google Scholar] [CrossRef]
- Waleed, K.; Mirza, F.M. Examining behavioral patterns in household fuel consumption using two-stage-budgeting framework for energy and environmental policies: Evidence based on micro data from Pakistan. Energy Policy 2020, 147, 111835. [Google Scholar] [CrossRef]
- Li, R.; Leung, G.C. The relationship between energy prices, economic growth and renewable energy consumption: Evidence from Europe. Energy Rep. 2021, 7, 1712–1719. [Google Scholar] [CrossRef]
- Tovar Reaños, M.A.; Lynch, M.A. Measuring carbon tax incidence using a fully flexible demand system. Vertical and horizontal effects using Irish data. Energy Policy 2022, 160, 112682. [Google Scholar] [CrossRef]
- Cavallari, L.; Etro, F. Demand, markups and the business cycle. Eur. Econ. Rev. 2020, 127, 103471. [Google Scholar] [CrossRef]
- Liu, J.; Gong, N.; Qin, J. How would the carbon tax on energy commodities affect consumer welfare? Evidence from China’s household energy consumption system. J. Environ. Manag. 2022, 317, 115466. [Google Scholar] [CrossRef] [PubMed]
- Galeotti, M.; Lanza, A. Desperately seeking environmental Kuznets. Environ. Model. Softw. 2005, 20, 1379–1388. [Google Scholar] [CrossRef]
- Ma, G.; Qin, J.; Zhang, Y. Does the carbon emission trading system reduce carbon emissions by promoting two-way FDI in developing countries? Evidence from Chinese listed companies and cities. Energy Econ. 2023, 120, 106581. [Google Scholar] [CrossRef]
- Bartocci, A.; Notarpietro, A.; Pisani, M. “Green” fiscal policy measures and nonstandard monetary policy in the euro area. Econ. Model. 2024, 136, 106743. [Google Scholar] [CrossRef]
- Gelfer, S. Examining business cycles and optimal monetary policy in a regional DSGE model. Econ. Model. 2024, 136, 106750. [Google Scholar] [CrossRef]
- Annicchiarico, B.; Dio, F.D. GHG Emissions Control and Monetary Policy. Environ. Resour. Econ. 2017, 67, 823–851. [Google Scholar] [CrossRef]
- Borenstein, S.; Bushnell, J.; Wolak, F.A.; Zaragoza-Watkins, M. Expecting the Unexpected: Emissions Uncertainty and Environmental Market Design. Am. Econ. Rev. 2019, 109, 3953–3977. [Google Scholar] [CrossRef]
- Rozenberg, J.; Vogt-Schilb, A.; Hallegatte, S. Instrument choice and stranded assets in the transition to clean capital. J. Environ. Econ. Manag. 2020, 100, 102183. [Google Scholar] [CrossRef]
- Sun, J.; Wang, F.; Yin, H.; Zhang, B. Money Talks: The Environmental Impact of China’s Green Credit Policy. J. Policy Anal. Manag. 2019, 38, 653–680. [Google Scholar] [CrossRef]
- Blazquez, J.; Galeotti, M.; Manzano, B.; Pierru, A.; Pradhan, S. Effects of Saudi Arabia’s economic reforms: Insights from a DSGE model. Econ. Model. 2021, 95, 145–169. [Google Scholar] [CrossRef]
- Hou, R.; Lei, L.; Jin, K.; Lin, X.; Xiao, L. Introducing electric vehicles? Impact of network effect on profits and social welfare. Energy 2022, 243, 123002. [Google Scholar] [CrossRef]
- Matsumura, K.; Naka, T.; Sudo, N. Analysis of the transmission of carbon taxes using a multi-sector DSGE. Energy Econ. 2024, 136, 107642. [Google Scholar] [CrossRef]
- Garcia-Villegas, S.; Martorell, E. Climate transition risk and the role of bank capital requirements. Econ. Model. 2024, 135, 106724. [Google Scholar] [CrossRef]
- Crocker, T. The Structuring of Atmospheric Pollution Control Systems. Econ. Air Pollut. 1966, 61, 81–84. [Google Scholar] [CrossRef]
- Bel, G.; Joseph, S. Emission abatement: Untangling the impacts of the EU ETS and the economic crisis. Energy Econ. 2015, 49, 531–539. [Google Scholar] [CrossRef]
- Schäfer, S. Decoupling the EU ETS from subsidized renewables and other demand side effects: Lessons from the impact of the EU ETS on CO2 emissions in the German electricity sector. Energy Policy 2019, 133, 110858. [Google Scholar] [CrossRef]
- Liu, Y.; Tan, X.J.; Yu, Y.; Qi, S.Z. Assessment of impacts of Hubei Pilot emission trading schemes in China—A CGE-analysis using TermCO2 model. Appl. Energy 2017, 189, 762–769. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, W.; Zhang, N. The Potential Gains from Carbon Emission Trading in China’s Industrial Sectors. Comput. Econ. 2018, 52, 1175–1194. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, S.; Luo, T.; Gao, J. The effect of emission trading policy on carbon emission reduction: Evidence from an integrated study of pilot regions in China. J. Clean. Prod. 2020, 265, 121843. [Google Scholar] [CrossRef]
- Li, R.; Ramanathan, R. Exploring the relationships between different types of environmental regulations and environmental performance: Evidence from China. J. Clean. Prod. 2018, 196, 1329–1340. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, Q.; Dong, X.; Dong, K. Would environmental regulation improve the greenhouse gas benefits of natural gas use? A Chinese case study. Energy Econ. 2020, 87, 104712. [Google Scholar] [CrossRef]
- Du, Z.; Xu, C.; Lin, B. Does the Emission Trading Scheme achieve the dual dividend of reducing pollution and improving energy efficiency? Micro evidence from China. J. Environ. Manag. 2022, 323, 116202. [Google Scholar] [CrossRef]
- Tan, X.; Liu, Y.; Cui, J.; Su, B. Assessment of carbon leakage by channels: An approach combining CGE model and decomposition analysis. Energy Econ. 2018, 74, 535–545. [Google Scholar] [CrossRef]
- Wen, F.; Wu, N.; Gong, X. China’s carbon emission trading and stock returns. Energy Econ. 2020, 86, 104627. [Google Scholar] [CrossRef]
- Cui, L.B.; Fan, Y.; Zhu, L.; Bi, Q.H. How will the emission trading scheme save cost for achieving China’s 2020 carbon intensity reduction target? Appl. Energy 2014, 136, 1043–1052. [Google Scholar] [CrossRef]
- Wesseh, P.K.; Lin, B. Optimal carbon taxes for China and implications for power generation, welfare, and the environment. Energy Policy 2018, 118, 1–8. [Google Scholar] [CrossRef]
- Geng, W.; Fan, Y. Emission trading in an imperfectly competitive product market: A comparison of social welfare under mass- and rate-based schemes. Comput. Ind. Eng. 2021, 162, 107761. [Google Scholar] [CrossRef]
- Mayer, J.; Dugan, A.; Bachner, G.; Steininger, K.W. Is carbon pricing regressive? Insights from a recursive-dynamic CGE analysis with heterogeneous households for Austria. Energy Econ. 2021, 104, 105661. [Google Scholar] [CrossRef]
- Heutel, G. How should environmental policy respond to business cycles? Optimal policy under persistent productivity shocks. Rev. Econ. Dyn. 2012, 15, 244–264. [Google Scholar] [CrossRef]
- Fischer, C.; Springborn, M. Emissions targets and the real business cycle: Intensity targets versus caps or taxes. J. Environ. Econ. Manag. 2011, 62, 352–366. [Google Scholar] [CrossRef]
- Annicchiarico, B.; Di Dio, F. Environmental policy and macroeconomic dynamics in a new Keynesian model. J. Environ. Econ. Manag. 2015, 69, 1–21. [Google Scholar] [CrossRef]
- Dissou, Y.; Karnizova, L. Emissions cap or emissions tax? A multi-sector business cycle analysis. J. Environ. Econ. Manag. 2016, 79, 169–188. [Google Scholar] [CrossRef]
- Katircioglu, S.; Katircioglu, S. Testing the role of fiscal policy in the environmental degradation: The case of Turkey. Environ. Sci. Pollut. Res. 2018, 25, 5616–5630. [Google Scholar] [CrossRef]
- Economides, G.; Xepapadeas, A. Monetary Policy under Climate Change; CESifo Working Paper 7021; Munich Society for the Promotion of Economic Research-CESifo GmbH: Munich, Germany, 2018. [Google Scholar]
- Jacobs, B.W.; Singhal, V.R.; Subramanian, R. An empirical investigation of environmental performance and the market value of the firm. J. Oper. Manag. 2010, 28, 430–441. [Google Scholar] [CrossRef]
- Kumar, A.; Jain, V.; Kumar, S. A comprehensive environment friendly approach for supplier selection. Omega 2014, 42, 109–123. [Google Scholar] [CrossRef]
- Ji, J.; Zhang, Z.; Yang, L. Carbon emission reduction decisions in the retail-/dual-channel supply chain with consumers’ preference. J. Clean. Prod. 2017, 141, 852–867. [Google Scholar] [CrossRef]
- Xia, L.; Hao, W.; Qin, J.; Ji, F.; Yue, X. Carbon emission reduction and promotion policies considering social preferences and consumers’ low-carbon awareness in the cap-and-trade system. J. Clean. Prod. 2018, 195, 1105–1124. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, F. Production and emission reduction decisions considering the differentiated carbon tax regulation across new and remanufactured products and consumer preference. Urban Clim. 2021, 40, 100992. [Google Scholar] [CrossRef]
- Dogan, E.; Muhammad, I. Willingness to pay for renewable electricity: A contingent valuation study in Turkey. Electr. J. 2019, 32, 106677. [Google Scholar] [CrossRef]
- Ndebele, T. Assessing the potential for consumer-driven renewable energy development in deregulated electricity markets dominated by renewables. Energy Policy 2020, 136, 111057. [Google Scholar] [CrossRef]
- Liobikienė, G.; Dagiliūtė, R. Do positive aspects of renewable energy contribute to the willingness to pay more for green energy? Energy 2021, 231, 120817. [Google Scholar] [CrossRef]
- Cardella, E.; Ewing, B.T.; Williams, R.B. Green is Good—The Impact of Information Nudges on the Selection of Voluntary Green-Power Plans. Energy J. 2022, 43, 1–42. [Google Scholar] [CrossRef]
- Sun, C.; Wang, Y.; Zhu, Z.; Qiu, L. Decoupling carbon emissions from the economy and low-carbon ecological city construction-based on 196 cities in China. Sustain. Cities Soc. 2024, 107, 105458. [Google Scholar] [CrossRef]
- Bertoletti, P.; Etro, F. Monopolistic Competition when Income Matters. Econ. J. 2017, 127, 1217–1243. [Google Scholar] [CrossRef]
- Erceg, C.; Henderson, D.; Levin, A. Optimal Monetary Policy With Staggered Wage and Price Contracts. J. Monet. Econ. 2000, 46, 281–313. [Google Scholar] [CrossRef]
- Calvo, G.A. Staggered prices in a utility-maximizing framework. J. Monet. Econ. 1983, 12, 383–398. [Google Scholar] [CrossRef]
- Gourio, F. Disaster Risk and Business Cycles. Am. Econ. Rev. 2012, 102, 2734–2766. [Google Scholar] [CrossRef]
- Christiano, L.J.; Trabandt, M.; Walentin, K. Chapter 7–DSGE Models for Monetary Policy Analysis. In Handbook of Monetary Economics; Elsvier: Amsterdam, The Netherlands, 2010; Volume 3, pp. 285–367. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, Y. Examining the economic and environmental effects of emissions policies in China: A Bayesian DSGE model. J. Clean. Prod. 2020, 266, 122026. [Google Scholar] [CrossRef]
- Annicchiarico, B.; Diluiso, F. International transmission of the business cycle and environmental policy. Resour. Energy Econ. 2019, 58, 101112. [Google Scholar] [CrossRef]
- Pan, X.; Xu, H.; Li, M.; Zong, T.; Lee, C.T.; Lu, Y. Environmental expenditure spillovers: Evidence from an estimated multi-area DSGE model. Energy Econ. 2020, 86, 104645. [Google Scholar] [CrossRef]
- Xiao, B.; Fan, Y.; Guo, X.; Voigt, S.; Cui, L. Effects of linking national carbon markets on international macroeconomics: An open-economy E-DSGE model. Comput. Ind. Eng. 2022, 169, 108166. [Google Scholar] [CrossRef]
- Chan, Y.T. Are macroeconomic policies better in curbing air pollution than environmental policies? A DSGE approach with carbon-dependent fiscal and monetary policies. Energy Policy 2020, 141, 111454. [Google Scholar] [CrossRef]
- Noureen, S.; Iqbal, J.; Chishti, M. Exploring the dynamic effects of shocks in monetary and fiscal policies on the environment of developing economies: Evidence from the CS-ARDL approach. Environ. Sci. Pollut. Res. 2022, 29, 45665–45682. [Google Scholar] [CrossRef]
- Schmitt-Grohé, S.; Uribe, M. Solving dynamic general equilibrium models using a second-order approximation to the policy function. J. Econ. Dyn. Control. 2004, 28, 755–775. [Google Scholar] [CrossRef]



| Parameter | Description | Value | Literature Backed |
|---|---|---|---|
| Discount factor | 0.9904 | Chan [62] | |
| Parameter of labor disutility | Calculated by steady-state | ||
| Inverse of Frisch elasticity | 1.0000 | Christiano et al. [57] | |
| Parameter of emissions disutility | 0.2000 | Zhang and Zhang [58] | |
| Depreciation rate of capital | 0.0250 | Chan [62] | |
| Parameter of price adjustment cost | 2.0000 | Pan et al. [60], Xiao et al. [61] | |
| Parameter of capital utilization cost | Calculated by steady-state | ||
| Parameter of capital utilization cost | 0.0100 | Christiano et al. [57] | |
| Elasticity of substitution of energy products | 6.0000 | Annicchiarico and Diluiso [59] | |
| Parameter of non-homothetic | 1.0000 | Bertoletti and Etro [53] | |
| Parameter of wage stickiness | 0.7500 | Calvo [55] | |
| Elasticity of substitution of labor supply | 6.0000 | Chan [62] | |
| Share of capital in production | Annicchiarico and Diluiso [59] | ||
| Damage parameter of carbon emissions | 0.0026 | Heutel [37] | |
| Technological efficiency parameter of abatement efforts | 0.4500 | Annicchiarico and Dio [14] | |
| Scale parameter of controlling abatement costs | 0.1850 | Annicchiarico and Dio [14] | |
| Elasticity of abatement costs to abatement efforts | 2.8000 | Annicchiarico and Dio [14] | |
| Steady-state carbon price in carbon markets | 0.0500 | Chan [62] | |
| Steady-state share of government expenditures | 0.2000 | Chan [62] | |
| Parameter of price stickiness | 0.7500 | Calvo [55] |
| Parameter | Prior Distribution | Posterior Distribution | |||
|---|---|---|---|---|---|
| Prior Dist | Prior Mean | Prior SD | Posterior Mean | 90% Confidence Interval | |
| Beta | 0.5000 | 0.1000 | 0.4032 | ||
| Normal | 1.5000 | 0.1000 | 1.7460 | ||
| Beta | 0.5000 | 0.2000 | 0.1458 | ||
| Normal | 1.6000 | 0.1000 | 1.5643 | ||
| Normal | 0.1000 | 0.0500 | 0.4088 | ||
| Normal | 0.1200 | 0.2000 | 0.0851 | ||
| Beta | 0.5000 | 0.2000 | 0.9569 | ||
| Normal | 0.0500 | 0.0200 | 0.0443 | ||
| Beta | 0.7000 | 0.2000 | 0.7721 | ||
| Beta | 0.7000 | 0.2000 | 0.9883 | ||
| Beta | 0.5000 | 0.0200 | 0.5328 | ||
| Shock | Non-Homotheticity | |||||||
|---|---|---|---|---|---|---|---|---|
| Policy Mix | Policy Mix | |||||||
| Baseline | C + F | C + M | M + F | Baseline | C + F | C + M | M + F | |
| All Shocks | 1.895 | 2.046 | −0.034 | −0.004 | −0.930 | −4.389 | 0.757 | 0.013 |
| (3.597) | (4.502) | (−0.090) | (−0.012) | (0.894) | (−1.486) | (0.711) | (0.003) | |
| Carbon price | −0.246 | −0.036 | −0.179 | 0.364 | −3.757 | −7.314 | 0.774 | 0.014 |
| (−0.593) | (−0.160) | (−0.360) | (0.867) | (−3.757) | (−7.314) | (0.774) | (0.014) | |
| Monetary | 2.159 | 2.346 | −0.031 | −0.015 | −0.922 | −4.378 | 0.746 | 0.004 |
| (3.672) | (4.527) | (−0.074) | (−0.029) | (0.560) | (−1.984) | (0.715) | (−0.005) | |
| Fiscal | 0.002 | 0.008 | 0.006 | −0.053 | −3.755 | −7.314 | 0.774 | 0.014 |
| (0.009) | (0.001) | (0.001) | (−0.116) | (−3.752) | (−7.314) | (0.775) | (0.014) | |
| Technology | −0.026 | −0.016 | −0.008 | 0.001 | −3.696 | −7.241 | 0.771 | 0.014 |
| (−0.050) | (−0.028) | (−0.017) | (0.002) | (−3.663) | (−7.191) | (0.768) | (0.014) | |
| Investment | −0.234 | −0.277 | 0.005 | 0.010 | −3.828 | −7.398 | 0.786 | 0.022 |
| (−0.025) | (0.004) | (0.005) | (0.014) | (−3.536) | (−6.967) | (0.774) | (0.022) | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, X.; Ma, G.; Cao, J. The Emission-Reduction Effect of Green Demand Preference in Carbon Market and Macro-Environmental Policy: A DSGE Approach. Sustainability 2024, 16, 6741. https://doi.org/10.3390/su16166741
Ding X, Ma G, Cao J. The Emission-Reduction Effect of Green Demand Preference in Carbon Market and Macro-Environmental Policy: A DSGE Approach. Sustainability. 2024; 16(16):6741. https://doi.org/10.3390/su16166741
Chicago/Turabian StyleDing, Xuyi, Guangcheng Ma, and Jianhua Cao. 2024. "The Emission-Reduction Effect of Green Demand Preference in Carbon Market and Macro-Environmental Policy: A DSGE Approach" Sustainability 16, no. 16: 6741. https://doi.org/10.3390/su16166741
APA StyleDing, X., Ma, G., & Cao, J. (2024). The Emission-Reduction Effect of Green Demand Preference in Carbon Market and Macro-Environmental Policy: A DSGE Approach. Sustainability, 16(16), 6741. https://doi.org/10.3390/su16166741






