Research on Coordination of Fresh Supply Chain Considering Supplier Misreporting and Consumer Return

Abstract

Misreporting is prevalent in supply chain characterized by asymmetric information, and its impact on the supply chain is substantial and cannot be overlooked. In order to explore the impact of fresh supplier’s misreporting decisions on fresh supply chain, this paper takes the fresh supply chain with a single fresh supplier and a single e-commerce enterprise as the research object, and constructs five Stackelberg game models based on the differences of supply chain information transparency and power structure. Particularly, the effect of fresh-keeping level on the after-sales rate and market demand of the product is incorporated into the model, and the following conclusions are drawn by solving and analyzing the decision results of the different models: (1) When the supplier has the decision advantage, it will not choose to misreport. But when it loses the decision advantage, it will produce the misreporting behavior. Supplier misreporting is detrimental to the retailer and the supply chain; specifically, it can lead to lower fresh-keeping level and higher after-sales rates. (2) In the decentralized decision-making model, it is more beneficial for the supply chain that the supplier has the leading right of decision-making. In the absence of misreporting, the leader’s profit is always higher than that of the follower. When there is misreporting, even if the retailer is the dominant player, its profit is still lower than the manufacturer’s. (3) Both supply chain profit and fresh-keeping level are positively correlated with the coefficient of consumer perception of freshness and the coefficient of sensitivity to fresh-keeping technology, and are more significant under the centralized decision-making model. Furthermore, in response to supplier misreporting behavior, this paper achieves coordination in the fresh supply chain by designing a joint contract and confirms the effectiveness of this contract through an arithmetic analysis.

1. Introduction

With the enhancement of living standards, consumers are increasingly demanding freshness from fresh commodities. Freshness serves as a crucial indicator of the quality of fresh commodities and an important consideration for consumers when buying such fresh commodities, and significantly influences consumers’ purchasing decisions. Commonly known fresh commodities like vegetables, fruits, and meats are prone to deterioration and damage during circulation due to their perishable nature [1,2]. Unlike the conventional retail model of fresh commodities, online shopping precludes consumers from assessing product quality until delivery. Upon receiving damaged goods, customers will apply to the e-commerce enterprise for after-sales applications, such as refunds or exchanges [3]. Investing in fresh-keeping technology during transport not only improves the freshness of fresh commodities, thereby encouraging consumer purchases, but also reduces the refund behavior arising from product spoilage or loss.

Currently, numerous studies are focused on optimizing supply chain management by leveraging fresh-keeping technology. Zhang et al. [4] quantified the fresh-keeping level in grey scale and constructed a grey-game-based study of supply chain fresh-keeping behavior, which provides a theoretical basis for decision optimization in supply chain management. Indrajitsingha and Sahu [5] studied an optimized inventory model and effectively reduced the deterioration rate of products by investing in preservation technology. Chen et al. [6] improved the deterioration inventory model based on the level of preservation, and discussed the time-varying demand rate under the influence of factors such as product freshness. Mahata and Debnath [7] set the investment cap of fresh-keeping technology as the constraint of the model, constructed a two-level supply chain inventory model, and analyzed the coordination mechanism under different investment strategies. Jiao et al. [8] designed a “cost sharing + revenue sharing” incentive mechanism to optimize the supply chain in view of the information asymmetry between freshness and preservation efforts. Cao et al. [9] found in their study that the input of fresh-keeping efforts will increase with the increase in freshness sensitivity, and it will form an inverted U-shape with the increase in effective supply time. From the perspective of positive externalities of the market, Xu [10] used evolutionary game theory to analyze the fresh-keeping investment behavior of supplier and retailer under bounded rationality. The existing research has widely involved the effectiveness of fresh-keeping technology in improving the freshness of fresh commodities, but the research on how fresh-keeping technology affects the after-sales rate of fresh commodities is still relatively insufficient.

Regarding consumers’ after-sales behavior in fresh chain, Huang and Hu [11] found that third-party logistics provides consumers with fresh-keeping services, thus reducing consumers’ after-sales behavior. Li et al. [12] discussed the coordination of the cold chain home delivery supply chain considering the return period, and pointed out the importance of setting a reasonable return period to encourage all parties in the supply chain to maintain a high level of fresh-keeping efforts. Based on the return demand of fresh products due to deterioration loss, Guo and Wang [13] constructed a cross-regional closed-loop logistics network and distribution vehicle path optimization model considering carbon trading. Yang and Guo [14,15] studied the problem of the uncertain closed-loop logistics network based on fresh product demand and return under the background of new retail through fuzzy programming method, and proposed a fuzzy environment fresh closed-loop logistics network system considering the multi-decision-making situation of the cycle, which highlights the high attention to uncertainty and its management in modern supply chain design. Gu et al. [16] and Zhang and Ma [17] pointed out the impact of consumer return policies on supply chain performance and consumer satisfaction, and the potential facilitation of the design of coordination mechanisms under information symmetry on the improvement of fresh-keeping levels from the perspectives of consumer after-sales behavior and dual-channel supply chain coordination, respectively. The above studies considering consumer returns are based on the assumption of supply chain information symmetry, and studies on supply chain after-sales problems when information asymmetry is present are less common.

Information asymmetry is prevalent in supply chains. Each member of the supply chain has different information, leading to an unequal distribution of information, and this asymmetry may lead to one party having an advantage in decision making. One of the supply chain members with information advantage may resort to misreporting strategy to gain more profit. Zhou et al. [18] studied the quality information misreporting behavior of vertical product differentiation, and revealed the phenomenon of quality misreporting that is common in enterprises in monopoly markets. Cai et al. [19] pointed out in their study that information asymmetry in product quality can lead to damage to consumer welfare, as evidenced by the “Google penalty case” in the United States and the “Wei Zexi incident” in China, which emphasizes the importance of information symmetry for the healthy development of the market. Jia and Chen [20] constructed a single-cycle newsboy model for the asymmetry of freshness of fresh agricultural products, and discussed how to deal with the misreporting behavior of producers through the supply chain coordination mechanism. Chen et al. [21] and Liu and Li [22] both demonstrated the role of blockchain technology in curbing the behavior of suppliers misreporting the freshness of commodities in the fresh commodity supply chain, suggesting that the input of new technologies can improve information transparency and reduce the negative impact of information asymmetry on the supply chain. Song et al. [23] considered the retailer’s sales cost misreporting behavior when studying supply chain pricing and green decision making, and explored the impact of risk aversion strategies on the decision-making process. Dong et al. [24] considered the manufacturer’s misreporting of cost information, and found that the manufacturer’s misreporting behavior would lead to damage to the overall performance of the retailer and the supply chain. In addition, Feng and Liu [25] and Wu et al. [26] both built supply chain models around supplier misreporting cost information, and proposed that when the retailer is dominant, the supplier will adopt a misreporting strategy. The misreporting behavior under information asymmetry may not only lead to market turmoil, but also weaken the overall interests of the supply chain. Therefore, it is of great significance to study the information misreporting behavior of fresh supply chains under different information transparency conditions for optimizing the management of fresh supply chains.

Information asymmetry is one of the causes of reduced supply chain performance. When information is symmetric, timely and accurate sharing of information can be achieved between various links and participants in the supply chain, thus promoting the efficient operation of the supply chain. In order to inhibit the information asymmetry phenomenon and enhance the efficiency of the supply chain, many scholars have researched the supply chain coordination problem under information asymmetry. Tang et al. [27] introduced a revenue sharing mechanism and option contract to realize the information sharing of commodity freshness and the coordination of the supply chain. To promote freshness sharing in the fresh supply chain, Zheng et al. [28] optimized the revenue sharing contract and facilitated the supply chain to achieve Pareto optimality. Zheng and Fan [29] constructed a contractual incentive model for the fresh produce supply chain based on principal–agent theory to address the information asymmetry of the fresh produce supply chain under the “agricultural super-docking” model. Kerkkamp et al. [30] designed a principal–agent contract model to coordinate the asymmetry of cost information between supplier and retailer. Avinadav [31] studied the misreporting behavior of retailers regarding market demand information, and pointed out that asymmetric information would affect the double marginalization problem. To overcome the information asymmetry problem and improve supply chain performance, Patidar et al. [32] developed an appropriate ICT strategy by exploring a feasible combination of internal advantages and external opportunities. Dan et al. [33] designed an incentive contract for demand information sharing to achieve Pareto improvement of supply chain members’ profits. In addition, references [34,35,36,37] achieved perfect coordination of the fresh commodity supply chain through combinatorial contracts.

In summary, among the existing research on fresh supply chain, few studies have considered the correlation between fresh-keeping level and consumer after-sales behavior in the model. At the same time, there is a lack of research on how information symmetry and after-sales behavior affect supply chain decision making together, as shown in

Table 1. Summary of existing research.

Reference	Research Purpose	Research Method	Information Transparency	Research Findings
[5]	Explore the impact of fresh-keeping level on the supply chain.	Construct an inventory model and introduce fresh-keeping level factors.	Information symmetry.	Retailers investing in fresh-keeping technology can reduce product deterioration rate.
[10]	Explore the impact of fresh produce preservation inputs on market.	Constructing an evolutionary game model for supplier and retailer with finite rationality properties.	Information symmetry.	Improving fresh-keeping level can help to address the “free-riding” problem of supply chain members.
[17]	Explore the impact of return behavior on supply chain performance.	A Stackelberg game model is constructed, in which the consumer’s return behavior is considered.	Information symmetry.	Consumers’ return behavior of deteriorating products can encourage fresh e-commerce to improve their fresh-keeping efforts.
[19]	Explore the negative impact of information asymmetry on supply chains.	The game model of the three parties is constructed by means of game theory.	Information asymmetry	Information asymmetry makes consumer welfare suffer double losses due to the adverse selection of sellers.
[20]	Explore the coordination of fresh agricultural products supply chain with information asymmetry.	The model is constructed by combining the one-cycle newsboy model and Stackelberg game theory.	Information asymmetry	Designing revenue sharing contracts to effectively curb supply chain misrepresentation and improve supply chain stability.

. Based on the in-depth analysis of the existing research, this paper proposes a new research perspective for the decision-making problem of the fresh supply chain. From the perspective of information asymmetry, a two-level supply chain model, including a single fresh supplier and an e-commerce enterprise, is constructed. Considering the supplier’s misreporting behavior and consumer’s after-sales behavior, as well as the potential impact of fresh-keeping level on after-sales rate, this paper explores the impact of supplier misreporting timing and misreporting behavior on the supply chain, as well as the impact of consumer return behavior on the supply chain. In addition, this paper designs a combination contract of “fresh-keeping cost sharing + wholesale price discount + revenue sharing”, which aims to optimize the decision making of the fresh supply chain through the coordination of the contract.

2. Problem Description and Research Hypothesis

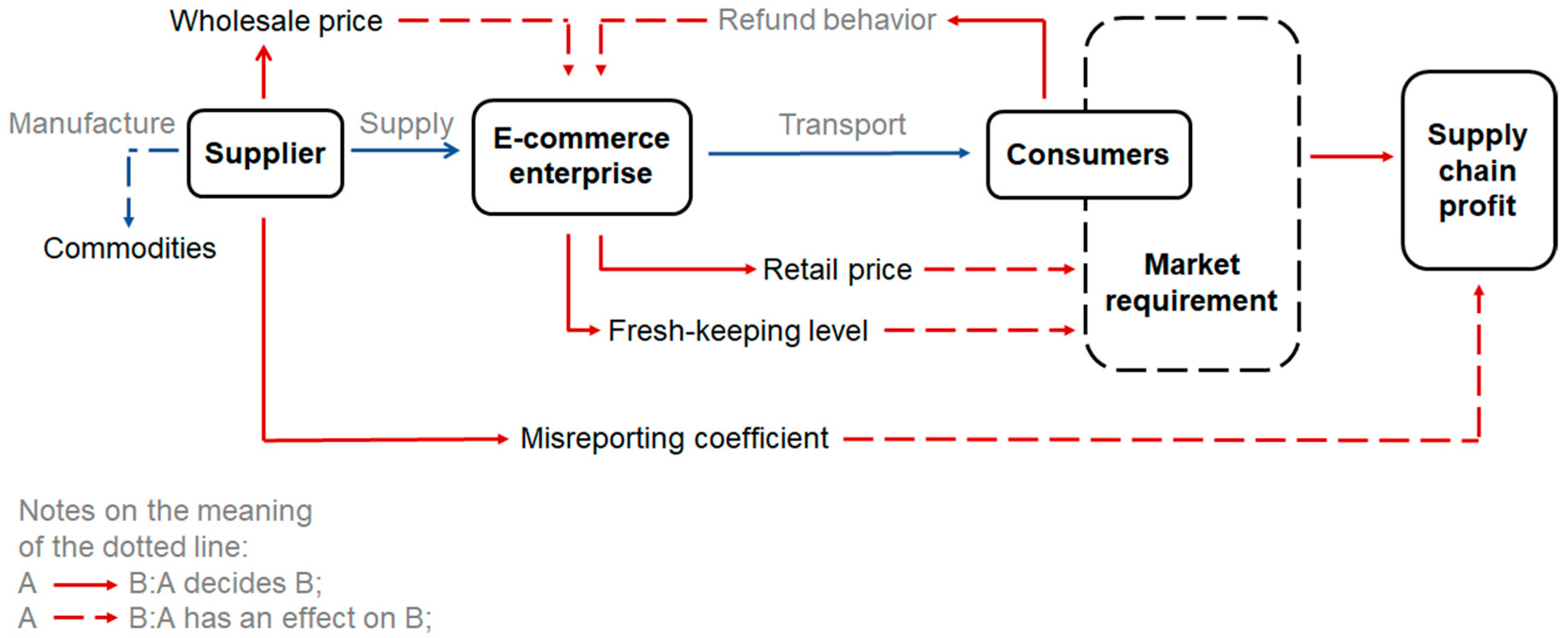
The purpose of this paper is to study the fresh supply chain composed of a single supplier and a single e-commerce enterprise, focusing on the misreporting strategy and the available coordination mechanism in the supply chain under the condition of cost information asymmetry. As shown in Figure 1, the fresh supply chain consists of two main participants: supplier and e-commerce enterprise.

Referring to Zeng et al. [36], it is assumed that the market demand of fresh commodities $Q$ is influenced by the dual influence of the retail price of commodities ($p$) and the fresh-keeping level ($g$): $Q=a-bp+fg$. Here, $a$ is the potential size of the market for fresh commodities, $b$ is the price sensitivity coefficient, and $f$ is the freshness sensitivity coefficient. The parameters $a$, $b$, and $f$ are constants greater than zero.

Fresh commodities are prone to deterioration in circulation, which in turn leads to after-sales problems for supply chain, so the after-sales rate of fresh commodities is also affected by the deterioration rate of fresh commodities, which in turn is negatively affected by fresh-keeping technology. Referring to Zhang et al.’s [14] study, $m=n-\beta g$, $n$ is the initial shipment loss rate of commodities, $\beta$ is the sensitivity coefficient of fresh-keeping technology, and $\beta >0$.

Due to the special characteristics of fresh commodities, almost all fresh commodities have no residual value after deterioration. It is assumed that consumers will apply for after-sales service when they receive deteriorating commodities, and the e-commerce platform will give consumers a certain after-sales compensation $k$ according to the deterioration of fresh commodities. Considering the positive impact of fresh-keeping level on the supply chain, e-commerce enterprise will invest costs to improve the fresh-keeping level of fresh commodities. Referring to the research of Chen et al. [36], when the fresh-keeping level is $g$, the cost to be invested is $c(g)={\displaystyle \frac{1}{2}}\epsilon g^2$, $\epsilon$ represents the fresh-keeping investment cost coefficient, and $\epsilon >0$.

The production cost of fresh commodities is complex, so the cost information of fresh commodities is often the private information of the supplier. When the supply chain information is opaque, the supplier may falsely report the production cost for personal gain. When the production cost of fresh commodities is $c$, the cost announced by the supplier (false cost) is $xc$, where $x$ is the misreporting coefficient and $x>0$. If $x=1$, then the supplier does not lie about the cost of commodity production. If $0<x<1$, then the supplier understates the production cost. If $x>1$, then the supplier overstates the production cost.

In summary, in the supply chain studied in this paper, the supplier determines the wholesale price $w$ and the cost misreporting coefficient $x$, and the e-commerce enterprise determines the market retail price $p$ and the fresh-keeping level $g$.

3. Supply Chain Decision Model

In this paper, five supply chain models are constructed, including one centralized decision-making model (CDM model), two decentralized decision-making models when information is transparent, and two decentralized decision-making models when information is opaque. The classification of decentralized decision-making models is shown in

Table 2. Supply chain decision-making model table.

	Supplier-First Decision (Supplier-Led)	E-Commerce-First Decision (E-Commerce-Led)
Information symmetry	AS model (Supplier-led under information symmetry)	AE model (E-commerce-led under information symmetry)
Information asymmetry	BS model (Supplier-led under information asymmetry)	BE model (Supplier-led under information asymmetry)

.

According to the Stackelberg game theory, the centralized decision-making model refers to the decision making of supply chain members with the optimal total profit of the supply chain as the goal; the decentralized decision-making model refers to that whereby the supply chain members make decisions according to their own status, and the decision-making goal is to maximize their own interests.

To facilitate the distinction, ${\Pi }_s$ represents the supplier’s profit; ${\Pi }_r$ represents e-commerce enterprise’s profit; ${\Pi }_c$ represents supply chain profit. When the information is asymmetric, the real profits of the supplier and the e-commerce enterprise and the profit disclosed by the supplier are

$${\Pi }_{s\left(BS/BE\right)}=\left(w-c\right)Q,$$

(1)

$${\Pi }_{r\left(BS/BE\right)}=\left(p-w\right)Q-{\displaystyle \frac{1}{2}}\epsilon g^2-mkQ,$$

(2)

$${\Omega }_{s\left(BS/BE\right)}=\left(w-xc\right)Q.$$

(3)

When the information is symmetrical, the profit functions of the supplier and the e-commerce enterprise are

$${\Pi }_{s\left(AS/AE\right)}=\left(w-c\right)Q,$$

(4)

$${\Pi }_{r\left(AS/AE\right)}=\left(p-w\right)Q-{\displaystyle \frac{1}{2}}\epsilon g^2-mkQ.$$

(5)

The total profit of the supply chain is equal to the sum of the real profit of the supplier and the real profit of the e-commerce enterprise.

3.1. BS Model

In the BS model, the supply chain information is opaque, so the supplier has a motive to misreport. At this point, the supplier as the leader first determines the misreporting coefficient $x$, and then determines the wholesale price $w$. The e-commerce enterprise as a follower then decides the retail price $p$.

According to Equation (2), we have

$${\displaystyle \frac{\partial {\Pi }_{r\left(BS\right)}}{\partial p_{\left(BS\right)}}}=a+f{g}_{\left(BS\right)}-b{p}_{\left(BS\right)}-b\left(p_{\left(BS\right)}-w_{\left(BS\right)}\right)+bk\left(n-\beta g_{\left(BS\right)}\right),$$

(6)

$${\displaystyle \frac{\partial {\Pi }_{r\left(BS\right)}}{\partial g_{\left(BS\right)}}}=f\left(p_{\left(BS\right)}-w_{\left(BS\right)}\right)-\epsilon g_{\left(BS\right)}-fk\left(n-\beta g_{\left(BS\right)}\right)+\beta k\left(a+f{g}_{\left(BS\right)}-b{p}_{\left(BS\right)}\right).$$

(7)

In the following discussion, we always suppose that the following condition (A), i.e., $2b\epsilon -2\beta bkr-f^2-{\beta }^2{b}^2{k}^2>0$, is satisfied. It is easily proved that the Hessian matrix of ${\Pi }_{r(BS)}$ over $p_{\left(BS\right)}$ and $g_{(BS)}$ is a negative definite matrix under condition (A). Then, a unique optimal solution $(p_{\left(BS\right)}^{\ast },g_{\left(BS\right)}^{\ast })$ for the e-commerce profit function ${\Pi }_{r\left(BS\right)}$ can be obtained by solving the equations ${\displaystyle \frac{\partial {\Pi }_{r\left(BS\right)}}{\partial p_{\left(BS\right)}}}=0$ and ${\displaystyle \frac{\partial {\Pi }_{r\left(BS\right)}}{\partial g_{\left(BS\right)}}}=0$.

Letting $B_1=-\epsilon bkn+\beta bfk{w}_{\left(BS\right)}+\beta bf{k}^{2}n$, we can obtain

$$p_{\left(BS\right)}^{\ast }={\displaystyle \frac{f^2{w}_{\left(BS\right)}-\epsilon a-\epsilon b{w}_{\left(BS\right)}+f^{2}kn+{\beta }^{2}ab{k}^2+\beta afk+B_1}{{\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2}},$$

(8)

$$g_{\left(BS\right)}^{\ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(b{w}_{\left(BS\right)}-a+bkn\right)}{{\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2}}.$$

(9)

Substituting Equations (8) and (9) into the supplier’s public profit function ${\Omega }_{s\left(BS\right)}$, the first- and second-order derivatives of $w_{(BS)}$ can be obtained as $2b\epsilon -2\beta bkf-f^2-{\beta }^2{b}^2{k}^2>0$, so ${\displaystyle \frac{{\partial }^2{\Pi }_{s\left(BS\right)}}{\partial w_{\left(BS\right)}^2}}<0$, and there exists an optimal solution for $w_{(BS)}$. Let ${\displaystyle \frac{\partial {\Pi }_{s\left(BS\right)}}{\partial w_{\left(BS\right)}}}=0$, then the optimal $w_{\left(BS\right)}^{\ast }$ can be obtained:

$$w_{\left(BS\right)}^{\ast }={\displaystyle \frac{a-bkn+bcx}{2b}}.$$

(10)

Substituting $w_{\left(BS\right)}^{\ast }$ into Equations (8) and (9), the optimal retail price $p_{\left(BS\right)}^{\ast }$ and the optimal fresh-keeping level $g_{\left(BS\right)}^{\ast }$ can be obtained in the BS model:

$$p_{\left(BS\right)}^{\ast }={\displaystyle \frac{2a{\beta }^2{b}^2{k}^2+n\beta b^{2}f{k}^2+cx\beta b^{2}fk+3a\beta bfk-\epsilon n{b}^{2}k-\epsilon cx{b}^2+B_2}{2b\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(11)

$$g_{\left(BS\right)}^{\ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(bkn-a+bcx\right)}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}}.$$

(12)

where $B_2=nb{f}^{2}k+cxb{f}^2-3\epsilon ab+a{f}^2$.

At this point, the supplier, the e-commerce enterprise, and the supply chain as a whole are optimally profitable, respectively:

$${\Pi }_{s\left(BS\right)}^{\ast }=-{\displaystyle \frac{\epsilon \left(a^2-2abc-2abkn-b^2{c}^2{x}^2+2b^2{c}^{2}x+2b^{2}ckn+b^2{k}^2{n}^2\right)}{4\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(13)

$${\Pi }_{r\left(BS\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bkn-a+bcx\right)}^2}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(14)

$${\Pi }_{c\left(BS\right)}^{\ast }=-{\displaystyle \frac{\epsilon \left(\begin{array}{l}3a^2-2abcx-4abc-6abkn-b^2{c}^2{x}^2\\ +4b^2{c}^{2}x+2b^{2}cknx+4b^{2}ckn+3b^2{k}^2{n}^2\end{array}\right)}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}}.$$

(15)

Proposition 1.

In the BS model, the supplier’s misreporting coefficient $x=1$.

Proof of Proposition 1.

It is obvious that ${\displaystyle \frac{{\partial }^2{\Pi }_{s\left(BS\right)}^{\ast }}{\partial x^2}}={\displaystyle \frac{\epsilon b^2{c}^2}{2{\beta }^2{b}^2{k}^2+4\beta bfk-4\epsilon b+2f^2}}<0$. Then, there exists an optimal misreporting coefficient $x$ that maximizes the supplier’s profit.

Let ${\displaystyle \frac{\partial {\Pi }_{s\left(BS\right)}^{\ast }}{\partial x}}=0$, then we can obtain $x_{\left(BS\right)}=1$. Therefore, Proposition 1 is proved. □

Remark 1.

According to Proposition 1, when the supply chain information is opaque and the supplier dominates the supply chain, the supplier will not misreport the cost information.

3.2. BE Model

In the BE model, the e-commerce enterprise, as the dominant player in the supply chain, prioritizes the decision on the retail price of the commodities $p_{(BE)}$ ($p_{\left(BE\right)}=w_{\left(BE\right)}+y$, $y$ denotes the profit of the commodities) and the fresh-keeping level $g_{(BE)}$. The supplier, as a follower, later decides on the wholesale price $w_{(BE)}$ and the misreporting coefficient $x$. However, in order to obtain higher profit, the supplier may take advantage of its information and misreport the information on the production cost of commodities.

The second-order derivative of ${\Omega }_{s\left(BE\right)}$ with respect to $w_{\left(BE\right)}$ is ${\displaystyle \frac{{\partial }^2{\Omega }_{r\left(BE\right)}}{\partial w_{\left(BE\right)}^2}}=-2b<0$. Then, ${\Omega }_{s\left(BE\right)}$ has an optimal solution. Letting ${\displaystyle \frac{\partial {\Omega }_{s\left(BE\right)}}{\partial w_{\left(BE\right)}}}=0$, the optimal solution (i.e., the optimal wholesale price) can be obtained as follows:

$$w_{\left(BE\right)}^{\ast }={\displaystyle \frac{a+f{g}_{\left(BE\right)}-by+bcx}{2b}}.$$

(16)

Substituting $w_{\left(BE\right)}^{\ast }$ into the e-commerce profit function ${\Pi }_{r\left(BE\right)}$, and calculating the first derivative of $y$ and $g_{\left(BE\right)}$, respectively, we can obtain

$${\displaystyle \frac{\partial {\Pi }_{r\left(BE\right)}}{\partial y}}={\displaystyle \frac{a+f{g}_{\left(BE\right)}-2by+bkn-bcx-\beta b{g}_{\left(BE\right)}k}{2}},$$

(17)

$${\displaystyle \frac{\partial {\Pi }_{r\left(BE\right)}}{\partial g_{\left(BE\right)}}}={\displaystyle \frac{fy-2\epsilon g_{\left(BE\right)}+\beta ak-fkn+2\beta f{g}_{\left(BE\right)}k-\beta bky-\beta bckx}{2}}.$$

(18)

The Hessian matrix of ${\Pi }_{r(BE)}$ with respect to $y$ and $g_{(BE)}$ is

$$H_{r(BE)}=\left[\begin{array}{cc}-b& {\displaystyle \frac{f-\beta bk}{2}}\\ {\displaystyle \frac{f-\beta bk}{2}}& \beta fk-\epsilon \end{array}\right].$$

Since $-b<0$, then if the condition (A) is satisfied, we know that the Hesse matrix $H_{r(BE)}$ is negative definite. Therefore, $y$ and $g_{(BE)}$ have unique optimal values. Letting ${\displaystyle \frac{\partial {\Pi }_{r\left(BE\right)}}{\partial y}}=0$ and ${\displaystyle \frac{\partial {\Pi }_{r\left(BE\right)}}{\partial g_{\left(BE\right)}}}=0$, we can obtain $y^{\ast }$, $g_{\left(BE\right)}^{\ast }$ as follows:

$$y^{\ast }={\displaystyle \frac{-cx{\beta }^2{b}^2{k}^2+a{\beta }^{2}b{k}^2+n\beta bf{k}^2-cx\beta bfk+a\beta fk+B_3}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}},$$

(19)

$$g_{\left(BE\right)}^{\ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(bkn-a+bcx\right)}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}}.$$

(20)

where $B_3=-2\epsilon nbk+2\epsilon cxb+n{f}^{2}k-2\epsilon a$, $B_4=-\epsilon bcx+\beta bf{k}^{2}n+\beta bcfkx$.

Substituting $y^{\ast }$ and $g_{\left(BE\right)}^{\ast }$ into Equation (16), $w_{\left(BE\right)}^{\ast }$ can be obtained:

$$w_{\left(BE\right)}^{\ast }={\displaystyle \frac{cx{\beta }^2{b}^2{k}^2+2cx\beta bfk+\epsilon nbk-3\epsilon cxb+cx{f}^2-\epsilon a}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}},$$

(21)

Because $p_{\left(BE\right)}=w_{\left(BE\right)}+y$, we can obtain

$$p_{\left(BE\right)}^{\ast }={\displaystyle \frac{f^{2}kn-3\epsilon a+c{f}^{2}x+{\beta }^{2}ab{k}^2+\beta afk-\epsilon bkn+B_4}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}}.$$

(22)

Supplier and e-commerce enterprise profits and total supply chain profit are maximized when the e-commerce enterprise optimal retail price is $p_{\left(BE\right)}^{\ast }$, the optimal fresh-keeping level is $g_{\left(BE\right)}^{\ast }$, and the supplier optimal wholesale price is $w_{\left(BE\right)}^{\ast }$, respectively:

$${\Pi }_{s\left(BE\right)}^{\ast }=-{\displaystyle \frac{\epsilon b{B}_5\left(\begin{array}{l}\epsilon a+c{f}^2-4\epsilon bc-c{f}^{2}x-\epsilon bkn+3\epsilon bcx+\\ {\beta }^2{b}^{2}c{k}^2+2\beta bcfk-{\beta }^2{b}^{2}c{k}^{2}x-2\beta bcfkx\end{array}\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}},$$

(23)

$${\Pi }_{r\left(BE\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bkn-a+bcx\right)}^2}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}},$$

(24)

$${\Pi }_{c\left(BE\right)}^{\ast }={\displaystyle \frac{\epsilon B_5\left(\begin{array}{l}a{f}^2-6\epsilon ab+8\epsilon b^{2}c-2bc{f}^2+6\epsilon b^{2}kn-2\epsilon b^{2}cx-b{f}^{2}kn\\ +bc{f}^{2}x+{\beta }^{2}a{b}^2{k}^2-2{\beta }^2{b}^{3}c{k}^2-{\beta }^2{b}^3{k}^{3}n-2\beta b^{2}f{k}^{2}n\\ +2\beta abfk+{\beta }^2{b}^{3}c{k}^{2}x-4\beta b^{2}cfk+2\beta b^{2}cfkx\end{array}\right)}{2{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}}.$$

(25)

where $B_5=bkn-a+bcx$.

Proposition 2.

In the BE model, the supplier’s misreporting coefficient $x_{\left(BE\right)}={\displaystyle \frac{\begin{array}{l}-n{\beta }^2{b}^3{k}^3+c{\beta }^2{b}^3{k}^2+a{\beta }^2{b}^2{k}^2-2n\beta b^{2}f{k}^2+2c\beta b^{2}fk\\ +2a\beta bfk+2\epsilon n{b}^{2}k-4\epsilon c{b}^2-nb{f}^{2}k+cb{f}^2-2\epsilon ab+a{f}^2\end{array}}{2bc\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}}\ne 1$.

Proof of Proposition 2.

Through direct calculation, we obtain

$${\displaystyle \frac{{\partial }^2{\Pi }_{s\left(BE\right)}^{\ast }}{\partial x^2}}={\displaystyle \frac{2\epsilon b^2{c}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}}<0.$$

Then, there exists an optimal misreporting coefficient $x$ that allows the supplier to maximize profit. Letting ${\displaystyle \frac{\partial {\Pi }_{s\left(BE\right)}^{\ast }}{\partial x}}=0$, we can obtain

$$x_{\left(BE\right)}={\displaystyle \frac{\begin{array}{l}-n{\beta }^2{b}^3{k}^3+c{\beta }^2{b}^3{k}^2+a{\beta }^2{b}^2{k}^2-2n\beta b^{2}f{k}^2+2c\beta b^{2}fk\\ +2a\beta bfk+2\epsilon n{b}^{2}k-4\epsilon c{b}^2-nb{f}^{2}k+cb{f}^2-2\epsilon ab+a{f}^2\end{array}}{2bc\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}}\ne 1.$$

Proposition 2 is proved. □

Remark 2.

It can be seen from Proposition 2 that when the supply chain information is opaque and the e-commerce enterprise dominates the supply chain, the supplier will misreport the cost information.

Proposition 3.

When the supplier’s misreporting coefficient is $x_{\left(BE\right)}$, substituting $x_{\left(BE\right)}$ into Equations (20)–(25), the optimal decision of the supply chain members when the supplier misreports is $\left(g_{\left(BE\right)}^{\ast \ast },p_{\left(BE\right)}^{\ast \ast },w_{\left(BE\right)}^{\ast \ast }\right)$, and the profits of the supplier, the e-commerce enterprise, and the overall supply chain are $\left({\Pi }_{s\left(BE\right)}^{\ast \ast },{\Pi }_{r\left(BE\right)}^{\ast \ast },{\Pi }_{c\left(BE\right)}^{\ast \ast }\right)$.

Among them,

$$w_{\left(BE\right)}^{\ast \ast }={\displaystyle \frac{a+bc-bkn}{2b}},$$

(26)

$$p_{\left(BE\right)}^{\ast \ast }={\displaystyle \frac{\begin{array}{l}2a{\beta }^2{b}^2{k}^2+n\beta b^{2}f{k}^2+c\beta b^{2}fk+3a\beta bfk\\ -\epsilon n{b}^{2}k-\epsilon c{b}^2+nb{f}^{2}k+cb{f}^2-5\epsilon ab+a{f}^2\end{array}}{2b\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}},$$

(27)

$$g_{\left(BE\right)}^{\ast \ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(bc-a+bkn\right)}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}},$$

(28)

$${\Pi }_{r\left(BE\right)}^{\ast \ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}{8{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}},$$

(29)

$${\Pi }_{s\left(BE\right)}^{\ast \ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2}{4\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}},$$

(30)

$${\Pi }_{c\left(BE\right)}^{\ast \ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2\left(3{\beta }^2{b}^2{k}^2+6\beta bfk-10\epsilon b+3f^2\right)}{8{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}.$$

(31)

3.3. AS Model

Proposition 4.

In the AS model, under information symmetry, there is no information gap in the supply chain and the supplier cannot misreport the cost information, so $x=1$. Substituting $x_{\left(AS\right)}=x_{\left(BS\right)}=1$ into Equations (8)–(13) yields the optimal decision without misreporting behavior under supplier dominance as well as the profits of each member and the supply chain as a whole as $\left(g_{\left(AS\right)}^{\ast },p_{\left(AS\right)}^{\ast },w_{\left(AS\right)}^{\ast }\right)$, $\left({\Pi }_{s\left(AE\right)}^{\ast },{\Pi }_{r\left(AE\right)}^{\ast },{\Pi }_{c\left(AE\right)}^{\ast }\right)$, respectively.

Among them,

$$w_{\left(AS\right)}^{\ast }={\displaystyle \frac{a+bc-bkn}{2b}},$$

(32)

$$p_{\left(AS\right)}^{\ast }={\displaystyle \frac{\begin{array}{l}2a{\beta }^2{b}^2{k}^2+n\beta b^{2}f{k}^2+c\beta b^{2}fk+3a\beta bfk\\ -\epsilon n{b}^{2}k-\epsilon c{b}^2+nb{f}^{2}k+cb{f}^2-3\epsilon ab+a{f}^2\end{array}}{2b\left({\beta }^2{b}^2{k}^2-2\epsilon b+2\beta bfk+f^2\right)}},$$

(33)

$$g_{\left(AS\right)}^{\ast }={\displaystyle \frac{\left(\beta bk+f\right)\left(bc-a+bkn\right)}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(34)

$${\Pi }_{r\left(AS\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(35)

$${\Pi }_{s\left(AS\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2}{4\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}},$$

(36)

$${\Pi }_{c\left(AS\right)}^{\ast }=-{\displaystyle \frac{3\epsilon {\left(bc-a+bkn\right)}^2}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}}.$$

(37)

3.4. AE Model

Proposition 5.

In the AE model, when the e-commerce enterprise dominates the supply chain decision, when the supplier misreporting coefficient $x_{\left(AE\right)}=1$, substituting it into Equations (20)–(25), the optimal decision of the supply chain members without misreporting is $\left(g_{\left(AE\right)}^{\ast },p_{\left(AE\right)}^{\ast },w_{\left(AE\right)}^{\ast }\right)$, and the profits of the supplier, the e-commerce enterprise, and the overall supply chain are $\left({\Pi }_{s\left(AE\right)}^{\ast },{\Pi }_{r\left(AE\right)}^{\ast },{\Pi }_{c\left(AE\right)}^{\ast }\right)$. Let $B_6=-\epsilon bkn+\beta bcfk+\beta bf{k}^{2}n$. Then, we have

$$w_{\left(AE\right)}^{\ast }={\displaystyle \frac{c{\beta }^2{b}^2{k}^2+2c\beta bfk+\epsilon nbk-3\epsilon cb+c{f}^2-\epsilon a}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}},$$

(38)

$$p_{\left(AE\right)}^{\ast }={\displaystyle \frac{c{f}^2-3\epsilon a-\epsilon bc+f^{2}kn+{\beta }^{2}ab{k}^2+\beta afk+B_6}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}},$$

(39)

$$g_{\left(AE\right)}^{\ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(bc-a+bkn\right)}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}},$$

(40)

$${\Pi }_{r\left(AE\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}},$$

(41)

$${\Pi }_{s\left(AE\right)}^{\ast }={\displaystyle \frac{{\epsilon }^{2}b{\left(bc-a+bkn\right)}^2}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}},$$

(42)

$${\Pi }_{c\left(AE\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-6\epsilon b+f^2\right)}{2{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}}.$$

(43)

3.5. CDM Model

The CDM model is a centralized decision-making model in which the information in the supply chain is completely symmetric and the overall profit function of the supply chain is

$${\Pi }_{c\left(SC\right)}=\left(p_{\left(SC\right)}-c\right)Q-{\displaystyle \frac{1}{2}}\epsilon {g_{\left(SC\right)}}^2-mkQ.$$

(44)

The first-order partial derivatives of ${\Pi }_{c(SC)}$ with respect to the retail price $p_{\left(SC\right)}$ and the fresh-keeping level $g_{\left(SC\right)}$ are as follows:

$${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}}{\partial p_{\left(SC\right)}}}=a+f{g}_{\left(SC\right)}-b{p}_{\left(SC\right)}+b\left(c-p_{\left(SC\right)}\right)+bk\left(n-\beta g_{\left(SC\right)}\right),$$

(45)

$${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}}{\partial g_{\left(SC\right)}}}=\beta k\left(a+f{g}_{\left(SC\right)}-b{p}_{\left(SC\right)}\right)-f\left(c-p_{\left(SC\right)}\right)-fk\left(n-\beta g_{\left(SC\right)}\right)-\epsilon g_{\left(SC\right)}$$

(46)

Further, one obtains the Hessian matrix of ${\Pi }_{c(SC)}$ with respect to $p_{(SC)}$ and $g_{(SC)}$ as follows:

$$H_{c(SC)}=\left[\begin{array}{cc}-2b& f-\beta bk\\ f-\beta bk& 2\beta fk-\epsilon \end{array}\right].$$

Since $-2b<0$, then if the condition (A) is satisfied, we know that the Hesse matrix $H_{c(SC)}$ is negative definite. Therefore, ${\Pi }_{c\left(SC\right)}$ is a joint concave function with respect to $p_{(SC)}$ and $g_{(SC)}$. There exists a unique optimal value for $p_{(SC)}$ and $g_{(SC)}$. The joint equations ${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}}{\partial p_{\left(SC\right)}}}=0$ and ${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}}{\partial g_{\left(SC\right)}}}=0$ lead to the optimal solution:

$$p_{\left(SC\right)}^{\ast }={\displaystyle \frac{c{f}^2-\epsilon a-\epsilon bc+f^{2}kn+{\beta }^{2}ab{k}^2+\beta afk+B_7}{{\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2}},$$

(47)

$$g_{\left(SC\right)}^{\ast }={\displaystyle \frac{\left(f+\beta bk\right)\left(bc-a+bkn\right)}{{\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2}}.$$

(48)

where $B_7=-\epsilon bkn+\beta bcfk+\beta bf{k}^2$.

In the centralized decision-making model, the supply chain profit is optimal when the retail price of the commodities is $p_{(SC)}^{\ast }$ and the fresh-keeping level is $g_{(SC)}^{\ast }$. The total profit of the supply chain is

$${\Pi }_{c\left(SC\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2}{2\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}}.$$

(49)

3.6. Comparison and Analysis of Decision Models

Proposition 6.

${\Pi }_{s\left(AE\right)}^{\ast }<{\Pi }_{s\left(BE\right)}^{\ast \ast }$, ${\Pi }_{r\left(BE\right)}^{\ast \ast }<{\Pi }_{r\left(AE\right)}^{\ast }$, $g_{\left(AE\right)}^{\ast }>g_{\left(BE\right)}^{\ast \ast }$, ${\Pi }_{c\left(BE\right)}^{\ast \ast }<{\Pi }_{c\left(AE\right)}^{\ast }$.

Proof of Proposition 6.

Through direct calculation, we obtain

$$\begin{array}{l}{\Pi }_{s\left(AE\right)}^{\ast }-{\Pi }_{s\left(BE\right)}^{\ast \ast }={\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}{4\left({\beta }^2{b}^2{k}^2-3\epsilon b+2\beta bfk+f^2\right){\left({\beta }^2{b}^2{k}^2-4\epsilon b+2\beta bfk+f^2\right)}^2}}<0,\\ {\displaystyle \frac{{\Pi }_{r\left(BE\right)}^{\ast \ast }}{{\Pi }_{r\left(AE\right)}^{\ast }}}={\displaystyle \frac{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)\left(2{\beta }^2{b}^2{k}^2+4\beta bfk-8\epsilon b+2f^2\right)}{8{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}<1,\\ {\displaystyle \frac{g_{\left(AE\right)}^{\ast }}{g_{\left(BE\right)}^{\ast \ast }}}={\displaystyle \frac{2{\beta }^2{b}^2{k}^2+4\beta bfk-6\epsilon b+2f^2}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}}>1,\\ x_{\left(BE\right)}-1=-{\displaystyle \frac{\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}{2bc\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}}>0,\\ {\Pi }_{c\left(BE\right)}^{\ast \ast }-{\Pi }_{c\left(AE\right)}^{\ast }=-{\displaystyle \frac{{\epsilon }^{2}b{\left(bc-a+bkn\right)}^2\left(2{\beta }^2{b}^2{k}^2+4\beta bfk-7\epsilon b+2f^2\right)}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right){\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}<0.\end{array}$$

Proposition 2 is proved. □

Remark 3.

It can be seen from Proposition 6 that supplier misreporting is not conducive to the sustainable development of the supply chain, which is mainly reflected in the decline in supply chain profit and e-commerce profit, and the decline in the commodity fresh-keeping level.

Proposition 7.

${\Pi }_{s\left(AS\right)}^{\ast }>{\Pi }_{r\left(AS\right)}^{\ast }$, ${\Pi }_{s\left(AE\right)}^{\ast }<{\Pi }_{r\left(AE\right)}^{\ast }$, ${\Pi }_{s\left(BE\right)}^{\ast \ast }>{\Pi }_{r\left(BE\right)}^{\ast \ast }$, ${\Pi }_{s\left(BE\right)}^{\ast \ast }<{\Pi }_{s\left(AS/BS\right)}^{\ast }$.

Proof of Proposition 7.

Through direct calculation, we obtain

$$\begin{array}{l}{\displaystyle \frac{{\Pi }_{s\left(AS\right)}^{\ast }}{{\Pi }_{r\left(AS\right)}^{\ast }}}=2>1,\\ {\Pi }_{r\left(AE\right)}^{\ast }-{\Pi }_{s\left(AE\right)}^{\ast }={\displaystyle \frac{\epsilon {(bc-a+bkn)}^2(2b\epsilon -{\beta }^2{b}^2{c}^2-2\beta bcf-f^2)}{2{(4b\epsilon -{\beta }^2{b}^2{k}^2-2\beta bcf-f^2)}^2}}>0,\\ {\Pi }_{r\left(BE\right)}^{\ast \ast }-{\Pi }_{s\left(BE\right)}^{\ast \ast }={\displaystyle \frac{\beta {\left(bc-a+bkn\right)}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}{8{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}<0,\\ {\displaystyle \frac{{\Pi }_{s\left(BE\right)}^{\ast \ast }}{{\Pi }_{s\left(AS/BS\right)}^{\ast }}}={\displaystyle \frac{{\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2}{{\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2}}<1.\end{array}$$

Proposition 7 is proved. □

Remark 4.

Proposition 7 shows that when the supply chain information is transparent, the leader’s profit is higher than that of the follower; when the supply chain information is opaque and the supplier has a false report, the profit of the e-commerce enterprise as the leader is lower than that of the supplier.

Proposition 8.

$g_{\left(SC\right)}^{\ast }>g_{\left(AS/BS\right)}^{\ast }>g_{\left(AE\right)}^{\ast }>g_{\left(BE\right)}^{\ast \ast }$, $p_{\left(SC\right)}^{\ast }<p_{\left(AS/BS\right)}^{\ast }<p_{\left(BE\right)}^{\ast \ast }$, ${\Pi }_{c\left(AS/BS\right)}^{\ast }<{\Pi }_{c\left(SC\right)}^{\ast }$, ${\Pi }_{c\left(BE\right)}^{\ast \ast }<{\Pi }_{c\left(AE\right)}^{\ast }<{\Pi }_{c\left(SC\right)}^{\ast }$.

Proof of Proposition 8.

It holds when ${\beta }^2{b}^2{k}^2+2\beta bfk+f^2-\epsilon b<0$.

Let $B_8=-5\epsilon b\left({\beta }^2{b}^2{k}^2+2\beta bfk+f^2-\epsilon b\right)$. Through direct calculation, we obtain

$$\begin{array}{l}\{\begin{array}{l}{\displaystyle \frac{g_{\left(SC\right)}^{\ast }}{g_{\left(AS/BS\right)}^{\ast }}}=2>1\\ {\displaystyle \frac{g_{\left(AS/BS\right)}^{\ast }}{g_{\left(AE\right)}^{\ast }}}={\displaystyle \frac{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}{2{\beta }^2{b}^2{k}^2+4\beta bfk-4\epsilon b+2f^2}}>1\\ {\displaystyle \frac{g_{\left(AE\right)}^{\ast }}{g_{\left(BE\right)}^{\ast \ast }}}={\displaystyle \frac{2{\beta }^2{b}^2{k}^2+4\beta bfk-6\epsilon b+2f^2}{{\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2}}>1\end{array},\\ \{\begin{array}{l}{p}_{\left(SC\right)}^{\ast }-p_{\left(AS/BS\right)}^{\ast }={\displaystyle \frac{\left(f^2+\beta bkf-\epsilon b\right)\left(bc-a+bkn\right)}{2b\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}}<0\\ p_{\left(AS/BS\right)}^{\ast }-p_{\left(BE\right)}^{\ast \ast }=-{\displaystyle \frac{\epsilon \left(f^2+\beta bkf-\epsilon b\right)\left(bc-a+bkn\right)}{2\left({\beta }^4{b}^4{k}^4+4{\beta }^3{b}^{3}f{k}^3+6{\beta }^2{b}^2{f}^2{k}^2+4\beta b{f}^{3}k+f^4+{\epsilon }^2{b}^2+B_8\right)}}<0\end{array},\\ {\Pi }_{c\left(SC\right)}^{\ast }-{\Pi }_{c\left(AS/BS\right)}^{\ast }=-{\displaystyle \frac{\epsilon {\left(bc-a+bkn\right)}^2{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right){\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}>0,\\ \{\begin{array}{l}{\displaystyle \frac{{\Pi }_{c\left(AE\right)}^{\ast }}{{\Pi }_{c\left(SC\right)}^{\ast }}}={\displaystyle \frac{3}{4}}<1\\ {\Pi }_{c\left(BE\right)}^{\ast \ast }-{\Pi }_{c\left(AE\right)}^{\ast }=-{\displaystyle \frac{{\epsilon }^{2}b{\left(bc-a+bkn\right)}^2\left(2{\beta }^2{b}^2{k}^2+4\beta bfk-7\epsilon b+2f^2\right)}{8\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right){\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^2}}<0\end{array}\end{array}$$

Proposition 8 is proved. □

Remark 5.

Proposition 8 shows that the centralized decision-making model has the highest commodity fresh-keeping level and the lowest retail price, while the BE decision-making model has the lowest commodity fresh-keeping level and the highest retail price. In addition, the total profit of the supply chain under the centralized decision-making model is greater than that under the four decentralized decision-making models.

3.7. Sensitivity Analysis of $f$ and $\beta$

Proposition 9.

${\displaystyle \frac{\partial g_{\left(SC\right)}^{\ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}^{\ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial g_{\left(AS/BS\right)}^{\ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(AS/BS\right)}^{\ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial g_{\left(BE\right)}^{\ast \ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(BE\right)}^{\ast \ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial g_{\left(AE\right)}^{\ast }}{\partial f}}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(AE\right)}^{\ast }}{\partial f}}>0$.

Proof of Proposition 9.

Since $g_{\left(AS\right)}^{\ast }>0$, combined with $2b\epsilon -2\beta bkr-f^2-{\beta }^2{b}^2{k}^2>0$, it follows that $bc-a+bkn>0$ when $3{\beta }^2{b}^2{k}^2+6\beta bfk-11\epsilon b+3f^2<0$; we have

$$\begin{array}{l}{\displaystyle \frac{\partial g_{\left(SC\right)}^{\ast }}{\partial f}}=-{\displaystyle \frac{\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+2\beta bfk+2\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}^{\ast }}{\partial f}}={\displaystyle \frac{\epsilon \left(f+\beta bk\right){\left(bc-a+bkn\right)}^2}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial g_{\left(AS/BS\right)}^{\ast }}{\partial f}}=-{\displaystyle \frac{\left(bc-a+bkn\right)\left(2\epsilon b+{\beta }^2{b}^2{k}^2+2\beta bfk+f^2\right)}{2{\left({\beta }^2{b}^2{k}^2-2\epsilon b+2\beta bfk+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(AS/BS\right)}^{\ast }}{\partial f}}={\displaystyle \frac{3\epsilon \left(f+\beta bk\right){\left(bc-a+bkn\right)}^2}{4{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial g_{\left(BE\right)}^{\ast \ast }}{\partial f}}=-{\displaystyle \frac{\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+3\epsilon b+2\beta bfk+f^2\right)}{2{\left({\beta }^2{b}^2{k}^2-3\epsilon b+2\beta bfk+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(BE\right)}^{\ast \ast }}{\partial f}}={\displaystyle \frac{\epsilon \left(f+\beta bk\right){\left(bc-a+bkn\right)}^2\left(3{\beta }^2{b}^2{k}^2+6\beta bfk-11\epsilon b+3f^2\right)}{4{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^3}}>0,\\ {\displaystyle \frac{\partial g_{\left(AE\right)}^{\ast }}{\partial f}}=-{\displaystyle \frac{\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+2\beta bfk+4\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(AE\right)}^{\ast }}{\partial f}}={\displaystyle \frac{\epsilon \left(f+\beta bk\right){\left(bc-a+bkn\right)}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-8\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^3}}>0.\end{array}$$

Proposition 9 is proved. □

Remark 6.

Proposition 9 shows that under the five decision-making models, the fresh-keeping level of fresh commodities and the total profit of the supply chain are directly proportional to the sensitivity coefficient of consumers to the freshness of commodities.

Proposition 10.

${\displaystyle \frac{\partial g_{\left(SC\right)}^{\ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}^{\ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial g_{\left(AS/BS\right)}^{\ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(AS/BS\right)}^{\ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial g_{\left(BE\right)}^{\ast \ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(BE\right)}^{\ast \ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial g_{\left(AE\right)}^{\ast }}{\partial \beta }}>0$, ${\displaystyle \frac{\partial {\Pi }_{c\left(AE\right)}^{\ast }}{\partial \beta }}>0$.

Proof of Proposition 10.

When $3{\beta }^2{b}^2{k}^2+6\beta bfk-11\epsilon b+3f^2<0$, we can obtain

$$\begin{array}{l}{\displaystyle \frac{\partial g_{\left(SC\right)}^{\ast }}{\partial \beta }}=-{\displaystyle \frac{bk\left(bc-a+bkn\right)\left(2\epsilon b+2\beta bfk+{\beta }^2{b}^2{k}^2+f^2\right)}{{\left({\beta }^2{b}^2{k}^2-2\epsilon b+2\beta bfk+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(SC\right)}^{\ast }}{\partial \beta }}={\displaystyle \frac{\epsilon bk\left(f+\beta bk\right){\left(bc-a+bkn\right)}^2}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial g_{\left(AS/BS\right)}^{\ast }}{\partial \beta }}=-{\displaystyle \frac{bk\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+2\beta bfk+2\epsilon b+f^2\right)}{2{\left({\beta }^2{b}^2{k}^2-2\epsilon b+2\beta bfk+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(AS/BS\right)}^{\ast }}{\partial \beta }}={\displaystyle \frac{3\epsilon bk\left(f+\beta bk\right){\left(bc-a+bkn\right)}^2}{4{\left({\beta }^2{b}^2{k}^2+2\beta bfk-2\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial g_{\left(BE\right)}^{\ast \ast }}{\partial \beta }}=-{\displaystyle \frac{bk\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+3\epsilon b+2\beta bfk+f^2\right)}{2{\left({\beta }^2{b}^2{k}^2-3\epsilon b+2\beta bfk+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(BE\right)}^{\ast \ast }}{\partial \beta }}={\displaystyle \frac{\epsilon bk\left(f+\beta bk\right){\left(bc-a+bkn\right)}^2\left(3{\beta }^2{b}^2{k}^2+6\beta bfk-11\epsilon b+3f^2\right)}{4{\left({\beta }^2{b}^2{k}^2+2\beta bfk-3\epsilon b+f^2\right)}^3}}>0,\\ {\displaystyle \frac{\partial g_{\left(AE\right)}^{\ast }}{\partial \beta }}=-{\displaystyle \frac{bk\left(bc-a+bkn\right)\left({\beta }^2{b}^2{k}^2+2\beta bfk+4\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^2}}>0,\\ {\displaystyle \frac{\partial {\Pi }_{c\left(AE\right)}^{\ast }}{\partial \beta }}={\displaystyle \frac{\epsilon bk\left(f+\beta bk\right){\left(bc-a+bkn\right)}^2\left({\beta }^2{b}^2{k}^2+2\beta bfk-8\epsilon b+f^2\right)}{{\left({\beta }^2{b}^2{k}^2+2\beta bfk-4\epsilon b+f^2\right)}^3}}>0.\end{array}$$

Proposition 10 is proved. □

Remark 7.

Proposition 10 shows that the level of fresh-keeping of commodities and the total profit of the supply chain under the five decision-making models gradually increase as the sensitivity coefficient of fresh-keeping technology of fresh commodities increases.

4. Construction and Analysis of Supply Chain Contract Model

4.1. Supply Chain Combination Contract Model

When supply chain members adopt decentralized decision-making, the supply chain cannot achieve optimal performance. At this time, the supplier’s misreporting will further aggravate the imbalance of the supply chain. In this paper, the “cost sharing + revenue sharing + wholesale price discount” combination contract is used to coordinate the fresh supply chain (taking the AS model as an example): Considering the important impact of freshness of fresh commodities on fresh supply chain performance, the supplier gives the e-commerce enterprise a discounted wholesale price while also helping the e-commerce enterprise to share part of the input cost of improving the fresh-keeping level, with a sharing ratio of $1-\theta (0<\theta <1)$; in return, the e-commerce enterprise shares part of the revenue to the supplier, with a sharing ratio of $1-\phi (0<\phi <1)$.

The profit function of each member under this combination contract is, respectively,

$${\Pi }_{s\left(C\right)}=(w_{\left(C\right)}-c)Q+(1-\phi )p_{\left(C\right)}Q-{\displaystyle \frac{1}{2}}(1-\theta )\epsilon g_{\left(C\right)}^2,$$

(50)

$${\Pi }_{r\left(C\right)}=(\phi p_{\left(C\right)}-w_{\left(C\right)})Q-{\displaystyle \frac{1}{2}}\theta \epsilon g_{\left(C\right)}^2-mkQ.$$

(51)

Similar to solving the optimal decision in the decentralized decision-making model, the inverse inductive solution method is adopted. First, we find the first-order partial derivatives for $p_{(C)}$ and $g_{(C)}$:

$${\displaystyle \frac{\partial {\Pi }_{r\left(C\right)}}{\partial p_{\left(C\right)}}}=b\left(w-\phi p_{\left(C\right)}\right)+\phi \left(a+f{g}_{\left(C\right)}-b{p}_{\left(C\right)}\right)+bk\left(n-\beta g_{\left(C\right)}\right),$$

(52)

$${\displaystyle \frac{\partial {\Pi }_{r\left(C\right)}}{\partial g_{\left(C\right)}}}=\beta k\left(a+f{g}_{\left(C\right)}-b{p}_{\left(C\right)}\right)-fk\left(n-\beta g_{\left(C\right)}\right)-f\left(w_{\left(C\right)}-\phi p_{\left(C\right)}\right)-\epsilon \theta g_{\left(C\right)}.$$

(53)

The Hessian matrix of ${\Pi }_{r(C)}$ can be obtained as follows:

$$H_{r(C)}=\left[\begin{array}{cc}-2\phi b& \phi f-\beta bk\\ \phi f-\beta bk& 2\beta kf-\theta \epsilon \end{array}\right].$$

Since $-2\phi b<0$, the Hessian matrix is negative definite when its second-order principal subequation $2\phi \theta b\epsilon -2\phi \beta bkf-{\phi }^2{f}^2-{\beta }^2{b}^2{k}^2>0$. At this point, ${\Pi }_{r(C)}$ is a joint concave function of $p_{(C)}$ and $g_{(C)}$. There exists a unique optimal solution for $p_{(C)}$ and $g_{(C)}$. Letting ${\displaystyle \frac{\partial {\Pi }_{r\left(C\right)}}{\partial p_{\left(C\right)}}}=0$ and ${\displaystyle \frac{\partial {\Pi }_{r\left(C\right)}}{\partial g_{\left(C\right)}}}=0$, we obtain

$$p_{\left(C\right)}^{\ast }={\displaystyle \frac{\begin{array}{l}\phi f^2{w}_{\left(C\right)}+\phi f^{2}kn+{\beta }^{2}ab{k}^2-\epsilon \theta \phi a-\epsilon \theta b{w}_{\left(C\right)}\\ +\beta \phi afk-\epsilon \theta bkn+\beta bfk{w}_{\left(C\right)}+\beta bf{k}^{2}n\end{array}}{{\beta }^2{b}^2{k}^2+2\beta \phi bfk+{\phi }^2{f}^2-2\epsilon \theta \phi b}},$$

(54)

$$g_{\left(C\right)}^{\ast }={\displaystyle \frac{\left(\phi f+\beta bk\right)\left(b{w}_{\left(C\right)}-\phi a+bkn\right)}{{\beta }^2{b}^2{k}^2+2\beta \phi bfk+{\phi }^2{f}^2-2\epsilon \theta \phi b}}.$$

(55)

Here, $w_{\left(C\right)}$ is the adjustment variable. When the supplier preferentially decides the wholesale price $w_{(C)}$, if the retail price and fresh-keeping level of the commodities decided by the e-commerce enterprise are $p_{(C)}^{\ast }$ and $g_{(C)}^{\ast }$, respectively, the profits of the supplier and the e-commerce enterprise will reach the maximum.

4.2. Coordination and Improvement of the Contract Model

In the combination contract, the existence of $\phi$ and $\theta$ fulfilling certain conditions can bring the supply chain into coordination. At this time, the following conditions must be met:$p_{\left(C\right)}^{\ast }=p_{\left(SC\right)}^{\ast }$, $g_{\left(C\right)}^{\ast }=g_{\left(SC\right)}^{\ast }$. At this time, the total supply chain profit under the contract is also equal to the total supply chain profit under the centralized decision-making model. The joint contract parameters $(w,\phi ,\theta )$ can be obtained by combining Equations (47), (48), (54) and (55). If the contract parameters meet the following conditions, the overall profit of the supply chain can be optimized:

$$\{\begin{array}{c}\phi =-{\displaystyle \frac{b\left(w_{\left(CS\right)}+kn-\beta g_{\left(SC\right)}^{\ast }k\right)}{a+f{g}_{\left(SC\right)}^{\ast }-2b{p}_{\left(SC\right)}^{\ast }}}\\ \theta =-{\displaystyle \frac{\left(a+f{g}_{\left(SC\right)}^{\ast }-b{p}_{\left(SC\right)}^{\ast }\right)\left(f{w}_{\left(CS\right)}-\beta ak+fkn-2\beta f{g}_{\left(SC\right)}^{\ast }k+2\beta bk{p}_{\left(SC\right)}^{\ast }\right)}{\epsilon g_{\left(SC\right)}^{\ast }\left(a+f{g}_{\left(SC\right)}^{\ast }-2b{p}_{\left(SC\right)}^{\ast }\right)}}\end{array},$$

(56)

Taking the AS/BS model as an example, if the profit of each supply chain member can be optimized (i.e., ${\Pi }_{s\left(C\right)}^{\ast }>{\Pi }_{s\left(AS/BS\right)}^{\ast }$, ${\Pi }_{r\left(C\right)}^{\ast }>{\Pi }_{r\left(AS/BS\right)}^{\ast }$) under the coordination of a joint contract, it means that the contract can achieve Pareto improvement. The joint inequality yields the following range of values for the adjustment variable $w_{\left(C\right)}$:

$${\displaystyle \frac{-(A_6+A_7+2{\Pi }_{r\left(AS/BS\right)}^{\ast }f{g}_{\left(SC\right)}^{\ast })}{A_5}}<w_{\left(C\right)}<{\displaystyle \frac{2A_1({\Pi }_{s\left(AS/BS\right)}^{\ast }+c{A}_2-A_3-A_4)}{A_5}},$$

where

• $A_1=a+f{g}_{\left(SC\right)}^{\ast }-2b{p}_{\left(SC\right)}^{\ast }$, $A_2=a+f{g}_{\left(SC\right)}^{\ast }-b{p}_{\left(SC\right)}^{\ast }$,
• $A_3={\displaystyle \frac{p_{\left(SC\right)}^{\ast }\left(A_4+bkn-\beta b{g}_{\left(SC\right)}^{\ast }k\right)A_5}{A_4}}$,
• $A_4={\displaystyle \frac{k\epsilon {g_{\left(SC\right)}^{\ast }}^2{A}_5\left(\beta a-fn+2\beta f{g}_{\left(SC\right)}^{\ast }-2\beta b{p}_{\left(SC\right)}^{\ast }\right)}{2\epsilon g_{\left(SC\right)}^{\ast }{A}_1}}-{\displaystyle \frac{1}{2}}\epsilon {g_{\left(SC\right)}^{\ast }}^2$,
• $A_5=2a^2-4ab{p}_{\left(SC\right)}^{\ast }+3af{g}_{\left(SC\right)}^{\ast }+2b^2{p_{\left(SC\right)}^{\ast }}^2-3bf{g}_{\left(SC\right)}^{\ast }{p}_{\left(SC\right)}^{\ast }+f^2{g_{\left(SC\right)}^{\ast }}^2$,
• $A_6=-\beta k{a}^2{g}_{\left(SC\right)}^{\ast }+2kn{a}^2+\beta kab{g}_{\left(SC\right)}^{\ast }{p}_{\left(SC\right)}^{\ast }-4knab{p}_{\left(SC\right)}^{\ast }-\beta kaf{g_{\left(SC\right)}^{\ast }}^2$,
• $A_7=3knaf{g}_{\left(SC\right)}^{\ast }+2{\Pi }_{r\left(AS/BS\right)}^{\ast }a+2kn{b}^2{p_{\left(SC\right)}^{\ast }}^2-3knbf{g}_{\left(SC\right)}^{\ast }{p}_{\left(SC\right)}^{\ast }-4{\Pi }_{r\left(AS/BS\right)}^{\ast }b{p}_{\left(SC\right)}^{\ast }+kn{f}^2{g_{\left(SC\right)}^{\ast }}^2$.

5. Example Analysis

To further validate the conclusions mentioned above, this section presents a simulation example that conforms to the actual market situation of the fresh supply chain. Reference [17], which details parameter settings in fresh supply chain research, along with the aforementioned assumptions, serves as a reference for the parameter settings in

Table 3. Selection of example values.

Symbol	$\mathit{a}$	$\mathit{c}$	$\mathit{b}$	$\mathit{\epsilon }$	$\mathit{k}$	$\mathit{f}$	$\mathit{\beta }$	$\mathit{n}$
Value	100	10	0.5	100	12	0.8	0.1	0.1

of this paper.

5.1. Model Comparison

According to

Table 4. Supply chain model decision results and profit value table.

Model	${\mathit{p}}^{\ast }$	${\mathit{f}}^{\ast }$	${\Pi }_{\mathbf{s}}^{\ast }$	${\Pi }_{\mathbf{r}}^{\ast }$	${\Pi }_{\mathbf{c}}^{\ast }$
AS/BS model	152.9348	0.6740	2272.3786	1136.1893	3408.5679
AE model	153.6968	0.6673	1136.0780	2249.8889	3385.9669
BE model	168.8309	0.4464	1504.8906	1006.5810	2511.4717
CDM model	105.8696	1.3480	——	——	4544.7572

, we can draw the following points:

(1) Under the centralized decision-making model, the total supply chain profit is better than the total supply chain profit under several decentralized decision-making models. This is because the decentralized decision-making model reduces the overall efficiency of the supply chain due to the bilateral effect. Specifically, in the centralized decision-making model, both supplier and e-commerce enterprise make decisions together to maximize the profit of the supply chain system. The final decision result is to improve the fresh-keeping level and reduce the retail price. This will enhance the commodity quality and reduce quality loss, thereby reducing consumer after-sales behavior, increasing market demand, and ultimately achieving the optimization of total supply chain profit.

(2) The total supply chain profit in the BE model is much lower than that in the AE model. This is because in the BE model, the supplier employs a strategy of misreporting cost, resulting in higher retail prices for commodity. Higher retail prices diminish market demand, thereby adversely impacting the overall supply chain performance. Further comparison shows that compared with the AE model, the supplier profit in the BE model increases, but the e-commerce enterprise profit decreases. This indicates that manufacturer misreporting is detrimental to other supply chain members but advantageous to itself.

(3) Observing the profits of each supply chain member in the AS/BS and AE models, it can be found that the supply chain dominator always has higher profit than its followers due to its decision-making priority. Specifically, when there is no misreporting in the supply chain, the dominator can make more profits. However, in the BE model, the supplier profit as a decision follower is higher than the e-commerce enterprise profit. This is because when there is information asymmetry, the supplier obtains a large portion of the gains through misreporting, resulting in its profit being higher than the dominator’s profit.

Based on the above research conclusions, the following management implications can be obtained:

When the supply chain information is symmetrical, members should prioritize maximizing the overall interests of the supply chain as the common goal and adopt centralized decision-making whenever feasible. While this approach optimizes the supply chain’s overall profit, it does not necessarily optimize individual gains. Nonetheless, supply chain members can ensure they benefit from centralized decision making through various forms of interest transfer. When the supply chain information is asymmetric, the supplier has an information advantage. If the e-commerce enterprise dominates the supply chain, the supplier may misreport cost information for its own benefit, thereby harming the overall profits of the e-commerce enterprise and the supply chain. In such case, the e-commerce enterprise should proactively communicate and cooperate with the supplier to break information barriers. For example, both parties can establish an information disclosure mechanism, achieve the information visualization, and foster an open and fair trading environment to mitigate supply chain information asymmetry.

5.2. Sensitivity Analysis of $\beta$ and $f$

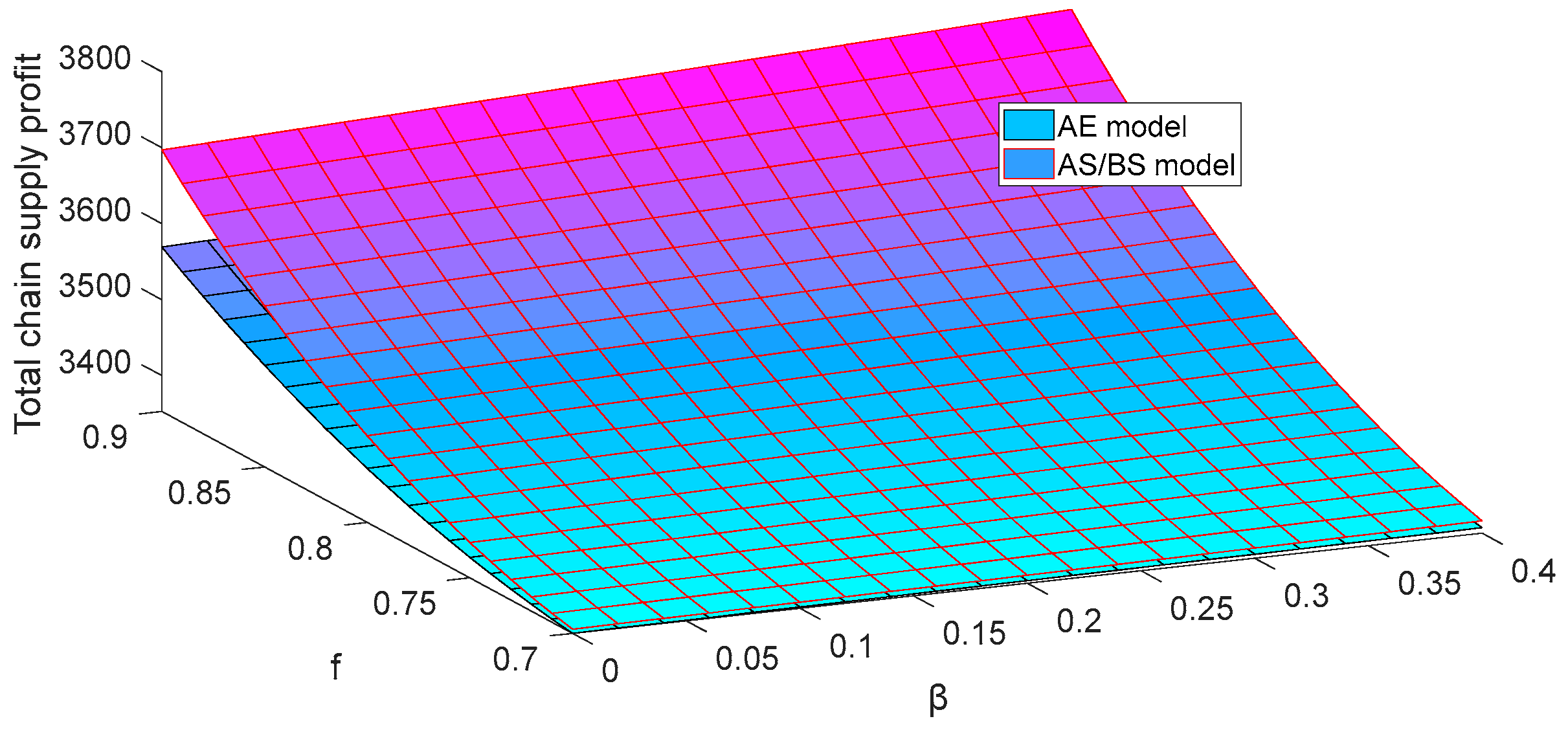
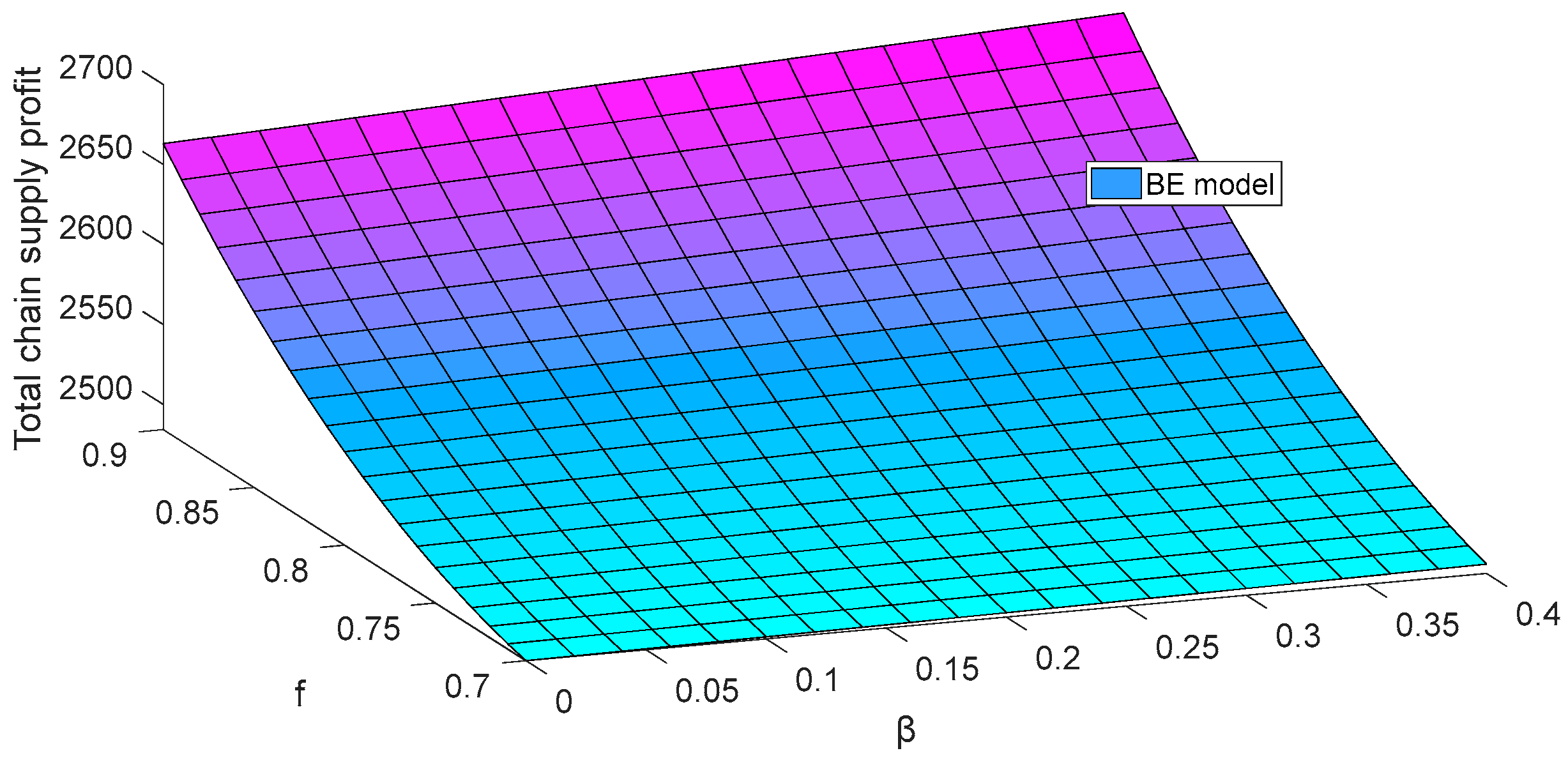
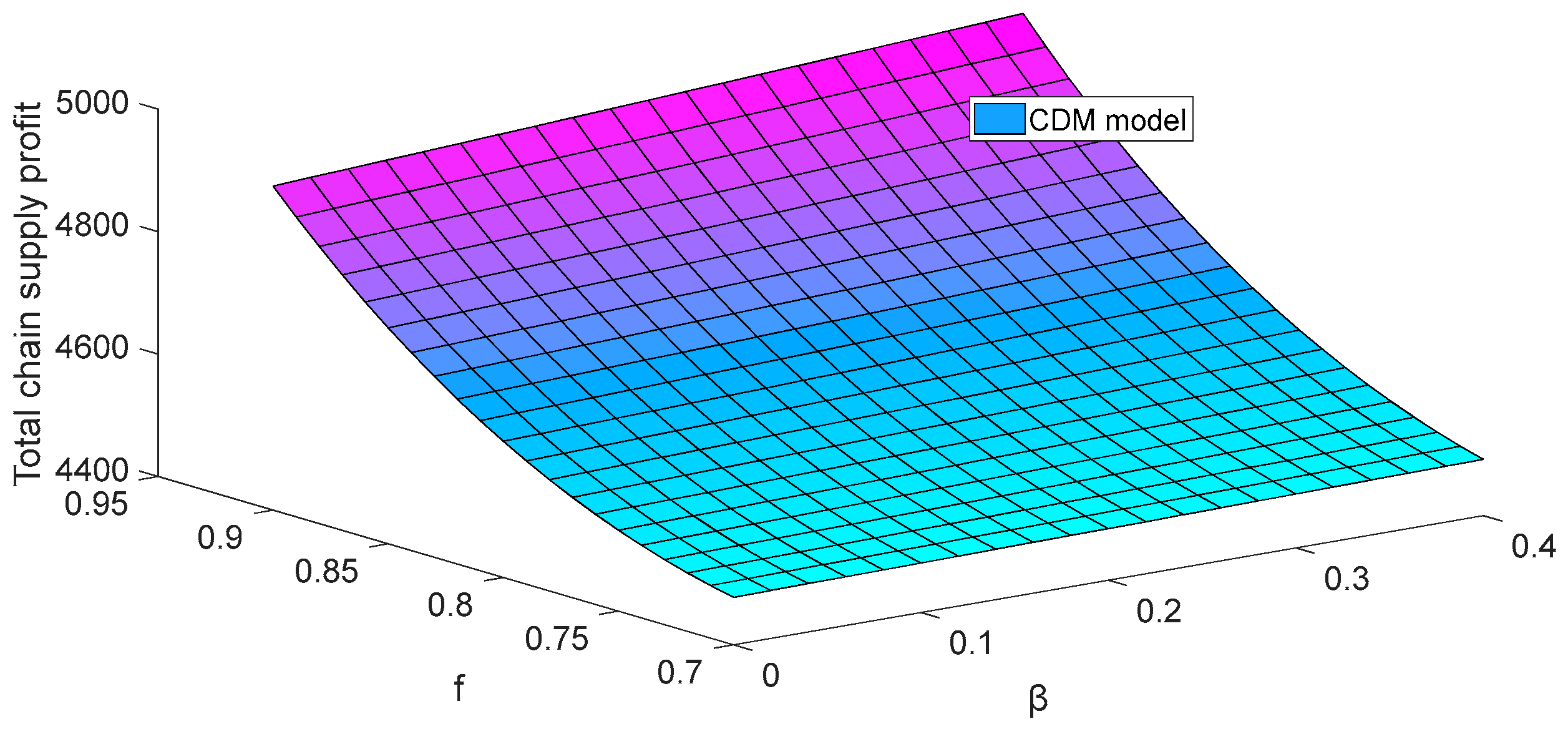
In order to explore the influence of fresh-keeping technology sensitivity coefficient $\beta$ and freshness sensitivity coefficient $f$ on the total supply chain profit, Figure 2, Figure 3 and Figure 4 are drawn.

As can be seen from Figure 2, Figure 3 and Figure 4, with the increase in $\beta$ and $f$, the total supply chain profits in the decentralized model and the centralized model are both on the rise.

The main reasons why the sensitivity coefficient of fresh-keeping technology has a positive impact on the supply chain are as follows: On the one hand, as $\beta$ increases, the deterioration rate and after-sales rate of commodities decrease, resulting in reduced supply chain loss. On the other hand, the higher the value of $\beta$ is, the more pronounced the fresh-keeping effect of fresh-keeping technology becomes, encouraging supply chain members to enhance the fresh-keeping level. This improvement boosts market demand and increases supply chain profit.

The main reasons why the freshness sensitivity coefficient $f$ has a positive impact on the supply chain are as follows: With the growing consumer preference for freshness in fresh commodities, e-commerce enterprise will increase its investment in fresh-keeping technology to meet the market demands. This will reduce commodities loss due to deterioration, decrease the after-sales rate, and minimize supply chain loss. Additionally, as consumers are more willing to purchase commodities with higher freshness, the market demand will increase with the improved freshness, leading to an increase in the total supply chain profit.

When optimizing the fresh commodities supply chain, managers should prioritize consumers’ preference for freshness. Simultaneously, they should increase investment in fresh-keeping technology to enhance commodity quality and mitigate deterioration and loss during transportation.

5.3. Misreporting Coefficient Analysis

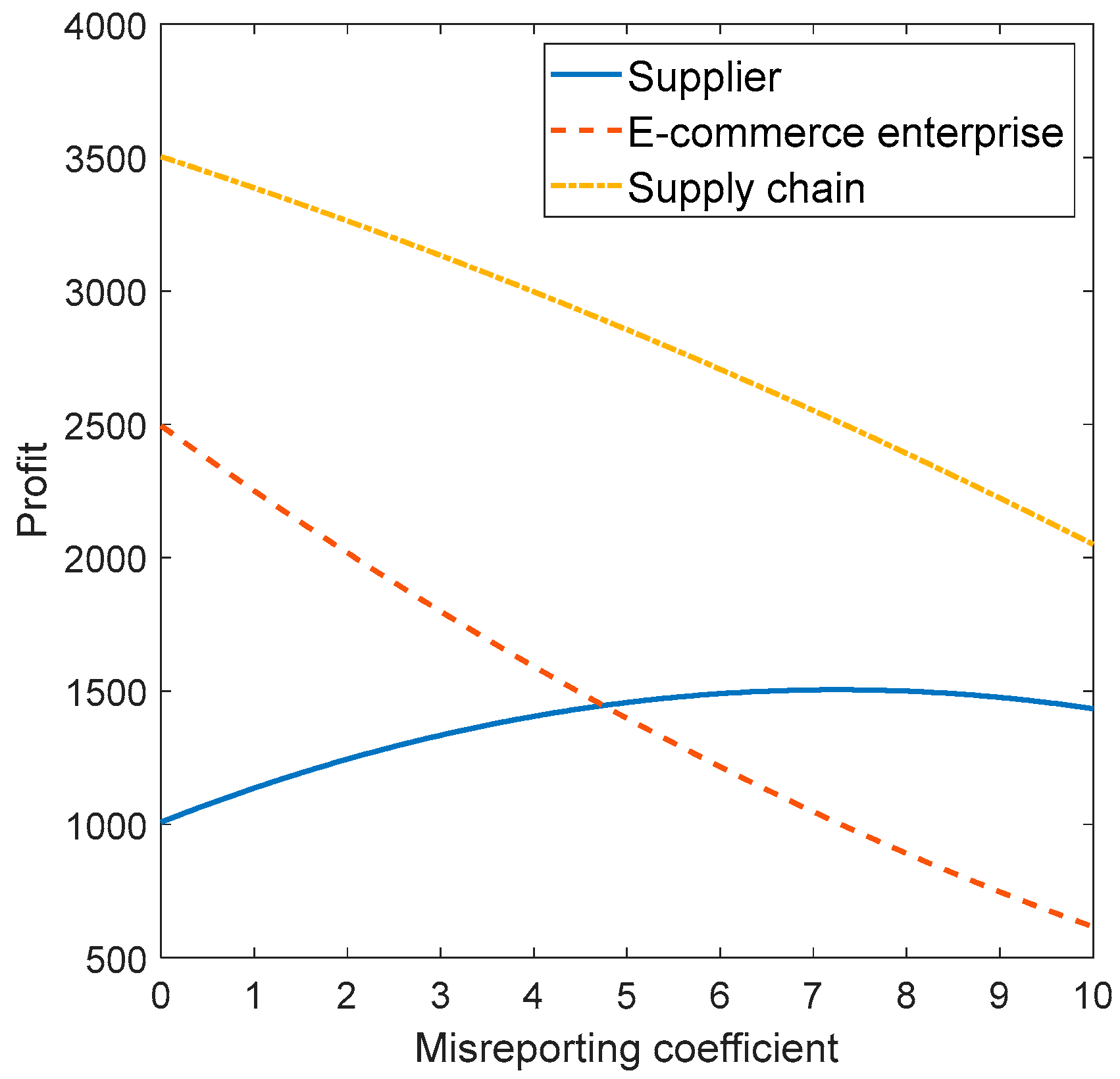
In the BE model, the supplier will engage in misreporting. Figure 5 shows the impact of the misreporting coefficient on the profit of all parties in the supply chain.

Observing Figure 5, the supplier’s optimal misreporting strategy is $x=7.2$; at this time, the supplier’s profit is optimal. By comparing the e-commerce enterprise profit and the total supply chain profit when $x=1$ (the supplier does not misreport) and $x=7.2$, it can be found that the supplier’s optimal misreporting strategy will reduce the overall profit of the e-commerce enterprise and the supply chain. When $x<1$, the supplier understates the cost, the e-commerce enterprise profit, and the total supply chain profit increase, but the supplier’s profit decreases. Consequently, the supplier will not understate the cost.

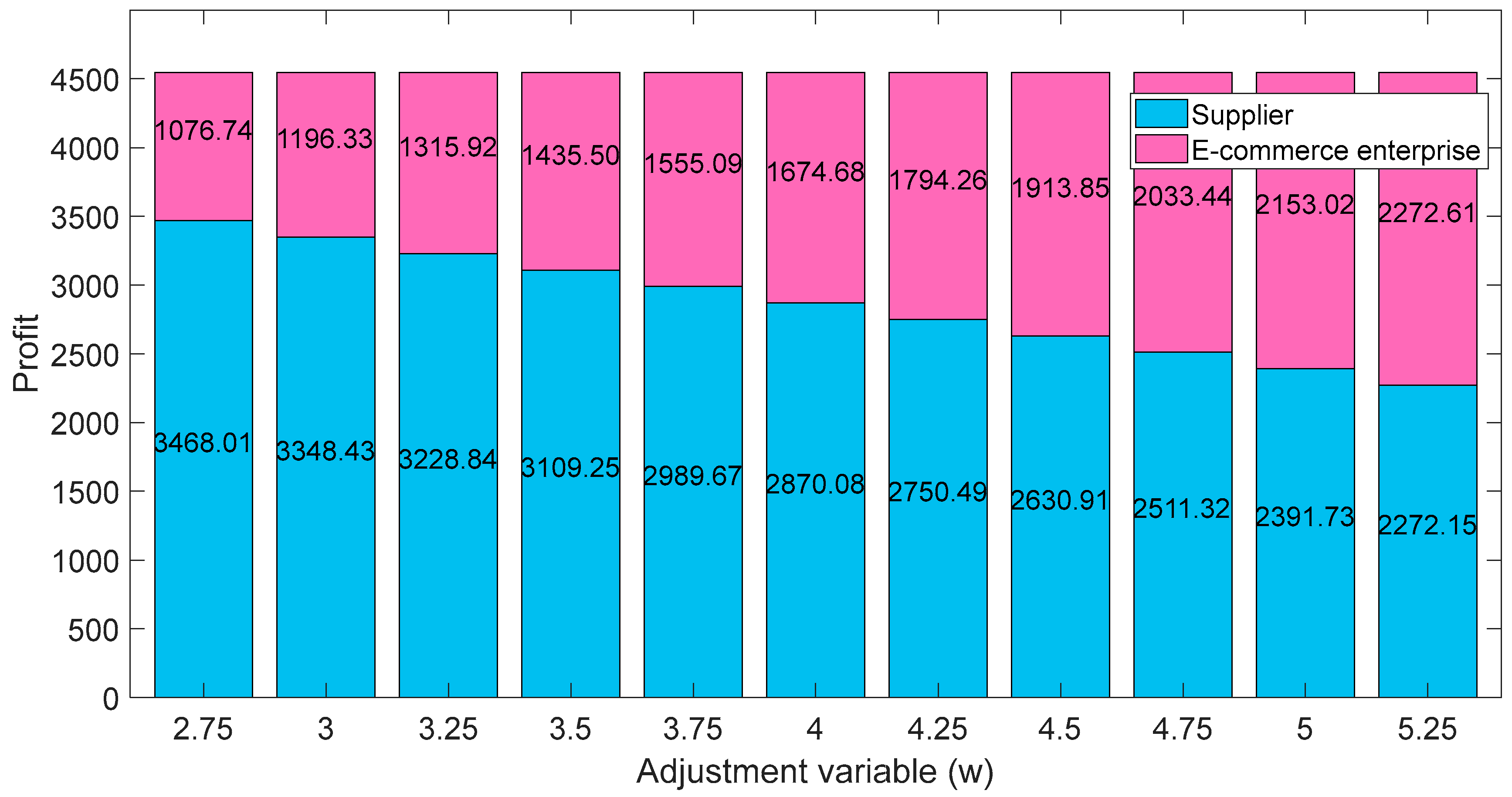
5.4. Parameter Analysis of Contract

According to the set parameter values, under the coordination of the combined contract, the fluctuation range of the adjustment variable is [2.8742, 5.2495]. Within this range, the profits of each supply chain member are higher than their respective profits before contract coordination, that is, the contract is valid. Figure 6 verifies the validity of the contract.

Observing Figure 6, when the adjustment variable fluctuates within the interval [2.8742, 5.2495], the profits of supplier and e-commerce enterprise are higher than their respective profits before coordination (reference value: ${\Pi }_{s(AS)}^{\ast }=2272.3786$, ${\Pi }_{r(AS)}^{\ast }=1136.1893$). If $w=2.75$, the profit of e-commerce enterprise is lower than that before coordination, that is, the coordination is not successful. If $w=5.25$, then the supplier’s profit is lower than the pre-coordination profit, that is, the coordination is also unsuccessful. In addition, the change in the adjustment variable does not affect the total profit of the supply chain under contract coordination.

6. Conclusions

Based on the influence of fresh-keeping level on the after-sales rate and market demand of fresh commodities, this paper constructs five supply chain decision models considering information asymmetry and power structure, and uses Stackelberg knowledge to solve the optimal decision and profit of each member under different decision-making models. Through the analysis, the following conclusions are obtained:

(1) Under information asymmetry, the supplier will not misreport cost information if the supplier dominates the supply chain; if e-commerce enterprise dominates the supply chain, the supplier will overstate costs. This misreporting behavior will damage the profits of e-commerce enterprise and the whole supply chain.

(2) Compared with decentralized decision making, the overall supply chain profit, the retail price, and the fresh-keeping level under centralized decision making are better. In a decentralized decision-making model, the decisions led by the supplier are superior to those led by the retailer. This superiority is evident in the higher fresh-keeping level, lower retail price, and increased total supply chain profit.

(3) Under information symmetry, the profit of the supply chain leader is higher than that of its followers. Under information asymmetry, when the e-commerce enterprise is the leader, its profit is lower than the supplier.

(4) Under different supply chain models, the fresh-keeping level and total profit are positively correlated with the sensitivity coefficients of consumer freshness and fresh-keeping technology.

In addition, aiming at the supplier’s misreporting behavior under asymmetric information, this paper introduces a joint contract of “cost sharing + revenue sharing + wholesale price discount” to coordinate the supply chain under the decentralized model, so that the supply chain profit can achieve Pareto optimal improvement.

According to the aforementioned research findings, this paper offers decision-making recommendations for supply chain stakeholders in various scenarios. For instance, under conditions of symmetrical information, centralized decision making is advisable. However, in situations where centralized decision making is not feasible, allowing the supplier to lead the supply chain proves more advantageous. In cases of asymmetric information, the retailer should diligently monitor and prevent supplier misreporting only when it has the advantage of decision making. While this study’s results and recommendations provide theoretical reference for the harmonized advancement of the fresh supply chain, it still has some limitations. For example, the results of this paper are only applicable to the supply chain of a single-channel e-commerce model. Therefore, it is necessary to further consider the coordination of multichannel fresh supply chains in future research.