Connectedness of Carbon Price and Energy Price under Shocks: A Study Based on Positive and Negative Price Volatility
Abstract
1. Introduction
2. Literature Review
3. Pre-Analysis of the Connectedness Mechanism
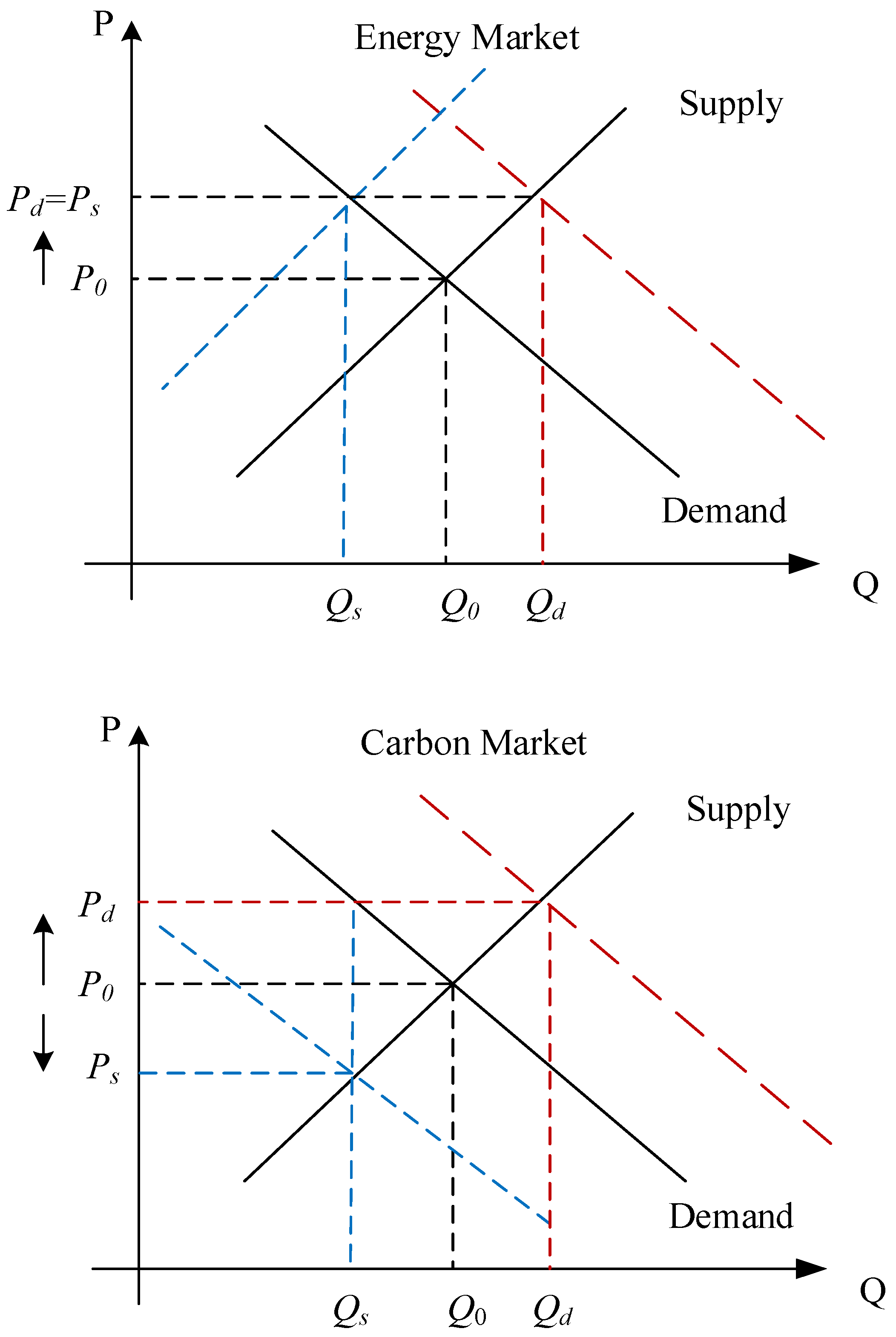
3.1. Supply and Demand Mechanism
3.2. Common Risk Exposure
3.3. Price Elasticity Analysis
3.4. Brief Summary
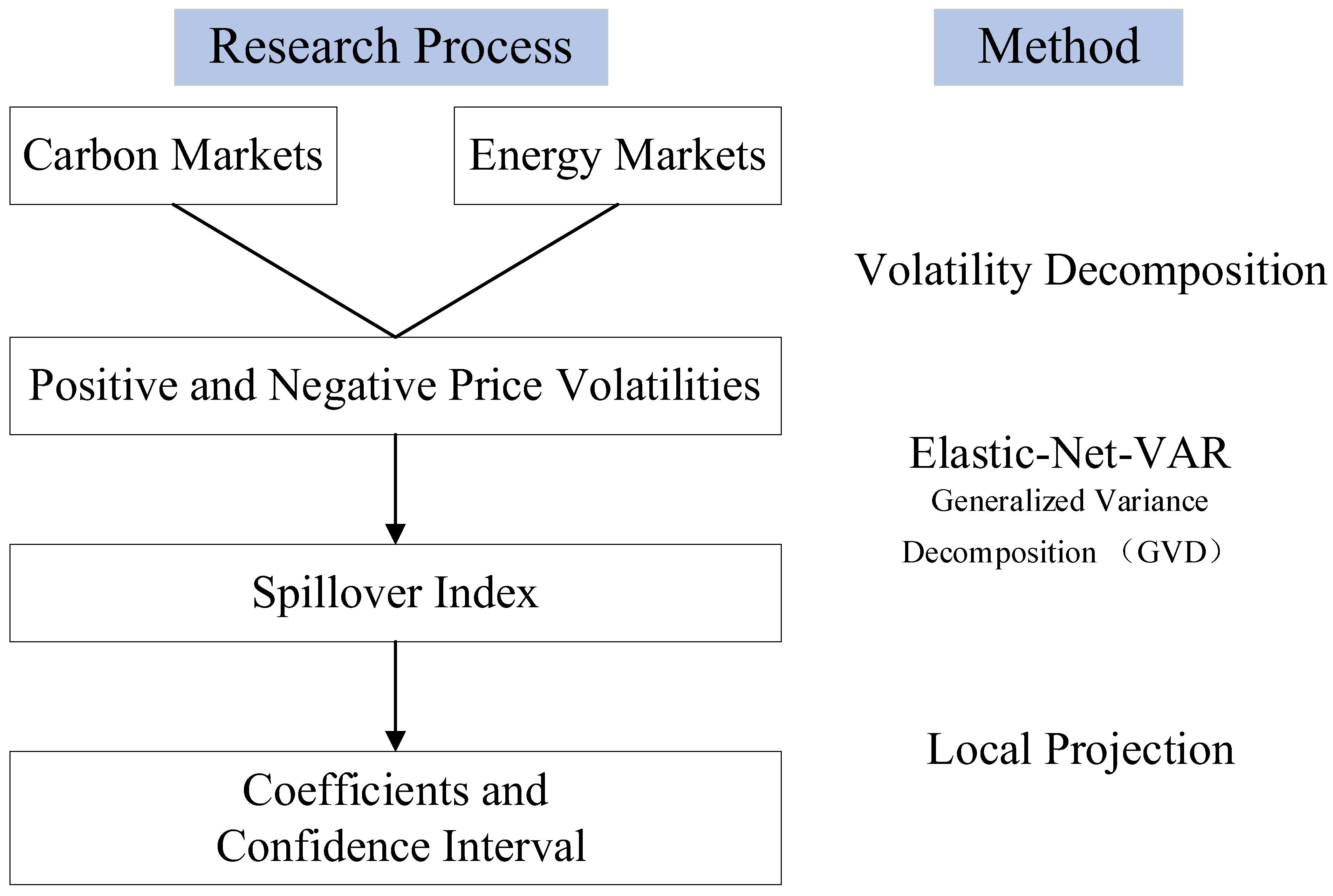
4. Methods and Data Description
4.1. Realized Semi-Variance
4.2. Elastic-Net-VAR Model
4.3. Spillover Effect Analysis Based on Elastic-Net-VAR Model
4.4. Local Projection
4.5. Data
5. Results
5.1. Full Sample Static Spillover Analysis
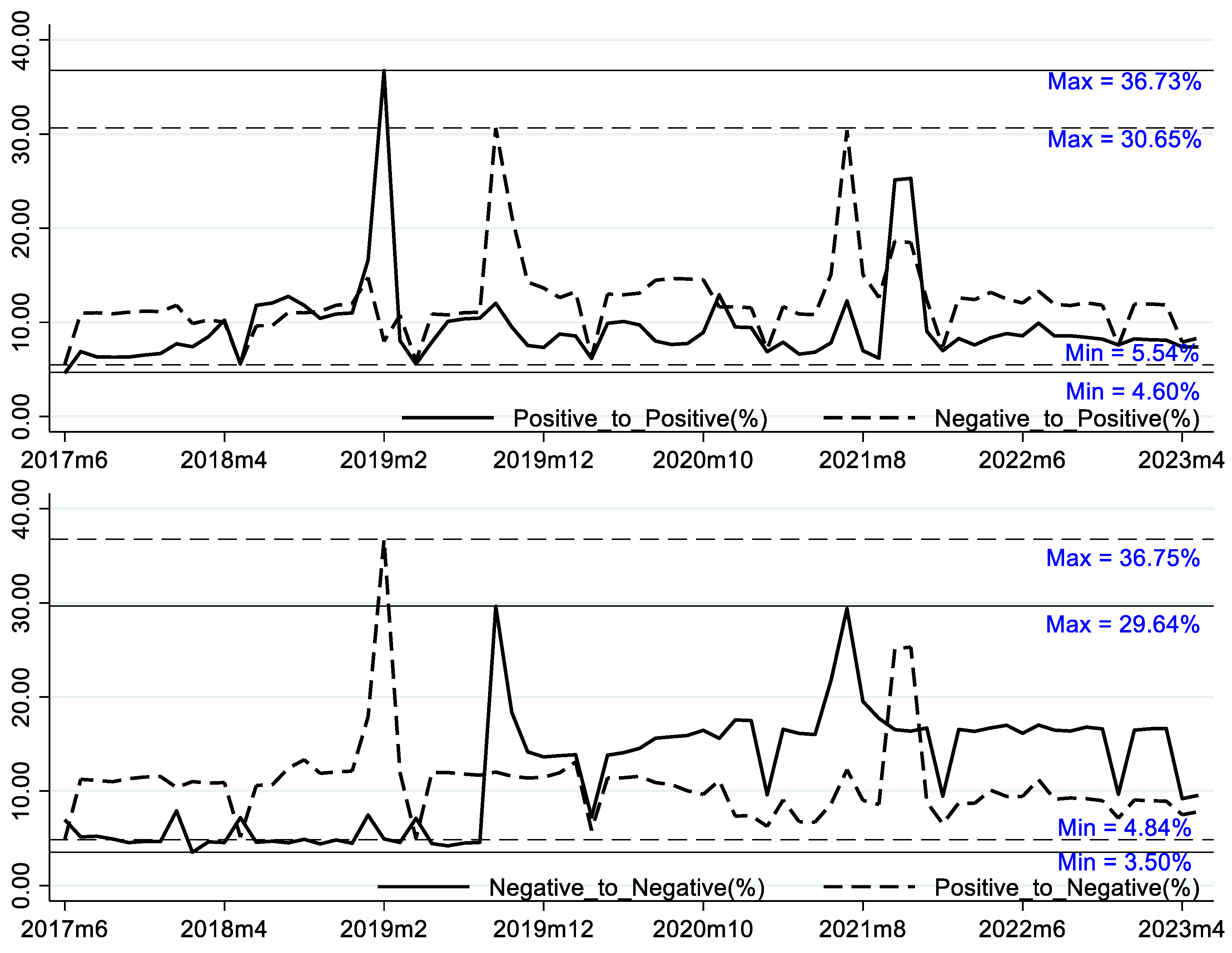
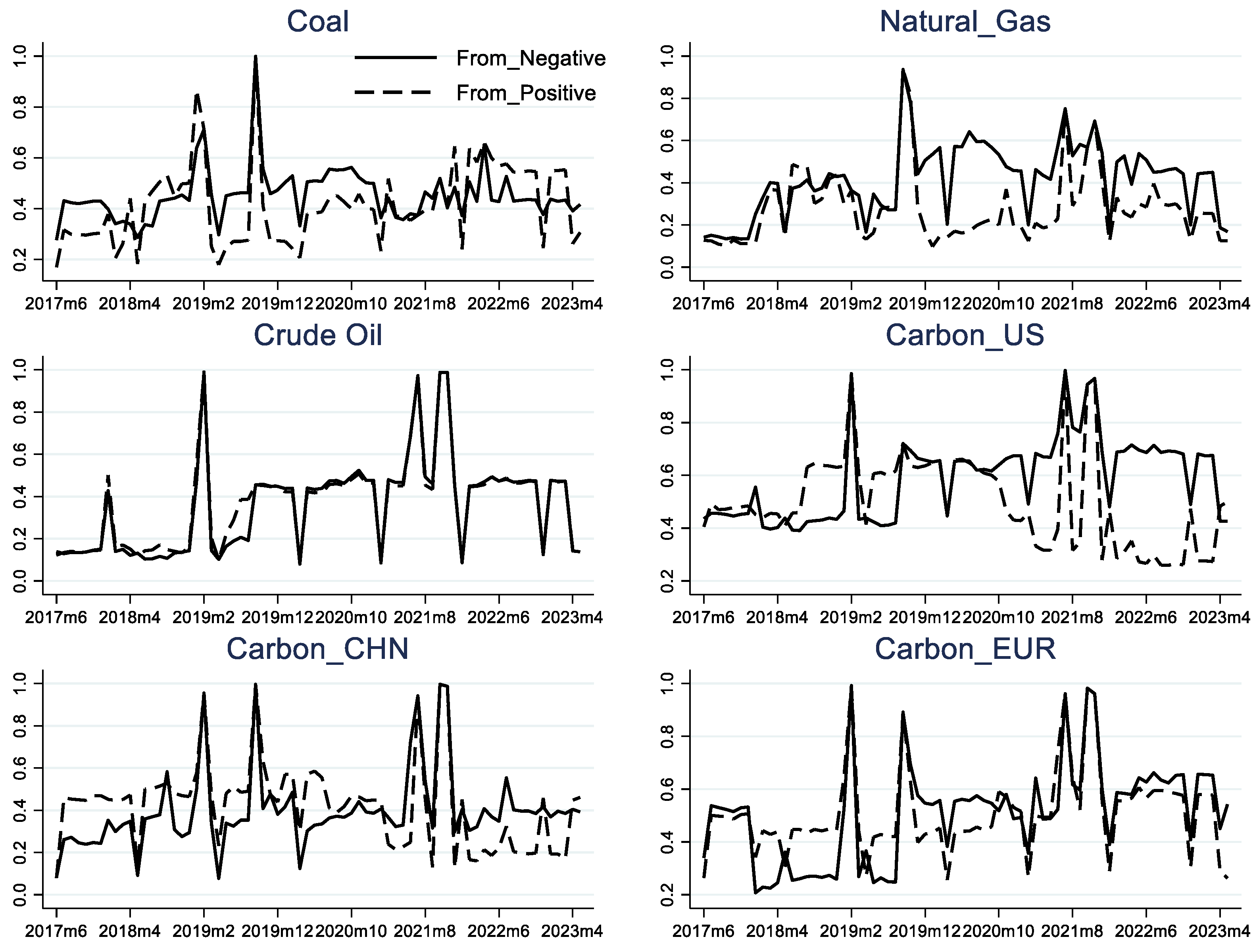
5.2. Dynamic Spillover Analysis of Rolling Samples
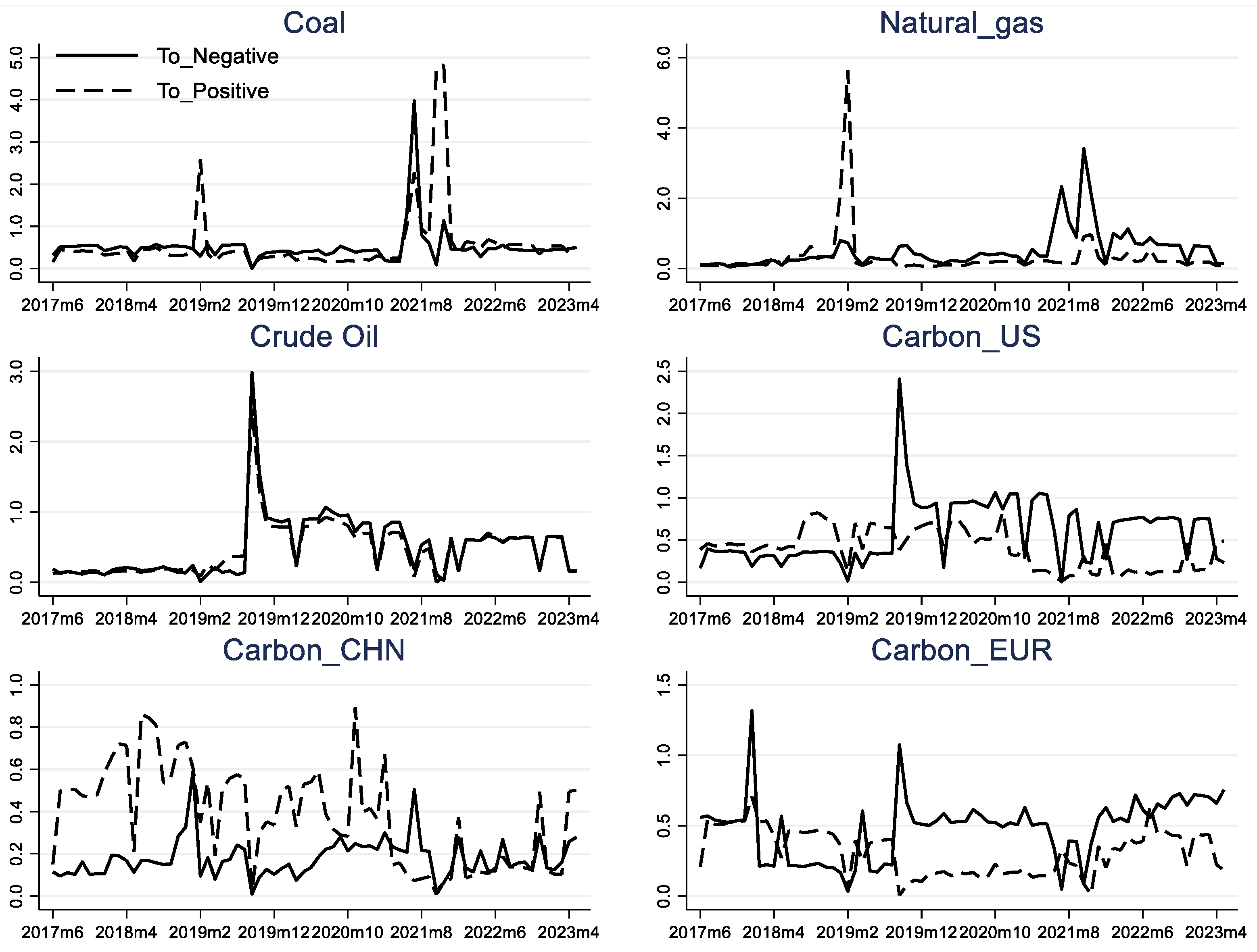
5.3. Directional Spillover Level
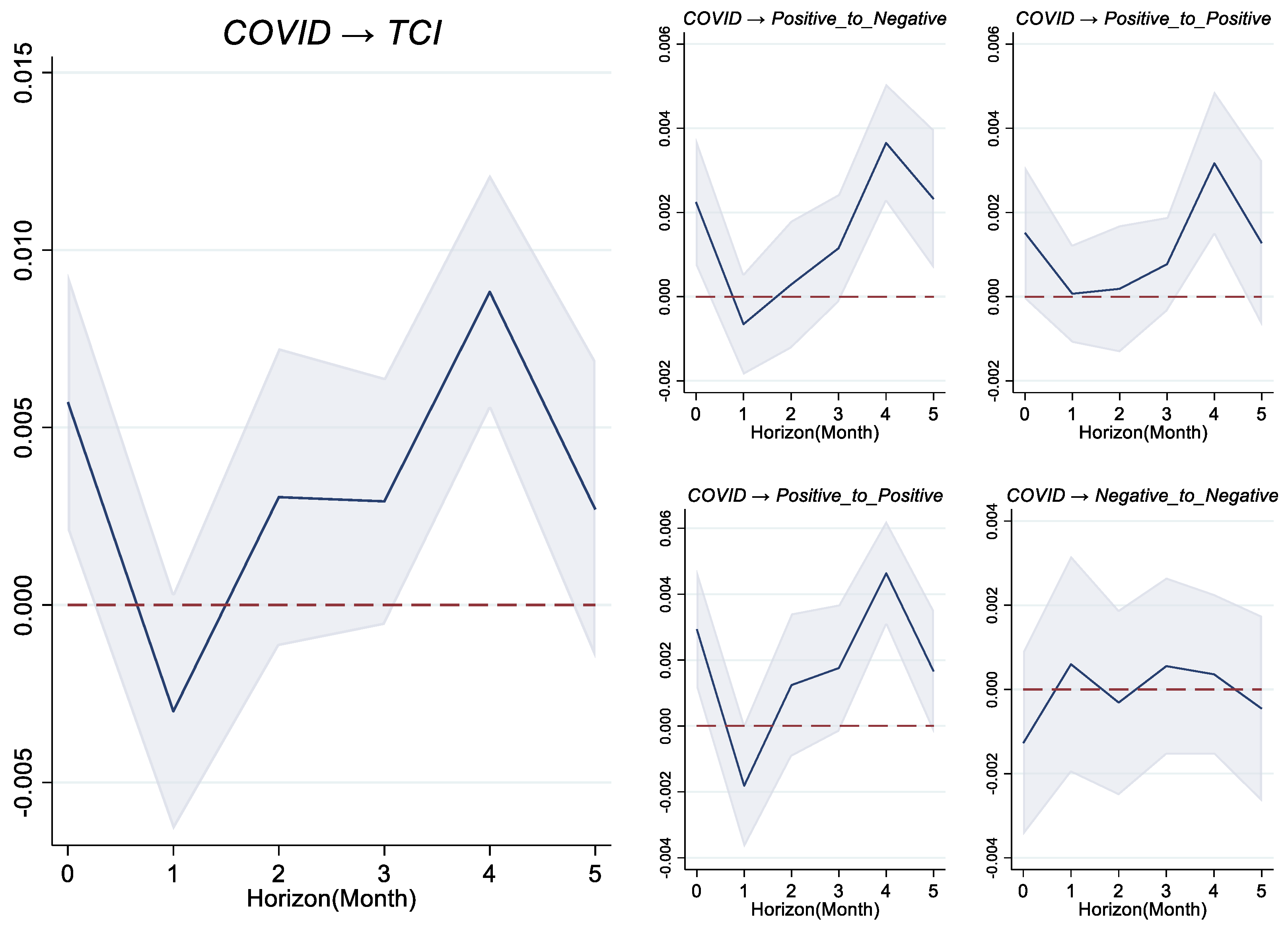
5.4. Testing the Impact of Shocks
6. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Chevallier, J. A model of carbon price interactions with macroeconomic and energy dynamics. Energy Econ. 2011, 33, 1295–1312. [Google Scholar] [CrossRef]
- Doda, B. Evidence on business cycles and CO2 emissions. J. Macroecon. 2014, 40, 214–227. [Google Scholar] [CrossRef]
- Khan, H.; Metaxoglou, K.; Knittel, C.R.; Papineau, M. Carbon emissions and business cycles. J. Macroecon. 2019, 60, 1–19. [Google Scholar] [CrossRef]
- Fan, J.; Zhang, X.; Wang, J.; Qian, D. Measuring the Impacts of International Trade on Carbon Emissions Intensity: A Global Value Chain Perspective. Emerg. Mark. Financ. Trade 2021, 57, 972–988. [Google Scholar] [CrossRef]
- Glosten, L.R.; Jagannathan, R.; Runkle, D.E. On the Relation between the Expected Value and the Volatility of the Nominal Excess Return on Stocks. J. Financ. 1993, 48, 1779–1801. [Google Scholar] [CrossRef]
- Barndorff-Nielsen, O.; Kinnebrock, S.; Shephard, N. Measuring Downside Risk-Realised Semivariance; 2008-W02; Department of Economics, University of Oxford: Oxford, UK, 2008. [Google Scholar]
- Shahzad, S.J.H.; Naeem, M.A.; Peng, Z.; Bouri, E. Asymmetric volatility spillover among Chinese sectors during COVID-19. Int. Rev. Financ. Anal. 2021, 75, 101754. [Google Scholar] [CrossRef] [PubMed]
- Bakas, D.; Triantafyllou, A. The impact of uncertainty shocks on the volatility of commodity prices. J. Int. Money Financ. 2018, 87, 96–111. [Google Scholar] [CrossRef]
- Segal, G.; Shaliastovich, I.; Yaron, A. Good and bad uncertainty: Macroeconomic and financial market implications. J. Financ. Econ. 2015, 117, 369–397. [Google Scholar] [CrossRef]
- Xu, W.; Ma, F.; Chen, W.; Zhang, B. Asymmetric volatility spillovers between oil and stock markets: Evidence from China and the United States. Energy Econ. 2019, 80, 310–320. [Google Scholar] [CrossRef]
- Diebold, X.F.; Yılmaz, K. On the network topology of variance decompositions: Measuring the connectedness of financial firms. J. Econom. 2014, 182, 119–134. [Google Scholar] [CrossRef]
- Demirer, M.; Diebold, F.X.; Liu, L.; Yilmaz, K. Estimating global bank network connectedness. J. Appl. Econom. 2018, 33, 1–15. [Google Scholar] [CrossRef]
- Ma, R.; Liu, Z.; Zhai, P. Does economic policy uncertainty drive volatility spillovers in electricity markets: Time and frequency evidence. Energy Econ. 2022, 107, 105848. [Google Scholar] [CrossRef]
- Balcilar, M.; Ozdemir, H.; Agan, B. Effects of COVID-19 on cryptocurrency and emerging market connectedness: Empirical evidence from quantile, frequency, and lasso networks. Phys. A Stat. Mech. Its Appl. 2022, 604, 127885. [Google Scholar] [CrossRef]
- Jordà, Ò. Estimation and Inference of Impulse Responses by Local Projections. Am. Econ. Rev. 2005, 95, 161–182. [Google Scholar] [CrossRef]
- Keppler, J.H.; Mansanet-Bataller, M. Causalities between CO2, electricity, and other energy variables during phase I and phase II of the EU ETS. Energy Policy 2010, 38, 3329–3341. [Google Scholar] [CrossRef]
- Lutz, B.J.; Pigorsch, U.; Rotfuß, W. Nonlinearity in cap-and-trade systems: The EUA price and its fundamentals. Energy Econ. 2013, 40, 222–232. [Google Scholar] [CrossRef]
- Aatola, P.; Ollikainen, M.; Toppinen, A. Price determination in the EU ETS market: Theory and econometric analysis with market fundamentals. Energy Econ. 2013, 36, 380–395. [Google Scholar] [CrossRef]
- Zhang, Y.-J.; Sun, Y.-F. The dynamic volatility spillover between European carbon trading market and fossil energy market. J. Clean. Prod. 2016, 112, 2654–2663. [Google Scholar] [CrossRef]
- Zhu, B.; Han, D.; Chevallier, J.; Wei, Y.-M. Dynamic multiscale interactions between European carbon and electricity markets during 2005–2016. Energy Policy 2017, 107, 309–322. [Google Scholar] [CrossRef]
- Ji, Q.; Zhang, D.; Geng, J.-b. Information linkage, dynamic spillovers in prices and volatility between the carbon and energy markets. J. Clean. Prod. 2018, 198, 972–978. [Google Scholar] [CrossRef]
- Batten, A.J.; Maddox, E.G.; Young, R.M. Does weather, or energy prices, affect carbon prices? Energy Econ. 2021, 96, 105016. [Google Scholar] [CrossRef]
- Nazifi, F.; Milunovich, G. Measuring the Impact of Carbon Allowance Trading on Energy Prices. Energy Environ. 2010, 21, 367–383. [Google Scholar] [CrossRef]
- Jin, Y.; Zhao, H.; Bu, L.; Zhang, D. Geopolitical risk, climate risk and energy markets: A dynamic spillover analysis. Int. Rev. Financ. Anal. 2023, 87, 102597. [Google Scholar] [CrossRef]
- Liu, D.; Liu, X.; Guo, K.; Ji, Q.; Chang, Y. Spillover Effects among Electricity Prices, Traditional Energy Prices and Carbon Market under Climate Risk. Int. J. Environ. Res. Public Health 2023, 20, 1116. [Google Scholar] [CrossRef] [PubMed]
- Meng, B.; Wei, B.; Yang, M.; Kuang, H. Measuring the time-frequency spillover effect among carbon markets and shipping energy markets: A global perspective. Energy Econ. 2023, 128, 107133. [Google Scholar] [CrossRef]
- Naeem, M.A.; Arfaoui, N. Exploring downside risk dependence across energy markets: Electricity, conventional energy, carbon, and clean energy during episodes of market crises. Energy Econ. 2023, 127, 107082. [Google Scholar] [CrossRef]
- Wang, T.; Wu, F.; Zhang, D.; Ji, Q. Energy market reforms in China and the time-varying connectedness of domestic and international markets. Energy Econ. 2023, 117, 106495. [Google Scholar] [CrossRef]
- Hoque, M.E.; Soo-Wah, L.; Billah, M. Time-frequency connectedness and spillover among carbon, climate, and energy futures: Determinants and portfolio risk management implications. Energy Econ. 2023, 127, 107034. [Google Scholar] [CrossRef]
- Naeem, M.A.; Peng, Z.; Suleman, M.T.; Nepal, R.; Shahzad, S.J.H. Time and frequency connectedness among oil shocks, electricity and clean energy markets. Energy Econ. 2020, 91, 104914. [Google Scholar] [CrossRef]
- Girardi, G.; Tolga Ergün, A. Systemic risk measurement: Multivariate GARCH estimation of CoVaR. J. Bank. Amp; Financ. 2013, 37, 3169–3180. [Google Scholar] [CrossRef]
- Xu, Y. Risk spillover from energy market uncertainties to the Chinese carbon market. Pac. -Basin Financ. J. 2021, 67, 101561. [Google Scholar] [CrossRef]
- Dutta, A. Modeling and forecasting the volatility of carbon emission market: The role of outliers, time-varying jumps and oil price risk. J. Clean. Prod. 2018, 172, 2773–2781. [Google Scholar] [CrossRef]
- Balcılar, M.; Demirer, R.; Hammoudeh, S.; Nguyen, D.K. Risk spillovers across the energy and carbon markets and hedging strategies for carbon risk. Energy Econ. 2016, 54, 159–172. [Google Scholar] [CrossRef]
- Fleming, J.; Kirby, C.; Ostdiek, B. Information and volatility linkages in the stock, bond, and money markets. J. Financ. Econ. 1998, 49, 111–137. [Google Scholar] [CrossRef]
- Kilian, L. Understanding the estimation of oil demand and oil supply elasticities. Energy Econ. 2022, 107, 105844. [Google Scholar] [CrossRef]
- Gabaix, X.; Koijen, R.S. In Search of the Origins of Financial Fluctuations: The Inelastic Markets Hypothesis; National Bureau of Economic Research: Cambridge, MA, USA, 2021. [Google Scholar]
- Caldara, D.; Cavallo, M.; Iacoviello, M. Oil price elasticities and oil price fluctuations. J. Monet. Econ. 2019, 103, 1–20. [Google Scholar] [CrossRef]
- Patton, A.J.; Sheppard, K. Good Volatility, Bad Volatility: Signed Jumps and The Persistence of Volatility. Rev. Econ. Stat. 2015, 97, 683–697. [Google Scholar] [CrossRef]
- Duan, Y.; El Ghoul, S.; Guedhami, O.; Li, H.; Li, X. Bank systemic risk around COVID-19: A cross-country analysis. J. Bank. Financ. 2021, 133, 106299. [Google Scholar] [CrossRef]
- Caldara, D.; Iacoviello, M. Measuring geopolitical risk. Am. Econ. Rev. 2022, 112, 1194–1225. [Google Scholar] [CrossRef]
- Duan, K.; Ren, X.; Shi, Y.; Mishra, T.; Yan, C. The marginal impacts of energy prices on carbon price variations: Evidence from a quantile-on-quantile approach. Energy Econ. 2021, 95, 105131. [Google Scholar] [CrossRef]
- Hamilton, J.D. What is an oil shock? J. Econom. 2003, 113, 363–398. [Google Scholar] [CrossRef]
- Cross, J.; Nguyen, B.H. Time varying macroeconomic effects of energy price shocks: A new measure for China. Energy Econ. 2018, 73, 146–160. [Google Scholar] [CrossRef]
- Lau, C.K.; Soliman, A.M.; Albasu, J.; Gozgor, G. Dependence structures among geopolitical risks, energy prices, and carbon emissions prices. Resour. Policy 2023, 83, 103603. [Google Scholar] [CrossRef]



| Variable | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| GDP_EU27 (Millions of euros) | 116 | 269,2603.00 | 697,915.60 | 1,552,569.00 | 4,313,506.00 |
| GPD_Italy (Millions of euros) | 116 | 381,641.90 | 69,262.39 | 213,695.30 | 527,492.20 |
| GDP_France (Millions of euros) | 116 | 484,117.90 | 107,143.50 | 301,164.00 | 712,521.80 |
| GDP_Spain (Millions of euros) | 116 | 239,373.10 | 65,905.82 | 112,945.80 | 375,161.00 |
| GDP_Germany (Millions of euros) | 116 | 673,202.00 | 152,719.40 | 485,577.20 | 1,053,040.00 |
| GDP_UK (Millions of euros) | 116 | 402,398.10 | 124,626.00 | 207,126.00 | 678,310.00 |
| Carbon emission_EU27 and England(kton) | 1947 | 8.23 | 1.56 | 4.46 | 12.28 |
| Carbon emission_France(kton) | 1947 | 0.78 | 0.19 | 0.29 | 1.25 |
| Carbon emission_Germany(kton) | 1947 | 1.73 | 0.46 | 0.77 | 3.01 |
| Carbon emission_Italy(kton) | 1947 | 0.84 | 0.18 | 0.39 | 1.28 |
| Carbon emission_Spain(kton) | 1947 | 0.64 | 0.12 | 0.29 | 0.98 |
| Carbon emission_UK(kton) | 1947 | 0.92 | 0.18 | 0.45 | 1.46 |
| Carbon emission_Others (kton) | 1947 | 3.32 | 0.58 | 1.89 | 4.96 |
| Variables | |
|---|---|
| 0.0527 *** | |
| (0.0198) | |
| Constant | −0.345 ** |
| (0.137) | |
| Observations | 260 |
| R-squared | 0.021 |
| Robust standard errors in parentheses |
| Data Type | Variable | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|---|
| Prices | Carbon_US(USD) | 2588 | 13.57 | 4.178 | 8.868 | 23.84 |
| Carbon EU(USD) | 2588 | 28.91 | 21.07 | 9.611 | 83.25 | |
| Carbon CHN(USD) | 2588 | 5.137 | 2.384 | 2.093 | 21.47 | |
| IPE Rotterdam Coal(USD) | 1831 | 99.71 | 77.3 | 38.55 | 459 | |
| IPE Brent Crude Oil(USD) | 2547 | 69.62 | 22.5 | 23 | 129.5 | |
| IPE UK Natural Gas(USD) | 2474 | 78.98 | 85.91 | 9.04 | 606.2 | |
| Shocks | GPR(Index) | 72 | 77.13 | 22.88 | 46.86 | 167.3 |
| COVID_19(%) | 72 | 0.856 | 3.655 | 0 | 29.47 |
| Positive Price Volatilities | Negative Price Volatilities | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Crude Oil | Coal | Natural Gas | Carbon_ EU | Carbon_ US | Carbon_ CHN | Crude oil | Coal | Natural Gas | Carbon_EU | Carbon_ US | Carbon_ CHN | ||
| Positive Price Volatilities | Crude oil | 5.35 | 0.10 | 1.49 | 1.14 | 0.82 | 1.68 | 0.55 | 11.20 | 0.08 | 0.15 | ||
| Coal | 6.27 | 0.93 | 5.66 | 1.24 | 0.10 | 2.53 | 14.09 | 12.06 | 0.03 | 0.01 | |||
| Natural Gas | 0.28 | 1.80 | 0.64 | 0.12 | 0.96 | 0.09 | 0.92 | 0.36 | 1.46 | 0.07 | |||
| Carbon_ EU | 4.82 | 11.02 | 0.26 | 0.64 | 0.73 | 6.05 | 4.83 | 5.28 | 2.42 | 0.22 | |||
| Carbon_ US | 3.64 | 0.73 | 0.08 | 1.07 | 1.32 | 8.03 | 1.32 | 0.54 | 3.46 | 0.02 | |||
| Carbon_ CHN | 0.30 | 0.32 | 0.56 | 0.65 | 0.76 | 0.69 | 0.54 | 1.76 | 0.49 | 0.02 | |||
| Negative Price Volatilities | Crude oil | 3.43 | 0.05 | 1.75 | 1.25 | 0.75 | 2.09 | 1.10 | 13.87 | 0.18 | 0.16 | ||
| Coal | 3.22 | 0.24 | 1.57 | 1.32 | 0.26 | 2.98 | 12.63 | 5.47 | 0.07 | 0.04 | |||
| Natural Gas | 0.66 | 10.91 | 3.11 | 1.17 | 1.11 | 0.88 | 8.56 | 5.66 | 1.38 | 0.10 | |||
| Carbon_ EU | 9.20 | 13.68 | 0.28 | 0.63 | 0.25 | 11.90 | 5.03 | 6.23 | 0.31 | 0.07 | |||
| Carbon_ US | 0.68 | 0.22 | 2.17 | 4.22 | 0.19 | 0.97 | 0.15 | 2.81 | 2.74 | 0.41 | |||
| Carbon_ CHN | 0.29 | 0.13 | 0.34 | 1.06 | 0.01 | 0.48 | 0.23 | 0.75 | 0.25 | 0.27 | |||
| Market | From+ | From− | To+ | To− | From | To |
|---|---|---|---|---|---|---|
| Crude oil | 22.57 | 24.63 | 29.36 | 34.60 | 2.06 | 5.24 |
| Coal | 42.92 | 27.8 | 47.59 | 25.35 | −15.12 | −22.24 |
| Natural gas | 6.71 | 33.53 | 5.02 | 45.74 | 26.83 | 40.73 |
| Carbon_EU | 36.29 | 47.58 | 21.21 | 55.56 | 11.29 | 34.35 |
| Carbon_US | 20.2 | 14.55 | 8.29 | 6.22 | −5.66 | −2.07 |
| Carbon_CHN | 6.1 | 3.8 | 6.49 | 1.25 | −2.29 | −5.23 |
| Spillover (%) | Negative Price Volatility | Positive Price Volatility | Difference | t-Statistic | p-Value | ||
|---|---|---|---|---|---|---|---|
| Mean | Standard Error | Mean | Standard Error | ||||
| Coal | 51.02 | 5.31 | 56.88 | 9.57 | −5.86 | −0.53 | 0.30 |
| Natural Gas | 51.24 | 6.43 | 31.55 | 8.22 | 19.69 | 1.89 | 0.03 |
| Crude oil | 49.65 | 5.33 | 46.37 | 4.45 | 3.29 | 0.47 | 0.32 |
| Carbon_US | 59.85 | 4.52 | 39.89 | 2.76 | 19.96 | 3.77 | 0.00 |
| Carbon_CHN | 17.89 | 1.09 | 37.80 | 2.79 | −19.91 | −6.65 | 0.00 |
| Carbon_EU | 48.21 | 2.65 | 31.19 | 1.93 | 17.02 | 5.19 | 0.00 |
| Inflow (%) | Negative Price Volatility | Positive Price Volatility | Difference | t-Statistic | p-Value | ||
|---|---|---|---|---|---|---|---|
| Mean | Standard Error | Mean | Standard Error | ||||
| Coal | 45.33 | 1.22 | 41.41 | 1.88 | 3.93 | 1.75 | 0.04 |
| Natural Gas | 41.39 | 2.02 | 27.62 | 1.99 | 13.78 | 4.86 | 0.00 |
| Crude oil | 35.93 | 2.67 | 36.92 | 2.57 | −0.99 | −0.27 | 0.40 |
| Carbon_US | 58.98 | 1.82 | 49.98 | 2.09 | 9.00 | 3.24 | 0.00 |
| Carbon_CHN | 39.81 | 2.22 | 42.55 | 2.43 | −2.74 | −0.83 | 0.20 |
| Carbon_EU | 50.88 | 2.23 | 50.75 | 1.90 | 0.13 | 0.05 | 0.48 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Chang, Z. Connectedness of Carbon Price and Energy Price under Shocks: A Study Based on Positive and Negative Price Volatility. Sustainability 2024, 16, 5226. https://doi.org/10.3390/su16125226
Yu B, Chang Z. Connectedness of Carbon Price and Energy Price under Shocks: A Study Based on Positive and Negative Price Volatility. Sustainability. 2024; 16(12):5226. https://doi.org/10.3390/su16125226
Chicago/Turabian StyleYu, Bo, and Zhijia Chang. 2024. "Connectedness of Carbon Price and Energy Price under Shocks: A Study Based on Positive and Negative Price Volatility" Sustainability 16, no. 12: 5226. https://doi.org/10.3390/su16125226
APA StyleYu, B., & Chang, Z. (2024). Connectedness of Carbon Price and Energy Price under Shocks: A Study Based on Positive and Negative Price Volatility. Sustainability, 16(12), 5226. https://doi.org/10.3390/su16125226






