An Assessment Method of Deviation Electricity Responsibility in China’s Forward Electricity Market Based on Time-Sharing Trading Prices
Abstract
1. Introduction
1.1. Literature Review
1.2. Aims and Contributions
- (1)
- This paper refines the settlement rule of “monthly clearing and monthly settlement” for DE in the forward electricity market and proposes a novel settlement method of “hourly basic calculation and monthly settlement” for DE, which refines the time-sharing deviation responsibility for a BRP. At the same time, the EDS mechanism with smaller granularity of calculation time strengthens the connection with the electricity spot market.
- (2)
- We examine how DE participates in the spot market through CFDs within an electricity market where both spot and forward markets coexist. We propose that DE in the forward electricity market can also be settled using CFDs at time-sharing prices, allowing for a more comprehensive response to the economic responsibility of DE.
- (3)
- To enhance the price signal for deviation settlement, we comprehensively consider the supply–demand relationship and power supply costs. We analyze four typical scenarios and their pricing methods, and propose a time-sharing price model. Both the BRP and BSP refer to this price for settlement, allowing the grid to avoid generating imbalance funds that should not be borne by itself due to differences in settlement prices.
2. Methods and Models
2.1. Principle Analysis of the EDS Mechanism
2.1.1. Causes of Deviation Electricity
- Product specificity: Electric energy products encompass power generation, transmission, distribution, and consumption simultaneously. Consequently, power system operation and market transactions require real-time power balance to ensure grid safety.
- Contract default penalties: Given the inevitable generation of DE, the power grid must establish a settlement mechanism with varying constraint strengths based on market players’ performance awareness and ability. This encourages market players to fulfill balancing responsibilities outlined in the trading contract.
- Total deviation settlement: Electric energy delivery in the forward electricity market cannot be individually measured at specific moments. The grid accumulates the total deviation of electric energy transactions over the PTU and establishes uniform settlement and assessment rules.
2.1.2. The ESD Mechanism
- (1)
- SO: The SO bears the responsibility for instantaneous deviations at each moment, and the EDS mechanism with longer settlement periods overlooks the cost incurred by the SO to maintain real-time power balance. Additionally, the deviation penalty price is artificially set by the grid and will be used for a long time once it is determined. However, the cost incurred by the SO for procuring balancing services from BSPs is dynamic, fluctuating with the supply cost and the supply–demand conditions. Consequently, the SO may risk that the deviation assessment fees charged do not fully cover the deviation balancing costs.
- (2)
- BRPs: DE by BRPs is penalized regardless of its direction if it exceeds the threshold. However, the contribution and impact of DE vary significantly under different conditions. If there is a surplus in the deviation assessment cost after covering the balancing service cost, the SO will distribute this surplus in an electricity proportion, allowing the BRP to receive a portion of the revenue. This reduces the actual economic responsibility of the BRP and weakens the constraining effect of the EDS mechanism.
- (3)
- BSPs: The cost of balancing services varies with the market’s supply and demand conditions and the cost of power supply. The SO should develop a more economical and accurate pricing guide for BSPs, fully considering the economics of deviation adjustments.
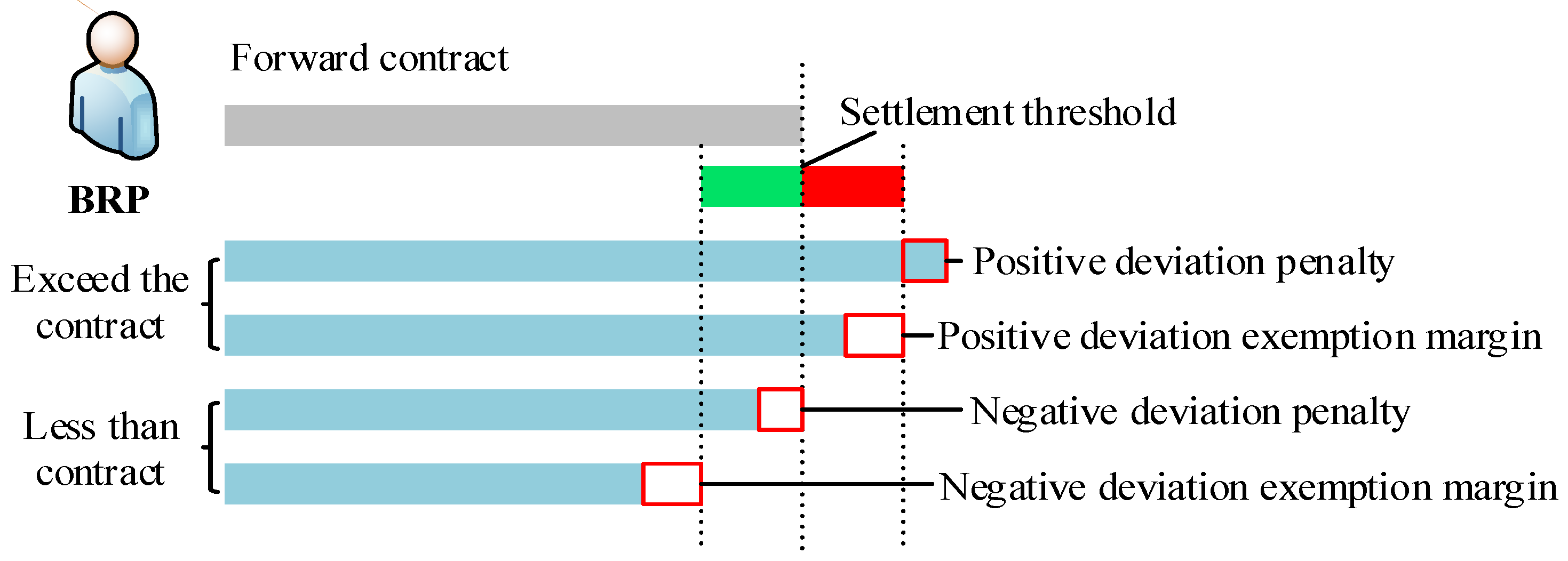
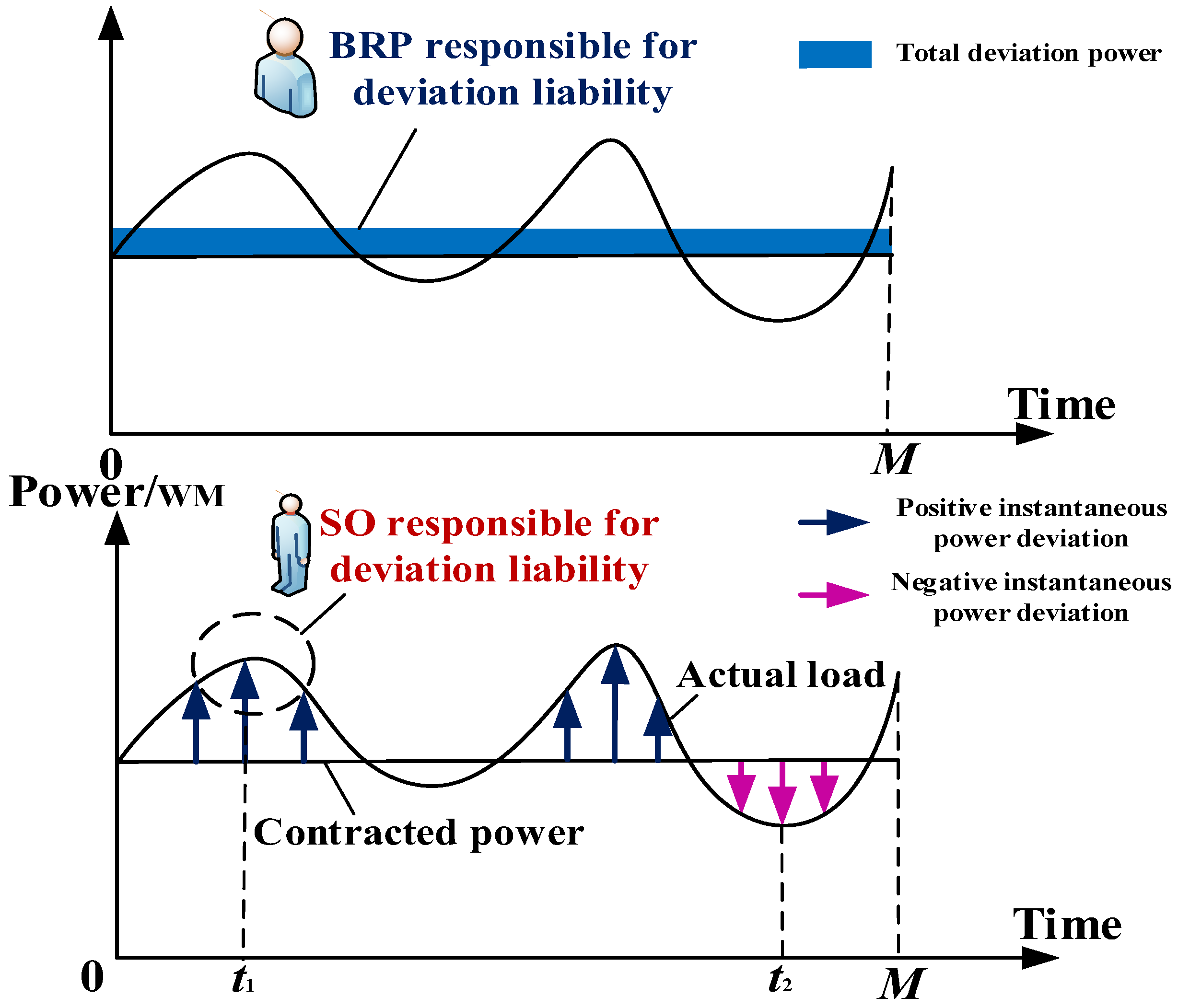
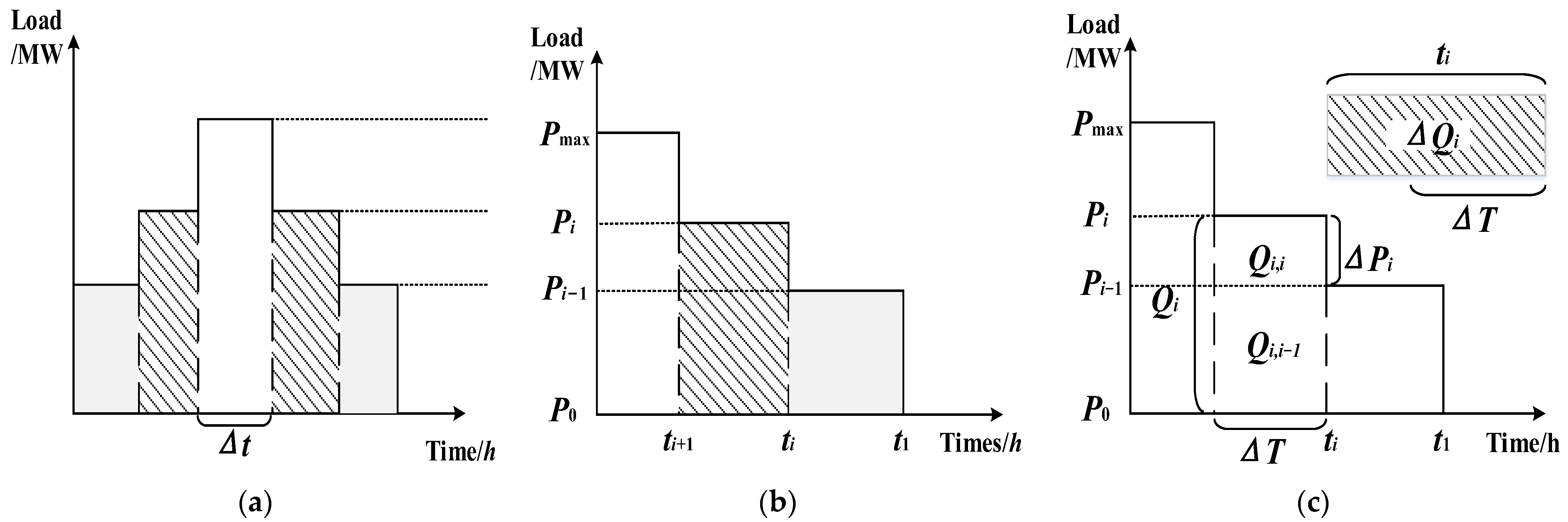
2.1.3. Misalignment in Deviation Responsibility
- (1)
- Inconsistency in assumed balancing responsibilities: As illustrated in Figure 3 below, the BRP is solely accountable for balancing corresponding to its total deviation power within each settlement unit (typically monthly), corresponding to the blue rectangle in the figure, without bearing the costs associated with positive and negative offsetting DE within the unit. Conversely, the SO must procure balancing services from the BSP to maintain system supply–demand equilibrium at each moment, corresponding to the positive and negative instantaneous DE—blue and purple arrow markings. The former concerns the total DE of a settlement unit, while the latter pertains to the instantaneous DE of each moment. This disparity in balancing responsibilities between the SO and BRP can result in inaccuracies in the financial responsibility attributed to measured BRP deviation.
- (2)
- Disparities in DE settlement prices exist: To safeguard the interests of all stakeholders and incentive market players to minimize their deviations, many countries or regions incorporate punitive pricing into their balancing mechanisms. For instance, Spain and Belgium implement the “two-price method,” assigning distinct prices for positive and negative deviations. Similarly, the EDS mechanism in China’s forward market penalizes deviation behavior among market players, as indicated by the deviation punitive prices in select provinces outlined in Table 2. However, this variability in settlement prices for positive and negative DE can result in discrepancies in economic responsibility assessment.
2.2. Methodology for Evaluating Deviation Responsibility
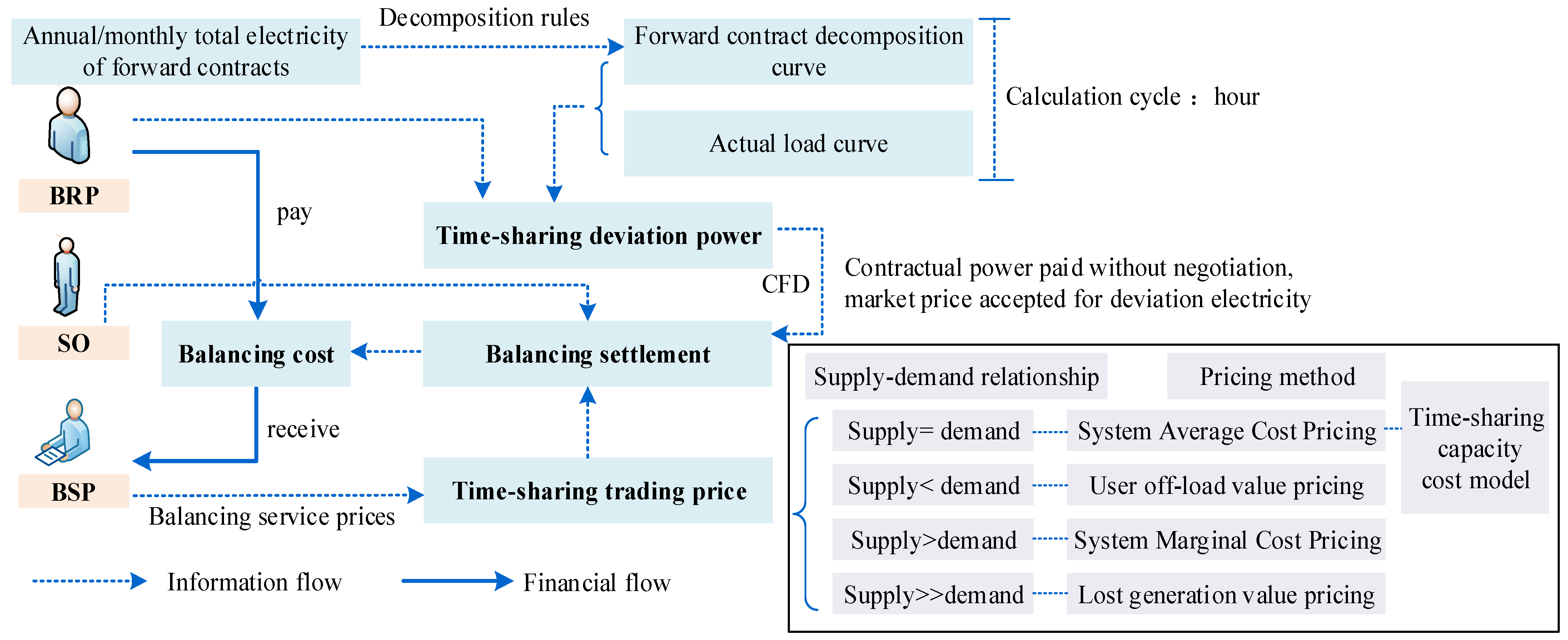
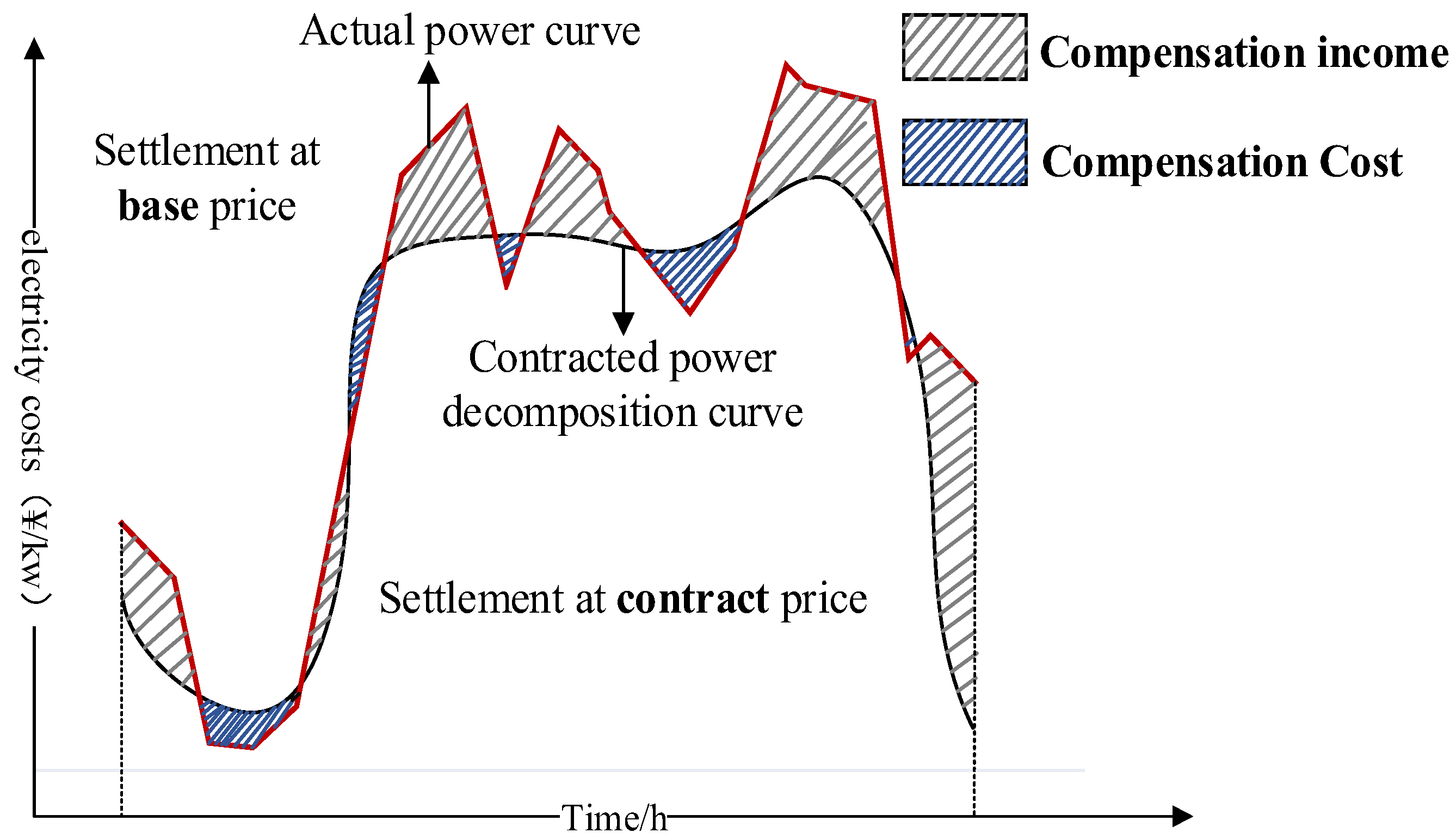
2.2.1. EDS Mechanism Based on CFDs
2.2.2. Time-Sharing Trading Pricing Model
- Pricing model
- 2.
- Time-sharing capacity cost model
2.2.3. Unit Output Model
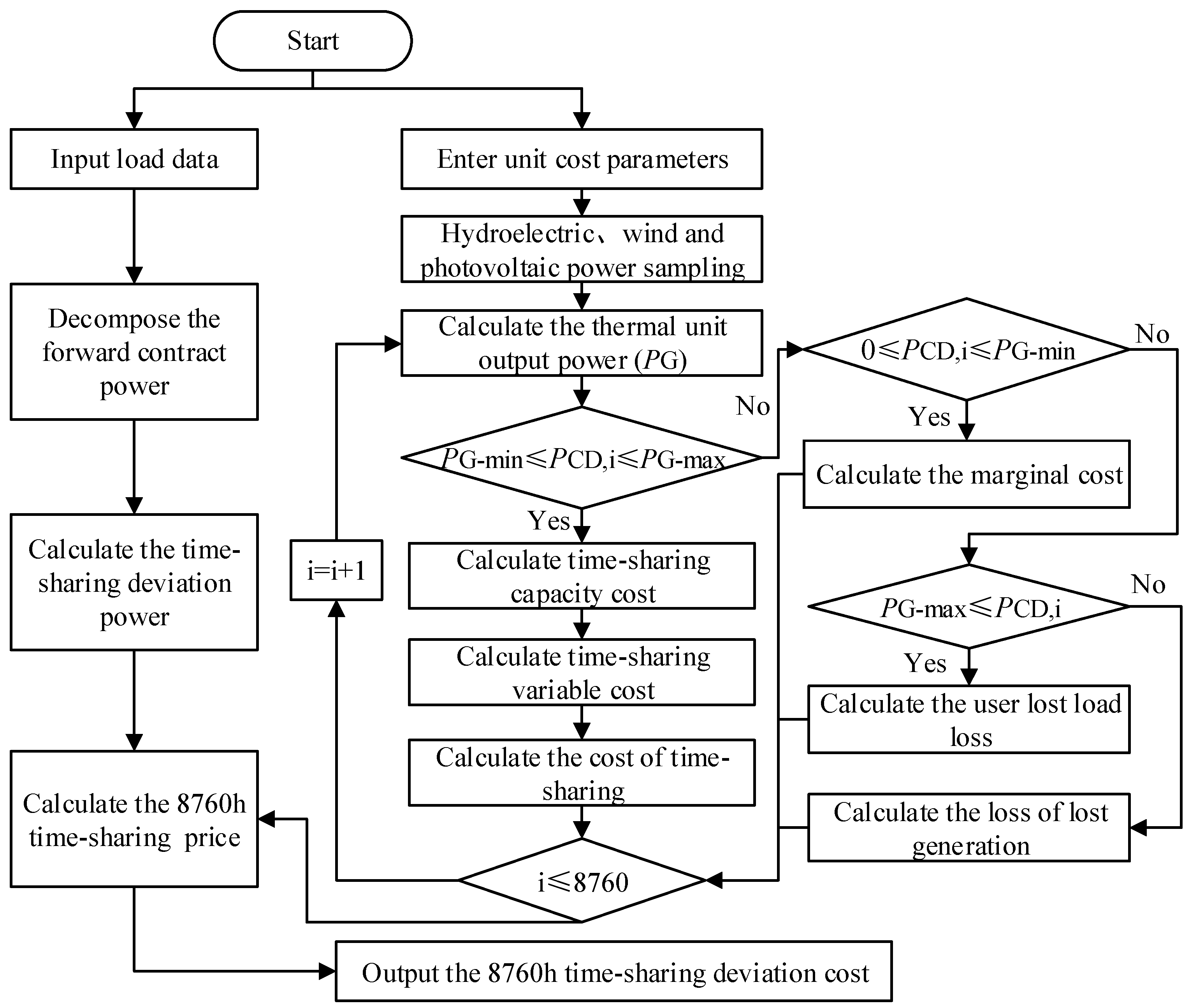
2.2.4. Solution Flow
3. Simulation Results and Discussion
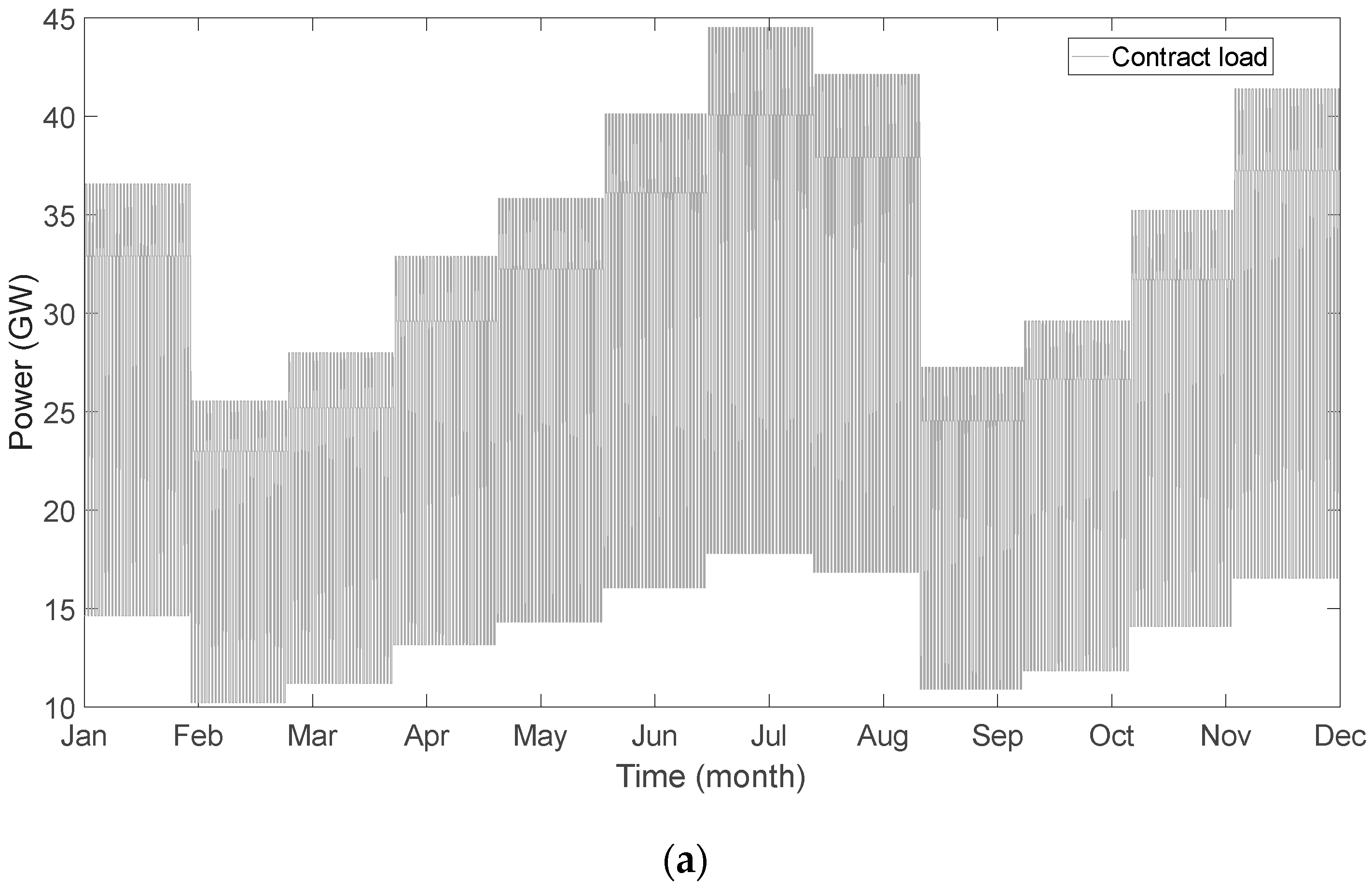
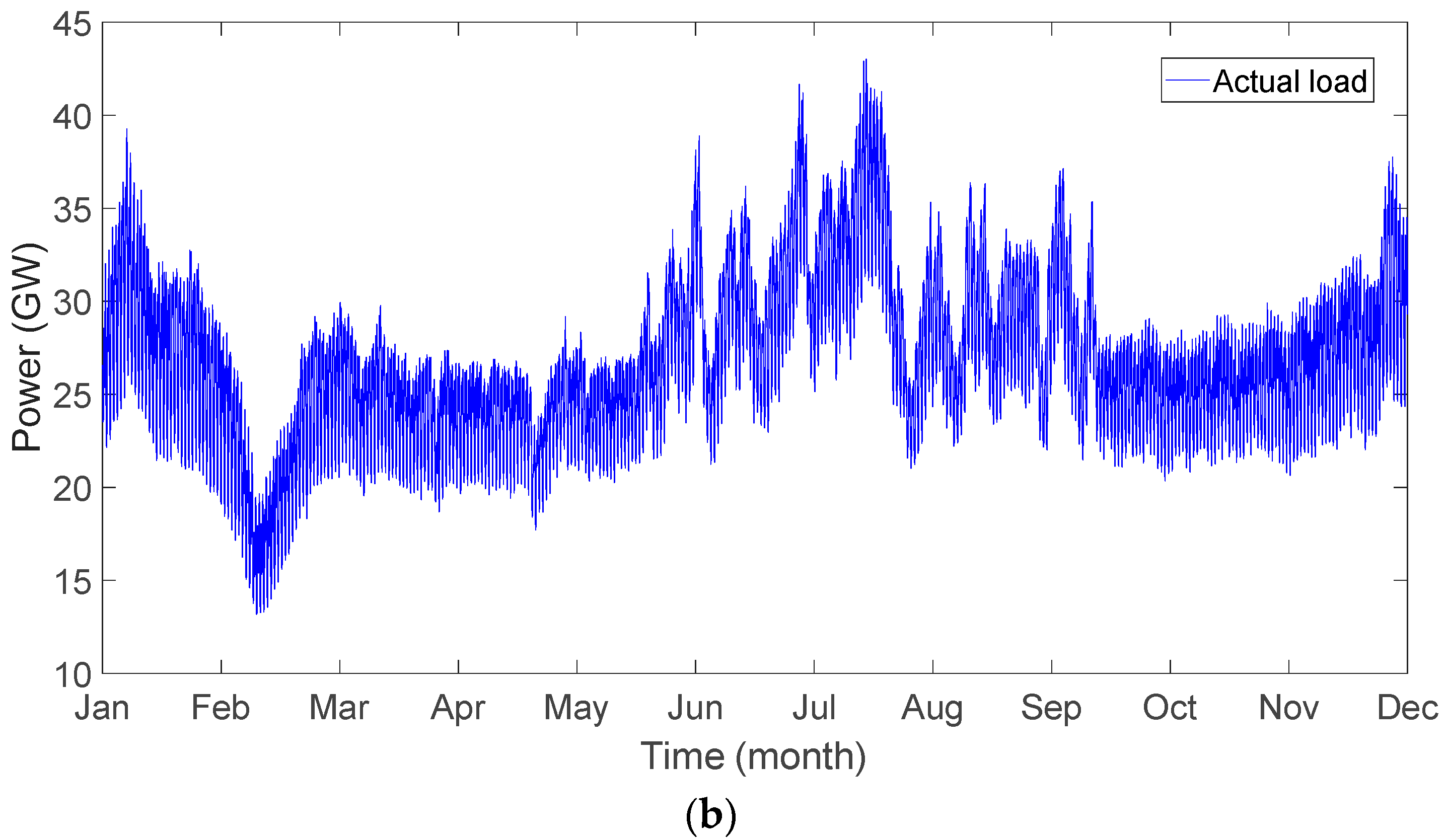
3.1. Basic Settings
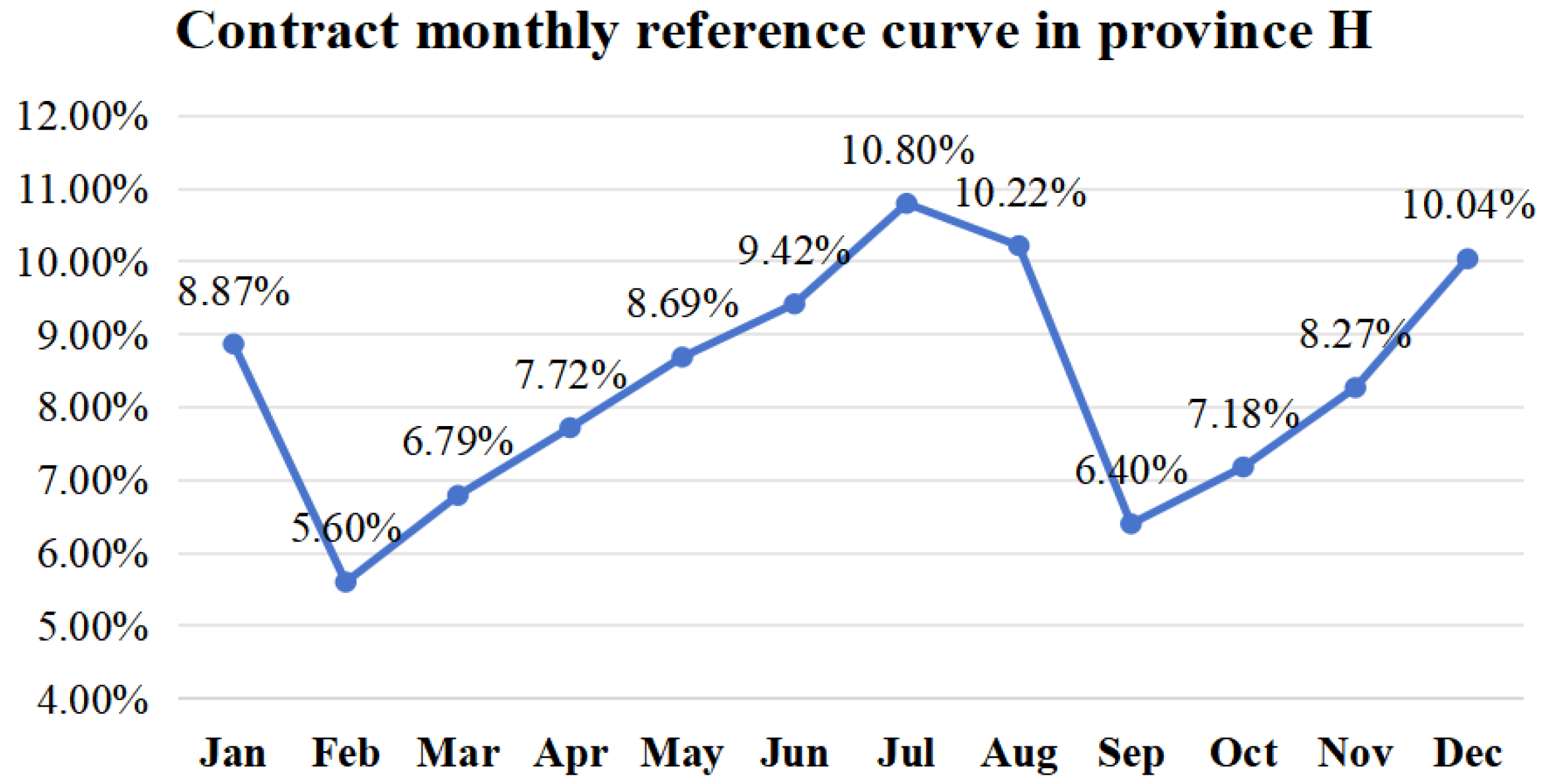
- Decomposition of forward contract
- Decompose the total annual contract power into monthly contract power, guided by the reference curve. The reference decomposition curve is depicted in Figure 7.
- Breakdown monthly total power into daily power on an average basis by days.
- Decompose daily power into hourly power, referencing the integrated daily typical curve. The decomposition ratios are as follows: 20% of electricity within the time period 0:00~9:00; 50% within 9:00~18:00; and 30% within 18:00~24:00.
- 2.
- Time-sharing deviation electricity
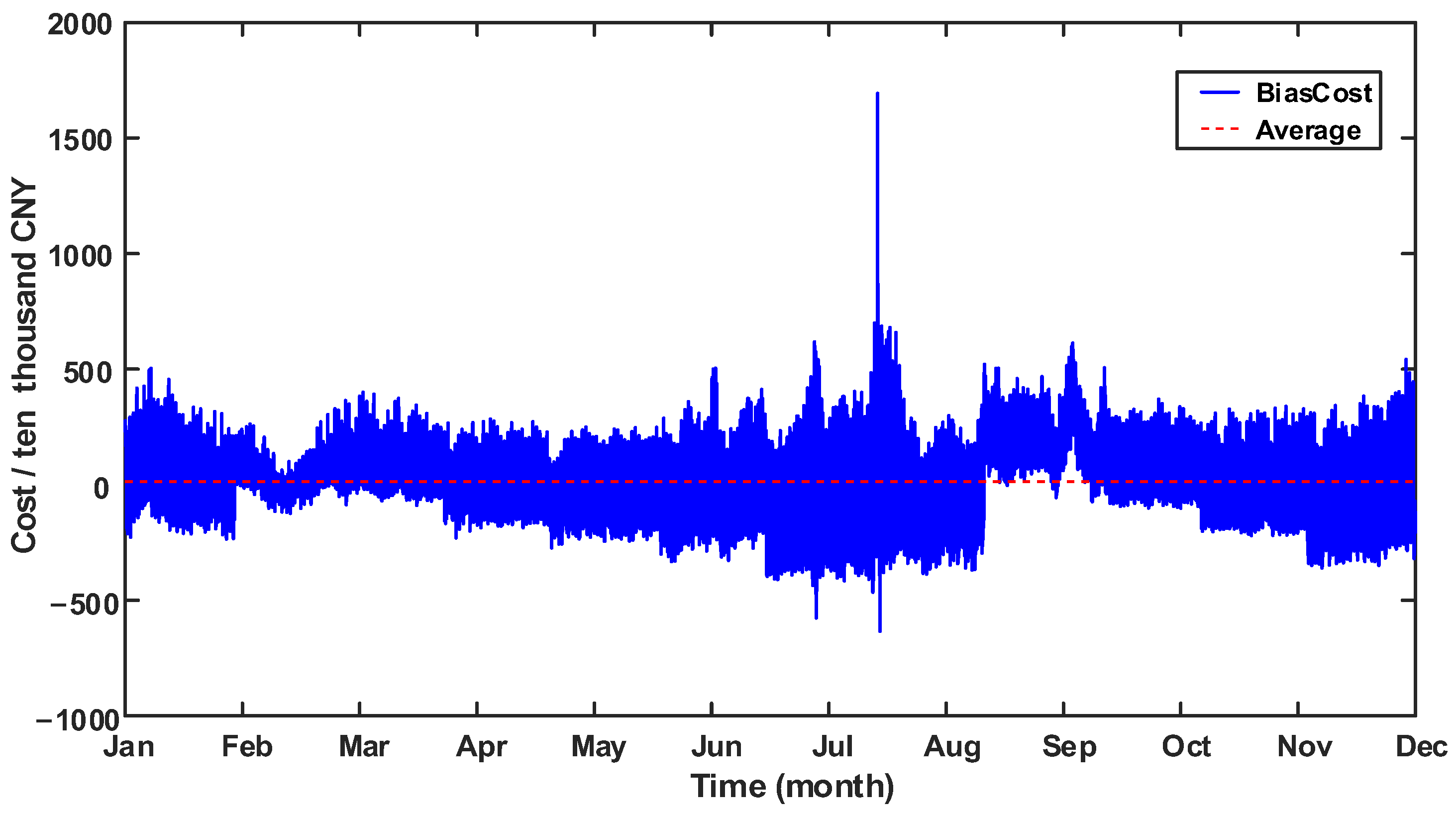
3.2. Simulation Results
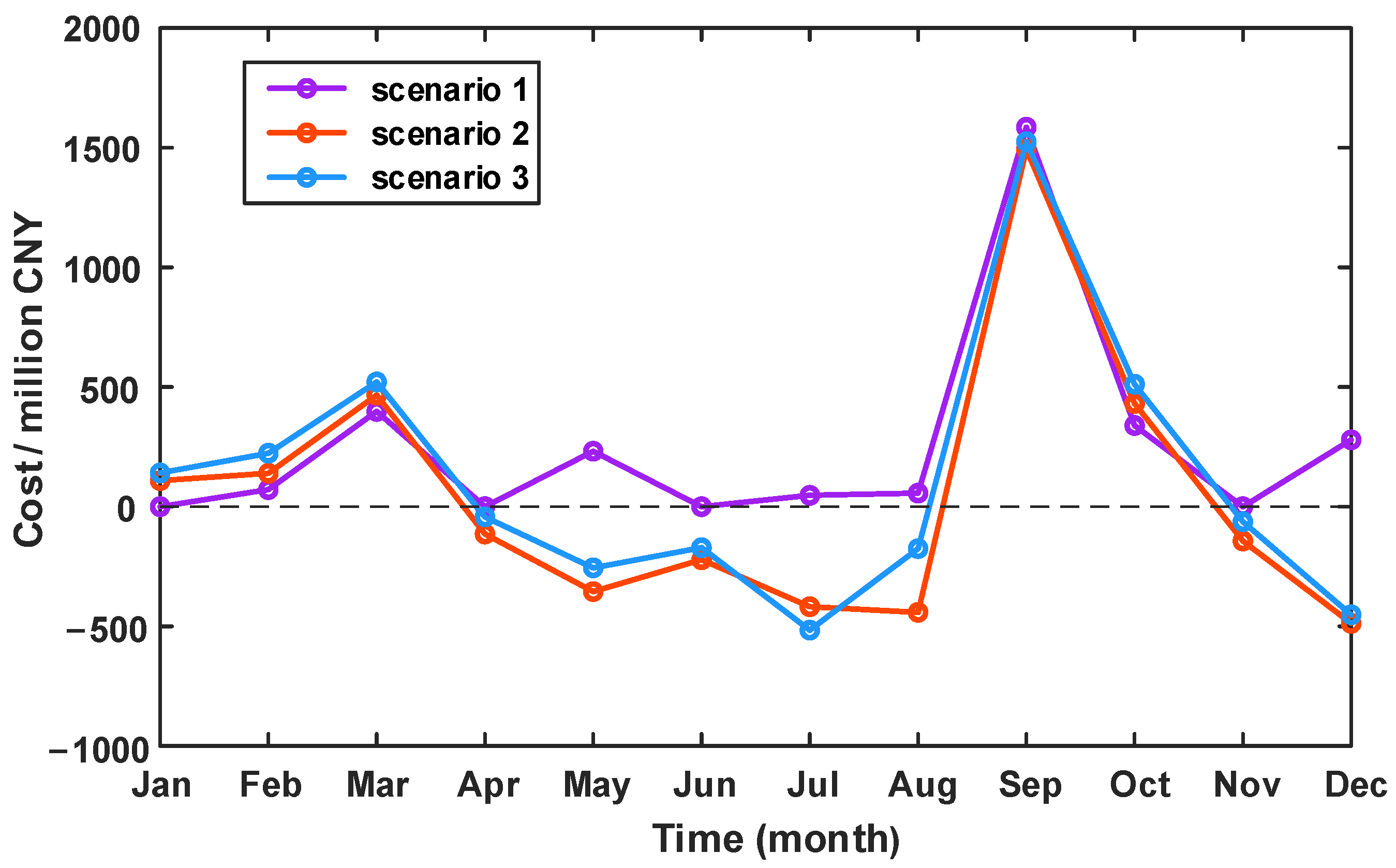
3.3. Comparative Analysis of Different Scenarios
3.4. Sensitivity Analysis
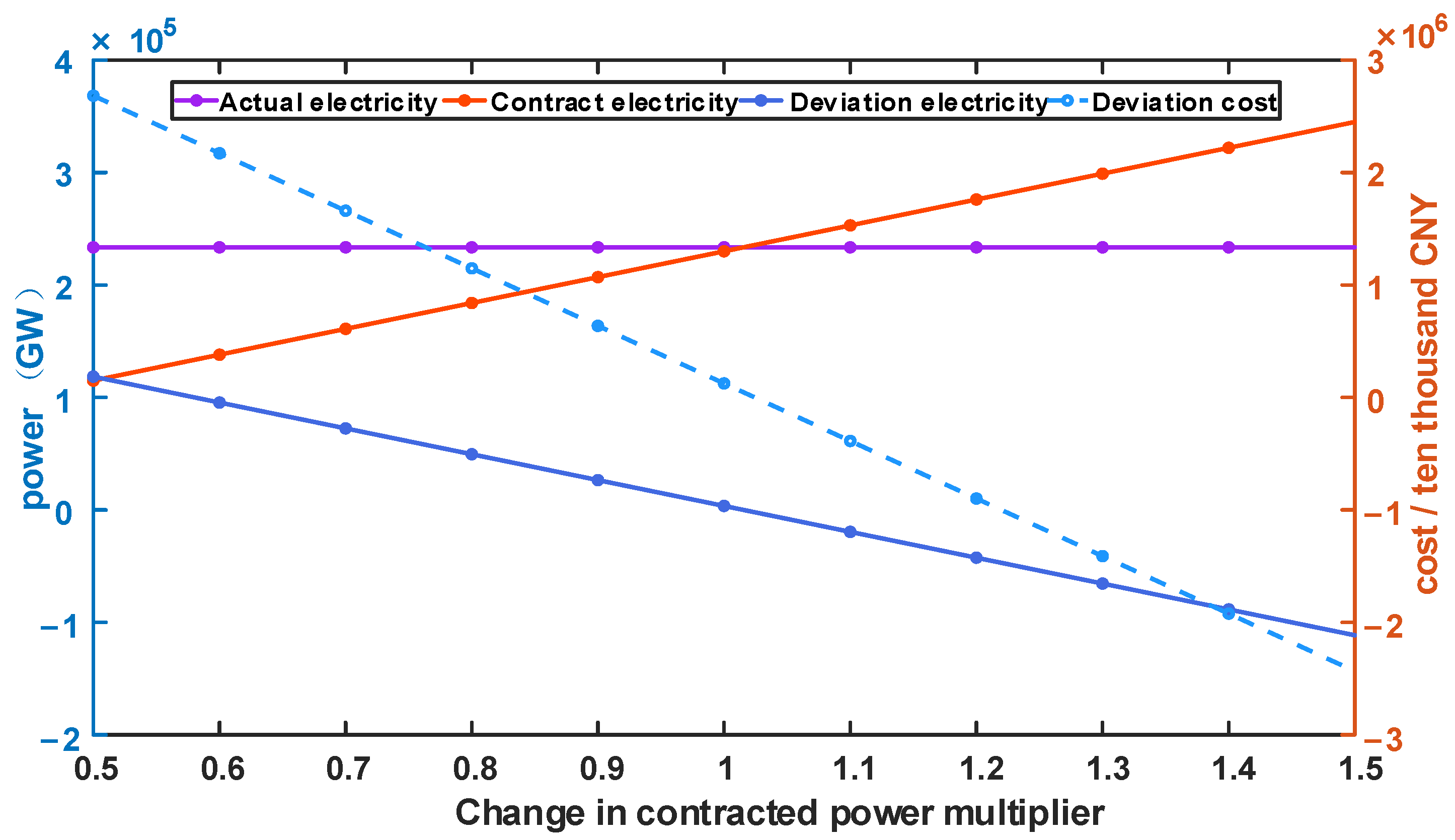
3.4.1. Contracted Electricity
3.4.2. Decomposition Methods
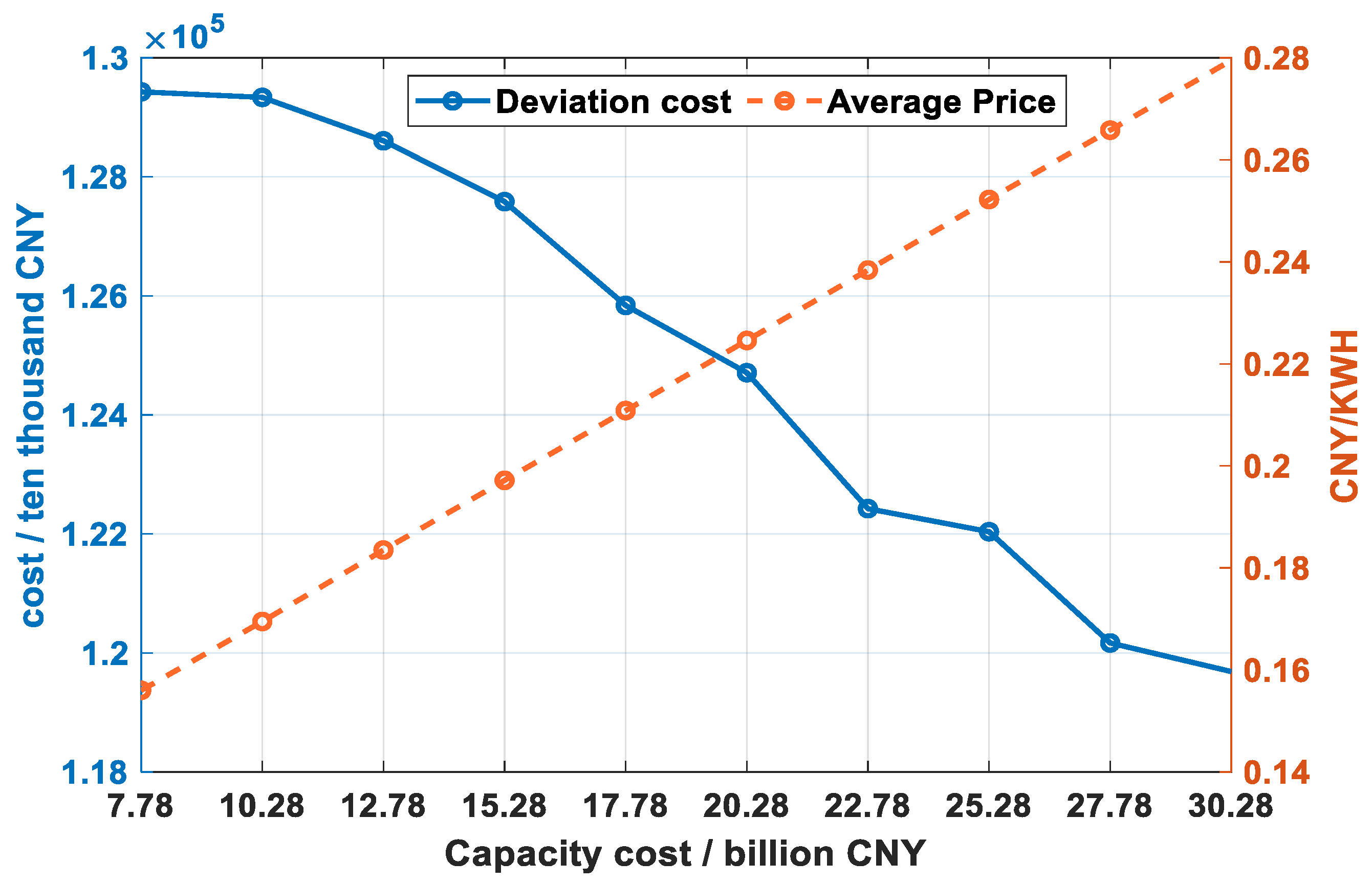
3.4.3. Capacity Cost
4. Conclusions and Policy Implications
- (1)
- The unique characteristics of electric power products and the uncertainty in electric power consumption and production are the primary causes of DE. Many countries manage and settle DE through the electricity spot market, while China, dominated by the forward electricity market, utilizes the EDS mechanism to address DE.
- (2)
- The existing EDS mechanism has shortcomings for stakeholders such as a BRP, BSP, and SO, and it hinders future market development. Inconsistencies in balancing responsibilities and disparities in settlement prices are the primary causes of inaccurate deviation responsibility measurement.
- (3)
- Deviation costs are influenced by the calculation and settlement period, DE, deviation price, and deviation direction. The proposed method for measuring deviation responsibility, based on time-sharing transaction prices, features a shorter calculation cycle, facilitating a detailed demonstration of the deviation responsibility borne by the BRP. The developed time-sharing trading price model offers price guidance for BRPs to settle DE and for BSPs to settle balancing services. The lower annual average price and wider price change range reflect supply and demand relationships and power supply costs in different time periods while ensuring overall price stability.
- (4)
- Sensitivity analysis results indicate that the quantity of contracted power and the way it is broken down affect the deviation cost by influencing the amount of DE. The system’s fixed capacity cost impacts deviation costs by affecting deviation prices. It is evident that the absolute values of the DE, deviation price, and deviation cost are positively correlated, while the direction of DE determines whether the deviation cost is positive or negative.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Hydropower output model
- 2.
- Wind power output model
- 3.
- PV output model
References
- Ye, Z. The “Chinese Characteristics” of Electricity Markets. China Power Enterp. Manag. 2021, 1, 35–40. [Google Scholar]
- Qian, C.; Yun, Y.; Jing, Z. Discussion on the Target and Structure of Electricity Market and the Key Issues in the Construction of China’s Electricity Market. J. Glob. Energy Interconnect. 2020, 3, 508–517. [Google Scholar]
- Xu, C.; Zhang, L.; Chen, D.; Tang, C. A Monthly Balancing Mechanism Based on Pre-bidding and Its Multi-period Generation Schedule Optimization Model. Proc. CSEE 2019, 39, 5085–5094. [Google Scholar]
- Wang, Y.; Zhang, B.; Sun, H.; Shang, J.; Huang, Y. An Introduction to Foreign Balancing Market Mechanism and Suggestions on Constructing Real-Time Balancing Market in China. Power Syst. Technol. 2003, 27, 10–13. [Google Scholar]
- Zhou, M.; Yan, Y.; Ding, Q.; Wu, Z.; He, Y.; Long, S. Transaction and Settlement Mechanism for Foreign Representative Power Markets and Its Enlightenment for Chinese Power Market. Autom. Electr. Power Syst. 2017, 41, 1–8. [Google Scholar]
- He, Y.; Zhou, M.; Wu, Z.; Long, S.; Xun, J. Study on Operation Mechanism of Foreign Representative Balancing Markets and Its Enlightenment for China. Power Syst. Technol. 2018, 42, 3520–3528. [Google Scholar]
- Chen, Z.; Lin, Z.; He, C.; Qian, H.; Zhang, Z.; Lin, Z.; Wen, F. An assessment mechanism for contract energy deviation in a medium and long-term electricity market. J. Electr. Power Sci. Technol. 2020, 35, 31–39. [Google Scholar]
- Wang, D.; Ding, W.; Gao, F.; Xu, Y.; Miao, Q. A Method to Deal With Inter-Regional and Inter-Provincial Transaction Settlement Deviation Quantity Based on Kernel Density–Entropy Weight. Front. Energy Res 2021, 9, 667163. [Google Scholar] [CrossRef]
- Zhu, D.; Ma, R.; Xia, X.; Zhang, S.; Liu, J. Construction of Real-Time Deviation Electric Quantity Control Model for Regional Electricity Spot Market. Meas. Control 2022, 55, 595–602. [Google Scholar] [CrossRef]
- Gupta, M.; Gupta, S.; Thakur, T. Implementation of New Electricity Regulatory Norms for Deviation Settlement Mechanism: A Case Study of India. Cogent Eng. 2019, 6, 1623152. [Google Scholar] [CrossRef]
- Turker, B.; Arroyo Klein, S.; Komsiyska, L.; Trujillo, J.J.; Von Bremen, L.; Kühn, M.; Busse, M. Utilizing a Vanadium Redox Flow Battery to Avoid Wind Power Deviation Penalties in an Electricity Market. Energy Convers. Manag. 2013, 76, 1150–1157. [Google Scholar] [CrossRef]
- Miao, S.; Luo, B.; Shen, J.; Cheng, C.; Li, G.; Sun, Y. Short-Term Multi-Objective Hydro-Thermal Generation Dispatch Considering Electricity Market Transition and Mid-and Long-Term Contract Decomposition. Power Syst. Technol. 2018, 42, 2221–2231. [Google Scholar]
- Song, S.; Guo, H.; Yang, P.; Xu, Z.; He, T.; Lu, Z. Research on Demand Response Strategy of the Electricity Deviation Assessment. J. Eng. 2017, 2017, 2221–2225. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, K.; Zhang, S.; Wu, L. Equilibrium Analysis of Electricity Market With Demand Response Exchange to Counterbalance Bid Deviations of Renewable Generators. IEEE Syst. J. 2020, 14, 2713–2724. [Google Scholar] [CrossRef]
- Fabbri, A.; GomezSanRoman, T.; RivierAbbad, J.; MendezQuezada, V.H. Assessment of the Cost Associated With Wind Generation Pre-diction Errors in a Liberalized Electricity Market. IEEE Trans. Power Syst. 2005, 20, 1440–1446. [Google Scholar] [CrossRef]
- Yang, J.; Dong, Z.Y.; Wen, F.; Chen, Q.; Luo, F.; Liu, W.; Zhan, J. A Penalty Scheme for Mitigating Uninstructed Deviation of Generation Outputs from Variable Renewables in a Distribution Market. IEEE Trans. Smart Grid 2020, 11, 4056–4069. [Google Scholar] [CrossRef]
- Koul, B.; Singh, K.; Brar, Y.S. Improvements in Deviation Settlement Mechanism of Indian Electricity Grid System through Demand Response Management. Int. J. Emerg. Electr. Power Syst. 2022, 23, 605–620. [Google Scholar] [CrossRef]
- Van Der Veen, R.A.; Abbasy, A.; Hakvoort, R.A. Agent-Based Analysis of the Impact of the Imbalance Pricing Mechanism on Market Behavior in Electricity Balancing Markets. Energy Econ. 2012, 34, 874–881. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, M.; Zhang, T.; Li, G.; Zhang, Y.; Liu, X. Imbalance Settlement Evaluation for China’s Balancing Market Design via an Agent-Based Model with a Multiple Criteria Decision Analysis Method. Energy Policy 2020, 139, 111297. [Google Scholar] [CrossRef]
- Zani, A.; Rossi, S. Nodal Pricing Applied to Imbalance Settlement: Issues for Implementation in Zonal Markets. In Proceedings of the 2018 15th International Conference on the European Energy Market (EEM), Lodz, Poland, 27–29 June 2018; pp. 1–5. [Google Scholar]
- Zhang, Z.; Jiang, Y.; Lin, Z.; Wen, F.; Ding, Y.; Yang, L.; Lin, Z.; Li, Y.; Qian, H.; Li, J.; et al. Optimal Alliance Strategies Among Retailers Under Energy Deviation Settlement Mechanism in China’s Forward Electricity Market. IEEE Trans. Power Syst. 2020, 35, 2059–2071. [Google Scholar] [CrossRef]
- Lu, Z.; Wang, J.; Yong, W.; Tang, Z.; Yang, M.; Zhang, B. Coordinated P2P Electricity Trading Model with Aggregated Alliance and Reserve Purchasing for Hedging the Risk of Deviation Penalty. Energy Rep. 2021, 7, 426–435. [Google Scholar] [CrossRef]
- Liu, F.; Xu, Y.; Zhu, D.-D.; Wei, S.-M.; Tang, C.-P. Equilibrium Risk Decision Model for Bidding Electricity Quantity Deviation of Cascade Hydropower Stations. J. Electr. Eng. Technol 2024, 19, 977–991. [Google Scholar] [CrossRef]
- Li, L.; Dou, X.; Yang, H.; Fu, Y.; Yu, J.; Huo, X.; Pang, C. Dynamic Aggregation Method for Load Aggregators Considering Users’ Deviation Electricity. Electronics 2024, 13, 278. [Google Scholar] [CrossRef]
- Huang, M.; Wang, X.; Zhang, S. Analysis of an Electricity Market Equilibrium Model with Penalties for Wind Power’s Bidding Deviation. In Proceedings of the 2015 5th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Changsha, China, 26–29 November 2015; pp. 35–40. [Google Scholar]
- Momoh, J.A. Electric Power System Applications of Optimization, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-21895-3. [Google Scholar]
- Biggar, D.R.; Hesamzadeh, M.R. The Economics of Electricity Markets; John Wiley & Sons: Hoboken, NJ, USA, 2014; ISBN 978-1-118-77572-1. [Google Scholar]
- Kreps, D.M. Game Theory and Economic Modelling; Oxford University Press: Oxford, UK, 1990; ISBN 978-0-19-828381-2. [Google Scholar]
- Rau, N.S. Optimization Principles: Practical Applications to the Operation and Markets of the Electric Power Industry; John Wiley & Sons: Hoboken, NJ, USA, 2003; ISBN 978-0-471-45130-3. [Google Scholar]
- Zhang, L.; Xu, C.; Chen, C.; Yang, S. Research on Decoupling and Settlement Mechanism of Electric Energy Market in Electricity Spot Market Environment. Price Theory Pract. 2020, 30–36. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, M.; Kou, Y.; Sun, P.; Wang, X.; Li, G. Imbalance Capital Allocation Mechanism Based on Agent-based Model. Power Syst. Technol. 2021, 45, 3408–3416. [Google Scholar]
- Chen, X.; Liu, J.; Song, Y.; Wang, P.; Su, S. Use of CFDS and FTRS to Hedge Against Risks of Power Market. Proc. CSEE 2005, 75–81. Available online: https://kns.cnki.net/kcms2/article/abstract?v=bnAgTRNiloI5N-pKpKlFzkydwMiccsgwf4iobybEf1Hn_BlnjVDG09xD7hJmGGqm2a1u63Ubl3rGJlOvJWDQuX8e_dqjIKga1AXOTl5EIhG6BMe4ZOqHteDYPxxUHHQM&uniplatform=NZKPT&language=CHS (accessed on 10 June 2024).
- Kristiansen, T. Pricing of Contracts for Difference in the Nordic Market. Energy Policy 2004, 32, 1075–1085. [Google Scholar] [CrossRef]
- Luo, Z.; Ji, T.; Jing, Z.; He, A. Design and Application of Contract for Difference in Electricity Market. Power Syst. Technol. 2019, 43, 2743–2751. [Google Scholar]
- Ye, Z.; Li, M. Analysis on Generation Companies’ Trading Strategy for Medium and Long-term Electricity Contracts Based on CfD. Electr. Power Technol. Econ. 2008, 24–27. Available online: https://kns.cnki.net/kcms2/article/abstract?v=bnAgTRNiloIVUja-jlufBQCG3AnrysuOKZl8UoBEzu6fxp0rFppG9ZSjK7nESsaIFmC6R2Iy7arM84nubYrRp_v64kyrK7nE-Iu7mlhkJ66TiGrNSt4LMAYZqVG91yKLFW7HS1xhuTMGM7LiSebDnQ==&uniplatform=NZKPT&language=CHS (accessed on 10 June 2024).
- Ye, Z. The principle of marginal cost pricing and its application in the formulation or formation of electricity price. China Power Enterp. Manag. 2020, 33–37. Available online: https://kns.cnki.net/kcms2/article/abstract?v=bnAgTRNiloLwzHO6OImjNYs-HfV4Zv_X0skLNbLjoKZEXU6YbT1iMjy-uMPhZWbCK685_HkuupLZDQdQZZs9YUGv1otd06CsGuV2bYvo1K40hkLERifUEIfwQ58LtN4mlJwnIXRQcEk=&uniplatform=NZKPT&language=CHS (accessed on 10 June 2024).
- Huang, S.; Ye, Z.; Luo, M.; Chen, L.; Wei, W.; Yao, J. Time-Sharing Trading Price Formation Mechanism and Model of China’s Mid to Long-Term Electricity Market. Electr. Power 2023, 56, 17–27. [Google Scholar]
- Jia, X.; Xia, Q.; Chen, Q.; Ding, M.; Ning, B. Electricity Pricing Mechanism Based on Effective Capacity Cost of Power Generation. Autom. Electr. Power Syst. 2013, 37, 6–13. [Google Scholar]



| Country or Region | Market Model | Treatment | 1 Energy Consumption/EJ | 1 Energy Generation/TWH |
|---|---|---|---|---|
| Australia | Centralized wholesale market | a. No deviation electricity settlement b. All actual electricity is accepted for settlement at real-time market prices | 5.98 | 273.6 |
| American PJM | a. Spot market dual settlement system b. Hedging of spot price risk through CFDs and future financial transactions | 7.31 | 4547.7 | |
| UK | Decentralized electricity market | a. Forward trading contracts for physical delivery b. Real-time power balancing is guaranteed through the BM | 1.36 | 326 |
| Northern Europe | a. Establishment of co-regulated markets b. Adoption of a pre-listed balancing mechanism | 1.9 (Norway) | 146.8 (Norway) |
| Province | Exemption Margin | Penalty Price 1 | |
|---|---|---|---|
| Exceed | Less | ||
| Shandong | −2~6% | 5% of the contractual weighted average electricity purchase price | Reduction in the power compensation tariff |
| Guangdong | −5~5% | 2× absolute monthly market clearing spreads | |
| Sichuan | −2~2% | Hydroelectricity trading tariff cap | 70% of hydroelectricity trading tariff cap |
| Hubei | −5~5% | Assessed at 0.05 CNY/KWH | |
| Scenarios | Supply–Demand Relationship | Pricing Methods | Concrete Operation |
|---|---|---|---|
| 1 | Basic balance | System average cost pricing | Time-sharing capacity costs overlaid on time-sharing variable costs |
| 2 | Supply less than demand | User off-load value pricing clearing spreads | General use of KWH GDP value added |
| 3 | Supply exceeds demand | System marginal cost pricing | Recovery of time-sharing variable costs only |
| 4 | Extreme oversupply | Lost generation value pricing | Generally use unit start or stop costs |
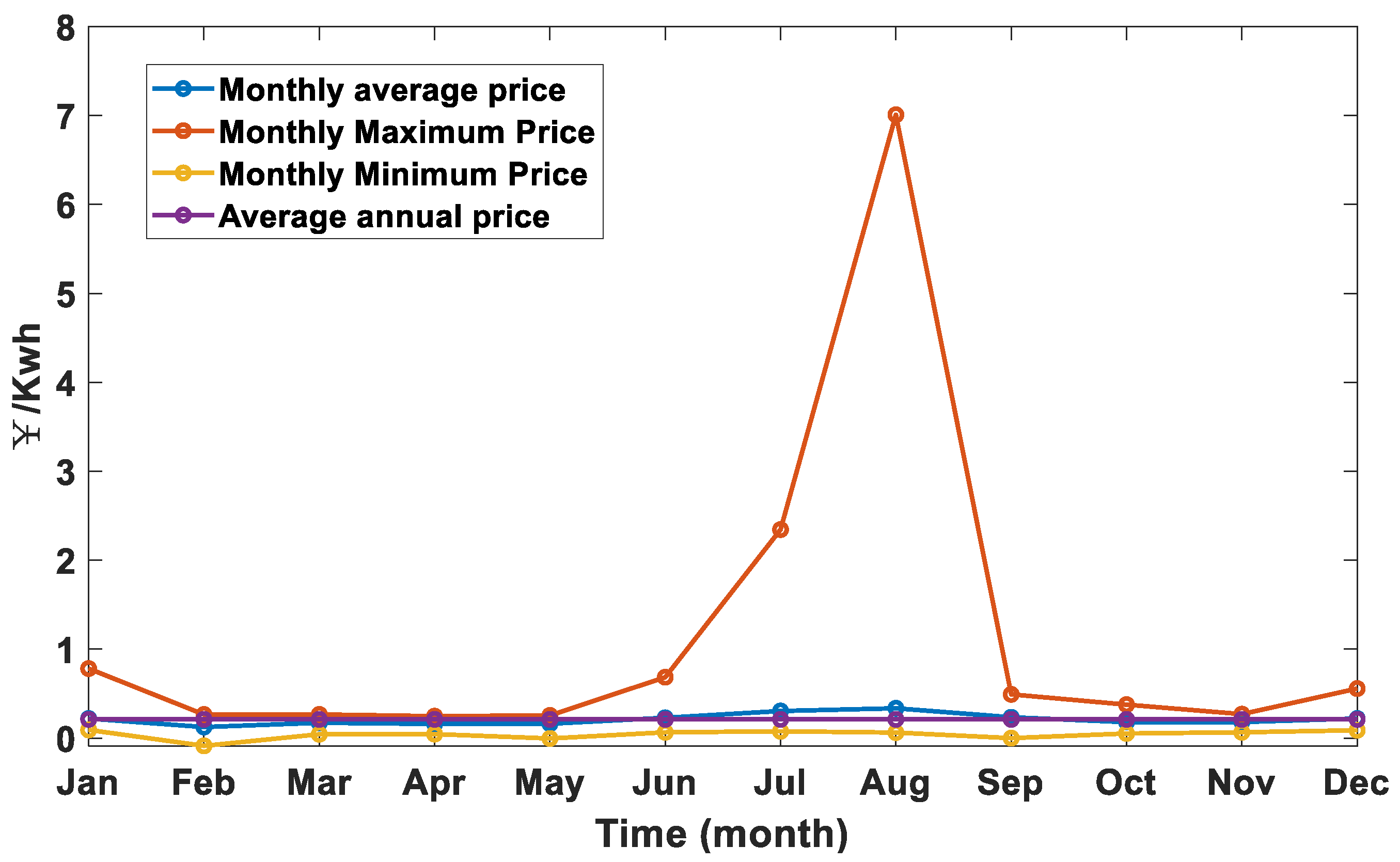
| Month | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| monthly average | 0.2200 | 0.1244 | 0.1721 | 0.1592 | 0.1616 | 0.2287 | 0.3046 | 0.3353 | 0.2344 | 0.1795 | 0.1805 | 0.2203 |
| monthly maximum | 0.7818 | 0.2654 | 0.2663 | 0.2467 | 0.2553 | 0.6848 | 2.3447 | 7.0085 | 0.4918 | 0.3762 | 0.2695 | 0.5570 |
| monthly minimum | 0.0921 | −0.0869 | 0.0434 | 0.0450 | −0.0039 | 0.0649 | 0.0764 | 0.0624 | 0.0000 | 0.0519 | 0.0653 | 0.0883 |
| Scenarios | 1 | 2 | 3 |
|---|---|---|---|
| Total contracted electricity/GW | 230,000 | ||
| Total actual electricity/GW | 233,500 | ||
| Total deviation electricity/GW | 3500 | ||
| Deviation assessment costs/CNY million | 3009.5 | 459.52 | 1247.24 |
| DE base/GW | 12,128 | 22,663 | 67,516 |
| BSP balance service fee/CNY million | 459.52 | 459.52 | 459.52 |
| Additional costs borne by SO/CNY million | 2550.02 | 0 | 0 |
| Average deviation cost/CNY/KWH | 0.2481 | 0.0203 | 0.0185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, Z.; Liang, D.; Wang, M.; Huang, S.; Luo, O. An Assessment Method of Deviation Electricity Responsibility in China’s Forward Electricity Market Based on Time-Sharing Trading Prices. Sustainability 2024, 16, 5130. https://doi.org/10.3390/su16125130
Ye Z, Liang D, Wang M, Huang S, Luo O. An Assessment Method of Deviation Electricity Responsibility in China’s Forward Electricity Market Based on Time-Sharing Trading Prices. Sustainability. 2024; 16(12):5130. https://doi.org/10.3390/su16125130
Chicago/Turabian StyleYe, Ze, Deping Liang, Meihui Wang, Shanshan Huang, and Ouzhe Luo. 2024. "An Assessment Method of Deviation Electricity Responsibility in China’s Forward Electricity Market Based on Time-Sharing Trading Prices" Sustainability 16, no. 12: 5130. https://doi.org/10.3390/su16125130
APA StyleYe, Z., Liang, D., Wang, M., Huang, S., & Luo, O. (2024). An Assessment Method of Deviation Electricity Responsibility in China’s Forward Electricity Market Based on Time-Sharing Trading Prices. Sustainability, 16(12), 5130. https://doi.org/10.3390/su16125130





