Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments
Abstract
1. Introduction
| Method | Resilience Indicator Type | Resilience Indicator |
|---|---|---|
| Agent-based method | Proxy metric | Resilience index [16]; combination of resilience index, reliability and redundancy [17]; modified resilience index [18]; flow entropy [20]. |
| Simulation method | Hydraulic metric | Satisfaction degree index [12,23,24]; pressure, demand, water serviceability, and population impacted [25]. |
| Network theory method | Topological metric | Statistical and spectral metrics [27]; weighted K-level shortest-path-based topological metric [28]; edge-betweenness-based topological metric [29]; minimum cut set-based system reliability [30]; topological resilience metric (TRM) [31]; modified TRM [11,32]. |
2. Methodology
2.1. Corrosion Model of Buried Pipelines with Different Service Ages
2.2. Seismic Fragility of Pipelines
2.3. Hydraulic Analysis Model
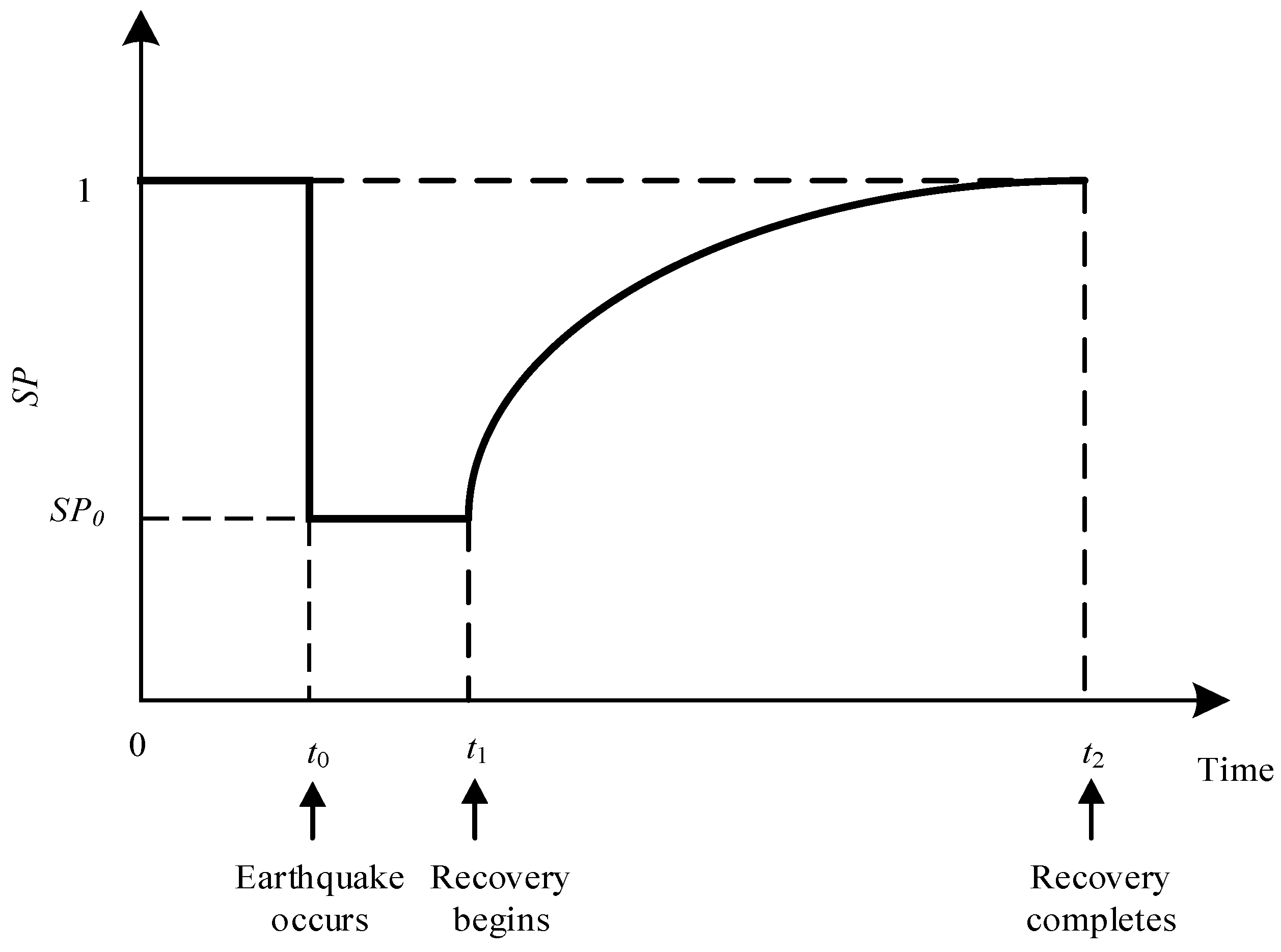
2.4. Seismic Resilience Assessment Method for WDS
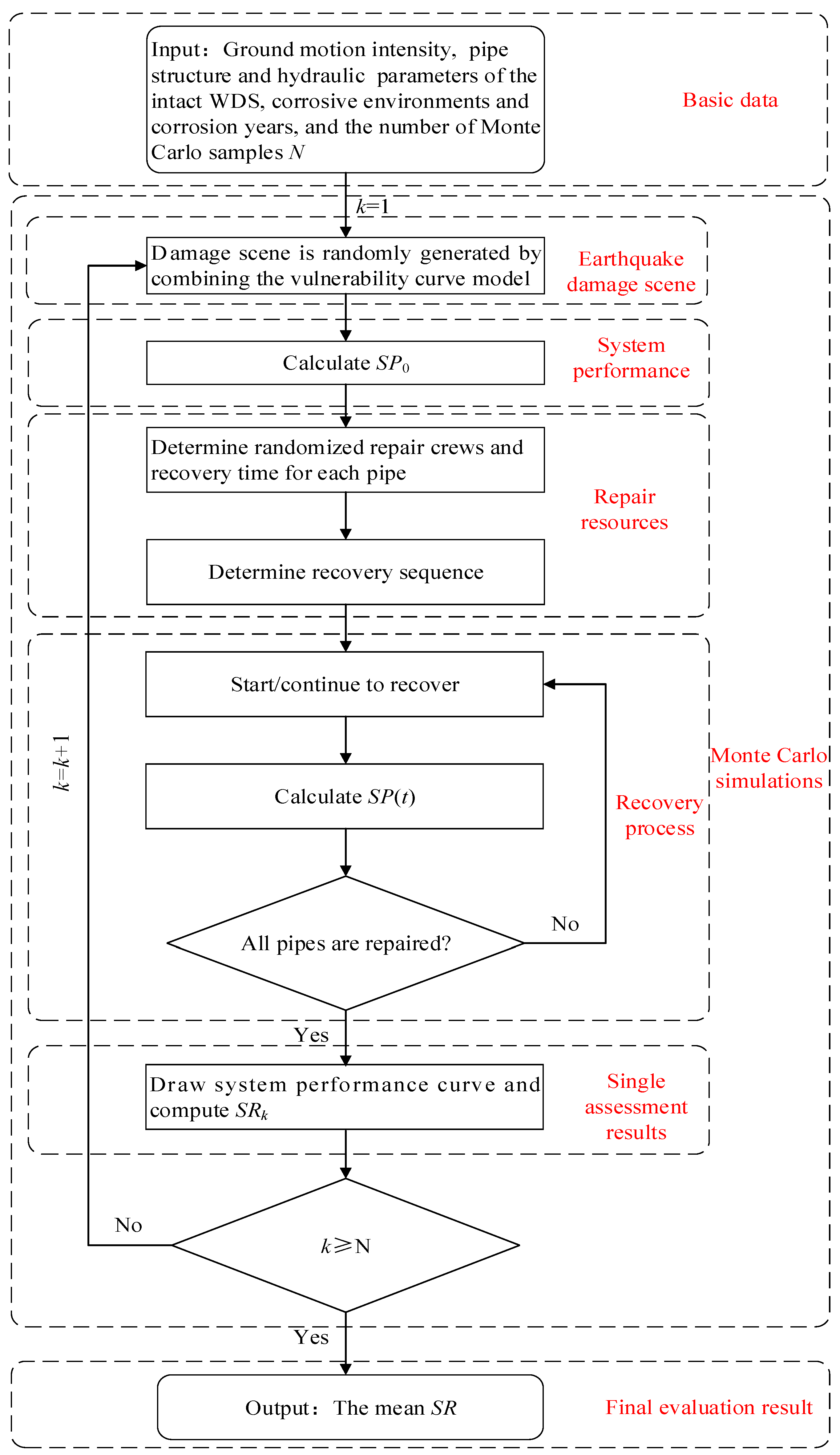
2.5. Monte Carlo Simulation
3. Case Study
3.1. Results of Hydraulic Analysis under Different Working Conditions
3.2. Seismic Resilience Evaluation Results
3.3. Results of Seismic Resilience Assessment Based on Empirical Data
4. Conclusions
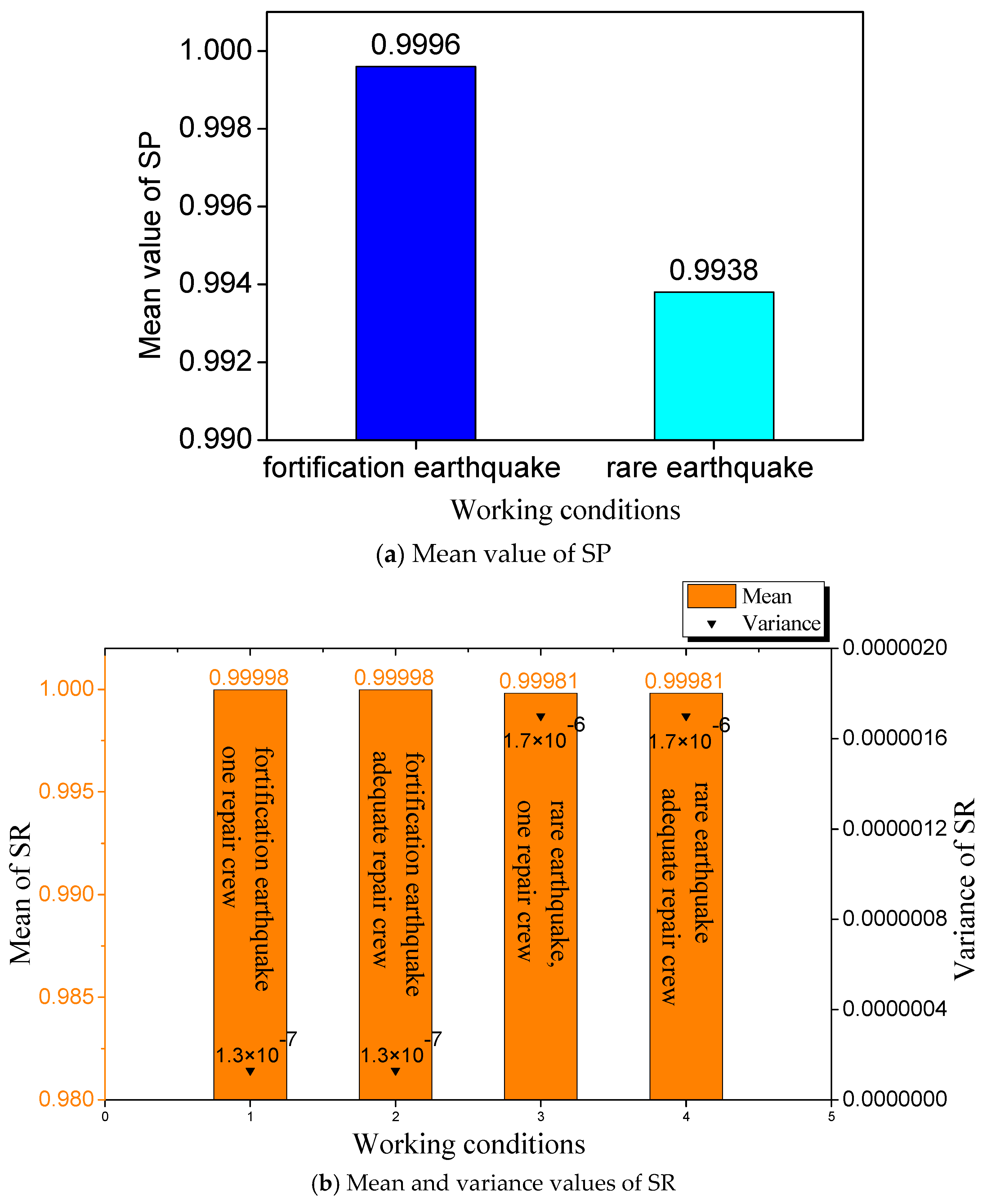
- The simulation results indicated that both SP and SR remained at 100% across various service ages and soil conditions when subjected to frequent earthquakes.
- The SP and SR for the four service ages in the three soil environments did not differ significantly under the effects of a fortification earthquake. Compared with the simulation results under frequent earthquakes, there was a slight decrease, but the overall decrease was not significant.
- Under rare earthquake conditions, SP and SR varied significantly, especially in acidic environments where performance notably declined, with the worst recorded SP being 0.68 for pipelines with a service age of 40 years. Despite this, the overall performance across different conditions remained relatively high, with SP values ranging from a minimum of 83.8% to a maximum of 98.2%, and an average SP of 91%. This showed that post-earthquake restoration resources are a key factor in guaranteeing a high level of the SP.
- Holding the service age and soil environment constant, the SR diminished progressively as seismic activity intensified. Under identical service ages and high seismic intensities, the SR was lowest in acidic soil environments and highest in near-neutral soil environments. Considering a constant soil environment and high seismic activity, the SR progressively declined with the advancing service age. The assignment of multiple repair crews universally resulted in a high SR for the WDSs.
- Based on evaluations using empirical data, the SP and SR, when assessed without accounting for variations in soil corrosion conditions and the service age of the pipelines, tended to be estimated on the higher side.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhai, C.; Zhao, Y.; Wen, W.; Qin, H.; Xie, L. A novel urban seismic resilience assessment method considering the weighting of post-earthquake loss and recovery time. Int. J. Disaster Risk Reduct. 2023, 84, 103453. [Google Scholar] [CrossRef]
- Taghizadeh, M.; Mahsuli, M.; Poorzahedy, H. Probabilistic framework for evaluating the seismic resilience of transportation systems during emergency medical response. Reliab. Eng. Syst. Saf. 2023, 236, 109255. [Google Scholar] [CrossRef]
- Liu, J.; Tian, L.; Yang, M.; Meng, X. Probabilistic framework for seismic resilience assessment of transmission tower-line systems subjected to mainshock-aftershock sequences. Reliab. Eng. Syst. Saf. 2024, 242, 109755. [Google Scholar] [CrossRef]
- Li, Z.; Lim, H.W.; Li, N.; Long, Y.; Fang, D. Assessing the seismic resilience of a healthcare system: A hybrid modeling. Int. J. Disaster Risk Reduct. 2023, 93, 103730. [Google Scholar] [CrossRef]
- Liu, W.; Wu, Q.X. Seismic resilience analysis of water distribution networks with multi-components and resilience improvement strategies. J. Seismol. Res. 2023, 46, 271–279. [Google Scholar] [CrossRef]
- Scawthorn, C. Water Supply in Regard to Fire Following Earthquakes; Pacific Earthquake Engineering Research Center: Berkeley, CA, USA, 2011. [Google Scholar]
- Miyajima, M. Damage analysis of water supply facilities in the 2011 great east japan earthquake and tsunami. In Proceedings of the 15th World Conference in Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 24–28. [Google Scholar]
- Manyena, S.B. The concept of resilience revisited. Disasters 2006, 30, 433–450. [Google Scholar] [CrossRef] [PubMed]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Pagano, A.; Giordano, R.; Portoghese, I. A pipe ranking method for water distribution network resilience assessment based on graph-theory metrics aggregated through Bayesian belief networks. Water Resour. Manag. 2022, 36, 5091–5106. [Google Scholar] [CrossRef]
- Li, W.; Mazumder, R.K.; Li, Y. Topology-based resilience metrics for seismic performance evaluation and recovery analysis of water distribution systems. J. Pipeline Syst. Eng. Pract. 2023, 14, 04022070. [Google Scholar] [CrossRef]
- Song, Z.; Liu, W.; Shu, S. Resilience-based post-earthquake recovery optimization of water distribution networks. Int. J. Disaster Risk Reduct. 2022, 74, 102934. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.; Ouyang, M.; Li, J. Recovery-based seismic resilience enhancement strategies of water distribution networks. Reliab. Eng. Syst. Saf. 2020, 203, 107088. [Google Scholar] [CrossRef]
- Creaco, E.; Franchini, M.; Todini, E. Generalized resilience and failure indices for use with pressure-driven modeling and leakage. J. Water Resour. Plan. Manag. 2016, 142, 04016019. [Google Scholar] [CrossRef]
- Jeong, G.; Wicaksono, A.; Kang, D. Revisiting the resilience index for water distribution networks. J. Water Resour. Plan. Manag. 2017, 143, 04017035. [Google Scholar] [CrossRef]
- Todini, E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water 2000, 2, 115–122. [Google Scholar] [CrossRef]
- Prasad, T.D.; Park, N.S. Multi-objective genetic algorithms for design of water distribution networks. J. Water Resour. Plan. Manag. 2004, 130, 73–82. [Google Scholar] [CrossRef]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44, W01417. [Google Scholar] [CrossRef]
- Awumah, K.; Goulter, I.; Bhatt, S.K. Entropy-Based Redundancy Measures in Water-Distribution Networks. J. Hydraul. Eng. 1991, 117, 595–614. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Templeman, A.B. Calculating Maximum Entropy Flows in Networks. J. Oper. Res. Soc. 1993, 44, 383–396. [Google Scholar] [CrossRef]
- Lee, E.H.; Lee, Y.S.; Joo, J.G.; Jung, D.; Kim, J.H. Investigating the impact of proactive pump operation and capacity expansion on urban drainage system resilience. J. Water Resour. Plan. Manag. 2017, 143, 04017024. [Google Scholar] [CrossRef]
- Klise, K.A.; Bynum, M.; Moriarty, D.; Murray, R. A software framework for assessing the resilience of drinking water systems to disasters with an example earthquake case study. Environ. Model. Softw. 2017, 95, 420–431. [Google Scholar] [CrossRef]
- Liu, W.; Song, Z.; Ouyang, M. Lifecycle operational resilience assessment of urban water distribution networks. Reliab. Eng. Syst. Saf. 2020, 198, 106859. [Google Scholar] [CrossRef]
- Long, L.; Zheng, S.S.; Yang, Y.; Zhou, Y. Research on the recovery strategy of the urban water supply networks after an earthquake. J. Seismol. Res. 2022, 45, 352–361. [Google Scholar] [CrossRef]
- Bata, M.H.; Carriveau, R.; Ting, D.S.-K. Urban water supply systems’ resilience under earthquake scenario. Sci. Rep. 2022, 12, 20555. [Google Scholar] [CrossRef] [PubMed]
- Hou, B.; Huang, J.; Miao, H.; Zhao, X.; Wu, S. Seismic resilience evaluation of water distribution systems considering hydraulic and water quality performance. Int. J. Disaster Risk Reduct. 2023, 93, 103756. [Google Scholar] [CrossRef]
- Yazdani, A.; Otoo, R.A.; Jeffrey, P. Resilience enhancing expansion strategies for water distribution systems: A network theory approach. Environ. Model. Softw. 2011, 26, 1574–1582. [Google Scholar] [CrossRef]
- Herrera, M.; Abraham, E.; Stoianov, I. A graph-theoretic framework for assessing the resilience of sectorised water distribution networks. Water Resour. Manag. 2016, 30, 1685–1699. [Google Scholar] [CrossRef]
- Li, W.; Mazumder, R.K.; Bastidas-Arteaga, E.; Li, Y. Seismic Performance Evaluation of Corroded Water Distribution Systems Considering Firefighting. J. Water Resour. Plan. Manag. 2024, 150, 04023075. [Google Scholar] [CrossRef]
- BÃűde, E.; Peikenkamp, T.; Rakow, J.; Wischmeyer, S. Model based importance analysis for minimal cut sets. In Automated Technology for Verification and Analysis; Series Lecture Notes in Computer Science; Cha, S., Choi, J.-Y., Kim, M., Lee, I., Viswanathan, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5311, pp. 303–317. [Google Scholar]
- Farahmandfar, Z.; Piratla, K.R. Comparative evaluation of topological and flow-based seismic resilience metrics for rehabilitation of water pipeline systems. J. Pipeline Syst. Eng. Pract. 2018, 9, 04017027. [Google Scholar] [CrossRef]
- Meng, F.; Fu, G.; Farmani, R.; Sweetapple, C.; Butler, D. Topological attributes of network resilience: A study in water distribution systems. Water Res. 2018, 143, 376–386. [Google Scholar] [CrossRef]
- Liu, H.J. Research on the Resilience of Urban Water Distribution Networks Based on Energy and Topology. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2021. [Google Scholar]
- Pietrucha-Urbanik, K.; Rak, J. Water, Resources, and Resilience: Insights from Diverse Environmental Studies. Water 2023, 15, 3965. [Google Scholar] [CrossRef]
- Bolzoni, F.; Fassina, P.; Fumagalli, G.; Lazzari, L.; Mazzola, E. Application of probabilistic models to localised corrosion study. Metall. Ital. 2006, 98, 9–15. [Google Scholar]
- Timashev, S.A.; Malyukova, M.G.; Poluian, L.V.; Bushinskaya, A.V. Markov Description of Corrosion Defects Growth and Its Application to Reliability Based Inspection and Maintenance of Pipelines. Am. Soc. Mech. Eng. 2008, 48609, 525–533. [Google Scholar]
- Huang, T.; Chen, X.P.; Wang, X.D.; Mi, F.Y.; Liu, R.; Li, X.Y. Effect of pH Value on Corrosion Behavior of Q235 Steel in an Artificial Soil. J. Chin. Soc. Corros. Prot. 2016, 36, 31–38. [Google Scholar]
- Li, H.K.; Zhu, F.Y.; Lou, Y.X.; Han, C.C.; Liu, Z.J.; Wang, Y. Distribution of Free Corrosion Rate of Pipeline Steel in Soil with Different Resistivity. Corros. Prot. 2017, 38, 598–601. [Google Scholar]
- Cai, Y.L. Seismic Vulnerability Analysis of Water Supply System. Master’s Thesis, Xi’an University of Architecture & Technology, Xi’an, China, 2019. [Google Scholar]
- Tarbotton, C.; Dall’Osso, F.; Dominey-Howes, D.; Goff, J. The use of empirical vulnerability functions to assess the response of buildings to tsunami impact: Comparative review and summary of best practice. Earth-Sci. Rev. 2015, 142, 120–134. [Google Scholar] [CrossRef]
- Shabani, A.; Kioumarsi, M.; Zucconi, M. State of the art of simplified analytical methods for seismic vulnerability assessment of unreinforced masonry buildings. Eng. Struct. 2021, 239, 112280. [Google Scholar] [CrossRef]
- Jaiswal, K.S.; Aspinall, W.; Perkins, D.; Wald, D.; Porter, K.A. Use of expert judgment elicitation to estimate seismic vulnerability of selected building types. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012; pp. 1–10. [Google Scholar]
- He, J.C.; Han, F.; Zheng, S.S.; Xie, X.Q.; Cai, Y.L. Seismic Vulnerability Analysis of Multi-Age Buried Steel Pipes in an Acidic Soil Environment. J. Tianjin Univ. (Sci. Technol.) 2020, 53, 881–889. [Google Scholar]
- Liu, A.W.; Hu, Y.X.; Zhao, F.X.; Li, X.J.; Takada, S.; Zhao, L. An equivalent-boundary method for the shell analysis of buried pipelines under fault movement. Acta Seismol. Sin. 2004, 17, 141–147. [Google Scholar] [CrossRef]
- Crisfield, M.A. A faster modified Newton-Raphson iteration. Comput. Methods Appl. Mech. Eng. 1979, 20, 267–278. [Google Scholar] [CrossRef]
- Hou, B.W. Seismic Performance Assessment and Performance-Based Design of Water Distribution System. Ph.D. Thesis, Beijing University of Technology, Beijing, China, 2014. [Google Scholar]
- Shi, P. Seismic Response Modeling of Water Supply Systems. Ph.D. Dissertation, Cornell University, Ithaca, NY, USA, 2006. [Google Scholar]
- Choi, J.; Kang, D. Improved hydraulic simulation of valve layout effects on post-earthquake restoration of a water distribution network. Sustainability 2020, 12, 3492. [Google Scholar] [CrossRef]
- Han, Z.; Ma, D.; Hou, B.; Wang, W. Seismic resilience enhancement of urban water distribution system using restoration priority of pipeline damages. Sustainability 2020, 12, 914. [Google Scholar] [CrossRef]
- Gupta, R.; Bhave, P.R. Comparison of methods for predicting deficient-network performance. J. Water Resour. Plan. Manag. 1996, 122, 214–217. [Google Scholar] [CrossRef]
- Long, L.; Yang, H.; Zhou, Y.; Yang, Y. Research on Seismic Connectivity Reliability Analysis of Water Distribution System Based on CUDA. Water 2023, 15, 2087. [Google Scholar] [CrossRef]
- Rak, J.; Pietrucha, K. Some factors of crisis management in water supply system. Environ. Prot. Eng. 2008, 34, 57. [Google Scholar]
- FEMA. Multi-Hazard Loss Estimation Methodology, Earthquake Model (HAZUS-MHMR4); FEMA: Washington, DC, USA, 2003.
- JWWA. Seismic Damage Prediction of Water Supply Pipelines; Japan Water Works Association (JWWA): Tokyo, Japan, 1998. [Google Scholar]














Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Long, L.; Yang, H.; Zheng, S.; Cai, Y. Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments. Sustainability 2024, 16, 5126. https://doi.org/10.3390/su16125126
Long L, Yang H, Zheng S, Cai Y. Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments. Sustainability. 2024; 16(12):5126. https://doi.org/10.3390/su16125126
Chicago/Turabian StyleLong, Li, Huaping Yang, Shansuo Zheng, and Yonglong Cai. 2024. "Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments" Sustainability 16, no. 12: 5126. https://doi.org/10.3390/su16125126
APA StyleLong, L., Yang, H., Zheng, S., & Cai, Y. (2024). Seismic Resilience Evaluation of Urban Multi-Age Water Distribution Systems Considering Soil Corrosive Environments. Sustainability, 16(12), 5126. https://doi.org/10.3390/su16125126






