Low-Carbon Economic Dispatch Model of Integrated Energy System Accounting for Concentrating Solar Power and Hydrogen-Doped Combustion
Abstract
:1. Introduction
- (1)
- A CSP-P2G-HCHP coupled integrated energy system based on the carbon trading mechanism is proposed. The results show that the proposed method takes into account the carbon reduction effect and operation efficiency and effectively improves the new energy consumption capacity.
- (2)
- The use of P2G technology to absorb excess wind power for hydrogen production and methanation effectively improves the utilization efficiency of new energy and the recycling of CO2.
- (3)
- Considering the hydrogen blending operation mode of cogeneration units and gas boilers, the utilization efficiency of hydrogen energy is improved, and the emission reduction potential of hydrogen energy is explored.
2. Integrated Energy Dispatch Modeling of CSP with Hydrogen-Doped Combustion
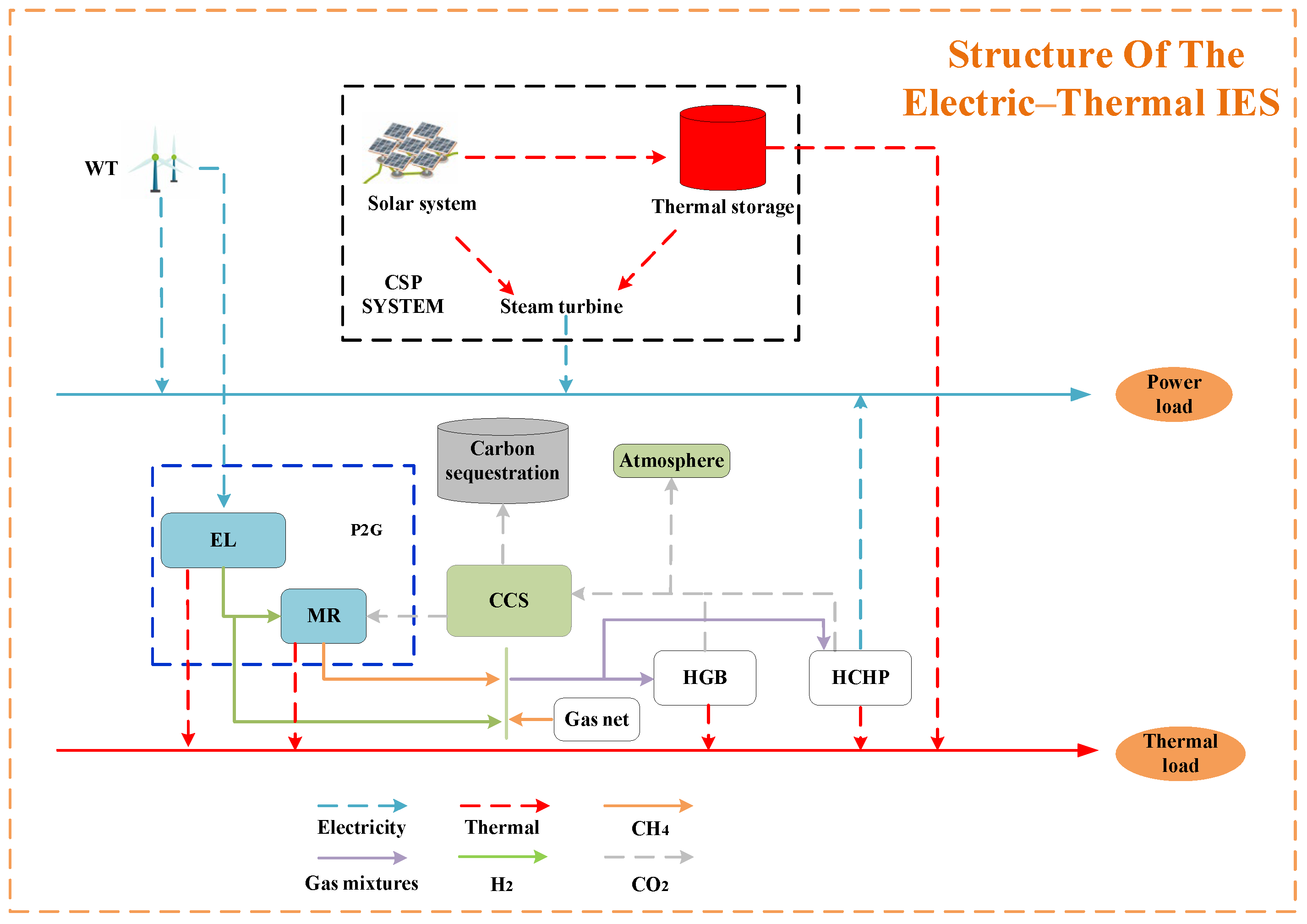
2.1. Structure of the Electric–Thermal Integrated Energy System
2.2. System Operation Strategy Analysis
2.3. Mechanism of Joint Operation of CSP and CHP
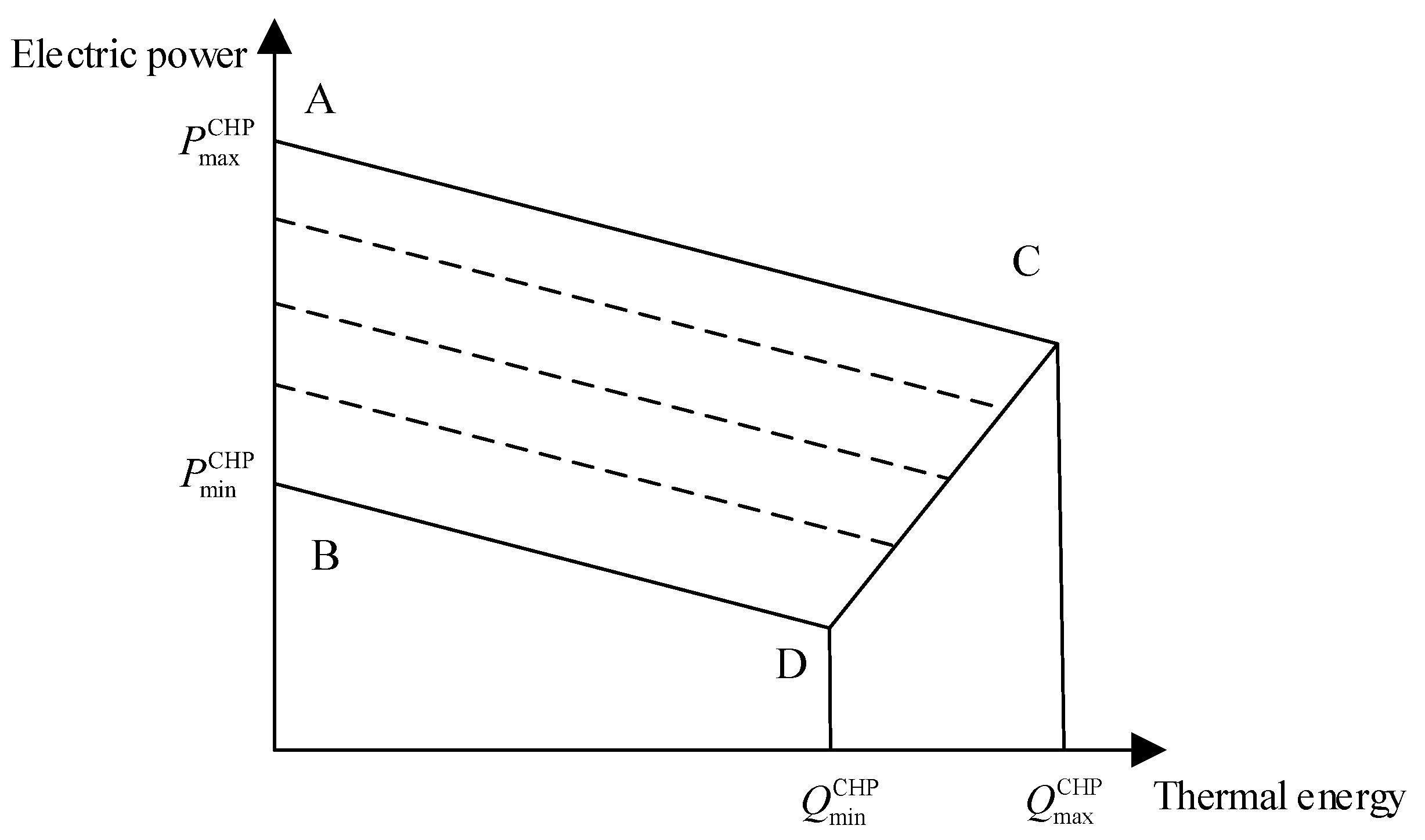
2.3.1. Electro-Thermal Characteristics of the CHP Operating Mode
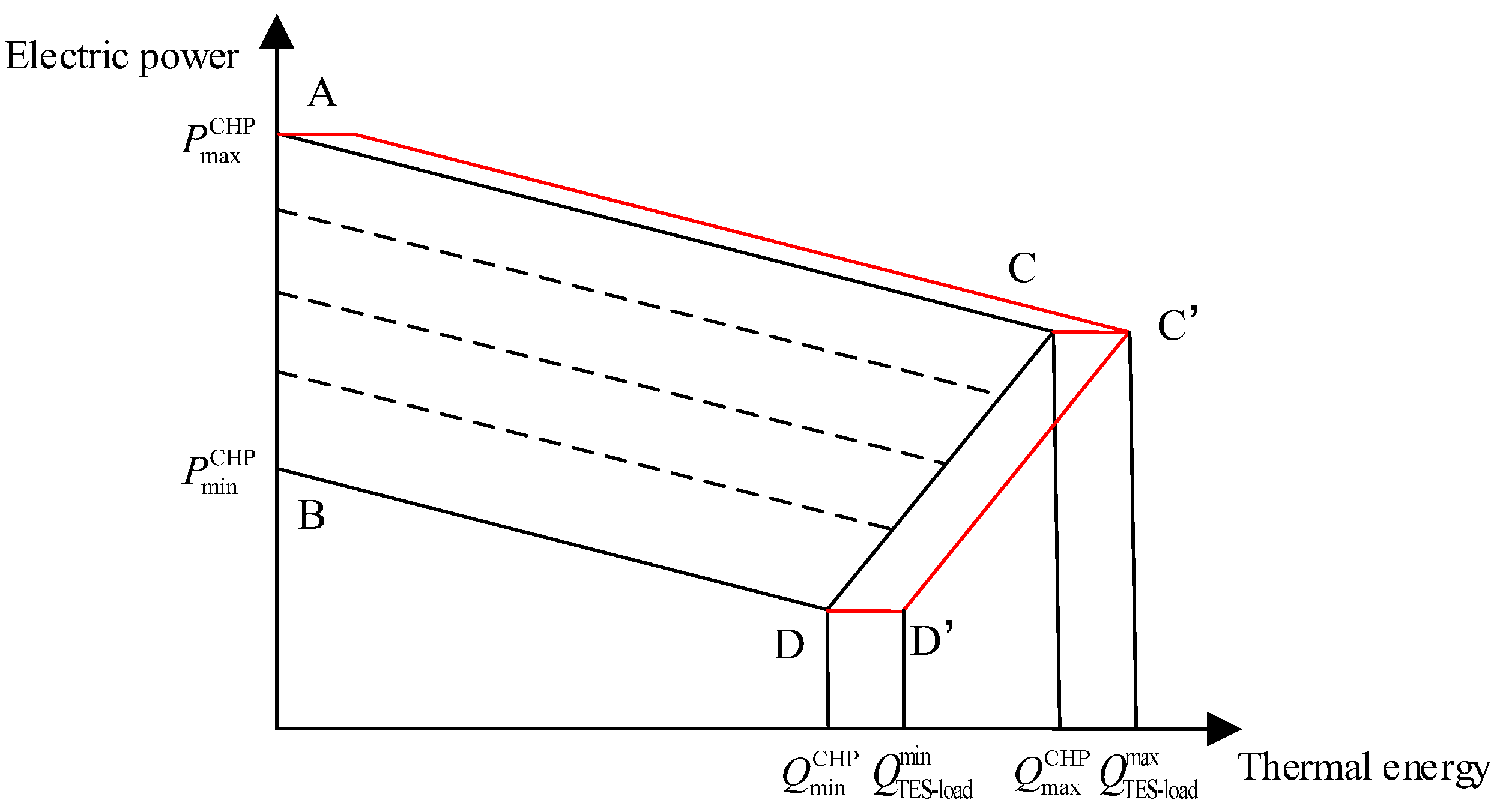
2.3.2. Joint Operation of CSP and CHP
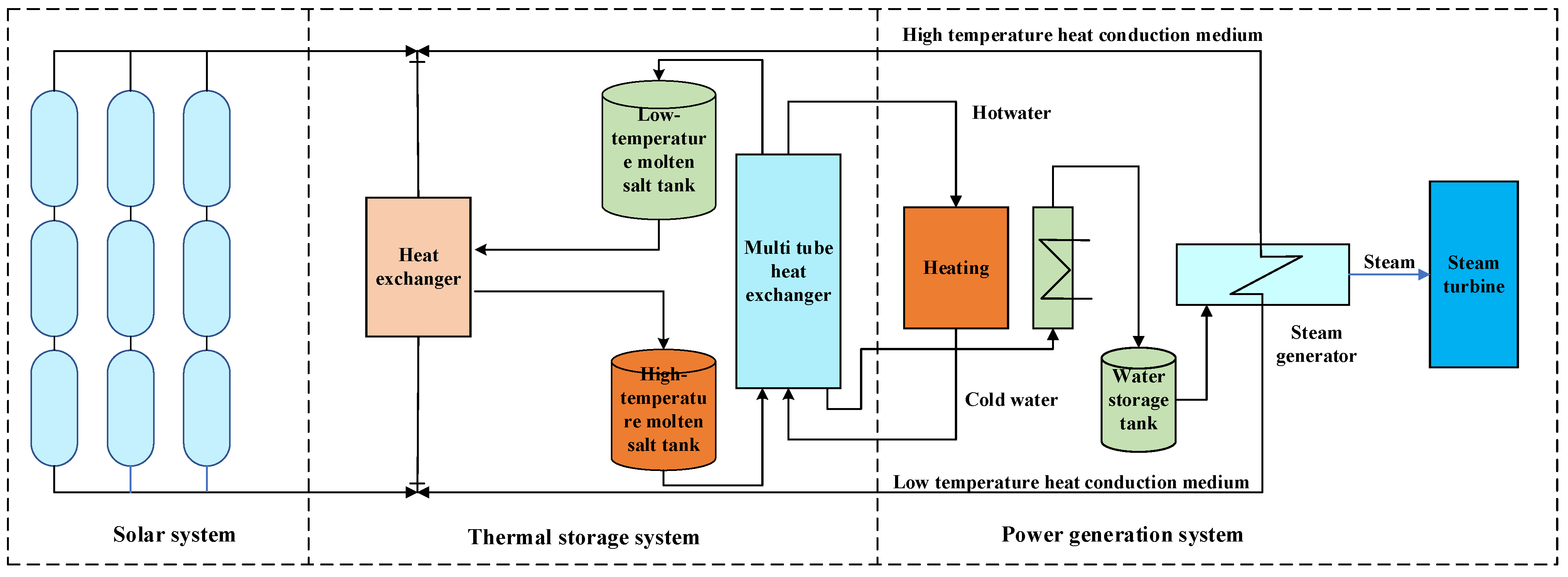
2.4. CSP Mathematical Model
2.5. HCHP and HGB Mathematical Modeling
2.5.1. HCHP Modeling
2.5.2. HGB Modeling
2.5.3. Electrolyzer Modeling
2.5.4. MR Modeling
3. Scheduling Strategy Based on Joint Operation of CSP and Hydrogen-Doped Combustion
3.1. Objective Function
- (1)
- Equipment operation and maintenance costs:
- (2)
- Purchased energy costs:
- (3)
- Wind abandonment costs:
- (4)
- Cost of carbon emissions:
3.2. Constraints
- (1)
- Electrical power balance constraints:
- (2)
- Thermal energy balance constraints:
- (3)
- Natural gas balance constraints:
- (4)
- Hydrogen equilibrium constraints:
- (5)
- WT output constraints:
- (6)
- CSP operational constraints:
- (7)
- HCHP unit constraints:
- (8)
- HGB unit constraints:
- (9)
- CCS unit constraints:
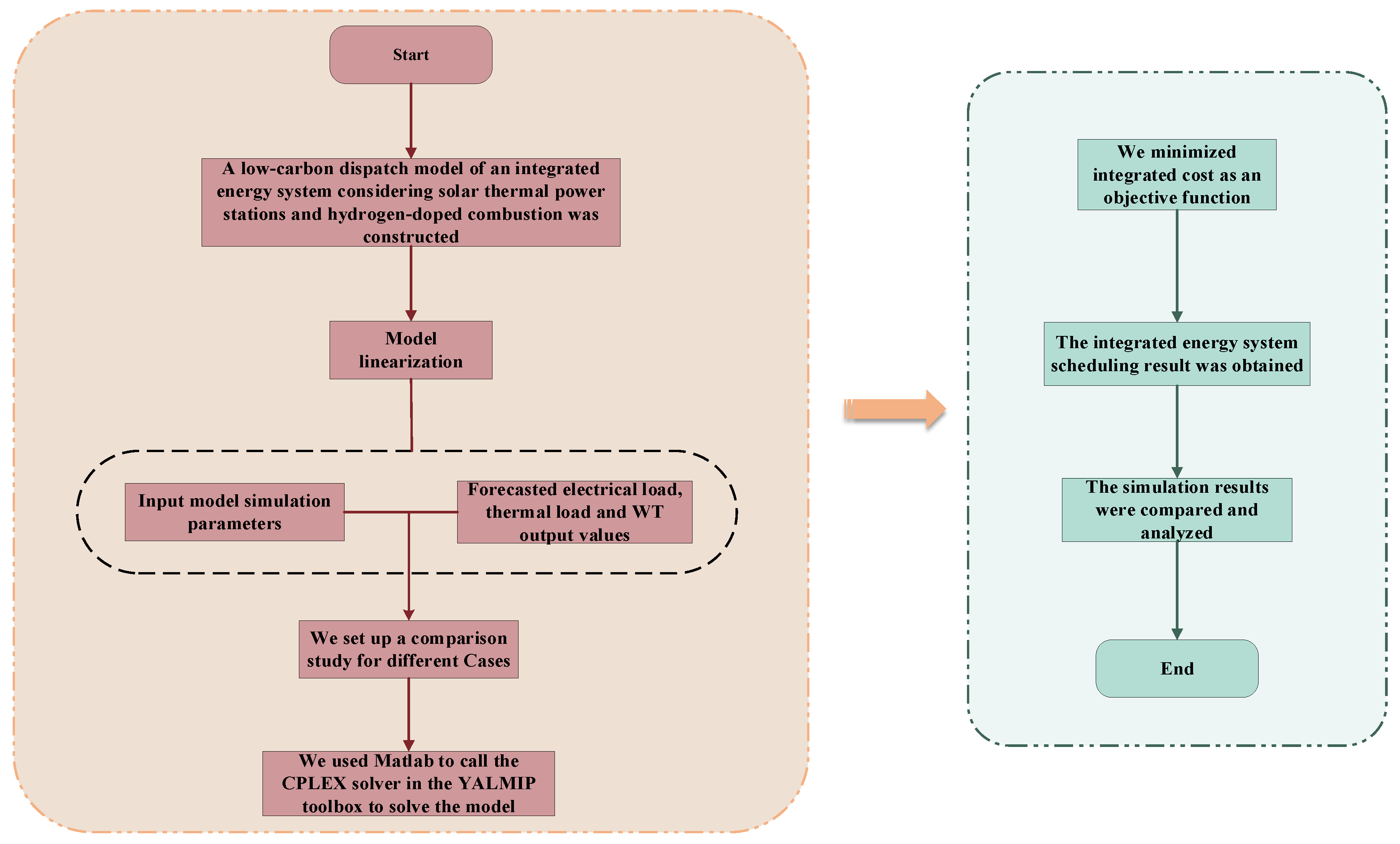
3.3. Solution Process
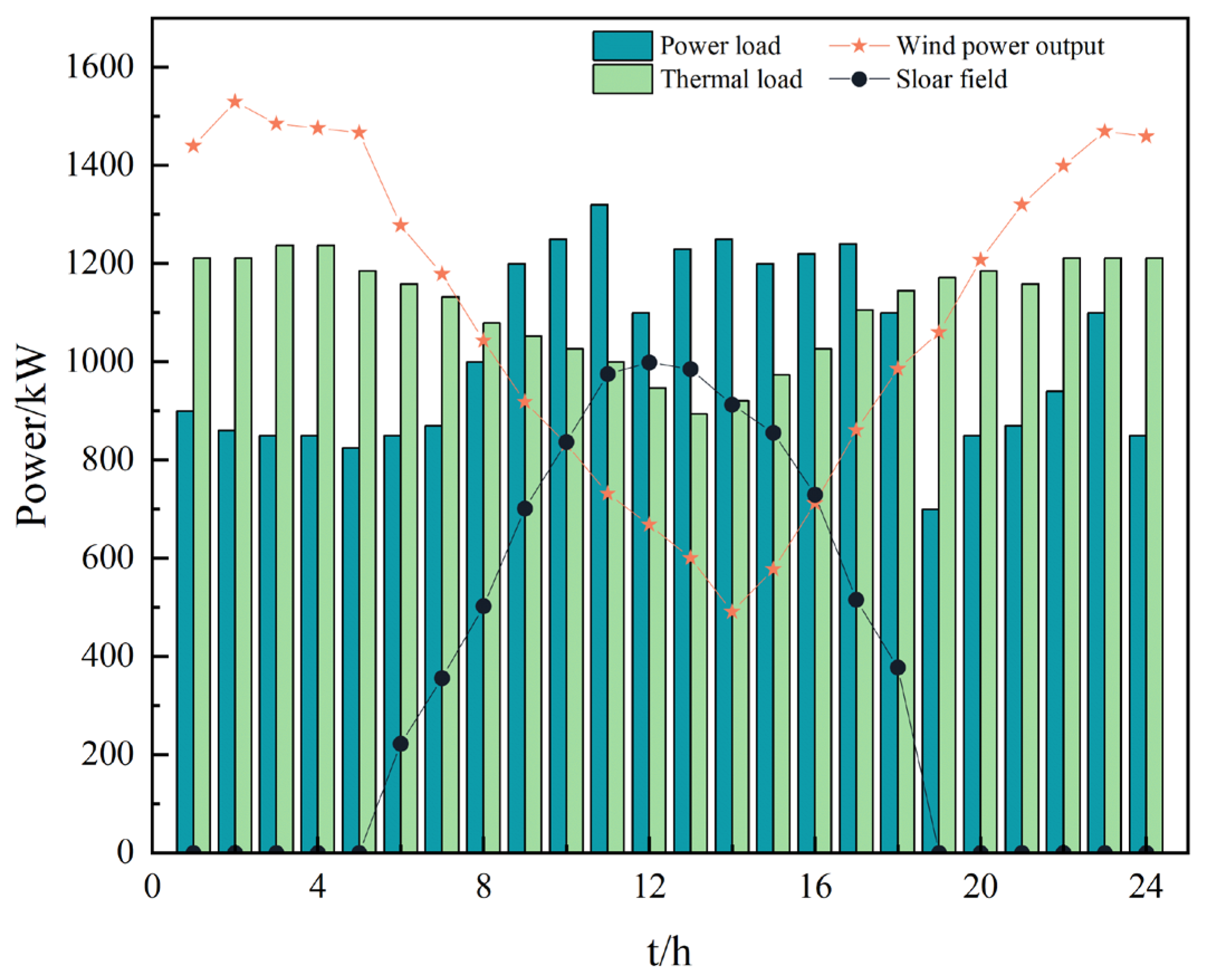
3.4. Case Setup
4. Results and Discussion
4.1. Cost Analysis
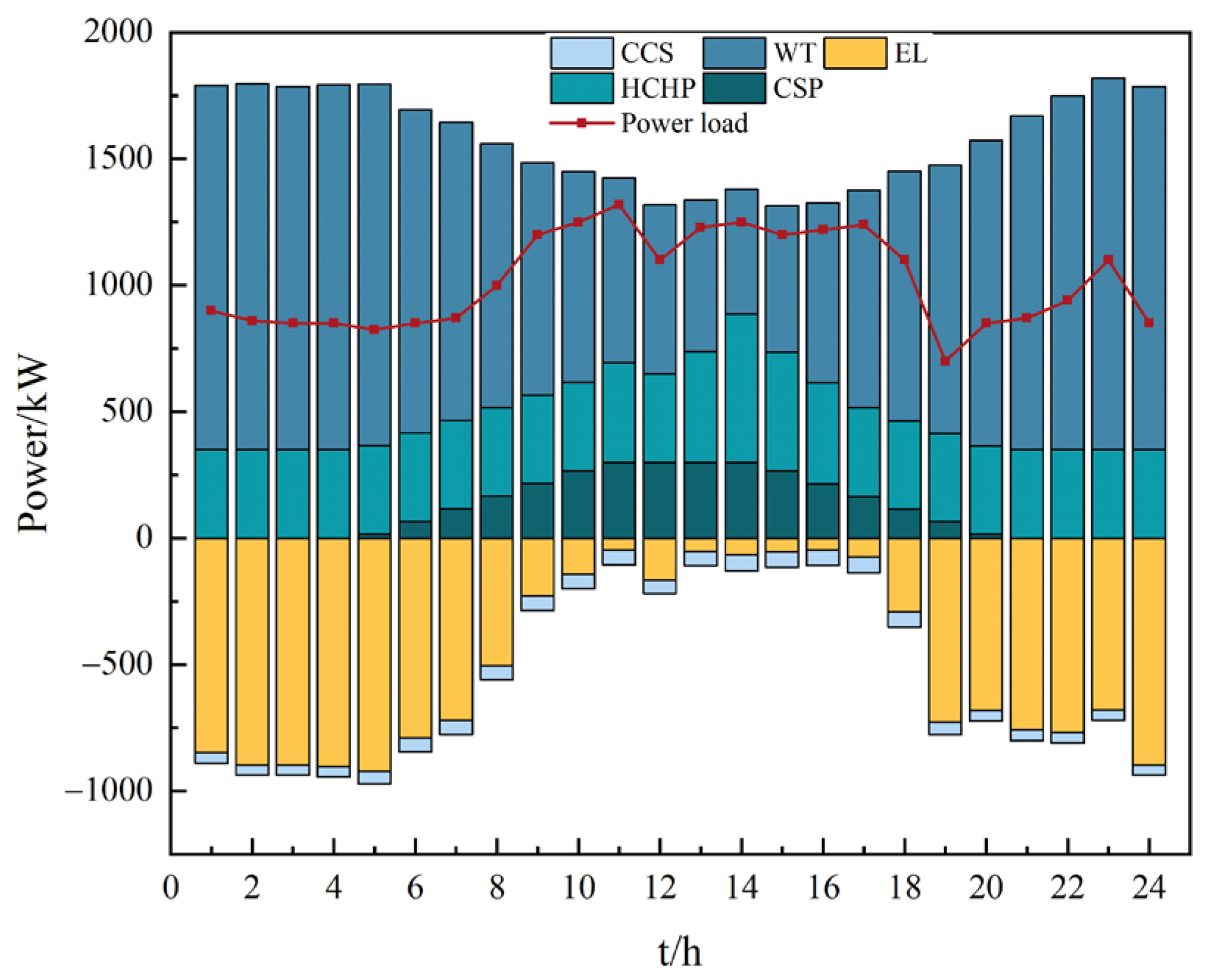
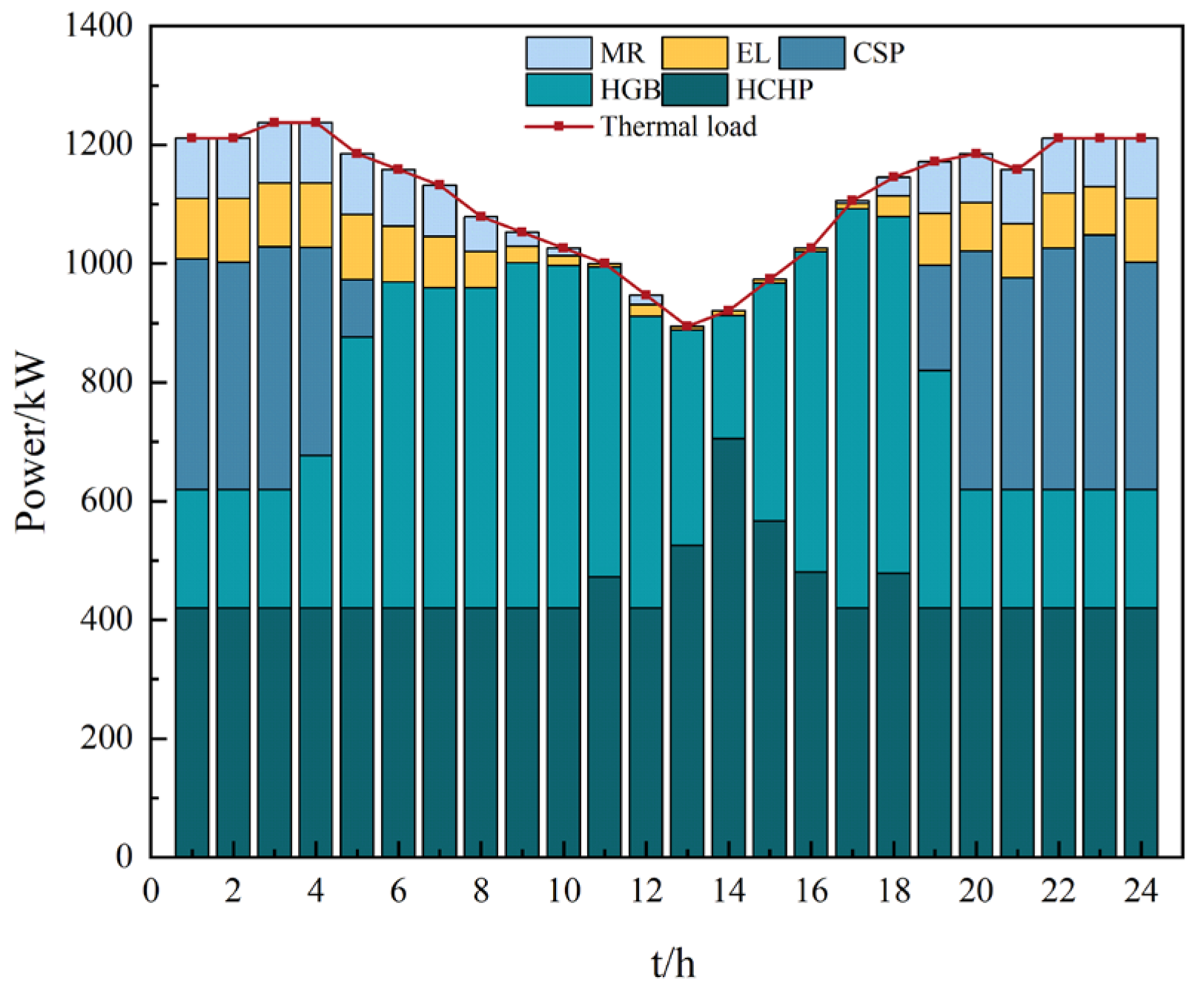
4.2. Unit Output Analysis
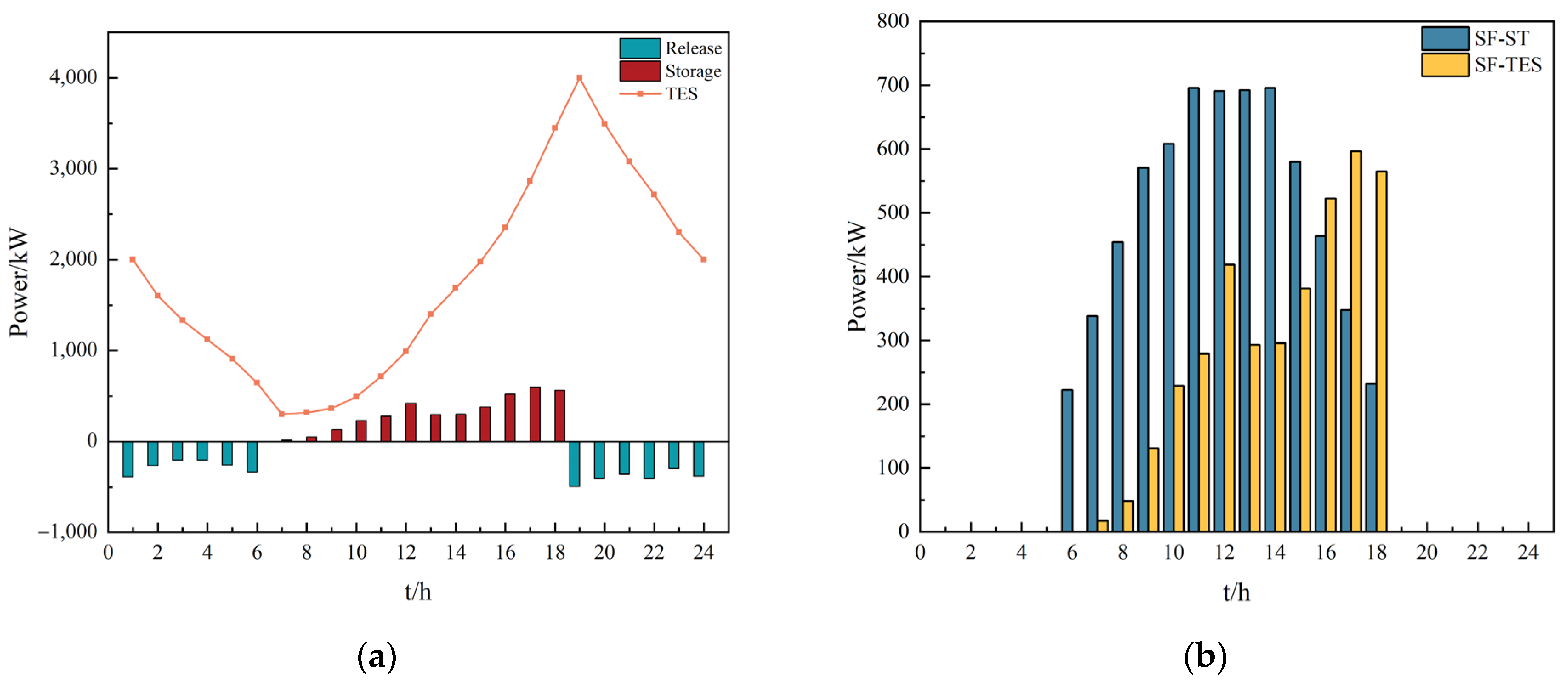
4.3. Analysis of CSP Operations
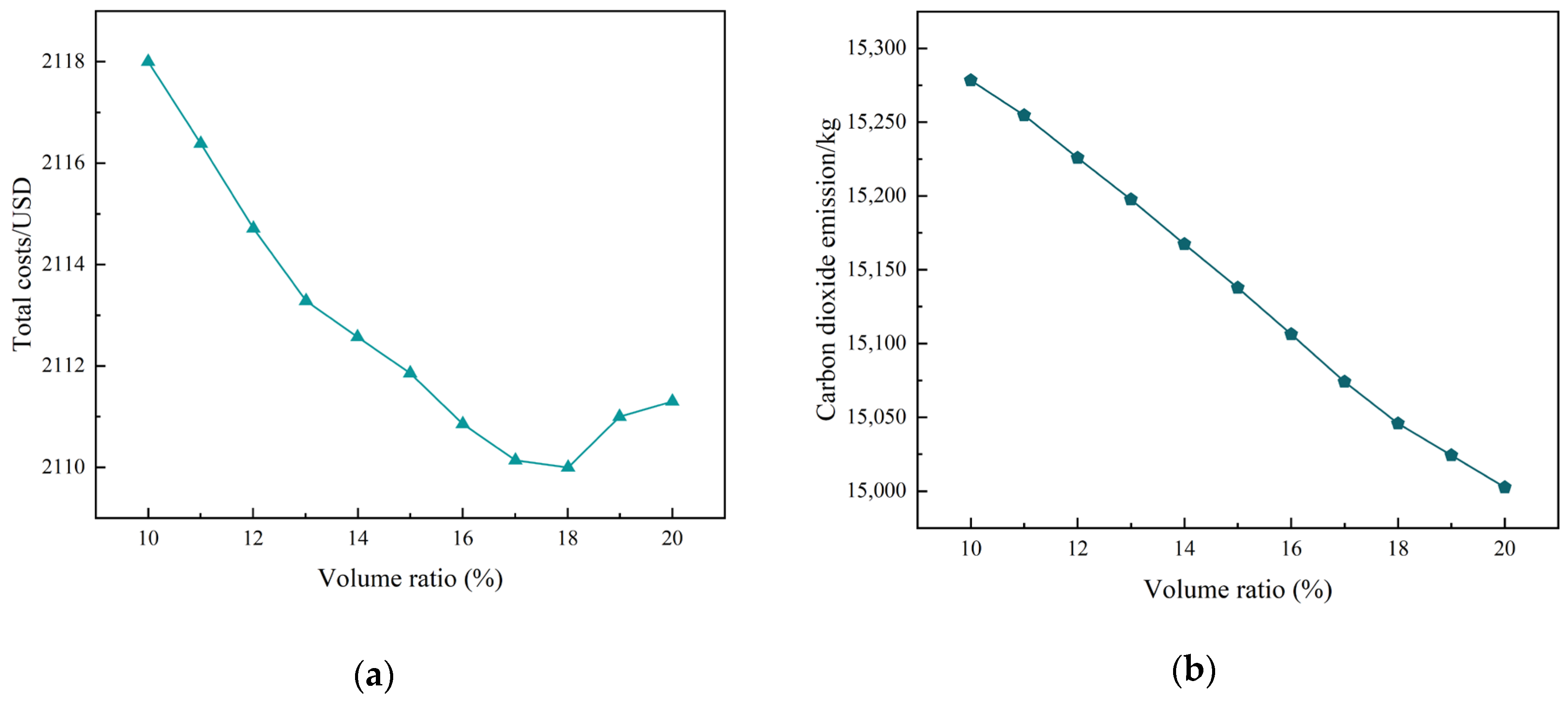
4.4. Analysis of the Impact of TES Thermal Storage Capacity on the Operational Efficiency of the System
4.5. Analysis of CO2 Emissions
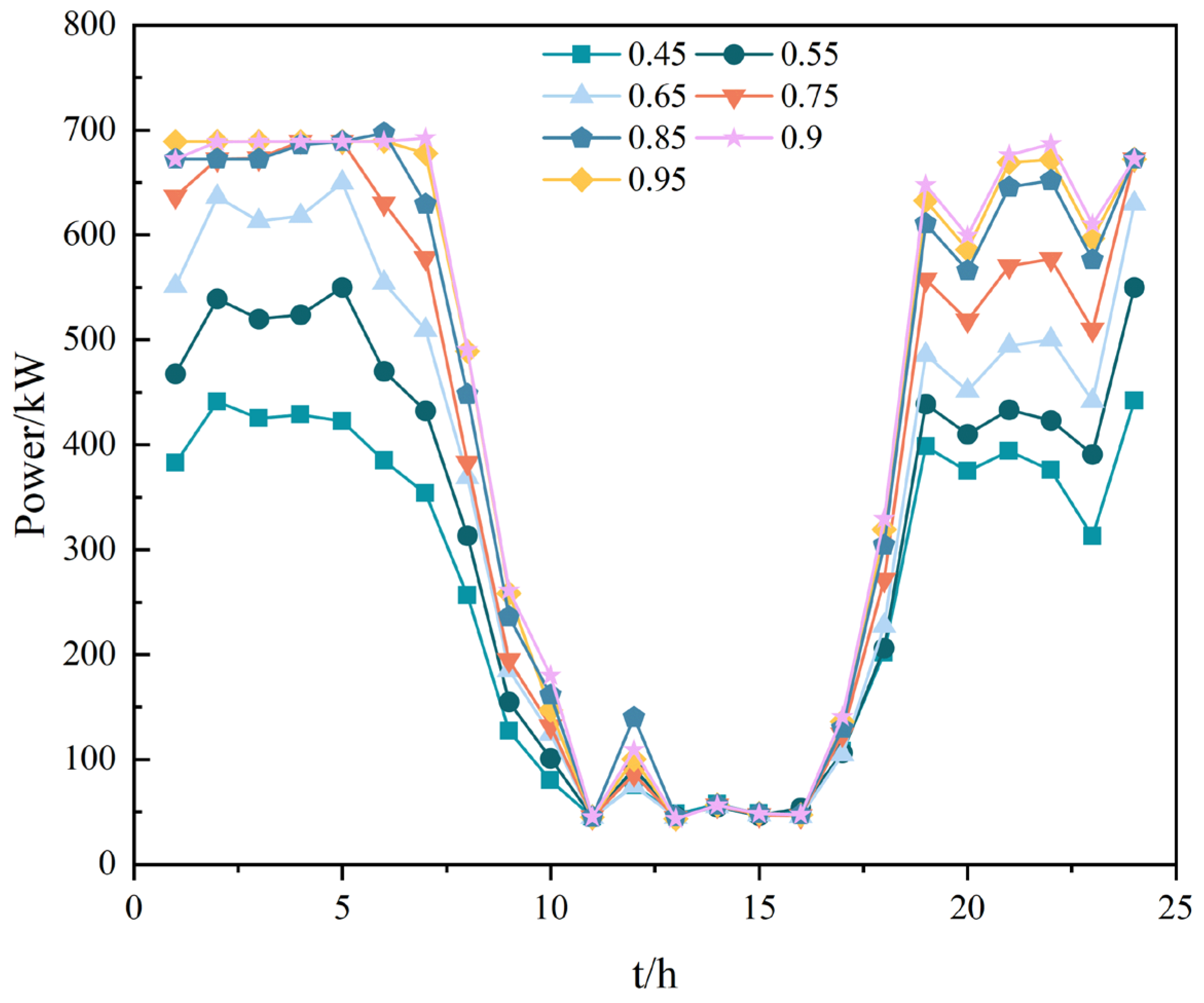
4.6. Impact Analysis of EL Hydrogen Production Efficiency
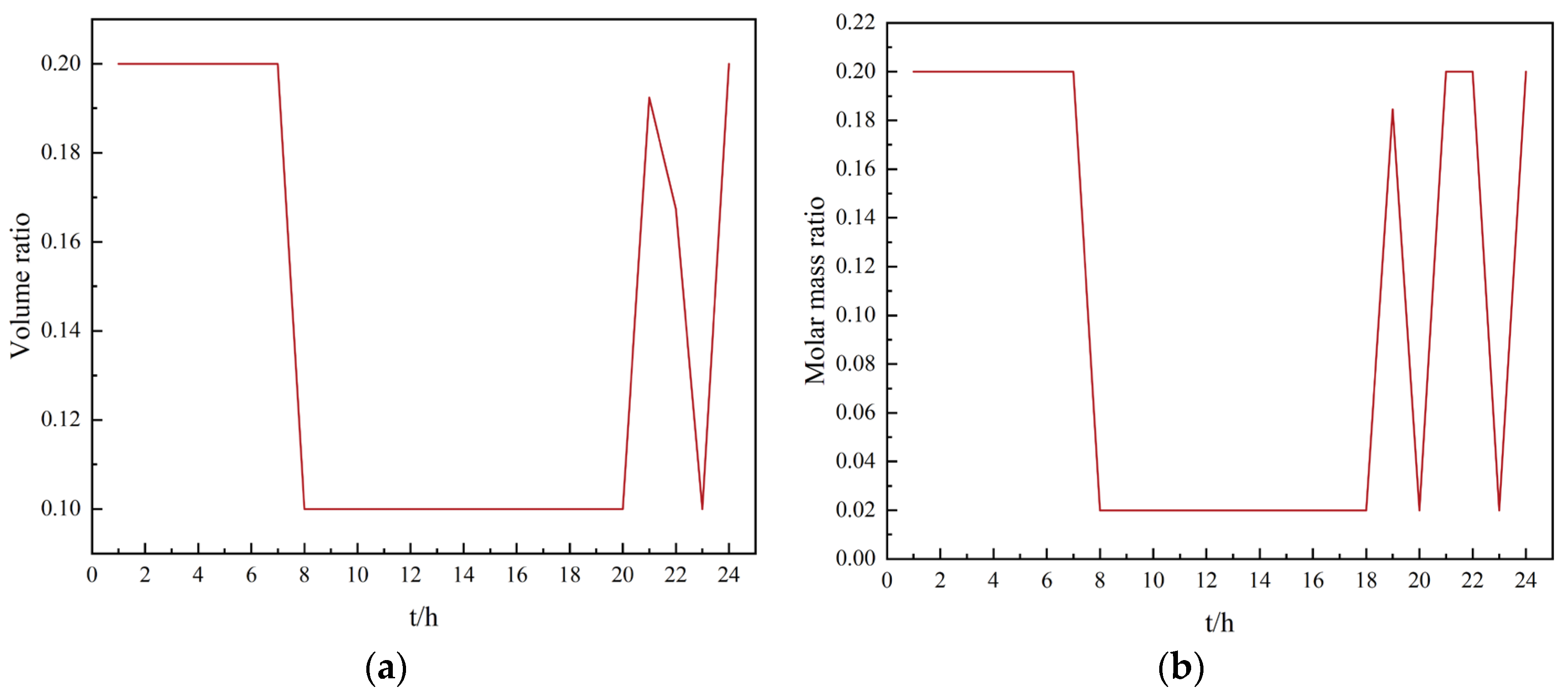
4.7. System Hydrogen Doping Analysis
5. Conclusions
- (1)
- Based on the carbon trading mechanism, the introduction of CSP and hydrogen mixing into natural gas combustion reduces the carbon emission level of the system, while the carbon allowance of the system is increased, which improves the carbon trading benefits of the system. Compared with the other cases, the total system cost can be significantly reduced while improving the CO2 reduction problem.
- (2)
- P2G is refined into a two-stage model, and HCHP and an HGB are introduced to achieve hydrogen-doped combustion. Four simulation comparisons are set up, and even though the CSP-P2G-HCHP coupling model does not exhibit the highest wind power utilization, it has the lowest the total system cost and CO2 emissions. Therefore, CSP-P2G-HCHP coupling can further reduce the overall carbon emission level of the system and the overall total cost of the IES.
- (3)
- Comparing the fixed hydrogen doping ratio with the variable hydrogen doping ratio, the former does not yield many benefits and even produces results contrary to expectations when the ratio reaches a certain level. Therefore, a variable hydrogen doping ratio is used to maximize the cost and emission reduction capability of the system.
- (4)
- This study proposes a low-carbon and low-cost dispatch model of an integrated energy system comprising concentrating solar power and hydrogen-doped combustion. Secondly, the introduction of P2G improves the economic value and environmental impact of the system and achieves the mutual transformation of multiple energy cycles. In order to better improve the operational efficiency of the system, future research will focus on the uncertainty of wind power prediction and dynamic carbon trading.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| IES | Integrated energy system |
| P2G | Power to gas |
| SF | Solar field |
| CSP | Concentrating solar power |
| TES | Thermal energy storage |
| CCS | Carbon capture and storage |
| CVR | Conditional value at risk |
| EL | Electrolyzer |
| MR | Methanization reaction |
| CHP | Combined heat and power |
| GB | Gas boiler |
| HCHP | Hydrogen-doped combined heat and power |
| HGB | Hydrogen-doped gas boiler |
| WT | Wind turbine |
| SPD | Solar parabolic dish |
| PTC | Parabolic trough collector |
| SPT | Solar power tower |
| LFR | Linear Fresnel reflector |
| AE | Alkaline electrolysis |
| PEM | Proton exchange membrane |
| HTSO | High-temperature solid oxide electrolysis |
| The density of hydrogen, kg/m3 | |
| The molar mass of hydrogen, kg/mol | |
| The efficiency of the EL | |
| The calorific value of hydrogen, kJ/kg | |
| The converted thermal energy absorbed by SF at time t, kW | |
| The thermal energy transferred directly by SF to the turbine for power generation at time t, kW | |
| The thermal energy stored in the TES from the heat absorbed by SF at time t, kW | |
| The electric power emitted by the CSP at moment t, kW | |
| The thermal energy transferred to the turbine by the TES at moment t, kW | |
| The heat in the TES at moment t, kW | |
| The heat loss coefficient in the TES | |
| The efficiency coefficient of heat storage | |
| The efficiency coefficient of heat release | |
| The heat charged to the TES at moment t, kW | |
| The heat released by the TES at moment t, kW | |
| The thermal energy transferred to the load from the TES at moment t, kW | |
| The heat released into the TES during the operation of the P2G equipment, kW | |
| The electrical power of HCHP at time t, kW | |
| The natural gas power consumed by HCHP at time t, kW | |
| The hydrogen power consumed by HCHP at time t, kW | |
| The electrical efficiency of HCHP | |
| The thermal energy of HCHP at time t, kW | |
| The thermal efficiency of HCHP | |
| The ratio of thermoelectricity | |
| The calorific value of hydrogen, kJ/m3 | |
| The calorific value of natural gas, kJ/m3 | |
| The quality of hydrogen produced at time t, kg | |
| The electric power consumed by the EL at moment t | |
| The hydrogen input at time t, kg |
Appendix A
References
- Huang, W.; Zhang, B.; Ge, L.; He, J.; Liao, W.; Ma, P. Day-ahead optimal scheduling strategy for electrolytic water to hydrogen production in zero-carbon parks type microgrid for optimal utilization of electrolyzer. J. Energy Storage 2023, 68, 107653. [Google Scholar] [CrossRef]
- Ge, L.; Zhang, B.; Huang, W.; Li, Y.; Hou, L.; Xiao, J.; Mao, Z.; Li, X. A review of hydrogen generation, storage, and applications in power system. J. Energy Storage 2024, 75, 109307. [Google Scholar] [CrossRef]
- Du, E.; Zhang, N.; Kang, C.; Miao, M. Reviews and prospects of the operation and planning optimization for grid integrated concentrating solar power. Proc. CSEE 2016, 36, 5765–5775. [Google Scholar]
- Wang, Z.; Zhang, X.; Zhang, X.; Huang, S. Low-carbon Optimal Dispatch of Integrated Energy System Considering Concentrating Solar Plant. In Proceedings of the 2022 IEEE/IAS Industrial and Commercial Power System Asia (I&CPS Asia), Shanghai, China, 8–11 July 2022; pp. 1239–1244. [Google Scholar]
- Cui, Y.; Jia, R.; Wu, Z. Optimal scheduling of concentrating solar power plant with thermal energy storage and wind farm considering electric-thermal conversion. Proc. CSEE 2020, 40, 6482–6494. [Google Scholar]
- Zhang, D.; Yun, Y.; Wang, X.; He, J.; Dong, H. Economic dispatch of integrated electricity-heat-gas energy system considering generalized energy storage and concentrating solar power plant. Autom. Electr. Power 2021, 45, 33–42. [Google Scholar]
- Chen, R.; Sun, H.; Guo, Q.; Li, Z.; Deng, T.; Wu, W.; Zhang, B. Reducing generation uncertainty by integrating CSP with wind power: An adaptive robust optimization-based analysis. IEEE Trans. Sustain. Energy 2015, 6, 583–594. [Google Scholar] [CrossRef]
- Li, X.; Gui, D.; Zhao, Z.; Li, X.; Wu, X.; Hua, Y.; Guo, P.; Zhong, H. Operation optimization of electrical-heating integrated energy system based on concentrating solar power plant hybridized with combined heat and power plant. J. Clean. Prod. 2021, 289, 125712. [Google Scholar] [CrossRef]
- He, L.; Lu, Z.; Zhang, J.; Geng, L.; Zhao, H.; Li, X. Low-carbon economic dispatch for electricity and natural gas systems considering carbon capture systems and power-to-gas. Appl. Energy 2018, 224, 357–370. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y. Environment-friendly and economical scheduling optimization for integrated energy system considering power-to-gas technology and carbon capture power plant. J. Clean. Prod. 2020, 276, 123348. [Google Scholar] [CrossRef]
- Liu, J.; Sun, W.; Yan, J. Effect of P2G on flexibility in integrated power-natural gas-heating energy systems with gas storage. Energies 2021, 14, 196. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Ji, X.; Ye, P.; Li, J. Unit commitment of integrated energy system considering conditional value-at-risk and P2G. Electr. Power Syst. Res. 2023, 221, 109398. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, H.; Yang, C.; Li, K. Research on optimization scheduling of integrated electricity-gas system considering carbon trading and P2G operation characteristics. Electr. Power Syst. Res. 2023, 225, 109797. [Google Scholar] [CrossRef]
- Li, X.; Li, T.; Liu, L.; Wang, Z.; Li, X.; Huang, J.; Huang, J.; Guo, P.; Xiong, W. Operation optimization for integrated energy system based on hybrid CSP-CHP considering power-to-gas technology and carbon capture system. J. Clean. Prod. 2023, 391, 136119. [Google Scholar] [CrossRef]
- Meziane, S.; Bentebbiche, A. Numerical study of blended fuel natural gas-hydrogen combustion in rich/quench/lean combustor of a micro gas turbine. Int. J. Hydrogen Energy 2019, 44, 15610–15621. [Google Scholar] [CrossRef]
- Rajpara, P.; Shah, R.; Banerjee, J. Effect of hydrogen addition on combustion and emission characteristics of methane fuelled upward swirl can combustor. Int. J. Hydrogen Energy 2018, 43, 17505–17519. [Google Scholar] [CrossRef]
- Yun, Y.; Zhang, D.; Yang, S.; Li, Y.; Yan, J. Low-carbon optimal dispatch of integrated energy system considering the operation of oxy-fuel combustion coupled with power-to-gas and hydrogen-doped gas equipment. Energy 2023, 283, 129127. [Google Scholar] [CrossRef]
- Guo, C.; Abuduwayiti, X.; Shang, Y.; Huang, L.; Cui, C. Optimized Scheduling of Integrated Energy Systems Accounting for Hydrogen Energy Multi-Utilization Models. Sustainability 2024, 16, 1198. [Google Scholar] [CrossRef]
- Zhu, X.; Xue, J.; Hu, M.; Liu, Z.; Gao, X.; Huang, W. Low-carbon economy dispatching of integrated energy system with P2G-HGT coupling wind power absorption based on stepped Carbon emission trading. Energy Rep. 2023, 10, 1753–1764. [Google Scholar] [CrossRef]
- Roy, P.K.; Paul, C.; Sultana, S. Oppositional teaching learning based optimization approach for combined heat and power dispatch. Int. J. Electr. Power Energy Syst. 2014, 57, 392–403. [Google Scholar] [CrossRef]
- Islam, M.T.; Huda, N.; Abdullah, A.B.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2018, 91, 987–1018. [Google Scholar] [CrossRef]
- Yang, H.; Zhou, M.; Wu, Z.; Zhang, M.; Liu, S.; Guo, Z.; Du, E. Exploiting the operational flexibility of a concentrated solar power plant with hydrogen production. Sol. Energy 2022, 247, 158–170. [Google Scholar] [CrossRef]
- Jiang, P.; Dong, J.; Huang, H. Optimal integrated demand response scheduling in regional integrated energy system with concentrating solar power. Appl. Therm. Eng. 2020, 166, 114754. [Google Scholar] [CrossRef]
- Cui, Y.; Liu, X.; Chen, M. Experimental study of natural gas doping full pressure of F-class heavy-duty gas turbine burner. Gas Turbine Technol. 2021, 34, 38–42. [Google Scholar]
- Luo, Z.; Wang, J.; Xiao, N.; Yang, L.; Zhao, W.; Geng, J.; Lu, T.; Luo, M.; Dong, C. Low Carbon Economic Dispatch Optimization of Regional Integrated Energy Systems Considering Heating Network and P2G. Energies 2022, 15, 5494. [Google Scholar] [CrossRef]
- Liu, J.; Sun, W.; Harrison, G. Optimal low-carbon economic environmental dispatch of hybrid electricity-natural gas energy systems considering P2G. Energies 2019, 12, 1355. [Google Scholar] [CrossRef]
- Yan, Q.; Ai, X.; Li, J. Low-carbon economic dispatch based on a CCPP-P2G virtual power plant considering carbon trading and green certificates. Sustainability 2021, 13, 12423. [Google Scholar] [CrossRef]
- Lau, J.; Dey, G.; Licht, S. Thermodynamic assessment of CO2 to carbon nanofiber transformation for carbon sequestration in a combined cycle gas or a coal power plant. Energy Convers. Manag. 2016, 122, 400–410. [Google Scholar] [CrossRef]
- Zheng, L.; Wen, Z.; Qiu, Z. Low-carbon optimized operation of an integrated energy system that takes into account solar thermal power plants and hydrogen storage. Electr. Meas. Instrum. 2022, 1–9. [Google Scholar]
- Yun, Y.; Zhang, D.; Wang, X.; Ni, P.; He, J. Low-Carbon Operational Optimization of Integrated Electricity-Heat-Gas Energy System Considering Concentrating Solar Power Plant and Oxygen-Enriched Combustion Capture Technology. Trans. China Electrotech. Soc. 2023, 24, 6709–6726. [Google Scholar]
- Chen, D.; Liu, F.; Liu, S. Optimization of virtual power plant scheduling coupling with P2G-CCS and doped with gas hydrogen based on stepped carbon trading. Power Syst. Technol. 2022, 46, 2042–2054. [Google Scholar]


| Equipment Type | Parameter | Value | Equipment Type | Parameter | Value |
|---|---|---|---|---|---|
| CSP | (kW) | 600 | CCS | (kWh/kg) | 0.893 |
| (kW) | 0 | 0.9 | |||
| (kW) | 50 | P2G | (kW) | 1000 | |
| (kW) | 50 | (kW) | 10 | ||
| 0.431 | (%) | 88 | |||
| HCHP | (kW) | 900 | HGB | (kW) | 600 |
| (kW) | 200 | (kW) | 200 | ||
| (kW) | 1020 | 0.88 | |||
| (kW) | 260 | / | / | ||
| 1.2–1.5 | / | / |
| Equipment Type | Unit Price (USD/kW) | Equipment Type | Unit Price (USD/kW) |
|---|---|---|---|
| WT | 0.007 | HGB | 0.014 |
| HCHP | 0.013 | EL | 0.0026 |
| CSP | 0.013 | / | / |
| Case | CSP | Hydrogen-Doped Combustion | P2G | Conventional CHP |
|---|---|---|---|---|
| 1 | × | × | × | √ |
| 2 | × | √ | √ | √ |
| 3 | √ | × | √ | √ |
| 4 | √ | √ | √ | √ |
| Category | Case 1 | Case 2 | Case 3 | Case 4 |
|---|---|---|---|---|
| Operation and maintenance costs | 572 | 673.92 | 643.51 | 660.35 |
| Cost of energy purchases | 2324.97 | 1843.68 | 1421.74 | 1384.3 |
| Wind abandonment costs | 128.31 | 0.054 | 23.3 | 11.13 |
| Cost of carbon emissions | 355.86 | 313.6 | 25.24 | 24.46 |
| Total cost | 3381.14 | 2831.25 | 2113.79 | 2080.24 |
| Actual carbon emissions (kg) | 2106.3 | 1893 | 323.2 | 302.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, J.; Xiao, J.; Zhang, B.; Zhang, Z.; Mao, Z.; He, J. Low-Carbon Economic Dispatch Model of Integrated Energy System Accounting for Concentrating Solar Power and Hydrogen-Doped Combustion. Sustainability 2024, 16, 4818. https://doi.org/10.3390/su16114818
Chen J, Xiao J, Zhang B, Zhang Z, Mao Z, He J. Low-Carbon Economic Dispatch Model of Integrated Energy System Accounting for Concentrating Solar Power and Hydrogen-Doped Combustion. Sustainability. 2024; 16(11):4818. https://doi.org/10.3390/su16114818
Chicago/Turabian StyleChen, Jun, Jianbo Xiao, Bohan Zhang, Zuoming Zhang, Zimu Mao, and Jun He. 2024. "Low-Carbon Economic Dispatch Model of Integrated Energy System Accounting for Concentrating Solar Power and Hydrogen-Doped Combustion" Sustainability 16, no. 11: 4818. https://doi.org/10.3390/su16114818
APA StyleChen, J., Xiao, J., Zhang, B., Zhang, Z., Mao, Z., & He, J. (2024). Low-Carbon Economic Dispatch Model of Integrated Energy System Accounting for Concentrating Solar Power and Hydrogen-Doped Combustion. Sustainability, 16(11), 4818. https://doi.org/10.3390/su16114818





